Abstract
With the continuous development of wireless sensor network (WSN) technology, WSN has gradually become one of the key technologies of the Internet, and is widely used in indoor target location technology. However, the obstacles will have a great influence on the distance measurement, and it will result in a large positioning error. Therefore, how to deal with the non-line-of-sight (NLOS) error becomes an important problem. In this paper, Interacting Multiple Model (IMM) was used to identify NOLS/LOS. The NLOS probability was calculated by Markov transform probability, and the likelihood function was calculated by extended Kalman filter (EKF). The NLOS probability was compared with the LOS probability to judge whether the measurement contained the NLOS error. A robust algorithm combining IMM model with semidefinite programming (IMM-SDP) was proposed. The improved convex programming algorithm was proposed to reduce the NLOS error. Simulation and experimental results showed that the proposed algorithm can effectively reduce the influence of NLOS error and achieve higher positioning accuracy compared with the existing positioning methods.
1. Introduction
A wireless sensor network (WSN) consists of a large number of sensor nodes, network gateways, and clients. The sensor node could communicate with each other and share information in a network. Since GPS navigation systems are very expensive and not suitable for indoor positioning, we need to use other positioning methods. Wireless sensor positioning technology is a kind of bidirectional wireless technology with a short distance, low power consumption, low data transmission rate, and low cost. WSN is a revolutionary way of information collection in an information communication system. Therefore, it is widely applied in indoor positioning.
According to anchor node and unknown node, there are two localization methods based on WSN: one is the location method with a known distance, and the other is the location method with an unknown distance. This paper adopts the distance-based localization method. Kalman filter is used to process the data and get the correct location. However, in the process of positioning, many obstacles will have a great influence on the distance measurement, resulting in a large positioning error, so how to correctly deal with the NLOS error in the process of positioning has always been the focus and difficulty. Distance-based WSN localization mainly adopts time difference of arrival (TDOA), time of arrival (TOA), angle of arrival (AOA), and received signal strength (RSSI) systems, which have been widely studied and used to identify and mitigate NLOS errors. An IMM algorithm based on an extended Kalman filter is proposed to reduce the impact of simulation results error []. A new semidefinite programming algorithm is proposed [], which transforms the TDOA model into the TOA model and adds new variables and constraints to improve positioning accuracy and reduce positioning errors.
In this paper, an improved IMM model is used to identify NLOS/LOS errors, and two convex programming methods are improved to deal with NLOS and LOS errors respectively. The algorithm has the following advantages:
- (1)
- In order to solve the problem of NLOS error, the semi-definite programming algorithm of the TOA/TDOA model transformation is improved in this paper. It can effectively alleviate the influence of NLOS error, and improve the positioning accuracy.
- (2)
- The proposed convex programming algorithm is more accurate than maximum likelihood estimation and residual estimation.
The structure of this article is as follows. Section 2 introduces relevant work and summarizes existing techniques from the literature. The signal model is introduced in Section 3. The proposed algorithm is analyzed in Section 4. The simulation and the experimental results are analyzed in Section 5. The conclusion is drawn in Section 6.
2. Related Work
Because NLOS error is the main influencing factor, the influence of NLOS error can be dealt with by suppressing the NLOS error algorithm, or directly using the filtering algorithm to filter the NLOS error. These algorithms may lose some data more or less and may not have good positioning accuracy and robustness. Therefore, through continuous research and development. Many ways of dealing with various problems have been put forward. A rough position estimation algorithm for TDOA positioning based on a non-linear least squares algorithm is proposed []. This algorithm is a rough position estimation algorithm based on scaling. The algorithm is robust to the initial position by optimizing the complex location function of arrival time difference. In the system [], A moving target location tracking algorithm based on TOA measurement in a non-line-of-sight environment is proposed. In the NLOS model, the EKF standard algorithm is transformed into a linear regression model by the REKF algorithm, and the Robust technology in Hammes and Zoubir is used to solve the model. In the algorithm [], an iterative minimum residual algorithm combined with AOA/TOA is proposed to improve the estimation performance through sequential detection and elimination of non-LOS nodes. In [], a smoothing algorithm based on an extended Kalman smoothing filter (EK-IMM) is proposed, which combines the time of arrival (TOA) and received signal strength (RSS) algorithm for the target location. The extended Kalman filter and IMM scheme are combined to reduce the influence of NLOS on the measurement distance error. In [], a robust NLOS bias mitigation algorithm for target location based on RSS-TOA is proposed. The algorithm transforms the location algorithm into a generalized trust region subproblem, which is solved only by dichotomy. Literature [] proposed a low-complexity NLOS suppression method, which uses a sparse pseudo-input Gaussian process to directly eliminate LOS bias and NLOS conditions without non-line-of-sight recognition. In [], Estimate the expected value of the NLOS error to correct the measurement. The NLOS error is eliminated by subtracting the expectation of the NLOS error. The classical multidimensional scale (MDS) algorithm is redesigned for non-LOS localization problems. In [], the general equality constraint of spatial correlation of NLOS error is captured by establishing a maximum posterior (MAP) estimate, and the algorithm is optimized by using the specific constraint function of Gaussian process (GP) regression.
In [], A random variable is introduced into the RSS model to simulate the path loss data, and a new robust algorithm is proposed to improve the positioning accuracy of the measurement model under unknown parameters. The effect of NLOS error can be effectively alleviated by effectively recognizing LOS distance and NLOS distance. In [], an improved joint Probabilistic Data Association location (MJPDA) algorithm is proposed. An improved JPDA algorithm based on EKF is proposed to identify LOS and NLOS. In the case of NLOS. The improved JPDA is used to deal with the data association between virtual points and granules. Experiments show that the proposed method has better positioning accuracy and robustness when the NLOS error is large. In [], the author proposed an NLOS recognition method based on a multidimensional scale and quasi-accurate detection. NLOS awakening can be identified effectively by mapping the NLOS awakening problem to the coarse error problem by building a model. A new NLOS recognition method based on a convolution algorithm is proposed []. In [], model probability and hypothesis testing are used to identify NLOS, and then the innovation covariance matrix is used to identify NLOS for the second time in hypothesis testing Location estimates polluted by NLOS errors are dumped. The correct position estimate is aggravated by correlation probability. In [], an NLOS classifier based on AdaBoost is proposed to identify NLOS and be used for wireless sensor positioning.
Convex programming is also used to solve NLOS problems []. A semi-static location method based on TDOA in a non-LOS environment is proposed, and a statistical location method based on empirical location data in an NLOS environment is proposed. Error model []. A soft minimum method based on convex optimization to alleviate TOA localization is proposed to solve the infeasible problem and improve the localization accuracy of NLOS. Literature [] proposed a robust convex approximation method based on TDOA localization in an NLOS environment. Two convex relaxation approximations are used to transform robust least squares from a non-convex set to a convex set. Literature [] proposed a new robust second-order cone relaxation method, and the NLOS error did not have much influence on this method. This method does not need to consider the prior information of NLOS error, but only needs to consider the upper and lower limits of NLOS error. In [], two low-complexity heuristic algorithms, namely optimal selection filling (BOF) algorithm and iterative commutative greed (ISG) algorithm, are proposed to deal with non-convex problems and transform them into semidefinite programming (SDP). The problem is TDOA localization in NLOS conditions. In [], in order to alleviate the NLOS problem, an “equilibrium parameter” related to the NLOS error is introduced, and a new robust weighted least squares problem is constructed with source position and NLOS equilibrium parameters as estimation variables, and transformed into a semidefinite programming problem. In [], the authors use the sparsity of LOS/ NLOS measurement bias to mitigate NLOS
3. System Model UNITS
When a mobile node is moving, the information received by the base station will be interfered with noise. This interference is constantly changing between LOS and NLOS, so we need to identify whether the state of interference is LOS. This process is called As a Markov transformation process, we need to build a model to distinguish between LOS and NLOS.
We set up N base stations to detect the signals of mobile nodes, We use , k = 1, 2,…N. Use to represent the mobile node, so represents the real distance between the k-th base station and the mobile node at moment n, where k = 1, 2,…N. Since the received signal will have two situations, LOS and NLOS, we can model the true distance of the beacon node as:
where, is expressed as the measured distance between the k base station and the mobile node, and is the measurement noise.
The size of the noise is divided into two cases, LOS and NLOS, when it is in the case of NLOS:
where, is expressed as Gaussian white noise with mean and variance . Thus, when the NLOS error is 0, . is expressed as Gaussian white noise with a mean value of 0 and a variance of , which is:
According to the above distance measurement model, we build a state space model, so the state model based on all beacon nodes is expressed as:
where, represents the speed at which a node is moved, so the non-linear state space model of the mobile node can be obtained as:
where, is the sampling period, and is the noise of the mobile node during the movement [].
4. The Proposed Algorithm
In Figure 1, the initial states of state estimation and skew variance are known, and the transformation problem of LOS/NLOS is modeled as a Markov transformation problem by means of set model probability and transition matrix. We use two parallel extended Kalman filters (LOS and NLOS) for synchronous processing to achieve model matching. By calculating the probability of LOS and NLOS and the probability of the initial state estimation of the next iteration, we judge by comparing the probability of the two models (LOS/NLOS). If the probability of NLOS is greater than the probability of LOS, the input signal is considered to be the NLOS signal; otherwise, it is the LOS signal. The two kinds of data are respectively processed by two different convex optimizations. Finally, the data after the two convex optimization processing are fused to get the final result. As shown in Figure 1, it is mainly composed of four aspects: likelihood function update, NLOS/LOS probability, semidefinite programming, and data fusion. Figure 2 shows the Process of Markov transformation.
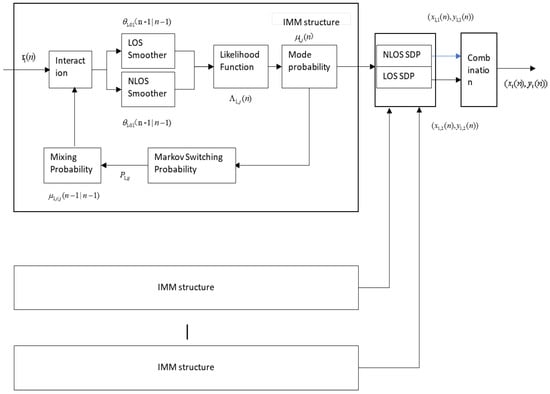
Figure 1.
The flow chart of the proposed algorithm.
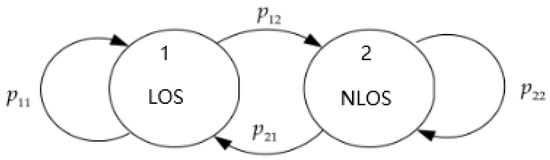
Figure 2.
Markov transformation process.
4.1. Markov Transformation Process
The conversion probability of Markov’s model is []:
4.2. The Initial Input of the MODEL
It is known that can be expressed as a base station, k = 1…N. [1 for the LOS smoother, 2 for the NLOS smoother], We know that the prior probability at time n − 1 is , and the Markov transition probability from i to mode j in is . Therefore, the mixed probability from mode i to mode j can be obtained as:
where, is the normalization factor, which can be expressed as:
4.3. Interaction
The mixed state estimation in j [LOS smoother, NLOS smoother] mode is , and the covariance matrix at time n-1 in j [LOS smoother, NLOS smoother] mode is , and we can obtain from the above:
Among them , are the state estimation and covariance matrix of each beacon node in i mode.
4.4. Kalman Filter Algorithm
So we introduce the above-mentioned nonlinear state space model into the scalable Kalman filter algorithm:
where, is the alman gain, is the deviation of the observed estimated value, the residual covariance of state prediction was calculated by the deviation value of available observation estimation.
From the above formula, the extended Kalman gain and error covariance matrix can be obtained as:
. are the noise generated during the movement, is the covariance of the state prediction residuals.
So we can predict the covariance of the state as:
We can get that the likelihood function and model probability of the Kalman filter of the beacon node in j mode are:
We use the obtained NLOS/LOS probability to judge whether the input signal is LOS or NLOS, so when , we think that the possibility of LOS is high, and we input the output data into the SDP algorithm that processes LOS data, on the contrary, we think it is more likely to be NLOS.
4.5. NLOS Situation
The system model can be described as:
where, is the length of the sensor itself, which is a very small number. Squaring both sides of it can get:
Since is small, we discard it, so we make:
We set new variable parameters:
We can get the nonlinear least squares estimate of the unknown :
It can be seen that is the weight value, which is generally taken as 1, and the θ value is the position estimation of the mobile node. We obtain the final location of the mobile node by calculating the value of θ. From the above model, we can see that is the coordinates of the base station, and is the coordinates, so we can get:
Convert it to matrix vector mode to get:
Therefore, by increasing the variable l, more constraints are added to make the final positioning more accurate. Because of variable , the semi-definite condition is satisfied, So I can be solved by convex optimization:
where, L is a penalty factor, which is a small number, is a newly added variable.
It can be known from the geometric relationship that the sum of both sides of a triangle is greater than the sum of the third side:
From the above description, we can get:
It can be seen from the above that in the NLOS environment, the noise is very large, and the noise is generally positive, so you can get:
So we can introduce a new variable , which satisfies the condition of , so change (38) to:
A new variable is added, which makes the constraint relaxed, so it is necessary to add the newly added variable to the objective function , increase L(>0). The value of a determines the result of the objective function, which can be obtained by calculation. Constrained by the above constraint conditions, combined with the new objective function to make it more accurate.
The objective function of the new semi-definite programming is:
4.6. LOS Situation
The system model can be described as . We can get by squaring both sides:
Shift it to get:
We set , so we can get the nonlinear least squares estimate of the unknown :
where, is the weight value, which is generally taken as 1, and the value is the position estimation of the mobile node. We obtain the final location of the mobile node by calculating the value of θ.
In the above model, we can see that is the coordinates of the base station, and is the coordinates, so we can get . Convert to matrix vector mode , and .
Therefore, by increasing the variable l, more constraints are added to make the final positioning more accurate and reduce errors. It can be known from the above variables:
Since the above variables satisfy the positive semi-definite, it can be transformed into a convex optimization problem:
where, L is a penalty factor, and the variable is a newly added variable.
It can be known from the geometric relationship that the sum of both sides of a triangle is greater than the sum of the third side:
Therefore, we can obtain:
As can be seen from the above, in the LOS environment, since is not true, the measured distance is not necessarily greater than the real distance, so we can introduce a new variable that satisfies the condition of constraint:
A new variable is added, which makes the constraint relaxed, so the newly added variable needs to be added to the objective function . Among them, (>0), the value of (>0) determines the result of the objective function, which can be obtained by calculation. Constrained by the above constraint conditions, combined with the new objective function to make it more accurate.
The objective function of the new semi-definite programming is:
4.7. Data Fusion
After NLOS convex optimization and LOS convex optimization, two coordinate points are output respectively. The final coordinates are obtained by data fusion. Thus, we can get:
5. Simulation and Experimental Results
This section mainly introduces the simulation results. As shown the Figure 3, we have deployed eight beacon nodes in the space, where we set the sampling period as 0.5 s and the sampling times as 100. The following figure shows the mobile node moving along a fixed trajectory. The initial position was denoted as , the initial velocity was set as , and the initial error covariance matrix was . In order to make the simulation environment more similar to the real environment, a parameter and NLOS threshold were given. This parameter is generated randomly and is more suitable for the actual environment. When the parameter value is less than the given threshold value, we judge him as NLOS, otherwise, we consider him as LOS. In this experiment, we simulate different noises such as Gaussian distribution, exponential distribution and uniform distribution. In this paper, we also compare extended Kalman filter (IMM-EKF) [], reduced extended Kalman filter (IMM-REKF) [], JPDA [] and SU-SDP [] algorithms. A total of 1000 Monte Carlo simulations were run for the simulation results. This paper uses root mean square error (RMSE) to evaluate the performance of the algorithm.
where, MC represents the moving steps of the mobile node, MC = 1000 is the number of Monte Carlo cycles, is the measured position of the mobile node, and is the real position of the mobile node.
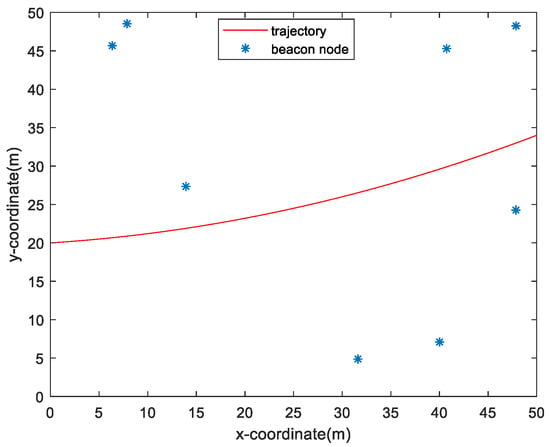
Figure 3.
The trajectory of a mobile node.
5.1. Gaussian Distribution
We suppose that the NLOS error comply the Gaussian distribution, that is, . The measurement noise of the system, that is, the LOS noise, also obeys the Gaussian distribution, that is, . The size of the LOS noise has nothing to do with the measurement distance. The Gaussian distribution map of the default parameters is given in the following Table 1.

Table 1.
Gaussian distribution parameter map.
As shown in the following Figure 4, we took the NLOS error mean from 3 to 8, and we find that RSME increases with the increase of the NLOS error mean, indicating that the NLOS error mean has a certain influence on the simulation results. When the mean value of NLOS changes from 3 to 8, the mean value of NLOS error of IMM-EKF, IMM-REKF and JPDA increases, and the RMSE of JPDA is approximately linear with the increase of NLOS. While the error of IMM-EKF and IMM-REKF increases with the increase of the mean value, the RMSE increases very quickly, and the RMSE of the SU-SDP method does not change significantly. It can be seen from the figure that our algorithm is better than IMM-EKF, IMM-REKF, JPDA, and SU-SDP algorithms. The positioning accuracy of this algorithm is 55.7%, 54.9%, 23.9% and 59.2% higher than that of IMM-EKF, IMM-REKF, JPDA and SU-SDP, respectively.
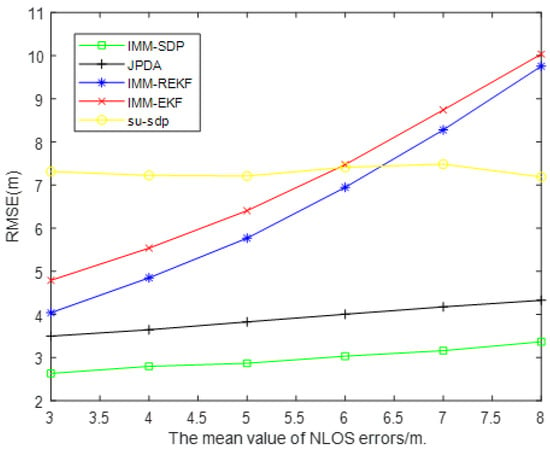
Figure 4.
RMSE versus the mean value of NLOS errors.
As shown in Figure 5, we changed the variance of NLOS from 3 to 8, and RMSE increased with the increase of variance, indicating that the variance of NLOS range had an impact on simulation results. When NLOS variance varies from 3 to 8, the errors of IMM-EKF, IMM-REKF and JPDA all increase with the increase of variance. As can be seen from the figure, our algorithm is superior to IMM-EKF, IMM-REKF, JPDA and SU-SDP algorithms. In the case of the VARIANCE of NLOS. Compared with IMM-EKF, IMM-REKF, JPDA and SU-SDP, the accuracy of the proposed algorithm is improved by 71.1%, 69.6%, 34.0%, and 60.7, respectively.
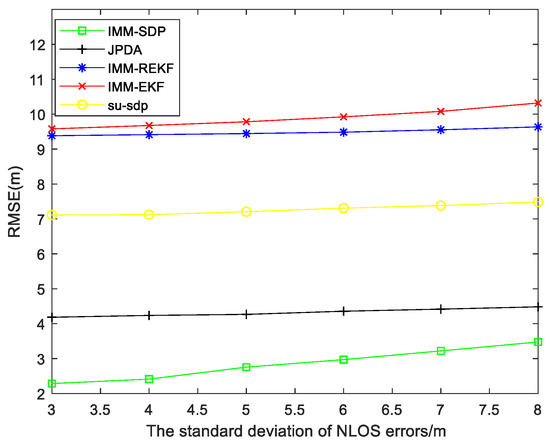
Figure 5.
RMSE versus the standard deviation of NLOS errors.
As shown in the following Figure 6, we change the probability of NLOS from 0.7 to 0.95, we find that RSME increases with the increase of the mean, but the increase in speed is relatively slow, indicating that it is very Strong robustness. When the NLOS probability changes from 0.7 to 0.95, the errors of IMM-EKF, IMM-REKF, and JPDA all increase with the increase of the mean, while the errors of IMM-EKF and IMM-REKF increase with the increase of the mean. The RMSE increases very quickly, and the RMSE of the SU-SDP method does not change significantly. It can be seen from the figure that our algorithm is better than IMM-EKF, IMM-REKF, and JPDA and SU-SDP algorithms. In the case of NLOS probability, the accuracy of this algorithm is 67.3%, 65.1%, 20.1%, and 55.3% higher than IMM-EKF, IMM-REKF, JPDA, and SU-SDP, respectively.
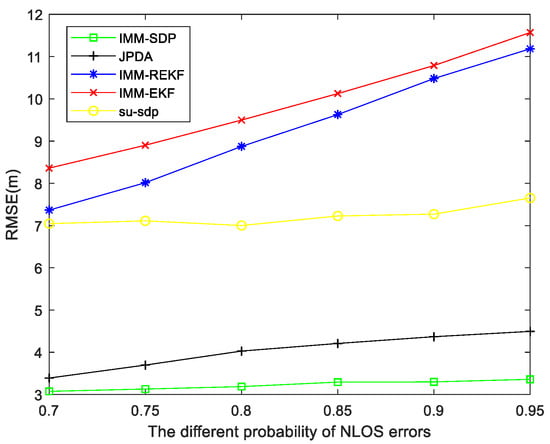
Figure 6.
RMSE versus the different probability of NLOS errors.
As shown in Figure 7, we change the variance of the LOS from 0.5 to 3, and we find that RSME increases with the increase of the variance of the LOS, indicating that the magnitude of the variance of the LOS has an impact on the simulation. It has a big impact. When the variance of the LOS varies from 0.5 to 3, IMM-EKF, IMM-REKF, and JPDA all increase slowly with the increase of the variance of the LOS and the RMSE increases very slowly. The RMSE of the SU-SDP method basically does not change much, indicating that it is extremely robust. It can be seen from the figure that our algorithm is better than IMM-EKF, IMM-REKF, and JPDA and SU-SDP algorithms. When the NLOS average value is 3, our positioning accuracy is better than IMM-EKF, IMM-REKF, and JPDA respectively. The SU-SDP algorithm is 64.8%, 63.4%, 11.0%, 50.8% higher.
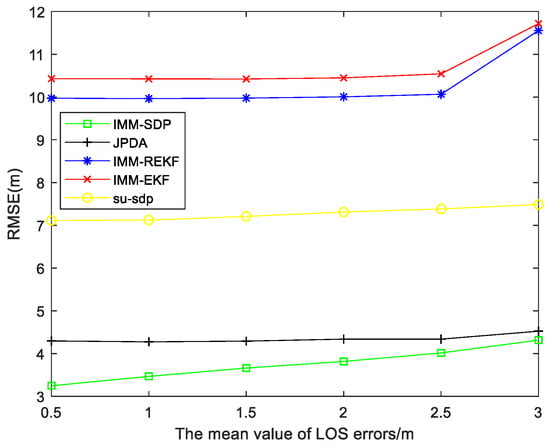
Figure 7.
RMSE versus the different probability of LOS errors.
5.2. Exponential Distribution
We suppose that the NLOS error complies with an exponential distribution, namely . The measurement noise of the system, the NLOS, also obeys the Gaussian distribution, namely . The size of the LOS noise has nothing to do with the measurement distance. The default parameter distribution map is given in Table 2 below.

Table 2.
Exponential distribution parameter diagram.
It can be seen from the Figure 8 below that we change the index parameter data from 4 to 9. We find that RSME increases as the parameter increases. When the exponential distribution parameter changes from 4 to 9, IMM -EKF, IMM-REKF, and JPDA all increase the error with the increase of the mean value, the RMSE increases very fast, and the RMSE of the SU_SDP method fluctuates up and down within a certain range. It can be seen from the figure that our algorithm is better than IMM-EKF, IMM-REKF, and JPDA and SU-SDP algorithms. Under the exponential distribution, our positioning accuracy is better than IMM-EKF, IMM-REKF, and JPDA, and SU-SDP respectively. The average of the algorithm is 68.7%, 61.6%, 25.9%, and 57.1% higher.
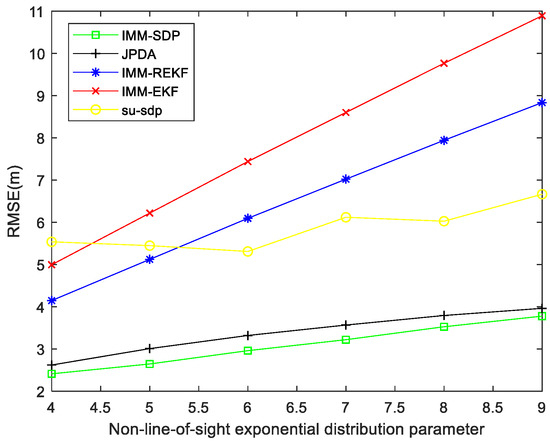
Figure 8.
NLOS exponential distribution parameter.
5.3. Uniform Distribution
We suppose that the NLOS error comply an exponential distribution, namely . The measurement noise of the system, namely the line-of-sight noise, also obeys the Gaussian distribution, namely . The size of the LOS noise has nothing to do with the measurement distance. The default parameter distribution map is given in Table 3 below.

Table 3.
Uniform distribution parameter map.
As can be seen from the Figure 9 below, when NLOS error is uniformly distributed and its parameters change from 6 to 14, we find that RMSE increases as a whole, but the change is not obvious. The size of uniform distribution has little influence on simulation results. When the NLOS errors are uniformly distributed and the parameters change from 6 to 14, the errors of IMM-EKF, IMM-REKF and JPDA all increase with the increase of the mean value, while RMSE of the SU-SDP method does not change significantly. As can be seen from the figure, our algorithm is superior to IMM-EKF, IMM-REKF, JPDA and SU-SDP algorithms. Compared with IMM-EKF, IMM-REKF, JPDA, AND SU-SDP algorithms, our positioning accuracy is 65.3%, 64.3%, 42.6%, and 63.2%, respectively, when NLOS errors are evenly distributed.
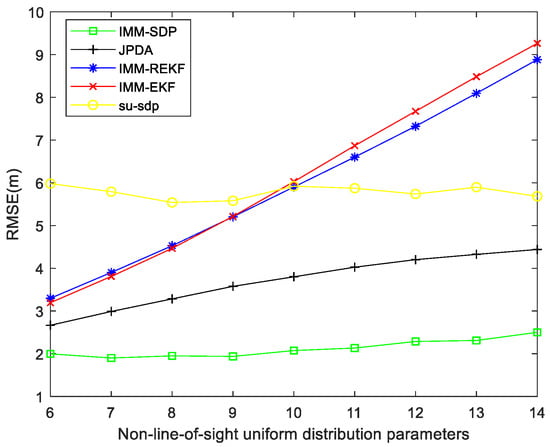
Figure 9.
NLOS uniform distribution parameters.
5.4. Experiment
5.4.1. Experimental Environment
In order to test the performance of the proposed algorithm, we conducted a localization experiment in an indoor environment. The signal transmission between the mobile node and beacon nodes was based on ultra-wideband (UWB) technology. UWB technology has been widely used in indoor positioning in recent years because of its low complexity and high positioning accuracy. The principle of UWB ranging is to approximate the distance between nodes based on the two-way propagation time of signals. In this experiment, both the mobile node and the beacon nodes adopted the UWB node. The difference was that the mobile node was connected with the power supply as shown in Figure 10, and was held by a pedestrian during the movement, while a beacon node was connected with a computer to transmit the collected data to the computer.

Figure 10.
The ultra-wideband (UWB) node is connected with the power supply.
The experimental scene is depicted in Figure 11. The coordinates of eight beacon nodes are n1 (13.2, 3.6), n2 (9, 1.2), n3 (10.2, 8.4), n4 (3.6, 16.8), n5 (6,8.4), n6 (9.6, 13.8), n7 (6.6, 13.8), n8 (3.6, 4.8). The mobile node moves at a speed of 0.6 m/s along the true trajectory in the figure from the initial position R1 (12, 1.2) until it reaches R4 (4.8, 15.6). To avoid ground reflection, all nodes are placed 1.2 m above the ground. The sampling frequency is 1 Hz. Every 60 cm, one sampling point is recorded and there are 25 sampling points in the whole true trajectory. Twenty measurements are collected at every sampling point, and an average of 20 measurements at every sampling point is utilized as the measurement distance. The parameter settings for the experiment were the same as those in the simulation.
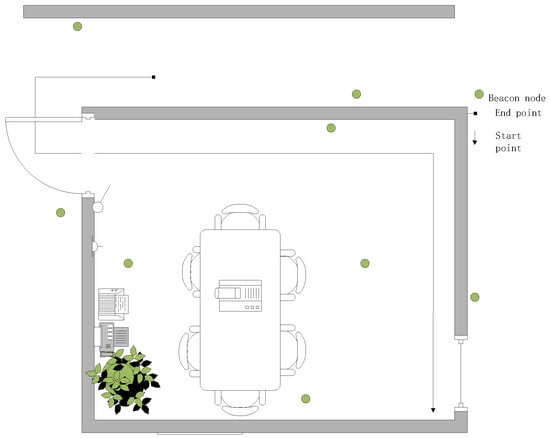
Figure 11.
The experimental scene.
5.4.2. Experimental Results
The positioning error of each sampling point is shown in Figure 12. We can find that the positioning error of this algorithm is almost always minimal. It shows that our algorithm can effectively suppress the influence of strong NLOS error. According to experiments, the average errors of the IMM-EKF, IMM-REKF, JPDA, SU-SDP, and IMM-SDP algorithms are 0.9577, 0.9002, 0.9321, 6.7144, and 0.7834, respectively. The accuracies of our algorithm are 18.19%, 12.19%, 15.95%, and 88.33% higher than theirs, respectively.
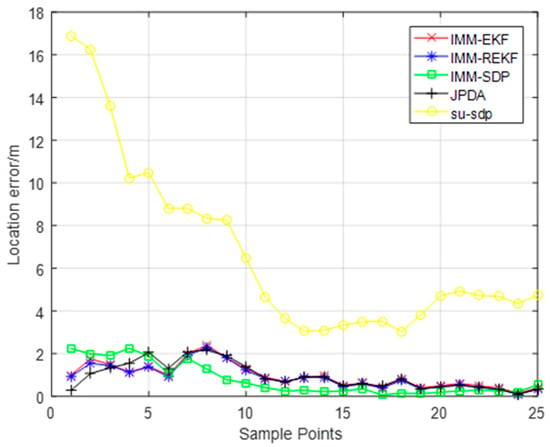
Figure 12.
The localization error at each sampling point.
5.4.3. Computation Time Comparison
Table 4 shows the running time of each algorithm. Coded using MATLAB R2018a and tested on Windows 10 Professional workstation and Intel(R) Core (TM) i7-8700 @ 3.20 GHz and 8.00 GB RAM. IMM-SDP is more time-consuming, and the running time is longer due to the use of multiple convex programs.

Table 4.
Running time of each algorithm.
6. Conclusions
In order to reduce NLOS errors, an improved NLOS/LOS hybrid localization algorithm was proposed. This paper proposed a robust IMM-SDP algorithm. In this paper, the IMM model was used to identify LOS and NLOS. The probability of LOS and NLOS was calculated by Markov transformation probability, and the visual distance and non-visual data were separated and processed, respectively. Finally, an improved convex programming algorithm was proposed to reduce NLOS errors, compared with IMM-EKF, IMM-REKF, JPDA and SU-SDP. Simulation and experimental results showed that the proposed algorithm has good positioning accuracy and strong robustness.
Author Contributions
Conceptualization, Y.W. and Y.C.; methodology, Y.W.; software, L.C.; investigation, Y.C.; writing—original draft preparation, Y.W. and Y.C.; writing—review and editing, Y.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant No. 61803077; Natural Science Foundation of Hebei Province under Grant No. F2020501012.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
References
- Chen, B.; Yang, C.; Liao, F.; Liao, J. Mobile Location Estimator in a Rough Wireless Environment Using Extended Kalman-Based IMM and Data Fusion. IEEE Trans. Veh. Technol. 2009, 58, 1157–1169. [Google Scholar] [CrossRef]
- Su, Z.; Shao, G.; Liu, H. Semidefinite Programming for NLOS Error Mitigation in TDOA Localization. IEEE Commun. Lett. 2018, 22, 1430–1433. [Google Scholar] [CrossRef]
- Qiao, T.; Redfield, S.; Abbasi, A.; Su, Z.; Liu, H. Robust Coarse Position Estimation for TDOA Localization. IEEE Wirel. Commun. Lett. 2013, 2, 623–626. [Google Scholar] [CrossRef]
- Hammes, U.; Zoubir, A.M. Robust MT Tracking Based on M-Estimation and Interacting Multiple Model Algorithm. IEEE Trans. Signal Process. 2011, 59, 3398–3409. [Google Scholar] [CrossRef]
- Horiba, M.; Okamoto, E.; Shinohara, T.; Matsumura, K. An improved NLOS detection scheme for hybrid-TOA/AOA-based localization in indoor environments. In Proceedings of the 2013 IEEE International Conference on Ultra-Wideband (ICUWB), Sydney, Australia, 15–18 September 2013; pp. 37–42. [Google Scholar] [CrossRef]
- Liao, J.; Chen, B. Robust Mobile Location Estimator with NLOS Mitigation using Interacting Multiple Model Algorithm. IEEE Trans. Wirel. Commun. 2006, 5, 3002–3006. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M. A Robust NLOS Bias Mitigation Technique for RSS-TOA-Based Target Localization. IEEE Signal Process. Lett. 2019, 26, 64–68. [Google Scholar] [CrossRef]
- Yang, X.F. NLOS Mitigation for UWB Localization based on spars pseudo-input Gaussian process. IEEE Sens. J. 2018, 18, 4311–4316. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, Y.W.; Jia, Z.X. An indoor mobile localization strategy for robot in NLOS environment. Int. J. Distrib. Sens. Netw. 2013, 2013, 758749. [Google Scholar] [CrossRef]
- Li, S.; Hedley, M.; Collings, I.B.; Humphrey, D. Joint Trajectory and Ranging Offset Estimation for Accurate Tracking in NLOS Environments. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3–14. [Google Scholar] [CrossRef]
- Cheng, L.; Li, Y.; Xue, M.; Wang, Y. An Indoor Localization Algorithm Based on Modified Joint Probabilistic Data Association for Wireless Sensor Network. IEEE Trans. Ind. Inform. 2021, 17, 63–72. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, S.; Wang, G.; Chen, H. Robust RSS-Based Source Localization With Unknown Model Parameters in Mixed LOS/NLOS Environments. IEEE Trans. Veh. Technol. 2021, 70, 3926–3931. [Google Scholar] [CrossRef]
- Zhu, Y.; Ma, T.; Li, Z.; Sun, D.; Sun, X.; Zhao, X.; Hu, F. NLOS Identification and Correction Based on Multidimensional Scaling and Quasi-Accurate Detection. IEEE Access 2019, 7, 53977–53987. [Google Scholar] [CrossRef]
- Cheng, L.; Xue, M.; Wang, Y.; Wang, Y.; Bi, Y. A Robust Tracking Algorithm Based on Modified Generalized Probability Data As-sociation for Wireless Sensor Network. IEEE Trans. Ind. Electron. 2021, 69, 2136–2146. [Google Scholar] [CrossRef]
- Zeng, Z.; Liu, S.; Wang, L. NLOS Identification for UWB Based on Channel Impulse Response. In Proceedings of the 2018 12th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, Australia, 17–19 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, Y.; Xia, W.; Yan, F.; Shen, L. NLOS Identification via AdaBoost for Wireless Network Localization. IEEE Commun. Lett. 2019, 23, 2234–2237. [Google Scholar] [CrossRef]
- Li, S.; Hedley, M.; Collings, I.B.; Humphrey, D. TDOA-Based Localization for Semi-Static Targets in NLOS Environments. IEEE Wirel. Commun. Lett. 2015, 4, 513–516. [Google Scholar] [CrossRef]
- Su, Z.; Shao, G.; Liu, H. A Soft-Minimum Method for NLOS Error Mitigation in TOA Systems. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Wang, G.; So, A.M.; Li, Y. Robust Convex Approximation Methods for TDOA-Based Localization Under NLOS Conditions. IEEE Trans. Signal Process. 2016, 64, 3281–3296. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, S.; Wang, G.; Li, Y. Robust NLOS Error Mitigation Method for TOA-Based Localization via Second-Order Cone Relaxation. IEEE Commun. Lett. 2015, 19, 2210–2213. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Z.; Hao, B.; Shi, J. Sensor Selection for TDOA-Based Localization in Wireless Sensor Networks With Non-Line-of-Sight Condition. IEEE Trans. Veh. Technol. 2019, 68, 9935–9950. [Google Scholar] [CrossRef]
- Chen, H.; Wang, G.; Ansari, N. Improved Robust TOA-Based Localization via NLOS Balancing Parameter Estimation. IEEE Trans. Veh. Technol. 2019, 68, 6177–6181. [Google Scholar] [CrossRef]
- Jin, D.; Yin, F.; Zoubir, A.M.; So, H.C. Exploiting Sparsity of Ranging Biases for NLOS Mitigation. IEEE Trans. Signal Process. 2021, 69, 3782–3795. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).