Development and Analysis of Key Components of a Multi Motion Mode Soft-Bodied Pipe Robot
Abstract
:1. Introduction
2. Structural Design and Deformation Analysis of Hexagonal Prism Soft-Bodied Bionic Actuator
2.1. Principal Design
2.2. Deformation Mode Analysis
3. Mechanical Model Analysis
3.1. Constitutive Model of Silicone Rubber
3.2. Establishment of the Mechanical Model of Hexagonal Prism Soft-Bodied Bionic Actuator
4. Verification of Numerical Simulation Algorithm and Preparation of Physical Model
4.1. Numerical Simulation Algorithm Verification
- (1)
- Model establishment
- (2)
- Soft-bodied actuator material and load setting
- (3)
- Soft-bodied actuator meshing
- (4)
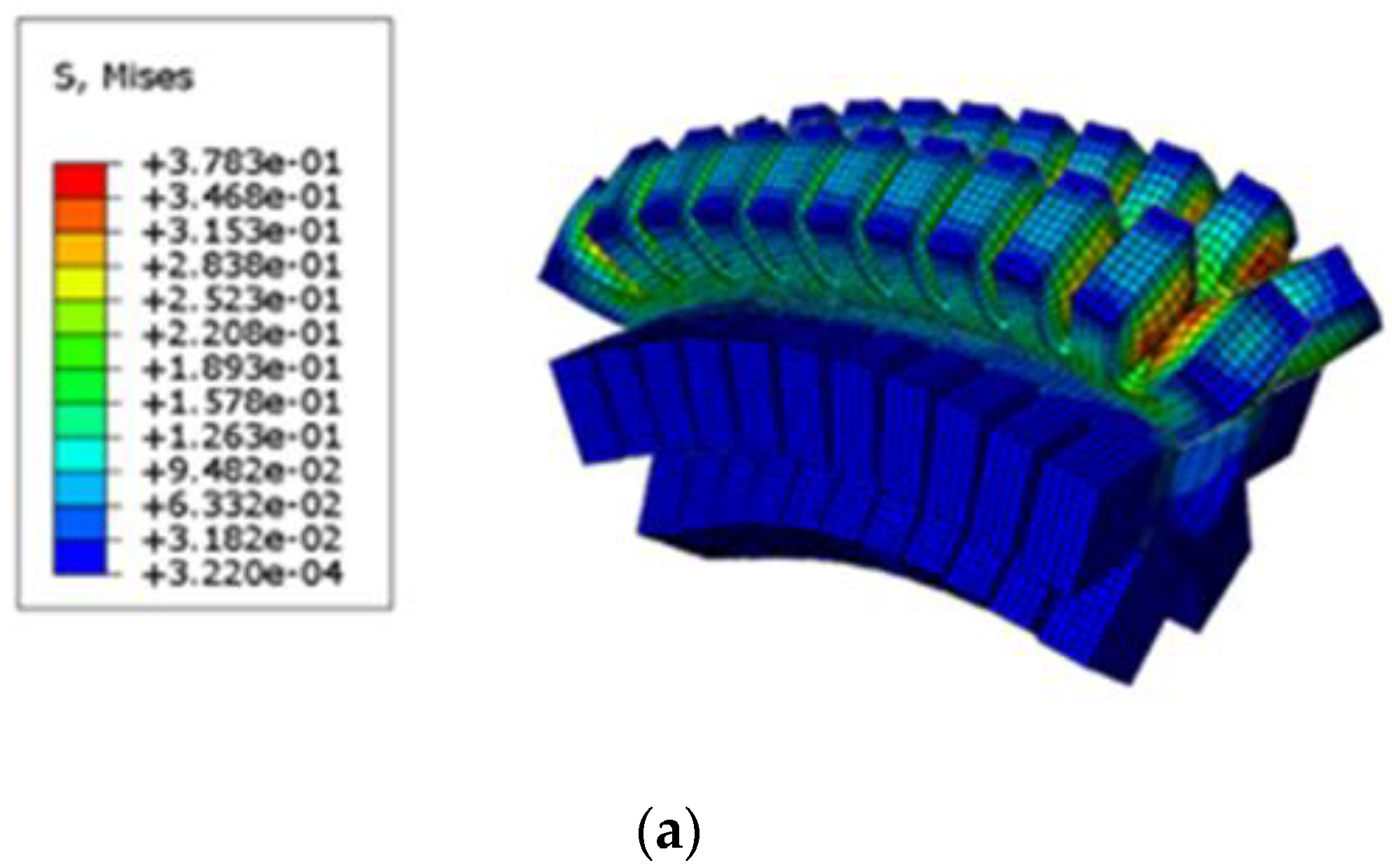
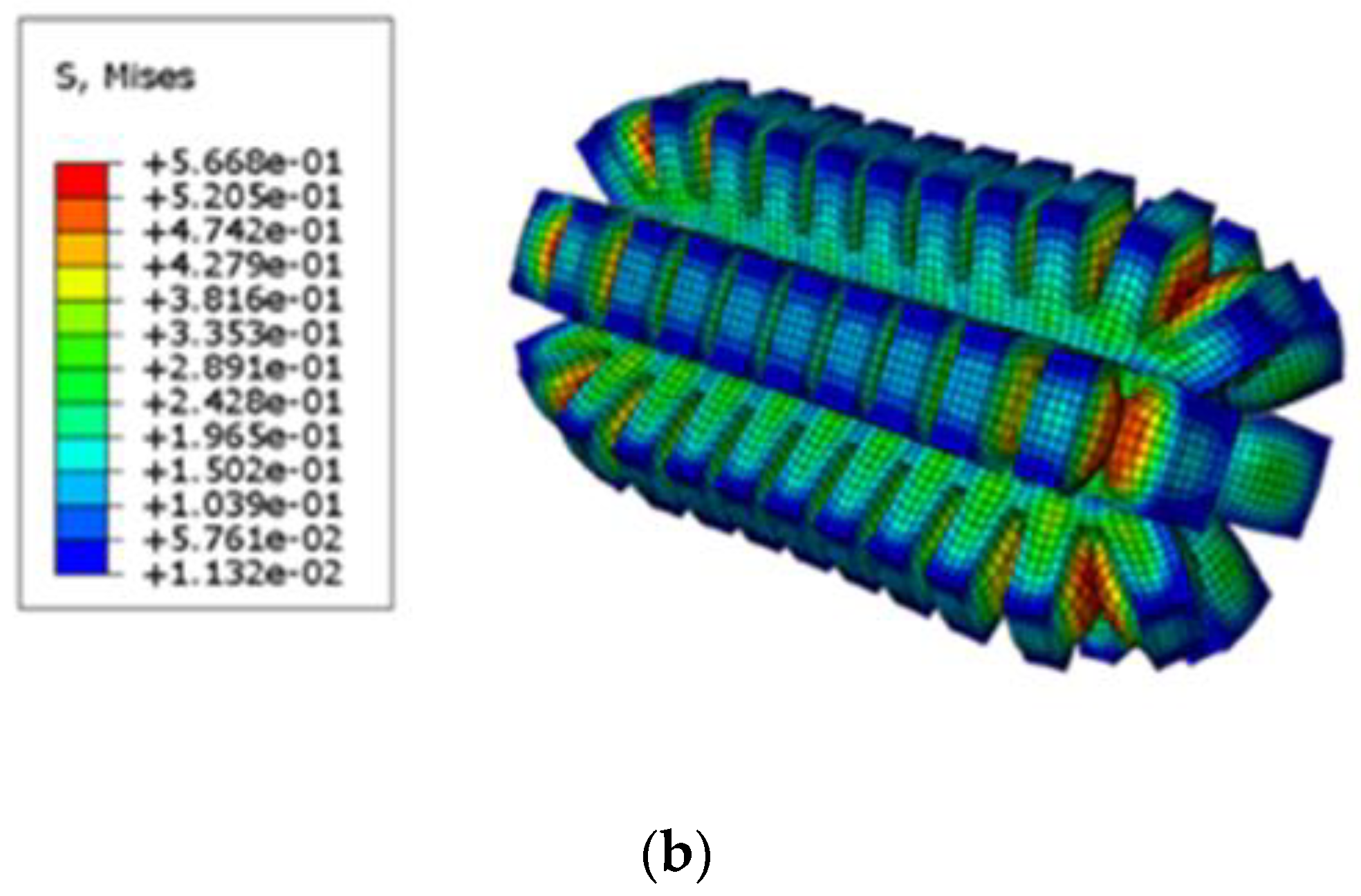
- Create a working file and conduct simulation analysis to obtain the deformation analysis diagram of hexagonal prism soft-bodied actuator, as shown in Figure 7.
4.2. Physical Model Preparation
5. Experimental Test and Analysis of Hexagonal Prism Soft-Bodied Bionic Actuator
5.1. Experimental Analysis of Axial Bending Deformation of Hexagonal Prism Soft-Bodied Bionic Actuator
5.1.1. Analysis of Motion Characteristics of Hexagonal Prism Soft-Bodied Bionic Actuator
5.1.2. Dynamic Characteristics Analysis of Hexagonal Prism Soft-Bodied Bionic Actuator
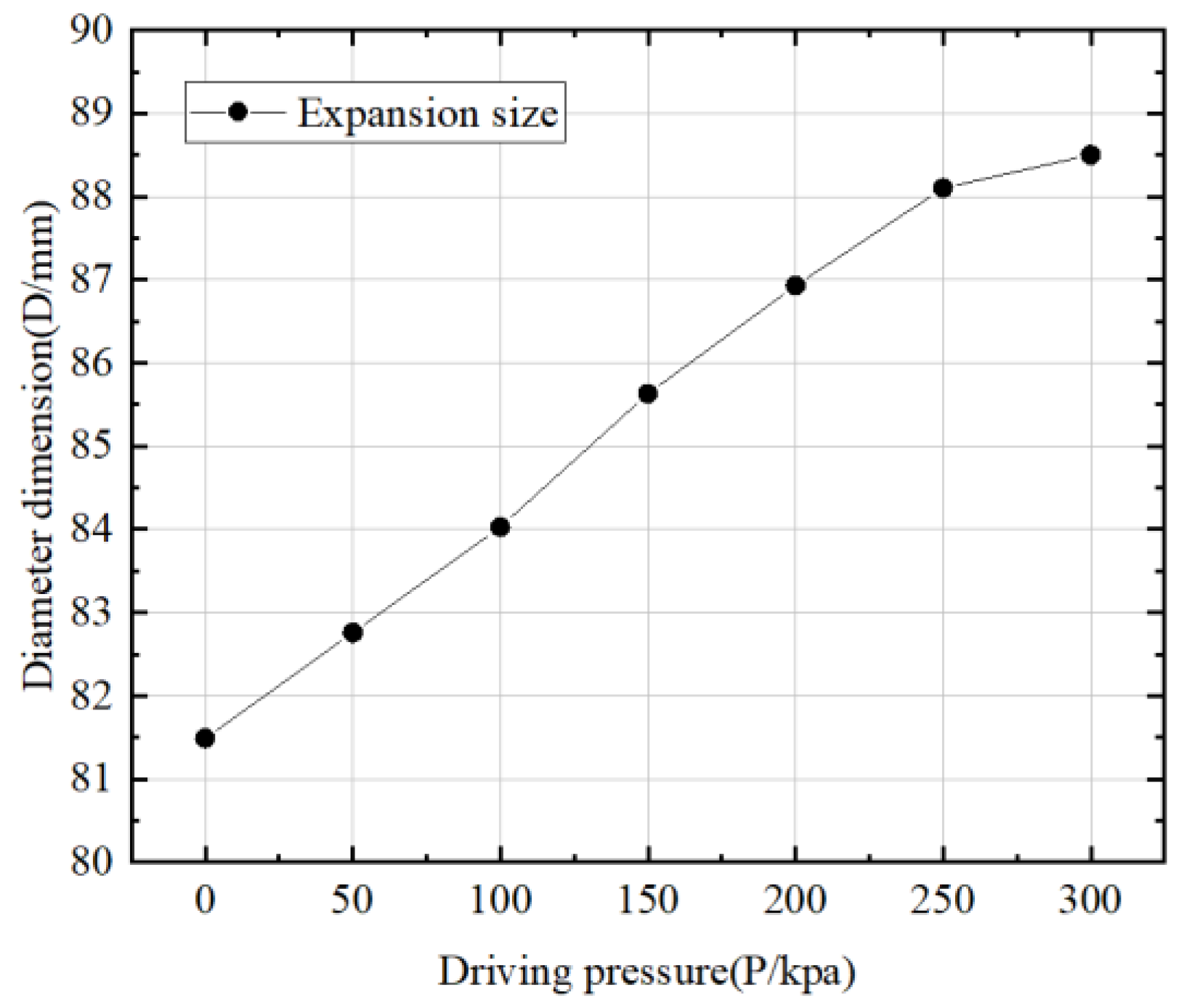
5.2. Experimental Analysis of Radial Expansion Deformation of Hexagonal Prism Soft-Bodied Bionic Actuator
6. Conclusions
- (1)
- Based on the Yeoh binomial parameter silicone constitutive model, a deformation analysis model of the actuator is established to obtain the relationship between the bending angle of the actuator and the driving pressure, which can provide a theoretical reference for the structural design and deformation analysis of the soft-bodied actuator.
- (2)
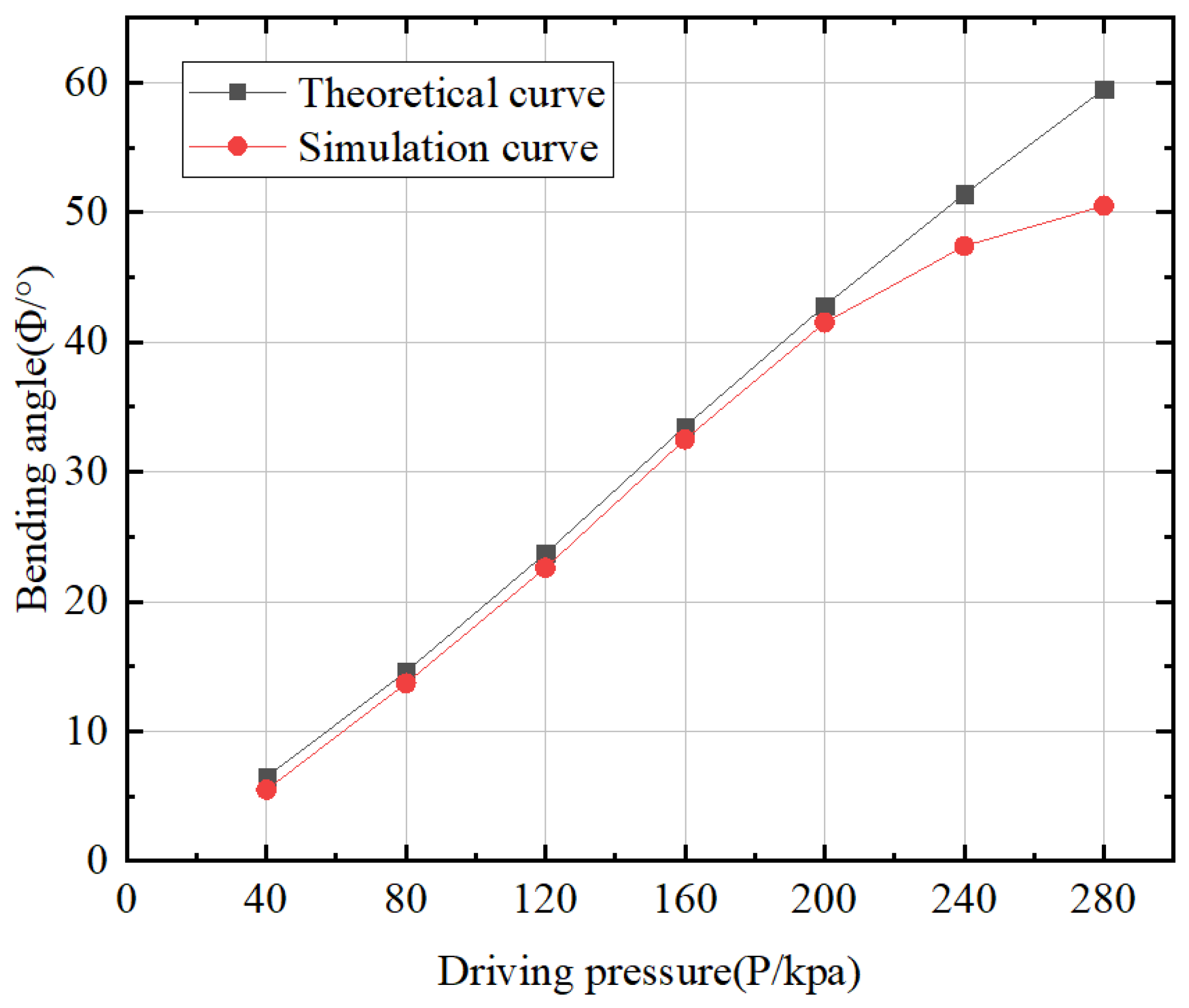
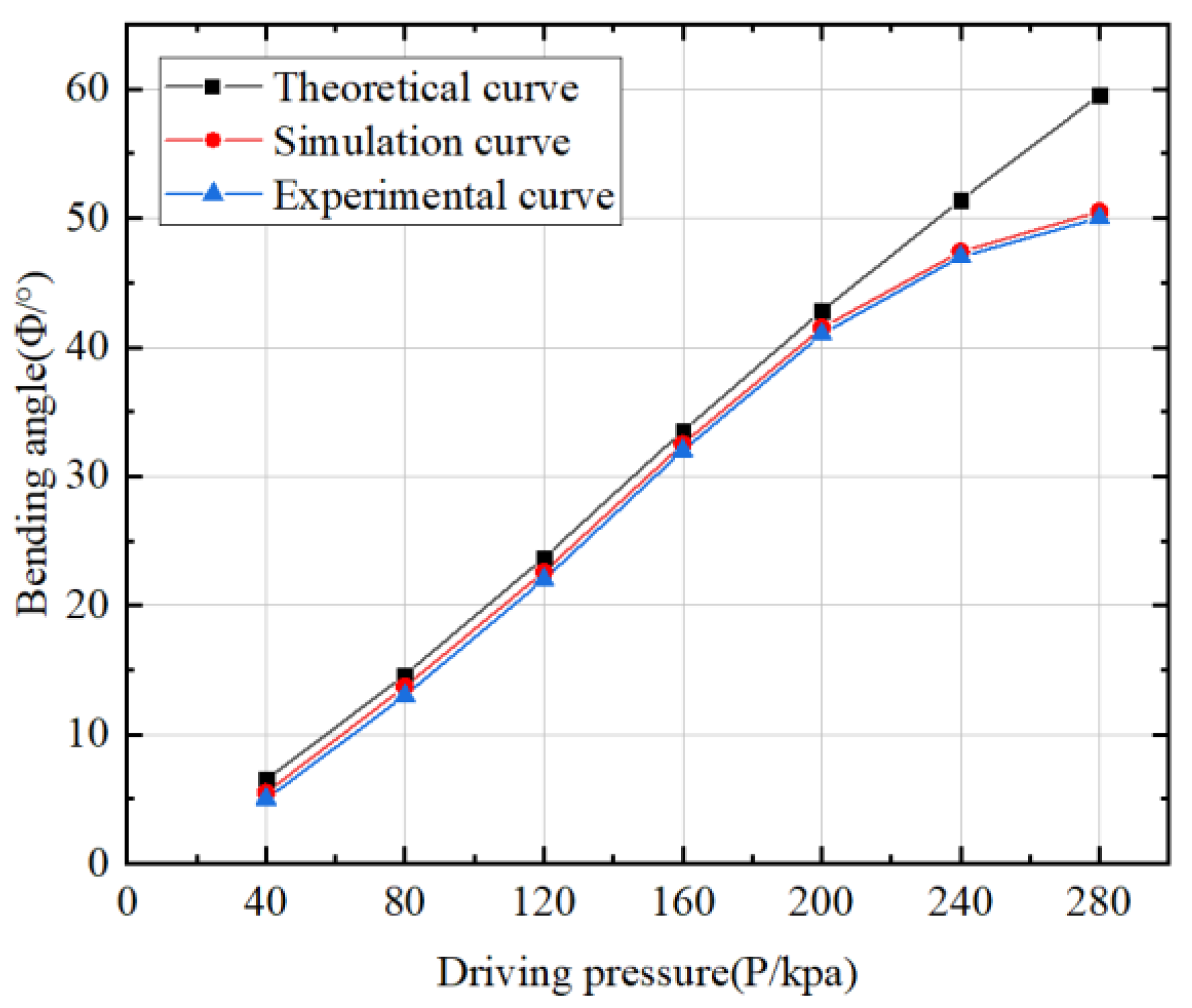
- Using numerical simulation technology, the rationality of the structure and function of the actuator is verified. When the driving pressure is not more than 200 kPa, the comparison error between the numerical simulation results and the theoretical model is 7.18%, which verifies that the deformation analysis model has a certain accuracy.
- (3)
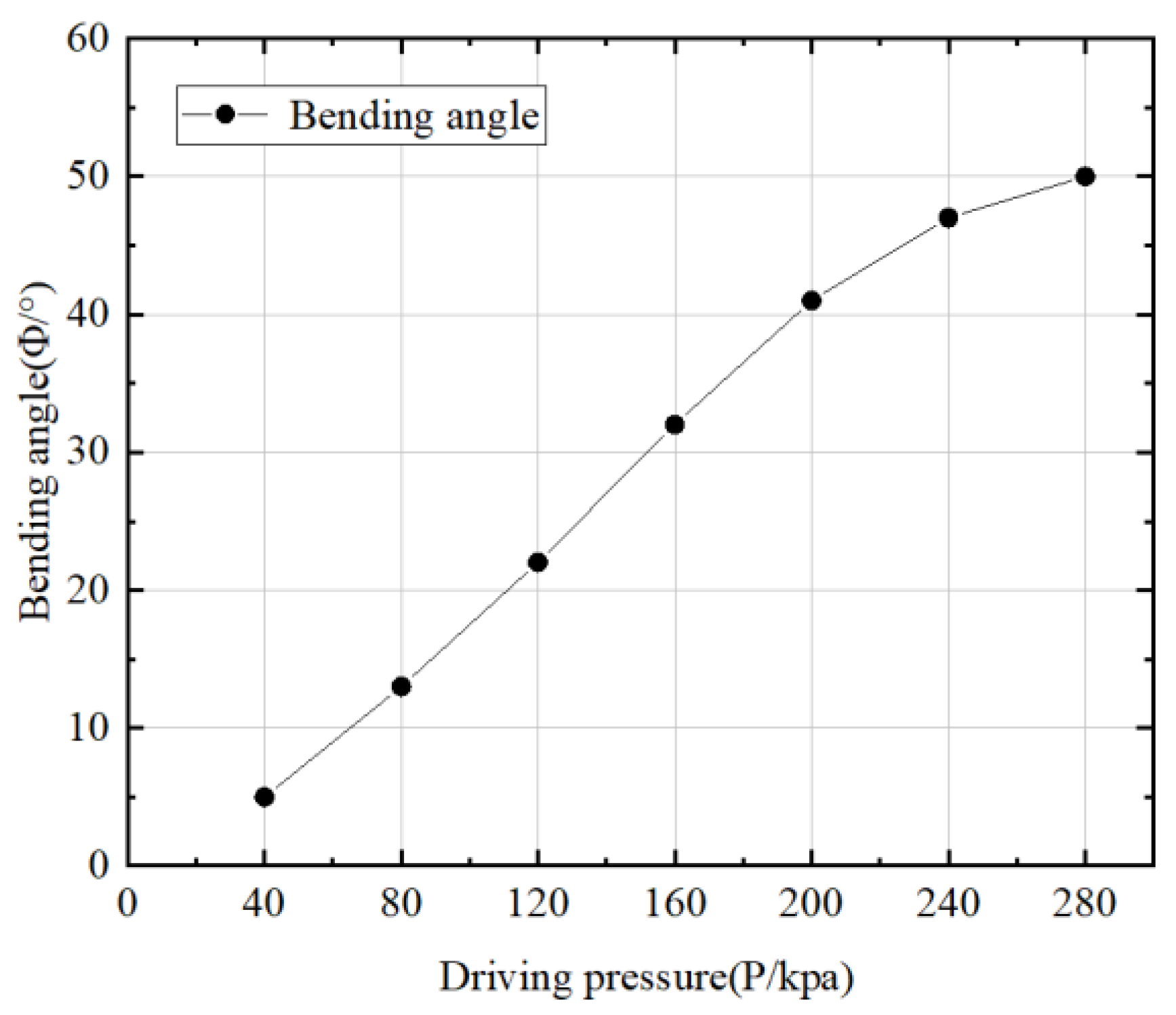
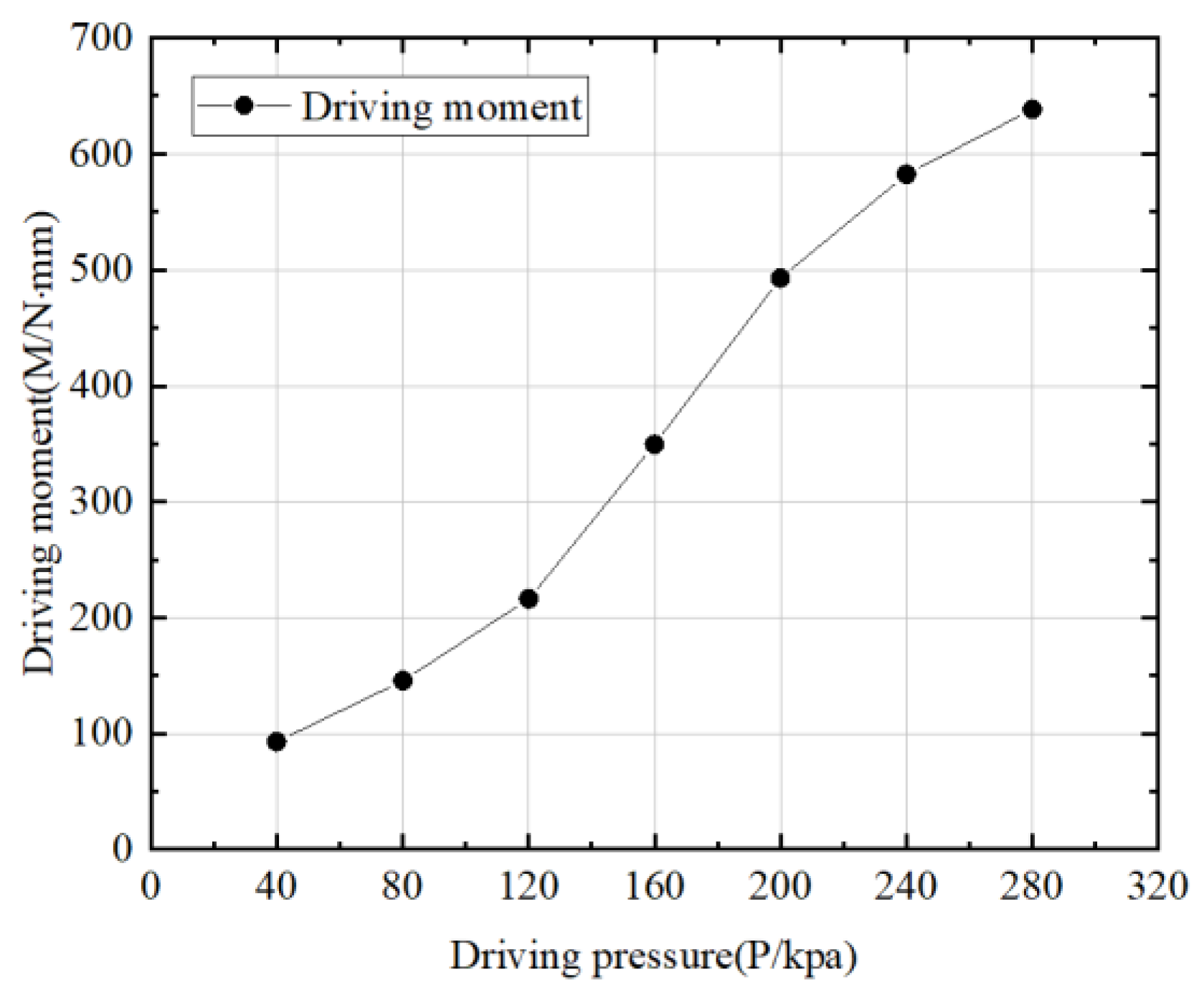
- An experimental platform is built to verify and analyze the performance of the prepared actuator. According to the input driving air pressure value, matching a certain range of motion and power output, the characteristic curves of actuator bending angle and driving moment are obtained, and the empirical formula is fitted. The accuracy of the deformation analysis model and numerical simulation algorithm is verified, and the radial expansion deformation characteristics of the actuator are experimentally studied. Finally, it is determined that the actuator is reasonable and feasible, and can be used as the driving mechanism of a multi-motion mode soft-bodied pipe crawling robot.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abidin, A.S.Z.; Zaini, M.H.; Pauzi, M.F.A.M.; Sadini, M.M.; Chie, S.C.; Mohammadan, S.; Jamali, A.; Muslimen, R.; Ashari, M.F.; Jamaludin, M.S.; et al. Development of Cleaning Device for In-pipe Robot Application. Procedia Comput. Sci. 2015, 76, 506–511. [Google Scholar] [CrossRef] [Green Version]
- Singh, P.; Ananthasuresh, G.K. A Compact and Compliant External Pipe-Crawling Robot. IEEE Trans. Robot. 2012, 29, 251–260. [Google Scholar] [CrossRef]
- Alnaimi, F.B.I.; Mazraeh, A.A.; Sahari, K.S.M.; Weria, K.; Moslem, Y. Design of a multi-diameter in-line cleaning and fault detection pipe pigging device. In Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Langkawi, Malaysia, 18–20 October 2015; pp. 258–265. [Google Scholar]
- Patricio, R.A.C.; Baptista, R.M.; Rachid, F.B.D.F.; Bodstein, G.C. Numerical simulation of pig motion in gas and liquid pipelines using the Flux-Corrected Transport method. J. Pet. Sci. Eng. 2020, 189, 106970. [Google Scholar] [CrossRef]
- Kim, Y.-G.; Shin, D.-H.; Moon, J.-I.; An, J. Design and implementation of an optimal in-pipe navigation mechanism for a steel pipe cleaning robot. In Proceedings of the 2011 8th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Incheon, Korea, 23–26 November 2011; pp. 772–773. [Google Scholar]
- Oya, T.; Okada, T. Development of a steerable, wheel-type, in-pipe robot and its path planning. Adv. Robot. 2005, 19, 635–650. [Google Scholar] [CrossRef]
- Dewei, T.; Qingkai, L.; Shengyuan, J.; Deng, Z. Analysis of differential characteristics and drag force of three-axis differential pipeline robot when passing through elbow. Robot 2010, 32, 91–96. [Google Scholar]
- Gunatilake, A.; Piyathilaka, L.; Kodagoda, S.; Barclay, S.; Vitanage, D. Real-Time 3D Profiling with RGB-D Mapping in Pipelines Using Stereo Camera Vision and Structured IR Laser Ring. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 19–21 June 2019; pp. 916–921. [Google Scholar]
- Zhang, L.; Wang, X. Stable motion analysis and verification of a radial adjustable pipeline robot. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 1023–1028. [Google Scholar]
- Chen, X.; Wu, Z.; He, S.; Xiao, X. Trafficability design of adaptive supporting pipeline inspection robot. J. Cent. South Univ. (Nat. Sci. Ed.) 2018, 49, 2953–2962. [Google Scholar]
- Matuliauskas, A.; Spruogis, B.; Pikūnas, A. Wall Press Walking In-Pipe Robot. Solid State Phenom. 2006, 113, 296–300. [Google Scholar] [CrossRef]
- Yu, X.; Chen, Y.; Chen, M.Z.Q.; Lam, J. Development of a Novel In-Pipe Walking Robot. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 364–368. [Google Scholar]
- Savin, S. Parameter Optimization for Walking Patterns and the Geometry of in-Pipe Robots. In Proceedings of the 2018 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Moscow, Russia, 15–18 May 2018. [Google Scholar]
- Qiao, J.; Shang, J.; Chen, X. Development of an Inchworm In-pipe Robot Based on the Cam Self-locked Principle. J. Mech. Eng. 2010, 46, 83–88. [Google Scholar] [CrossRef]
- Ishikawa, R.; Tomita, T.; Yamada, Y.; Nakamura, T. Development of the Attachment for the Cable of Peristaltic Crawling Robot to Reduce Friction in Elbow Pipe. In Intelligent Robotics and Applications. ICIRA 2016. Lecture Notes in Computer Science; Part I; Kubota, N., Kiguchi, K., Liu, H., Obo, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 589–595. [Google Scholar]
- Kamata, M.; Yamazaki, S.; Tanise, Y.; Yamada, Y.; Nakamura, T. Morphological change in peristaltic crawling motion of a narrow pipe inspection robot inspired by earthworm’s locomotion. Adv. Robot. 2018, 32, 386–397. [Google Scholar] [CrossRef]
- Tao, R.; Chen, Y.; Qingyou, L. A helical drive in-pipe robot based on compound planetary gearing. Adv. Robot. 2014, 28, 1165–1175. [Google Scholar] [CrossRef]
- Liu, Q.; Li, Y.; Ren, T.; Chen, Y. Active screw driven pipeline robot. Robot 2014, 36, 711–718. [Google Scholar]
- Zhang, Z.; Wang, X.; Wang, S.; Meng, D.; Liang, B. Design and Modeling of a Parallel-Pipe-Crawling Pneumatic Soft Robot. IEEE Access 2019, 7, 134301–134317. [Google Scholar] [CrossRef]
- Kellaris, N.; Venkata, V.G.; Smith, G.M.; Mitchell, S.K.; Keplinger, C. Peano-HASEL actuators: Muscle-mimetic, electrohydraulic transducers that linearly contract on activation. Sci. Robot. 2018, 3, eaar3276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mao, Z.; Iizuka, T.; Maeda, S. Bidirectional electrohydrodynamic pump with high symmetrical performance and its application to a tube actuator. Sens. Actuators A Phys. 2021, 332, 113168. [Google Scholar] [CrossRef]
- Calderon, A.A.; Ugalde, J.C.; Zagal, J.C.; Perez-Arancibia, N.O. Design, fabrication and control of a multi-material-multi-actuator soft robot inspired by burrowing worms. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 31–38. [Google Scholar]
- Connolly, F.; Polygerinos, P.; Walsh, C.J.; Bertoldi, K. Mechanical Programming of Soft Actuators by Varying Fiber Angle. Soft Robot. 2015, 2, 26–32. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, S.; Tanise, Y.; Yamada, Y.; Nakamura, T. Development of axial extension actuator for narrow pipe inspection endoscopic robot. In Proceedings of the 2016 IEEE/SICE International Symposium on System Integration (SII), Sapporo, Japan, 13–15 December 2016; pp. 634–639. [Google Scholar]
- Verma, M.; Ainla, A.; Yang, D.; Harburg, D.; Whitesides, G.M. A Soft Tube-Climbing Robot. Soft Robot. 2018, 5, 133–1377. [Google Scholar] [CrossRef]
- Heung, H.; Chiu, P.W.; Li, Z. Design and prototyping of a soft earthworm-like robot targeted for GI tract inspection. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; pp. 497–502. [Google Scholar]
- Liang, J.; Wu, Y.; Yim, J.K.; Chen, H.; Miao, Z.; Liu, H.; Liu, Y.; Liu, Y.; Wang, D.; Qiu, W.; et al. Electrostatic footpads enable agile insect-scale soft robots with trajectory control. Sci. Robot. 2021, 6, eabe7906. [Google Scholar] [CrossRef]
- Fan, X.; Dai, N.; Wang, H. Prediction method of bending deformation of pneumatic mesh soft actuator. China Mech. Eng. 2020, 31, 1108–1114. [Google Scholar]
- Jiang, C. Design and Application of Worm like Pneumatic Pipeline Robot with Fabric Skin. Master’s Thesis, Donghua University, Shanghai, China, 2021. [Google Scholar]
- Zhang, Y.; Wang, N.; Zhao, W. Design and test of peristaltic soft pipe robot. Food Mach. 2020, 36, 82–86. [Google Scholar]
- Yirmibesoglu, O.D.; Morrow, J.; Walker, S.; Gosrich, W.; Canizares, R.; Kim, H.; Daalkhaijav, U.; Fleming, C.; Branyan, C.; Menguc, Y. Direct 3D Printing of Silicone Elastomer Soft Robots and Their Performance Comparison with Molded Counterparts. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 295–302. [Google Scholar]
- Mei, Y.; Stover, B.; Kazerooni, N.A.; Srinivasa, A.; Hajhashemkhani, M.; Hematiyan, M.; Goenezen, S. A comparative study of two constitutive models within an inverse approach to determine the spatial stiffness distribution in soft materials. Int. J. Mech. Sci. 2018, 140, 446–454. [Google Scholar] [CrossRef]
- Panda, S.K.; Buist, M.L. A finite nonlinear hyper-viscoelastic model for soft biological tissues. J. Biomech. 2018, 69, 121–128. [Google Scholar] [CrossRef] [PubMed]
- Matouš, K.; Geers, M.G.; Kouznetsova, V.; Gillman, A. A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials. J. Comput. Phys. 2017, 330, 192–220. [Google Scholar] [CrossRef] [Green Version]
- Chanda, A.; Callaway, C. Tissue Anisotropy Modeling Using Soft Composite Materials. Appl. Bionics Biomech. 2018, 2018, 4838157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; Zhang, Y.; Wang, N. Soft Robotics: Research, Challenges, and Prospects. J. Robot. Mechatron. 2021, 33, 45–68. [Google Scholar] [CrossRef]
- Wang, H.; Kang, R.; Wang, X.; Dai, J. Design and modeling of soft bending actuator. J. Beijing Univ. Aeronaut. Astronaut. 2017, 43, 1053–1060. [Google Scholar]
- Kao, Y.-T.; Zhang, Y.; Wang, J.; Tai, B.L. Bending behaviors of 3D-printed Bi-material structure: Experimental study and finite element analysis. Addit. Manuf. 2017, 16, 197–205. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, J.; Qu, L. Dynamic modeling for silicone beams using higher-order ANCF beam elements and experiment investigation. Multibody Syst. Dyn. 2019, 46, 307–328. [Google Scholar] [CrossRef]
- Chen, W.-M.; Lee, T.; Lee, P.V.S.; Lee, J.W.; Lee, S.-J. Effects of internal stress concentrations in plantar soft-tissue—A preliminary three-dimensional finite element analysis. Med. Eng. Phys. 2010, 32, 324–331. [Google Scholar] [CrossRef]
- Kindo, S.; Vashistha, R.; Raj, S.; Ravishankar, G.P.; Padwale, M.P. Selection and validation of hyperelastic finite element model for analysis of silicone rubber. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM), Thessaloniki, Greece, 25–30 September 2017. [Google Scholar]
- Launhardt, M.; Ebel, N.; Kondruweit, M.; Weyand, M.; Volk, T.; Drummer, D. Developing a Patient Individualized Flexible Silicone Implant using SLS and Vacuum Die Casting. In Proceedings of the Europe/Africa Regional Dresden Conference of the Polymer-Processing-Society (PPS), Dresden, Germany, 27–29 June 2017. [Google Scholar]

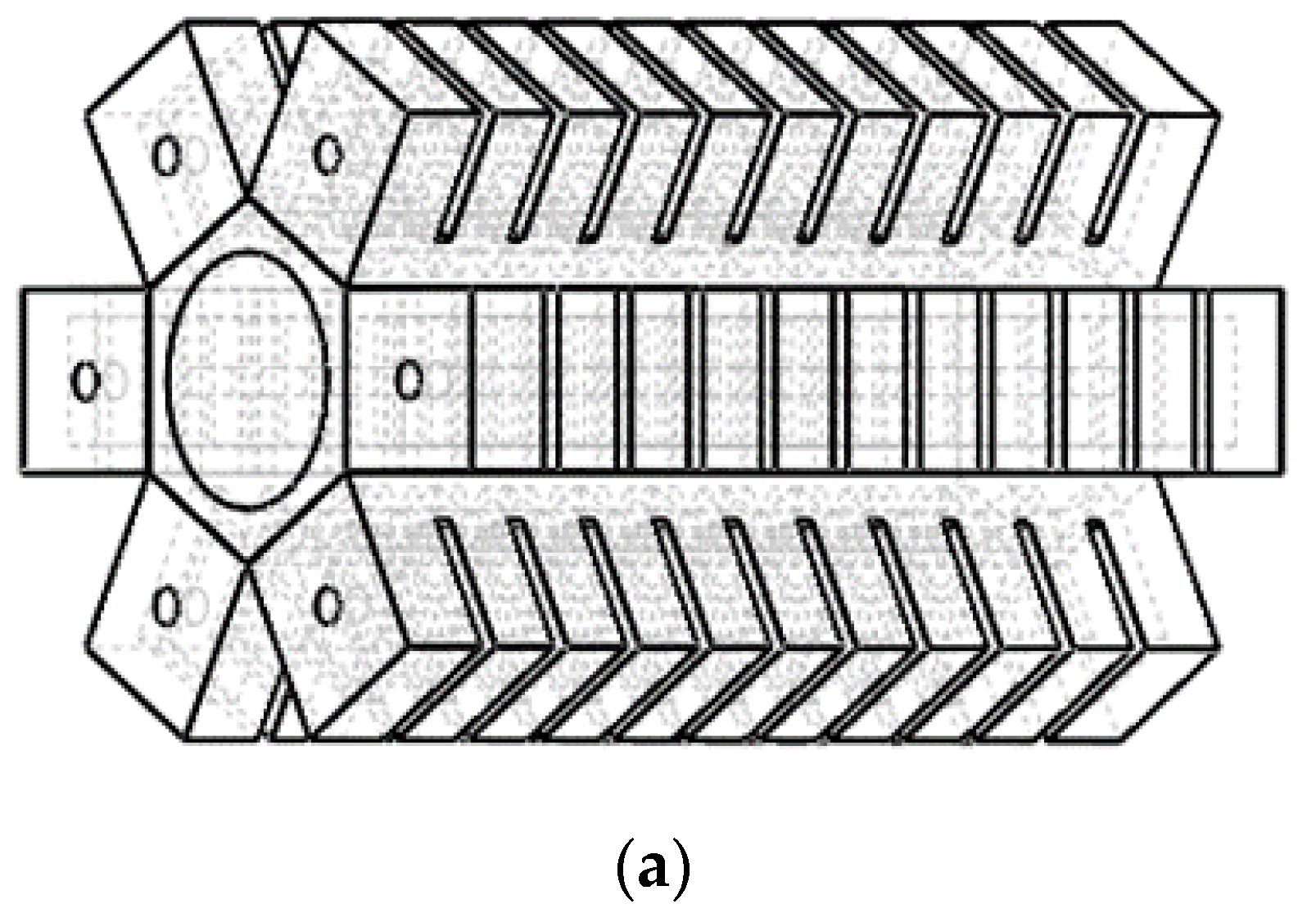
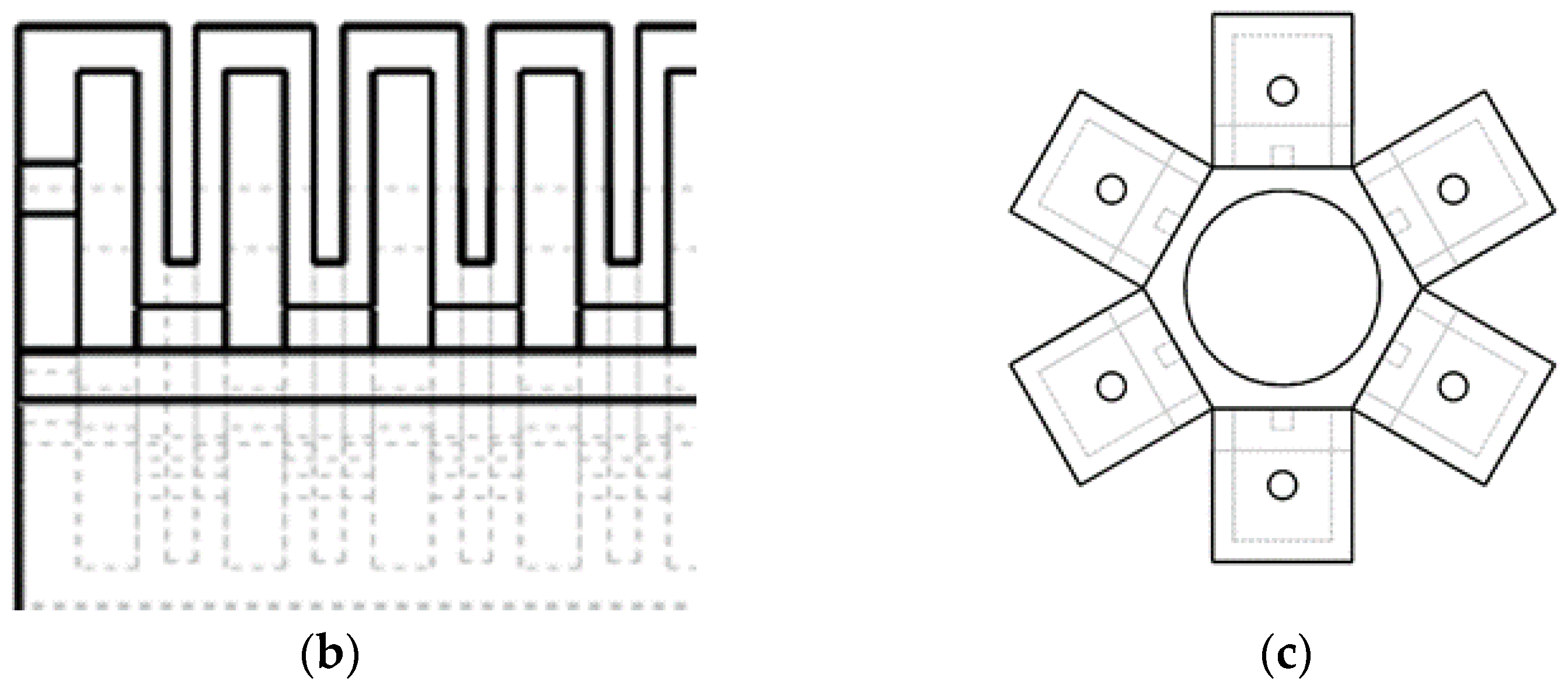
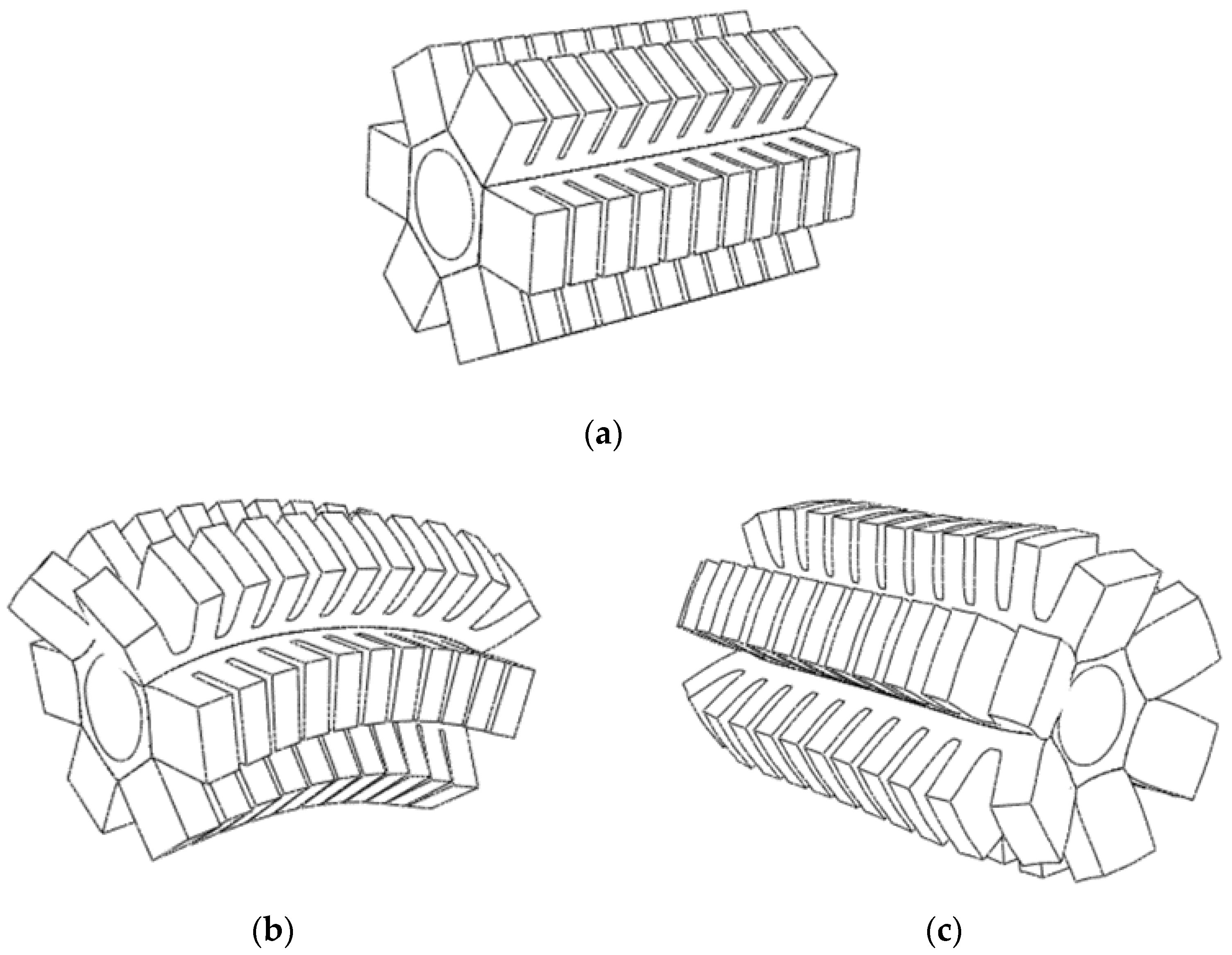
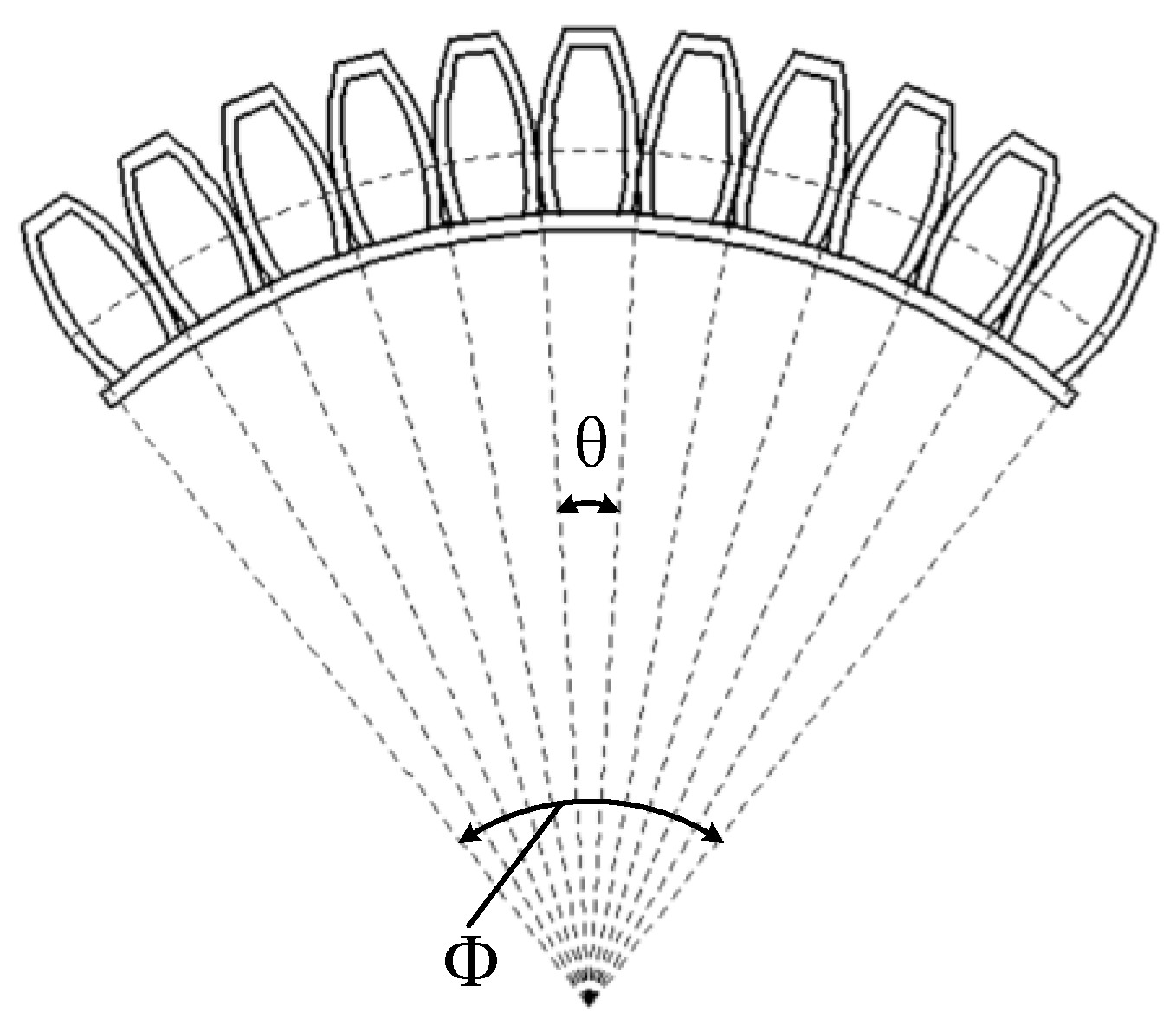
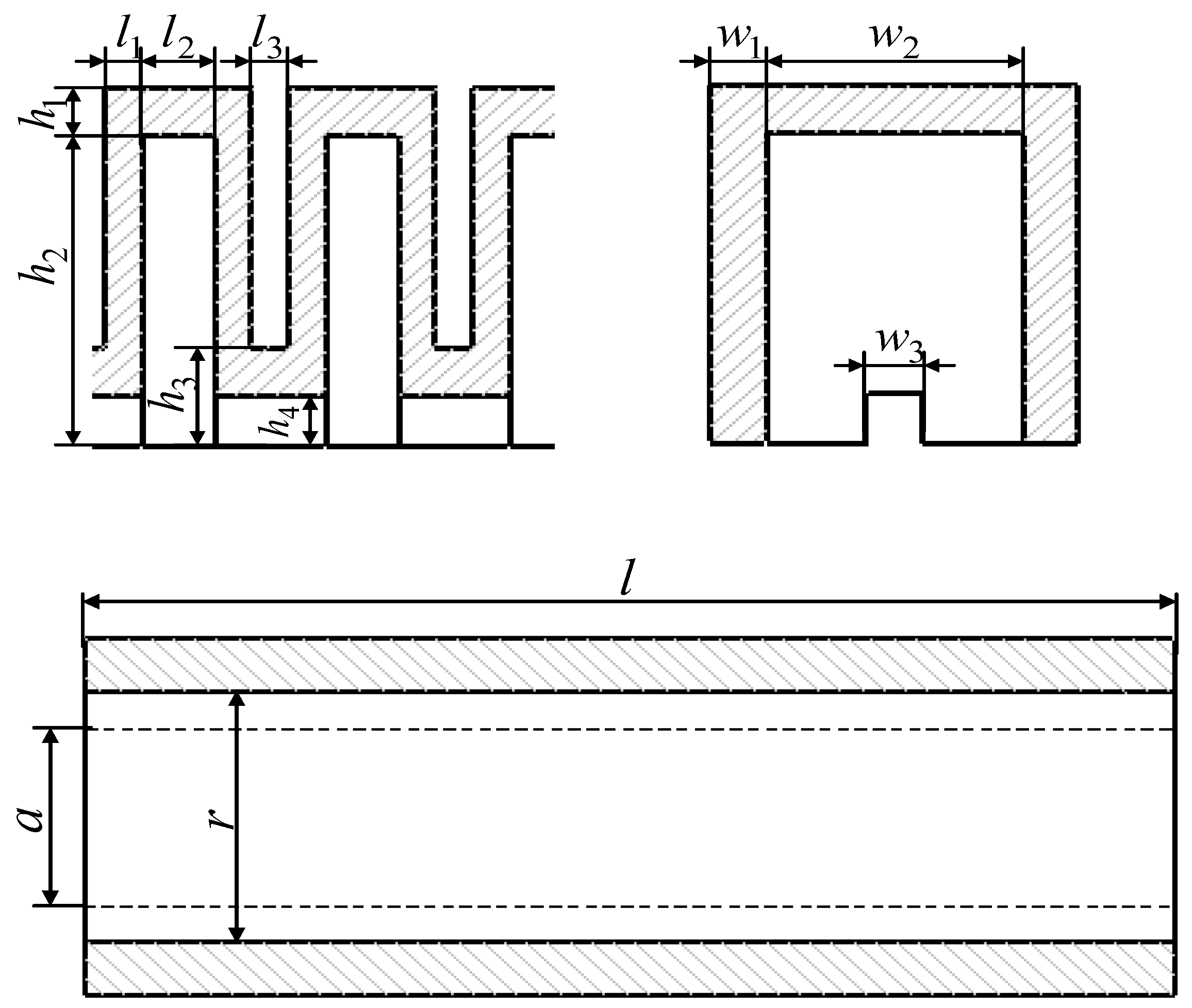




| No. | Size | Num |
|---|---|---|
| 1 | Height of rectangular cavity | 19 mm |
| 2 | Length of rectangular cavity | 14 mm |
| 3 | Width of rectangular cavity | 4 mm |
| 4 | Thickness of expansion wall of rectangular cavity | 2 mm |
| 5 | Side length of hexagonal silicone rubber column | 20 mm |
| 6 | Length of hexagonal silicone rubber column | 112 mm |
| 7 | Dimensions of hollow structure of hexagonal silicone rubber column | 14 mm |
| 8 | Number of air chamber structures | 11 |
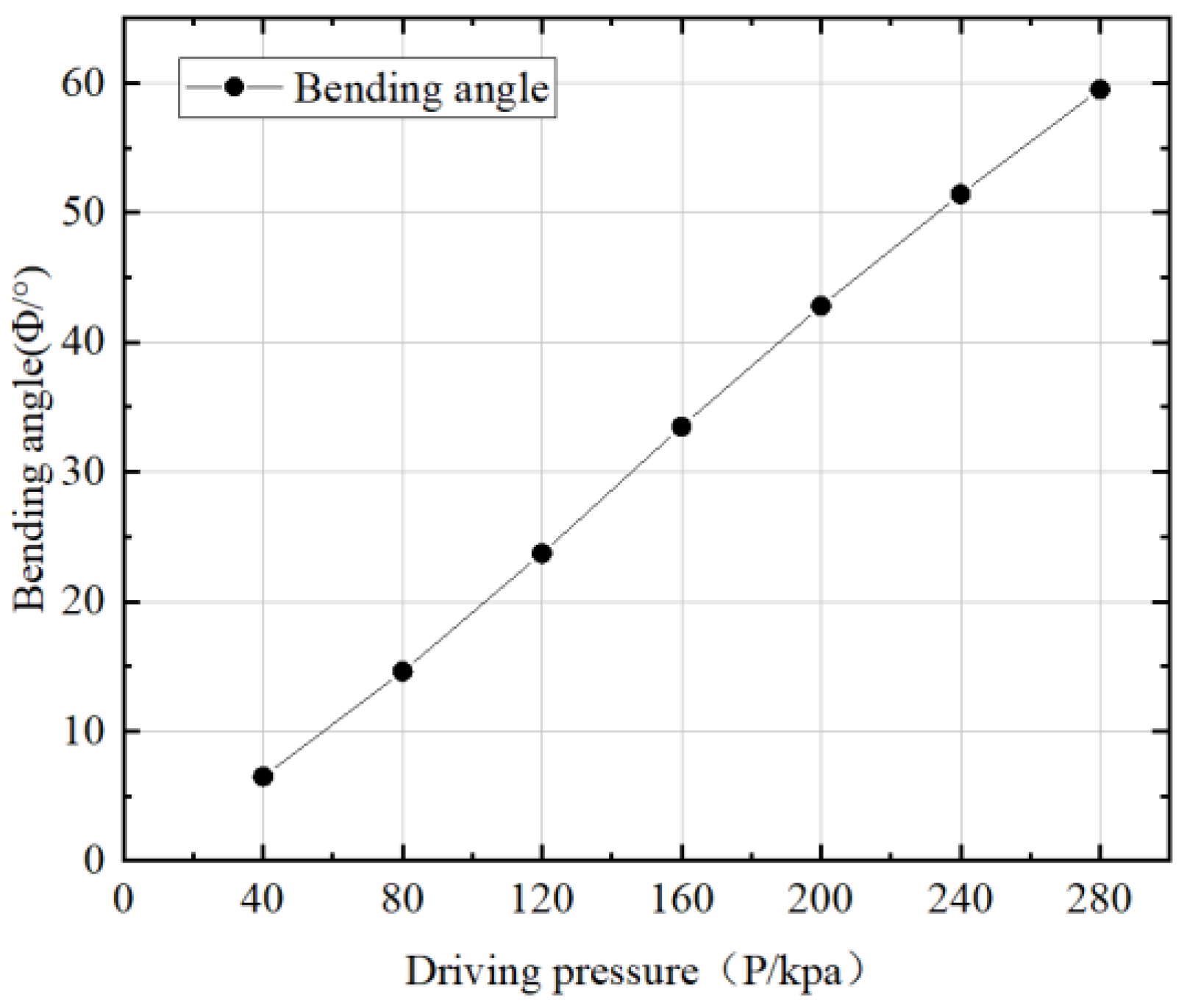
| Driving pressure | 40 | 80 | 120 | 160 | 200 | 240 | 280 |
| Bending angle | 5.5 | 13.7 | 22.6 | 32.5 | 41.5 | 47.4 | 50.5 |
| Preparation of Required Consumables | Material Details |
|---|---|
| Rectangular cavity | Shore A45 platinum silicone rubber |
| Hexagonal silicone rubber column | Shore A45 platinum silicone rubber |
| Pouring mould | PLA |
| adhesive | silicone adhesive |
| Coefficient | |||||
|---|---|---|---|---|---|
| 1.1097 × 10−8 | −9.4894 × 10−6 | 0.0024 | 0.0146 | 1.2143 |
| Coefficient | |||||
|---|---|---|---|---|---|
| −1.4254 × 10−7 | 1.8295 × 10−5 | 0.0163 | −0.9734 | 107.200 |
| Tilt Angle (°) | 0 | 30 | 60 | 90 |
|---|---|---|---|---|
| Driving pressure (kPa) | 160 | 175 | 195 | 225 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Zhang, Y.; Zhang, G.; Zhao, W.; Peng, L. Development and Analysis of Key Components of a Multi Motion Mode Soft-Bodied Pipe Robot. Actuators 2022, 11, 125. https://doi.org/10.3390/act11050125
Wang N, Zhang Y, Zhang G, Zhao W, Peng L. Development and Analysis of Key Components of a Multi Motion Mode Soft-Bodied Pipe Robot. Actuators. 2022; 11(5):125. https://doi.org/10.3390/act11050125
Chicago/Turabian StyleWang, Ning, Yu Zhang, Guofeng Zhang, Wenchuan Zhao, and Linghui Peng. 2022. "Development and Analysis of Key Components of a Multi Motion Mode Soft-Bodied Pipe Robot" Actuators 11, no. 5: 125. https://doi.org/10.3390/act11050125
APA StyleWang, N., Zhang, Y., Zhang, G., Zhao, W., & Peng, L. (2022). Development and Analysis of Key Components of a Multi Motion Mode Soft-Bodied Pipe Robot. Actuators, 11(5), 125. https://doi.org/10.3390/act11050125







