An LADRC Controller to Improve the Robustness of the Visual Tracking and Inertial Stabilized System in Luminance Variation Conditions
Abstract
:1. Introduction
- The theory that the disturbance of the identification influences the control system was studied. The TD of the LADRC can track the missing distance with random disturbance generated by a visual sensor, which provides a smooth and real-time angular velocity order to the inner loop control. In this way, it reduces the influences of the luminance variation on the VTISP.
- Considering the high-frequency random noise from the data of the low-cost MEMS gyroscope, an improved LESO is modified with TD processing and used to observe the total disturbance and the high-order state variables. The dynamic response time and stability of the system can be ensured by the high-order inner velocity loop control and compensation of the total disturbance.
- An approximate model of the system is built for the controller design. The feasibility of the LADRC in the VTISP with an inaccuracy model and random disturbance in varying illuminations is verified by the simulation and experiments.
2. Mathematical Models and Definitions
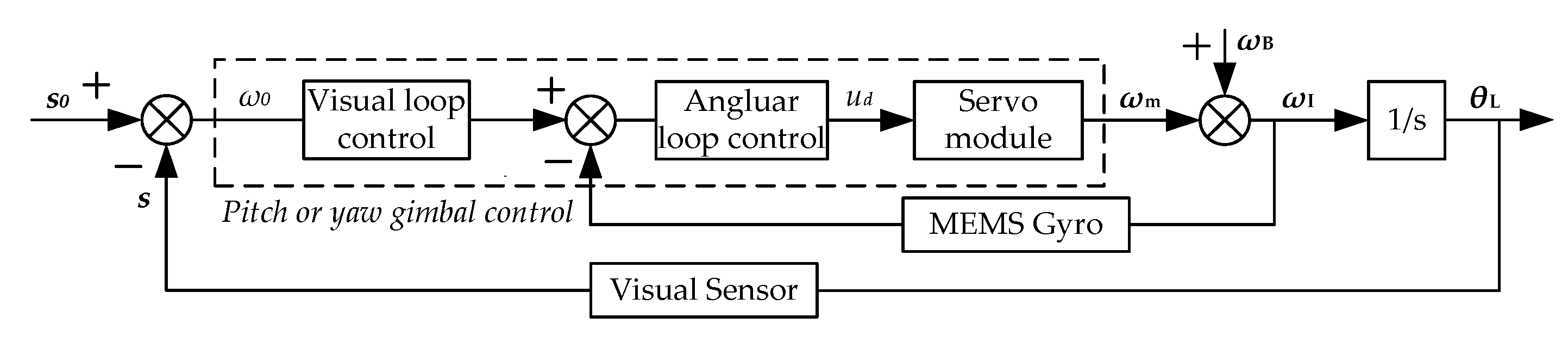
2.1. Gimbal Kinematic Model
2.2. Gear-Driven Actuator
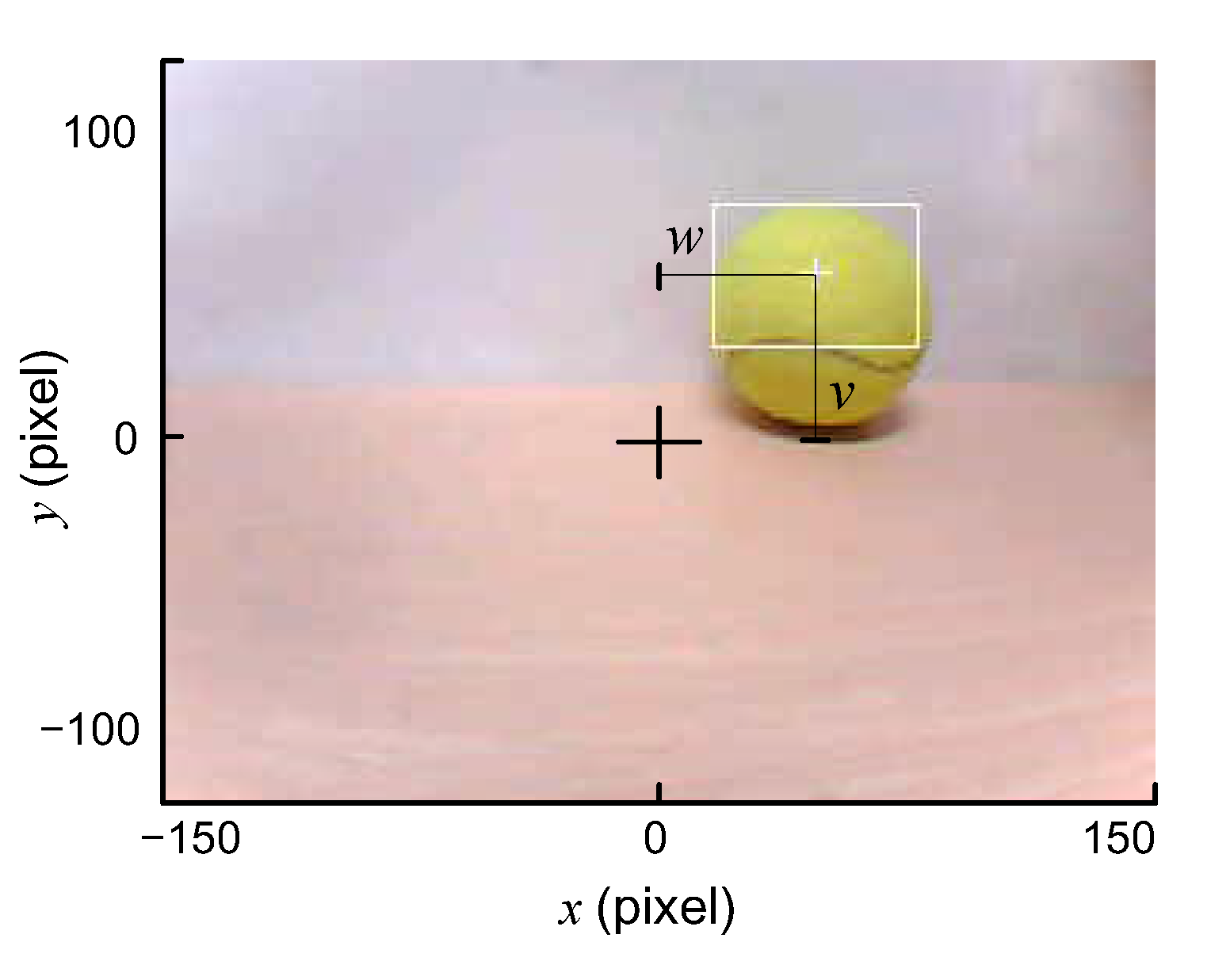
2.3. 2D Visual Model
2.4. Visual Tracking Control Model
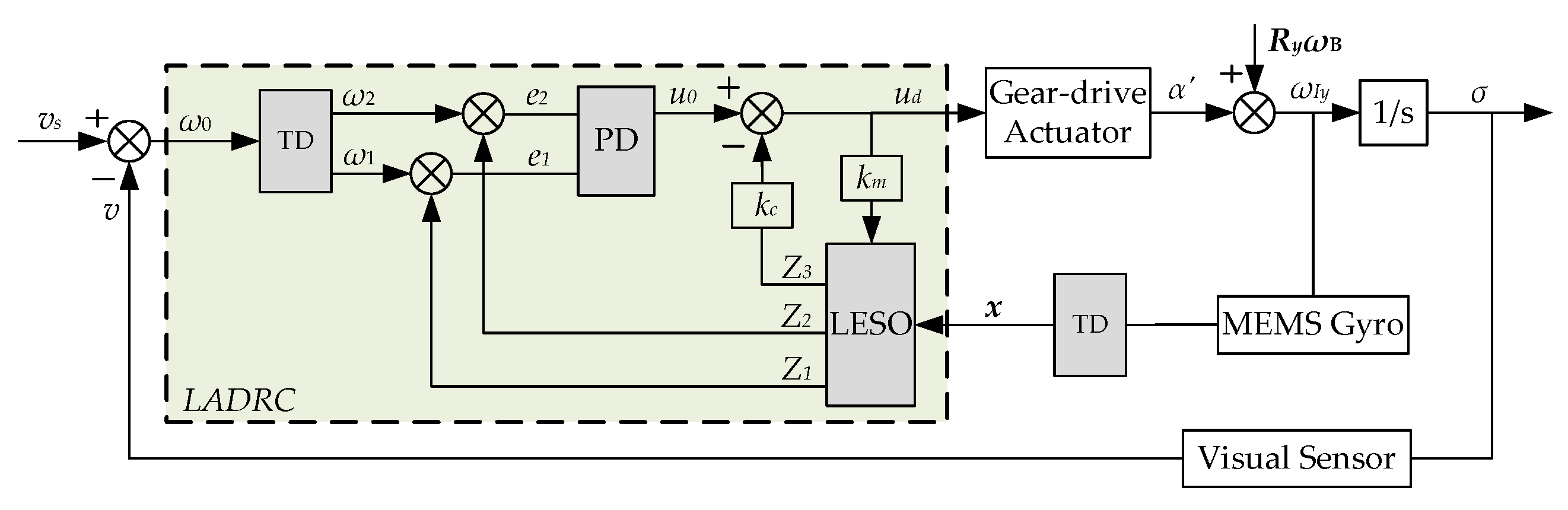
3. LADRCin VTISP
3.1. Tracking Differentiator (TD)
3.2. Linear Extended State Observer (LESO)
3.3. Disturbance Compensation and PD Controller
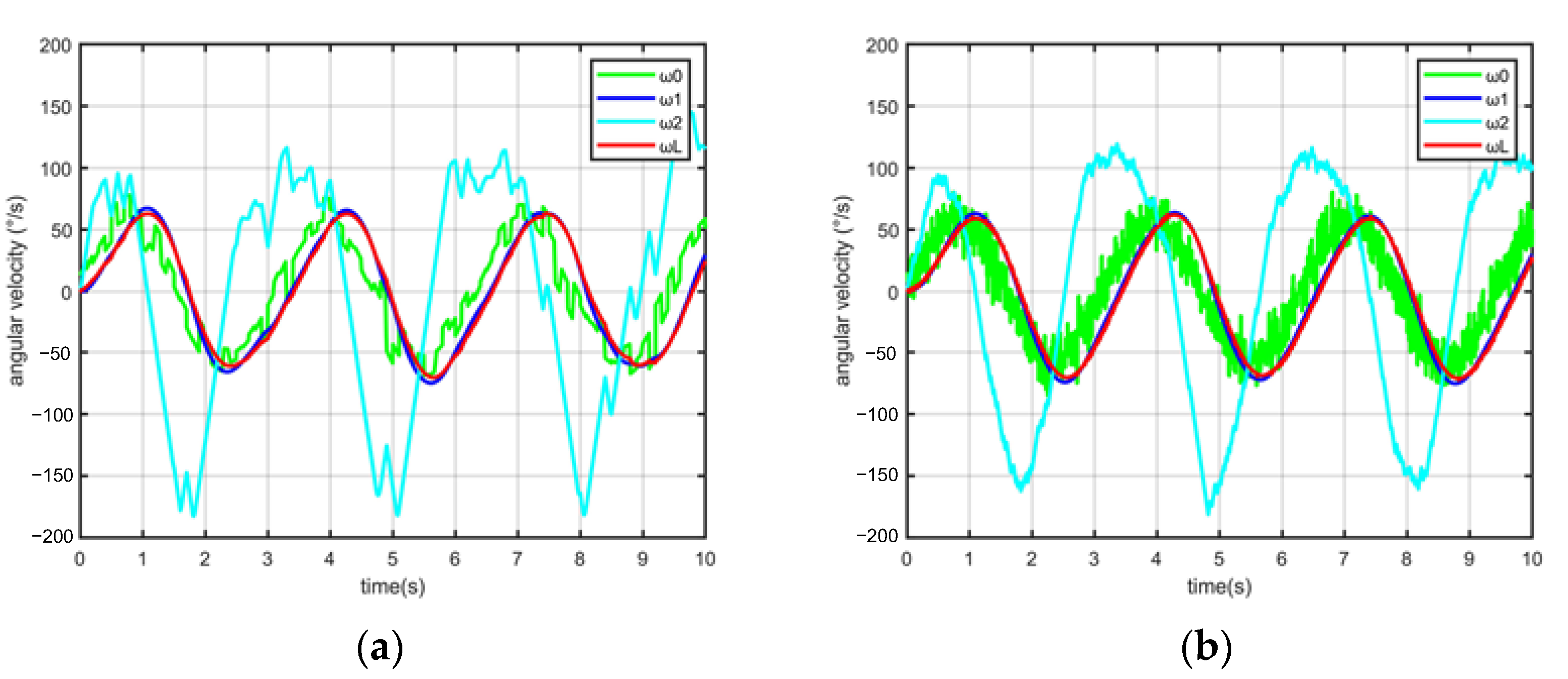
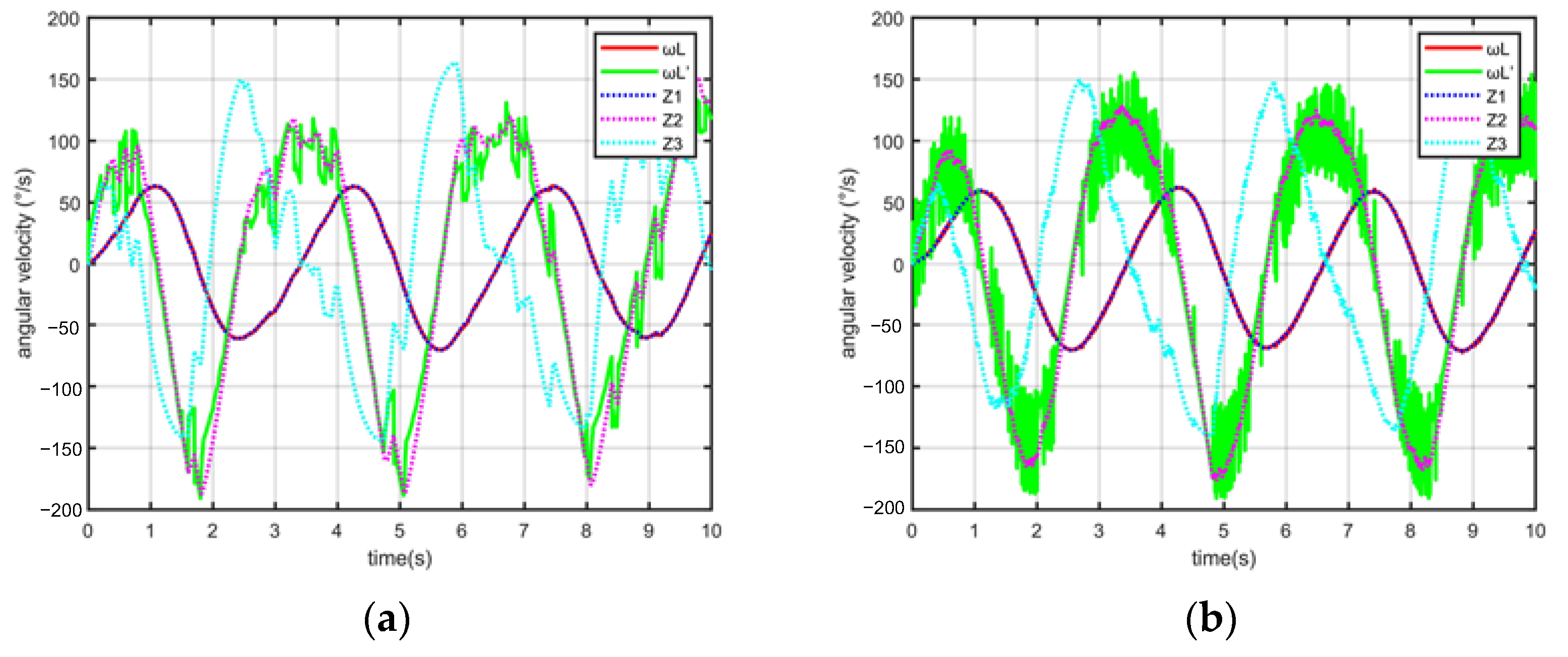
4. Simulation and Verification
4.1. Influence of Luminance Variation
4.2. Simulation of Control System
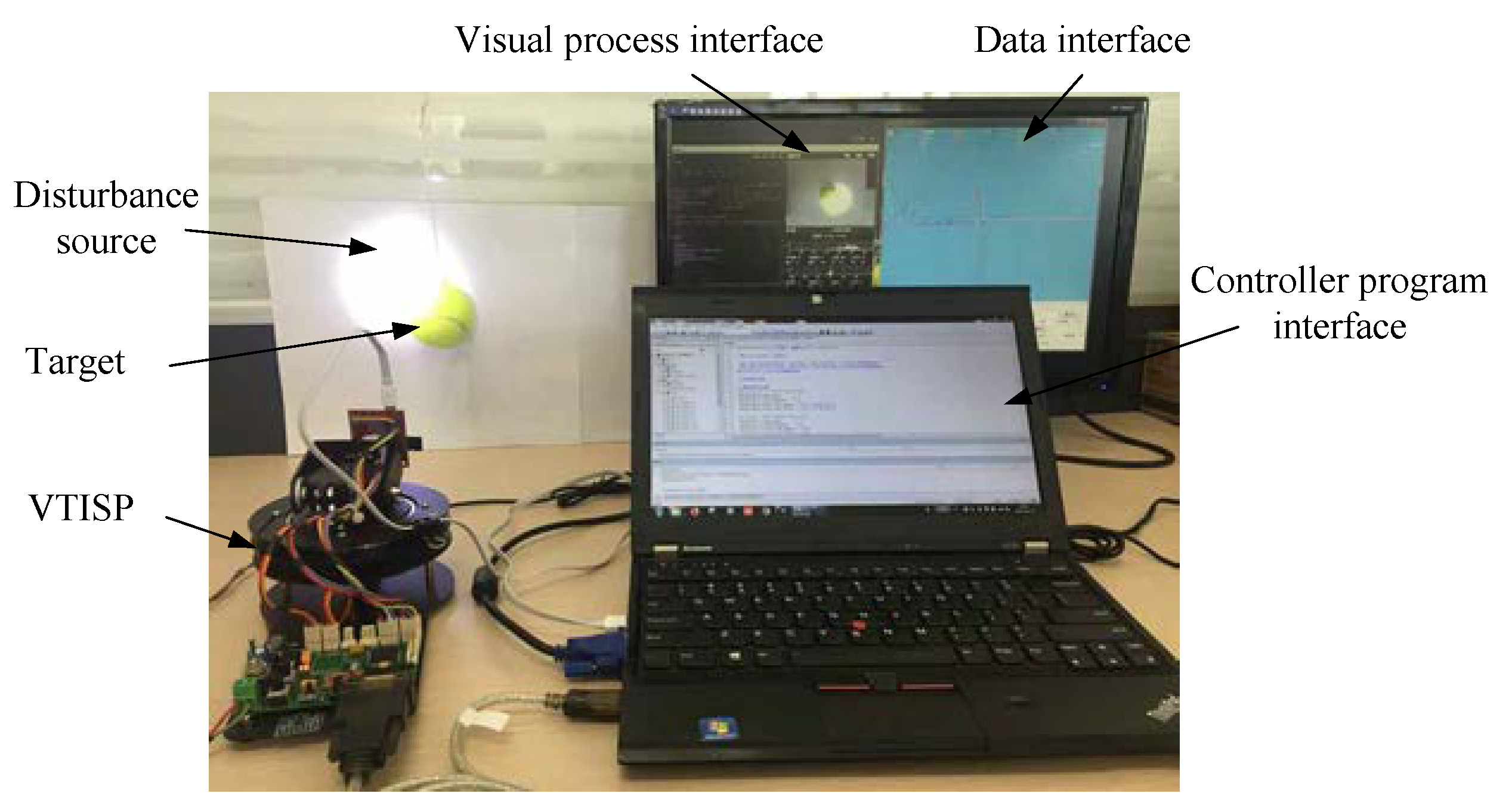
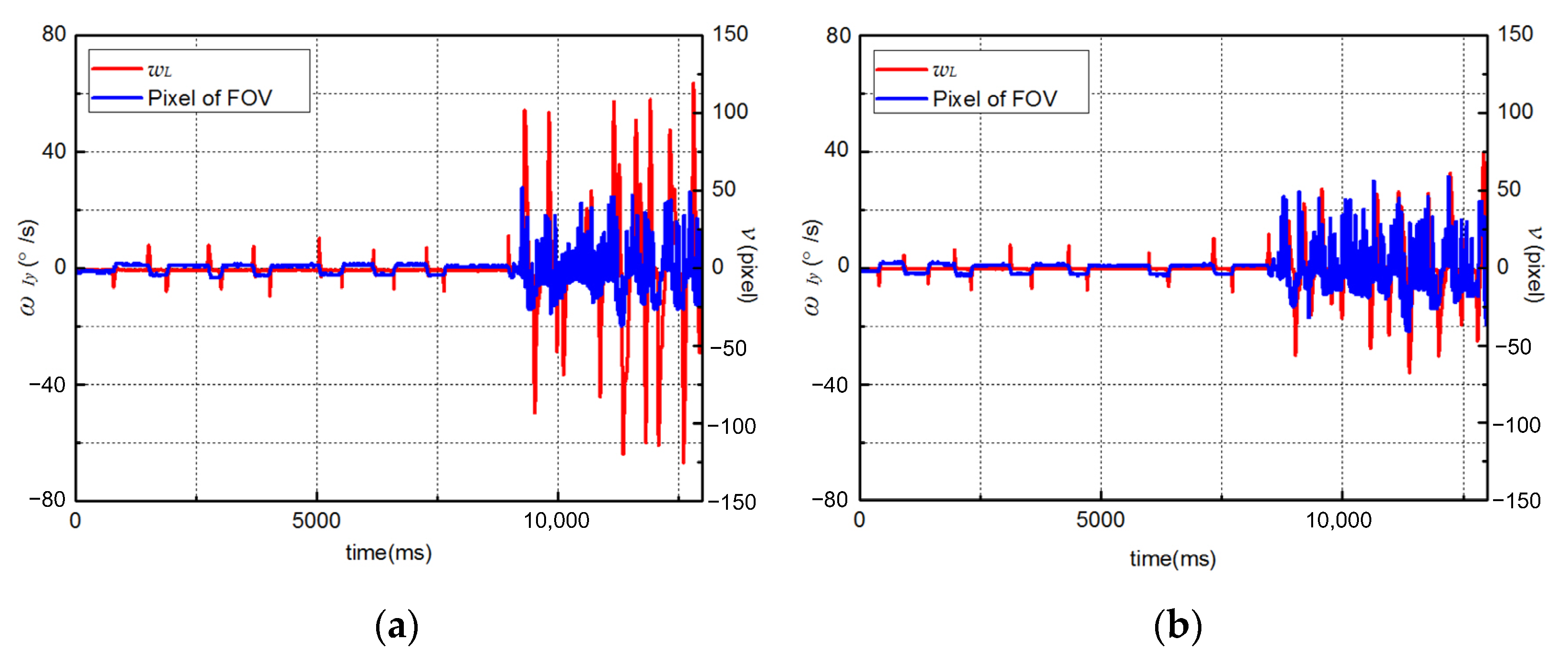
5. Experiment and Results
5.1. System for Experiments
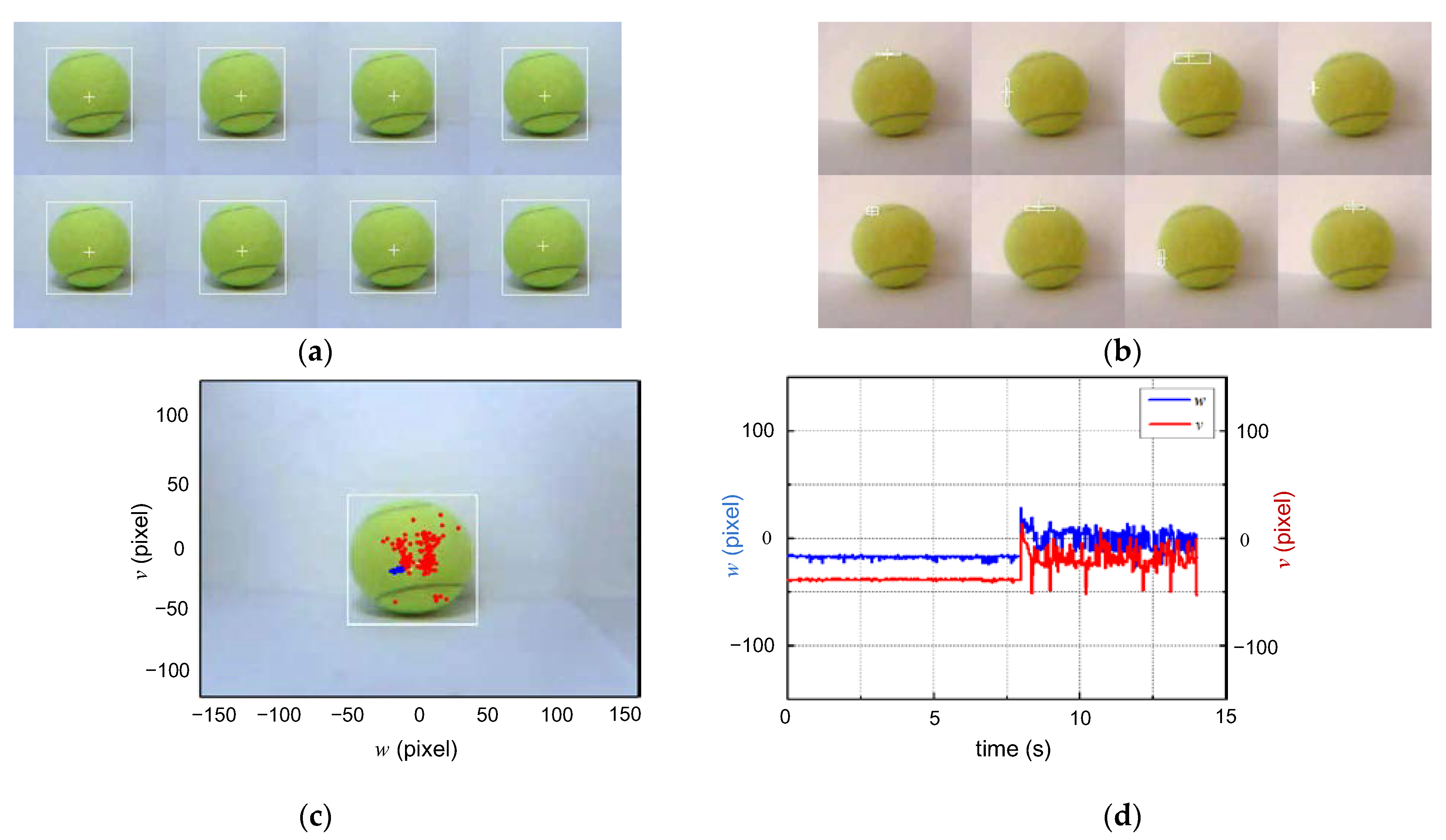
5.2. Performance of TD
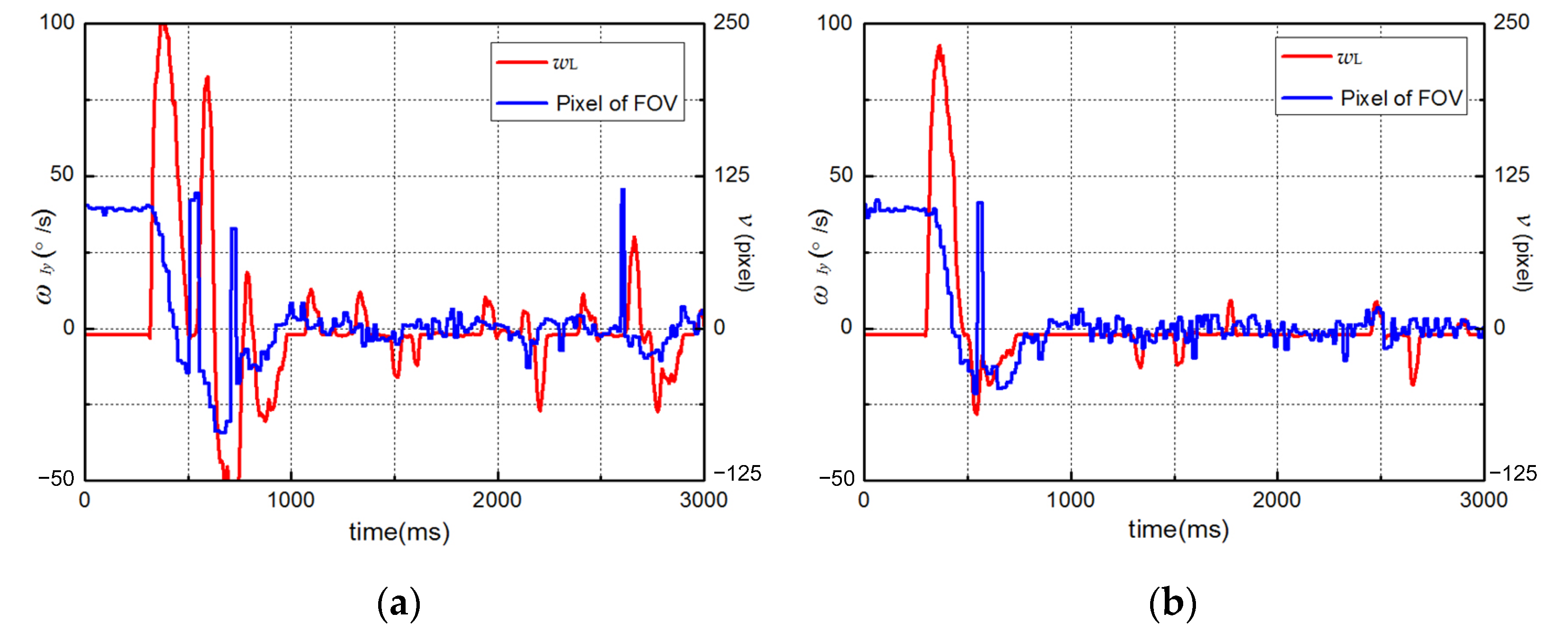
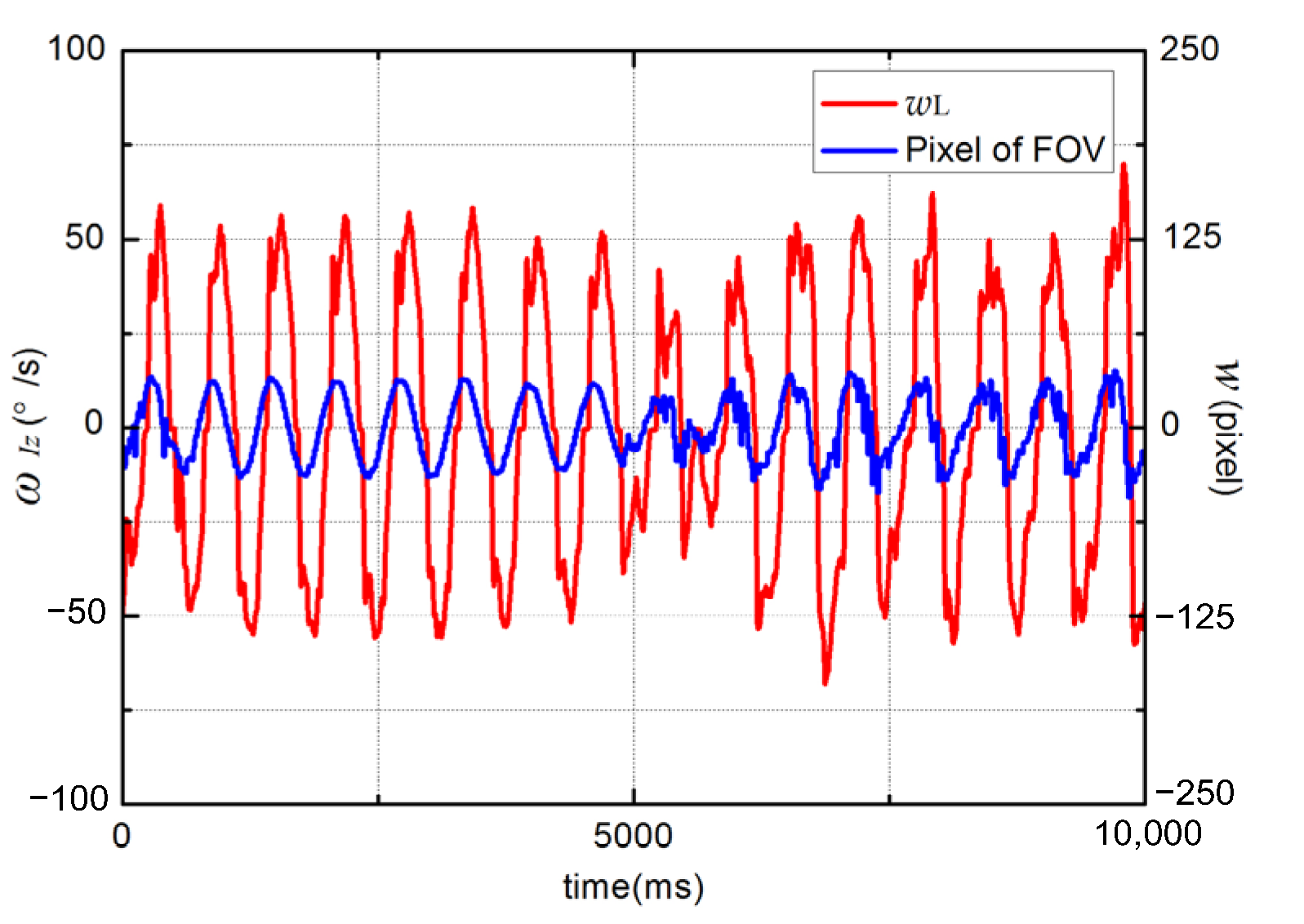
5.3. Dynamic Performanceof Controller
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Das, S.; Kale, A.; Vaswani, N. Particle filter with a mode tracker for visual tracking across illumination changes. IEEE Trans. Image Process. 2012, 21, 2340–2346. [Google Scholar] [CrossRef] [PubMed]
- Al Delail, B.; Bhaskar, H.; Zemerly, M.J.; Al-Mualla, M. Robust likelihood model for illumination invariance in particle filtering. IEEE Trans. Circ. Syst. Video Technol. 2018, 28, 2836–2848. [Google Scholar] [CrossRef]
- Gurkan, F.; Gunsel, B.; Ozer, C. Robust object tracking via integration of particle filtering with deep detection. Digit. Signal Process. 2019, 87, 112–124. [Google Scholar] [CrossRef]
- Wu, H.; Xu, X.R.; Chu, J.B.; Duan, L.; Siebert, P. Particle swarm optimization-based optimal real Gabor filter for surface inspection. Assenbly Autom. 2019, 39, 963–972. [Google Scholar] [CrossRef]
- Moghaddasi, S.S.; Faraji, N. A hybrid algorithm based on particle filter and genetic algorithm for target tracking. Expert Syst. Appl. 2020, 147, 113188. [Google Scholar] [CrossRef]
- Wang, F.S.; Wang, Y.B.; He, J.J.; Sun, F.M.; Li, X.C.; Zhang, J.X. Visual object tracking via iterative ant particle filtering. IET Image Process. 2020, 14, 1636–1644. [Google Scholar] [CrossRef]
- Luo, M.; Chang, X.; Nie, L.; Yang, Y.; Alexander, G.; Zheng, Q. An Adaptive Semisupervised Feature Analysis for Video Semantic Recognition. IEEE Trans. Cybern. 2018, 48, 648–660. [Google Scholar] [CrossRef]
- Chen, K.; Yao, L.; Zhang, D.; Wang, X.; Chang, X.; Nie, F. A Semisupervised Recurrent Convolutional Attention Model for Human Activity Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1747–1756. [Google Scholar] [CrossRef]
- Miller, R.; Mooty, G.; Hilkert, J.M. Gimbal system configurations and line-of-sight control techniques forsmall UAV applications. In Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications X; SPIE: Paris, France, 2013; p. 8713. [Google Scholar]
- Gasparovic, M.; Jurjevic, L. Gimbal Influence on the Stability of Exterior Orientation Parameters of UAV Acquired Images. Sensors 2017, 17, 401. [Google Scholar] [CrossRef] [Green Version]
- Rodin, C.D.; Andrade, F.A.D.; Hovenburg, A.R.; Johansen, T.A. A survey of practical design considerations of optical imaging stabilization systems for small unmanned aerial systems. Sensors 2019, 19, 4800. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Yao, L.; Chen, X.; Wang, S.; Chang, X.; Liu, Y. Making Sense of Spatio-Temporal Preserving Representations for EEG-Based Human Intention Recognition. IEEE Trans. Cybern. 2020, 50, 3033–3044. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.Y.; Gong, G.H.; Li, J.P.; Zhang, H.Y.; Yu, R.X. Decoupling control for a three-axis inertially stabilized platform used for aerial remote sensing. Trans. Inst. Meas. Control 2015, 37, 1135–1145. [Google Scholar] [CrossRef]
- Ke, D.; Shuang, C.; Dejie, K.; Honghai, S. Discrete-Time Direct Model Reference Adaptive Control Application in a High-Precision Inertially Stabilized Platform. IEEE Trans. Ind. Electron. 2019, 66, 358–367. [Google Scholar]
- Altan, A.; Hacioglu, R. Model predictive control of three-axis gimbal system mounted on UAV for real-time target tracking under external disturbances. Mech. Syst. Signal Process. 2020, 138, 106548. [Google Scholar] [CrossRef]
- Kim, S.B.; Kim, S.H.; Kwak, Y.K. Robust control for a two-axis gimbaled sensor system with multivariable feedback systems. IET Control. Theory Appl. 2010, 4, 539–551. [Google Scholar] [CrossRef]
- Hong, S.; Cho, K.D. Kinematic algorithms and robust controller design for inertially stabilized system. IEEE-ASME Trans. Mechatron. 2014, 19, 76–87. [Google Scholar] [CrossRef]
- Songoing, J.; Zhou, D.; Sun, J.; Qi, Z. Robust control with compensation of adaptive model for dual-stage inertially stabilized platform. J. Cent. South Univ. 2018, 25, 2615–2625. [Google Scholar] [CrossRef]
- Safa, A.; Abdolmalaki, R.Y. Robust output feedback tracking control for inertially stabilized platforms with matched and unmatched uncertainties. IEEE Trans. Control Syst. Technol. 2019, 27, 118–131. [Google Scholar] [CrossRef]
- Lee, D.H.; Tran, D.Q.; Kim, Y.B.; Chakir, S. A robust double active control system design for disturbance suppression of a two-Axis gimbal system. Electronics 2020, 9, 1638. [Google Scholar] [CrossRef]
- Zou, Y.; Lei, X.S. A compound control method based on the adaptive neural network and sliding mode control for inertial stable platform. EuroCmputing 2015, 155, 286–294. [Google Scholar] [CrossRef]
- Zhou, Z.M.; Zhang, B.; Mao, D.P. MIMO fuzzy sliding mode control for three-axis inertially stabilized platform. Sensors 2019, 19, 1658. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, Z.; Feng, Z.; Liang, Y.; Zhe, J.; Zhu, J. Anti-Disturbance Neural-Sliding Mode Control for Inertially Stabilized Platform With Actuator Saturation. IEEE Access 2019, 7, 92220–92231. [Google Scholar] [CrossRef]
- Kumar, S.S.; Anitha, G. A novel self-tuning fuzzy logic-based PID controllers for two-axis gimbal stabilization in a missile seeker. Int. J. Aerosp. Eng. 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterizationbased controller tuning. In proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Xia, Y.; Dai, L.; Fu, M.; Li, C.; Wang, C. Application of active disturbance rejection control in tank gun control system. J. Frankl. Inst. 2014, 351, 2299–2314. [Google Scholar] [CrossRef]
- Zhou, X.; Chao, Y.; Zhao, B.; Zhao, L.; Zhu, Z. A High-Precision Control Scheme Based on Active Disturbance Rejection Control for a Three-Axis Inertially Stabilized Platform for Aerial Remote Sensing Applications. J. Sens. 2018, 2018, 7295852. [Google Scholar] [CrossRef]
- Changrui, B.; Zhou, Z. A least mean square based active disturbance rejection control for an inertially stabilized platform. Opt-Int. J. Light Electron Opt. 2018, 174, 609–622. [Google Scholar]
- Behzad, A.; Amin, N. Hardware Implementation of an ADRC Controller on a Gimbal Mechanism. IEEE Trans. Control Syst. Technol. 2018, 26, 2268–2275. [Google Scholar]
- Wang, F.; Wang, R.; Li, E.; Zhang, W. Stabilization Control Method for Two-Axis Inertia Stabilized Platform Based on Active Disturbance Rejection Control with Noise Reduction Disturbance Observe. IEEE Access 2019, 7, 99521–99529. [Google Scholar] [CrossRef]
- Zhou, X.; Yuan, J.; Qiang, Z.; Cai, T. Dual-rate-loop control based on disturbance observer of angular acceleration for a three-axis aerial inertially stabilized platform. ISA Trans. 2016, 63, 288–298. [Google Scholar] [CrossRef]
- Zhou, X.; Zhun, J.; Zhao, B.; Li, J. Extended state observer/proportion integration differentiation compound control based on dynamic modelling for an aerial inertially stabilized platform. Int. J. Adv. Robot. Syst. 2017, 2017, 1–10. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, H.; Zhao, B.; Zhao, L. A GA-based parameters tuning method for an ADRC controller of ISP for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar] [CrossRef] [PubMed]
- Huynh, T.; Tran, M.T.; Lee, D.H. A Study on Vision-Based Back-stepping Control for a Target Tracking System. Actuators 2021, 10, 105. [Google Scholar] [CrossRef]
- Guo, J.; Yuan, C.; Zhang, X.; Chen, F. Vision-based target detection and tracking for a miniature pan-tilt inertially stabilized platform. Electronics 2021, 10, 2243. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, Y. ADRC based input disturbance rejection for minimum-phase plants with unknown orders and/or uncertain relative degrees. J. Syst. Sci. Complex. 2012, 25, 625–640. [Google Scholar] [CrossRef]
- Ekstrand, B. Equations of motion for a two-axes gimbal system. IEEE Trans. Aerosp. Eelctron. Syst. 2001, 37, 1083–1091. [Google Scholar] [CrossRef]
- Hurak, Z.; Rezac, M. Image-based pointing and tracking for inertially stabilized airborne camera platform. IEEE Trans. Control Syst. Technol. 2012, 20, 1146–1159. [Google Scholar] [CrossRef]
- Masten, M.K. Inertially stabilized platforms for optical imaging systems—Tracking dynamic targets with mobile sensors. IEEE Control Syst. Mag. 2008, 28, 47–64. [Google Scholar]
- Zhang, Z.; Cheng, J.; Guo, Y. PD-Based Optimal ADRC with Improved Linear Extended State Observer. Entropy 2021, 23, 888. [Google Scholar] [CrossRef]


| Module | Hardware | Interface Form |
|---|---|---|
| Visual module | Core: STM32H743VET6 | USB |
| Camera: OV7725 | ||
| Control module | Core: STM32F407VET6 | RS232 |
| Gyro: MPU6050 | ||
| Servo module | KS-3518 | Voltage square signal |
| Terms | Scope Range | Accuracy |
|---|---|---|
| Pitch angle | 0~90° | 0.043° (233 LSB/°) |
| Yaw angle | −45°~45° | 0.043° (233 LSB/°) |
| Pitch angle speed | ±190°/s | Gyro:0~±250°/s, 131 LSB/(°/s) |
| Yaw angle speed | ±180°/s | Gyro:0~±250°/s, 131 LSB/(°/s) |
| Visual resolution | 320 × 240 | 1 pixel |
| Terms | Value | |
|---|---|---|
| TD | r = 5 | h = 4 |
| r2 = 1 | h2 = 2 | |
| PD | k1 = 0.15 | k2 = 0.07 |
| LESO | β1 = 1.2 | β2 = 0.7 |
| β3= 0.8 | kc = 0.3 |
| Terms | SMC | LADRC |
|---|---|---|
| dv | 50 | 50 |
| ωIy | ±80°/s | ±40°/s |
| Terms | SMC | LADRC |
|---|---|---|
| dv | 25 | 25 |
| ωIy | 80°/s | −25°/s |
| tc | 0.7 s | 0.45 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, T.; Gao, Y.; Guan, L.; Qin, C. An LADRC Controller to Improve the Robustness of the Visual Tracking and Inertial Stabilized System in Luminance Variation Conditions. Actuators 2022, 11, 118. https://doi.org/10.3390/act11050118
Fu T, Gao Y, Guan L, Qin C. An LADRC Controller to Improve the Robustness of the Visual Tracking and Inertial Stabilized System in Luminance Variation Conditions. Actuators. 2022; 11(5):118. https://doi.org/10.3390/act11050118
Chicago/Turabian StyleFu, Tianlei, Yanbin Gao, Lianwu Guan, and Chao Qin. 2022. "An LADRC Controller to Improve the Robustness of the Visual Tracking and Inertial Stabilized System in Luminance Variation Conditions" Actuators 11, no. 5: 118. https://doi.org/10.3390/act11050118
APA StyleFu, T., Gao, Y., Guan, L., & Qin, C. (2022). An LADRC Controller to Improve the Robustness of the Visual Tracking and Inertial Stabilized System in Luminance Variation Conditions. Actuators, 11(5), 118. https://doi.org/10.3390/act11050118






