Local Path Planning of the Autonomous Vehicle Based on Adaptive Improved RRT Algorithm in Certain Lane Environments
Abstract
:1. Introduction
- This method uses the sampling node method based on heuristic information to make the random tree grow more directionally and utilizes the adaptive sampling space and the adaptive step size to speed up its convergence.
- The road environment constraints and the vehicle’s constraint method gained by a magnifying mechanism considering the motion characteristics of the vehicle are considered to make the vehicle achieve an excellent behavior of avoiding obstacles.
- A heuristic node selection mechanism is introduced to select the nearest tree node so that the vehicle moves smoothly at less cost.
- The post-processing, including the pruning method and the cubic B-spline, is used to optimize the generated path to make the path satisfy the requirement of autonomous vehicle driving.
2. Preliminaries
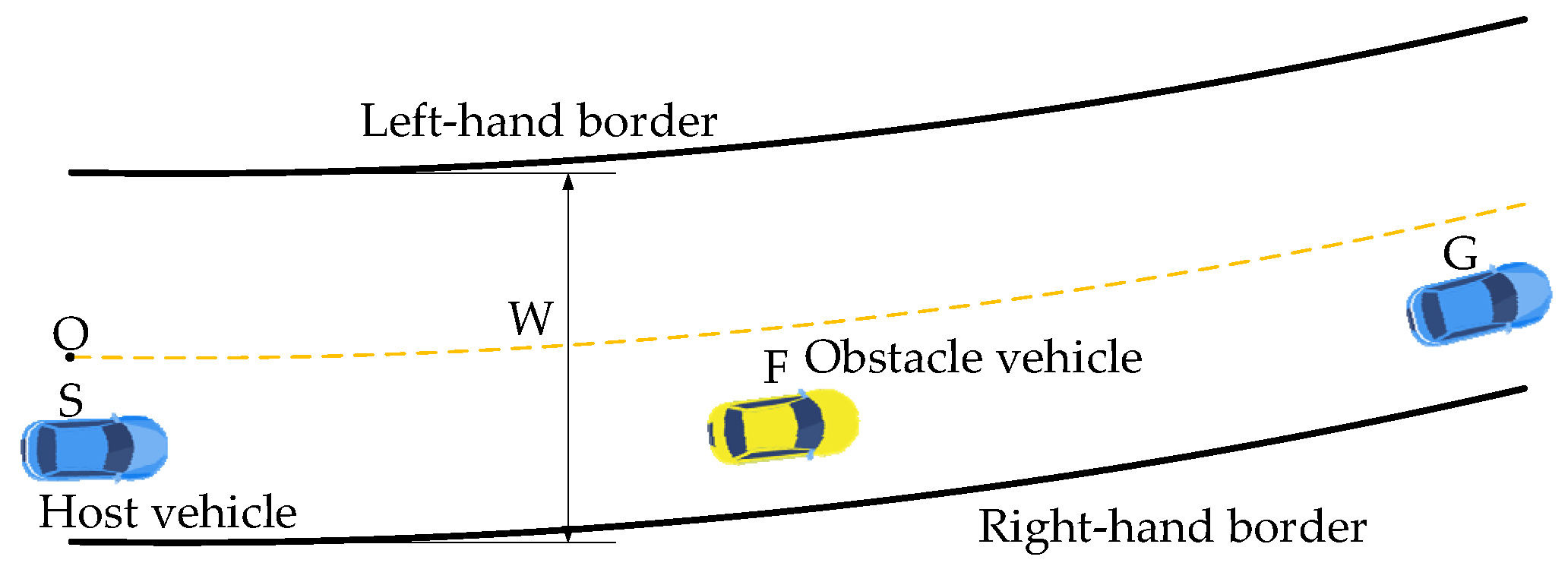
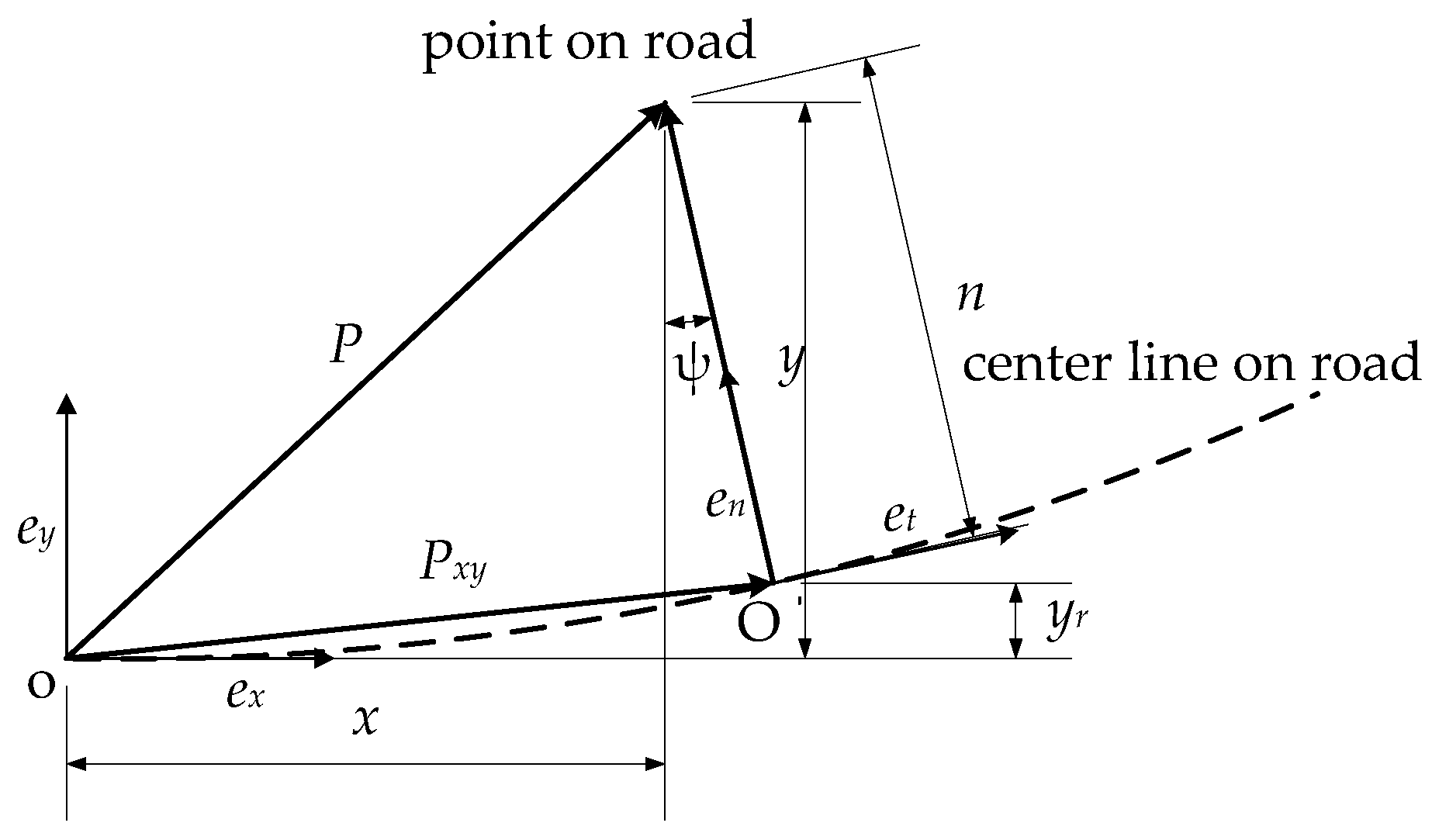
2.1. Road Environment Method
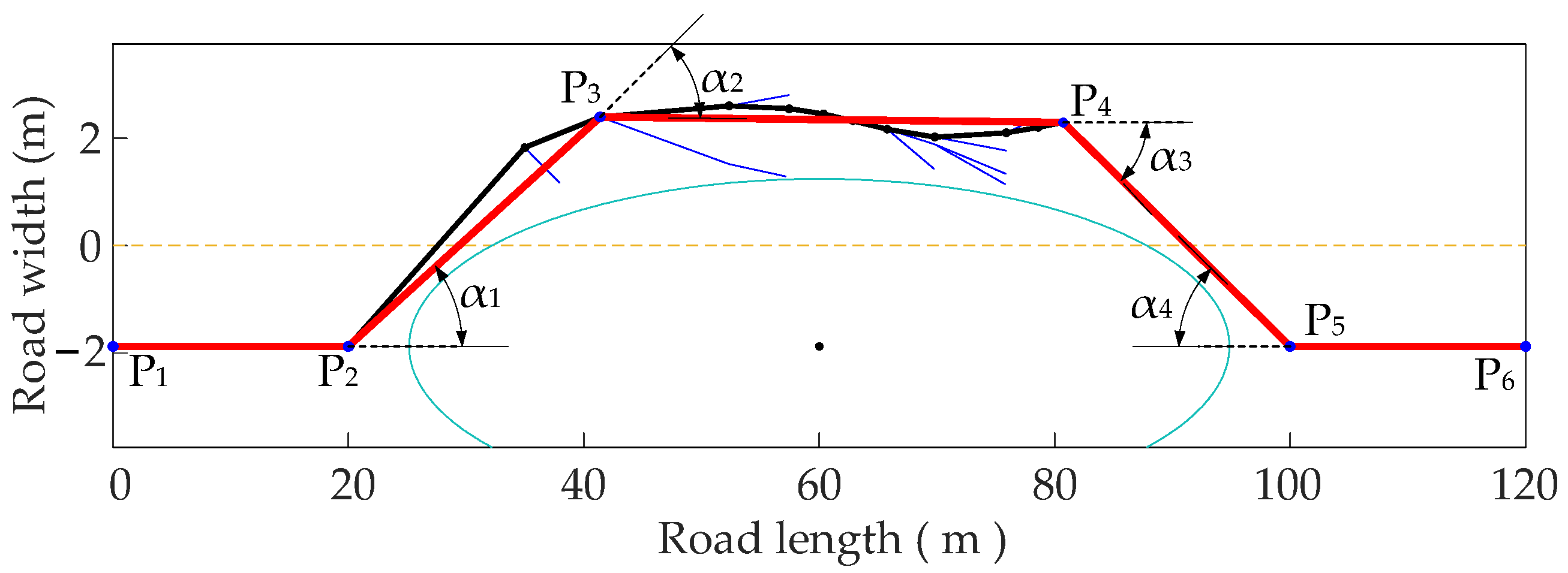
2.1.1. Road Environment Geometries
2.1.2. Constraints of Road Environment
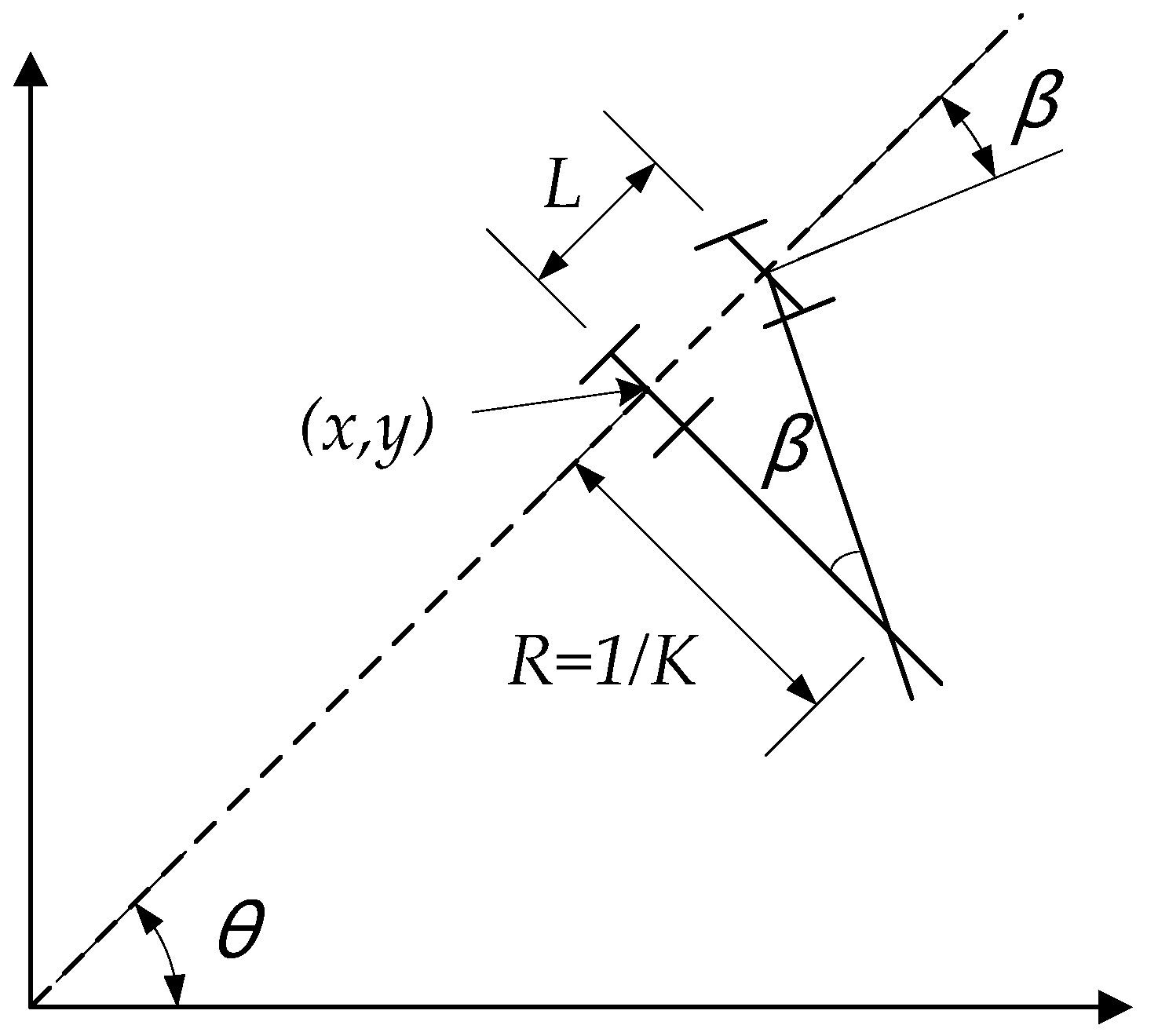
2.2. The Vehicle Model with Non-Integrality Constraint
3. Adaptive Improved RRT Path Planning
3.1. Basic RRT
| Algorithm 1:) |
| ) |
| ) do |
| ←RANDOM_STATE ( ) |
| ←) |
| ←) |
| then |
| 7. Return T |
| 8. endif |
| 9. endWhile |
| 10. path←GET_PATH (T) |
| Algorithm 2: Function GET_PATH (T) |
| 1. Var path_set; ); 3. while 4. i←; ); 6. if i = 1 7. break; 8. endif 9. i←i + 1; 10. endwhile 11. path←path_set |
3.2. Adaptive Improved RRT Algorithm
| Algorithm 3:) |
| ) |
| do |
| ←EFFECTIVE_RANDOM_STATE ( ) |
| ←EFFECTIVE_NEAREST_NEIGHBOR ( ) |
| ←EFFECTIVE_EXTEND ( ) |
| then |
| 7. Return T |
| 8. endif |
| 9. endWhile |
| 10. path←GET_PATH (T) |
| 11. path←PRUNING (path) |
| 12. trajectory←SMOOTHING (path) |
3.2.1. Collision Detection
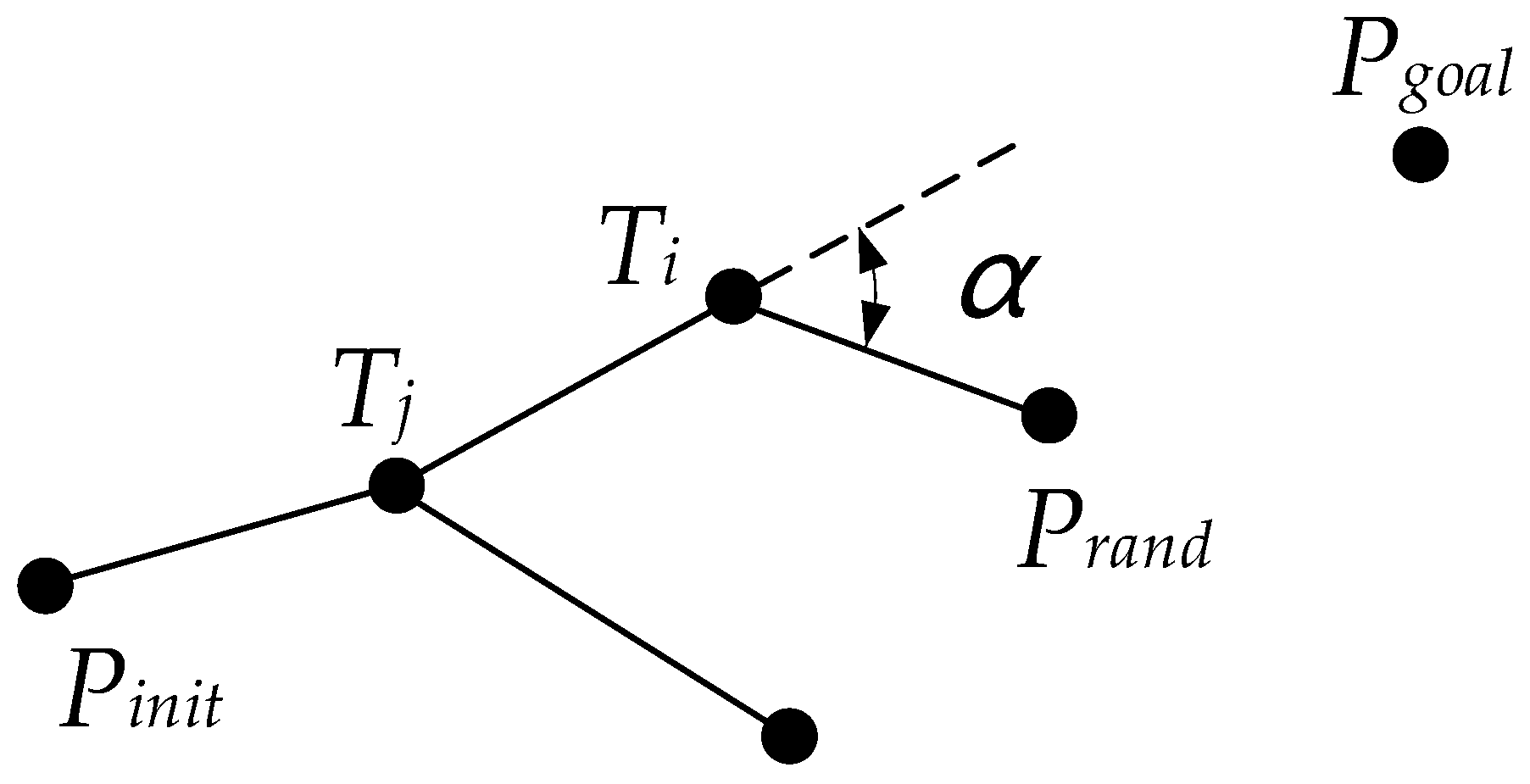
3.2.2. Adaptive Directed Sampling Strategy
Adaptive Sampling Space
Dynamic Sampling
| Algorithm 4: Adaptive Improved RRT EFFECTIVE_RANDOM_STATE ( ) |
| 1. Sample_zone←,T) |
| ←RANDOM_VALUE (0,1) |
| ←Double_Rand ( ) |
| 5. else |
| ←; |
| 7. endif |
3.2.3. Reasonable Node Selection Strategy
3.2.4. Adaptive Node Extension Strategy
3.2.5. Post-Processing Strategy
| Algorithm 5: Adaptive Improved RRT POST_PROCESSING ( ) |
| : path |
| )←GET_PATH (T) |
| ←←; |
| ←) |
| ←) |
| do |
| ←←) |
| ∈ |
| ) |
| ); |
| 11. else |
| ); break |
| 13. end if |
| 14. end for |
| ∈∈ |
| ←←; |
| ); |
| ←←; a←k; break |
| 20. end if |
| 21. end for |
| ← |
| ←) |
| 24. endWhile |
| ) |
| 26. trajectory←) |
Path Pruning
Cubic B-Spline Smoothing Method
4. Simulation Experiments
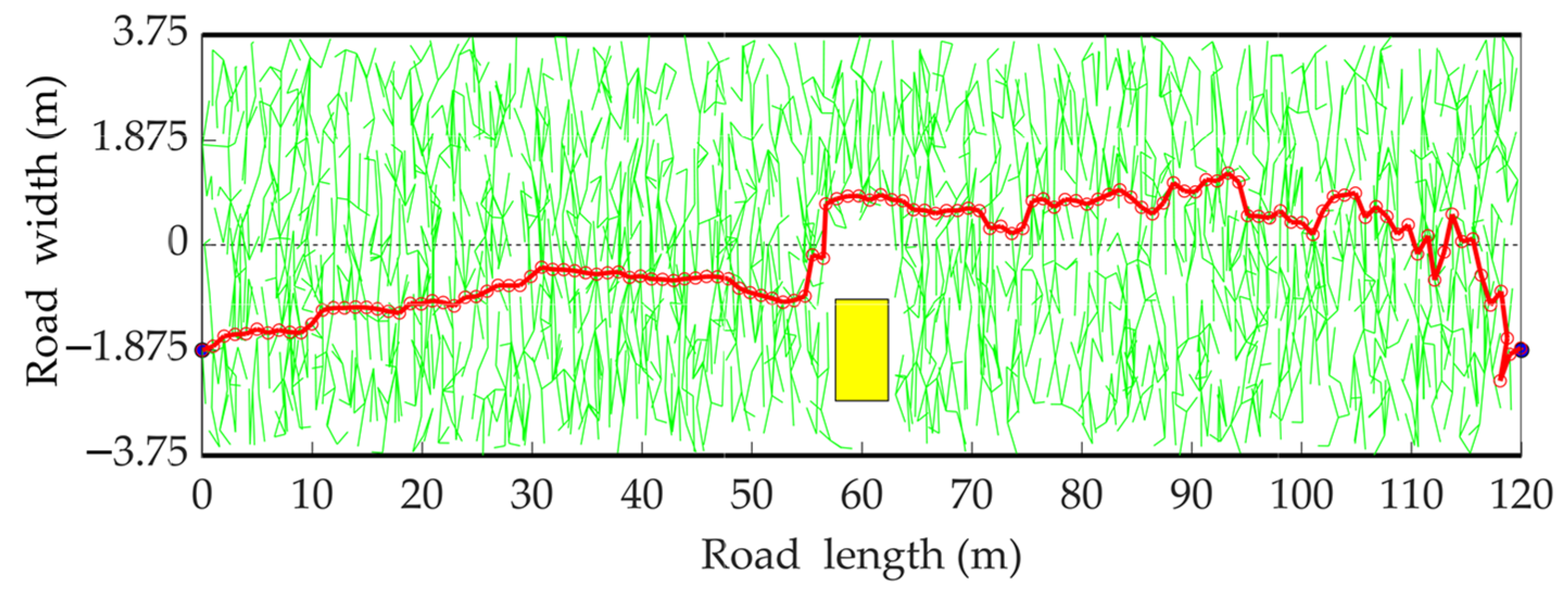
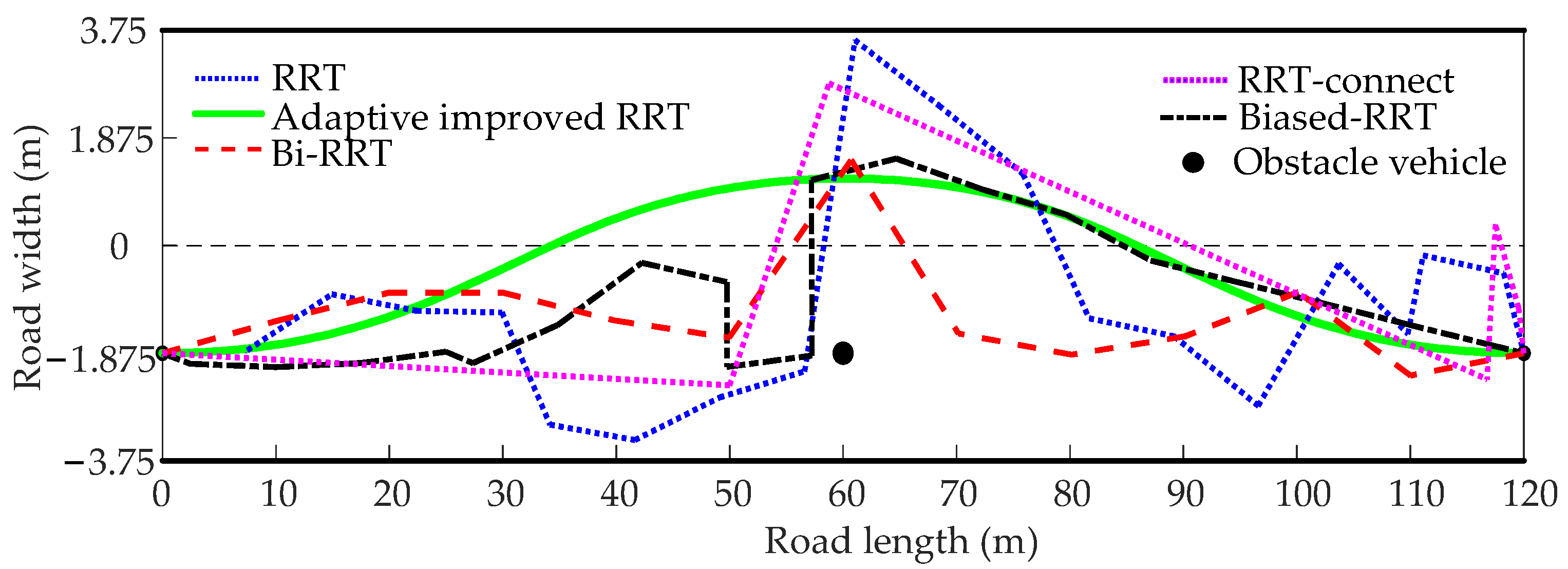
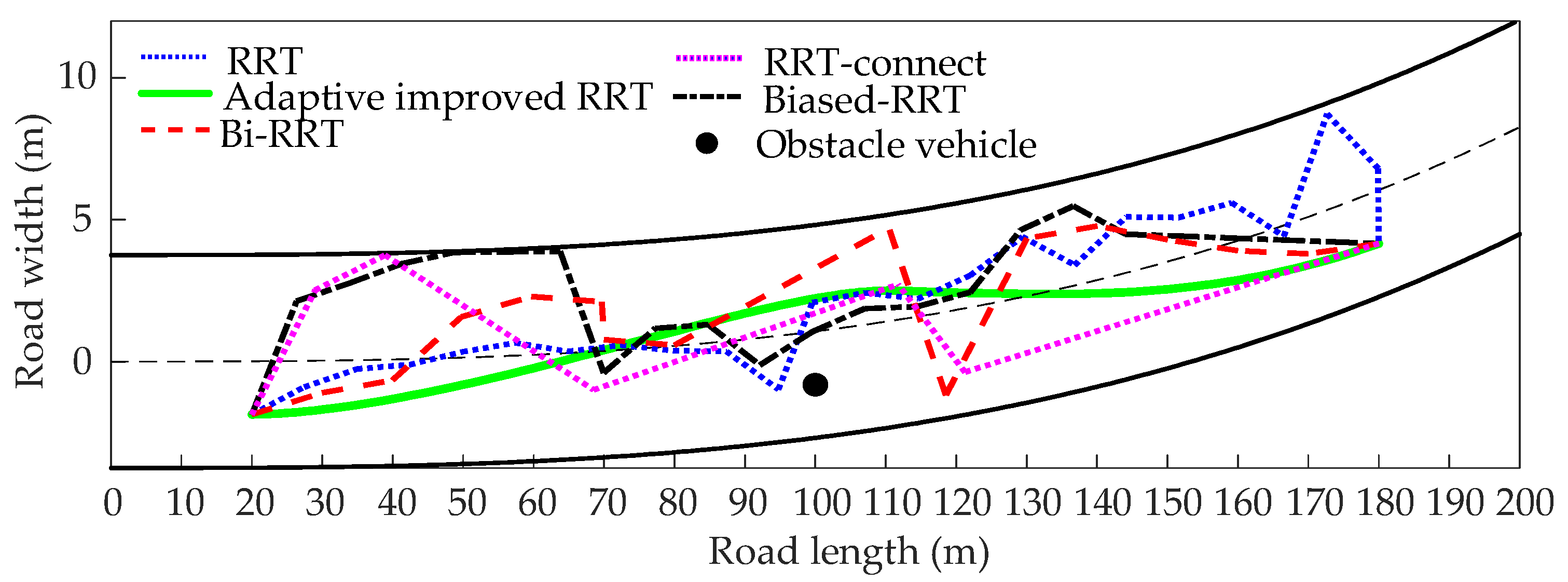
4.1. Performance Comparison of Several RRT Algorithms
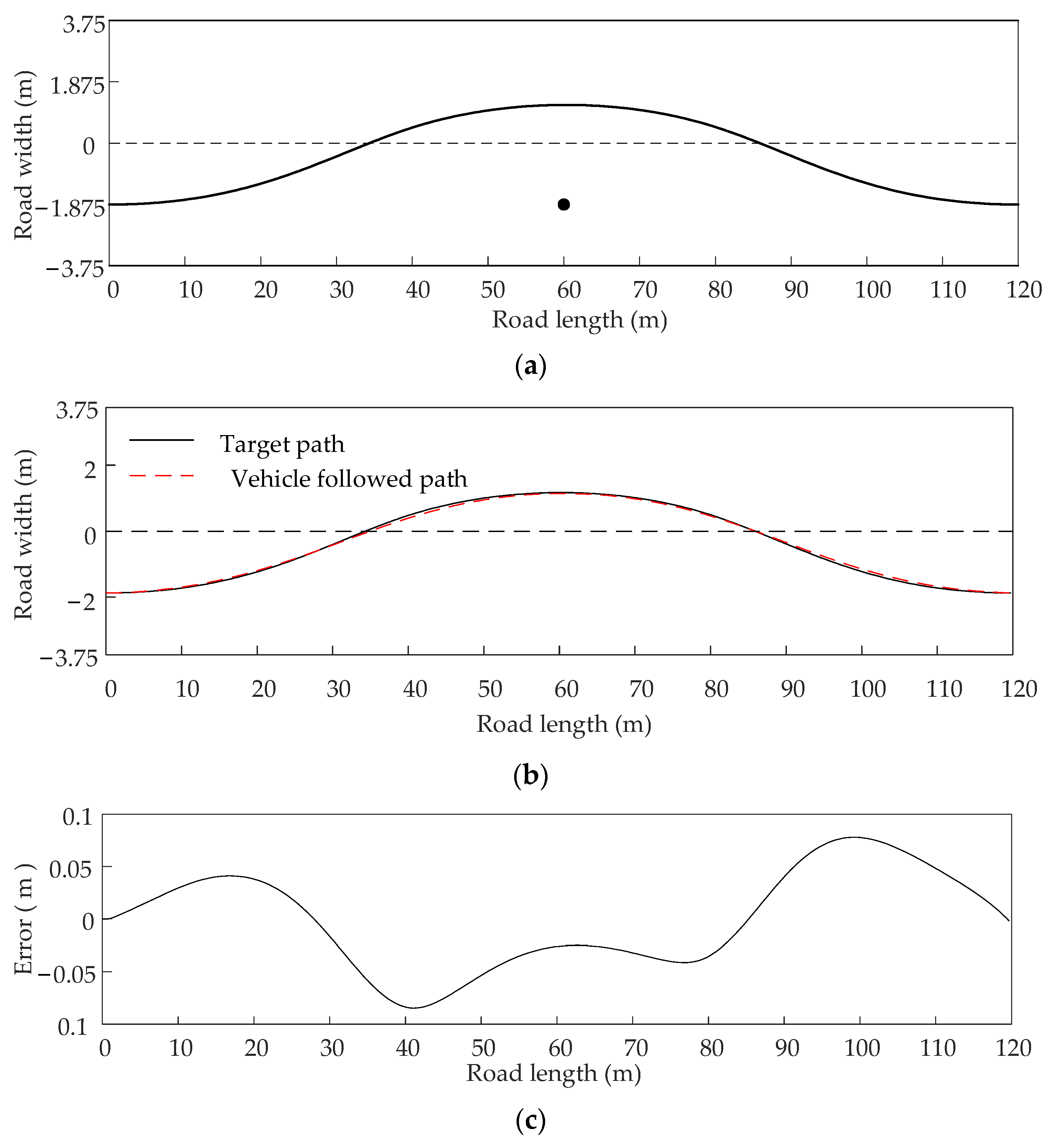
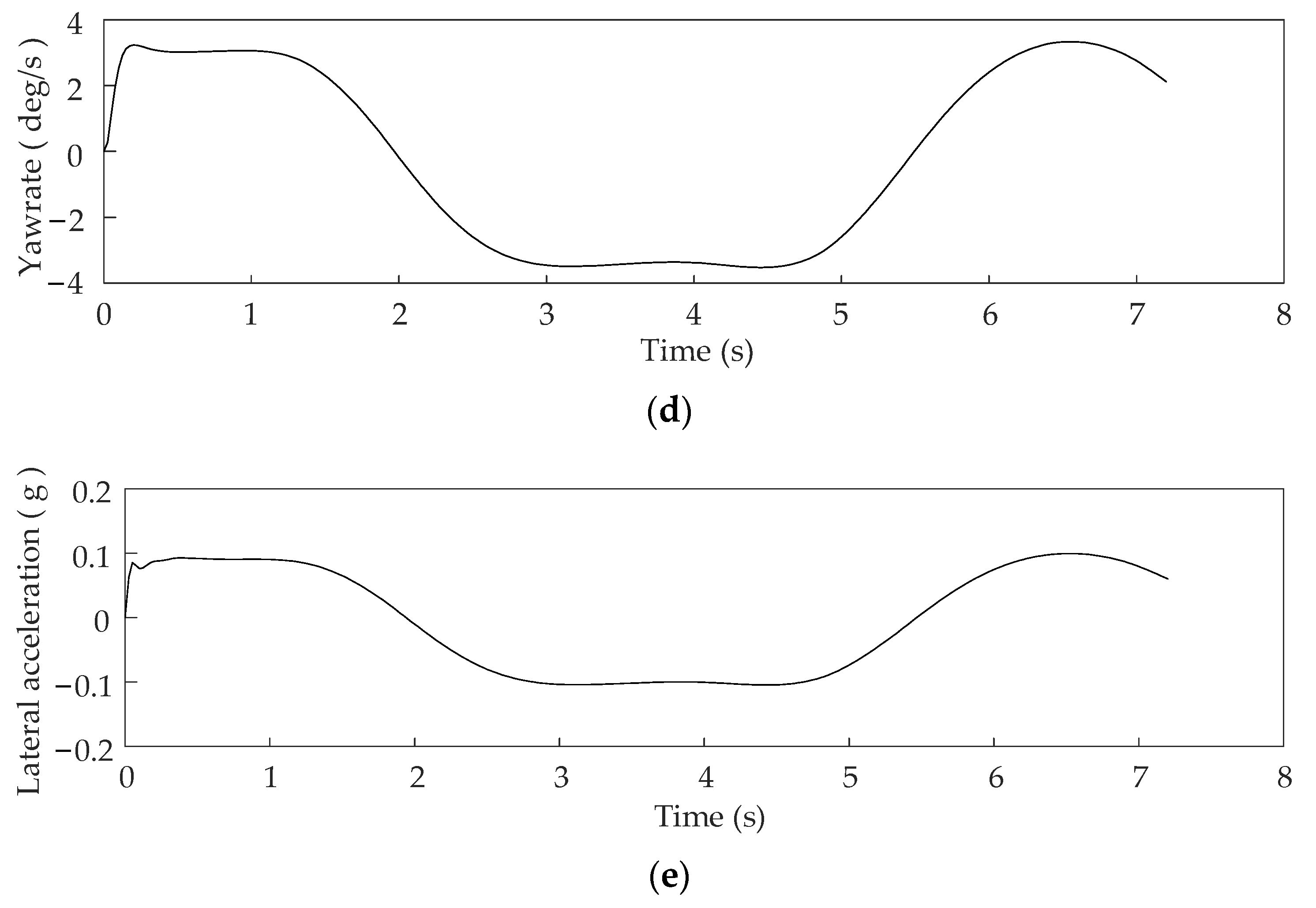
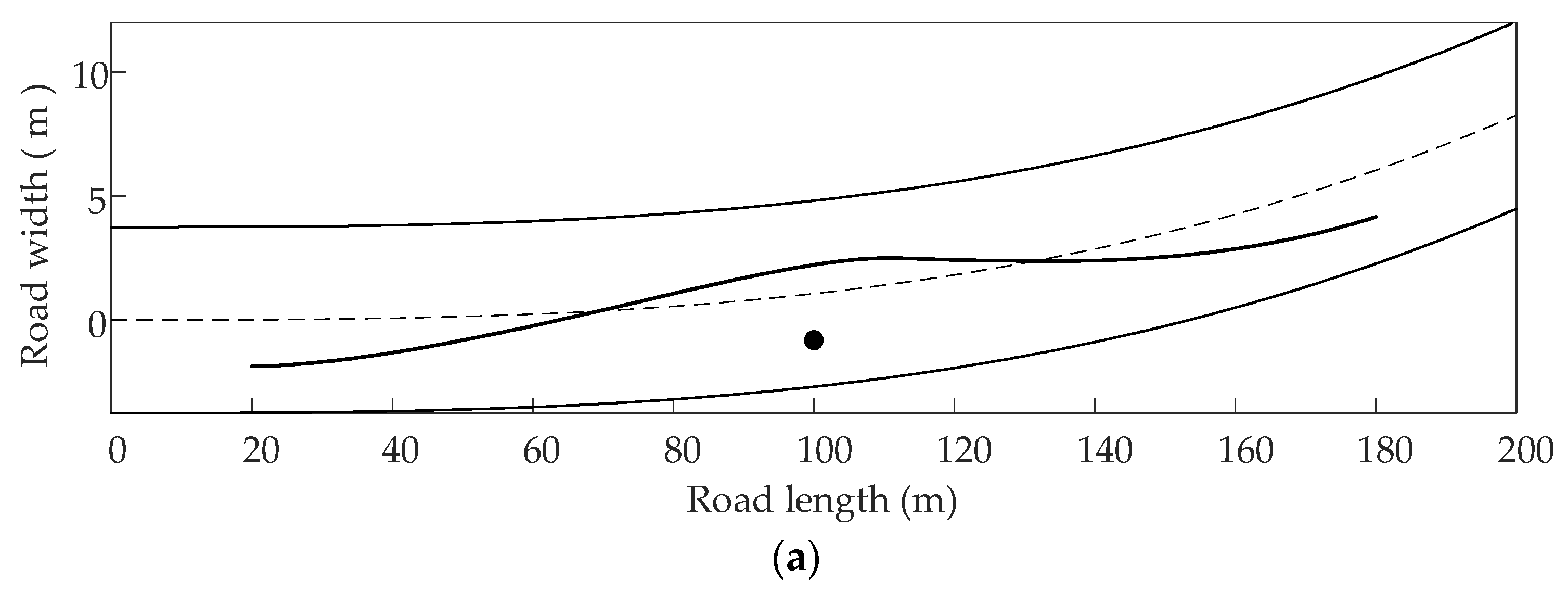
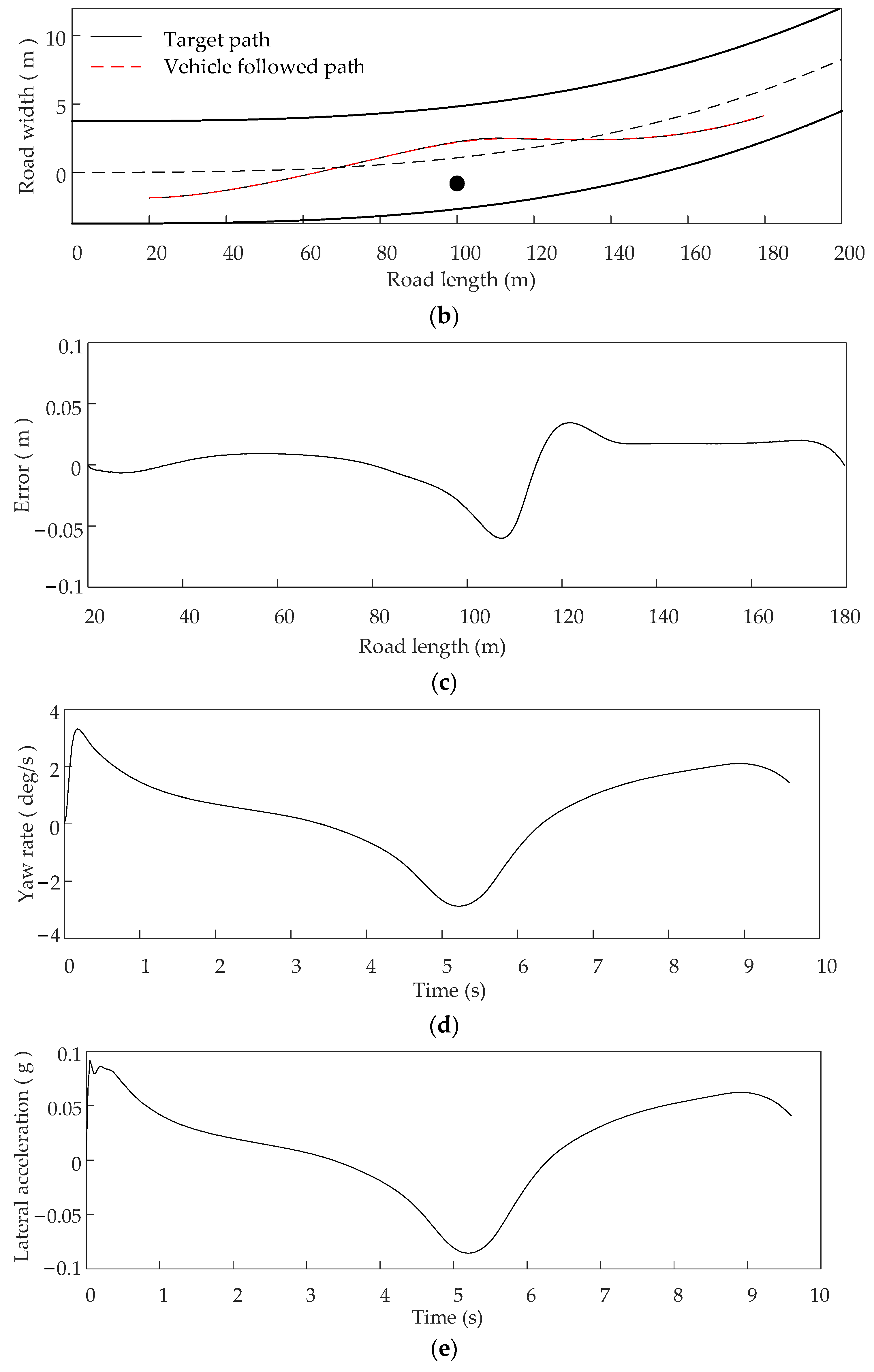
4.2. Path Following Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Malik, S.; Khattak, H.A.; Ameer, Z.; Shoaib, U.; Rauf, H.T.; Song, H. Proactive Scheduling and Resource Management for Connected Autonomous Vehicles: A Data Science Perspective. IEEE Sens. J. 2021, 21, 25151–25160. [Google Scholar] [CrossRef]
- Claussmann, L.; Revilloud, M.; Gruyer, D.; Glaser, S. A Review of Motion Planning for Highway Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1826–1848. [Google Scholar] [CrossRef] [Green Version]
- Hang, P.; Chen, X.B. Towards Autonomous Driving: Review and Perspectives on Configuration and Control of Four-Wheel Independent Drive/Steering Electric Vehicles. Actuators 2021, 10, 184. [Google Scholar] [CrossRef]
- Hnewa, M.; Radha, H. Object Detection Under Rainy Conditions for Autonomous Vehicles: A Review of State-of-the-Art and Emerging Techniques. IEEE Signal Process. Mag. 2021, 38, 53–67. [Google Scholar] [CrossRef]
- Kim, K.; Kim, J.S.; Jeong, S.; Park, J.H.; Kim, H.K. Cybersecurity for autonomous vehicles: Review of attacks and defense. Comput. Secur. 2021, 103, 27. [Google Scholar] [CrossRef]
- Li, X.C.; Zhu, S.; Aksun-Guvenc, B.; Guvenc, L. Development and Evaluation of Path and Speed Profile Planning and Tracking Control for an Autonomous Shuttle Using a Realistic, Virtual Simulation Environment. J. Intell. Robot. Syst. 2021, 101, 23. [Google Scholar] [CrossRef]
- Kim, J.; Jo, K.; Chu, K.; Sunwoo, M. Road-model-based and graph-structure-based hierarchical path-planning approach for autonomous vehicles. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2014, 228, 909–928. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 500–505. [Google Scholar]
- Qi, B.K.; Li, M.; Yang, Y.; Wang, X.Y. Research on UAV path planning obstacle avoidance algorithm based on improved artificial potential field method. 2nd International Conference on Internet of Things. In Proceedings of the Artificial Intelligence and Mechanical Automation, Hangzhou, China, 14–16 May 2021; Volume 1948, p. 012060. [Google Scholar]
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C.A. Motion Planning and Tracking Framework for Autonomous Vehicles Based on Artificial Potential Field-Elaborated Resistance Network Approach. IEEE Trans. Ind. Electron. 2020, 67, 1376–1386. [Google Scholar] [CrossRef]
- Sang, H.; You, Y.; Sun, X.; Zhou, Y.; Liu, F. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations. Ocean. Eng. 2021, 223, 108709. [Google Scholar] [CrossRef]
- Song, X.L.; Cao, H.T.; Huang, J. Vehicle path planning in various driving situations based on the elastic band theory for highway collision avoidance. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2013, 227, 1706–1722. [Google Scholar] [CrossRef]
- Zhang, H.M.; Li, M.L. Rapid path planning algorithm for mobile robot in dynamic environment. Adv. Mech. Eng. 2017, 9, 12. [Google Scholar] [CrossRef]
- Liu, L.S.; Lin, J.F.; Yao, J.X.; He, D.W.; Zheng, J.S.; Huang, J.; Shi, P. Path Planning for Smart Car Based on Dijkstra Algorithm and Dynamic Window Approach. Wirel. Commun. Mob. Comput. 2021, 2021, 12. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Y. Mobile Robot Path Planning Algorithm Based on Improved a Star. In Proceedings of the 4th International Conference on Advanced Algorithms and Control Engineering, Sanya, China, 29–31 January 2021; Volume 1848, p. 012013. [Google Scholar]
- Desaraju, V.R.; How, J.P. Decentralized path planning for multiple agents in complex environments using rapidly-exploring random trees. In Proceedings of the IEEE International Conference on Robotics & Automation, Shanghai, China, 9–13 May 2011; pp. 4956–4961. [Google Scholar]
- Palmieri, L.; Kai, O.A. Distance metric learning for RRT-based motion planning with constant-time inference. In Proceedings of the IEEE International Conference on Robotics and Automation, Seattle, WA, USA, 26–30 May 2015; pp. 637–643. [Google Scholar]
- Jaillet, L.; Cortés, J.; Siméon, T. Sampling-Based Path Planning on Configuration-Space Costmaps. IEEE Trans. Robot 2010, 26, 635–646. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.Y.; Zhang, X.B.; Wen, J.; Wang, R.H.; Chen, X. Goal-biased Bidirectional RRT based on Curve-smoothing. In Proceedings of the 5th IFAC Symposium on Telematics Applications, Chengdu, China, 25–27 September 2019; Volume 52, pp. 255–260. [Google Scholar]
- Meng, L.; Song, Q.; Zhao, Q.J. UAV path re-planning based on improved bidirectional RRT algorithm in dynamic environment. In Proceedings of the 3rd IEEE International Conference on Control, Automation and Robotics, Nagoya, Japan, 22–24 April 2017; pp. 658–661. [Google Scholar]
- Wei, K.; Ren, B. A Method on Dynamic Path Planning for Robotic Manipulator Autonomous Obstacle Avoidance Based on an Improved RRT Algorithm. Sensors 2018, 18, 571. [Google Scholar] [CrossRef] [Green Version]
- Yang, K. Anytime synchronized-biased-greedy rapidly-exploring random tree path planning in two dimensional complex environments. Int. J. Control Autom. Syst. 2011, 9, 750–758. [Google Scholar] [CrossRef]
- Chen, L.; Shan, Y.; Tian, W.; Li, B.; Cao, D. A Fast and Efficient Double-Tree RRT* Like Sampling-Based Planner Applying on Mobile Robotic Systems. IEEE/ASME Trans. Mechatron. 2018, 24, 2568–2578. [Google Scholar] [CrossRef]
- Kang, J.G.; Lim, D.W.; Choi, Y.S.; Jang, W.J.; Jung, J.W. Improved RRT-Connect Algorithm Based on Triangular Inequality for Robot Path Planning. Sensors 2021, 21, 333. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.; Kim, H.J. Planning and Control for Collision-Free Cooperative Aerial Transportation. IEEE Trans. Autom. Sci. Eng. 2018, 15, 189–201. [Google Scholar] [CrossRef]
- Rodriguez, S.; Tang, X.; Lien, J.M.; Amato, N.M. An obstacle-based rapidly-exploring random tree. In Proceedings of the IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; pp. 895–900. [Google Scholar]
- Gan, Y.; Zhang, B.; Ke, C.; Zhu, X.; He, W.; Ihara, T. Research on Robot Motion Planning Based on RRT Algorithm with Nonholonomic Constraints. Neural Process. Lett. 2021, 53, 3011–3029. [Google Scholar] [CrossRef]
- Chen, J.G.; Zhao, Y.; Xu, X. Improved RRT-Connect Based Path Planning Algorithm for Mobile Robots. IEEE Access. 2021, 9, 145988–145999. [Google Scholar] [CrossRef]
- Ge, Q.; Li, A.; Li, S.; Du, H.; Huang, X.; Niu, C. Improved Bidirectional RRT * Path Planning Method for Smart Vehicle. Math. Probl. Eng. 2021, 2021, 6669728. [Google Scholar] [CrossRef]
- Kuwata, Y.; Teo, J.; Fiore, G.; Karaman, S.; Frazzoli, E.; How, J.P. Real-time motion planning with applications to autonomous urban driving. IEEE Trans. Control Syst. Technol. 2009, 17, 1105–1118. [Google Scholar] [CrossRef]
- Lau, B.; Sprunk, C.; Burgard, W. Kinodynamic motion planning for mobile robots using splines. In Proceedings of the IEEE RSJ International Conference on Intelligent Robots and Systems, St Louis, MO, USA, 10–15 October 2009; pp. 2427–2433. [Google Scholar]
- Thanh, P.H.; Nguyen, V.H.; Konigorski, U. A Time-optimal Trajectory Generation Approach with Non-uniform B-splines. Int. J. Control Autom. Syst. 2021, 19, 3947–3955. [Google Scholar]
- Pappas, G.J.; Kyriakopoulos, K.J. Stabilization of non-holonomic vehicles under kinematic constraints. Int. J. Control 1995, 61, 933–947. [Google Scholar] [CrossRef]
- Rodrigues, R.T.; Aguiar, A.P.; Pascoal, A. A coverage planner for AUVs using B-splines. In Proceedings of the IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018; pp. 1–6. [Google Scholar]
- Noreen, I. Collision Free Smooth Path for Mobile Robots in Cluttered Environment Using an Economical Clamped Cubic B-Spline. Symmetry 2020, 12, 1567. [Google Scholar] [CrossRef]
- Elbanhawi, M.; Simic, M.; Jazar, R. Continuous-curvature bounded trajectory planning using parametric splines. In Proceedings of the KES International Conference on Smart Digital Futures, Chania, Greece, 18–20 June 2014; Volume 262, pp. 513–522. [Google Scholar]


| Road Type | Road Length (m) | Single Lane Width (m) | Initial Point | Target Point | Obstacle Point |
|---|---|---|---|---|---|
| Straight | 120 | 3.75 | 0, −1.875 | 120, −1.875 | 60, −1.875 |
| Curve | 200 | 3.75 | 20, −1.865 | 180, 4.160 | 100, −0.813 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Obstacle vehicle width (m) | 1.8 | Terminal step size δ (m) | 20 |
| Obstacle vehicle length (m) | 4.8 | Constraint angle (°) | 30 |
| Expansion coefficient | Weighted coefficient | 0.5 | |
| Friction coefficient | 0.8 | Weighted coefficient | 0.5 |
| Acceleration of gravity (m/s2) | 9.8 | Weighted coefficient | 0.5 |
| Host vehicle speed (km/h) | 60 | Weighted coefficient | 0.7 |
| Biased probability | 0.1 | Weighted coefficient | 0.3 |
| Maximum step size (m) | 20 |
| Algorithm | Node | Length | Segment | Time |
|---|---|---|---|---|
| Basic | 37.47 | 124.435 | 15.7 | 0.026 |
| Biased | 25.77 | 122.746 | 11.57 | 0.017 |
| Bi | 14.90 | 122.105 | 10.03 | 0.016 |
| Connect | 10.50 | 124.378 | 4.43 | 0.011 |
| Adaptive-Improved | 22.50 | 120.290 | 5.23 | 0.024 |
| Algorithm | Node | Length | Segment | Time |
|---|---|---|---|---|
| Basic | 26.93 | 162.634 | 16.57 | 1.755 |
| Biased | 21.13 | 161.884 | 14.10 | 1.411 |
| Bi | 14.00 | 161.032 | 12.13 | 0.386 |
| Connect | 4.87 | 162.243 | 3.30 | 0.299 |
| Adaptive-Improved | 26.37 | 160.141 | 4.23 | 3.257 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhu, T.; Xu, Y.; Liu, H.; Liu, F. Local Path Planning of the Autonomous Vehicle Based on Adaptive Improved RRT Algorithm in Certain Lane Environments. Actuators 2022, 11, 109. https://doi.org/10.3390/act11040109
Zhang X, Zhu T, Xu Y, Liu H, Liu F. Local Path Planning of the Autonomous Vehicle Based on Adaptive Improved RRT Algorithm in Certain Lane Environments. Actuators. 2022; 11(4):109. https://doi.org/10.3390/act11040109
Chicago/Turabian StyleZhang, Xiao, Tong Zhu, Yu Xu, Haoxue Liu, and Fei Liu. 2022. "Local Path Planning of the Autonomous Vehicle Based on Adaptive Improved RRT Algorithm in Certain Lane Environments" Actuators 11, no. 4: 109. https://doi.org/10.3390/act11040109
APA StyleZhang, X., Zhu, T., Xu, Y., Liu, H., & Liu, F. (2022). Local Path Planning of the Autonomous Vehicle Based on Adaptive Improved RRT Algorithm in Certain Lane Environments. Actuators, 11(4), 109. https://doi.org/10.3390/act11040109





