Analysis of Magnetic Field Characteristics of a Giant Magnetostrictive Actuator with a Semi-Closed Magnetic Circuit
Abstract
:1. Introduction
2. Principles and Methods
2.1. Basic Theory of Model Solving
2.2. COMSOL Multiphysics Finite Element Model Establishment
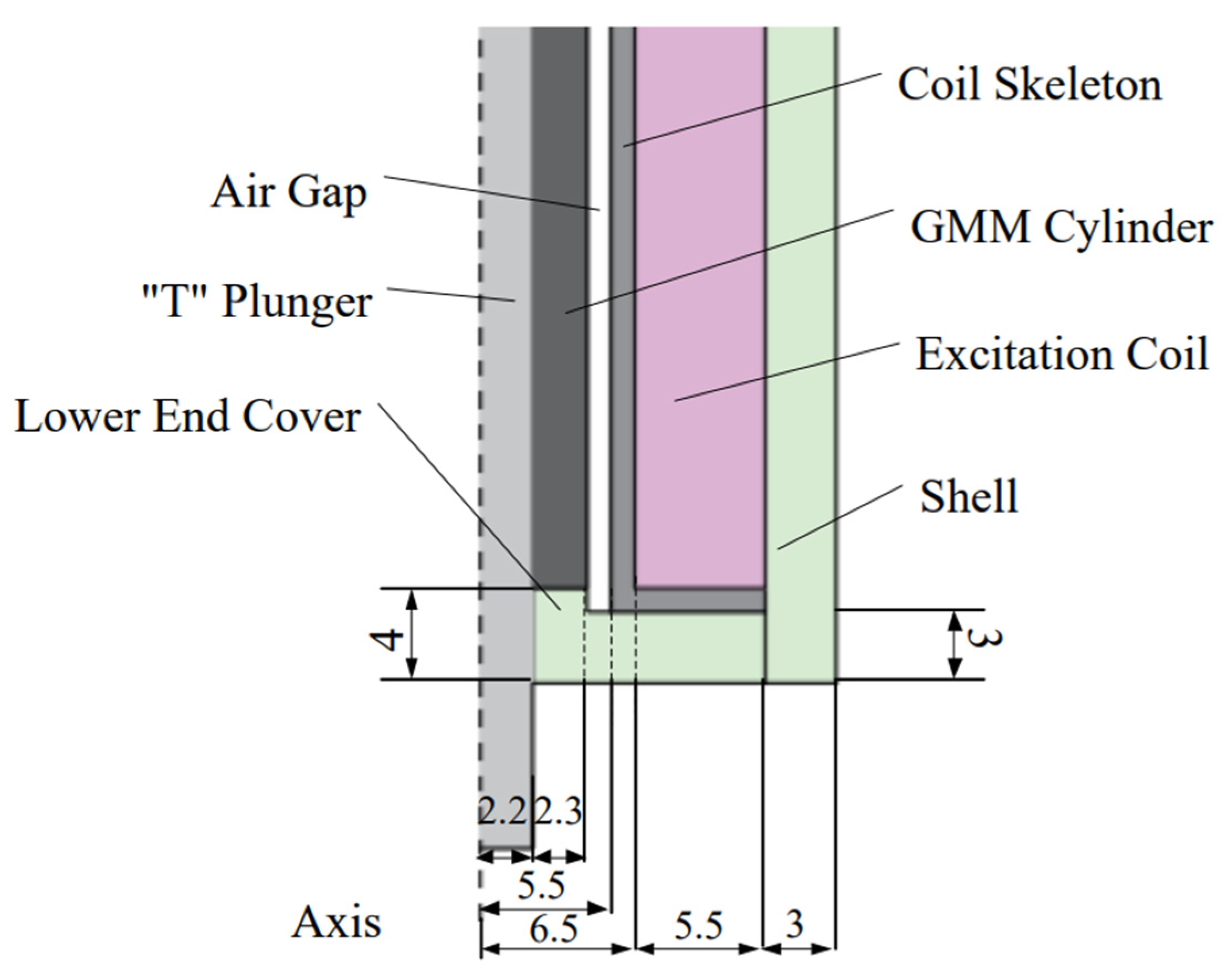
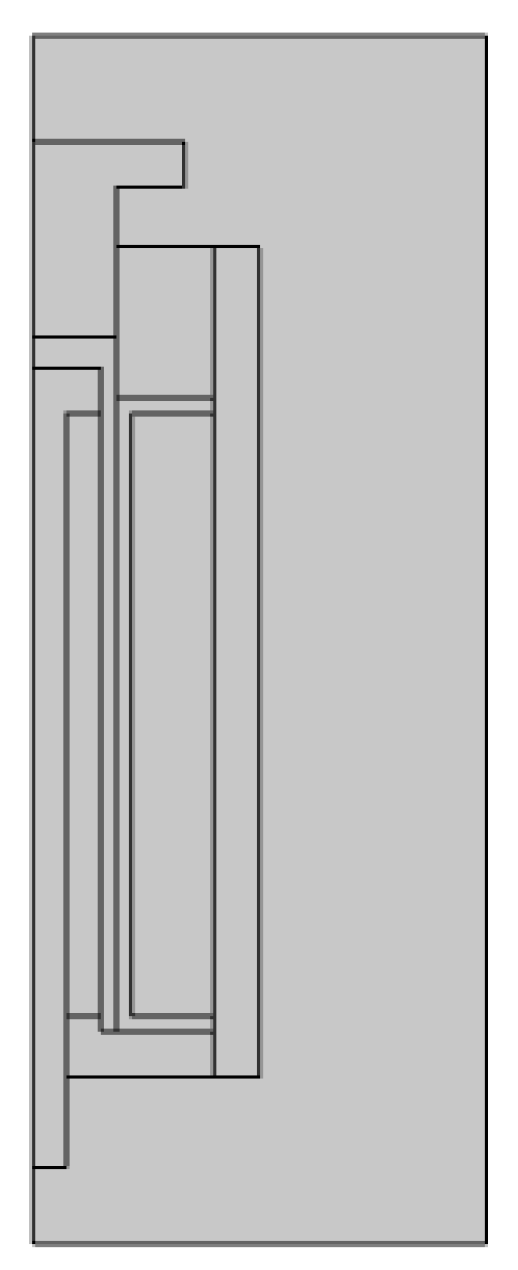
2.2.1. Finite Element Model
2.2.2. Setting Boundary Conditions and Loads
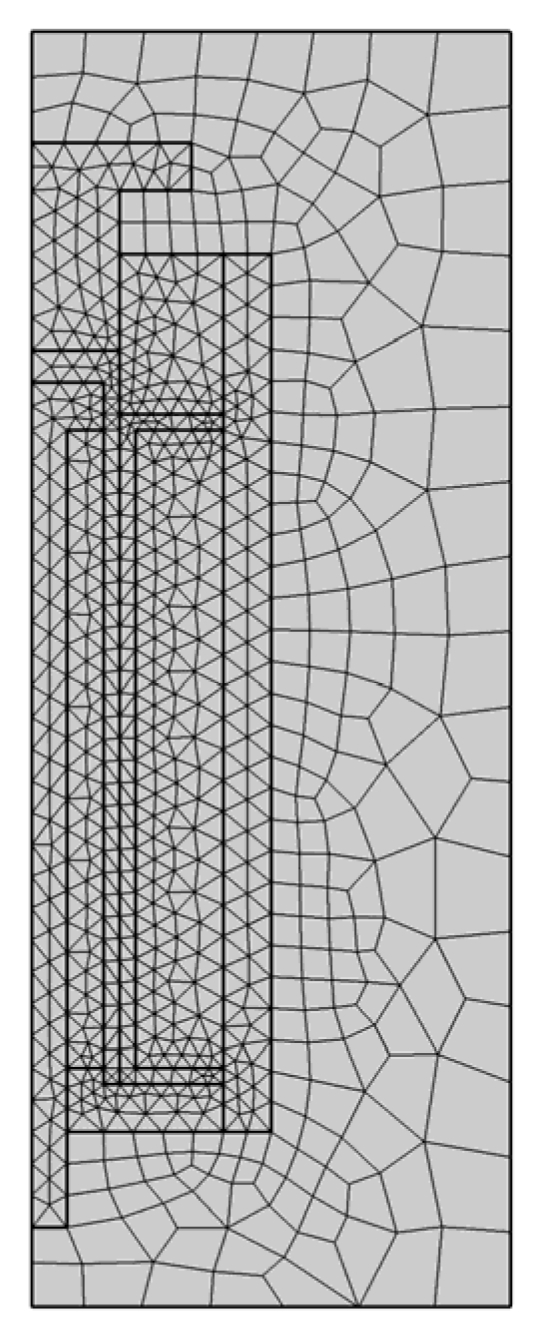
2.2.3. Meshing
2.2.4. Model Solution and Postprocessing
2.3. Establishing a Coordinate System
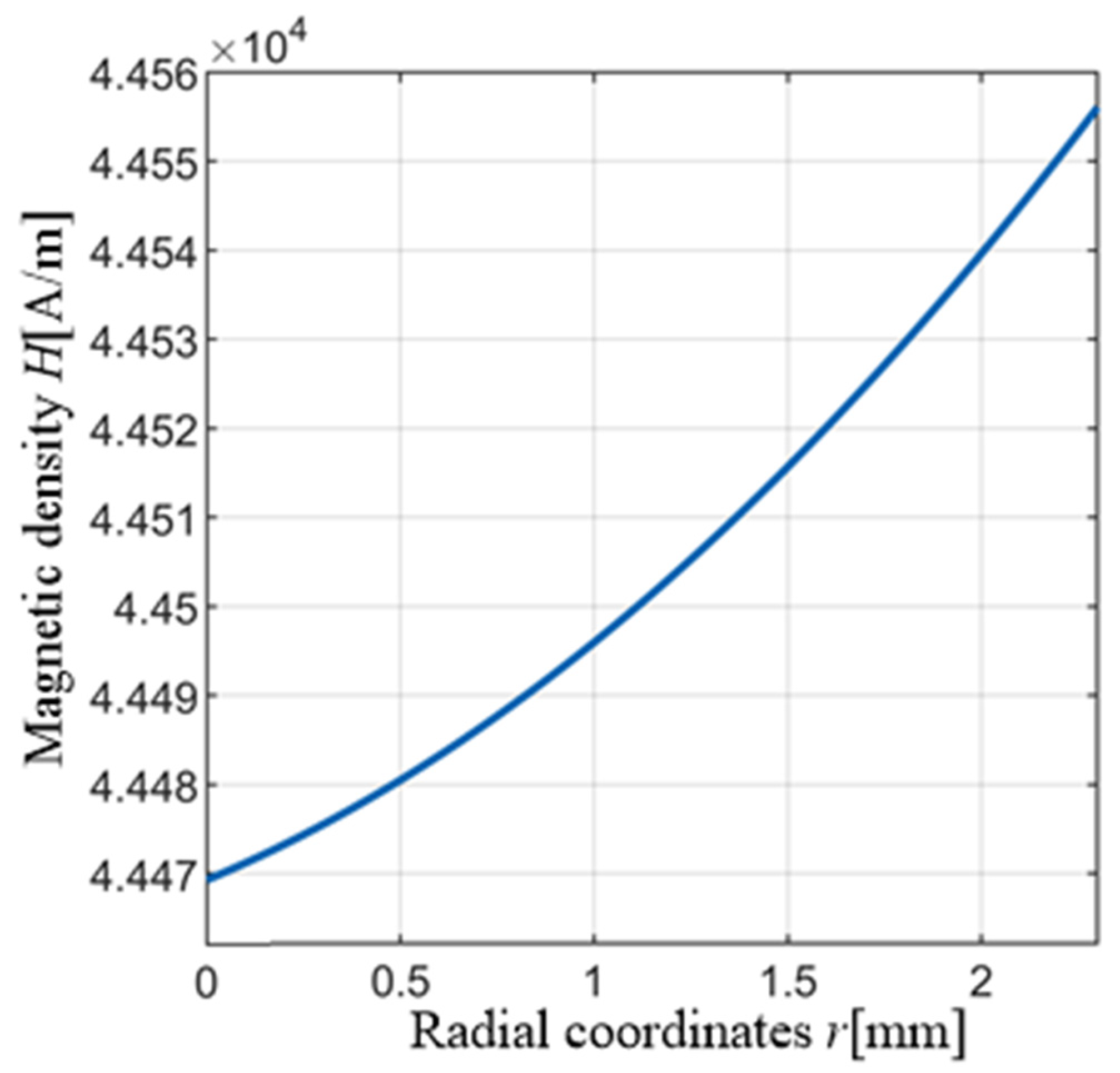
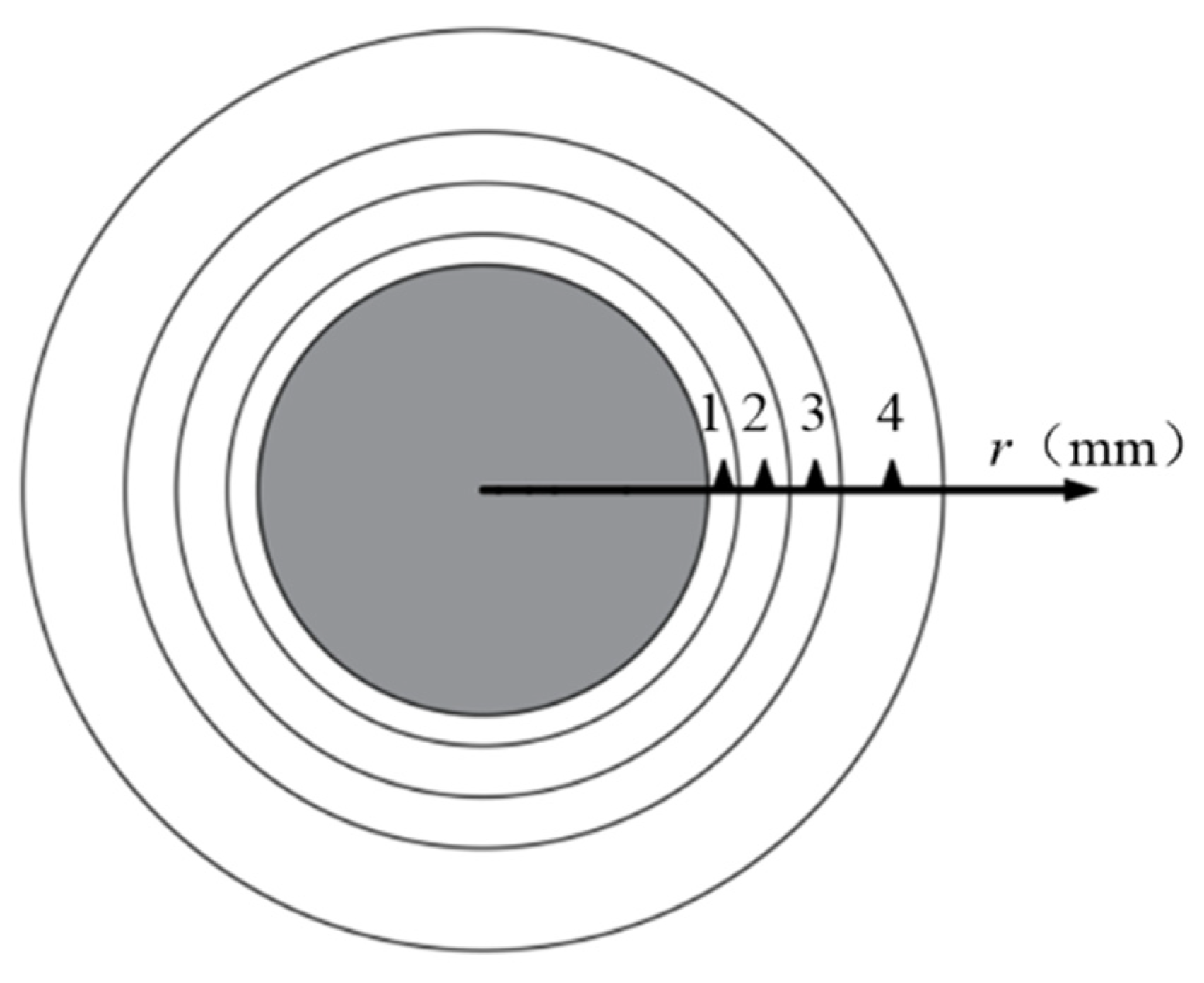
2.4. Solving the Cross-Sectional Magnetic Density
3. Results and Discussion
3.1. Simulation Verification
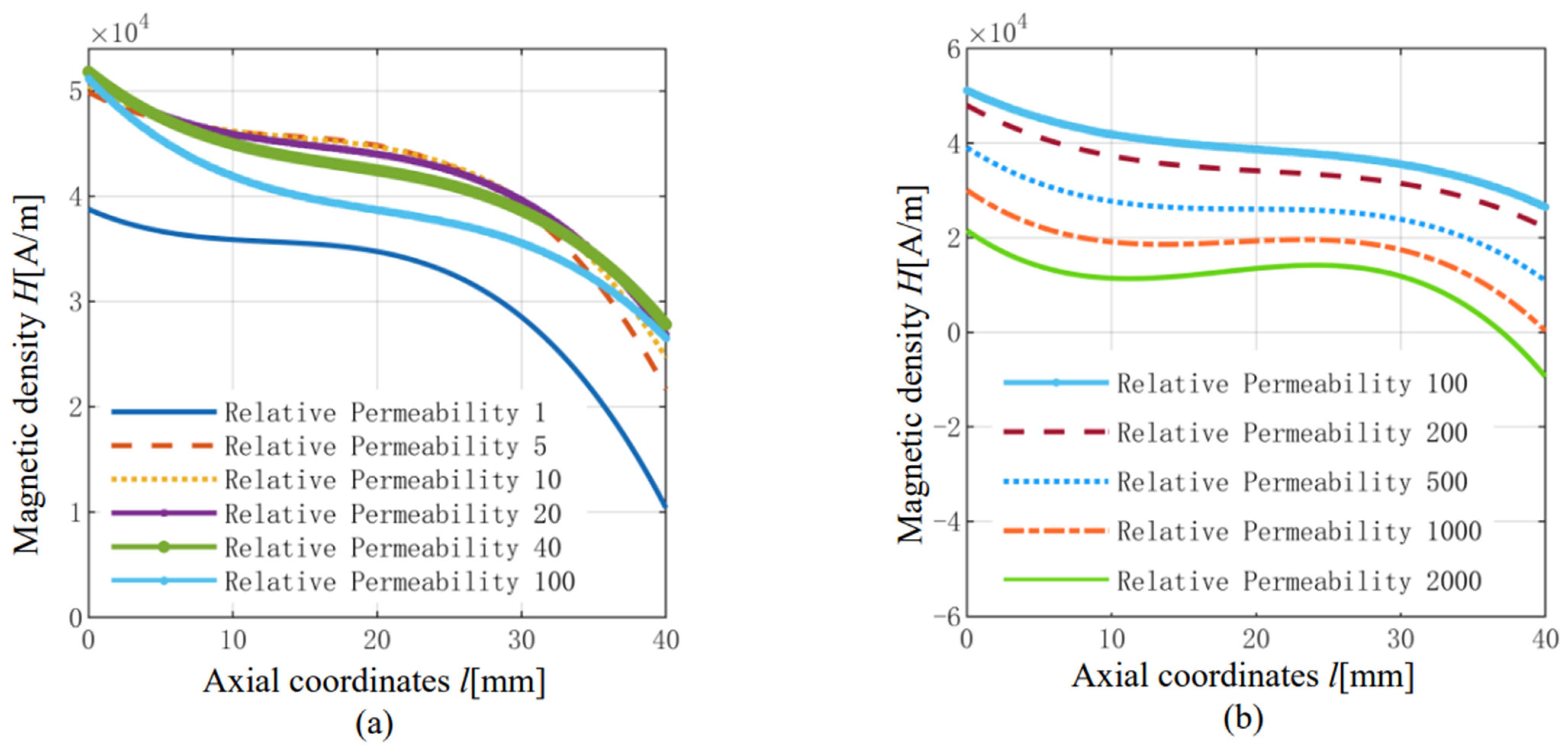
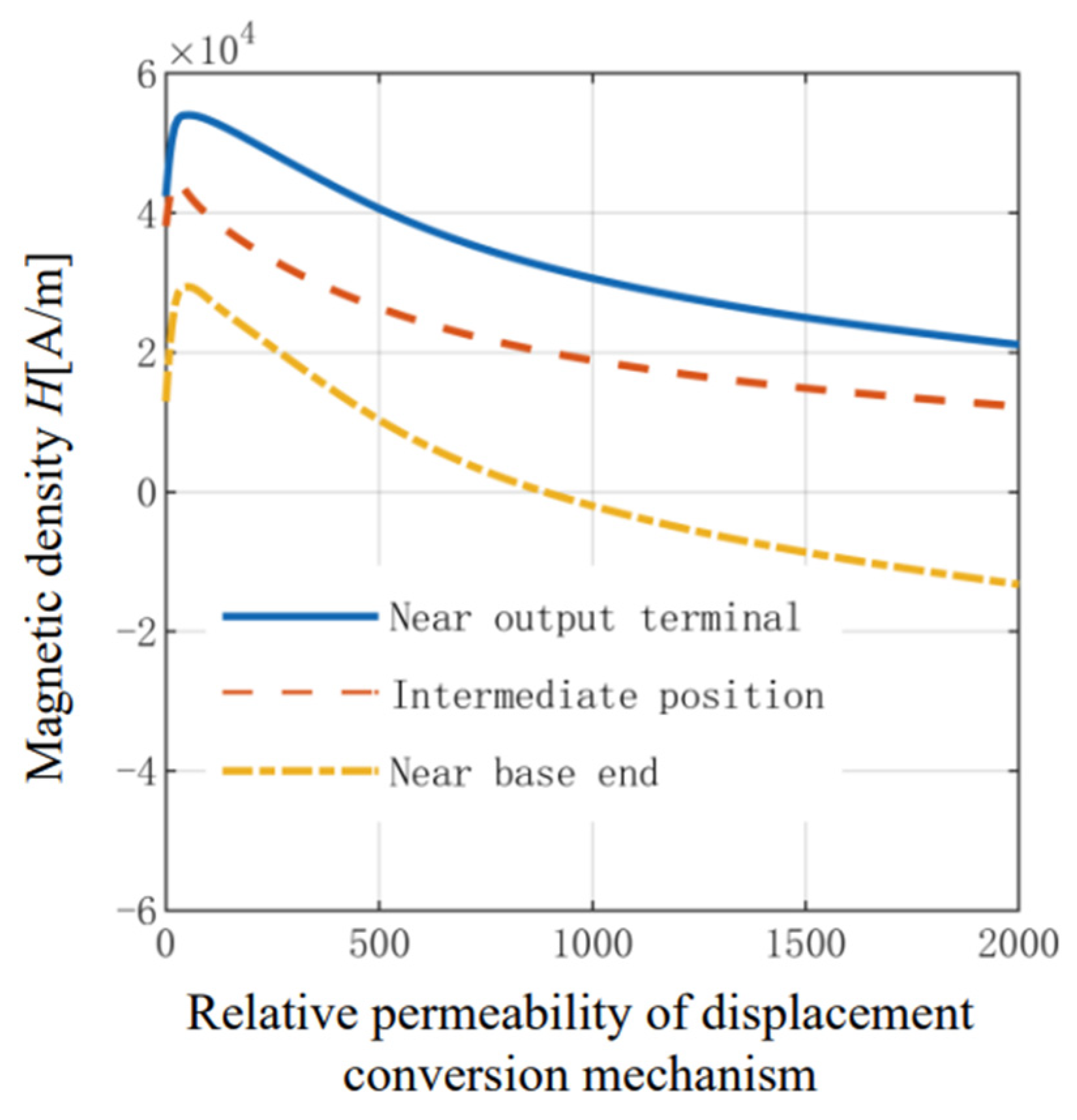
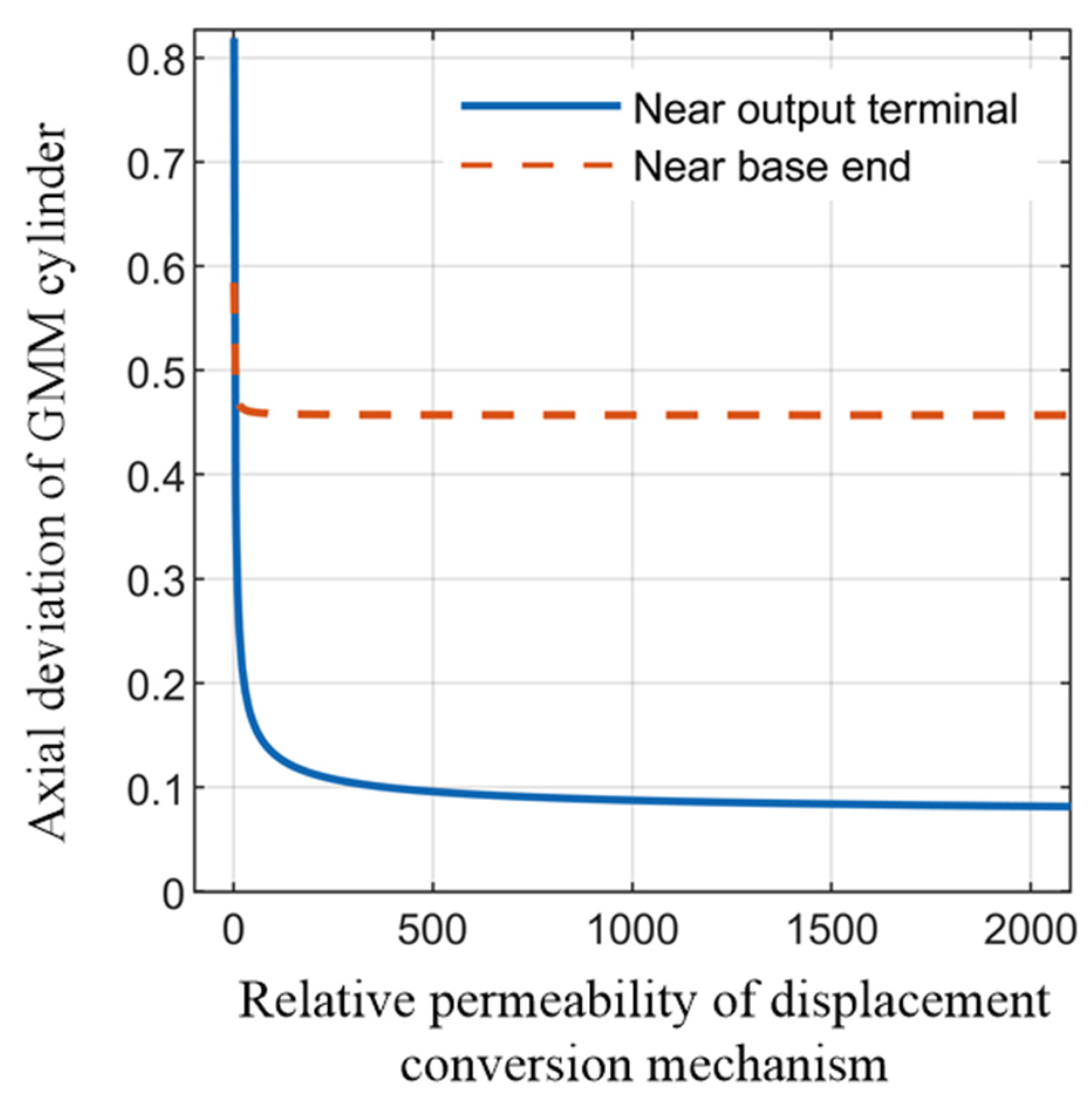
3.1.1. Influence of Displacement Conversion Mechanism on Magnetic Field Distribution Characteristic
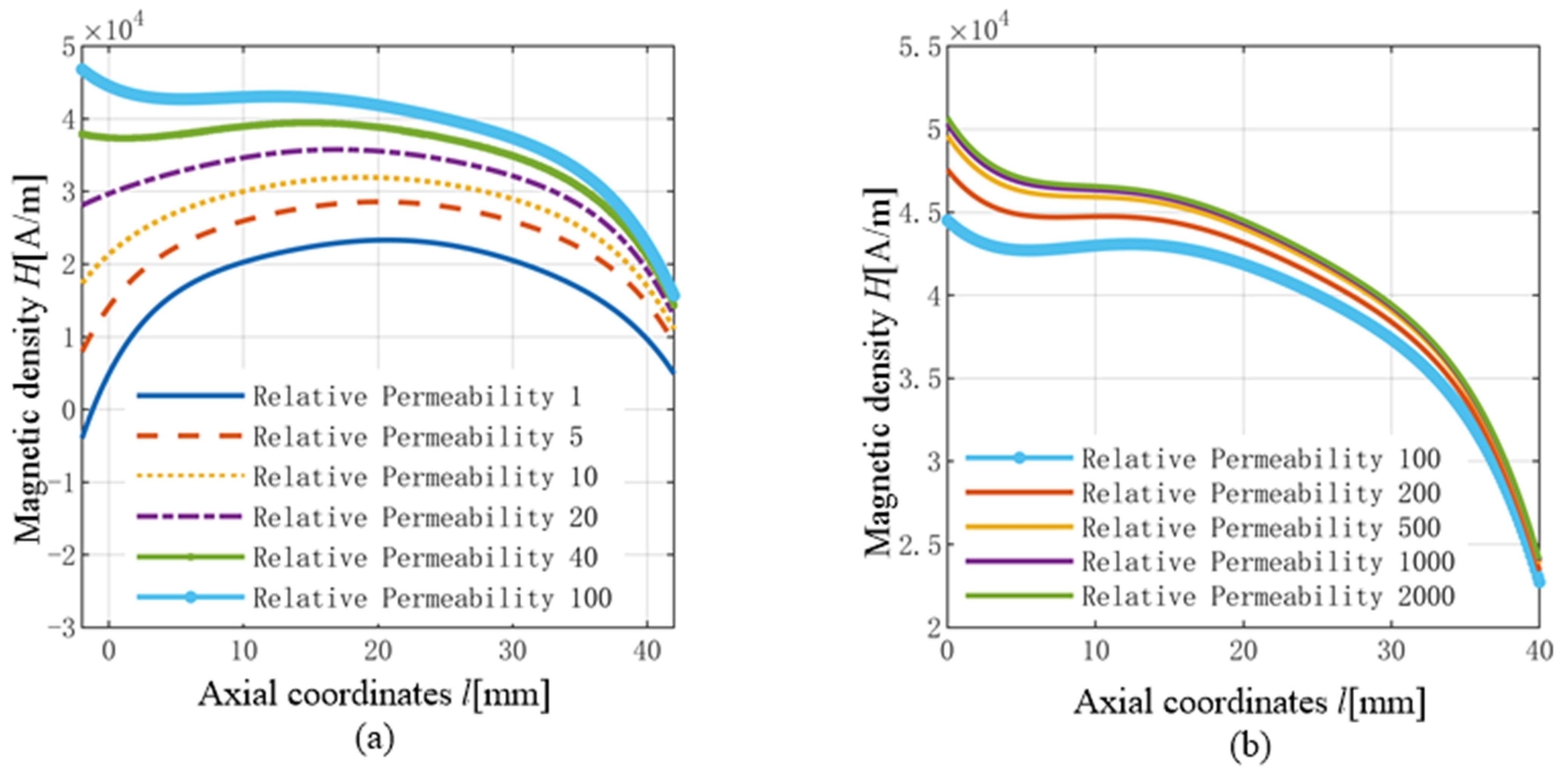
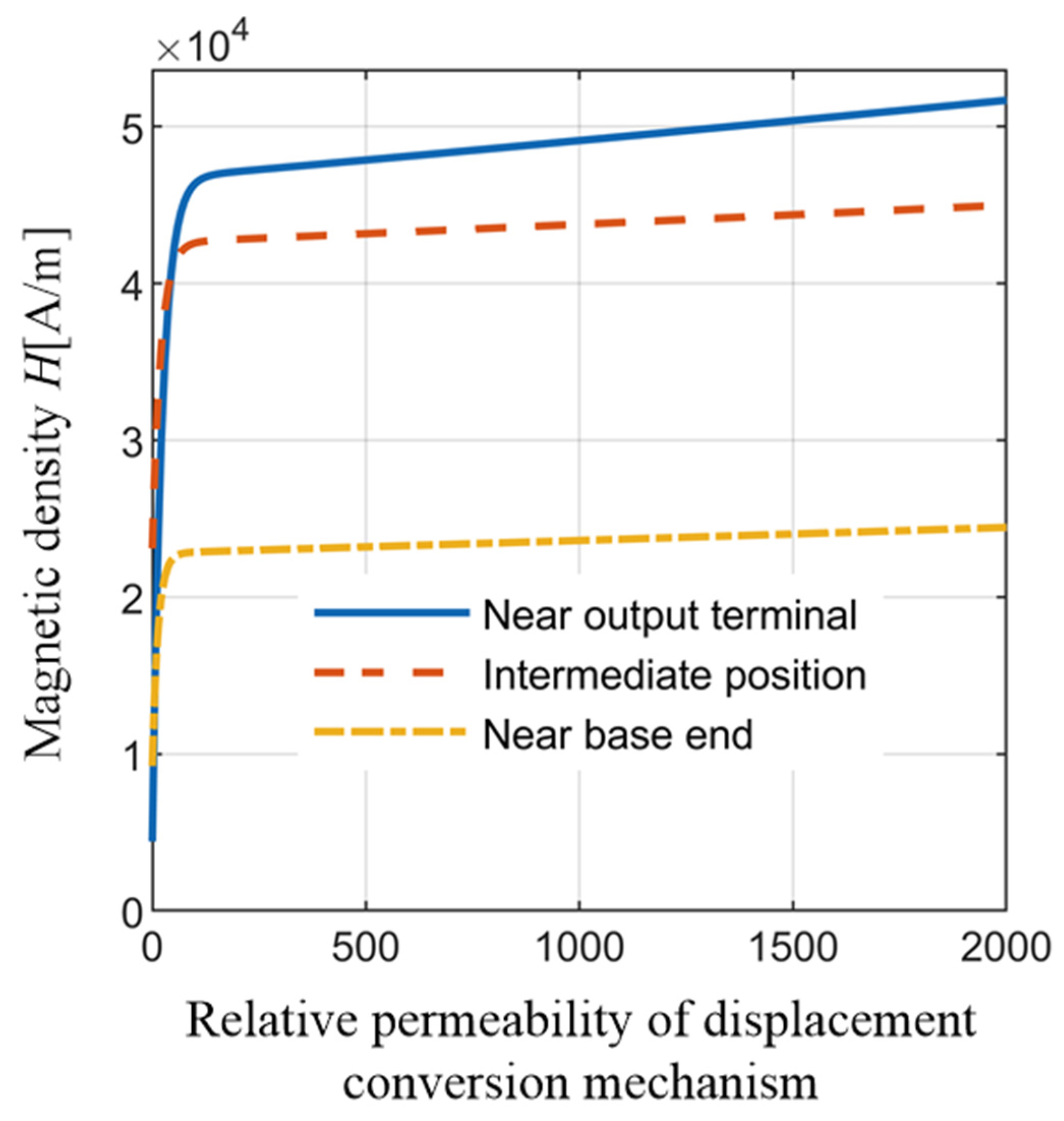
3.1.2. Influence of Shell on Magnetic Field Distribution Characteristic
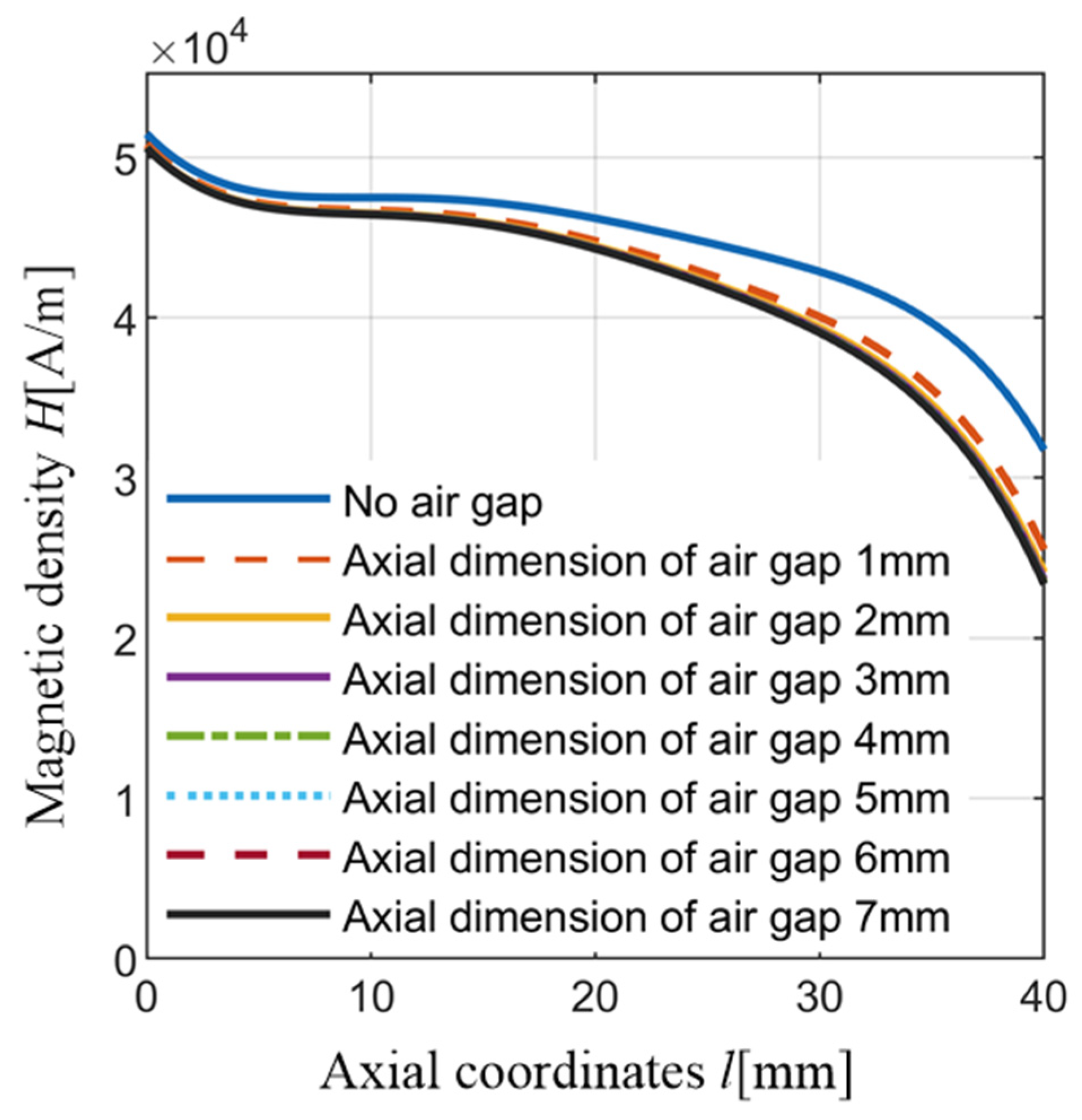
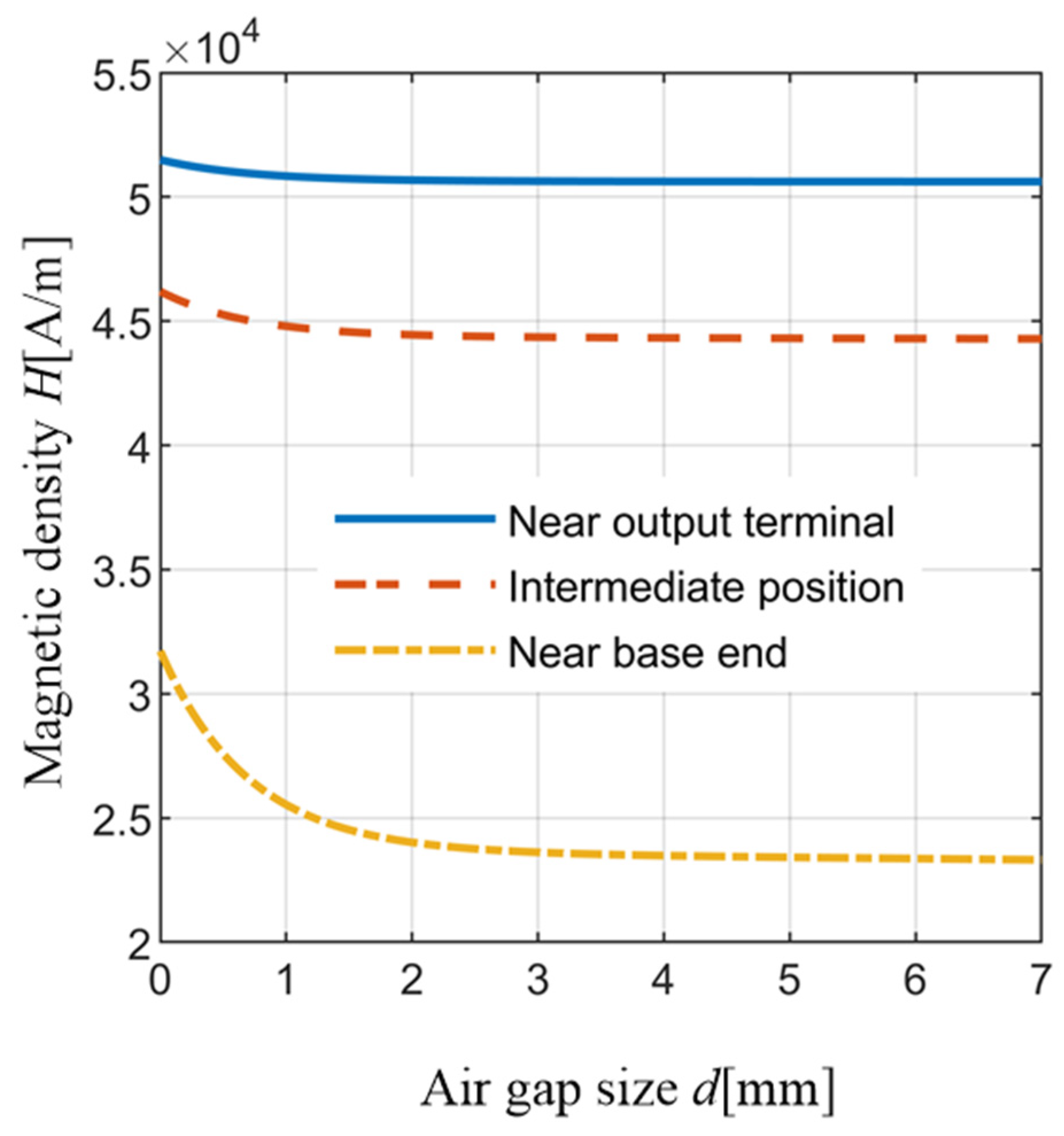
3.1.3. Influence of Air Gap Geometry on Axial Magnetic Density of GMM Cylinder
3.2. Experimental Verification
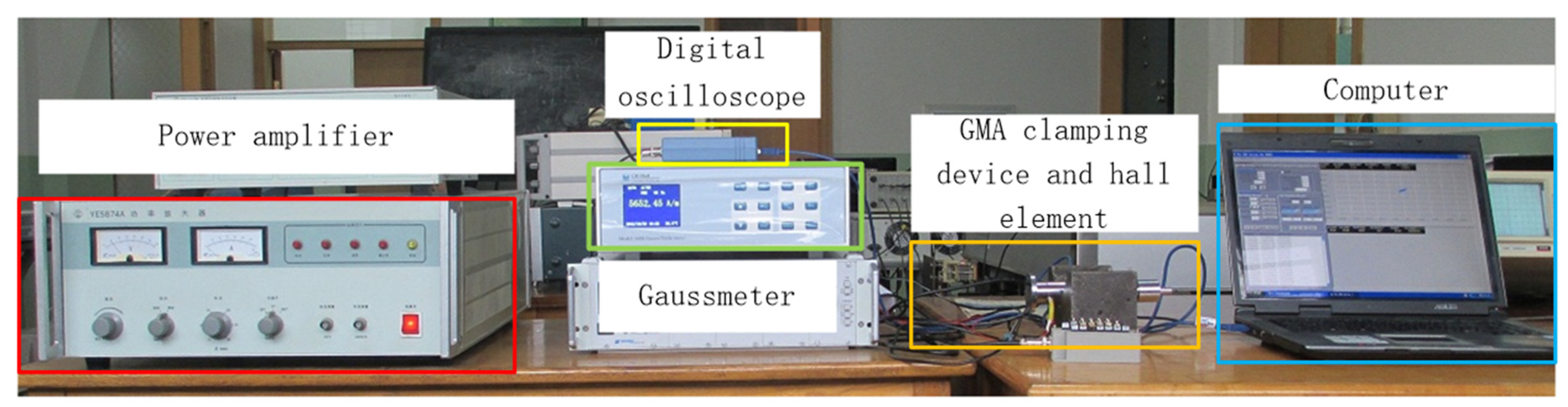
3.2.1. Experimental System
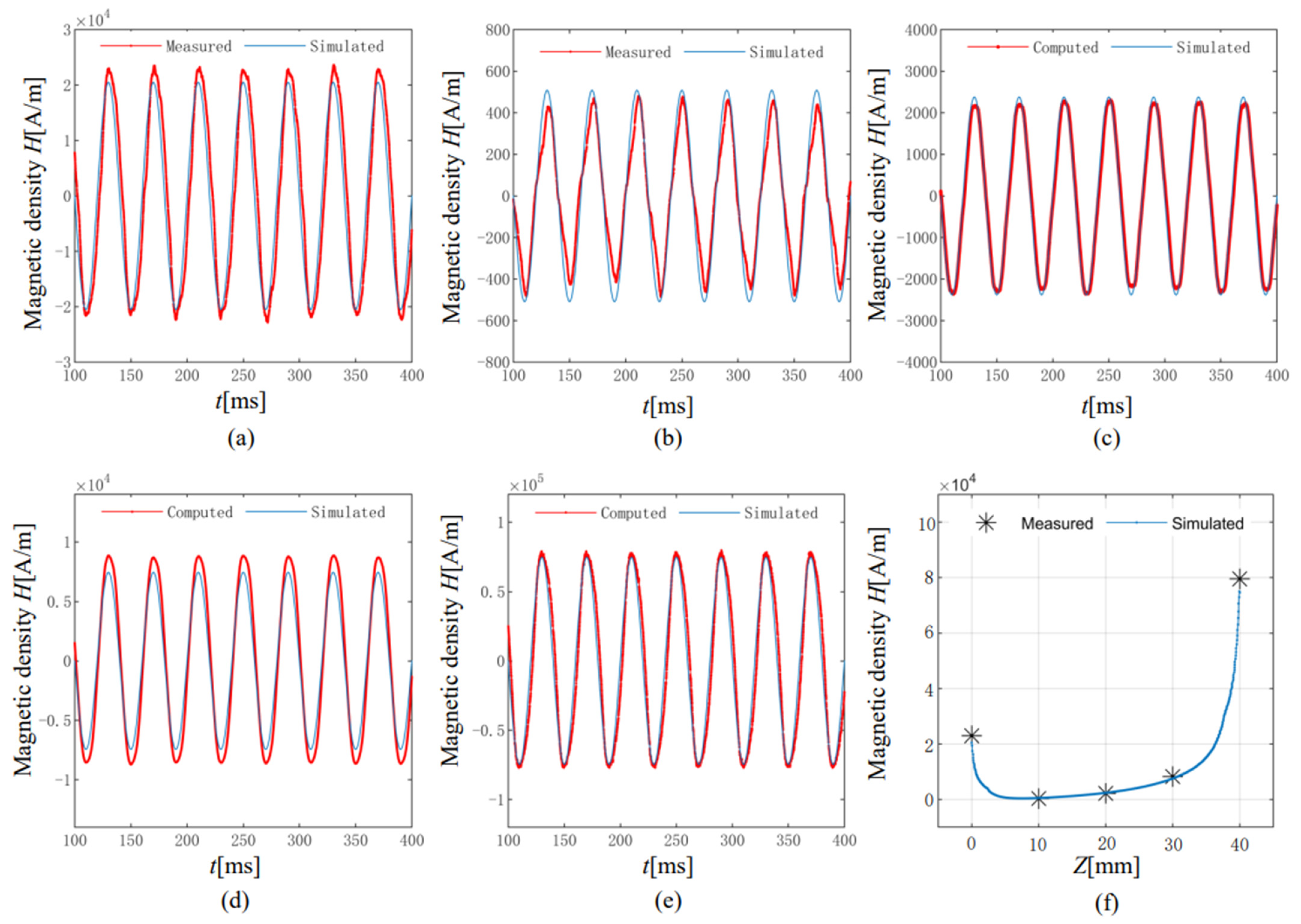
3.2.2. Comparison between Simulation Results and Experimental Results
4. Conclusions
- (1)
- By increasing the relative permeability of the transfer mechanism, the magnetic field intensity on the GMM cylinder first increased and then decreased, whereas the deviation of the average magnetic field intensity at both ends first decreased and then increased. In order to make the axial magnetic field intensity of the GMM cylinder larger and more uniform, the displacement conversion mechanism should be made of materials with low magnetic permeability.
- (2)
- When the relative permeability of the shell increased, the magnetic field density on the GMM cylinder increased monotonously, and the deviation of magnetic field density at both ends decreased monotonously. In order to make the axial magnetic field intensity of the GMM cylinder large and uniform, the device shell should be made of high-permeability material.
- (3)
- With the increase in air gap size, its constraint on magnetic field lines weakened, the magnetic field density on the GMM cylinder decreased, and the deviation degree of magnetic field density increased. Therefore, in order to improve the utilization efficiency of the excitation magnetic field, the geometric size of the air gap should be reduced as much as possible under the condition of meeting the pretightening force requirements.
- (4)
- The experimental test results showed that the established simulation model can correctly reflect the actual physical characteristics of GMA, and it was also verified that it is feasible to use the averaging method based on magnetic circuit theory to solve the magnetic field intensity of GMM cylinder axial section.
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, S.; Gao, X. Magnetostrictive Materia, 1st ed.; Metallurgical Industry Press: Beijing, China, 2017; pp. 1–10. [Google Scholar]
- Engdahl, G. Handbook of Giant Magnetostrictive Materials; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Liu, J.; Jiang, C.; Xu, H. Giant magnetostrictive materials. Sci. China Technol. Sci. 2012, 55, 1319–1326. [Google Scholar] [CrossRef]
- Xue, G.; Ge, J.; Ning, P.; Zhou, J.; Wang, K.; Cheng, Z.; Pei, G. Simulation studies on the boot shape injection of a giant magnetostrictive injector. Sci. Rep. 2021, 11, 22999. [Google Scholar] [CrossRef] [PubMed]
- Xue, G.; Zhang, P.; He, Z.; Li, D.; Yang, Z.; Zhao, Z. Displacement model and driving voltage optimization for a giant magnetostrictive actuator used on a high-pressure common-rail injector. Mater. Des. 2016, 95, 501–509. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, P.; He, Z. A simple magnetization model for giant magnetostrictive actuator used on an electronic controlled injector. J. Magn. Magn. Mater. 2019, 472, 59–65. [Google Scholar] [CrossRef]
- Gahodsi, M.; Ozer, A.; Yahmadi, A.A. Development of Gasoline Direct Injector Using Giant Magnetostrictive Materials. In Proceedings of the 2014 International Conference on Renewable Energy Research and Application (ICRERA), Milwaukee, WI, USA, 19–22 October 2014. [Google Scholar]
- Xu, B. Structure Design and Characterstic Analysis of High Pressure Common Rail Injector Based on Giant Magnetostrictive Actuator; Anhui University of Science and Technology: Huainan, China, 2020. [Google Scholar]
- Xue, G.; He, Z.; Li, D. Magnetic field intensity model for giant magnetostrictive rodand coil optimization analysis. Nanotechnol. Precis. Eng. 2014, 12, 85–90. [Google Scholar]
- Chen, J.; Wang, L.; Tang, Y.; Zhou, H. GMA internal magnetic field measurement based on FBG.In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation. SPIE 2019, 11053, 213–221. [Google Scholar]
- Li, D. Study on 3D internal magnetic field distribution and dynamic mechanics of a giant magnetostrictive actuator. J. Supercond. Nov. Magn. 2018, 31, 4013–4020. [Google Scholar] [CrossRef]
- Liu, H.; Gao, S.; Wang, H. Study on eddy current loss characteristics of precision giant magnetostrictive actuator considering magnetic field distribution. Int. J. Nanomanuf. 2019, 15, 343–354. [Google Scholar] [CrossRef]
- Zheng, J.; He, Z.; Zhou, J. Distribution Structure Design on Bias Magnetic Field of Giant Magnetostrictive Actuator for Hydraulic Valve. Chin. Hydraul. Pneum. 2018, 9, 33. [Google Scholar]
- Wang, G.; An, L. COMSOL Multiphysics Engineering Practice and Theoretical Simulation: Numerical Analysis Technology of Multiple Physical Fields, 1st ed.; Electronic Industry Press: Beijing, China, 2012; pp. 67–81. [Google Scholar]
- Xue, G.; He, Z.; Li, D. Analysis on magnetic field distribution of giant magnetostrictive actuator based on a displacement transmission mechanism. Mech. Sci. Technol. Aerosp. Eng. 2014, 33, 1259–1263. [Google Scholar]
- Reddy, J.N. Introduction to the Finite Element Method, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2019; pp. 591–668. [Google Scholar]
- Fan, W.; Lin, M.; Ju, X. Research and simulation of magnetic field of cylindrical hypermagnetic actuator. J. Funct. Mater. 2017, 48, 5054–5060. [Google Scholar]
- Tu, J.; Liu, Z.; Li, Z. Magnetic circuit optimization design andfinite element analysis of giant magnetostrictive actuator. J. Chongqing Univ. 2021, 44, 52–63. [Google Scholar]
- Yu, Z.; Zhao, H.; Zhang, C. Modeling and simulation of axial non-uniform magnetic field for giant magnetostrictive actuator. J. Magn. Mater. Devices 2019, 50, 10–16. [Google Scholar]
- Tan, X.; Yang, B.; Meng, G.; Xu, P.; Yang, D. Displacement Model and Finite Element Analysis of Two-dimensional Axisymmetric Nonlinear Drive for Giant magnetostrictive Actuator. Astron. Res. Technol. 2010, 7, 362–368. [Google Scholar]
- Gang, W.; Mei, D.; Chen, Z.; Fu, L. Finite Element Analysis of Magnetic Field for Giant Magnetostrictive Microactuator. China Mech. Eng. 2003, 22, 79–81. [Google Scholar]
- Yu, C.; Wang, C.; Deng, H.; He, T.; Wei, B. Giant magnetostrictive actuator magnetic field performance analysis and optimization. Mod. Manuf. Eng. 2015, 8, 136–140. [Google Scholar]
- Yu, C.; Wang, C.; Wei, B. Finite element analysis of magnetostrictive model of giant magnetostrictive actuator. Mach. Tools Hydraul. 2016, 44, 120–124. [Google Scholar]
- Liu, G.; He, Z.; Bai, G. Modeling and experimental study of oil-cooled stacked giant magnetostrictive actuator for servo valve. Actuators 2020, 9, 37. [Google Scholar] [CrossRef]
- Yan, H.; Gao, H.; Hao, H. Design and simulation of exciting coil in rare earth giant magnetostrictive actuator. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 1569–1575. [Google Scholar]
- Yan, R.; Wang, B.; Cao, S. Magneto-mechanical strong coupled model for a giant magnetostrictive actuator. Proc. CSEE 2003, 23, 107–111. [Google Scholar]
- He, Z.; Rong, C.; Li, D. Modeling and analysis of magnetic field distribution for stack giant magnetostrictive actuator. Opt. Precis. Eng. 2017, 25, 2347–2358. [Google Scholar]
- Chen, S.; Zhao, L.; Zhou, J. The magnetic circuit design and simulation of rare earth giant magnetostrictive transducer. Mach. Des. Manuf. 2018, 2, 43–46. [Google Scholar]
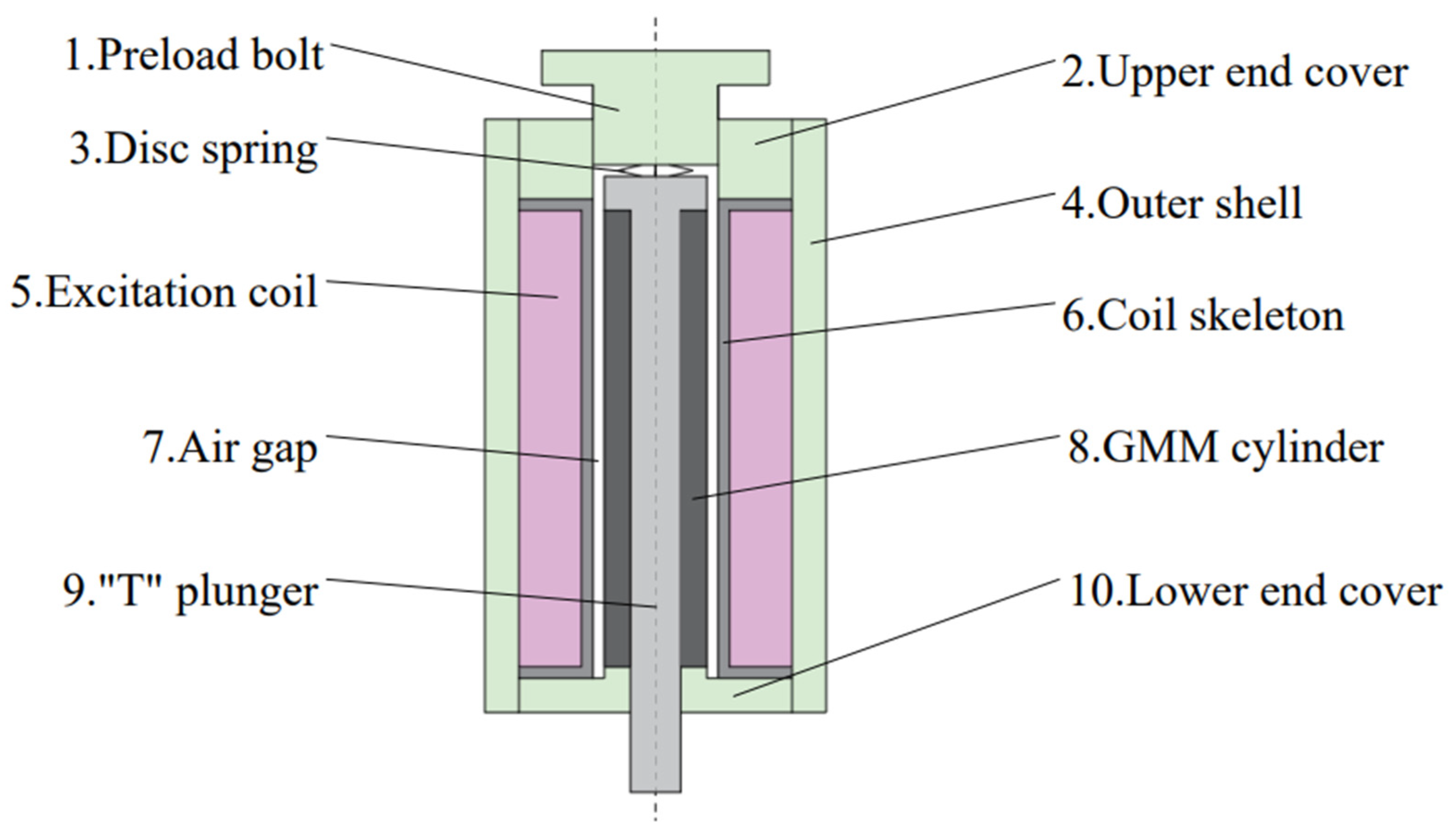

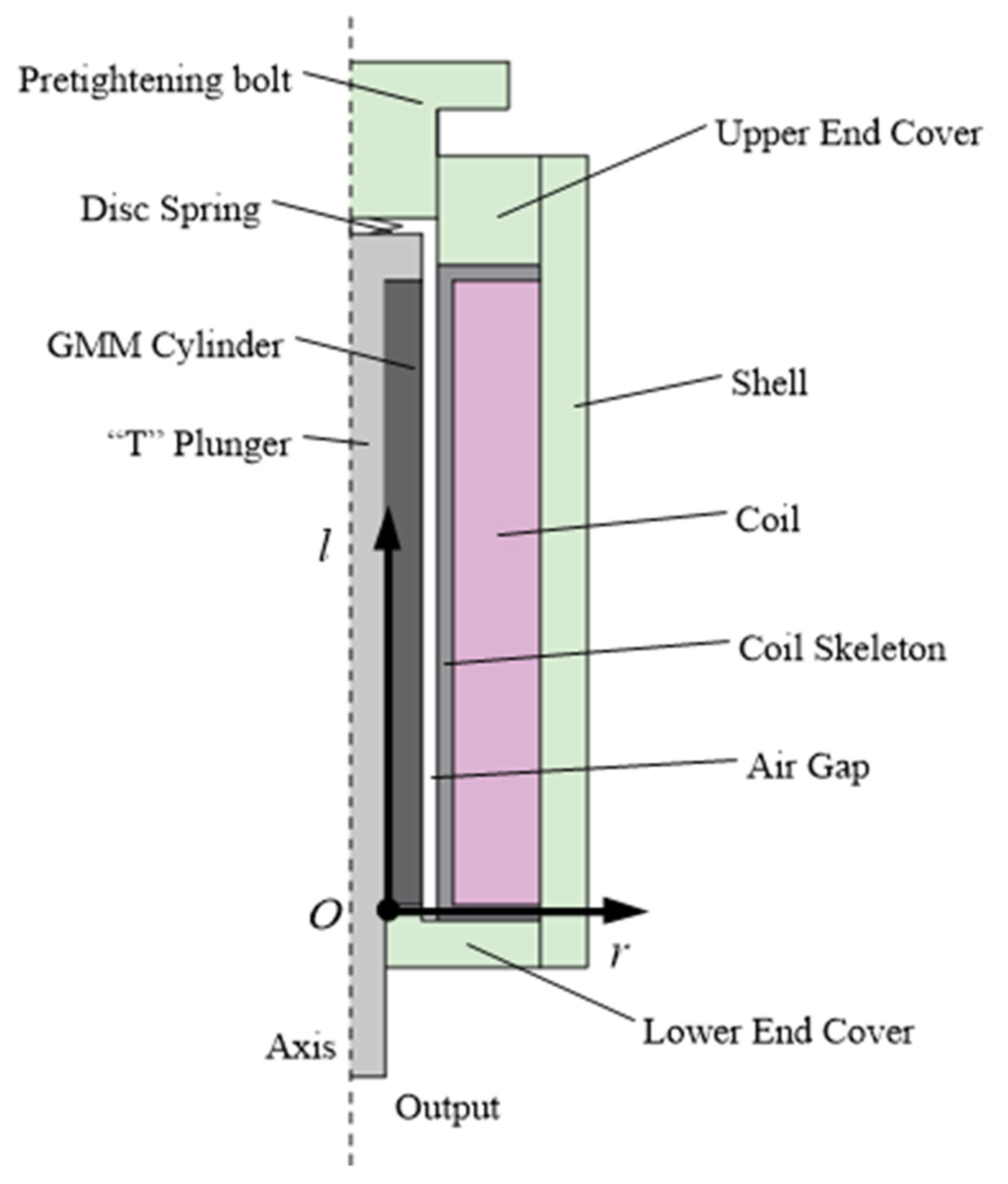
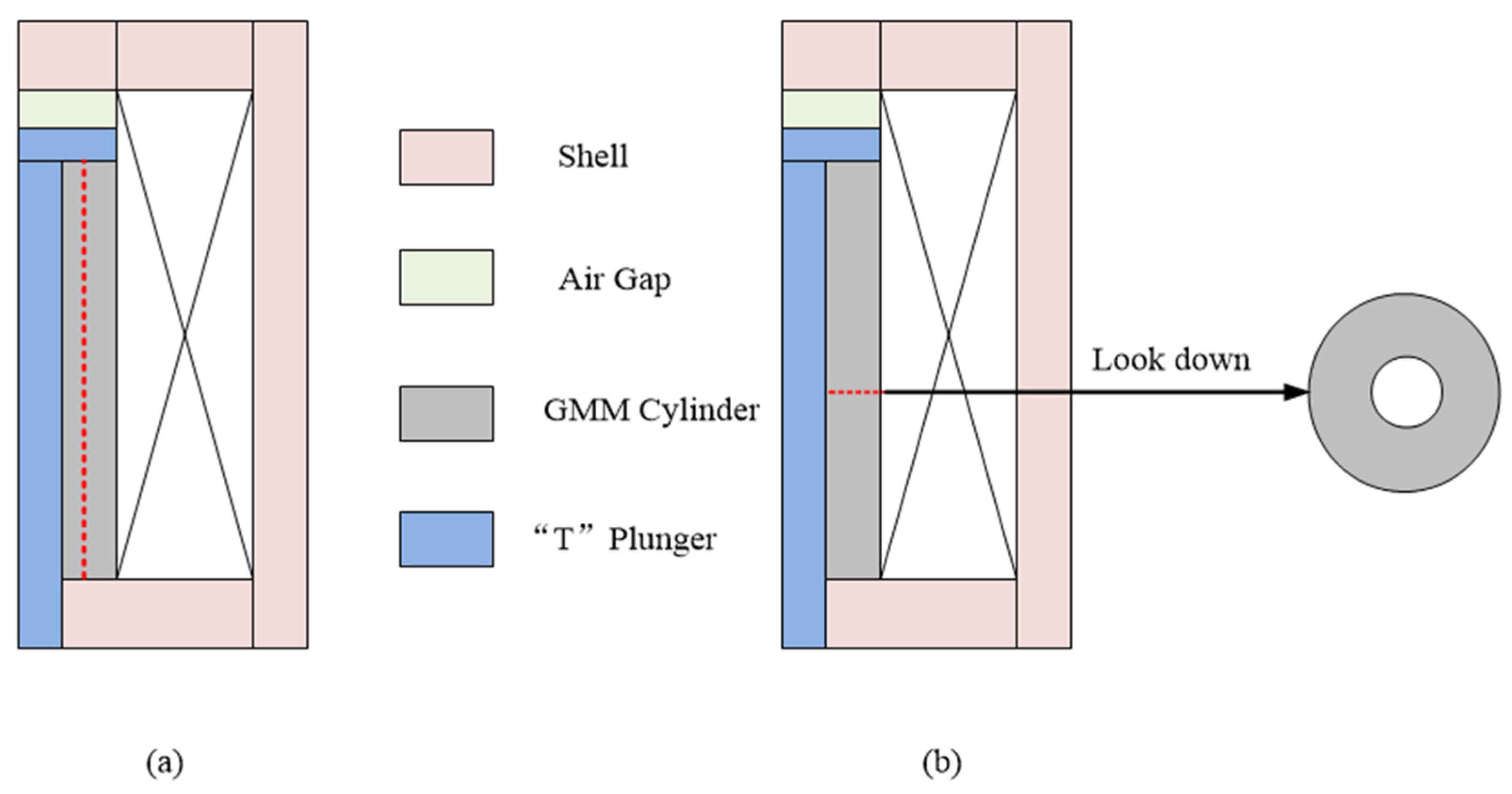





| NO. | Structure Name | Material ur |
|---|---|---|
| 1 | Preload bolt | 2000 |
| 2 | Upper-end cover | 2000 |
| 3 | Disc spring | — |
| 4 | Outer shell | 2000 |
| 5 | Excitation coil | 1 |
| 6 | Coil skeleton | 1 |
| 7 | Air gap | 1 |
| 8 | GMM cylinder | 20 |
| 9 | “T” plunger | 10 |
| 10 | Lower end cover | 2000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; He, Z.; Xue, G.; Zhou, J.; Rong, C.; Liu, G. Analysis of Magnetic Field Characteristics of a Giant Magnetostrictive Actuator with a Semi-Closed Magnetic Circuit. Actuators 2022, 11, 108. https://doi.org/10.3390/act11040108
Zhou Z, He Z, Xue G, Zhou J, Rong C, Liu G. Analysis of Magnetic Field Characteristics of a Giant Magnetostrictive Actuator with a Semi-Closed Magnetic Circuit. Actuators. 2022; 11(4):108. https://doi.org/10.3390/act11040108
Chicago/Turabian StyleZhou, Zhaoqi, Zhongbo He, Guangming Xue, Jingtao Zhou, Ce Rong, and Guoping Liu. 2022. "Analysis of Magnetic Field Characteristics of a Giant Magnetostrictive Actuator with a Semi-Closed Magnetic Circuit" Actuators 11, no. 4: 108. https://doi.org/10.3390/act11040108
APA StyleZhou, Z., He, Z., Xue, G., Zhou, J., Rong, C., & Liu, G. (2022). Analysis of Magnetic Field Characteristics of a Giant Magnetostrictive Actuator with a Semi-Closed Magnetic Circuit. Actuators, 11(4), 108. https://doi.org/10.3390/act11040108







