Abstract
Motivated for improving the efficiency and reliability of wind turbine energy conversion, this paper presents an advanced control design that enhances the power regulation efficiency and reliability. The constrained behavior of the wind turbine is taken into account, by using the barrier Lyapunov function in the analysis of the Lyapunov direct method. This, consequently, guarantees that the generated power remains within the desired bounds to satisfy the grid power demand. Moreover, a Nussbaum-type function is utilized in the control scheme, to cope with the unpredictable wind speed. This eliminates the need for accurate wind speed measurement or estimation. Furthermore, via properly designed adaptive laws, a robust actuator fault-tolerant capability is integrated into the scheme, handling the model uncertainty. Numerical simulations are performed on a high-fidelity wind turbine benchmark model, under different fault scenarios, to verify the effectiveness of the developed design. Furthermore, a Monte-Carlo analysis is exploited for the evaluation of the reliability and robustness characteristics against the model-reality mismatch, measurement errors and disturbance effects.
1. Introduction
Horizontal Axis Wind Turbines (HAWTs) have dominated the Wind Energy Conversion (WEC) industry over the last few decades [1,2]. Modern HAWTs are designed larger and are located in remote places, e.g., offshore sites, to increase the WEC capacity. The HAWT is a complex highly nonlinear dynamic system [3]. So, in the presence of high wind speed variation, it is challenging to retain HAWT operation with the prescribed WEC efficiency [4]. The high wind speed may cause HAWT out-of-control operation with catastrophic overspeeding of the rotor. In this case, either the HAWT is stalled to stop, or the mechanical brake is engaged. As a result, only a conservative WEC is achieved and the efficiency is cumulatively less than that desired [1].
The HAWT efficiency is a trade-off between capturing the maximum energy and satisfying the structural/operational safety [1]. In this regard, modern HAWT manufacturers define the so-called ideal power curve, which characterizes the HAWT operation with optimal efficiency. The key solution for the enhancement of the HAWT efficiency relies on the development of proper control strategies to retain the operation on the ideal power curve [4]. Accordingly, in high wind speed conditions, the generated power is regulated at its nominal value to maintain safe operation and to avoid overspeeding. This region of operation is known as the full load region, where power regulation represents the main objective. In the HAWT, the power regulation is fulfilled by adjusting the pitch angle of the blades, which leads to regulating the rotor speed [5]. Therefore, it is crucial to control the pitch angle such that the rotor speed is kept within the predefined safe-to-operate bound around the nominal value and, consequently, to avoid conservative WEC control solutions [1].
The long-term operation of HAWTs may increase the incidence of pitch actuator faults [1]. The fault occurrence reduces the availability of the plant and increases the WEC cost. Pitch actuator bias, effectiveness loss and dynamic change are the most commonly reported pitch actuator fault types [1,6]. In WTs with hydraulic actuators, the dynamic change is caused by a pressure drop due to hydraulic oil leak, high air content in the oil and pump wear, for those installations using hydraulic actuation. In the case of electric actuators, dynamic change is due, for example, to the wear or ageing of the electric motor, whose response becomes slower due to the friction increase [1,6]. This, in turn, leads to a slower response of the pitch actuator, and, consequently, inefficient power regulation. The pitch actuator bias can be caused when blades are installed to the pitch actuator, and small misalignments can be thus generated. This problem can be present in both electric and hydraulic actuators. The effectiveness loss can be derived from a mechanical fault affecting the electric motor actuating the blades, e.g., some deflection angles (for the complete range of motion) are no longer available due to the wear out of the bearings. The same issue arises also in hydraulic actuators, where the increased friction of the mechanical parts is due to the aging of the hydraulic cylinders. On the other hand, debris build-up and blade erosion are inevitable, which leads to the Blade Aerodynamic Profile Change (BAPC) [1]. These issues motivate the need for maintenance procedures. However, the increased maintenance downtime leads to reduce the power generation rate at a higher cost, especially for offshore installations, due to the reachability difficulties of harsh environments [5]. Therefore, the pitch angle control should integrate fault-tolerance capabilities to compensate possible fault effects [6].
The power regulation control design has gained significant attention and viable solutions are proposed (see, e.g., [7] and the references therein). However, most of the available solutions fail to operate satisfactorily in the presence of pitch actuator faults. Consequently, Fault-Tolerant Control (FTC) has emerged recently and different schemes have been designed, such as robust linear parameter varying control [6], adaptive sliding mode control [5], and fuzzy control [8,9]. Nevertheless, in all the aforementioned works, the constrained rotor speed has not been considered. The constrained HAWT performance may be tackled using Model Predictive Control (MPC) approaches [10,11,12,13]. However, as mentioned in [12], if the constraints are selected inadequately the optimization problem is difficult or even impossible to solve, or the closed-loop system may become unstable. Furthermore, most MPC approaches may suffer from the heavy online computation burden as the solution should be obtained between every two sampling times [14]. The pitch angle control design for efficient power regulation represents a long-lasting challenge, i.e., the mathematical relationship between aerodynamic torque and the pitch angle is not completely known as it is a function of the uncertain wind speed variation [1,15]. This is considered as the unknown control gain problem [16]. It is worth noting that wind speed can be roughly measured on-site by an anemometer, placed on the rotor hub, or by Light Detection and Ranging (LiDAR) devices. However, the accurate measurement of the effective wind speed over the blades is impossible, due to spatial/temporal distribution of the effective wind speed over the blade plane, turbulence, wind shear and tower shadow effects, which is even more important for large rotor installations [1,4]. On the other hand, different numerical approaches have been proposed for wind speed estimation (see, e.g., [17] and references therein), though they remain complicated for practical implementation and, thus, ineffective. Finally, BAPC can be tackled by feeding the measured power into a controller with an integral action [18,19]. However, constructing the pitch angle control on the measured power basis requires the design of generator torque control simultaneously, which is mainly reserved for the low wind speed region [1]. Furthermore, in the mentioned works other pitch actuator faults, and consequent unknown control gain are not considered. Moreover, the control integral action might be dangerous in the presence of faults, caused by the integration of the error, which can be due to a fault.
Motivated by these considerations, in this paper, a pitch angle control is designed for the safe and reliable power regulation purpose, constraining the rotor speed and the generated power within the safe-to-operate bounds. This is a resolution to the overspeeding and the conservative WEC problems. In the proposed controller the unknown control gain is resolved. Furthermore, the designed control tolerates the pitch angle faults, without the need for complex wind estimation schemes. The main features of the proposed controller are summarized in Figure 1.
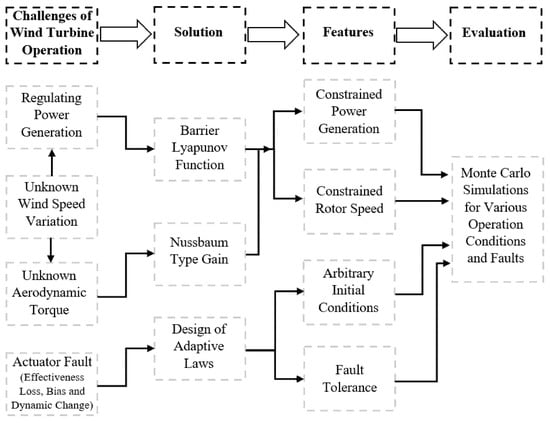
Figure 1.
The proposed solution qualitative features.
To highlight the main contributions, the following comments can be drawn.
The unknown control gain problem, due to uncertain wind speed variation, is tackled by utilizing the Nussbaum-type function. In contrast to the available solutions, e.g., [15,17,20], no computationally expensive and complicated algorithm for the wind speed estimation is required. Therefore, this paper presents an industrially viable scheme.
The constrained power generation is achieved in the control design by the development of a Barrier Lyapunov Function (BLF) to constrain the rotor speed and the generated power, with guaranteed stability and no online optimization burden, in contrast to MPC approaches [10,11,12,13]. Furthermore, the assumption of bounded initial conditions is relaxed. The control parameter selection is formulated as an offline optimization problem.
The fault tolerance capability is inherently included in the proposed solution. By that means, contrary to [15,21,22], the designed control automatically and systematically compensates for the pitch actuator faults. In this manner, neither fault detection nor control reconfiguration schemes are needed. In contrast to the robust solutions, e.g., optimization [1], in which the worst-case scenario is presumed, the conservatism is avoided.
The rest of this paper is organized as follows. Section 2 briefly recalls the HAWT model with some technical preliminaries. In Section 3, a baseline Nonlinear Adaptive Constrained Control (NACC) approach is constructed, with the assumption of known control gain. This restrictive assumption is relaxed in Section 4 and the Modified NACC (MNACC) approach is proposed. In Section 5, asymmetric time variable constraints are constructed to handle arbitrary initial conditions. The fault tolerance characteristics of the proposed MNACC are analysed in Section 6. In Section 7, the feasibility of the proposed solution is studied. The numerical evaluation is addressed in Section 8, and the results are discussed. Furthermore, a Monte-Carlo analysis is exploited for the evaluation of the reliability and robustness features against the model-reality mismatch and measurement errors. The Monte-Carlo analysis represents an effective tool for the preliminary validation of the proposed solution prior to application to real systems. Finally, some concluding remarks and future research issues are summarized in Section 9.
2. HAWT Operational Model and Preliminaries
In this section, the HAWT operational model is briefly introduced with the pitch actuator faults. Furthermore, BAPC is also considered. Finally, some technical preliminaries are given. Hereafter, to simplify the subsequent notation if there is no confusion, function arguments are omitted.
2.1. HAWT Operational Model
The wind energy is converted into the rotor kinetic energy by the blades. The effective wind speed induces the aerodynamic torque , thrust , and power modelled as [1]:
where and are the air density and the rotor radius, respectively. Additionally,, and are torque, power and thrust coefficients, respectively. These factors are functions of the blade pitch angle, , and the tip speed ratio, , defined as [1]. is the rotor angular speed. Furthermore, the aerodynamic power is as , which leads to the relation . The effect of on the tower causes a bending oscillation [6]. The displacement of the nacelle is represented by , measured from its equilibrium position. The effective wind speed at the rotor plane is then obtained as , where is the free wind speed, i.e., the wind speed before the blades [23].
The kinetic energy of the rotor shaft is transferred into the generator shaft, via the drivetrain, with efficiency and speed ratio . The rotor and generator shafts inertia are represented by and , respectively. Furthermore, the rotor and the generator speeds are denoted by and , respectively. Moreover, the drivetrain is modelled as a two-mass system, including the torsion stiffness and the torsion damping . Therefore, a torsion angle is considered, where and are the rotation angle of the rotor and generator shafts, respectively. On the other hand, the bearings of the rotor and generator shafts impose the viscous friction, modelled by the coefficients and , respectively. The generator converts kinetic energy into electrical energy. Additionally, between the generator and the electrical grid, a converter is placed, regulating the power frequency [6]. The internal electronic controller of the generator is much faster than the HAWT mechanical dynamic behaviour. So, it is reasonable to assume that the generator torque is adjusted according to the generator reference torque fast enough to ignore the generator dynamic response. As a result, the electrical power can be approximated by the following static function [6]:
where is the generator efficiency. The power regulation objective can be stated as the generation of the nominal power under uncertain wind speed variation, while avoiding overspeeding and consequent brake engagement. Accordingly, taking Equation (2) into account, this objective is achieved by the following operation requirements: (i) setting at its nominal value ; (ii) regulating at its nominal value .
The nominal power generation is then achieved as , where [6]. The operation requirement (i) can be simply fulfilled by setting the generator reference torque at . The operation requirement (ii) can be fulfilled by the pitch angle control. In this manner, the induced aerodynamic torque is controlled. Consequently, the rotor and the generator angular speeds are regulated [5]. Therefore, the main objective of this paper is to satisfy the requirement (ii).
In order to reduce drivetrain stress, the drivetrain torsion angle variation is to be kept as small as possible. In this regard, the ideal case can be stated as , i.e., keeping the rotor and generator speeds at the drivetrain ratio [24]. As the generator speed is kept at , then the rotor speed is maintained at . This represents the reduced drivetrain stress trajectory. Accordingly, the HAWT operational model is given by [16]:
where, , , , , , , , and .
Considering Equations (1) and (3), the pitch angle control leads to the adjustment of , and consequently, the aerodynamic torque. This, in turn, regulates the rotor speed. The aerodynamic torque is not a singular function in the operational range of HAWT [16]. By that means, in the presence of wind speed variation, there always exists a given pitch angle , and by setting the reference pitch angle at , the consequent aerodynamic torque leads to the nominal power generation [23]. Therefore, the pitch angle controller has to maintain the reference pitch angle at , which retains at nominal values . This, consequently, regulates at , which meets the operation requirement (ii). However, due to uncertain wind speed variation, retaining exactly at is impossible and there is always an error [1]. Therefore, the main aim of this paper is to retain the tracking error as close as possible to zero within the safe-to-operate bounds, i.e., to avoid hazardous overspeeding.
As this work considers a hydraulic pitch actuator, it moves the blades to regulate at the actuated angle . The pitch actuator is modelled as [5]:
with the natural frequency and the damping ratio . The pitch actuator operational ranges are limited as and . In this paper and indicate the maximum and minimum allowable value of the variable , respectively. Note that HAWT operation in a harsh environment may lead to pitch actuator dynamic change, which reduces the power regulation efficiency. This causes the variation in the natural frequency and the damping ratio of the pitch actuator, which in turn leads to a slower pitch actuator response [6]. The dynamic change is modelled by the additive signal in the pitch actuator model, defined later [5]. Moreover, the pitch actuator may suffer from bias, and effectiveness loss. These lead to the deviation of the actuated pitch angle from the reference one , defined by the pitch angle controller [16], modelled as:
with the unknown pitch actuator bias and the unknown effectiveness [9]. Note that , where represents full effectiveness and is total loss [9,25]. More importantly, is an unknown lower bound of the actuator effectiveness, below which the actuator is unable to keep controlling the system and it practically becomes uncontrollable [26]. The signal is the reference pitch angle, which is generated by the pitch angle controller. Clearly, in the case of full effectiveness and no bias, . Associating the pitch actuator dynamic behaviour of Equation (4), with the pitch actuator dynamic change, bias and effectiveness loss, yields:
Environmental situations, such as rain, snow and dirt, lead to erosion or debris build-up on blades. This, in turn, causes BAPC. As a result, the captured aerodynamic power is reduced [15]. Consequently, the power regulation is not efficiently achieved. BAPC can be modelled as an aerodynamic torque change , due to a change in the power coefficient described as [18]. These changes are challenging to detect due to their slow-developing (incipient) characteristics. Therefore, it is difficult to determine if the decreased generated power is due to BAPC or reduced wind speed. However, as BAPC occurs slowly, this change is mostly assumed to be solved by the planned annual maintenance, when the blades are cleaned or replaced. Therefore, this paper aims to design a pitch angle controller that is insensitive to BAPC, thus guaranteeing nominal power generation up to the next planned maintenance.
Considering Equations (1) and (3), the rotor dynamic relation is represented by a non-affine function of the pitch angle [23]. As stated earlier, is not a singular function. Accordingly, this problem is resolved by using the mean value theorem [15], i.e., for any given pair of , there exists such that , where and . It is worth noting that with constants . It can be seen that as effective wind speed increases, by increasing pitch angle, the aerodynamic torque decreases. Therefore, by taking the time derivative of , the following relation is obtained:
where is an aerodynamic torque change due to BAPC [18]. Moreover, it is worth noting that, as the wind speed is not accurately measurable, in Equation (7) is an unknown variable. Now, by using Equations (6) and (7) in Equation (3), one can obtain:
This describes the HAWT rotor dynamic response, which takes into account possible pitch actuator dynamic change, bias, effectiveness loss and BAPC. It is worth noting that the HAWT sensor is affected by measurement error, modelled by stochastic processes. For the sake of notation, the measured variable is represented by the signal , with , where represents a Gaussian white noise process [1,27]. Considering this measurement error, the computable expression of the rotor dynamic of Equation (8) has the following form:
where , ,
and .
Assumption 1.
The bounded achievable values of pitch angle, i.e., and , are limited which leads to the boundedness of as [28]. As varies due to the variation in and , the signal is bounded as [5,16]. The debris build-up and erosion occur very slowly when compared to the scheduled maintenance of the blades. Therefore, it is reasonable to assume that is bounded as [18]. It should be noted that , and are unknown positive constants. Moreover, it is assumed that the noise processes used to represent the measurements errors have a limited bandwidth [1,24]. By considering the bounded variation in , i.e., , is bounded as , where is a positive unknown constant. It can be shown that in Equation (9) is unknown yet bounded, due to the presence of as well as [15]. More importantly, it is assumed that there is always a pitch actuator effort, i.e., , the control gain never becomes zero. Finally, considering the limited generator torque and drivetrain dynamic response of the industrial HAWTs with limited operation range, it can be shown that the induced aerodynamic torque is bounded as [16].
Considering Assumption 1, based on the information extraction technique from the system nonlinearities [16], there is an unknown non-negative constant and a computable non-negative function , i.e., a core function, such that the following inequality is satisfied:
where and .
2.2. Technical Preliminaries
The following definitions and lemmas are introduced, which are used for the stability analysis.
The BLF function is defined as follows, which is used for the design of the constrained control.
Definition 1
[29]. Let’s assume that is positive definite continuous with respect to the solution of the system on an open region . If approaches to infinity, as approaches to the boundary of the region , then is a BLF with continuous first order partial derivatives within all . Consequently, the inequality , holds along with the solution of for , and some positive constant .
The following definition is given, thus demonstrating the boundedness of the closed-loop system.
Definition 2
[30]. is Uniformly Ultimately Bounded (UUB) if there exists a number , and a such that for any compact set and all , , for all .
Definition 3
[16]. Any continuous function is a Nussbaum-type function of , satisfying and , for .
Lemma 1
[16]. Let’s assume that and are smooth functions for any . Then, if
where and are positive constants, and the function takes values in the unknown closed intervals with . Then , and must be bounded on .
Lemma 2
[15]. For a real variable in , the inequality holds true.
3. Baseline NACC Design
In this section, the baseline NACC of the pitch actuator is designed to achieve the control operation requirement (ii), as described in Section 2. Furthermore, the constrained rotor speed and generated power requirements are guaranteed, with the closed-loop stability analysis. In this section the control gain is assumed to be known, i.e., the aerodynamic torque variation with respect to pitch angle is available. This assumption will be relaxed in Section 4 and the NCCA is modified. Moreover, in this section, the design procedure is developed on the fault-free case, i.e., , , , and . The fault-tolerance capability is discussed in Section 6.
The baseline NACC is designed based on the rotor speed tracking error and its time derivative , defined as:
where is the desired rotor speed. The measured rotor speed is affected by noise. So, its differentiation might lead to noise amplification. Therefore, the rotor acceleration is obtained via a Gaussian regression of [31,32,33]. As stated earlier, in the full load region is . The function corresponds to a virtual control, designed as:
where is a positive design parameter and , with is the modified tracking error and is a constraint on . A BLF is chosen as:
which is positive definite and continuous in the set . This imposes the constrained characteristic on , according to Definition 1. Taking the first-time derivative of , the following expression is obtained:
On the other hand, the first-time derivative of has the following form:
By replacing Equation (12) into Equation (15), the following relation is obtained:
Based on Young’s inequality, it is easy to show that
Considering Lemma 2, the inequality holds. Consequently, Equation (16) is rewritten as:
Now, the baseline NACC is designed as:
with the control gain defined as:
and is a virtual control designed as:
where , with is the modified tracking error and is a constraint on . is a positive design parameter. The signal represents the estimation of , updated by the following adaption law:
where and are positive design parameters. A Lyapunov function is chosen as:
where is the estimation error of , defined as . The Lyapunov function is positive definite and continuous in the set . This imposes the constrained characteristic on , according to Definition 1. The first-time derivative of is obtained as:
By replacing the baseline NACC of Equation (18) and the adaption law of Equation (21) into Equation (23), the following expression is obtained:
Considering the trivial inequality , , and Equation (10), it can be shown that .
Additionally, considering Lemma 2, the inequality holds. Finally, it is easy to show that . Consequently, Equation (24) is rewritten as:
where and , which are positive constants. The main properties of the baseline NACC are stated in Theorem 1.
Theorem 1.
Consider the HAWT dynamic model of Equation (8) for the fault-free case, i.e., , , , and . If the initial conditions belong to set for , by using the pitch angle control of Equation (18), with the gain of Equation (19), the virtual controls of Equations (12) and (20), together with the adaption law of Equation (21), then the following propositions hold:
- P1. All the closed-loop system states are bounded;
- P2. For , the constraint sets are not violated;
- P3. By the proper choice of the design parameters, the tracking error can be made arbitrarily small.
Proof.
Multiplying Equation (25) by , the following inequality is obtained:
The integration of Equation (26) over yields the expression:
where . It should be noted that and . Therefore, Equation (27) can be rewritten as:
where is an unknown positive constant. Accordingly, it can be stated that the Lyapunov function is bounded. Consequently, and are bounded. Therefore, it can be inferred that belongs to , hence, it is bounded. In this sense, Equation (17) can be rewritten as:
where is an unknown positive constant. Multiplying both sides of Equation (29) by the following inequality is obtained:
The integration of Equation (30) over yields to:
where . It should be noted that and . Therefore, Equation (31) can be rewritten as:
where is an unknown positive constant. Accordingly, it can be stated that the Lyapunov function is bounded. Consequently, is bounded. Therefore, it can be inferred that belongs to , and hence it is bounded. In the light of the above-mentioned analysis, Propositions P1, P2 and P3, stated in Theorem 1, are proven as follows.
P1. Consider the boundedness of , , and . Therefore, and are bounded. Hence, Equation (12) implies the boundedness of . This, in turn, leads to the boundedness of and , considering Equation (11) and the assumptions on the error processes affecting the measured signals. Provided the boundedness of , the boundedness of is inferred. Therefore, considering Equation (20), is bounded. Consequently, is bounded.
P2. The tracking errors and belong to the sets and , respectively, for .
P3. Considering Equations (13) and (31), it can be shown that . Given , if , then, it holds that . If , since , then it can be concluded that for any given , there exists such that , for any . Therefore, the expression holds for any . Since is an increasing function of its argument, it can be concluded that . As is a design parameter, this implies that can be made arbitrarily small by an appropriate selection of the design parameter. This guarantees that the closed-loop system is UUB based on Definition 2. □
4. MNACC Design with Unknown Control Gain
The control gain in Equation (19) is unknown as it is a function of the pitch actuator effectiveness, i.e., , and the aerodynamic torque variation with respect to pitch angle, i.e., . The former is represented by an unknown time-dependent variable. The latter depends on the wind speed and the aerodynamic blade profile. Some studies, e.g., [15,17,20], suggest estimating the effective wind speed and the blade aerodynamic profile. Besides the computational expensiveness of solutions, the estimation error is unavoidable, especially with high wind speed variations. This, in turn, leads to the degraded performance of the HAWT. On the other hand, some works, e.g., [6], use a look-up table to compute the , based on the in-site measurements by a linear interpolation. This has led to computationally-practical solutions. However, a small amount of measurement data and the linear interpolation approach cannot capture the nonlinear dynamic response of HAWTs accurately. More importantly, both approaches fail to operate desirably in the case of pitch actuator effectiveness loss and BAPC.
The aforementioned unknown control gain problem is resolved in this section, by the adoption of a Nussbaum-type function for the control gain. The MNACC is designed for the fault-free pitch actuator, i.e., and . The fault tolerance capability of the proposed MNACC is discussed in Section 6. The structure of MNACC is given by Equation (18), with the control gain, defined as follows:
where is a Nussbaum-type function, which satisfies Definition 3. Furthermore, is obtained via the following adaption laws:
Now, the main properties of the MNACC are stated in Theorem 2.
Theorem 2.
Consider the HAWT dynamic model ofEquation (8) for the fault-free case, i.e., , , , and . If the initial conditions belong to set for , by using the pitch angle control law of Equation (18), with the gain of Equation (33), the virtual controls of Equations (12) and (20), and the adaption law of Equations (21) and (34), then Propositions P1, P2 and P3, stated in Theorem 1, hold.
Proof.
Consider the Lyapunov functions and , described by Equations (13) and (22), respectively. By substituting the control law of Equation (18) with the gain of Equation (33) and the adaption laws of Equations (21) and (34) into the first-time derivative of , given in Equation (23), one can obtain:
It is readily shown that:
Therefore, from Equation (35) the following inequality can be derived:
The multiplication of Equation (36) by , yields the following inequality:
Therefore, the integration of Equation (37) over yields to:
It should be noted that and . Therefore, Equation (38) can be rewritten as:
Moreover, the variable in Equation (39) satisfies the conditions stated for in Lemma 1. Furthermore, and are unknown positive constants. Therefore, considering Equation (39), it can be shown that and are bounded. The rest of the proof is similar to that of Theorem 1 and is thus omitted here (see from Equation (29) to the end of the proof). □
Remark 1.
Regarding the MNACC of Equation (18) with the gain of Equation (33), it is worth noting that in the design procedure of the pitch angle control, there is no need to estimate the aerodynamic torque variation with respect to pitch angle, i.e.,, and Propositions P1–P3 are still satisfied. This represents one significant key of the proposed MNACC.
5. MNACC Control with Arbitrary Initial Conditions
The initial conditions of HAWT are not necessarily close to the desired trajectory, i.e., for . In this section, the case of arbitrary initial condition is handled.
If the initial conditions do not belong to the constraint sets, the stability analysis given in Theorem 2, is no longer valid. This might lead to HAWT over speeding or, even to more dangerous catastrophic consequences. This requires the initial conditions to be manually set within the constraint sets, which is not a practical approach. As an example, in [34,35,36,37] the authors adopted too large and conservative constraints to include the initial conditions. Nevertheless, such a constraint may be ineffective in practice. Instead, it is beneficial to have a systematic and automatic approach to handle arbitrary initial conditions. To relax this requirement, the constraints are initially enlarged based on the assigned initial conditions. Then, the constraints converge exponentially to the intended bounds, in which the desired performance is achieved. In this manner, the arbitrary initial condition is systematically handled. The exponential convergence of the constraints to the given bounds offers more degrees of freedom that can be exploited in the control design. To this end, the constraint for , are designed according to the following relation:
where
Furthermore, if , then and , otherwise and . The term is a positive design parameter. The terms and represent positive upper and lower thresholds, respectively, between the desired trajectory and constraints, which can be constant or variable. The terms and are defined based on the initial condition values. Accordingly, the constraint is initially enlarged to cover the arbitrary initial condition. On the other hand, approaches to zero as time increases. This provides further degrees of freedom in the design, i.e., the rate of the distance vanishes. For example, for large inertia and slow dynamic systems the term is selected in order to have a suitable convergence time and avoid a large control effort. Finally, and define a small bound, within which desirable performance is achieved.
The constraint , defined in Equation (40), is obviously a time variable and thus affects the closed-loop performance. This effect leads to extra terms contributing to the time derivative of and . These functions are represented by the expression:
for , which is added to Equations (15) and (23), respectively. Accordingly, in order to remove their effects, the virtual control in Equation (12) and in Equation (20) are modified as follows:
where
for . It is worth noting that can be defined by the following relation:
where
The achieved results valid for the arbitrary initial condition are summarized as follows.
Theorem 3.
Consider the HAWT dynamic model of Equation (8) for the fault-free case, i.e., , , , and . The pitch angle control law of Equation (18) is designed with the gain of Equation (33) and the virtual controls of Equations (41) and (42), the adaption laws of Equations (21) and (34), and the constraints defined by Equation (40). For any initial conditions Propositions P1, P2 and P3, stated in Theorem 1, hold.
Proof.
The proof is straightforward (similar to that of Theorem 2), and thus omitted here. □
Remark 2.
Considering the definition of in Equations (41) and (42) for , when approaches to zero, the term approaches to zero, by using L’Hospital’s rule. Therefore, the singularity does not occur. However, since digital processors are not able to evaluate indeterminate form 0/0, the Maclaurin series with the first term is used in the implementation step to solve this problem. Accordingly, in the term is replaced with , when , where is a small positive design constant.
6. Fault-Tolerance Capability of MNACC
The pitch actuator might suffer from effectiveness loss, bias and dynamic change. On the other hand, the long-term operation might lead to BAPC. This section aims to analyse the fault-tolerant capability of the proposed controller. It is proven that the control law of Equation (18), integrated with the gain of Equation (33), is able to compensate for the fault effects from the closed-loop performance automatically, and no control modification is required. This represents a key feature of the proposed pitch angle control, i.e., the constrained power generation is guaranteed, while no redundant hardware components are required. Furthermore, an extra computationally expensive scheme to detect, isolate and identify the faults is not needed. This is an important advantage in general for HAWTs, especially for offshore deployments. To this end, the main results on the fault tolerance capability of the proposed MNACC are summarized in the following theorem.
Theorem 4.
Consider the HAWT dynamic model of Equation (8) under pitch actuator effectiveness loss, bias, dynamic changeand the BAPC. The pitch angle control exploits Equation (18), with the gain of Equation (33) and, the virtual controls of Equations (41) and (42), the adaption law of Equations (21) and (34), and the constraints defined by Equation (40). For any initial conditions, Propositions P1, P2 and P3, stated in Theorem 1, hold.
Proof.
Consider the Lyapunov functions and , given in Equations (13) and (22), respectively. By using the control of Equation (18) with the gain of Equation (33) and the adaption laws of Equations (21) and (34), and the virtual control of Equations (41) and (42), the first-time derivative of satisfies the following inequality:
where . Therefore, the integration of Equation (43) over leads to the following inequality:
It should be noted that and . Therefore, Equation (44) can be rewritten as:
Moreover, as , then the term satisfies the conditions on in Lemma 1. Furthermore, and are unknown positive constants. Therefore, considering Equation (45), it can be shown that and are bounded. The rest of the proof is similar to that of Theorem 1 and is, thus, omitted here (see from Equation (29) to the end of the proof). □
Remark 3.
In Theorem 4, Proposition P1 implies that the closed-loop HAWT including the MNACC controller is stable. Proposition P2 guarantees the fulfilment of the constraints on the rotor speed and its acceleration. Consequently, the generator speed and the generated power are kept within the prescribed bounds. Considering Section 3, the efficient power regulation requirements are also met, hence, the required power grid demand is satisfied. Moreover, both the rotor overspeeding and the mechanical brake engagement is avoided. Proposition P3 indicates the expert’s knowledge in the implementation stage, to satisfactorily make the tracking error small. These objectives are also satisfied in the presence of uncertain wind speed variation, pitch actuator effectiveness loss, bias, dynamic change, and BAPC, for any initial conditions. So, efficient power regulation is satisfied without the need for unplanned maintenance. Accordingly, the reliability and availability properties are improved. Furthermore, downtime and maintenance costs are reduced.
Remark 4.
It should be noted that in [27], different faults, either sensor or actuator, mechanical or electrical, were introduced. In the current study, the pitch actuator dynamic change, bias and effectiveness loss are considered. This is mainly motivated by considering the severity of these faults [1]. Meanwhile, the effects of BAPC and drivetrain efficiency reduction are evaluated. However, the rest of the mentioned faults [27] are not included. This stems from two reasons. In the full load region, the generator control is not active, and the generator torque load is just set at the nominal value. Therefore, the faults on the generator are not considered. More importantly, the proposed controller can be used in parallel to the available solutions, which are designed to compensate, for instance, for the sensor faults (for the other faults see the suggested strategies in [38]).
7. Feasibility Check and Design Algorithm
In the proposed controller, the constraints are imposed on the tracking error. However, from a practical point of view, the state constraints are given directly on the HAWT rotor speed and its derivative, rather than the tracking error. In that sense, the operational requirements are defined as and . In practice, it is assumed that . From Equation (41), it can be stated that if the virtual control is bounded with respect to the specified constrained , the inequality is guaranteed. As , and also since , it can be verified that . An important issue is that the feasibility condition may be violated when the approaches the constraint [30]. Therefore, must be satisfied by choosing the appropriate design parameter [29]. On the other hand, considering effect of as in Equation (42), may become very large when gets very close to [29]. Therefore, the state constraints cannot be arbitrarily selected, and a given feasibility constraint has to be satisfied, which is based on . The feasibility condition depends on the existence of the design parameters to satisfy the state constraints. To this end, if the constraints are too small, such a control may not exist. In this regard, the feasibility condition is formulated as a static optimization and solved prior to the implementation of the controller. Let us assume there exists an upper bound , such that:
where . From Proposition P3 in Theorem 3, it is evident that the design parameters are to be selected large enough to achieve good tracking performance. However, this increases in Equation (41), and consequently, . This may violate the state constraint . Accordingly, a tradeoff has to be defined, which is formulated as a feasibility condition. Specifically, it checks if there exists a solution for the following static Optimization Problem (OP).
It should be noted that this is a sufficient condition. In such a case, with the state constraints are not violated. The design procedure is summarized in Algorithm 1. It should be noted that this algorithm can be solved by using, e.g., the fmincon routine in MATLAB [39]. Additionally, the design structure is summarized in Figure 2.
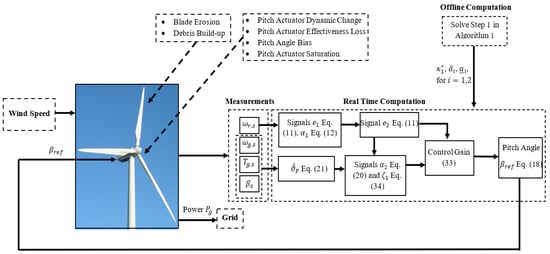
Figure 2.
Block diagram of the design procedure.
| Algorithm 1 Proposed controller design procedure |
| 1. Offline computation: |
| 1.1. For the given and , solve OP to obtain . Select , , and , for i = 1,2, in accordance with Remark 2. |
| 1.2. For the given initial condition, compute and , then select , and , for i = 1,2. |
| 2. Online computation: |
| 2.1. Integrate the virtual controls Equations (41) and (42), the adaptive laws Equations (21) and (34). |
| 2.2. Compute the control gain Equation (33) and then the control signal Equation (18). |
8. Simulations and Discussion
This section presents and discusses the numerical simulations conducted on the high-fidelity 4.8 MW HAWT benchmark to evaluate the effectiveness of the MANCC [6,27]. Different fault scenarios are applied to the benchmark, i.e., single and simultaneous faults. It is shown that in both cases the considered constraints are not violated, satisfying the operation requirement (ii). Uncertainties represent the key point in the case of offshore HAWTs. Indeed, in remote harsh locations, BAPC and drivetrain efficiency reduction are unavoidable. This issue is important, as this may lead to less captured power. Accordingly, to assess the robustness of the proposed MANCC, a Monte-Carlo analysis is performed with different measurement errors, modelled as Gaussian processes, and the model-reality mismatch. To numerically evaluate the nominal power generation the following normalized Power Metric (PM) is defined as follows:
8.1. Control Parameters
The constraints on the rotor speed and its time derivative are selected as and . Accordingly, by solving OP, the parameters of the MANCC are , , . Furthermore, the initial conditions vector is . Consequently, the parameters of the tracking error constraints in Equation (40) are , , , , , , , , and . The Nussbaum-type function is used, according to Definition 3. Finally, considering Remark 2, is selected.
8.2. Fault Model
The fault in Equation (6) is due to the pitch actuator dynamic change, which in turn causes the variation in the natural frequency and the damping ratio . As described in [1], the fault can be modelled as a convex functions depending on the nominal values of the natural frequency and the damping ratio, as described by the following relation [1,6]:
where , , and are fault indicators, and are the natural frequency and the damping ratio, respectively, in the condition . Additionally, the acronyms , , , and stand for normal, hydraulic leaks, pump wear, and high air content conditions, respectively. The parameters of these conditions are summarized in Table 1. On the other hand, to precisely investigate the effects of faults and the performance of the proposed controller, different fault types, sizes and periods are considered.

Table 1.
Pitch actuator dynamic change parameters [1,6].
Furthermore, single faults occurring once per time are simulated, as well as simultaneous ones. To summarize, two fault scenarios, including single and simultaneous fault conditions with different sizes and types are implemented, as described in Table 2 and Table 3, respectively. Additionally, it should be noted that
can be implemented as a reduction in the power coefficient. BAPC is described as a 10% reduction in the power coefficient in the simulations. On the other hand, the drivetrain friction may lead to decreased efficiency. This is modelled by a 5% reduction in drivetrain efficiency.

Table 2.
Single fault scenario.

Table 3.
Simultaneous fault scenario.
8.3. Parameters of Measurement Errors
To have a realistic simulation analysis, the sensor measurements are affected by measurement errors, modelled as Gaussian processes, which is a common assumption in many works [27]. The measurement error parameters are described by the variables of in Table 4. It is worth noting that the measurement error of the sensors may be variable over a long period of operation. These effects are investigated through the evaluation of the robustness feature via the Monte-Carlo tool. Accordingly, three sets of measurement errors with different standard deviations are considered, which are reported in Table 4, i.e., , and . It should be pointed out that, as the paper focuses on the pitch angle control, larger variations in pitch angle standard deviation are considered.

Table 4.
Parameters of the different measurement error conditions.
8.4. Simulation Results and Discussion
The considered wind speed sequence is shown in Figure 3, with the mean 17.84 (m/s) and the standard deviation of 1.94 (m/s). It is worth noting that other wind sequences can be used to study the robustness of the performance. In this work, however, the robustness is analysed via the Monte-Carlo tool in the presence of measurement errors. Therefore, for the sake of brevity, the wind speed sequence depicted in Figure 3 is only used. Under single and simultaneous fault scenarios, the results are shown in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
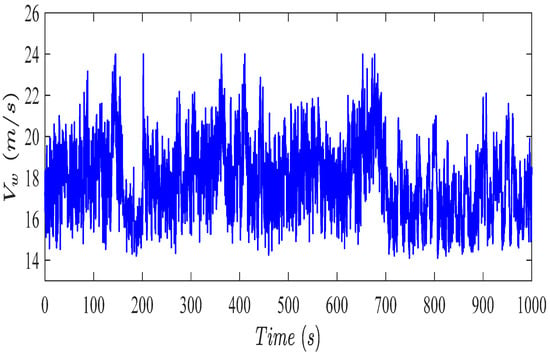
Figure 3.
Free wind speed profile.
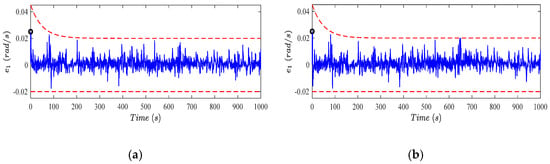
Figure 4.
Tacking error (blue line) with constructed constraints (red dashed lines), under single (a) and simultaneous faults (b). The circle represents the initial value.
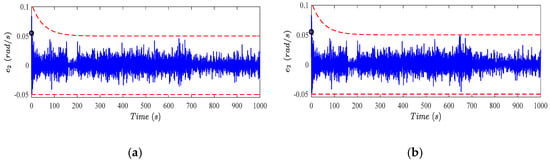
Figure 5.
Tacking error (blue line) with constructed constraints (red dashed lines), under single (a) and simultaneous faults (b). The circle represents the initial value.
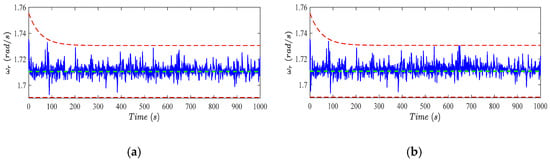
Figure 6.
Rotor speed (blue line) with constructed constraints (red dashed lines) and nominal value (green dashed line), under single (a) and simultaneous faults (b).
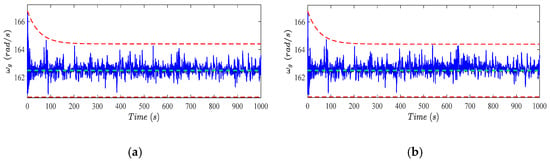
Figure 7.
Generator speed (blue line) with constructed constraints (red dashed lines) and nominal value (green dashed line), under single (a) and simultaneous faults (b).
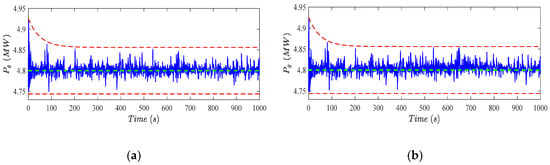
Figure 8.
Generated power (blue line) with constructed constraints (red dashed lines) and nominal value (green dashed line), under single (a) and simultaneous faults (b).
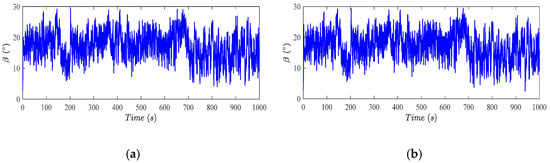
Figure 9.
Reference pitch angle under single (a) and simultaneous faults (b).
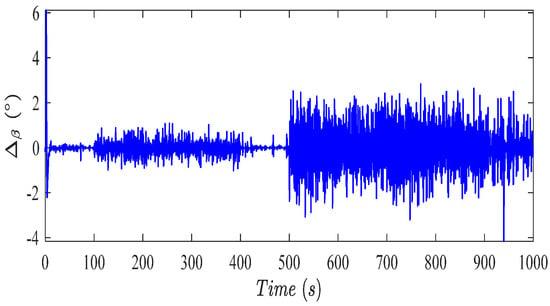
Figure 10.
Profile of .
It can be seen that the tracking errors and are within the considered constraints, considering Figure 4 and Figure 5. Accordingly, both the rotor and the generator speed signals, illustrated in Figure 6 and Figure 7, are quite close to the corresponding nominal values despite the wind speed variation and faults. As a result, the generated power is regulated at the nominal value, as shown in Figure 8. These results imply that the wind turbine is successfully controlled by pitch angle regulation, i.e., the nominal power is generated, despite the wind speed high variation and the faults. Furthermore, the given operation bounds are not violated. This enables safe operation and avoids conservative WEC. Especially, considering the bounded rotor speed, the engagement of the mechanical brake on the rotor shaft can be avoided. On the other hand, as indicated in Figure 4 and Figure 5, the proposed scheme is able to construct the bounds to handle the initial conditions outside of these bounds, as discussed in Section 5.
The reference pitch angle computed by the proposed controller is shown in Figure 9. The pitch angles in Figure 9 are very similar to each other. Therefore, to accurately investigate the performance of the proposed controller, the difference between these two pitch angles, defined as , is reported in Figure 10. Considering Table 1 and Table 2, and Figure 10, it is clear that the main difference is in the periods that the pitch actuator bias and effectiveness loss commence, i.e., and . Considering Figure 10 and Table 2 and Table 3, the effects of the pitch actuator dynamic change have led to more variations, compared to bias and effectiveness loss. Indeed, the dynamic change causes the slower pitch actuator dynamic response. In this case, the controller has to vary the pitch angle faster with larger values to retain the rotor speed within the bounds.
Now to extensively evaluate the performance, the Monte-Carlo analysis is performed to assess the robustness and reliability of the proposed controller, in terms of nominal power generation, considering different measurement errors and the PM(%) index. Additionally, BAPC is included as a 10% reduction in the power coefficient. On the other hand, the drivetrain decreased efficiency is considered by a 5% reduction in this parameter. Accordingly, two cases with and without BAPC and drivetrain efficiency reduction are represented by Case 1 (C1) and Case 2 (C2), respectively. The Monte-Carlo analysis is performed under a single fault scenario. For each case, 100 simulations are performed. For each simulation, the PM(%) is computed over the simulation time. Then, the maximum, minimum, standard deviation and mean values of each PM(%) index for each simulation are computed. Accordingly, for the sake of brevity, the Worst (W), the Average (A) and the Best (B) values over 100 simulations are considered, as indicated in Table 5. It is worth noting that the PM(%) index, as defined in Equation (48), is ideally close to zero. Therefore, the worst, the average and the best values represent the largest, average and smallest values, respectively. The rationale behind this is that the largest PM(%) represents the largest deviation from the nominal power generation. Therefore, this is selected as the worst performance index. Similar justifications can be given for average and the best values. All Monte-Carlo simulation results reported in Table 5 highlight that the proposed control scheme is robust with respect to the model efficiency reduction, measurement errors, wind speed variations as well as faults. Indeed, in terms of nominal power generation, which is the main operational objective of the wind turbine in the full load region, the proposed pitch angle controller is able to keep the generated power very close to the nominal value.

Table 5.
Monte-Carlo simulation results in terms of PM% index. Letters B, A and W stand for best, average and worst values, respectively.
Table 5 summarises the Monte-Carlo analysis results. As these simulations are performed under random noise processes 600 times, cumulatively, it can be concluded that the achievement of this objective is guaranteed by using the proposed controller. This highlights the robustness and reliability of the developed solution, in terms of nominal power generation. This is verified considering the PM(%) in Table 5. The deviation of the generated power from the nominal value is negligible for all the simulations with different measurement errors and faults. Even the worst cases, i.e., the largest PM(%), have led to small deviations.
9. Conclusions
This paper proposed a novel pitch actuator controller to improve the power regulation efficiency of the horizontal axis wind turbine. It also guaranteed safe operation with efficient wind energy conversion. The constrained control was designed, using the barrier Lyapunov function, to retain the rotor speed and the generated power within the safe-to-operate bounds. Therefore, the rotor overspeeding, the mechanical brake engagement, and the conservative energy conversion are avoided. The proposed controller was able to handle the uncertain wind speed variation effects without requiring accurate wind speed measurement, using the Nussbaum-type function. It was also able to compensate for pitch actuator faults and aerodynamic characteristic change. Accordingly, unplanned maintenance and consequent cost are reduced. Numerical simulations were performed to validate the effectiveness of the proposed controller under various faults. The Monte-Carlo tool was exploited for the evaluation of reliability and robustness against the model uncertainty and measurement noise.
This paper suggests some future research issues that need to be investigated. One of the most crucial issues is the experimental analysis of the proposed scheme, which needs to be conducted before industrial applications. However, the development of the proposed solution for real wind turbines is promising. Furthermore, the numerical calculation of the captured wind energy can be evaluated, considering the reduced downtime, operation and maintenance costs. This can further highlight the economic benefits of the proposed controller.
Author Contributions
Conceptualization, H.H., I.H. and S.S.; methodology, H.H., I.H. and S.S.; software, H.H.; validation, H.H., I.H. and S.S.; formal analysis, H.H. and S.S.; investigation, H.H., I.H. and S.S.; resources, H.H., I.H. and S.S.; data curation, H.H. and S.S.; writing—original draft preparation, H.H.; writing—review and editing, H.H., I.H. and S.S.; visualization, H.H.; supervision, I.H. and S.S.; Revision, H.H., I.H. and S.S.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Habibi, H.; Howard, I.; Simani, S. Reliability improvement of wind turbine power generation using model-based fault detection and fault tolerant control: A review. Renew. Energy 2019, 135, 877–896. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X. An overview on fault diagnosis, prognosis and resilient control for wind turbine systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Yang, S.; Wang, R.; Zhou, J.; Chen, B. Intermediate-Variable-Based Distributed Fusion Estimation for Wind Turbine Systems. Actuators 2022, 11, 15. [Google Scholar] [CrossRef]
- Mahdizadeh, A.; Schmid, R.; Oetomo, D. LIDAR-Assisted Exact Output Regulation for Load Mitigation in Wind Turbines. IEEE Trans. Control Syst. Technol. 2020, 29, 1102–1116. [Google Scholar] [CrossRef]
- Lan, J.; Patton, R.J.; Zhu, X. Fault-tolerant wind turbine pitch control using adaptive sliding mode estimation. Renew. Energy 2018, 116, 219–231. [Google Scholar] [CrossRef]
- Sloth, C.; Esbensen, T.; Stoustrup, J. Robust and fault-tolerant linear parameter-varying control of wind turbines. Mechatronics 2011, 21, 645–659. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, R.; Babu, N.R. Recent developments of control strategies for wind energy conversion system. Rene. Sustain. Energy Rev. 2016, 66, 268–285. [Google Scholar] [CrossRef]
- Simani, S.; Farsoni, S.; Castaldi, P. Fault diagnosis of a wind turbine benchmark via identified fuzzy models. IEEE Trans. Ind. Electron. 2015, 62, 3775–3782. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Fuzzy gain-scheduled active fault-tolerant control of a wind turbine. J. Franklin Inst. 2014, 351, 3677–3706. [Google Scholar] [CrossRef]
- Ghanbarpour, K.; Bayat, F.; Jalilvand, A. Wind turbines sustainable power generation subject to sensor faults: Observer-based MPC approach. Int. Trans. Electr. Energy Syst. 2020, 30, e12174. [Google Scholar] [CrossRef]
- Kong, X.; Ma, L.; Liu, X.; Abdelbaky, M.A.; Wu, Q. Wind turbine control using nonlinear economic model predictive control over all operating regions. Energies 2020, 13, 184. [Google Scholar] [CrossRef] [Green Version]
- Petrović, V.; Jelavić, M.; Baotić, M. MPC framework for constrained wind turbine individual pitch control. WiEn 2021, 24, 54–68. [Google Scholar] [CrossRef]
- Khooban, M.H. An Optimal Non-Integer MPC-based Load Frequency Control for Modern AC Power Grids with V2G Technology. IEEE Trans. Energy Convers. 2020. [Google Scholar]
- Zhao, K.; Song, Y.; Chen, C.P.; Chen, L. Control of nonlinear systems under dynamic constraints: A unified barrier function-based approach. Autom 2020, 119, 109102. [Google Scholar] [CrossRef]
- Habibi, H.; Nohooji, H.R.; Howard, I.; Simani, S. Fault-Tolerant Neuro Adaptive Constrained Control of Wind Turbines for Power Regulation with Uncertain Wind Speed Variation. Energies 2019, 12, 4712. [Google Scholar] [CrossRef] [Green Version]
- Habibi, H.; Nohooji, H.R.; Howard, I. Adaptive PID Control of Wind Turbines for Power Regulation With Unknown Control Direction and Actuator Faults. IEEE Access 2018, 6, 37464–37479. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Cai, Z.; Dong, M.; Su, M.; Wang, Y. Wind estimation with a non-standard extended Kalman filter and its application on maximum power extraction for variable speed wind turbines. Appl. Energy 2017, 190, 670–685. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Fault-tolerant cooperative control in an offshore wind farm using model-free and model-based fault detection and diagnosis approaches. Appl. Energy 2017, 201, 284–307. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Pillay, P.; Rakheja, S. Application of FMRAC to fault-tolerant cooperative control of a wind farm with decreased power generation due to blade erosion/debris buildup. Int. J. Adapt. Control Signal Process. 2018, 32, 628–645. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Geng, S.; Wu, L. Nonlinear Control of Variable Speed Wind Turbines via Fuzzy Techniques. IEEE Access 2017, 5, 27–34. [Google Scholar] [CrossRef]
- Rahnavard, M.; Ayati, M.; Yazdi, M.R.H.; Mousavi, M. Finite time estimation of actuator faults, states, and aerodynamic load of a realistic wind turbine. Renew. Energy 2019, 130, 256–267. [Google Scholar] [CrossRef]
- Li, M.; Yu, D.; Chen, Z.; Xiahou, K.; Ji, T.; Wu, Q. A data-driven residual-based method for fault diagnosis and isolation in wind turbines. IEEE Trans. Sustain. Energy 2019, 10, 895–904. [Google Scholar] [CrossRef]
- Jafarnejadsani, H.; Pieper, J.; Ehlers, J. Adaptive control of a variable-speed variable-pitch wind turbine using radial-basis function neural network. IEEE Trans. Control Syst. Technol. 2013, 21, 2264–2272. [Google Scholar] [CrossRef]
- Habibi, H.; Howard, I.; Habibi, R. Bayesian Fault Probability Estimation: Application in Wind Turbine Drivetrain Sensor Fault Detection. Asian J. Control 2020, 22, 624–647. [Google Scholar] [CrossRef]
- Badihi, H.; Zhang, Y.; Hong, H. Wind turbine fault diagnosis and fault-tolerant torque load control against actuator faults. IEEE Trans. Cont. Syst. Technol. 2015, 23, 1351–1372. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.; Wen, C. Computationally inexpensive fault tolerant control of uncertain non-linear systems with non-smooth asymmetric input saturation and undetectable actuation failures. IET Control. Theory Appl. 2016, 10, 1866–1873. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Contr. Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, S.; Fitzgerald, B.; Basu, B. Individual Blade Pitch Control of Floating Offshore Wind Turbines for Load Mitigation and Power Regulation. IEEE Trans. Control Syst. Technol. 2020, 29, 305–315. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.S. Control of nonlinear systems with full state constraint using a barrier Lyapunov function. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC), Shanghai, China, 15–18 December 2009; pp. 8618–8623. [Google Scholar]
- Tang, Z.-L.; Ge, S.S.; Tee, K.P.; He, W. Robust adaptive neural tracking control for a class of perturbed uncertain nonlinear systems with state constraints. IEEE Trans. Syst. Man Cyb. Syst. 2016, 46, 1618–1629. [Google Scholar] [CrossRef]
- Leithead, W.E.; Dominguez, S. Wind turbine rotor acceleration: Identification using Gaussian regression. In Proceedings of the International Conference on Informatics in Control, Automation, Barcelona, Spain, 14–17 September 2005. [Google Scholar]
- Leithead, W.; Hardan, F.; Leith, D. Identification of aerodynamics and drive-train dynamics for a variable speed wind turbine. In Proceedings of the European Wind Energy Conference and Exhibition, Madrid, Spain, 16–19 June 2003. [Google Scholar]
- Rommel, D.; Di Maio, D.; Tinga, T. Calculating wind turbine component loads for improved life prediction. Renew. Energy 2020, 146, 223–241. [Google Scholar] [CrossRef]
- Wu, L.B.; Park, J.H.; Zhao, N.N. Robust Adaptive Fault-Tolerant Tracking Control for Nonaffine Stochastic Nonlinear Systems With Full-State Constraints. IEEE Trans. Cybern. 2019, 50, 3793–3805. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.J.; Tong, S. Barrier Lyapunov functions for Nussbaum gain adaptive control of full state constrained nonlinear systems. Autom 2017, 76, 143–152. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Chen, C.L.P. Adaptive Neural Control of Uncertain MIMO Nonlinear Systems With State and Input Constraints. IEEE Trans. Neural Net. Learn. Syst. 2017, 28, 1318–1330. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.J.; Song, Y.D. Barrier Function-Based Neural Adaptive Control With Locally Weighted Learning and Finite Neuron Self-Growing Strategy. IEEE Trans. Neural Net. Learn. Syst. 2017, 28, 1439–1451. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Stoustrup, J. A benchmark evaluation of fault tolerant wind turbine control concepts. IEEE Trans. Cont. Syst. Technol. 2015, 23, 1221–1228. [Google Scholar] [CrossRef]
- Tang, Z.-L.; Tee, K.P.; He, W. Tangent barrier Lyapunov functions for the control of output-constrained nonlinear systems. IFAC Proc. Vol. 2013, 46, 449–455. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).