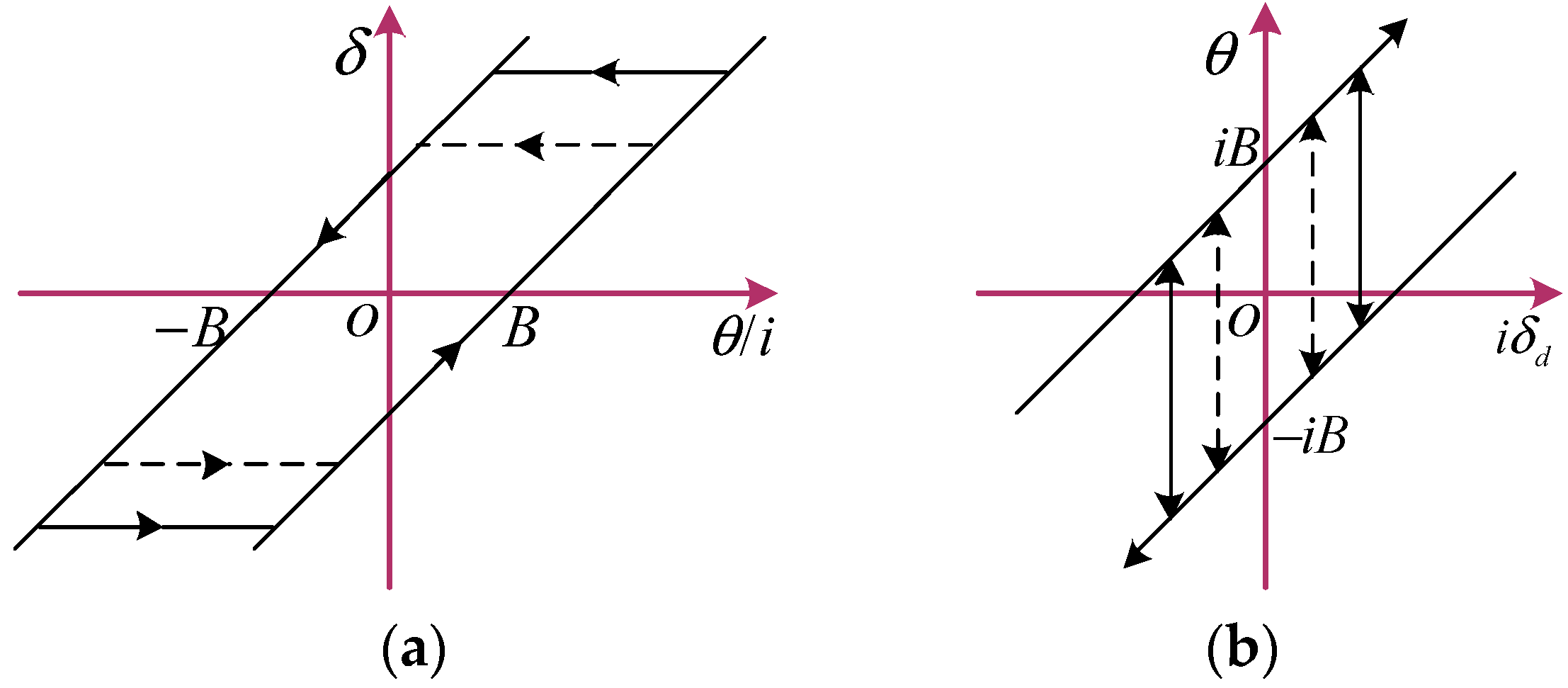Abstract
A compound scheme, based on an improved active disturbance rejection controller (ADRC) and nonlinear compensation, is developed for the electromechanical actuator (EMA) system in this paper. First, considering the influences of backlash, friction on the EMA system, a model for the EMA system is presented. The LuGre model and Hysteresis inverse model are used to compensate for the friction and backlash phenomenon. Then, the method of improved ADRC, based on the Fal function filter and a Linear extended state observer (LESO), is investigated. Simultaneously, since the controller parameters of the improved ADRC are complicated, the non-dominated sorting genetic algorithm II (NSGA-II) is presented to optimize the controller parameters, to achieve the best dynamic response. Finally, simulation and experiment are presented to validate the effectiveness of the proposed method. Under the nonlinear compensation, the performance of the proposed compound scheme is compared with the conventional proportional integral (PI) controller, in terms of step response analysis and sine wave response analysis. Simulation and experiments show that the proposed controller provides high-performance dynamic characteristics.
1. Introduction
The electromechanical actuator (EMA) system is vital in missiles. It is used to receive instructions from the navigation control system and deflect, according to the instructions, to change the flight attitude of the missile. With the development of high-performance guidance weapons, higher requirements are put forward for the EMA system. The EMA system is a typical mechatronic system, and the nonlinearity of internal and external disturbance, friction, and backlash [1,2] seriously affect the system’s performance. It is vital to study the nonlinearity of the EMA system and propose effective control methods.
Friction compensation based on the friction model is a widely used method to alleviate the effect of friction. There are many friction models, such as the classic model [3], Dahl model [4], Boliman and sorine model [5], elasto-plastic model [6], LuGre model [7], Karnopp model [8], Borello model [9] and Generalized maxwell-slip model [10], although these models have some applications in different systems. Among them, the LuGre model provides a perfect approximation for the friction phenomenon and is widely used in many applications to describe friction [11,12]. It is regarded as a dynamic friction model, which can completely describe the pre-sliding and gross sliding periods of the motion in the mechanical transmission device [13]. Especially compared with the Karnopp model [8] and Borello model [9], the LuGre algorithm can more comprehensively describe the friction characteristics. Therefore, this model is used to describe the friction torque of the EMA system. Due to the play between adjacent movable parts of the EMA system, the backlash is a common phenomenon in the EMA system. The backlash can cause oscillations and inaccuracy in the system [14]. There are two methods to alleviate the backlash effects: the mechanical solution [13] and the controller solution. The former uses pre-load-spring to reduce the disadvantage of the backlash. However, it is not suitable for a rapid system like the EMA system. The latter uses a backlash compensation method to reduce the effect of the backlash, which is a widely used method. There are many backlash models, such as describing function [15], inverse model [16], dead zone model [17,18], novel fuzzy backlash model [19], and Hysteresis nonlinear model [20,21]. Among them, the Hysteresis nonlinear model is widely used, and the core of the compensation is to use the hysteresis inverse model to cancel the effect of the backlash [22].
A proportional integral derivative (PID) controller is usually used to control the EMA system, but considering the nonlinear characteristics of the EMA system, the traditional PID controller has disadvantages. Because of this, many scholars put forward different control strategies for the EMA system. In [23,24], a sliding-mode variable structure controller is proposed to improve the dynamic characteristics. However, it has the problem of chattering. In [25], the Genetic algorithm (GA) optimized fuzzy supervisory PID controller is adopted in the EMA system. Since the rules of a fuzzy controller consist of an antecedent part and a consequent part, it is difficult to define the fuzzy rules. In [26], an inner-loop control strategy is implemented in the electromechanical actuator. Each of the proposed methods has different models and assumptions, which cannot be applied easily to other cases, and some trade-off is necessary to achieve the performance. It is essential to improve the controller to achieve better performance.
ADRC is an improved version of the PID controller. ADRC consists of three core components: a tracking-differentiator (TD), an extended state observer (ESO), and a nonlinear state error feedback (NLSEF). The feasibility of the ADRC to control systems depends upon estimating the disturbance, in a timely and accurate manner. Conventional ADRC is widely used in various applications [27]. However, take the second order plant, for example, where the conventional ADRC has 11 parameters that need to be tuned. Parameters of the conventional ADRC and various forms of improvement of ADRC [28,29] are usually tuned by trial and error. There are two research methods of conventional ADRC, which are tuning parameters and making the algorithm linear, respectively. The former proposed the time scale method and genetic algorithm to describe the ADRC [30,31], and the latter represents the linear extended state observer (LESO) [32]. Meanwhile, the concept of bandwidth parameters is proposed. LESO is popular to estimate state and disturbance for many systems, such as permanent magnet brushless direct current (DC) motor [33] and rigid-body vehicle moving control [34].
Inspired by the recent papers and studies above, the synthesis of improved ADRC and nonlinear compensation is proposed for the EMA system in this paper. The method of improved ADRC is based on the LESO and Fal function filter. The LuGre model and Hysteresis inverse model are used to identify and compensate the friction and backlash phenomenon, respectively. Besides, for the purpose of optimizing the controller parameters, the non-dominated sorting genetic algorithm II (NSGA-II) is adopted. The main contribution of this paper is to provide a compound controller, which can not only effectively improve the dynamic performance and anti-disturbance ability of the system, but also improve the steady-state performance of the system, as a result of adopting the Fal function filter.
2. Problem Formulation
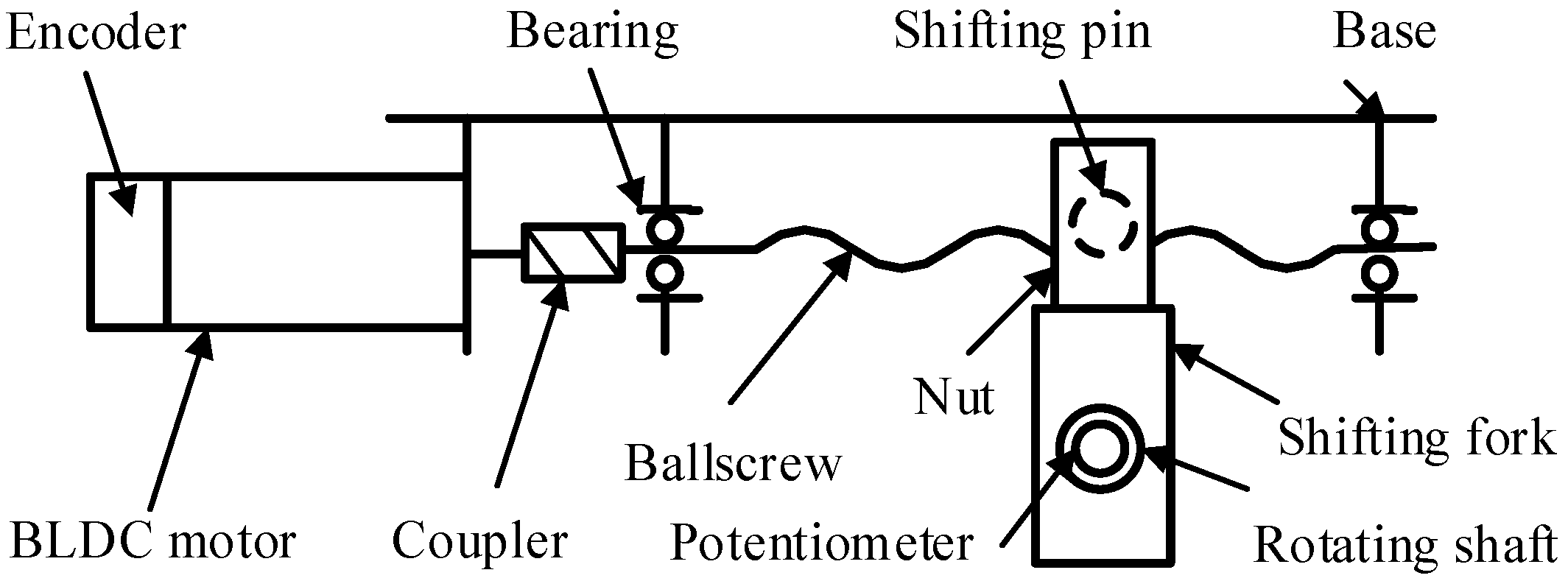
The simplified diagram of the EMA system is shown in Figure 1. The EMA mechanism consists of a ball screw, nut, shifting pin, shifting fork, rotating shaft, brushless direct current motor, and coupler.
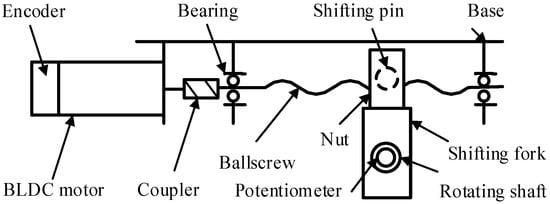
Figure 1.
The diagrammatic sketch of the EMA system.
2.1. System Model
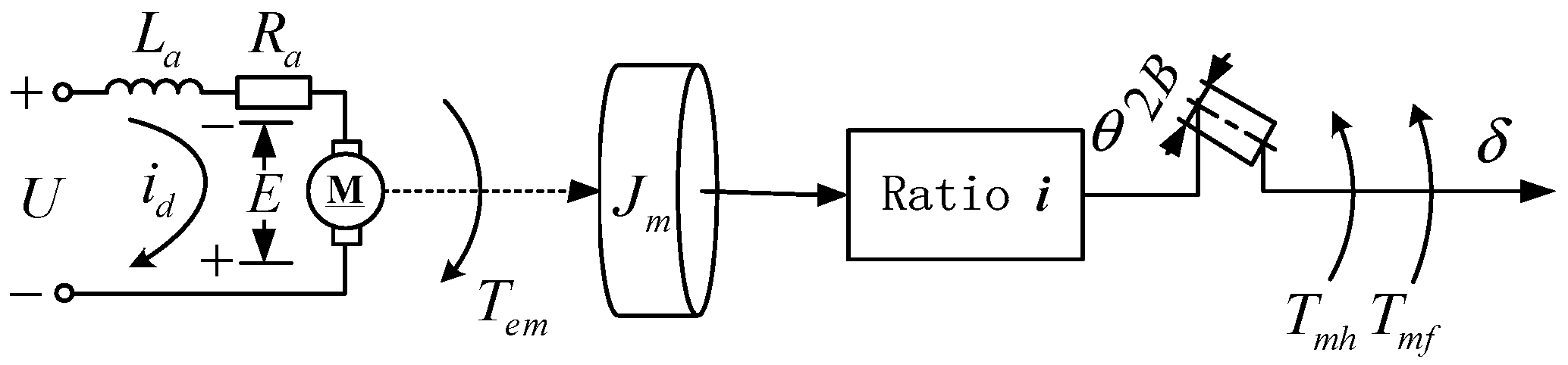
The system model of the EMA system is presented in Figure 2.
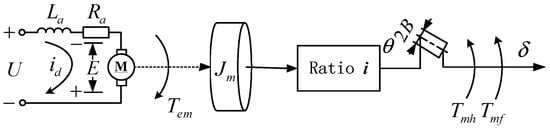
Figure 2.
Dynamic transfer model of the EMA system.
The brushless direct current motor (BLDCM) (shown in Figure 2, represented by the symbol M) is used to drive the mechanism of the EMA system. The transmitted torque and the motion relationship between the actual position and backlash is expressed by Equation (1).
where represents the equivalent moments of inertia. , , , denote the pulse width modulation (PWM) coefficient, the armature resistance, the armature inductance, and the armature current, respectively. , , and denote the rotor speed, the motor torque, the torque constant, and the electrical constant, respectively. is the friction torque, is the load torque, is the equivalent backlash of the output shaft, is the actual position with backlash, and is the position without backlash. As shown in Equation (1), if the load of the EMA system is determined, the motor selection is determined, and the model of nonlinear characteristics is clear, meaning the dynamic characteristics of the EMA system can be analyzed. In Section 2.2, the nonlinear model will be analyzed.
2.2. Nonlinear Factors
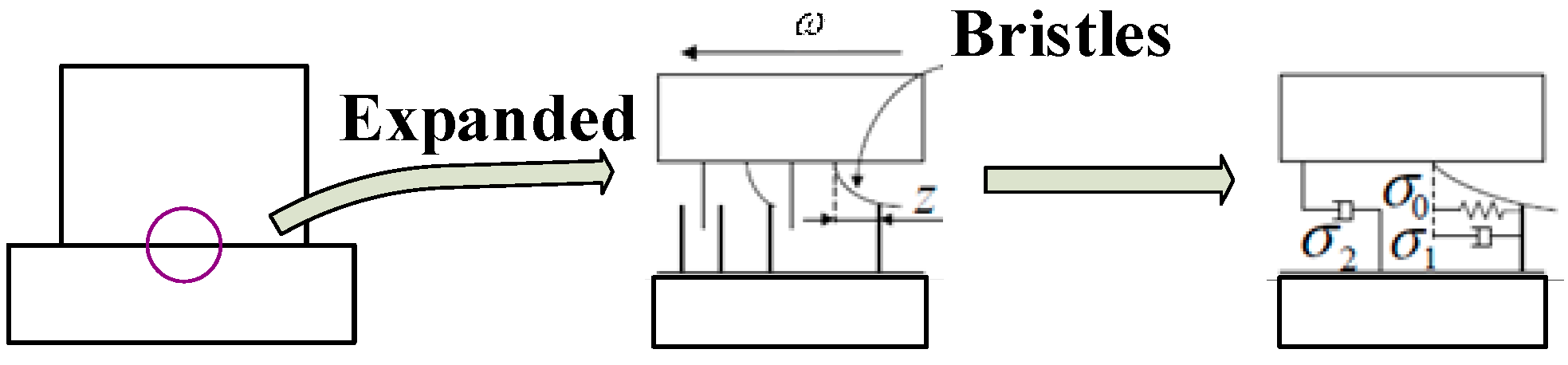
In the EMA system, nonlinear factors are inevitable, and they seriously degrade system performance. It is urgent to carry out research on the nonlinear model. Introduction and identification of the friction model are first presented. The LuGre model is a popular friction model. The schematic of the LuGre model is illustrated in Figure 3.
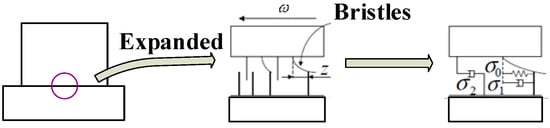
Figure 3.
The schematic of the LuGre model.
Friction torque is as follows [35]:
where is the friction torque, is the coulomb friction torque, is the static friction torque, is the bristle stiffness, is the bristle damping, is the viscous friction coefficient, is the Stribeck velocity, is the velocity of the system, is the dynamics of the deformation of bristles. also appears in Equation (1). If the parameters of the friction model in Equation (2) of the system can be determined, the value of can be obtained. When the value of is obtained, it can be combined with Equation (1) to calculate the performance of the EMA system. Static parameters, such as , , and , are obtained by identification with the constant speed motion method. Thus, (as a result ), and can be described by the following equation:
Equation (3) is the intermediate equation for friction parameter identification. Substituting Equations (2) and (3) into Equation (1), (shown in Equation (1)) is set as 0, and the friction torque is as follows:
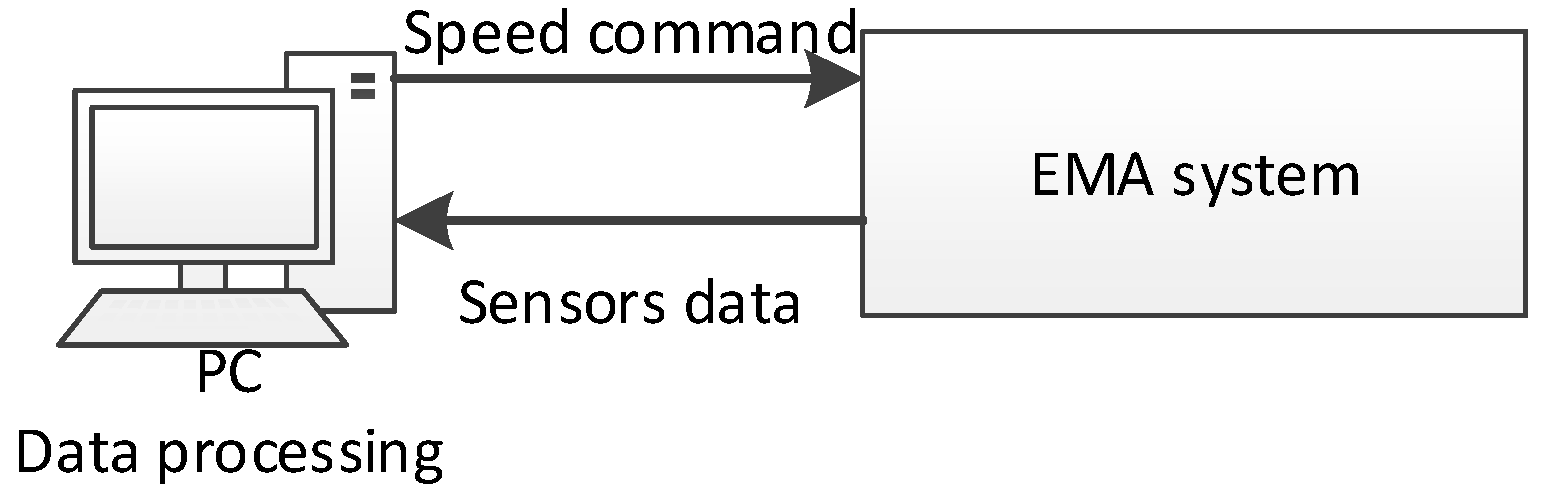
where the subscript denotes the steady state, that is, the speed is the data measured at a constant speed. It can be seen from Equation (4) that we can measure the armature current to obtain the friction torque. The test bench is shown in Figure 4. The test bench consists of a PC and the EMA system. The PC is used to send commands to the EMA system and receive the sensors’ output from the EMA system. Then, the PC processes the data to identify the friction parameters.
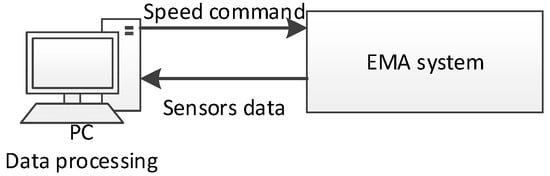
Figure 4.
Schematic diagram of test bench.
According to the type selection and constituent units of the EMA system, shown in Figure 1, ignoring the high-order factors, this paper uses the second-order model in Equation (1) to study the characteristics of the system. Therefore, in the next identification process, our physical model is consistent with the mathematical model shown in Equation (1).
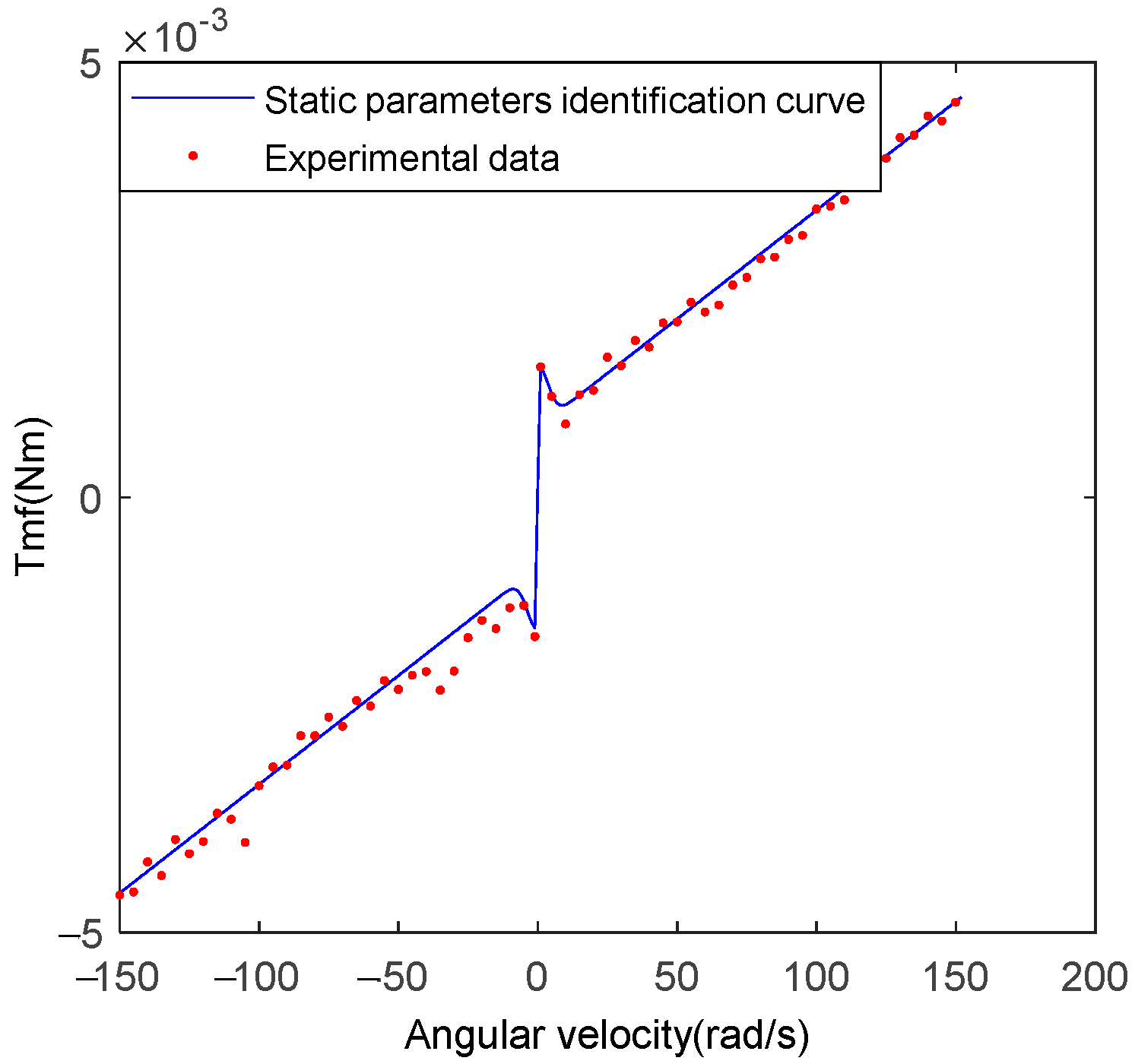
The identification process is as follows: run the EMA system at a uniform speed and measure the corresponding speed and current to obtain a set of values, and then the speed increases continuously from a small value to a large value (the curve type shown in Figure 5). Then, the static parameters in the corresponding Equation (4) can be obtained by the least square method. Static parameters are identified by using the least square method and are shown in Table 1.
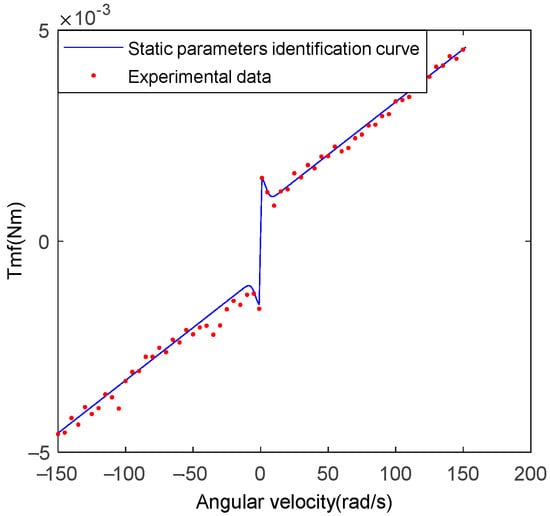
Figure 5.
Static parameters identification curve.

Table 1.
Static parameters of the LuGre model.
The identification of dynamic parameters is also very important. The dynamic parameters of the LuGre model can be obtained as follows: firstly, model linearization is adopted at and , and then , and should be replaced in Equation (3), shown in Equation (1) can be written as:
In order to deduce how to obtain dynamic parameters, set and combine Equation (1), Equation (2), and Equation (5) by Laplace transform, and we can get:
According to the form of Equation (6), we can use the second-order system theory to analyze the dynamic parameters. Set , , Equation (6) can be described as:
As shown in Equation (7), the theory of second-order damping systems can be used to deal with the system’s friction problem. Using the experimental platform shown in Figure 4, the input command is the position command. By obtaining the step response curve of the system, then, according to the principle of a second-order system, , is obtained. Based on classical second-order control theory, and are obtained. Dynamic parameters are presented in Table 2.

Table 2.
Dynamic parameters of the LuGre model.
Introduction and identification of the backlash model are presented. The Hysteresis model is applied to describe backlash and is shown in Equation (8). The inverse model is presented in Equation (9) [36]:
where is the desired output of the EMA system, is Dirac function, which compensates the backlash instantaneously when the backlash is , is the reduction ratio.
The schematic diagrams of the Hysteresis and Hysteresis inverse model are shown in Figure 6. The backlash characteristic is shown in Figure 6a. The backlash inverse shown in Figure 6b is used to cancel the effect of the backlash [16].
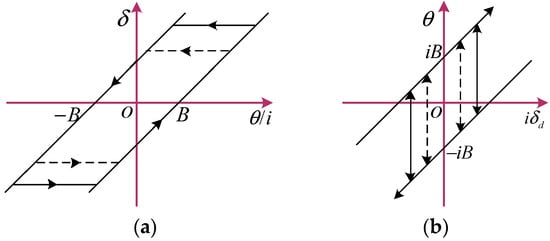
Figure 6.
Schematic diagrams of Hysteresis model and Hysteresis inverse model. (a) Hysteresis model; (b) Hysteresis inverse model.
The total length of the screw is 40 mm, and the total length of the nut is 16 mm. Thus, the nut needs to move 24 mm, since the backlash is different at each point, with eight points of 10 mm, 12 mm, 14 mm, 16 mm, 18 mm, 20 mm, 22 mm, 24 mm. They are set to measure the backlash. Finally, the average value of the backlash, obtained above, is the system backlash. The test bench shown in Figure 4 is applied to implement the experiment to measure the backlash. Finally, the system backlash is obtained by collecting and processing the position information.
The backlash is measured in the following steps. Firstly, rotate the motor in a clockwise direction until the nut cannot be rotated due to reaching the bracket wall. Here, the backlash is eliminated. Meanwhile, stop rotating the motor, and the value of the potentiometer is recorded at this position. Secondly, fix the output shaft of the EMA system using the chucking appliance, and then rotate the motor in an anticlockwise direction with a slow speed. The potentiometer records the position at that moment. The difference between the position at that moment and the position of the last time is the backlash at this point. The backlash of the different point is measured by the above method. Finally, the average of the backlash is 0.142°, namely the system backlash.
3. Controller Design
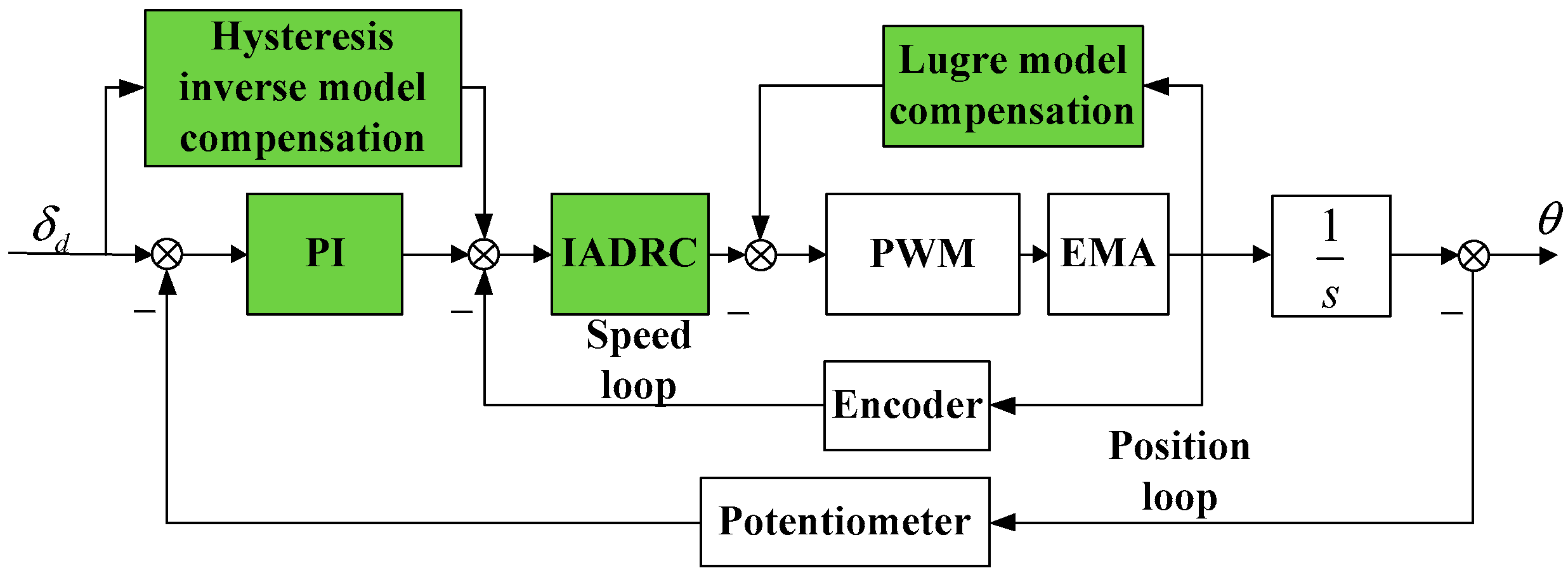
The control block diagram of the EMA system is illustrated in Figure 7. Improved ADRC is used for speed loop control and LuGre model compensation, and Hysteresis inverse model compensation is utilized for controller design. Both of them comprise the compound controller. Friction compensation is carried out by feedback. Backlash compensation is based on the idea of inverse compensation by feedforward.
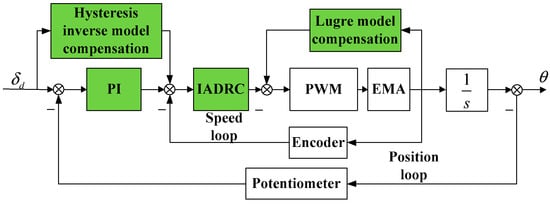
Figure 7.
Control block diagram of the system.
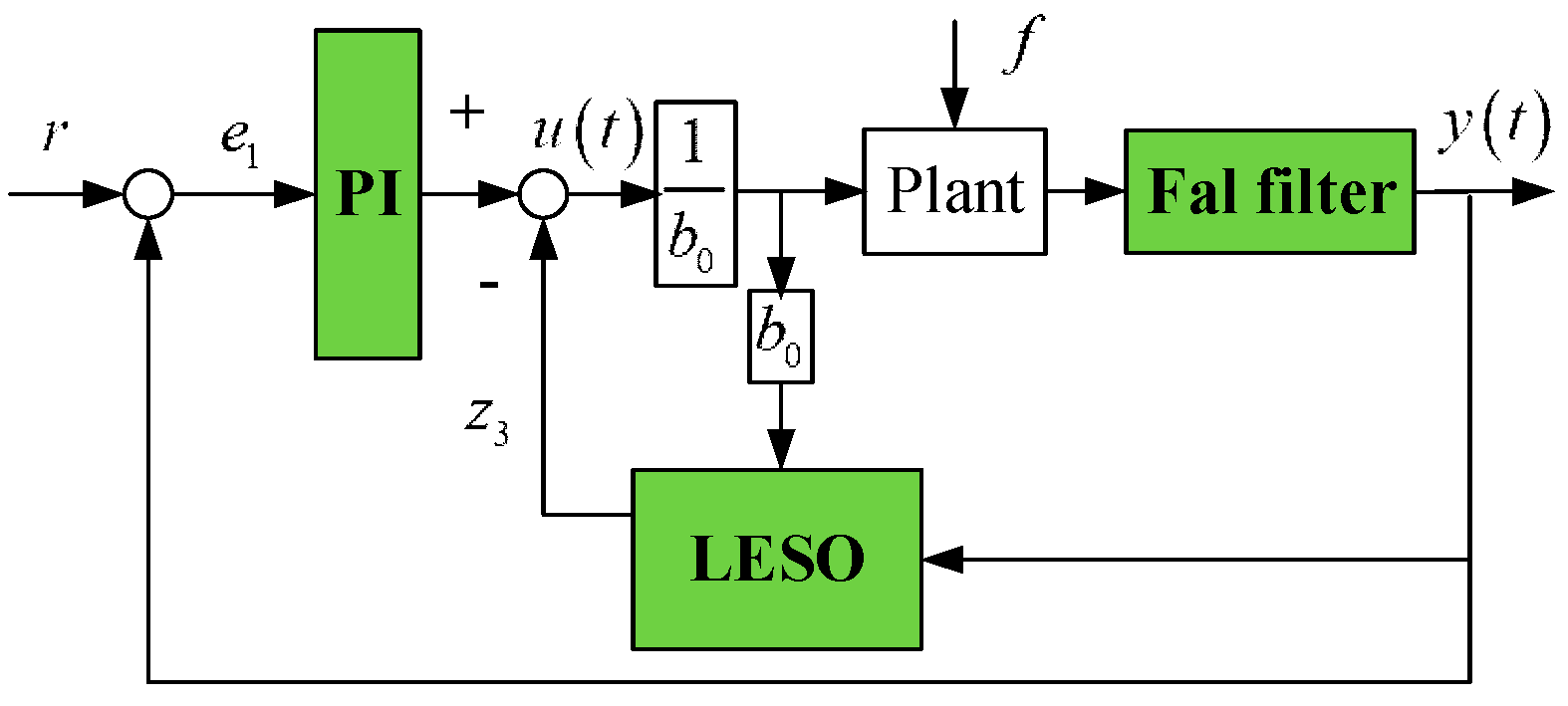
The improved ADRC is established by employing a proportional integral (PI) controller, LESO, and Fal function filter. Figure 8 shows the components of the improved ADRC.
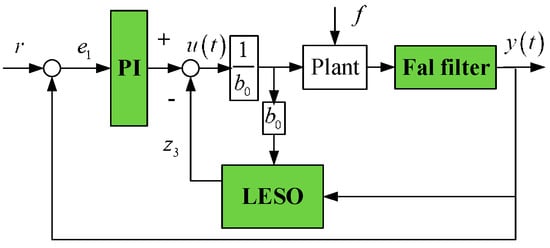
Figure 8.
Block diagram of improved ADRC.
In Figure 8, is the reference input, is the disturbance, is the reference signal, is the system output. is the angular velocity of the system.
3.1. LESO
The LESO estimates the state variables and the unknown disturbances of the system, including internal disturbance [37], including variation of parameters, back electromotive forces, torque ripples unmodeled dynamics, and the external disturbance, such as load disturbances of the EMA system.
These disturbances may affect the performance of the system. The state equation is as follows:
where , , . All the disturbances can be taken as .
Based on the pole placement (pole placement can be used to achieve the regulation), all the observer poles are placed at . and are the observer state variables. The LESO is shown in Equation (11) [38,39].
The control design problem is to process a double integral system. The control law is as follows:
where and are the proportional gain and the integral gain of the speed loop, respectively.
3.2. Fal Function Filter
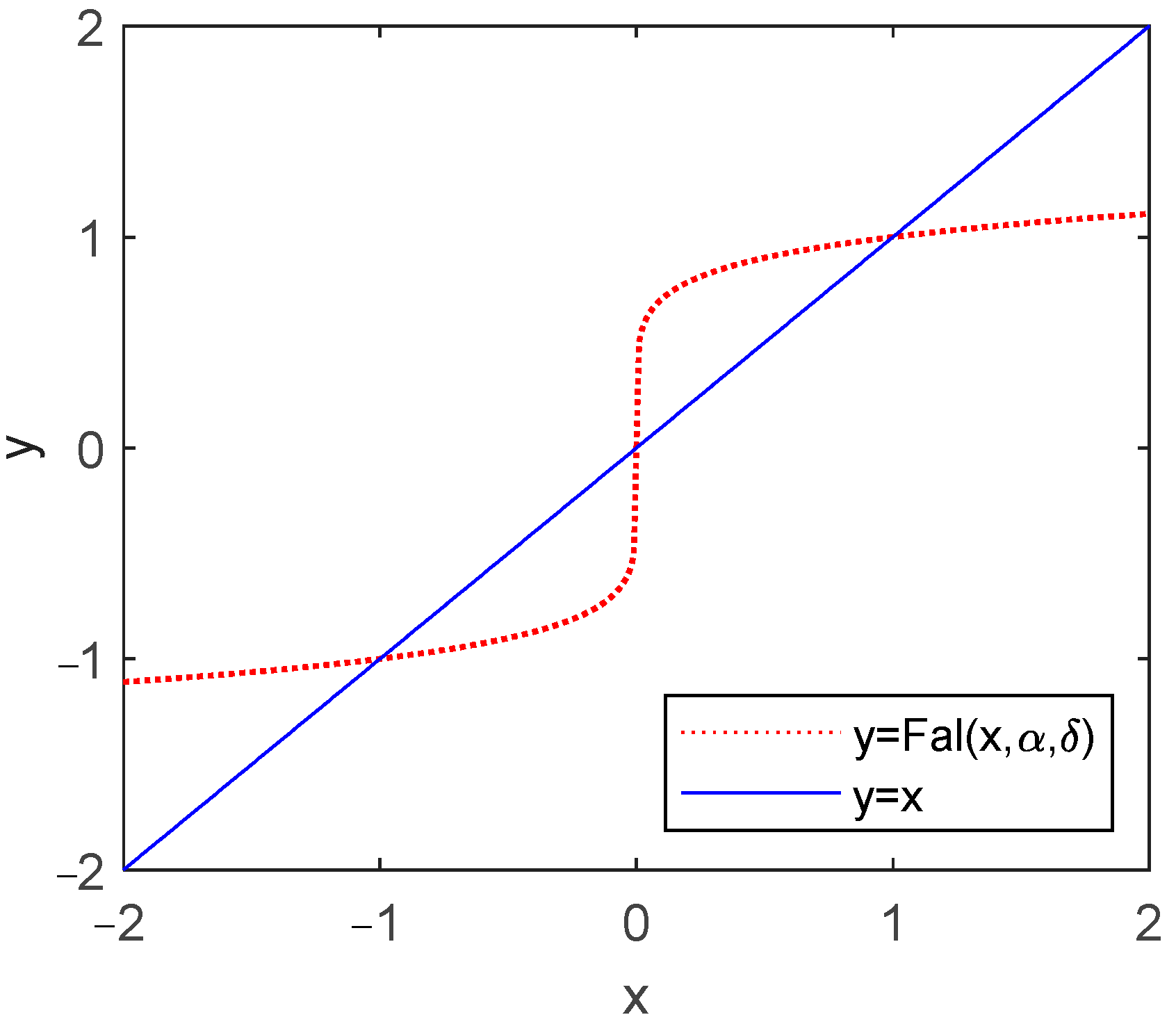
The fitting curve of the Fal function [40] is presented in Figure 9. It implies that the larger the error between input and output, the smaller the gain, and vice versa [41]. The Fal function filter is as follows:
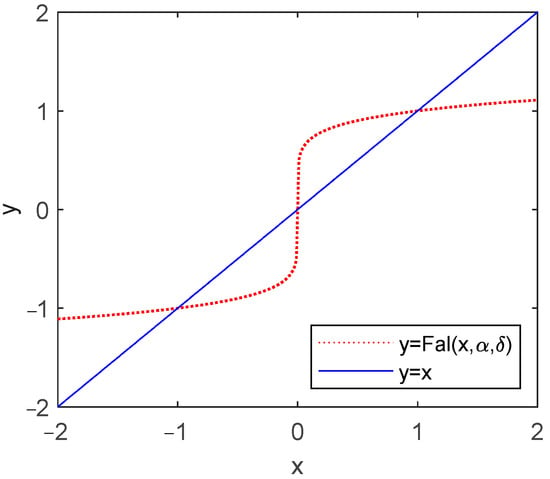
Figure 9.
Fitting schematic diagram of Fal function.
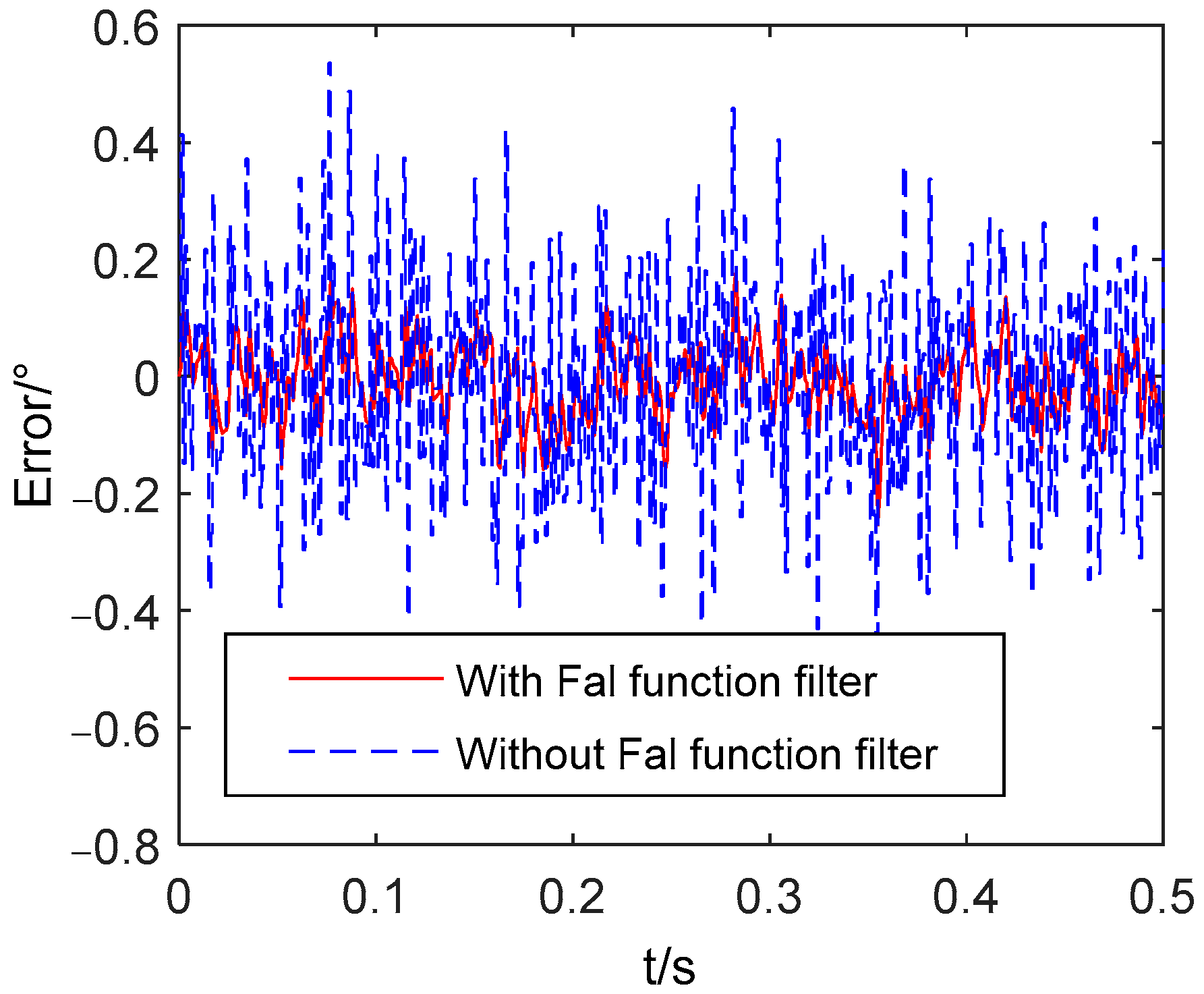
A comparison of unit step response with band-limited white noise power of 0.003 between the system with the filter and the system without the filter is executed to validate the performance of the Fal function filter. The filter parameters are: k = 1000, δ = 0.8, α = 0.5. Figure 10 shows the error comparison for the filter performance. The standard deviation of the error between the reference input and the actual system output are 0.1721° and 0.0612°, respectively. The result shows that this Fal function filter has a good performance of state tracking for the system with noise.
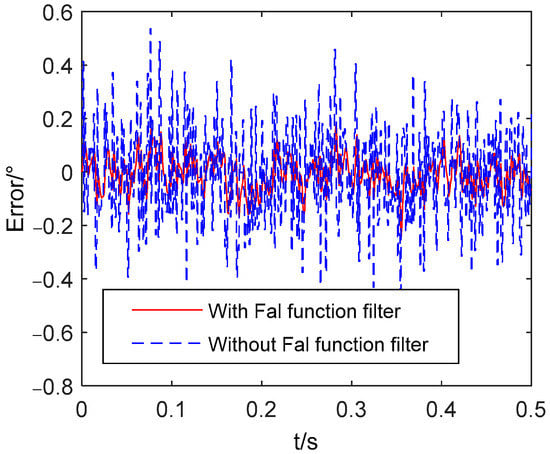
Figure 10.
Error comparison for filter performance.
3.3. Parameter Tuning for the Controller
This part of the paper outlines a method to tune the controller parameters. Controller parameters can be generally obtained by trial and error. Empirical methods may become unworkable if physical systems are complex or too expensive. Here, NSGA-II with multiple constraints handling, is adopted to optimize the improved ADRC parameters.
The objectives include overshoot, integrated time and absolute error (ITAE), and rise time. Overshoot and rise time are performance indexes of step response, and they are chosen as objectives to be minimized. ITAE as an optimal controller index is regarded as an objective to be minimized. According to the control strategy, the improved ADRC has the following input parameters: , , , , , . The multi-objective optimization problem is posed in Equation (14).
where is the error between the system’s input and the system’s output. represents ITAE, here the unit of J is set as . represents the rise time, represents overshoot. Thus, the controller parameters are tuned by NSGA-II so that the performance indexes Fitness1, Fitness2, and Fitness3 are all minimized. The steps are as follows: give a certain initial value and corresponding range of controller parameters, and then combine them into different combinations of controller parameters. Using these controller parameters to control the system, take the step response as the evaluation standard to obtain Fitness1, Fitness2, and Fitness3. If Fitness1, Fitness2, and Fitness3 meet the requirements under the current parameter control, stop the system and record the controller combination under the current state, that is, the optimal controller parameters. If Fitness1, Fitness2, and Fitness3 are not the minimum, continue to simulate until the required simulation results are obtained.
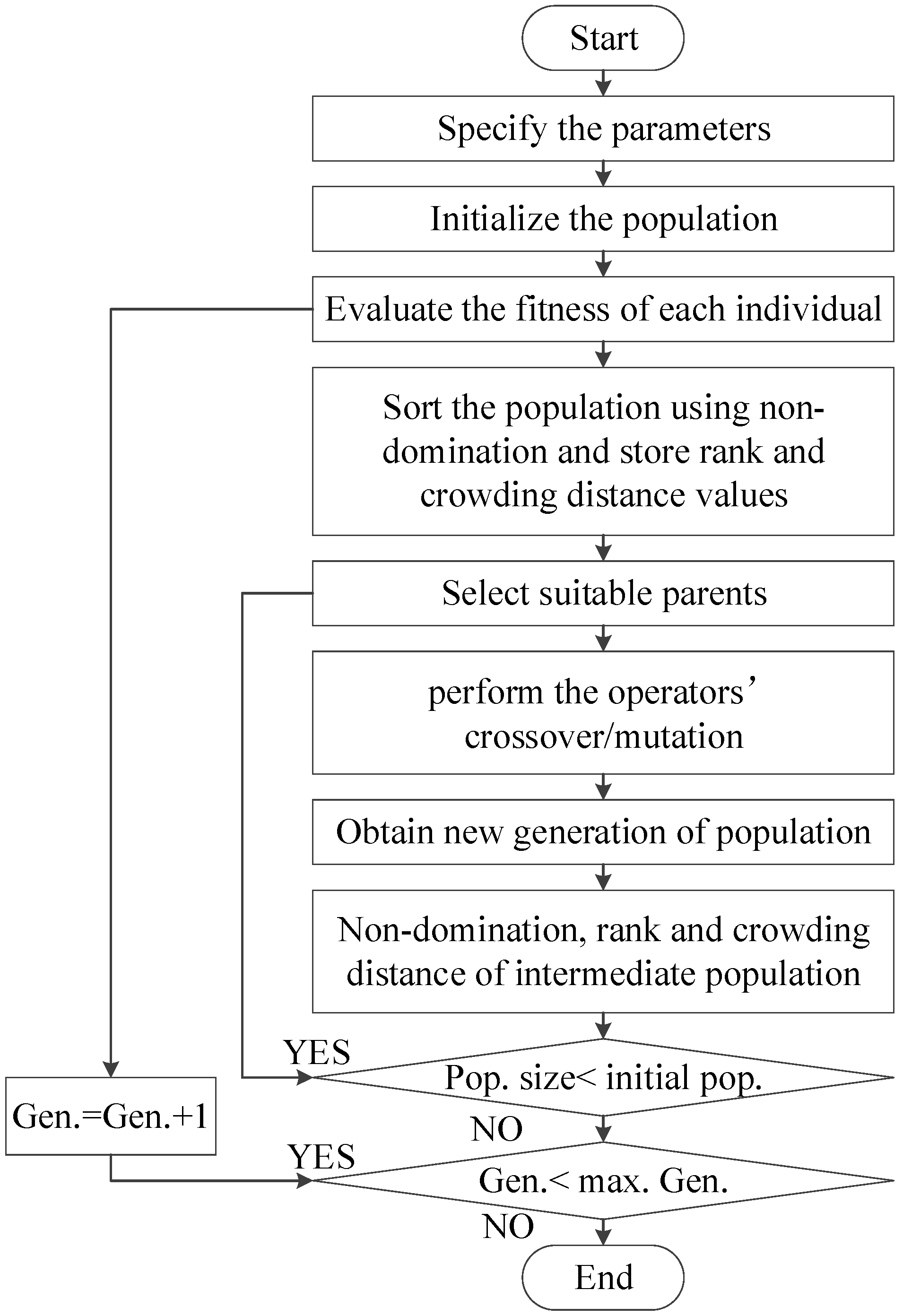
The NSGA-II is an improved approach of the genetic algorithm (GA) for the multi-objective optimization of process responses. Non-dominated solutions of NSGA-II have high crowding distance, which are used to provide diversified Pareto optimal solutions. A Pareto optimal solution cannot be improved with respect to any objective without worsening at least one other objective [42]. The set of feasible non-dominated solutions in the solution space is referred to as the Pareto optimal set. The NSGA-II encompasses advanced concepts like elitism, fast non-dominated sorting, and diversity maintenance along the Pareto optimal front. The flowchart of the NSGA-II is shown in Figure 11.
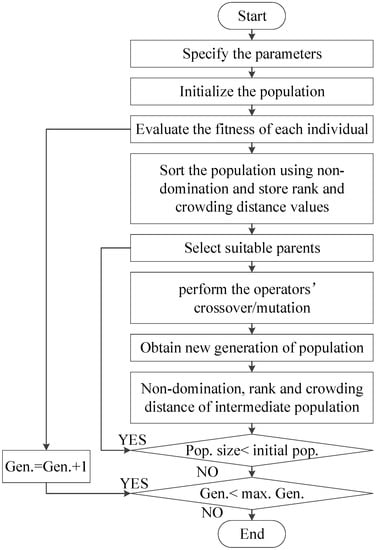
Figure 11.
The flowchart of the NSGA-II algorithm.
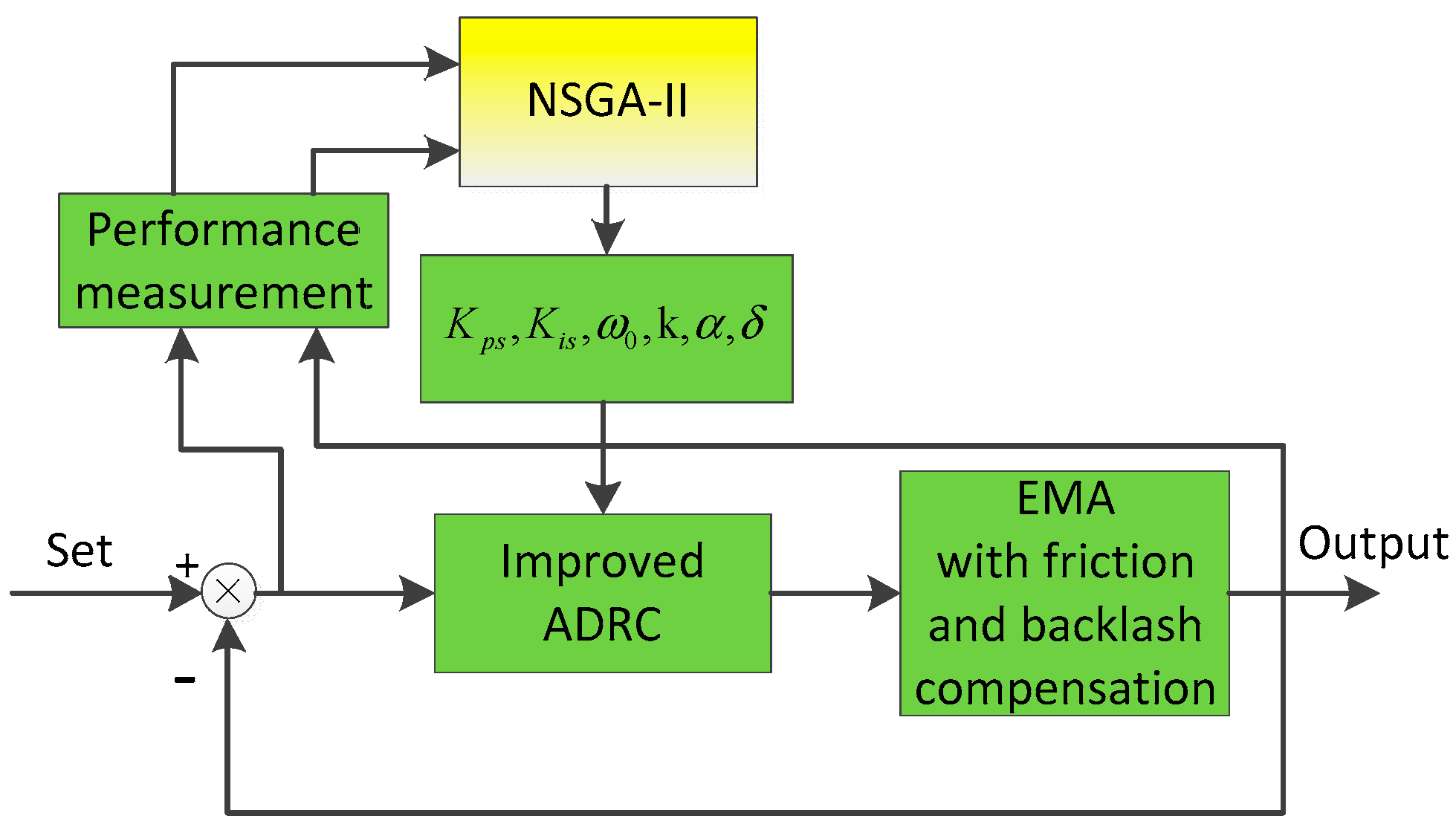
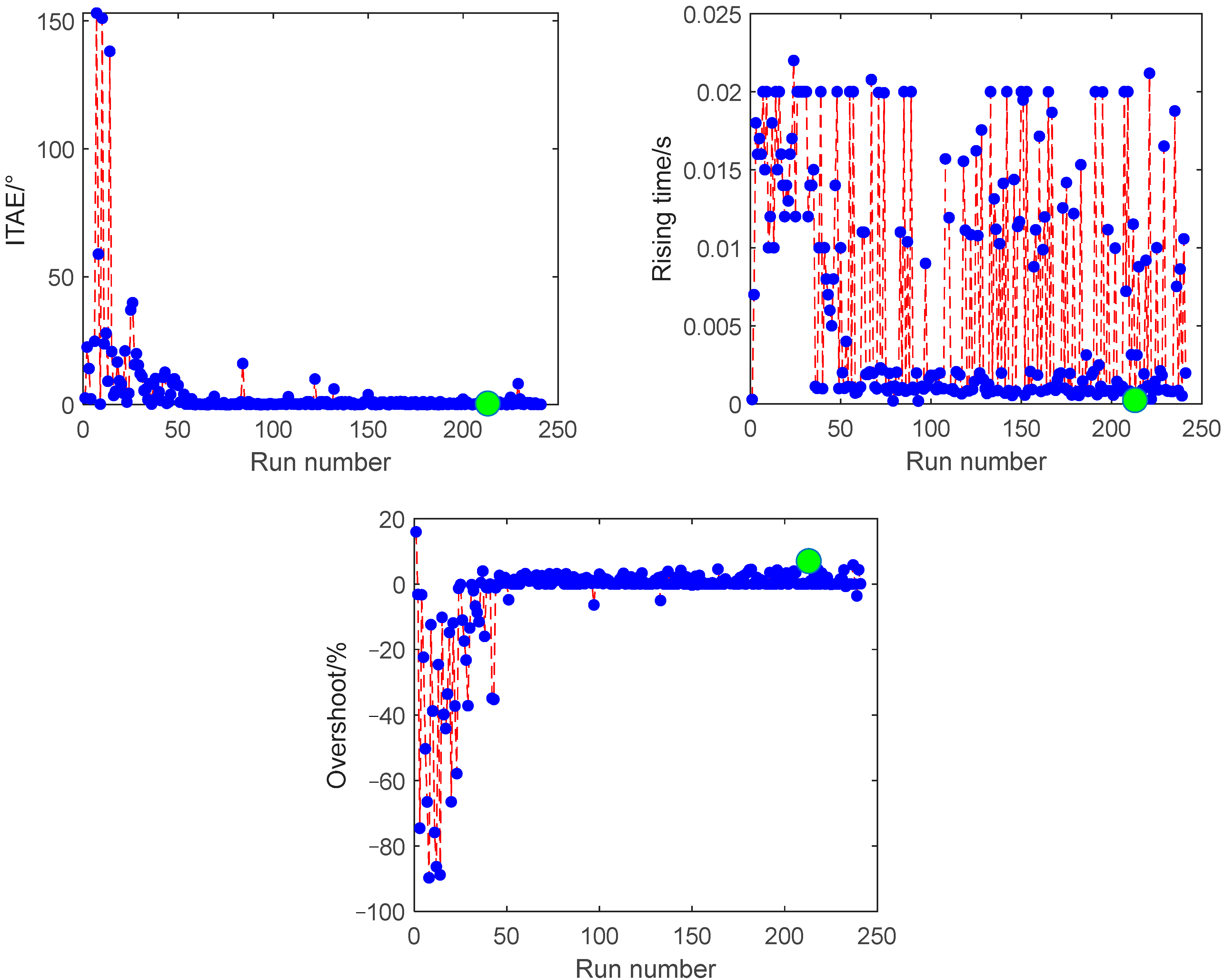
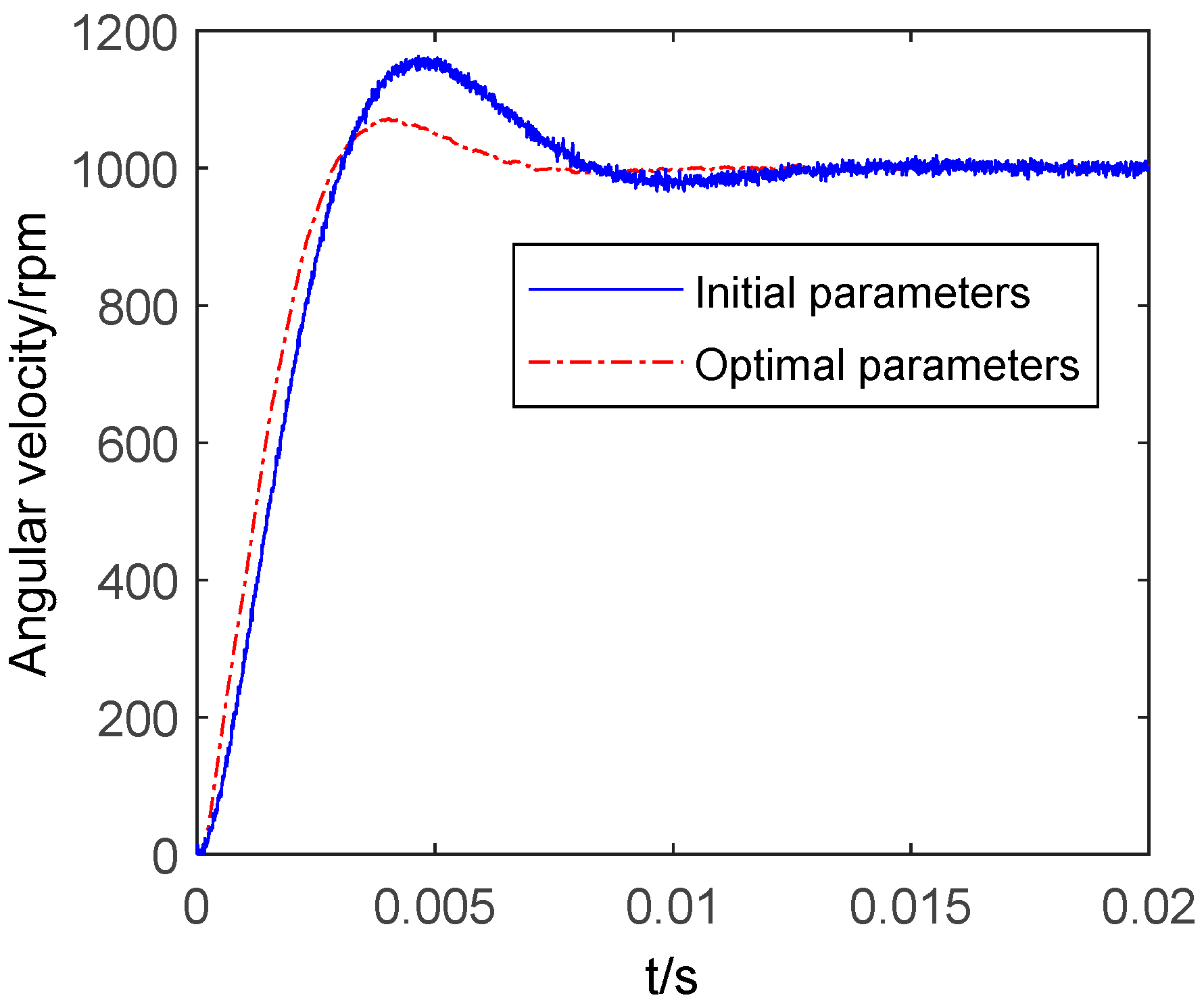
Figure 12 shows the optimization procedure of tuning improved the ADRC parameters, in order to investigate the effectiveness of NSGA-II for the improved ADRC. The population size and maximum generation numbers are set as 12 and 20, respectively. The crossover probability is 0.7, and mutation probability is 0.001. Further, a 1000 rpm step input signal, including band-limited white noise with noise power 0.0003, is given as the command. The Pareto front for triple objective optimization is shown in Figure 13. It can be seen from Figure 13 that green points express the Pareto solution. The optimal parameters and the corresponding optimized values of the objective functions, obtained above, are presented in Table 3. It can be seen from Table 3, that the overshoot is 7.01%, ITAE is 0.43, the rise time is 0.0024 with the optimized parameters. The step response of the EMA system adopting improved ADRC with optimal controller parameters is given in Figure 14. Hence, it can be concluded that the optimal parameters are feasible.
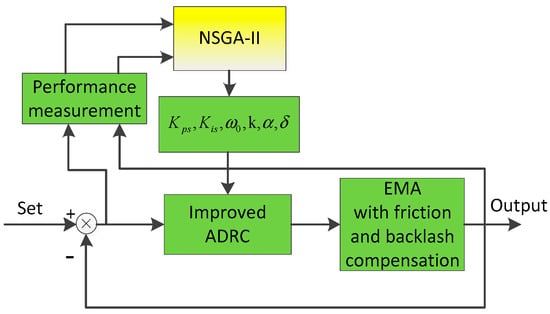
Figure 12.
The optimization procedure of tuning improved ADRC parameters.
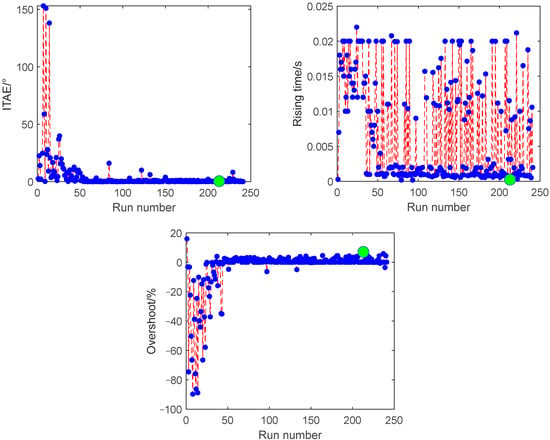
Figure 13.
Pareto front for objective optimization of speed loop.

Table 3.
Optimized controller parameters and their objective values of the speed loop.
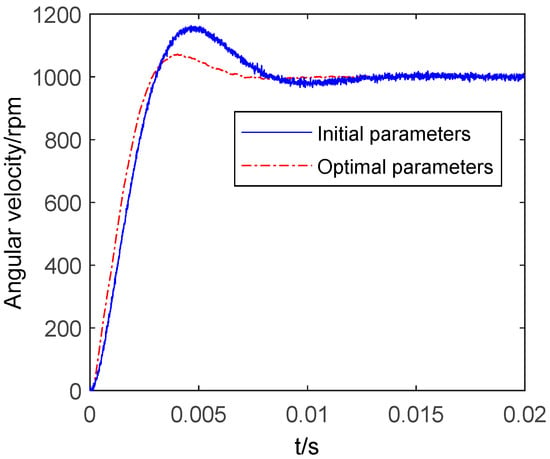
Figure 14.
Step response comparison of 1000 rpm speed input.
The results show that this approach presents a perfect solution for optimizing the controller parameters of the proposed controller with multiple constraints.
4. Simulation Results
The simulation model plays a key role in analyzing the control system design. Based on the above analysis, the performances of the PI controller and proposed controller are compared in the EMA system. The overall simulation model of the EMA system has been prepared in MATLAB/Simulink, used to establish the model of the EMA system. The adopted controllers of the position loop for the two speed loops are PI controllers.
4.1. Sine Wave Response
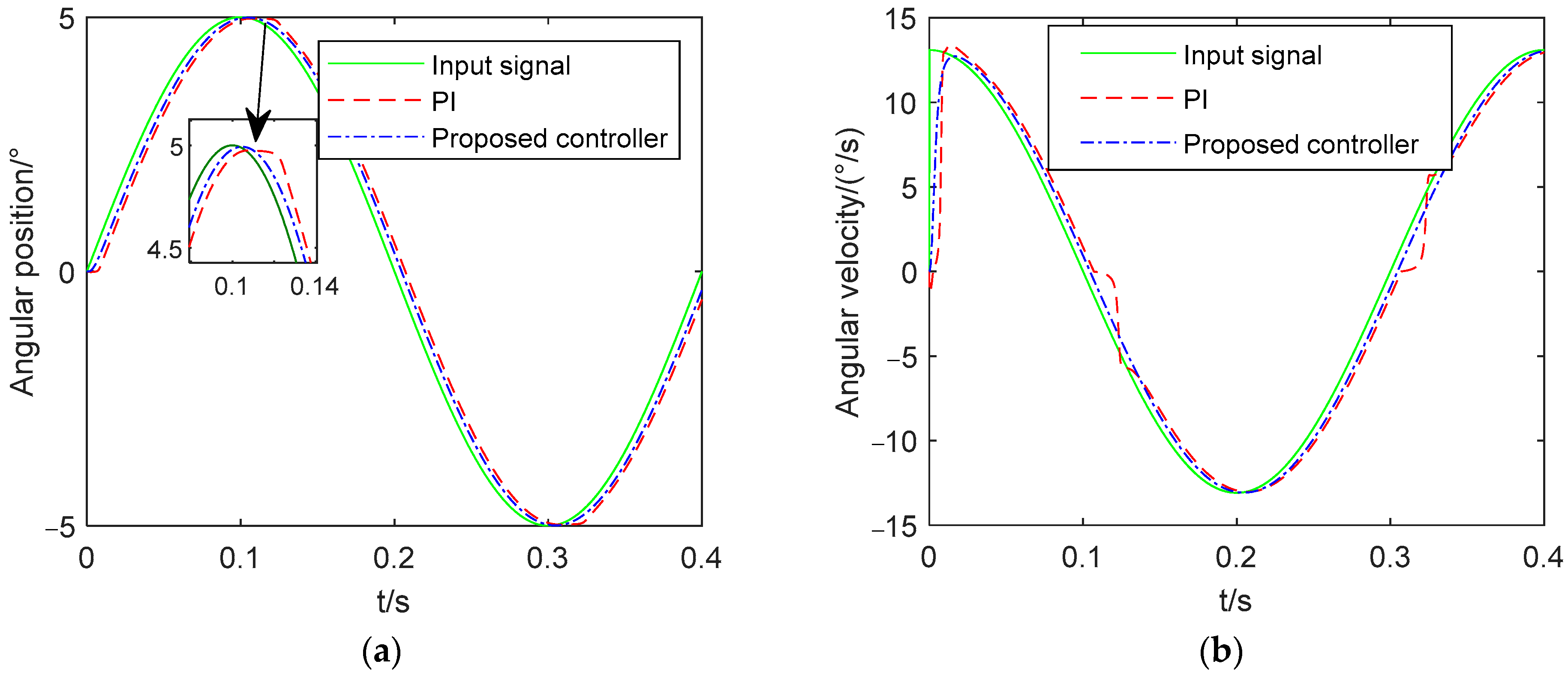
Figure 15 shows the sine wave response for the PI controller and proposed controller. It is seen from Figure 15 that the PI controller cannot deal with the phenomenon of the speed dead zone and position flattening, when the system speed tends to 0, but the new compound controller can solve this problem well. It can be seen that the proposed controller effectively suppresses the nonlinear factors.
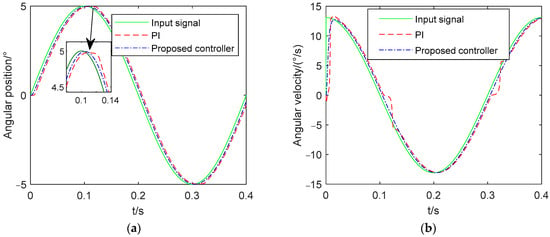
Figure 15.
Response of 5sin (5πt) (a) Position tracking curve; (b) Speed tracking curve.
4.2. Disturbance Rejection Ability Verification
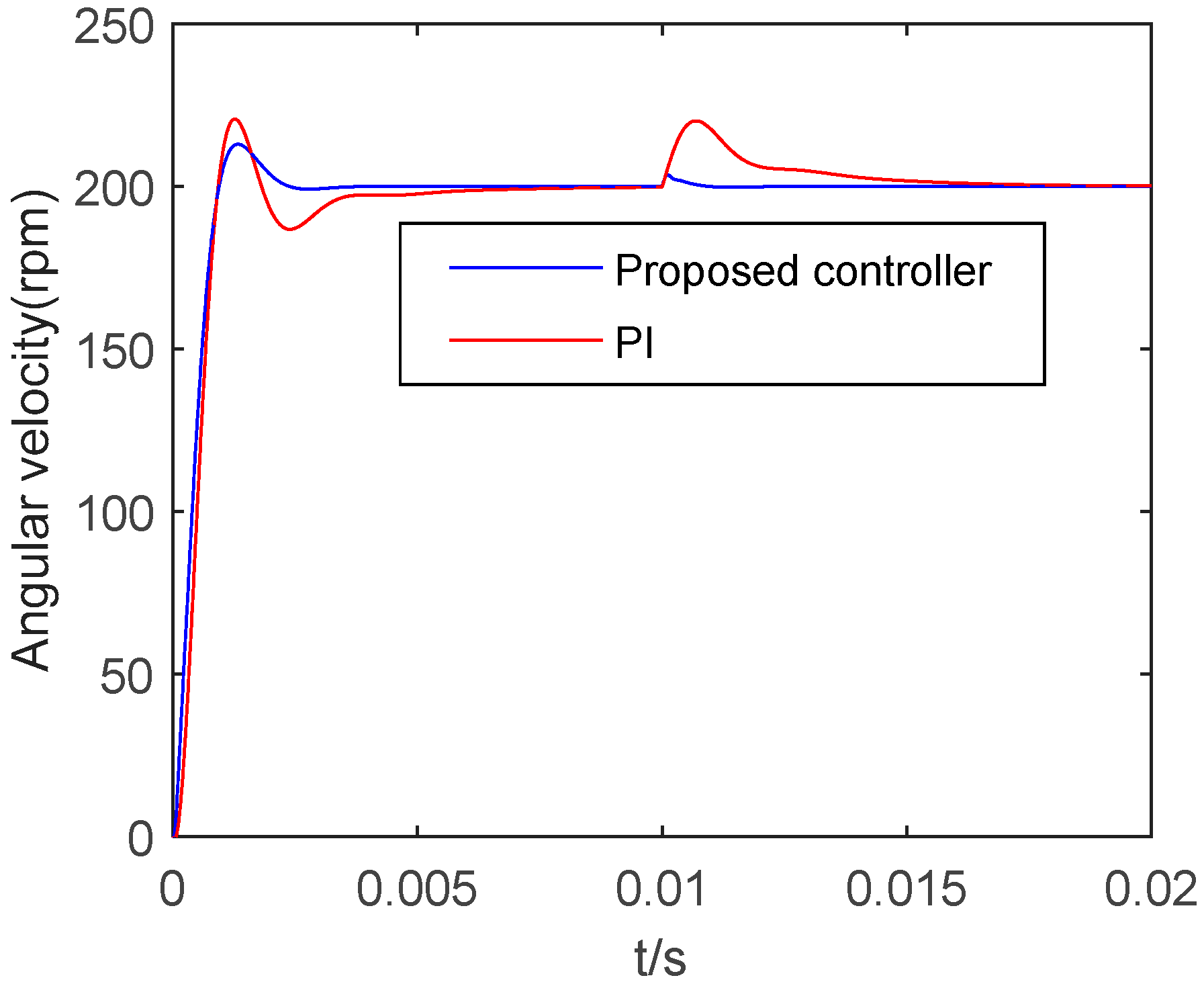
To validate the disturbance rejection ability, a step signal with an amplitude 200 rpm is set as the input of the system. A step disturbance is also added to the system at 0.01 s. The response curve is shown in Figure 16. It is seen from Figure 16 that the rise time and overshoot by the proposed controller are shorter than the conventional PI controller. The peak value and the tuning time of the disturbance by the proposed controller are better than the PI controller. It can be seen that the proposed controller can effectively improve the anti-disturbance ability of the system, on the premise of ensuring the dynamic characteristics of the system.
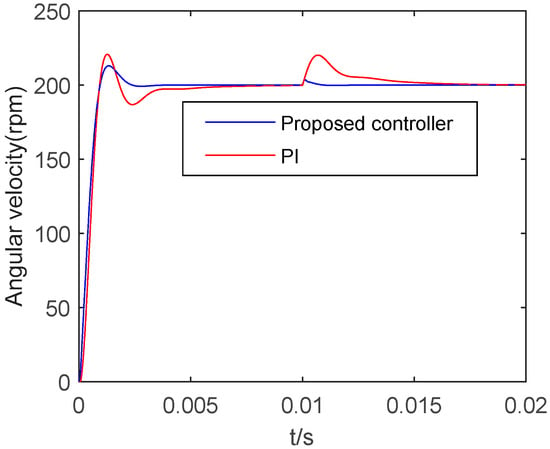
Figure 16.
Step response with disturbance.
5. Experiment Testing
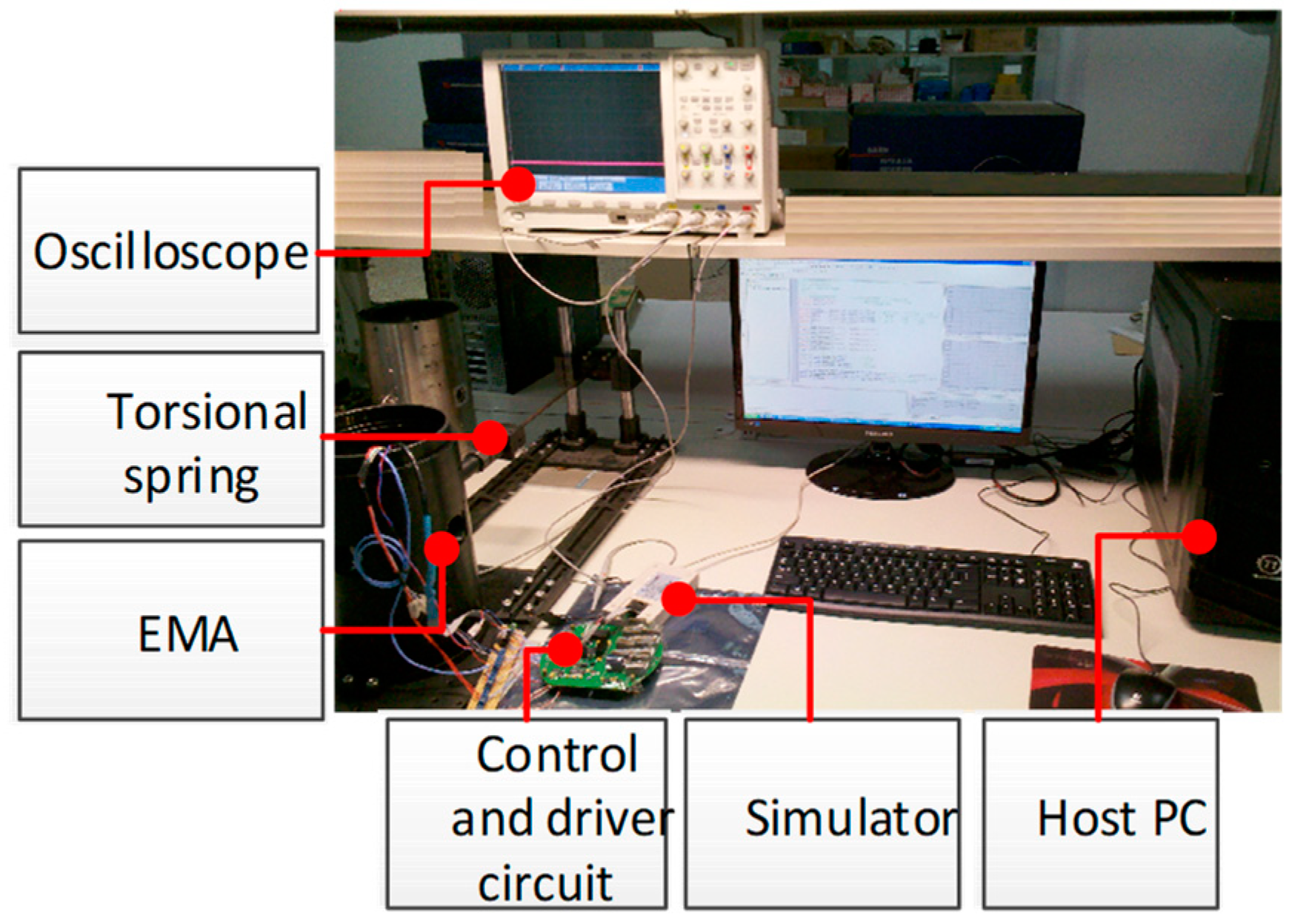
As discussed in the preceding section, the PI controller and the proposed compound controller are applied to the EMA system. The sample time is 1 ms, and the controller is carried out on a Digital Signal Processing chip (DSP). The experimental facility of the EMA system is illustrated in Figure 17. A host PC is used as the upper computer to record and monitor the system in real time. The simulator is used to download the program to the DSP. The torsional spring is used as the load torque of the EMA surface. The oscilloscope is used to monitor the output of the digital signals.
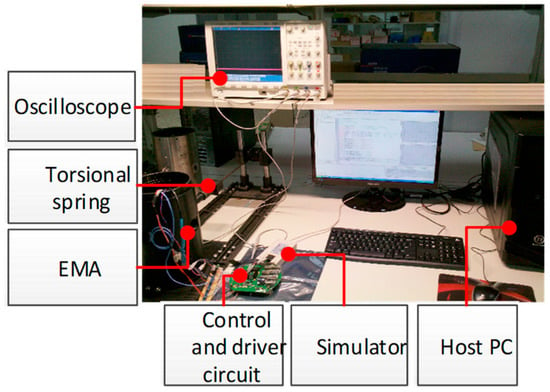
Figure 17.
Experimental facility of the EMA system.
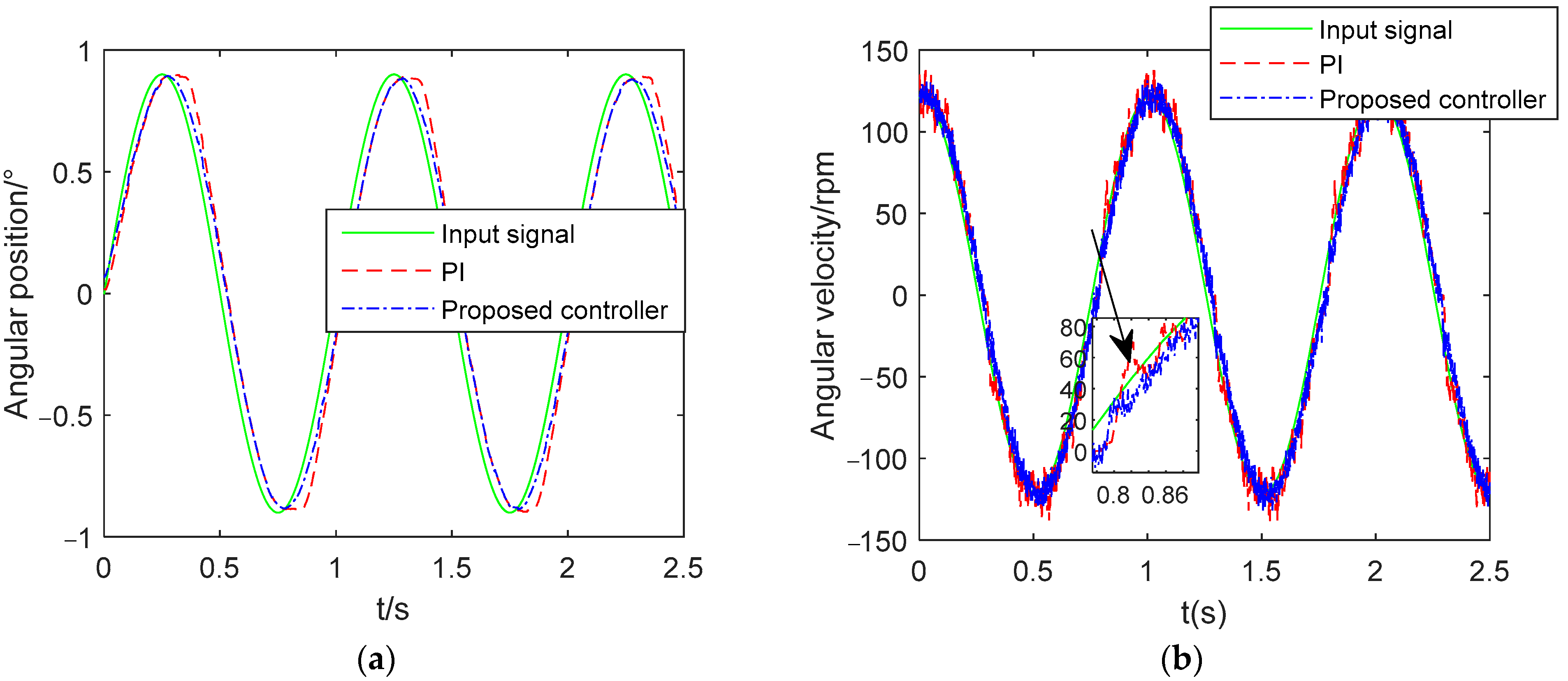
The sine wave response is illustrated in Figure 18. The input of the sine is 0.9sin (0.9πt). It can be seen from Figure 18 that, compared with the system controlled by the PI controller, there is a shorter position flat crest and smaller speed dead zone by the proposed controller of the system output. Under the action of the proposed controller, the system output effectively suppresses the influence of friction and backlash nonlinearity. The comparison results are shown in Table 4. In addition, the noise effect is also alleviated by the proposed controller. Thus, the performance of the proposed controller is better than the PI controller.
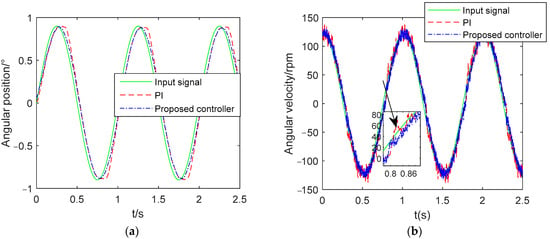
Figure 18.
Curve of tracking (a) Position tracking curve; (b) Speed tracking curve.

Table 4.
Comparison of tracking performance of 0.9sin (0.9πt).
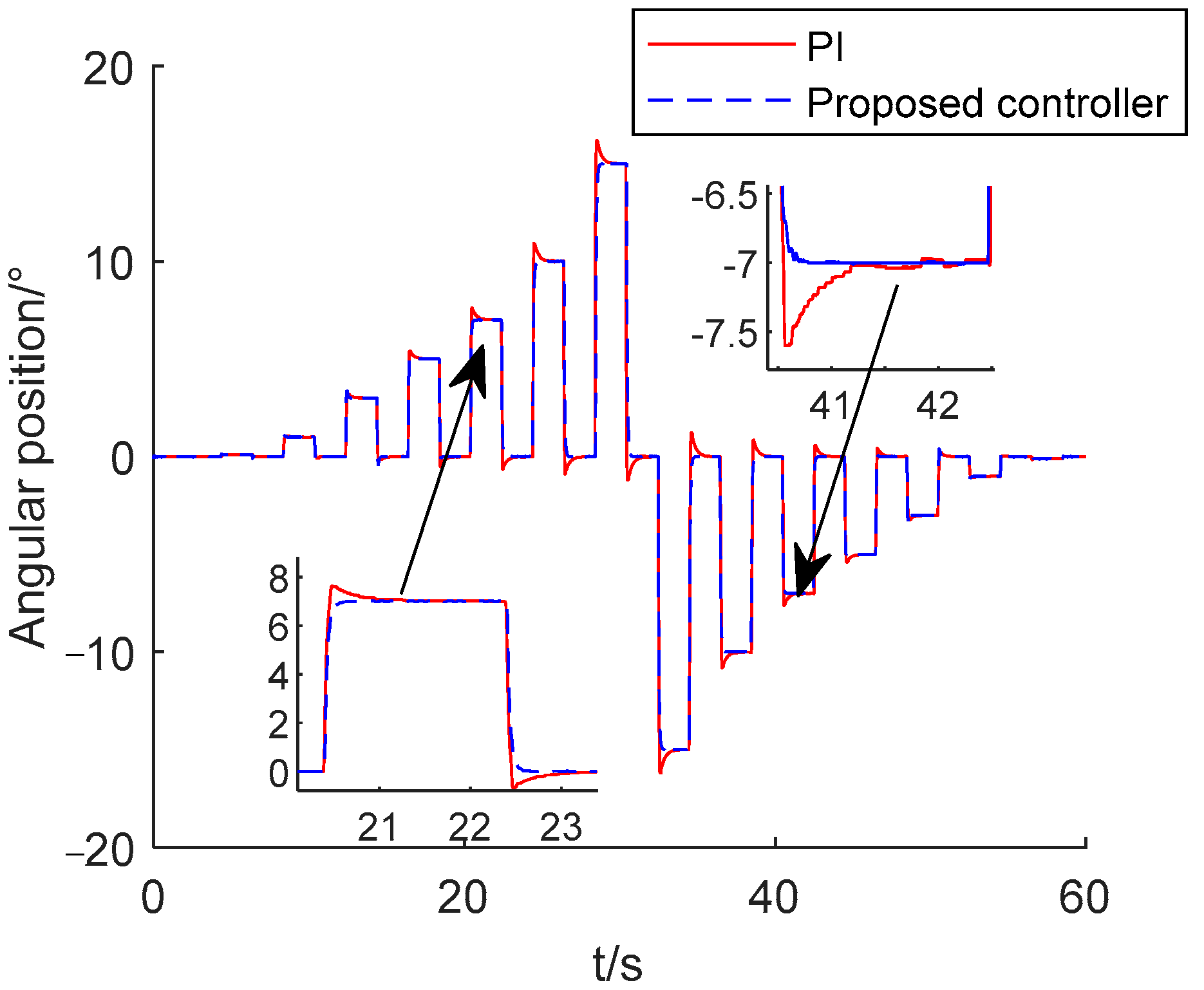
Since the EMA system deflections are limited to ±15°, the performance comparisons of the tracking angular position, from ±1° to ±15°, by different controllers, are shown in Figure 19. Equivalent load torque is added to the EMA system using a torsional spring, which can be regarded as the disturbance. The elastic coefficient of the torsional spring is 0.62 N·m/°. It can be seen from Figure 19 that the PI controller has a long tuning time and a large overshoot, while the proposed controller has a small overshoot and a short tuning time. Taking the response of ±1° and ±15° as examples, the comparison data are shown in Table 5. For the four positions ±1° and ±15°, the three indexes of the proposed controller (tr, Mp, standard deviation) are smaller than the PI controller. It can be seen from the experiments that the proposed controller shows useful properties of good performance and robustness compared with the PI controller.
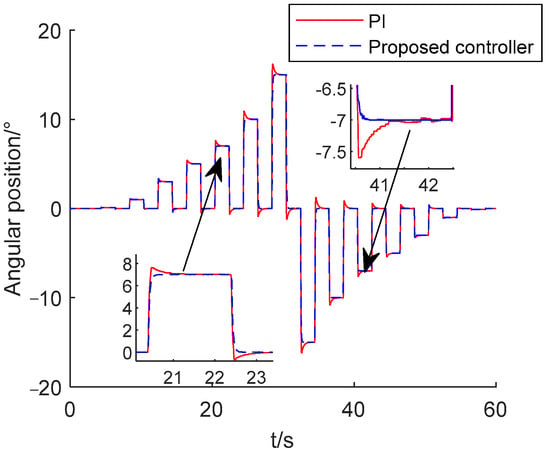
Figure 19.
Step response curve of tracking angular position by different controllers in speed loop.

Table 5.
Comparison of tracking performance of step signals.
6. Conclusions
In this paper, the compound scheme, based on improved ADRC and nonlinear compensation, is developed for the EMA system. The influences of backlash and friction on the EMA system are considered in this paper. The LuGre model and Hysteresis inverse model are used to compensate for the friction and backlash phenomenon, respectively. The improved ADRC, based on the Fal function filter and LESO, is investigated. The non-dominated sorting genetic algorithm II (NSGA-II) is presented to optimize the controller parameters, to achieve the best dynamic response. Simulations and experiments are presented to validate the effectiveness of the proposed method. As shown in Figure 18 and Figure 19, Table 4 and Table 5, the experimental results of the improved ADRC, with nonlinear compensation, indicate that rise time, overshoot and the steady state standard deviation of the EMA system are all improved by the proposed controller. In summary, it can be seen from the obtained results that the proposed controller has a quick response, slight overshoot, and strong anti-disturbance ability. Thus, the dynamic performance and steady precision of the system are both improved. Although the proposed controller does have some advantages, the proposed controller also requires some improvements. For example, how to make the system performance evaluation standard more perfect and reduce the controller parameters through the optimization algorithm are also very worthy of research.
Author Contributions
Conceptualization, M.Z. and Q.L.; methodology, M.Z.; software, M.Z.; validation, M.Z.; formal analysis, M.Z.; investigation, M.Z.; resources, M.Z.; data curation, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, Q.L.; visualization, M.Z.; supervision, M.Z.; project administration, M.Z.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded, in part, by the Tai Shan Scholar Foundation (tshw201502042), and in part by Shandong Province Key Research and Development Plan: 2017CXGC0607.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| List of Symbols | |
| equivalent moments of inertia on motor | |
| armature resistance | |
| armature current | |
| motor output torque | |
| electrical constant | |
| load torque | |
| actual position with backlash | |
| coulomb friction torque | |
| bristle stiffness | |
| viscous friction coefficient | |
| velocity of the system, unit rpm | |
| desired output of the EMA system | |
| reduction ratio | |
| reference signal | |
| , | state variables of the EMA system |
| angular velocity of the system, unit rad/s | |
| output tracking error | |
| controller output | |
| integral gain of the speed loop | |
| integrated time and absolute error (ITAE) | |
| overshoot of step response | |
| pulse width modulation (PWM) coefficient | |
| armature inductance | |
| rotor speed | |
| torque constant | |
| friction torque | |
| equivalent backlash of the output shaft | |
| position without backlash | |
| static friction torque | |
| bristle damping | |
| Stribeck velocity | |
| dynamics of deformation of bristles | |
| Dirac function | |
| reference input | |
| system output | |
| all the disturbances of the EMA system | |
| bandwidth of the LESO | |
| , | observer state variables |
| proportional gain of the speed loop | |
| ,, | parameters of the Fal function |
| rise time of the step response | |
| List of Acronyms | |
| ADRC | active disturbance rejection controller |
| LESO | linear extended state observer |
| PI | proportional integral controller |
| GA | genetic algorithm |
| ESO | extended state observer |
| DC | direct current |
| ITAE | integrated time and absolute error |
| EMA | electromechanical actuator |
| NSGA-II | non-dominated sorting genetic algorithm II |
| PID | proportional integral derivative controller |
| TD | tracking differentiator |
| NLSEF | nonlinear state error feedback |
| BLDCM | brushless direct current motor |
| DSP | digital signal processing chip |
References
- Aravind, M.A.; Dinesh, N.S.; Rajanna, K. Application of empc for precise position control of dc-motor system with backlash. Control Eng. Pract. 2020, 100, 104422. [Google Scholar]
- Lichtsinder, A.; Gutman, P.O. On the dual properties of friction and backlash in servo control systems. IFAC-PapersOnLine 2019, 52, 340–345. [Google Scholar] [CrossRef]
- Olsson, H.; Astrom, K.J.; Wit, C.C.D. Friction models and friction compensation. Eur. J. Control 1998, 4, 176–195. [Google Scholar] [CrossRef] [Green Version]
- Piatkowski, T. Dahl and lugre dynamic friction models—The analysis of selected properties. Mech. Mach. Theory 2014, 73, 91–100. [Google Scholar] [CrossRef]
- Gafvert, M. Comparisons of Two Dynamic Friction Models. In Proceedings of the IEEE International Conference on Control Applications, Hartford, CT, USA, 5–7 October 1997. [Google Scholar]
- Dupont, P.; Hayward, V.; Armstrong, B.; Altpeter, F. Single state elastoplastic friction models. IEEE Trans. Autom. Control 2002, 47, 787–792. [Google Scholar] [CrossRef]
- Jin, X.; Wang, Y.; Huang, Z. Approximately analytical technique for random response of lugre friction system. Int. J. Non-Linear Mech. 2018, 104, 1–7. [Google Scholar] [CrossRef]
- Karnopp, D. Computer simulation of stick-slip friction in mechanical dynamic systems. J. Dyn. Syst. Meas. Control 1985, 107, 100–103. [Google Scholar] [CrossRef]
- Borello, L.; Vedova, M. A dry friction model and robust computational algorithm for reversible or irreversible motion transmissions. Int. J. Mech. Control 2012, 13, 37–48. [Google Scholar]
- Al-Bender, F.; Vincent, V.; Swevers, J. The generalized maxwell-slip model: A novel model for friction simulation and compensation. IEEE Trans. Autom. Control 2005, 50, 1883–1887. [Google Scholar] [CrossRef]
- Pikunov, D.; Stefanski, A. Numerical analysis of the friction-induced oscillator of duffing’s type with modified lugre friction model. J. Sound Vib. 2019, 440, 23–33. [Google Scholar] [CrossRef]
- Fengfa, Y.; Xingfei, L. Robust adaptive integral backstepping control for opto-electronic tracking system based on modified lugre friction model. ISA Trans. 2018, 80, 312–321. [Google Scholar]
- Lotfi, B.; Zhong, Z.W.; Khoo, L.P. A novel algorithm to generate backlash-free motions. Mech. Mach. Theory 2010, 45, 1171–1184. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Z.; Zhang, Y.; Chen, C.L.P.; Xie, S. Actuator backlash compensation and accurate parameter estimation for active vibration isolation system. IEEE Trans. Ind. Electron. 2016, 63, 1643–1654. [Google Scholar] [CrossRef]
- Freeman, E.A. The effect of speed-dependent friction and backlash on the stability of automatic control systems. Am. Inst. Electr. Eng. Part II Appl. Ind. Trans. 1959, 77, 680–692. [Google Scholar] [CrossRef]
- Gang, T.; Kokotovic, P.V. Adaptive control of systems with backlash. Automatica 1993, 29, 323–335. [Google Scholar]
- Nordin, M.; Galic’, J.; Gutman, P.O. New models for backlash and gear play. Int. J. Adapt. Control Signal Process. 1997, 11, 49–63. [Google Scholar] [CrossRef]
- Nordin, M.; Gutman, P.-O. Controlling mechanical systems with backlash—A survey. Automatica 2002, 38, 1633–1649. [Google Scholar] [CrossRef]
- Lyu, Z.; Liu, Z.; Xie, K.; Philip Chen, C.L.; Zhang, Y. Adaptive tracking control for switched nonlinear systems with fuzzy actuator backlash. Fuzzy Sets Syst. 2020, 385, 60–80. [Google Scholar] [CrossRef]
- Lai, G.; Zhi, L.; Yun, Z.; Chen, C.L.P.; Xie, S. Asymmetric actuator backlash compensation in quantized adaptive control of uncertain networked nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 294–307. [Google Scholar] [CrossRef]
- Zhu, Z.; Pan, Y.; Zhou, Q.; Lu, C. Event-triggered adaptive fuzzy control for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis. IEEE Trans. Fuzzy Syst. 2020, 29, 1273–1283. [Google Scholar] [CrossRef]
- Jang, J.; Jeon, G. Backlash compensation of nonlinear systems using fuzzy logic. Int. J. Syst. Sci. 2006, 37, 485–492. [Google Scholar] [CrossRef]
- Han, S.I.; Lee, J.M. Adaptive dynamic surface control with sliding mode control and rwnn for robust positioning of a linear motion stage. Mechatronics 2012, 22, 222–238. [Google Scholar] [CrossRef]
- Yongjian, L. Adaptive Back-Stepping Control Based on Recurrent Neural Network for BLDCM EMA. In Proceedings of the 2009 IEEE 6th International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009. [Google Scholar]
- Ristanović, M.; Ćojbašić, Ž.; Lazić, D. Intelligent control of dc motor driven electromechanical fin actuator. Control Eng. Pract. 2012, 20, 610–617. [Google Scholar] [CrossRef]
- Sayed, M.A.E.; Habibi, S. Inner-Loop Control for Electro-Hydraulic Actuation Systems. In Proceedings of the ASME 2009 Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2010; pp. 114–133. [Google Scholar]
- Han, J. The Technique for Estimating and Compensating the Uncertainties: Active Disturbance Rejection Control Technique; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Rcr, A.; Repa, B.; Emp, C. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Chen, Q.; Chen, H.; Zhu, D.; Li, L. Design and analysis of an active disturbance rejection robust adaptive control system for electromechanical actuator. Actuators 2021, 10, 307. [Google Scholar] [CrossRef]
- Li, S.-Q.; Zang, S.-X.; Liu, Y.N.; Zhou, S.-W. Parameter-tuing in active disturbance rejection controller using time scale. Control Theory Appl. 2012, 29, 125–129. [Google Scholar]
- Wenying, C.; Fulei, C.; Shaoze, Y. Stepwise optimal design of active disturbances rejection vibration controller for intelligent truss structure based on adaptive genetic algorithm. J. Mech. Eng. 2010, 46, 74–81. [Google Scholar]
- Ren, C.; Ding, Y.; Ma, S. A structure-improved extended state observer based control with application to an omnidirectional mobile robot. ISA Trans. 2020, 101, 335–345. [Google Scholar] [CrossRef]
- Guerra, A.d.L.; Alvarez-Icaza, L.; Torres, L. Brushless dc motor control with unknown and variable torque load. IFAC-PapersOnLine 2018, 51, 644–649. [Google Scholar] [CrossRef]
- Michalek, M.M.; Lakomy, K.; Adamski, W. Robust output-feedback cascaded tracking controller for spatial motion of anisotropically-actuated vehicles. Aerosp. Sci. Technol. 2019, 92, 915–929. [Google Scholar] [CrossRef]
- Felix, J.L.P.; Balthazar, J.M.; Brasil, R.M.L.R.F.; Pontes, B.R. On lugre friction model to mitigate nonideal vibrations. J. Comput. Nonlinear Dyn. 2009, 4, 340–341. [Google Scholar] [CrossRef]
- Suraneni, S.; Kar, I.N.; Murthy, O.V.R.; Bhatt, R.K.P. Adaptive stick–Slip friction and backlash compensation using dynamic fuzzy logic system. Appl. Soft Comput. J. 2006, 6, 26–37. [Google Scholar] [CrossRef]
- Rida Mokhtari, M.; Choukchou Braham, A.; Cherki, B. Extended state observer based control for coaxial-rotor UAV. ISA Trans. 2016, 61, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Gao, Z. Frequency Response Analysis of Active Disturbance Rejection Based Control System. In Proceedings of the IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1595–1599. [Google Scholar]
- Hu, Y.; Wang, H. Robust tracking control for vehicle electronic throttle using adaptive dynamic sliding mode and extended state observer. Mech. Syst. Signal Process. 2020, 135, 106375. [Google Scholar] [CrossRef]
- Yi, H.; Han, J. Analysis and design for the second order nonlinear continuous extended states observer. Sci. Bull. 2000, 45, 1938–1944. [Google Scholar]
- Gao, Z.; Huang, Y.; Han, J. An Alternative Paradigm for Control System Design. In Proceedings of the IEEE Conference on Decision and Control, Orlando, FL, USA, 4–7 December 2001; pp. 4578–4585. [Google Scholar]
- Suthar, H.A.; Gadit, J.J. Multiobjective optimization of 2dof controller using evolutionary and swarm intelligence enhanced with topsis. Heliyon 2019, 5, e01410. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).