Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model
Abstract
:1. Introduction
2. Kinamatic Models
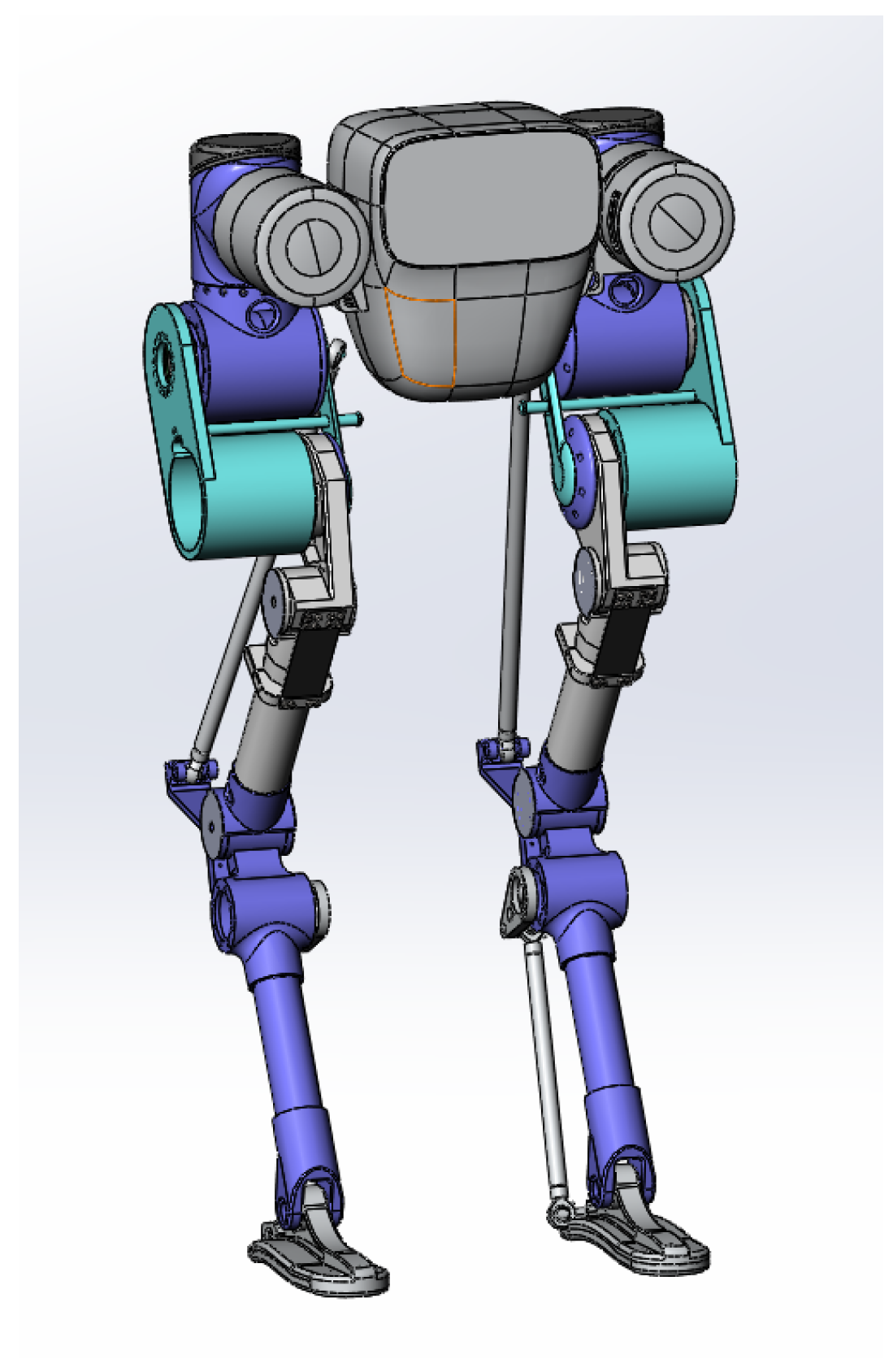
2.1. Configuration of the Legs of the Biped Robot
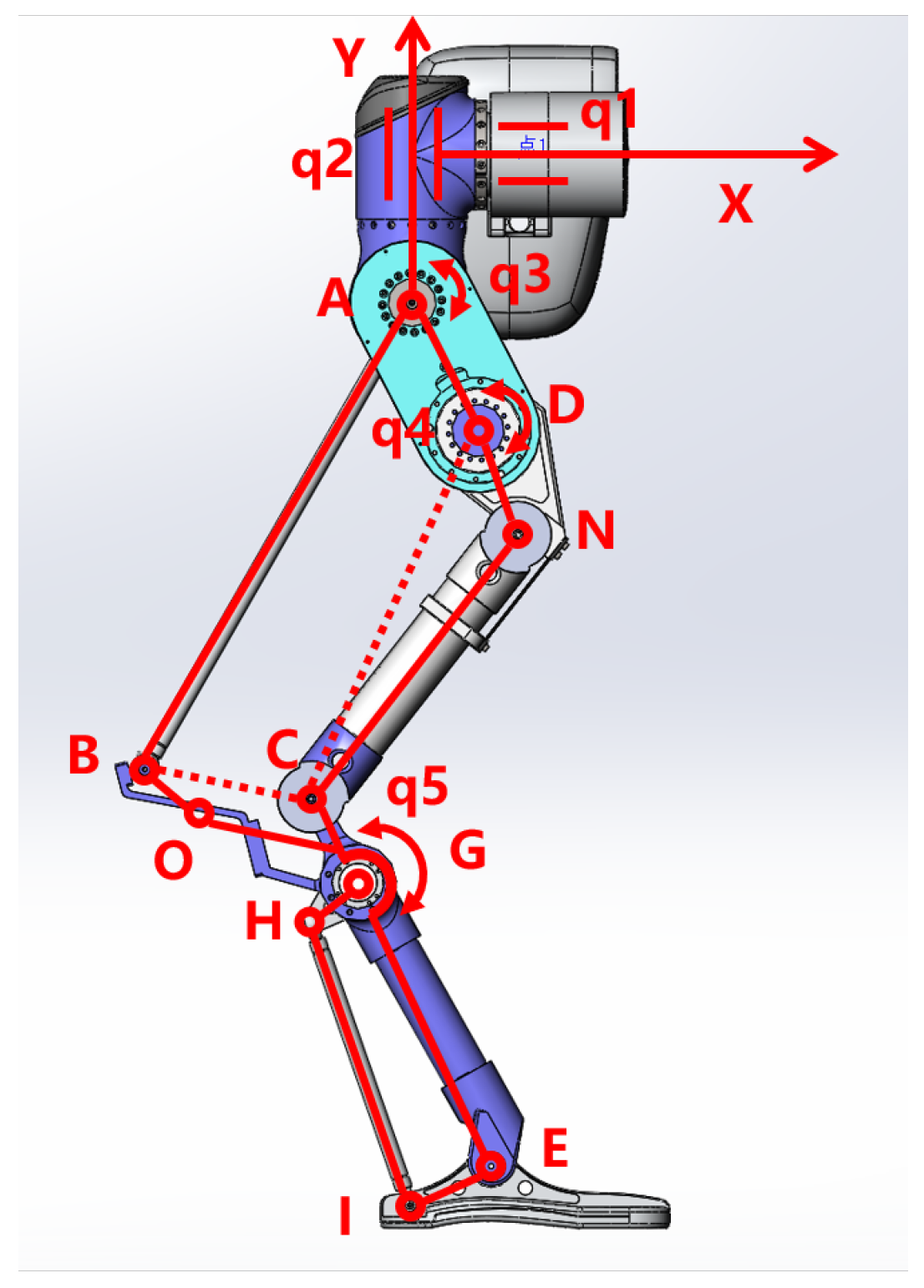
2.2. Forward Kinematic Models
2.3. Inverse Kinematics
2.3.1. Solving
2.3.2. Solving
2.3.3. Coordinate Conversion
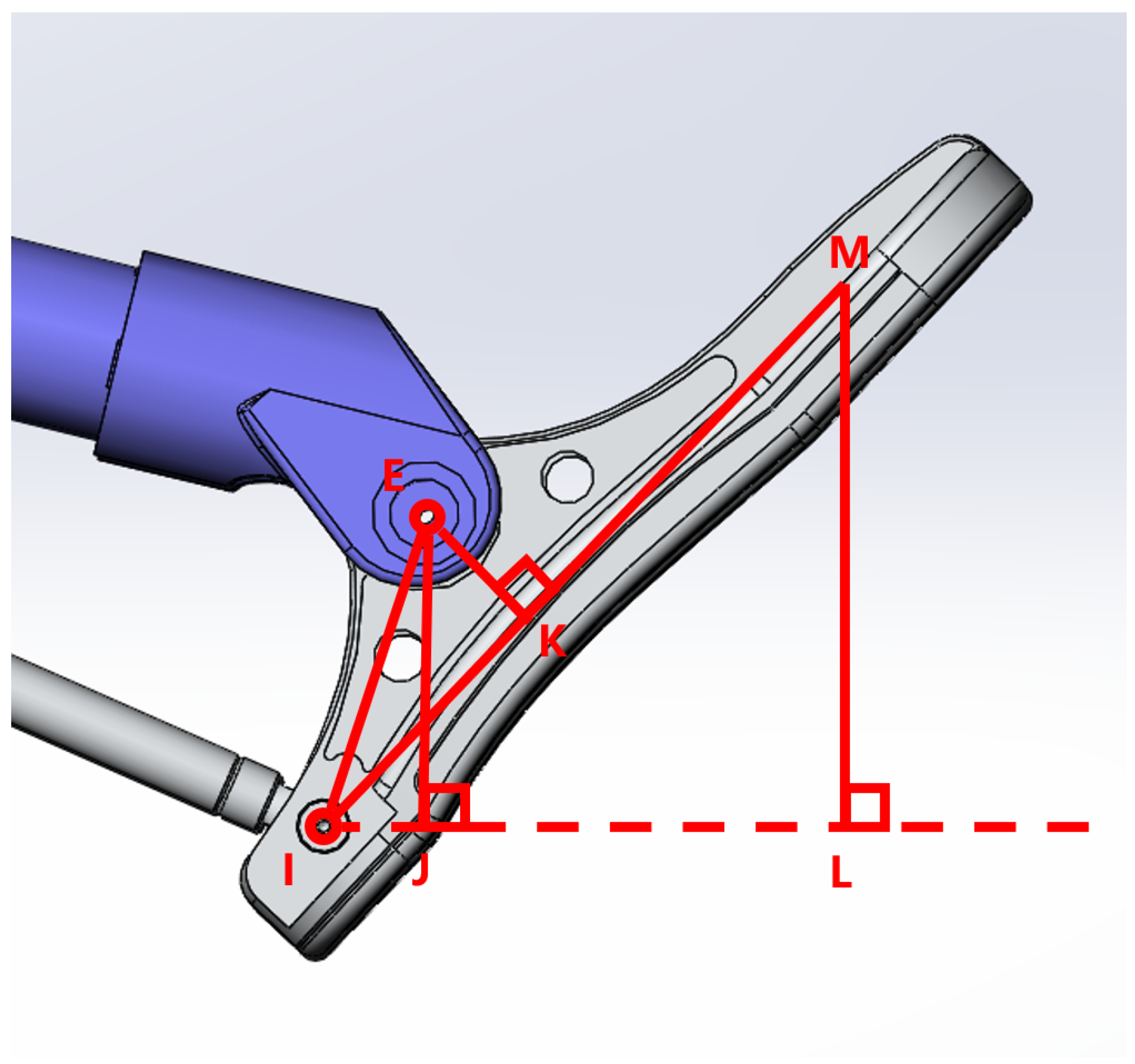
2.3.4. Solving and
2.3.5. Solving
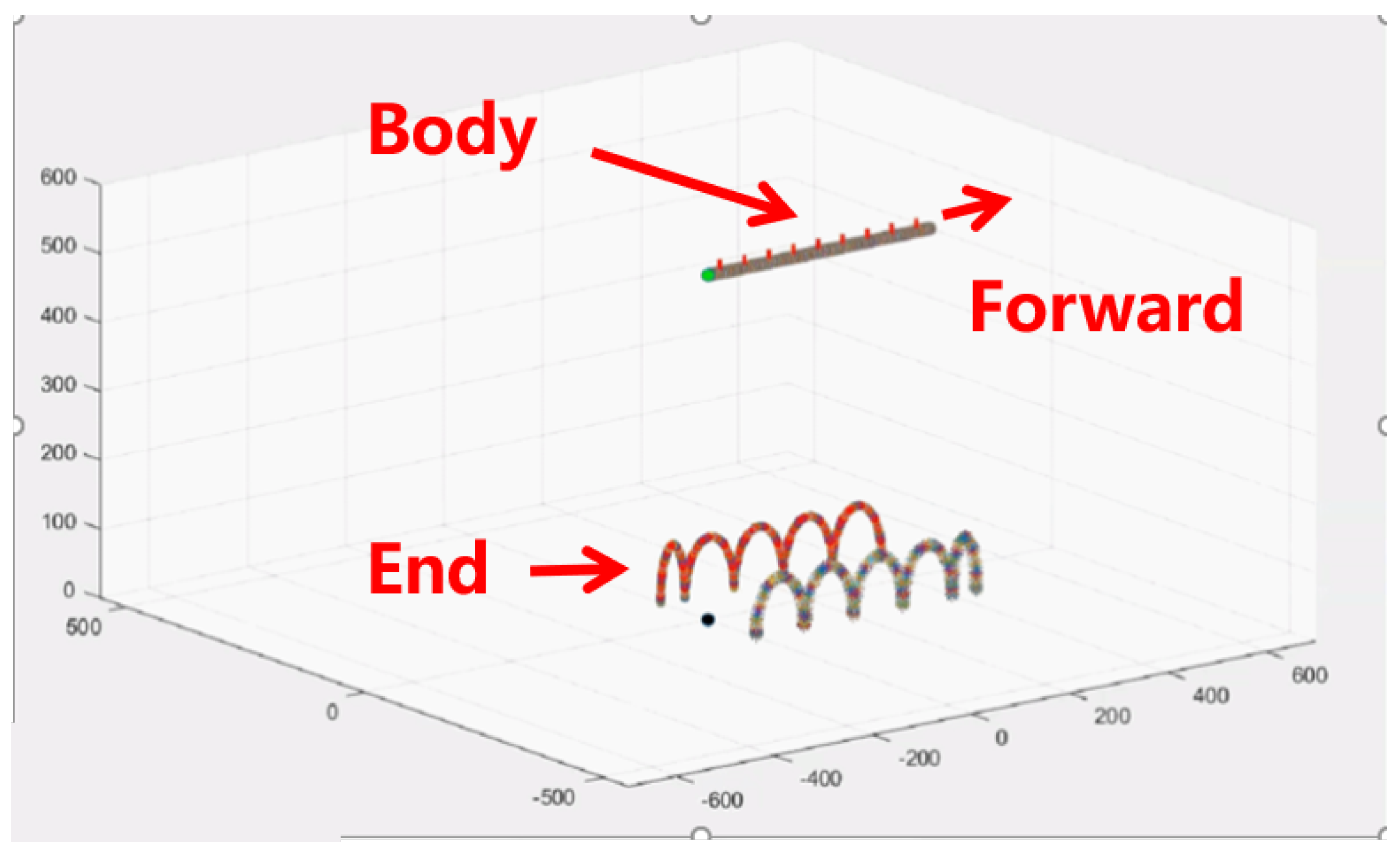
2.4. Verification of Kinematic Model
3. Experimental Prototype and Its Construction
3.1. Structural Component Design
3.2. Driver Design
3.3. Control
4. Prototype Performance Test
4.1. Experiment
4.2. Experiments Result
4.2.1. Experiments A
4.2.2. Experiments B
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dynamics, B. Atlas. [EB/OL]. Available online: https://www.bostondynamics.com/atlas (accessed on 20 December 2021).
- Dynamics, B. Do You Like Me? [EB/OL]. Available online: https://www.youtube.com/watch?v=fn3KWM1kuAw&ab_channel=BostonDynamics (accessed on 20 December 2021).
- Honda. ASIMO. [EB/OL]. Available online: https://global.honda/innovation/robotics/ASIMO.html (accessed on 20 December 2021).
- Shigemi, S.; Goswami, A.; Vadakkepat, P. ASIMO and humanoid robot research at Honda. In Humanoid Robotics: A Reference; Springer Nature B.V.: Dordrecht, The Netherlands, 2019; pp. 55–90. [Google Scholar]
- Lohmeier, S.; Buschmann, T.; Ulbrich, H. Humanoid robot LOLA. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 775–780. [Google Scholar]
- ubtRobot. Walker. [EB/OL]. Available online: https://www.ubtrobot.com/cn/products/walker/?area=cn (accessed on 20 December 2021).
- Akachi, K.; Kaneko, K.; Kanehira, N.; Ota, S.; Miyamori, G.; Hirata, M.; Kajita, S.; Kanehiro, F. Development of humanoid robot HRP-3P. In Proceedings of the 5th IEEE-RAS International Conference on Humanoid Robots, Tsukuba, Japan, 5 December 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 50–55. [Google Scholar]
- Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; Kajita, S.; Morisawa, M.; Kumagai, I.; Kanehiro, F. Humanoid robot HRP-5P: An electrically actuated humanoid robot with high-power and wide-range joints. IEEE Robot. Autom. Lett. 2019, 4, 1431–1438. [Google Scholar] [CrossRef]
- Englsberger, J.; Werner, A.; Ott, C.; Henze, B.; Roa, M.A.; Garofalo, G.; Burger, R.; Beyer, A.; Eiberger, O.; Schmid, K.; et al. Overview of the torque-controlled humanoid robot TORO. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 916–923. [Google Scholar]
- Mesesan, G.; Englsberger, J.; Garofalo, G.; Ott, C.; Albu-Schäffer, A. Dynamic walking on compliant and uneven terrain using DCM and passivity-based whole-body control. In Proceedings of the 2019 IEEE-RAS 19th International Conference on Humanoid Robots (Humanoids), Toronto, ON, Canada, 15–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 25–32. [Google Scholar]
- Hubicki, C.; Grimes, J.; Jones, M.; Renjewski, D.; Spröwitz, A.; Abate, A.; Hurst, J. Atrias: Design and validation of a tether-free 3d-capable spring-mass bipedal robot. Int. J. Robot. Res. 2016, 35, 1497–1521. [Google Scholar] [CrossRef]
- Hobbelen, D.; De Boer, T.; Wisse, M. System overview of bipedal robots flame and tulip: Tailor-made for limit cycle walking. In Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2486–2491. [Google Scholar]
- Collins, S.; Ruina, A.; Tedrake, R.; Wisse, M. Efficient bipedal robots based on passive-dynamic walkers. Science 2005, 307, 1082–1085. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russo, M.; Cafolla, D.; Ceccarelli, M. Development of LARMbot 2, A Novel Humanoid Robot with Parallel Architectures. In IFToMM Symposium on Mechanism Design for Robotics; Springer: Berlin/Heidelberg, Germany, 2018; pp. 17–24. [Google Scholar]
- Bhounsule, P.A.; Cortell, J.; Grewal, A.; Hendriksen, B.; Karssen, J.D.; Paul, C.; Ruina, A. Low-bandwidth reflex-based control for lower power walking: 65 km on a single battery charge. Int. J. Robot. Res. 2014, 33, 1305–1321. [Google Scholar] [CrossRef]
- Renjewski, D.; Spröwitz, A.; Hurst, J. Exciting passive dynamics in a versatile bipedal robot. IEEE Trans. Robot. 2014; submitted. [Google Scholar]
- Blickhan, R.; Seyfarth, A.; Geyer, H.; Grimmer, S.; Wagner, H.; Günther, M. Intelligence by mechanics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 199–220. [Google Scholar] [CrossRef] [PubMed]
- Robotics, A. Agility Robotics. [EB/OL]. Available online: https://www.agilityrobotics.com/robots#digit (accessed on 20 December 2021).
- Abate, A.M. Mechanical Design for Robot Locomotion. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2018. [Google Scholar]
- Apgar, T.; Clary, P.; Green, K.; Fern, A.; Hurst, J.W. Fast Online Trajectory Optimization for the Bipedal Robot Cassie. Robot. Sci. Syst. 2018, 101, 14. [Google Scholar]
- Gong, Y.; Hartley, R.; Da, X.; Hereid, A.; Harib, O.; Huang, J.K.; Grizzle, J. Feedback control of a cassie bipedal robot: Walking, standing, and riding a segway. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 4559–4566. [Google Scholar]
- Westervelt, E.R.; Grizzle, J.W.; Chevallereau, C.; Choi, J.H.; Morris, B. Feedback Control of Dynamic Bipedal Robot Locomotion; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Che, J.; Pan, Y.; Yan, W.; Yu, J. Kinematics Analysis of Leg Configuration of An Ostrich Bionic Biped Robot. In Proceedings of the 2021 International Conference on Robotics and Control Engineering, Tokyo, Japan, 22–25 April 2021; pp. 19–22. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Che, J.; Pan, Y.; Yan, W.; Yu, J. Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model. Actuators 2022, 11, 75. https://doi.org/10.3390/act11030075
Che J, Pan Y, Yan W, Yu J. Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model. Actuators. 2022; 11(3):75. https://doi.org/10.3390/act11030075
Chicago/Turabian StyleChe, Junjie, Yang Pan, Wei Yan, and Jiexian Yu. 2022. "Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model" Actuators 11, no. 3: 75. https://doi.org/10.3390/act11030075
APA StyleChe, J., Pan, Y., Yan, W., & Yu, J. (2022). Leg Configuration Analysis and Prototype Design of Biped Robot Based on Spring Mass Model. Actuators, 11(3), 75. https://doi.org/10.3390/act11030075




