Experimental Study of Dynamical Airfoil and Aerodynamic Prediction
Abstract
1. Introduction
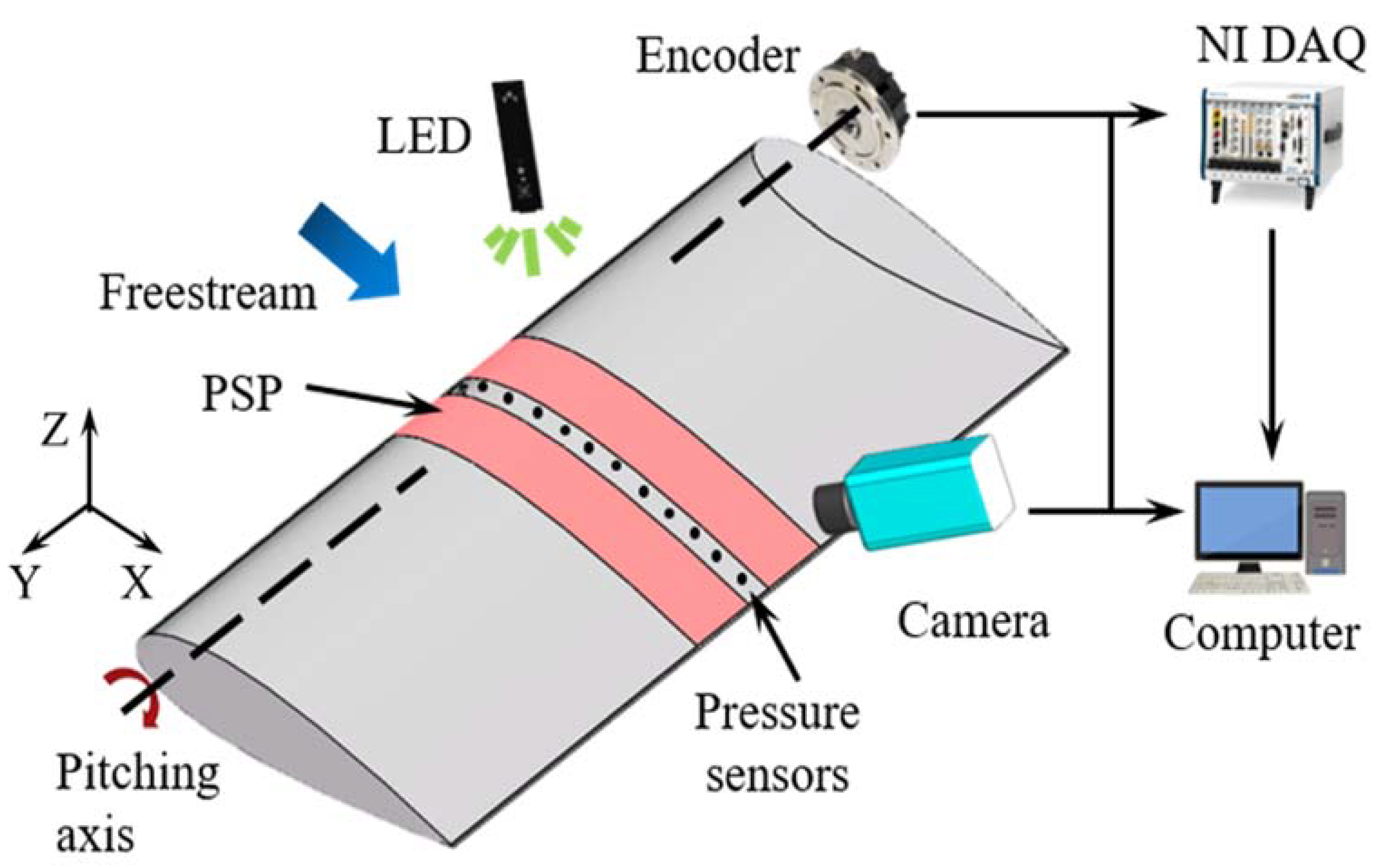
2. Experimental Setup and Methodology
2.1. Measurement Setup
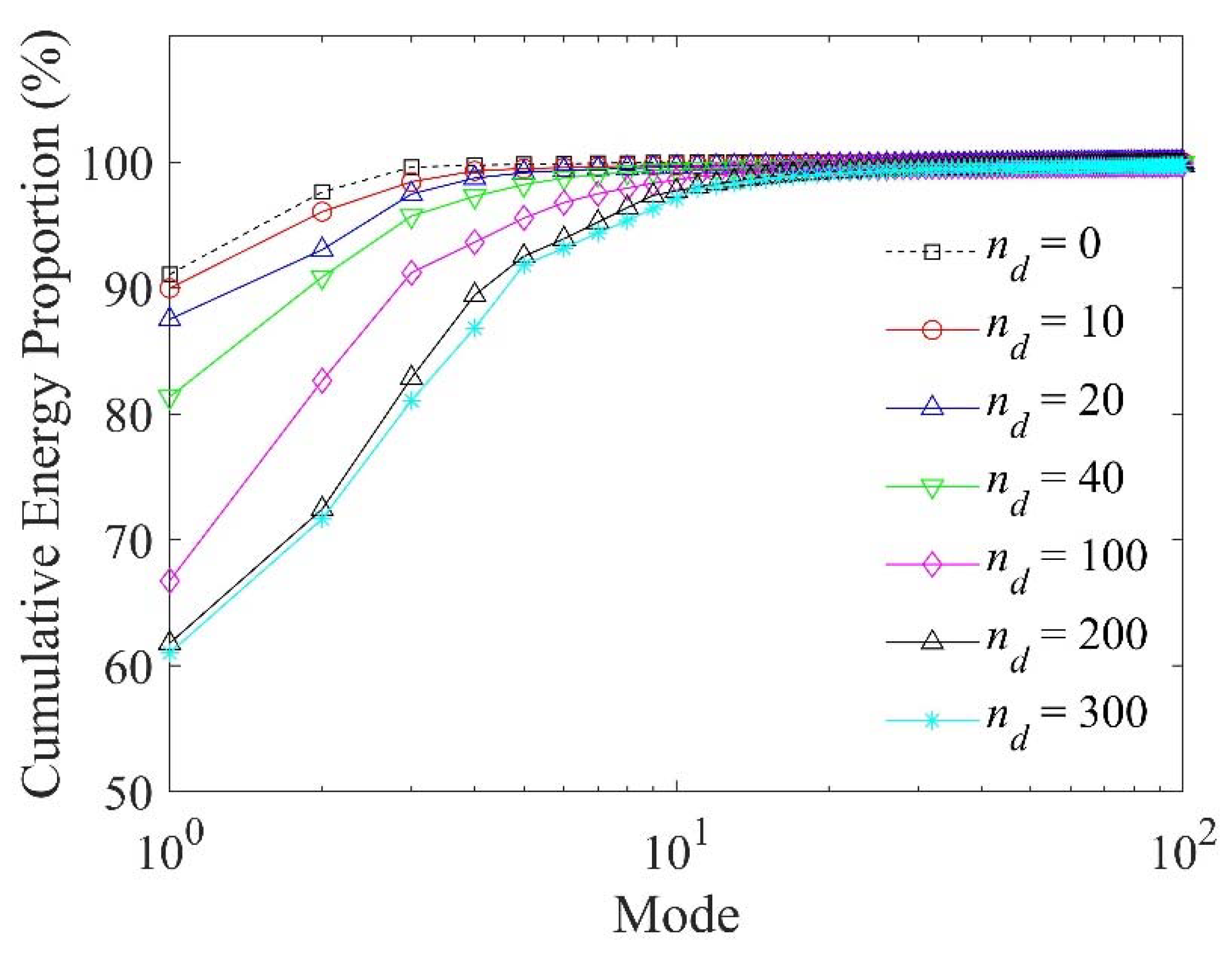
2.2. Dynamic Mode Decomposition with Time-Delay Embedding
3. Results and Discussion
3.1. Dynamic Stall
3.1.1. Flow Visualization
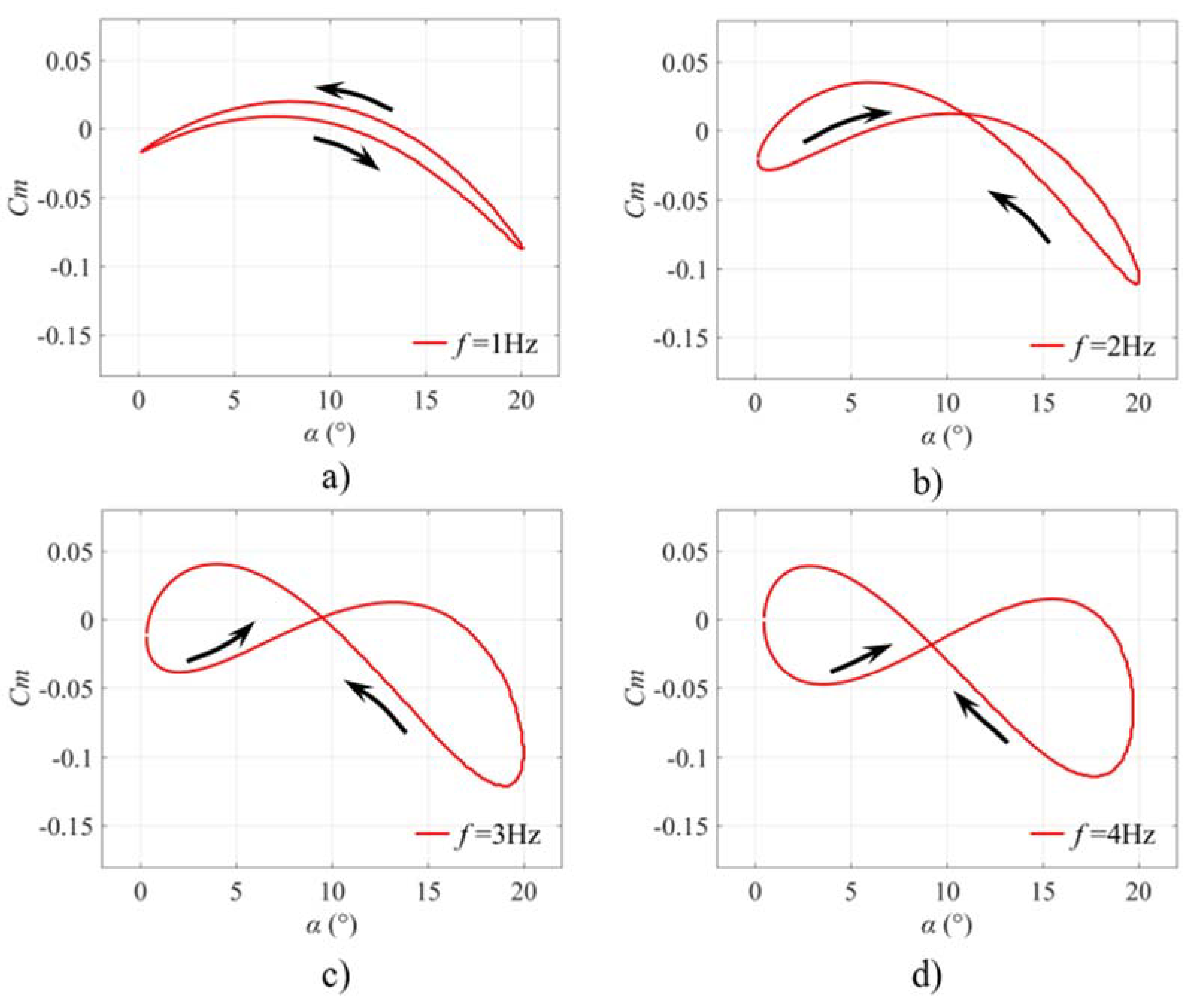
3.1.2. Aerodynamic Loads
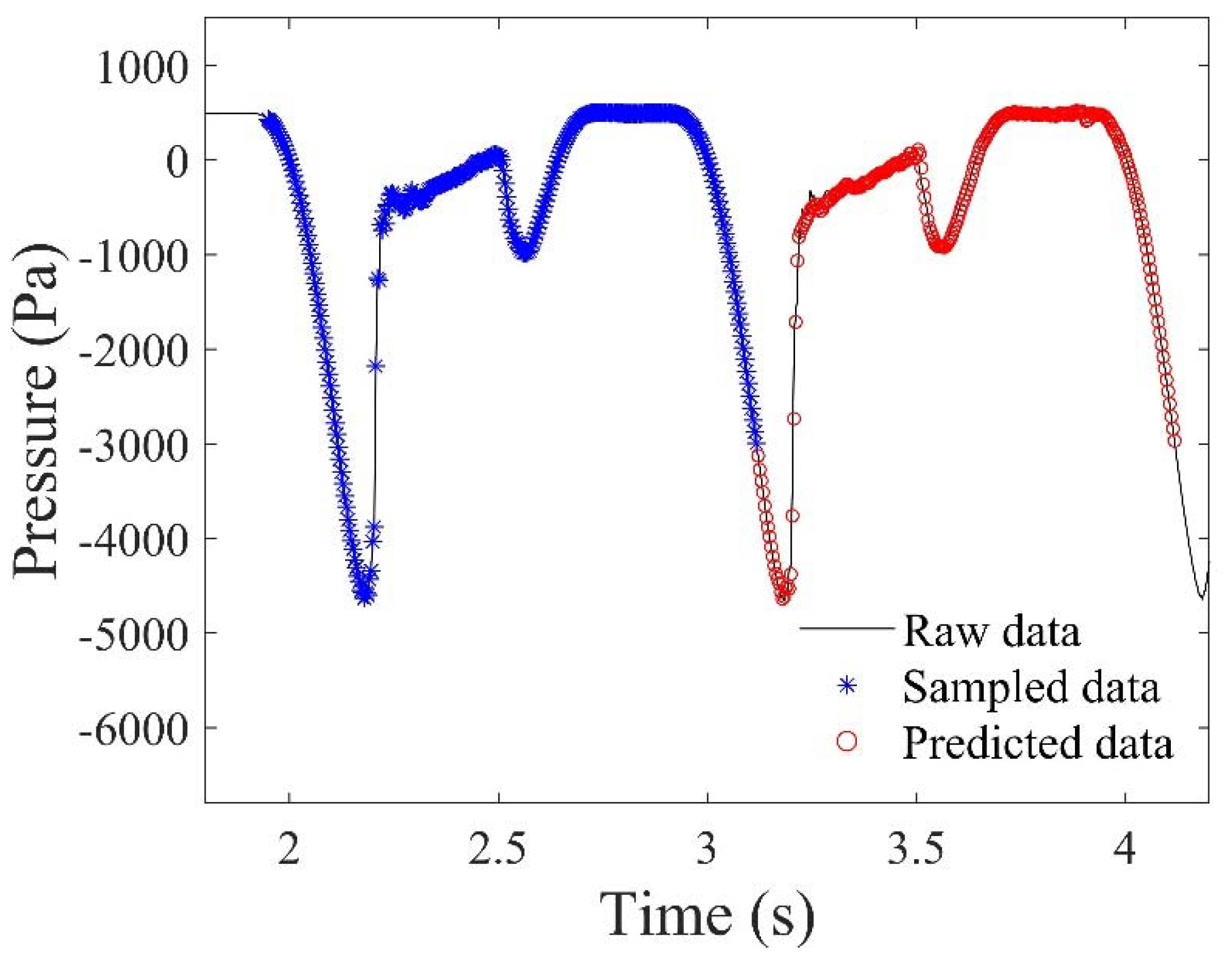
3.2. Prediction of Future Data
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| α | angle of attack, ° |
| α0 | mean angle of attack, ° |
| α1 | pitching amplitude, ° |
| c | chord length, m |
| Cl | lift coefficient |
| Cm | pitching moment coefficient |
| e | the error rate between reconstructed data and true data |
| f | pitching frequency, Hz |
| nd | the number of delay steps |
| U∞ | freestream velocity, m/s |
| s | span length, m |
| k | reduced frequency, Hz |
| Re | Reynolds number |
| ρ | air density, kg/m3Pi = the static pressure obtained from a pressure tap, Pa |
| P∞ | the static pressure of the incoming flow, Pa |
| H1, H2 | time-delay-embedded matrices |
| X1, X2 | raw data matrices |
| A, B | Koopman operator |
| Acronyms | |
| DMD | dynamic mode decomposition |
| PIV | particle image velocimetry |
| POD | proper orthogonal decomposition |
| PSP | pressure sensitive paint |
References
- McCroskey, W.J. The Phenomenon of Dynamic Stall. NASA Tech. Memo. 1981, 81264, 1–28. [Google Scholar]
- Mulleners, K.; Raffel, M. The onset of dynamic stall revisited. Exp. Fluids 2012, 52, 779–793. [Google Scholar] [CrossRef]
- Chandrasekhara, M.S.; Carr, L.W.; Wilder, M.C. Interferometric investigations of compressible dynamic stall over a transiently pitching airfoil. AIAA J. 1994, 32, 586–593. [Google Scholar] [CrossRef][Green Version]
- Visbal, M.R. Dynamic stall of a constant-rate pitching airfoil. J. Aircraft 1990, 27, 400–407. [Google Scholar] [CrossRef]
- Rival, D.; Tropea, C. Characteristics of pitching and plunging airfoils under dynamic-stall conditions. J. Aircraft 2010, 47, 80–86. [Google Scholar] [CrossRef]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircraft 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Geissler, W.; Dietz, G.; Mai, H.; Bosbach, J.; Richard, H. Dynamic Stall and its passive control investigations on the OA209 airfoil section. In Proceedings of the 31st European Rotorcraft Forum 2005 (ERF31), Florence, Italy, 13–15 September 2005. [Google Scholar]
- Heine, B.; Mulleners, K.; Joubert, G.; Raffel, M. Dynamic stall control by passive disturbance generators. AIAA J. 2013, 51, 2086–2097. [Google Scholar] [CrossRef]
- Konstantinidis, E.; Balabani, S. Symmetric vortex shedding in the near wake of a circular cylinder due to streamwise perturbations. J. Fluids Struct. 2007, 23, 1047–1063. [Google Scholar] [CrossRef]
- Melton, L.P.; Koklu, M.; Andino, M.; Lin, J.C. Active flow control via discrete sweeping and steady jets on a simple-hinged flap. AIAA J. 2018, 56, 2961–2973. [Google Scholar] [CrossRef]
- Schmidt, H.J.; Woszidlo, R.; Nayeri, C.N.; Paschereit, C.O. Separation control with fluidic oscillators in water. Exp. Fluids 2017, 58, 1–17. [Google Scholar] [CrossRef]
- Gao, D.; Chen, G.; Chen, W.; Huang, Y.; Li, H. Active control of circular cylinder flow with windward suction and leeward blowing. Exp. Fluids 2019, 60, 26. [Google Scholar] [CrossRef]
- Patel, M.P.; Carver, R.; Lisy, F.J.; Prince, T.S.; Ng, T. Detection and control of flow separation using pressure sensors and micro-vortex generators. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Saini, A.; Gopalarathnam, A. Leading-edge flow sensing for aerodynamic parameter estimation. AIAA J. 2018, 56, 4706–4718. [Google Scholar] [CrossRef]
- Le Provost, M.; He, X.; Williams, D.R. Real-time roll moment identification with distributed surface pressure sensors on a rolling UCAS wing. In Proceedings of the AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Juliano, T.J.; Peng, D.; Jensen, C.; Gregory, J.W.; Liu, T.; Montefort, J.; Palluconi, S.; Crafton, J.; Fonov, S. PSP measurements on an oscillating NACA 0012 airfoil in compressible flow. In Proceedings of the 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- An, X.; Williams, D.R.; Eldredge, J.D.; Colonius, T. Lift coefficient estimation for a rapidly pitching airfoil. Exp. Fluids 2021, 62, 1–12. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, Q.; Wang, L. Measurement of unsteady transition on a pitching airfoil using dynamic pressure sensors. J. Mech. Sci. Technol. 2016, 30, 4571–4578. [Google Scholar] [CrossRef]
- Sabater, C.; Stürmer, P.; Bekemeyer, P. Fast Predictions of Aircraft Aerodynamics using Deep Learning Techniques. In Proceedings of the AIAA AVIATION 2021 FORUM, Online, 2–6 August 2021. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-learning-augmented predictive modeling of turbulent separated flows over airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Meyer, K.E.; Pedersen, J.M.; Özcan, O. A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 2007, 583, 199–227. [Google Scholar] [CrossRef]
- Dawson, S.T.M.; Schiavone, N.K.; Rowley, C.W.; Williams, D.R. A data-driven modeling framework for predicting forces and pressures on a rapidly pitching airfoil. In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Bright, I.; Lin, G.; Kutz, J.N. Compressive sensing based machine learning strategy for characterizing the flow around a cylinder with limited pressure measurements. Phys. Fluids 2013, 25, 127102. [Google Scholar] [CrossRef]
- Zhou, K.; Zhou, L.; Zhao, S.; Qiang, X.; Liu, Y.; Wen, X. Data-Driven Method for Flow Sensing of Aerodynamic Parameters Using Distributed Pressure Measurements. AIAA J. 2021, 59, 3504–3516. [Google Scholar] [CrossRef]
- Saini, A.; Narsipur, S.; Gopalarathnam, A. Leading-edge flow sensing for detection of vortex shedding from airfoils in unsteady flows. Phys. Fluids 2021, 33, 21–28. [Google Scholar] [CrossRef]
- Pinier, J.T.; Ausseur, J.M.; Glauser, M.N.; Higuchi, H. Proportional closed-loop feedback control of flow separation. AIAA J. 2007, 45, 181–190. [Google Scholar] [CrossRef]
- Zhao, X.; Kania, R.; Kebbie-Anthony, A.; Azarm, S.; Balachandran, B. Dynamic data-driven aeroelastic response prediction with discrete sensor observations. In Proceedings of the 2018 AIAA Non-Deterministic Approaches Conference, Kissimmee, FL, USA, 8–12 January 2018; pp. 1–12. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Berger, E.; Sastuba, M.; Vogt, D.; Jung, B.; Ben Amor, H. Dynamic Mode Decomposition for perturbation estimation in human robot interaction. In Proceedings of the The 23rd IEEE International Symposium on Robot and Human Interactive Communication, Edinburgh, UK, 25–29 August 2014; pp. 593–600. [Google Scholar] [CrossRef]
- Le Clainche, S.; Vega, J.M. Higher order dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 2017, 16, 882–925. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kaiser, E.; Nathan Kutz, J. Chaos as an intermittently forced linear system. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef]
- Murshed, M.N.; Monir Uddin, M. Time delay coordinate based dynamic mode decomposition of a compressible signal. In Proceedings of the 2019 22nd International Conference on Computer and Information Technology, ICCIT, Dhaka, Bangladesh, 18–20 December 2019; pp. 18–20. [Google Scholar]
- Susuki, Y.; Sako, K. Data-Based Voltage Analysis of Power Systems via Delay Embedding and Extended Dynamic Mode Decomposition. IFAC-PapersOnLine 2018, 51, 221–226. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. On the structure of time-delay embedding in linear models of non-linear dynamical systems. Chaos 2020, 30, 073135. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhou, K.; Zhou, W.; Wen, X.; Liu, Y. Flow prediction using dynamic mode decomposition with time-delay embedding based on local measurement. Phys. Fluids 2021, 33, 095109. [Google Scholar] [CrossRef]
- Arbabi, H.; Korda, M.; Mezić, I. A data-driven Koopman model predictive control framework for nonlinear ows. In Proceedings of the The 57th IEEE Conference on Decision and Control, Miami Beach, FL, USA, 17–19 December 2018; pp. 6409–6414. [Google Scholar]
- Miller, S.D. Lift, Drag and Moment of a NACA 0015 Airfoil. Available online: https://smiller.sbyers.com/temp/AE510_03%20NACA%200015%20Airfoil.pdf (accessed on 6 December 2021).
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data–Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Dellnitz, M.; Von Molo, M.H.; Ziessler, A. A kernel-based method for data-driven Koopman spectral analysis. J. Comput. Dyn. 2016, 2, 247–265. [Google Scholar] [CrossRef]
- Mai, H.; Dietz, G.; Geißler, W.; Richter, K.; Bosbach, J.; Richard, H.; Groo, K. De Dynamic stall control by leading edge vortex generators. Annu. Forum Proc. AHS Int. 2006, III, 1728–1739. [Google Scholar]





| Upper Surface | Lower Surface | ||||||
|---|---|---|---|---|---|---|---|
| No. | x/c | No. | x/c | No. | x/c | No. | x/c |
| 1 | 0.01 | 11 | 0.24 | 21 | 0 | 31 | 0.25 |
| 2 | 0.02 | 12 | 0.3 | 22 | 0.0125 | 32 | 0.3 |
| 3 | 0.03 | 13 | 0.36 | 23 | 0.025 | 33 | 0.35 |
| 4 | 0.04 | 14 | 0.42 | 24 | 0.0375 | 34 | 0.4 |
| 5 | 0.05 | 15 | 0.48 | 25 | 0.05 | 35 | 0.5 |
| 6 | 0.06 | 16 | 0.57 | 26 | 0.075 | 36 | 0.6 |
| 7 | 0.09 | 17 | 0.66 | 27 | 0.1 | 37 | 0.7 |
| 8 | 0.12 | 18 | 0.75 | 28 | 0.125 | 38 | 0.8 |
| 9 | 0.15 | 19 | 0.84 | 29 | 0.15 | 39 | 0.9 |
| 10 | 0.18 | 20 | 0.93 | 30 | 0.2 | 40 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Zhou, K.; Qin, C.; Wen, X. Experimental Study of Dynamical Airfoil and Aerodynamic Prediction. Actuators 2022, 11, 46. https://doi.org/10.3390/act11020046
Shi Z, Zhou K, Qin C, Wen X. Experimental Study of Dynamical Airfoil and Aerodynamic Prediction. Actuators. 2022; 11(2):46. https://doi.org/10.3390/act11020046
Chicago/Turabian StyleShi, Zheyu, Kaiwen Zhou, Chen Qin, and Xin Wen. 2022. "Experimental Study of Dynamical Airfoil and Aerodynamic Prediction" Actuators 11, no. 2: 46. https://doi.org/10.3390/act11020046
APA StyleShi, Z., Zhou, K., Qin, C., & Wen, X. (2022). Experimental Study of Dynamical Airfoil and Aerodynamic Prediction. Actuators, 11(2), 46. https://doi.org/10.3390/act11020046







