Abstract
In lower-limb rehabilitation systems, exoskeleton robots are one of the most important components. These robots help patients to execute repetitive exercises under the guidance of physiotherapists. Recently, pneumatic artificial muscles (PAM), a kind of actuator that acts similarly to human muscles, have been chosen to power the exoskeleton robot for better human–machine interaction. In order to enhance the performance of a PAM-based exoskeleton robot, this article implements an active disturbance rejection control (ADRC) strategy with a nonlinear extended state observer (NLESO). Moreover, the stability of the closed-loop system is proved by Lyapunov’s theory. Finally, the experimental results show that with the proposed control strategy, the rehabilitation robot can effectively track the desired trajectories even when under external disturbance.
1. Introduction
In rehabilitation devices, exoskeleton robots play an essential role in assisting/replacing physical therapy for patients. Among them, lower-limb rehabilitation robots, which can recover one’s ability to move, have attracted much attention [1]. Developments have been carried out in multiple stages, from research to commercial products [2]. In this kind of robot, the actuators generate torque to the subject’s limbs and move them along the designated path. Thus, choosing a suitable actuator is a crucial factor. Various types have been used such as electric motors, hydraulic cylinders, and PAMs. Due to their outstanding features, such as being lightweight and compliant, having the capability of generating a high peak torque, and their spring-like behavior similar to biological muscles, PAMs have been widely used to actuate exoskeleton robots in recent years [3,4]. However, PAMs have some inherent drawbacks, such as uncertainty, time variance, and strong hysteresis, which require great effort to overcome.
Trajectory tracking control is the essential requirement of a rehabilitation exoskeleton robot, to ensure the desired trajectory generation and high tracking accuracy. Multiple control strategies have been applied to PAM-based robots. Conventional tracking control strategies such as PID-based controllers [5,6,7,8] and modified computed torque [9] are often used at the early stage of the system’s development to verify the mechanism of the robot without a subject. Since these types of control strategies do not require much knowledge about system modeling and control theory, they are the most common choice for researchers to test the tracking performance of the robot. However, these linear controllers can not deal with the uncertainty and hysteresis of PAM-based robots. To handle the nonlinearity problem, some nonlinear control strategies such as backstepping control [10,11], energy-based control [12], and adaptive control [13,14] have been reported in the literature. These controllers, however, are sensitive to model uncertainty and disturbance. Another prominent nonlinear control algorithm is the sliding mode control (SMC). The SMC with various improved versions proposed in [15,16,17,18,19,20,21,22] was shown to be effective with a robust control strategy in the presence of the uncertainties and disturbances of PAMs. However, these control algorithms, more or less, still require the PAM model.
Due to the difficulty in modeling pneumatic artificial muscles, some intelligent control strategies that require less information about the actuator model have recently been reported [23,24,25,26,27,28]. In [23], a sliding mode control with an adaptive sliding surface was applied to control the PAM. Fuzzy logic was utilized to adjust the discontinue term in the sliding mode controller to reduce the chattering of the sliding mode control. Although the result was acceptable, the controller was too complicated. A fuzzy logic controller was also used to estimate the PAM’s inverse model in [24]. However, the fuzzy set must be large enough to obtain a satisfactory result, which requires a high computation effort. In [25], the backstepping technique was used to design the controller for PAM with fuzzy logic and neural networks to approximate the unknown parts. To control the PAM robot, [26] applied a sliding mode control and fuzzy logic to estimate the PAM-model-based part. An artificial neural network was trained to approximate the inverse PAM robot model in [27] and then used as a feedforward controller in combination with PID feedback to control the PAM robot. The Takagi–Sugeno fuzzy model was combined with model predictive control in [29] to handle changing load scenarios. These intelligent control strategies enhanced the effectiveness of the artificial muscles in terms of control due to their extraordinary capacity for learning nonlinear characteristics. However, they were generally complicated and required a high level of computation; having to select a fuzzy rule or neural network structure for an effective controller is rather complex and sometimes unsuccessful.
In order to overcome these problems, the active disturbance rejection control (ADRC) method [30] has been considered. In the ADRC technique, the plant was regarded as a linear system, the ignored dynamics and disturbance were considered as a total disturbance, and an extended observer was established to determine the uncertainty. This ADRC method did not require as much knowledge about the system and its disturbances compared to other disturbance observer-based control approaches. In practice, the linear ADRC has been implemented in many applications [31,32,33,34]. A nonlinear ADRC scheme was also developed that not only maintained the advantages of the linear ADRC but also utilized the beneficial nonlinearities to enhance the control performance [35]. However, they focused only on the trajectory tracking of the actuators instead of the overall robot. In addition, the developed nonlinear ESO-based ADRC in [35] only tracked the 0.2 Hz sinusoidal and needed further improvement. In addition, the number of research works concerning the practical aspects of the nonlinear ADRC scheme for exoskeleton robots is limited.
This paper implements the nonlinear ADRC for the trajectory controller in a two-DOF PAMs-based rehabilitation exoskeleton. This robot simulates human hip and knee joints to help patients rehabilitate after surgery or injury. Due to the use of PAMs for actuators, the robot is strongly nonlinear with time-variant parameters and unknown disturbance. So, to effectively control the robot, a nonlinear extended state observer (ESO) is established. Then, a nonlinear feedback controller is designed to enable the system to follow the desired trajectory. In addition, a tracking differentiator (TD) is also proposed to create a physically feasible reference trajectory. In summary, the paper contributes the following:
- We build a mathematical model of the PAM-based exoskeleton robot named BK-Gait.
- We improve the tracking performance of the robot by implementing an NLESO-based ADRC controller, which utilizes a nonlinear ESO that can accurately approximate the system disturbance.
- We develop a feedback controller based on the Lyapunov stability theory. The controller shows outstanding effectiveness when guiding the robot to follow a gait pattern trajectory.
2. Problem Statement
2.1. System Description
This research was carried out on the exoskeleton robot of the BK-Gait rehabilitation system, as shown in Figure 1. The weight of the support system was not taken into account in this work. The robot’s skeleton was made of aluminum, designed with two DOF to cover the thigh and leg of the patient and support them during training. The length of the robot’s link could be first adjusted with sliders and fixed with the screw afterward. The movement limitation of the hip joint was 45 degrees, and it was 90 degrees for the knee joint. The robot was controlled by an embedded controller, the Myrio-1900 from NI. A computer was used to monitor and collect data from the reference trajectory and its measured counterpart.

Figure 1.
The lower-limb exoskeleton of the BK-gait rehabilitation system.
Each robot joint (hip or knee) was actuated by two opposing pneumatic muscles. These PAMs were fabricated (25 mm diameter) with 500 mm in length for the hip joint and 350 mm for the knee and could stretch up to 30%. The air pressure in the PAM was adjusted through the pressure regulator valve ITV-2030-212S-X26 of SMC. For the joints’ angles, a potentiometer WDD35D8 was used to measure the deflection.
2.2. System Modeling
Two opposing PAMs can convert axial motion to rotation movement by changing the pressure difference between both PAMs, which can be called the antagonistic configuration. In this setup, the two PAMs were supplied with and pressures to initialize the rotation angle.
Reynolds’s model [36] of a single PAM is the most common choice of researchers when developing a model of PAM-based systems:
with
where y is the length of the PAM. The spring, damping, and contractile elements of the model are denoted by K, B, and F. , , and (i = 0, 1) are the linear components. when the PAM contracts, and when it deflates, . Based on Reynold’s model, many reports [20,37,38] have constructed a mathematical model of PAMs in an antagonistic setup. In that setup, two PAMs affect a torque on the actuator as:
where
We considered the robot dynamics with two rotating joints as follows:
where M, H, and G are the inertia, viscous moment and radial force, and the gravity torque matrices, respectively. is the matrix torque created by the PAMs’ effect on the robot’s joints, and are the coordinates of the robot joints.
3. Nonlinear Eso-Based ADRC Controller
ADRC controllers are designed to eliminate disturbances in control. Here, disturbances can be understood as external influences on the model or the components of the model that have not been mathematically modeled [30,39,40].
Figure 2 demonstrates the model of the ADRC controller. The ADRC controller had the following main components:
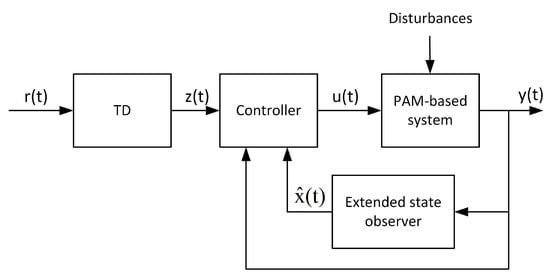
Figure 2.
ADRC controller model.
- Tracking Differentiator (TD), which avoids a sharp deviation of the output signal from its reference. Alternatively, one can create a desirable reference orbit that is physically feasible;
- Extended State Observer (ESO), which estimates the function to remove the unknown component in the model control;
- Nonlinear Feedback Controller (), which controls the state variables of the model to follow the desired trajectory.
3.1. Tracking Differentiator (Td)
The conventional tracking differentiator of the signal is:
where is the time sample ( very small). If the signal contains a high-frequency noise component of , the signal input becomes , and the delay component can be filtered.
Thus, the differential estimator is sensitive to noise in the signal r(t) because it is multiplied by the gain . To solve this difficulty, Han developed an enhanced TD [30] that is resistant to noise as follows:
with the condition: . All the components in (10) are delay signals, so we can avoid the effect of the noise. We considered the corresponding state-space model of (10) by setting as follows:
It can be seen that the smaller is, the faster tracks r. In this research, we employed the modified version of (11) by adding a tuning parameter as the following equation:
where and are positive constants, and is the tuning parameter.
We considered the estimation error of the tracking differentiator as follows:
We assume that the reference signal satisfies , for , and the matrix is Hurwitz. The linear TD (12) is convergent with double poles as ; then, we have
In this research, we chose
3.2. Extended State Observer (Eso)
The ESO is an improved development based on the fundamental state observer. The ESO can estimate both the state variables and the system disturbances. The unmodeled system dynamics, unknown control coefficients, external noise, etc., can cause system disturbance. We considered the state-space model of the PAM-based robot (7):
By setting , the model (7) becomes:
As reported in the research [39], we treat as a new state variable, and the model (17) becomes the observable system:
where is the control signal, and is the measured output.
Based on the state-space model (18), a linear high-gain extended state observer (LESO) and its enhanced versions have been developed by many researchers to estimate the system variables [30,41]:
in which is chosen to satisfy that the characteristic polynomial is Hurwitz, and the tuning parameter . However, the faster the change in the disturbance, the larger the tuned parameter is. A detailed analysis of the LESO’s convergence was reported in [42]. Consequently, the following assumptions were considered.
Assumption 1.
Assume that two nonlinear functions and are continuously differentiable concerning their variables, and
for some constants .
Assumption 2.
The state variables and the system disturbance in the model of PAM-based robot satisfy , for some positive constant b.
Assumption 3.
For , there are existing constants α and R and functions (V, W: ), which are positive definite and continuous differentiable, such that
- •
- is bounded for any ,
- •
- ,
- •
- .
Theorem 1.
With Assumptions 1 and 2, and if the following matrix E,
- •
- uniformly in , for every constant .
- •
- For any , there is , so that , where is an initial value independent constant.
Following this, the proposed nonlinear ESO with one tuning parameter is:
where are pertinent chosen functions, such that the assumption holds.
Theorem 2.
Under Assumption 3, the following special case of (22) was chosen to estimate the state variables of the proposed PAM-based robot:
where is the adjustment parameter and .
3.3. Feedback Controller
The last important part of the ADRC approach is the feedback controller, which was developed as the following equation:
in which is the state variable of the model (7), and is the state variable of the TD (12). serves to cancel the “total disturbance” effect of the object model. The function was selected according to the following model asymptotic stabilization:
in which is the estimation error of the tracking differentiator (13). The main aim of the ADRC controller is for the state variables of function (25) to converge to zero , or
There are many ways to choose a function in order for (25) to be asymptotically stable to zero.
In this research, we chose the following Lyapunov function:
We can easily conclude that , and . We consider the derivative of :
Function (25) will be asymptotically stable if we choose
with . Substituting (28) into (25), we have
As a result, the feedback controller was selected as:
4. Experimental Results
To determine the efficiency of the nonlinear ESO-based ADRC controller on an exoskeleton robot of the BK-gait rehabilitation system shown in Figure 1, the control performance when tracking a gait-pattern trajectory was investigated. In addition, an external force was also added to the system to test the capability of the proposed nonlinear ESO to cancel the external disturbance. The proposed control approach was also compared with the LESO-based ADRC in all experimental conditions. Both controllers were discretized and programed using the LabVIEW MyRIO Toolkit of National Instrument (NI) with 5 ms of sampling time. The controller NI MyRIO-1900 was the hardware used to execute the coding program. Based on the trial and error method, the finetuned parameters of the two controllers are provided in Table 1 and Table 2. The parameters of both controllers were similar.

Table 1.
LESO-based controller’s parameters.

Table 2.
NLESO-based controller’s parameters.
In the first experiment, each controller was used to guide the rehabilitation robot to follow a cycling human-gait pattern trajectory. The trajectory frequency was 0.5 Hz, equivalent to a 2.5 km/h walking speed. The results are shown in Figure 3. The NLESO-based ADRC achieved a better performance than the LESO-based ADRC, with the RMSTEs at for the hip joint and 1.27 for the knee joint. These values in the counterpart were and . There was alarge deviation in the absolute value of the RMSTE. The NLESO-based controller significantly improved by over the LESO-based controller.
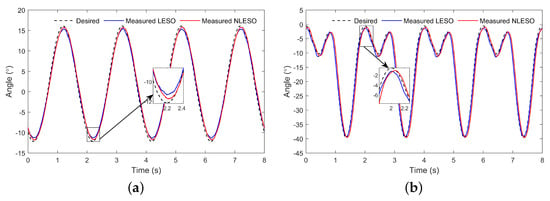
Figure 3.
Comparison of the results of tracking the gait-pattern trajectory with the LESO-based and NLESO-based controller: (a) hip and (b) knee joints.
Figure 4 and Figure 5 illustrate the knee joint’s measured state variables and the unknown disturbance together with their estimations. The nonlinear ESO achieved a high accuracy with the state variables, especially when estimating the variable , which contained the unknown disturbance. For example, in the knee joint, the trajectory was not as “smooth” as the hip’s trajectory; so, there were some sharp points in the of the LESO-based controller. As a result, the NLESO-based controller showed better tracking performance.
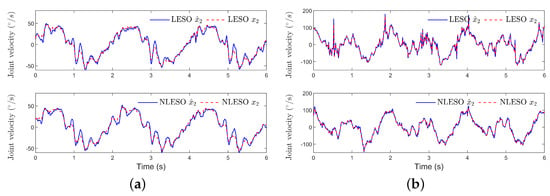
Figure 4.
The state variable and its estimation from the LESO (upper subfigure) and NLESO (lower subfigure) observers for the hip (a) and knee (b) joints.
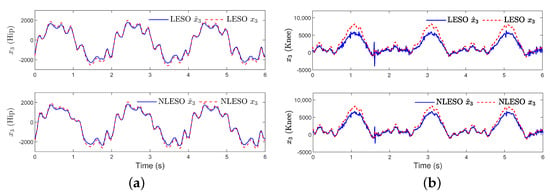
Figure 5.
The state variable and its estimation from the LESO (upper subfigure) and NLESO (lower subfigure) observers for the hip (a) and knee (b) joints.
To evaluate the ability to cancel the external disturbance of the NLESO-based controller, at s from the system startup, a cycling force ranging from 35 N to 40 N was added to the system as a disturbance component. The cycling force was generated by using a bicycle tube attached to the knee link of the exoskeleton robot. The length of the bicycle tube was reduced by supplying a slight pressure to create the external force at the needed time. Figure 6 illustrates the experimental results of the LESO-based and NLESO-based controllers. The NLESO-based controller achieved a better tracking accuracy with about error in the steady state. Both controllers maintained good tracking performance and excellently dealt with the external disturbance, which was the main aim of the ADRC approach. Table 3 provides the quantitative comparison results of both controllers.
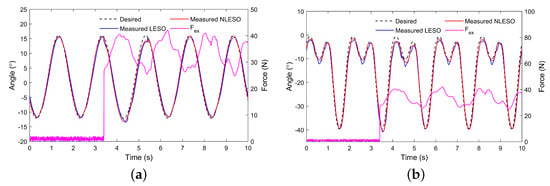
Figure 6.
The system’s response to disturbance (NLESO): (a) hip and (b) knee joints.

Table 3.
The RMSE value of the two ESOs.
5. Conclusions
In this paper, a nonlinear ESO-based ADRC control approach was used to enhance the trajectory tracking quality of the PAM-based exoskeleton robot of the BK-gait rehabilitation system. First, selecting the tracking differentiator with a transient profile helped to avoid the jump between the desired signal and the system’s output. In practical application, it made the desired trajectory smooth as well as the control output, which is valuable for any system. Second, a nonlinear ESO was implemented to estimate the inherent disturbance of the PAM-based robot. The theoretical and experimental results showed that the nonlinear observer achieved higher accuracy than the linear one in terms of approximation. Third, the feedback control law, developed based on the Lyapunov stability theory, showed outstanding effectiveness when guiding the exoskeleton robot to a gait-pattern trajectory. Overall, the systems were validated through experiments on a PAM-based robot in cases with and without external disturbance. Although experiments with a subject’s participation were not investigated in this research, the proposed NLESO-based controller showed the promising applicability of PAM-based robots in the rehabilitation field. The PAM-based robot’s mechanism and control approach must be improved more before allowing a subject to participate in the experiments. In addition, the assist-as-needed training function will also be integrated into the system by implementing an impedance controller. A body weight support system and its control system will also be implemented in future works. In addition, some wearable biomedical sensors, such as electromyography (EMG), should be included in the system to provide information about muscle recovery during the training process. It is a valuable assessment of the health of the muscles. Based on this, physical therapists can determine suitable exercises for the patients.
Author Contributions
Conceptualization, Q.-T.D. and M.-D.D.; Data curation, M.-C.T. and V.-L.N.; Formal analysis, V.-V.D.; Investigation, M.-C.T.; Methodology, M.-D.D. and N.-T.B.; Resources, V.-L.N.; Software, V.-L.N. and V.-C.T.; Validation, V.-V.D., M.-C.T. and V.-L.N.; Writing—original draft, V.-C.T. and N.-T.B.; Writing—review and editing, Q.-T.D. and M.-D.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Hanoi University of Science and Technology (HUST) under project number T2022-PC-002.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PAM | Pneumatic Artificial Muscle |
| ADRC | Active Disturbance Rejection Control |
| ESO | Extended State Observer |
| LESO | Linear Extended State Observer |
| NLESO | Nonlinear Extended State Observer |
| TD | Tracking Differentiator |
| RMSE | Root Mean Square Error |
| EMG | Electromyography |
References
- Zhou, J.; Yang, S.; Xue, Q. Lower limb rehabilitation exoskeleton robot: A review. Adv. Mech. Eng. 2021, 13, 16878140211011862. [Google Scholar] [CrossRef]
- Hussain, F.; Goecke, R.; Mohammadian, M. Exoskeleton robots for lower limb assistance: A review of materials, actuation, and manufacturing methods. Proc. Inst. Mech. Eng. Part J. Eng. Med. 2021, 235, 1375–1385. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J. Wearable Robotics: Systems and Applications; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Zhang, J.; Sheng, J.; O’Neill, C.T.; Walsh, C.J.; Wood, R.J.; Ryu, J.H.; Desai, J.P.; Yip, M.C. Robotic Artificial Muscles: Current Progress and Future Perspectives. IEEE Trans. Robot. 2019, 35, 761–781. [Google Scholar] [CrossRef]
- Andrikopoulos, G.; Nikolakopoulos, G.; Manesis, S. Advanced Nonlinear PID-Based Antagonistic Control for Pneumatic Muscle Actuators. IEEE Trans. Ind. Electron. 2014, 61, 6926–6937. [Google Scholar] [CrossRef]
- Vo-Minh, T.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. A New Approach to Modeling Hysteresis in a Pneumatic Artificial Muscle Using The Maxwell-Slip Model. IEEE/ASME Trans. Mechatron. 2011, 16, 177–186. [Google Scholar] [CrossRef]
- Kosaki, T.; Minesaki, A.; Sano, M. Adaptive Hysteresis Compensation with a Dynamic Hysteresis Model for Control of a Pneumatic Muscle Actuator. J. Environ. Eng. 2012, 7, 53–65. [Google Scholar] [CrossRef][Green Version]
- Xie, S.; Mei, J.; Liu, H.; Wang, Y. Hysteresis modeling and trajectory tracking control of the pneumatic muscle actuator using modified Prandtl–Ishlinskii model. Mech. Mach. Theory 2018, 120, 213–224. [Google Scholar] [CrossRef]
- Dao, Q.T.; Yamamoto, S.i. Assist-as-Needed Control of a Robotic Orthosis Actuated by Pneumatic Artificial Muscle for Gait Rehabilitation. Appl. Sci. 2018, 8, 499. [Google Scholar] [CrossRef]
- Taheri, B.; Case, D.; Richer, E. Force and Stiffness Backstepping-Sliding Mode Controller for Pneumatic Cylinders. IEEE/ASME Trans. Mechatronics 2014, 19, 1799–1809. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, H.; Xia, Y.; Liu, B. Angle Tracking Adaptive Backstepping Control for a Mechanism of Pneumatic Muscle Actuators via an AESO. IEEE Trans. Ind. Electron. 2019, 66, 4566–4576. [Google Scholar] [CrossRef]
- Liang, D.; Sun, N.; Wu, Y.; Chen, Y.; Fang, Y.; Liu, L. Energy-Based Motion Control for Pneumatic Artificial Muscle Actuated Robots With Experiments. IEEE Trans. Ind. Electron. 2022, 69, 7295–7306. [Google Scholar] [CrossRef]
- Sun, N.; Liang, D.; Wu, Y.; Chen, Y.; Qin, Y.; Fang, Y. Adaptive Control for Pneumatic Artificial Muscle Systems With Parametric Uncertainties and Unidirectional Input Constraints. IEEE Trans. Ind. Inform. 2020, 16, 969–979. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Ibraheem, I.K.; Azar, A.T.; Sadiq, M.E. A new adaptive synergetic control design for single link robot arm actuated by pneumatic muscles. Entropy 2020, 22, 723. [Google Scholar] [CrossRef]
- Estrada, A.; Plestan, F. Second order sliding mode output feedback control with switching gains—Application to the control of a pneumatic actuator. J. Frankl. Inst. 2014, 351, 2335–2355. [Google Scholar] [CrossRef]
- Dao, Q.T.; Mai, D.H.; Nguyen, D.K.; Ly, N.T. Adaptive Parameter Integral Sliding Mode Control of Pneumatic Artificial Muscles in Antagonistic Configuration. J. Control. Autom. Electr. Syst. 2022, 33, 1116–1124. [Google Scholar] [CrossRef]
- Hussain, S.; Xie, S.Q.; Jamwal, P.K. Adaptive Impedance Control of a Robotic Orthosis for Gait Rehabilitation. IEEE Trans. Cybern. 2013, 43, 1025–1034. [Google Scholar] [CrossRef] [PubMed]
- Dao, Q.T.; Nguyen, M.L.; Yamamoto, S.i. Discrete-Time Fractional Order Integral Sliding Mode Control of an Antagonistic Actuator Driven by Pneumatic Artificial Muscles. Appl. Sci. 2019, 9, 2503. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, H.; Zhang, J.; Xia, Y. Adaptive control for a motion mechanism with pneumatic artificial muscles subject to dead-zones. Mech. Syst. Signal Process. 2021, 148, 107155. [Google Scholar] [CrossRef]
- Hodgson, S.; Tavakoli, M.; Pham, M.T.; Leleve, A. Nonlinear Discontinuous Dynamics Averaging and PWM-Based Sliding Control of Solenoid-Valve Pneumatic Actuators. IEEE/ASME Trans. Mechatron. 2015, 20, 876–888. [Google Scholar] [CrossRef]
- Lin, C.J.; Sie, T.Y.; Chu, W.L.; Yau, H.T.; Ding, C.H. Tracking Control of Pneumatic Artificial Muscle-Activated Robot Arm Based on Sliding-Mode Control. Actuators 2021, 10, 66. [Google Scholar] [CrossRef]
- Dao, Q.T.; Tri, T.K.L.; Nguyen, V.A.; Nguyen, M.L. Discrete-time sliding mode control with power rate exponential reaching law of a pneumatic artificial muscle system. Control Theory Technol. 2022, 19, 221–238. [Google Scholar] [CrossRef]
- Rezoug, A.; Hamerlain, F.; Hamerlain, M. Application of Fuzzy Sliding Mode to control of Manipulator Robot actuated by Pneumatic artificial Muscles. In Proceedings of the 2nd IFAC Conference on Intelligent Control Systems and Signal Processing, Istanbul, Turkey, 21–23 September 2009; pp. 580–585. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Rattan, K. Feedforward control of a non-linear pneumatic muscle system using fuzzy logic. In Proceedings of the 12th IEEE International Conference on Fuzzy Systems, FUZZ ’03, Glasgow, UK, 25–28 May 2003; Volume 1, pp. 272–277. [Google Scholar] [CrossRef]
- Wang, T.; Chen, X.; Qin, W. A novel adaptive control for reaching movements of an anthropomorphic arm driven by pneumatic artificial muscles. Appl. Soft Comput. 2019, 83, 105623. [Google Scholar] [CrossRef]
- Pham, H.A.H.; Cao Van Kien, N.N.S.; Nam, N.T. New approach of sliding mode control for nonlinear uncertain pneumatic artificial muscle manipulator enhanced with adaptive fuzzy estimator. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418773204. [Google Scholar] [CrossRef]
- Huy Anh Ho Pham, N.N.S.; Kien, C.V. Adaptive neural compliant force-position control of serial PAM robot. J. Intell. Robot. Syst. 2018, 89, 351–369. [Google Scholar] [CrossRef]
- Xia, X.; Cheng, L. Adaptive Takagi-Sugeno fuzzy model and model predictive control of pneumatic artificial muscles. Sci. China Technol. Sci. 2021, 64, 2272–2280. [Google Scholar] [CrossRef]
- Ahn, K.K.; Anh, H.P.H. Design & Implementation an Adaptive Takagi-Sugeno Fuzzy Neural Networks Controller for the 2-Links Pneumatic Artificial Muscle (PAM) Manipulator using in Elbow Rehabilitation. In Proceedings of the 2006 First International Conference on Communications and Electronics, Hanoi, Vietnam, 10–11 Octobetr 2006; pp. 356–361. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Huang, C.; Zheng, Q. Application of linear active disturbance rejection control to power system load frequency control. Int. J. Intell. Control Syst. 2014, 19, 1–7. [Google Scholar]
- Alvarez, U.; Olascoaga, A.; Rivera, D.; Mendoza, A.R.; Garcia, O.; Amezquita-Brooks, L. Active disturbance rejection control for micro air vehicles using frequency domain analysis. In Proceedings of the Congreso Nacional de Control Automático, Nuevo León, Mexico, 4–6 October 2017; pp. 683–688. [Google Scholar]
- Suhail, S.A.; Bazaz, M.A.; Hussain, S. Active disturbance rejection control applied to a DC motor for position control. In Proceedings of the ICETIT 2019, Delhi, India, June 2019; pp. 437–448. [Google Scholar]
- Aole, S.; Elamvazuthi, I.; Waghmare, L.; Patre, B.; Meriaudeau, F. Improved Active Disturbance Rejection Control for Trajectory Tracking Control of Lower Limb Robotic Rehabilitation Exoskeleton. Sensors 2020, 20, 3681. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, X.; Wang, T. Trajectory tracking control for double-joint manipulator systems driven by pneumatic artificial muscles based on a nonlinear extended state observer. Mech. Syst. Signal Process. 2019, 122, 307–320. [Google Scholar] [CrossRef]
- Reynolds, D.; Repperger, D.; Phillips, C.; Bandry, G. Modeling the dynamic characteristics of pneumatic muscle. Ann. Biomed. Eng. 2003, 31, 310–317. [Google Scholar] [CrossRef]
- Lilly, J.; Quesada, P. A two-input sliding-mode controller for a planar arm actuated by four pneumatic muscle groups. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 349–359. [Google Scholar] [CrossRef] [PubMed]
- Choi, T.Y.; Lee, J.J. Control of Manipulator Using Pneumatic Muscles for Enhanced Safety. IEEE Trans. Ind. Electron. 2010, 57, 2815–2825. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. Active disturbance rejection control: Theoretical perspectives. Commun. Inf. Syst. 2015, 15, 361–421. [Google Scholar] [CrossRef]
- Herbst, G. A Simulative Study on Active Disturbance Rejection Control (ADRC) as a Control Tool for Practitioners. Electronics 2013, 2, 246–279. [Google Scholar] [CrossRef]
- Zhao, Z.L.; Guo, B.Z. On convergence of nonlinear active disturbance rejection control for MIMO systems. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 434–441. [Google Scholar] [CrossRef]
- Zheng, Q.; Gaol, L.Q.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).