Force Characteristics of Centrifugal Pump as Turbine during Start-Up Process under Gas–Liquid Two-Phase Conditions
Abstract
1. Introduction
2. Numerical Simulation and Verification
2.1. Control Equation
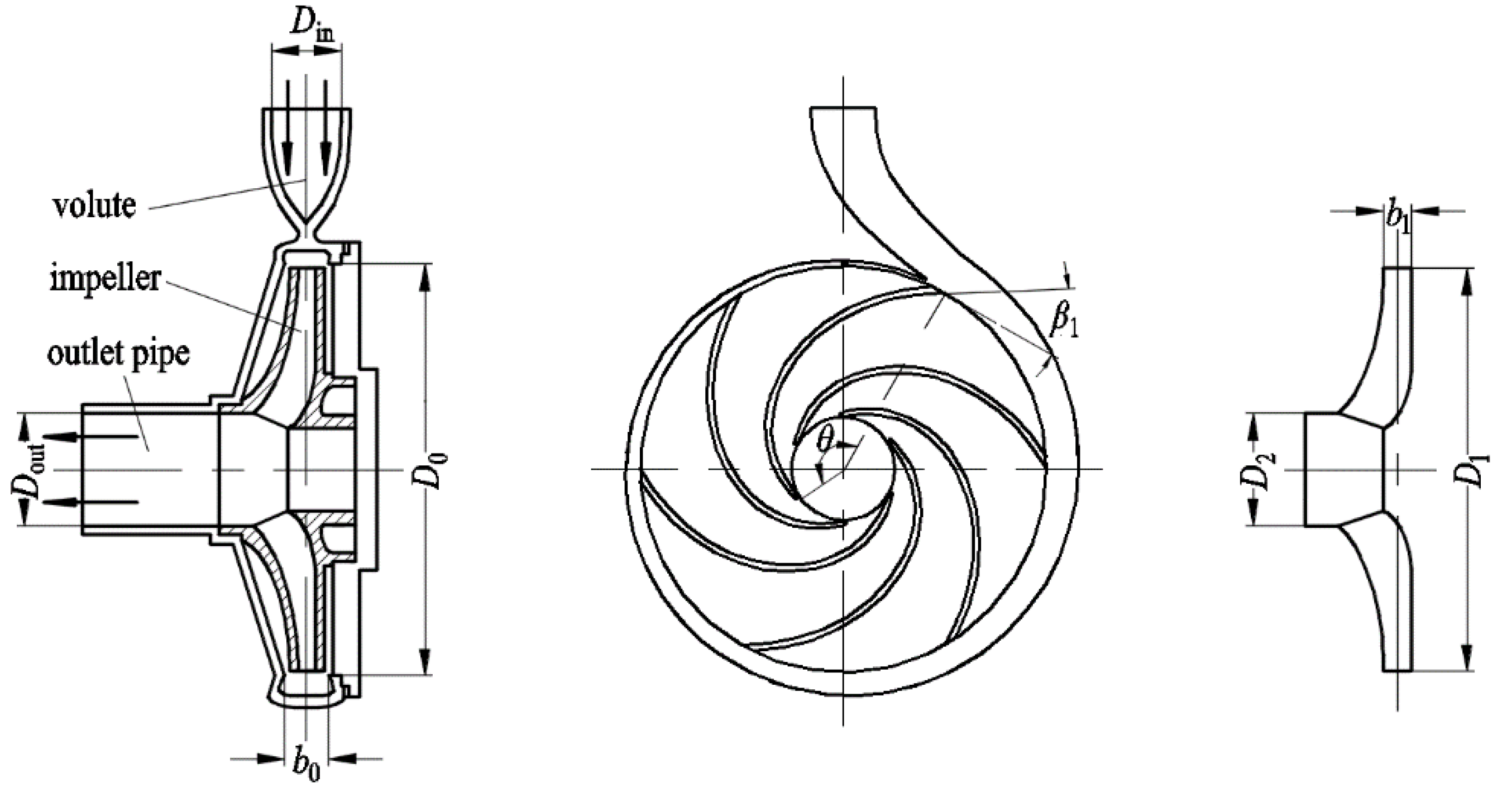
2.2. Calculation Model
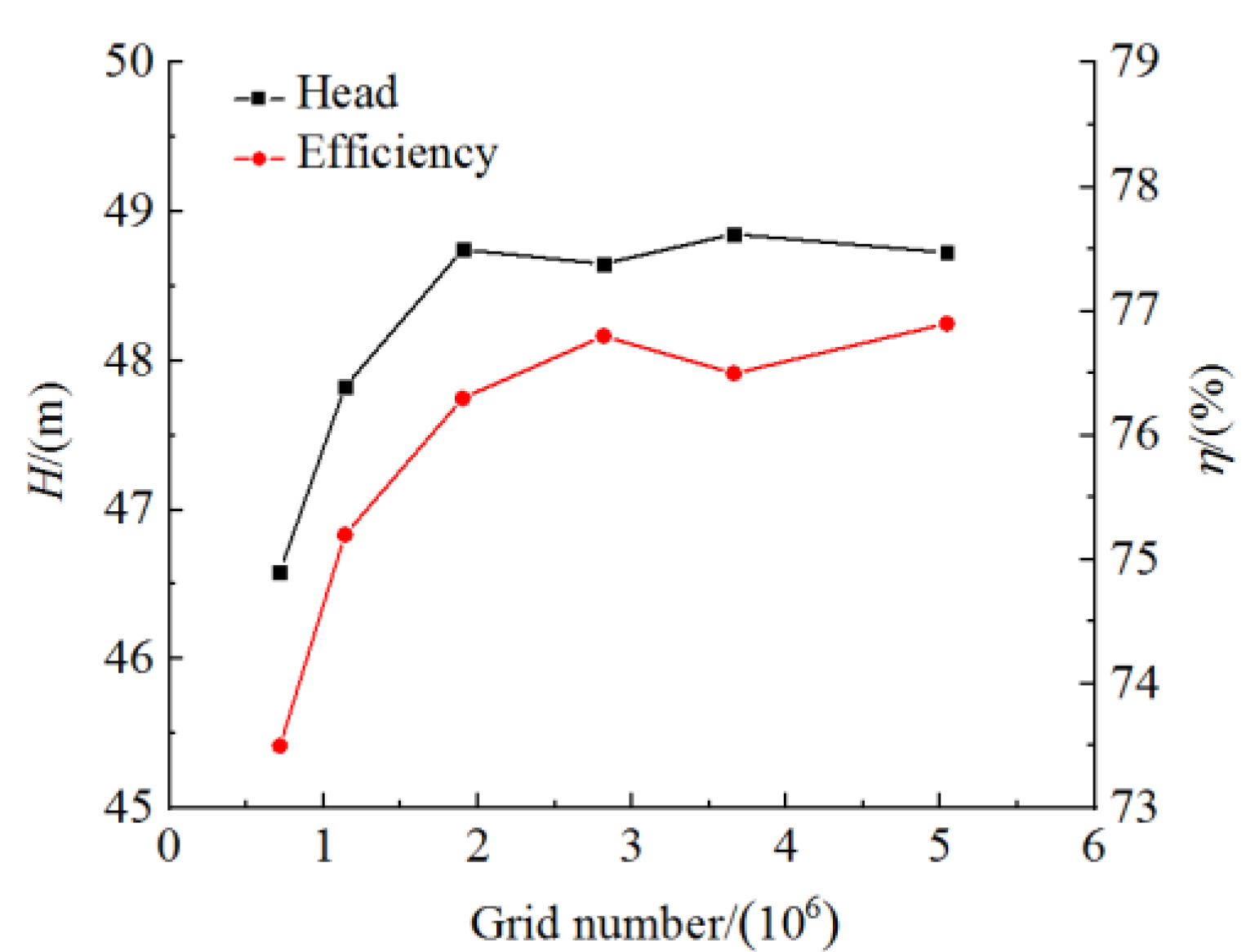
2.3. Calculation Method
2.4. Boundary Condition
2.5. Experimental Verification
3. Results and Analysis
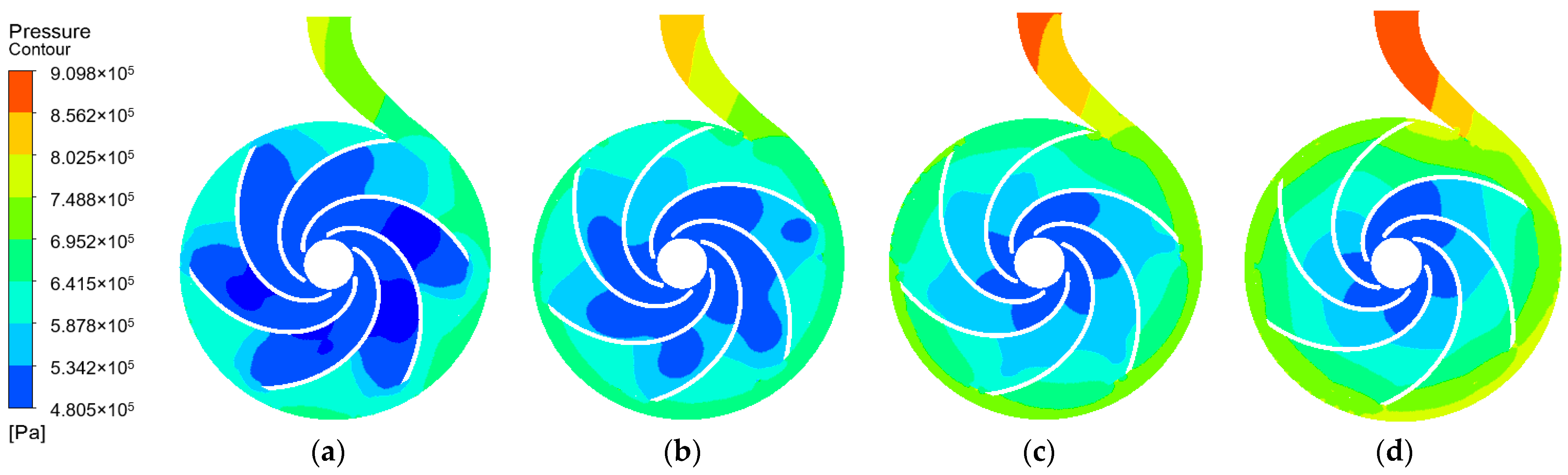
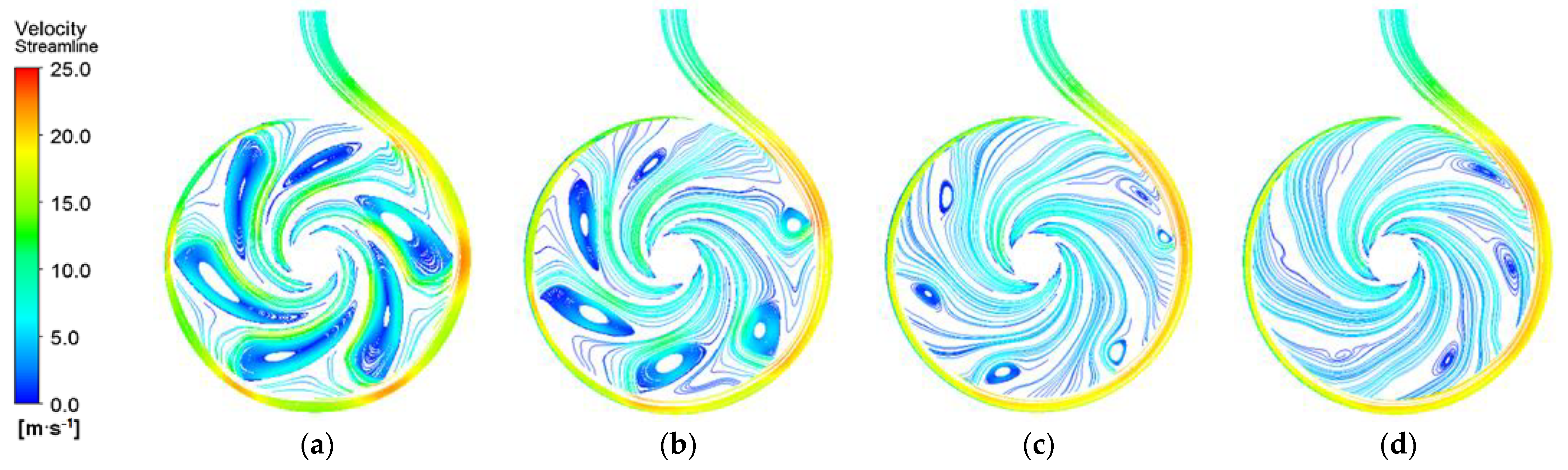
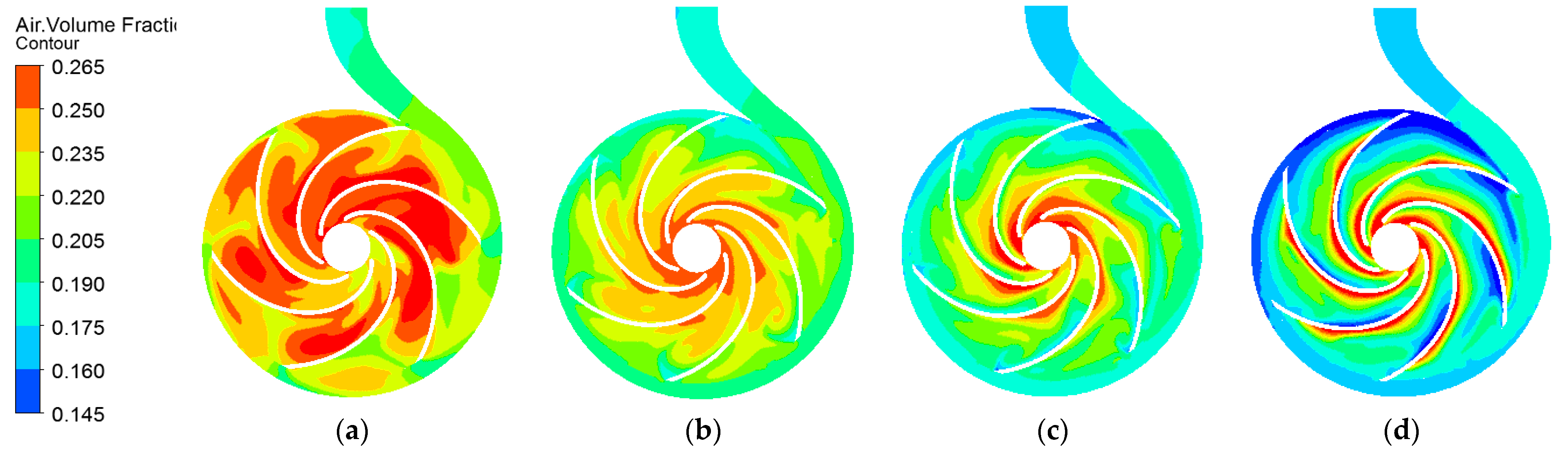
3.1. Internal Flow Field Distribution
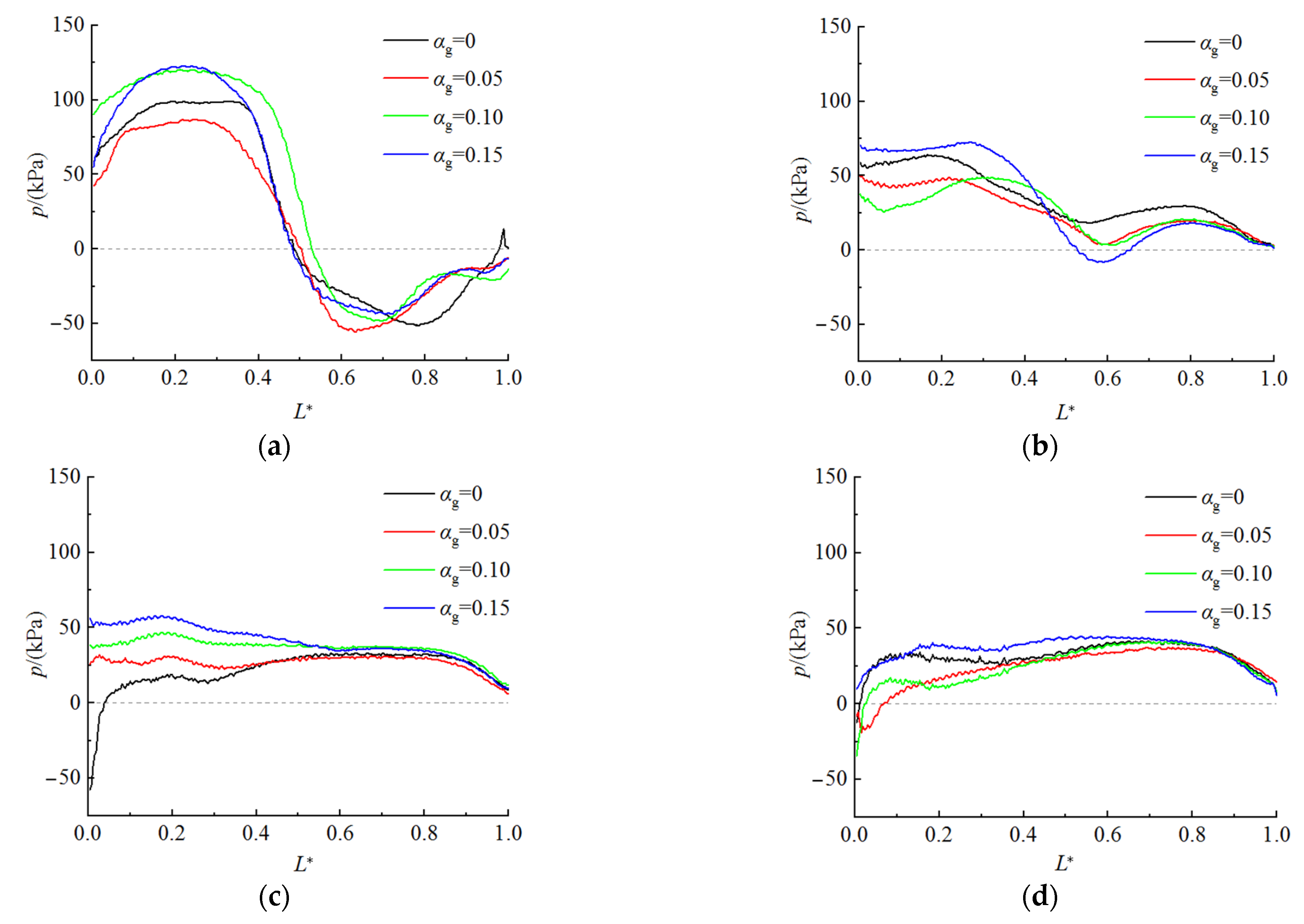
3.2. Blade Load Distribution
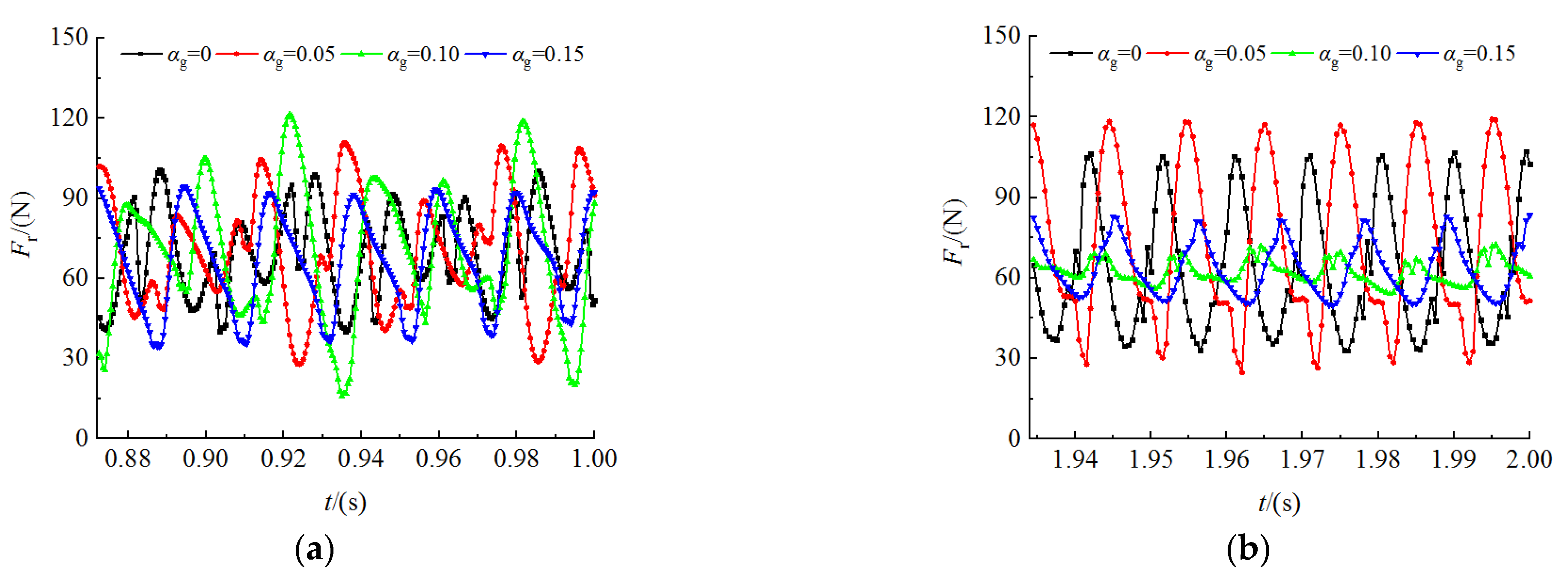
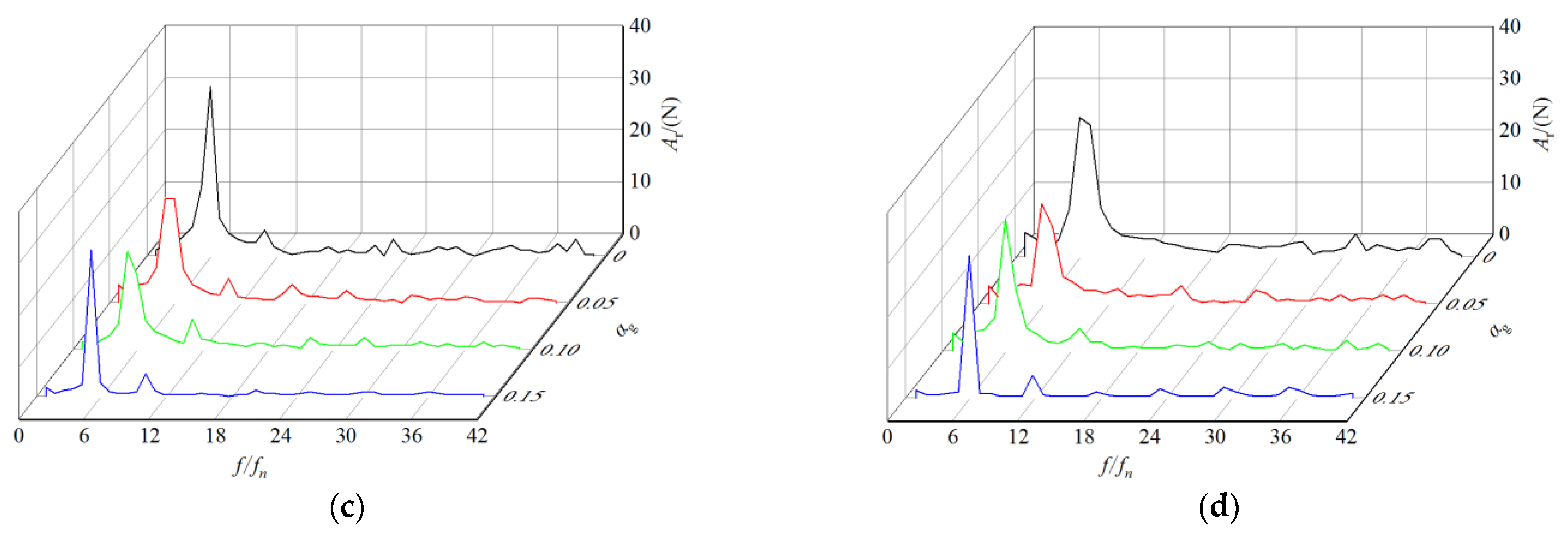
3.3. Radial Force Analysis
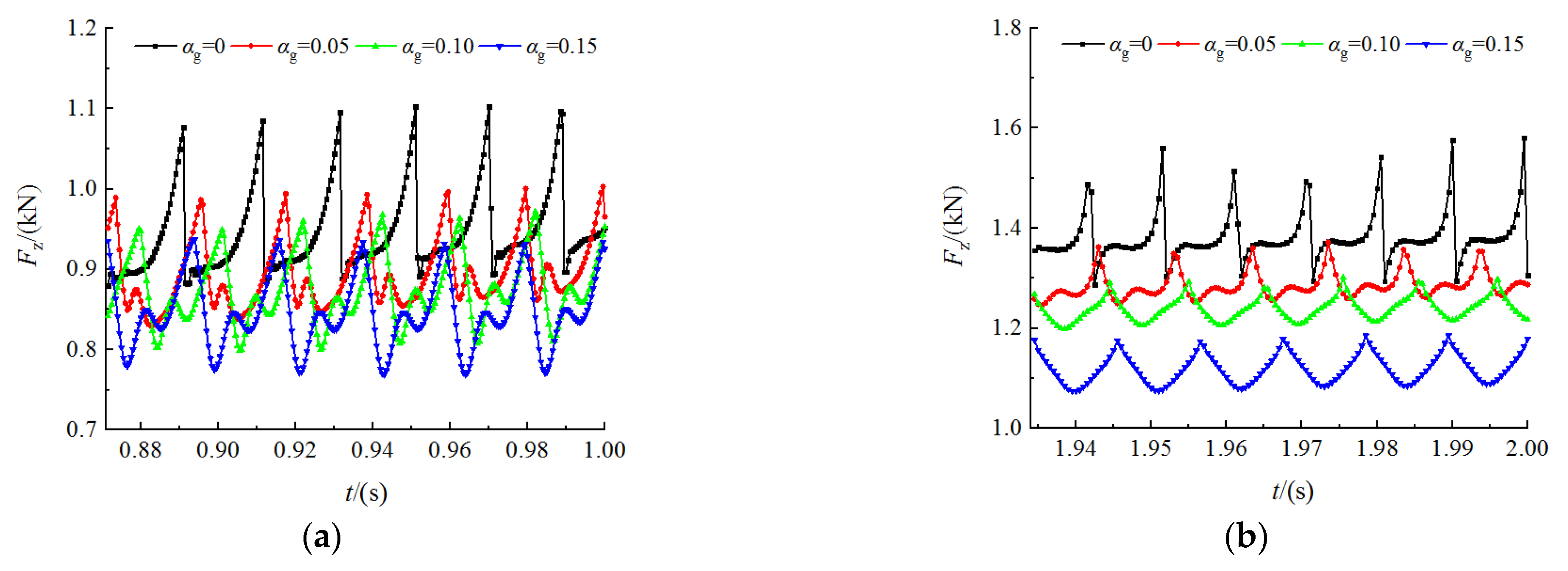
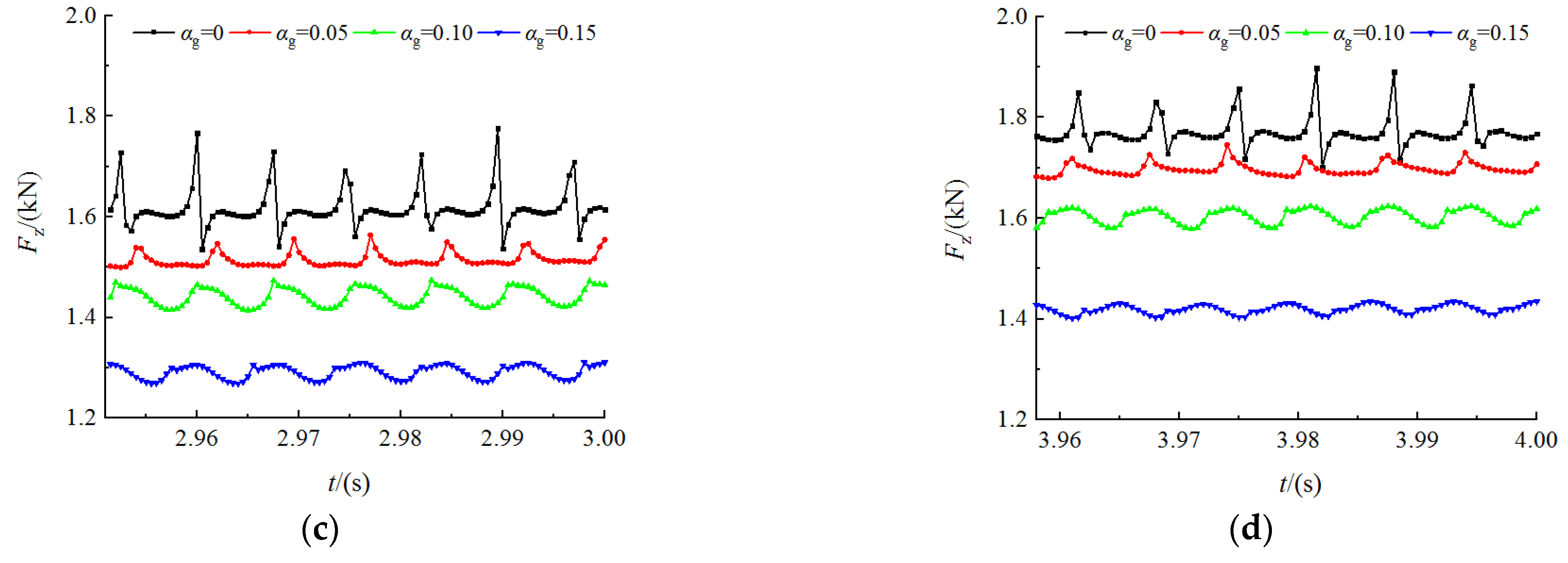
3.4. Axial Force Analysis
4. Conclusions
- (1)
- At the beginning of start-up, the gas volume fraction is high, its distribution is uneven in the impeller, and the area with high gas phase concentration corresponds to a strong vortex. With the increase in rotational speed, the low-pressure area, the high-concentration gas phase region, and the vortex intensity in the impeller gradually decrease. The gas phase gradually converges to the inner edge of the impeller, and the gas volume fraction of the blade suction surface is more significant than that of the blade pressure surface.
- (2)
- At the beginning of start-up, the blade load oscillates violently, and the maximum load is distributed near the outer edge of the blade. As the rotational speed increases, the oscillation of the blade load gradually weakens, and the maximum load is distributed near the inner edge of the blade after the rotational speed is stable. The larger the IGVF, the more severe the blade load oscillation during the start-up process. Therefore, reducing the IGVF is helpful in improving the stability of the PAT start-up process.
- (3)
- The periodic unbalanced radial force is produced in the start-up process. From the pure liquid conditions to the gas–liquid two-phase conditions with increasing IGVF, the dominant frequency amplitude of radial force shows a similar trend of decreasing first but then increasing. After the rotational speed tends to be stable, the dominant frequency of radial force is equal to the rotational frequency of the blade. With the increase in IGVF, the dominant frequency amplitude of radial force decreases slightly at the same time.
- (4)
- At the beginning of start-up, the axial force shows the maximum amplitude and fluctuates twice in a fluctuation cycle under gas–liquid two-phase conditions. With the increase in rotational speed, the dominant frequency amplitude of axial force decreases gradually. The higher the IGVF, the greater the dominant frequency amplitude of axial force at the same time.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jain, S.; Patel, R. Investigations on pump running in turbine mode: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2014, 30, 841–868. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Shi, F. Status and prospect of study on energy recovery hydraulic turbines. J. Drain. Irrig. Mach. Eng. 2014, 32, 742–747. [Google Scholar]
- Maxime, B.; Su, W.; Li, X.; Li, F.; Wei, X.; An, S. Investigation on pump as turbine (PAT) technical aspects for micro hydropower schemes: A state of the art review. Renew. Sustain. Energy Rev. 2017, 79, 148–179. [Google Scholar]
- Barrios, L. Visualization and Modeling of Multiphase Performance Inside an Electrical Submersible Pump. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2007. [Google Scholar]
- Gamboa, J. Prediction of the Transition in Two-Phase Performance of an Electrical Submersible Pump. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2008. [Google Scholar]
- Li, G.; Wang, Y.; Zheng, Y.; Ma, X.; Liang, L.; Hu, R. Unsteady internal flow and thrust analysis of centrifugal pump under gas-liquid two-phase flow conditions. J. Drain. Irrig. Mach. Eng. 2016, 34, 369–374. [Google Scholar]
- Yuan, J.; Zhang, K.; Si, Q.; Zhou, B.; Tang, Y.; Jin, Z. Numerical investigation of gas-liquid two-phase flow in centrifugal pumps based on inhomogeneous model. Trans. Chin. Soc. Agric. Mach. 2017, 48, 89–95. [Google Scholar]
- Luo, X.; Yan, S.; Feng, J.; Zhu, G.; Sun, S.; Chen, S. Force characteristics of gas-liquid two-phase centrifugal pump. Trans. Chin. Soc. Agric. Eng. 2019, 35, 66–72. [Google Scholar]
- Michael, M.; Saketh, K.; Dominique, T. Investigations on the effect of rotational speed on the transport of air-water two-phase flows by centrifugal pumps. Int. J. Heat Fluid Flow 2022, 94, 108939. [Google Scholar]
- Yan, S.; Luo, X.; Feng, J.; Zhu, G.; Zhang, L.; Chen, S. Numerical simulation of a gas-liquid centrifugal pump under different inlet gas volume fraction conditions. Int. J. Fluid Mach. Syst. 2019, 12, 56–63. [Google Scholar]
- Zhang, W.; Yu, Z.; Zahid, M.; Li, Y. Study of the gas distribution in a multiphase rotodynamic pump based on interphase force analysis. Energies 2018, 11, 1069. [Google Scholar] [CrossRef]
- Anthony, C.; Laurent, G.; Daniel, P. Characteristics of centrifugal pumps working in direct or reverse mode: Focus on the unsteady radial thrust. Int. J. Rotating Mach. 2013, 2013, 279049. [Google Scholar]
- Shi, F.; Yang, J.; Wang, X. Numerical prediction of radial force in hydraulic turbine based on fluent. Adv. Mater. Res. 2013, 716, 717–720. [Google Scholar] [CrossRef]
- Qu, X.; Kong, F.; Chen, H. A numerical simulation and analysis of impeller axial force of pumps as turbines. China Rural. Water Hydropower 2013, 7, 96–102. [Google Scholar]
- Yang, J.; Li, T. Influence of volute configurations on radial force of hydraulic turbine. J. Drain. Irrig. Mach. Eng. 2015, 33, 651–656. [Google Scholar]
- Dai, C.; Kong, F.; Dong, L.; Zhang, H.; Feng, Z. Effect of blade wrap angle on the radial force of centrifugal pump as turbine. J. Vib. Shock 2015, 34, 69–72. [Google Scholar]
- Shi, F.; Yang, J.; Wang, X. Unsteady analysis of on effect hydraulic turbine under variable gas content. J. Aerosp. Power 2017, 32, 2265–2272. [Google Scholar]
- Shi, F.; Yang, J.; Miao, S.; Wang, X. Investigation on the power loss and radial force characteristics of pump as turbine under gas-liquid two-phase condition. Adv. Mech. Eng. 2019, 11, 1687814019843732. [Google Scholar]
- Shi, G.; Liu, Y.; Luo, K. Analysis of gas-liquid two-phase flow field in hydraulic turbine considering gas compressibility. J. Eng. Therm. Energy Power 2018, 33, 40–45. [Google Scholar]
- Sun, K.; Li, Y.; Zhao, J. Transient starting performance analysis of vertical axis tidal turbine. Huazhong Univ. Sci. Tech. Nat. Sci. Ed. 2017, 45, 51–56. [Google Scholar]
- Chen, W.; Liu, Y.; Chen, L.W. Study on hydrodynamic performance of horizontal tidal turbine rotating passively based on UDF. Ocean Eng. 2018, 36, 119–126. [Google Scholar]
- Untaroiu, A.; Wood, H.; Allaire, P.; Ribando, R. Investigation of self-starting capability of vertical axis wind turbines using a computational fluid dynamics approach. J. Sol. Energy Eng. 2011, 133, 125–134. [Google Scholar] [CrossRef]
- Barrio, R.; Fernandez, J.; Blanco, E.; Parrondo, J. Estimation of radial load in centrifugal pumps using computational fluid dynamics. Eur. J. Mech.-B/Fluids 2011, 3, 316–324. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, B.; Yang, J.; Wang, X. Force Characteristics of Centrifugal Pump as Turbine during Start-Up Process under Gas–Liquid Two-Phase Conditions. Actuators 2022, 11, 370. https://doi.org/10.3390/act11120370
Chai B, Yang J, Wang X. Force Characteristics of Centrifugal Pump as Turbine during Start-Up Process under Gas–Liquid Two-Phase Conditions. Actuators. 2022; 11(12):370. https://doi.org/10.3390/act11120370
Chicago/Turabian StyleChai, Baodui, Junhu Yang, and Xiaohui Wang. 2022. "Force Characteristics of Centrifugal Pump as Turbine during Start-Up Process under Gas–Liquid Two-Phase Conditions" Actuators 11, no. 12: 370. https://doi.org/10.3390/act11120370
APA StyleChai, B., Yang, J., & Wang, X. (2022). Force Characteristics of Centrifugal Pump as Turbine during Start-Up Process under Gas–Liquid Two-Phase Conditions. Actuators, 11(12), 370. https://doi.org/10.3390/act11120370





