Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller
Abstract
:1. Introduction
- We present a new control structure to demonstrate the capability of the RST controller combined with inverse LSSVM model-based control to reject disturbances and further improve the robustness of the design.
- We evaluate the proposed control scheme using a nanopositioning platform and provide a comparison with the results from our previous work.
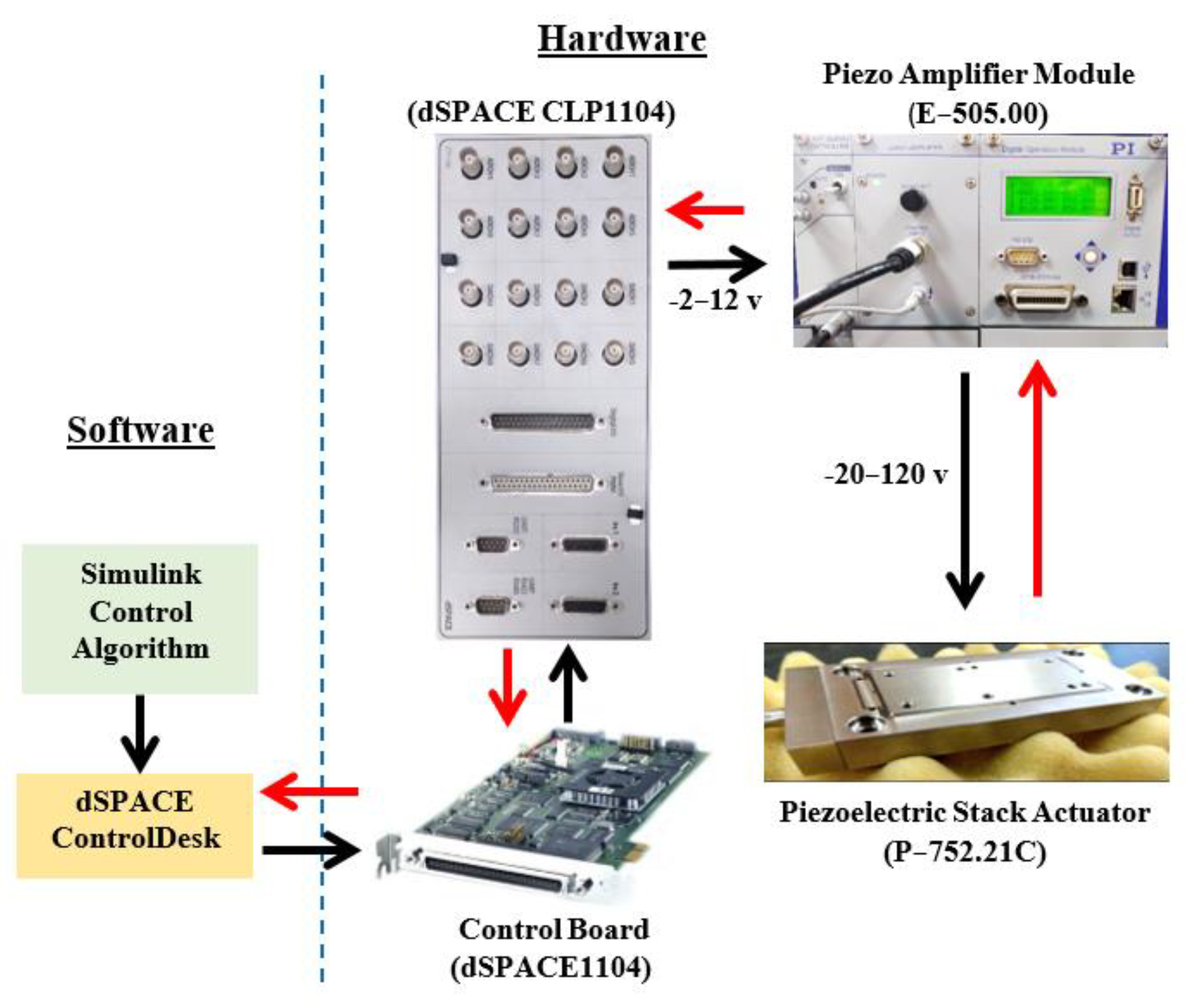
2. Hardware, Software, and Data Description
2.1. Hardware and Software Description
2.2. Data Description
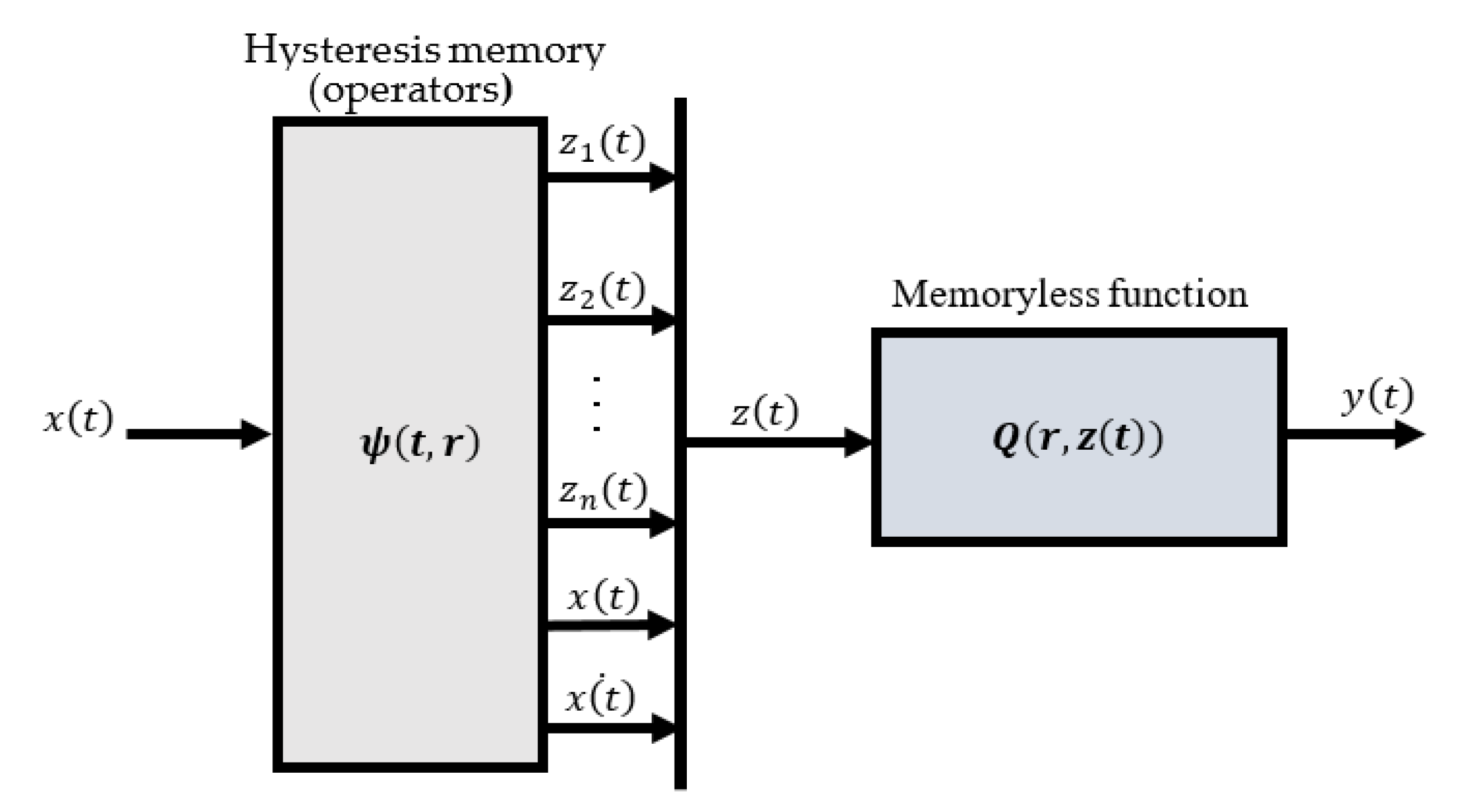
3. Model Structure
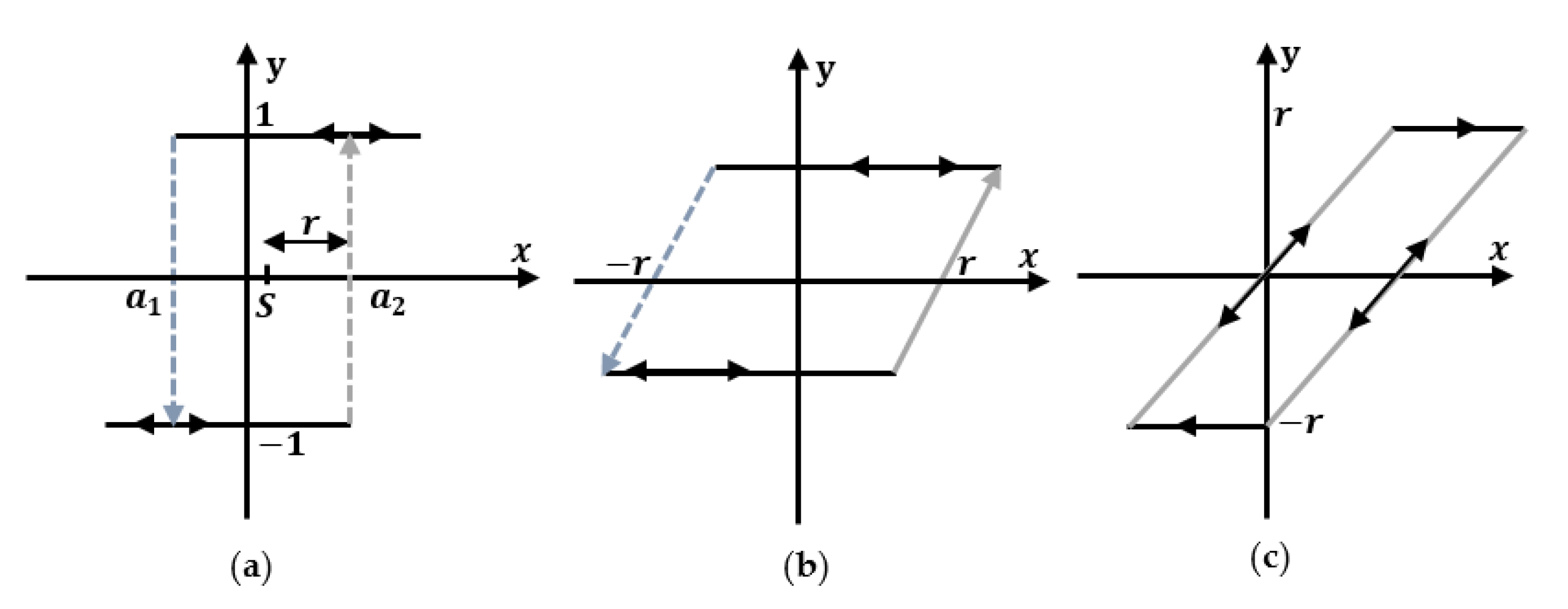
3.1. Proposed Hysteresis Memory
3.2. Memoryless Function
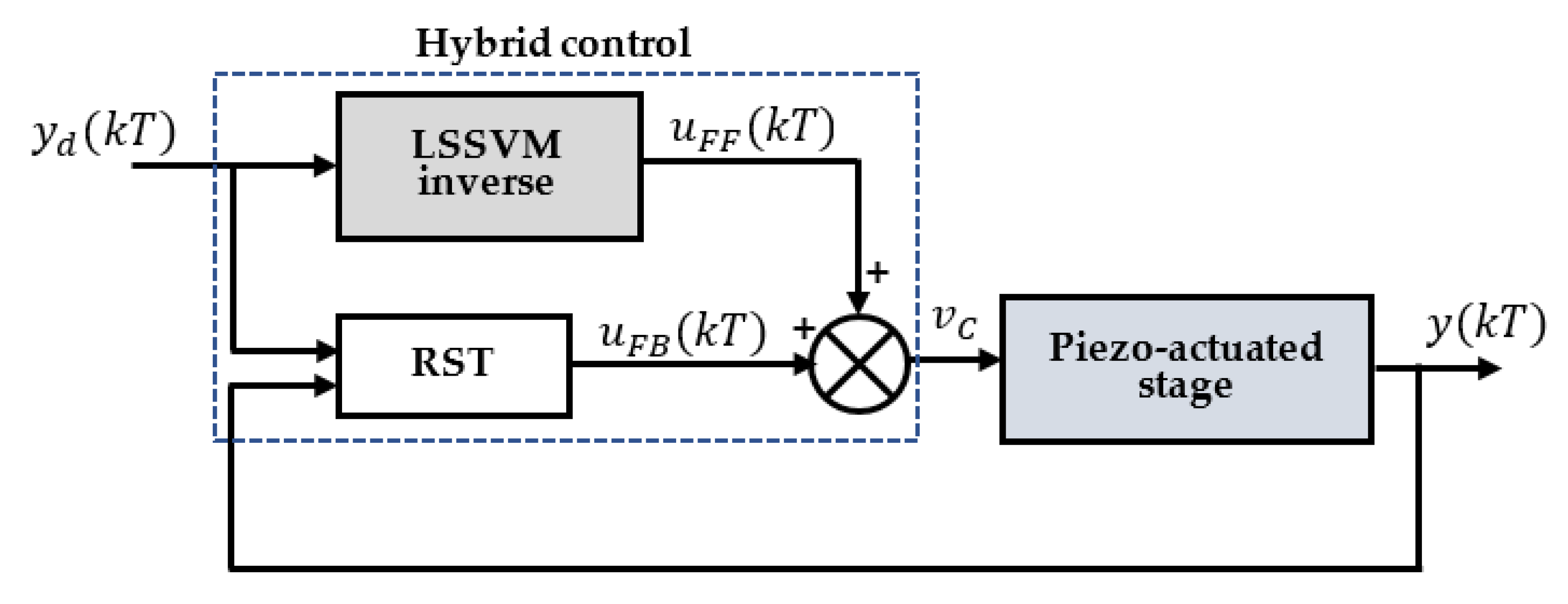
4. Control Design
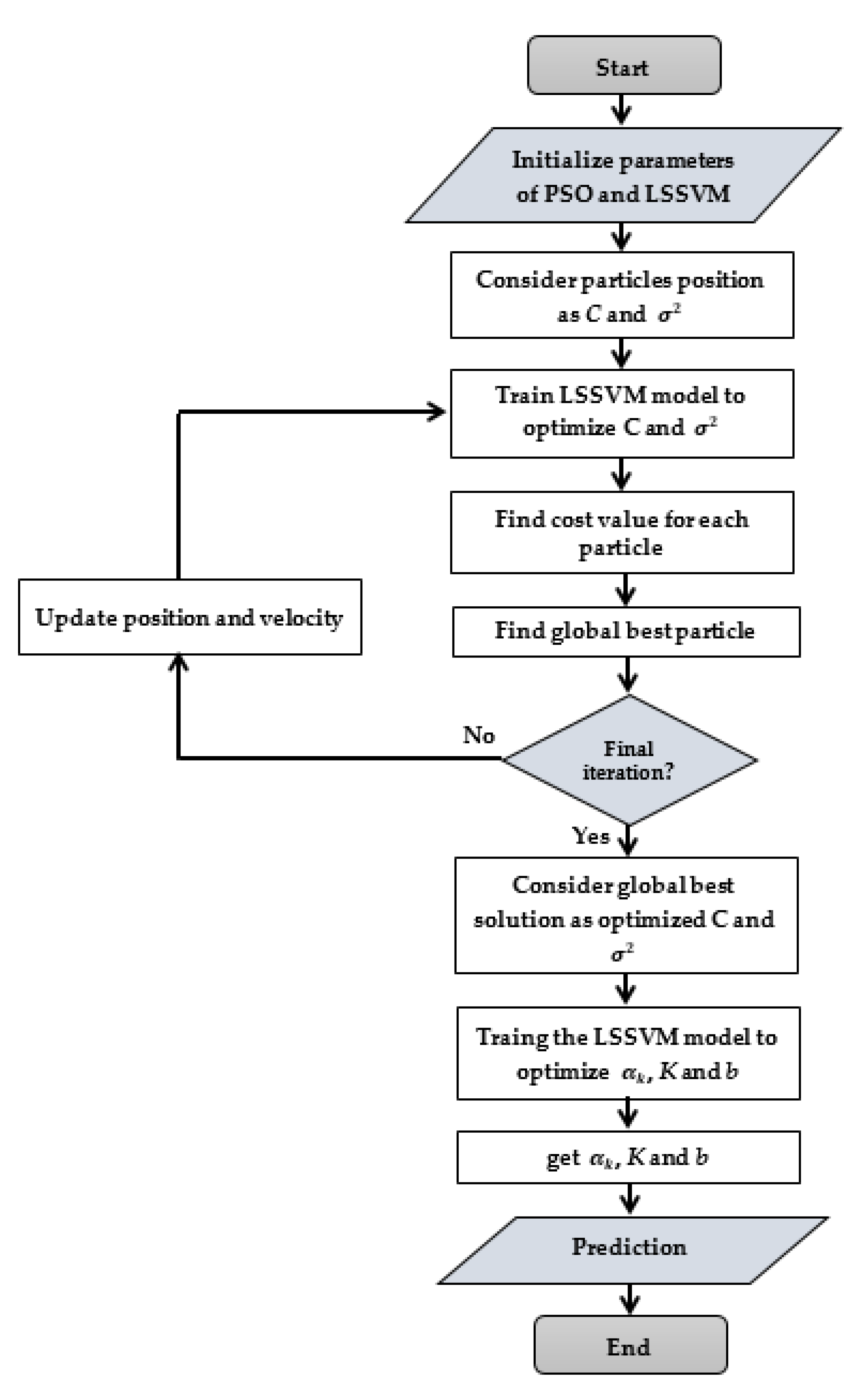
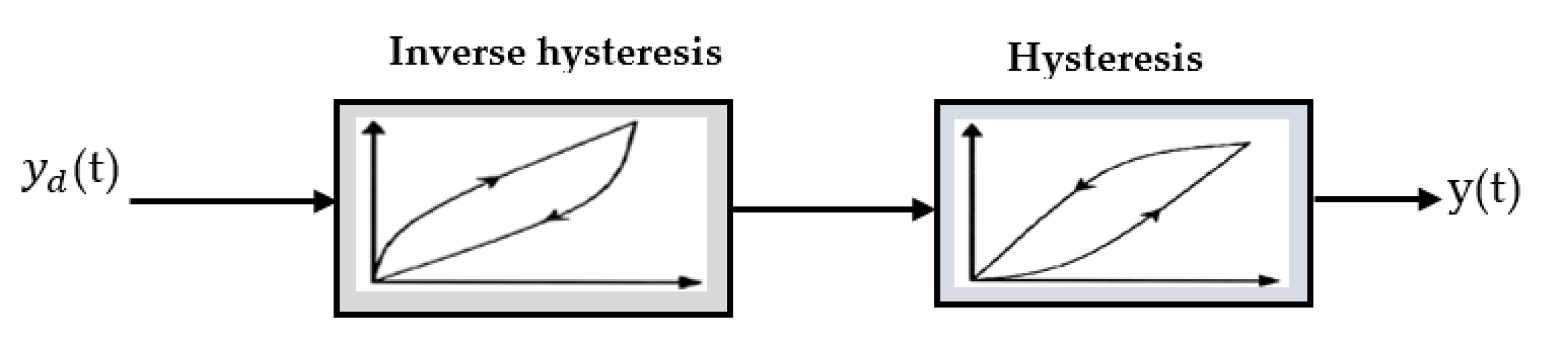
4.1. Inverse LSSVM Hysteresis Model
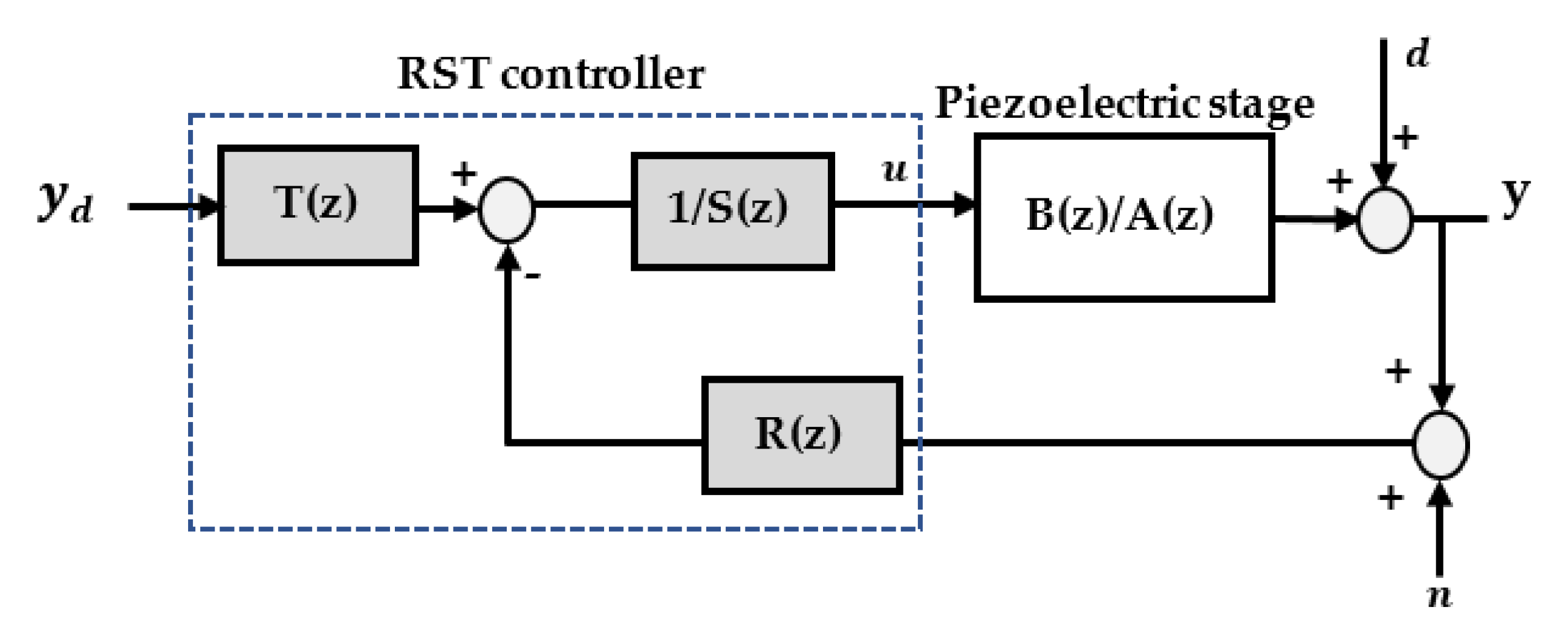
4.2. RST Controller
- Estimate the transfer function of the piezoelectric stage model and obtain ) and ).
- Choose dominant poles and determine , and .
- From Equation (33), solve and
- Compute and using Equations (31) and (32), respectively.
- Compute from the equation = R(1).
- Compute the sensitivity functions , , and by Equations (26)–(28), respectively.
- Evaluate the shaping of the sensitivity functions using the considered constraints and performance specifications.
- Repeat steps 2 to 7 until the optimum solution is reached.
5. Results and Discussion
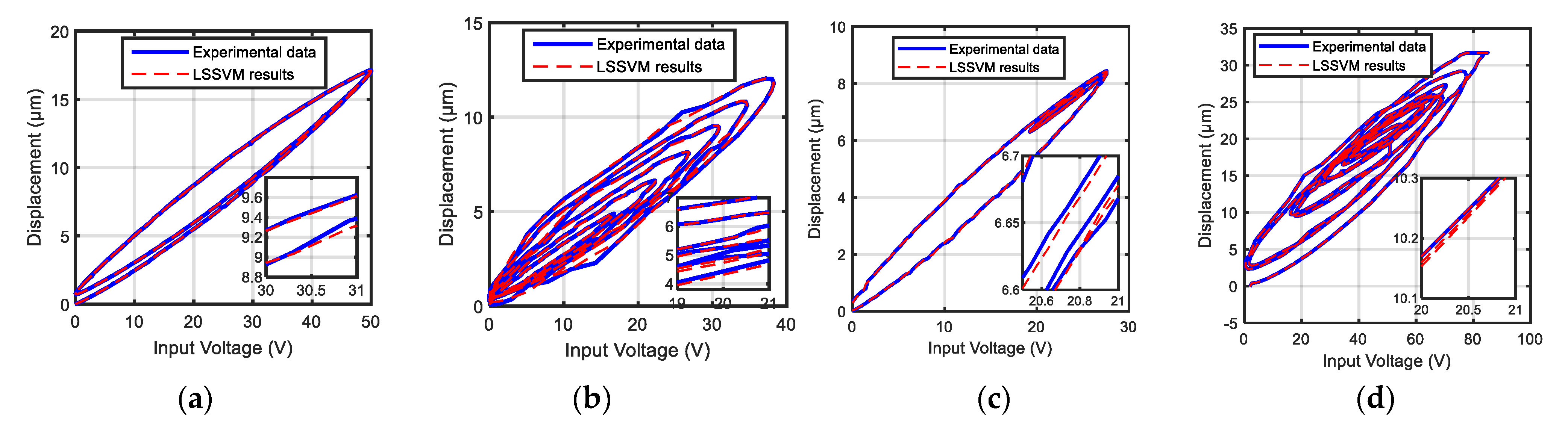
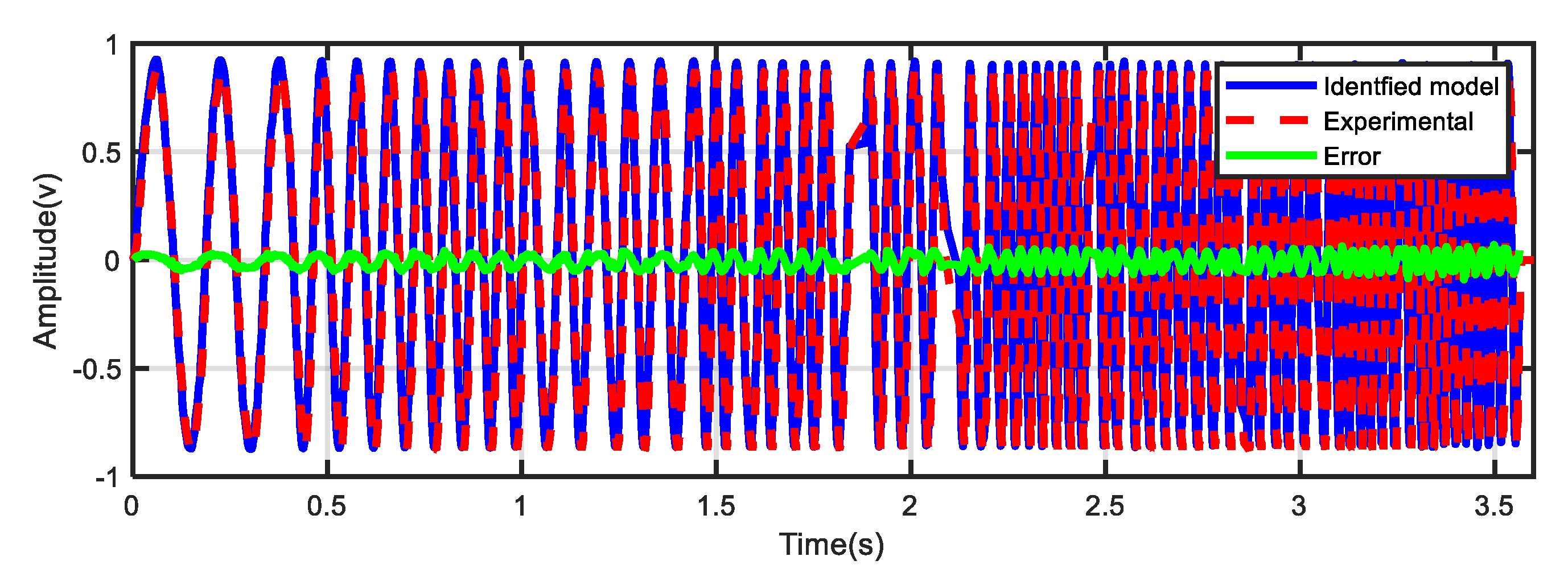
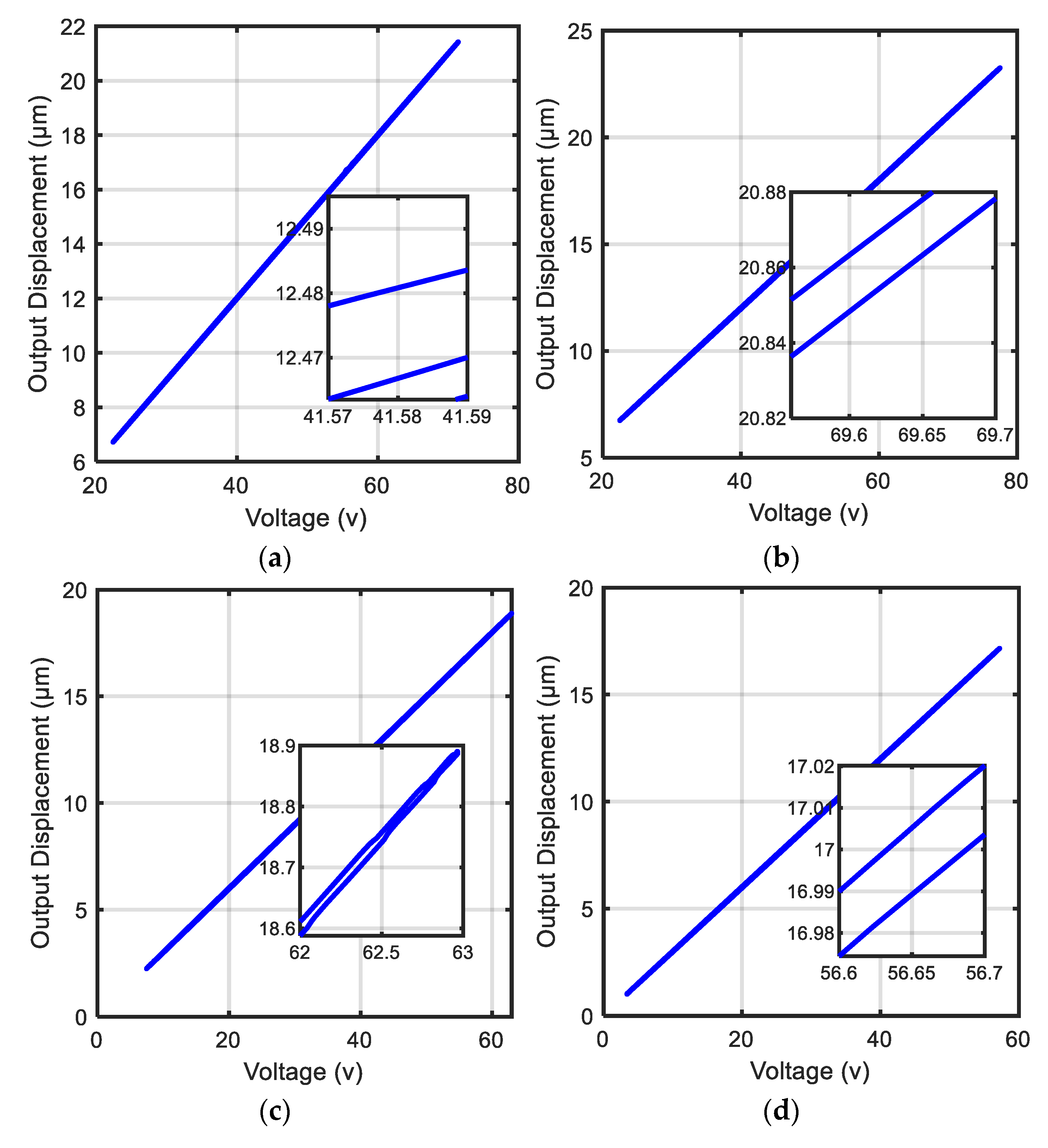
5.1. Modeling Examination
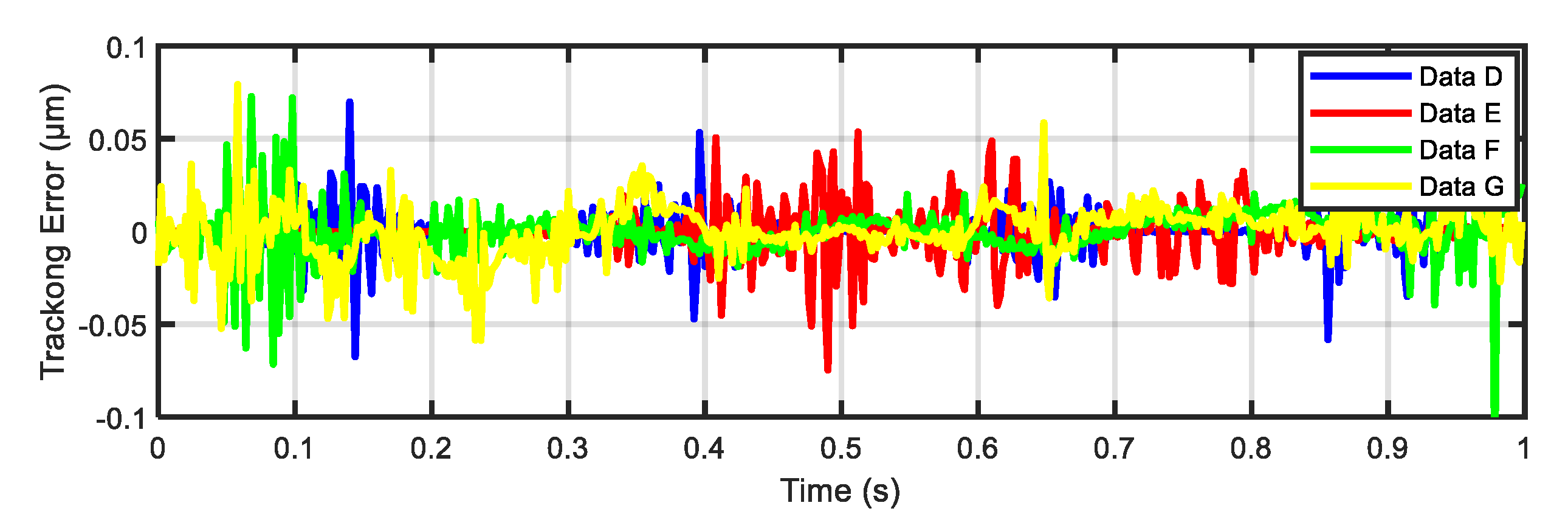
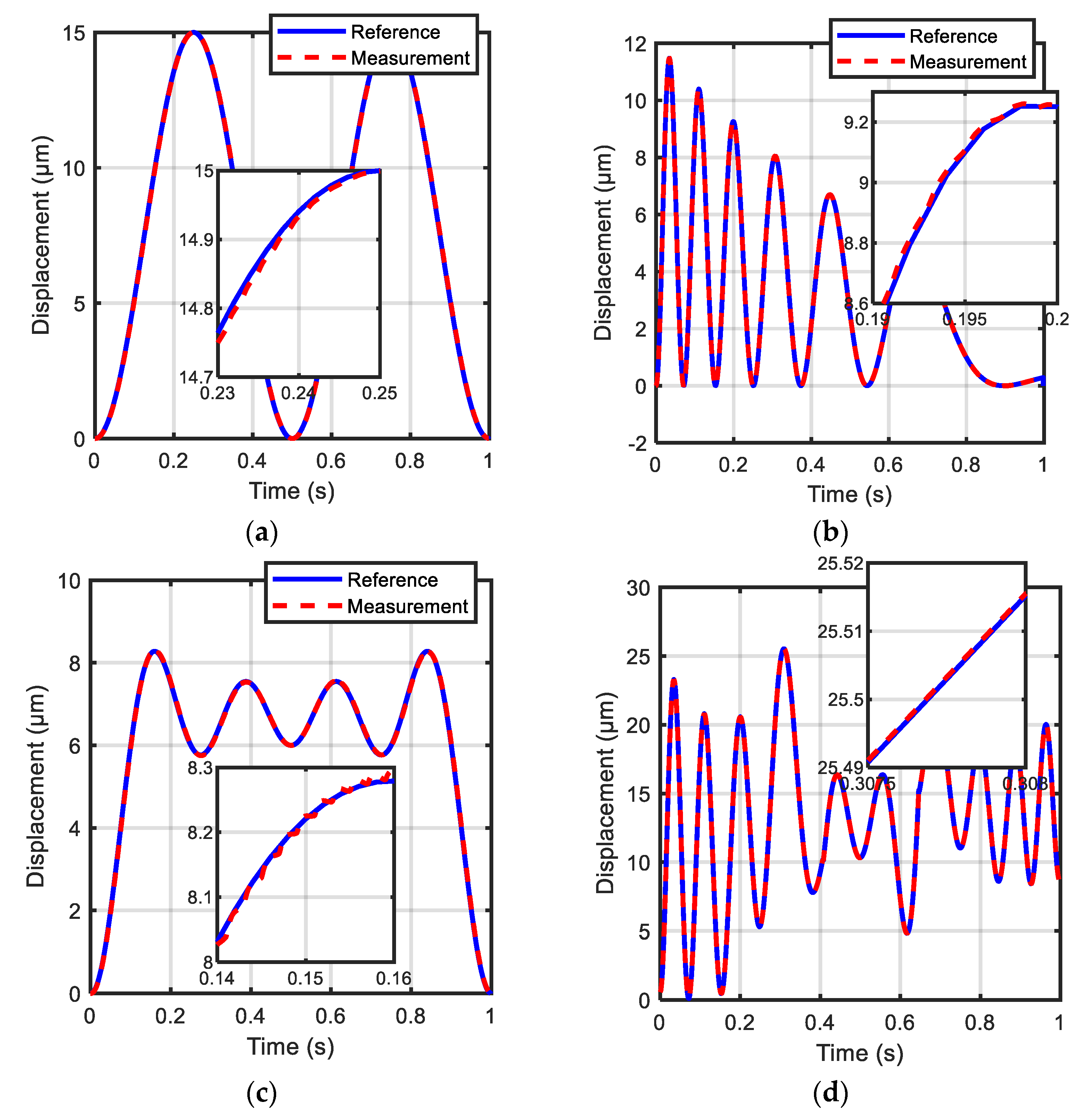
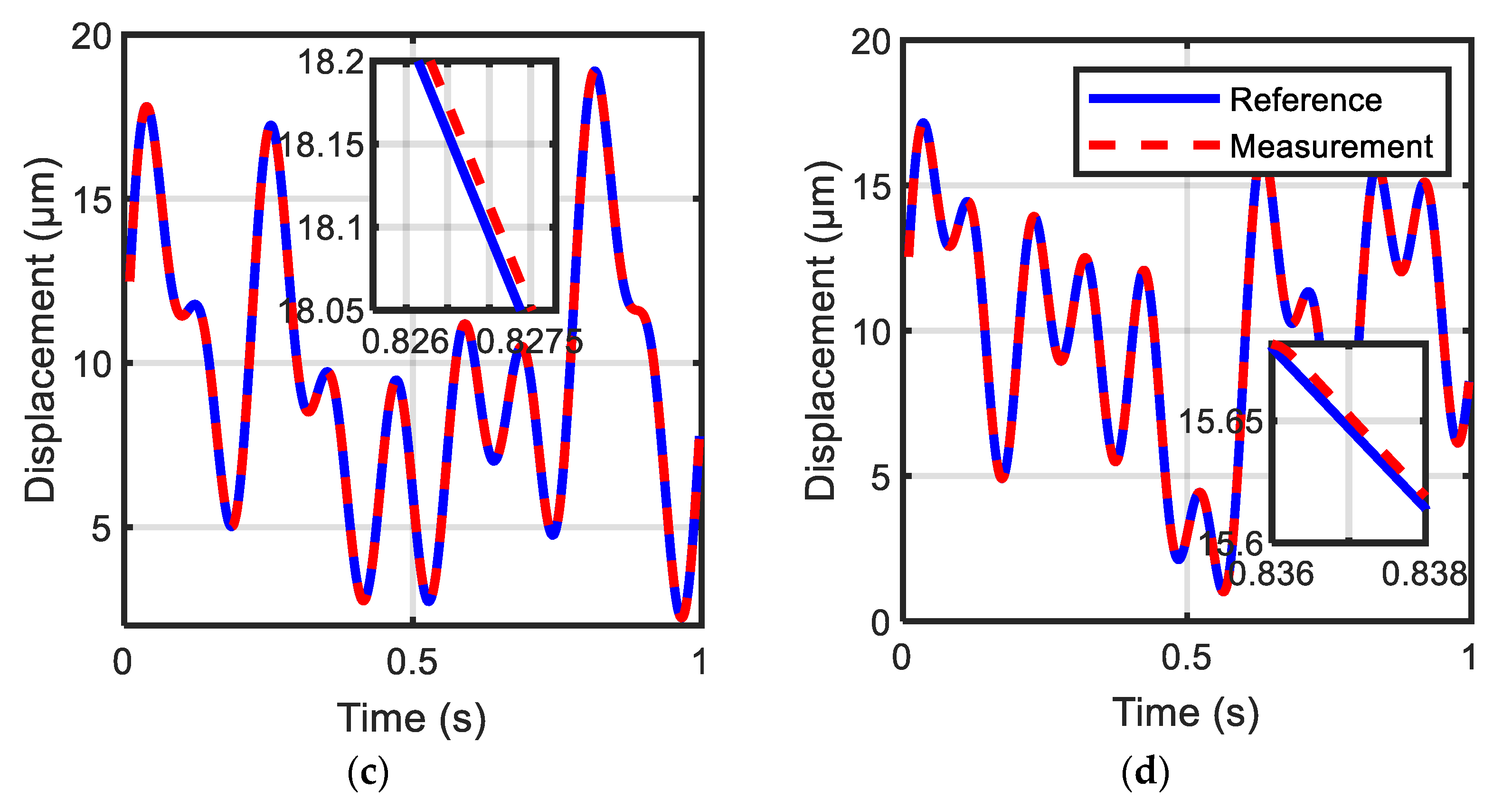
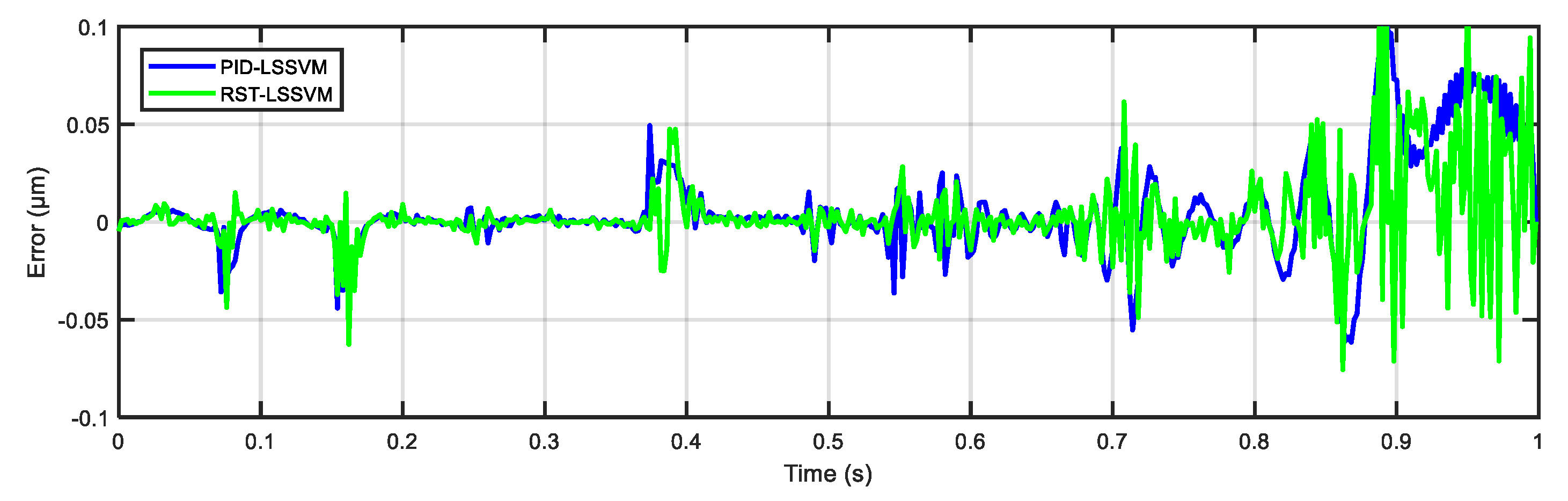
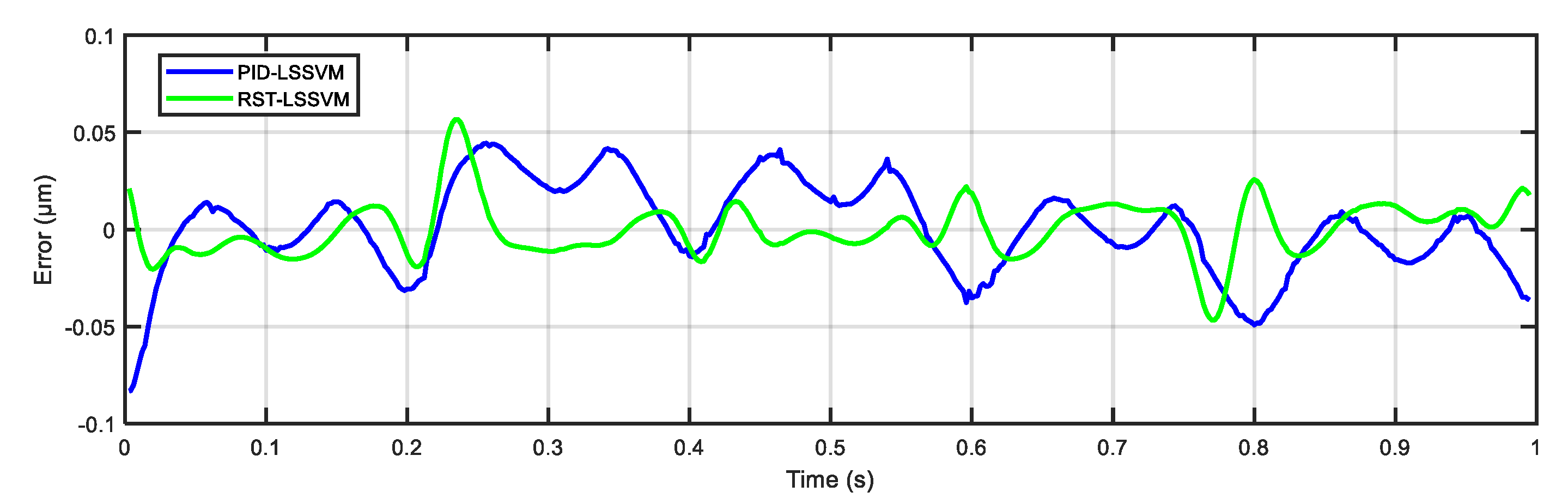
5.2. Experimental Results of Reference Tracking
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ewing, J.A. X. Experimental researches in magnetism. Philos. Trans. R. Soc. Lond. 1885, 176, 523–640. [Google Scholar]
- Gan, J.; Zhang, X. A review of nonlinear hysteresis modeling and control of piezoelectric actuators. AIP Adv. 2019, 9, 40702. [Google Scholar] [CrossRef] [Green Version]
- Gu, G.-Y.; Zhu, L.-M.; Su, C.-Y.; Ding, H.; Fatikow, S. Modeling and control of piezo-actuated nanopositioning stages: A survey. IEEE Trans. Autom. Sci. Eng. 2014, 13, 313–332. [Google Scholar] [CrossRef]
- Sabarianand, D.V.; Karthikeyan, P.; Muthuramalingam, T. A review on control strategies for compensation of hysteresis and creep on piezoelectric actuators based micro systems. Mech. Syst. Signal Process. 2020, 140, 106634. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Rakheja, S.; Su, C.-Y. Experimental characterization and modeling of rate-dependent hysteresis of a piezoceramic actuator. Mechatronics 2009, 19, 656–670. [Google Scholar] [CrossRef]
- Webb, G.V.; Lagoudas, D.C.; Kurdila, A.J. Hysteresis modeling of SMA actuators for control applications. J. Intell. Mater. Syst. Struct. 1998, 9, 432–448. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.-h. Non-symmetrical Bouc–Wen model for piezoelectric ceramic actuators. Sens. Actuators A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Ji, H.; Lv, B.; Ding, H.; Yang, F.; Qi, A.; Wu, X.; Ni, J. Modeling and Control of Hysteresis Characteristics of Piezoelectric Micro-Positioning Platform Based on Duhem Model. Actuators 2022, 11, 122. [Google Scholar] [CrossRef]
- Xiao, S.; Li, Y. Modeling and high dynamic compensating the rate-dependent hysteresis of piezoelectric actuators via a novel modified inverse Preisach model. IEEE Trans. Control. Syst. Technol. 2012, 21, 1549–1557. [Google Scholar] [CrossRef]
- Zhou, C.; Feng, C.; Aye, Y.N.; Ang, W.T. A digitized representation of the modified Prandtl–Ishlinskii hysteresis model for modeling and compensating piezoelectric actuator hysteresis. Micromachines 2021, 12, 942. [Google Scholar] [CrossRef]
- Meng, Y.; Wang, X.; Li, L.; Huang, W.; Zhu, L. Hysteresis Modeling and Compensation of Piezoelectric Actuators Using Gaussian Process with High-Dimensional Input. Actuators 2022, 11, 115. [Google Scholar] [CrossRef]
- Yang, L.; Ding, B.; Liao, W.; Li, Y. Identification of Preisach Model Parameters Based on an Improved Particle Swarm Optimization Method for Piezoelectric Actuators in Micro-Manufacturing Stages. Micromachines 2022, 13, 698. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Fang, Y.; Wang, H. Intelligent rate-dependent hysteresis control compensator design with Bouc-Wen model based on RMSO for piezoelectric actuator. IEEE Access 2020, 8, 63993–64001. [Google Scholar] [CrossRef]
- Ahmed, K.; Yan, P. Modeling and identification of rate dependent hysteresis in piezoelectric actuated nano-stage: A gray box neural network based approach. IEEE Access 2021, 9, 65440–65448. [Google Scholar] [CrossRef]
- Xiong, Y.; Jia, W.; Zhang, L.; Zhao, Y.; Zheng, L. Feedforward Control of Piezoelectric Ceramic Actuators Based on PEA-RNN. Sensors 2022, 22, 5387. [Google Scholar] [CrossRef]
- Raj, R.A.; Samikannu, R.; Yahya, A.; Mosalaosi, M. Performance evaluation of natural esters and dielectric correlation assessment using artificial neural network (ANN). J. Adv. Dielectr. 2020, 10, 2050025. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Van Gestel, T.; De Brabanter, J.; De Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific Publishing: Singapore, 2002; pp. 71–100. [Google Scholar]
- Kaytez, F.; Taplamacioglu, M.C.; Cam, E.; Hardalac, F. Forecasting electricity consumption: A comparison of regression analysis, neural networks and least squares support vector machines. Int. J. Electr. Power Energy Syst. 2015, 67, 431–438. [Google Scholar] [CrossRef]
- Huang, L.; Hu, Y.; Zhao, Y.; Li, Y. Modeling and control of IPMC actuators based on LSSVM-NARX paradigm. Mathematics 2019, 7, 741. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Ma, Z.; Mao, X.; Shan, J.; Wang, Y. A fast and accurate piezoelectric actuator modeling method based on truncated least squares support vector regression. Rev. Sci. Instrum. 2019, 5, 055004. [Google Scholar]
- Xu, Q. Identification and compensation of piezoelectric hysteresis without modeling hysteresis inverse. IEEE Trans. Ind. Electron. 2012, 60, 3927–3937. [Google Scholar] [CrossRef]
- Mao, X.; Wang, Y.; Liu, X.; Guo, Y. A hybrid feedforward-feedback hysteresis compensator in piezoelectric actuators based on least-squares support vector machine. IEEE Trans. Ind. Electron. 2017, 65, 5704–5711. [Google Scholar] [CrossRef] [Green Version]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neural Networks, Fuzzy Models, and Gaussian Processes; Springer Nature: Berlin/Heidelberg, Germany, 2020; p. 4. [Google Scholar]
- Farrokh, M. Hysteresis simulation using least-squares support vector machine. J. Eng. Mech. 2018, 144, 04018084. [Google Scholar] [CrossRef]
- Baziyad, A.G.; Nouh, A.S.; Ahmad, I.; Alkuhayli, A. Application of Least-Squares Support-Vector Machine Based on Hysteresis Operators and Particle Swarm Optimization for Modeling and Control of Hysteresis in Piezoelectric Actuators. Actuators 2022, 11, 217. [Google Scholar] [CrossRef]
- Landau, I.D. The RST digital controller design and applications. Control Eng. Pract. 1998, 6, 155–165. [Google Scholar] [CrossRef]
- Landau, I.D.; Karimi, A. Robust digital control using pole placement with sensitivity function shaping method. Int. J. Robust Nonlinear Control. IFAC-Affil. J. 1998, 8, 191–210. [Google Scholar] [CrossRef]
- Langer, J.; Landau, I.D. Combined pole placement/sensitivity function shaping method using convex optimization criteria. Automatica 1999, 35, 1111–1120. [Google Scholar] [CrossRef]
- Ahmad, I.; Abdurraqeeb, A.M. Tracking control of a piezoelectric actuator with hysteresis compensation using RST digital controller. Microsyst. Technol. 2017, 23, 2307–2317. [Google Scholar] [CrossRef]
- Rakotondrabe, M.; Al Janaideh, M. An RST control design based on interval technique for piezomicropositoning systems with rate-dependent hysteresis nonlinearities. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 1–8. [Google Scholar]
- Abdurraqeeb, A.M.; Al-Shamma’a, A.A.; Alkuhayli, A.; Noman, A.M.; Addoweesh, K.E. RST Digital Robust Control for DC/DC Buck Converter Feeding Constant Power Load. Mathematics 2022, 10, 1782. [Google Scholar] [CrossRef]
- Ali, Z.A.; Li, X. Controlling of an under-actuated quadrotor UAV equipped with a manipulator. IEEE Access 2020, 8, 34664–34674. [Google Scholar] [CrossRef]
- Physik Instrumente. P-752 High-Precision Nanopositioning Stage. Available online: https://www.physikinstrumente.com/en/products/nanopositioning-piezo-flexure-stages/linear-piezo-flexure-stages/p-752-high-precision-nanopositioning-stage-200800/ (accessed on 14 July 2022).
- Physik Instrumente. E-505 Piezo Amplifier Module. Available online: https://www.physikinstrumente.com/en/products/controllers-and-drivers/nanopositioning-piezo-controllers/e-505-piezo-amplifier-module-602300/ (accessed on 15 July 2022).
- dSPACE. DS1104 R&D Controller Board. Available online: https://www.dspace.com/en/inc/home/products/hw/singbord/ds1104.cfm (accessed on 14 July 2022).
- Lai, X.; Pan, H.; Zhao, X. Adaptive control for pure-feedback nonlinear systems preceded by asymmetric hysteresis. Energies 2019, 12, 4675. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Ge, H.; Li, H.; Xie, S.; Xu, S. Rate-Dependent Hysteresis Modeling and Displacement Tracking Control Based on Least-Squares SVM for Axially Pre-Compressed Macro-Fiber Composite Bimorph. Materials 2022, 15, 6480. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, X.; Shao, X. Design and real-time implementation of Takagi–Sugeno fuzzy controller for magnetic levitation ball system. IEEE Access 2020, 8, 38221–38228. [Google Scholar] [CrossRef]
- Mayergoyz, I. Mathematical models of hysteresis. IEEE Trans. Magn. 1986, 22, 603–608. [Google Scholar] [CrossRef] [Green Version]
- Brokate, M.; Sprekels, J. Hysteresis and Phase Transitions; Springer: New York, NY, USA, 1996; pp. 52–105. [Google Scholar]
- Suykens, J.A.; Vandewalle, J.; De Moor, B. Optimal control by least squares support vector machines. Neural Netw. 2001, 14, 23–35. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2001; pp. 287–324. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarms optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4. [Google Scholar]
- Mueller, A. (Ed.) Recent Advances in Robust Control-Novel Approaches and Design Methods; IntechOpen: London, UK, 2011; pp. 341–360. [Google Scholar]
- Li, Z.; Shan, J.; Gabbert, U. A direct inverse model for hysteresis compensation. IEEE Trans. Ind. Electron. 2020, 68, 4173–4181. [Google Scholar] [CrossRef]
- Ahmad, I.; Ali, A.E.A.; Salamah, Y.B. MIMO H μ Feedback Controller with Feedforward Compensator for Scanning Tunneling Microscope Having 3D Cross-Coupled Piezoelectric Actuator. IEEE Access 2021, 9, 153750–153766. [Google Scholar] [CrossRef]
- De Brabanter, K.; Karsmakers, P.; Ojeda, F.; Alzate, C.; De Brabanter, J.; Pelckmans, K.; De Moor, B.; Vandewalle, J.; Suykens, J.A. LS-SVMlab Toolbox User’s Guide: Version 1.7; Katholieke Universiteit Leuven: Leuven, Belgium, 2010. [Google Scholar]
- Chen, Q.; Wang, G. PSO-driven micromechanical identification of in-situ properties of fiber-reinforced composites. Compos. Struct. 2019, 220, 608–621. [Google Scholar] [CrossRef]
- Rezaee Jordehi, A.; Jasni, J. Parameter selection in particle swarm optimisation: A survey. J. Exp. Theor. Artif. Intell. 2013, 25, 527–542. [Google Scholar] [CrossRef]
- Xu, Q.; Wong, P.-K. Hysteresis modeling and compensation of a piezostage using least squares support vector machines. Mechatronics 2011, 21, 1239–1251. [Google Scholar] [CrossRef]





| Data | RMSE (µm) | RMSE Percentage % to Travel Range |
|---|---|---|
| A | 1.7466 | 4.990% |
| B | 2.0566 | 5.876% |
| C | 0.8623 | 2.463% |
| D | 1.7708 | 5.059% |
| E | 0.7140 | 2.040% |
| F | 0.4443 | 1.2695% |
| G | 5.8008 | 16.5736% |
| Properties | Values |
|---|---|
| Driven input voltage (V) | −20 to 120 |
| Resonant frequency (Hz) | 2100 |
| Resolution (nm) | 0.1 |
| Travel range (μm) | 0–35 |
| Stage mass (kg) | 0.35 |
| Electrical capacitance (μF) | 3.7 |
| Load capacity (N) | 30 |
| Stiffness in motion direction (N/μm) | 20 |
| Parameter | Symbol | Value |
|---|---|---|
| Sampling rate | 0.002 s | |
| Maximum absolute input | 8.5 | |
| Stop operator order | n | 55 |
| No. of particles | 30 | |
| Maximum number of iterations | i | 100 |
| Learning factors | 2 | |
| Inertia weights | [0.4, 0.9] | |
| Regularization factor | C | |
| Kernel parameter | 3.13544 | |
| Bias | b | 1.831 |
| Model | RMSE (μm) | Mean | ||||
|---|---|---|---|---|---|---|
| Data D | Data E | Data F | Data G | Mean Percentage % to Travel Range | ||
| PID-LSSVM | 0.0214 | 0.0267 | 0.0195 | 0.0250 | 0.0232 | 0.0663% |
| RST-LSSVM | 0.0182 | 0.0219 | 0.0162 | 0.0227 | 0.0198 | 0.0566% |
| Model | RMSE (μm) | Mean | ||||
|---|---|---|---|---|---|---|
| Data H | Data I | Data J | Data K | Mean Percentage % to Travel Range | ||
| PID-LSSVM | 0.0233 | 0.0281 | 0.020 | 0.0264 | 0.0244 | 0.0697% |
| RST-LSSVM | 0.0164 | 0.0158 | 0.0187 | 0.0181 | 0.0173 | 0.0494% |
| Contributor | Method | RMSE |
|---|---|---|
| Qingsong Xu [50] | Feedforward–feedback scheme based on the least squares support vector machine without modeling hysteresis inverse. | 0.62 |
| Yongcheng Xiong et al. [15] | Control scheme based on recurrent neural networks. | 0.465 |
| Wei Tech Ang et al. [12] | Control scheme based on the improved Preisach. | 0.15 |
| Liangsong Huang et al. [19] | Feedforward–feedback scheme based on the least squares support vector machine, combined with NARX model and PID controller. | 0.03 |
| PID-LSSVM [25] | Feedforward–feedback scheme based on particle swarm optimization and least squares support vector machine, combined with discrete memory (stop operators) and incremental PID controller. | 0.0238 |
| The proposed RST-LSSVM | Feedforward–feedback scheme based on particle swarm optimization and least squares support vector machine, combined with discrete memory (stop operators) and RST controller. | 0.0186 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baziyad, A.G.; Ahmad, I.; Salamah, Y.B.; Alkuhayli, A. Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller. Actuators 2022, 11, 324. https://doi.org/10.3390/act11110324
Baziyad AG, Ahmad I, Salamah YB, Alkuhayli A. Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller. Actuators. 2022; 11(11):324. https://doi.org/10.3390/act11110324
Chicago/Turabian StyleBaziyad, Ayad G., Irfan Ahmad, Yasser Bin Salamah, and Abdulaziz Alkuhayli. 2022. "Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller" Actuators 11, no. 11: 324. https://doi.org/10.3390/act11110324
APA StyleBaziyad, A. G., Ahmad, I., Salamah, Y. B., & Alkuhayli, A. (2022). Robust Tracking Control of Piezo-Actuated Nanopositioning Stage Using Improved Inverse LSSVM Hysteresis Model and RST Controller. Actuators, 11(11), 324. https://doi.org/10.3390/act11110324







