Abstract
Dynamic modeling of soft pneumatic actuators are a challenging research field. In this paper, a dynamic modeling method used for a bi-directionaly soft pneumatic actuator with symmetrical chambers is proposed. In this dynamic model, the effect of uninflated rubber block on bending deformation is considered. The errors resulting from the proposed dynamic equilibrium equation are analyzed, and a compensation method for the dynamic equilibrium equation is proposed. The equation can be solved quickly after simplification. The results show that the proposed dynamic model can describe the motion process of the bi-directional pneumatic actuator effectively.
1. Introduction
With the development of robotics, robotic applications are becoming more and more widespread. However, in many applications, traditional rigid robots have a lot of limitations, such as safety in human-robot interaction [1,2]. Soft robotics technologies can significantly solve these problems. The actuation of soft robots is an important part in the research of soft robotics. There are many ways to actuate soft robots, such as pneumatic methods [3], tendon-driven systems [4,5], shape memory materials [6], etc. The tendon-driven systems simulate human muscles with good flexibility and easier control but have higher structural requirements. Shape memory materials rely on material properties for deformation; they do not require a complex actuation system, but the actuation force is smaller. Among them, the pneumatic methods are frequently used, due to their easy design and the simple fabrication of their actuator [3,7]. They can also provide relatively large driving forces.
The control of pneumatic soft actuators presents great challenges because many control methods, such as Model Predictive Control, rely heavily on suitable and sufficiently accurate model representations of the system dynamics [8]. Due to the materials of the actuators, the large deformability and infinite degrees of freedom bring extreme difficulties when modeling the actuators [9]. Researchers have produced many works with the aim of establishing a general modeling method for soft actuators [10,11]. Most of these methods are static or quasi-static modeling, but control of actuators requires accurate dynamic modeling. Dynamic modeling of soft actuators remains challenging. The conventional mass-spring-damper model is often used for dynamic modeling [12,13]. However, due to the complexity of soft actuators, such a modeling approach requires a combination of system identification and fitting techniques. Lagrangian methods are also a common modeling approach, but their modeling process is relatively complex, and model solving is usually difficult. In order to reduce the difficulty of the solution, the proposed model is often simplified or reduced in order [14].
Data driven approaches can effectively solve these problems [8]. One of the most common approaches is to use neural networks. Neural networks are widely used in soft actuators modeling [15,16,17]. However, it is well known that neural networks require a large amount of training data, and the accuracy of the model is dependent on the quality of the training set. In addition, the neural network approaches are time consuming, making it impossible to use a high control frequency while controlling the actuator, which also greatly limits the control accuracy. Therefore, model-based modeling methods still have advantages. They are used in the control of soft robots and have good results [18].
This paper proposed a dynamic modeling method for the pneumatic soft actuator. The method utilizes D’Alembert’s principle and realizes the dynamic model of the actuator based on the static model using the dynamic equilibrium equation. The errors resulting from the proposed dynamic equilibrium equation are analyzed, and a compensation method for the dynamic equilibrium equation is proposed. The model obtained by this method is easy to solve, and the model accuracy is high after compensation. As a result, the model can be used in applications where the soft actuator is controlled in real time. The bi-directional motion experiments are performed for validating the proposed dynamic model, and the experimental results prove that the model has good accuracy and can describe the motion process of the bi-directional pneumatic soft actuator effectively. Section 2 presents the methodology of the dynamic equilibrium equation. Section 3 presents the description of the experiment. Section 4 presents the experimental results and discussion.
2. Methodology
According to D’Alembert’s principle, the dynamic equilibrium equation of the soft actuator can be presented as
In this equation, is the moment generated by the inertia force, that is, dynamic moment. is the moment generated by the driving force, which is mainly generated by the pressure. is the moment generated by the internal force of the actuator. and are static moments. When the driving force keep constant, the equation becomes when the actuator reaches the equilibrium position.
2.1. Static Moment
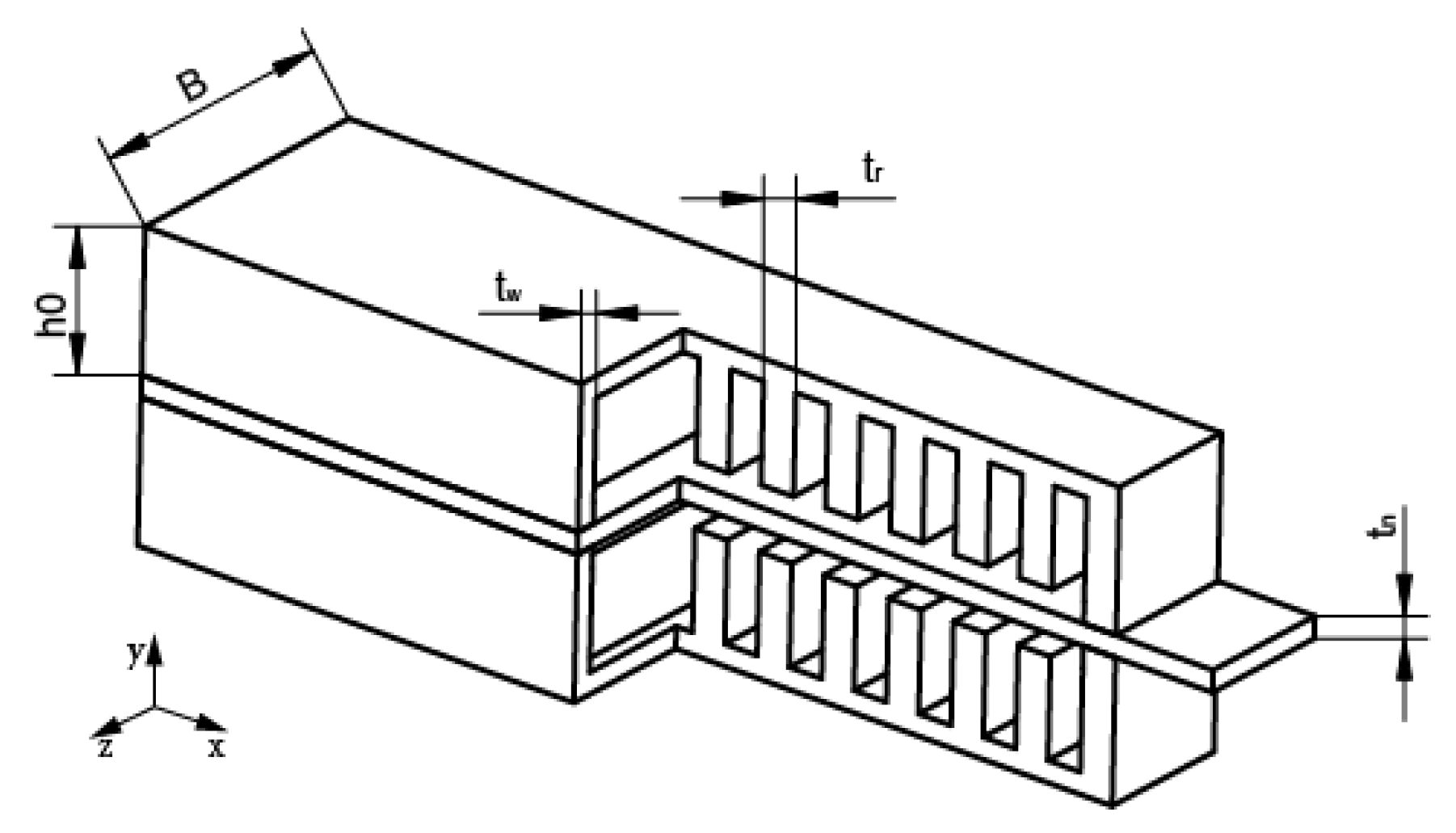
The dimension of the soft actuator can be shown in Figure 1. B is the width of the chamber, is the height of the chamber after inflation, is the thickness of the neutral layer, is the thickness of the chamber, and is the thickness of the rib.
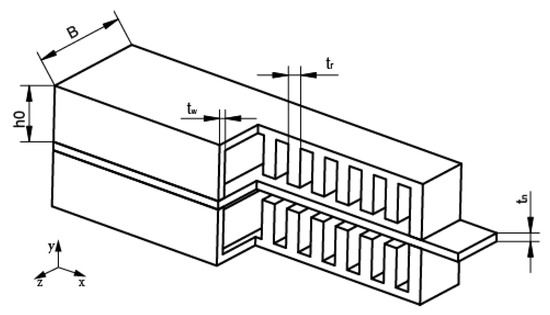
Figure 1.
The dimensions of the bi-directionally pneumatic actuator.
For analytical purposes, the static moment study is carried out with the end of the neutral layer of the actuator. The driving force comes from the pressure in the chambers, and the torque produced by it can be expressed as
where p is the pressure in the inflated side of the actuator, and y is the direction shown in Figure 1. A resistive moment is generated in the neutral layer during the bending motion of the actuator. It can be presented as
where E is the Young modulus of ABS, I is the moment of inertia about z-axis of the neutral layer. is the bending angle of the actuator, and L is the length of the actuator. The ABS plate has a Young’s modulus of 2 GPa and a Poisson ratio of 0.395, and I can be calculated as
In addition, the tensile, compressive and shear stresses are generated by the deformation of the actuator. The circumferential stress of the actuator’s upper wall on the inflated side is denoted by , the circumferential stress of the actuator’s sidewall on the inflated side is denoted by , the compressive stress of the upper wall on the uninflated side is denoted by , and the compressive stress of the side wall on the uninflated side is denoted by . They can induce moments , , and , respectively. These moments can be presented as
The derivation process for all these moments can be found in our previous work on the static analysis [11]. These moments, as well as , prevent the soft pneumatic actuator from bending. These moments are defined as the moment generated by the internal force of the actuator. Then the can be presented as
2.2. Dynamic Moment
Based on the analysis of static moments, the dynamic moment balancing study is also carried out with the end of the neutral layer of the actuator. The moment of inertia, that is , consists of two moments, the rotational moment and the bending moment.
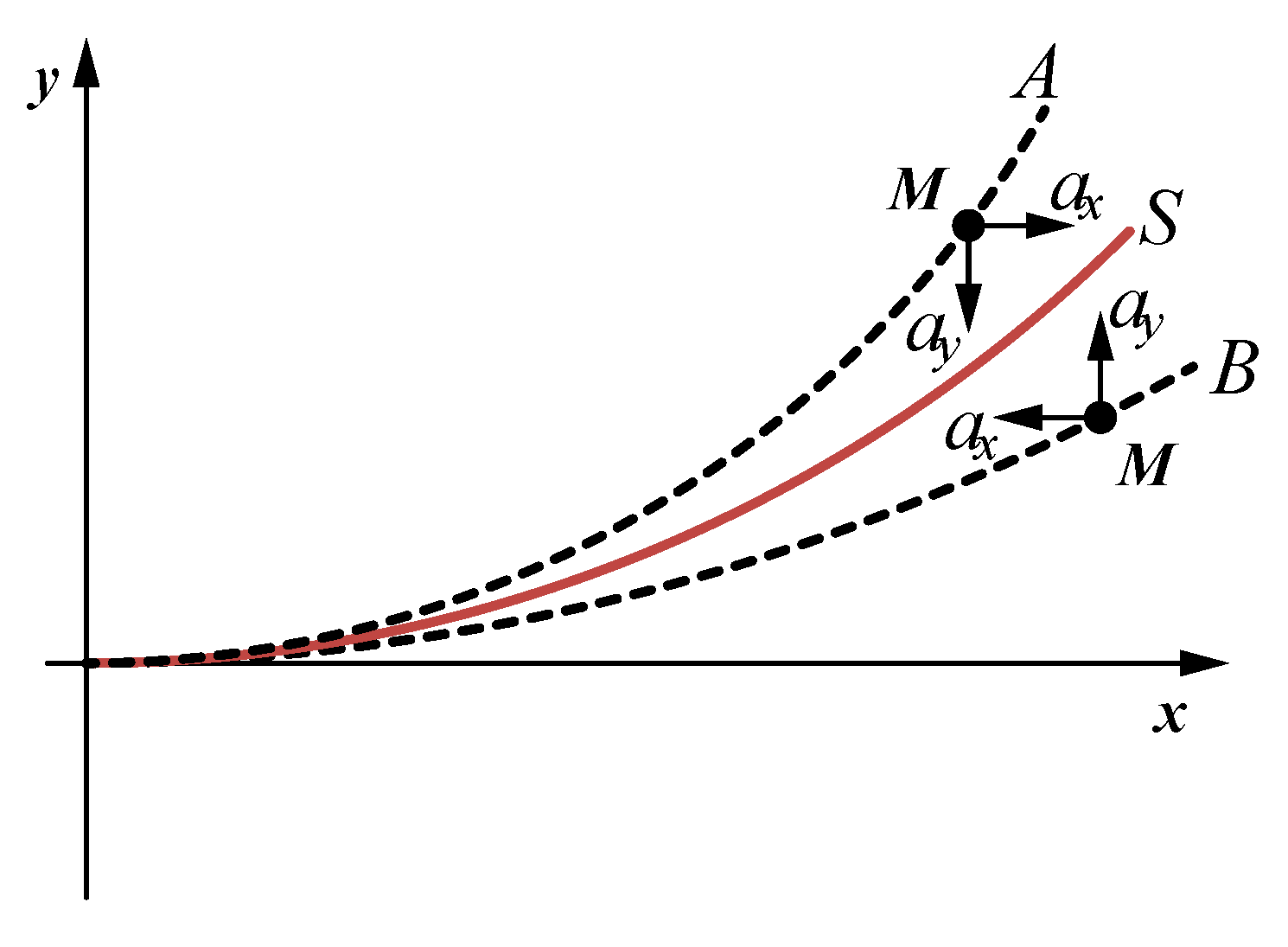
Assume that the static equilibrium position of the neutral layer of the actuator under the pressure p condition is S. A and B are the two transient positions of the actuator during the motion when the pressure in the chambers is p, respectively. The acceleration of the mass point M generated by the inertia force and its direction are shown in Figure 2.
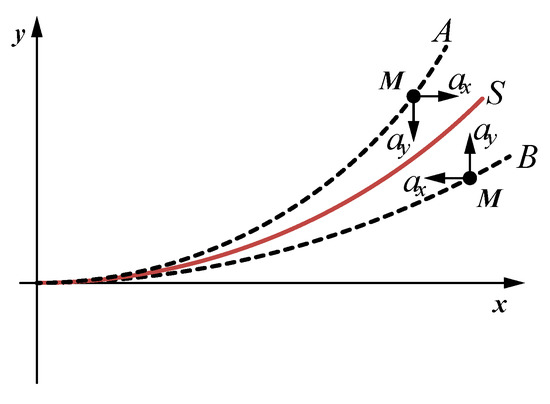
Figure 2.
The acceleration of the mass point generated by the inertia force.
Then the bending moment generated by the inertia force can be presented as
where is the bending moment, is the mass of the mass point, and are the accelerations of the mass point, and and are the projections of the distance from the mass point to O on the x and y axes.
If the length of the arc from the point in the Figure 2 to O is r, the accelerations and can be presented as
Since the actuator itself is a symmetrical structure, the center of mass of the whole actuator is on the neutral layer. In order to simplify the calculation, the height change on the inflatable side and the mass shift due to shear deformation are ignored. The form of mass distribution of the actuator is simplified to a distribution along the midline of the constrained layer. It can be expressed by the line density. The density of the actuator is different at the chamber and ribbed positions, so using and denotes the linear density at the air cavity and rib plate, respectively.
Then, the bending moment can be obtained by integrating Equation (10) over the length. Due to the density being different at the chamber and ribbed positions, the integrations are performed at different positions and finally summed.
where N is the number of the chambers.
From the density distribution, it can also be concluded that the rotational moment of the actuator differs for different positions on the neutral layer with respect to the rotation axis. They are expressed as and .
Assume that the distance from a mass point of the actuator to the origin is r. When the actuator is bent to , the angular velocity of each point of the actuator is , and the angular acceleration is . By integrating the rotational inertia of the mass point over the entire length of the actuator, the rotational moment of the actuator can be expressed
The final dynamic equilibrium equation can be obtained by substituting the Equations (2), (6), (10) and (12) into Equation (1), and the state of motion of the actuator can be obtained by solving this equation.
2.3. Compensation and Solution of the Dynamic Equilibrium Equation
Although the dynamic equilibrium equation has been established, this equation is very complex and difficult to solve. The equilibrium equation can be expanded to obtain the following form
where and are the function with respect to ; C is a constant, and is a function with respect to p. In this equation, the expression for the coefficient of the term is more complex, mainly due to the and functions. In order to facilitate the solution and improve the computational efficiency, it is necessary to make appropriate simplifications to the equation. Taylor expansions are performed for the and functions in Equation (8), respectively, and the fourth order terms are retained. The dynamic equilibrium equation is simplified. This equation can be solved with the Runge–Kutta methods.
By solving this differential equation, it is shown that the process of motion solved by this model is oscillatory and cannot eventually reach the equilibrium state. This is mainly because the damping of the system is not considered, so the damping of the model needs to be compensated. The compensation is performed by adding a term to the dynamic equilibrium equation. Due to the material properties, the movement of the actuator causes a change in the mass distribution. However, the mass distribution of the actuator is simplified to a distribution along the midline of the constrained layer, which is expressed by the line density. This can lead to errors in the dynamic moment calculation, so the changes in the mass distribution need to be compensated. is added into the dynamic equilibrium equation. The equilibrium equation after adding compensation can expressed as
The can be presented as , and the can be presented as .
3. Dynamic Model Validating Experiment of the Soft Pneumatic Actuator
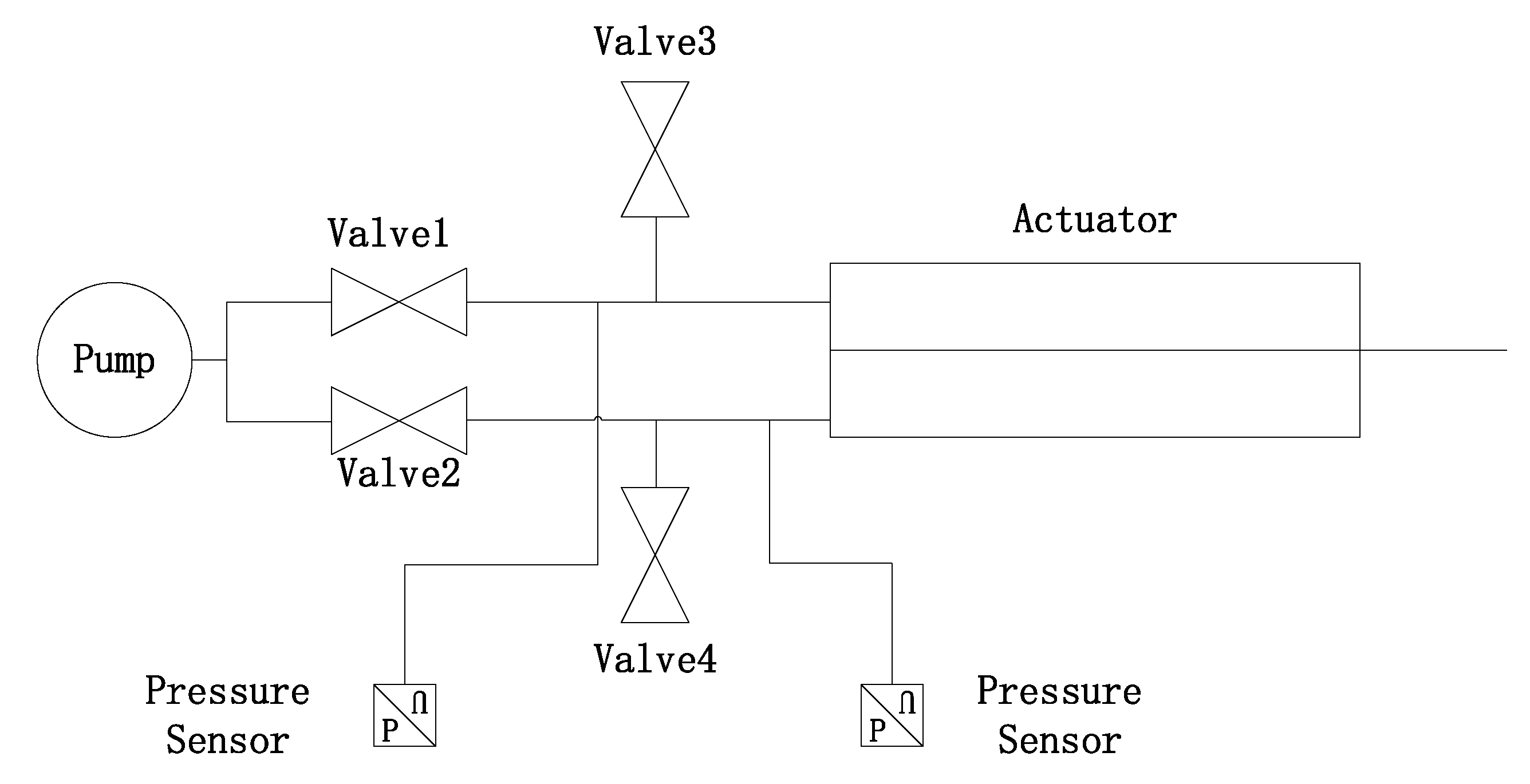
A pneumatic control system was established for the bi-directional pneumatic actuator in our previous work [15]. This system is used to validate the proposed dynamic model. The dynamic data of the bending motion are obtained from this system, and the structure of the system is shown in Figure 3.
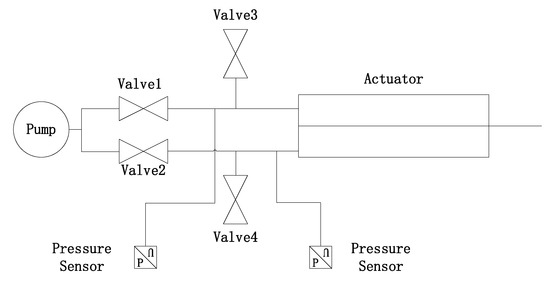
Figure 3.
The schematic of control system for the bi-directionally pneumatic actuator.
The air valves shown in the figure are controlled by a microcontroller unit (MCU). By controlling the air to inflate the chambers on one side of the actuator, the actuator bends in the corresponding direction. The pressure sensors are used to collected the pressure in the chambers of on each side of the actuator. The proposed dynamic model considers both the expansion side and compression side of the actuator. In order to validate the dynamic model, we inflate the chambers on one side of the actuator to a determined pressure and hold it. The actuator is bent from the starting position and stabilized in the equilibrium position. The dynamic data of the whole process are obtained. The bending angle is measured by the gyroscope which is mounted on the end of the neutral layer. The air pressure is measured by the pressure sensors after the inlet valves. Figure 4 is a photograph of the experimental bench, which shows the state of the actuator reaching the equilibrium position after bending motion.

Figure 4.
The experimental setup of the pneumatic actuator.
4. Results and Discussion
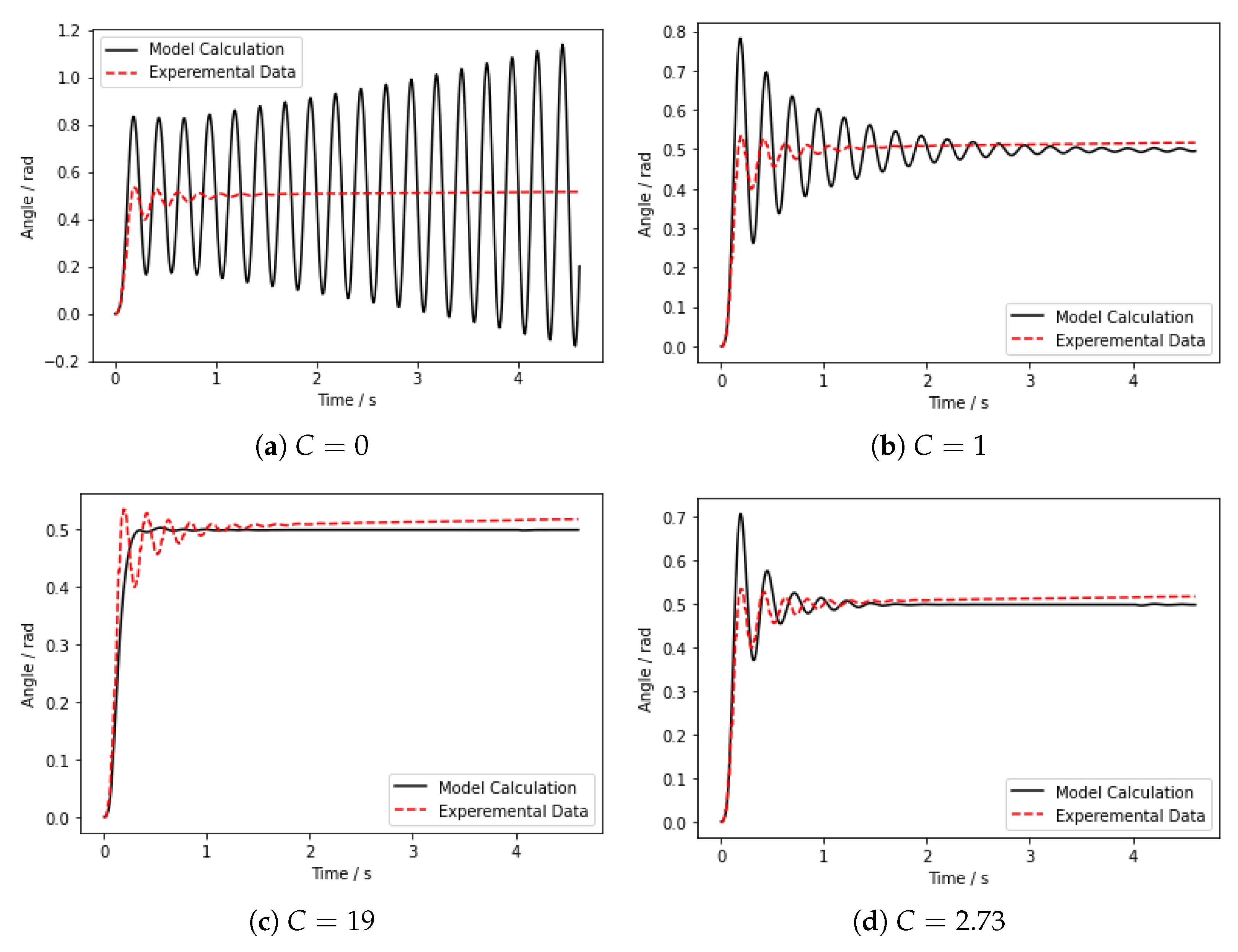
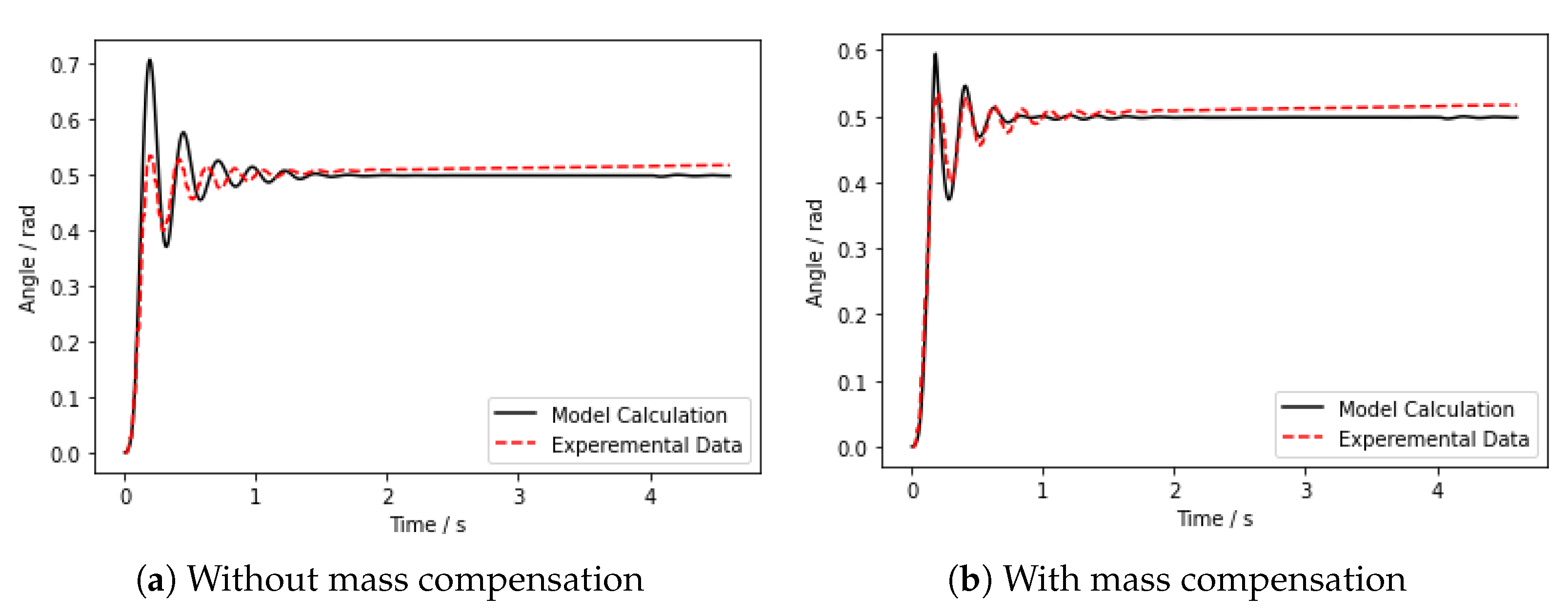
In the experiment, we inflate the chambers to 20 kPa on one side of the actuator and hold it, and the actuator bends to one side to reach the equilibrium position after several oscillations. According to the experimental conditions, the results by solving the dynamic equilibrium equation of the actuator are shown in Figure 5. In order to verify the compensation effect of the model, the results for different damping compensation were calculated separately, and the results were compared with the experimental data.
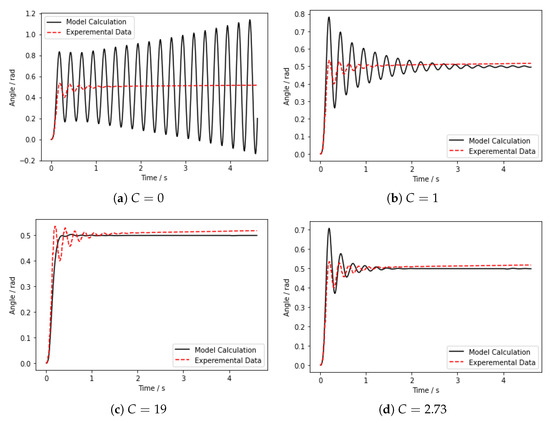
Figure 5.
Comparison of the results with the experimental data under different damping compensation.
In Figure 5a, damping compensation is not performed, and it can be seen that the calculated motion curve does not converge, which also indirectly indicates that the system will oscillate without considering damping in the proposed dynamic model. Figure 5b–d shows compensated damping. The motion curve converges after damping compensation. As C increases, the system changes from an underdamped state to an overdamped state, and the number of system oscillations is directly related to the different damping compensation. Its final equilibrium position remains consistent with the experimental results regardless of how the system oscillates. This also proves the correctness of the static part of the proposed model. From the results, it can be seen that Figure 5b is the underdamped state, Figure 5c is the over-damped state, and Figure 5d shows the optimal compensation coefficient, the number of its oscillations is basically consistent with the experimental data. It can be seen that there is a small error between the experimental data and the calculated results after the actuator reaches the equilibrium position in the figure. This is due to the drift of the gyroscope that measures the angle, i.e., the angle shows a small linear increase with time. This phenomenon has little effect on the measurement results.
With the damping compensation, the number of system oscillations is generally consistent with the experiment, but the frequency of oscillation still has an error. Therefore, it is necessary to compensate for the mass, which is also explained in the previous section. Figure 6 shows the comparison of the results of mass compensation. Figure 6a shows that the frequency of oscillation is much different from the experimental data without compensation, while Figure 6b shows that the frequency of oscillation is generally the same as the experimental data after adding mass compensation. In Figure 6b, we can see that although the error of the model becomes smaller after compensation, there is still a little overshoot, which is caused by the hysteresis of the pneumatic circuit, and the actual response is smaller than the result calculated by the model. The results show that the proposed dynamic model can describe the motion process of this bi-directional pneumatic actuator effectively.
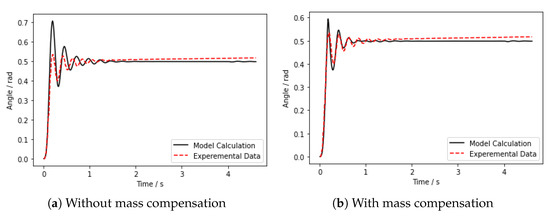
Figure 6.
Comparison of results with experimental data under different damping compensation (after damping compensation).
5. Conclusions
This paper proposed a dynamic modeling method for a bi-directional pneumatic actuator. The method utilizes D’Alembert’s principle and proposes a dynamic model of the actuator based on the static model. The errors resulting from the proposed dynamic equilibrium equation are analyzed, and a compensation method for the dynamic equilibrium equation is proposed. The solution process of the equation is also analyzed, and the equation can be calculated very quickly by using the Runge–Kutta method. According to the calculating tests, solving the model can be controlled within 1ms, so the actual control frequency can reach 1khz, which can meet the requirements of real-time control. At the end of this paper, the bi-directional motion experiments are performed for validating the proposed dynamic model, and the experimental results prove that the model still has a good accuracy. This model will also be applied to the actuator trajectory tracking control in our future work.
Author Contributions
Conceptualization, Y.L. and W.Z.; methodology, Y.L. and W.Z.; validation J.W.; investigation G.H.; writing-orginal draft preparation Y.L.; writing-review and editing W.Z. and J.W.; visualization, G.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Natural Science Foundation of Shaanxi Province (No. 2020JQ-813).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khan, S.G.; Herrmann, G.; Al Grafi, M.; Pipe, T.; Melhuish, C. Compliance control and human–robot interaction: Part 1—Survey. Int. J. Hum. Robot. 2014, 11, 1430001. [Google Scholar] [CrossRef] [Green Version]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marchese, A.D. Design, Fabrication, and Control of Soft Robots with Fluidic Elastomer Actuators. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2015. [Google Scholar]
- In, H.; Kang, B.B.; Sin, M.; Cho, K.J. Exo-glove: A wearable robot for the hand with a soft tendon routing system. IEEE Robot. Autom. Mag. 2015, 22, 97–105. [Google Scholar] [CrossRef]
- Ren, T.; Li, Y.; Xu, M.; Li, Y.; Xiong, C.; Chen, Y. A novel tendon-driven soft actuator with self-pumping property. Soft Robot. 2020, 7, 130–139. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Kumar, K.; Jawed, M.K.; Nasab, A.M.; Ye, Z.; Shan, W.; Majidi, C. Chasing biomimetic locomotion speeds: Creating untethered soft robots with shape memory alloy actuators. Sci. Robot 2018, 3, 7557. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait soft robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hewing, L.; Wabersich, K.P.; Menner, M.; Zeilinger, M.N. Learning-based model predictive control: Toward safe learning in control. Annu. Rev. Control. Robot. Auton. Syst. 2020, 3, 269–296. [Google Scholar] [CrossRef]
- Sadati, S.; Naghibi, S.E.; Shiva, A.; Noh, Y.; Gupta, A.; Walker, I.D.; Althoefer, K.; Nanayakkara, T. A geometry deformation model for braided continuum manipulators. Front. Robot. AI 2017, 4, 22. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Agheli, M.; Onal, C.D. Theoretical modeling and experimental analysis of a pressure-operated soft robotic snake. Soft Robot. 2014, 1, 136–146. [Google Scholar] [CrossRef]
- Zhou, W.; Li, Y. Modeling and analysis of soft pneumatic actuator with symmetrical chambers used for bionic robotic fish. Soft Robot. 2020, 7, 168–178. [Google Scholar] [CrossRef] [PubMed]
- Saunders, F.; Golden, E.; White, R.D.; Rife, J. Experimental verification of soft-robot gaits evolved using a lumped dynamic model. Robotica 2011, 29, 823–830. [Google Scholar] [CrossRef] [Green Version]
- Kanada, A.; Giardina, F.; Howison, T.; Mashimo, T.; Iida, F. Reachability improvement of a climbing robot based on large deformations induced by tri-tube soft actuators. Soft Robot. 2019, 6, 483–494. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Zhang, Y.; Zhu, Y.; Zhu, S. A computationally efficient dynamical model of fluidic soft actuators and its experimental verification. Mechatronics 2019, 58, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Cao, Y.; Jia, F. A Neural Network Based Dynamic Control Method for Soft Pneumatic Actuator with Symmetrical Chambers. Actuators 2021, 10, 112. [Google Scholar] [CrossRef]
- George Thuruthel, T.; Renda, F.; Iida, F. First-Order Dynamic Modeling and Control of Soft Robots. Front. Robot. AI 2020, 7, 95. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, M.T.; Best, C.M.; Townsend, E.C.; Wingate, D.; Killpack, M.D. Learning nonlinear dynamic models of soft robots for model predictive control with neural networks. In Proceedings of the 2018 IEEE International Conference on Soft Robotics (RoboSoft), Livorno, Italy, 24–28 April 2018; pp. 39–45. [Google Scholar]
- Johnson, C.C.; Quackenbush, T.; Sorensen, T.; Wingate, D.; Killpack, M.D. Using First Principles for Deep Learning and Model-Based Control of Soft Robots. Front. Robot. AI 2021, 8, 654398. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).