Abstract
An optimal mission assignment and path planning method of multiple unmanned aerial vehicles (UAVs) for disaster rescue is proposed. In this application, the UAVs include the drug delivery UAV, image collection UAV, and communication relay UAV. When implementing the modeling and simulation, first, three threat sources are built: the weather threat source, transmission tower threat source, and upland threat source. Second, a cost-revenue function is constructed. The flight distance, oil consumption, function descriptions of UAV, and threat source factors above are considered. The analytic hierarchy process (AHP) method is utilized to estimate the weights of cost-revenue function. Third, an adaptive genetic algorithm (AGA) is designed to solve the mission allocation task. A fitness function which considers the current and maximum iteration numbers is proposed to improve the AGA convergence performance. Finally, an optimal path plan between the neighboring mission points is computed by an improved artificial bee colony (IABC) method. A balanced searching strategy is developed to modify the IABC computational effect. Extensive simulation experiments have shown the effectiveness of our method.
1. Introduction
Different from traditional disaster rescue applications [1] which utilize 3D terrain reconstruction or ground target recognition, the multiple unmanned aerial vehicles (UAVs)-based disaster rescue plan [2] utilizes the UAVs with distinct functions to realize people searching, complete injury identification, and provide medical assistance in the disaster zones [3]. In our past research works, a multi-UAV system is developed; this system includes [4] the drug delivery UAV, image collection UAV, and communication relay UAV. Compared with the single UAV system, the multiple UAVs can increase the resource delivery ability, intensify the flight security, and reduce the mission cost. Many factors will affect the rescue task including the environment factor [5] (such as the weather, terrain, and artificial facilities), UAV performance factor [6] (such as the maximum flight distance, oil consumption, or typical rescue function), and mission complexity itself. Currently, when implementing the disaster rescue using the multi-UAV-based system, how to assign the amount and combination mode of UAVs reasonably [7,8] and how to plan their flight paths are the issues that should be researched carefully.
Much research has been done to solve the UAV-based mission assignment and path planning tasks. In [9], a distributed control law was developed to solve the issue of mission assignment of multi-UAV. The coordination task was solved by reaching a consensus on a defined coordination state. In [10], a coordinated standoff target tracking strategy which considered the path shaping for multiple UAVs was presented. A new path shaping technique was developed in that application. In [11], online path planning for joint detection and tracking of multiple unknown radio-tagged objects was developed. This research could be used for information collection using UAVs with on-board sensors. In general, the research on mission assignment and path planning can be transferred into the optimization modelling problem [12]. To solve that problem, the proper cost-revenue function should be designed firstly, and then some optimization methods can be developed to solve it. Currently, many research studies have been done in the fields of mission assignment and path planning; however, the corresponding research in disaster rescue is still rare.
The essence of multi-UAV mission assignment and path planning is to use interactive information and data analysis measurement to realize collaborative work of UAVs. Table 1 presents an algorithm review of multi-UAV mission assignment and path planning. Regarding mission assignment, the heuristic algorithm [13,14,15] uses the intuitive experiences to build its computational strategy; the mathematical programming [16,17] employs the classic algebra or matrix theory to solve optimal computation with various of constraints; and the stochastic intelligent optimization [18,19,20] considers the typical theories, such as biological or physical rules, to accomplish optimal computation. As for path planning, the mathematical programming [21,22] can solve path generation with the consideration of environment and kinematics factors; the artificial potential field method [23,24] considers the balance between the attractive and repulsive forces to implement path searching; the graph-based method [25,26,27,28] uses the modeling and computation of graph theory to accomplish path planning; and the intelligent optimization [29,30] can carry out path creation using typical biological imitation algorithms.

Table 1.
Review of mission assignment and path planning methods.
In this paper, an optimal mission assignment and path planning method of multiple UAVs for the disaster rescue application is proposed. The drug delivery UAV, image collection UAV, and communication relay UAV are considered in this system. When carrying out mission assignment, first, three threat sources [31] are designed, they are the weather threat source, i.e., the wind and rain, transmission tower threat source, i.e., the electromagnetic interference disturbance, and terrain threat source, i.e., the upland. Second, a cost-revenue function is proposed. The flight distance, oil consumption, UAV function descriptions, together with the threat source factors, are all employed to construct that function. The analytic hierarchy process (AHP) method [32] is used to estimate the weights of this model. Third, an adaptive genetic algorithm (AGA) [33] is considered to estimate the optimal mission assignment. The new fitness function is proposed to improve the performance of AGA. Finally, an improved artificial bee colony (IABC)-based optimal path planning [34] for neighboring mission points is developed. The balanced searching strategy is considered for a fast optimal computation.
The main contributions of this paper include: (1) a modelling method of the multi-UAV optimal mission assignment and path planning for the disaster rescue is proposed. Three threat source factors are defined, and a new cost-revenue function is built. (2) Both an AGA and an IABC algorithms are developed. The new fitness function and the new searching strategy are proposed to improve the computational performance of AGA and IABC, respectively.
In the following sections, first, the problem formulation of multi-UAV mission assignment and path planning will be presented. Second, the optimization modelling including the threat sources, cost-revenue function, together with AGA and IABC will be introduced. Third, some experiment results, such as the evaluations of AGA and IABC or disaster rescue simulations, will be shown.
2. Problem Formulation
Figure 1 shows the sketch map of our investigated application. The multiple UAVs are used to carry out the disaster medical rescue task from a start point; and after the drug deliveries to each mission point, they will fly to a recovery point. The natural or manmade environment factors will influence the flight security of UAVs; thus, how to assign mission points to UAVs reasonably and how to plan their flight path safely, economically, and efficiently should be considered. In Figure 1, the UAVs include the drug delivery UAV, image collection UAV, and communication relay UAV. The drug delivery UAV can take the first-aid kit and necessary medical supplies to the disaster zone. The image collection UAV is equipped with various kinds of camera for video information collection. The communication relay UAV carries the communication relay device to guarantee the information transmission of entire system. Several villages locate in different sites of disaster zone; each one of them needs to be rescued by these UAVs. Many environmental factors can threaten the flight security of UAV. For example, the nimbus cloud [35] can damage the motor or sensor of UAV, and it may also contaminate the drugs. The upland may reduce the flight security of UAV. Furthermore, the transmission tower can influence the communication system of UAV. Other factors, such as the maximum flight distance or oil consumption will also affect this mission.
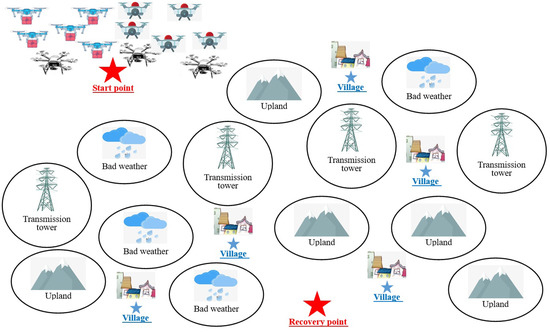
Figure 1.
Sketch map of multi-UAV-based disaster rescue.
3. Optimization Modelling and Its Solution
3.1. The Proposed Computational Flow Chart
Regarding the multi-UAV-based disaster rescue, two questions should be answered. The first question is how to plan the optimal mission allocation. That means the quantity and combination mode of multiple UAVs should be designed for a rescue task. The second question is how to plan their optimal flight paths between two neighboring mission points. Many factors, such as the threat sources and flight parameters will influence the cruise path of UAV. To answer these questions, a novel method is proposed. Figure 2 shows its computational flow chart. After the threat source modelling, a cost-revenue function is designed. The AHP method is used to estimate the weights of cost-revenue function. A kind of AGA is used to solve the optimal mission assignment and an IABC is considered to estimate the optimal path between the neighboring mission points. The main inputs of this model include the amount of UAV, coordinates of mission points (the villages in Figure 1) and threat source centers, and control parameters of AGA and IABC algorithms. The outputs of this model are the mission assignment results of UAVs and their flight paths.
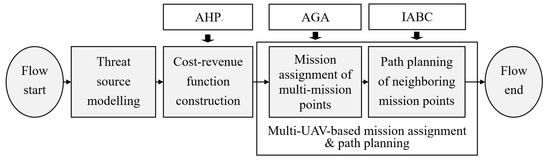
Figure 2.
Proposed computational flow chart.
3.2. The Threat Source Modelling Methods
In this study, it is supposed three types of exterior threat factor will influence the UAV flight security: the severe weather, transmission tower, and upland.
- (1)
- The severe weather threat source
In this study, the severe weather points to the wind and rain. Many methods can be used to evaluate the intensity of wind and rain in a certain area, such as the remote sensing satellite-based method [36] or atmosphere sensor-based technique [37]. Regarding the remote sensing satellite-based method, some models, such as the weather research and forecasting (WRF) model or the large Eddy simulations (LES) model [38], can be employed; however, these models are too complex for our application currently. Without loss of generality, the atmosphere observation data which are collected by the weather station are considered in this model. Figure 3 shows the 3D sketch map of weather station and the actual remote sensing map. In many cases, the weather station will be distributed in the peak of highland. Then it can assess the atmosphere state around highland. Table 2 presents the definition of wind speeds and their threat degrees. Equation (1) gives out the computational method of the severe weather threat source. In this paper, it is supposed that the 2D shape of weather threat source is a circle; the circle center is set in the weather station and the circle radius comes from the expert advice which consider the terrain and local historical climate. From Table 2 and Equation (1) it can be seen if there is a rain, the threat degree PWR will be high (PWR = 1); and if no rain appears in that zone, the threat degree would be higher with the increment of wind speed.
where Pi,j,p,WR represents the threat degree of rain and wind, i means the ith UAV, j means the jth threat source, p is the pth iteration number, WR indicates the wind and rain threat sources; Pi,j,p,R and Pi,j,p,W are the threat degrees of rain and wind, respectively; dWR is the distance between the UAV and weather threat source center; DWR is the radius of weather threat source; symbols “||” and “&” represent the relationship operators “or” and “and” between two variables; Pi,p,WR is the integrated severe weather threat degree of the ith UAV; and M1 is the total amount of weather threat source (weather station).
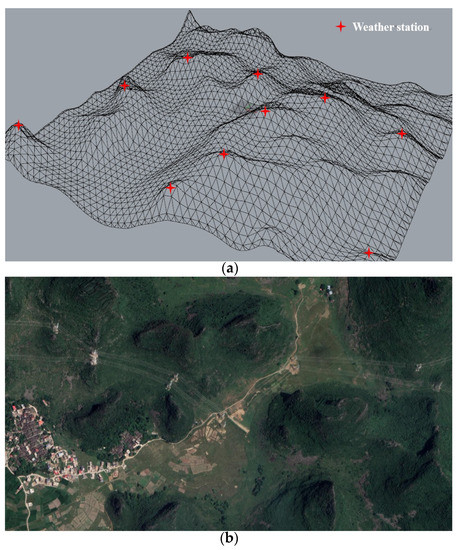
Figure 3.
Sketch map of weather station and its actual remote sensing map. (a) Sketch map of weather station. (b) Actual remote sensing map which comes from Google earth (https://www.google.com/earth/ accessed on 19 January 2020).

Table 2.
Definitions of wind speeds and their threat degrees.
- (2)
- The transmission tower threat source
The transmission tower is extensive erected in the mountain area in China which will create electromagnetic disturbance [39] to the navigation system of UAV. Although many anti-disturbance techniques have been developed to decrease that negative effect for UAV [40]; however, it is better to avoid the across-tower flight phenomenon. Figure 4 shows the sketch maps of transmission tower and a simplified model of intensity distribution of electromagnetic disturbance. In this paper, a bi-Gaussian mixed model (bi-GMM) [41] is used to construct the intensity distribution model of electromagnetic disturbance. In Figure 4a shows the sketch maps of electromagnetic radiation intensity distribution over the transmission tower from the front view and side view; Figure 4b,c is the 2D and 3D images of bi-GMM. Equations (3)–(5) are the computational methods of bi-GMM and the total electromagnetic disturbances of transmission tower.
where fi,j,p,q(x, y) (q = 1, 2) is the probability density function of bi-GMM function, i means the ith UAV, j is of the jth threat source (transmission tower), p is the pth iteration number, q is the number of Gaussian function; μ1i,j,p,q and μ2i,j,p,q are the means, σ1i,j,p,q and σ2i,j,p,q are the variances, ρi,j,p,q is the correlation coefficient; Pi,j,p,TT is the security threat degree of the jth transmission tower; wj,p,q is the weight of two Gaussian functions; TT means the transmission tower threat source; Pi,p,TT is the integrated transmission tower threat degree of the ith UAV; M2 is the total number of transmission tower in the investigated area.
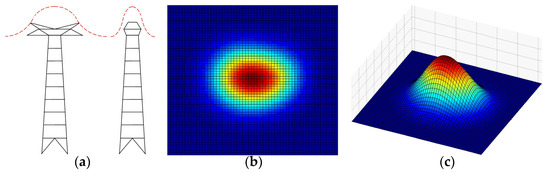
Figure 4.
Sketch map of transmission tower and its simplified model of radio interference distribution. (a) Front and side views of transmission tower. (b) 2D image of bi-GMM. (c) 3D image of bi-GMM.
- (3)
- The upland threat source
The upland will threaten the flight security of UAV because a crash may happen if the UAV is controlled improperly or flies too close to upland; therefore, the distance between the UAV and upland should affect the intensity of upland threat source. For the sake of simpleness, a circular cone model [42] is built in this study to imitate upland threat source. This kind of simplified model is like the actual terrain in China’s Sichuan or Guangxi Province. Figure 5 shows the sketch map of the upland threat source model. Three situations are considered in this model. In the first situation, if the flight height of UAV is larger than the height of upland () or the maximum security flight distance of upland (), the collision probability is 0. In the second situation, if the flight height of UAV is between the minimum security flight distance of upland () and the maximum security flight distance of upland (), the collision probability will be proportional to the UAV flight height from the upland surface. In the third situation, if the flight height of UAV is lower than the minimum security flight distance of upland (), the collision probability would be 1 in this model. From Figure 5 the larger the distance between UAV and upland surface is, the smaller the threat degree of upland would be. Equations (6)–(8) show the threat degree estimation method of one circular cone upland, some geometry relationships are employed here; and Equation (9) presents the total threat degree of multiple uplands in the disaster area.
where the symbols θi,j,p, , , , , , , are defined in Figure 5; i means the ith UAV, j is the jth upland threat source, p is the pth iteration number, m means the circle center of the circular cone in bottom; t is the circle center of circular cone in middle; “||” and “&” represent the relationship operators of “or” and “and” between two variables; Pi,j,p,UT represents the threat source of the jth upland; UT means the upland threat source; Pi,p,UT is the integrated upland threat effect of the ith UAV; M3 is the total number of upland in the disaster zone.
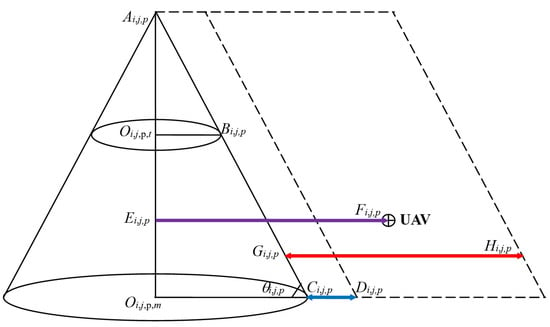
Figure 5.
Sketch map of the upland threat source model.
3.3. The Cost-Revenue Function
Both a cost function and a revenue function [43] are designed to accomplish the optimal mission assignment and path planning of multi-UAVs. When constructing the cost function, the flight distance, oil consumption, UAV function descriptions, UAV recovery issue, and threat source factors are considered. Equations (10)–(12) present the computational methods of these factors. From these equations, the threat degree can be decreased if the mission group contains the image collection UAV and communication relay UAV. The revenue function can represent the mission accomplishment degree of rescue mission. Equation (13) gives out its computational method. Finally, the definition of cost-revenue function is shown in Equations (14) and (15). In this model, regarding Equations (11) and (12), many weights are used. To determine their values objectively, the AHP method is utilized. The AHP is an operation method which can estimate the specific weight values of varied factors by comparing their importance in pairs. Figure 6 shows the hierarchy structure of AHP. Table 3 shows its evaluation criterion.
where Ci,p,Total is the total cost and revenue in the pth iteration computation of the ith UAV; Ci,p,MP is the cost function of the mission point; Ci,p,RP is the cost function of the recovery point; , , , , are the weights of distance factor, oil consumption factor, weather threat factor, transmission tower threat factor, and upland threat factor, respectively; K is the total number of mission points; similarly, , , , , and are the corresponding weights of recovery point; Pi,p,D(k), Pi,p,O(k), Pi,p,WR(k), Pi,p,TT(k), and Pi,p,UT(k) are the cost values of distance factor, oil consumption factor, costs of weather threat factor, transmission tower factor, and upland threat factor of the mission point k; and Pi,p,D(c), Pi,p,O(c) Pi,p,WR(c), Pi,p,TT(c), and Pi,p,UT(c) are the corresponding cost values in recovery point; rp, sp, and tp are the amounts of drug delivery UAV, image collection UAV, and communication relay UAV in the pth iteration, respectively; α is the parameter of drug delivery UAV which means the rate of a successful drug delivery; β is the parameter of image collection UAV which indicates the improvement probability of a drug delivery; γ is the parameter of communication relay UAV which presents the decreasing probability of all kinds of threat degrees; R(k) is the revenue of the kth mission point; ω1 and ω2 are weights, ω1 = 1.0 and ω2 = 10.0; I is the total number of UAVs.
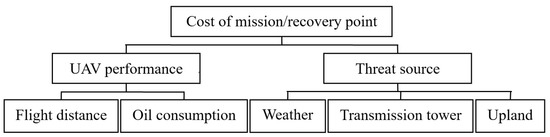
Figure 6.
Hierarchy structure of AHP.

Table 3.
Evaluation criterion of AHP.
3.4. The Optimal Computational Methods: AGA and IABC
Two optimal computational methods are designed for mission assignment and path planning: an AGA is proposed for mission assignment and a kind of IABC method is considered for path planning of neighboring mission points.
- (1)
- The optimal mission assignment of multiple mission points using AGAThe multi-UAV can be allocated into different UAV groups by AGA to accomplish the rescue task. The computational steps of AGA are listed below.
- (a)
- The population initialization. The initial population is generated, i.e., a series of initial solutions of mission assignment are created by the random number. The population size N_AGA, the current iteration number p_AGA, the maximum iteration number p_AGAmax, the crossing probability Pp_AGA,C, and the mutation probability Pp_AGA,M etc., are set.
- (b)
- The fitness function calculation [44]. The calculation method of the fitness function is shown by Equation (16).where fp_AGA is the fitness function in the p_AGAth iteration; T2p_AGA is defined in (15).
- (c)
- The iterative computation of AGA. Three kinds of computations are implemented [45]: the selection operation, crossover operation, and mutation operation. First, the selection operation considers the estimation result of fitness function, and its probability is defined in Equation (17). The roulette wheel selection method is utilized in this study. Second, the crossover processing is carried out by exchanging several gene fragments at the positions of two randomly selected individuals. Third, the mutation step is achieved by switching two genes of one randomly selected individual. The probabilities of crossover and mutation operations are defined in (18) and (19).where Pp_AGA,S is the selection probability; fp_AGA is the fitness function in the p_AGAth iteration; N_AGA is the maximum population number; Pp_AGA,C is the cross probability; ap_AGA, bp_AGA, cp_AGA, and dp_AGA are the control parameters in the p_AGAth iteration, ap_AGA = 1.0, bp_AGA = 1.2, cp_AGA = 1.0, and dp_AGA = 1.35 in this study; Pp_AGA,C_max is the maximum of cross probability; fp_AGA,max is the maximum of fitness function; fp_AGA,mean is the mean of fitness function; Pp_AGA,M is the mutation probability; Pp_AGA,M_max is the maximum of mutation probability.
Due to the convergence speed of traditional GA is slow with the accumulation of iteration number; an adjustment parameter is defined which is related with the iteration number. Then the new fitness function can be computed. Equations (20)–(22) present the corresponding computational methods.
where KAGA is an adjustment parameter; hi is a variable; is the maximum of cost-revenue function; p_AGAmax is the maximum iteration number.
Without loss of generality, let us take the mission allocation issue of two UAV groups as an example. Figure 7 shows the sketch map of chromosome coding method [46] of proposed AGA. In Figure 7, two code sequences compose this chromosome fragment; which also means we only consider dividing the mission implementation units into two parts. Two code sequences have the equal size and the same gene definition method. For example, in the left code sequence, the first three codes indicate the amounts of drug delivery UAV, image collection UAV, and communication relay UAV, respectively; and its left codes mean the mission points which can be filled by “0” or “1”; where “0” means this UAV group will not go to this mission point, while “1” is this group will go to this mission point. Clearly, the amount of these left codes should equal to the amount of the mission point. After coding, this chromosome fragment can be used to implement the selection, crossover, and mutation operations.

Figure 7.
Sketch map of the chromosome coding method of AGA.
- (2)
- The optimal path planning between neighboring mission points using IABCAn IABC algorithm is used to find the optimal path between neighboring mission points. The basic computational steps of artificial bee colony (ABC) algorithm are presented below.
- (a)
- The population initialization. The random solutions of ABC algorithm are created. The corresponding computation method [47] can be written by (23). The maximum iteration is also set, and the initial iteration number is 0.where xij is the coordinate of flight path; xjmin and xjmax are the minimum and maximum values of xij; i = 1, 2, …, NP, and NP is the total number of bees; j = 1, 2, …, D. Here D is the dimension of estimated parameter, D = 2 in this study.
- (b)
- The path updating of employed foragers. First, the solutions vij of employed foragers can be computed by (24), and then the fitness function will be estimated. Here, the fitness function uses the cost-revenue function in Equation (14) to estimate its fitness degree by Equation (25). The classical greedy algorithm [48] is used to select the proper solution. Second, the probability Pp_IABC is calculated by (26) and the corresponding scouter can be selected properly. Third, the solution vij of the onlooker from the solutions xij selected depending on Pp_IABC will also be computed by (24); and the greedy algorithm will be used again to select the proper solution. Fourth, the abandoned solution of scouter will be determined, and a new randomly solution will be considered for them. Fifth, the best solution will be recorded in this round and the iteration counter will be added by 1.where i = 1, 2, …, NP; j = 1, 2, …, D, and k = 1, 2, …, NP; k and j are the randomly chosen indexes, and k ≠ i; fp_IABC is the fitness function of solution which is proportional to the nectar amount; T1p_IABC is the cost-revenue function of the p_IABCth iteration.
- (c)
- The iteration computation will be terminated if the iteration counter reach its upper limitation.
The traditional ABC algorithm may have a shallow search depth, a low evolution efficiency of excellent individual, and a high abandon probability of good nectar source. To conquer these drawbacks to some extent, a balanced searching strategy is proposed. Equations (27)–(29) present its computational method. Clearly, during the early iteration computations, δ(p_IABC) > ε(p_IABC), this algorithm will have a good global searching ability in that stage; and with the implementation of iteration, the global optimal solution of current population xbest,j will avoid the local minimum solution, fasten convergence speed, and keep algorithm to hold the global searching ability to some extent. In that stage, the convergence speed still can high.
where xbest,j is the jth dimension component of global optimal solution of current population; ε(p_IABC) and δ(p_IABC) are the balanced searching factors, p_IABC is the current iteration number, p_IABCmax is the maximum iteration number.
4. Results and Discussions
A series of test and evaluation experiments are performed to assess the validity and effectiveness of proposed models and methods. All the simulation programs are written by Python (Pycharm2020) in our PC (4.0 GB RAM, 1.70 GHz Intel (R) Core(TM) i3-4005U CPU). To evaluate the effectiveness of proposed system and method, first, an assessment experiment of AGA is made; second, an evaluation experiment of IABC is performed; third, the experiment of multi-UAV optimal mission assignment and path planning for disaster rescue is implemented; finally, some discussions, extended experiments, and applications are illustrated.
4.1. The Evaluation Experiment of AGA
A mission assignment comparison between the GA and our AGA was made. The task assignment for the sole UAV was used for evaluation. Only the air-line distance between mission points was considered for simulation. The all-permutation of mission point was employed as the chromosome coding method. Both an 8 and an 18 mission points tests were considered in the evaluation experiments. The initial population size was 60, the maximum crossover probability was 0.8, the maximum mutation probability was 0.01; and the maximum iteration numbers were 300, 400, and 500. The coordinates of mission point are presented in Table 4. Table 5 shows the comparison results of fitness function and processing time of GA and AGA. Regarding GA and AGA, the fitness function means the difference between the cost function and revenue function (see Equation (16)); thus, the smaller the fitness function is the better the optimal computation effect will be. From Table 5, our AGA can achieve the better computational performance. The processing time of AGA is larger because it uses more resource for the selection, crossover, and mutation operations. A statistical evaluation of GA and AGA was also performed. After implementing the mission assignment experiment for 50 times [49], we investigated the average minimum and mean fitness functions of GA and AGA when the iteration times were 300, 400, and 500, respectively. Figure 8 gives out the results. From Figure 8, our AGA can acquire better performance. Table 6 illustrates the mission assignment results of GA and AGA: when the number of mission points are small, GA and AGA will get the similar assignment result; while the results will have remarkable differences when the amount of mission point is large.

Table 4.
Coordinates of mission point in the AGA evaluation experiment.

Table 5.
Population evaluation indices comparisons of GA and AGA.
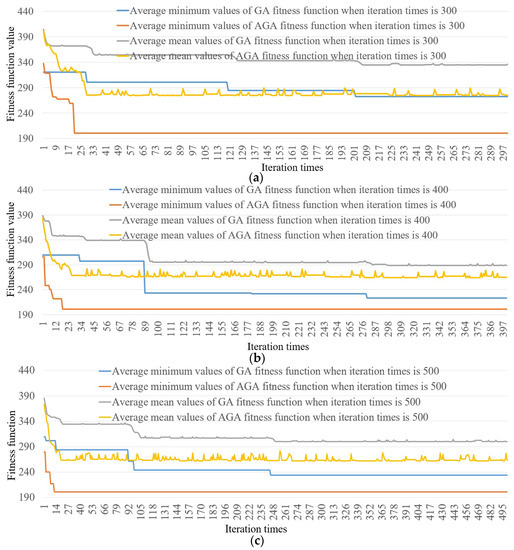
Figure 8.
Average minimum and mean fitness function values of GA and AGA when the iteration times are 300, 400, and 500. (a) Statistical evaluation results of fitness function when the iteration times is 300. (b) Statistical evaluation results of fitness function when the iteration times is 400. (c) Statistical evaluation results of fitness function when the iteration times is 500.

Table 6.
Evaluation results of GA and AGA using different experiments and iteration times.
4.2. The Evaluation Experiment of IABC
An optimal path planning comparison experiment between ABC and IABC was investigated. In this experiment, only the cost function was used to build the fitness function (see (14)). Table 7 presents the parameter settings of threat sources. The initial parameters of ABC and IABC were: the population size was 100; the data dimension was 15; the coordinates of start and end points were (0, 85) and (120, 30). To assess the performance of ABC and IABC, the optimal fitness function, path length, and processing time were considered. Table 8 presents the corresponding results. Regarding ABC and IABC, the larger the fitness function is the better the algorithm performance will be. Because the IABC employs a balanced searching strategy which adds more amounts of computation, the processing speed of proposed IABC is slow. However, there is no processing time requirement in our application currently, thus the corresponding result is acceptable. Finally, from Table 8, our method can get better fitness function and use less path length, as a result we think its performance is better than the traditional method.

Table 7.
Parameters setting methods of threat sources.

Table 8.
Evaluation results of ABC and IABC using different indices and iteration times.
The simulation results of fitness function, path length, and processing time using different iteration times are illustrated in Table 9. The best, worst, mean, and standard deviation values of fitness function, path length, and processing time of different populations are presented. From Table 9, our IABC can get the larger fitness function, shorter flight path length, while longer processing time. Since the processing time is acceptable (i.e., not important) for our application, our IABC is better than ABC in Table 9. Figure 9, Figure 10 and Figure 11 present the visualization examples of optimal path planning and the statistical results of fitness function using different iteration times. The total experiment times of ABC and IABC were 30. The best fitness function values of populations in each simulation were used to compute the statistical data in Figure 9, Figure 10 and Figure 11. From Figure 9, Figure 10 and Figure 11, the IABC can get smoother flight path and its fitness function indices are larger than those of ABC most of time; therefore, we think our IABC has better performance instead of ABC.

Table 9.
Performance evaluation results of ABC and IABC using different iteration times.
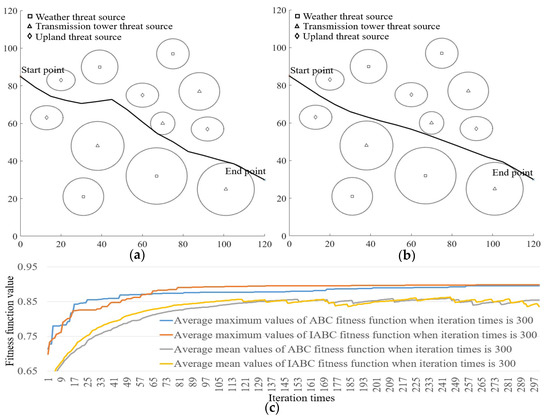
Figure 9.
Examples of path planning and statistical results of fitness function using 300 iterations. (a,b) Path planning examples of ABC and IABC when iteration times is 300. (c) Statistical results of fitness function of ABC and IABC when iteration times is 300.
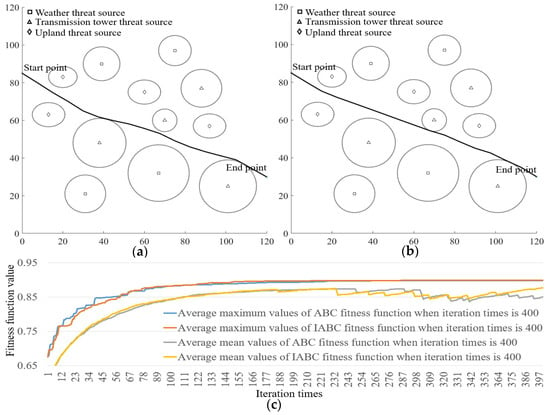
Figure 10.
Examples of path planning and statistical results of fitness function using 400 iterations. (a,b) Path planning examples of ABC and IABC when iteration times is 400. (c) Statistical results of fitness function of ABC and IABC when iteration times is 400.
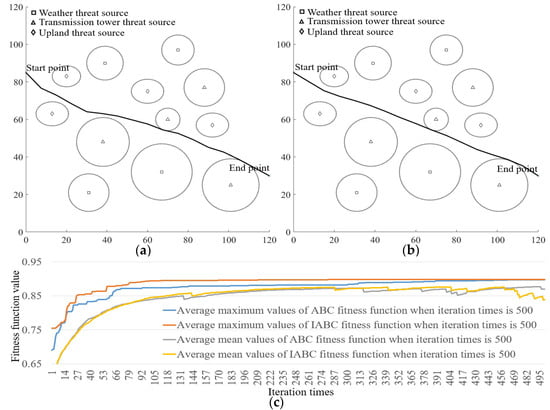
Figure 11.
Examples of path planning and statistical results of fitness function using 500 iterations. (a,b) Path planning examples of ABC and IABC when iteration times is 500. (c) Statistical results of fitness function of ABC and IABC when iteration times is 500.
4.3. The Evaluation Experiment of Disaster Rescue Simulation
An evaluation experiment of disaster rescue was performed. The AHP was used to estimate the weights of cost-revenue function in Equations (11) and (12). In this experiment, Table 10, Table 11, Table 12 and Table 13 give out the judgmental matrixes of AHP criteria hierarchy of mission point, the judgmental matrixes of UAV performance alternative hierarchy of mission point, the judgmental matrixes of threat source alternative hierarchy of mission point, and the final importance weights of mission point. Table 14, Table 15, Table 16 and Table 17 present the corresponding judgmental matrixes and final importance weights of recovery point. Regarding the data in Table 10, Table 11 and Table 12 and Table 14, Table 15 and Table 16, the judgmental matrixes come from the advice of disaster rescue experts. From Table 13 and Table 17, the weather threat source is the most important factor; while the flight distance is the least important factor for mission points and the oil consumption factor is the least important factor for recovery point. Since the recovery point will always be selected in the site which does not have too many threat sources, this result is reasonable for our application.

Table 10.
Judgmental matrixes of AHP criteria hierarchy of mission point.

Table 11.
Judgmental matrixes of UAV performance alternative hierarchy of mission point.

Table 12.
Judgmental matrixes of threat source alternative hierarchy of mission point.

Table 13.
Final estimated importance weights of AHP of mission point.

Table 14.
Judgmental matrixes of AHP criteria hierarchy of recovery point.

Table 15.
Judgmental matrixes of UAV performance alternative hierarchy of recovery point.

Table 16.
Judgmental matrixes of threat source alternative hierarchy of recovery point.

Table 17.
Final estimated importance weights of AHP of recovery point.
An integrated evaluation of mission assignment and path planning was performed, the initial experiment parameters were: the amounts of drug delivery, image collection, and communication relay UAVs were 15, 3; and 2; the UAVs were classified into two groups; the coordinates of start point of UAV groups were (0, 50) and (0, 52); the coordinate of recovery point was (120, 50); α = 0.5, β = 0.1 and γ = 0.1; R(k) = {1.0, 1.3, 1.2, 1.5, 1.4, 1.2}. Other parameters of threat sources, GA, AGA, ABC, and IABC were the same to the parameters in Section 4.2 and Section 4.3. The mission point coordinates are shown in Table 18. Table 19 shows the results. In Table 19, methods of GA+ABC, GA+IABC, AGA+ABC, and AGA+IABC are investigated; the results of group assignment, mission assignment, total revenue (see (13)), total cost (see (10)), processing time, and path length are simulated. From Table 19, the AGA+IABC can get the best performance except for the processing time. Figure 12 shows our visualization results. Table 20 illustrates the statistical results of average revenue, average cost, average processing time, and average path length. From Table 20, our AGA+IABC can get the best revenue, the least cost, and the shortest path length most of time; thus we believe this method to be good enough for our application.

Table 18.
Coordinates of mission point in the disaster rescue evaluation experiment.

Table 19.
Results of multi-UAV optimal mission assignment and path planning using different optimization methods.
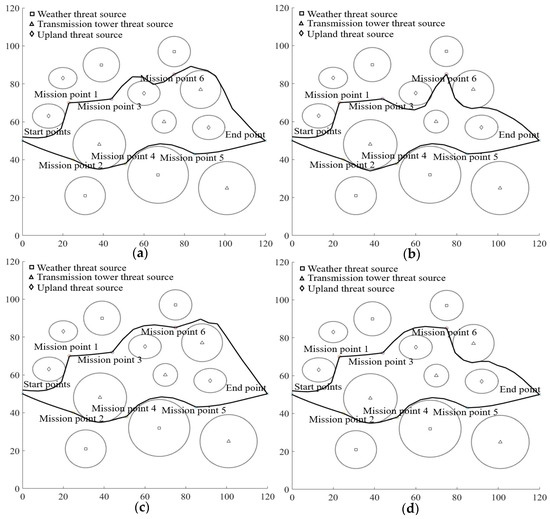
Figure 12.
Results of multi-UAV optimal mission assignment and path planning using different methods. (a) Visualization results of GA+ABC. (b) Visualization results of GA+IABC. (c) Visualization results of AGA+ABC. (d) Visualization results of AGA+IABC.

Table 20.
Statistical results of average revenue, average cost, average processing time, and average path length using different mission assignment and path planning methods.
4.4. Discussions
With the fast technique advancement, the multi-UAV and multi-UAV mission formation [50] have been widely studied to assist the disaster rescue of villages which locate far away from the big city. Currently, the familiar hypothetical rescue task always happens in the southwest China because the earthquake belt crosses this area. The terrain in southwest China always has the basin or karst landform [51] (see Figure 3b), the weather there is rainy and windy most of the year. Thus, it is necessary to make a careful design of task assignment of medical rescue before the serious earthquake damage happens. Comparing with a single UAV, the multiple UAVs can take larger amount of rescue resources, accomplish more rescue functions, and behave better flight stability. Thus, how to assign the proper UAVs for different rescue points and how to plan their flight paths should be studied before the implementation of rescue. To conquer these problems to some extent, an intelligent algorithm is developed in this study which considers the flight factor, the UAV function factor, the threat source factor, and the UAV recovery factor, etc. This research work can be used for the decision support of disaster medical rescue.
Three types of threat source models were considered in this study, i.e., the weather threat source, transmission tower threat source, and upland threat source. The modeling of weather phenomenon really is a complex task because too many factors will affect the local weather, such as the wind, temperature, humidity, sun light, and even the local terrain. In this study, a simplified weather threat source was proposed for a fast computation purpose; only the factors of wind and rain were considered. The influence scope of bad weather was abstracted by a circle around the weather station. In future, the atmosphere temperature model [52] can be researched for our application. The electromagnetic disturbance cannot be omitted for any UAV applications. The manmade disturbance source, i.e., the transmission tower, was modeled in this study. In fact, the power line itself and the nature disturbance sources (such as the thunder, ground radiation, etc.) can also be studied in future. A simplified upland model was used in our model. The distance from the ground was considered to assess the degree of threat source intensity. Clearly, the 3D terrain model can be used to replace that circular cone in our next research step.
A kind of revenue-cost function was designed to guide the optimal computation of mission assignment and path planning. Both the revenue and cost in the mission point and recovery point were considered. The revenue function reflects the rescue value of typical mission point (i.e., the village); the larger the revenue function value is the better the optimal computation will be. The cost function indicates the risk, material cost, and mission complexity during the disaster rescue; the smaller the cost function value is the better the model computation effect will be. The function assignment of UAVs is controlled by the parameters in the revenue and cost functions. In this study, the flight distance, oil consumption, UAV function descriptions, threat source factors, and mission point revenue participated the construction of revenue–cost function. To improve the modeling objectivity, the AHP model was used to estimate the weights of revenue-cost function. The opinions of disaster rescue experts were used to build the AHP model. The meeting discussion can be considered for expert opinion collection. Clearly, more factors can be considered in the design of revenue-cost function in future, such as the minimum turning radius of UAV, precision of satellite navigation, and other threat source factors, etc.
Both an AGA and an IABC [53] were developed for mission assignment and path planning in the disaster rescue task. Regarding the mission assignment, the GA-based method [54,55] has been proofed to be the best scheduling method in our former research; thus it is not necessary to consider other techniques for solving this task. Differently, as for the path planning problem, many other optimization methods can be considered, such as the particle swarm optimization (PSO) [56] method, artificial potential field algorithm (APFA) [57], or bat algorithm [58], etc. After a series of tests, it can be found the performance of bat algorithm cannot fulfill our application requirement; thus, only the PSO and APFA were evaluated. Figure 13 presents the visualization results of multi-UAV optimal mission assignment and path planning using GA, AGA, PSO, and APFA. From Figure 13, the PSO-based method can get a smoother flight path. Table 21 gives out the statistical evaluation result of average revenue, average cost, average processing time, and average path length using GA, AGA, PSO, and APFA. The simulation times was 40. From Table 21, similar to the results in Table 20, the methods of AGA+PSO and AGA+APFA can get better performances than the methods of GA+PSO and GA+APFA, respectively. These results can illustrate the effectiveness of proposed AGA to some extent.
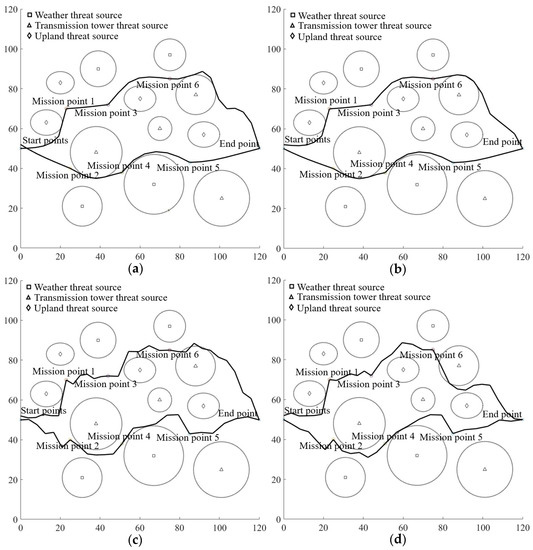
Figure 13.
Visualization results of multi-UAV optimal mission assignment and path planning using GA, AGA, PSO, and APFA. (a) Visualization results of GA+PSO. (b) Visualization results of AGA+PSO. (c) Visualization results of GA+APFA. (d) Visualization results of GA+APFA.

Table 21.
Statistical evaluation results of average revenue, average cost, average processing time, and average path length using GA, AGA, PSO, and APFA.
A series of evaluation experiments were performed to assess the effect of proposed computational method in this study. Many evaluation indices, such as the statistical value of fitness function, iteration times, or program processing time, were used. For example, regarding the IABC algorithm, it needs more computational resource for the computation of balanced searching strategy (see Equations (27)–(29)) than the ABC method; however its convergence speed is faster than ABC. The experiment results showed if we investigated the algorithm performance of 1000 iterations, the convergence times (i.e., the value of fitness function would not be changed) of ABC and IABC were 440 and 316, respectively; and the processing time of ABC and IABC were 12.1826 s and 15.0539 s; thus, the average convergence time of ABC and IABC were 5.3603 s and 4.757 s, respectively. As for the iteration times in the GA and AGA evaluation experiments, the larger the iteration times is the smaller the fitness function will be (see Figure 8). When it comes to the iteration times of ABC and IABC, the path length will decrease firstly and then increase slightly with the rise of iteration times; and the fitness function will increase, the processing time will rise distinctly. Clearly, all these results can illustrate the good performance of our proposed methods.
The proposed algorithm can be used for practical application. An optimal computation module together with a visualization simulation software [59] were developed for the disaster rescue task in our application. Currently, both the fixed wing UAV and the multi-rotor unmanned helicopter can be used for this application. In our software, the 3D terrain came from the satellite remote sensing data. Figure 14 presents the corresponding visualization results. In Figure 14, the color 3D terrain is illustrated; the optimal paths are presented by the white dash lines; the threat sources are marked by the hemispheres with blue or red color; and multiple helicopters are also displayed in that scene. In Figure 14, the UAVs are classified into two groups. Regarding this software, because the optimal computation will cost too much time, as a result the optimal mission assignment and path planning will be computed firstly, and then the corresponding results will be displayed by the 3D visualization program. Another issue in this study is: the height information of UAV is not considered in our model; this designing comes from the fact that the UAV uses the altimeter to control its flight height from the ground; and in many cases its flight height can be a fixed value.

Figure 14.
Visualization simulation examples of proposed method. (a) Global field view of simulation result. (b) Local field view of simulation result.
The proposed algorithm has at least three advantages. First, our model considers the practical engineering application of disaster rescue carefully. As we have stated above, this method is designed for the medical rescue in southwest China. The typical terrain, weather condition, and artificial facility [60] are all considered when constructing the corresponding target functions. The typical multiple UAVs for the medical disaster rescue are also designed. The function characters of multi-UAV are also proposed for the optimal computation. Second, its computational precision is comparable high. Comparing with other application, an integrated evaluation of mission assignment and path planning is performed. This processing method can refine our computational result. Third, the model extensibility is good. Clearly, any other optimal methods can be used easily in our computational framework; this system and method can be popularized for any applications outside China only with limited model adjustments. Our algorithm also has some shortcomings. For example, the models of threat sources can be improved and the human-computer interactivity of this system is limited. In future more intelligent techniques can be used in our model.
5. Conclusions
In this study, a multi-UAV mission assignment and path planning method is proposed for the disaster medical rescue. The multiple UAVs include the drug delivery UAV, image collection UAV, and communication relay UAV. Three kinds of threat source models are considered: the severe weather, transmission tower, and upland. When building the cost-revenue function of optimization model, the flight distance, oil consumption, UAV function, and threat sources are utilized. The AHP model is utilized to estimate the weights in this model. Both the cost-revenue functions for the mission point and recovery point are designed. An AGA is designed to solve the optimal mission assignment for mission points; a fitness function which considers the current and maximum iteration numbers are employed to improve the algorithm convergence performance. An IABC method is considered to solve the optimal path planning between the neighboring mission points; a balanced searching strategy is developed to improve the algorithm computational effect. Many evaluation results have proofed the effect of proposed model. This research work can be used for decision support of disaster medical rescue in future.
Author Contributions
Conceptualization, H.L., J.G., J.L. (Jiacheng Li), K.D., Z.Z., Z.G., W.L. and J.L. (Jinhui Lan); Data curation, H.L.; Formal analysis, H.L., J.G., J.L. (Jiacheng Li), K.D., Z.Z., Z.G., W.L. and J.L. (Jinhui Lan); Funding acquisition, H.L.; Investigation, H.L., J.G., K.D., Z.Z. and J.L. (Jinhui Lan); Methodology, H.L., J.G., Y.W., J.L. (Jiacheng Li), K.D., Z.Z., Z.G. and W.L.; Project administration, K.D.; Resources, Z.Z.; Software, Y.W. and J.L. (Jiacheng Li); Supervision, H.L.; Validation, H.L., J.G., Y.W., J.L. (Jiacheng Li), Z.G. and J.L. (Jinhui Lan); Visualization, J.G., Y.W., J.L. (Jiacheng Li) and W.L.; Writing—Original draft, H.L.; Writing—Review & Editing, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fund of Science and Technology on Near-Surface Detection Laboratory under Grant TCGZ2019A003, the National Natural Science Foundation of China under Grant 61975011, the Fund of State Key Laboratory of Intense Pulsed Radiation Simulation and Effect under Grant SKLIPR2024, and the Fundamental Research Fund for the China Central Universities of USTB under Grant FRF-BD-19-002A. The authors declare no conflict of interest.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
Here is a list with the main abbreviations used in this article.
| ABC | Artificial bee colony |
| AGA | Adaptive Genetic algorithm |
| AHP | Analytic hierarchy process |
| APFA | Artificial potential field algorithm |
| GA | Genetic algorithm |
| GMM | Gaussian mixed model |
| IABC | Improved artificial bee colony |
| LES | Large Eddy Simulations |
| PC | Personal computer |
| PSO | Particle swarm optimization |
| UAV | Unmanned aerial vehicle |
| WRF | Weather research and forecasting |
Nomenclature
| The threat degree of rain and wind of the ith UAV in the jth threat source under the pth iterative computation. | |
| The threat degree of rain of the ith UAV in the jth threat source under the pth iterative computation. | |
| The threat degree of wind of the ith UAV in the jth threat source under the pth iterative computation. | |
| The distance between UAV and weather threat source center. | |
| The radius of weather threat source. | |
| The integrated weather threat degree of the ith UAV under the pth iterative computation. | |
| The total amount of weather threat source. | |
| The probability density function of bi-GMM function of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The mean of Gaussian function 1 of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The mean of Gaussian function 2 of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The variance of Gaussian function 1 of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The variance of Gaussian function 2 of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The correlation coefficient of bi-GMM of the ith UAV in the jth threat source under the pth iterative computation, q is the number of Gaussian function. | |
| The threat degree of transmission tower of the ith UAV in the jth threat source under the pth iterative computation. | |
| The weight of Gaussian function, j is the number of threat source, p is number of iteration times, q is the number of Gaussian function. | |
| The integrated transmission tower threat degree of the ith UAV in the pth threat source. | |
| The total number of transmission tower in the investigated area. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| Please see the definition in Figure 5. | |
| The threat degree of upland of the ith UAV in the jth threat source under the pth iterative computation. | |
| The integrated threat degree of upland of the ith UAV under the pth iterative computation. | |
| The total cost and revenue of the ith UAV in the pth iterative computation. | |
| The mission point cost function of the ith UAV under the pth iterative computation. | |
| The recovery point cost function of the ith UAV under the pth iterative computation. | |
| The weight of distance factor of mission point. | |
| The weight of oil consumption factor of mission point. | |
| The weight of weather threat factor of mission point. | |
| The weight of transmission tower threat factor of mission point. | |
| The weight of upland threat factor of mission point. | |
| The total number of mission point. | |
| The weight of distance factor of recovery point. | |
| The weight of oil consumption factor of recovery point. | |
| The weight of weather threat factor of recovery point. | |
| The weight of transmission tower threat factor of recovery point. | |
| The weight of upland threat factor of recovery point. | |
| The distance cost value of mission point k of the ith UAV under the pth iterative computation. | |
| The oil consumption cost value of mission point k of the ith UAV under the pth iterative computation. | |
| The weather cost value of mission point k of the ith UAV under the pth iterative computation. | |
| The transmission tower cost value of mission point k of the ith UAV under the pth iterative computation. | |
| The upland cost value of mission point k of the ith UAV under the pth iterative computation. | |
| The distance cost value of recovery point c of the ith UAV under the pth iterative computation. | |
| The oil consumption cost value of recovery point c of the ith UAV under the pth iterative computation. | |
| The weather cost value of recovery point c of the ith UAV under the pth iterative computation. | |
| The transmission tower cost value of recovery point c of the ith UAV under the pth iterative computation. | |
| The upland cost value of recovery point c of the ith UAV under the pth iterative computation. | |
| The amount of drug delivery UAV under the pth iterative computation. | |
| The amount of image collection UAV under the pth iterative computation. | |
| The amount of communication relay UAV under the pth iterative computation. | |
| The rate of successful drug delivery of drug delivery UAV. | |
| The improvement probability of drug delivery caused by image collection UAV. | |
| The decreasing probability of threat source caused by communication relay UAV. | |
| The revenue of the kth mission point. | |
| The weight of Gaussian function 1. | |
| The weight of Gaussian function 2. | |
| The total amount of UAV. | |
| The fitness function of AGA under the p_AGAth iteration. | |
| The AGA application of Equation (15). | |
| The selection probability of AGA under the p_AGAth iteration. | |
| The maximum population amount of AGA. | |
| The cross probability of AGA under the p_AGAth iteration. | |
| A control parameter of AGA fitness function under the p_AGAth iteration. | |
| A control parameter of AGA fitness function under the p_AGAth iteration. | |
| A control parameter of AGA fitness function under the p_AGAth iteration. | |
| A control parameter of AGA fitness function under the p_AGAth iteration. | |
| The maximum of cross probability of AGA under the p_AGAth iteration. | |
| The maximum of fitness function of AGA under the p_AGAth iteration. | |
| The mean of fitness function of AGA under the p_AGAth iteration. | |
| The mutation probability of AGA under the p_AGAth iteration. | |
| The maximum of mutation probability of AGA under the p_AGAth iteration. | |
| The adjustment parameter of fitness function of AGA. | |
| The iteration times-related variable of AGA algorithm. | |
| The maximum of cost-revenue function under the p_AGAth iteration. | |
| The maximum iteration number of AGA. | |
| The coordinate of flight path. | |
| The minimum value of xij. | |
| The maximum value of xij. | |
| The total amount of bee of ABC algorithm. | |
| The parameter dimension of ABC algorithm. | |
| The fitness function of IABC algorithm. | |
| The cost-revenue function of IABC algorithm under p_IABCth iteration. | |
| The jth dimension component of global optimal solution of current population. | |
| The balanced searching factor 1 of IABC algorithm. | |
| The balanced searching factor 2 of IABC algorithm. | |
| The current iteration number of IABC algorithm. | |
| The maximum iteration number of IABC algorithm. |
References
- Liu, H.; Yan, B.; Wang, W.; Li, X.; Guo, Z. Manhole cover detection from natural scene based on imaging environment perception. KSII Trans. Internet Inf. 2019, 13, 5059–5111. [Google Scholar]
- Lv, M.; Zheng, J.; Tong, Q.; Chen, J.; Liu, H.; Gao, Y. Modeling and simulation of scheduling medical materials using graph model for complex rescue. J. Inf. Process. Syst. 2017, 13, 1243–1258. [Google Scholar]
- Chen, J.; Liu, H.; Zheng, J.; Lv, M.; Yan, B.; Hu, X.; Gao, Y. Damage degree evaluation of earthquake area using UAV aerial image. Int. J. Aerosp. Eng. 2016, 216, 2052603. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, W.; He, Z.; Tong, Q.; Wang, X.; Yu, W.; Lv, M. The design of air-space integrative calamity information analysis and rescue system. In Proceedings of the IEEE International Conference on Cyber Technology in Automation, Control and Intelligent Systems, Shenyang, China, 8–12 June 2015; pp. 1997–2001. [Google Scholar]
- Yamazaki, F.; Miyazaki, S.; Liu, W. 3D visualization of landslide affected area due to heavy rainfall in Japan from UAV flights and SfM. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5685–5688. [Google Scholar]
- Fan, Q.; Wang, F.; Shen, X.; Luo, D. Path planning for a reconnaissance UAV uncertain environment. In Proceedings of the IEEE International Conference on Control and Automation, Kathmandu, Nepal, 1–3 June 2016; pp. 248–252. [Google Scholar]
- Hao, R.; Luo, D.; Duan, H. Multiple UAVs mission assignment based on modified pigeon-inspired optimization algorithm. In Proceedings of the IEEE Chinese Guidance, Navigation and Control Conference, Yantai, China, 8–10 August 2014; pp. 2692–2697. [Google Scholar]
- He, Z.; Zhao, L. The comparison of four UAV path planning algorithms based on geometry search algorithm. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2017; pp. 33–36. [Google Scholar]
- Cichella, V.; Kaminer, I.; Dobrokhodov, V.; Xargay, E.; Choe, R.; Hovakimyan, N.; Pedro Aguiar, A.; Pascoal, A.M. Cooperative path following of multiple multirotors over time-varying networks. IEEE Trans. Autom. Sci. Eng. 2015, 12, 945–957. [Google Scholar] [CrossRef]
- Oh, H.; Turchi, D.; Kim, S.; Tsourdos, A.; Pollini, L.; White, B. Coordinated standoff tracking using path shaping for multiple UAVs. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 348–363. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, H.V.; Rezatofighi, H.; Vo, B.-N.; Ranasinghe, D.C. Online UAV path planning for joint detection and tracking of multiple radio-tagged objects. IEEE Trans. Signal Process. 2019, 67, 5365–5379. [Google Scholar] [CrossRef] [Green Version]
- Xia, S.; Zhang, X. Constrained path planning for unmanned aerial vehicle in 3D terrain using modified multi-objective particle swarm optimization. Actuators 2021, 10, 255. [Google Scholar] [CrossRef]
- Shahzad, A.; Ur-Rehman, R. An artificial intelligence based novel approach for real-time allocation of armament to hostile targets. In Proceedings of the 10th International Bhurban Conference on Applied Sciences & Technology, Islamabad, Pakistan, 15–19 January 2013; pp. 141–146. [Google Scholar]
- Huang, T.; Wang, Y.; Cao, X.; Xu, D. Multi-UAV mission planning method. In Proceedings of the 3rd International Conference on Unmanned Systems, Harbin, China, 27–28 November 2020; pp. 325–330. [Google Scholar]
- Luo, W. An efficient sensor-mission assignment algorithm based on dynamic alliance and quantum genetic algorithm in wireless sensor networks. In Proceedings of the International Conference on Intelligent Computing and Integrated Systems, Guilin, China, 22–24 October 2010; pp. 854–857. [Google Scholar]
- Fan, H.; Liu, F.; Xia, L. Cluster label aligning algorithm based on programming model. In Proceedings of the 24th Chinese Control and Decision Conference, Taiyuan, China, 23–25 May 2012; pp. 1768–1772. [Google Scholar]
- Ahner, D.; Parson, C. Weapon tradeoff analysis using dynamic programming for a dynamic weapon target assignment problem within a simulation. In Proceedings of the Winter Simulations Conference, Washington, DC, USA, 8–11 December 2013; pp. 2831–2841. [Google Scholar]
- Dumka, S.; Maheshwari, S.; Kala, R. Decentralized multi-robot mission planning using evolutionary computation. In Proceedings of the IEEE Congress on Evolutionary Computation, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Kang, S.; Li, J.; Li, J.; Xiong, J.; Liu, C. Application of the evolutionary algorithms for task allocation in uncertain environments with stochastic tuning. In Proceedings of the International Conference on Artificial Intelligence, Information Processing and Cloud Computing, Hangzhou, China, 26–28 June 2021; pp. 1–7. [Google Scholar]
- Wang, G.; Li, M.; Deng, Z.; Yang, B.; Yao, W. A new approach to solve the mission assignment problem for cooperative UCAVs using immune particle swarm optimizations. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 549–554. [Google Scholar]
- Mokrane, A.; Choukchou Braham, A.; Cherki, B. UAV path planning based on dynamic programming algorithm on photogrammetric DEMs. In Proceedings of the International Conference on Electrical Engineering, Istanbul, Turkey, 25–27 September 2020; pp. 1–5. [Google Scholar]
- Jing, W.; Feng, D.; Zhang, P.; Zhang, S.; Lin, S.; Tang, B. A multi-objective optimization-based path planning method for parallel parking of autonomous vehicle via nonlinear programming. In Proceedings of the 15th International Conference on Control, Automation, Robotics and Vision, Singapore, 18–21 November 2018; pp. 1665–1670. [Google Scholar]
- He, N.; Su, Y.; Guo, J.; Fan, X.; Liu, Z.; Wang, B. Dynamic path planning of mobile robot based on artificial potential field. In Proceedings of the International Conference on Intelligent Computing and Human-Computer Interaction, Sanya, China, 4–6 December 2020; pp. 259–264. [Google Scholar]
- Chen, Z.; Xu, B. AGV path planning based on improved artificial potential field method. In Proceedings of the IEEE International Conference on Power Electronics, Computer Applications, Shenyang, China, 22–24 January 2021; pp. 32–37. [Google Scholar]
- Guo, Q.; Zhang, Z.; Xu, Y. Path-planning of automated guided vehicle based on improved Dijkstra algorithm. In Proceedings of the 29th Chinese Control and Decision Conference, Chongqing, China, 28–30 May 2017; pp. 7138–7143. [Google Scholar]
- Li, X.; Hu, X.; Wang, Z.; Du, Z. Path planning based on combination of improved A-star algorithm and DWA algorithm. In Proceedings of the 2nd International Conference on Artificial Intelligence and Advanced Manufacture, Manchester, UK, 15–17 October 2020; pp. 99–103. [Google Scholar]
- Chen, X.; Chen, X.-M. The UAV dynamic path planning algorithm research based on Voronoi diagram. In Proceedings of the 26th Chinese Control and Decision Conference, Changsha, China, 31 May–2 June 2014; pp. 1069–1071. [Google Scholar]
- Santiago, R.M.C.; De Ocampo, A.L.; Ubando, A.T.; Bandala, A.A.; Dadios, E.P. Path planning for mobile robots using genetic algorithm and probabilistic roadmap. In Proceedings of the IEEE 9th International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management, Manila, Philippines, 1–3 December 2017; pp. 1–5. [Google Scholar]
- Liu, Z.; Kong, J. Path planning of parafoil system based on particle swarm optimization. In Proceedings of the International Conference on Computational Intelligence and Natural Computing, Wuhan, China, 6–7 June 2009; pp. 450–453. [Google Scholar]
- Tang, J.; Zhao, Y.; Li, F. On the use of ant colony algorithm with weighted penalty strategy to optimize path searching. In Proceedings of the International Conference on Intelligent Computing, Automation and Systems, Chongqing, China, 11–13 December 2020; pp. 309–312. [Google Scholar]
- Pierpaoli, P.; Egerstedt, M.; Rahmani, A. Altering UAV flight path by threatening collision. In Proceedings of the Digital Avionics Systems Conference, Prague, Czech Republic, 13–17 September 2015; pp. 1–13. [Google Scholar]
- Yaraghi, N.; Tabesh, P.; Guan, P.; Zhuang, J. Comparison of AHP and Monte Carlo AHP under different levels of uncertainty. IEEE Trans. Eng. Manag. 2015, 62, 122–132. [Google Scholar] [CrossRef]
- Xhafa, F.; Herrero, X.; Barolli, A.; Takizawa, M. A struggle genetic algorithm for ground stations scheduling problem. In Proceedings of the International Conference on Intelligent Networking and Collaborative Systems, Bucharest, Romania, 19–21 September 2012; pp. 70–76. [Google Scholar]
- Wang, Q.; Liu, G.; Guo, K. Research on path planning of UAV based on improved ABC algorithm. Mach. Tool Hydraul. 2017, 45, 68–72. [Google Scholar]
- Gallaher, D.W.; Campbell, G.G.; Meier, W.N. Anomalous variability in Antarctic sea ice extents during the 1960s with the use of nimbus data. IEEE J.-STARS 2014, 7, 881–887. [Google Scholar] [CrossRef]
- Ziouh, A.; Abbou, A.; Marhraoui, S. Efficiency of ripple correlation control compared to fuzzy logic MPPT algorithm in space climate conditions for Nimbus 2 Satellite. In Proceedings of the International Renewable and Sustainable Energy Conference, Tangier, Morocco, 4–7 December 2017; pp. 1–5. [Google Scholar]
- Du, P. Ensemble machine learning-based wind forecasting to combine NWP output with data from weather station. IEEE Trans. Sustain. Energy 2019, 10, 2133–2141. [Google Scholar] [CrossRef]
- Mallick, Z.; Kuhn, T.; Korhonen, H.; Kokkola, H.; Laaksonen, A.; Romakkaniemi, S. Effect aerosol concentration and absorbing aerosol on the radiation fog life cycle. Atmos. Environ. 2016, 133, 26–33. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Xue, H.; Yang, C.; Yan, T. Research on the electromagnetic environment of 110kV six-circuit transmission line on the same tower. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Tianjin, China, 21–24 May 2012; pp. 1–5. [Google Scholar]
- Zheng, T.; Sun, L.; Lou, T.; Guo, X.; Liu, Q. Determination method of safe flight area for UAV inspection for transmission line based on the electromagnetic field calculation. ShanDong Electr. Power 2018, 45, 27–30. [Google Scholar]
- Xu, N.; Shao, X.; Yang, Z. A novel voice morphing system using Bi-GMM for high quality transformation. In Proceedings of the ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing, Phuket, Thailand, 6–8 August 2008; pp. 485–489. [Google Scholar]
- Hu, Z. Research on Some Key Techniques of UAV Path Planning Based on Intelligent Optimization Algorithm. Ph.D. Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, April 2011. [Google Scholar]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- San, K.T.; Lee, E.Y.; Chang, Y.S. The delivery assignment solution for swarms of UAVs dealing with multi-dimensional chromosome representation of genetic algorithm. In Proceedings of the IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication, New York, NY, USA, 20–22 October 2016; pp. 1–7. [Google Scholar]
- Lin, C.-J.; Sie, T.-Y.; Chu, W.-L.; Yau, H.-T.; Ding, C.-H. Tracking control of pneumatic artificial muscle-activated robot arm based on sliding-mode control. Actuators 2021, 10, 66. [Google Scholar] [CrossRef]
- Xiong, X.; Dong, L. A self-adaptive genetic algorithm for labeling line drawings of planar objects. J. Graph. 2018, 39, 1104–1111. [Google Scholar]
- Kubicek, J.; Vilimek, D.; Krestanova, A.; Penhaker, M.; Kotalova, E.; Faure-Brac, B.; Noel, C.; Scurek, R.; Augustynek, M.; Cerny, M.; et al. Prediction model of alcohol intoxication from facial temperature dynamics based on K-means clustering driven by evolutionary computing. Symmetry 2019, 11, 995. [Google Scholar] [CrossRef] [Green Version]
- Trongratsameethong, A.; Mitrpanont, J.L. Exhaustive greedy algorithm for optimizing intermediate result sizes of join queries. In Proceedings of the IEEE/ACIS International Conference on Computer and Information Science, Shanghai, China, 1–3 June 2009; pp. 463–468. [Google Scholar]
- Carrano, E.G.; Wanner, E.F.; Takahashi, R.H.C. A multicriteria statistical based comparison methodology for evaluating evolutionary algorithms. IEEE Trans. Evol. Comput. 2011, 15, 848–870. [Google Scholar] [CrossRef]
- Liu, H.; Wang, W.; Wang, X.; Yu, W.; Lv, M. Multiple rotor UAVs formation flight and its application on level evaluation of earthquake damage. In Proceedings of the International Symposium on Computational Intelligence and Design, Hangzhou, China, 13–14 December 2014; pp. 333–336. [Google Scholar]
- Zhou, Q.; Luo, Y.; Zhou, X.; Cai, M.; Zhao, C. Response of vegetation to water balance conditions at different time scales across the karst area of southwestern China–a remote sensing approach. Sci. Total Environ. 2018, 645, 460–470. [Google Scholar] [CrossRef]
- Huang, L.; Peng, H.; Liu, L.; Li, C.; Kang, C.; Xie, S. An empirical atmospheric weighted mean temperature model considering the lapse rate function for China. Acta Geod. Et Cartogr. Sin. 2020, 49, 432–442. [Google Scholar]
- Kubicek, J.; Penhaker, M.; Augustynek, M.; Cerny, M.; Oczka, D. Segmentation of articular cartilage and early osteoarthritis based on the fuzzy soft thresholding approach driven by modified evolutionary ABC optimization and local statistical aggregation. Symmetry 2019, 11, 861. [Google Scholar] [CrossRef] [Green Version]
- Bernal-Romero, D.L.; Montoya, O.D.; Arias-Londono, A. Solution of the optimal reactive power flow problem using a discrete-continuous CBGA implemented in the DigSILENT programming language. Computers 2021, 10, 151. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Grisales-Norena, L.F.; Hincapie, R.A.; Granada, A. Improved genetic algorithm for phase-balancing in three-phase distribution networks: A master-slave optimization approach. Computation 2021, 9, 67. [Google Scholar] [CrossRef]
- Cai, Q.; Long, T.; Wang, Z.; Wen, Y.; Kou, J. Multiple paths planning for UAVs using particle swarm optimization with sequential niche technique. In Proceedings of the Chinese Control and Decision Conference, Yinchuan, China, 28–30 May 2016; pp. 4730–4734. [Google Scholar]
- Yao, Q.; Zheng, Z.; Qi, L.; Yuan, H.; Guo, X.; Zhao, M.; Liu, Z.; Yang, T. Path planning method with improved artificial potential field–a reinforcement learning perspective. IEEE Access 2020, 8, 135513–135523. [Google Scholar] [CrossRef]
- Chen, D.-F.; Chiu, S.-P.-C.; Cheng, A.-B.; Ting, J.-C. Electromagnetic actuator system using Witty control system. Actuators 2021, 10, 65. [Google Scholar] [CrossRef]
- Potena, C.; Khanna, R.; Nieto, J.; Siegwart, R.; Nardi, D.; Pretto, A. AgriColMap: Aerial-ground collaborative 3D mapping for precision farming. IEEE Robot. Autom. Lett. 2019, 4, 1086–1092. [Google Scholar] [CrossRef] [Green Version]
- Rezinkina, M.; Rezinkin, O.; Lytvynenko, S.; Tomashevskyi, R. Electromagnetic compatibility at UAVs usage for power transmission lines monitoring. In Proceedings of the IEEE International Conference Actual Problems of Unmanned Aerial Vehicles Developments, Kiev, Ukraine, 22–24 October 2019; pp. 157–160. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).