A Novel Design and Performance Evaluation Technique for a Spool-Actuated Pressure-Reducing Valve
Abstract
:1. Introduction
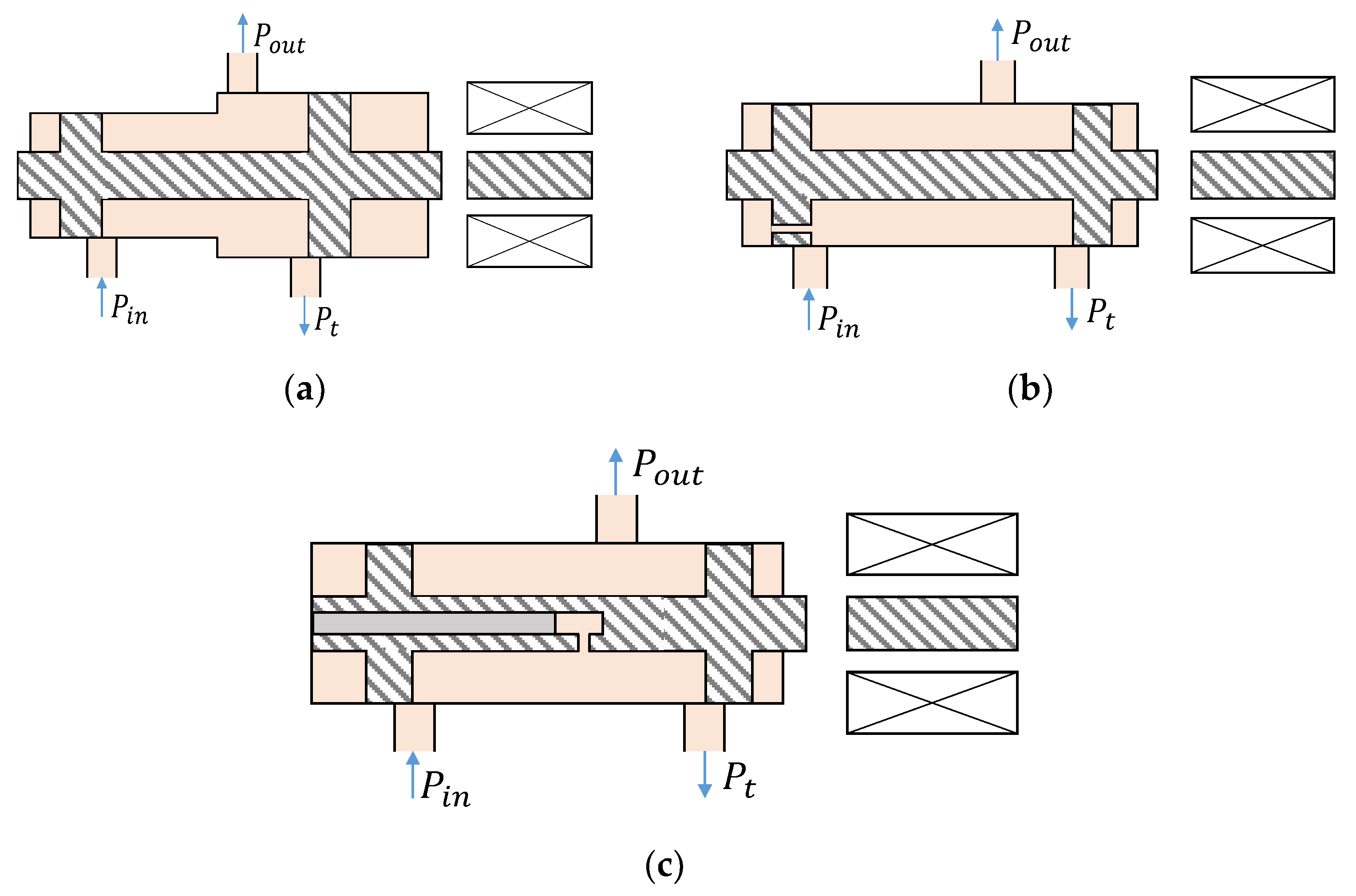
2. Types of Pressure-Reducing Valves Based on Spool Geometry
3. Mathematical Modeling
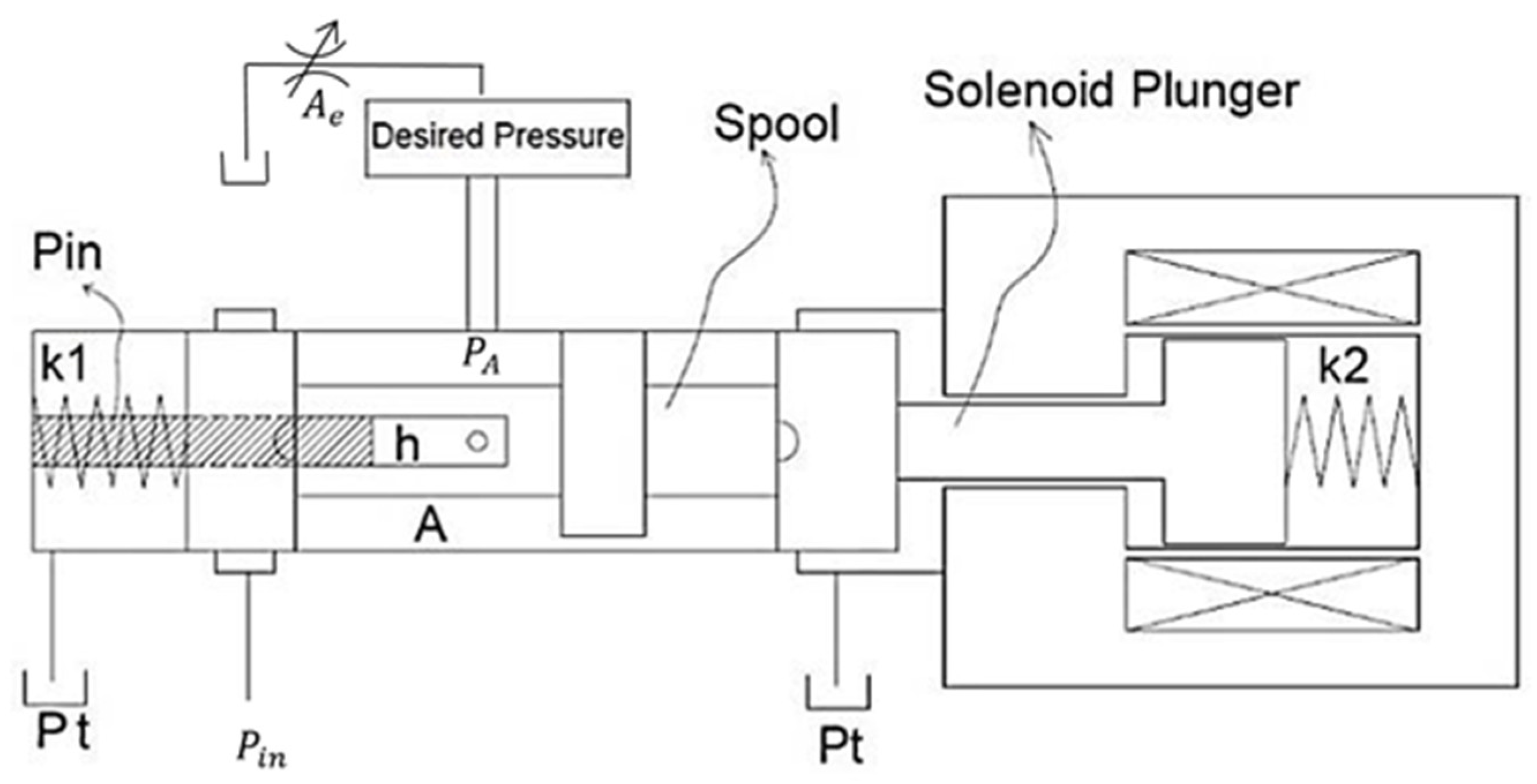
3.1. Details of the Valve Mechanism and Pin-Type Spool Actuator
3.2. Governing Equations
3.3. Assumptions and Simplification
- Initially, the spool position is centered, i.e., .
- As reflected in Equation (6), leakage flow through the pin-spool clearance is assumed to be fully developed and laminar due to its high length to cross-section ratio and small fluid velocity justified later through results.
- Temperature variations are ignored, and an operating temperature of 25 °C is used for the determination of oil properties.
- HLP-46 is used as the working fluid.
- All the edges are assumed to be perfectly sharp.
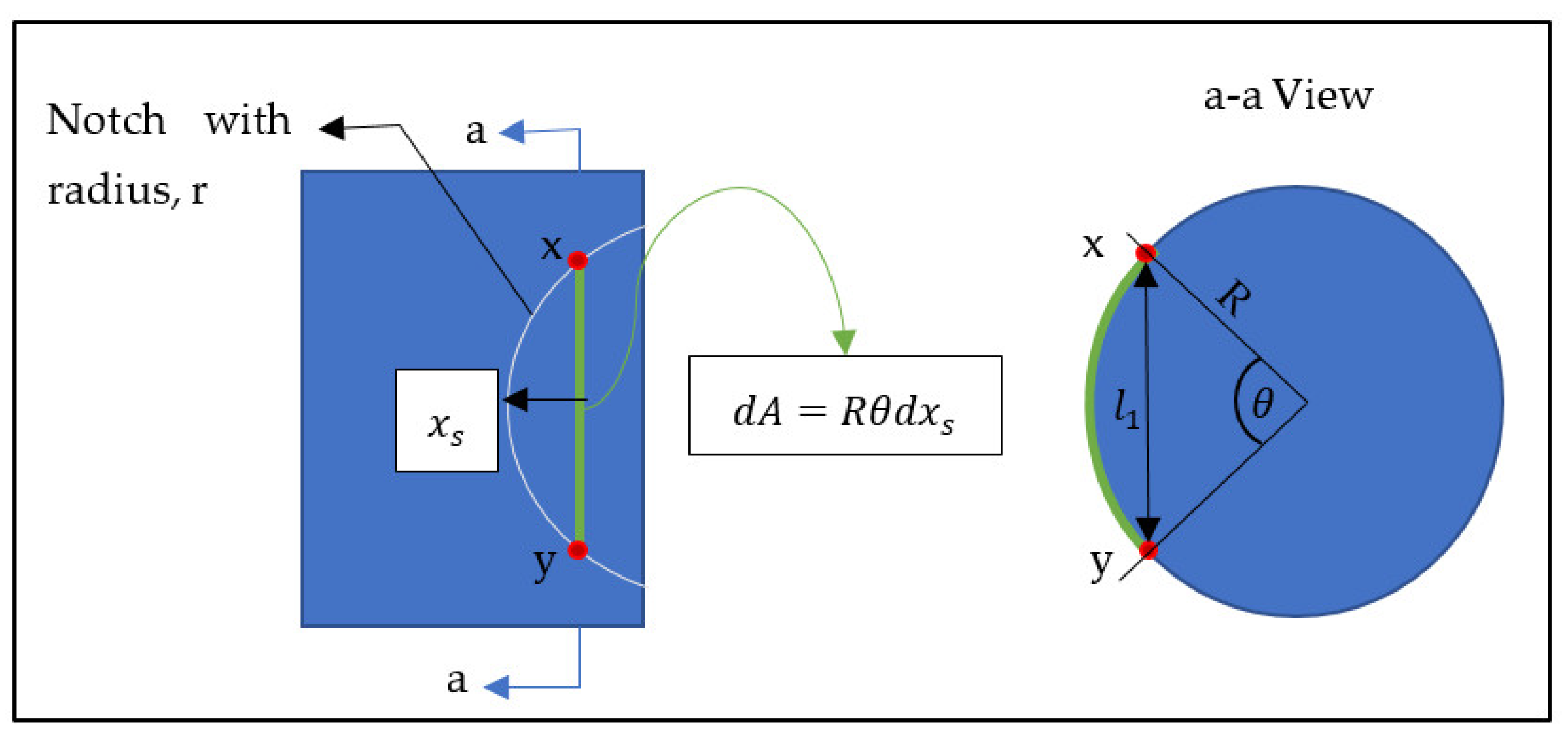
- The spool lands are perfectly round in shape with circular notches on each edge.
- The spatial pressure variation in Chamber A or Chamber h is negligible.
- Inlet pressure is assumed to be the same as that of the actual piston pump.
- The ratio of spool displacement to spool-sleeve clearance was assumed to be close to 1 in order to be consistent with the details given in Section 3.4.
3.4. Actual Valve Model Parameters
4. Modeling Using Simulink
5. Experimental Results for Use in Simulation
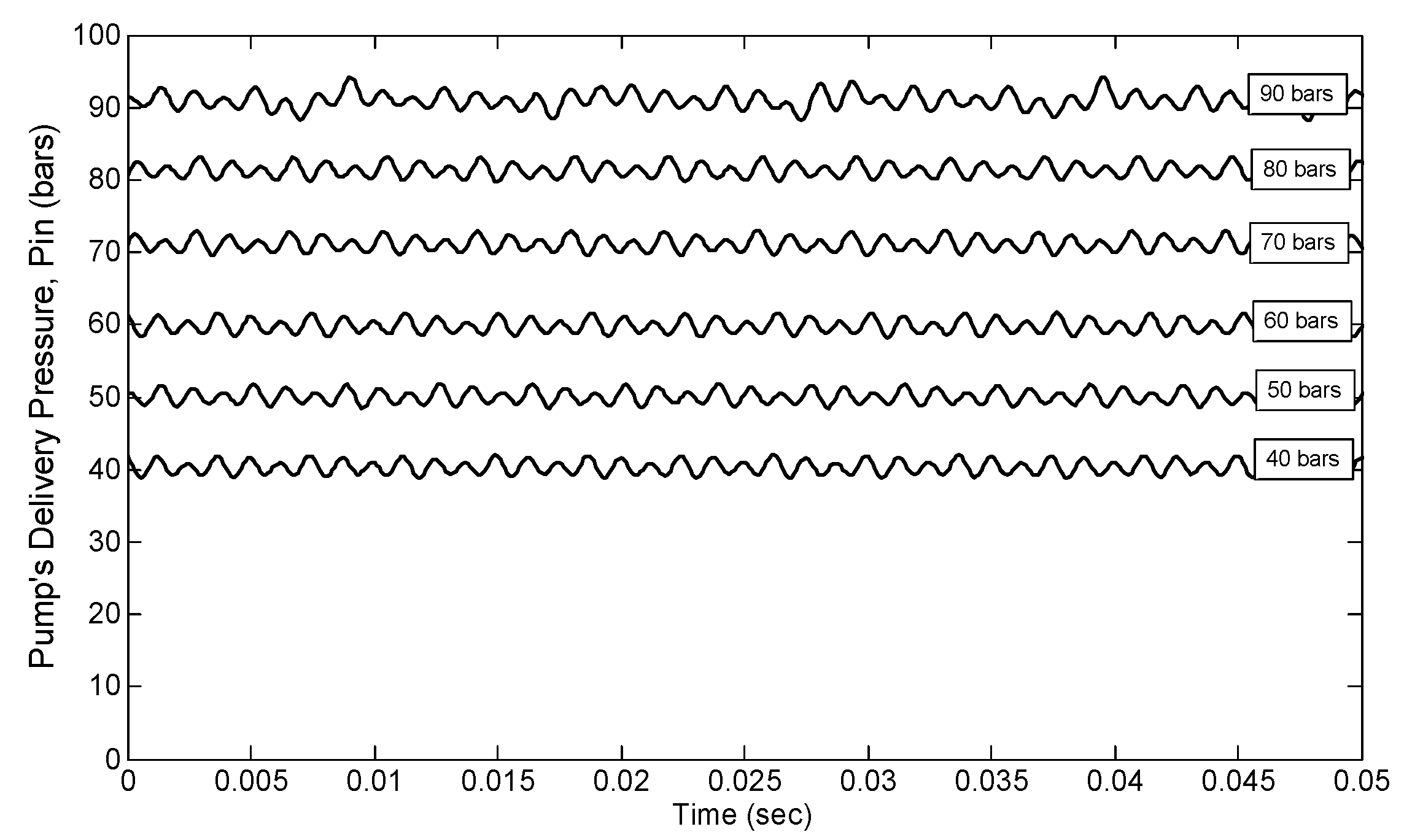
5.1. Test Setup for Pump Pressure Measurement
5.2. Pump Pressure Results
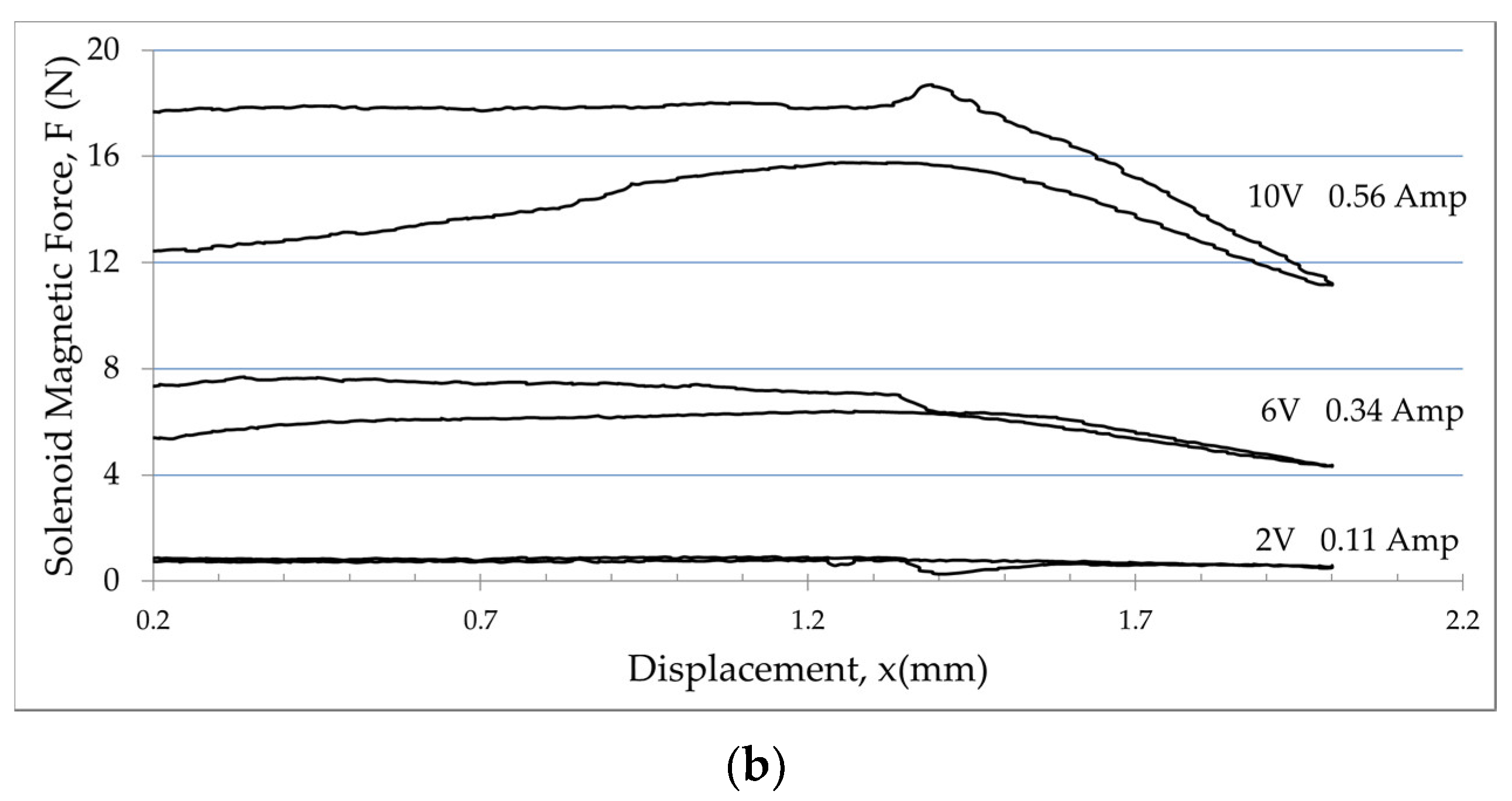
5.3. Solenoid Force Measurement
6. Simulation Results and Discussion
6.1. No Load-Flow Condition
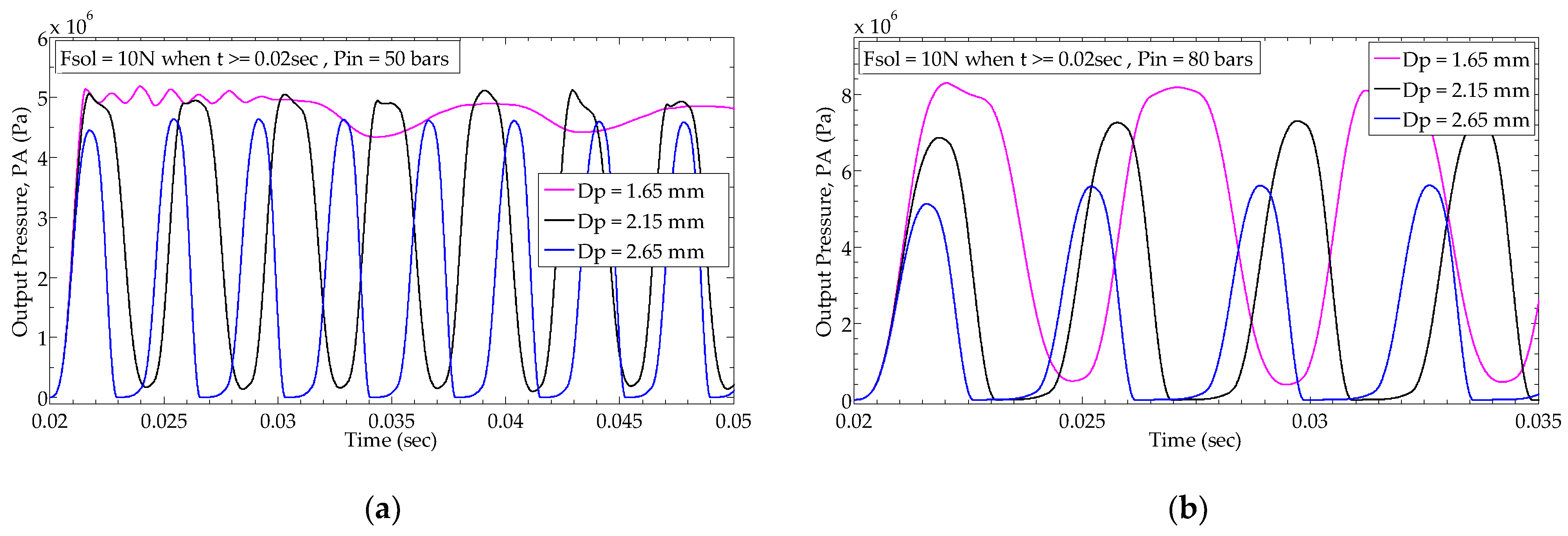
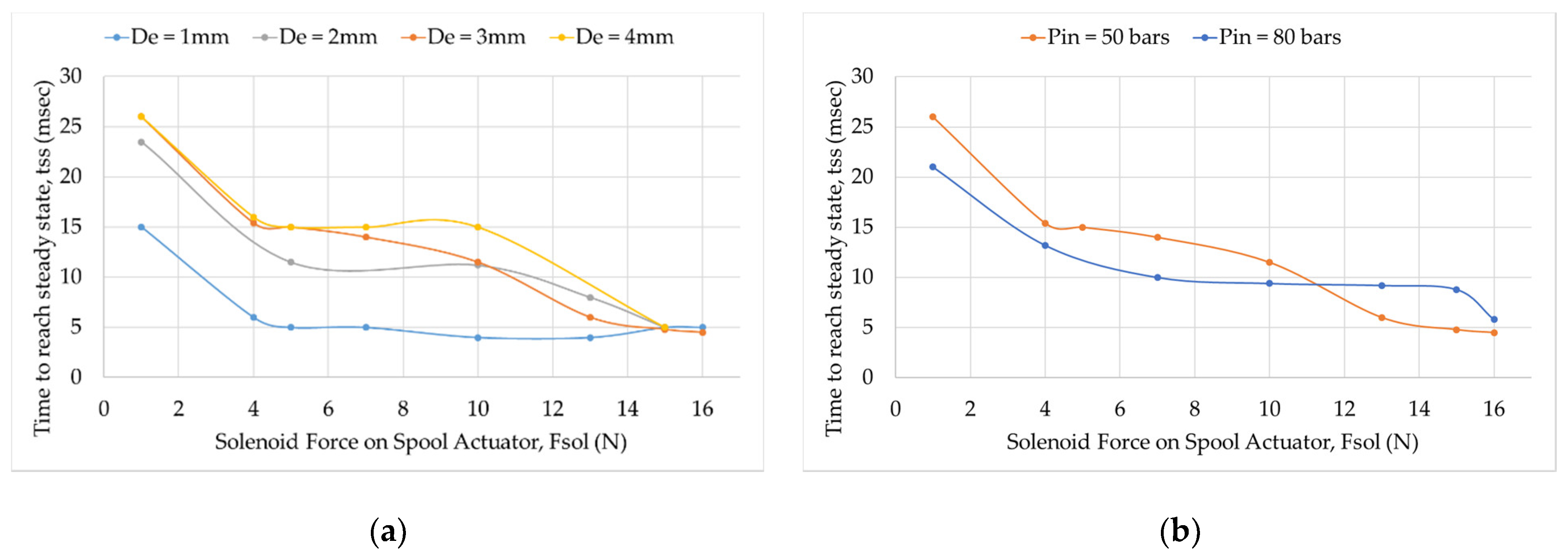
6.1.1. Criteria for Selection of Inlet Pressure and Pin Diameter
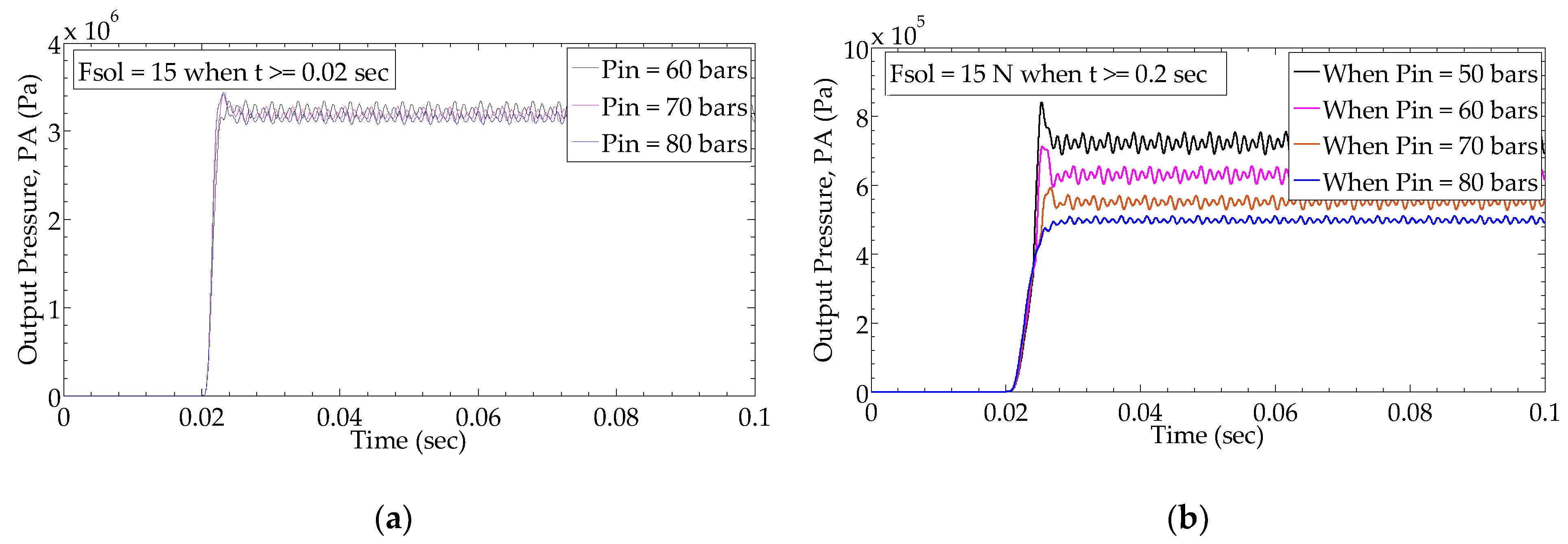
6.1.2. Influence of Pin Diameter and Inlet Pressure on Outlet Pressure
6.2. Results with Opened Outlet
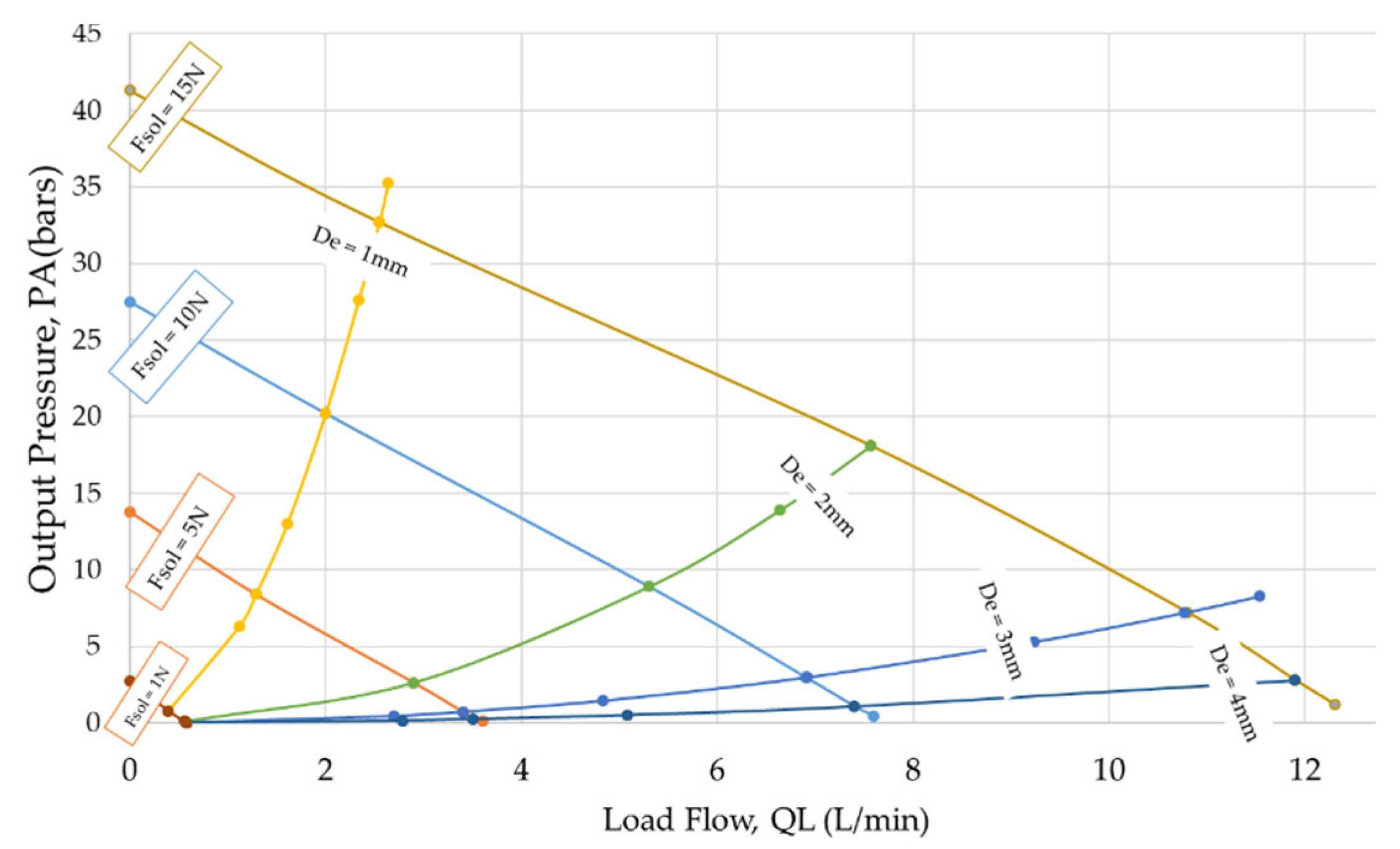
6.2.1. Steady-State Results
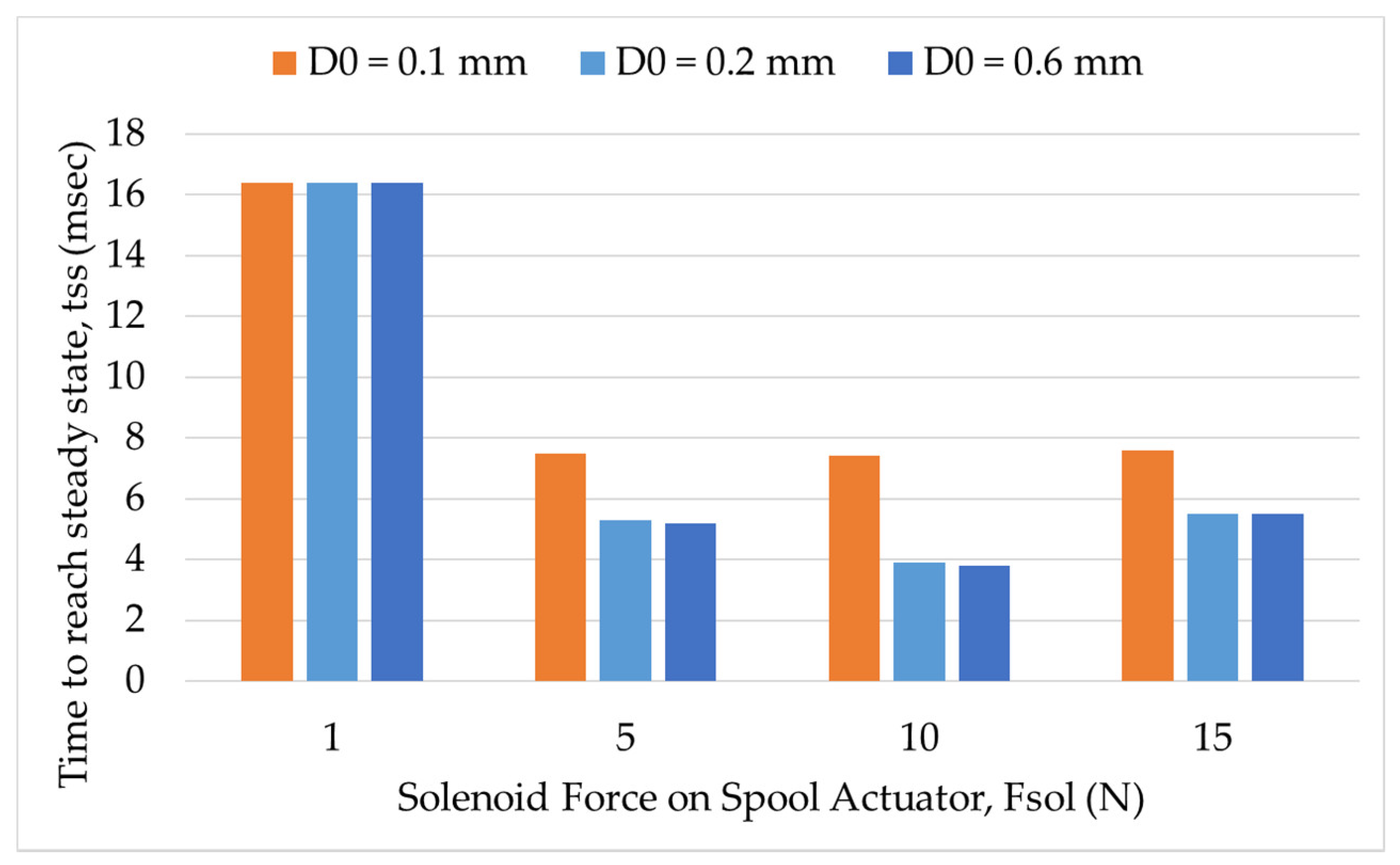
6.2.2. Step Response Results for Different Valve Openings and Inlet Pressure Settings
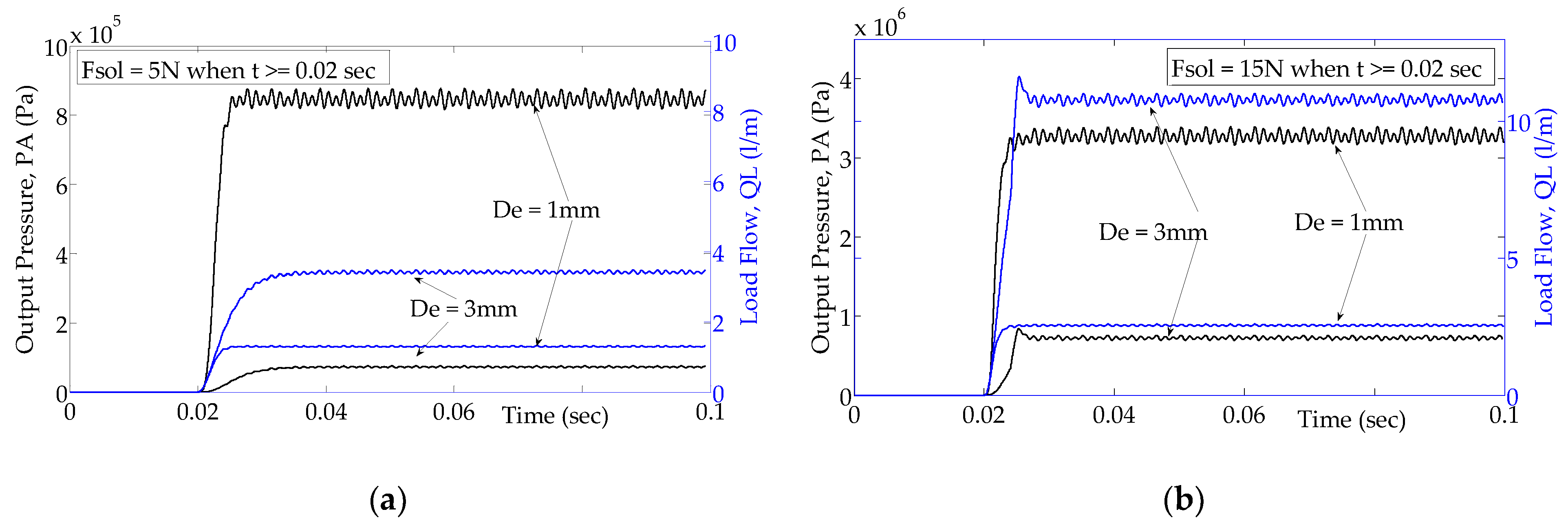
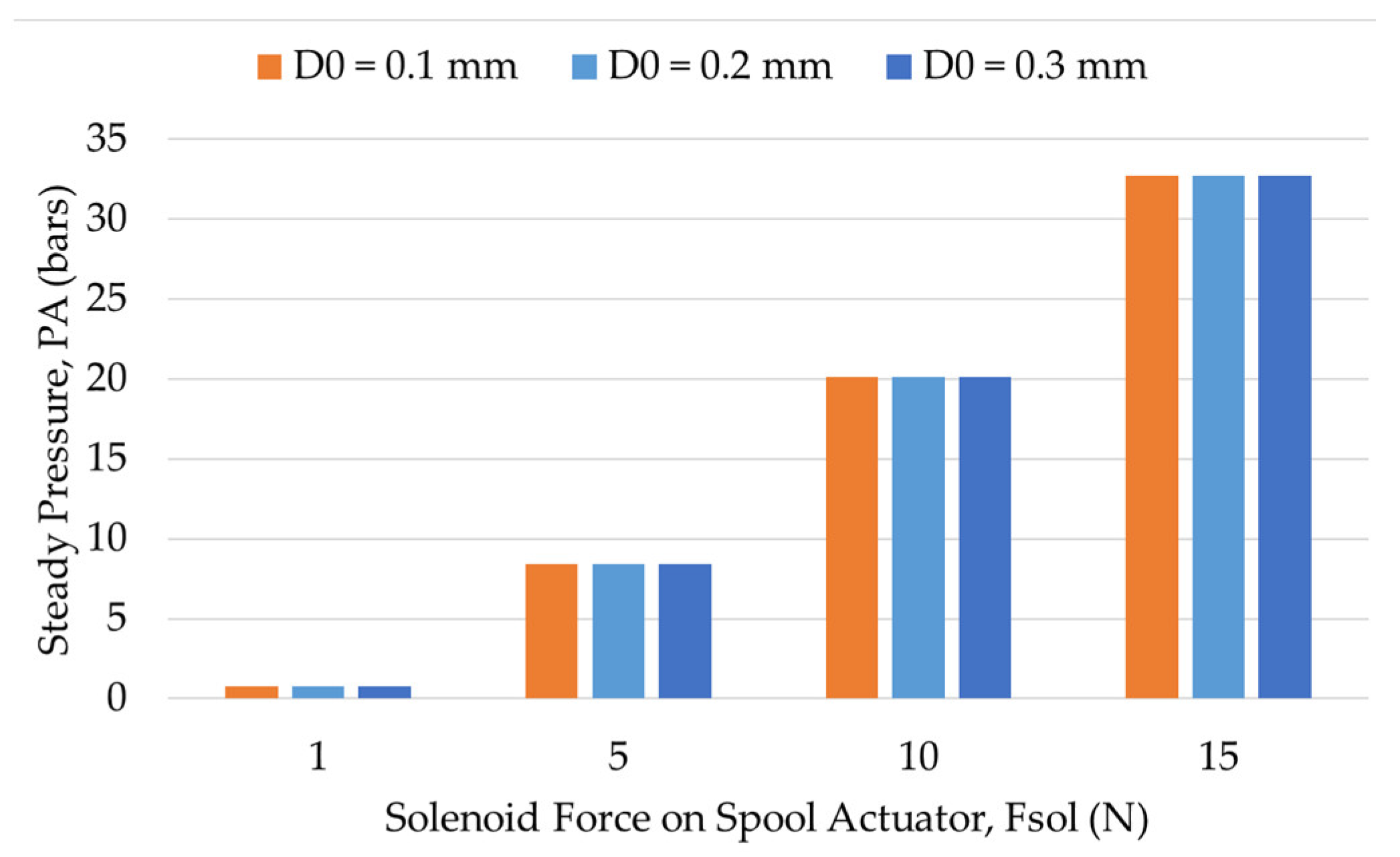
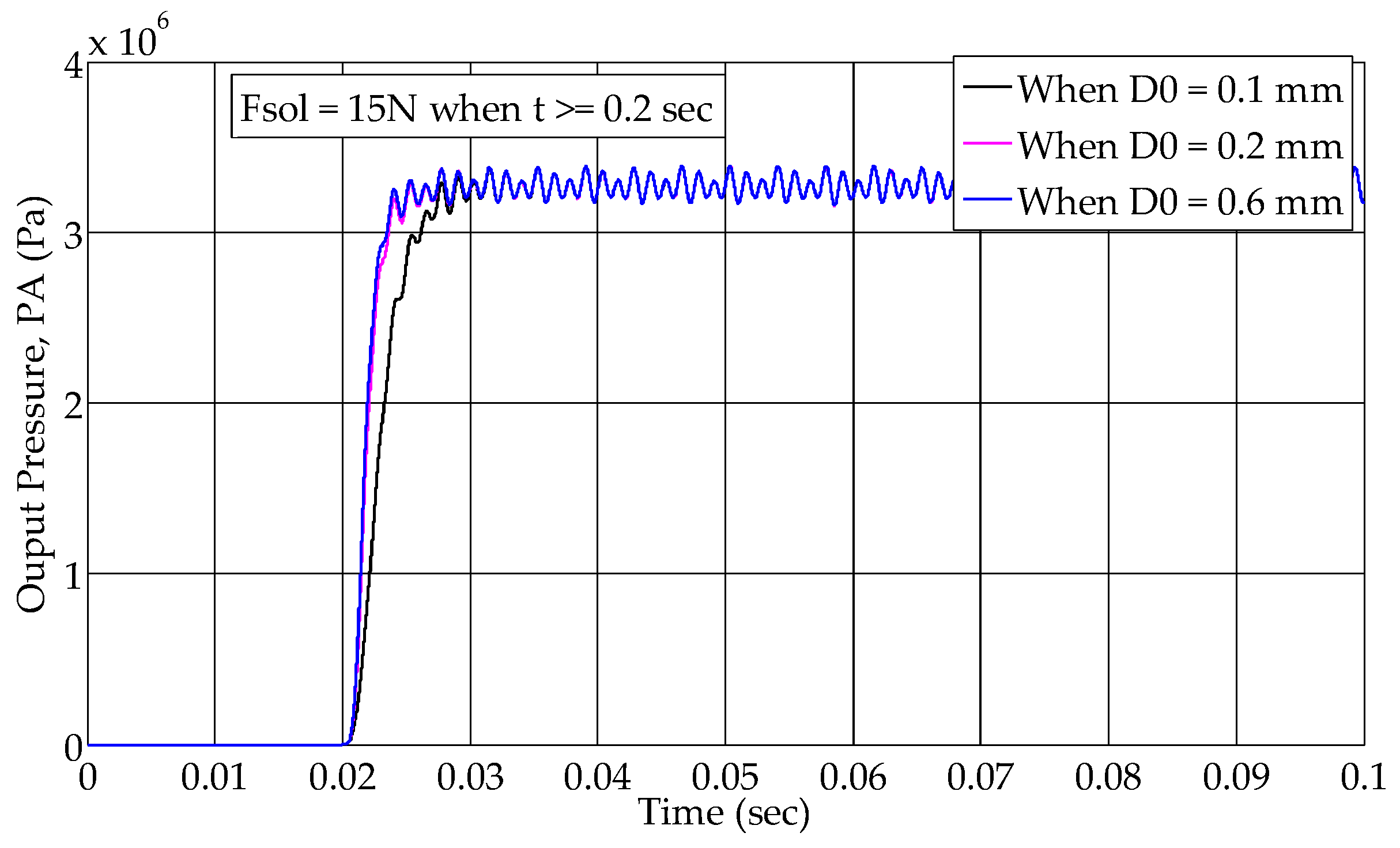
6.2.3. Influence of Damping Orifice on Output
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviation/Nomenclature
| Inlet flow rate | |
| Outlet flow rate | |
| Flow rate across the tank port | |
| Rate of flow into the pin-hole chamber | |
| Leakage flow through the pin-spool clearance | |
| Volume of valve chamber | |
| Bulk modulus of the working fluid | |
| Density of the working fluid | |
| Discharge coefficient | |
| Velocity coefficient, i.e., actual jet velocity divided by inviscid jet velocity | |
| Fluid jet angle with the spool axis | |
| Fluid pressure at the valve inlet | |
| Fluid pressure in the valve chamber | |
| Steady-state pressure in the valve chamber | |
| Fluid pressure in the pin-hole chamber | |
| Curtain area that allows fluid flow from the valve inlet to the valve chamber | |
| Curtain area that allows fluid flow from the valve chamber to the valve’s tank port | |
| Orifice area allowing flow between Chamber A and Chamber h | |
| Area of orifice installed at the valve’s outlet to simulate load flow | |
| Cross-sectional area of the pin | |
| Annular clearance flow area between spool and pin | |
| Radius of the spool land cross-section | |
| Radius of the notch on the spool land | |
| Spring constant of the spring to the left side of the spool | |
| Spring constant of the spring to the right side of the spool | |
| Spool displacement as in Figure 2 | |
| Mass of spool actuator | |
| Friction coefficient | |
| Axial length of the pin-hole chamber | |
| Damping length number 1 (from inlet spool land to outlet) | |
| Damping length number 2 (from outlet spool land to tank port) | |
| Electromagnetic force exerted by the solenoid | |
| Time taken by the output pressure to reach the average steady value after step input is applied |
Appendix A
References
- Slama, V.; Mrozek, L.; Tajc, L.; Klimko, M.; Zitek, P. Flow Analysis in a Steam Turbine Control Valve with Through-Flow Valve Chamber. J. Nucl. Eng. Radiat. Sci. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Wu, D.; Li, S.; Wu, P. CFD simulation of flow-pressure characteristics of a pressure control valve for automotive fuel supply system. Energy Convers. Manag. 2015, 101, 658–665. [Google Scholar] [CrossRef]
- Frosina, E.; Senatore, A.; Buono, D.; Stelson, K.A. A Modeling Approach to Study the Fluid-Dynamic Forces Acting on the Spool of a Flow Control Valve. J. Fluids Eng. 2017, 139, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Sánchez, M.; López-Jiménez, A.P.; Ramos, M.H. PATs operating in water networks under unsteady flow conditions: Control valve manoeuvre and overspeed effect. J. Water (Switzerland) 2018, 10, 529. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Cheng, M. Motion control of multi-actuator hydraulic systems for mobile machineries: Recent advancements and future trends. Front. Mech. Eng. 2017, 13, 151–166. [Google Scholar] [CrossRef]
- Fang, X.; Ouyang, X.; Yang, H. Investigation into the Effects of the Variable Displacement Mechanism on Swash Plate Oscillation in High-Speed Piston Pumps. Appl. Sci. 2018, 8, 658. [Google Scholar] [CrossRef] [Green Version]
- Jung, D.-S.; Kim, H.-E.; Kang, E.-S. Multi-function Control of Hydraulic Variable Displacement Pump with EPPR Valve. Trans. Korean Soc. Automot. Eng. 2006, 14, 160–170. [Google Scholar]
- Jin, Z.-J.; Chen, F.-Q.; Qian, J.-Y.; Zhang, M.; Chen, L.-L.; Wang, F.; Fei, Y. Numerical analysis of flow and temperature characteristics in a high multi-stage pressure reducing valve for hydrogen refueling station. Int. J. Hydrogen Energy 2016, 41, 5559–5570. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A Review of High-Speed Electro-Hydrostatic Actuator Pumps in Aerospace Ap-plications: Challenges and Solutions. J. Mech. Des. Trans. ASME 2019, 141, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Carravetta, A.; Chacon, C.M.; Fecarotta, O.; McNabola, A.; Ramos, M.H. Chapter 13—Energy harvesting in water supply systems. In Sustainable Water Engineering; Charlesworth, S., Booth, C., Adeyeye, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 229–254. [Google Scholar]
- Balau, A.E.; Caruntu, C.F.; Patrascu, D.I.; Lazar, C.; Matcovschi, M.H.; Pastravanu, O.; Lazǎr, C. Modeling of a pressure reducing valve actuator for automotive applications. In Proceedings of the 2009 IEEE International Conference on Control Applications, Saint Petersburg, Russia, 8–10 July 2009; pp. 1356–1361. [Google Scholar]
- He, X.; Zhao, D.; Sun, X.; Zhu, B. Theoretical and Experimental Research on a Three-Way Water Hydraulic Pressure Reducing Valve. J. Press. Vessel. Technol. 2017, 139, 1–9. [Google Scholar] [CrossRef]
- Janus, T.; Ulanicki, B. Improving Stability of Electronically Controlled Pressure-Reducing Valves through Gain Compensation. J. Hydraul. Eng. 2018, 144, 1–13. [Google Scholar] [CrossRef]
- Ulanicki, B.; Skworcow, P. Why PRVs Tends to Oscillate at Low Flows. Procedia Eng. 2014, 89, 378–385. [Google Scholar] [CrossRef] [Green Version]
- Prescott, S.L.; Ulanicki, B. Dynamic Modeling of Pressure Reducing Valves. J. Hydraul. Eng. 2003, 129, 804–812. [Google Scholar] [CrossRef]
- Meniconi, S.; Brunone, B.; Mazzetti, E.; Laucelli, D.B.; Borta, G. Hydraulic characterization and transient response of pressure reducing valves: Laboratory experiments. J. Hydroinform. 2017, 19, 798–810. [Google Scholar] [CrossRef]
- Aung, Z.N.; Peng, J.; Li, S. Reducing the steady flow force acting on the spool by using a simple jet-guiding groove. In Proceedings of the 2015 International Conference on Fluid Power and Mechatronics (FPM), Harbin, China, 5–7 August 2015; pp. 289–294. [Google Scholar]
- Stone, J.A. Discharge Coefficients and Steady-State Flow Forces for Hydraulic Poppet Valves. J. Basic Eng. 1960, 82, 144–154. [Google Scholar] [CrossRef]
- Yun, S.-N.; Lee, Y.-L.; Khan, H.A.; Kang, C.-N.; Ham, Y.-B.; Park, J.-H. Proportional Flow Control Valve for Construction Vehicle. In Proceedings of the 2019 23rd International Conference on Mechatronics Technology (ICMT), Salerno, Italy, 23–26 October 2019; pp. 1–3. [Google Scholar]
- Khan, H.A.; Yun, S.-N. Modeling and Simulation of an EPPR Valve Coupled with a Spool Valve. J. Drive Control 2019, 16, 30–35. [Google Scholar]
- Munson, R.B.; Young, F.D. Fundamentals of Fluid Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Merritt, E.H. Hydraulic Control Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1967. [Google Scholar]
- Choose an ODE Solver. Available online: https://www.mathworks.com/help/matlab/math/choose-an-ode-solver.html#bu7wegm-1 (accessed on 1 August 2021).
- Baker, T.; Dormand, J.; Gilmore, J.; Prince, P. Continuous approximation with embedded Runge-Kutta methods. Appl. Numer. Math. 1996, 22, 51–62. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. Soc. Ind. Appl. Math. 1997, 18, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Dormand, J.; Prince, P. A reconsideration of some embedded Runge–Kutta formulae. J. Comput. Appl. Math. 1986, 15, 203–211. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Li, X.; Li, B.; Jia, X.-Q.; Zhu, Z. Influence of Impeller Sinusoidal Tubercle Trailing-Edge on Pressure Pulsation in a Centrifugal Pump at Nominal Flow Rate. J. Fluids Eng. 2021, 143, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, T.; Tan, C.; Fu, J.; Guo, S. Research Status, Critical Technologies, and Development Trends of Hydraulic Pressure Pulsation Attenuator. Chin. J. Mech. Eng. 2021, 34, 1–17. [Google Scholar] [CrossRef]
- Masuda, S.; Shimizu, F.; Fuchiwaki, M.; Tanaka, K. Modelling and Reducing Fuel Flow Pulsation of a Fuel-Metering System by Improving Response of the Pressure Control Valve During Pump Mode Switching in a Turbofan Engine. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019; Volume 240, pp. 1–10. [Google Scholar]
- Ye, J.; Zeng, W.; Zhao, Z.; Yang, J.; Yang, J. Optimization of pump turbine closing operation to minimize water hammer and pulsating pressures during load rejection. Energies 2020, 13, 1000. [Google Scholar] [CrossRef] [Green Version]
- Bostan, M.; Akhtari, A.A.; Bonakdari, H.; Gharabaghi, B.; Noori, O. Investigation of a new shock damper system efficiency in reducing water hammer excess pressure due to the sudden closure of a control valve. ISH J. Hydraul. Eng. 2020, 26, 258–266. [Google Scholar] [CrossRef]
- Hosseini, R.S.; Ahmadi, A.; Zanganeh, R. Fluid-structure interaction during water hammer in a pipeline with different per-formance mechanisms of viscoelastic supports. J. Sound Vib. 2020, 487, 1–26. [Google Scholar] [CrossRef]
- Liao, Y.; Lian, Z.; Feng, J.; Yuan, H.; Zhao, R. Effects of multiple factors on water hammer induced by a large flow directional valve. J. Mech. Eng. 2018, 64, 329–338. [Google Scholar]
- Brunone, B.; Morelli, L. Automatic Control Valve–Induced Transients in Operative Pipe System. J. Hydraul. Eng. 1999, 125, 534–542. [Google Scholar] [CrossRef]
- Wei, W.; Jian, H.; Yan, Q.; Luo, X.; Wu, X. Nonlinear modeling and stability analysis of a pilot-operated valve-control hydraulic system. Adv. Mech. Eng. 2018, 10, 1–8. [Google Scholar] [CrossRef]
- Jian, H.; Wei, W.; Li, H.; Yan, Q. Optimization of a pressure control valve for high power automatic transmission considering stability. Mech. Syst. Signal Process. 2018, 101, 182–196. [Google Scholar] [CrossRef]
- Zhou, F.; Gu, L.; Chen, Z. Model Linearization and Stability Analysis of Thruster System Controlled by Proportional Pressure Reducing Valves. Jixie Gongcheng Xuebao/J. Mech. Eng. J. 2017, 53, 187–194. [Google Scholar] [CrossRef]
- Janus, T.; Ulanicki, B. Hydraulic Modelling for Pressure Reducing Valve Controller Design Addressing Disturbance Rejection and Stability Properties. Procedia Eng. 2017, 186, 635–642. [Google Scholar] [CrossRef]
- Hayashi, S.; Hayase, T.; Kurahashi, T. Chaos in hydraulic control valve. J. Fluids Struct. 1997, 11, 693–716. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, B.; Zhu, Y.; Li, Z. Flow and cavitation characteristics of a damping orifice in water hydraulics. Proc. Inst. Mech. Eng. Part A J. Power Energy 2006, 220, 933–942. [Google Scholar]
- Watton, J. The Effect of Drain Orifice Damping on the Performance Characteristics of a Servovalve Flapper/Nozzle Stage. J. Dyn. Syst. Meas. Control 1987, 109, 19–23. [Google Scholar] [CrossRef]




| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 4 mm | |||
| 1 mm | |||
| 3000 N/m | |||
| 0.62 | 1840 N/m | ||
| 0.98 | 32 g | ||
| 80 Ns/m | |||
| 50 bar (approximately) | 9 mm | ||
| 10 mm | |||
| 8 mm |
| Model | PCH-100K | Safe Over Load | 150% of Rated Current |
|---|---|---|---|
| Capacity | 100 bar | Non-linearity | 0.2% of rated output |
| Rated Output | 1.503 mV/V | Hysteresis | 0.2% of rated output |
| Model | LRM-100N | Safe Over Load | 120% of Rated Current |
|---|---|---|---|
| Capacity | 100 N | Non-linearity | 0.05% of rated output |
| Rated Output | 1.5 mV/V | Hysteresis | 0.05% of rated output |
| 10 N | 1.65 mm | 46.8 bar | 50 bar or greater |
| 2.15 mm | 27.5 bar | 30 bar or greater | |
| 2.65 mm | 18.1 bar | 20 bar or greater | |
| 15 N | 1.65 mm | 70.2 bar | 70 bar or greater |
| 2.15 mm | 41.3 bar | 50 bar or greater | |
| 2.65 mm | 27.2 bar | 30 bar or greater |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.A.; Yun, S.-N.; Jeong, E.-A.; Park, J.-W.; Choi, B.-I. A Novel Design and Performance Evaluation Technique for a Spool-Actuated Pressure-Reducing Valve. Actuators 2021, 10, 232. https://doi.org/10.3390/act10090232
Khan HA, Yun S-N, Jeong E-A, Park J-W, Choi B-I. A Novel Design and Performance Evaluation Technique for a Spool-Actuated Pressure-Reducing Valve. Actuators. 2021; 10(9):232. https://doi.org/10.3390/act10090232
Chicago/Turabian StyleKhan, Haroon Ahmad, So-Nam Yun, Eun-A Jeong, Jeong-Woo Park, and Byung-Il Choi. 2021. "A Novel Design and Performance Evaluation Technique for a Spool-Actuated Pressure-Reducing Valve" Actuators 10, no. 9: 232. https://doi.org/10.3390/act10090232
APA StyleKhan, H. A., Yun, S.-N., Jeong, E.-A., Park, J.-W., & Choi, B.-I. (2021). A Novel Design and Performance Evaluation Technique for a Spool-Actuated Pressure-Reducing Valve. Actuators, 10(9), 232. https://doi.org/10.3390/act10090232






