Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm
Abstract
:1. Introduction
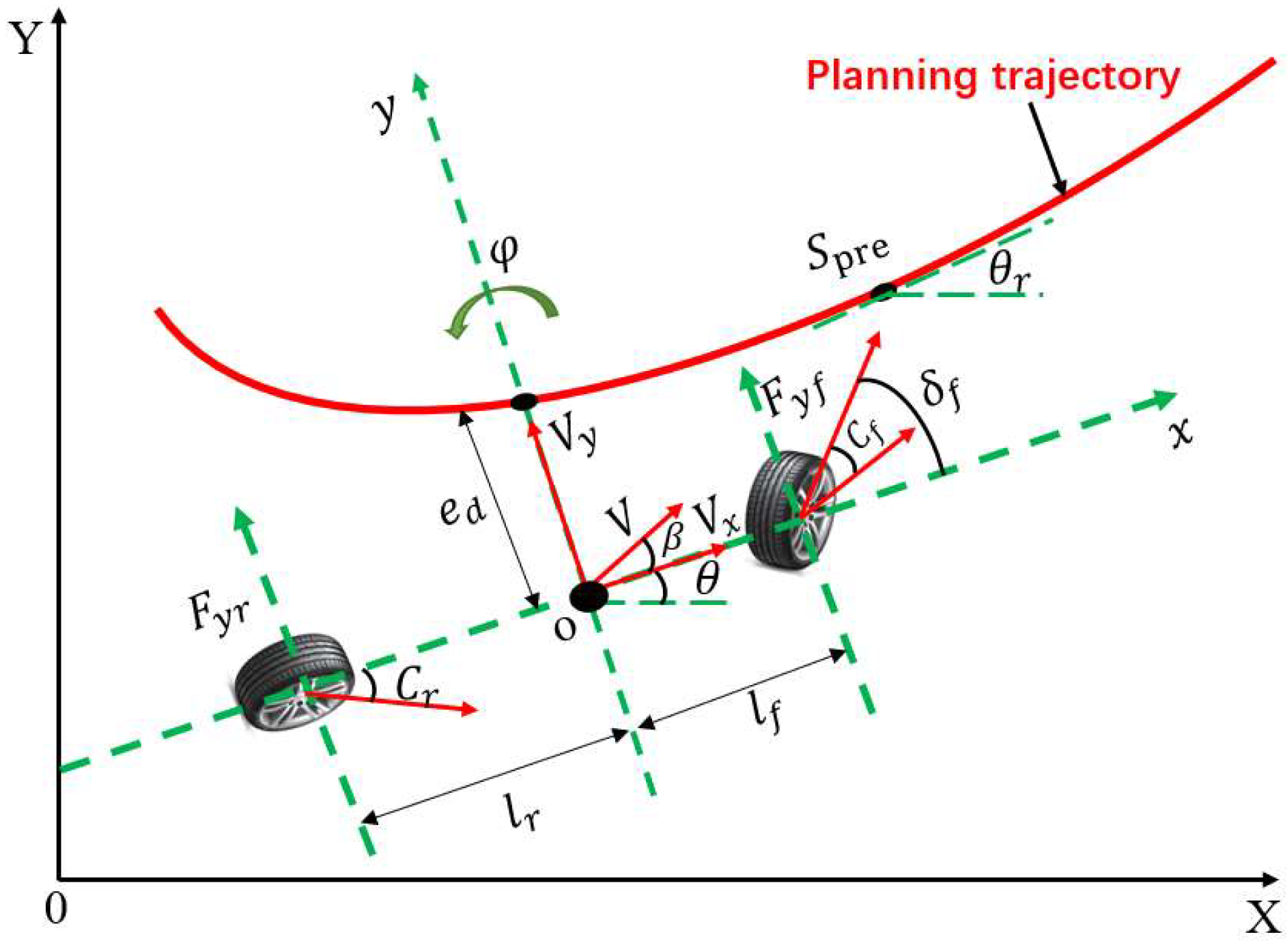
2. Establishment of a Vehicle Dynamics Model
Vehicle Dynamics Tracking Error Model
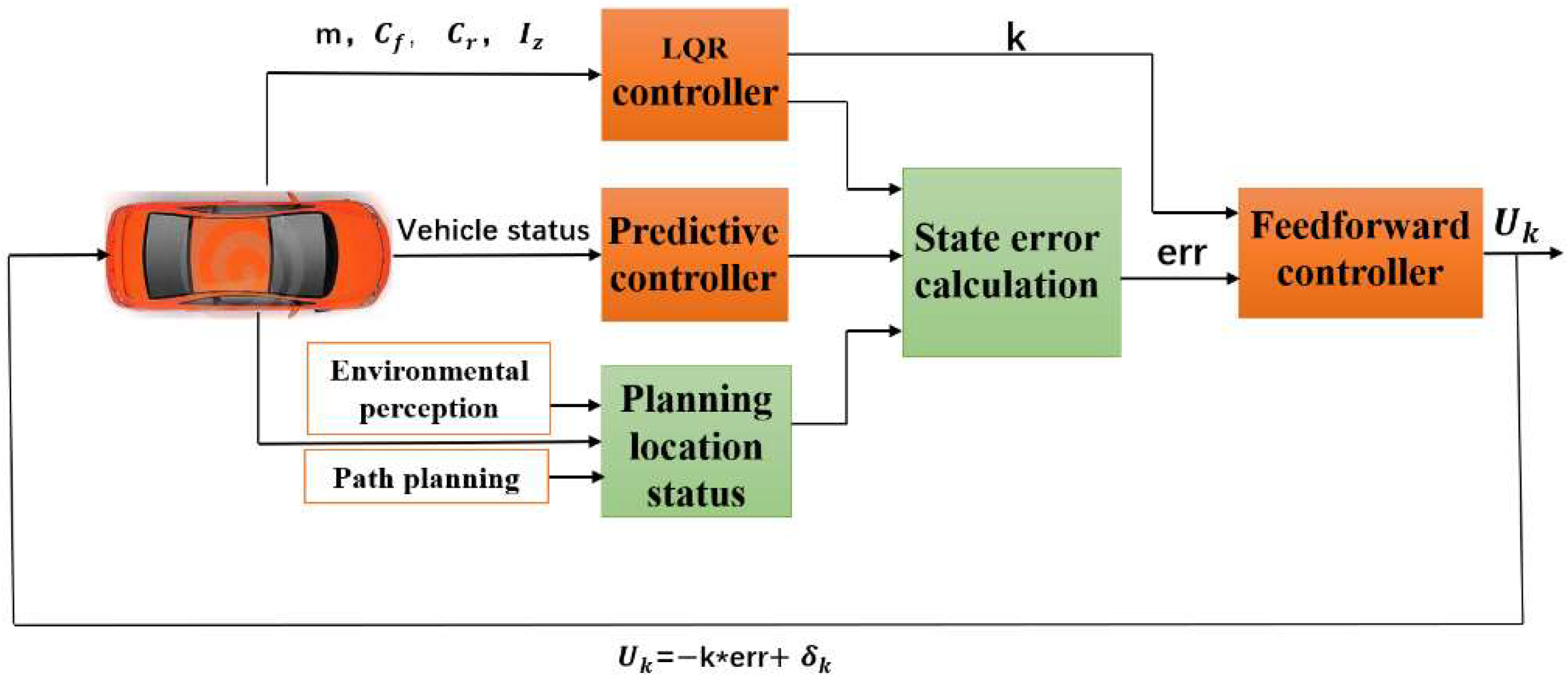
3. Lateral Control System Design
3.1. LQR Controller Design
3.2. Feedforward Controller Design
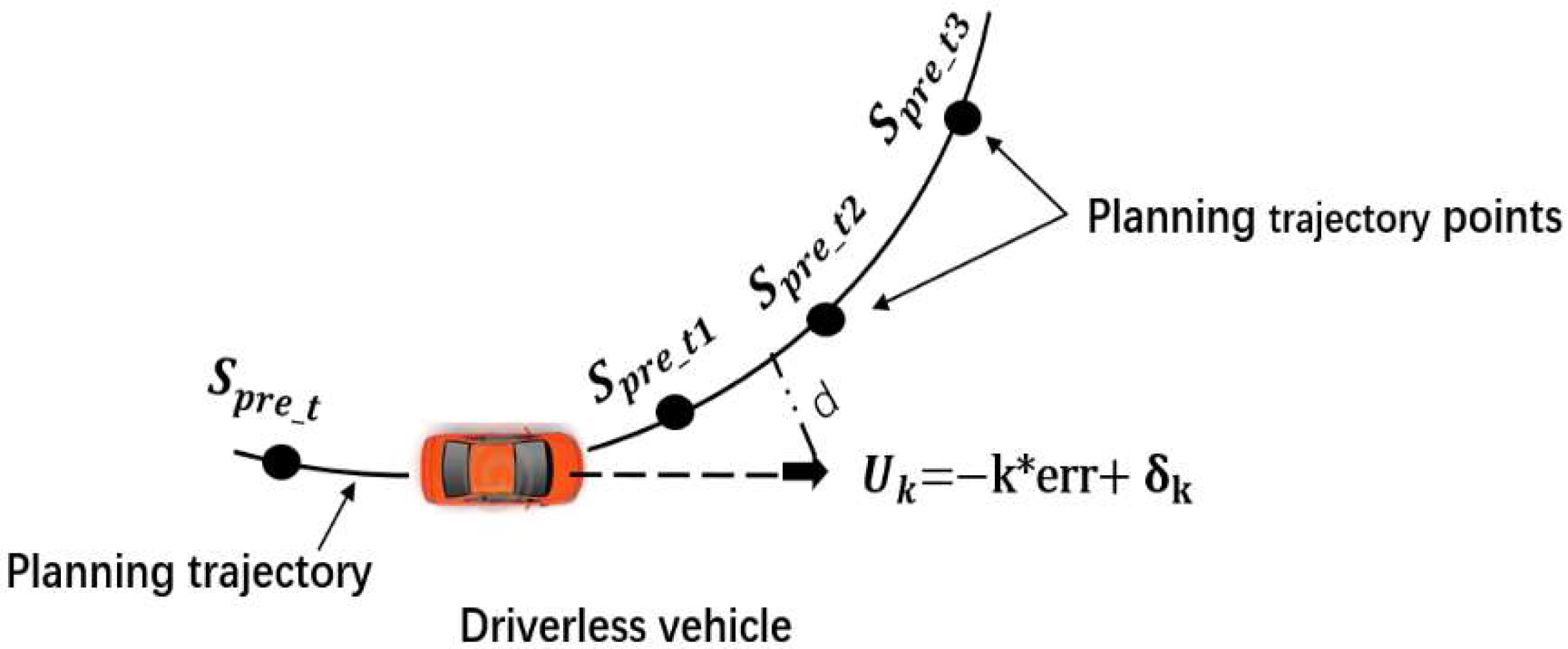
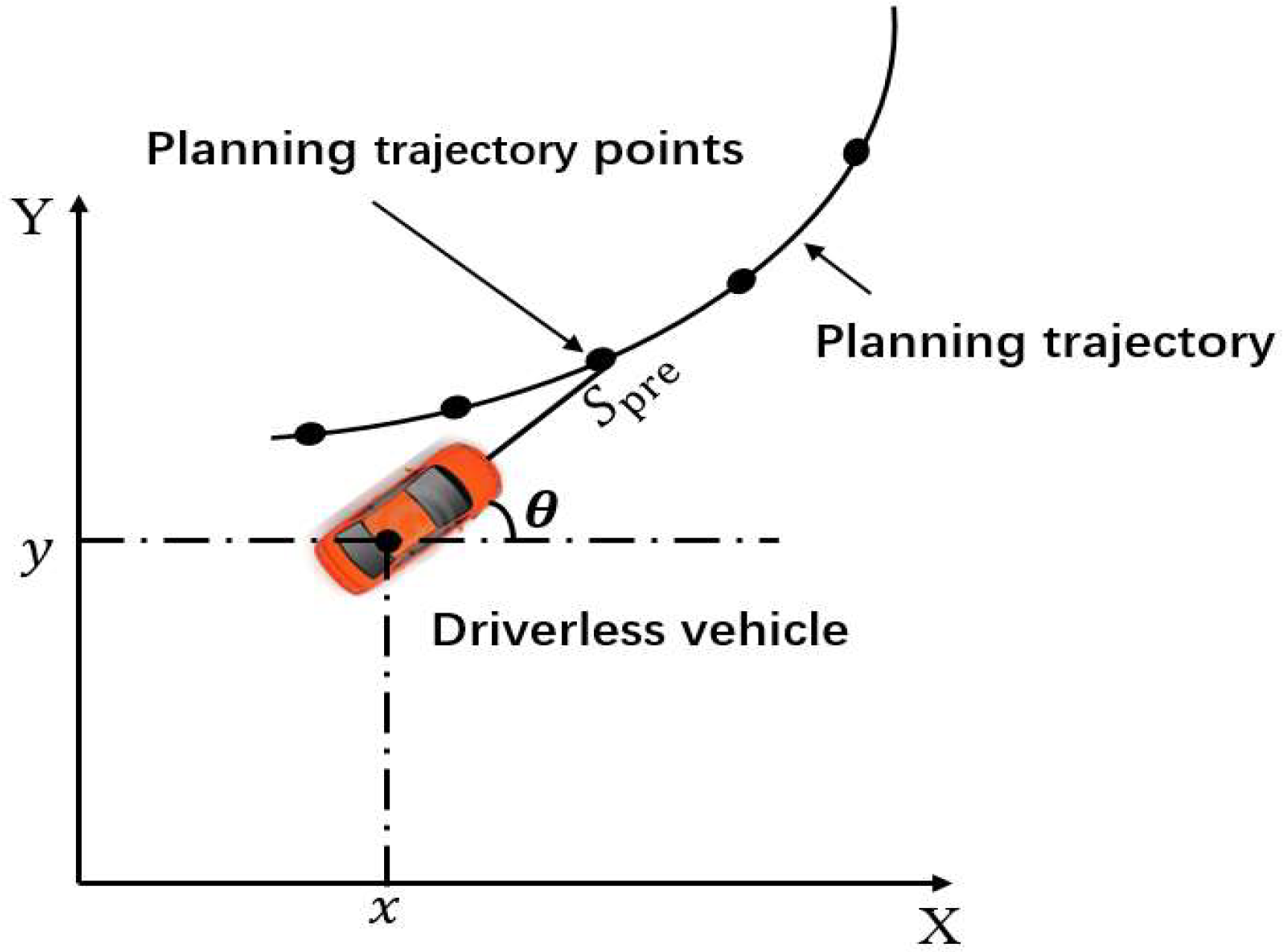
3.3. Predictive Controller Design
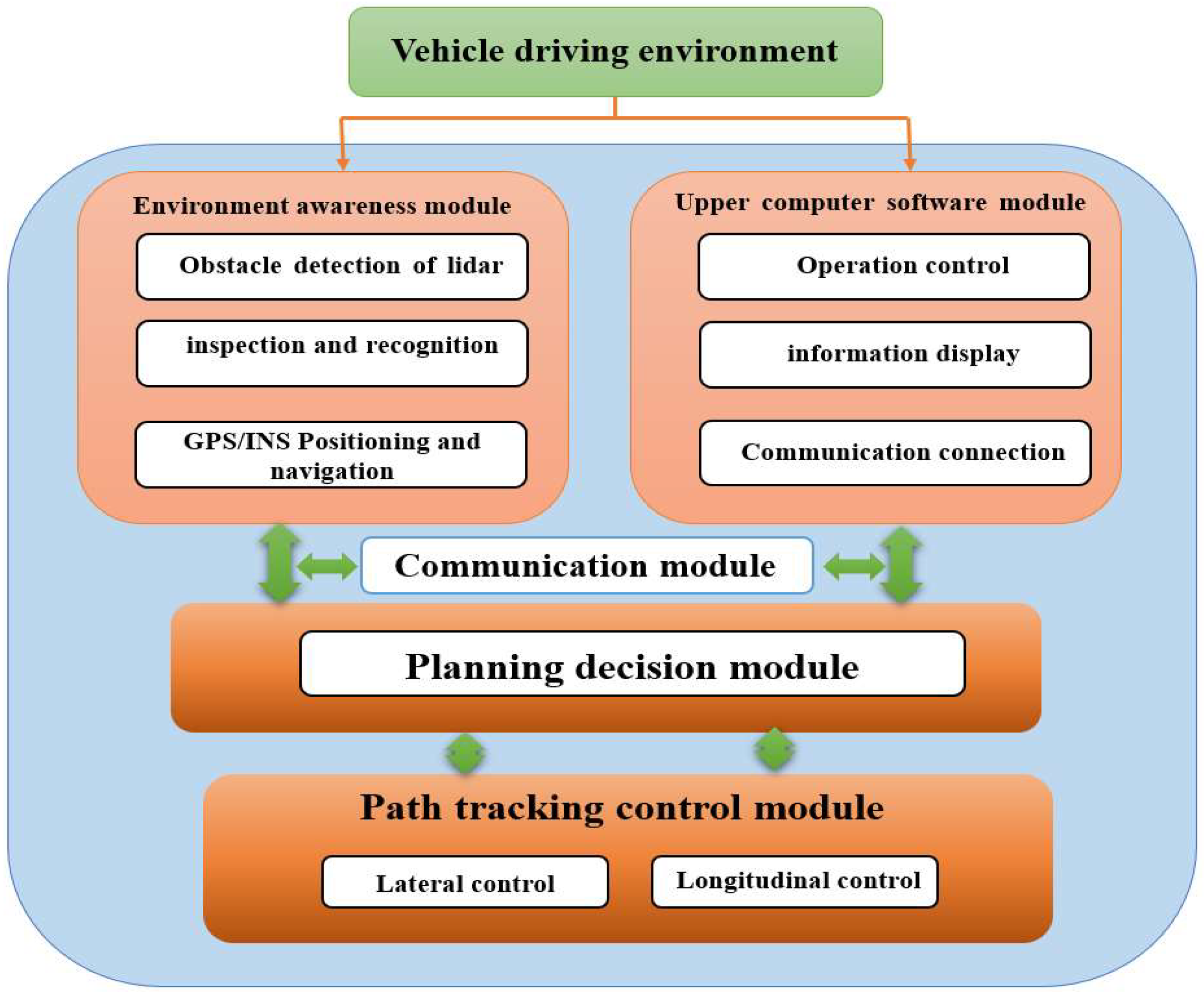
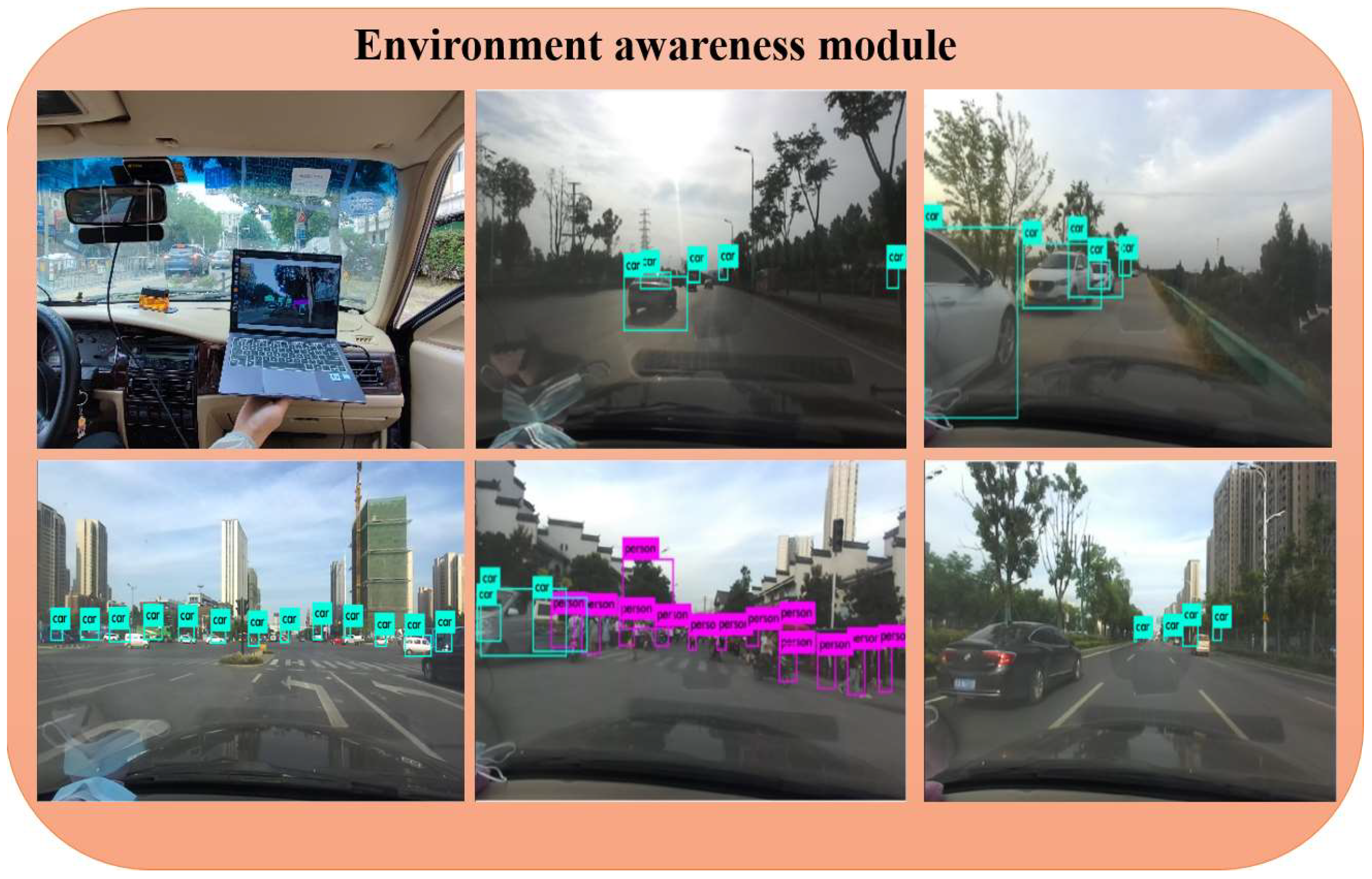
3.4. Establishment of Environmental Awareness System
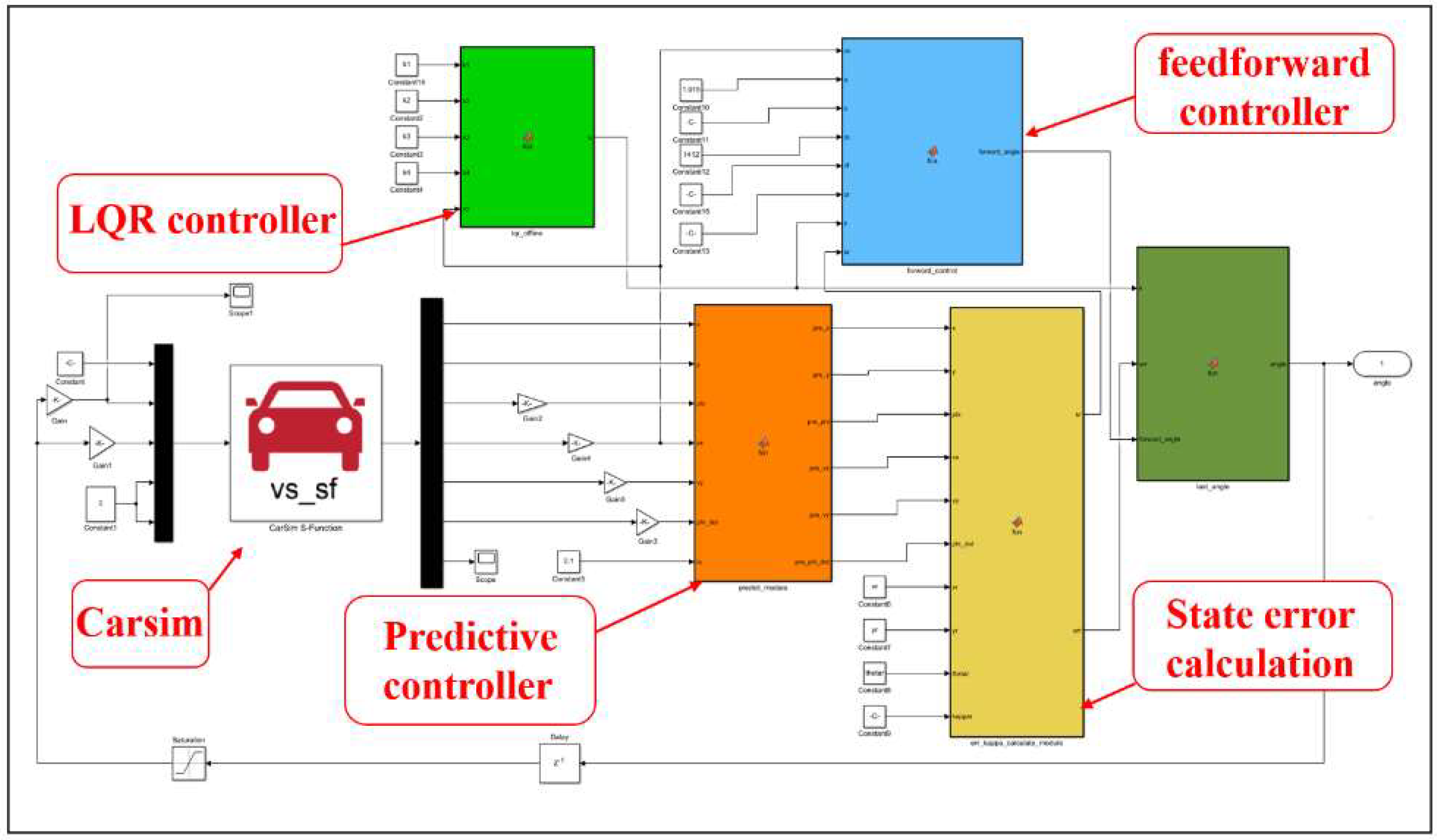
4. Simulation and Hardware in the Loop Test
4.1. Simulation Test and Analysis under Different Working Conditions
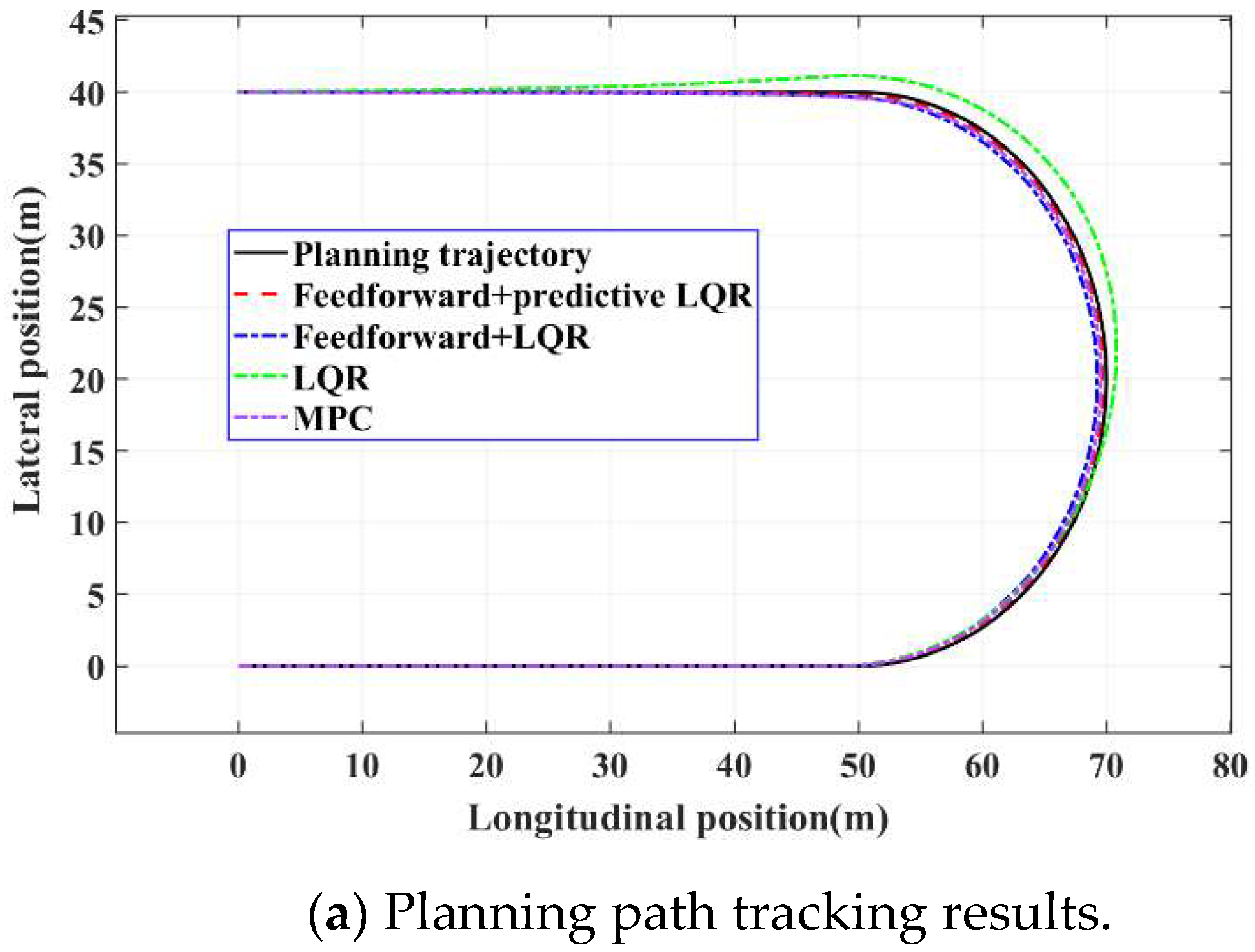
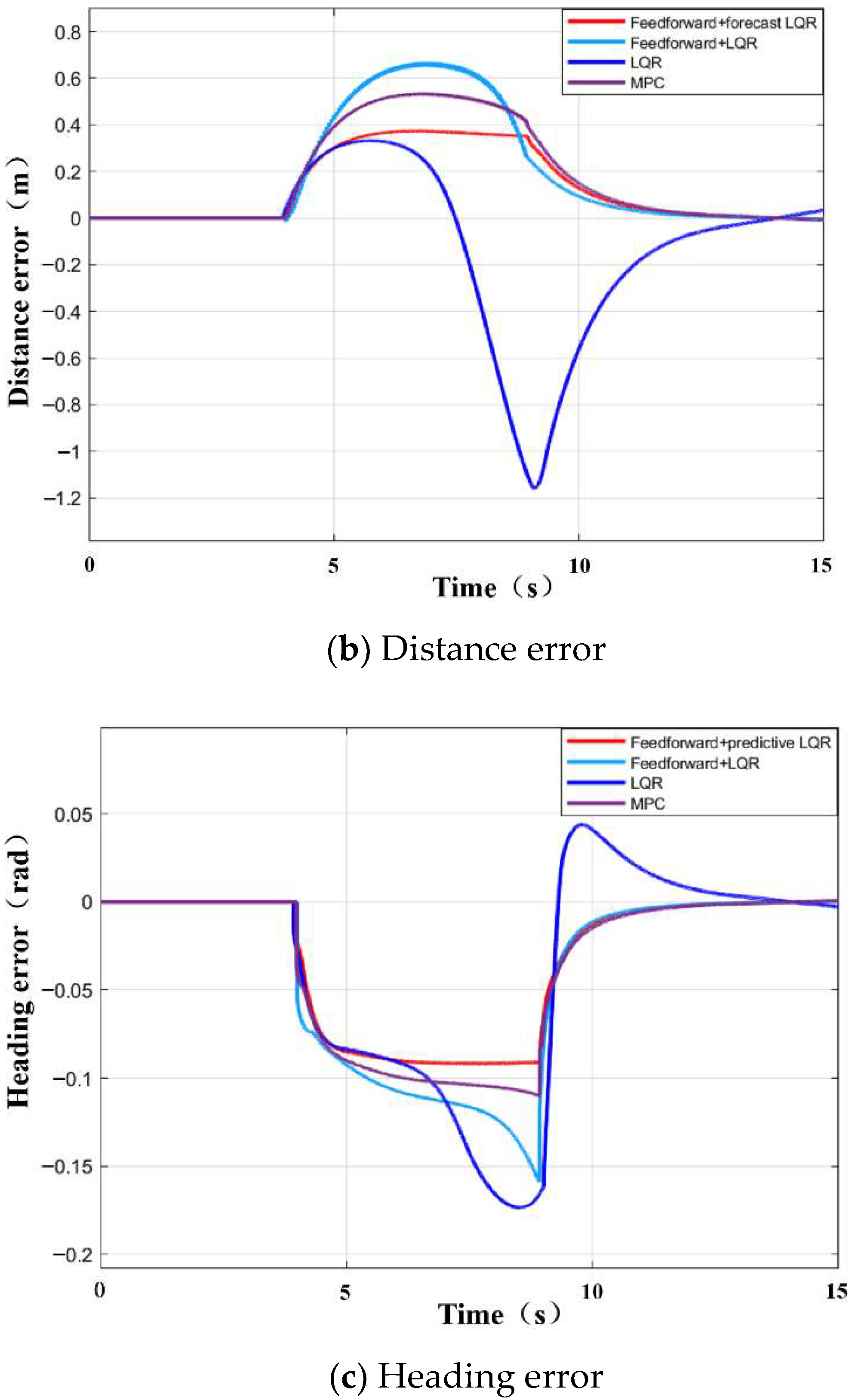
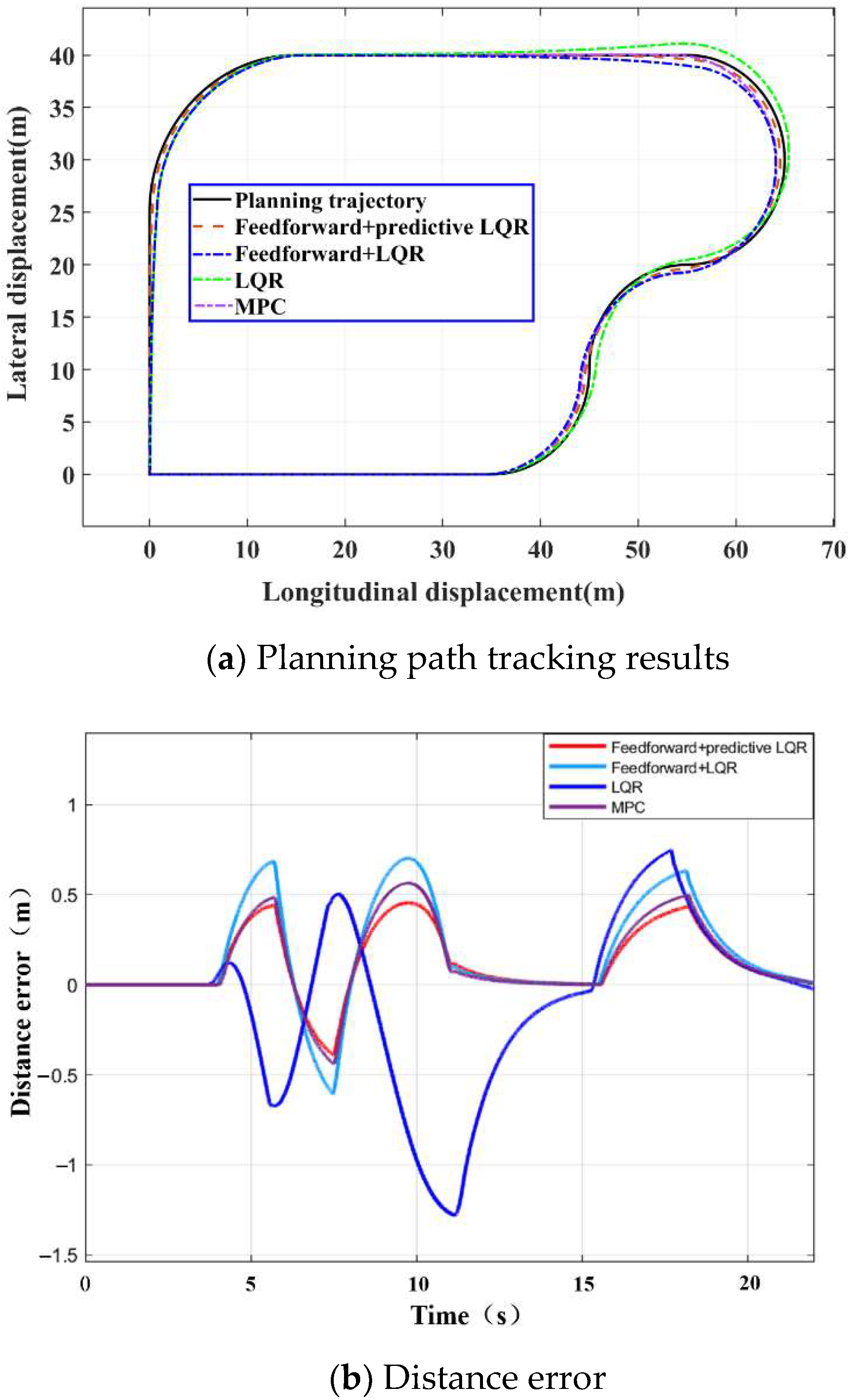
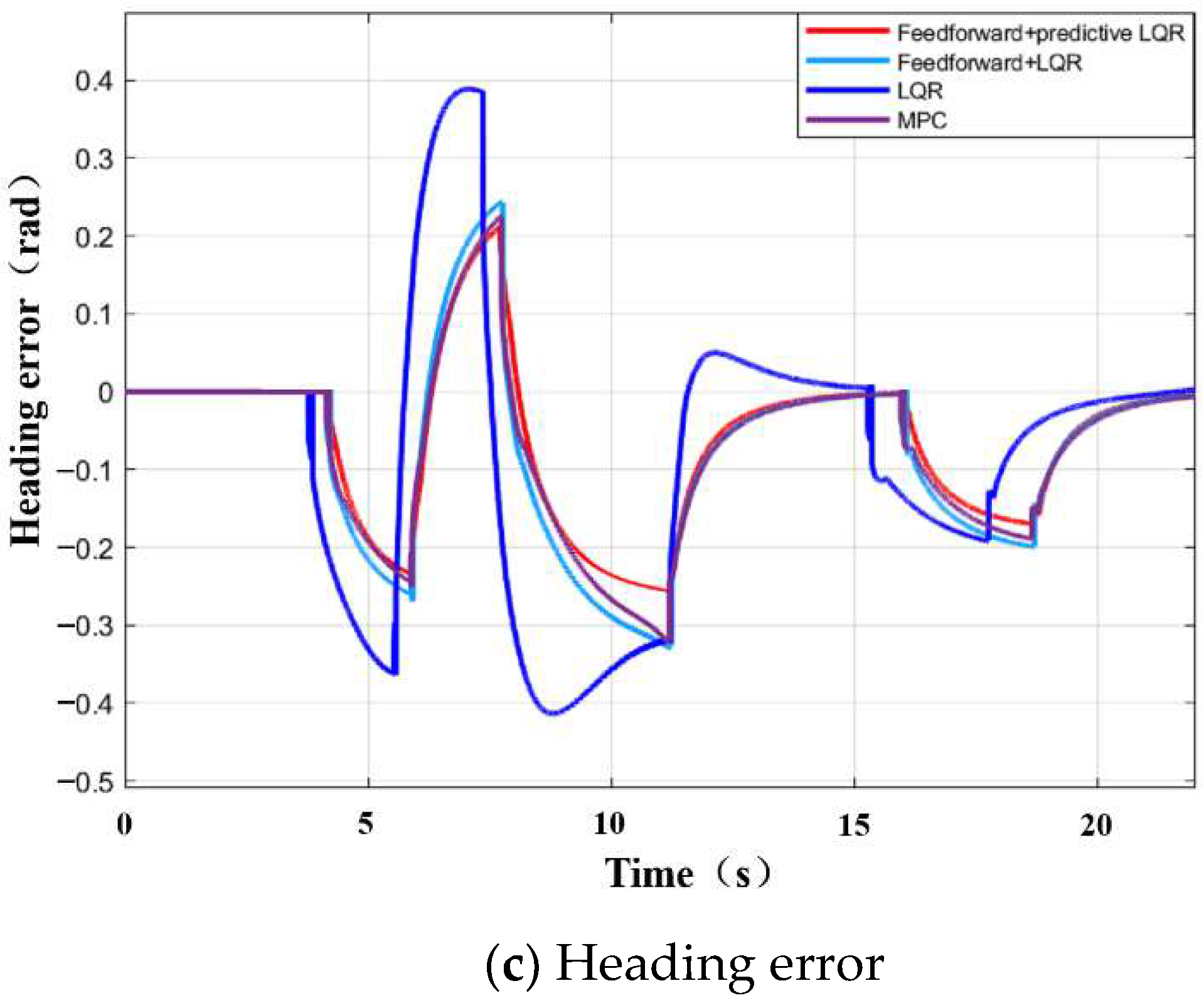
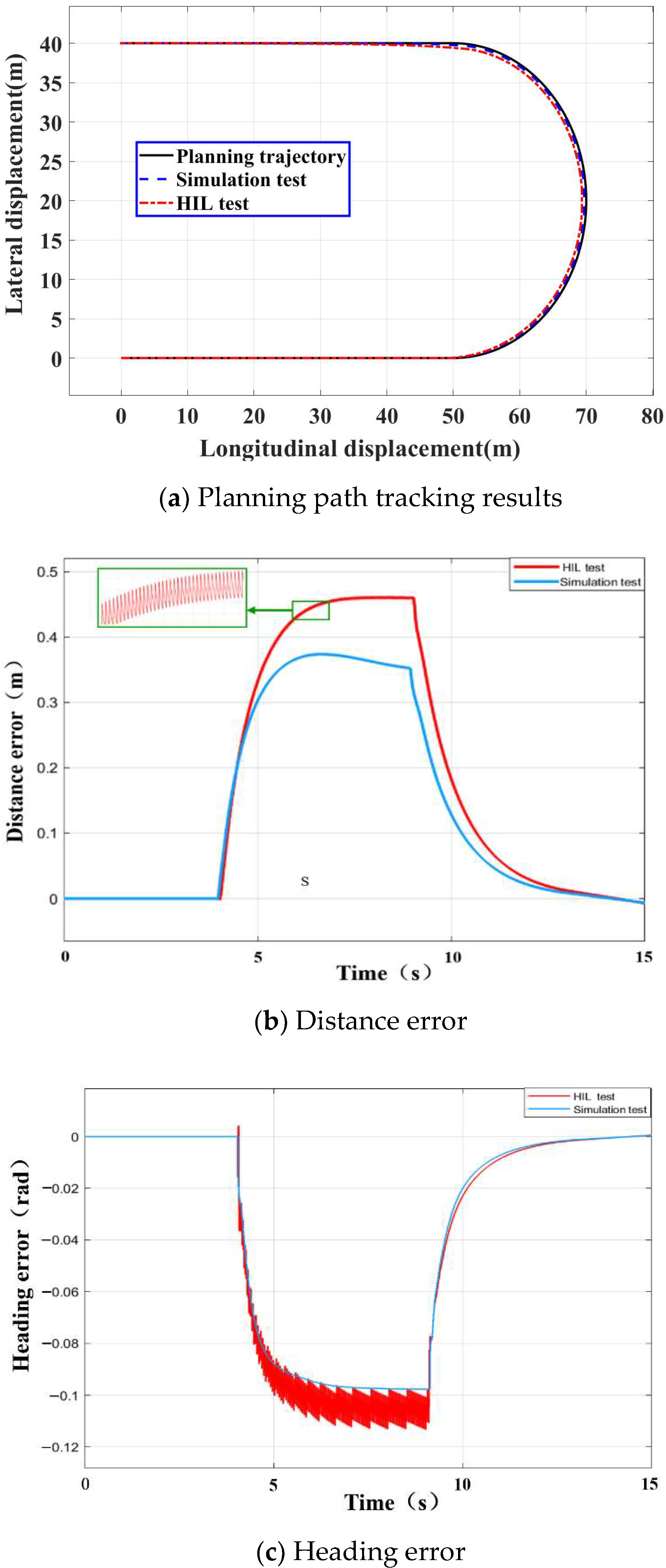
4.1.1. Simulation Test of the Roundabout Working Condition
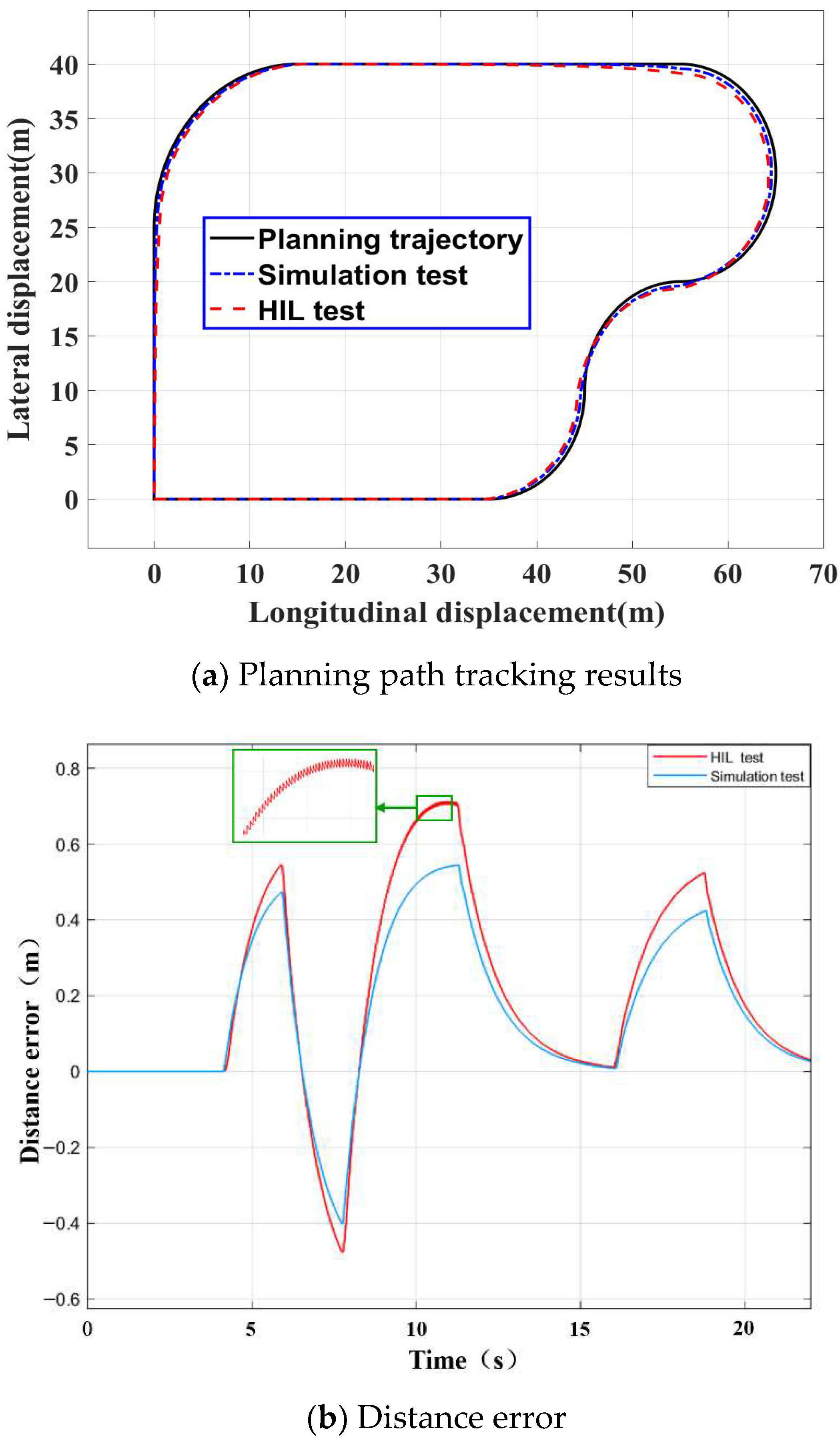
4.1.2. Simulation Test of Complex Steering Conditions
4.2. Hardware in the Loop Test and Analysis
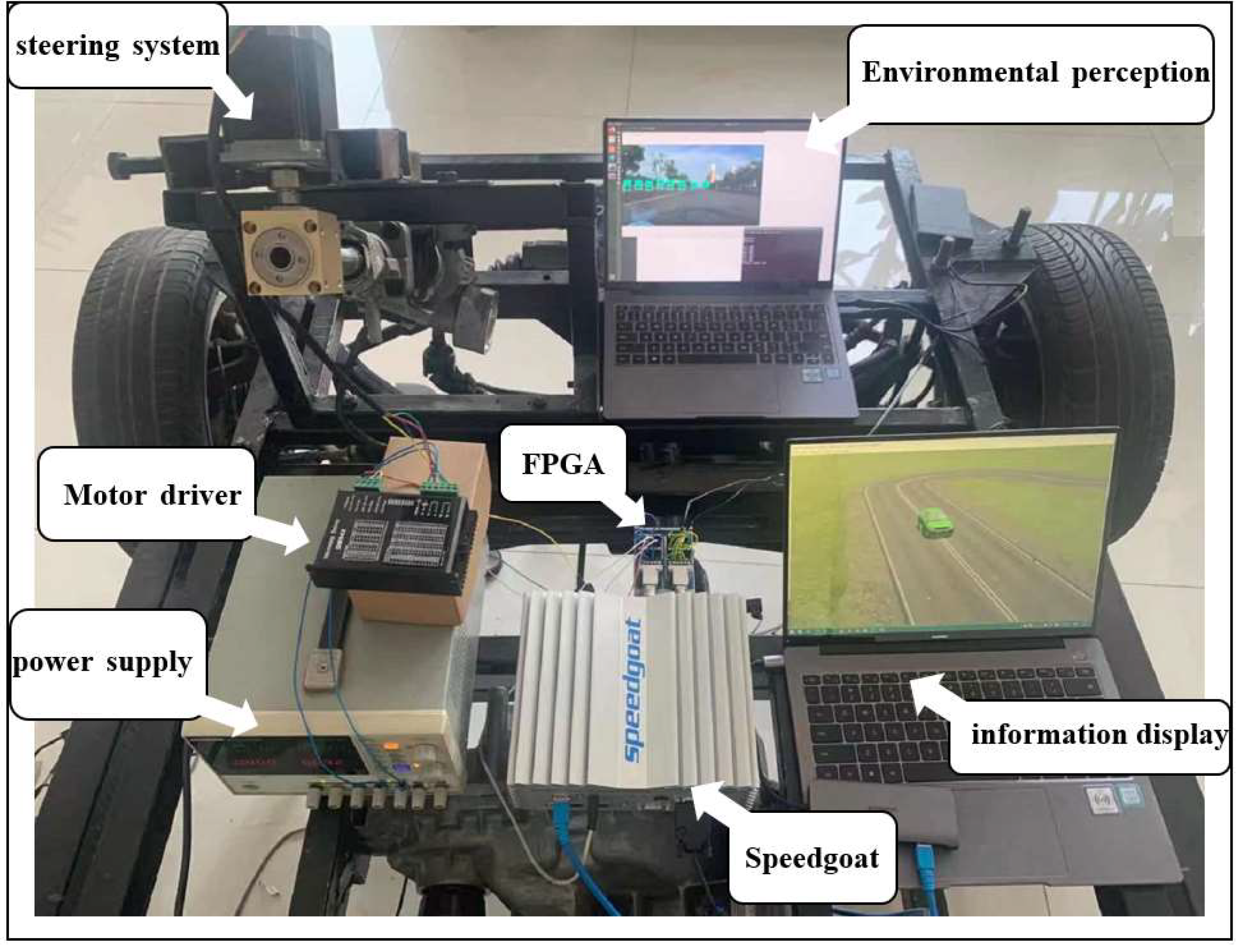
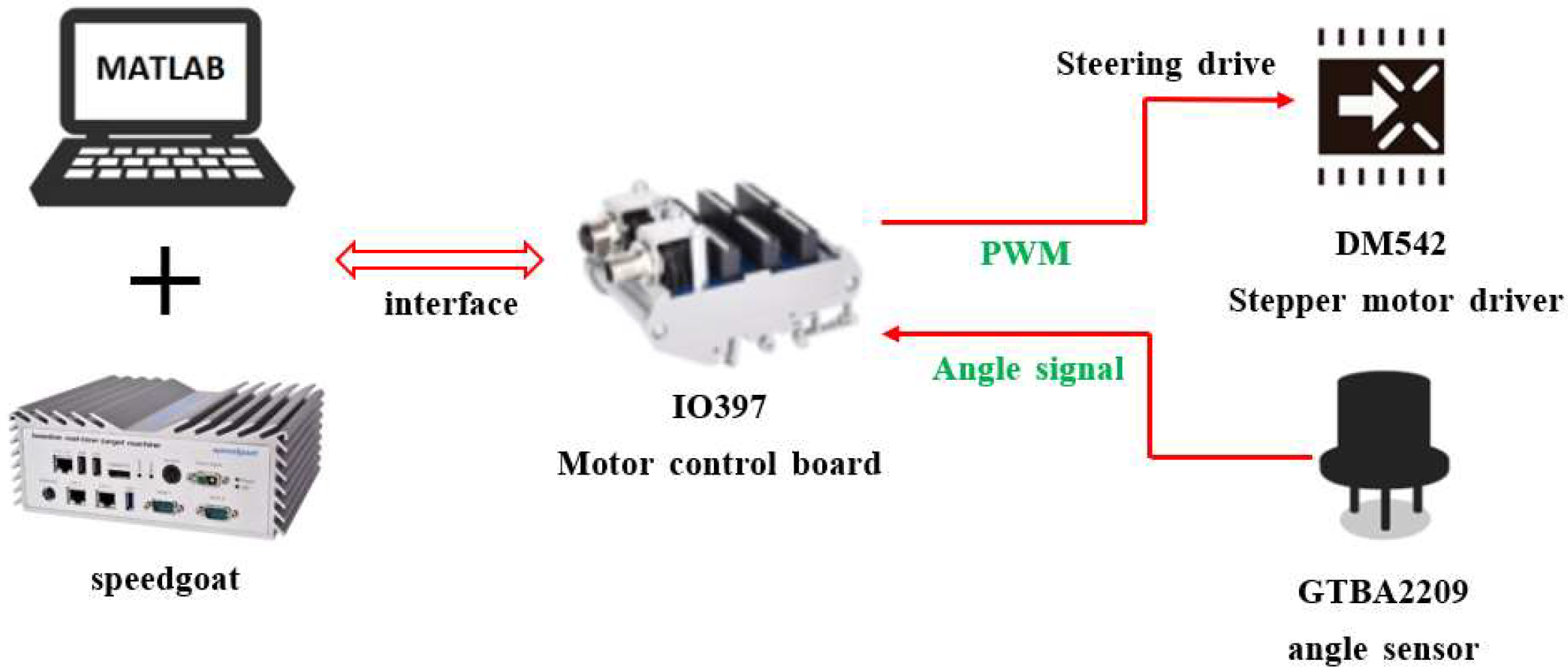
4.2.1. Introduction of Hardware in the Loop Test Platform
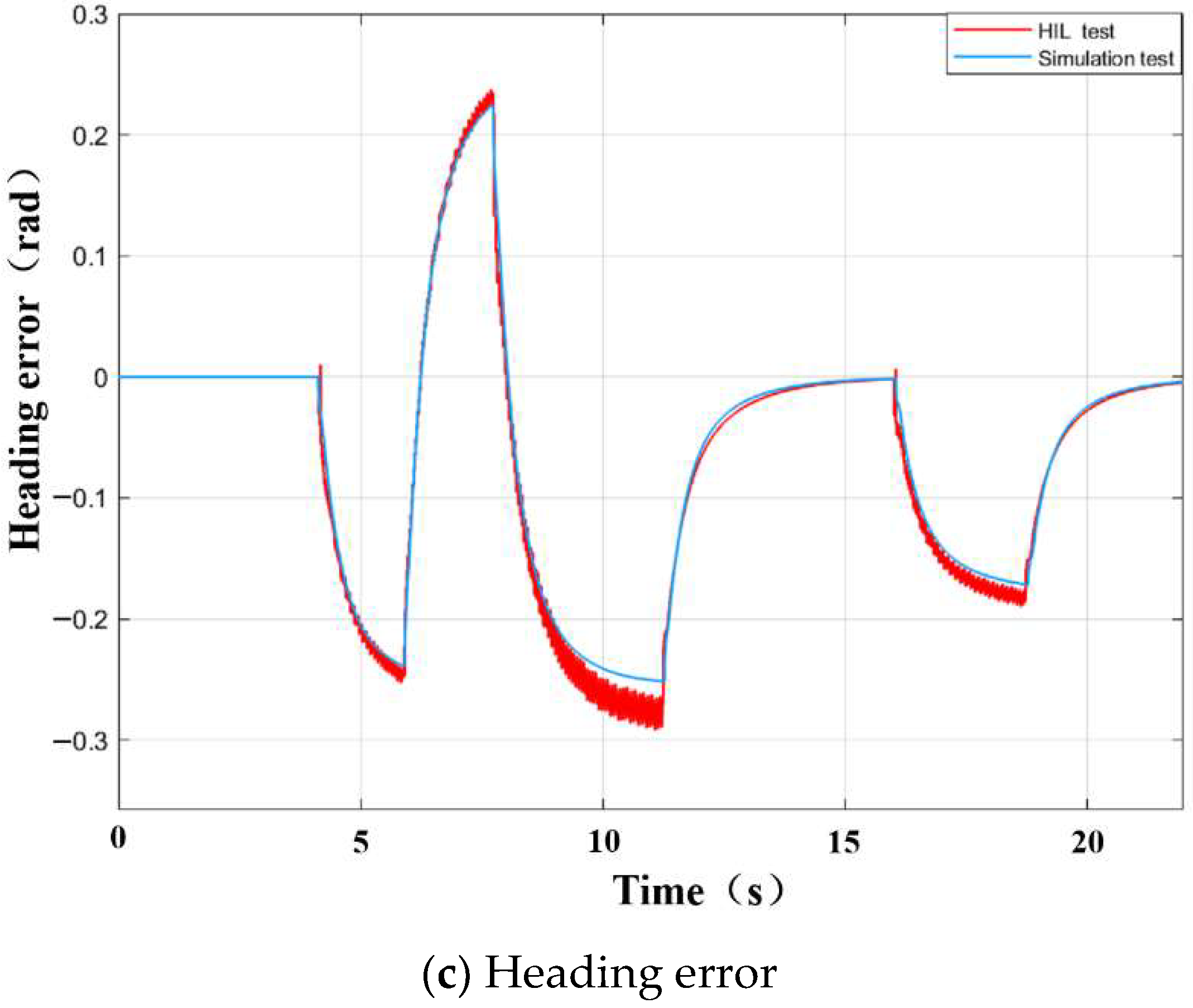
4.2.2. Analysis of Hardware in the Loop Test Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Li, Z.; Yang, J.; Song, Y. Lateral Stability Control of Four-Wheel-Drive Electric Vehicle Based on Coordinated Control of Torque Distribution and ESP Differential Braking. Actuators 2021, 10, 135. [Google Scholar] [CrossRef]
- Cao, K.; Li, Z.; Gu, Y.; Zhang, L.; Chen, L. The control design of transverse interconnected electronic control air suspension based on seeker optimization algorithm. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 235, 2200–2211. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Fioravanti, A.R.; Moutinho, A.; de Paiva, E.C. Nonlinear state-feedback design for vehicle lateral control using sum-of-squares programming. Veh. Syst. Dyn. 2020, 1844905. [Google Scholar] [CrossRef]
- Ando, T.; Kugimiya, W.; Hashimoto, T.; Momiyama, F.; Aoki, K.; Nakano, K. Lateral Control in Precision Docking Using RTK-GNSS/INS and LiDAR for Localization. IEEE Trans. Intell. Veh. 2020, 6, 78–87. [Google Scholar] [CrossRef]
- Lu, X.; Xing, Y.; Guirong, Z. Overview of the development status of motion control of unmanned vehicles. J. Mech. Eng. 2020, 56, 17. [Google Scholar]
- Choi, W.Y.; Kim, D.J.; Kang, C.M.; Lee, S.; Chung, C.C. Autonomous Vehicle Lateral Maneuvering by Approximate Explicit Predictive Control. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4739–4744. [Google Scholar] [CrossRef]
- Guo, N.; Zhang, X.; Zou, Y.; Lenzo, B.; Zhang, T. A Computationally Efficient Path-Following Control Strategy of Autonomous Electric Vehicles With Yaw Motion Stabilization. IEEE Trans. Transp. Electrif. 2020, 6, 728–739. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, Y.; Zhao, Y.; Zhao, Y.; Yin, G.; Zhang, H.; Wang, K. Trajectory Tracking of Autonomous Vehicle with the Fusion of DYC and Longitudinal–Lateral Control. Chin. J. Mech. Eng. 2019, 32, 1–16. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Rath, J.J.; Guerra, T.M.; Rath, J.; Zhang, H.; Palhares, R. Robust Set-Invariance Based Fuzzy Output Tracking Control for Vehicle Autonomous Driving Under Uncertain Lateral Forces and Steering Constraints. IEEE Trans. Intell. Transp. Syst. 2020, 1–7. [Google Scholar] [CrossRef]
- Chen, C.; Lv, J.; Song, G.; Liu, H. Adaptive fuzzy sliding mode control algorithm based on input-output linearization for vehicle’s lateral control. In Proceedings of the 2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC), Nanjing, China, 12–14 August 2016; IEEE: Piscataway Township, NJ, USA, 2016. [Google Scholar]
- Brown, M.; Funke, J.; Erlien, S.; Gerdes, J.C. Safe driving envelopes for path tracking in autonomous vehicles ScienceDirect. Control. Eng. Pract. 2017, 61, 307–316. [Google Scholar] [CrossRef]
- Zhang, W. A robust lateral tracking control strategy for autonomous driving vehicles. Mech. Syst. Signal Process. 2021, 150, 107238. [Google Scholar] [CrossRef]
- Bao, C.; Feng, J. Model predictive control of steering torque in shared driving of autonomous vehicles. Sci. Prog. 2020, 103, 1–22. [Google Scholar] [CrossRef]
- Goodarzi, A.; Sabooteh, A.; Esmailzadeh, E. Automatic path control based on integrated steering and external yaw-moment control. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2008, 222, 189–200. [Google Scholar] [CrossRef]
- Cui, Q.; Ding, R.; Wei, C.; Zhou, B. Path-tracking and lateral stabilisation for autonomous vehicles by using the steering angle envelope. Veh. Syst. Dyn. 2020, 1–25. [Google Scholar] [CrossRef]
- Li, P.; Nguyen, A.T.; Du, H.; Wang, Y.; Zhang, H. Polytopic LPV Approaches for Intelligent Automotive Systems: State of the Art and Future Challenges. Mech. Syst. Signal. Process. 2021, 161, 107931. [Google Scholar] [CrossRef]
- Guo, N.; Lenzo, B.; Zhang, X.; Zou, Y.; Zhai, R.; Zhang, T. A Real-time Nonlinear Model Predictive Controller for Yaw Motion Optimization of Distributed Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 4935–4946. [Google Scholar] [CrossRef] [Green Version]
- Benariba, H.; Boumediene, A. Lateral Sliding Mode Control of an Electric Vehicle. In Proceedings of the 2018 6th International Conference on Control Engineering & Information Technology (CEIT), Istanbul, Turkey, 25–27 October 2018. [Google Scholar]
- Wang, Z.; Wang, M.; Zhang, Y.; Guan, T.; Song, X.; Liu, J.; Zhen, Y.; Zhang, D. Driverless simulation of path tracking based on PID control. IOP Conf. Ser. Mater. Sci. Eng. 2020, 892, 012050. [Google Scholar] [CrossRef]
- Qian, X.; Arnaud, D.; Moutarde, F. A Hierarchical Model Predictive Control Framework for On-road Formation Control of Autonomous Vehicles. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 376–381. [Google Scholar]
- Tang, F.; Li, C. Intelligent vehicle lateral tracking control based on multiple model prediction. AIP Adv. 2020, 10, 075107. [Google Scholar] [CrossRef]
- Li, Z.; Wang, P.; Liu, H.; Hu, Y.; Chen, H. Coordinated longitudinal and lateral vehicle stability control based on the combined-slip tire model in the MPC framework. Mech. Syst. Signal Process. 2021, 161, 107947. [Google Scholar] [CrossRef]
- Olalla, C.; Leyva, R.; Aroudi, A.E.; Queinnec, I. Robust LQR Control for PWM Converters: An LMI Approach. IEEE Trans. Ind. Electron. 2009, 56, 2548–2558. [Google Scholar] [CrossRef]
- Sharp, R.S.; Peng, H. Vehicle dynamics applications of optimal control theory: Vehicle System Dynamics. Veh. Syst. Dyn. 2011, 49, 1073–1111. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic steering methods for autonomous automobile path tracking. In Robotics Institute; CMURITR-09-08; Carnegie Mellon University: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Kapania, N.R.; Gerdes, J.C. Design of a feedback-feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Peng, H. Design, Analysis, and Experiments of Preview Path Tracking Control for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 48–58. [Google Scholar] [CrossRef]
- Zhen, Z.A.; Xi, A.; Tao, Y.A.; Gu, Y.; Wang, W.; Chen, L. Multi-objective optimization of lubricant volume in an ELSD considering thermal effects. Int. J. Therm. Sci. 2021, 164, 106884. [Google Scholar]
- Cheng, S.; Li, L.; Guo, H.Q.; Chen, Z.-G.; Song, P. Longitudinal Collision Avoidance and Lateral Stability Adaptive Control System Based on MPC of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Zheng, J.; Cao, Z.; Man, Z.; Yu, M.; Chen, L. Adaptive Sliding Mode-based Lateral Stability Control of Steer-by-Wire Vehicles with Experimental Validations. IEEE Trans. Veh. Technol. 2020, 69, 9589–9600. [Google Scholar] [CrossRef]
- Katebi, J.; Shoaei-Parchin, M.; Shariati, M.; Trung, N.T.; Khorami, M. Developed comparative analysis of metaheuristic optimization algorithms for optimal active control of structures. Eng. Comput. 2020, 36, 1539–1558. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, L.; Qu, Z. Lyapunov, Adaptive, and Optimal Design Techniques for Cooperative Systems on Directed Communication Graphs. IEEE Trans. Ind. Electron. 2012, 59, 3026–3041. [Google Scholar] [CrossRef]
- Xu, S.; Peng, H.; Song, Z.; Chen, K.; Tang, Y. Accurate and Smooth Speed Control for an Autonomous Vehicle. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018; IEEE: Piscataway Township, NJ, USA, 2018. [Google Scholar]
- Bencloucif, A.M.; Nguyen, A.T.; Sentouh, C.; Popieul, J. Cooperative Trajectory Planning for Haptic Shared Control between Driver and Automation in Highway Driving. IEEE Trans. Ind. Electron. 2019, 66, 9846–9857. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Miao, F.; Tian, Y.; Jin, L. Vehicle Direction Detection Based on YOLOv3. In Proceedings of the 2019 11th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 24–25 August 2019; pp. 268–271. [Google Scholar] [CrossRef]
- Gu, Y.; Li, Z.; Zhang, Z.; Li, J.; Chen, L. Path Tracking Control of Field Information-Collecting Robot Based on Improved Convolutional Neural Network Algorithm. Sensors 2020, 20, 797. [Google Scholar] [CrossRef] [Green Version]

| Definition | Symbol | Value (Unit) |
|---|---|---|
| Vehicle weight | m | 1412 (kg) |
| Gravitational acceleration | g | 9.8 () |
| wheelbase | 2.91 (m) | |
| Distance from centroid to front axle | 1.01 (m) | |
| Centroid height | 0.52 (m) | |
| Front wheel turning stiffness | 43,664.21 () | |
| Rear wheel turning stiffness | 80,384.32 () | |
| Moment of inertia about X axis | 536.6 (kg ) | |
| Moment of inertia about Y axis | 1536.7 (kg ) | |
| Moment of inertia about Z axis | 1536.7 (kg ) | |
| Rolling radius of the tire | R | 0.304 (m) |
| Tire-road friction factor | 0.65 (-) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Bai, Z.; Li, Z.; Feng, N.; Chen, L. Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm. Actuators 2021, 10, 228. https://doi.org/10.3390/act10090228
Yang T, Bai Z, Li Z, Feng N, Chen L. Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm. Actuators. 2021; 10(9):228. https://doi.org/10.3390/act10090228
Chicago/Turabian StyleYang, Tao, Ziwen Bai, Zhiqiang Li, Nenglian Feng, and Liqing Chen. 2021. "Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm" Actuators 10, no. 9: 228. https://doi.org/10.3390/act10090228
APA StyleYang, T., Bai, Z., Li, Z., Feng, N., & Chen, L. (2021). Intelligent Vehicle Lateral Control Method Based on Feedforward + Predictive LQR Algorithm. Actuators, 10(9), 228. https://doi.org/10.3390/act10090228







