Stabilization of Unstable Second-Order Delay Plants under PID Control: A Nyquist Curve Analysis
Abstract
:1. Introduction
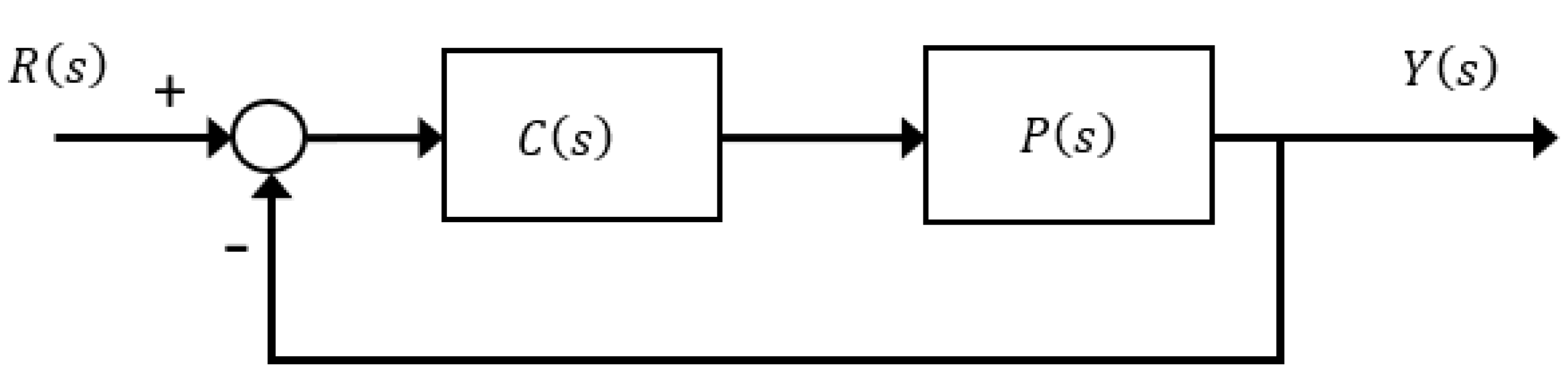
2. Preliminaries and Problem Formulation
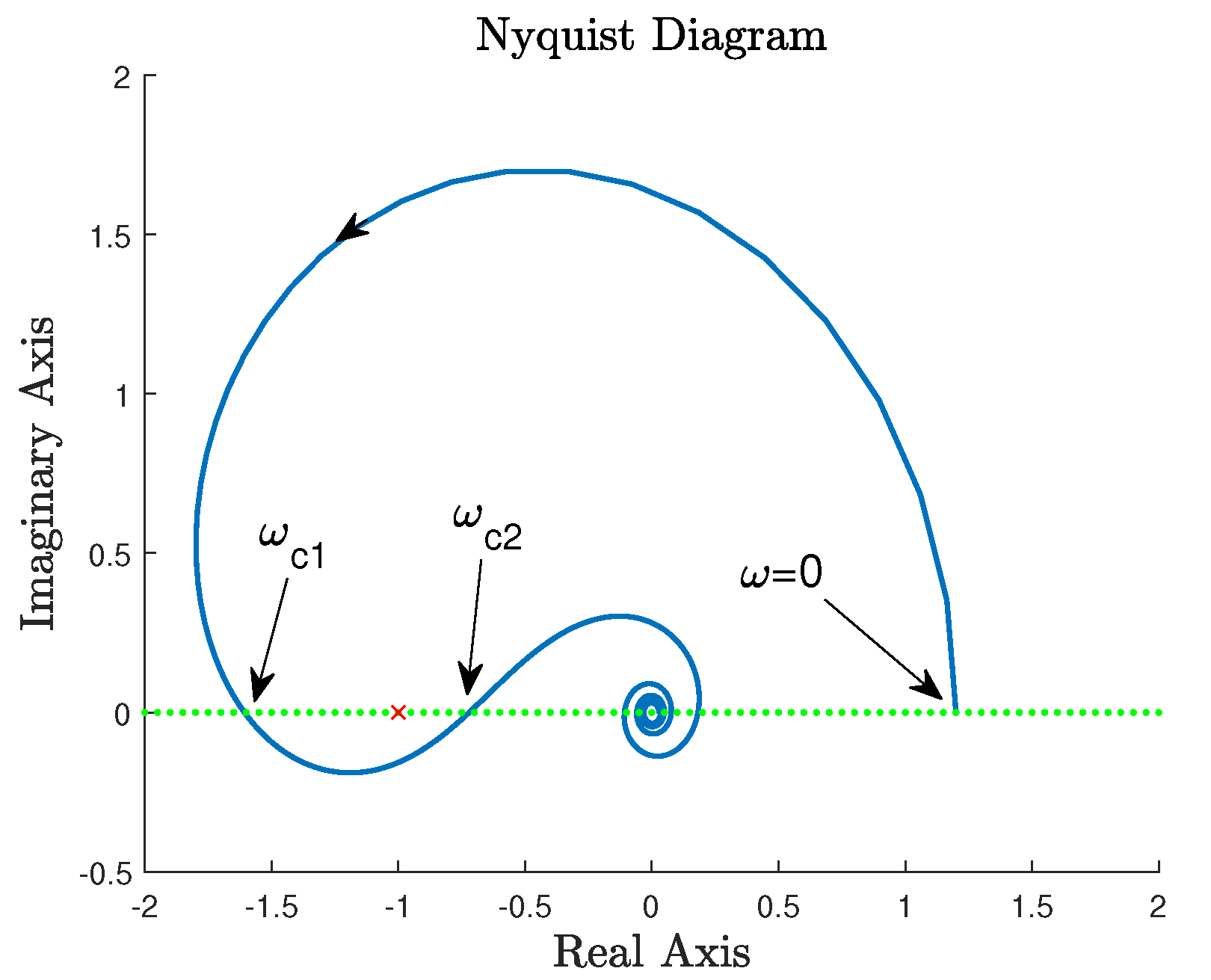
3. Stabilization of Delay Plants with Two Real Poles under PD Control
3.1. A Necessary and Sufficient Condition for Stabilization by Fixed PD Parameters
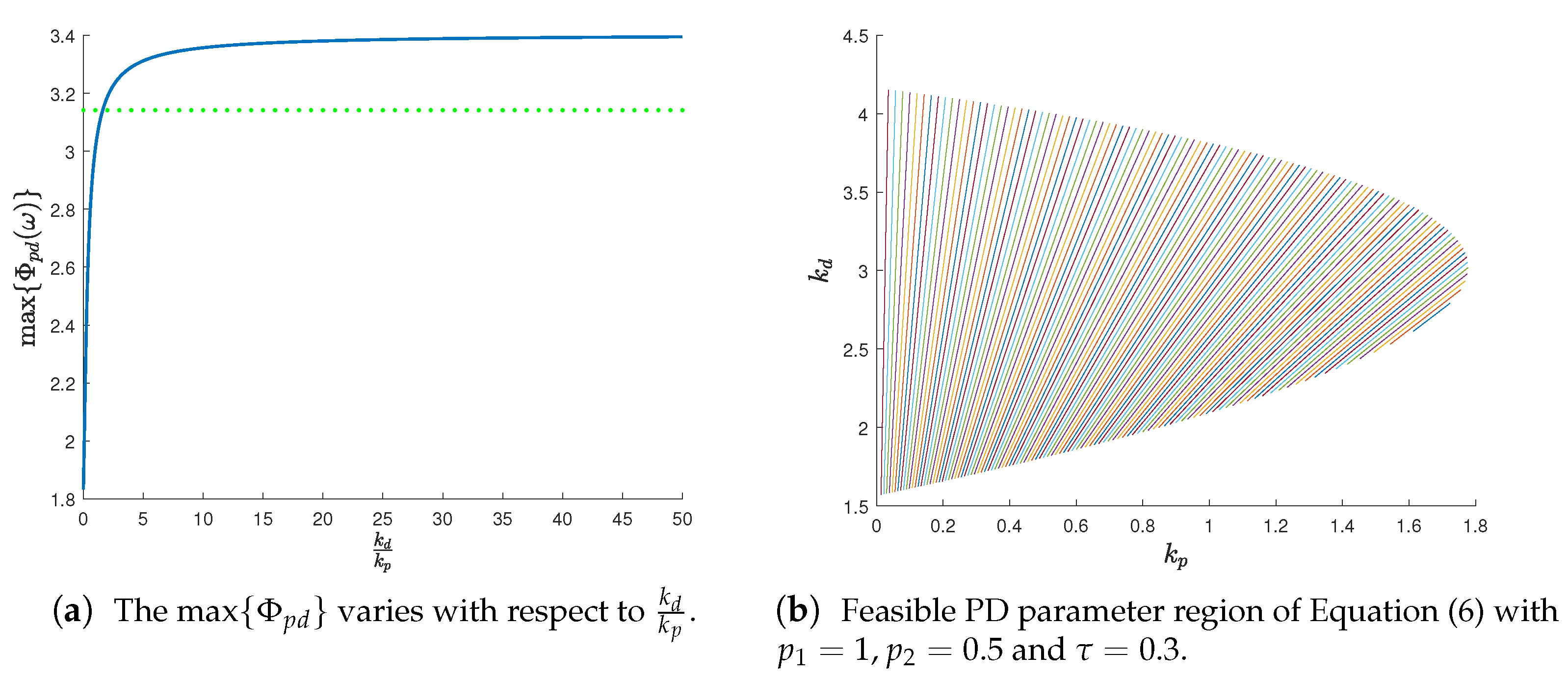
3.2. An Algorithm for Feasible Parameter Region of PD Control
| Algorithm 1 The algorithm for the feasible PID parameter region of the plant (6). |
|
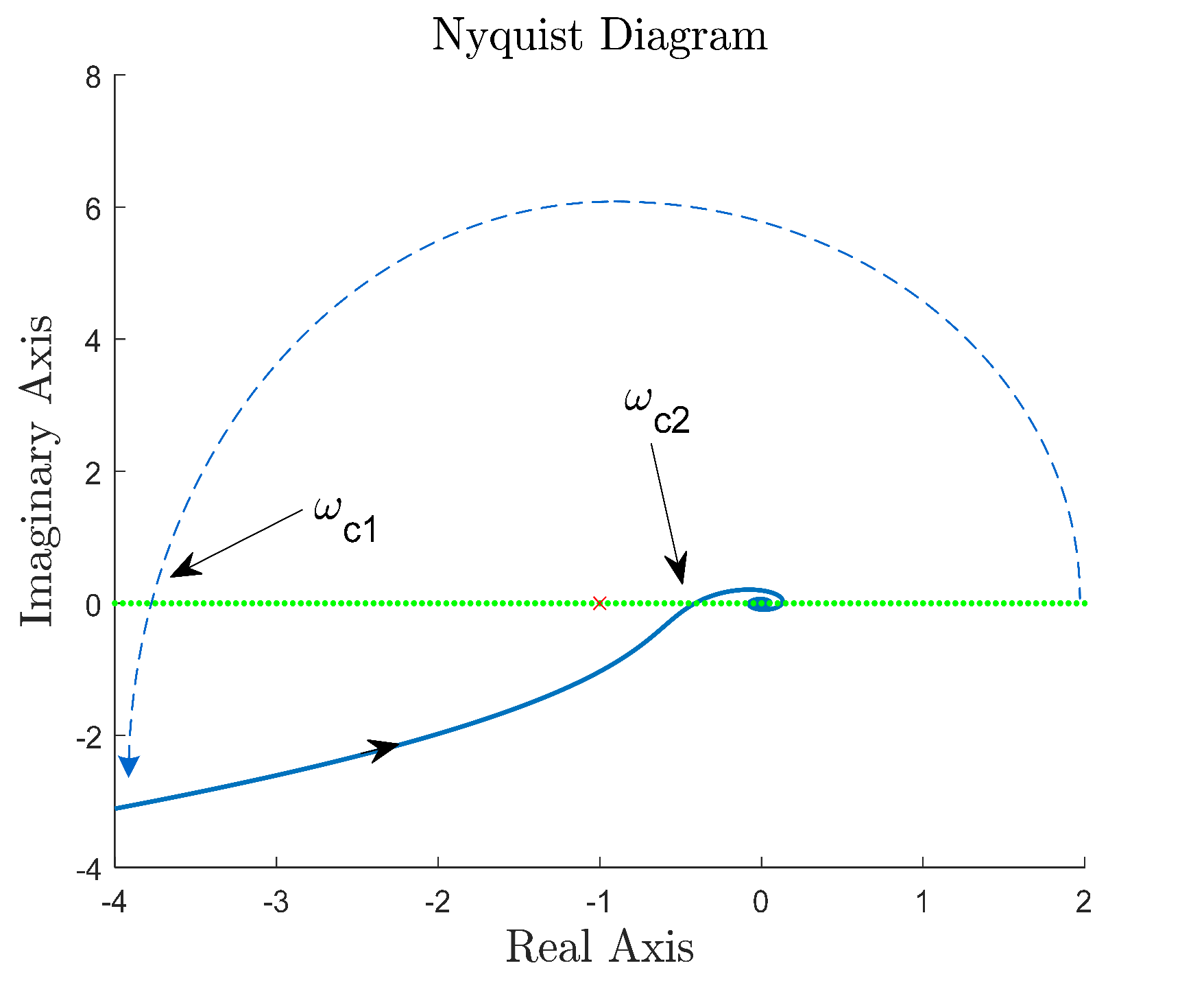
4. Stabilization of Delay Plants with Two Unstable Real Poles under PID Control
4.1. A Sufficient Condition for Stabilization by Fixed PID Parameters
4.2. An Algorithm for Feasible Parameter Region of PID Control
| Algorithm 2 The algorithm for the feasible PID parameter region of the plant (6). |
|
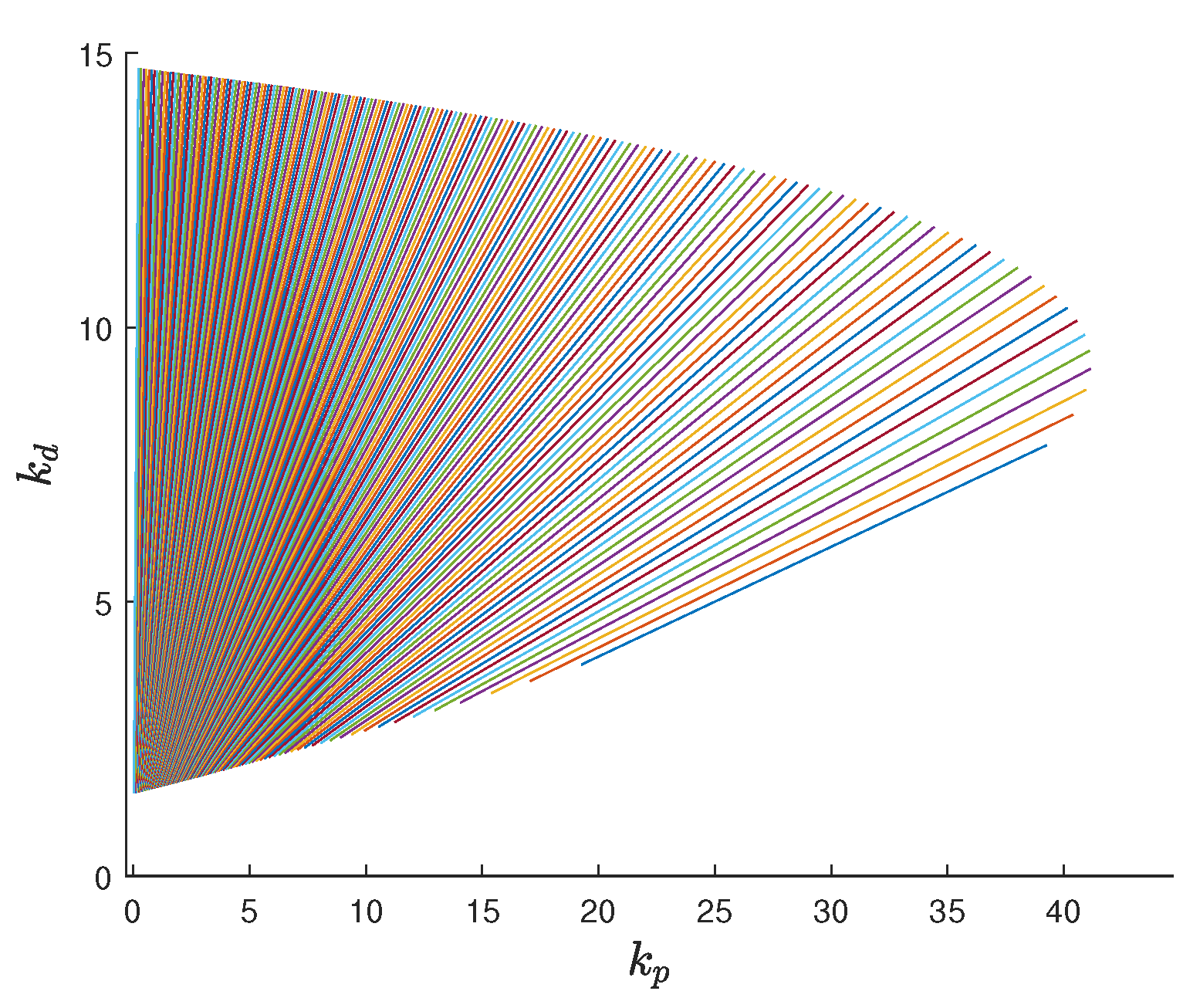
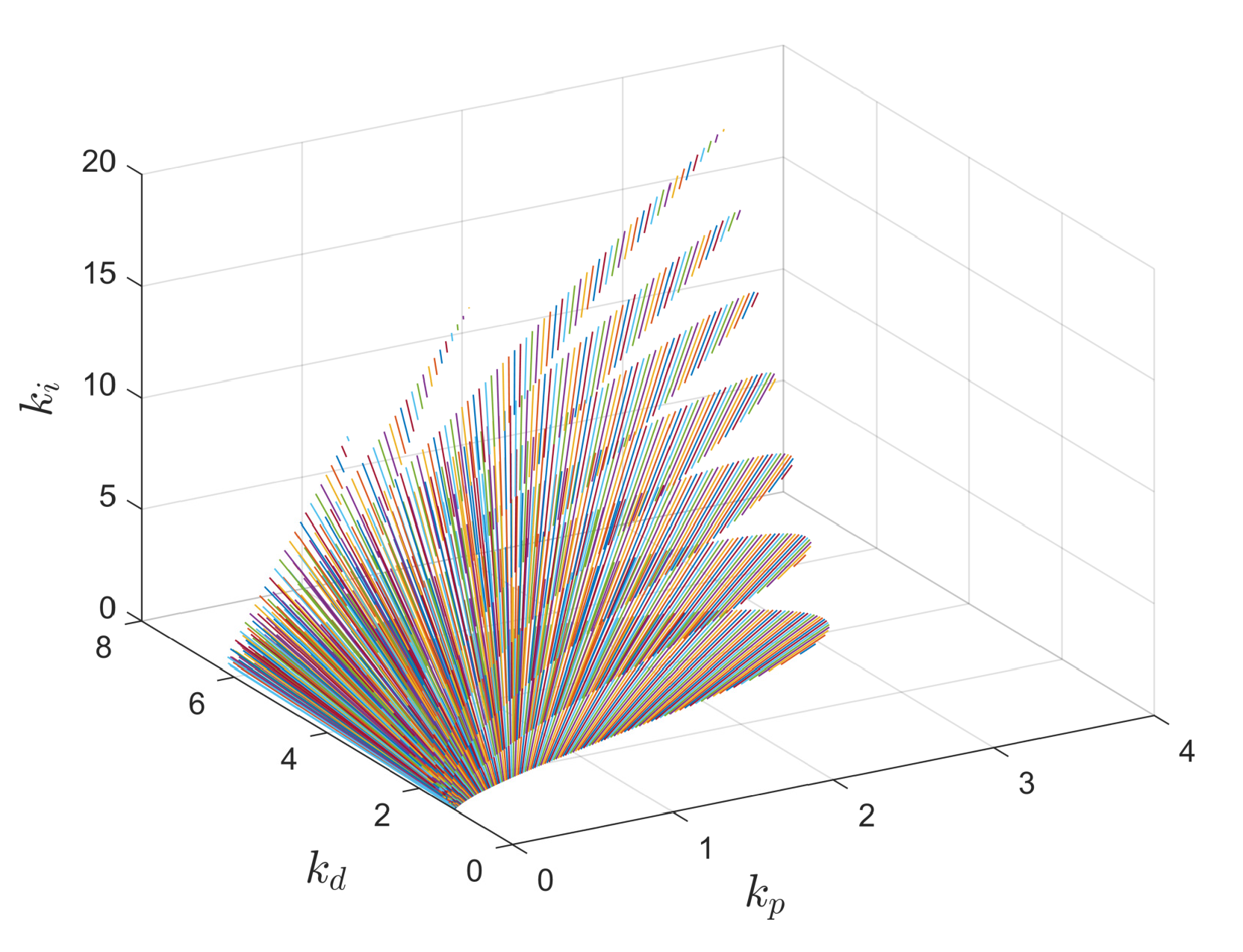
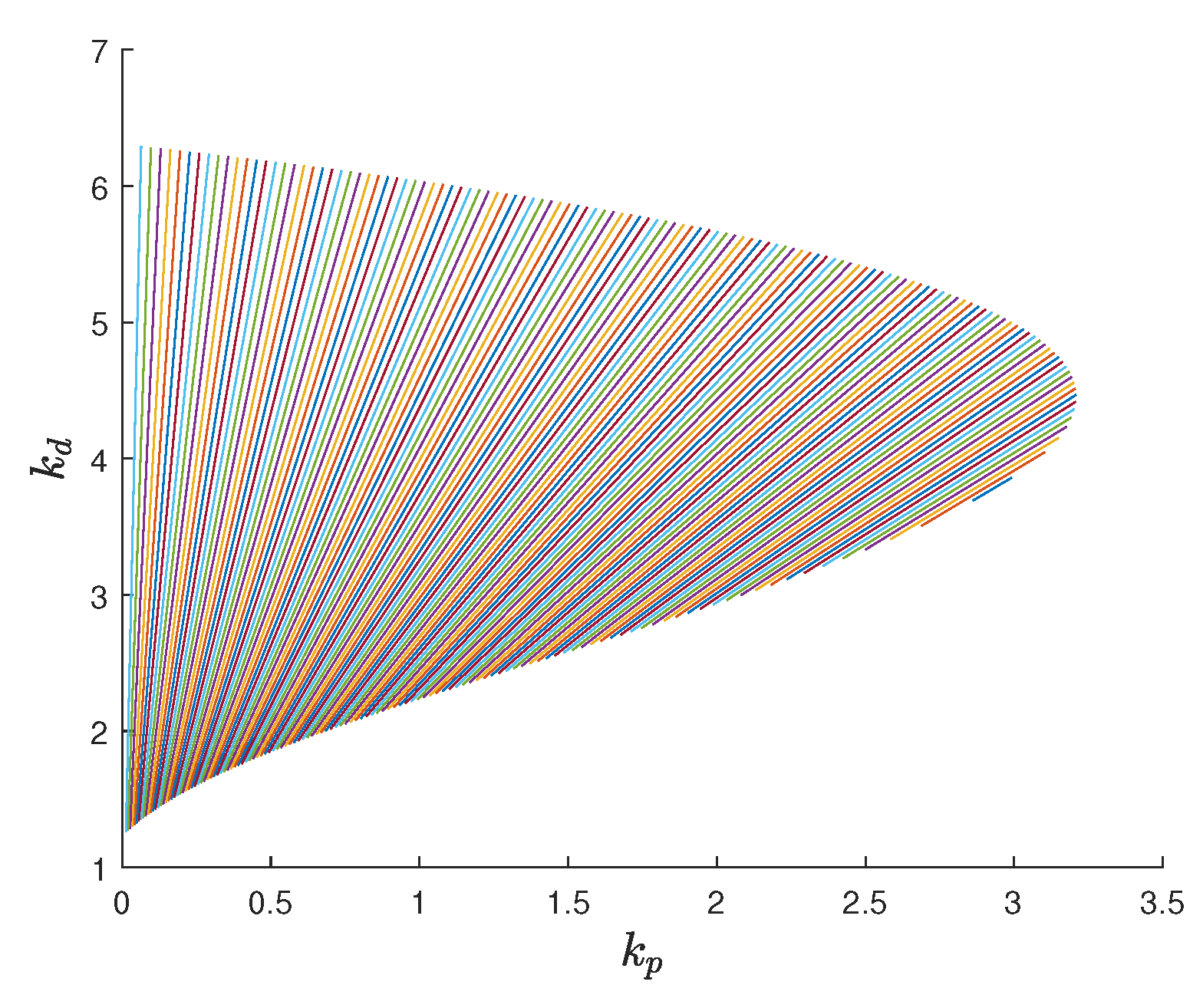
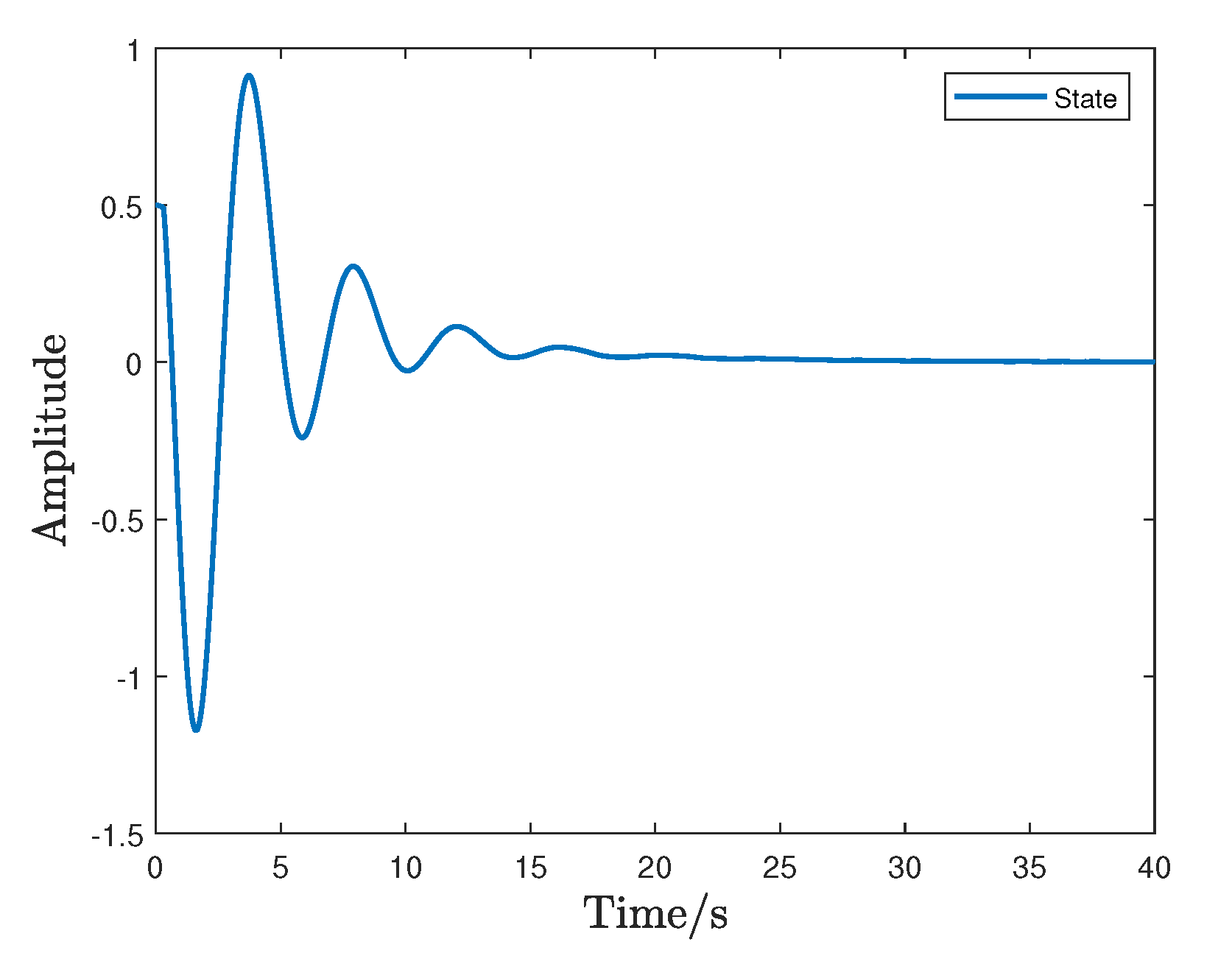
5. Illustrative Examples
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sipahi, R.; Niculescu, S.; Abdallah, C.T.; Michiels, W.; Gu, K. Stability and Stabilization of Systems with Time Delay. IEEE Control Syst. Mag. 2011, 31, 38–65. [Google Scholar]
- Lee, Y.; Lee, J.; Park, S. PID controller tuning for integrating and unstable processes with time delay. Chem. Eng. Sci. 2000, 55, 3481–3493. [Google Scholar] [CrossRef]
- Thowsen, A. An analytic stability test for a class of time-delay systems. IEEE Trans. Autom. Control 1981, 26, 735–736. [Google Scholar] [CrossRef]
- Walton, K.; Marshall, J.E. Direct method for TDS stability analysis. IEEE Proc. Control Theory Appl. 1987, 134, 101–107. [Google Scholar] [CrossRef]
- Sipahi, R.; Olgac, N. Complete stability robustness of third-order LTI multiple time-delay systems. Automatica 2005, 41, 1413–1422. [Google Scholar] [CrossRef]
- Olgac, N.; Sipahi, R. An exact method for the stability analysis of time-delayed linear time-invariant (LTI) systems. IEEE Trans. Autom. Control 2002, 47, 793–797. [Google Scholar] [CrossRef]
- Gu, K.; Niculescu, S.I.; Chen, J. On stability crossing curves for general systems with two delays. J. Math. Anal. Appl. 2005, 311, 231–253. [Google Scholar] [CrossRef] [Green Version]
- Naghnaeian, M.; Gu, K. Stability crossing set for systems with two scalar-delay channels. Automatica 2013, 49, 2098–2106. [Google Scholar] [CrossRef]
- Lanzkron, R.; Higgins, T. D-decomposition analysis of automatic control systems. IRE Trans. Autom. Control 1959, 4, 150–171. [Google Scholar] [CrossRef]
- De Paor, A.M.; O’Malley, M. Controllers of Ziegler-Nichols type for unstable process with time delay. Int. J. Control 1989, 49, 1273–1284. [Google Scholar] [CrossRef]
- Vanavil, B.; Chaitanya, K.K.; Rao, A.S. Improved PID controller design for unstable time delay processes based on direct synthesis method and maximum sensitivity. Int. J. Syst. Sci. 2015, 46, 1349–1366. [Google Scholar] [CrossRef]
- Tan, W.; Marquez, H.J.; Chen, T. IMC design for unstable processes with time delays. J. Process Control 2003, 13, 203–213. [Google Scholar] [CrossRef] [Green Version]
- Seer, Q.H.; Nandong, J. Stabilization and PID tuning algorithms for second-order unstable processes with time-delays. ISA Trans. 2017, 67, 233–245. [Google Scholar] [CrossRef]
- Srivastava, S.; Misra, A.; Thakur, S.K.; Pandit, V.S. An optimal PID controller via LQR for standard second order plus time delay systems. ISA Trans. 2016, 60, 244–253. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Zhang, Y. New results on eigenvalue distribution and controller design for time delay systems. IEEE Trans. Autom. Control 2016, 62, 2886–2901. [Google Scholar] [CrossRef]
- Das, S.; Halder, K.; Gupta, A. Delay handling method in dominant pole placement based PID controller design. IEEE Trans. Ind. Inf. 2019, 16, 980–991. [Google Scholar] [CrossRef]
- Dincel, E.; Söylemez, M.T. Digital PI-PD controller design for arbitrary order systems: Dominant pole placement approach. ISA Trans. 2018, 79, 189–201. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Cui, Y.; Ding, X. An improved analytical tuning rule of a robust PID controller for integrating systems with time delay based on the multiple dominant pole-placement method. Symmetry 2020, 12, 1449. [Google Scholar] [CrossRef]
- Fišer, J.; Zítek, P. PID controller tuning via dominant pole placement in comparison with Ziegler-Nichols tuning. IFAC—PapersOnLine 2019, 52, 43–48. [Google Scholar] [CrossRef]
- Silva, G.J.; Datta, A.; Bhattacharyya, S.P. PID Controllers for Time-Delay Systems, 1st ed.; Springer: Boston, MA, USA, 2007; pp. 135–189. [Google Scholar]
- Yu, X.; Ding, P.; Yang, F.; Zou, C.; Ou, L. Stabilization parametric region of distributed PID controllers for general first-order multi-agent systems with time delay. IEEE/CAA J. Autom. Sin. 2020, 7, 1555–1564. [Google Scholar] [CrossRef]
- Firouzbahrami, M.; Nobakhti, A. Reliable computation of PID gain space for general second-order time-delay systems. Int. J. Control 2017, 90, 2124–2136. [Google Scholar] [CrossRef]
- Hwang, C.; Hwang, J.H. Stabilisation of first-order plus dead-time unstable processes using PID controllers. IEE Proc. Control Theory Appl. 2004, 151, 89–94. [Google Scholar] [CrossRef]
- Zalluhoglu, U.; Kammer, A.S.; Olgac, N. Feedback stabilization of a thermoacoustic device with experiments. In Proceedings of the 2015 American Control Conference, Chicago, IL, USA, 1–3 July 2015. [Google Scholar]
- Lee, S.C.; Wang, Q.G.; Xiang, C. Stabilization of all-pole unstable delay processes by simple controllers. J. Process Control 2010, 20, 235–239. [Google Scholar] [CrossRef]
- Middleton, R.H.; Miller, D.E. On the achievable delay margin using LTI control for unstable plants. IEEE Trans. Autom. Control 2007, 52, 1194–1207. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Chen, J. Delay margin of low-order systems achievable by PID controllers. IEEE Trans. Autom. Control 2019, 64, 1958–1973. [Google Scholar] [CrossRef]
- Ma, D.; Chen, J.; Liu, A.; Chen, J.; Niculescu, S.I. Explicit bounds for guaranteed stabilization by PID control of second-order unstable delay systems. Automatica 2019, 100, 407–411. [Google Scholar] [CrossRef]
- Chen, J.; Ma, D.; Xu, Y.; Chen, J. Delay Robustness of PID Control of Second-Order Systems: Pseudo-Concavity, Exact Delay Margin, and Performance Trade-Off. IEEE Trans. Autom. Control 2021. early access. [Google Scholar] [CrossRef]
- Srivastava, S.; Pandit, V.S. A PI/PID controller for time delay systems with desired closed loop time response and guaranteed gain and phase margins. J. Process Control 2016, 37, 70–77. [Google Scholar] [CrossRef]
- Ma, D.; Tian, R.; Zulfiqar, A.; Chen, J.; Chai, T. Bounds on Delay Consensus Margin of Second-Order Multiagent Systems with Robust Position and Velocity Feedback Protocol. IEEE Trans. Autom. Control 2019, 64, 3780–3787. [Google Scholar] [CrossRef]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 7th ed.; Pearson: New York, NY, USA, 2015; pp. 333–335. [Google Scholar]
- Xiang, C.; Wang, Q.G.; Lu, X.; Nguyen, L.A.; Lee, T.H. Stabilization of second-order unstable delay processes by simple controllers. J. Process Control 2007, 17, 675–682. [Google Scholar] [CrossRef]
- Panda, R.C. Synthesis of PID controller for unstable and integrating processes. Chem. Eng. Sci. 2009, 64, 2807–2816. [Google Scholar] [CrossRef]
- Fan, S.K.S.; Chang, Y.J. An integrated advanced process control framework using run-to-run control, virtual metrology and fault detection. J. Process Control 2013, 23, 933–942. [Google Scholar] [CrossRef]
- Fan, S.K.S.; Chang, Y.J. Multiple-input multiple-output double exponentially weighted moving average controller using partial least squares. J. Process Control 2010, 20, 734–742. [Google Scholar] [CrossRef]

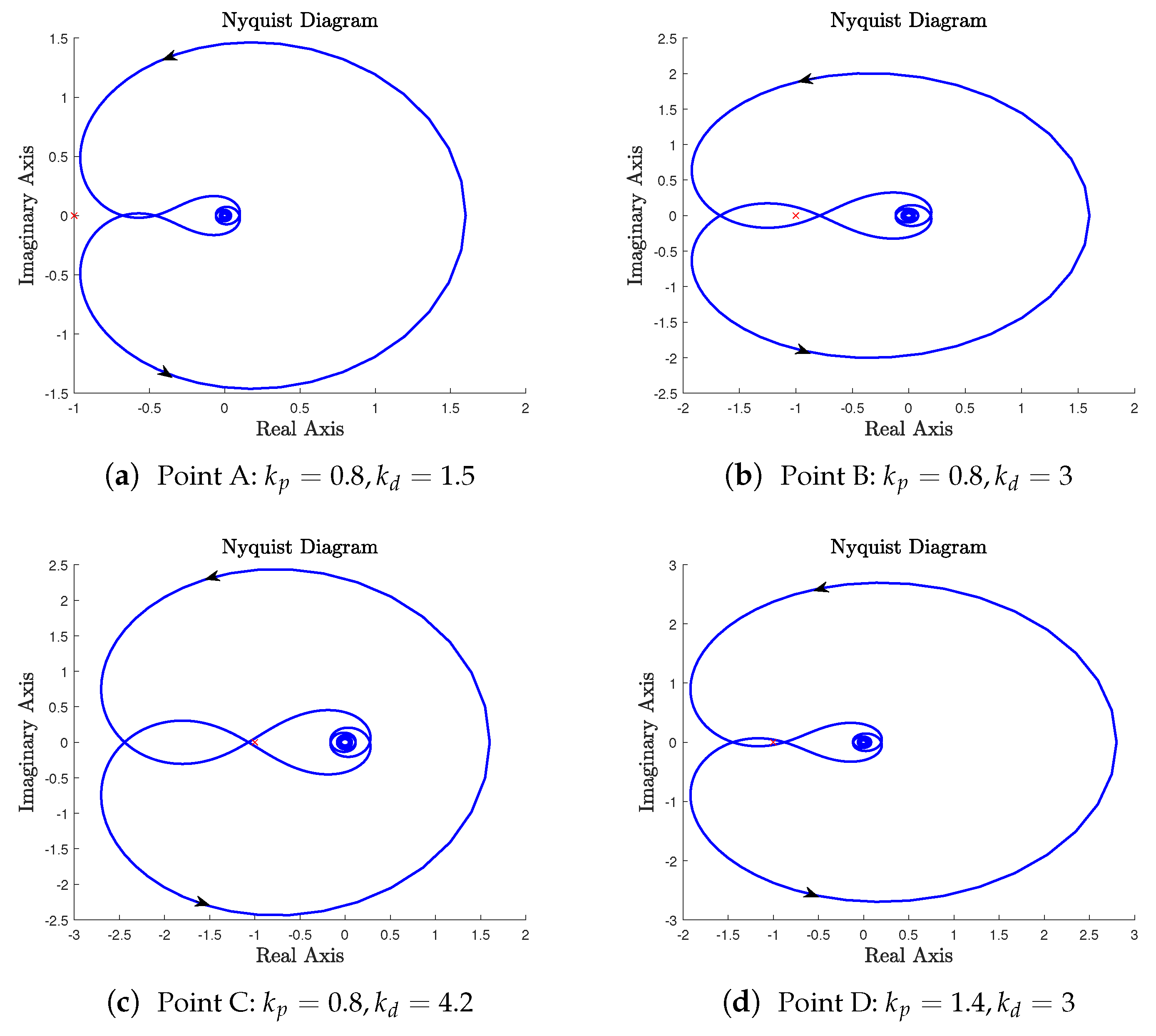


| A | B | C | D | |
|---|---|---|---|---|
| 0.8 | 0.8 | 0.8 | 1.4 | |
| 1.5 | 3 | 4.2 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Ma, D. Stabilization of Unstable Second-Order Delay Plants under PID Control: A Nyquist Curve Analysis. Actuators 2021, 10, 227. https://doi.org/10.3390/act10090227
Sun L, Ma D. Stabilization of Unstable Second-Order Delay Plants under PID Control: A Nyquist Curve Analysis. Actuators. 2021; 10(9):227. https://doi.org/10.3390/act10090227
Chicago/Turabian StyleSun, Li, and Dan Ma. 2021. "Stabilization of Unstable Second-Order Delay Plants under PID Control: A Nyquist Curve Analysis" Actuators 10, no. 9: 227. https://doi.org/10.3390/act10090227
APA StyleSun, L., & Ma, D. (2021). Stabilization of Unstable Second-Order Delay Plants under PID Control: A Nyquist Curve Analysis. Actuators, 10(9), 227. https://doi.org/10.3390/act10090227






