Trajectory Tracking Control for Reaction–Diffusion System with Time Delay Using P-Type Iterative Learning Method
Abstract
1. Introduction
2. Problem Formulation and Preliminaries
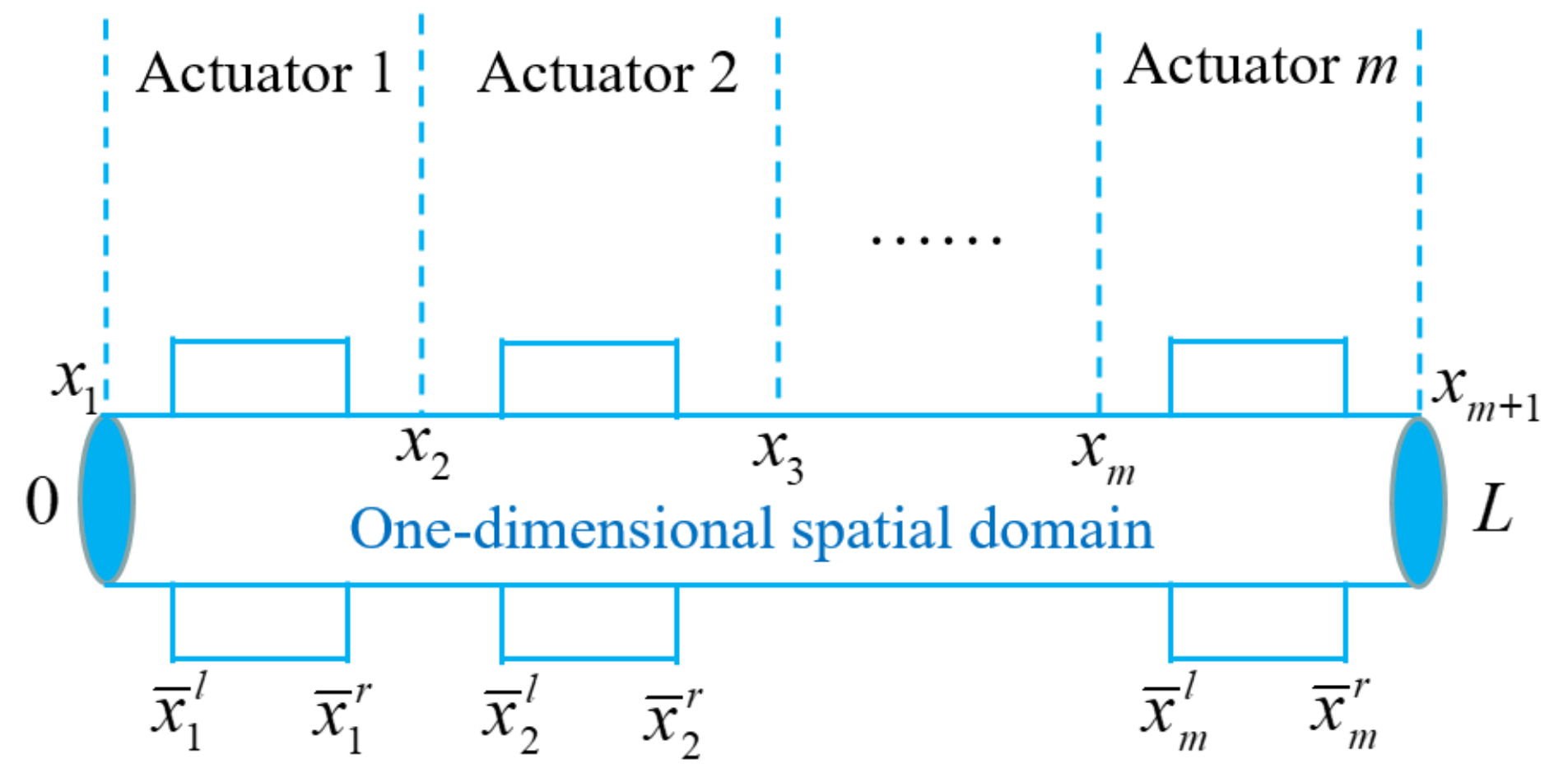
2.1. Problem Formulation
2.2. Preliminaries
3. Iterative Learning Control Design
3.1. Open-Loop P-Type Iterative Learning Control Design
3.2. Closed-Loop P-Type Iterative Learning Control Design
4. Convergence Analysis
4.1. Open-Loop ILC Convergence Analysis
4.2. Closed-Loop ILC Convergence Analysis
5. Numerical Simulation
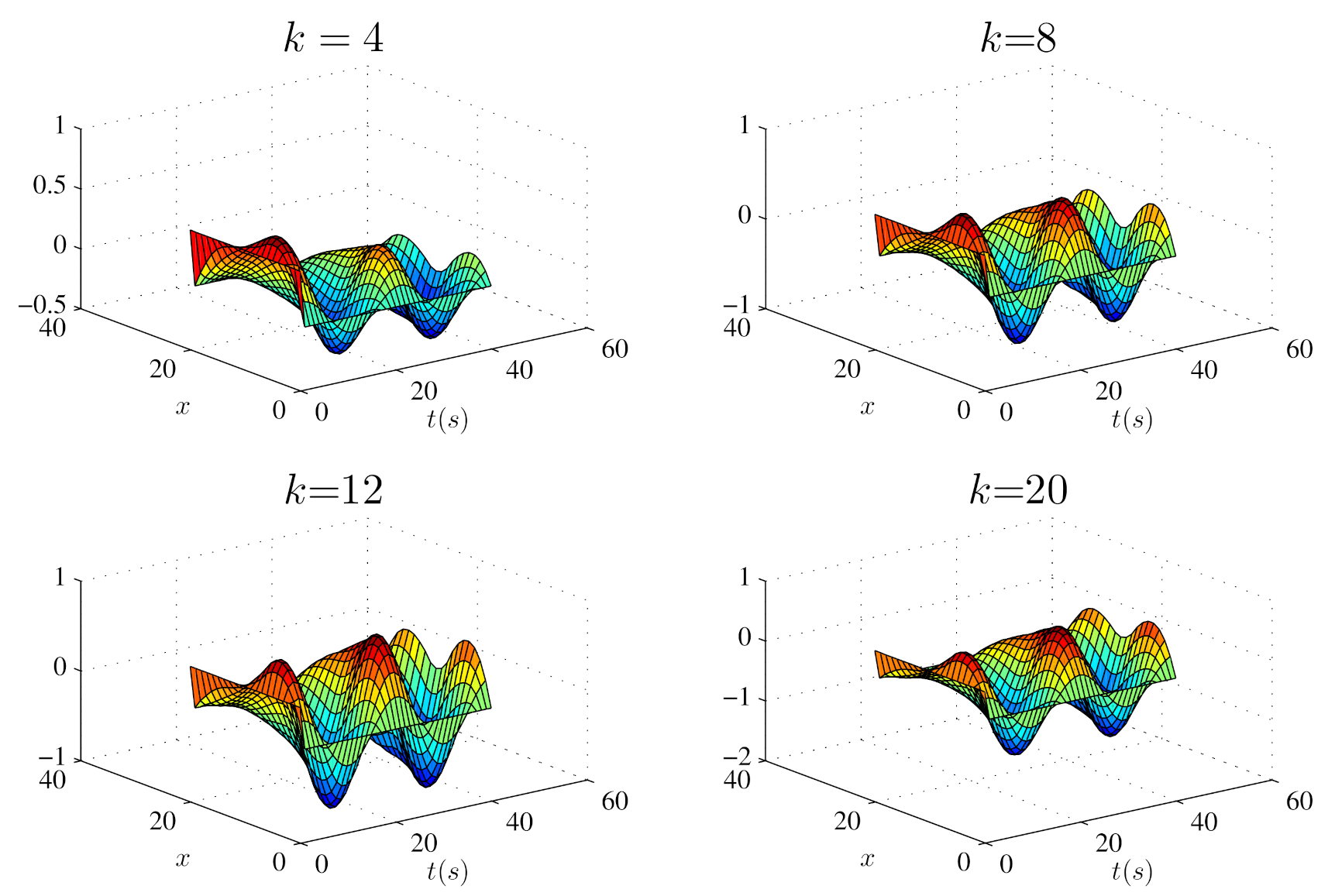
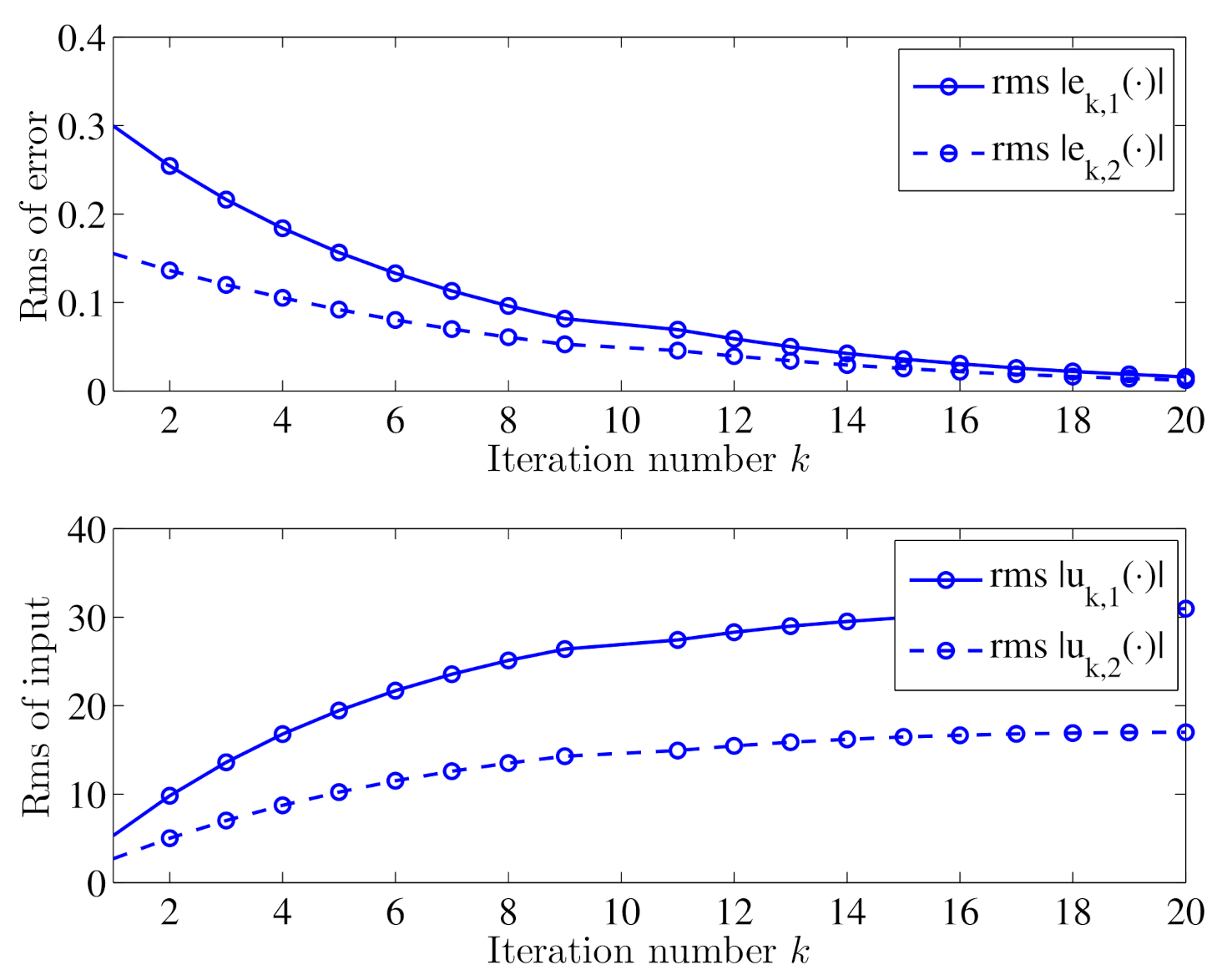
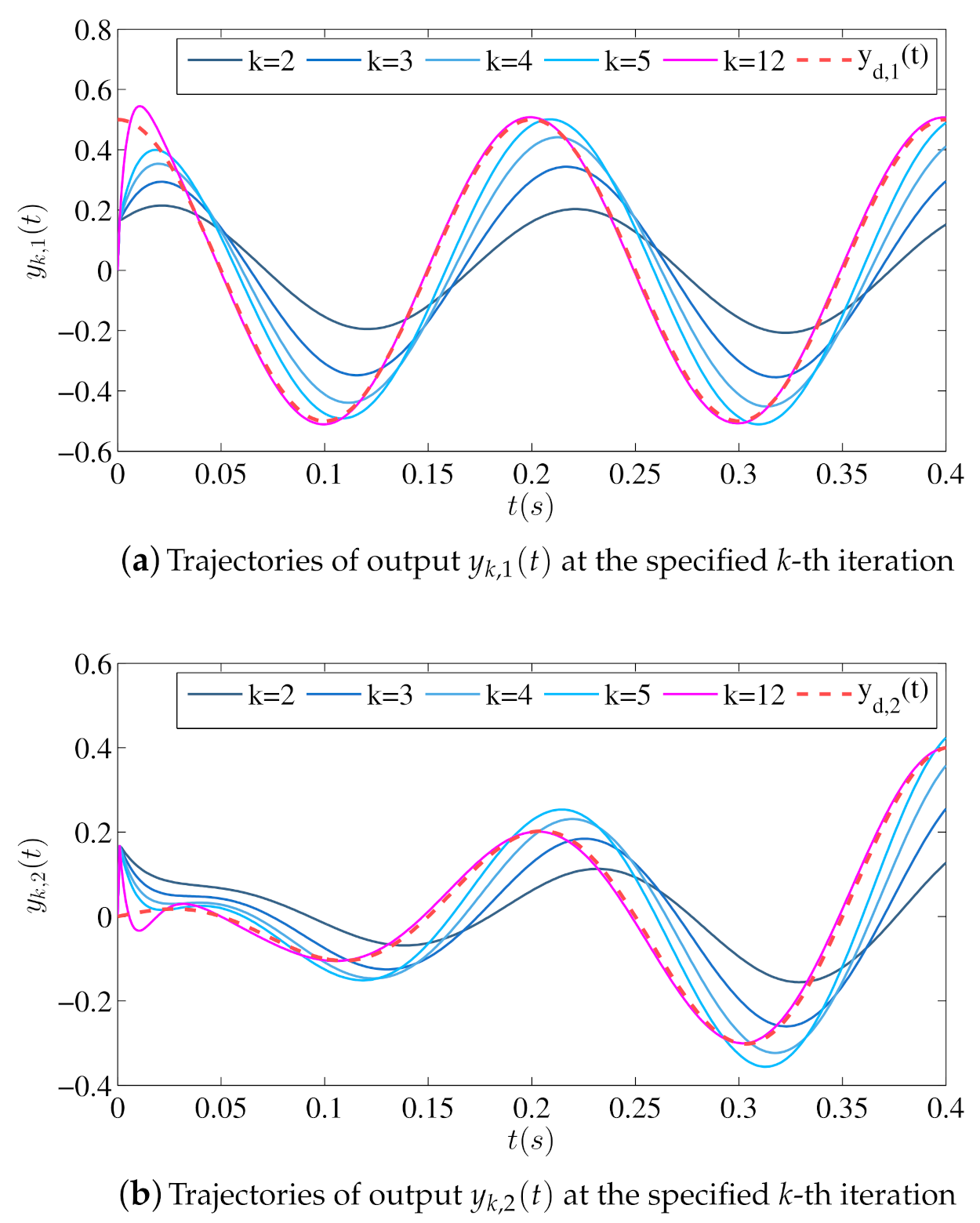
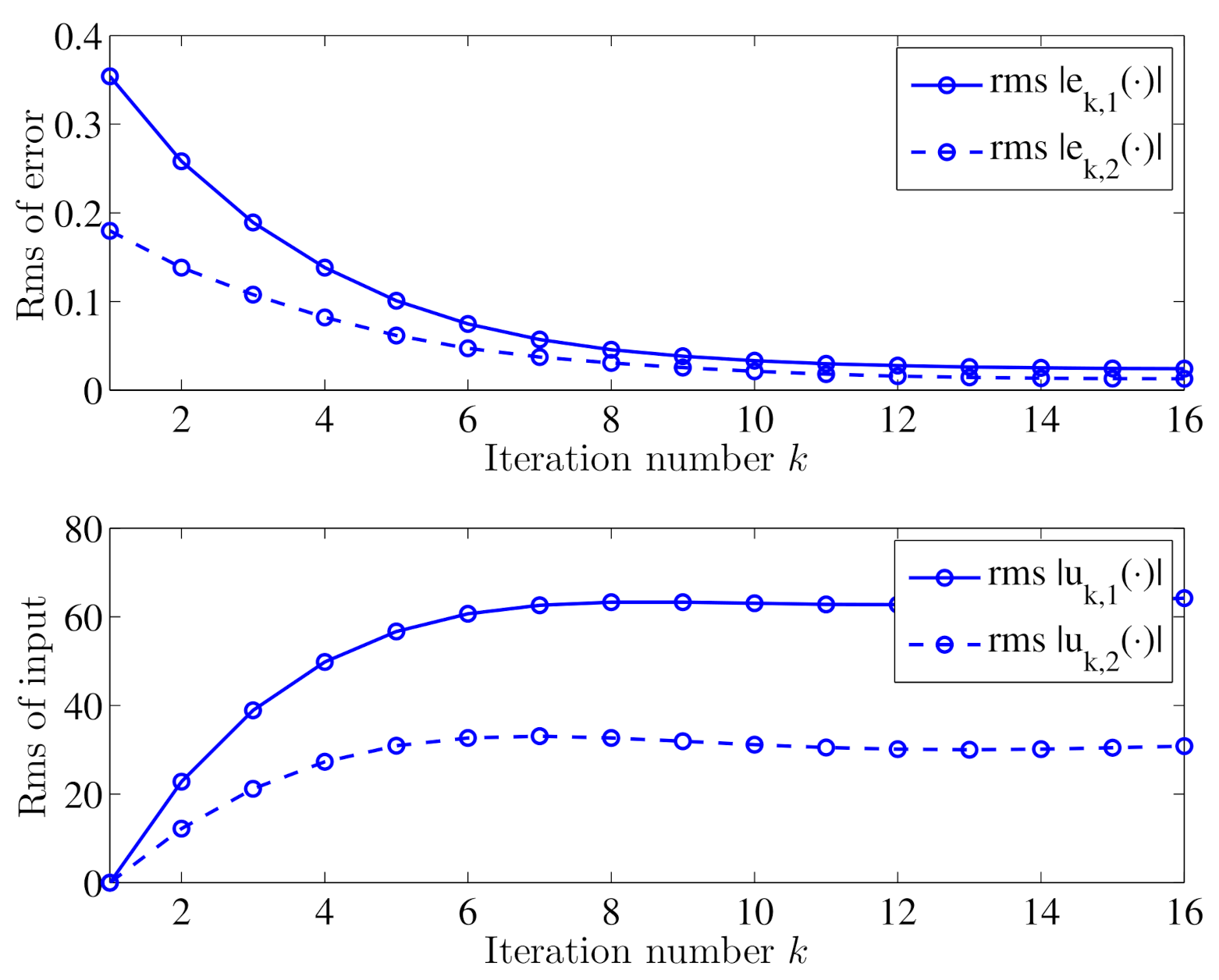
5.1. Open-Loop ILC Simulation
5.2. Closed-Loop ILC Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ILC | Iterative Learning Control |
| PDE | Partial Differential Equation |
| D-PDE | Delay Partial Differential Equation |
| MIMO | Multiple Inputs and Multiple Outputs |
| RMS | Root Mean Square |
References
- Wu, M.; He, Y.; She, J.H.; Liu, G.P. Delay-dependent criteria for robust stability of time-varying delay systems. Automatica 2004, 40, 1435–1439. [Google Scholar] [CrossRef]
- Wu, M.; He, Y.; She, J.H. New delay-dependent stability criteria and stabilizing method for neutral systems. IEEE Trans. Autom. Control. 2004, 49, 2266–2271. [Google Scholar] [CrossRef]
- He, Y.; Wu, M.; She, J.H.; Liu, G.P. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays. Syst. Control Lett. 2004, 51, 57–65. [Google Scholar] [CrossRef]
- Zhang, X.M.; Wu, M.; She, J.H.; He, Y. Delay-dependent stabilization of linear systems with time-varying state and input delays. Automatica 2005, 41, 1405–1412. [Google Scholar] [CrossRef]
- Zhang, C.K.; He, Y.; Jiang, L.; Wu, M. Stability analysis for delayed neural networks considering both conservativeness and complexity. IEEE Trans. Neural Netw. Learn. Syst. 2015, 27, 1486–1501. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Wu, M.; He, Y. Stubborn state estimation for delayed neural networks using saturating output errors. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1982–1994. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Zhang, X.M.; Wu, M.; Han, Q.L.; He, Y. Receding horizon synchronization of delayed neural networks using a novel inequality on quadratic polynomial functions. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–11. [Google Scholar] [CrossRef]
- Lin, Z.; Fang, H. On asymptotic stabilizability of linear systems with delayed input. IEEE Trans. Autom. Control 2007, 52, 998–1013. [Google Scholar] [CrossRef]
- Zhou, B.; Lin, Z.; Duan, G. Stabilization of linear systems with input delay and saturation–a parametric Lyapunov equation approach. Int. J. Robust Nonlinear Control 2010, 20, 1502–1519. [Google Scholar] [CrossRef]
- Zhou, B.; Gao, H.; Lin, Z.; Duan, G.R. Stabilization of linear systems with distributed input delay and input saturation. Automatica 2012, 48, 712–724. [Google Scholar] [CrossRef]
- Zhang, S.; Han, W.; Zhang, Y. Finite time convergence incremental nonlinear dynamic inversion-based attitude control for flying-wing aircraft with actuator faults. Actuators 2020, 9, 70. [Google Scholar] [CrossRef]
- Tran, M.T.; Lee, D.H.; Chakir, S.; Kim, Y.B. A novel adaptive super-twisting sliding mode control scheme with time-delay estimation for a single ducted-fan unmanned aerial vehicle. Actuators 2021, 10, 54. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Y.; He, H.; Sun, C. Team-triggered practical fixed-time consensus of double-integrator agents with uncertain disturbance. IEEE Trans. Cybern. 2020, 51, 3263–3272. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhang, Y.; Yu, Y.; Liu, H.; Sun, C. A Zeno-Free Self-Triggered Approach to Practical Fixed-Time Consensus Tracking With Input Delay. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Ji, H.; Hou, Z.; Fan, L. Multi-agent-based data-driven distributed adaptive cooperative control in urban traffic signal timing. Energies 2019, 12, 1402. [Google Scholar] [CrossRef]
- Wang, J.W.; Wu, H.N. Some extended Wirtinger’s inequalities and distributed proportional-spatial integral control of distributed parameter systems with multi-time delays. J. Frankl. Inst. 2015, 352, 4423–4445. [Google Scholar] [CrossRef]
- Wang, J.W.; Sun, C.Y. Delay-dependent exponential stabilization for linear distributed parameter systems with time-varying delay. J. Dyn. Syst. Meas. Control 2018, 140, 051003. [Google Scholar] [CrossRef]
- Wu, H.N. Delay-dependent stability analysis and stabilization for discrete-time fuzzy systems with state delay: A fuzzy Lyapunov–Krasovskii functional approach. IEEE Trans. Syst. Man Cybern. Part B 2006, 36, 954–962. [Google Scholar]
- Wu, H.N.; Li, H.X. New approach to delay-dependent stability analysis and stabilization for continuous-time fuzzy systems with time-varying delay. IEEE Trans. Fuzzy Syst. 2007, 15, 482–493. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N. Robust guaranteed cost sampled-data fuzzy control for uncertain nonlinear time-delay systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 964–975. [Google Scholar] [CrossRef]
- Wang, Z.P.; Wu, H.N.; Huang, T. Sampled-Data Fuzzy Control for Nonlinear Delayed Distributed Parameter Systems. IEEE Trans. Fuzzy Syst. 2020, 1. [Google Scholar] [CrossRef]
- Krstic, M. Delay Compensation for Nonlinear, Adaptive and PDE Systems; Spring: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ye, X. Adaptive stabilization of time-delay feedforward nonlinear systems. Automatica 2011, 47, 950–955. [Google Scholar] [CrossRef]
- Zhu, Y.; Krstic, M.; Su, H. Adaptive global stabilization of uncertain multi-input linear time-delay systems by PDE full-state feedback. Automatica 2018, 96, 270–279. [Google Scholar] [CrossRef]
- Zhang, H.; Pal, N.R.; Sheng, Y.; Zeng, Z. Distributed adaptive tracking synchronization for coupled reaction–diffusion neural network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1462–1475. [Google Scholar] [CrossRef]
- Steeves, D.; Camacho-Solorio, L.; Benosman, M.; Krstic, M. Prescribed-time tracking for triangular systems of reaction–diffusion PDEs. IFAC-PapersOnLine 2020, 53, 7629–7634. [Google Scholar] [CrossRef]
- Nevins, T.D.; Kelley, D.H. Front tracking for quantifying advection-reaction–diffusion. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 043105. [Google Scholar] [CrossRef]
- Cristofaro, A. Robust tracking control for a class of perturbed and uncertain reaction–diffusion equations. IFAC Proc. Vol. 2014, 47, 11375–11380. [Google Scholar] [CrossRef]
- Xu, J.X. A survey on iterative learning control for nonlinear systems. Int. J. Control 2011, 84, 1275–1294. [Google Scholar] [CrossRef]
- Bien, Z.; Xu, J.X. Iterative Learning Control: Analysis, Design, Integration and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Shen, D.; Wang, Y. Survey on stochastic iterative learning control. J. Process Control 2014, 24, 64–77. [Google Scholar] [CrossRef]
- Tayebi, A. Adaptive iterative learning control for robot manipulators. Automatica 2004, 40, 1195–1203. [Google Scholar] [CrossRef]
- Shi, J.; Xu, J.; Sun, J.; Yang, Y. Iterative Learning Control for time-varying systems subject to variable pass lengths: Application to robot manipulators. IEEE Trans. Ind. Electron. 2019, 67, 8629–8637. [Google Scholar] [CrossRef]
- Xing, X.; Liu, J. Modeling and robust adaptive iterative learning control of a vehicle-based flexible manipulator with uncertainties. Int. J. Robust Nonlinear Control 2019, 29, 2385–2405. [Google Scholar] [CrossRef]
- Dai, X.; Tian, S.; Peng, Y.; Luo, W. Closed-loop P-type iterative learning control of uncertain linear distributed parameter systems. IEEE/CAA J. Autom. Sin. 2014, 1, 267–273. [Google Scholar]
- Dai, X.S.; Tian, S.P.; Guo, Y.J. Iterative learning control for discrete parabolic distributed parameter systems. Int. J. Autom. Comput. 2015, 12, 316–322. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Cui, B.; Dai, X.; Jiang, Z. Iterative learning control for distributed parameter systems based on non-collocated sensors and actuators. IEEE/CAA J. Autom. Sin. 2019, 7, 865–871. [Google Scholar] [CrossRef]
- Dai, X.; Wang, C.; Tian, S.; Huang, Q. Consensus control via iterative learning for distributed parameter models multi-agent systems with time-delay. J. Frankl. Inst. 2019, 356, 5240–5259. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, B.; Lou, X.Y. Iterative learning control for semi-linear distributed parameter systems based on sensor-actuator networks. IET Control Theory Appl. 2020, 14, 1785–1796. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Tian, Y.; Dai, X. Iterative learning control-based tracking synchronization for linearly coupled reaction–diffusion neural networks with time delay and iteration-varying switching topology. J. Frankl. Inst. 2021, 358, 3822–3846. [Google Scholar] [CrossRef]
- He, W.; Meng, T.; Huang, D.; Li, X. Adaptive boundary iterative learning control for an Euler–Bernoulli beam system with input constraint. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1539–1549. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Meng, T.; He, X.; Ge, S.S. Unified iterative learning control for flexible structures with input constraints. Automatica 2018, 96, 326–336. [Google Scholar] [CrossRef]
- Meng, T.; He, W. Iterative Learning Control for Flexible Structures; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Liu, Y.Q.; Wang, J.W.; Sun, C.Y. Observer-based output feedback compensator design for linear parabolic PDEs with local piecewise control and pointwise observation in space. IET Control Theory Appl. 2018, 12, 1812–1821. [Google Scholar] [CrossRef]
- Wang, J.W.; Liu, Y.Q.; Sun, C.Y. Pointwise exponential stabilization of a linear parabolic PDE system using non-collocated pointwise observation. Automatica 2018, 93, 197–210. [Google Scholar] [CrossRef]
- Curtain Ruth, F.Z.H. An Introduction to Infinite-Dimensional Linear Systems Theory; Springer Science & Business Media: New York, NY, USA, 2012; Volume 2. [Google Scholar]

| Symbol | Explanation | Value |
|---|---|---|
| L | Spatial Length | 1 |
| T | Finite Time Interval | 0.4 |
| Model Parameter | 4 | |
| Delay-Model Parameter | 1 | |
| Time Delay Parameter | 0.1 | |
| Scalar Parameter | 1 | |
| Coefficient Parameter | 0.01 | |
| p | Lyapunov Parameter | 0.6272 |
| Scalar Parameter | 0.5824 | |
| Sampling Time | 0.001s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, J.; Jin, Z. Trajectory Tracking Control for Reaction–Diffusion System with Time Delay Using P-Type Iterative Learning Method. Actuators 2021, 10, 186. https://doi.org/10.3390/act10080186
Liu Y, Li J, Jin Z. Trajectory Tracking Control for Reaction–Diffusion System with Time Delay Using P-Type Iterative Learning Method. Actuators. 2021; 10(8):186. https://doi.org/10.3390/act10080186
Chicago/Turabian StyleLiu, Yaqiang, Jianzhong Li, and Zengwang Jin. 2021. "Trajectory Tracking Control for Reaction–Diffusion System with Time Delay Using P-Type Iterative Learning Method" Actuators 10, no. 8: 186. https://doi.org/10.3390/act10080186
APA StyleLiu, Y., Li, J., & Jin, Z. (2021). Trajectory Tracking Control for Reaction–Diffusion System with Time Delay Using P-Type Iterative Learning Method. Actuators, 10(8), 186. https://doi.org/10.3390/act10080186






