A Twisted String, Flexure Hinges Approach for Design of a Wearable Haptic Thimble
Abstract
:1. Introduction
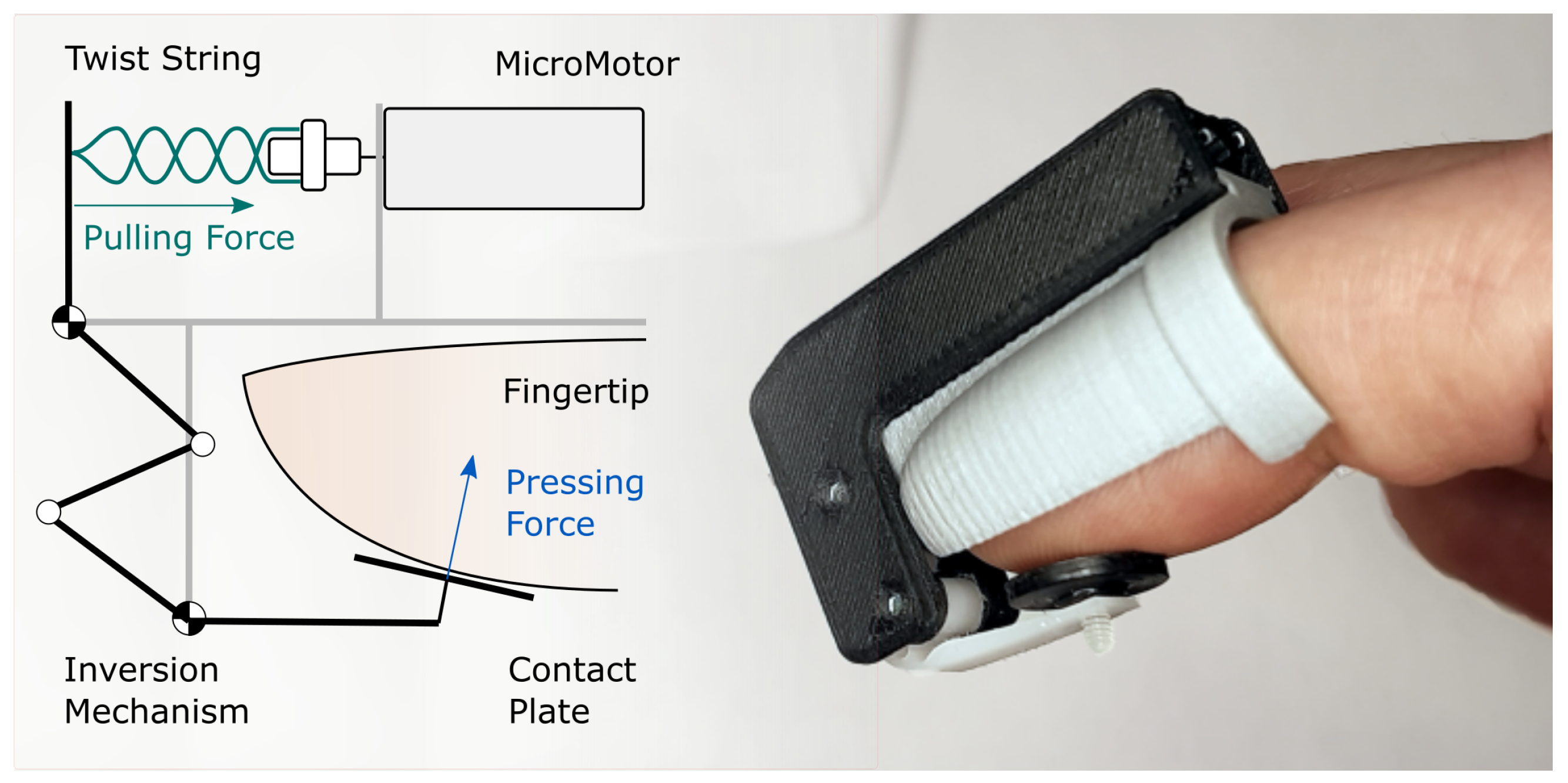
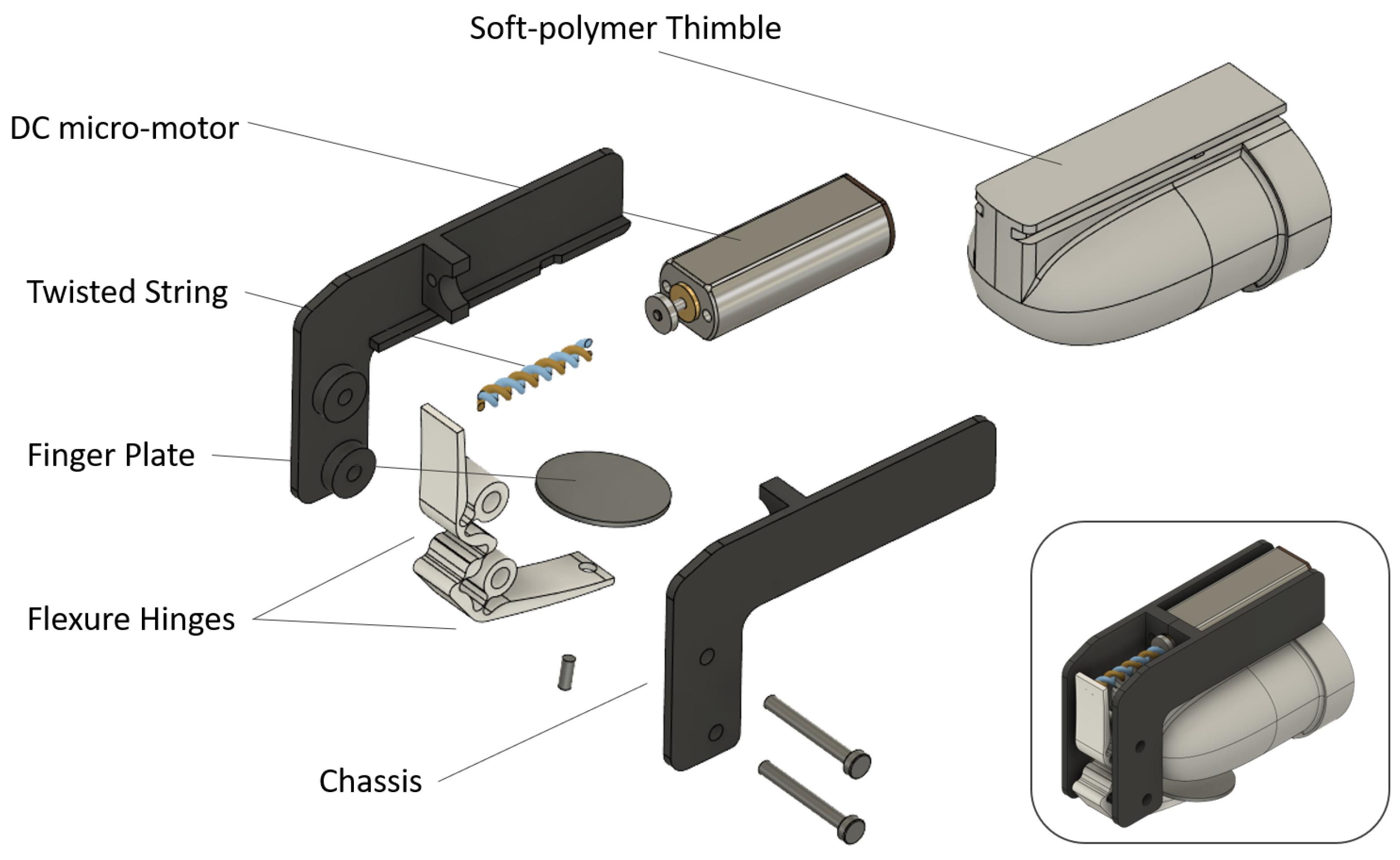
2. The Twisted String and Flexure Hinge Approach
- Compact and lightweight mechanism with respect to rotoidal joints with shaft and bearings.
- Limited number of moving parts.
- No introduced friction or backlash, relevant for high-quality haptic feedback.
- Residual elastic force needed to move the plate in the out of contact direction.
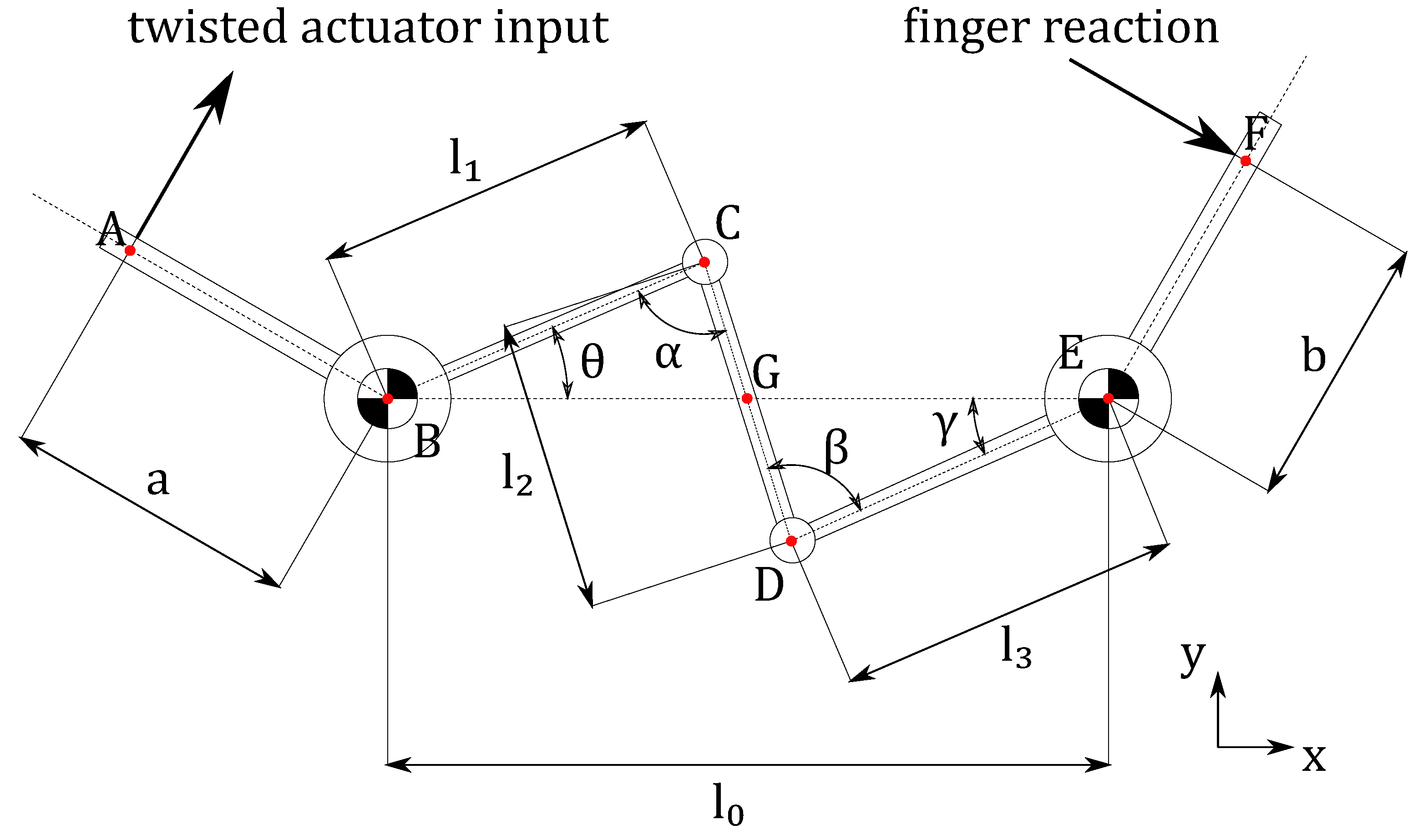
2.1. Synthesis and Optimization of the Mechanism
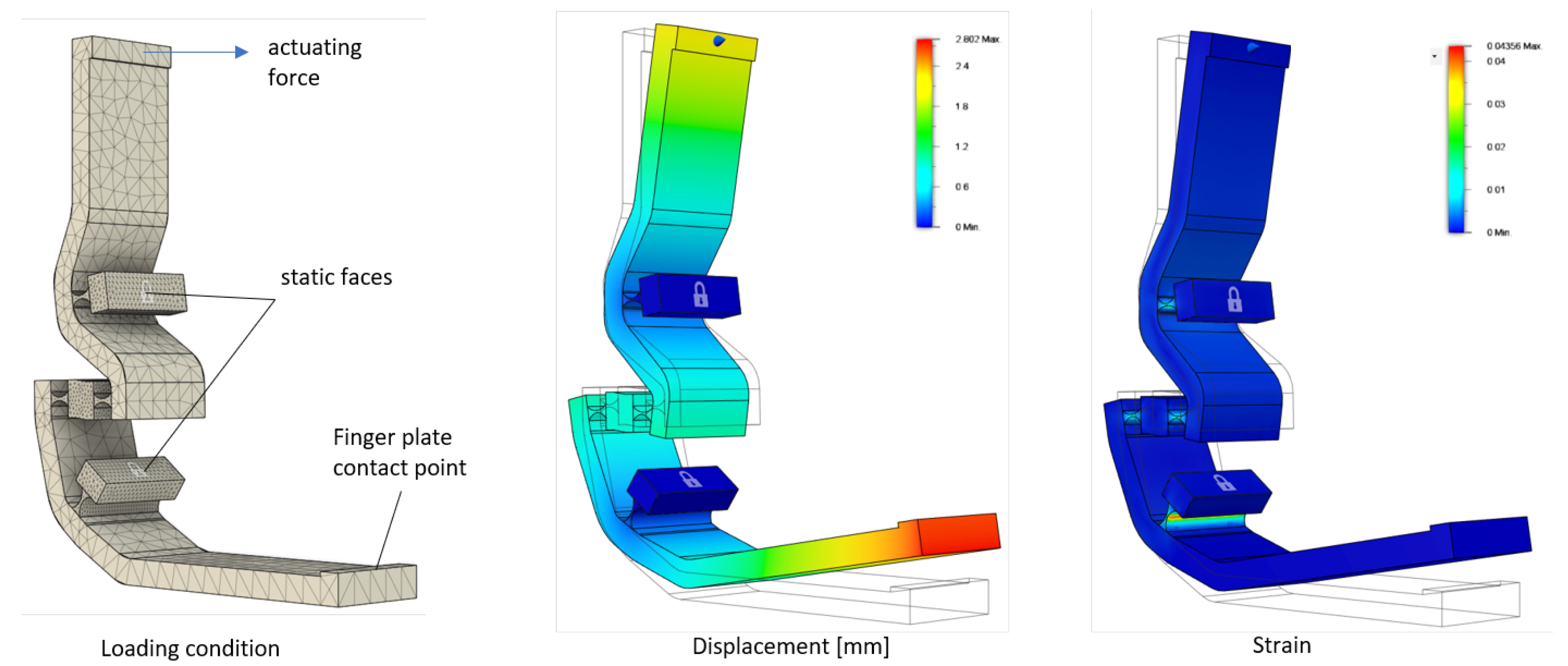
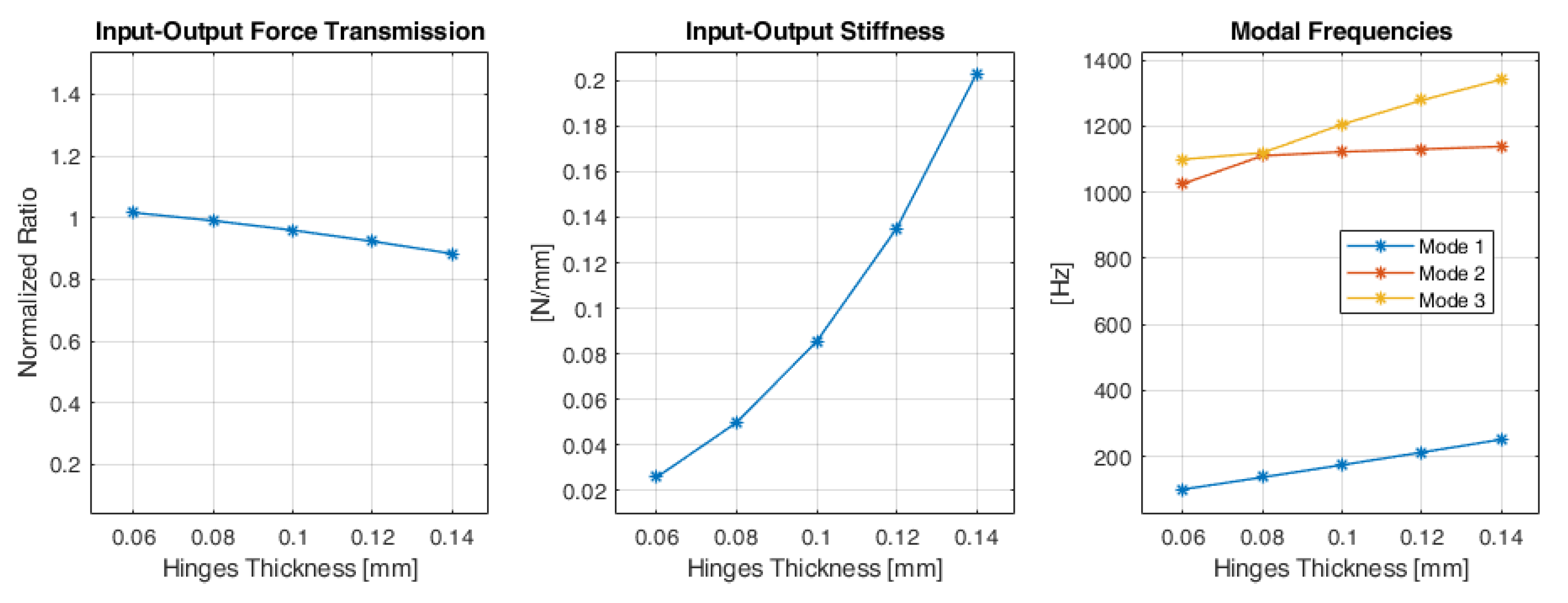
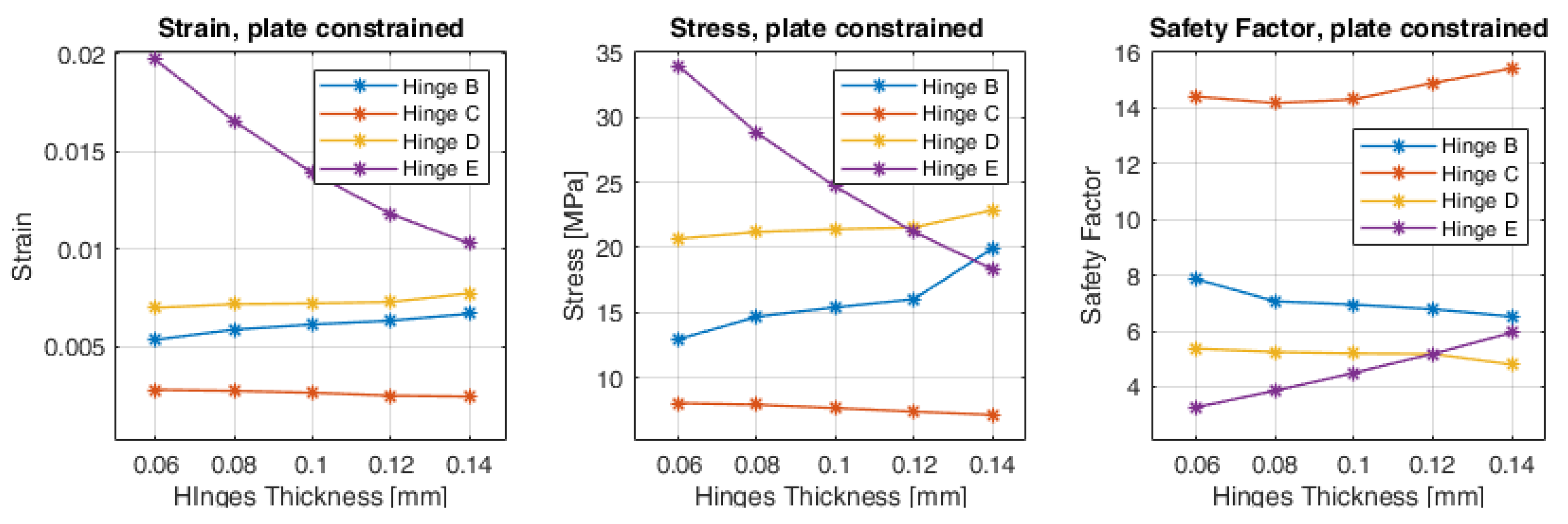
2.2. FEM Analysis of the Flexure Hinges
3. Design and Implementation of the Twisted String Haptic Thimble
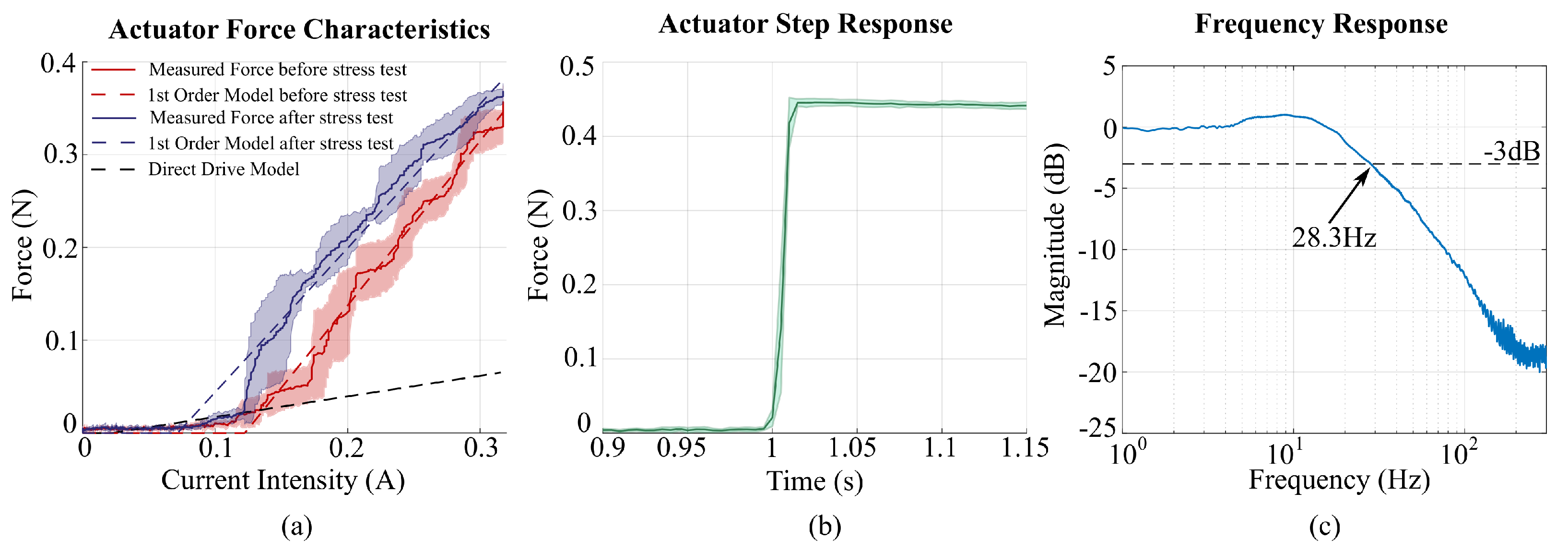
4. Experimental Characterization
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bortone, I.; Barsotti, M.; Leonardis, D.; Crecchi, A.; Tozzini, A.; Bonfiglio, L.; Frisoli, A. Immersive Virtual Environments and Wearable Haptic Devices in rehabilitation of children with neuromotor impairments: A single-blind randomized controlled crossover pilot study. J. Neuroeng. Rehabil. 2020, 17, 1–14. [Google Scholar] [CrossRef]
- Gutiérrez, Á.; Farella, N.; Gil-Agudo, Á.; de los Reyes Guzmán, A. Virtual Reality Environment with Haptic Feedback Thimble for Post Spinal Cord Injury Upper-Limb Rehabilitation. Appl. Sci. 2021, 11, 2476. [Google Scholar] [CrossRef]
- Klamt, T.; Schwarz, M.; Lenz, C.; Baccelliere, L.; Buongiorno, D.; Cichon, T.; DiGuardo, A.; Droeschel, D.; Gabardi, M.; Kamedula, M.; et al. Remote mobile manipulation with the centauro robot: Full-body telepresence and autonomous operator assistance. J. Field Robot. 2020, 37, 889–919. [Google Scholar] [CrossRef] [Green Version]
- Solazzi, M.; Frisoli, A.; Bergamasco, M. Design of a novel finger haptic interface for contact and orientation display. In Proceedings of the Haptics Symposium, Waltham, MA, USA, 25–26 March 2010; pp. 129–132. [Google Scholar]
- Chinello, F.; Malvezzi, M.; Pacchierotti, C.; Prattichizzo, D. Design and development of a 3RRS wearable fingertip cutaneous device. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Korea, 7–11 July 2015; pp. 293–298. [Google Scholar]
- Fani, S.; Ciotti, S.; Battaglia, E.; Moscatelli, A.; Bianchi, M. W-FYD: A wearable fabric-based display for haptic multi-cue delivery and tactile augmented reality. IEEE Trans. Haptics 2017, 11, 304–316. [Google Scholar] [CrossRef] [Green Version]
- Leonardis, D.; Solazzi, M.; Bortone, I.; Frisoli, A. A wearable fingertip haptic device with 3 DoF asymmetric 3-RSR kinematics. In Proceedings of the 2015 IEEE World Haptics Conference (WHC), Evanston, IL, USA, 22–26 June 2015; pp. 388–393. [Google Scholar]
- Sonar, H.A.; Gerratt, A.P.; Lacour, S.P.; Paik, J. Closed-loop haptic feedback control using a self-sensing soft pneumatic actuator skin. Soft Robot. 2020, 7, 22–29. [Google Scholar] [CrossRef]
- Feng, Y.L.; Fernando, C.L.; Rod, J.; Minamizawa, K. Submerged haptics: A 3-DOF fingertip haptic display using miniature 3D printed airbags. In Proceedings of the ACM SIGGRAPH 2017 Posters, Los Angeles, CA, USA, 30 July–3 August 2017; pp. 1–2. [Google Scholar]
- Gallo, S.; Rognini, G.; Santos-Carreras, L.; Vouga, T.; Blanke, O.; Bleuler, H. Encoded and crossmodal thermal stimulation through a fingertip-sized haptic display. Front. Robot. AI 2015, 2, 25. [Google Scholar] [CrossRef] [Green Version]
- Gabardi, M.; Chiaradia, D.; Leonardis, D.; Solazzi, M.; Frisoli, A. A high performance thermal control for simulation of different materials in a fingertip haptic device. In International Conference on Human Haptic Sensing and Touch Enabled Computer Applications; Springer: Heidelberg, Germany, 2018; pp. 313–325. [Google Scholar]
- Wang, D.; Ohnishi, K.; Xu, W. Multimodal Haptic Display for Virtual Reality: A Survey. IEEE Trans. Ind. Electron. 2019, 67, 610–623. [Google Scholar] [CrossRef]
- Pacchierotti, C.; Sinclair, S.; Solazzi, M.; Frisoli, A.; Hayward, V.; Prattichizzo, D. Wearable haptic systems for the fingertip and the hand: Taxonomy, review, and perspectives. IEEE Trans. Haptics 2017, 10, 580–600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leonardis, D.; Solazzi, M.; Bortone, I.; Frisoli, A. A 3-RSR haptic wearable device for rendering fingertip contact forces. IEEE Trans. Haptics 2016, 10, 305–316. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.H.; Kim, K.S. A 2-speed small transmission mechanism based on twisted string actuation and a dog clutch. IEEE Robot. Autom. Lett. 2018, 3, 1338–1345. [Google Scholar] [CrossRef]
- Rodriguez, A.S.M.; Hosseini, M.; Paik, J. A hybrid control strategy for force and precise end effector positioning of a twisted string actuator. IEEE/ASME Trans. Mechatron. 2020. [Google Scholar] [CrossRef]
- Cho, K.H.; Song, M.G.; Jung, H.; Park, J.; Moon, H.; Koo, J.C.; Nam, J.D.; Choi, H.R. A robotic finger driven by twisted and coiled polymer actuator. Electroactive Polymer Actuators and Devices (EAPAD) 2016. Int. Soc. Opt. Photonics 2016, 9798. [Google Scholar] [CrossRef]
- Hosseini, M.; Meattini, R.; Palli, G.; Melchiorri, C. A wearable robotic device based on twisted string actuation for rehabilitation and assistive applications. J. Robot. 2017, 2017. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, M.; Sengül, A.; Pane, Y.; De Schutter, J.; Bruyninck, H. Exoten-glove: A force-feedback haptic glove based on twisted string actuation system. In Proceedings of the 2018 27th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Nanjing, China, 27–31 August 2018; pp. 320–327. [Google Scholar]
- Pepe, A.; Hosseini, M.; Scarcia, U.; Palli, G.; Melchiorri, C. Development of an haptic interface based on twisted string actuators. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 28–33. [Google Scholar]
- Van, Q.H.; Harders, M. Augmenting contact stiffness in passive haptics—Preliminary results with twisted string actuation. In Proceedings of the 2017 IEEE World Haptics Conference (WHC), Munich, Germany, 6–9 June 2017; pp. 148–153. [Google Scholar]
- Leonardis, D.; Tiseni, L.; Chiaradia, D.; Frisoli, A. Design of a Twisted String Actuated Haptic Thimble for Cutaneous Force Feedback. In The International Conference of IFToMM ITALY; Springer: Heidelberg, Germany, 2020; pp. 145–153. [Google Scholar]
- Leonardis, D.; Gabardi, M.; Solazzi, M.; Frisoli, A. A Parallel Elastic Haptic Thimble for Wide Bandwidth Cutaneous Feedback. In International Conference on Human Haptic Sensing and Touch Enabled Computer Applications; Springer: Heidelberg, Germany, 2020; pp. 389–397. [Google Scholar]
- Gleeson, B.T.; Horschel, S.K.; Provancher, W.R. Design of a fingertip-mounted tactile display with tangential skin displacement feedback. IEEE Trans. Haptics 2010, 3, 297–301. [Google Scholar] [CrossRef]
- Brown, J.D.; Ibrahim, M.; Chase, E.D.; Pacchierotti, C.; Kuchenbecker, K.J. Data-driven comparison of four cutaneous displays for pinching palpation in robotic surgery. In Proceedings of the 2016 IEEE Haptics Symposium (HAPTICS), Philadelphia, PA, USA, 8–11 April 2016; pp. 147–154. [Google Scholar]
- Gabardi, M.; Solazzi, M.; Leonardis, D.; Frisoli, A. A new wearable fingertip haptic interface for the rendering of virtual shapes and surface features. In Proceedings of the 2016 IEEE Haptics Symposium (HAPTICS), Philadelphia, PA, USA, 8–11 April 2016; pp. 140–146. [Google Scholar]




| Population Size | 400 |
| Max. Generations | 1000 |
| Function Tolerance | 1 × 10 |
| Max. Stall Generations | 100 |
| Crossover Function | Scattered |
| Selection Function | Tournament, 4 |
| Mutation Function | Adaptive & Feasible |
| Crossover Fraction | 0.5 |
| Elite Count | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonardis, D.; Tiseni, L.; Chiaradia, D.; Frisoli, A. A Twisted String, Flexure Hinges Approach for Design of a Wearable Haptic Thimble. Actuators 2021, 10, 211. https://doi.org/10.3390/act10090211
Leonardis D, Tiseni L, Chiaradia D, Frisoli A. A Twisted String, Flexure Hinges Approach for Design of a Wearable Haptic Thimble. Actuators. 2021; 10(9):211. https://doi.org/10.3390/act10090211
Chicago/Turabian StyleLeonardis, Daniele, Luca Tiseni, Domenico Chiaradia, and Antonio Frisoli. 2021. "A Twisted String, Flexure Hinges Approach for Design of a Wearable Haptic Thimble" Actuators 10, no. 9: 211. https://doi.org/10.3390/act10090211
APA StyleLeonardis, D., Tiseni, L., Chiaradia, D., & Frisoli, A. (2021). A Twisted String, Flexure Hinges Approach for Design of a Wearable Haptic Thimble. Actuators, 10(9), 211. https://doi.org/10.3390/act10090211








