Abstract
The development of powered assistive devices that integrate exoskeletal motors and muscle activation for gait restoration benefits from actuators with low backdrive torque. Such an approach enables motors to assist as needed while maximizing the joint torque muscles, contributing to movement, and facilitating ballistic motions instead of overcoming passive dynamics. Two electromechanical actuators were developed to determine the effect of two candidate transmission implementations for an exoskeletal joint. To differentiate the transmission effects, the devices utilized the same motor and similar gearing. One actuator included a commercially available harmonic drive transmission while the other incorporated a custom designed two-stage planetary transmission. Passive resistance and mechanical efficiency were determined based on isometric torque and passive resistance. The planetary-based actuator outperformed the harmonic-based actuator in all tests and would be more suitable for hybrid exoskeletons.
1. Introduction
With an estimated 17,000 new cases of spinal cord injury (SCI) per year [1], restoration of standing and walking are consistently rated as top priorities for people with SCI [2,3,4]. Commercial exoskeletons provide interventions for improving mobility after paralysis [5,6,7]. These devices have been optimized for functional replacement, with the robotic device providing all of the joint torques required for motion. This approach is effective for people without any volitional movement. These robot-enabled gait devices typically follow pre-programmed kinematic trajectories, without any influence from the user. With this control scheme, passive dynamics such as joint friction are not an important consideration in the design process; instead, the focus is on overall device size, weight, and ease of use. In many ways, the goal is to make a robotic system that is as unintrusive to the wearer as possible.
Individuals with partial paralysis such as incomplete spinal cord injury, stroke, or multiple sclerosis may also benefit from active exoskeletal assistance [8,9,10,11,12]. A substantial difference in approach for these user populations is that the goal is for the robot to augment the user’s capabilities instead of producing the entire motion. A similar idea has been explored in hybrid systems for people with complete SCI where the biological torque component is supplied by Neuromuscluar Electrical Stimulation (NMES). Previous work in this area of hybrid human/orthotic gait restoration came in a variety of architectures, with the bracing ranging from passive exoskeletons [13], to semi-active orthoses with variable joint constraints [14,15,16], to fully active exoskeletons [17,18,19,20].
There is an additional important design criterion for hardware components in cooperative robot applications incorporating users’ muscle contributions. The goal of unintrusive hardware is maintained, however the definition of unintrusive expands for hybrid systems. In addition to physical properties such as size and mass, passive dynamics such as friction become critical for joint torques from muscles to generate movement rather than being lost to the friction of the system; these systems aim to extract as much propulsive effort from the wearer as possible.
Prior work engineering backdrivable actuators for hybrid human/robot cooperative applications has taken a variety of architectures and forms. Hydraulic approaches [21,22] have the advantage of remotely positioning the motor/pump, and thus minimizing the device weight collocated with the user’s limb. Despite being power dense, small scale hydraulics typically suffer from low efficiency. Electro-mechanical solutions have been researched in a variety of configurations, but all include an electric motor and transmission. The style of transmissions used varies widely. Examples include a single planetary gearbox plus one belt reduction stage [23], a single stepped planetary gearbox [24], a one stage belt/chain reduction [25], and a harmonic drive [17,19].
Selecting the size and style of transmission gearing is a complicated design decision based on the relative importance of several desired actuator properties. Small transmission ratio (low gearing) actuators tend to have low passive resistance and low part counts, but require large motors (and large motor currents) to achieve desired output torque. This may not be feasible when maintaining small actuator size or electrical current limits are important requirements. Large transmission ratios (very high gearing) can result in a more compact actuator at the expense of mechanical complexity, high part count, and excessive noise. With the diverse choices for implementation, it becomes difficult to determine specific solutions for new applications. The goal of this work is to assist in that decision process by directly comparing two compact, power dense approaches.
Harmonic drives and planetary gears are the focus of this study due to their ability to provide substantial gearing reduction within a compact form factor. Planetary gear mechanisms consist of three primary components—the internal sun gear, the external ring gear, and intermediate planet gears and their carrier [26]. In its simplest form, a constant gear ratio is formed by fixing one of these components, treating one as an input, and one as an output. For maximum gear reduction, the ring gear is fixed, the sun gear is treated as the input, and the planet carrier is treated as output. Dividing the input torque load amongst multiple planet gears allows for a smaller size compared to a single spur gear mesh of equivalent torque/gear ratio. Multiple stages can be implemented concentrically for greater reduction in a compact package.
The structure of a harmonic drive is similar to a planetary gear set—it consists of an input wave generator (analogous to a sun gear), a rigid circular spline (a circular, internally splined piece that functions much like a planetary ring gear), and a flexspline—a cup shaped, externally splined part similar to the planetary gears/carrier [27]. In operation, the circular spline is fixed, the wave generator (which features an eccentric bearing) is treated as the transmission input, and the flexspline is deformed under the influence of the wave generator, resulting in its external teeth ratcheting around the internal teeth of the circular spline. This creates a large gear reduction—anywhere from 50:1 to 150:1. This unique structure and operation results in several non-linear dynamic elements in use [27] that require additional design consideration (for example—a more robust input and output bearing to handle radial forces and vibrations that are not found in other transmissions). Despite these complexities, the compact design and low backlash qualities of harmonic drives make them a favored choice in applications with strict packaging and precision requirements.
While it is convenient to evaluate an actuator’s performance in isolation, the interplay between motor and transmission makes it more difficult to draw conclusions about the value of different transmission implementations between technologies. This study compares two joint actuators that were designed and constructed with these two different gearbox styles. The actuators incorporate identical motors and similar gear ratios to directly compare their potential as transmissions for hybrid exoskeleton applications. Bench top testing results evaluating the passive resistance, torque production capacity, and efficiency of these two transmission were performed to determine which approach is more appropriate for hybrid applications.
2. Methods: Mechatronic Design
2.1. Design Requirements
This work was motivated by the goal of determining appropriate actuators for muscle-first, gait restoration systems capable of matching gait speeds of able-bodied populations. Independent community ambulation requires walking at speeds greater than 1.2 m/s [28,29,30]. The necessary joint speeds for a robotic exoskeleton actuator were determined based on a prior study with a semi-active exoskeleton featuring hydraulic cylinders located bilaterally at the hip and knee [31]. Able-bodied participants walked as quickly as possible while angular velocities were measured at each joint. Walking at an average speed of 1.2 m/s resulted in a mean peak knee velocity of 234 deg/sec (individual maximums ranged from 169 to 328 deg/sec) and a mean peak hip angular velocity of 128 deg/sec (ranging from 117 to 142 deg/sec).
Torque requirements were difficult to define due to the hybrid nature of the systems. These actuators are for a hybrid system that supplements torque generated by the user’s muscles rather than to produce enough torque to move the joint by themselves. As a point of comparison, an exoskeleton with bilaterial hip and knee actuators capable of 40 Nm peak torque was able to restore gait to 0.22 m/s to a subject with a T10 complete SCI [32]. Other projects have reported peak torques in a similar range—36 Nm [17], 30 Nm [33], and 60 Nm [23]. For this work, a torque requirement was not defined—the objective was to achieve the necessary joint velocities (which defined the necessary gearing) as described above. However, the actuators were designed to be comparable in output torque to similar robotic systems.
2.2. Implementation
The two actuators consisted of the same motor and brake, similar internal frame, along with similar gearing ratios so the system could achieve the target knee angular velocities. The primary difference was that one actuator used a harmonic drive type transmission, while the other employed a custom two stage planetary gearbox.
The two units had comparable dimensions and overall designs (Figure 1). An ANSI size 25 roller chain connected the motor/brake unit to the transmission. Each actuator was the same size (231.8 mm long, 108 mm wide, and 76.7 mm deep) and mass (2.1 kg), and was small/light enough to be considered for biomedical exoskeleton applications. 50:1 overall gearing was targeted for each design—at 28.8 V (system voltage used in prior work [17]), the motor would spin at 3860 RPM without any load, and 463 deg/sec. output after the 50:1 reduction. Even accounting for unknown inefficiencies, this is higher than necessary for walking at speeds necessary for community ambulation.

Figure 1.
Top and side views of the actuators.
2.2.1. Motor/Brake Integration
Both units incorporated a brushless DC motor (Maxon Motors part No. 543673) and solenoid brake (Thomson Linear part No. SB-17B12-E04S). The motor was frameless, with only the rotor and stator supplied by the vendor, which allowed for customized integration leading to a compact design. For this application, a double ended shaft was engineered to allow the motor and brake to be stacked concentrically. A spherical ball bearing was press fit into the housing, and the two pieces of the shaft were clamped around it as shown in Figure 2. The second end of the shaft exited through the motor, and had an ANSI size 25 roller chain sprocket attached with set screws. Sprocket size varied between the two transmission implementations. A small electromagnetic solenoid brake was incorporated on the high speed side of the system, which multiplied the brake torque based on the gearing.
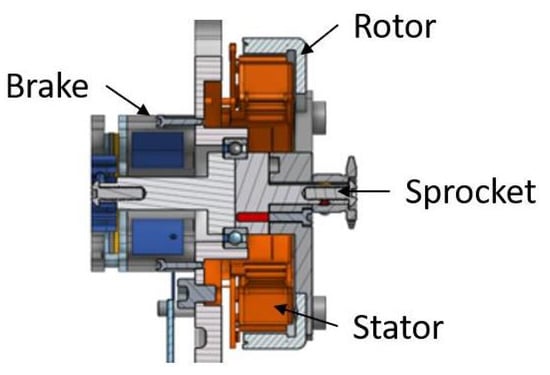
Figure 2.
Cutaway view of the motor/brake integration. This shows the double ended shaft and internal spherical roller bearing.
2.2.2. Harmonic Drive Integration
We selected a 50:1 reduction harmonic drive for this work (Part No. CCD-20-50-C-I, China Harmonic Drive). The input roller chain had a 1:1 transmission ratio which resulted in an overall transmission ratio of 50:1. The transmission was entirely self-contained, with a transmission and output cross roller bearing both integrated into a steel housing. A small spherical roller bearing was press fit into the housing to support the shaft attached to the wave generator.
2.2.3. Planetary Gearbox Integration
The planetary gearbox (Figure 3) consisted of two stages, with gear selection summarized below. In both stages, the sun gear was the input to the planetary and the ring gear was stationary while the planet carrier was the output. The two stages were housed in an aluminum casing, which contained a spherical roller bearing for the first stage sun gear/input sprocket. Both gear stages used four planet gears. The output of the second stage was held by a cross roller bearing embedded in the frame of the actuator.
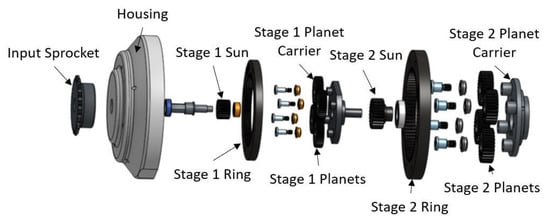
Figure 3.
An exploded view of the two stage planetary transmission.
To eliminate precision concentricity issues during manufacturing and operation, the ring gears were mounted with shoulder bolts in oversized clearance holes, which allowed them to float during operation. This floating gear allowed for the ring gears to shift for equal tooth force distribution, and eliminated high contact points that could produce areas of excessive passive resistance during operation due to errors in ring gear concentricity.
The first stage of gearing consisted of 0.5 mm module gears, and featured a 5.17:1 reduction ratio. The second stage of gearing consisted of 0.8 mm module gears, and featured a 4.33:1 reduction ratio. Combined with the 2.11:1 reduction ratio of the initial chain drive, this resulted in an overall reduction ratio of 47.3:1. All gears were made from unhardened 1045 steel and sourced from KHK Gear. Under maximum motor torque (1.07 Nm), the minimum factor of safety in all gears was 3.14, as calculated by the Lewis equation for gear tooth strength [34]. A summary of gear parameters and stress is found in Table 1.

Table 1.
A summary of gear parameters for the planetary gearbox.
2.3. Actuator Evaluation
Actuator bench testing was performed to determine isometric (zero speed) torque and passive resistance qualities of each transmission. Relationships between current and torque and current and steady state velocity were measured. The data were integrated to determine the net torque operating envelope. A custom control board controlled the actuator. The control board was comprised of a microcontroller, motor controller (Maxon Motors unit part No. 438725), and custom sensor input/processing. The motor controller could provide a 5 A continuous motor current, and peaks (3–5 s in length) of up to 15 A. The motor controller was operated in a closed-loop current control mode with a PI controller. It provided motor current and motor speed sensor signals. Motor speed was converted to joint speed with the known gear ratio.
2.3.1. Isometric Torque
Isometric torque is defined as the relationship between output torque and motor current at zero speed. Prior research established this relationship for electromechanical actuators to be linear [35,36]—the bench testing was performed to determine the slope (isometric torque constant, expressed as Nm per A) of that line. To determine this constant, the output arm of the actuator was attached to a load cell (JR3) that was fixed in place (Figure 4). Resultant torque was measured for a sequence of applied currents ranging from one to eight Amps, in one Amp increments. Each current command was issued for three seconds. Motor current and output torque were collected at 100 Hz. Torque data was only considered at steady state—early transient data in the three second period were discarded.

Figure 4.
Isometric Test Setup.
2.3.2. Passive Resistance
Passive resistance was determined as the torque required to move the actuator at a given speed without the presence of an external load. The procedure followed here was similar to what has been done by others when evaluating actuators [25]. Prior work has established that passive resistance for these types of devices is predominantly a function of joint speed [37,38]. The output arm was removed during this test to allow continuous rotation of the output stage. A continually increasing current command was sent to the motor, which began at zero current and increased at 0.25 A/sec. That rate was determined to be slow enough to approximate steady state. With the output arm removed, the only resistance to movement was the actuator’s internal friction. Motor speed (converted into joint speed via the known gear ratio) and motor current were recorded from the motor controller. Using the isometric current constant, this current command was translated into a torque. Polynomial trend lines were fit to the passive resistance data. Trend line powers were increased until a sufficiently good fit ( greater than 0.97) was achieved.
2.3.3. Net Torque Operating Envelope
Actuator net torque was calculated as the difference between isometric torque () and passive resistance torque () as shown in Equation (1). In this equation, represents the net actuator torque (Nm), is the actuator isometric torque constant, I is the motor current, and is the actuator passive resistance (as a function of joint speed). and were derived from the isometric torque testing and passive resistance testing, respectively. This represents the torque available to undertake useful work.
2.3.4. Mechanical Efficiency
The isometric torque and passive resistance test results were also combined to calculate mechanical efficiency of each gearbox, computed as the ratio of actuator input power (mechanical power delivered by the motor) to actuator output power. Motor power (mechanical power developed by the motor prior to the gearbox) was calculated according to the manufacturer’s specifications, as shown in the equation below.
In this equation, I is the motor current, is the actuator joint speed, n is the actuator gear ratio, is the manufacturer’s specified motor isometric torque constant (0.071 Nm/A, specified as constant across the entire speed range). These values are combined to calculate the motor power, . Output power is calculated according to the equation below:
In this equation, is the net actuator torque, taken from the bench testing. The actuator joint speed is represented by . Mechanical efficiency () was calculated as the ratio of output to input power.
3. Results
3.1. Isometric Torque
Isometric torque results are shown in Figure 5. The actuator with the planetary transmission generated significantly higher torque for a given current for all tested currents. On average, the planetary gearbox produced 3.39 Nm/A of commanded current, compared to 2.07 Nm/A for the harmonic gearbox. At maximum current (15 A), the planetary gearbox is capable of 50.9 Nm torque, compared to 31.1 Nm for the harmonic gearbox (extrapolated from testing results).
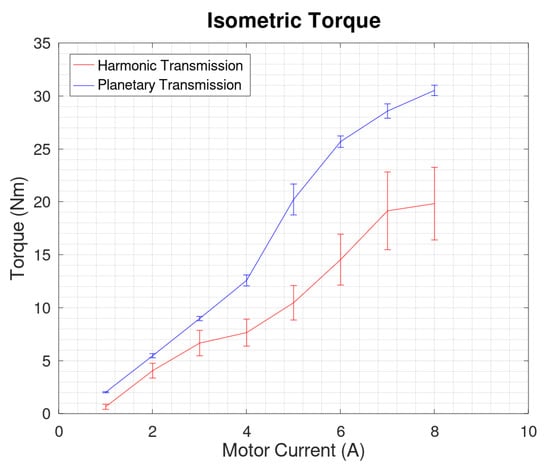
Figure 5.
Transmission Isometric Torque Comparison. Each Actuator’s isometric torque current constant is computed as the average of each data point’s mean torque divided by current command.
3.2. Passive Resistance
Test results for passive resistance are shown in Figure 6, along with best fit trend lines. Each point represents a data point taken during the current command sweep—measured motor current and measured joint velocity (derived from measured motor speed divided by actuator gear ratio) are shown in the plot. These equations are summarized below. In testing, the harmonic actuator did not achieve the same maximum output angular velocity as the planetary actuator. The planetary actuator testing was stopped at 330 deg/sec, the maximum design specification. The harmonic actuator test was stopped at 270 deg/sec due to excessive chain vibration which eventually resulted in the chain coming free of the sprocket. There were two sources of noise in this data. The first was from the closed loop current controller used for this test—the PI parameters in the controller were tuned when the actuator was loaded with significantly more inertia. When the output arm was removed for this test, these higher than optimal parameters resulted in noisier current commands. The areas of higher dispersion in the data indicate the resonant frequencies of the actuator—temporarily creating higher than normal levels of vibration as the speed swept through that point. The best fit trend line showed decreasing passive resistance at high speed. Prior testing of harmonic drives showed that passive resistance may not monotonically increase with speed [39].
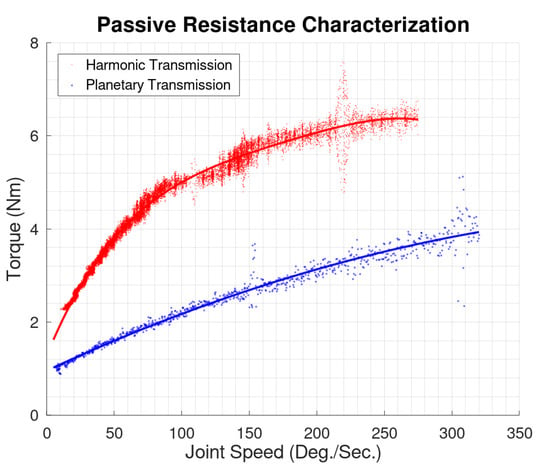
Figure 6.
No Load Passive Resistance vs. Speed Characterization Results. Raw data is shown as individual data points, with trend lines in solid.
3.3. Net Torque
Figure 7 shows the integration of the isometric torque and passive resistance results into the net torque operating envelope for each actuator. Each actuator is rated at 5 A continuous current, and 15 A peak (both limited by the motor controller). The greater isometric torque means the planetary actuator produces more torque for a given current at all speeds. The lower passive resistance translates to a greater torque gap at higher joint speeds.
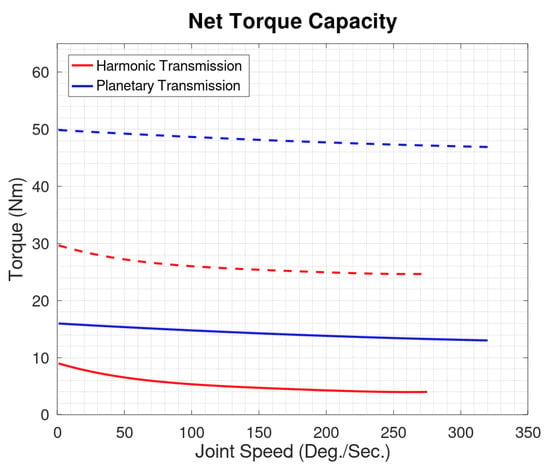
Figure 7.
Actuator Net Torque. The solid lines represent the continuous actuator torque capacity. The dashed lines represent peak actutator torque, which can be generated for 3–5 s bursts.
3.4. Compensation Current
The passive resistance characterization test showed that the planetary actuator had significantly less passive resistance torque at all joint speeds. This test, along with the isometric torque characterization test, can be used to develop a basic feed forward friction compensation controller to decrease passive resistance as felt by the user [40,41]. This calculation is a basic approximation that assumes joint friction is strictly a function of joint speed. Doing so, however, costs motor current. The motor current necessary to overcome passive resistance can be determined by rearranging Equation (1), with net torque equal to zero, and solving for current.
Figure 8 shows this compensation current based on the passive resistance model for both actuator configurations. Across all joint speeds, the decreased passive resistance of the planetary actuator results in roughly 2/3 less current needed to compensate for it. This result also decreases overall power consumption of the actuator, resulting in either a decrease in needed battery size and/or capacity or an increase in endurance. This comparison demonstrates potential for decreased current consumption in practice of the planetary actuator compared to the harmonic. More care would need to be applied in the implementation phase (and potentially additional variables added to the model).
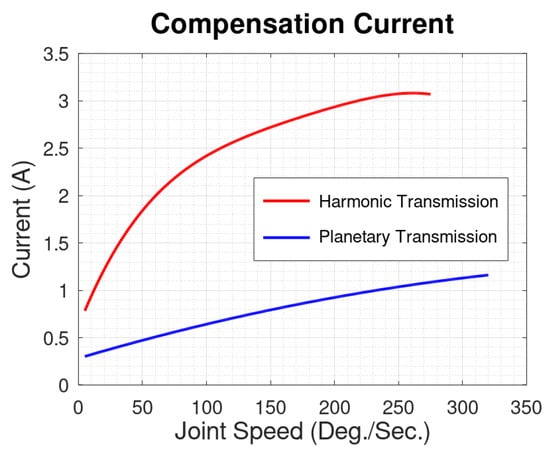
Figure 8.
Compensation Current Comparison.
3.5. Mechanical Efficiency
The results of the mechanical efficiency calculation are shown in Figure 9. Efficiency, as derived in Section 2.3.4 is a function of both motor current and joint speed. The figure shows peak (greatest) efficiency as a function of joint speed, which occurs as the greatest motor current of 15 A. The significant increase in isometric torque for the planetary actuator manifested as a significant increase the mechanical efficiency. The decreased passive resistance of the planetary actuator translated to less significant efficiency fall off with increasing joint speed. Overall, the planetary actuator approximately doubled the mechanical efficiency of the harmonic actuator.

Figure 9.
Transmission Efficiency Comparison.
4. Discussion
This work directly compared two transmissions that could be integrated into a hybrid exoskeleton. Aside from the transmissions, the rest of each actuator was designed to be as similar as possible—incorporating the same motor and brake components, and similar transmission ratios. Both actuators were implemented with the same form factor and had similar size and mass. A tightly integrated motor/brake was built into both designs. With this ability to lock, these actuators were also suitable for users with spinal cord injury who require full exoskeletal support during stance. The information presented here will allow for more informed future design criteria. The design objective was maximizing torque for a given required design speed. Future testing of a complete exoskeleton platform will reveal what joint torque is actually required to facilitate high speed hybrid gait. From this testing, it is clear the planetary transmission is the superior transmission—isometric torque increased by 38% while passive resistance decreased by approximately 30% across all joint speeds compared to the harmonic transmission. These two results combined to show a significant increase in peak and continuous output torque for the planetary transmission.
Low passive resistance was deemed critical for hybrid applications, where biological torques may be generated by NMES. Stimulation torques vary greatly, making it difficult to define the necessary criteria. For example, quadriceps stimulation for knee extension by surface stimulation can generate anywhere from less than 15 Nm to greater than 60 Nm, depending on joint angle and level of muscle fatigue [42]. With a maximum demonstrated passive resistance of 4 Nm for the planetary actuator, anywhere from 7% to 27% of the stimulation would required to overcome resistance of the actuator. For the harmonic actuator with maximum of 6.5 Nm passive resistance torque, 11% to 43% of the stimulation would be required. As discussed previously, a feed-forward model could also increase output torque to minimize resistance that must be overcome. At peak resistance, the planetary gearbox required 1.32 A (26% of the continuous current rating) to overcome resistance. The harmonic required 3.14 A (63% of the continuous current) for the same task.
Table 2 shows a comparison of these actuators compared to similar work. This comparison specifically targets other actuators used in self-contained assistive orthotic devices that utilize direct drive. We excluded series elastic actuators from this comparison for two reasons. First, series elastic actuators are more likely to use a high passive resistance motor/transmission, and rely on active controls and the spring element for the impedance transformation. Secondly, the presence of the series elastic element places an upward boundary on output stiffness, which may be significantly less than the high stiffness provided by the joint lock. The use of multiple planetary stages represented a unique setup amongst similar work. In comparison to our previous work [17], the motor used in this work had half the terminal resistance (0.226 Ohms vs. 0.573 Ohms)—thereby decreasing the resistive losses in the motor. At 15 A (the maximum current for both motors), this change in resistance decreases the motor resistive losses (and thereby decreasing heat production) from 128 W to 51 W. In context, these actuators are capable of 200–250 W maximum output mechanical power, while consuming 300–320 W of electrical power under similar load. Not only does this increase electrical efficiency, but helps the motor run at lower temperatures—which is an important consideration when operating near human skin. When compared to Zhu et al. (which used a significantly larger motor, only a single stage planetary transmission and half the gearing used here) [23], the planetary actuator is capable of producing 85% of their maximum torque, but required half the current (15 A vs. 30 A), and displayed half the maximum passive resistance (8 Nm vs. 4 Nm). More precise comparisons are difficult to make due to a difference in testing styles—instead of actuator bench testing as performed here, their actuator was benchmarked with a subject walking with it. Passive resistance as a function of joint speed was not reported, but instead a peak passive resistance value during passive walking trials served as their benchmark. Because of these characteristics, our planetary actuator requires smaller/lighter supporting electronics (motor controller, battery) to achieve its performance. While not able to compete in torque output compared to the electrohydraulic implementations, our planetary actuator showed a substantially higher mechanical efficiency. This is not unexpected—since while hydraulic actuation systems typically excel in torque density, small scale systems struggle with excessive seal friction causing poor efficiency [43]. In addition to the advantage of increased efficiency, elimination of high pressure hydraulic fluid near human skin also obviates the potential for injury from breach of the hydraulic circuit. The others did not characterize the actuators to the degree presented here, limiting potential comparisons.

Table 2.
Summary of parameters from assistive orthotic devices. Blank spaces indicate the metric was not reported.
There are several limitations associated with this work. First, the harmonic drive actuator was limited in output speed by input vibrations. This could be due to the unique operating principles of the harmonic drive, and may have been averted with a more substantial bearing arrangement at the input. This was initially considered in the design phase, but was not included as it would have unacceptably increased the medial/lateral width and overall mass. Second, the lack of stiffness of the isometric torque test setup led to non-linearity in the data and prevented testing up to the maximum motor current. Despite this, prior work has shown this relationship is linear amongst similar devices, and the assumption of linearity was used in the calculation of performance. The maximum torque data were extrapolated. Minimal motion was present in the data shown, as confirmed visually as well as with sensor data from the dynamometer angular displacement sensor and the actuator motor angular velocity sensor.
This review should not be considered an exhaustive comparison. These two implementations were identified as two of the most promising idealizations for the task at hand, but several additional were considered and rejected out of time and cost constraints. These tests were considered the most pertinent for identifying functional parameters, but other characteristics such as noise, size, and other physical properties were not evaluated. Future work should include methods of examining these properties as well as understanding the relative importance of all outcome measures in practice. Additionally, other fields can contribute more advanced methods of evaluation. Bench testing was selected to evaluate these actuators because of the ease of testing. Other, more complicated systems have demanded the advancement of alternative, online methods of parameter evaluation [44,45]. There may be lessons from these areas of research for paremeter identification or refinement for online control of these actuators.
The performance gains shown in these results indicate that the planetary style transmission requires approximately 30% less gearing to achieve the same torque as compared to the harmonic drive. While these two actuators were designed with similar gearing (and with similar mass) with a common speed goal, designing for a torque goal would allow for the planetary implementation to be constructed with less gearing, resulting in a smaller and lighter actuator. Initial exoskeleton research has adopted a four degrees of freedom system as standard, with powered hip and knee joints driving the legs in the sagittal plane of motion. As plans progress and additional degrees of freedom are introduced, the importance of lightweight, efficient, powerful, and lockable actuators will only grow.
5. Conclusions
Two actuators were designed, constructed, and tested to evaluate their suitability for hybrid cooperative robotic applications. Several unique design features were evaluated and their perfomances quantified for comparison. A unique multistage planetary gearbox with floating rings for equal tooth engagement was developed, and shown to offer similar or better performance in key parameters compared to other transmission arrangements. Both actuators were tested for isometric torque and passive resistance. Only one actuator was able to achieve the target angular velocity of 330 deg/sec required for community ambulation.
By all metrics presented here, this planetary transmission performance exceeds that of this harmonic transmission. For a given motor current, it produced substantially more isometric torque. There was less passive resistance at all joint speeds. These results combine for a greater output torque operating envelope for the planetary system. Such actuator configurations should be considered for future wearable robotic systems for rehabilitation that require backdrivability, low current consumption, and mechanical efficiency.
Author Contributions
Conceptualization, M.J.N., R.Q. and N.S.M.; methodology, M.J.N., N.S.M.; software, M.J.N.; validation, R.J.T., N.S.M. and R.Q.; formal analysis, M.J.N., M.H.; investigation, M.J.N., M.H.; resources, R.J.T. and N.S.M.; data curation, M.J.N.; writing—original draft preparation, M.J.N.; writing—review and editing, N.S.M., R.J.T. and R.Q.; visualization, M.J.N., M.H.; supervision, R.Q., N.S.M. and R.J.T.; project administration, R.Q. and R.J.T.; funding acquisition, R.Q., R.J.T. and N.S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Science Foundation grant number 1739800, US Department of Veterans Affairs Merit Review 1I01RX002275-01, and US Department of Veterans Affairs Merit Review RX-003056-01.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SCI | Spinal Cord Injury |
| NMES | Neuromuscular Electrical Stimulation |
References
- National Spinal Cord Injury Statistical Center. Spinal Cord Injury Facts and Figures at a Glance 2020 SCI Data Sheet; Technical Report; University of Alabama at Birmingham: Birmingham, AL, USA, 2020. [Google Scholar]
- Brown-Triolo, D.L.; Mary, C.; Roach, J.; Nelson, K.; Triolo, R.J. Consumer Perspectives on Mobility: Implications for Neuroprosthesis Design. J. Rehabil. Res. Dev. 2002, 39, 659–670. [Google Scholar]
- Ditunno, P.L.; Patrick, M.; Stineman, M.; Ditunno, J.F. Who wants to walk? Preferences for recovery after SCI: A longitudinal and cross-sectional study. Spinal Cord 2008, 46, 500–506. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.D. Targeting Recovery: Priorities of the Spinal Cord-Injured Population. J. Neurotrauma 2004, 21, 1371–1383. [Google Scholar] [CrossRef] [PubMed]
- Kolakowsky-Hayner, S.A. Safety and Feasibility of using the EksoTM Bionic Exoskeleton to Aid Ambulation after Spinal Cord Injury. J. Spine 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Hartigan, C.; Kandilakis, C.; Dalley, S.; Clausen, M.; Wilson, E.; Morrison, S.; Etheridge, S.; Farris, R. Mobility Outcomes Following Five Training Sessions with a Powered Exoskeleton. Top. Spinal Cord Inj. Rehabil. 2015, 21, 93–99. [Google Scholar] [CrossRef] [Green Version]
- Benson, I.; Hart, K.; Tussler, D.; van Middendorp, J.J. Lower-limb exoskeletons for individuals with chronic spinal cord injury: Findings from a feasibility study. Clin. Rehabil. 2016, 30, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Puyuelo-Quintana, G.; Cano-De-La-Cuerda, R.; Plaza-Flores, A.; Garces-Castellote, E.; Sanz-Merodio, D.; Goñi-Arana, A.; Marín-Ojea, J.; García-Armada, E. A new lower limb portable exoskeleton for gait assistance in neurological patients: A proof of concept study. J. Neuroeng. Rehabil. 2020, 17, 1–16. [Google Scholar] [CrossRef]
- Buesing, C.; Fisch, G.; Shahidi, I.; Thomas, L.; Mummidisetty, C.K.; Williams, K.J.; Takahashi, H.; Zev Rymer, W.; Jayaraman, A. Effects of a wearable exoskeleton stride management assist system (SMA®) on spatiotemporal gait characteristics in individuals after stroke: A randomized controlled trial. J. Neuroeng. Rehabil. 2015, 12, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Kawamoto, H.; Kamibayashi, K.; Nakata, Y.; Yamawaki, K.; Ariyasu, R.; Sankai, Y.; Sakane, M.; Eguchi, K.; Ochiai, N. Pilot study of locomotion improvement using hybrid assistive limb in chronic stroke patients. BMC Neurol. 2013, 13, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Byl, N.N. Mobility training using a bionic knee orthosis in patients in a post-stroke chronic state: A case series. J. Med. Case Rep. 2012, 6, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Maeshima, S.; Osawa, A.; Nishio, D.; Hirano, Y.; Takeda, K.; Kigawa, H.; Sankai, Y. Efficacy of a hybrid assistive limb in post-stroke hemiplegic patients: A preliminary report. Technical report. BMC Neurol. 2011, 11, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Solomonow, M.; Baratta, R.; Hirokawa, S.; Beaudette, C. The RGO Generation II: Muscle Stimulation Powered Orthosis as a practical walking system for thoracic paraplegics. Orthop. Oct Nurs. Allied Health Database Pg 1989, 12, 1309–1315. [Google Scholar]
- To, C.; Kirsch, R.; Kobetic, R.; Triolo, R. Simulation of a Functional Neuromuscular Stimulation Powered Mechanical Gait Orthosis With Coordinated Joint Locking. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 227–235. [Google Scholar] [CrossRef]
- Goldfarb, M.; Korkowski, K.; Harrold, B.; Durfee, W. Preliminary evaluation of a controlled-brake orthosis for FES-aided gait. IEEE Trans. Neural Syst. Rehabil. Eng. 2003, 11, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Nandor, M.; Li, L.; Foglyano, K.; Schnellenberger, J.; Kobetic, R.; Quinn, R.; Triolo, R. A stimulation-driven exoskeleton for walking after paraplegia. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Orlando, FL, USA, 16–20 August 2016. [Google Scholar] [CrossRef]
- Nandor, M.; Kobetic, R.; Audu, M.; Triolo, R.; Quinn, R. A Muscle-First, Electromechanical Hybrid Gait Restoration System in People With Spinal Cord Injury. Front. Robot. AI 2021, 8, 645588. [Google Scholar] [CrossRef] [PubMed]
- Ha, K.H.; Quintero, H.A.; Farris, R.J.; Goldfarb, M. Enhancing stance phase propulsion during level walking by combining fes with a powered exoskeleton for persons with paraplegia. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, San Diego, CA, USA, 28 August–1 September 2012. [Google Scholar] [CrossRef] [Green Version]
- Alibeji, N.A.; Molazadeh, V.; Moore-Clingenpeel, F.; Sharma, N. A muscle synergy-inspired control design to coordinate functional electrical stimulation and a powered exoskeleton: Artificial generation of synergies to reduce input dimensionality. IEEE Control. Syst. 2018, 38, 35–60. [Google Scholar] [CrossRef]
- del Ama, A.J.; Gil-Agudo, A.; Pons, J.L.; Moreno, J.C. Hybrid FES-robot cooperative control of ambulatory gait rehabilitation exoskeleton. J. Neuroeng. Rehabil. 2014, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Kaminaga, H.; Amari, T.; Niwa, Y.; Nakamura, Y. Development of knee power assist using backdrivable electro-hydrostatic actuator. In Proceedings of the IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems, IROS 2010—Conference Proceedings, Taipei, Taiwan, 18–22 October 2010; pp. 5517–5524. [Google Scholar] [CrossRef]
- Neubauer, B.C.; Nath, J.; Durfee, W.K. Design of a portable hydraulic ankle-foot orthosis. In Proceedings of the 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC, Chicago, IL, USA, 26–30 August 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway Township, NJ, USA, 2014; pp. 1182–1185. [Google Scholar] [CrossRef]
- Zhu, H.; Doan, J.; Stence, C.; Lv, G.; Elery, T.; Gregg, R. Design and validation of a torque dense, highly backdrivable powered knee-ankle orthosis. In Proceedings of the IEEE International Conference on Robotics and Automation, Singapore, 29 May–3 June 2017; Institute of Electrical and Electronics Engineers Inc.: Piscataway Township, NJ, USA, 2017; pp. 504–510. [Google Scholar] [CrossRef]
- Elery, T.; Rezazadeh, S.; Nesler, C.; Doan, J.; Zhu, H.; Gregg, R.D. Design and Benchtop Validation of a Powered Knee-Ankle Prosthesis with High-Torque, Low-Impedance Actuators. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway Township, NJ, USA, 2018; pp. 2788–2795. [Google Scholar] [CrossRef]
- Goo, A.; Laubscher, C.A.; Farris, R.J.; Sawicki, J.T. Design and Evaluation of a Pediatric Lower-Limb Exoskeleton Joint Actuator. Actuators 2020, 9, 138. [Google Scholar] [CrossRef]
- Levai, Z. Structure and Analysis of Planetary Gear Trains. J. Mech. 1968, 3, 131–148. [Google Scholar] [CrossRef]
- Tuttle, T. Understanding and Modeling the Behavior of a Harmonic Drive Gear Transmission. Master’s Thesis, MIT, Cambridge, MA, USA, 1992. [Google Scholar]
- Andrews, A.W.; Chinworth, S.A.; Bourassa, M.; Garvin, M.; Benton, D.; Tanner, S. Update on distance and velocity requirements for community ambulation. J. Geriatr. Phys. Ther. 2010, 33, 128–134. [Google Scholar] [CrossRef]
- Bohannon, R.W.; Williams Andrews, A.; Michael Thomas, B.W. Walking Speed: Reference Values and Correlates for Older Adults. J. Orthop. Sport. Phys. Ther. 1996, 24, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Bohannon, R.W. Comfortable and maximum walking speed of adults aged 20–79 years: Reference values and determinants. Age Ageing 1997, 26, 15–19. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.R.; Kobetic, R.; Triolo, R.J. Effect of exoskeletal joint constraint and passive resistance on metabolic energy expenditure: Implications for walking in paraplegia. PLoS ONE 2017, 12, e0183125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farris, R.J.; Quintero, H.A.; Goldfarb, M. Preliminary evaluation of a powered lower limb orthosis to aid walking in paraplegic individuals. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 652–659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaminaga, H.; Tanaka, H.; Nakamura, Y. Mechanism and Control of Knee Power Augmenting Device with Backdrivable Electro-Hydrostatic Actuator; Technical Report; World Congress in Mechanism and Machine Science: Guanajuato, Mexico, 2011. [Google Scholar]
- Juvinall, R.C.; Marshek, K.M. Fundamentals of Machine Component Design, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2006; pp. 604–612. [Google Scholar]
- Xiao, Z.G.; Menon, C. Towards the development of a portable wrist exoskeleton. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, ROBIO 2011, Karon Beach, Thailand, 7–11 December 2011; pp. 1884–1889. [Google Scholar] [CrossRef]
- Laubscher, C.A.; Farris, R.J.; Sawicki, J.T. Design and Preliminary Evaluation of a Powered Pediatric Lower Limb Orthosis. Proc. ASME Des. Eng. Tech. Conf. 2017, 58172, V05AT08A061. [Google Scholar] [CrossRef]
- Reyes, R.D.; Kobetic, R.; Nandor, M.; Makowski, N.; Audu, M.; Quinn, R.; Triolo, R. Effect of Joint Friction Compensation on a “Muscle-First” Motor-Assisted Hybrid Neuroprosthesis. Front. Neurorobot. 2020, 14, 588950. [Google Scholar] [CrossRef] [PubMed]
- Tuttle, T.D.; Seering, W.P. A Nonlinear Model of a Harmonic Drive Gear Transmission. IEEE Trans. Robot. Autom. 1996, 12, 368–374. [Google Scholar] [CrossRef]
- Marilier, T.; Richardt, J.A. Non-Linear Mechanic And Electric Behavior of a Robot Axis with a “Harmonic-Drive” Gear. Robot. Comput.-Integr. Manuf. 1989, 5, 129–136. [Google Scholar] [CrossRef]
- Kermani, M.R.; Patel, R.V.; Moallem, M. Friction identification and compensation in robotic manipulators. IEEE Trans. Instrum. Meas. 2007, 56, 2346–2353. [Google Scholar] [CrossRef]
- Hauschild, J.P.; Heppler, G.R. Control of harmonic drive motor actuated flexible linkages. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; pp. 3451–3456. [Google Scholar] [CrossRef]
- Levy, M.; Mizrahi, J.; Susak, Z. Recruitment, force and fatigue characteristics of quadriceps muscles of paraplegics isometrically activated by surface functional electrical stimulation. J. Biomed. Eng. 1990, 12, 150–156. [Google Scholar] [CrossRef]
- Xia, J.; Durfee, W.K. Analysis of small-scale hydraulic actuation systems. J. Mech. Des. Trans. ASME 2013, 135, 091001. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Pan, Y.; Zhou, Q.; Lu, C. Event-Triggered Adaptive Fuzzy Control for Stochastic Nonlinear Systems with Unmeasured States and Unknown Backlash-Like Hysteresis. IEEE Trans. Fuzzy Syst. 2021, 29, 1273–1283. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control. 2021, 58, 373–387. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).