Distributed Model Predictive Longitudinal Control for a Connected Autonomous Vehicle Platoon with Dynamic Information Flow Topology
Abstract
:1. Introduction
- Node dynamics: describes the single vehicle model.
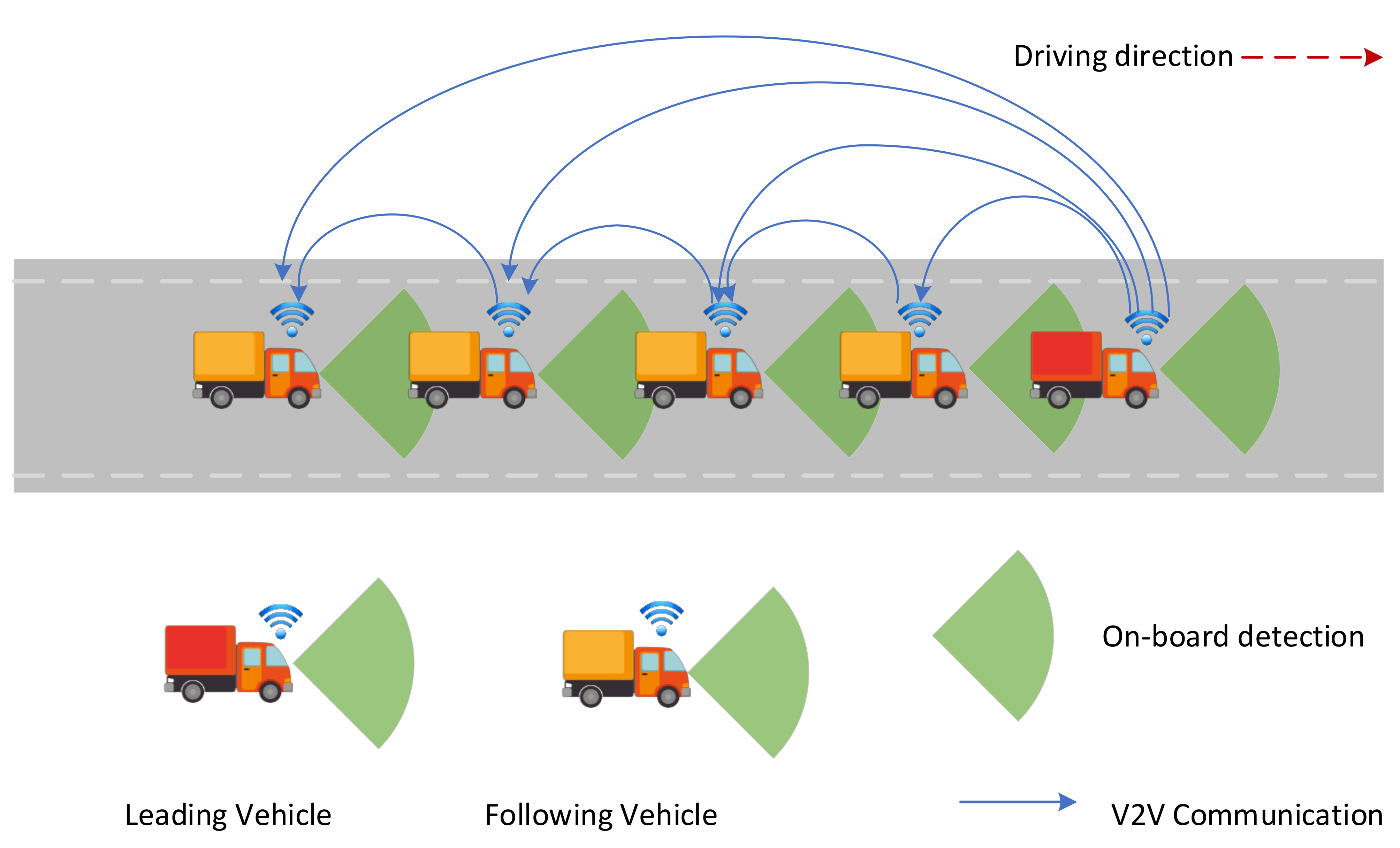
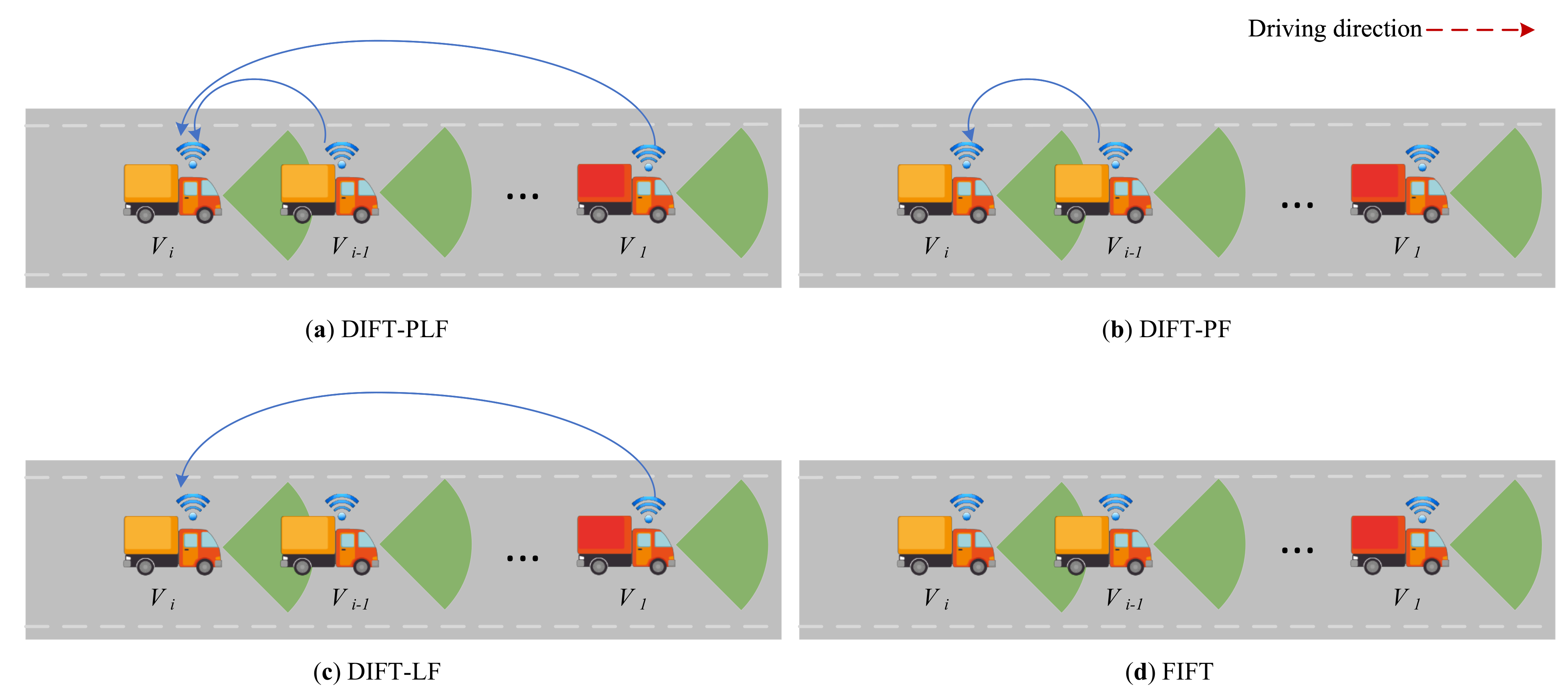
- Information flow topology (IFT): describes the information graph structure in the platooning nodes.
- Distributed controller: describes the control scheme of the platoon.
- Formation geometry: describes the spacing policy to maintain desired space between adjacent vehicles.
- A dynamic information topology with communication indicators is proposed to adapt to different communication conditions in platooning.
- A distributed model predictive control algorithm is designed to achieve satisfactory tracking performance of the platoon.
- The dynamics and fuel consumption are considered to simulate the realistic application of heavy-duty vehicles.
2. Problem Statement and Platoon Modeling
2.1. Formulation of DIFT
2.2. Platoon Formation
3. Distributed Model Predictive Controller
4. Results and Discussion
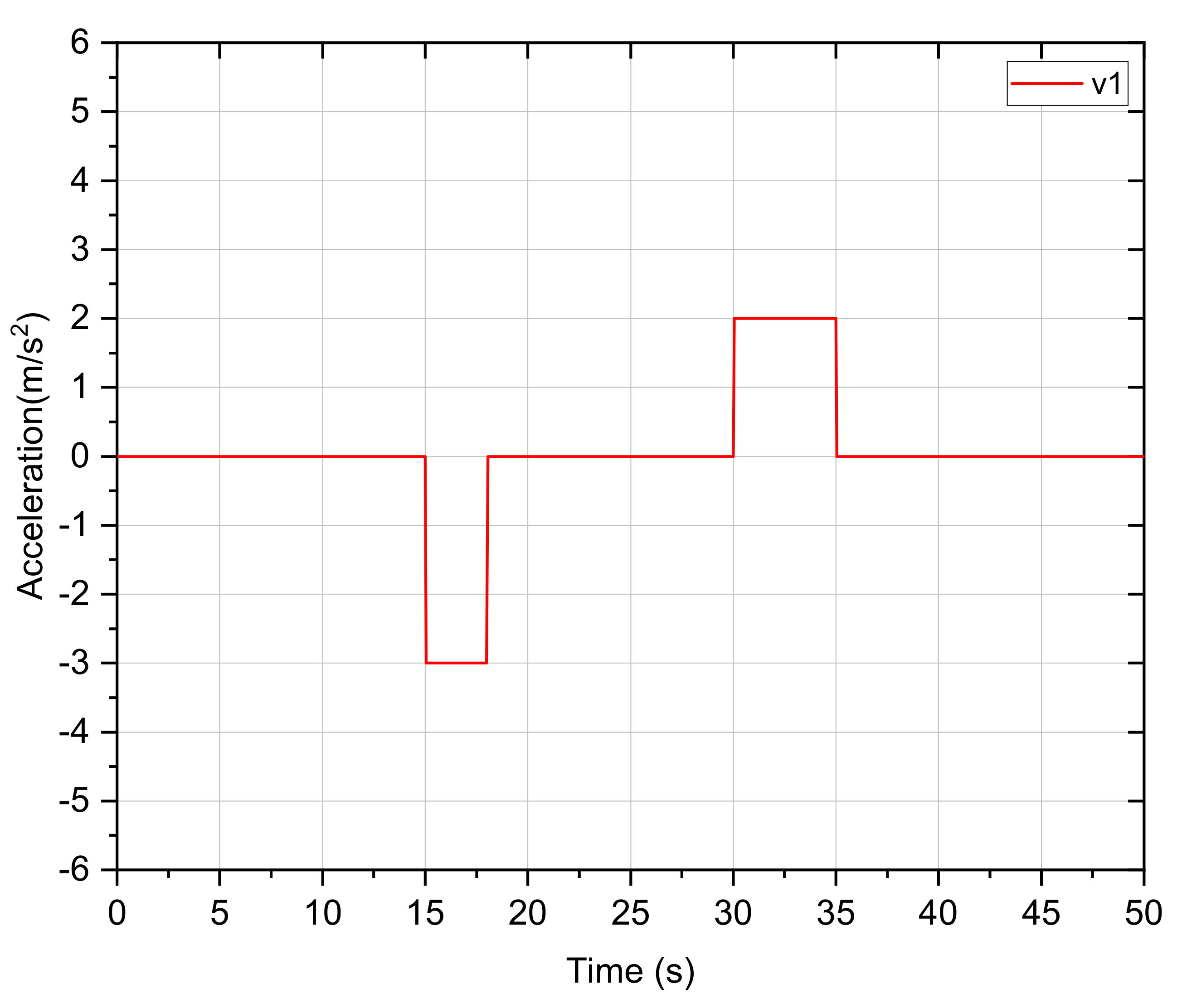
4.1. Simulation Setting
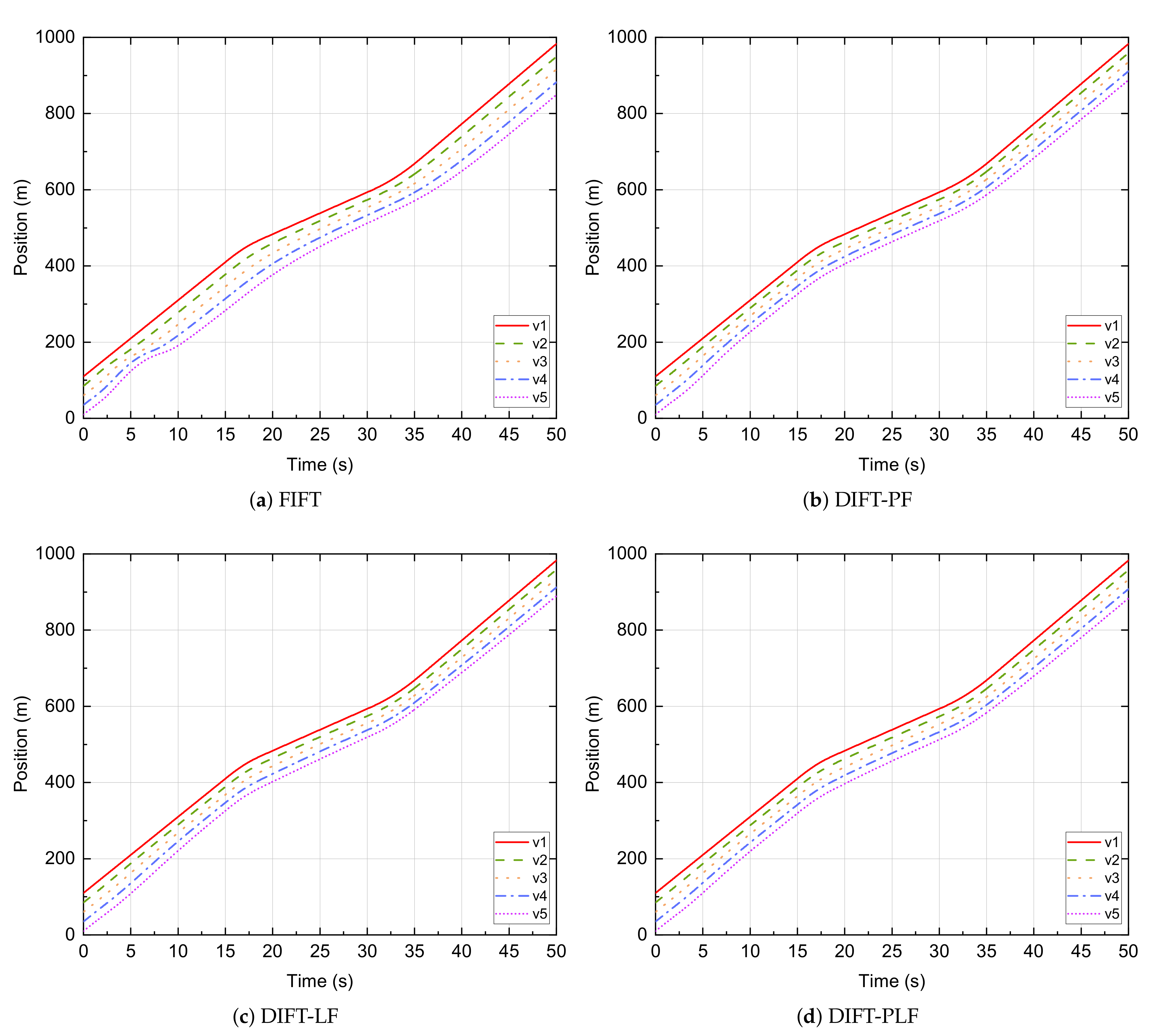
4.2. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| V2V | Vehicle to Vehicle |
| CAV | Connected Autonomous Vehicle |
| ACC | Adaptive Cruise Control |
| IFT | Information Flow Topology |
| FIFT | Fixed Information Flow Topology |
| DIFT | Dynamic Information Flow Topology |
| DMPC | Distributed Model Predicitive Control |
| CD | Constant Distance |
| CTH | Constant Time Headway |
| PF | Predecessor Following |
| LF | Leader Following |
| PLF | Predecessor–Leader Following |
References
- Din, S.; Paul, A.; Rehman, A. 5G-enabled Hierarchical architecture for software-defined intelligent transportation system. Comput. Netw. 2019, 150, 81–89. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Yan, M. An Optimization Design of Adaptive Cruise Control System Based on MPC and ADRC. Actuators 2021, 10, 110. [Google Scholar] [CrossRef]
- Xiao, L.; Gao, F. Practical string stability of platoon of adaptive cruise control vehicles. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1184–1194. [Google Scholar] [CrossRef]
- Sheikholeslam, S.; Desoer, C.A. Longitudinal control of a platoon of vehicles. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 291–296. [Google Scholar]
- Jia, D.; Lu, K.; Wang, J.; Zhang, X.; Shen, X. A survey on platoon-based vehicular cyber-physical systems. IEEE Commun. Surv. Tutor. 2015, 18, 263–284. [Google Scholar] [CrossRef] [Green Version]
- Tsugawa, S.; Kato, S.; Aoki, K. An automated truck platoon for energy saving. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 4109–4114. [Google Scholar]
- Michael, J.B.; Godbole, D.N.; Lygeros, J.; Sengupta, R. Capacity analysis of traffic flow over a single-lane automated highway system. J. Intell. Transp. Syst. 1998, 4, 49–80. [Google Scholar] [CrossRef]
- Robinson, T.; Chan, E.; Coelingh, E. Operating platoons on public motorways: An introduction to the sartre platooning programme. In Proceedings of the 17th World Congress on Intelligent Transport Systems, Venue, Sydney, 25–29 October 2010; Volume 1, p. 12. [Google Scholar]
- Bian, Y.; Zheng, Y.; Ren, W.; Li, S.E.; Wang, J.; Li, K. Reducing time headway for platooning of connected vehicles via V2V communication. Transp. Res. Part C Emerg. Technol. 2019, 102, 87–105. [Google Scholar] [CrossRef]
- Ma, F.; Yang, Y.; Wang, J.; Liu, Z.; Li, J.; Nie, J.; Shen, Y.; Wu, L. Predictive energy-saving optimization based on nonlinear model predictive control for cooperative connected vehicles platoon with V2V communication. Energy 2019, 189, 116120. [Google Scholar] [CrossRef]
- Li, S.E.; Zheng, Y.; Li, K.; Wang, J. An overview of vehicular platoon control under the four-component framework. In Proceedings of the 2015 IEEE Intelligent Vehicles Symposium (IV), Seoul, Korea, 28 June–1 July 2015; pp. 286–291. [Google Scholar]
- Hao, H.; Barooah, P. Stability and robustness of large platoons of vehicles with double-integrator models and nearest neighbor interaction. Int. J. Robust Nonlinear Control. 2013, 23, 2097–2122. [Google Scholar] [CrossRef]
- Ghasemi, A.; Kazemi, R.; Azadi, S. Stable decentralized control of a platoon of vehicles with heterogeneous information feedback. IEEE Trans. Veh. Technol. 2013, 62, 4299–4308. [Google Scholar] [CrossRef]
- Knorn, S.; Donaire, A.; Agüero, J.C.; Middleton, R.H. Passivity-based control for multi-vehicle systems subject to string constraints. Automatica 2014, 50, 3224–3230. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.E.; Wang, J.; Cao, D.; Li, K. Stability and scalability of homogeneous vehicular platoon: Study on the influence of information flow topologies. IEEE Trans. Intell. Transp. Syst. 2015, 17, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Shaw, E.; Hedrick, J.K. String stability analysis for heterogeneous vehicle strings. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 3118–3125. [Google Scholar]
- Peters, A.A.; Middleton, R.H.; Mason, O. Leader tracking in homogeneous vehicle platoons with broadcast delays. Automatica 2014, 50, 64–74. [Google Scholar] [CrossRef]
- Gong, S.; Zhou, A.; Peeta, S. Cooperative adaptive cruise control for a platoon of connected and autonomous vehicles considering dynamic information flow topology. Transp. Res. Rec. 2019, 2673, 185–198. [Google Scholar] [CrossRef]
- No, T.S.; Chong, K.T.; Roh, D.H. A Lyapunov function approach to longitudinal control of vehicles in a platoon. In Proceedings of the 2000 IEEE 51st Vehicular Technology Conference Proceedings (Cat. No. 00CH37026), Tokyo, Japan, 15–18 May 2000; Volume 1, pp. 336–340. [Google Scholar]
- Kwon, J.W.; Chwa, D. Adaptive bidirectional platoon control using a coupled sliding mode control method. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2040–2048. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.E.; Li, K.; Borrelli, F.; Hedrick, J.K. Distributed model predictive control for heterogeneous vehicle platoons under unidirectional topologies. IEEE Trans. Control. Syst. Technol. 2016, 25, 899–910. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Li, S.E.; Cortés, J.; Poolla, K. Distributed sliding mode control for nonlinear heterogeneous platoon systems with positive definite topologies. IEEE Trans. Control. Syst. Technol. 2019, 28, 1272–1283. [Google Scholar] [CrossRef]
- Syed, A.; Yin, G.; Pandya, A.; Zhang, H. Coordinated vehicle platoon control: Weighted and constrained consensus and communication network topologies. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 4057–4062. [Google Scholar]
- Kaku, A.; Mukai, M.; Kawabe, T. A centralized control system for ecological vehicle platooning using linear quadratic regulator theory. Artif. Life Robot. 2012, 17, 70–74. [Google Scholar] [CrossRef]
- Moaveni, B.; Movahedi, M. Centralized Controller Design for the Moving Vehicles in a Platoon to Achieve the Robust String Stability. J. Control. 2015, 9, 1–12. [Google Scholar]
- Mazzola, M.; Schaaf, G. Modeling and control design of a centralized adaptive cruise control system. Int. J. Inf. Commun. Eng. 2014, 8, 1177–1181. [Google Scholar]
- Guo, N.; Lenzo, B.; Zhang, X.; Zou, Y.; Zhai, R.; Zhang, T. A real-time nonlinear model predictive controller for yaw motion optimization of distributed drive electric vehicles. IEEE Trans. Veh. Technol. 2020, 69, 4935–4946. [Google Scholar] [CrossRef] [Green Version]
- Guo, N.; Zhang, X.; Zou, Y.; Guo, L.; Du, G. Real-time predictive energy management of plug-in hybrid electric vehicles for coordination of fuel economy and battery degradation. Energy 2021, 214, 119070. [Google Scholar] [CrossRef]
- Manfredi, S.; Petrillo, A.; Santini, S. Distributed PI Control For Heterogeneous Nonlinear Platoon of Autonomous Connected Vehicles. IFAC-Pap. 2020, 53, 15229–15234. [Google Scholar]
- Guo, G.; Li, D. Adaptive sliding mode control of vehicular platoons with prescribed tracking performance. IEEE Trans. Veh. Technol. 2019, 68, 7511–7520. [Google Scholar] [CrossRef]
- Gong, S.; Du, L. Cooperative platoon control for a mixed traffic flow including human drive vehicles and connected and autonomous vehicles. Transp. Res. Part B Methodol. 2018, 116, 25–61. [Google Scholar] [CrossRef]
- Li, M.; Cao, Z.; Li, Z. A Reinforcement Learning-Based Vehicle Platoon Control Strategy for Reducing Energy Consumption in Traffic Oscillations. IEEE Trans. Neural Networks Learn. Syst. 2021. [Google Scholar] [CrossRef]
- Kazemi, H.; Mahjoub, H.N.; Tahmasbi-Sarvestani, A.; Fallah, Y.P. A learning-based stochastic MPC design for cooperative adaptive cruise control to handle interfering vehicles. IEEE Trans. Intell. Veh. 2018, 3, 266–275. [Google Scholar] [CrossRef] [Green Version]
- Dunbar, W.B.; Caveney, D.S. Distributed receding horizon control of vehicle platoons: Stability and string stability. IEEE Trans. Autom. Control. 2011, 57, 620–633. [Google Scholar] [CrossRef]




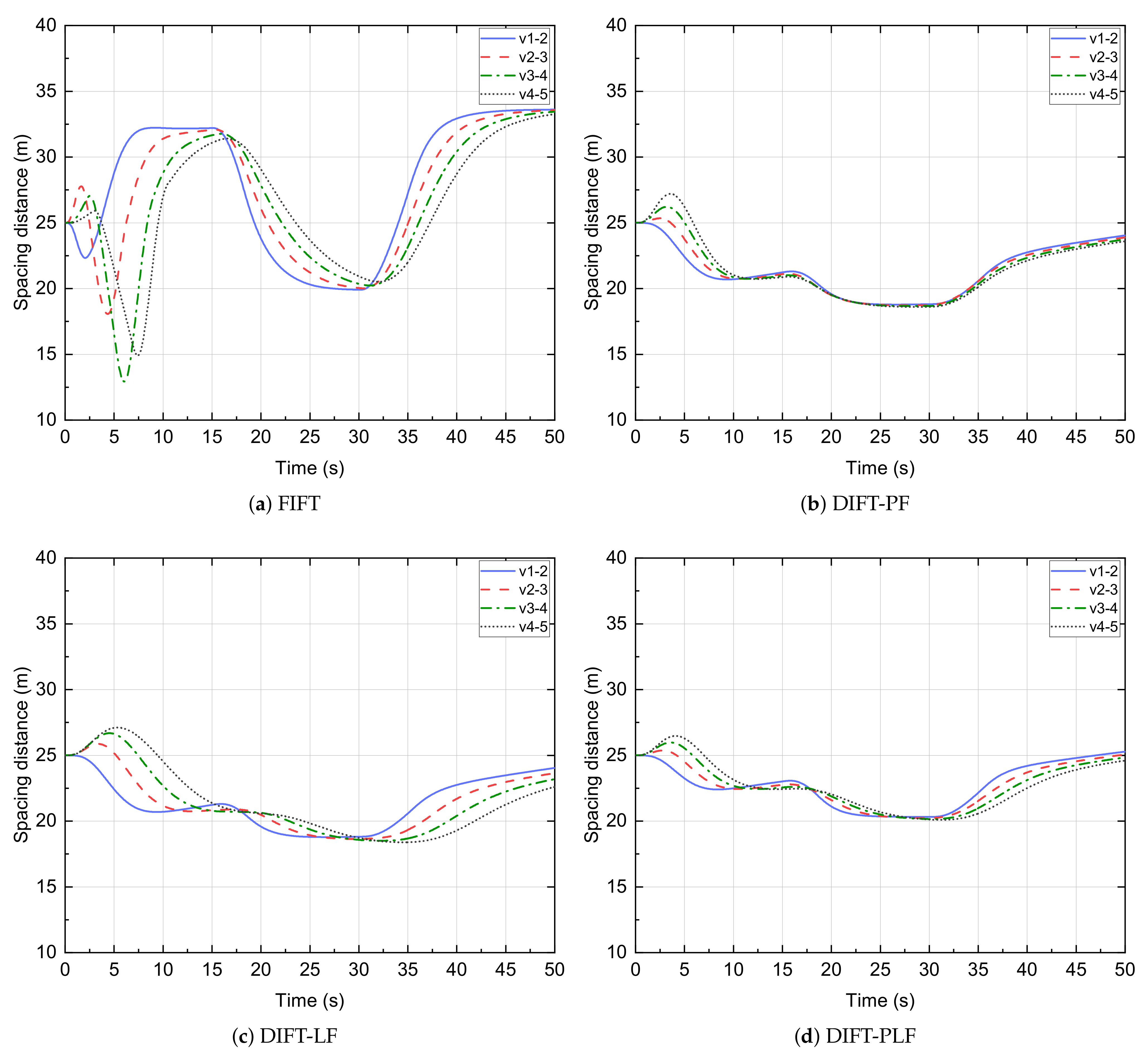

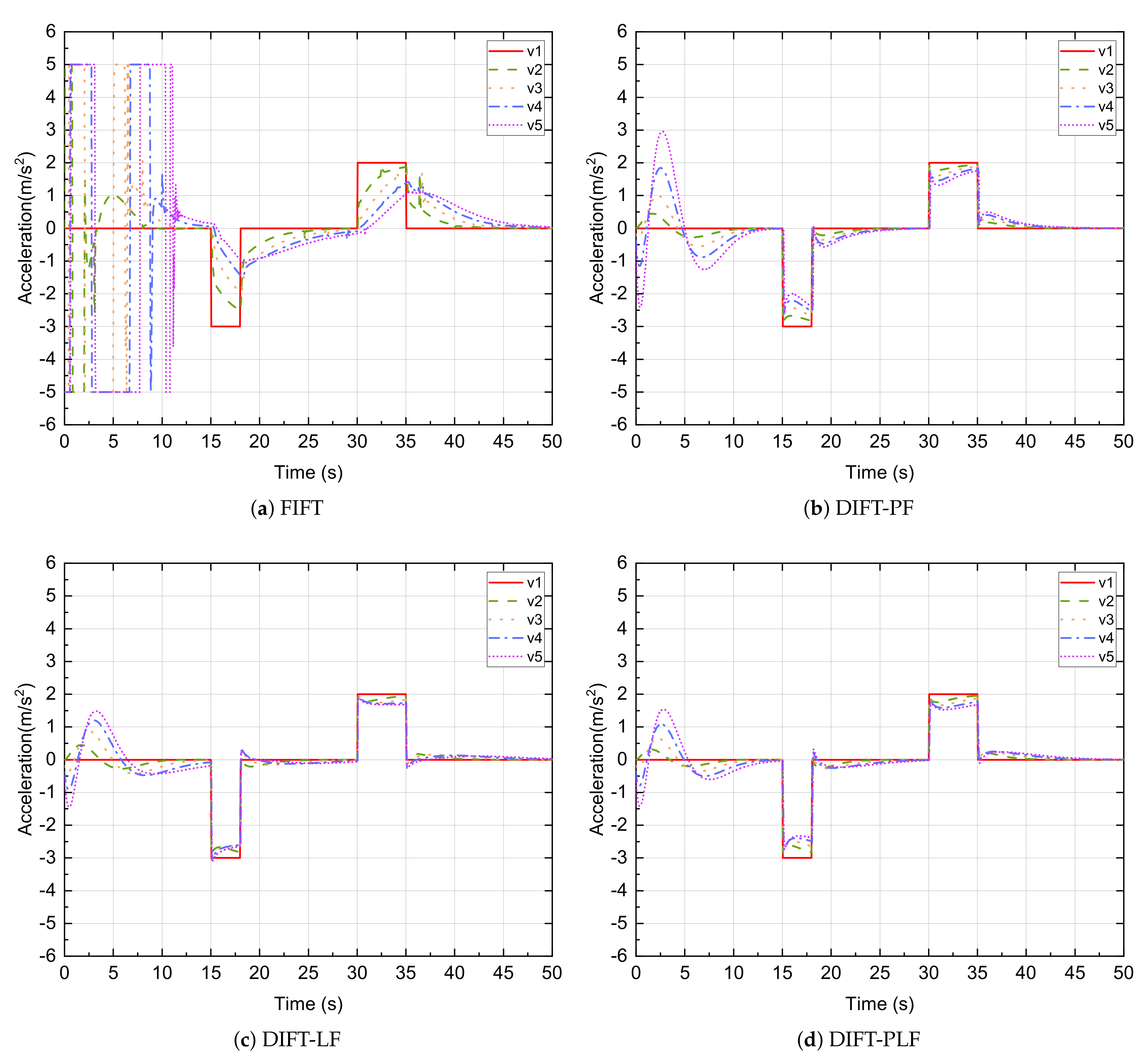
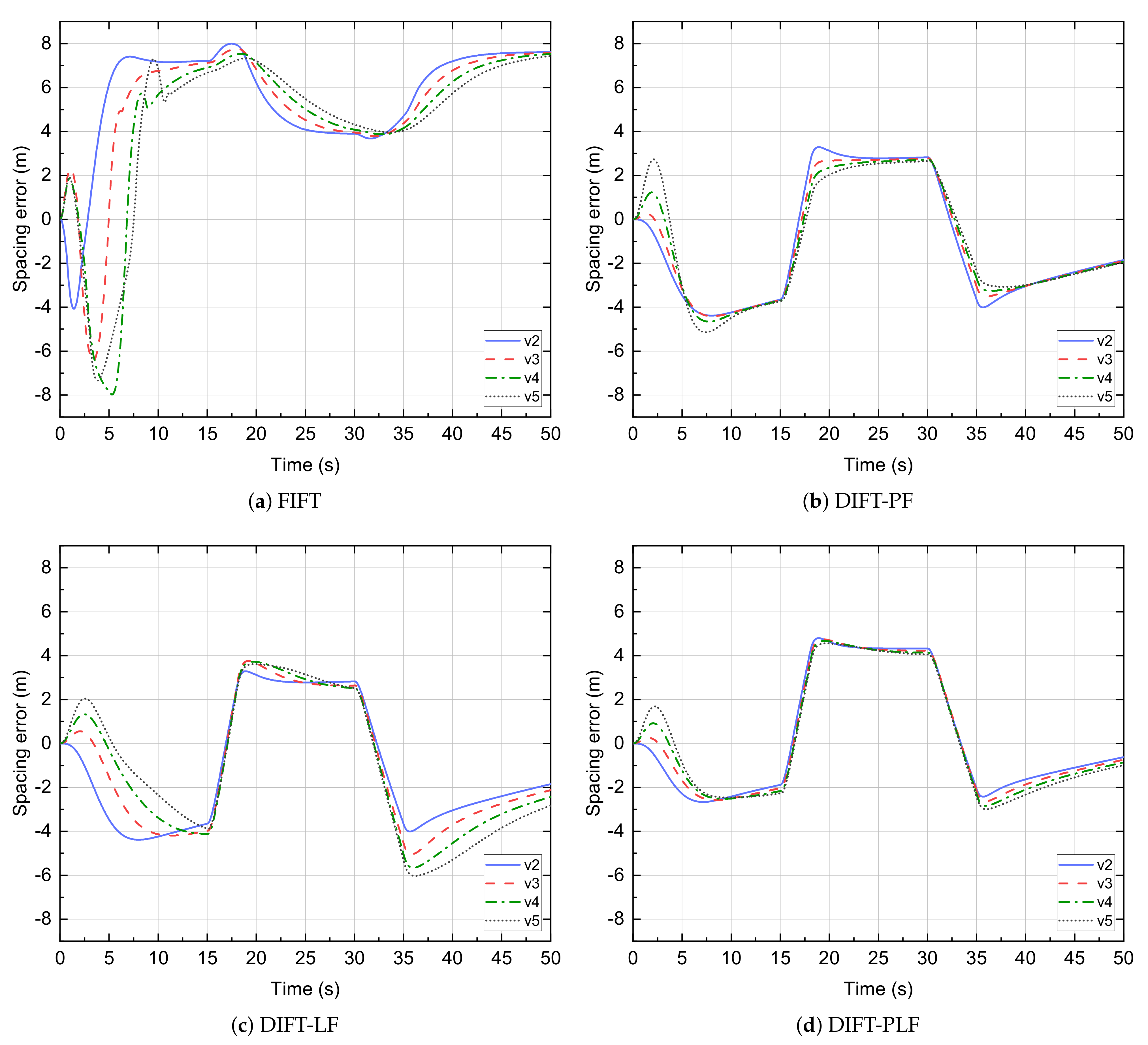

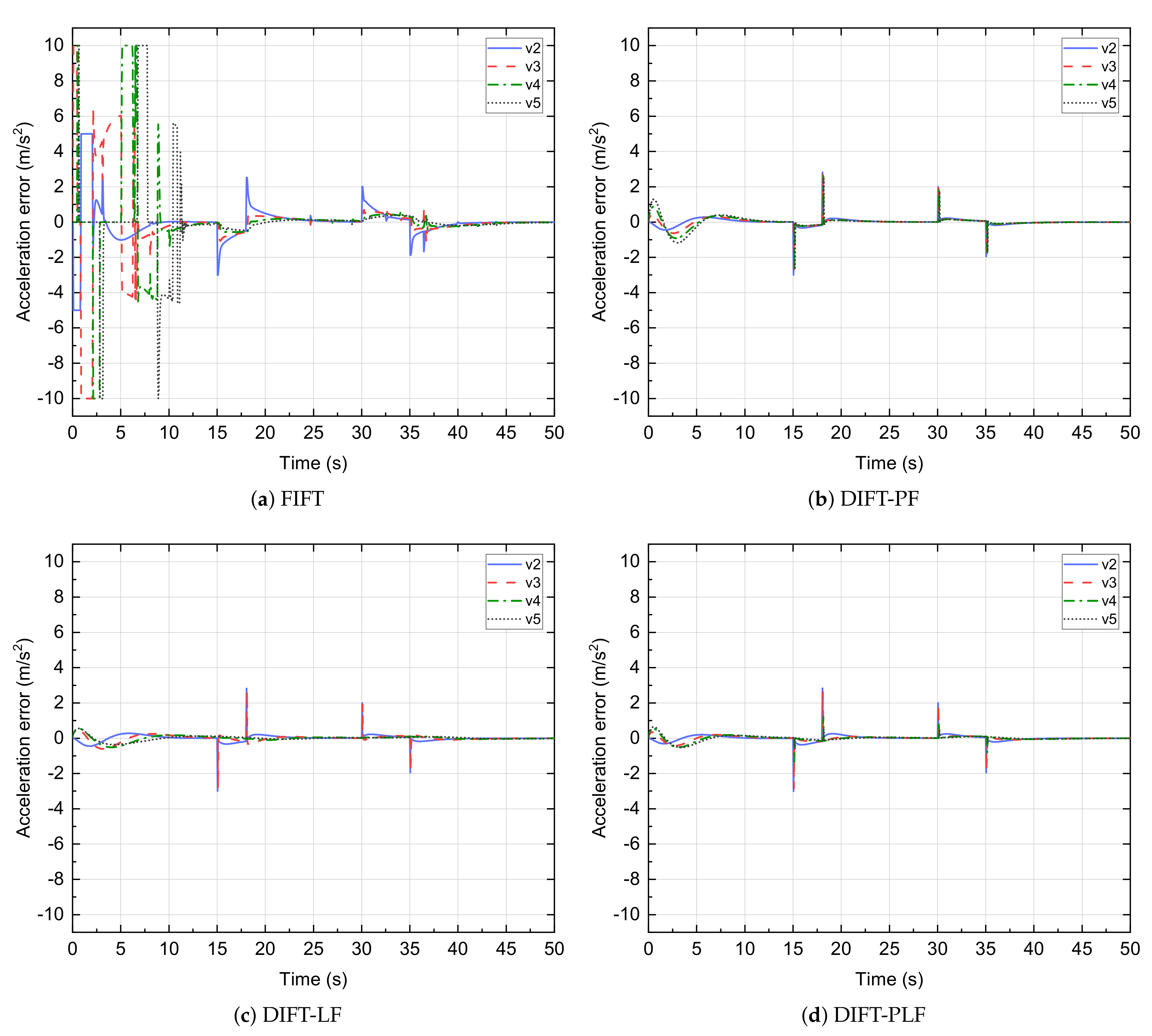
| Controller | R | ||||||
|---|---|---|---|---|---|---|---|
| FIFT | 0 | 0 | 10 | 0.1 | 0 | 0 | |
| DIFT-PF | 0 | 130 | 10 | 0.1 | 0 | 1 | |
| DIFT-LF | 130 | 0 | 10 | 0.1 | 1 | 0 | |
| DIFT-PLF | 105 | 105 | 10 | 0.1 | 1 | 1 |
| Controller | |||||
|---|---|---|---|---|---|
| (m) | (m/s) | (m) | (m/s) | (m/s2) | |
| FIFT | 4.785 | 0.171 | 7.999 | 6.913 | −4.505 |
| DIFT-PF | 1.132 | 0.031 | 5.142 | 1.472 | 2.962 |
| DIFT-LF | 1.157 | 0.025 | 6.032 | 1.031 | −3.119 |
| DIFT-PLF | 0.614 | 0.008 | 4.795 | 0.757 | −2.842 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Liu, Y.; Wang, J.; Wang, L. Distributed Model Predictive Longitudinal Control for a Connected Autonomous Vehicle Platoon with Dynamic Information Flow Topology. Actuators 2021, 10, 204. https://doi.org/10.3390/act10090204
Zhao F, Liu Y, Wang J, Wang L. Distributed Model Predictive Longitudinal Control for a Connected Autonomous Vehicle Platoon with Dynamic Information Flow Topology. Actuators. 2021; 10(9):204. https://doi.org/10.3390/act10090204
Chicago/Turabian StyleZhao, Fei, Yu Liu, Jian Wang, and Li Wang. 2021. "Distributed Model Predictive Longitudinal Control for a Connected Autonomous Vehicle Platoon with Dynamic Information Flow Topology" Actuators 10, no. 9: 204. https://doi.org/10.3390/act10090204
APA StyleZhao, F., Liu, Y., Wang, J., & Wang, L. (2021). Distributed Model Predictive Longitudinal Control for a Connected Autonomous Vehicle Platoon with Dynamic Information Flow Topology. Actuators, 10(9), 204. https://doi.org/10.3390/act10090204






