Experimental and Analytical Study of Secondary Path Transfer Function in Active Hydraulic Mount with Solenoid Actuator

Abstract

The active hydraulic mount with solenoid actuator (AHM-SNA) does not require permanent magnets, is of low cost, and has attracted wide attention. This paper focuses on each link of the secondary path in AHM-SNA, the transfer functions (TFs) were studied one by one, and a simple and efficient expression for the total secondary path is discussed. First, based on the mathematical model of the hydraulic mount with inertia track and decoupling membrane, the TF from actuator active force to output force at frame side was analyzed, the results show that the TF was constant in the mid-frequency band. Second, based on the geometric parameters and cone air gap of solenoid actuator, it was obtained that the TF from the square of current to actuator active force is also constant; based on the relationship that the active force frequency is twice of the harmonic current frequency, the full-wave-rectified current was introduced. Utilizing the fact that the second harmonic component of the current is the main component, it was concluded that the total TF of the secondary path from current to active force and then to output force at frame side was constant in the mid-frequency band. Finally, two sets of experiments with full-wave-rectified current as the excitation were carried out, and the analytical conclusion was verified that the TF of the secondary path was constant as a proportional link and was convenient for the active control algorithms.

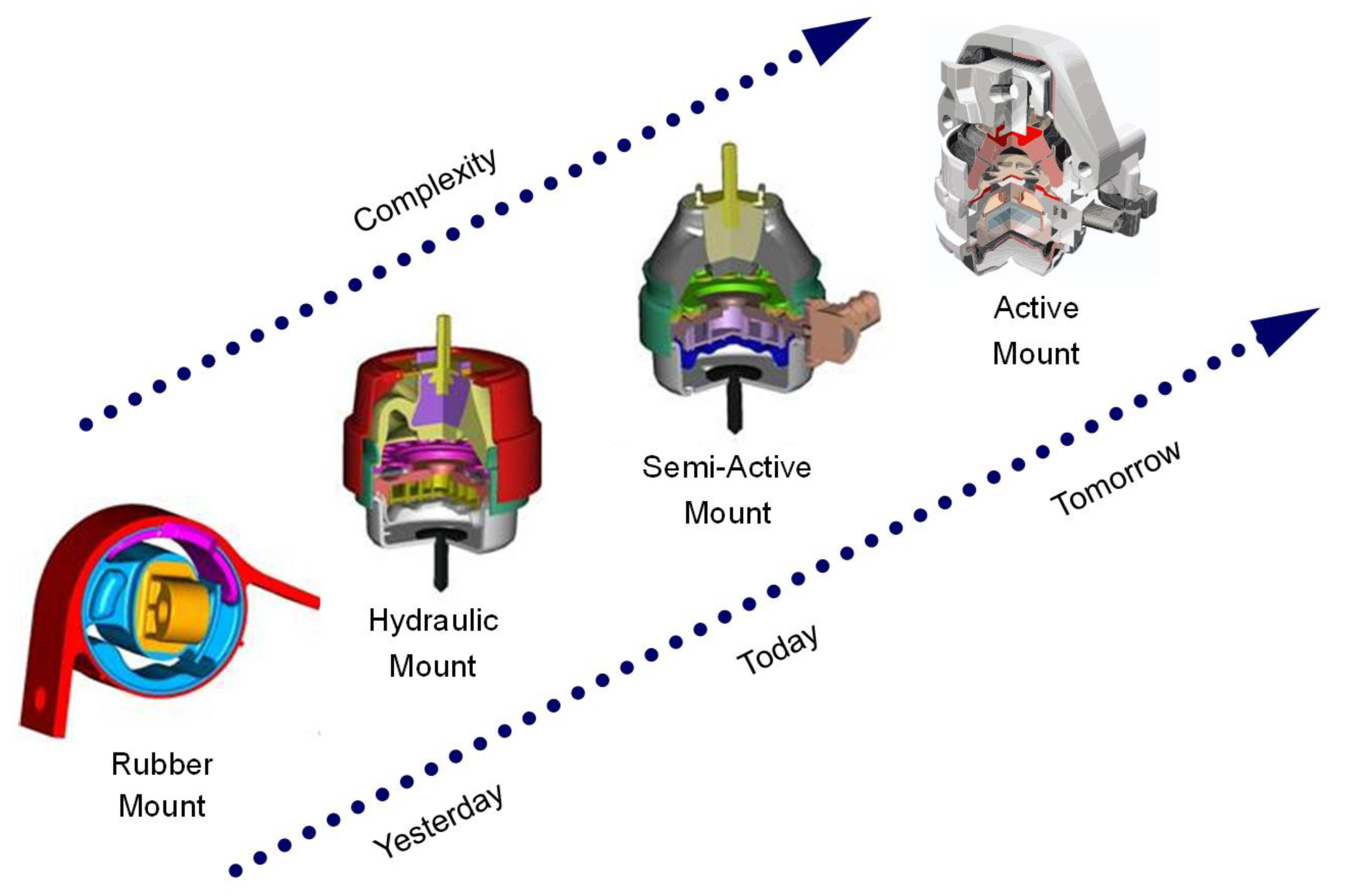
1. Introduction

Periodic unbalanced reciprocating inertia force and unbalanced overturning torque excitation of automobile engines are one of the main sources of vehicle vibration [1]. A vibration isolating device is installed between the powertrain and the frame/chassis to reduce the vibration transferred from the engine to the frame. With the development of society and the progress of science and technology, people have increasing demands for the dynamic quality of the vehicle with vibration noise as the main content, and the powertrain mount has developed from rubber mounts, hydraulic mounts, and semi-active mounts to active mounts [2]. The schematic diagram of the structure of these four mounts is shown in Figure 1.

If the excitation force generated by the engine operation is directly transferred to the frame, on the one hand, the passengers will feel discomfort, on the other hand, it will also reduce the service life of the engine installation position. In order to improve this situation, a rubber vibration isolating device can be added between the engine and the frame, which is the rubber mount. The rubber mount has a simple structure and low cost, but it has a significant disadvantage of dynamic hardening.

Dynamic hardening means that the dynamic stiffness of rubber increases as the excitation frequency increases. The dynamic stiffness is the stiffness when a dynamic load is applied to the rubber, which is related to the rubber formula. We hope that under low-frequency and large-amplitude excitation conditions such as road impact, engine startup, shutdown, and acceleration, the mount has the characteristics of large stiffness and large damping to better resist the large displacement of the engine and at the same time attenuate the energy of its vibration. When the engine speed increases, high-frequency and small-amplitude vibration are generated. At this time, we hope that the mount has the characteristics of small stiffness and small damping, so that the natural frequency of the mount system can be far away from the excitation frequency to achieve better vibration isolation. The rubber mount obviously cannot meet the requirements well, because as the frequency increases, its dynamic stiffness increases significantly and dynamic hardening occurs, which is contrary to the vibration isolation we want. In addition, the rubber mount relies on the friction of internal molecules to produce damping, and the effect is limited. Therefore, under the excitation of low-frequency and large-amplitude, the protective effect of rubber mount on the engine is average.

The emergence of hydraulic mount has improved the deficiency of rubber mount to a certain extent. Taking the hydraulic mount with inertia track and decoupling membrane as an example, when the excitation is low-frequency and large-amplitude vibration, the decoupling membrane will not work on the side of the upper and lower limit baffles. In addition to the role of the main rubber spring, the liquid will flow back and forth in the inertial track to form a certain damping effect, which achieves a large damping effect during low-frequency excitation. As the excitation frequency increases, the flow of the liquid in the inertial track is obstructed, and the decoupling membrane starts to play a role. The reciprocating motion between the upper and lower limits agitates the liquid, reducing the dynamic stiffness of the mount to a certain extent. Therefore, the mount performance is improved. However, as the excitation frequency further increases, the vibration amplitude of the decoupling membrane decreases, so that it cannot reduce the dynamic stiffness of the mount.

The semi-active mount is based on the hydraulic mount, adding a control method to adjust it when the dynamic stiffness cannot meet the demand, so that the performance of the mount is better [3]. The active mount is formed by adding an actuator in the hydraulic mount, which is used as the force generated by the actuator to offset the excitation force of the engine, thereby ensuring that the vibration transferred to the frame is reduced and improving the NVH performance of the vehicle. In recent years, both domestic and international are actively researching and developing active mounts. The difficulty of development and the high price have led to active mounts being found only in a few concept cars and luxury car. The affordable active mount for the mass market has become a hot research direction of mounts [2,3,4,5,6].

The active hydraulic mount with solenoid actuator is formed by adding a solenoid actuator to the passive hydraulic mount with inertia track and decoupling membrane. When the coil is loaded with alternating current, the solenoid produces a one-way alternating suction force on the armature, which converts electrical energy into mechanical energy. It has no permanent magnets and has the advantages of compact structure, low energy consumption, sensitive response, and large displacement. It is a current research hotspot [4,6]. Many researchers have devoted themselves to the study of solenoid actuator modeling and characteristics. Honggang Xiang et al. [7] used the finite element method to calculate the magnetic field related parameters, and Liang Mei et al. [8] derived the equation for the electromagnetic suction force of a circular solenoid. In addition, Bo-Ha Lee et al. [9] proposed an improved active mount model to study the active characteristics and passive characteristics, and introduced a shaping current as the input of the secondary path. Yoshiharu Nakaji et al. [10] developed an active mount system and measured the transfer function of the secondary path by measuring the step sine sweep excitation response.

Focusing on the transfer function of the secondary path of the active hydraulic mount with solenoid actuator, starting from each link of the transfer path, individually study the contribution and characteristics of the hydraulic mounts and the solenoid actuator to the transfer function of the secondary path, and introduce the full-wave-rectified current as the excitation, seek a simple and effective form of expression of the transfer function of the secondary path, and verify it by experiment, laying the foundation for the next step of realizing the active control algorithm.

2. Working Mechanism of the Active Hydraulic Mount with Solenoid Actuator

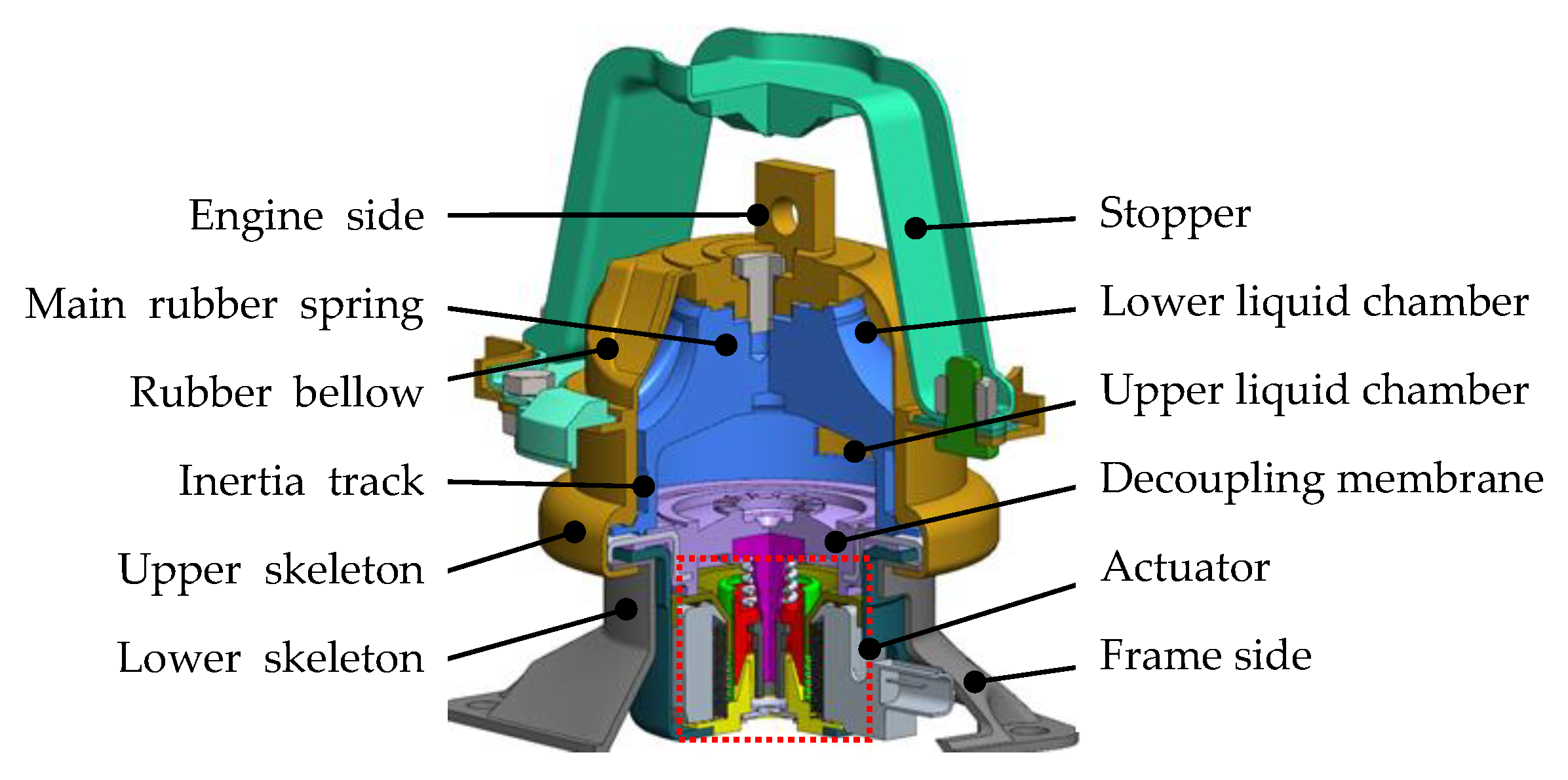
2.1. Structure of Active Hydraulic Mount

The active hydraulic mount with solenoid actuator structure uses the hydraulic mount with inertia track and decoupling membrane as the carrier, and its structure is shown in Figure 2. It mainly includes main rubber spring, inertia track, decoupling membrane, stopper, metal skeleton, and actuator. The stopper and the upper skeleton are connected by bolts and nuts. The inner surface of the stopper is vulcanized with stopper rubber to prevent excessive displacement of the engine and serve as a buffer; Rubber bellow vulcanized on the upper skeleton and vulcanized to the engine side support tab, covering the upper part of the main rubber spring to prevent impurities from entering; The main rubber spring is compressed on the decoupling membrane to prevent the liquid from leaking in the upper liquid chamber; The decoupling membrane is vulcanized with the ejector rod to enclose a sealed space for the solenoid actuator to prevent liquid immersion and affect the performance of the actuator; The support tab is vulcanized on the top of the main rubber spring as the engine installation point; The bottom of the lower skeleton has a hole, which is fixed to the frame by bolts.

In the low frequency band below 25 Hz, the actuator does not operate and relies on the large damping of the passive hydraulic mount at low frequency to attenuate the large amplitude vibration of the powertrain at rigid body modal frequency induced by shock conditions such as starting, stopping, and crossing speed bumps [11,12].

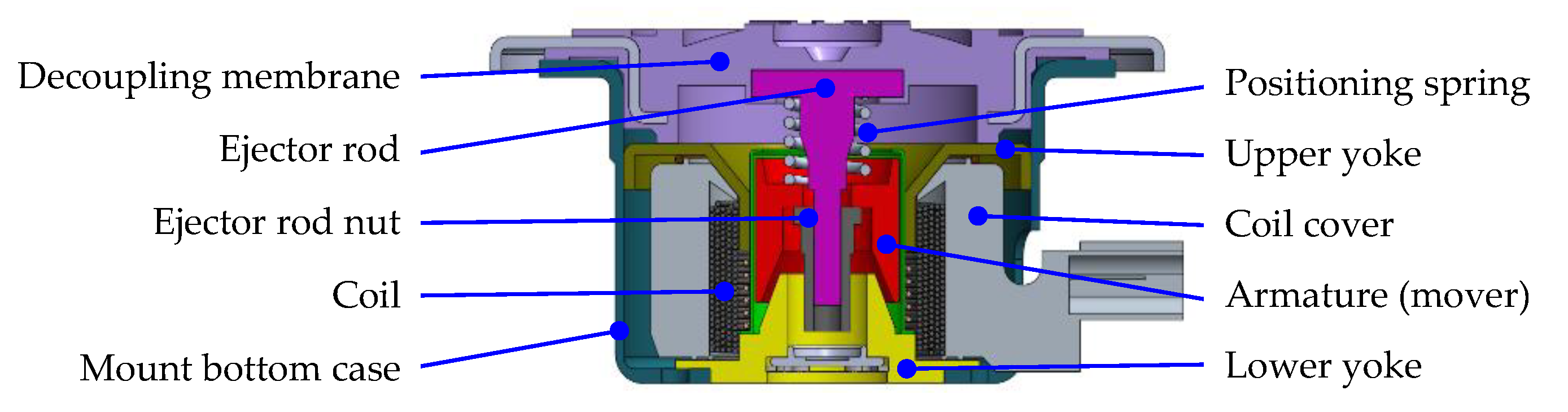
2.2. Structure and Working Principle of Solenoid Actuator

The solenoid actuator structure is shown in Figure 3, which forms a closed magnetic circuit through the armature (mover), upper yoke, coil cover, lower yoke, and air gap to reduce the magnetic resistance, so that the magnetic flux generated by the energized coil leaks less and enhances the suction force and power efficiency of the solenoid coil.

The solenoid actuator is installed in the lower skeleton of the hydraulic mount, below the decoupling membrane, and the mover is connected to the ejector rod embedded in the decoupling membrane with bolts. The coil is energized to generate a magnetic field, which produces a one-way suction force to the mover. If the suction force is reduced, the mover will rely on the elastic force of the decoupling membrane to return to its original position.

When the engine is running, its unbalanced reciprocating inertia force and unbalanced overturning torque are transferred to the frame side through the primary path of the active mount.

The actuator acts on the secondary path. The solenoid coil is energized with alternating current to produce an alternating magnetic field, and the suction force on the armature fixed to the decoupling membrane is used as the active force, which is transferred to the frame through the secondary path, offsetting the force transferred from the engine to the frame side through the primary path to reduce frame vibration. The action of the suction force on the decoupling membrane by the actuator also changes the dynamic characteristics of the hydraulic mount at the same time. The working mechanism of active hydraulic mounts for active attenuating can be understood from the perspective of the actuator actively reducing the force transferred from the engine to the frame side, and also from the perspective of the actuator actively changing the dynamic characteristics of the hydraulic mounts.

3. Active Characteristics of Active Hydraulic Mount

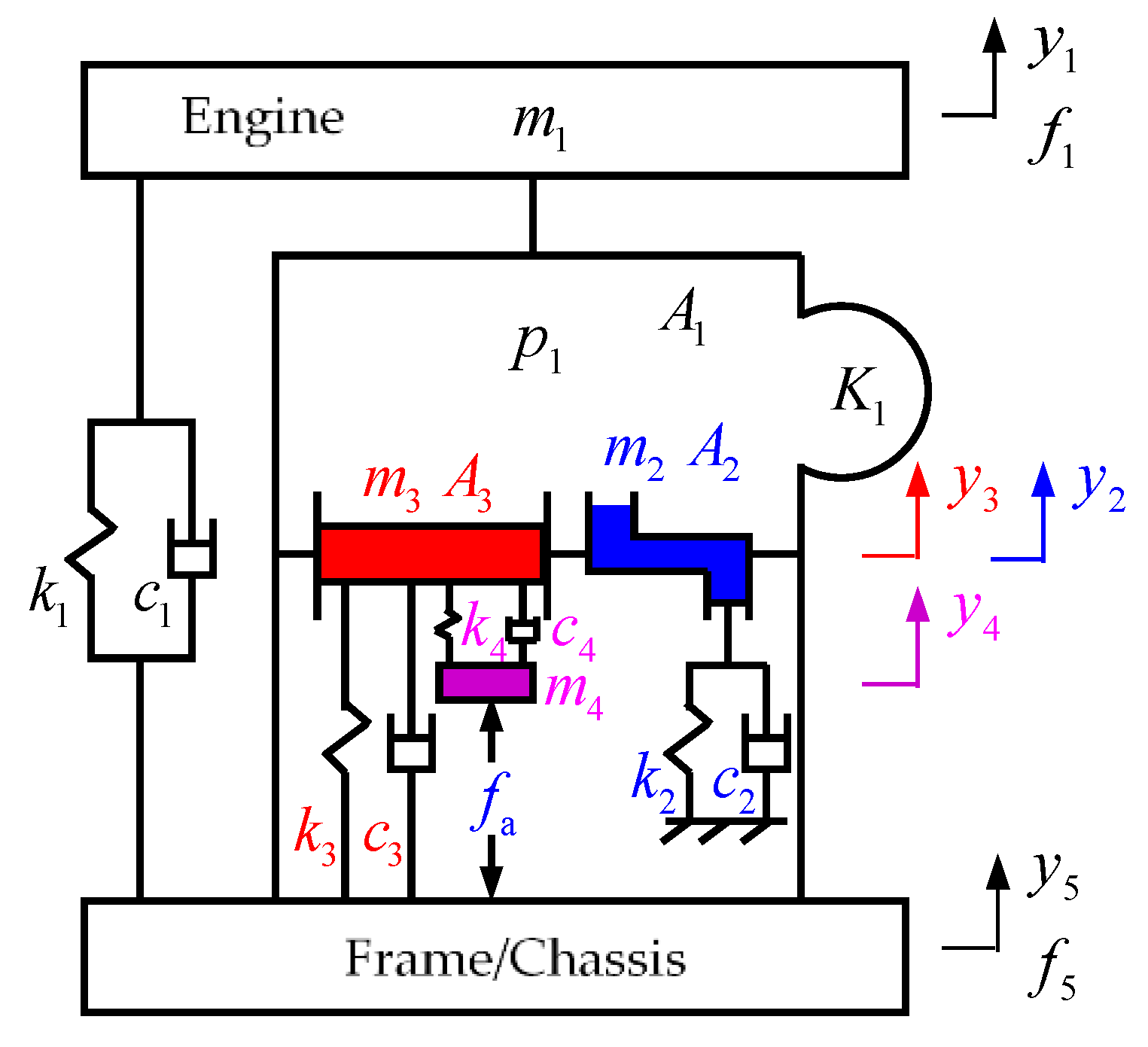
3.1. Model of Active Characteristic

The active hydraulic mount with solenoid actuator is formed by adding solenoid electromagnetic actuator with the passive hydraulic mount, with inertia track and decoupling membrane as the carrier [11,12,13,14]. With reference to the classical mechanical model of hydraulic mount [11,12,13], the mechanical model of inertial track-decoupling membrane-actuator type active hydraulic mount is established as shown in Figure 4. The displacement of the engine side is y₁ and the force is f₁; the displacement of the inertial liquid column relative to the inertial track wall is y₂, the displacement of the decoupling membrane is y₃, the displacement of the mover is y₄, and the displacement of the frame side is y₅; The pressure fluctuation of the upper liquid chamber relative to the static state is p₁; the active power of the actuator is f_a. The above are the variables in the lumped parameter model. Considering that the dynamic bulk stiffness K₂ of the lower liquid chamber surrounded by the wrinkled rubber bellow is almost zero, the pressure fluctuation p₂ of the lower liquid chamber is not considered in the model [11,12,13] and p₂ = 0.

The inertia track nature frequency f_n2 is generally in the range of 12~15 Hz. For the low frequency, large amplitude vibrations of the powertrain at rigid body modal frequency (about 8~15 Hz) are induced by shock conditions such as starting, stopping, and crossing speed bumps. Effective attenuation can be achieved by means of fluid damping, no active control is required, and the actuator does not work. The frequency band that needs to be actively controlled is above 25 Hz. At this time, the inertial track is almost closed due to the increase of fluid resistance. The degree of freedom of the inertial liquid column can be ignored, and y₂ = 0. When studying the transfer function of the secondary path of the force from the actuator to the frame side of the active mount, that is, the active characteristics, set m₁ = 0, k₂ = 0, y₁ = 0, y₅ = 0, and combine K₂ = 0, p₂ = 0, the mathematical model of the active characteristics of the active hydraulic mount with solenoid actuator in the filling state is obtained as Equation (1), and the relevant parameters and their meanings are shown in

Table 1. Parameters for AHM-SNA.

Parameter	Name	Value
c1	Viscous damping of main rubber spring in vertical direction/N·s·m−1	N/A
c2	Fluid damping/N·s·m−1	N/A
c3	Viscous damping of decoupling membrane/N·s·m−1	19.5
c4	Mover damping/N·s·m−1	16
k1	Dynamic stiffness in-phase of main rubber spring in vertical direction/N·m−1	N/A
k2	Fluid stiffness/N·m−1	N/A
k3	Dynamic stiffness of decoupling membrane/N·m−1	8.025 × 103
k4	Mover stiffness/N·m−1	1.547 × 106
m1	Mass at engine side/kg	N/A
m2	Mass of fluid in inertia track/kg	N/A
m3	Mass of ejector rod, decoupling membrane and attached liquid/kg	0.266
m4	Mass of mover/kg	7.1 × 10−2
p1	Pressure fluctuation of upper liquid chamber/Pa	N/A
p2	Pressure fluctuation of lower liquid chamber/Pa	N/A
A1	Equivalent piston area of main rubber spring/mm2	N/A
A2	Cross-sectional area of inertia track/mm2	N/A
A3	Decoupling membrane pump liquid piston area/mm2	1.3872 × 103
K1	Dynamic bulk stiffness of Main rubber spring/GN·m−5	22.67
K2	Dynamic bulk stiffness of lower liquid chamber/GN·m−5	0
K3	Dynamic bulk stiffness of decoupling membrane/GN·m−5	N/A
A0	Cross-sectional area of cone air gap/mm2	379.5
N	Number of turns of the coil	150
R	Total reluctance of the magnetic flux loop/H−1	N/A
Rm	Reluctance of core/H−1	N/A
Rδ	Reluctance of air gap/H−1	N/A
α	Cone angle/deg	45
dc	Outer diameter of mover/mm	26.5
di	Inner diameter of mover cone/mm	14.5
μ0	Magnetic permeability of vacuum/H·m−1	4π × 10−7
δ	Length of air gap/m	N/A

.

$$\{\begin{array}{l}{m}_3{\ddot{y}}_3+c_3{\dot{y}}_3+k_3{y}_3+c_4\left({\dot{y}}_3-{\dot{y}}_4\right)+k_4\left(y_3-y_4\right)+A_3{p}_1=0\\ m_4{\ddot{y}}_4+c_4\left({\dot{y}}_4-{\dot{y}}_3\right)+k_4\left(y_4-y_3\right)-f_{\mathrm{a}}=0\\ A_3{y}_3=p_1/K_1\\ f_1=-A_1{p}_1\\ f_5=c_3{\dot{y}}_3+k_3{y}_3-\left(A_1-A_3\right)p_1-f_{\mathrm{a}}=f_1-\left(m_3{\ddot{y}}_3+m_4{\ddot{y}}_4\right)\end{array}$$

(1)

Equations (4) and (5) of Equation (1) show that the active force f_a during the actuator operation is transferred partly to both the engine side and the frame side with the component f₁, and partly to the frame side only with the component $-\left(m_3{\ddot{y}}_3+m_4{\ddot{y}}_4\right)$ being the sum of the inertial forces of the mover mass m₄ and the ejector rod, decoupling membrane and its attached liquid mass m₃. The purpose of the active control of the actuator is to adjust the magnitude and phase of the active force f_a in real time, to offset the force transferred from the engine to the frame side through the primary path to the greatest extent, so as to achieve the purpose of vibration and noise reduction.

3.2. Analysis of Active Characteristic

From Equation (3) of Equation (1), we have:

$$p_1=A_3{K}_1{y}_3$$

(2)

Substituting Equations (1), (2), (4), and (5) in Equation (1), let $A_3^2{K}_3=k_3$, K₃ can be regarded as the equivalent dynamic bulk stiffness of the decoupling membrane line stiffness k₃, so there is:

$$\{\begin{array}{l}{m}_3{\ddot{y}}_3+c_3{\dot{y}}_3+A_3^2\left(K_1+K_3\right)y_3+c_4\left({\dot{y}}_3-{\dot{y}}_4\right)+k_4\left(y_3-y_4\right)=0\\ m_4{\ddot{y}}_4+c_4\left({\dot{y}}_4-{\dot{y}}_3\right)+k_4\left(y_4-y_3\right)=f_{\mathrm{a}}\\ f_1=-A_1{A}_3{K}_1{y}_3\\ f_5=f_1-\left(m_3{\ddot{y}}_3+m_4{\ddot{y}}_4\right)\end{array}$$

(3)

Considering the actual structure of the solenoid actuator, the ejector rod connecting the decoupling membrane and the mover armature is sufficiently rigid, so that the modal frequency f_n4 of the mover m₄ is much higher than the modal frequency f_n3 of the decoupling membrane m₃. Avoid introducing unnecessary modal in the active control frequency band. Therefore, in the mechanical model shown in Figure 4, m₃ and m₄ can be considered as a rigid connection, i.e., y₃ = y₄, at which point Equation (3) can be simplified as:

$$\{\begin{array}{l}\left(m_3+m_4\right){\ddot{y}}_3+c_3{\dot{y}}_3+A_3^2\left(K_1+K_3\right)y_3=f_{\mathrm{a}}\\ f_1=-A_1{A}_3{K}_1{y}_3\\ f_5=f_1-\left(m_3+m_4\right){\ddot{y}}_3\end{array}$$

(4)

This is a typical forced vibration of a single degree of freedom system, and its natural frequency is:

$$\begin{array}{cc}\hfill f_{\mathrm{n}3}& =\frac{1}{2\pi }\sqrt{\frac{A_3^2\left(K_1+K_3\right)}{m_3+m_4}}\hfill \\ \hfill {\omega }_{\mathrm{n}3}& =2\pi f_{\mathrm{n}3}\hfill \end{array}$$

(5)

Equation (5) shows that the dynamic bulk stiffness of the main rubber spring K₁ and the dynamic bulk stiffness of the decoupling membrane K₃ are in a parallel relationship in terms of the stiffness contribution of the decoupling membrane/mover vibration.

Suppose that in the state of steady-state simple harmonic motion, there is:

$$f_{\mathrm{a}}=F_{\mathrm{a}}{e}^{j\omega t}, y_3=Y_3{e}^{j\omega t}, f_1=F_1{e}^{j\omega t}, f_5=F_5{e}^{j\omega t}$$

(6)

where: $F_{\mathrm{a}}$ is the amplitude of active power, a positive real number; $Y_3$ is the displacement response amplitude of decoupling membrane, $F_1$ is the amplitude of the restraining reaction force at the engine side, and $F_5$ is the amplitude of the force transferred to the frame side, all of which are complex numbers.

Substituting into Equation (4), the frequency response functions of y₃, f₁, and f₅ are obtained as follows.

$$\frac{Y_3}{F_{\mathrm{a}}}=\frac{1}{A_3^2\left(K_1+K_3\right)\left(1-{\lambda }^2+j2\xi \lambda \right)}$$

(7)

$$-\frac{F_1}{F_{\mathrm{a}}}=\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}\cdot \frac{1}{1-{\lambda }^2+j2\xi \lambda }$$

(8)

$$-\frac{F_5}{F_{\mathrm{a}}}=\left(\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}-{\lambda }^2\right)\frac{1}{1-{\lambda }^2+j2\xi \lambda }$$

(9)

where: $K_{\mathrm{u}1}=K_1{K}_3/\left(K_1+K_3\right)$, is the series dynamic bulk stiffness of K₁ and K₃; $\lambda =\omega /{\omega }_{\mathrm{n}3}$ is the frequency ratio; $\xi =c_3/2\sqrt{\left(m_3+m_4\right)A_3^2\left(K_1+K_3\right)}$ is the damping ratio.

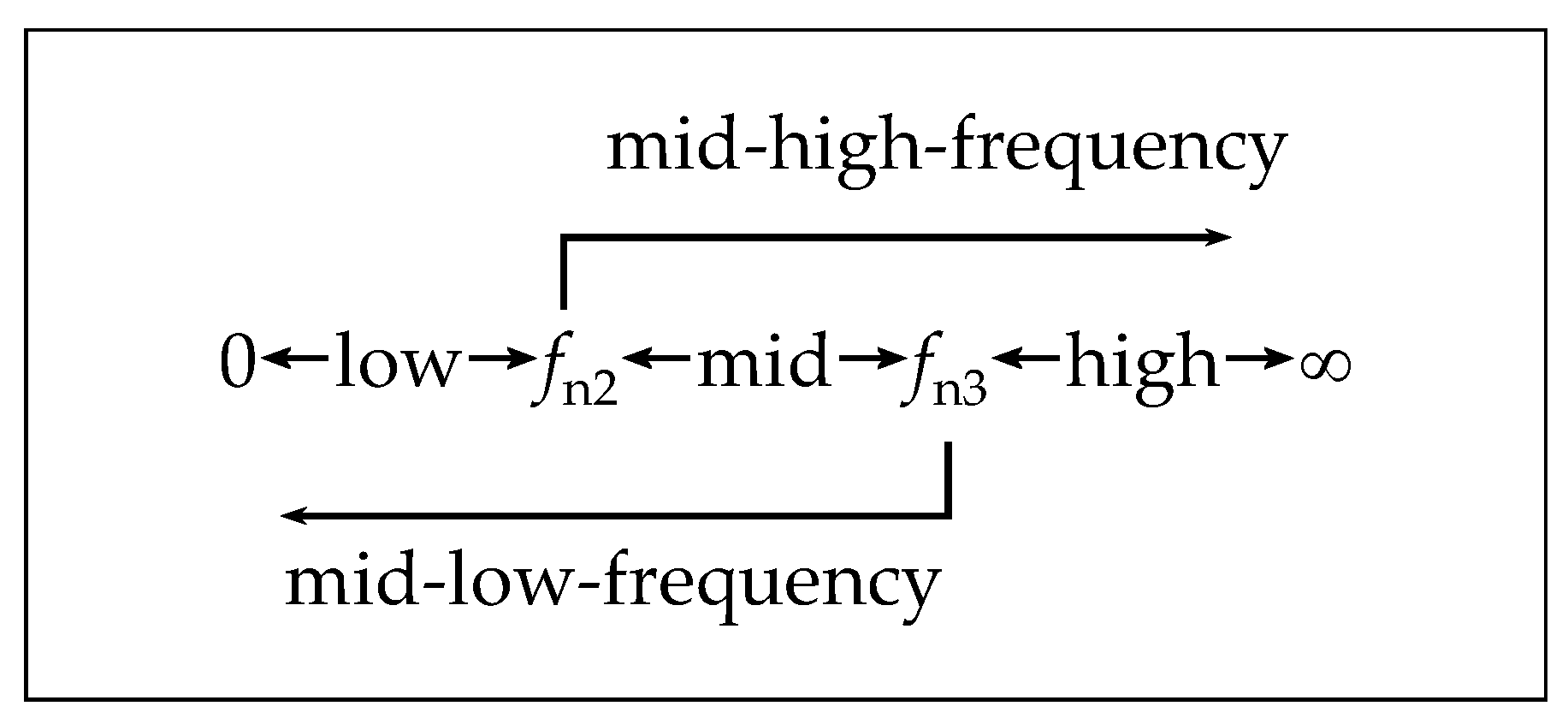
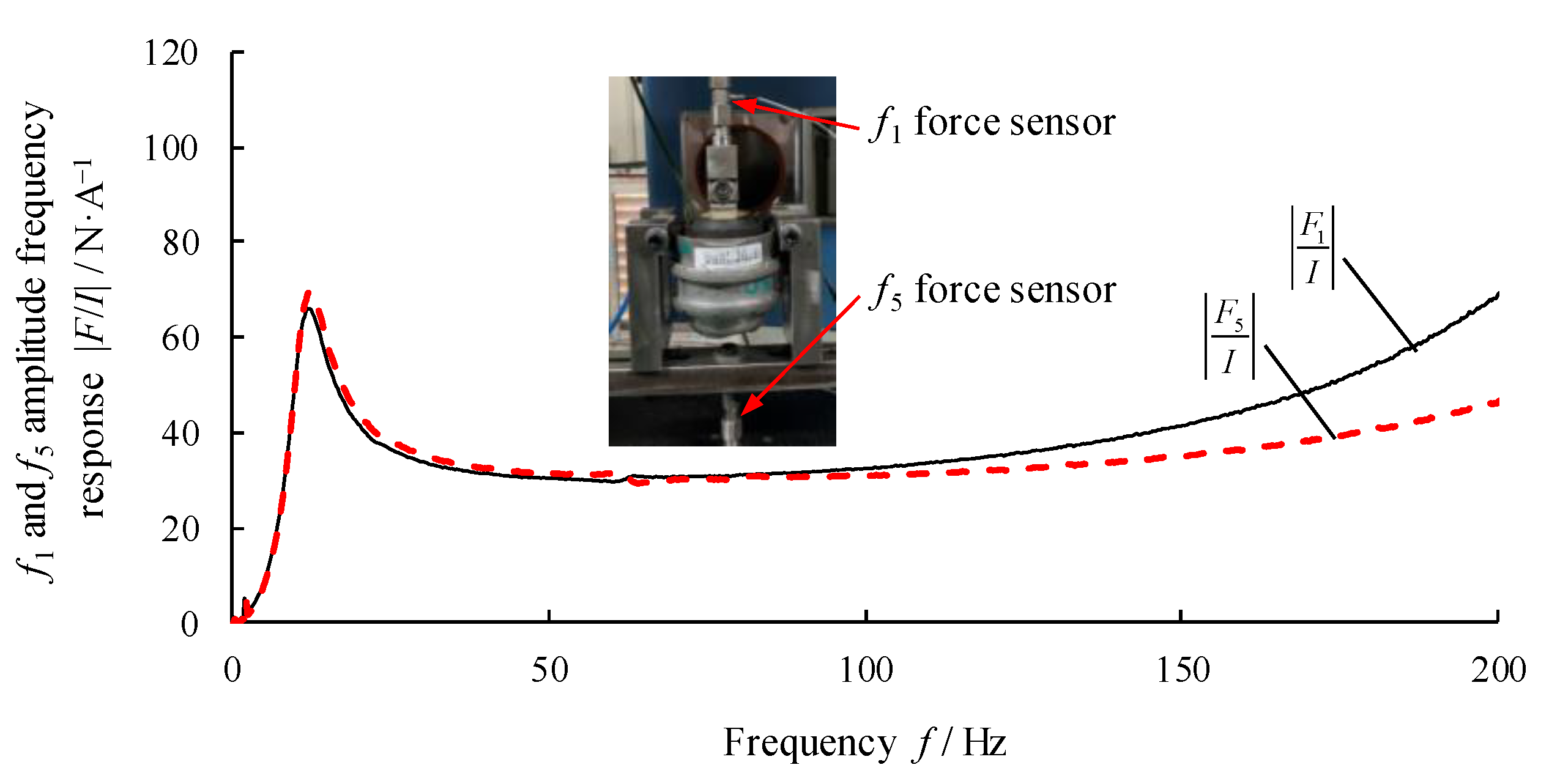
3.2.1. Frequency Response Characteristics of Engine Side Restraining Reaction Force f₁ in the Mid-High-Frequency Band

Since the natural frequency f_n3 of the decoupling membrane m₃ is much larger than the natural frequency f_n2 of the inertial track, considering that the mathematical model shown in Equation (1) is suitable for the frequency range of the excitation frequency much larger than f_n2, it is called the mid-high-frequency band. Accordingly, the frequency range much lower than f_n3 is called the mid-low-frequency band. The division of low-frequency, mid-frequency, and high-frequency band can be shown in Figure 5.

(1). Mid-frequency band when $\lambda \to 0$ (f_n2 << f << f_n3)

$$-{\frac{F_1}{F_{\mathrm{a}}}|}_{\lambda \to 0}=\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}=G$$

(10)

Equation (10) shows that in the mid-frequency band before the resonance frequency of the decoupling membrane, the force transfer rate from f_a to f₁ is a constant, and let it be G, because the parameters on the right side of the equation are constant in the case of the hydraulic mount with inertia track and decoupling membrane determined as active mounts carriers. Therefore, the active characteristic of the engine side is equivalent to a proportional link in the mid-frequency band, and the amplitude-frequency characteristic curve appears as a horizontal line.

(2). High-frequency band when $\lambda \to \infty$ (f >> f_n3)

$$-{\frac{F_1}{F_{\mathrm{a}}}|}_{\lambda \to \infty }=0$$

(11)

It can be seen that in the high frequency band (f >> f_n3) where the excitation frequency is much larger than the nature frequency of the decoupling membrane, the active power is not transferred to the engine side.

(3). When $\lambda =1$

$$-{\frac{F_1}{F_{\mathrm{a}}}|}_{\lambda =1}=\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}\cdot \frac{1}{2\xi }{e}^{-j\frac{\pi }{2}}$$

(12)

(4). The peak value of $-\frac{F_1}{F_{\mathrm{a}}}$ and the corresponding peak frequency are

$$\begin{array}{cc}\hfill {\lambda }_{\mathrm{p}}& =\sqrt{1-2{\xi }^2}\hfill \\ \hfill {\left|-\frac{F_1}{F_{\mathrm{a}}}\right|}_{\mathrm{p}}& =\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}\cdot \frac{1}{2\xi \sqrt{1-{\xi }^2}}\hfill \end{array}$$

(13)

The results of Equations (12) and (13) can be used for parameter identification.

3.2.2. Frequency Response Characteristics of the Force f₅ Transferred to the Frame Side in the Mid-High-Frequency Band

(1). Mid-frequency band when $\lambda \to 0$ (f_n2 << f << f_n3)

$$-{\frac{F_5}{F_{\mathrm{a}}}|}_{\lambda \to 0}=\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}=G$$

(14)

Equation (14) is consistent with the result of Equation (10), which shows that the active characteristic of the frame side is also equivalent to a proportional link in the mid-frequency band, and the amplitude-frequency characteristic curve behaves as a horizontal line, which is the linear section on which the active mount works and facilitates the realization of active control. It also shows that in the mid-frequency band, which is far below the natural frequency of the decoupling membrane, there is no difference in the frequency response characteristics of the engine and frame sides forces f₁ and f₅ of the mount due to the inertial forces of m₃ and m₄, so the inertial forces can be neglected; this conclusion is consistent with the mechanical vibration theory, and experimental verification has been done for this purpose.

(2). High-frequency band when $\lambda \to \infty$ (f >> f_n3)

$$-{\frac{F_5}{F_{\mathrm{a}}}|}_{\lambda \to \infty }=1$$

(15)

Equation (15) shows that in the high-frequency band (f >> f_n3) where the excitation frequency is much larger than the natural frequency of the decoupling membrane, the active power is reproduced at the frame/chassis side in reverse phase 1:1, and is not transferred to the engine side. This provides convenience for the control of the active power.

(3). When $\lambda =1$

$$-{\frac{F_5}{F_{\mathrm{a}}}|}_{\lambda =1}=\left(\frac{A_1{K}_{\mathrm{u}1}}{A_3{K}_3}-1\right)\frac{1}{2\xi }{e}^{-j\frac{\pi }{2}}$$

(16)

In order to verify the conclusion that the results of Equations (10) and (14) are consistent, and the reasonableness of ignoring the inertial force of the decoupling membrane/mover in the mid-frequency band, a special experiment was designed to verify. Figure 6 shows the force-frequency response characteristic curve at both ends of an inertial track-decoupling membrane-oscillating coil linear actuator active hydraulic mount. The hydraulic mount as the active mount carrier has the same form, all of which are the hydraulic mount with inertia track and decoupling membrane; its actuator is an oscillating coil actuator, the actuation force and current is linear, that is, f_a = k_M⋅i(t), for the actuation force f_a as the input frequency response curve and the current i as the input frequency response curve only differs by a constant k_M. As shown in Figure 6, the frequency response curves at both ends of the mount almost overlap within 100 Hz, indicating that the difference in frequency response characteristics between the engine and frame sides forces f₁ and f₅ of the mount caused by the inertial force in the mid-low-frequency band is negligible. Above 100 Hz, the influence of the decoupling membrane/mover mass inertial force gradually increases, and the influence of inertial force must be considered.

4. Actuating Force of Solenoid Actuator

The analysis of the active characteristics of the hydraulic mount in the previous section shows that if the input and output transfer function of the actuator are linear, such as the oscillating coil actuator, the above active characteristics can be directly multiplied by a scale factor to obtain the total transfer function of the secondary path. For solenoid actuators, the input and output characteristics are more complex and require further study. The AHM-SNA parameters involved in this chapter are included in Table 1.

4.1. Alternating Suction Force of Electromagnet

The electromagnet is an electrical appliance that uses the energized core coil to attract the armature, and the magnetic field in the alternating current electromagnet is also alternating at the same frequency [15]. Let the alternating magnetic field be:

$$B_0=B_{\mathrm{m}}\sin \omega t$$

(17)

where: B_m is the amplitude of magnetic induction intensity B₀ in the solenoid air gap, unit [T]. Then the alternating electromagnetic suction force is also known as the solenoid actuator active force instantaneous value f_a(t) and its amplitude F_a are:

$$f_{\mathrm{a}}\left(t\right)=F_{\mathrm{a}}\sin \left(2\omega t-\frac{\pi }{2}\right)$$

(18)

$$F_{\mathrm{a}}=\frac{1}{2}\frac{{10}^7}{8\pi }{B}_{\mathrm{m}}^2{A}_0=\frac{1}{2}\frac{{10}^7}{8\pi }\frac{{Ф}_{\mathrm{m}}^2}{A_0}$$

(19)

where: A₀ is the cross-sectional area of the cone air gap, 379.5 mm²; Φ_m is the maximum value of the magnetic flux in the core magnetic circuit, that is, the amplitude, the unit is [Wb], 1 Wb = 1 T·m² =1 V·s.

Note that the frequency of the alternating active power of the solenoid actuator is twice the frequency of the alternating magnetic field (that is, the alternating current), and it lags the alternating magnetic field π/2 in phase.

4.2. Alternating Suction Force of the Cone Air Gap Solenoid

The solenoid is also called electromagnet. Based on magnetic ohm’s law [15]

$${Ф}_{\mathrm{m}}R={Ф}_{\mathrm{m}}\left(R_{\mathrm{m}}+R_{\delta }\right)=N{I}_{\mathrm{m}}$$

(20)

where: I_m is the amplitude of the alternating current $i\left(t\right)=I_{\mathrm{m}}\sin \omega t$, unit [A]; N is the number of turns of the coil, 150; R is the total reluctance of the magnetic flux loop, R_m is the reluctance of the core, R_δ is the reluctance of the air gap, unit [H⁻¹].

Considering that the reluctance of air gap is much larger than the reluctance of iron core, the reluctance of iron core can be neglected in the total reluctance, i.e., $R=R_{\mathrm{m}}+R_{\delta }\approx R_{\delta }$, and the Equation (20) can be approximated as:

$${Ф}_{\mathrm{m}}{R}_{\delta }=N{I}_{\mathrm{m}}$$

(21)

Substituting Equation (19), there are:

$$F_{\mathrm{a}}=\frac{1}{2}\frac{{10}^7}{8\pi }\frac{N^2}{A_0}\frac{1}{R_{\delta }^2}{I}_{\mathrm{m}}^2$$

(22)

Note that the relationship of F_a~I_m is independent of the excitation current frequency f, but is squared with the reluctance of air gap as well as the current amplitude I_m, which has nonlinear characteristics.

The structure and parameters of the solenoid actuator are shown in Figure 7. For an electromagnet with a cone surface, the reluctance of air gap is [16]:

$$\begin{array}{cc}\hfill R_{\mathsf{\delta }}& =\frac{1}{{\mu }_0\times {10}^{-2}\left(\frac{100\pi d_{\mathrm{c}}^2}{4\delta {\sin }^2\alpha }-\frac{15.7d_{\mathrm{c}}}{{\sin }^2\alpha }+75d_{\mathrm{c}}\right)}\hfill \\ \hfill & =\frac{{10}^8}{\left(\frac{0.139}{\delta }+1.452\right)}\hfill \end{array}$$

(23)

where: α is the cone angle, 45°; d_c is the outer diameter of mover, 26.5 mm; d_i is the inner diameter of mover cone, 14.5 mm; ${\mu }_0$ is the magnetic permeability of the vacuum, 4π × 10⁻⁷ H·m⁻¹; $\delta$ is the length of air gap, unit [m].

Substituting Equation (23) into Equation (22), the amplitude of the alternating force of the solenoid actuator during the alternating current excitation is obtained as:

$$F_{\mathrm{a}}={\left(\frac{0.00476}{\delta }+0.04987\right)}^2{I}_{\mathrm{m}}^2$$

(24)

4.3. Frequency Response Characteristics of Full-Wave-Rectified Current Excitation

Considering the alternating suction force frequency of the solenoid actuator shown in Equation (18) is twice the frequency of the alternating current, it is not convenient to calculate the frequency response function from the input current to the output active power, the following considers the alternating suction force under the excitation of the full-wave-rectified current shown in Equation (25) because the fundamental frequency of the full-wave-rectified current is just twice the frequency of the alternating current before rectification, which is equal to the fundamental frequency of the alternating active power, and the frequency response function can be calculated.

Full-wave-rectified current, also called absolute value sine current, the harmonic decomposition of its Fourier series is as follows [15]:

$$\begin{array}{cc}\hfill i\left(t\right)& =\mathrm{abs}\left(I_{\mathrm{m},\mathrm{a}}\sin \omega t\right)\hfill \\ \hfill & =I_{\mathrm{m},\mathrm{a}}\cdot \mathrm{abs}\left(\sin \omega t\right)\hfill \\ \hfill & =\frac{2I_{\mathrm{m},\mathrm{a}}}{\pi }\left(1-\frac{2}{3}\cos 2\omega t-\frac{2}{15}\cos 4\omega t-\cdots \right)\hfill \\ \hfill & =I_{\mathrm{m},0}+I_{\mathrm{m},2}\cos 2\omega t+I_{\mathrm{m},4}\cos 4\omega t+\cdots \hfill \end{array}$$

(25)

where:

I_m,a is the amplitude of the alternating current before rectification;

I_m,0 is the direct current component, $I_{\mathrm{m},0}=\frac{2I_{\mathrm{m},\mathrm{a}}}{\pi }$;

I_m,2 is the second harmonic amplitude, $I_{\mathrm{m},2}=\frac{4I_{\mathrm{m},\mathrm{a}}}{3\pi }$;

I_m,4 is the fourth harmonic amplitude, $I_{\mathrm{m},4}=\frac{4I_{\mathrm{m},\mathrm{a}}}{15\pi }$, which is only 20% of the second harmonic amplitude I_m,2.

Although the full-wave-rectified current in addition to the second harmonic, there are high-order harmonics with small amplitudes such as fourth and sixth. Because of the small amplitude, the impact is ignored. Only considering the second harmonic excitation, from the full-wave-rectified current peak value I_m,a to the second harmonic amplitude I_m,2, then to the amplitude of the alternating active power of the solenoid actuator F_a, and then to the frequency response function of force F₅ at the frame side, by Equations (14), (24) and (25), there are:

$$\begin{array}{cc}\hfill \left|\frac{F_5}{I_{\mathrm{m},\mathrm{a}}^2}\right|& =\left|\frac{F_5}{F_{\mathrm{a}}}\cdot \frac{F_{\mathrm{a}}}{I_{\mathrm{m},2}^2}\cdot \frac{I_{\mathrm{m},2}^2}{I_{\mathrm{m},\mathrm{a}}^2}\right|\hfill \\ \hfill & =G{\left(\frac{0.00476}{\delta }+0.04987\right)}^2{\left(\frac{4}{3\pi }\right)}^2\hfill \\ \hfill & =K\hfill \end{array}$$

(26)

Considering that the parameters in equation are all constants under the action of a certain current, the right side of Equation (26) is directly equated to a constant K. Next, we will fit the constant K based on the experimental data to verify whether the assumption of the constant is valid. If it is true, the cumbersome process of parameter testing such as A₁, K_u1, A₃, K₃, δ and the errors caused by it can be eliminated, and the implementation of active control algorithms is facilitated.

5. Experimental of Secondary Path Transfer Function in Active Hydraulic Mount with Solenoid Actuator

In response to the conclusions of the previous analysis, the experiment setup shown in Figure 8 was designed and tested according to the following scheme.

In the experiment device in Figure 8, the active mount is fixed at both ends, and two force sensors are installed at the end of the frame. The solenoid actuator is loaded with full-wave-rectified current, the actuator is activated, the force sensor picks up the force transferred to the frame side, and the current sensor picks up the loading current. It has been verified that based on the symmetrical installation, the signals of the two force sensors are almost coincident, and the two are added together as a force on the end of the frame.

The first experiment scheme is fixed frequency variable current. Perform experiment at multiple frequencies such as 40, 50, 75 Hz; At each frequency, set multiple current amplitudes I_m,a between 0 and 4 A, and get several amplitude data pairs for different currents at that frequency F₅~I_m,a, forming a curve. Multiple curves can be obtained under multiple experiment frequencies, and the experiment results are shown in Figure 9. The curves of different frequencies in the figure basically overlap and conform to the shape of a quadratic curve. The fitting can be performed based on all the experimental data and according to Equation (26). The fitting result is K = 2.12.

The second experiment scheme: fixed current variable frequency. According to Equation (26), the ratio between the amplitude of alternating suction force and the square of the current amplitude $F_5/I_{\mathrm{m}}^2$ should be a constant 2.12 in the operating frequency band, so the second experiment was conducted to verify the fitting results again, i.e., the amplitude of the excitation current was fixed, and the frequency was gradually increased. Extract the amplitude F₅ of f₅ at each frequency, and get the curve of $F_5/I_{\mathrm{m}}^2$ changing with frequency. The experiment result is shown in Figure 10, and the curve appears as a horizontal line and coincides with the curve calculated by the fitting constant K = 2.12.

The above experiment shows that the fitting result is reliable and can be used for the calculation of electromagnetic suction force. The analysis result shown in Equation (26) is correct. It also verifies that the current-based alternating electromagnetic suction force is independent of frequency.

In addition to the second harmonic of the full-wave-rectified current, there are also higher harmonic quantities such as the fourth and sixth, although the amplitude is small, making the above frequency response characteristics only an approximate sense of the frequency response characteristics. The next step will be to study the shaping technology of the full-wave-rectified current to eliminate its higher harmonics and obtain the frequency response function from the current to the force at the frame side in the strict sense, so as to improve its accuracy and facilitate the active control.

6. Conclusions

(1)

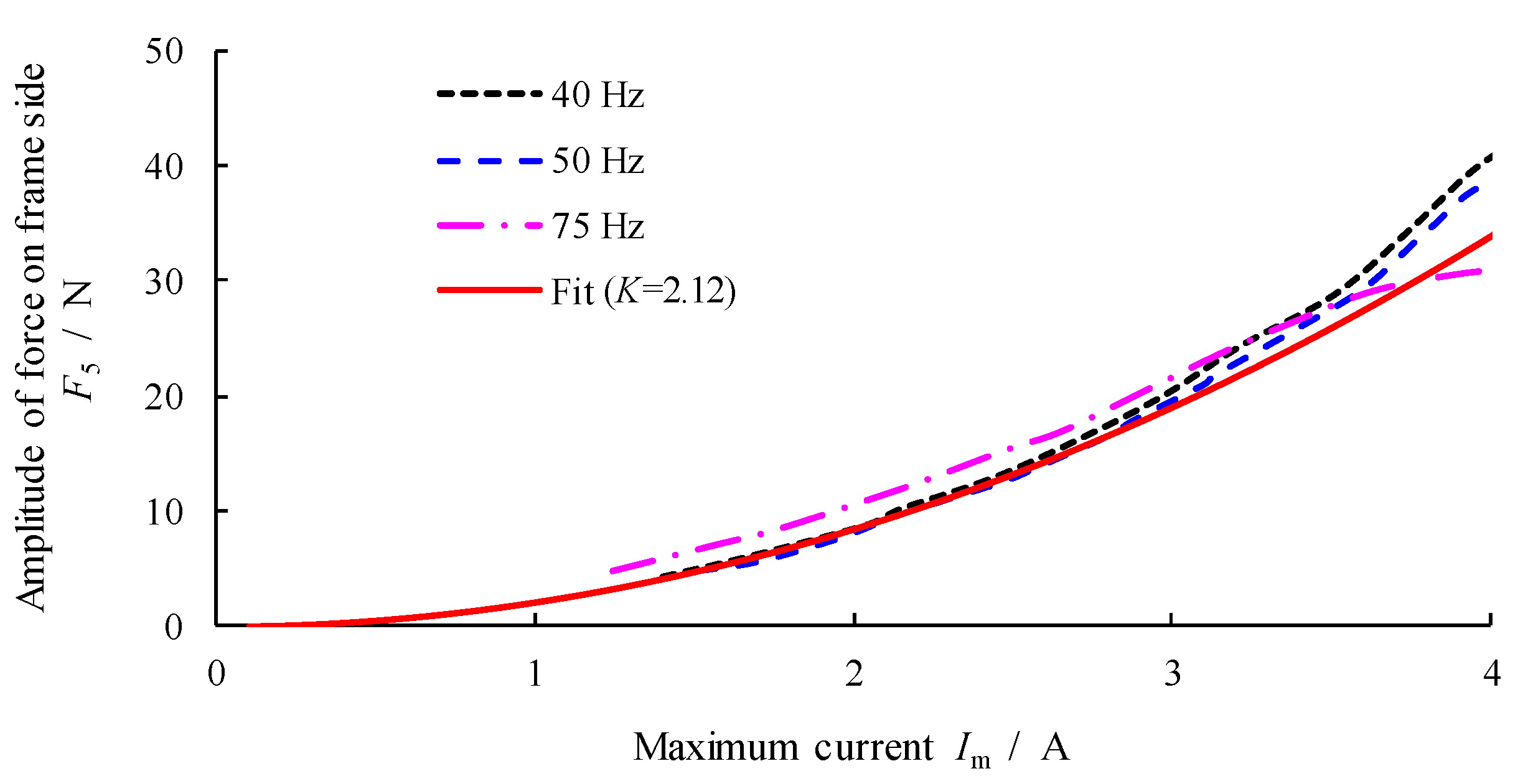
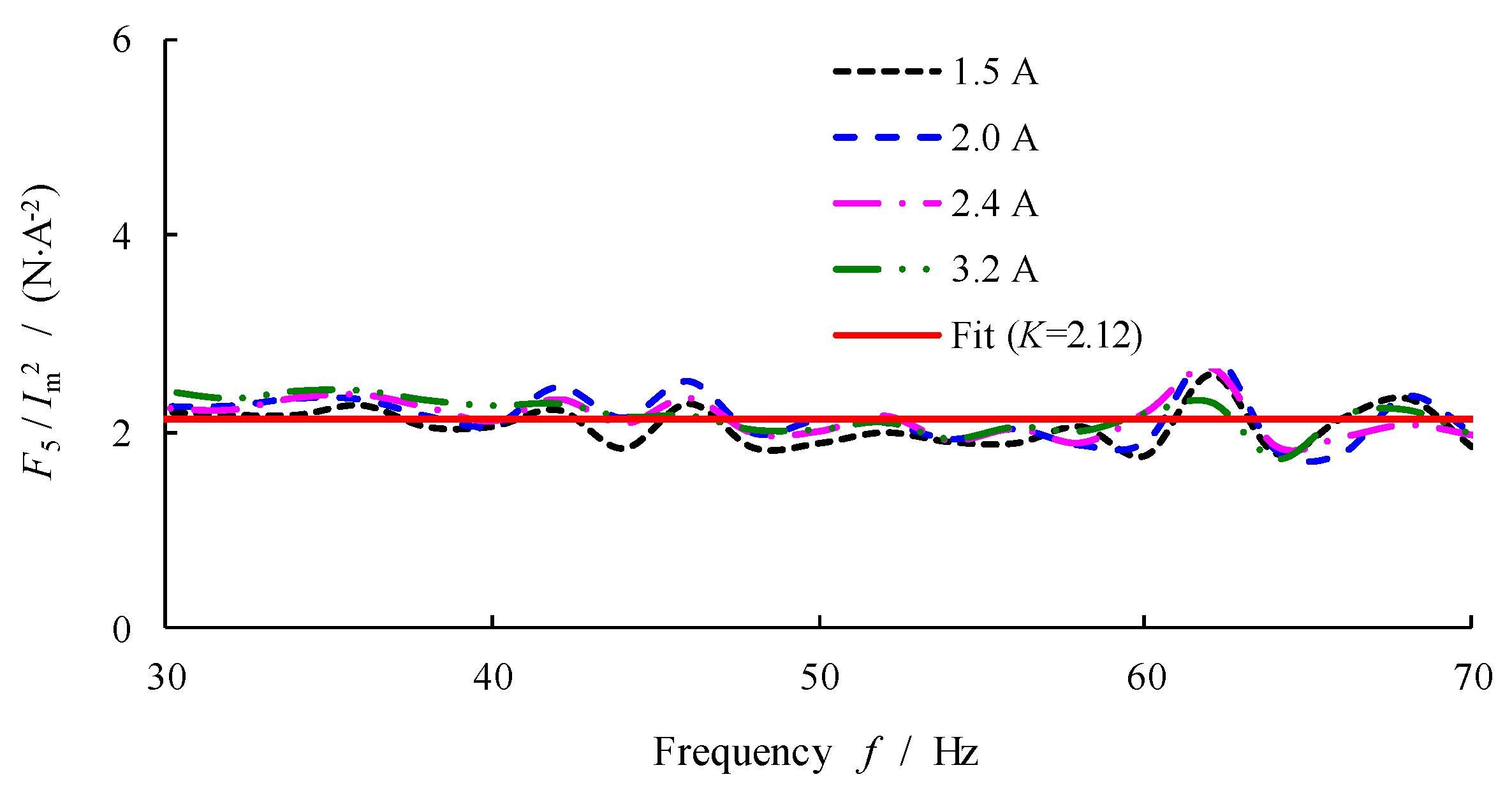
In the active hydraulic mount with the inertial track-decoupling membrane hydraulic mount as the carrier, the transfer function of the active power of the actuator to the force on the frame side is constant in the mid-frequency band, which is equivalent to the proportional link.

(2)

Under the action of harmonic current of solenoid actuator, the frequency of its alternating suction force is twice the frequency of current, and the amplitude of alternating suction force is independent of frequency. Under the action of full-wave-rectified current, the frequency of the current is the same as the second harmonic component of the main component of the alternating suction force, which is convenient to calculate and test the frequency response function in the approximate sense.

(3)

The analysis and experiment verify that the transfer function of the solenoid actuator from the full-wave-rectified current to the force on the frame side is constant, which not only provides convenience for active control, but also eliminates the tedious testing of the parameters related to the traditional hydraulic mount, reduces the error links, and improves the accuracy of the transfer function.

(4)

The next step will be to study a full-wave-rectified current shaping technology to eliminate its high-order harmonic components, so as to obtain higher-precision transfer function, which is conducive to active control.