Abstract
Model predictive torque control with duty cycle control (MPTC-DCC) is widely used in motor drive systems because of its low torque ripple and good steady-state performance. However, the selection of the optimal voltage vector and the calculation of the duration are extremely dependent on the accuracy of the motor parameters. In view of this situation, A modified MPTC-DCC is proposed in this paper. According to the variation of error between the measured value and the predicted value, the motor parameters are calculated in real-time. Meanwhile, Model reference adaptive control (MRAC) is adopted in the speed loop to eliminate the disturbance caused by the ripple of real-time update parameters, through which the disturbance caused by parameter mismatch is suppressed effectively. The simulation and experiment are carried out on MATLAB / Simulink software and dSPACE experimental platform, which corroborate the principle analysis and the correctness of the method.
1. Introduction
Permanent magnet synchronous motor (PMSM) was adopted as the driving machine of electric vehicles (EVs) because of its high efficiency, high torque density and low volume [1]. Nowadays, many mature control strategies have been proposed, which can be divided into two major categories: vector control (VC) and direct torque control (DTC) [2,3,4,5]. VC has good dynamic and steady-state performance, but its application in high-performance places is hindered by the limitation of bandwidth [2]. DTC has very fast torque response ability, but it can also cause higher torque ripple [3]. In order to overcome the shortcomings of traditional control methods, many control strategies have been proposed [4,5]. However, the complex operating environment of electric vehicles brings great challenges to the design of control methods [6,7].
In the EVs control system, torque is the most important control objective [8]. Model predictive torque control (MPTC) has been widely attended by many scholars because of its fast torque response and arbitrary synthesis of various constraints [9,10,11,12,13]. MPTC can directly predict the behavior of the machine at the next moment, and select the optimal voltage vector applied to the motor based on the designed cost function [9]. Compared with DTC, the optimal voltage vector selected by minimizing the cost function is more accurate and efficient [10]. Furthermore, other constraints can be integrated into the cost function to improve the control performance of the system [11]. Compared with VC, MPTC has faster torque response and is more suitable for applications requiring high torque response performance [12]. However, similar to DTC, MPTC also have the problems of high torque ripple and variable switching frequency [9]. In order to overcome this problem, the duty cycle control (DCC) idea of DTC control is introduced into MPTC, which can effectively reduce the torque ripple [13]. However, the machine behaviors predicted by model at the next extreme depend on the accuracy of the model parameters.
Recently, control techniques such as backstepping, model reference adaptive control (MRAC) and H-infinity method have been proposed to eliminate parameter mismatched disturbances [14,15,16,17]. The controller and observer designed by backstepping method can effectively improve the robustness of the system to eliminate the parameter mismatch disturbance and external disturbance [14,15]. Similar to the backstepping method, the H-infinity method also eliminates the disturbance by designing the controller [16]. In [17], MRAC regards parameter mismatch disturbance and external disturbance as a whole disturbance, and designs controller according to reference model to eliminate the whole disturbance by compensation. The designed controller can improve the robustness of the system to a certain extent, but its disturbance rejection ability is not enough to eliminate the large range of parameter mismatch. For example, the MRAC method proposed in [17] can only effectively eliminate the disturbance whose parameter error is less than .
In addition, many methods of utilizing observers to obtain the external disturbances and the actual parameters of the system have also been proposed by many scholars [18,19,20,21,22]. Sliding mode observer is widely used to improve system robustness [14]. According to the error signal, the rotor speed is estimated by the combination of sliding mode observer and model reference adaptive system, which is applied to the codeless induction motor control system [18]. The traditional method of flux linkage observation is extremely dependent on machine parameters [19,20]. A disturbance observer is designed in [19], which not only takes the load disturbance and parameter mismatch disturbance as observed variables, but also takes the digital delay disturbance into account [19]. In [20], when the rotor position angle is unknown, a flux observer based on phase self-tuning is proposed to eliminate the influence of parameter mismatch. A proportional integral observer combine with sliding mode and an extended sliding mode observer are designed in [21,22], respectively, through observation of disturbances caused by mismatch of various parameters, the accurate parameter of stator inductance for the former and viscous friction coefficient, rotational inertia for the latter can be obtained to improve performances. However, the iterative computation of MPTC in the process of minimizing the cost function will cause serious computational burden [23]. The use of observer will aggravate this phenomenon, and the parameter adjustment of observer is also very difficult.
Furthermore, it is an excellent solution to suppress parameter mismatch that the error between the predicted value and the actual value of the previous time is multiplied by the adjustment coefficient and introduced into the calculation of the predicted value of the next time [24,25,26,27,28,29]. However, in [24], when the adjacent switch states are the same, the adjustment coefficient is zero, which will deteriorate the control performance. In [25], the adjustment coefficient is obtained by trial and error, which cannot suppress the disturbance of continuous variation of parameters. An improved MPCC method with current update mechanism is proposed in [26]. According to the variation of error between the predicted value and the measured value of the adjacent period, the disturbance of parameter mismatch is introduced into the predicted current at the next moment, and the optimal voltage vector is selected more accurately. However, this method is only suitable for MPCC with cost function composed of current error, and the compensation obtained contains fluctuation due to the existence of differential process [29].
The contribution of this article is that this article proposes a modified MPTC-DCC method to suppress the parameter mismatch. Based on previous mentioned researches, according to the variation of error between the measured value and the predicted value, the motor parameters are calculated in real-time. Although the updated motor parameters contain noise under the influence of the differential process, they can be maintained near the actual parameters. Therefore, model reference adaptive control (MRAC) is adopted in the speed loop to eliminate the disturbance caused by the ripple of real-time update parameters, through which the disturbance caused by parameter mismatch is suppressed effectively.
This paper is organized as follows: the performance analysis of traditional MPTC is reviewed briefly in Section 2, including the mathematical model of PMSM, calculation of duration of optimal voltage vector. The proposed method is described in Section 3. In Section 4 and Section 5, simulation and experiment results are compared with other two methods: MRAC-SC proposed in [17], Current update mechanism proposed in [26] applied into MPTC to demonstrate the effectiveness. Finally, the conclusions are presented in Section 6.
2. Traditional Model Predictive Torque Control
The mathematical model of SPMSM on axis can be presented as follows [23]:
where stand for the stator currents, the stator voltages, the stator flux linkages, and the stator inductances on axis, respectively. For SPMSM, the stator inductances on d-axis and q-axis are approximately equal to synchronous inductance, i.e., , and stand for the stator resistance, rotor flux linkage, electromagnetic rotor angular velocity, number of pole pair, electromagnetic and load torque, respectively.
2.1. Model Predictive Torque Control
Cascade processing is used in traditional MPTC. The optimal voltage vector is first selected based on the minimization of the cost function, and then its duty cycle is obtained according to some principles [26]. According to Equation (1), based on the measured currents and the candidate voltage vectors the predicted currents can be obtained as [21]
where is sampling cycle. Prediction of torque and flux linkage can be obtained from Equations (2), (3) and (5). It is well known that in real-time implementation, there is one-step delay between the commanding voltage and the real voltage [21]. Therefore, one-step delay compensation is adopted. For the convenience of calculation, the detailed description is not given here. Then, prediction values are substituted into the cost function (6). The optimal voltage to minimize the cost function is selected.
where denote the reference values of electromagnetic torque and flux linkage. q denote the weight coefficient. It is determined by the ratio between rated torque and flux linkage of the motor [27].
2.2. Calculation of Time Duration of the Optimal Voltage Vector
The duty cycle determination method in [13] is adopted, which minimize the root mean square (RMS) value of torque ripple in one cycle. To reduce the control complexity, the optimal duration for the active vector is calculated in the stationary frame in order to avoid synchronous transformation [13]:
where stand for the value of the torque at the starting of the control period. are the stator voltage vector and stator flux linkage vector in the stationary frame, respectively. From the traditional MPTC cascade process with duty cycle control, it can be found that the selection of effective vector and the calculation of optimal duration are closely related to the accuracy of motor parameters, .
3. Proposed Modified MPTC with Parameters Robustness Improvement
In [17], a model reference adaptive control (MRAC) is proposed, the system control block diagram is shown in Figure 1. The experiment and simulation analysis in [17] shows that the control performance is excellent if the stator inductance, resistance and flux linkage are in the range of 80–125% of the actual values. In other words, only about error in parameters can be tolerated [17].
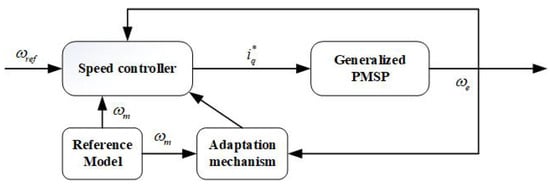
Figure 1.
Block diagram of the MRAC-SC proposed in [17].
Although the effect of MRAC-SC proposed in reference [17] on eliminating the disturbance caused by huge parameter mismatch is not satisfactory, the huge parameter change can be reduced to a small range by real-time updating method, and the superior performance of MRAC method can be fully utilized. The detailed process is described in Section 3.2.
In [26], an improved MPCC control method with current update mechanism was proposed, by which the predicted current can be update at the next moment according to the variation of error between the measured value and the predicted value.The system control block diagram is shown in Figure 2. The real motor parameters are not calculated directly, but the influence of parameter mismatch is eliminated by modifying the predicted current. However, the compensation obtained contains noises due to the existence of differential process [29]. Moreover, this method can not effectively compensate the predicted torque and flux in MPTC to eliminate the parameter mismatch disturbance.
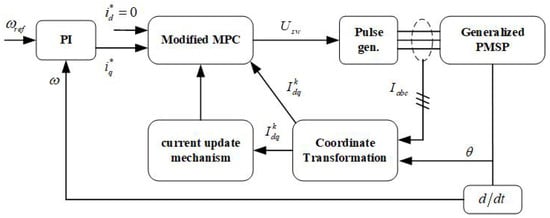
Figure 2.
Block diagram of the improved MPCC proposed in [26].
Based on the above results, a modified MPTC with parameters robustness improvement is proposed in the paper. The updated motor parameters can match the actual parameters in a certain range, and the noises caused by the existence of differential process can be completely eliminated by outer loop of MRAC method. Meanwhile, excellent speed tracking and anti-disturbance ability can be obtained.
3.1. Model Reference Adaptive Control
There exists a constant parameter vector such that [17]:
where
The reference model is selected as the first order differential form [17]
where is a strictly positive constant parameter. is the reference model output. c is the initial value of the reference model.
The reference model output is compared to the error between the actual speed and the desired speed [17], the dynamic equation can be obtained as:
where The tracking error is obtained as follows:
The reference torque is obtained as follows:
where the second term is the adaptive compensation term. is estimated value of the expected compensation value , the update law is given as . where .
The Lyapunov function is selected as:
where .
Then, the derivative of Lyapunov function is as follows:
According to Equations (10) and (14), the Equation (16) can be rearranged as follows:
Integrating both sides of (17) gives
Thus, the above-mentioned inequality can be rewritten as:
Which implies that , it is proved that the system is stable.The control block diagram is shown in Figure 1.
3.2. MPTC with Real-Time Update of Parameters
In MPTC with duty cycle control, an active vector and a null vector are applied to the motor in one cycle. In the steady-state process, the duration of the selected vector is less than the control cycle. The current at kth instant can be obtained base on the measured value at (k+1)th instant as
Then, rough prediction current can be obtained under parameters mismatch as
where stand for the rough predicted current. and are the measured values at ()th instant. stand for the durations of selected vector at ()th instant. are the inaccurate stator resistance, stator inductance and rotor flux linkage, respectively. The error between rough predicted current and actual measured value at kth instant is obtained based on the difference between Equations (20) and (21).
where , , .
Then, the error variation of adjacent cycle periods can be obtained as
Thanks for the analysis results in [24,25,26,29]. The right side of Equation (23), the current item is small enough to be ignored. Then, the Equation (24) can be rearranged as follows:
Then, the following relation can be obtained:
where stand for the updated stator inductance. It should be noted that there is a differential in Equation (5), which makes the updated stator inductance contain noise. The adjustment coefficient N is necessarily as
It should be noted that the latest obtained parameter will not be adopted until the new obtained parameter is acquired through Equation (26) [28]. Substituting into the second equation of Equation (23) results in
Then, the following relation can be obtained:
Substituting into the first equation of Equation (22) results in
The updated stator resistance can be obtained through Equation (30)
By substituting the above calculating results into (2)–(4), and (6)–(8), respectively, predicted torque and flux linkage, and the duration of the effective vector can be obtained. The updated motor parameters can change with the actual parameters, but it contains noise. The uncertainty caused by the noise and the external disturbance are compensated by the MRAC of the speed loop. The block diagram of the proposed method is shown in Figure 3.
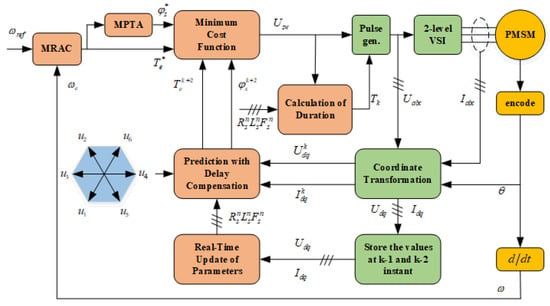
Figure 3.
Block diagram of the proposed method.
4. Simulation Study
The rated parameters of SPMSM are shown in Table 1. Simulation results of three methods under different conditions are compared in MTLAB/SIMULINK environment. The sampling time is set to 50 μs, and the DC side power supply voltage is set to 311 V. The weight coefficient q is set to 130 [27]. Method 1: MRAC-SC proposed in [17]. Method 2: Current update mechanism proposed in [26] applied to MPTC (MPTC-CUM). Method 3: The modified MPTC-DCC (MMPTC-DCC) method proposed in this paper.

Table 1.
Machine parameters.
Figure 4 and Figure 5 show the simulation response of MRAC-SC and MPTC-CUM at speed of 1000 r/min and load torque of 3 Nm when the inaccurate stator resistance changes from to . It is seen that when the stator resistance varies, the control performance of three methods does not deteriorate obviously, but there are slight differences among them. The speed and torque ripple of MRAC-SC increase and contain some spikes, especially at and . MPTC-CUM can maintain relatively good control performance, but its response curve contains some irregular ripples and spikes, which is caused by the fluctuation of compensation value, whether the parameters are accurate or not. The simulation response of MMPTC-DCC is shown in Figure 6; it works well at both accurate and inaccurate resistance. The details of the performance comparison of the three methods under stator resistance variation are shown in Table 2. The evaluation index of torque ripple is defined in [25], as shown in Equation (31).
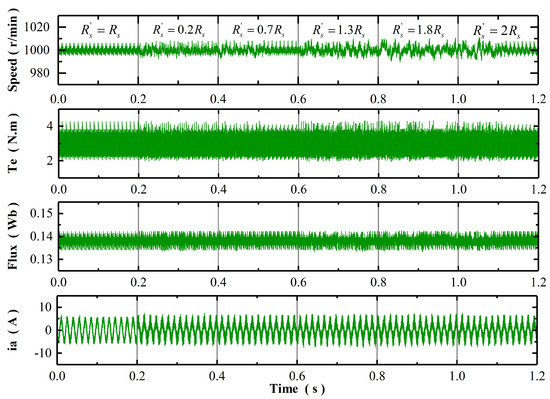
Figure 4.
Simulation result of MRAC-SC when stator resistance varies from to .
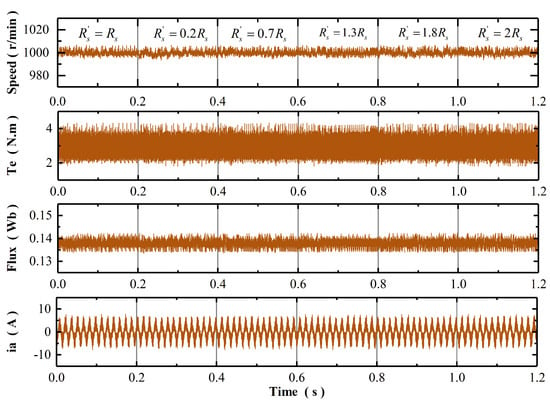
Figure 5.
Simulation result of MPTC-CUM when stator resistance varies from to .
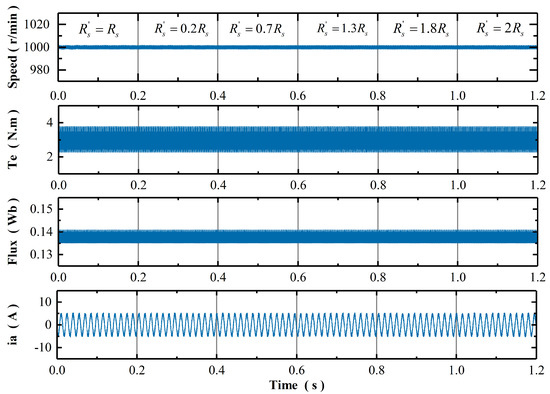
Figure 6.
Simulation result of MMPTC-DCC when stator resistance varies from to .

Table 2.
Performance comparison of three methods under stator resistance variation.
Then, ITAE is a comprehensive index to judge the performance during operating process, and the definition of ITAE is [23]:
The variations of rotor speed ITAE values within 1 s of MRAC-SC and MPTC-CUM under the machine parameters mismatch are shown in Figure 7 and Figure 8. From Figure 7 and Figure 8, it is seen that MRAC-SC maintain better control performance within of the parameter error, and the speed ITAE remains around . However, beyond the range of parameter error, the control performance of MRAC-SC is obviously deteriorated, and the maximum rotor speed ITAE can reach 29.4 at and . So, the performance of MRAC-SC deteriorates more seriously with the increase of parameter error. Similar simulation response can be obtained at MPTC-CUM, as show in Figure 8. It is clearly seen that MPTC-CUM has larger range of parameter error suppression and better robustness in a higher parameter error region. The maximum rotor speed ITAE can reach 17.499 at and . However, the jitter of the predicted current compensation in MPTC-CUM causes the ITAE value of the rotor speed to maintain around 1.3, in the range of to .
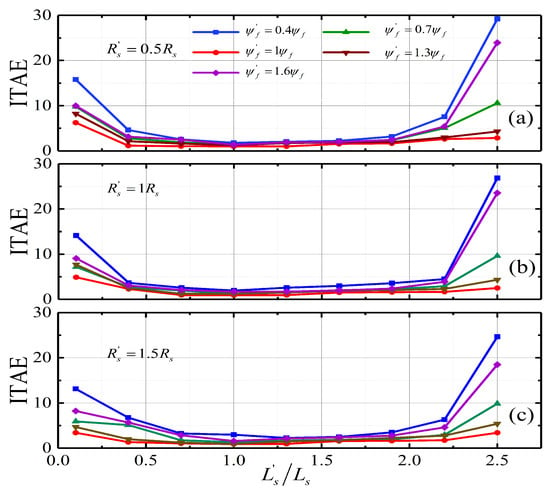
Figure 7.
The variation of ITAE value of rotor speed in MRAC-SC under parameters mismatch. (a) ITAE value of rotor speed under . (b) ITAE value of rotor speed under . (c) ITAE value of rotor speed under .
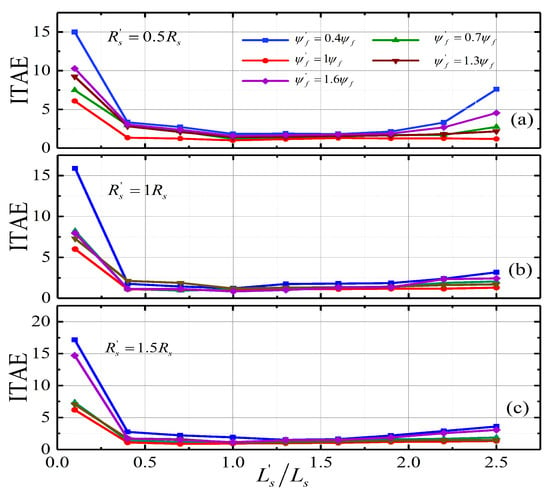
Figure 8.
The variation of ITAE value of rotor speed in MPTC-CUM under parameters mismatch. (a) ITAE value of rotor speed under . (b) ITAE value of rotor speed under . (c) ITAE value of rotor speed under .
The variation of ITAE value of rotor speed of MMPTC-DCC under machine parameters mismatch are shown in Figure 9. It is clearly seen that MMPTC-DCC has stronger robustness from to and to , and the maximum rotor speed ITAE is only 2.3. Compared with the maximum speed ITAE of MRAC-SC and MPTC-CUM, the performance of MMPTC-DCC has been significantly improved. In the range of to , the ITAE value of rotor speed of MMPTC-DCC can be maintained around 0.9. It should be noted that in the lower parameter error range, both of three methods can achieve better control performance. However, MMPTC-DCC overcomes the problems of the prediction current compensation jitter in MPTC-CUM and the lower range of parameter error suppression in MRAC-SC. It shows that MMPTC-DCC has stronger robustness.
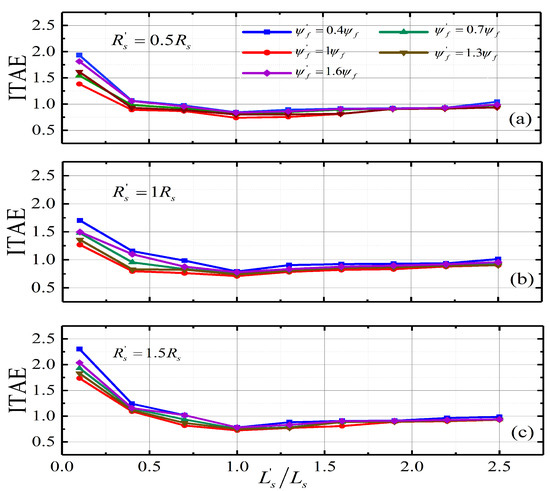
Figure 9.
The variation of ITAE value of rotor speed in MMPTC-DCC under parameters mismatch. (a) ITAE value of rotor speed under . (b) ITAE value of rotor speed under . (c) ITAE value of rotor speed under .
A numerical comparison of each method in term of current THD at variation of parameters is illustrated in Figure 10. It is seen that the MPTC-CUM presents the highest current THD without parameter mismatch, followed by MRAC-SC. From Figure 10a,b, when the variation of parameters is in the range of 20–30% of the real value, the current THD of MRAC-SC does not increase significantly. However, when the variation of parameters is beyond the range, the current THD increases obviously. In other words, only about error in parameters can be tolerated in MRAC-SC. The high current THD in MPTC-CUM is caused by the ripple of compensation without parameter mismatch. Moreover, the cost function of MPTC control method is composed of the error between the predicted value and the reference value of torque and flux. Therefore, MPTC-CUM only compensates the predicted current and cannot completely eliminate the parameter mismatch disturbance, resulting in higher current THD. It should be noted that the current THD of MRAC-SC and MPTC-CUM was reduced at , and , which is caused by the violent increase of stator current, as show in Figure 10c. Although the current THD is reduced, the increased stator current is more harmful to the safe and stable operation of the system. The current THD of MMPTC-DCC is maintained at a stable level, which is not affected by the variation range of parameters and the fluctuation of compensation. This shows that MMPTC-DCC is safer and more reliable
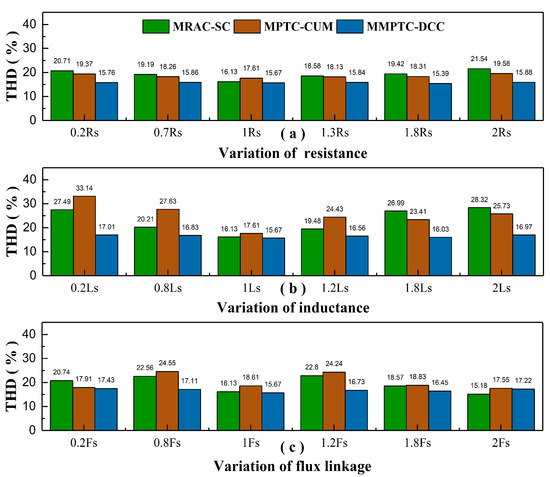
Figure 10.
Current THD of each method at various parameters with speed of 1000 r/min. (a) Variation of stator resistance. (b) Variation of stator inductance. (c) Variation of rotor flux linkage.
5. Experimental Result and Discussion
Apart from the simulation study, the verification experiment is carried out on a two-level inverter-fed PMSM drive platform. A 1-kW PMSM (110SJT-M040D) servo system experimental platform is shown in Figure 11. The control circuit includes dSPACE/MicroLabBox, IPM (PM50CLA120) drive circuit, measurement circuit, PC and power supply (62050H-600S). The PMSM parameters are the same as those listed in Table 1. From the analysis of the simulation section, it is seen that the control performance of the three methods in the low range of parameter error is almost the same. In order to show the difference of the three methods, large parameter mismatches (, , ) were used in the experimental process.

Figure 11.
Experimental platform.
First, the steady state performances for each method are investigated and illustrated in Figure 12 under parameter mismatches, where the speed increases from 800 r/min to rated speed (1000 r/min), and the load torque is rated torque (4.5 N.m). It is clearly seen that the speed error, torque and flux ripple of MRAC-SC increase significantly under the disturbance of huge parameter mismatches. Under the rated speed, the maximum speed error of MRAC-SC is 130 r/min, and the maximum torque error is 1.1 N.m. Although the speed and torque response of MPTC-CUM is improved, there are many peaks in the speed and torque response curve caused by the existence of differential process. Under the rate speed, the maximum speed peak of MPTC-CUM is 182 r/min, and the maximum torque error is 2.3 N.m. The existence of peak will seriously affect the driving experience of EVs. Meanwhile, the stator flux of MRAC-SC and MPTC-CUM is distorted by the rotor flux mismatch, which leads to the increase of harmonic content of stator current. At the rated speed, the current THD values of MRAC-SC and MPTC-CUM are and , respectively. It should be noted that the current THD value of MPTC-CUM is higher than that of MRAC-SC due to the existence of speed and torque response spikes. However, MMPTC-DCC presents much lower speed error (the maximum speed error is 22 r/min), torque (the maximum torque error is 0.9 N.m) and flux ripple. The THD of stator current is at 1000 r/min. This confirms that MMPTC-DCC can achieve better dynamic performance than MRAC-SC and MPTC-CUM under a large range of parameter errors.
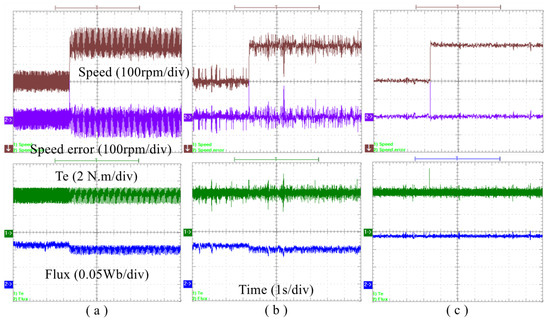
Figure 12.
The experimental results of speed, torques and flux linkage responses under the condition of , , , (a) MRAC-SC, (b) MPTC-CUM, (c) MMPTC-DCC.
Second, under the condition of parameter mismatches, the performance comparisons of the three methods are shown in Figure 13, where the speed increases from 0 r/min to 1000 r/min along the slope within 2.5 s, and then decreases to 800 r/min at 4 s, the load torque is 1 N.m in the start-up phase, and increases to 3 N.m at 6 s. Similar to the steady-state performance, the speed, torque and flux ripple of MRAC-SC are the largest, while the performance of MPTC-CUM is improved, but there are many spikes. MMPTC-DCC has the smallest speed and torque ripple in steady state. However, the speed dynamic tracking ability is poor when the motor starts up (the maximum tracking error is 87 r/min). The reason is that during this stage parameters of , and is updated frequently. The ITAE values of speed, torque and flux linkage of the three methods are shown in Table 3 within 1 s at 1000 r/min and during state-up stage.
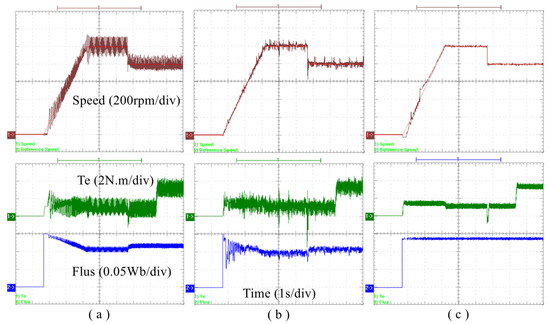
Figure 13.
The experimental results of speed, torques and flux linkage responses under the condition of , , , (a) MRAC-SC, (b) MPTC-CUM, (c) MMPTC-DCC.

Table 3.
ITAE analysis of three methods in different conditions.
Finally, under the condition of parameter mismatch (, , ), the response performance of the three methods at low speed is shown in Figure 14, where the speed increases from 100 r/min to 200 r/min at 3.5 s, and then decreases to 100 r/min at 7 s. With the decrease of speed, the load torque decreases from 4.5 N.m to 1 N.m. It is seen that the torque responses of the three methods are similar under the disturbance of small parameter mismatch. The difference is that the speed responses of MRAC-SC and MPTC-CUM contain some spikes and large flux ripples. The rising overshoots of three methods were 24 r/min, 21 r/min and 27 r/min, respectively. The maximum steady-state speed errors are 41 r/min, 49 r/min and 27 r/min at 100 r/min, respectively. The overshoot of three methods are 61 r/min, 35 r/min and 0 r/min, respectively, when the speed and load torque drop simultaneously. The ITAE values of speed, torque and flux linkage of the three methods are shown in Table 4 within 1 s at 100 r/min. It can be concluded that MMPTC-DCC has stronger robustness
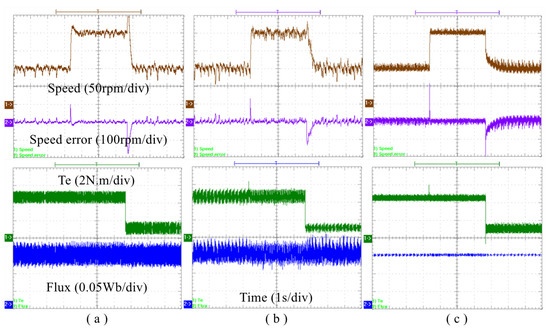
Figure 14.
The experimental results of speed, torques and flux linkage responses under the condition of , , (a) MRAC-SC, (b) MPTC-CUM, (c) MMPTC-DCC.

Table 4.
ITAE analysis of three methods at 100 r/min.
The comparison of torque ripple evaluation indexes of each method under parameter variation is shown in Figure 15 and Figure 16. It is seen that MMPTC-DCC presents much better torque ripple characteristics, which proves that MMPTC-DCC has stronger robustness. It should be noted that the torque ripples evaluation index of MRAC-SC and MPTC-CUM were reduced at and , which is caused by the violent increase of stator current, as show in Figure 15c and Figure 16c.
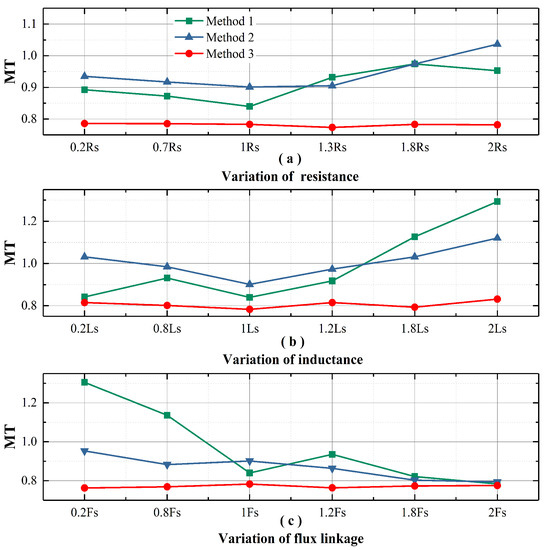
Figure 15.
Experimental result for of each method at various parameters, (a) Variation of stator resistance. (b) Variation of stator inductance. (c) Variation of rotor flux linkage.
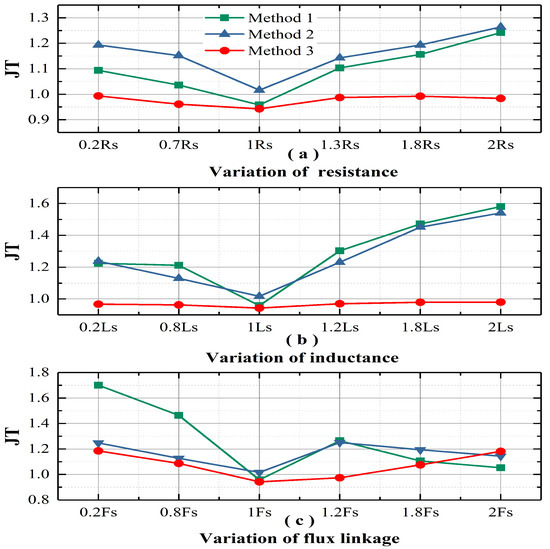
Figure 16.
Experimental result for of each method at various parameters (a) Variation of stator resistance. (b) Variation of stator inductance. (c) Variation of rotor flux linkage.
6. Conclusions
The complex driving conditions of EVs lead to the change of driving motor parameters, resulting in increased torque and flux ripples, and stator current harmonics, which are harmful to driving safety and vehicle system. In this paper, a modified MPTC with real-time updating of motor parameters is proposed to suppress the disturbance of parameter mismatch. Under the condition of parameter mismatch, according to the error between the actual measured value and the predicted value, the motor parameters are updated and corrected in real-time. Meanwhile, MRAC is used in the speed loop to eliminate the disturbance caused by the jitter of real-time update parameters. The simulation and experimental results compared with other methods also verify the much better robustness of this method. We can find that the proposed method can keep the excellent control performance of MPTC from the influence of parameter mismatch, and improve the operation safety of EVs. Moreover, from Figure 8, it is seen that the modified MPTC method can keep the harmonic content of stator current at a low level and reduce the harm of parameter mismatch on vehicle system.
Author Contributions
Conceptualization, H.Q. and S.G.; methodology, S.G.; software, S.G., D.Z. and Y.W. (Yao Wei); validation, Y.W. (Yao Wei) and D.Z.; formal analysis, Y.W. (Yanjun Wei); writing—original draft preparation, S.G.; writing—review and editing, H.Q. and Y.W. (Yanjun Wei); All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Project of Science and Technology Program for Colleges and Universities of Hebei Provincial Education Department grant number ZD2017081. and the Youth Fund Project of Science and Technology Program for Colleges and Universities of Hebei Provincial Education Department grant number QN2018134. and Natural Science Foundation of Hebei Province grant number E2019203297.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MPTC | Model predictive torque control |
| DCC | Duty cycle control |
| MRAC | Model reference adaptive control |
| PMSM | Permanent magnet synchronous motor |
| EVs | Electric vehicles |
| VC | Vector control |
| DTC | Direct torque control |
| MPTC-DCC | Model predictive torque control with duty cycle control |
| MRAC-SC | Model reference adaptive control based speed controller |
| MPTC-CUM | Current update mechanism used in model predictive torque |
| MMPTC-DCC | The modified Model predictive torque control with duty cycle control |
| RMS | Root mean square |
| ITAE | Integrated time and absolute error |
| THD | Total Harmonic Distortion |
References
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the Performances and Parameters of Interior PMSM Used for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Casadei, D.; Profumo, F.; Serra, G.; Tani, A. FOC and DTC: Two viable schemes for induction motors torque control. IEEE Trans. Power Electron. 2002, 17, 779–787. [Google Scholar] [CrossRef]
- Zhang, X.; Foo, G.H.B. A Constant Switching Frequency-Based Direct Torque Control Method for Interior Permanent-Magnet Synchronous Motor Drives. IEEE/ASME Trans. Mechatron. 2016, 21, 1455–1456. [Google Scholar] [CrossRef]
- Navardi, M.J.; Milimonfared, J.; Talebi, H.A. Torque and Flux Ripples Minimization of Permanent Magnet Synchronous Motor by a Predictive-Based Hybrid Direct Torque Control. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1662–1670. [Google Scholar] [CrossRef]
- Vafaie, M.H.; Dehkordi, B.M.; Zhao, J.; Moallem, P.; Kiyoumarsi, A. Minimizing Torque and Flux Ripples and Improving Dynamic Response of PMSM Using a Voltage Vector with Optimal Parameters. IEEE Trans. Ind. Electron. 2016, 63, 3876–3888. [Google Scholar] [CrossRef]
- Lara, J.; Xu, J.; Zhao, J.; Chandra, A. Effects of Rotor Position Error in the Performance of Field-Oriented-Controlled PMSM Drives for Electric Vehicle Traction Applications. IEEE Trans. Ind. Electron. 2016, 63, 4738–4751. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, C.; Xing, J. A Parameter-Independent Optimal Field-Weakening Control Strategy of IPMSM for Electric Vehicles Over Full Speed Range. IEEE Trans. Power Electron. 2021, 36, 4659–4671. [Google Scholar] [CrossRef]
- Li, L.; Liu, Q. Research on IPMSM Drive System Control Technology for Electric Vehicle Energy Consumption. IEEE Access 2019, 7, 186201–186210. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Torque ripple reduction of model predictive torque control of induction motor drives. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013. [Google Scholar]
- Zhang, Y.; Yang, H. Model predictive torque control with duty ratio optimization for two-level inverter-fed induction motor drive. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Korea, 26–29 October 2013. [Google Scholar]
- Zanma, T.; Tozawa, S.; Yu, T.; Koiwa, K.; Liu, K.Z. Optimal Voltage Vector in Current Control of PMSM Considering Torque Ripple and Reduction of Number of Switching Operations. IET Power Electron. 2020, 13, 1200–1206. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, D.; Liu, J.; Gao, S.; Xu, W. Performance Improvement of Model-Predictive Current Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2017, 53, 3683–3965. [Google Scholar] [CrossRef]
- Wu, M.; Sun, X.; Zhu, J.; Lei, G.; Guo, Y. Improved Model Predictive Torque Control for PMSM Drives Based on Duty Cycle Optimization. IEEE Trans. Magn. 2021, 57, 1–5. [Google Scholar]
- Sun, X.; Yu, H.; Yu, J.; Liu, X. Design and implementation of a novel adaptive backstepping control scheme for aPMSM with unknown load torque. IET Electr. Power Appl. 2019, 13, 445–455. [Google Scholar] [CrossRef]
- Uddin, M.N.; Rahman, M.M. Online Torque-Flux Estimation-Based Nonlinear Torque and Flux Control Scheme of IPMSM Drive for Reduced Torque Ripples. IEEE Trans. Power Electron. 2019, 34, 636–645. [Google Scholar] [CrossRef]
- Li, L.; Pei, G.; Liu, J.; Du, P.; Pei, L.; Zhong, C. 2-DOF Robust H∞ Control for Permanent Magnet Synchronous Motor with Disturbance Observer. IEEE Trans. Power Electron. 2021, 36, 636–645. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Rafaq, M.S.; Choi, H.H.; Jung, J. A Model Reference Adaptive Control Based Speed Controller for a Surface-Mounted Permanent Magnet Synchronous Motor Drive. IEEE Trans. Ind. Electron. 2018, 65, 9399–9409. [Google Scholar] [CrossRef]
- Xie, H.; Chen, Q.; Tang, Y.; Kennel, R.; Wang, F.; Xia, A.; Zhang, Z.; Rodriguez, J. Sliding-Mode MRAS based Encoderless Predictive Torque Control for Induction Machine. In Proceedings of the 2019 IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Quanzhou, China, 31 May–2 June 2019. [Google Scholar]
- Wang, J.; Wang, F.; Zhang, Z.; Li, S.; Rodríguez, J. Design and Implementation of Disturbance Compensation-Based Enhanced Robust Finite Control Set Predictive Torque Control for Induction Motor Systems. IEEE Trans. Ind. Inform. 2017, 13, 2645–2656. [Google Scholar] [CrossRef]
- Lin, X.; Huang, W.; Jiang, W.; Zhao, Y.; Zhu, S. A Stator Flux Observer with Phase Self-Tuning for Direct Torque Control of Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2020, 35, 6140–6152. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives with Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z. Sliding-Mode Observer-Based Mechanical Parameter Estimation for Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2016, 31, 5732–5745. [Google Scholar] [CrossRef]
- Wei, Y.; Wei, Y.; Sun, Y.; Qi, H.; Guo, X. Prediction Horizons Optimized Nonlinear Predictive Control for Permanent Magnet Synchronous Motor Position System. IEEE Trans. Ind. Electron. 2020, 67, 9153–9163. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rodríguez, J. Torque Ripple Reduction of Predictive Torque Control for PMSM Drives with Parameter Mismatch. IEEE Trans. Power Electron. 2017, 32, 7160–7168. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Abbaszadeh, A.; Rodríguez, J. Robustness Improvement of Predictive Current Control Using Prediction Error Correction for Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2016, 63, 3458–3466. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C. Improved Model Predictive Current Control for SPMSM Drives with Parameter Mismatch. IEEE Trans. Ind. Electron. 2020, 67, 852–862. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Generalized Two-Vector-Based Model-Predictive Torque Control of Induction Motor Drives. IEEE Trans. Power Electron. 2015, 30, 3818–3829. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H.; Xia, B. Model-Predictive Control of Induction Motor Drives: Torque Control Versus Flux Control. IEEE Trans. Ind. Appl. 2016, 52, 4050–4060. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, S.; Zhang, C.; Galassini, A.; Buticchi, G.; Degano, M. Improved Model Predictive Current Control for SPMSM Drives Using Current Update Mechanism. IEEE Trans. Ind. Electron. 2021, 68, 1938–1948. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).