Review of Magnetoelectric Sensors
Abstract
1. Introduction
2. Materials for ME Sensors
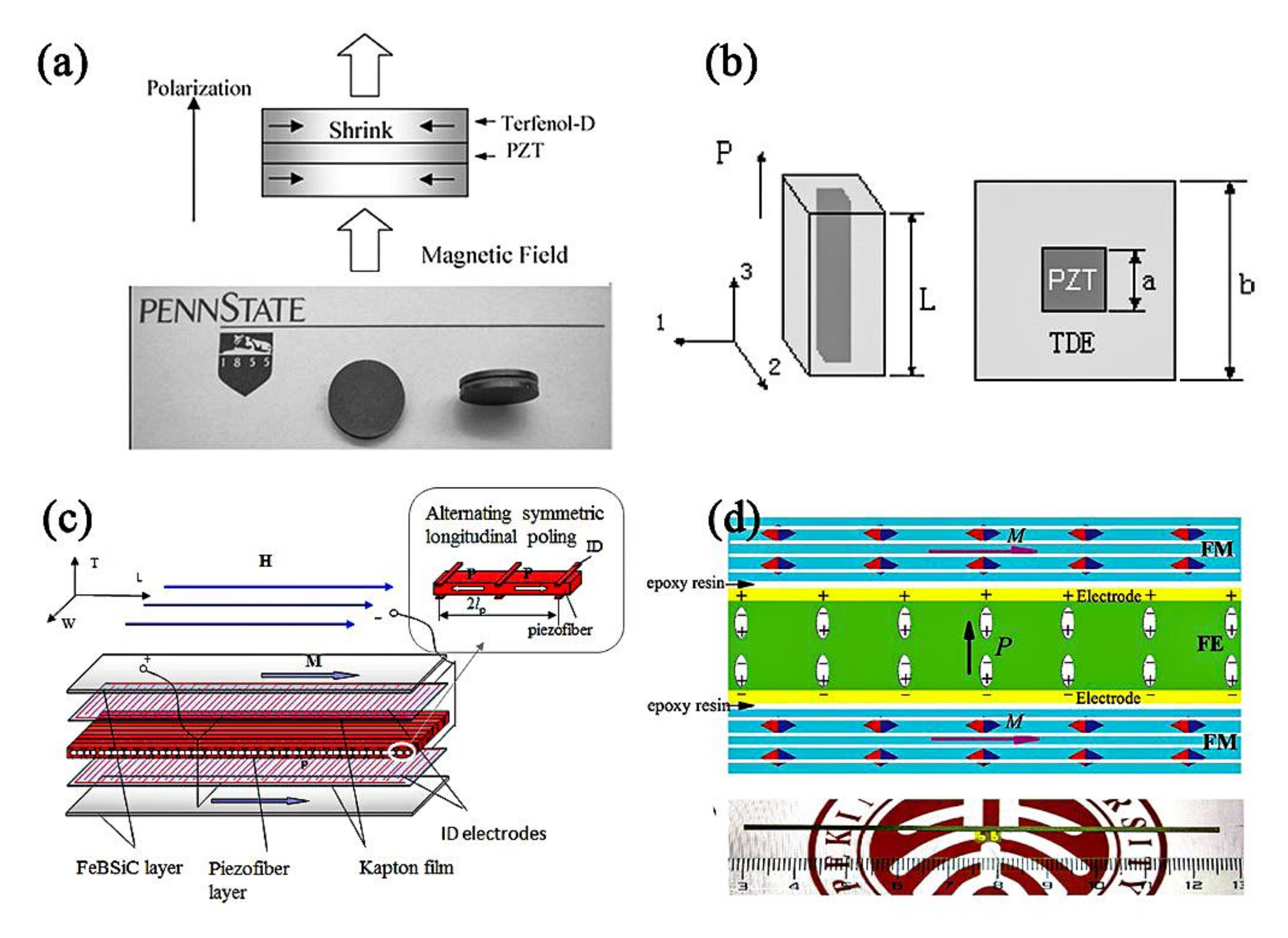
2.1. Bulk ME Laminates
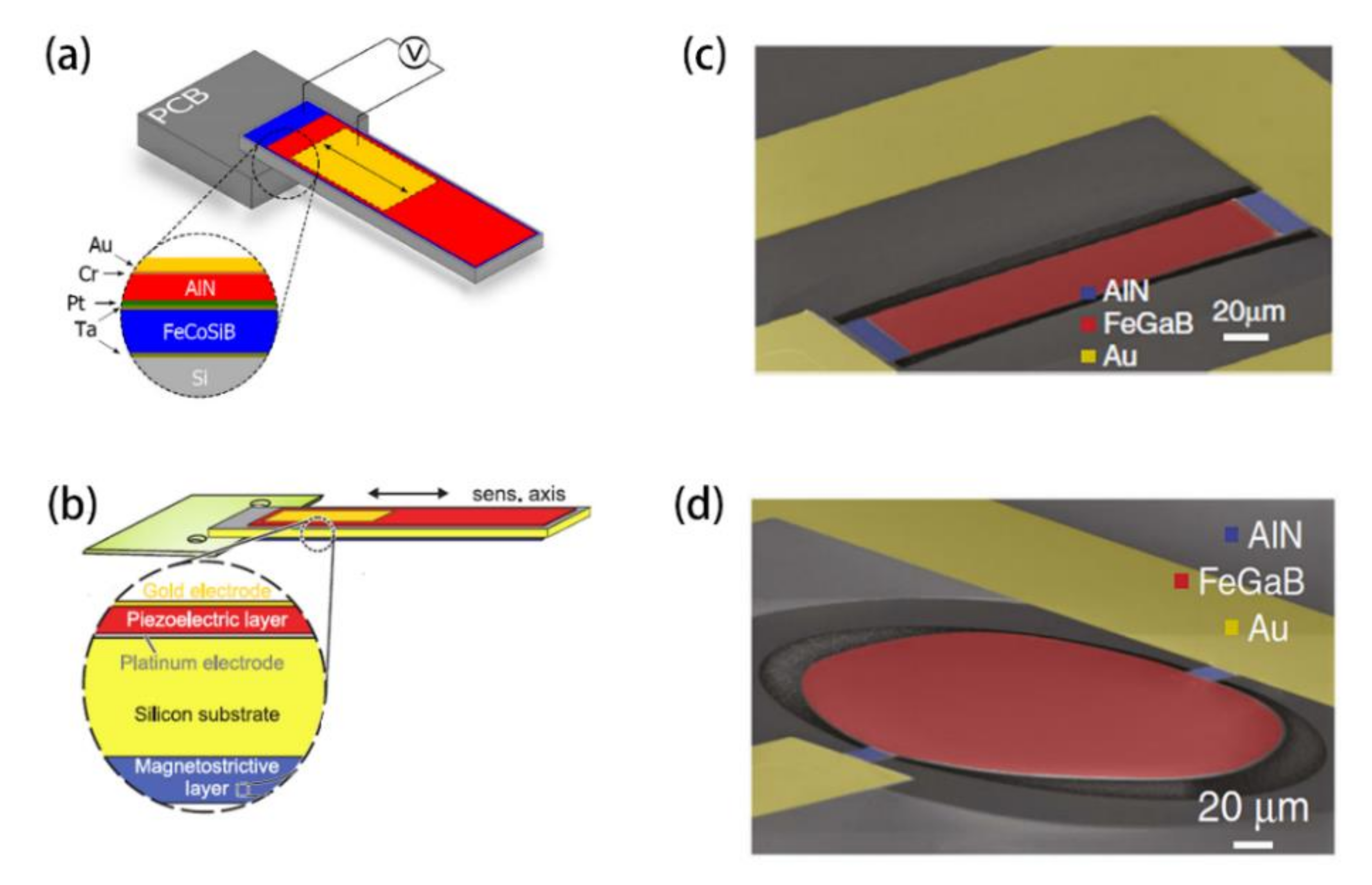
2.2. MEMS and NEMS ME Laminates
3. Advances in ME Sensors
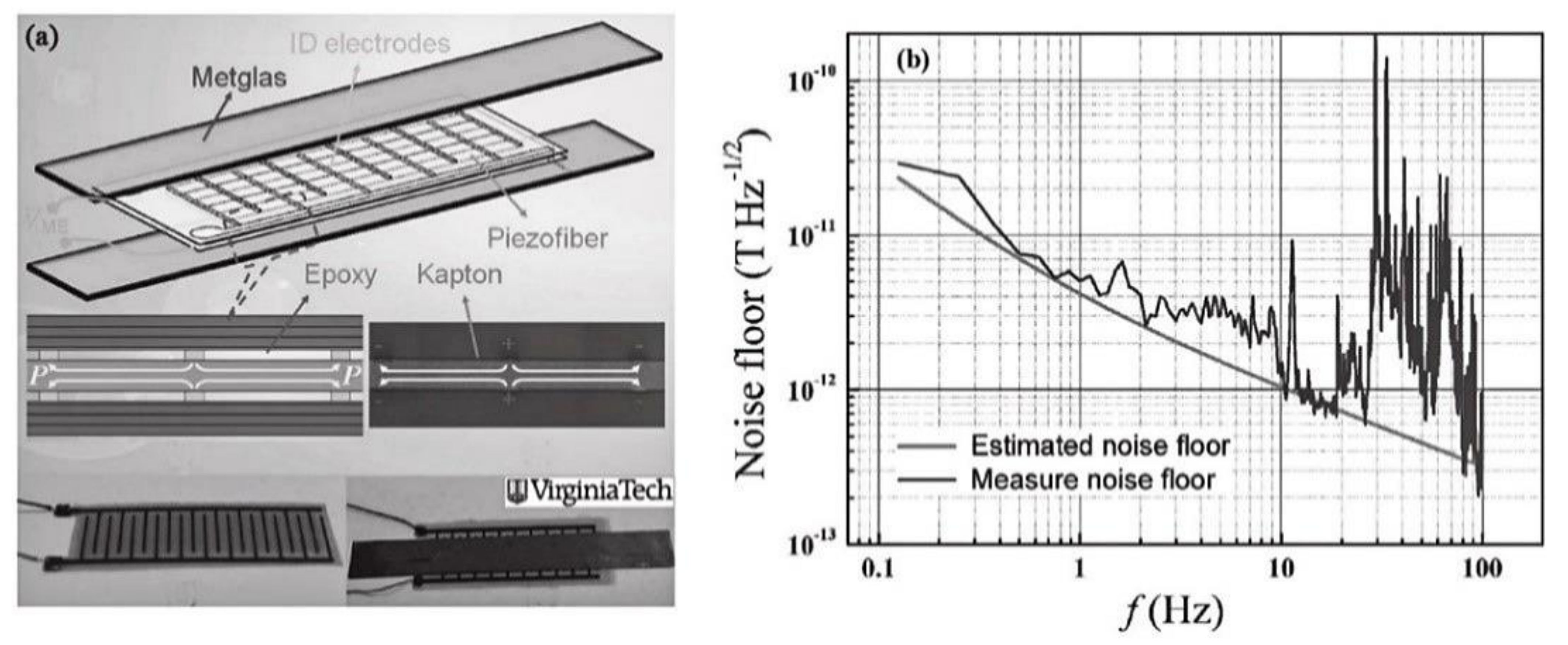
3.1. Low-Frequency Magnetic Sensor
3.2. Resonant-Frequency Magnetic Sensor
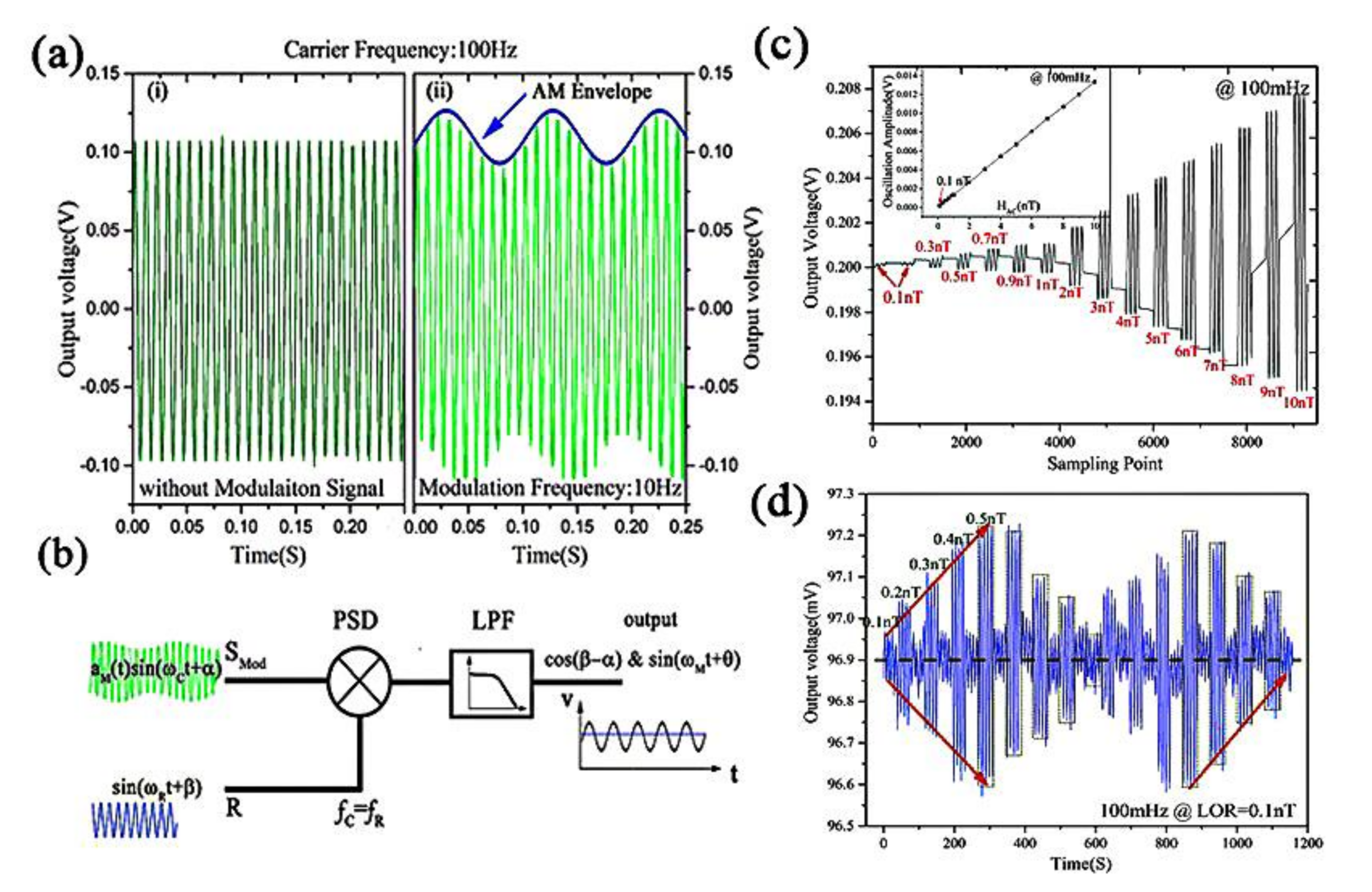
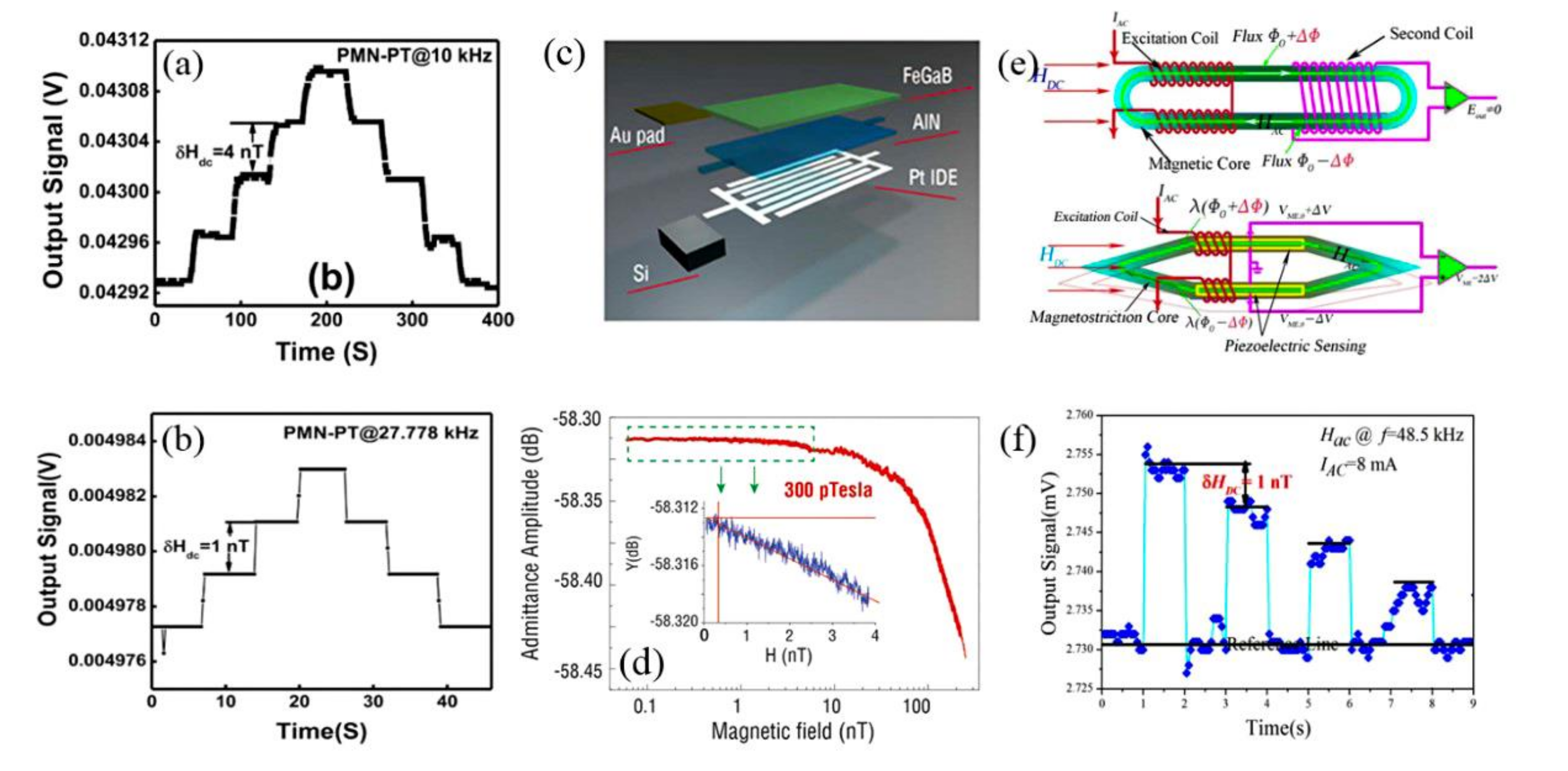
3.3. DC Magnetic Sensor
4. Engineering Applications of ME Sensors
4.1. Magnetic Target Detection and Localization
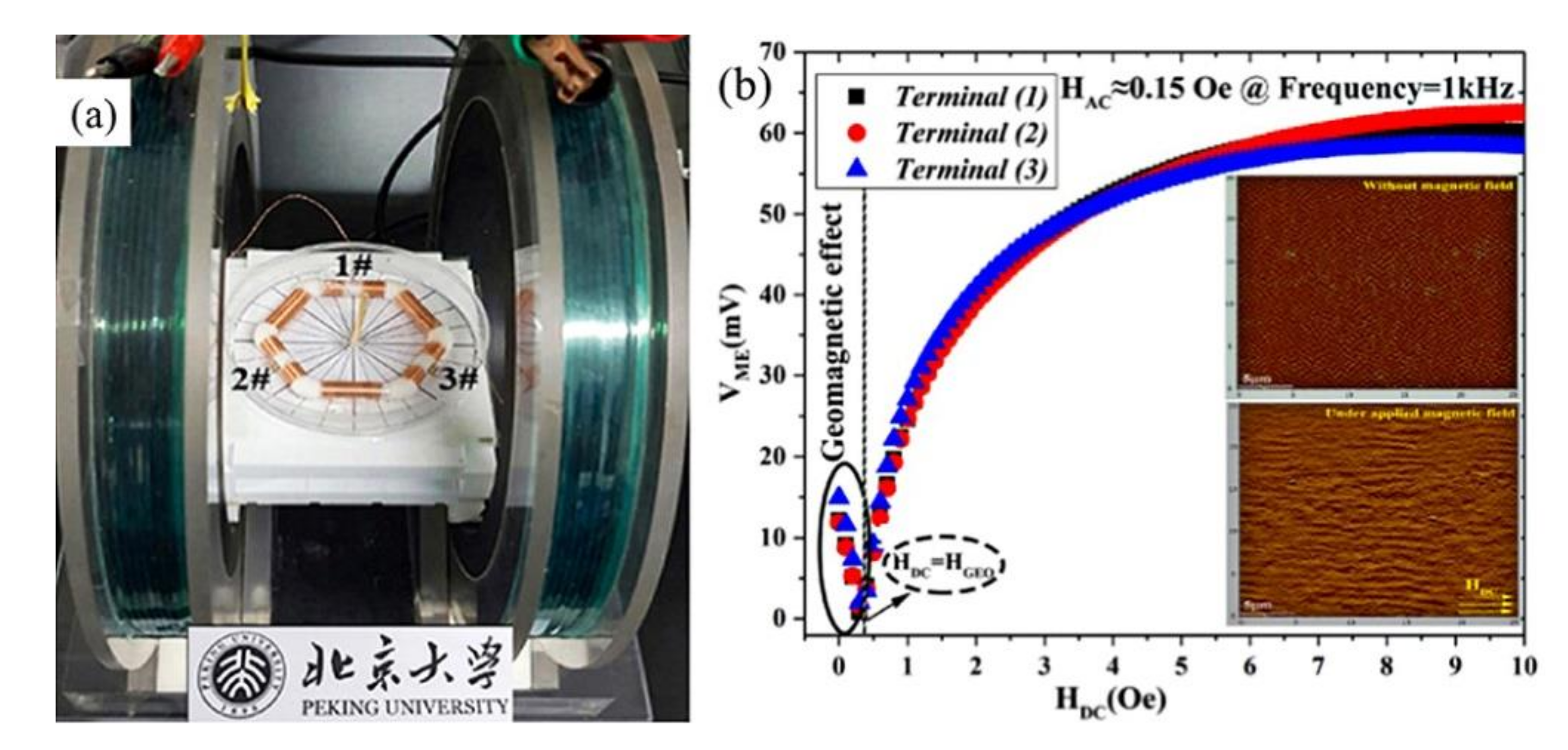
4.2. Geomagnetic Field Sensing
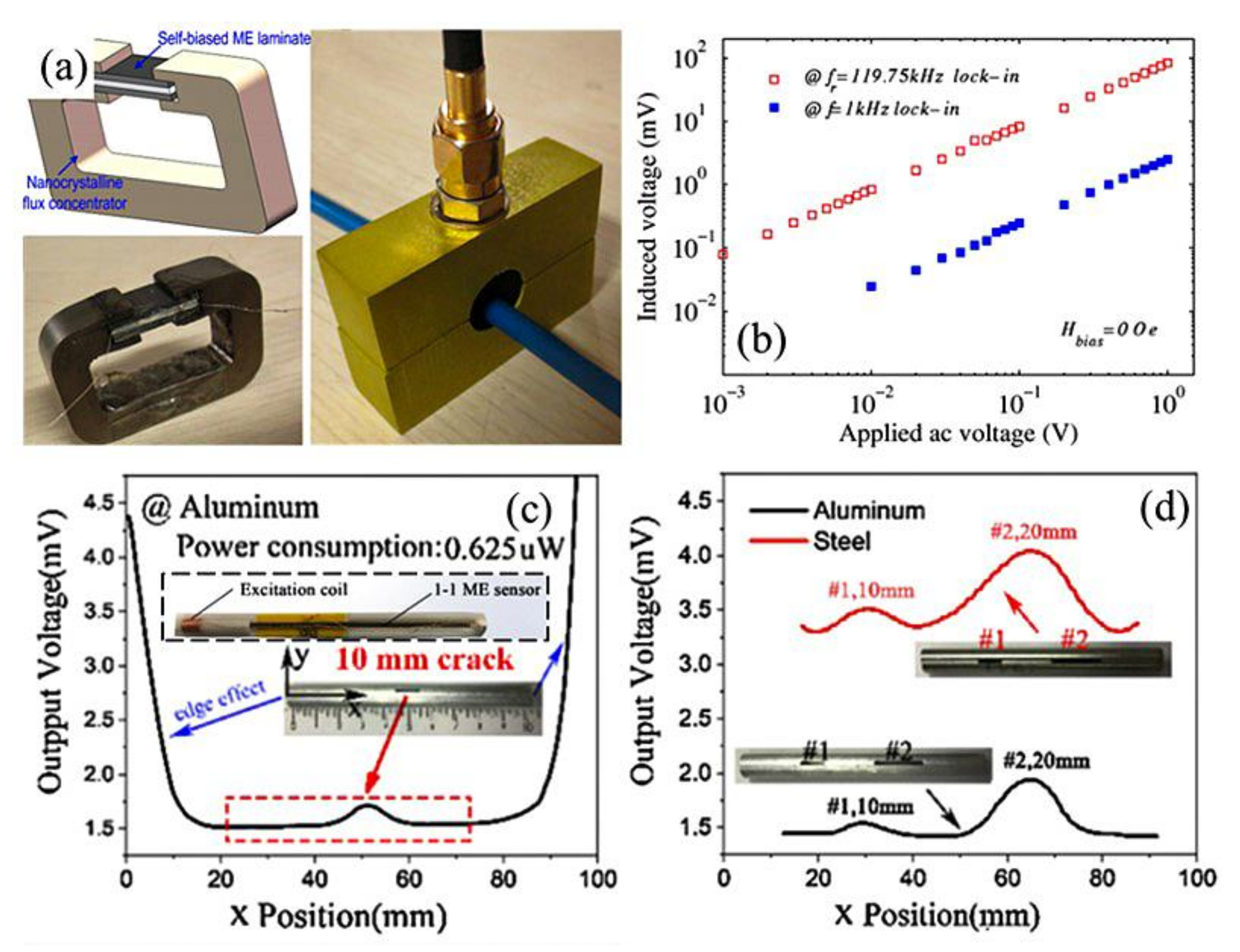
4.3. Current Sensing and Non-Destructive Detection
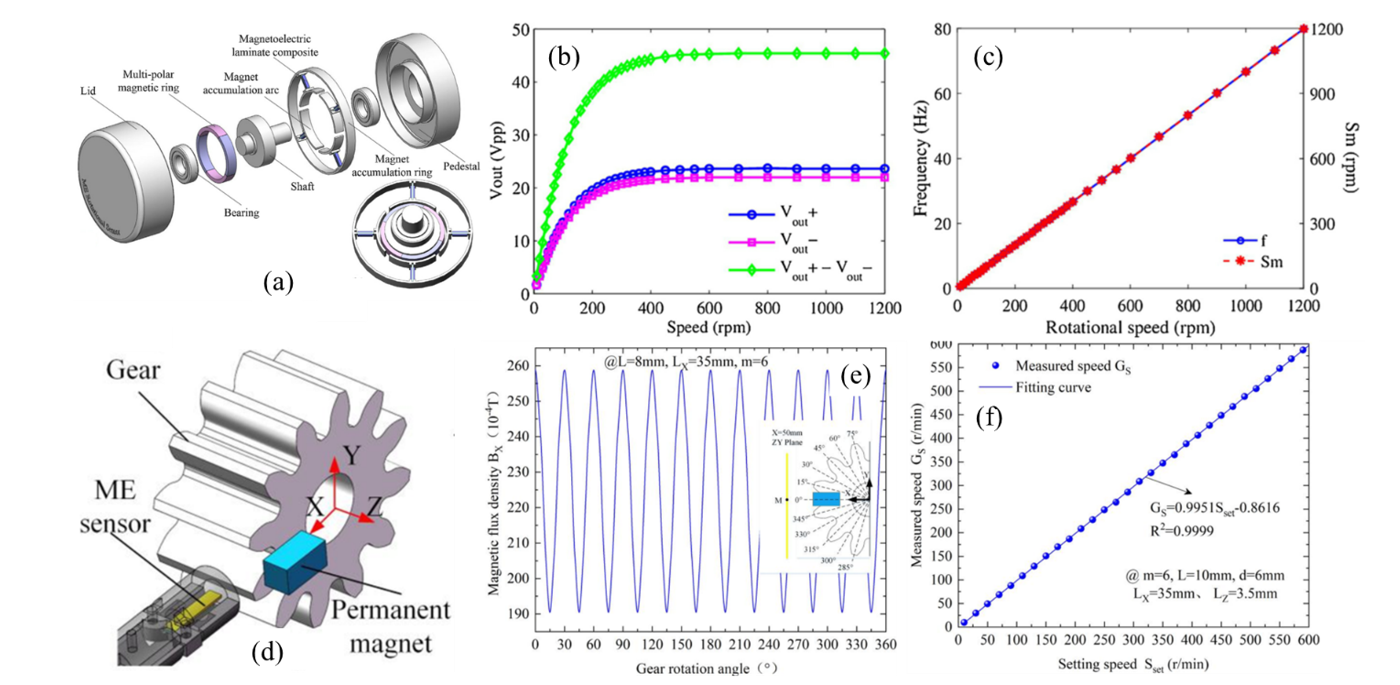
4.4. Velocity and Displacement Sensing
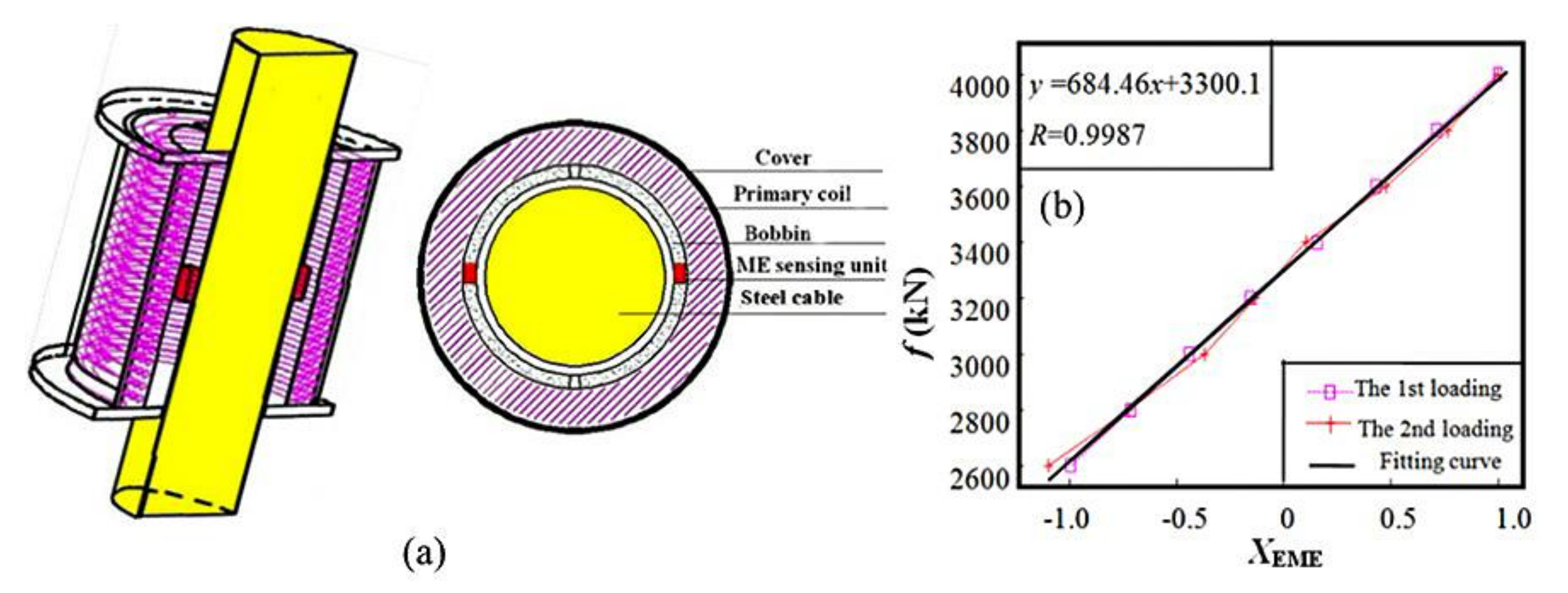
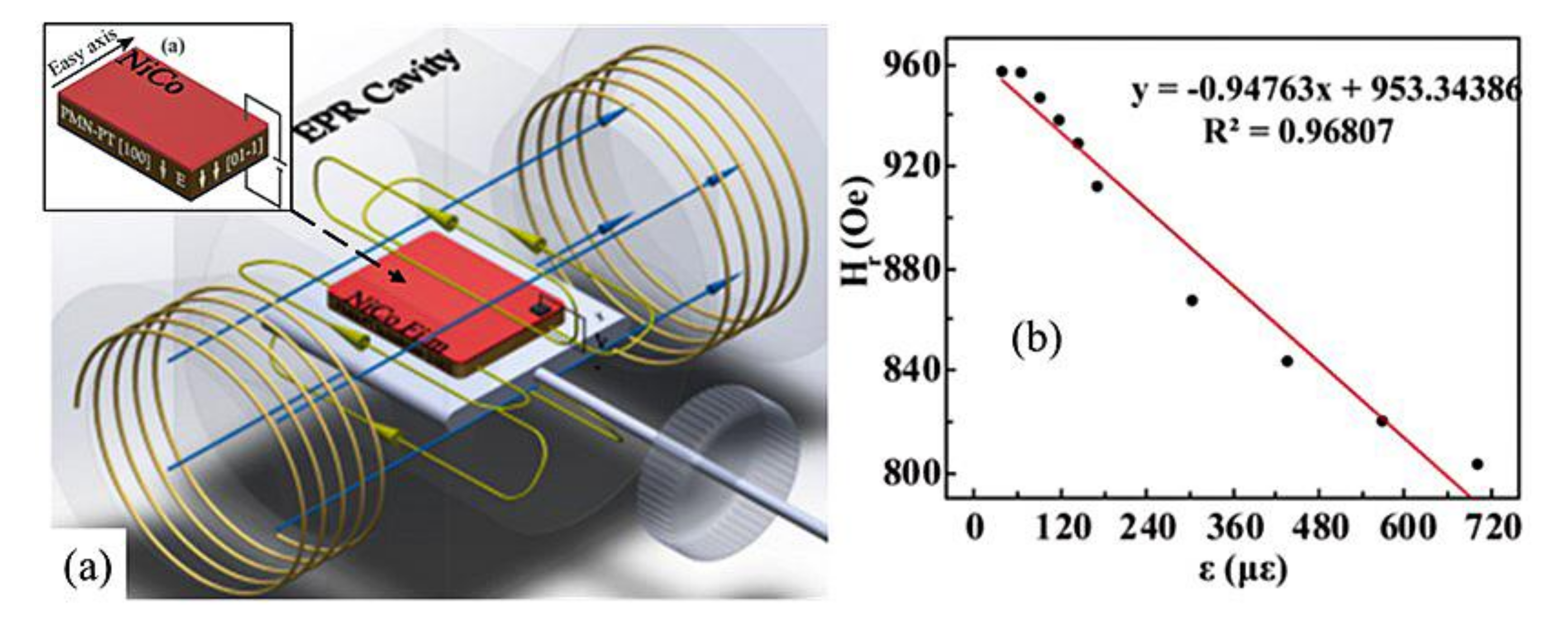
4.5. Stress and Strain Measurement
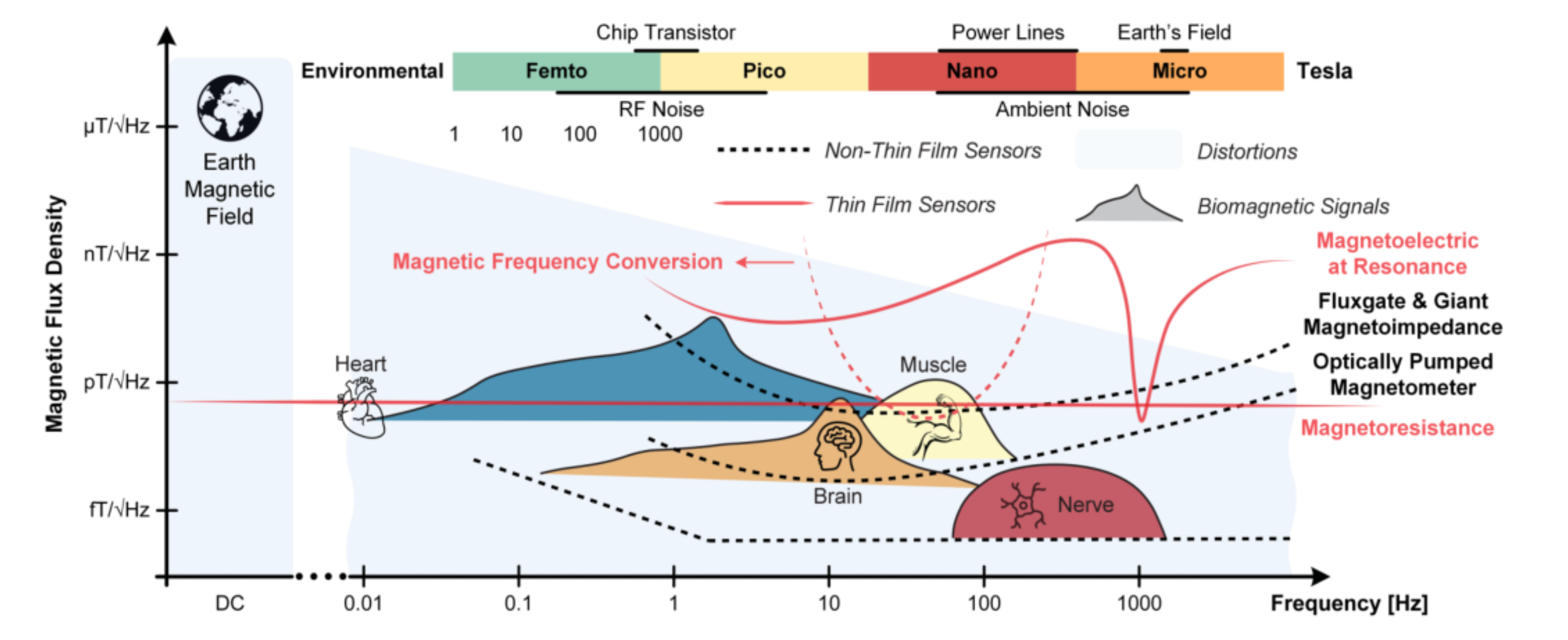
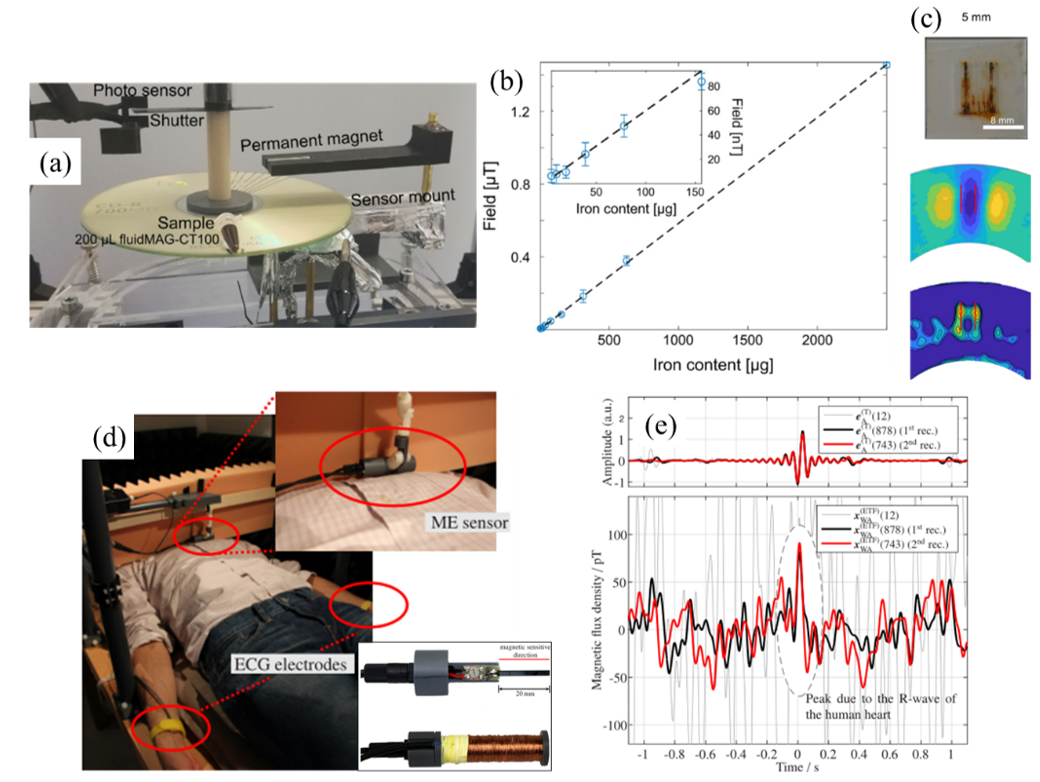
4.6. Biomagnetic Measurement
5. Future Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Hu, J.; Li, Z.; Nan, C.W. Recent progress in multiferroic magnetoelectric composites: From bulk to thin films. Adv. Mater. 2011, 23, 1062–1087. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.-M.; Nan, T.; Sun, N.X.; Chen, L.-Q. Multiferroic magnetoelectric nanostructures for novel device applications. MRS Bull. 2015, 40, 728–735. [Google Scholar] [CrossRef]
- Hu, J.-M.; Duan, C.-G.; Nan, C.-W.; Chen, L.-Q. Understanding and designing magnetoelectric heterostructures guided by computation: Progresses, remaining questions, and perspectives. NPJ Comput. Mater. 2017, 3, 1–21. [Google Scholar] [CrossRef]
- Kleemann, W. Multiferroic and magnetoelectric nanocomposites for data processing. J. Phys. D Appl. Phys. 2017, 50, 223001. [Google Scholar] [CrossRef]
- Lawes, G.; Srinivasan, G. Introduction to magnetoelectric coupling and multiferroic films. J. Phys. D Appl. Phys. 2011, 44, 243001. [Google Scholar] [CrossRef]
- Palneedi, H.; Annapureddy, V.; Priya, S.; Ryu, J. Status and Perspectives of Multiferroic Magnetoelectric Composite Materials and Applications. Actuators 2016, 5, 9. [Google Scholar] [CrossRef]
- Chu, Z.; PourhosseiniAsl, M.; Dong, S. Review of multi-layered magnetoelectric composite materials and devices applications. J. Phys. D Appl. Phys. 2018, 51, 243001. [Google Scholar] [CrossRef]
- Chu, Z.; Shi, H.; Shi, W.; Liu, G.; Wu, J.; Yalng, J.; Dong, S. Enhanced Resonance Magnetoelectric Coupling in (1-1) Connectivity Composites. Adv. Mater. 2017, 29, 1606022. [Google Scholar] [CrossRef]
- PourhosseiniAsl, M.; Gao, X.; Kamalisiahroudi, S.; Yu, Z.; Chu, Z.; Yang, J.; Lee, H.-Y.; Dong, S. Versatile power and energy conversion of magnetoelectric composite materials with high efficiency via electromechanical resonance. Nano Energy 2020, 70, 104506. [Google Scholar] [CrossRef]
- Nan, C.-W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Magnetoelectric Laminate Composites: An Overview. J. Am. Ceram. Soc. 2008, 91, 351–358. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Viehland, D. Magnetoelectrics for magnetic sensor applications: Status, challenges and perspectives. Mater. Today 2014, 17, 269–275. [Google Scholar] [CrossRef]
- Gutierrez, J.; Lasheras, A.; Martins, P.; Pereira, N.; Barandiaran, J.M.; Lanceros-Mendez, S. Metallic Glass/PVDF Magnetoelectric Laminates for Resonant Sensors and Actuators: A Review. Sensors 2017, 17, 1251. [Google Scholar] [CrossRef]
- Sreenivasulu, G.; Qu, P.; Petrov, V.; Qu, H.; Srinivasan, G. Sensitivity Enhancement in Magnetic Sensors Based on Ferroelectric-Bimorphs and Multiferroic Composites. Sensors 2016, 16, 262. [Google Scholar] [CrossRef]
- Annapureddy, V.; Palneedi, H.; Hwang, G.-T.; Peddigari, M.; Jeong, D.-Y.; Yoon, W.-H.; Kim, K.-H. Magnetic energy harvesting with magnetoelectrics: An emerging technology for self-powered autonomous systems. Sustain. Energy Fuels 2017, 1, 2039–2052. [Google Scholar] [CrossRef]
- Vopson, M.M. Fundamentals of Multiferroic Materials and Their Possible Applications. Crit. Rev. Solid State Mater. Sci. 2015, 40, 223–250. [Google Scholar] [CrossRef]
- Gao, X.; Yan, Y.; Carazo, A.V.; Dong, S.; Priya, S. Low-temperature cofired unipoled multilayer piezoelectric transformers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 65, 513–519. [Google Scholar] [CrossRef]
- Yang, N.; Wu, H.; Wang, S.; Yuan, G.; Zhang, J.; Sokolov, O.; Bichurin, M.I.; Wang, K.; Wang, Y. Ultrasensitive flexible magnetoelectric sensor. APL Mater. 2021, 9, 021123. [Google Scholar] [CrossRef]
- Dong, S.; Liu, J.-M.; Cheong, S.-W.; Ren, Z. Multiferroic materials and magnetoelectric physics: Symmetry, entanglement, excitation, and topology. Adv. Phys. 2015, 64, 519–626. [Google Scholar] [CrossRef]
- Astrov, D.N. Magnetoelectric Effect In Chromium Oxide. Sov. Phys. Jetp 1961, 13, 729–733. [Google Scholar]
- Schmid, H. Multi-ferroic magnetoelectrics. Ferroelectrics 1994, 162, 317–338. [Google Scholar] [CrossRef]
- Catalan, G.; Scott, J.F. Physics and Applications of Bismuth Ferrite. Adv. Mater. 2009, 21, 463–2485. [Google Scholar] [CrossRef]
- Yamauchi, K.; Picozzi, S. Orbital degrees of freedom as origin of magnetoelectric coupling in magnetite. Phys. Rev. B 2012, 85, 085131. [Google Scholar] [CrossRef]
- Pantinakis, A.; Jackson, D.A. High-sensitivity low-frequency magnetometer using magnetostrictive primary sensing and piezoelectric signal recovery. Electron. Lett. 1986, 22, 737–738. [Google Scholar] [CrossRef]
- Li, M.; Matyushov, A.; Dong, C.; Chen, H.; Lin, H.; Nan, T.; Qian, Z.; Rinaldi, M.; Lin, Y.; Sun, N.X. Ultra-sensitive NEMS magnetoelectric sensor for picotesla DC magnetic field detection. Appl. Phys. Lett. 2017, 110, 143510. [Google Scholar] [CrossRef]
- Ryu, J.; Priya, S.; Uchino, K.; Kim, H.-E. Magnetoelectric Effect in Composites of Magnetostrictive and Piezoelectric Materials. J. Electroceramics 2002, 8, 107–119. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.-F.; Viehland, D. Ultrahigh magnetic field sensitivity in laminates of TERFENOL-D and Pb(Mg1/3Nb2/3)O3–PbTiO3 crystals. Appl. Phys. Lett. 2003, 83, 2265–2267. [Google Scholar] [CrossRef]
- Dong, S.; Zhai, J.; Bai, F.; Li, J.-F.; Viehland, D. Push-pull mode magnetostrictive/piezoelectric laminate composite with an enhanced magnetoelectric voltage coefficient. Appl. Phys. Lett. 2005, 87, 062502. [Google Scholar] [CrossRef]
- Dong, S.; Zhai, J.; Li, J.; Viehland, D. Near-ideal magnetoelectricity in high-permeability magnetostrictive/piezofiber laminates with a (2-1) connectivity. Appl. Phys. Lett. 2006, 89, 252904. [Google Scholar] [CrossRef]
- Gao, J.; Shen, L.; Wang, Y.; Gray, D.; Li, J.; Viehland, D. Enhanced sensitivity to direct current magnetic field changes in Metglas/Pb(Mg1/3Nb2/3)O3–PbTiO3 laminates. J. Appl. Phys. 2011, 109, 074507. [Google Scholar] [CrossRef]
- Li, M.; Gao, J.; Wang, Y.; Gray, D.; Li, J.; Viehland, D. Enhancement in magnetic field sensitivity and reduction in equivalent magnetic noise by magnetoelectric laminate stacks. J. Appl. Phys. 2012, 111, 104504. [Google Scholar] [CrossRef]
- Wang, Y.; Gray, D.; Betrry, D.; Gao, J.; Li, M.; Li, J.; Viehland, D. An extremely low equivalent magnetic noise magnetoelectric sensor. Adv. Mater. 2011, 23, 4111–4114. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Berry, D.; Das, J.; Gray, D.; Li, J.; Viehland, D. Enhanced Sensitivity and Reduced Noise Floor in Magnetoelectric Laminate Sensors by an Improved Lamination Process. J. Am. Ceram. Soc. 2011, 94, 3738–3741. [Google Scholar] [CrossRef]
- Gao, J.; Das, J.; Xing, Z.; Li, J.; Viehland, D. Comparison of noise floor and sensitivity for different magnetoelectric laminates. J. Appl. Phys. 2010, 108, 084509. [Google Scholar] [CrossRef]
- Shi, Z.; Nan, C.W.; Zhang, J.; Cai, N.; Li, J.-F. Magnetoelectric effect of Pb(Zr,Ti)O3 rod arrays in a (Tb,Dy)Fe2/epoxy medium. Appl. Phys. Lett. 2005, 87, 012503. [Google Scholar] [CrossRef]
- Ma, J.; Shi, Z.; Nan, C.W. Magnetoelectric Properties of Composites of Single Pb(Zr,Ti)O3 Rods and Terfenol-D/Epoxy with a Single-Period of 1-3-Type Structure. Adv. Mater. 2007, 19, 2571–2573. [Google Scholar] [CrossRef]
- Palneedi, H.; Choi, S.-Y.; Kim, G.; Annapureddy, V.; Maurya, D.; Priya, S.; Lee, K.J.; Chung, S.; Kang, S.L.; Ryu, J. Tailoring the Magnetoelectric Properties of Pb(Zr,Ti)O3 Film Deposited on Amorphous Metglas Foil by Laser Annealing. J. Am. Ceram. Soc. 2016, 99, 2680–2687. [Google Scholar] [CrossRef]
- Palneedi, H.; Maurya, D.; Kim, G.-Y.; Priya, S.; Kang, S.-J.L.; Kim, K.-H.; Choi, S.-Y.; Ryu, J. Enhanced off-resonance magnetoelectric response in laser annealed PZT thick film grown on magnetostrictive amorphous metal substrate. Appl. Phys. Lett. 2015, 107, 012904. [Google Scholar] [CrossRef]
- Palneedi, H.; Yeo, H.G.; Hwang, G.-T.; Annapureddy, V.; Kim, J.-W.; Choi, J.-J.; Trolier-McKinstry, S.; Ryu, J. A flexible, high-performance magnetoelectric heterostructure of (001) oriented Pb(Zr0.52Ti0.48)O3 film grown on Ni foil. Appl. Mater. 2017, 5, 096111. [Google Scholar] [CrossRef]
- Palneedi, H.; Maurya, D.; Kim, G.-Y.; Annapureddy, V.; Noh, M.-S.; Kang, C.-Y.; Kim, J.-W.; Choi, J.-J.; Choi, S.-Y.; Chung, S.-Y.; et al. Unleashing the Full Potential of Magnetoelectric Coupling in Film Heterostructures. Adv. Mater. 2017, 29, 1605688. [Google Scholar] [CrossRef]
- Srinivasan, G.; Rasmussen, E.T.; Gallegos, J.; Srinivasan, R.; Bokhan, Y.I.; Laletin, V.M. Magnetoelectric bilayer and multilayer structures of magnetostrictive and piezoelectric oxides. Phys. Rev. B 2001, 64, 214408. [Google Scholar] [CrossRef]
- Zhai, J.; Dong, S.; Xing, Z.; Li, J.; Viehland, D. Giant magnetoelectric effect in Metglas/polyvinylidene-fluoride laminates. Appl. Phys. Lett. 2006, 89, 083507. [Google Scholar] [CrossRef]
- Jin, J.; Lu, S.-G.; Chanthad, C.; Zhang, Q.; Haque, M.A.; Wang, Q. Multiferroic Polymer Composites with Greatly Enhanced Magnetoelectric Effect under a Low Magnetic Bias. Adv. Mater. 2011, 23, 3853. [Google Scholar] [CrossRef]
- Sreenivasulu, G.; Fetisov, L.Y.; Fetisov, Y.K.; Srinivasan, G. Piezoelectric single crystal langatate and ferromagnetic composites: Studies on low-frequency and resonance magnetoelectric effects. Appl. Phys. Lett. 2012, 100, 052901. [Google Scholar] [CrossRef]
- Kirchhof, C.; Krantz, M.; Teliban, I.; Jahns, R.; Marauska, S.; Wagner, B.; Knoöchel, R.; Gerken, M.; Meyners, D.; Quandt, E. Giant magnetoelectric effect in vacuum. Appl. Phys. Lett. 2013, 102, 232905. [Google Scholar] [CrossRef]
- Yarar, E.; Salzer, S.; Hrkac, V.; Piorra, A.; Höft, M.; Knöchel, R.; Kienle, L.; Quandt, E. Inverse bilayer magnetoelectric thin film sensor. Appl. Phys. Lett. 2016, 109, 022901. [Google Scholar] [CrossRef]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Parkhomenko, Y.N.; Kobeleva, S.P.; Pakhomov, O.V.; Kholkin, A.L.; Sobolev, N.A. Magnetoelectric metglas/bidomain y + 140°-cut lithium niobate composite for sensing fT magnetic fields. Appl. Phys. Lett. 2018, 112, 262906. [Google Scholar] [CrossRef]
- Greve, H.; Woltermann, E.; Quenzer, H.-J.; Wagner, B.; Quandt, E. Giant magnetoelectric coefficients in (Fe90Co10)78Si12B10-AlN thin film composites. Appl. Phys. Lett. 2010, 96, 182501. [Google Scholar] [CrossRef]
- Jovičević Klug, M.; Thormählen, L.; Röbisch, V.; Toxværd, S.D.; Höft, M.; Knöchel, R.; Quandt, E.; Meyners, D.; McCord, J. Antiparallel exchange biased multilayers for low magnetic noise magnetic field sensors. Appl. Phys. Lett. 2019, 114, 192410. [Google Scholar] [CrossRef]
- Nan, T.; Hui, Y.; Rinaldi, M.; Sun, N.X. Self-biased 215 MHz magnetoelectric NEMS resonator for ultra-sensitive DC magnetic field detection. Sci. Rep. 2013, 3, 1985. [Google Scholar] [CrossRef] [PubMed]
- Tu, C.; Chu, Z.-Q.; Spetzler, B.; Hayes, P.; Dong, C.-Z.; Liang, X.-F.; Chen, H.-H.; He, Y.-F.; Wei, Y.-Y.; Lisenkov, I.; et al. Mechanical-Resonance-Enhanced Thin-Film Magnetoelectric Heterostructures for Magnetometers, Mechanical Antennas, Tunable RF Inductors, and Filters. Materials 2019, 12, 2259. [Google Scholar] [CrossRef] [PubMed]
- Nan, T.; Lin, H.; Gao, Y.; Matyushov, A.; Yu, G.; Chen, H.; Sun, N.; Wei, S.; Wang, Z.; Li, M.; et al. Acoustically actuated ultra-compact NEMS magnetoelectric antennas. Nat. Commun 2017, 8, 296. [Google Scholar] [CrossRef] [PubMed]
- Chu, Z.; Shi, H.; Gao, X.; Wu, J.; Dong, S. Magnetoelectric coupling of a magnetoelectric flux gate sensor in vibration noise circumstance. AIP Adv. 2018, 8, 015203. [Google Scholar] [CrossRef]
- Fang, C.; Jiao, J.; Ma, J.; Lin, D.; Xu, H.; Zhao, X.; Luo, H. Significant reduction of equivalent magnetic noise by in-plane series connection in magnetoelectric Metglas/Mn-doped Pb(Mg1/3Nb2/3)O3-PbTiO3laminate composites. J. Phys. D Appl. Phys. 2015, 48, 465002. [Google Scholar] [CrossRef]
- Liu, Y.; Jiao, J.; Ma, J.; Ren, B.; Li, L.; Zhao, X.; Luo, H.; Shi, L. Frequency conversion in magnetoelectric composites for quasi-static magnetic field detection. Appl. Phys. Lett. 2013, 103, 212902. [Google Scholar] [CrossRef]
- Petrie, J.R.; Fine, J.; Mandal, S.; Sreenivasulu, G.; Srinivasan, G.; Edelstein, A.S. Enhanced sensitivity of magnetoelectric sensors by tuning the resonant frequency. Appl. Phys. Lett. 2011, 99, 043504. [Google Scholar] [CrossRef]
- Petrie, J.; Mandal, S.; Gollapudi, S.; Viehland, D.; Gray, D.; Srinivasan, G.; Edelstein, A.S. Enhancing the sensitivity of magnetoelectric sensors by increasing the operating frequency. J. Appl. Phys. 2011, 110, 124506. [Google Scholar] [CrossRef]
- Ou-Yang, J.; Liu, X.; Zhou, H.; Zou, Z.; Yang, Y.; Li, J.; Zhang, Y.; Zhu, B.; Chetn, S.; Yang, X. Magnetoelectric laminate composites: An overview of methods for improving the DC and low-frequency response. J. Phys. D Appl. Phys. 2018, 51, 324005. [Google Scholar] [CrossRef]
- Chu, Z.; Dong, C.; Tu, C.; Liang, X.; Chen, H.; Sun, C.; Yu, Z.; Dong, S.; Sun, N.-X. A low-power and high-sensitivity magnetic field sensor based on converse magnetoelectric effect. Appl. Phys. Lett. 2019, 115, 162901. [Google Scholar] [CrossRef]
- Chu, Z.; Yu, Z.; PourhosseiniAsl, M.; Tu, C.; Dong, S. Enhanced low-frequency magnetic field sensitivity in magnetoelectric composite with amplitude modulation method. Appl. Phys. Lett. 2019, 114, 132901. [Google Scholar] [CrossRef]
- PourhosseiniAsl, M.; Yu, Z.; Chu, Z.; Yang, J.; Xu, J.; Hou, Y.; Dong, S. Enhanced self-bias magnetoelectric effect in locally heat-treated ME laminated composite. Appl. Phys. Lett. 2019, 115, 112901. [Google Scholar] [CrossRef]
- Li, J.; Ma, G.; Zhang, S.; Wang, C.; Jin, Z.; Zong, W.; Zhao, G.; Wang, X.; Xu, J.; Cao, D.; et al. AC/DC dual-mode magnetoelectric sensor with high magnetic field resolution and broad operating bandwidth. AIP Adv. 2021, 11, 045015. [Google Scholar] [CrossRef]
- Chu, Z.; Shi, H.; PourhosseiniAsl, M.J.; Wu, J.; Shi, W.; Galo, X.; Yuan, X.; Dong, S. A magnetoelectric flux gate: New approach for weak DC magnetic field detection. Sci. Rep. 2017, 7, 8592. [Google Scholar] [CrossRef]
- Burdin, D.A.; Chashin, D.V.; Ekonomov, N.A.; Fetisov, Y.K.; Stashkevich, A.A. High-sensitivity dc field magnetometer using nonlinear resonance magnetoelectric effect. J. Magn. Magn. Mater. 2016, 405, 244–248. [Google Scholar] [CrossRef]
- Burdin, D.; Chashin, D.; Ekonomov, N.; Fetisov, L.; Fetisov, Y.; Shamonin, M. DC magnetic field sensing based on the nonlinear magnetoelectric effect in magnetic heterostructures. J. Phys. D Appl. Phys. 2016, 49, 375002. [Google Scholar] [CrossRef]
- Burdin, D.A.; Ekonomov, N.A.; Chashin, D.V.; Fetisov, L.Y.; Fetisov, Y.K.; Shamonin, M. Temperature Dependence of the Resonant Magnetoelectric Effect in Layered Heterostructures. Materials 2017, 10, 1183. [Google Scholar] [CrossRef]
- Schmelz, M.; Stolz, R.; Zakosarenko, V.; Schönau, T.; Anders, S.; Fritzsch, L.; Mück, M.; Meyer, M.; Meyer, H.-G. Sub-fT/Hz1/2 resolution and field-stable SQUID magnetometer based on low parasitic capacitance sub-micrometer cross-type Josephson tunnel junctions. Phys. C Supercond. Its Appl. 2012, 482, 27–32. [Google Scholar] [CrossRef]
- Shen, Y.; Gao, J.; Hasanyan, D.; Wang, Y.; Li, M.; Li, J.; Viehland, D. Investigation of vehicle induced magnetic anomaly by triple-axis magnetoelectric sensors. Smart Mater. Struct. 2012, 21, 115007. [Google Scholar] [CrossRef]
- Shen, Y.; Hasanyan, D.; Gao, J.; Wang, Y.; Li, J.; Viehland, D. A magnetic signature study using magnetoelectric laminate sensors. Smart Mater. Struct. 2013, 22, 095007. [Google Scholar] [CrossRef]
- Xu, J.; Leung, C.M.; Zhuang, X.; Li, J.; Viehland, D. Spatial magnetic source detection based on active mode magnetoelectric gradiometer with 2D and 3D configurations. J. Phys. D Appl. Phys. 2020, 53, 365002. [Google Scholar] [CrossRef]
- Chu, Z.; Shi, W.; Shi, H.; Chen, Q.; Wang, L.; PourhosseiniAsl, M.J.; Xiao, C.; Xie, T.; Dong, S. A 1D Magnetoelectric Sensor Array for Magnetic Sketching. Adv. Mater. Technol. 2019, 4, 1800484. [Google Scholar] [CrossRef]
- Zhai, J.; Dong, S.; Xing, Z.; Li, J.; Viehland, D. Geomagnetic sensor based on giant magnetoelectric effect. Appl. Phys. Lett. 2007, 91, 123513. [Google Scholar] [CrossRef]
- Duc, N.H.; Tu, B.D.; Ngoc, N.T.; Lap, V.D.; Giang, D.T.H. Metglas/PZT-Magnetoelectric 2-D Geomagnetic Device for Computing Precise Angular Position. IEEE Trans. Magn. 2013, 49, 4839–4842. [Google Scholar] [CrossRef]
- PourhosseiniAsl, M.J.; Chu, Z.; Gao, X.; Dong, S. A hexagonal-framed magnetoelectric composite for magnetic vector measurement. Appl. Phys. Lett. 2018, 113, 092902. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Wen, Y.; He, W.; Yang, J.; Yang, A.; Lu, C.; Li, W. Enhanced sensitivity in magnetoelectric current-sensing devices with frequency up-conversion mechanism by modulating the magnetostrictive strain. J. Appl. Phys. 2014, 115, 17E505. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.-F.; Viehland, D. Vortex magnetic field sensor based on ring-type magnetoelectric laminate. Appl. Phys. Lett. 2004, 85, 2307–2309. [Google Scholar] [CrossRef]
- Zhang, J.; Li, P.; Wen, Y.; He, W.; Yang, A.; Lu, C. Packaged current-sensing device with self-biased magnetoelectric laminate for low-frequency weak-current detection. Smart Mater. Struct. 2014, 23, 095028. [Google Scholar] [CrossRef]
- Zhao, S.; Sun, L.; Gao, J.; Wang, J.; Shen, Y. Uniaxial ACFM detection system for metal crack size estimation using magnetic signature waveform analysis. Measurement 2020, 164, 108090. [Google Scholar] [CrossRef]
- Chu, Z.; Jiang, Z.; Mao, Z.; Shen, Y.; Gao, J.; Dong, S. Low-power eddy current detection with 1-1 type magnetoelectric sensor for pipeline cracks monitoring. Sens. Actuators A Phys. 2021, 318, 112496. [Google Scholar] [CrossRef]
- Wu, Z.; Bian, L.; Chen, S. Packaged angle-sensing device with magnetoelectric laminate composite and magnetic circuit. Sens. Actuators A Phys. 2018, 273, 232–239. [Google Scholar] [CrossRef]
- Lu, C.; Zhu, R.; Yu, F.; Jiang, X.; Liu, Z.; Dong, L.; Hua, Q.; Ou, Z. Gear rotational speed sensor based on FeCoSiB/Pb(Zr,Ti)O3 magnetoelectric composite. Measurement 2021, 168, 108409. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, B. Displacement Sensor with Nanometric resolution Based on Magnetoelectric Effect. IEEE Sens. J. 2021, 21, 12084–12091. [Google Scholar]
- Pereira, N.; Lima, A.C.; Correia, V.; Perinka, N.; Lanceros-Mendez, S.; Martins, P. Magnetic Proximity Sensor Based on Magnetoelectric Composites and Printed Coils. Materials 2020, 13, 1729. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Duan, Y.; Or, S.W.; Zhao, Y. Smart elasto-magneto-electric (EME) sensors for stress monitoring of steel cables: Design theory and experimental validation. Sensors 2014, 14, 13644–13660. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hu, C.; Wang, Z.; Li, Y.; Zhu, S.; Su, W.; Hu, Z.; Zhou, Z.; Liu, M. Wireless strain sensor based on the magnetic strain anisotropy dependent ferromagnetic resonance. AIP Adv. 2020, 10, 150310. [Google Scholar] [CrossRef]
- Hayes, P.; Klug, M.J.; Toxværd, S.; Durdaut, P.; Schell, V.; Teplyuk, A.; Burdin, D.; Winkler, A.; Weser, R.; Fetisov, Y.; et al. Converse Magnetoelectric Composite Resonator for Sensing Small Magnetic Fields. Sci. Rep. 2019, 9, 16355. [Google Scholar] [CrossRef]
- Xi, H.; Qian, X.; Lu, M.-C.; Mei, L.; Rupprecht, S.; Yang, Q.X.; Zhang, Q.M. A Room Temperature Ultrasensitive Magnetoelectric Susceptometer for Quantitative Tissue Iron Detection. Sci. Rep. 2016, 6, 29740. [Google Scholar] [CrossRef]
- Wikswo, J.P. SQUID magnetometers for biomagnetism and nondestructive testing: Important questions and initial answers. IEEE Trans. Appl. Supercond. 1995, 5, 74–120. [Google Scholar] [CrossRef]
- Zuo, S.; Schmalz, J.; Ozden, M.-O.; Gerken, M.; Su, J.; Niekiel, F.; Lofink, F.; Nazarpour, K.; Heidari, H. Ultrasensitive Magnetoelectric Sensing System for Pico-Tesla MagnetoMyoGraphy. IEEE Trans. Biomed. Circuits Syst 2020, 14, 971–984. [Google Scholar] [CrossRef]
- Ripka, P.; Janosek, M. Advances in Magnetic Field Sensors. IEEE Sens. J. 2010, 10, 1108–1116. [Google Scholar] [CrossRef]
- Lukat, N.; Friedrich, R.-M.; Spetzler, B.; Kirchhof, C.; Arndt, C.; Thormählen, L.; Faupel, F.; Selhuber-Unkel, C. Mapping of magnetic nanoparticles and cells using thin film magnetoelectric sensors based on the delta-E effect. Sens. Actuators A Phys. 2020, 309, 112023. [Google Scholar] [CrossRef]
- Gleich, B.; Weizenecker, J. Tomographic imaging using the nonlinear response of magnetic particles. Nature 2005, 435, 1214–1217. [Google Scholar] [CrossRef]
- Friedrich, R.M.; Zabel, S.; Galka, A.; Lukat, N.; Wagner, J.-M.; Kirchhof, C.; Quandt, E.; Mccord, J.; Selhuber-Unkel, C.; Siniatchkin, M.; et al. Magnetic particle mapping using magnetoelectric sensors as an imaging modality. Sci. Rep. 2019, 9, 2086. [Google Scholar] [CrossRef]
- Reermann, J.; Durdaut, P.; Salzer, S.; Demming, T.; Piorra, A.; Quandt, E.; Frey, N.; Höft, M.; Schmidt, G. Evaluation of magnetoelectric sensor systems for cardiological applications. Measurement 2018, 116, 230–238. [Google Scholar] [CrossRef]





| Composition | Year | Connectivity | Working Mode | ||
|---|---|---|---|---|---|
| Terfenol-D/PZT [37] | 2007 | 3-1 | L-L | 0.5 | 18.2 |
| NiFe2O4/PZT [42] | 2001 | 2-2 | L-T | 1.5 | / |
| Terfenol-D/PZT [27] | 2002 | 2-2 | L-T | 5 | / |
| Metglas/PVDF [43] | 2006 | 2-2 | L-T | 7.2 | 310 |
| Metglas/P(VDF-TrFE) [44] | 2011 | 2-2 | L-L | 17.7 | 383 |
| Lanthanum gallium tantalite/ permendur [45] | 2012 | 2-2 | / | 2.3 | 720 |
| FeCoSiB/(Pt)/AlN in vacuum [46] | 2013 | 2-2 | L-T | / | 20,000 |
| FeCoSiB/(Pt)/AlN [47] | 2016 | 2-2 | L-T | / | 5000 |
| Metglas/LiNbO3 [48] | 2018 | 2-2 | L-T | 1.9 | 1704 |
| FeBSiC/PZT [30] | 2006 | 2-1 | L-L | 22 | 500 |
| Metglas/PMN-PT [31] | 2011 | 2-1 | L-L | 45 | 1100 |
| Metglas/PMN-PT without laser treatment [8] | 2017 | 1-1 | L-T | 29.3 | 5500 |
| Metglas/PMN-PT with laser treatment [8] | 2017 | 1-1 | L-T | 22.9 | 7000 |
| Metglas/Mn-PMN-PZT with laser treatment [9] | 2020 | 1-1 | L-T | 23.6 | 12,500 |
| Composition | Working Mode | Sensing Mode | ||
|---|---|---|---|---|
| Low-frequency magnetic field sensing | Metglas/Mn-PMNT [55] | Longitudinal vibration (Multi-L-T) | Passive sensing | 0.87 pT/ @ 30 Hz |
| Metglas/PMN-PT [33] | Longitudinal vibration (Multi-push-pull) | Passive sensing | 5.1 pT/ @ 1 Hz | |
| Metglas/PMN-PZT [61] | Longitudinal vibration (L-T) | Active Modulation | 33 pT/ @ 0.1 Hz | |
| Resonant magnetic field sensing | Metglas/ LiNbO3 [48] | bending mode | Direct Sensing | 92 fT/√Hz |
| FeCoSiB/(Pt)/AlN [47] | bending mode | Direct Sensing | 400 fT/√Hz | |
| Metglas/PMN-PZT [8] | Longitudinal vibration (L-T) | Direct Sensing | 123 fT/√Hz | |
| DC magnetic field sensing | langatate-Metglas [65] | bending mode | Nonlinear ME effect | 10 nT |
| Metglas/PMN-PZT [9] | Longitudinal vibration (L-T) | Linear ME effect | 1 nT | |
| FeCoSiB/(Pt)/AlN [26] | Lateral vibration | Delta-E effect | 0.8 nT | |
| FeCoSiB/(Pt)/AlN [51] | Lateral vibration | Delta-E effect | 0.4 nT |
| Magnetometer | Working Temperature | Power Consumption (mW) | Typical Size | Limitations | |
|---|---|---|---|---|---|
| ME sensor [33] | 0 °C to +50 °C ① | <1 | 80 mm × 10 mm @ ME composites | 5.1 | Vibration interference |
| Magnetoresistive sensor ② | −40 °C to +125 °C | ~0.02 | 6 mm × 5 mm × 1.5 mm @ sensing element | 100 | Low sensitivity |
| Giant magneto-impedance sensor ③ | −20 °C to +60 °C | 75 | 35 mm × 11 mm × 4.6 mm @ sensing element | 15–25 | Low sensitivity |
| Fluxgate magnetometer ④ | −40 °C to +70 °C | 350 | ø100 mm × 125 mm @ system size | 2–6 | Power consumption |
| Optically pumped magnetometer ⑤ | −35 °C to +50 °C | >12,000 | 175 cm × 28 cm × 28 cm @ system size | 4 | Complex setup |
| SQUID magnetometer [68] | <−196 °C | >1000 | 12.5 mm × 12.5 mm @ chip size | <0.005 | Cooling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Jiang, Z.; Zhang, S.; Mao, Z.; Shen, Y.; Chu, Z. Review of Magnetoelectric Sensors. Actuators 2021, 10, 109. https://doi.org/10.3390/act10060109
Gao J, Jiang Z, Zhang S, Mao Z, Shen Y, Chu Z. Review of Magnetoelectric Sensors. Actuators. 2021; 10(6):109. https://doi.org/10.3390/act10060109
Chicago/Turabian StyleGao, Junqi, Zekun Jiang, Shuangjie Zhang, Zhineng Mao, Ying Shen, and Zhaoqiang Chu. 2021. "Review of Magnetoelectric Sensors" Actuators 10, no. 6: 109. https://doi.org/10.3390/act10060109
APA StyleGao, J., Jiang, Z., Zhang, S., Mao, Z., Shen, Y., & Chu, Z. (2021). Review of Magnetoelectric Sensors. Actuators, 10(6), 109. https://doi.org/10.3390/act10060109







