Adaptive Damping Variable Sliding Mode Control for an Electrohydrostatic Actuator
Abstract
1. Introduction
2. Mathematical Model of the EHA
2.1. Modeling of the Brushless DC Motor (BLDCM)
2.2. Modeling of Pump and Cylinder
3. Adaptive Damping Variable Sliding Mode Control Strategy
3.1. Problem Formulation
3.2. Nonlinear Projection Mapping
3.3. Design of the Extended State Observer (ESO)
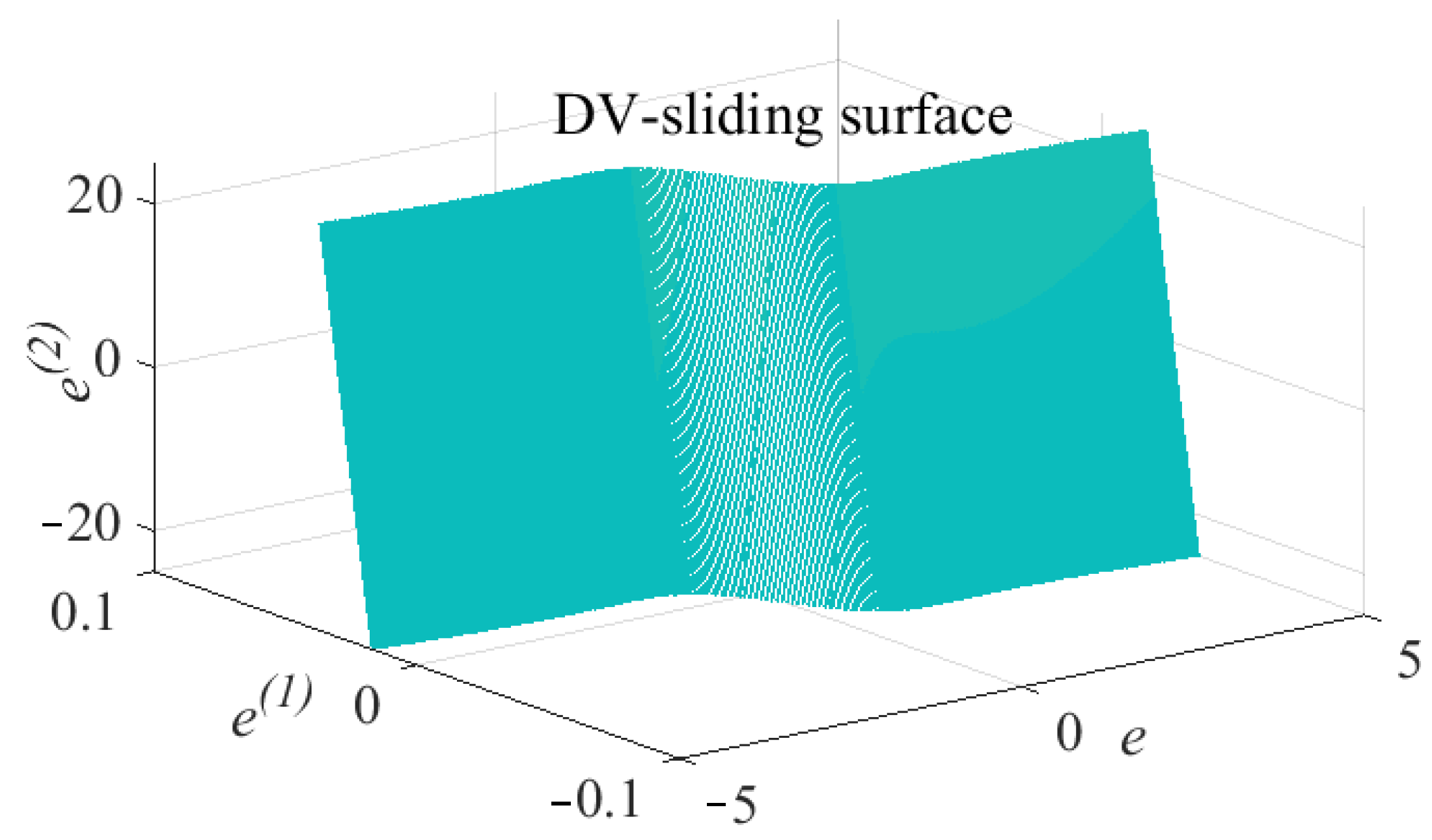
3.4. Design of the Adaptive Damping Variable Sliding Mode Controller (ADV-SMController)
3.5. Stability Analysis
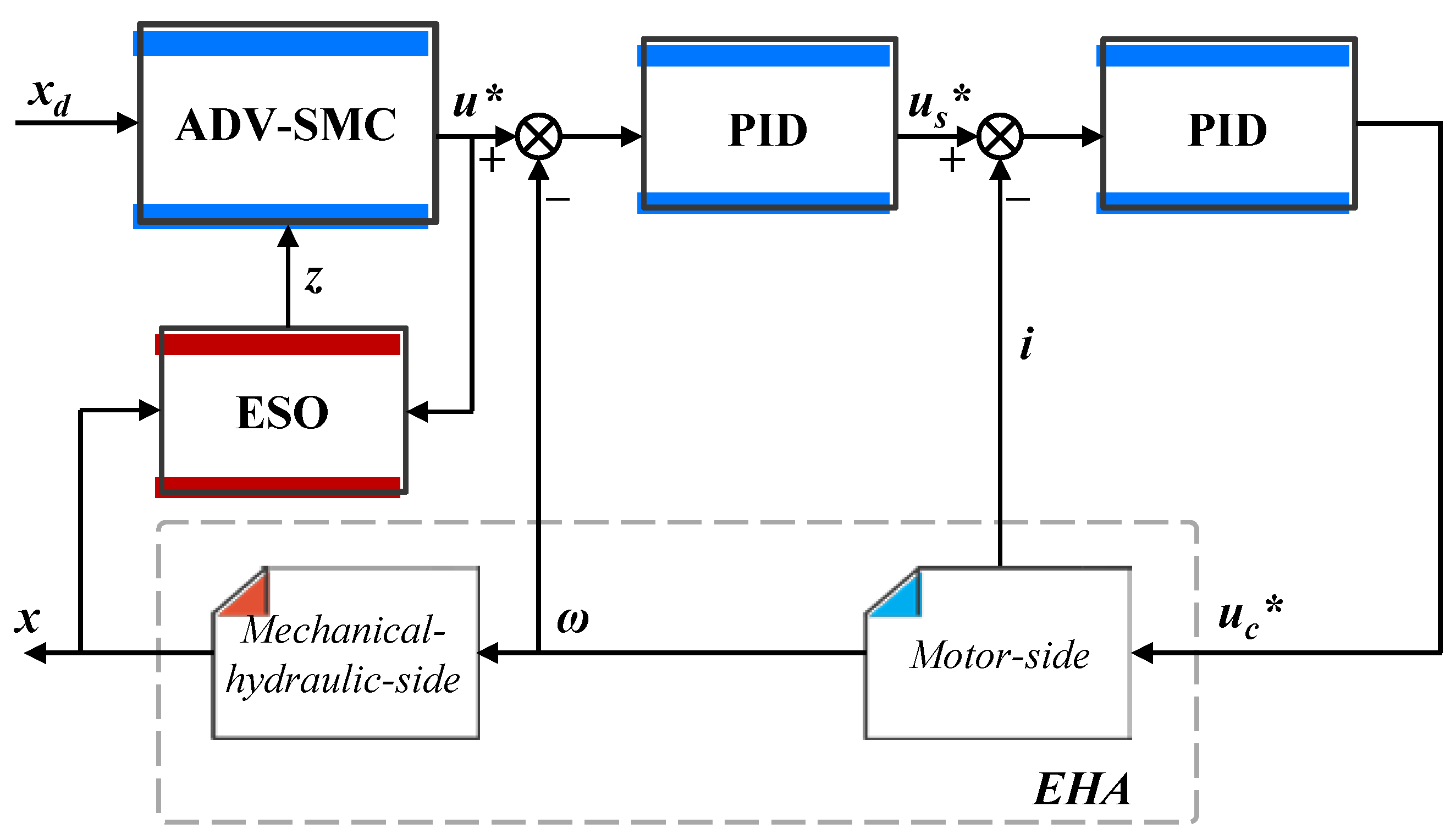
3.6. Control Method Design of the EHA
4. Experimental Verification
4.1. Experimental Setup
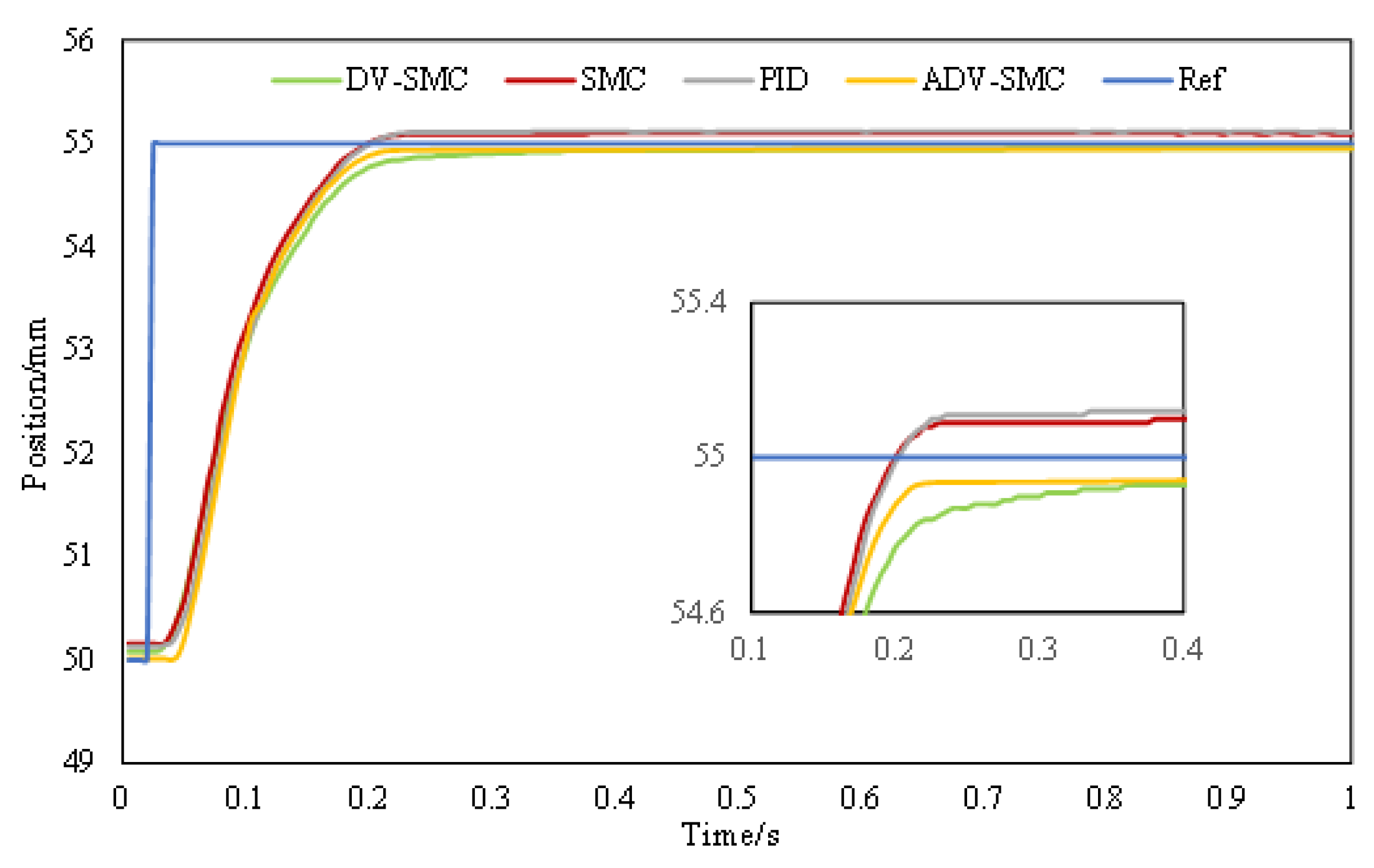
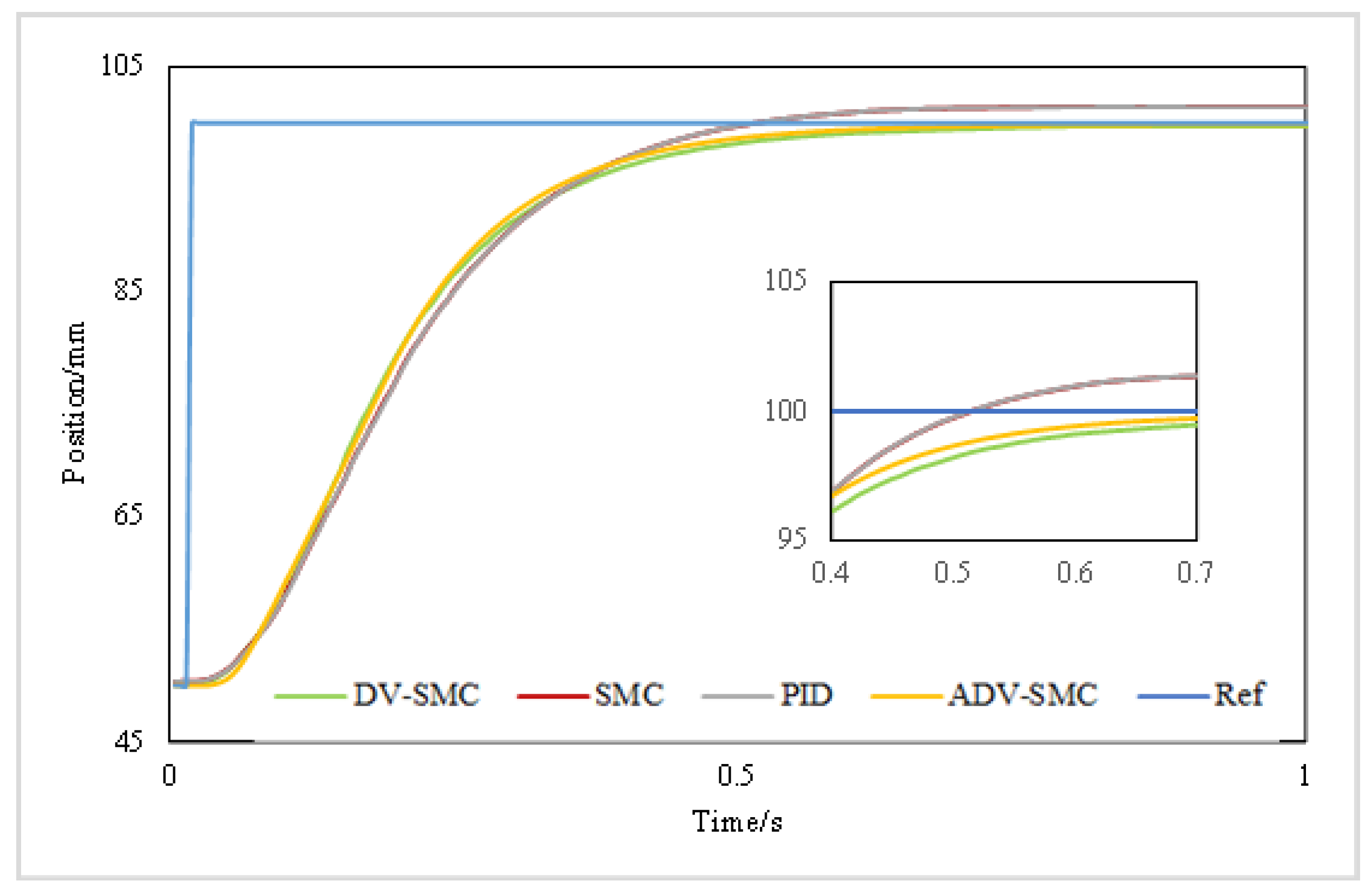
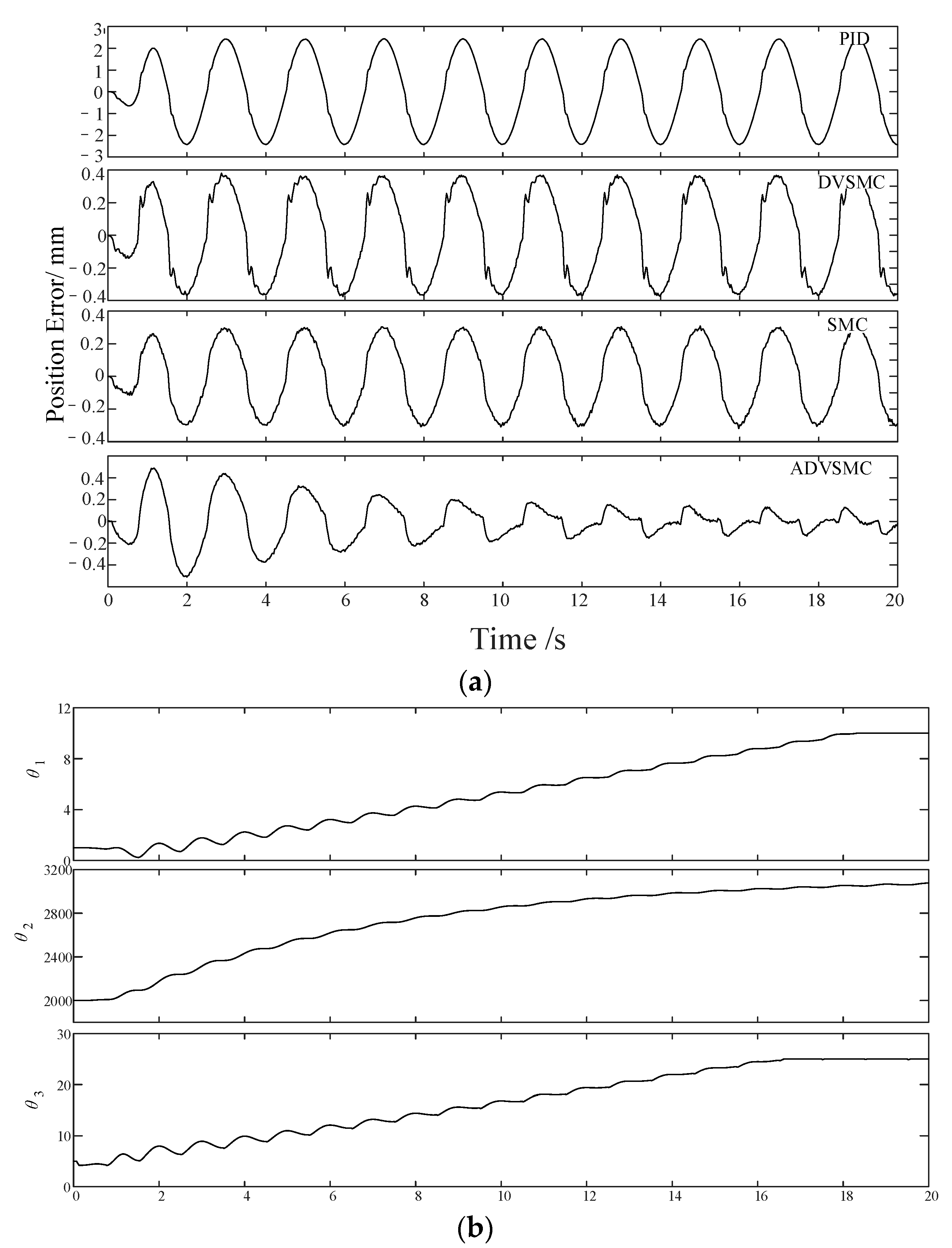
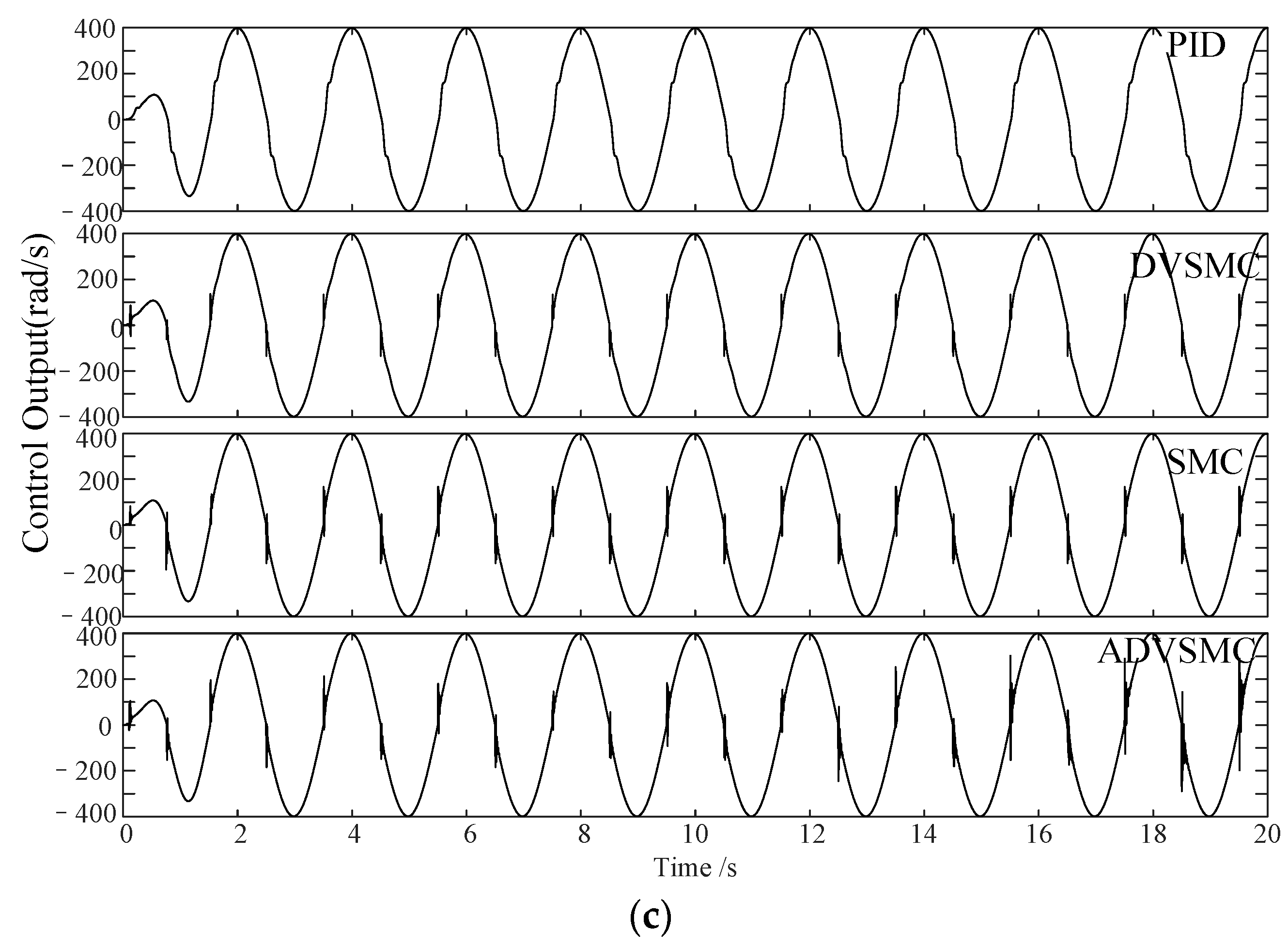
4.2. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maré, J.-C.; Fu, J. Review on signal-by-wire and power-by-wire actuation for more electric aircraft. Chin. J. Aeronaut. 2017, 30, 857–870. [Google Scholar] [CrossRef]
- Alle, N.; Hiremath, S.S.; Makaram, S.; Subramaniam, K.; Talukdar, A. Review on electro hydrostatic actuator for flight control. Int. J. Fluid Power 2016, 17, 125–145. [Google Scholar] [CrossRef]
- Shang, Y.; Li, X.; Qian, H.; Wu, S.; Pan, Q.; Huang, L.; Jiao, Z. A Novel Electro Hydrostatic Actuator System With Energy Recovery Module for More Electric Aircraft. IEEE Trans. Ind. Electron. 2020, 67, 2991–2999. [Google Scholar] [CrossRef]
- Marco, V.; Marco, T.; Giuseppe, F.; Luca, C. Electromechanical Actuator for Helicopter Rotor Damper Application. IEEE Trans. Ind. Appl. 2014, 50, 1007–1014. [Google Scholar]
- Qiao, G.; Liu, G.; Shi, Z.; Wang, Y.; Ma, S.; Lim, T.C. A review of electromechanical actuators for More/All Electric aircraft systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. Nov. 2017, 232, 4128–4151. [Google Scholar] [CrossRef]
- Bossche, D. The A380 flight control electro-hydrostatic actuators, achievements and lessons learnt. In Proceedings of the 25th International Congress of the Aeronautical Sciences, Hamburg, Germany, 3–8 September 2006; pp. 1–8. [Google Scholar]
- Qi, H.T.; Fu, Y.L.; Qi, X.Y.; Lang, Y. Architecture Optimization of More Electric Aircraft Actuation System. Chin. J. Aeronaut. 2011, 24, 506–513. [Google Scholar] [CrossRef]
- MOOG Inc. Electro Hydrostatic Actuators; MOOG Inc.: Salt Lake City, UT, USA, 2014. [Google Scholar]
- Zhao, J.A.; Fu, Y.L.; Ma, J.M.; Fu, J.; Chao, Q.; Wang, Y. Review of cylinder block/valve plate interface in axial piston pumps: Theoretical models, experimental investigations, and optimal design. Chin. J. Aeronaut. 2021, 34, 111–134. [Google Scholar] [CrossRef]
- Shea, A.; Jahns, T.M. Hardware integration for an integrated modular motor drive including distributed control. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 4881–4887. [Google Scholar]
- Wang, J.; Li, Y.; Han, Y. Integrated modular motor drive design with GaN power FETs. IEEE Trans. Ind. Appl. 2015, 51, 3198–3207. [Google Scholar] [CrossRef]
- Yang, Y.S.; Niu, W.Q.; Zhao, J. Design and Numerical Study of Electro-Hydrostatic Actuator. J. Phys. Conf. Ser. 2019, 012088, 1–9. [Google Scholar] [CrossRef]
- Ren, G.; Esfandiari, M.; Song, J.; Sepehri, N. Position Control of an Electro-hydrostatic Actuator with Tolerance to Internal Leakage. IEEE Trans. Control Syst. Technol. 2016, 24, 2224–2232. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Wang, J.; Karimi, H.R. Robust H∞ Sliding mode control with pole placement for a fluid power electrohydraulic actuator (EHA) system. Int. J. Adv. Manuf. Technol. 2014, 73, 1095–1104. [Google Scholar] [CrossRef]
- Wang, C.; Quan, L.; Jiao, Z.; Zhang, S. Nonlinear Adaptive Control of Hydraulic System With Observing and Compensating Mismatching Uncertainties. IEEE Trans. Control Syst. Technol. 2018, 26, 927–938. [Google Scholar] [CrossRef]
- Yao, Z.K.; Yao, J.Y.; Yao, F.Y. Model reference adaptive tracking control for hydraulic servo systems with nonlinear neural-networks. ISA Trans. 2019, 100, 396–404. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.K.; Fu, Y.L.; Zhao, J.A. A Novel Cascade Control Based on Damp Variable Sliding Mode Control for an Electro-hydrostatic Actuator. J. Beijing Univ. Aeronaut. Astronaut. 2020. (In Chinese) [Google Scholar] [CrossRef]
- Yang, R.R.; Fu, Y.L.; Zhang, G.L. A Novel Sliding Mode Control Framework for Electrohydrostatic Actuator. Math. Probl. Eng. 2018, 7159891. [Google Scholar] [CrossRef]
- Ataklti, E.A.; Fu, Y.L. Sliding mode control of electro-hydrostatic actuator based on extended state observer. In Proceedings of the 29th Chinese Control And Decision Conference, Chongqing, China, 28–30 May 2017; pp. 758–763. [Google Scholar]
- Wang, M.; Wang, Y.; Yang, R.; Fu, Y.; Zhu, D. A Sliding Mode Control Strategy for an ElectroHydrostatic Actuator with Damping Variable Sliding Surface. Actuators 2020, 10, 3. [Google Scholar] [CrossRef]
- Ali, S.A.; Christen, A.; Begg, S.; Langlois, N. Continuous–discrete time-observer design for state and disturbance estimation of electrohydraulic actuator systems. IEEE Trans. Ind. Electron. 2016, 63, 4314–4324. [Google Scholar] [CrossRef]
- Throne, D.; Martinez, F.; Marguire, R.; Arens, D. Integrated Motor/Drive Technology with Rockwell Connectivity. Rexroth, Bosch Group, Lohr am Main, Germany, Tech. Rep. Available online: http://www.cmafh.com/enewsletter/PDFs/IntegratedMotorDrives.pdf (accessed on 17 April 2021).
- Kim, H.-J.; Park, H.-S.; Kim, J.-M. Expansion of Operating Speed Range of High-Speed BLDC Motor Using Hybrid PWM Switching Method Considering Dead Time. Energies 2020, 13, 5212. [Google Scholar] [CrossRef]
- Berri, P.C.; Vedova, M.D.L.D.; Maggiore, P. A Simplified Monitor Model for EMA Prognostics. Matec Web Conf. 2018, 233, 00016. [Google Scholar] [CrossRef][Green Version]
- Yao, B.; Bu, F.; Reedy, J.; Chiu, G.C. Adaptive Robust Motion Control of Single-Rod Hydraulic Actuators: Theory and Experiments. IEEE/ASME Trans. Mechatron. 2000, 5, 79–91. [Google Scholar]


| Parameter | Value |
|---|---|
| Piston effective area (m2) | 1.134 × 10−4 |
| Effective stroke (m) | 0.1 |
| Fluid elastic modulus (N/m2) | 6.86 × 108 |
| Hydraulic cylinder volume (m3) | 4 × 10−4 |
| Mass of cylinder and load (kg) | 243 |
| Pump displacement (m3/rad) | 3.98 × 10−7 |
| Phase resistance (Ω) | 0.2 |
| Phase inductance (mH) | 1.33 |
| Motor spindle moment of inertia (kg⸱m2) | 4 × 10−4 |
| Torque coefficient (N⸱m/A) | 0.351 |
| Back EMF coefficient (V/(rad/s)) | 0.234 |
| Bus voltage (V) | 270 |
| 5 mm | 50 mm | |||
|---|---|---|---|---|
| ST/s | OS | ST/s | OS | |
| PID | 1+ | 0.024 | 1.8+ | 0.029 |
| SMC | 0.925 | 0.022 | 1.8+ | 0.029 |
| DV-SMC | 0.285 | 0 | 1.63 | 0 |
| ADV-SMC | 0.205 | 0 | 1.03 | 0 |
| Error | Average | Maximum | Variance |
|---|---|---|---|
| PID | 0.001589 | 0.002421 | 5.17 × 10−7 |
| DV-SMC | 0.000252 | 0.000362 | 1.02 × 10−8 |
| SMC | 0.000205 | 0.000297 | 6.64 × 10−9 |
| ADV-SMC | 4.42 × 10−5 | 0.000123 | 1.74 × 10−9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, M.; Yang, R.; Fu, Y.; Zhu, D. Adaptive Damping Variable Sliding Mode Control for an Electrohydrostatic Actuator. Actuators 2021, 10, 83. https://doi.org/10.3390/act10040083
Li L, Wang M, Yang R, Fu Y, Zhu D. Adaptive Damping Variable Sliding Mode Control for an Electrohydrostatic Actuator. Actuators. 2021; 10(4):83. https://doi.org/10.3390/act10040083
Chicago/Turabian StyleLi, Linjie, Mingkang Wang, Rongrong Yang, Yongling Fu, and Deming Zhu. 2021. "Adaptive Damping Variable Sliding Mode Control for an Electrohydrostatic Actuator" Actuators 10, no. 4: 83. https://doi.org/10.3390/act10040083
APA StyleLi, L., Wang, M., Yang, R., Fu, Y., & Zhu, D. (2021). Adaptive Damping Variable Sliding Mode Control for an Electrohydrostatic Actuator. Actuators, 10(4), 83. https://doi.org/10.3390/act10040083








