Examining Yam Production in Response to Climate Change in Nigeria: A Co-Integration Model Approach
Abstract
1. Introduction
2. Materials and Methods
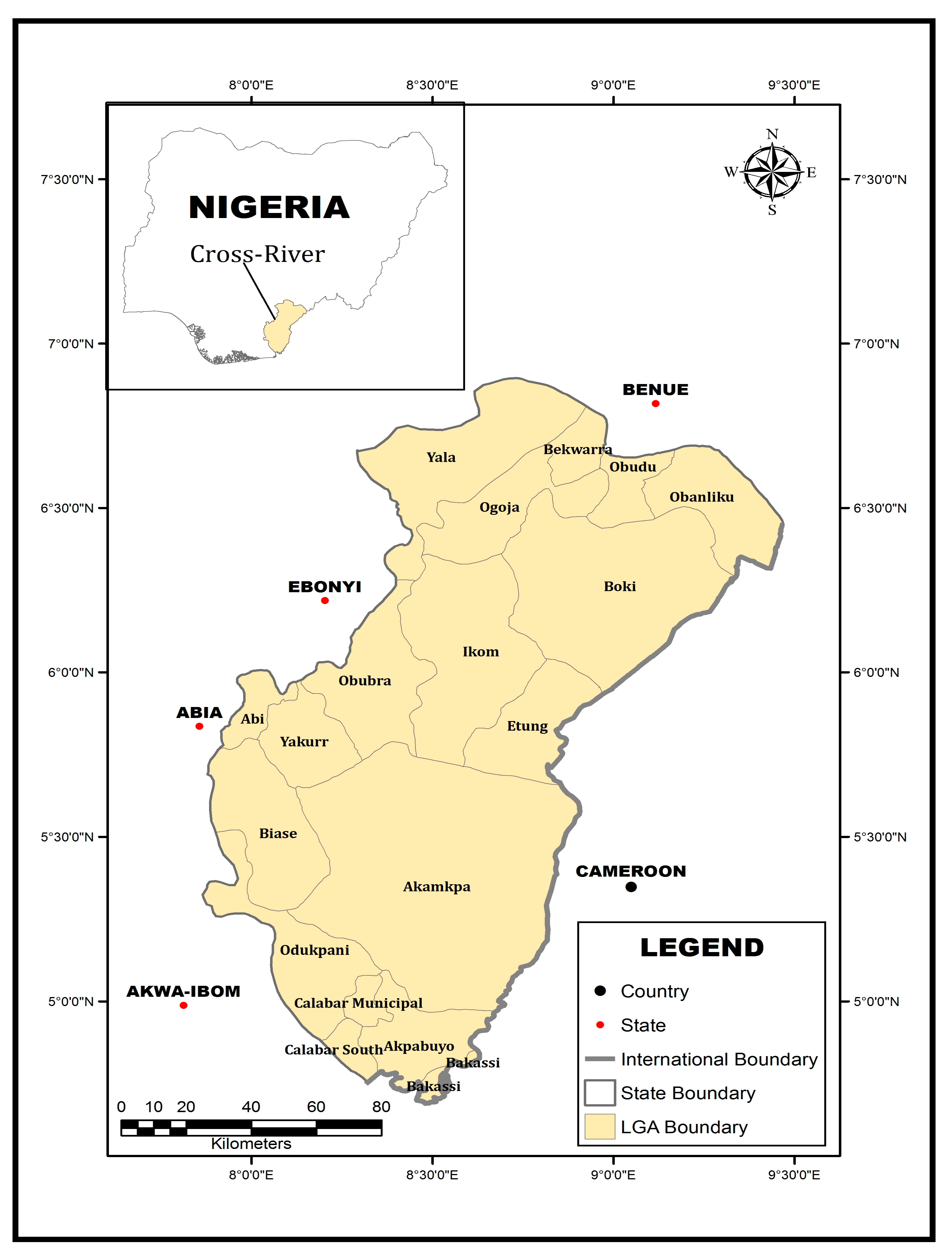
2.1. The Study Area
2.2. Data Collection
2.3. Data Analysis and Model Specification
2.3.1. Production Function Model Specification:
- Y = output of yam (kg)
- f = functional form
- X1 = rainfall (mm)
- X2 = temperature (°C)
- Y = output of yam (tonnes)
- R = rainfall (mm)
- T = temperature (°C)
- β = coefficients to be estimated
- e = stochastic variable
- Y = the dependent variable (output of yam)
- a = intercept of Y (constant)
- b = slope or coefficient of X
- X1 = rainfall (in mm)
- X2 = temperature (in °C)
- U = error term
2.3.2. Unit Root Test
2.3.3. The Co-Integration Test
2.3.4. Error Correction Model
2.3.5. Multivariate Model Specification
- β = regression coefficient
- Q = output of yam
- X1= mean annual temperature (degree centigrade)
- X2= mean annual rainfall (millimeter)
- U = random error term
- Yt = output of yam
- X1 = annual temperature (°C)
- X2 = annual rainfall (mm)
- Ut = stochastic error term
3. Results and Discussion
3.1. Trend Analysis of Yam Output and Climate Variables
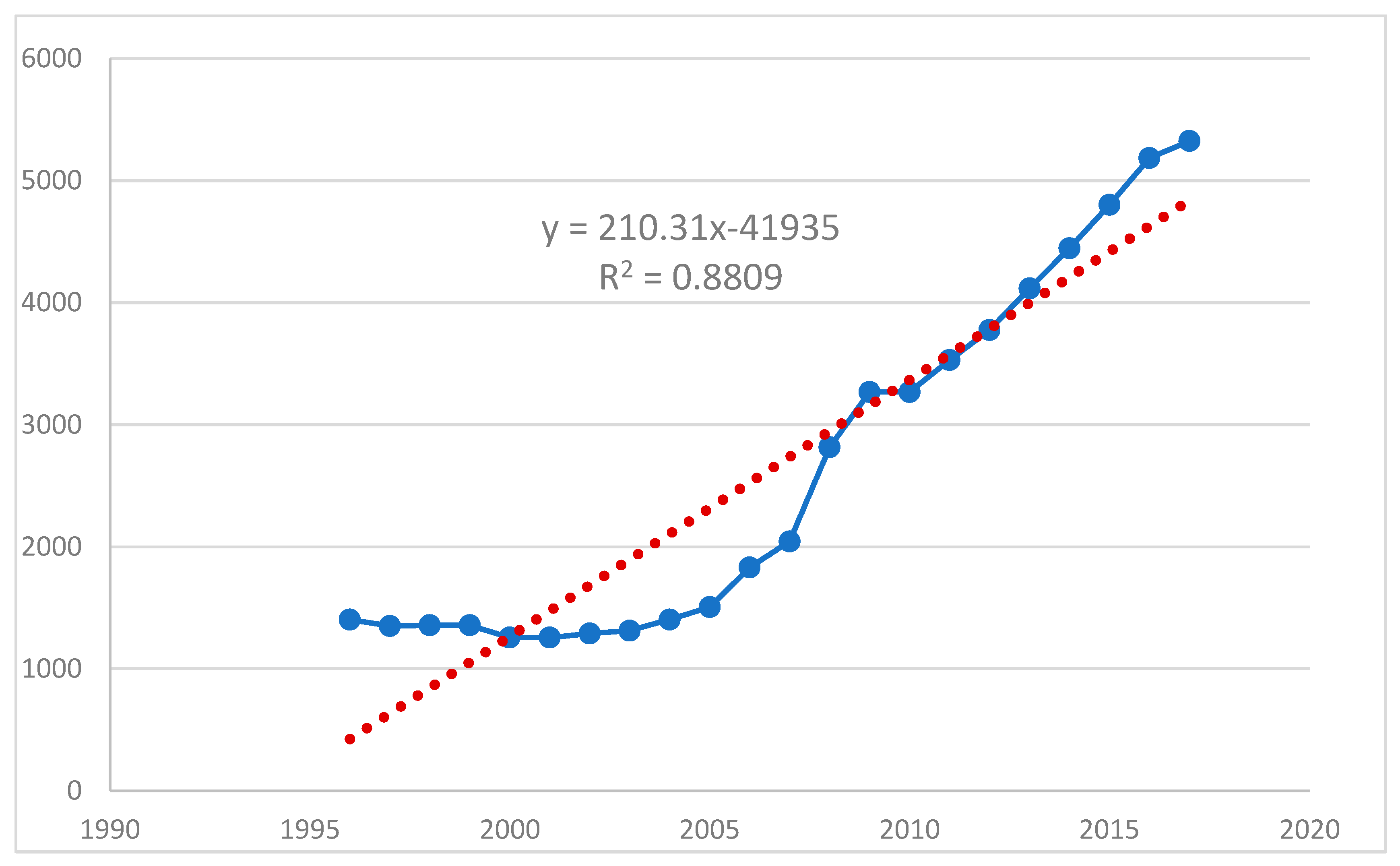
3.1.1. The Trend of Yam Production
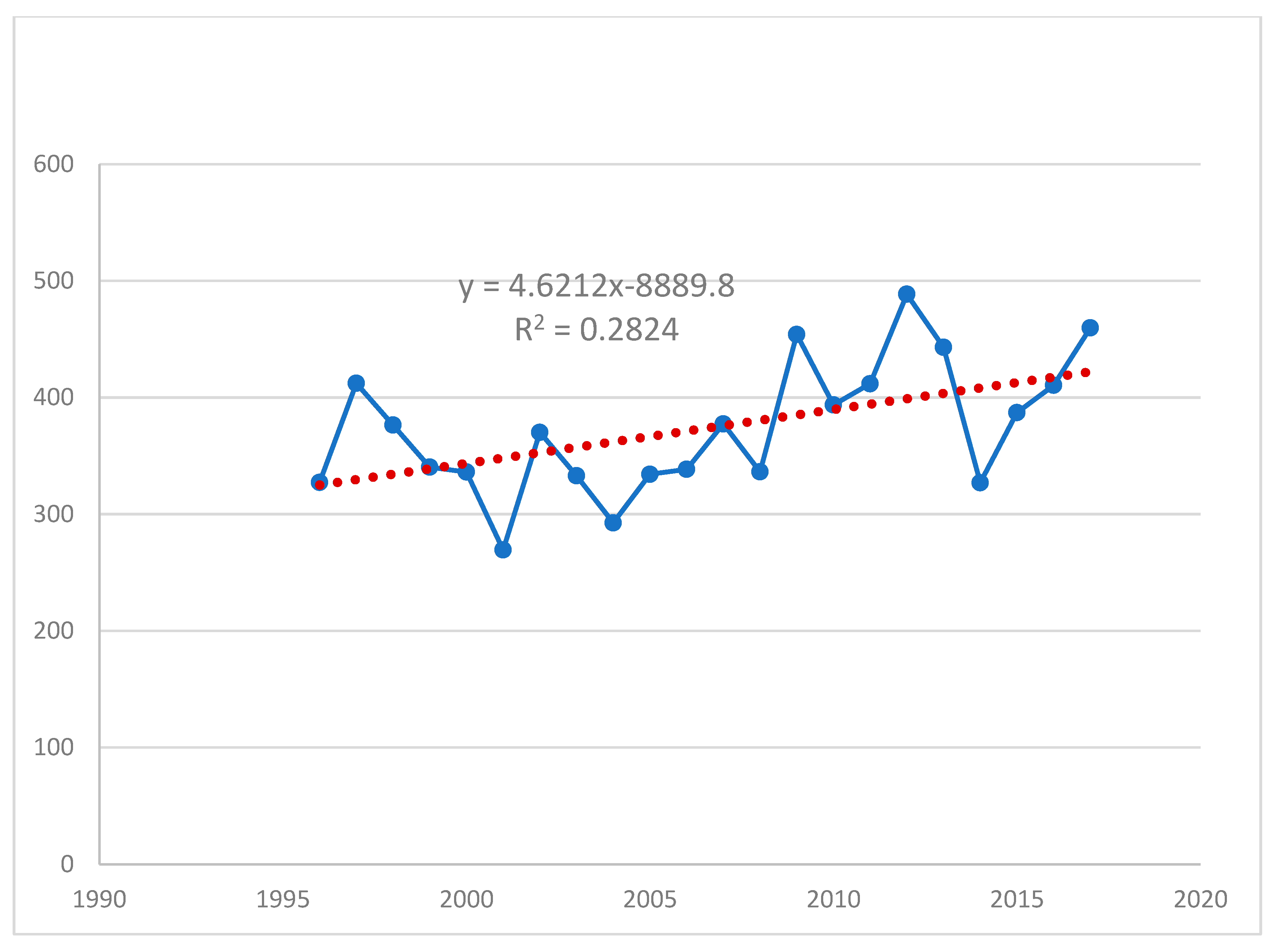
3.1.2. The Trend of Annual Rainfall
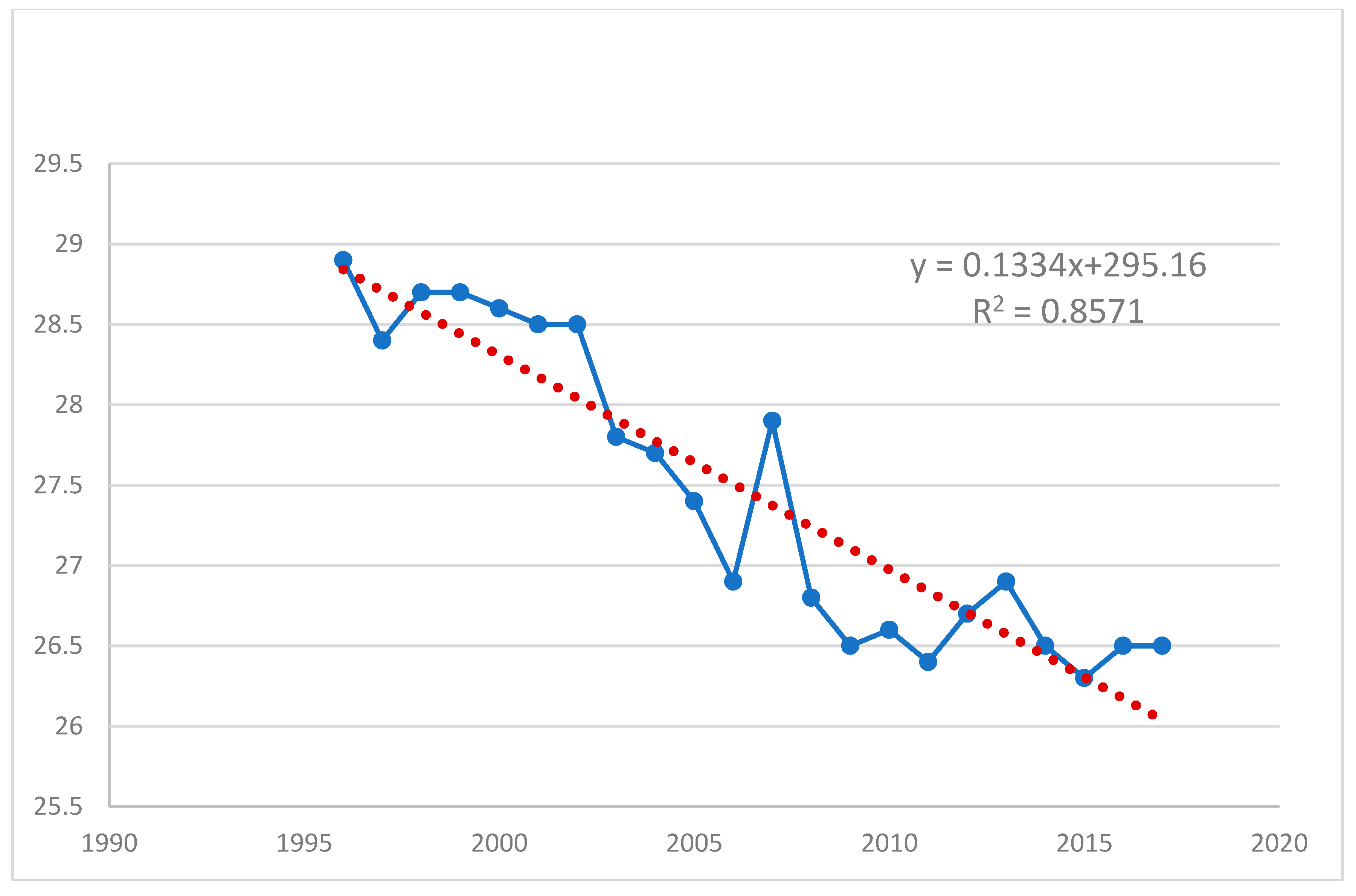
3.1.3. The Trend of Annual Temperature
3.2. Theoretical Overview and Evaluation of the Climate Change Variables on Yam Production
3.2.1. Stationarity and Non-Stationarity of Time Series
3.2.2. Unit Root (Stationarity) Test
3.2.3. Co-Integration Test (Long Term Co-Integrating Relationship)
3.2.4. Johansen Co-Integration Test Result
3.2.5. The Outcome from the Error Correction Model
3.2.6. Post Regression Test
4. Summary and Conclusions
5. Recommendations
- Given the observed adverse effect of temperature on yam production, policymakers need to create an enabling environment for independent researchers as well as institutes to develop pest- and disease-tolerant yam varieties.
- The agricultural policy to support farmers in Nigeria to concentrate more on the bottom-top participatory approach so that the existing and the developing adaptation practices and technologies could be focused at the farm level since the impact of climate change is crop and location-specific.
- The government should take appropriate steps to provide an effective weather forecast system that can facilitate the extension of weather information to local farmers to help them know when to expect temperature increase and thus take necessary adaptation action.
6. Limitations of the Study
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Agwu, Namak, Ifeanyi Nwachukwu, and Cynthia Anyanwu. 2012. Climate variability: Relative effect on Nigeria’s cassava productive capacity. Report Opinion 4: 11–14. Available online: http://www.sciencepub.net/report (accessed on 3 September 2018).
- Akinbobola, Temidayo, Tayo Adedokun, and Philip Nwosa. 2015. The impact of climate change on composition of agricultural output in Nigeria. American Journal of Environmental Protection 3: 44–47. [Google Scholar]
- Angba, Augustine Oko, Hilda Eta, and Cynthia W. Angba. 2018. Knowledge sharing and learning mechanisms for climate change adaptation among key stakeholders of yam and cassava production in cross river state, Nigeria. Journal of Teaching and Education 8: 177–86. [Google Scholar]
- Ater, Peter, and Goodness Aye. 2012. Economic impact of climate change on Nigerian maize sector: A Ricardian analysis. WIT Transactions on Ecology and the Environment 162: 231–39. [Google Scholar] [CrossRef]
- Ayinde, OOpeyemi, Mammo Muchie, and Gabriel Olatunji. 2011. Effect of climate change on agricultural productivity in Nigeria: A co−integration model approach. Journal of Human Ecology 35: 189–94. [Google Scholar] [CrossRef]
- Cerciello, Massimiliano, Massimiliano Agovino, and Antonio Garofalo. 2019. Estimating urban food waste at the local level: Are good practices in food consumption persistent? Economia Politica 36: 863–86. [Google Scholar] [CrossRef]
- Dinar, Ariel, Rashid Hassan, Robert Mendelsohn, and James Benhin. 2008. Climate Change and Agriculture in Africa: Impact Assessment and Adaption Strategies. London: Earthscan, pp. 1–105. [Google Scholar]
- Egbe, Cyprian, Margaret Yaro, Asuquo Okon, and Francis Bisong. 2014. Rural Peoples’ Perception to Climate Variability/Change in Cross River State-Nigeria. Journal of Sustainable Development 7: 25–37. [Google Scholar] [CrossRef]
- Elijah Samuel, Osuafor Ogonna, and Anarah Samuel. 2018. Effects of Climate Change on Yam Production in Cross River State, Nigeria. International Journal of Agriculture and Forestry 8: 104–11. [Google Scholar]
- Enete, Ifeanyi. 2014. Impacts of climate change on agricultural production in Enugu state, Nigeria. Journal of Earth Science & Climatic Change 5: 234. [Google Scholar]
- Eregha, Perekunah, Joseph Babatolu, and Rufus Akinnubi. 2014. Climate change and crop production in Nigeria: An error correction modelling approach. International Journal of Energy Economics and Policy 4: 297–311. [Google Scholar]
- Geospatial Analysis Mapping and Environmental Research Solutions. 2018. Available online: https://www.gamers.com.ng/map-of-cross-river-state-nigeria/ (accessed on 1 April 2020).
- Jalloh, Abdulahi, Gerald Nelson, Timothy Thomas, Robert Zougmore, and Harold Roy-Macauley. 2013. West African Agriculture and Climate Change: A Comprehensive Analysis. Washington: International Food Policy Research Institute, pp. 259–90. [Google Scholar]
- Knox, Jerry, Tim Hess, Andre Daccache, and Tim Wheeler. 2012. Climate change impacts on crop productivity in Africa and South Asia. Environmental Research Letters 7: 8. Available online: http://iopscience.iop.org/article/10.1088/1748−9326/7/3/034032/pdf (accessed on 12 March 2017). [CrossRef]
- Mbanasor, Jude, Ifeanyi Nwachukwu, Nnanna Agwu, and Ndubuisi Onwusiribe. 2015. Impact of climate change on the productivity of cassava in Nigeria. Journal of Agriculture and Environmental Sciences 4: 138–47. [Google Scholar]
- Moreira Campos da Cunha Amarante, Janaina, Tatiana Bach, Wesley Vieira da Silva, Daniela Matiollo, Alceu Souza, and Claudimar Pereira da Veiga. 2018. Econometric analysis of co-integration and causality between market prices toward futures contracts: Evidence from the live cattle market in Brazil. Cogent Business & Management 5: 1457861. [Google Scholar] [CrossRef]
- Natanelov, Valeri, Andrew McKenzie, and Guido Van Huylenbroeck. 2013. Crude oil-corn-ethanol-nexus: A contextual approach. Energy Policy 63: 504–13. [Google Scholar] [CrossRef]
- National Population Commission (NPC). 2011. Census enumeration survey N. P. C. Abuja, Nigeria. Federal Government Statistical Bulletin 2: 6–8. [Google Scholar]
- Nwaobiala, Chioma, and Do Nottidge. 2015. Effect of climate variability on output of cassava in Abia State, Nigeria. Nigeria Agricultural Journal 46: 81–86. [Google Scholar]
- Samuel, Ogalloh, Wandiga Shem, Olago Daniel, and Oriaso Silas. 2017. Impacts of climate variability and climate change on agricultural productivity of smallholder farmers in Southwest Nigeria. International Journal of Scientific & Engineering Research 8: 128–32. [Google Scholar]
- Sarker, Md. Abdur Rashid, Khorshed Alam, and Jeff Gow. 2012. Exploring the relationship between climate change and rice yield in Bangladesh: An analysis of time series data. Agricultural Systems 112: 11–16. [Google Scholar] [CrossRef]
- Tesso, Gutu, Bezabih Emana, and Mengistu Ketema. 2012. A time-series analysis of climate variability and its impacts on food production in North Shewa zone in Ethiopia. African Crop Science Journal 20: 261–74. [Google Scholar]
- Thomas-Hope, Elizabeth. 2017. Climate Change and Food Security: Africa and the Caribbean. Amsterdam: Routledge, pp. 1–112. [Google Scholar]
- Verter, Nahanga, and Věra Bečvářová. 2015. An Analysis of Yam Production in Nigeria. Acta Universitatis Agriculturae et Silviculturae Mendelianae Brunensis 63: 659–65. [Google Scholar] [CrossRef]
- Wang, Dan, Yu Hao, and Jianpei Wang. 2018. Impact of climate change on China’s rice production—An empirical estimation based on panel data (1979–2011) from China’s main rice-producing areas. The Singapore Economic Review 63: 535–53. [Google Scholar] [CrossRef]
- Zhang, Rongmao, Peter Robinson, and Qiwei Yao. 2019. Identifying co−integration by eigenanalysis. Journal of the American Statistical Association 114: 916–27. [Google Scholar] [CrossRef]
| Variables | @ Level | 1st Difference | Decision | ||||
|---|---|---|---|---|---|---|---|
| ADF Statistics | p-Value | Order of Integration | ADF Statistics | p-Value | Order of Integration | ||
| Yam output | −2.262092 | 0.4335 | I(1) | −2.576955 | 0.2927 | I(1) | Non-stationary |
| Rainfall | −3.526359 | 0.0623 | I(1) | −4.725198 | 0.0069 *** | I(0) | Stationary |
| Temperature | −3.000557 | 0.1550 | I(1) | −4.583192 | 0.0091 *** | I(0) | Stationary |
| Hypothesized No. of CE(s) | Eigenvalue | Trace Statistic | 0.05 Critical Value | Prob. |
|---|---|---|---|---|
| None * | 0.749 | 56.98 | 47.856 | 0.005 |
| At most 1 * | 0.562 | 30.72 | 29.797 | 0.039 |
| At most 2 | 0.444 | 15.04 | 15.495 | 0.068 |
| At most 3 * | 0.184 | 3.881 | 3.841 | 0.048 |
| Variable | Coefficient | Std. Error | t-Statistics | Prob. |
|---|---|---|---|---|
| C | 14.428 | 3.553 | 4.060 | 0.000 |
| LOG(AVRAINFALL) | 0.150 | 0.149 | 1.010 | 0.326 |
| LOG(AVTEMP) | −3.420 | 0.991 | −3.452 | 0.003 |
| R-Squared | 0.981 | Mean dependent variable | 7.730 | |
| Adjusted R-Squared | 0.979 | S.D. dependent variable | 0.550 | |
| SE of Regression | 0.080 | Akaike info criterion | −2.047 | |
| Sum Squared Residual | 0.116 | Schwarz criterion | −1.848 | |
| Log-Likelihood | 26.512 | Hannan–Quinn criterion | −1.999 | |
| F-Statistic | 323.743 | Durbin–Watson statistic | 1.188 | |
| Prob(F-Statistic) | 0.000 | |||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| ECM(−1) | −0.779 | 0.231 | −3.372 | 0.003 |
| D(ECM(−1)) | 0.353 | 0.204 | 1.729 | 0.100 |
| R-Squared | 0.386 | Mean dependent variable | 0.003 | |
| Adjusted R-Squared | 0.352 | S.D. dependent variable | 0.079 | |
| SE of Regression | 0.063 | Akaike info criterion | −2.572 | |
| Sum Squared Residual | 0.073 | Schwarz criterion | −2.472 | |
| Log-Likelihood | 27.72 | Hannan–Quinn criterion | −2.552 | |
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| C | 0.012 | 0.023 | 0.552 | 0.588 |
| DLOG(AVRAINFALL) | 0.119 | 0.104 | 1.140 | 0.271 |
| DLOG(AVTEMP) | −2.875 | 1.159 | −2.479 | 0.025 ** |
| ECM(−1) | −0.477 | 0.269 | −1.771466 | 0.0955 * |
| R-Squared | 0.405 | Mean dependent variable | 0.064 | |
| Adjusted R-Squared | 0.256 | S.D. dependent variable | 0.085 | |
| SE of Regression | 0.073 | Akaike info criterion | −2.181 | |
| Sum Squared Residual | 0.086 | Schwarz criterion | −1.933 | |
| Log-Likelihood | 27.909 | Hannan–Quinn criterion | −2.128 | |
| F-Statistic | 2.718 | Durbin–Watson statistics | 1.287 | |
| Prob(F-Statistic) | 0.067 | |||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
|---|---|---|---|---|
| C | 0.018701 | 0.019414 | 0.963238 | 0.3518 |
| DLOG(AVRAINFALL) | −0.034880 | 0.081811 | −0.426342 | 0.6763 |
| DLOG(AVTEMP) | 0.118822 | 0.900055 | 0.132016 | 0.8968 |
| ECM(−1) | −1.274533 | 0.451685 | −2.821732 | 0.0136 |
| RESID(−1) | 1.673803 | 0.482709 | 3.467521 | 0.0038 |
| RESID(−2) | 0.387120 | 0.312556 | 1.238562 | 0.2359 |
| R-squared | 0.476140 | Mean dependent variable | 7.23 × 10−18 | |
| Adjusted R-squared | 0.251629 | SD dependent varvariable | 0.065641 | |
| SE of Regression | 0.056785 | Akaike info criterion | −2.637900 | |
| Sum Squared Residual | 0.045143 | Schwarz criterion | −2.289726 | |
| Log-Likelihood | 34.69795 | Hannan–Quinn criterion | −2.562337 | |
| F-Statistic | 2.120784 | Durbin–Watson statatistic | 1.762265 | |
| Prob(F-Statistic) | 0.115641 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angba, C.W.; Baines, R.N.; Butler, A.J. Examining Yam Production in Response to Climate Change in Nigeria: A Co-Integration Model Approach. Soc. Sci. 2020, 9, 42. https://doi.org/10.3390/socsci9040042
Angba CW, Baines RN, Butler AJ. Examining Yam Production in Response to Climate Change in Nigeria: A Co-Integration Model Approach. Social Sciences. 2020; 9(4):42. https://doi.org/10.3390/socsci9040042
Chicago/Turabian StyleAngba, Cynthia W., Richard N. Baines, and Allan J. Butler. 2020. "Examining Yam Production in Response to Climate Change in Nigeria: A Co-Integration Model Approach" Social Sciences 9, no. 4: 42. https://doi.org/10.3390/socsci9040042
APA StyleAngba, C. W., Baines, R. N., & Butler, A. J. (2020). Examining Yam Production in Response to Climate Change in Nigeria: A Co-Integration Model Approach. Social Sciences, 9(4), 42. https://doi.org/10.3390/socsci9040042





