4.1. Efficiency of the State Maritime Policy
This article is devoted to the development and substantiation of theoretical/methodological and scientific/practical approaches to the formation of measures of efficiency in the maritime sector. The implementation of effective business models of sustainable development in seaports is aimed at maximizing the creation of the joint value at the macro and micro levels of the economy. The list of factors contributing to the efficiency of the state maritime policy was defined and separated into four groups: group 1 (infrastructural factors): Renewal of port infrastructure; coastal infrastructure of sea stations; ecological and physical safety; and convenience in reaching the port of departure by a cruise ship; group 2 (management factors): The effectiveness of management mechanisms; the level of automation and effective communications technologies; the coordination of various types of transport; and the efficiency of port services; group 3 (marketing factors): Tariff policies (size of tariffs, number of port fees, flexibility of price policy); and competition in the ports; group 4 (service factors): Attractiveness of logistics conditions; the development of international tourism; the development of sea leisure; the development of merchant shipping, shipbuilding, ship repair, and instrument making in the port; and the simplification of port entry procedures.
It has been established that the development the maritime business model at the macroeconomic level in state maritime policy has the following sequence: The desire to participate in global value added chains, which is ensured by the production of high-tech products in the areas of port processing and the provision of high-tech services with high added value; the introduction of complex measures of protectionism and free trade and dependence on the availability of national competitive advantages of the marine port industry for influencing the infrastructure, superstructure, and economic structure of the state maritime policy of Ukraine; and the creation of business models of seaports by basic types (creator, distributor, owner (landlord), broker (broker)) and depending on port type (land feudal lord, tool port, service port). At the same time, the following priorities of building a business model appear: An increase in the amount of taxes paid and the level of employment of the population; an increase in cargo turnover; improvement of the quality of transport services; and an increase in the number of tourists. Consideration of the following complementary assets as the basis for port business model development is suggested: Specialization (reputation, brand, formed clusters, distribution networks, experience and qualifications of experts, expertise, port society, information bases) and generalization (infrastructure, equipment, control facilities (customs processing)), computer systems and automation systems, social networks, ERP-networks, and agreements with state institutions and local self-government bodies). Monitoring of a business model’s performance at the macro and micro level should be carried out with information and analytical support to prevent the overall risk of bankruptcy of seaports (with the construction of a risk map). Qualitative and quantitative monitoring takes into account the interests of stakeholders in the maritime industry and is based on the creation of added value in port services as the basis for the shared value of the well-being of all stakeholders.
4.2. The Joint Value as a Measure of the Welfare of Stakeholders in the Maritime Industry
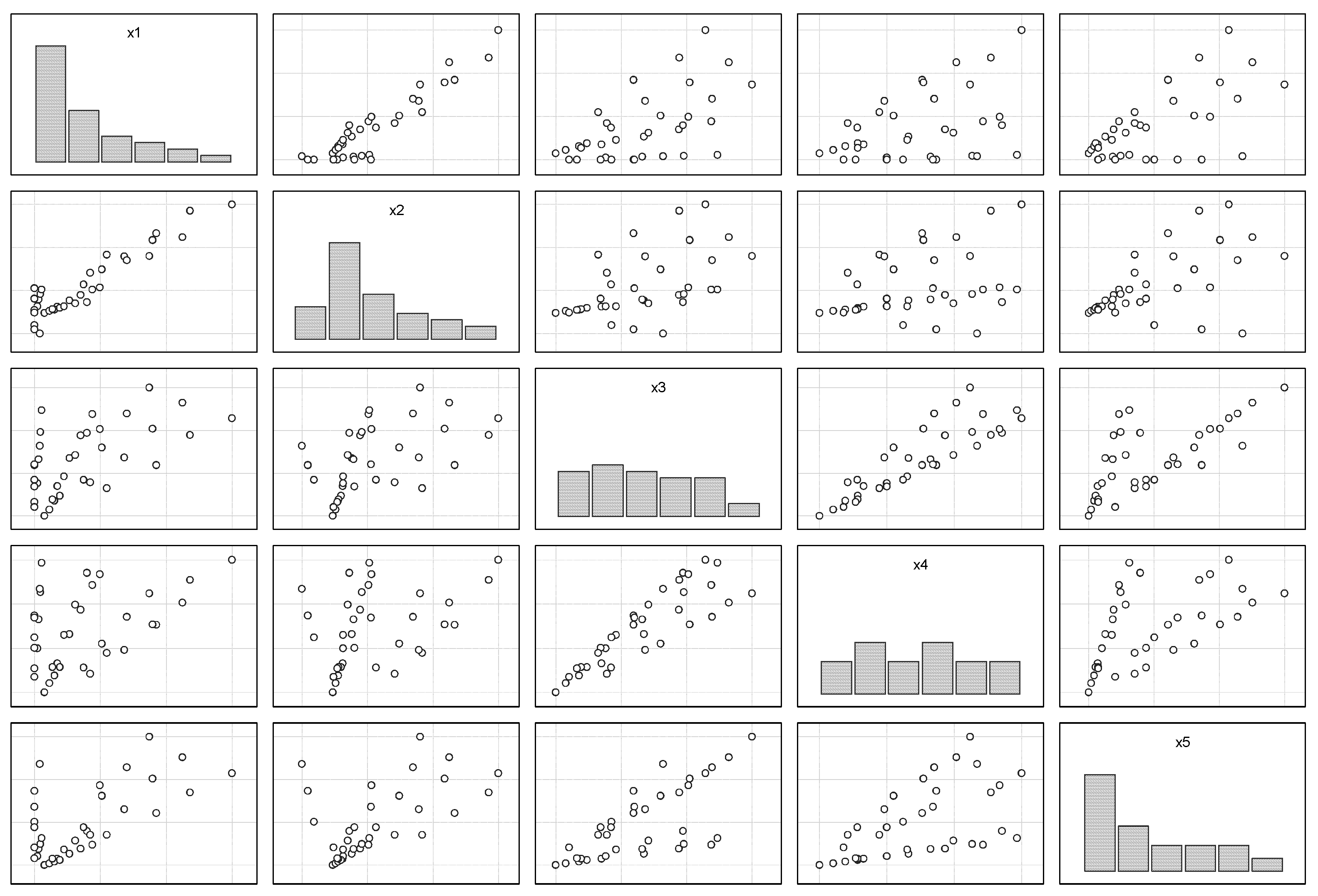
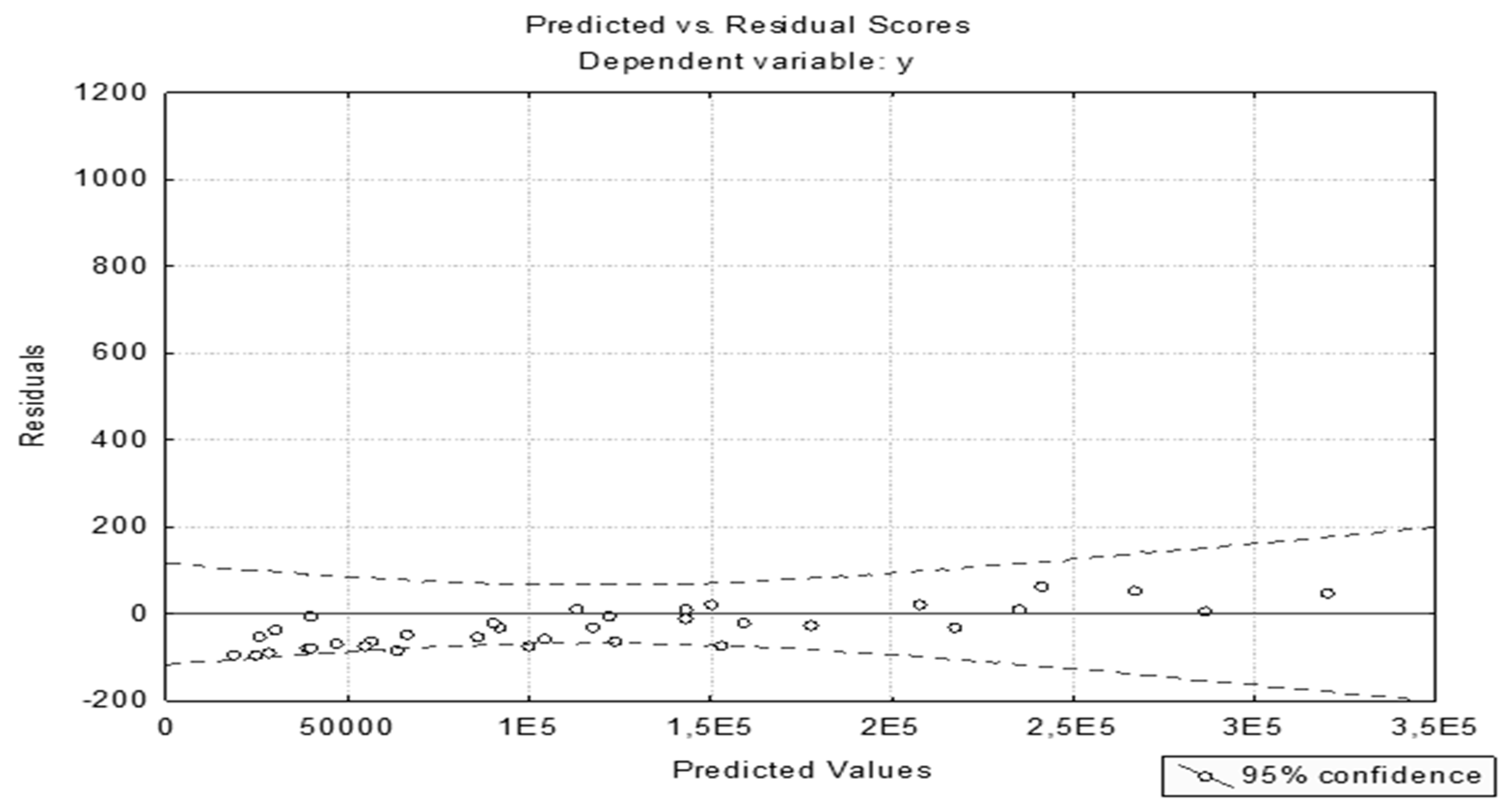
The joint value was considered to be a category at both a macroeconomic and microeconomic level, and it was combined with a multivariate regression model performed on the basis of statistical analysis and data processing system Statistics 8.0. The extrapolated data of the independent variables of the multifactor linear model of joint value created in the maritime industry field allowed us to proceed to the extrapolation process of the resulting indicator. The results of the approximation process, extrapolation, and the values of the upper and lower bounds of the confidence interval of the resulting indicator are presented in the Statistica 8.0 tool.
In the course of the calculations, an adequate multifactorial linear model of the joint value created in the marine port sector was obtained. The value of the determination coefficient indicated that the model explained 99.9937% of the total dispersion of its resulting value of the total value of the seaport services. For further investigation into the influence of objective and subjective indicators on the indicator of the joint value of the seaport services, we decided to use a method of expert evaluation, namely the method of analysis of hierarchies.
Using the hierarchy analysis method in the process of evaluating the common value of maritime merchant port services could allow for its decomposition into simple components, prioritizing each and evaluating the level of their interactions with the resulting indicator based on judgments and expert assessments (since they would be substantiated and supported by their experience), which would fill the information gap in the data analysis and significantly reduce the risk of ineffective management decisions regarding the operation of the maritime industry in Ukraine, especially at the macro level.
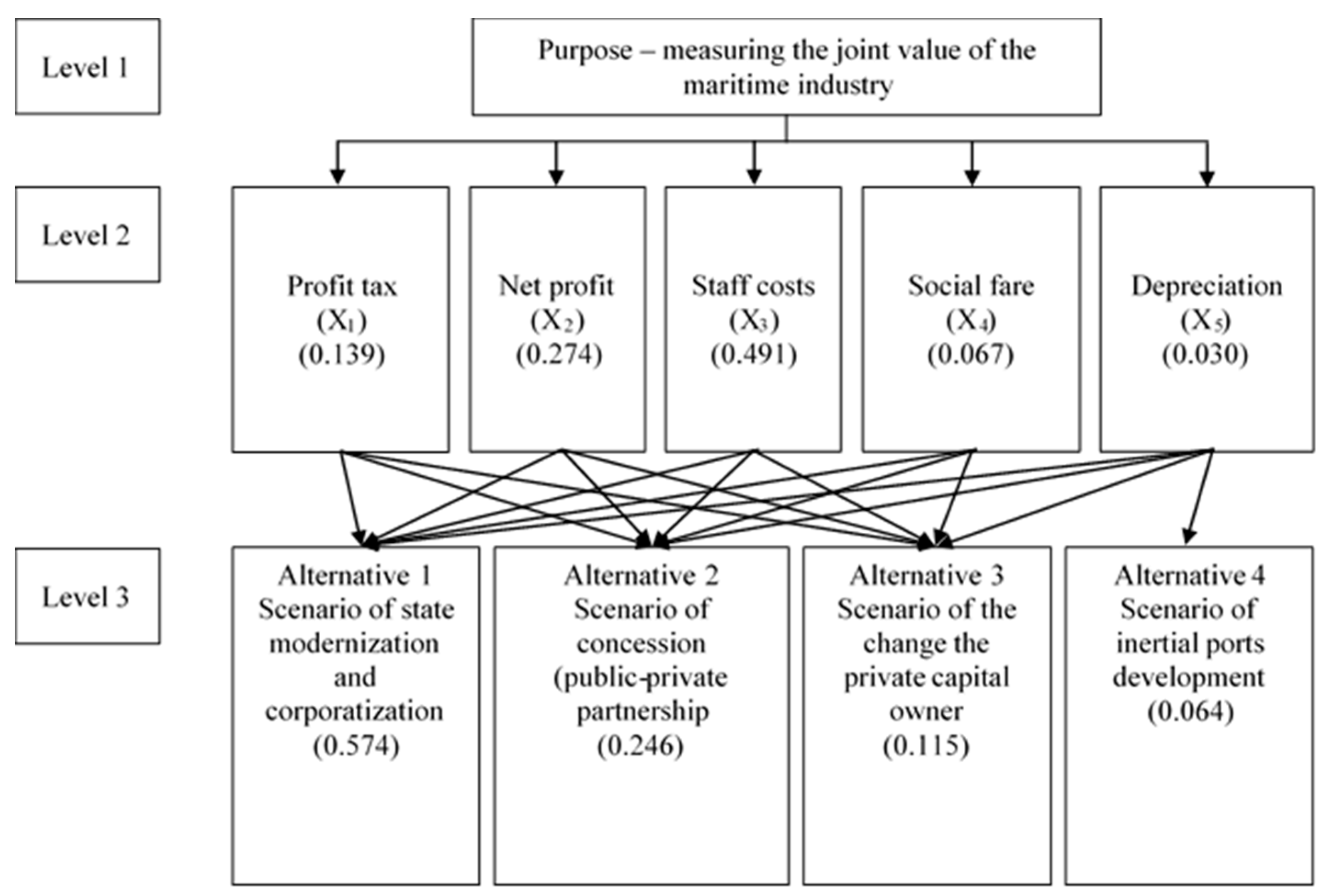
In the first step, the process of evaluating the joint value of the maritime trading port services in the form of a hierarchy and determining all elements of each level was performed. The first level of the hierarchical model for assessing the total value of the services of the sea trading port consisted of a single element, namely “The purpose is to assess the joint value of the services of the sea trading port”.
The elements of the second level were the independent variables of the multifactor linear model of joint value created in the maritime industry, since the relevance of using previous results in the study of the assessment of the joint value of the services of a maritime trading port had already been proven.
4.3. Scenarios of Sea Trade Port Industry Development
Based on the results of the fundamental analysis, structural modeling, and synthesis of approaches to business model development, the business model of the seaport was presented as a mechanism for generating a joint value for all stakeholders, considered through optimizing a logically complete set of economic relations within the framework of modeling the development and implementation of the business model. The results of the aggregate economic relations of stakeholders (the state, investors, owners, contractors of ports, the population of the port region, regular workers, invited specialists) within the framework of developing and implementing a business model were the following:
Alternative 1: A scenario of state modernization and corporatization;
Alternative 2: A scenario for managing the seaport as a concession (public–private partnership);
Alternative 3: A scenario for changing the owner of the port subject to attracting private capital; and
Alternative 4: A scenario of inertial development of the port provided there is stagnation in the macroeconomic environment.
The presented alternatives for assessing the total value of the services of the sea trading port were based on the obtained forecast values and the confidence intervals of the independent variables of the multifactor linear model of joint value created in the maritime port sector.
At the third level of the hierarchical model for assessing the joint value of the maritime merchant port services, the above alternatives are presented.
Graphic representation of the hierarchical model for assessing the joint value of the maritime industry is shown in
Figure 3.
The next step in working with the hierarchical model for evaluating the joint value of seaport services was to identify local priorities and assess the consistency of judgments.
Using the method of pairwise comparisons, we defined the following indicators: Priorities of the second-level criteria relative to the main goal and priorities of alternatives (scenarios of development) in relation to the second-level criteria.
To this end, we constructed the necessary matrices for pairwise comparisons. For each matrix, we defined the normalized priority vector, the maximal real number, the index, and the relation of the coherence.
The matrix of pairwise comparisons and the estimates of the priorities of the second-level elements in relation to the main goal obtained in its background are given in
Table 5.
The components of its own vector of local priorities are calculated by the formulas
where
—
is an element of the matrix column of the pairwise criteria comparison and
is the number of criteria, and
Corresponding calculations for the second-level hierarchical model for assessing the value of seaports were as follows:
The maximal proper value of the inverse-symmetric matrix of pairwise comparisons was determined by the following formula:
For elements of the second level of the hierarchical model of estimating the joint value of seaport industry services, we defined the following:
The coherence (homogeneity) of the matrices, which reflects the imitation of an expert’s logic in expressing his own judgments, is quite important in the process of constructing matrices of pairwise comparisons.
As an indicator of the degree of consistency of the elements of the matrix of pairwise comparisons, a homogeneity index (index of coherence) was used. It was calculated by the formula
To assess the acceptability of the degree of consistency of the matrix elements, the ratio of homogeneity (consistency), which was calculated by the following formula, was used:
where
is the average value of the homogeneity index of a randomly composed matrix of pairwise comparisons, based on experimental data (for
the table meaning equals
).
It was acceptable for further use of the obtained matrices of pairwise comparisons to be the value of the homogeneity relation (consistency), which was less than or equal to 0.1, (that is, ). The excess of the index of homogeneity (coherence) of the value of 0,1 indicated a significant violation of the logic of judgments, which the expert assumed when filling matrices of pairwise comparisons, so the expert should be asked to revise the data to improve this indicator. The result of the matrix of pairwise comparison of elements of the second level did not exceed a value of 0.1, which testified to the loyalty of the judgment logic of the research expert and the possibility of its use in subsequent calculations of the hierarchical model for evaluating the joint value of the services of the sea trading port.
In the next stage, we filled in matrices of pairwise comparisons for the third-level elements (alternatives) of the hierarchical model for assessing the total value of the services of sea merchant ports according to all of the criteria of the second level, and we determined their local priorities. The matrices of pairwise comparisons of elements of the third level according to all of the criteria of the second level of the hierarchical model for assessing the total value of services in the maritime industry are presented in
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10.
On the basis of the obtained results, we used the synthesis principle to determine the global priorities of the third-level elements. They were defined as the sum of applications of the local priorities of each element at the third level to the global priorities of the second-level elements of the hierarchical model for evaluating the joint value of the services of the maritime industry:
where
is the local priority of the
element of the third level in relation to the
element of the second level.
For the submitted alternatives at the third level of the hierarchical model for assessing the joint value of the services of the maritime industry of Ukraine:
The complex combination of results from the multifactor linear model of joint value created in the maritime port sector and the hierarchical model for assessing the joint value of the maritime merchant port services allowed us to obtain a calculated confirmation of the best further alternative for developing the port industry in Ukraine: Namely, a scenario of state modernization and corporatization.