Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review
Abstract
:1. Introduction
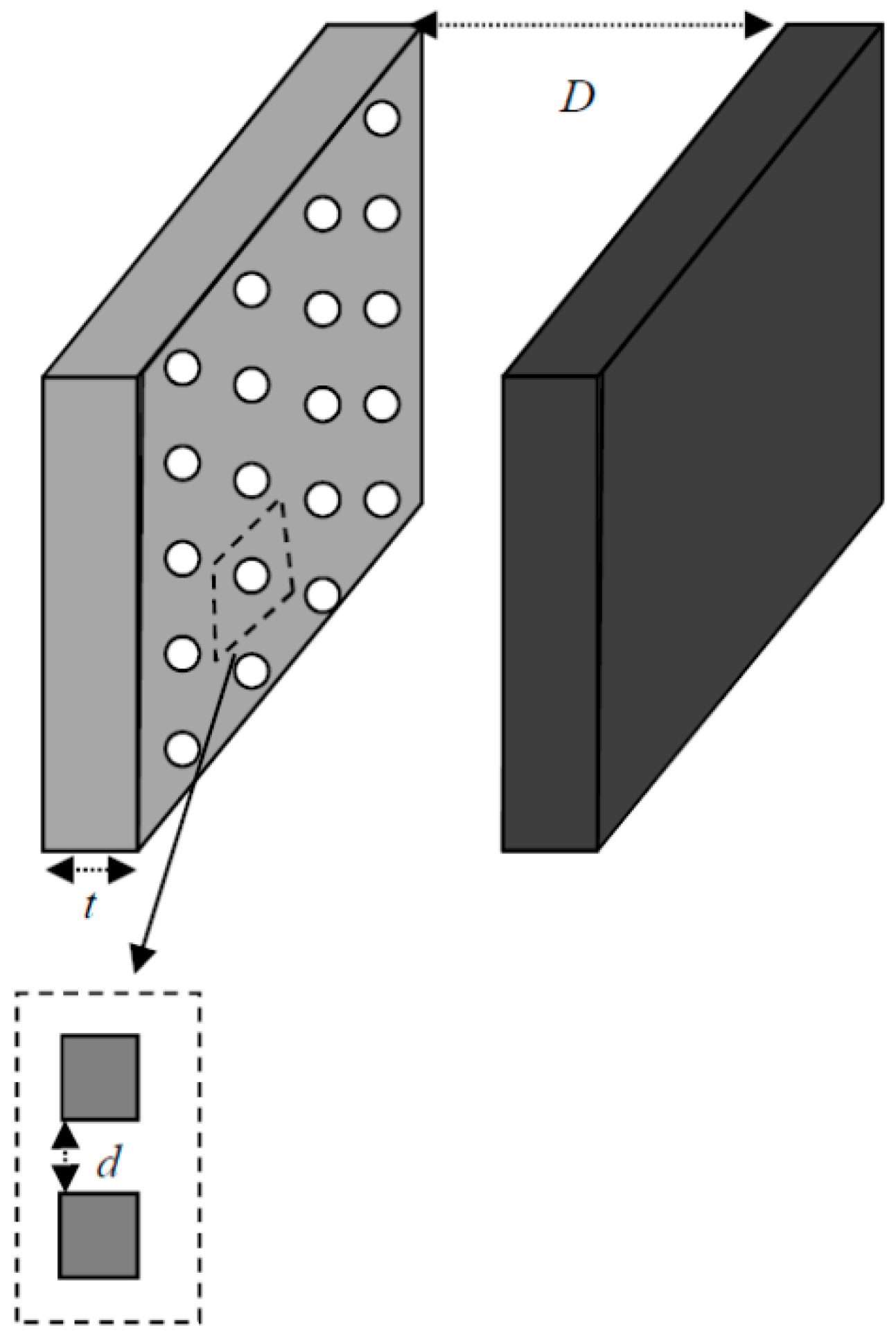
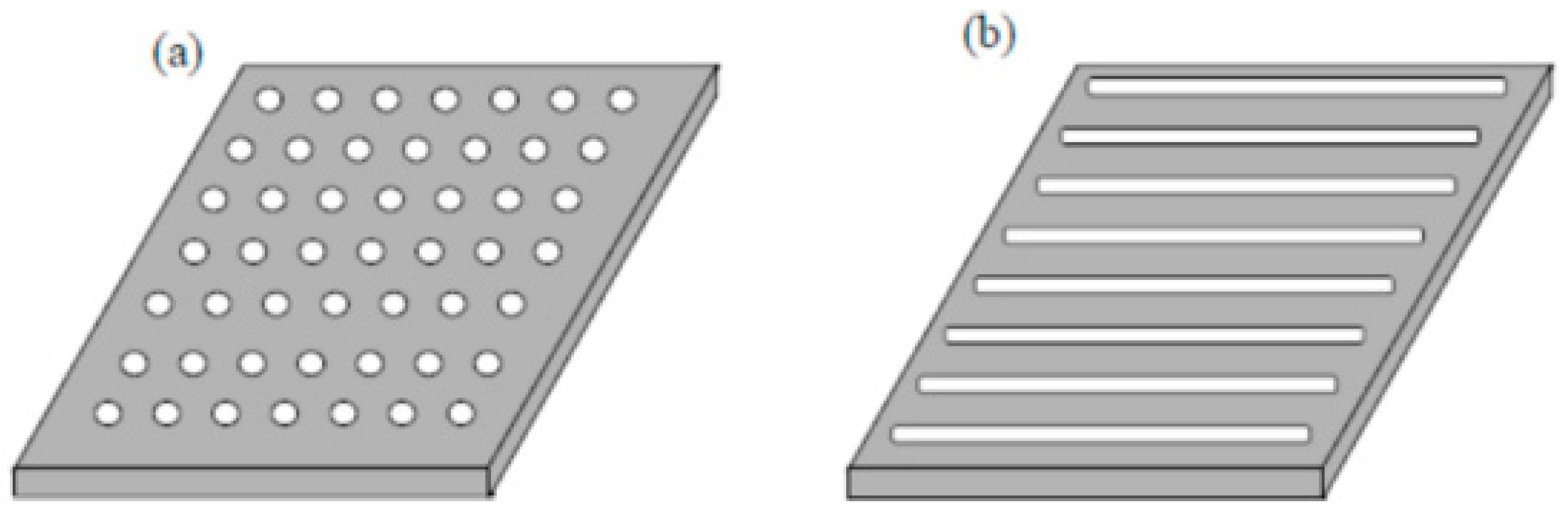
2. SL-MPP
- The visco-thermal dissipation within the holes, Zhole.
- The distortion of flow in the perforation edges, Zedge.
- The resonances in the air cavity, Zc.
- The structural vibrations of the panel, Zvib.
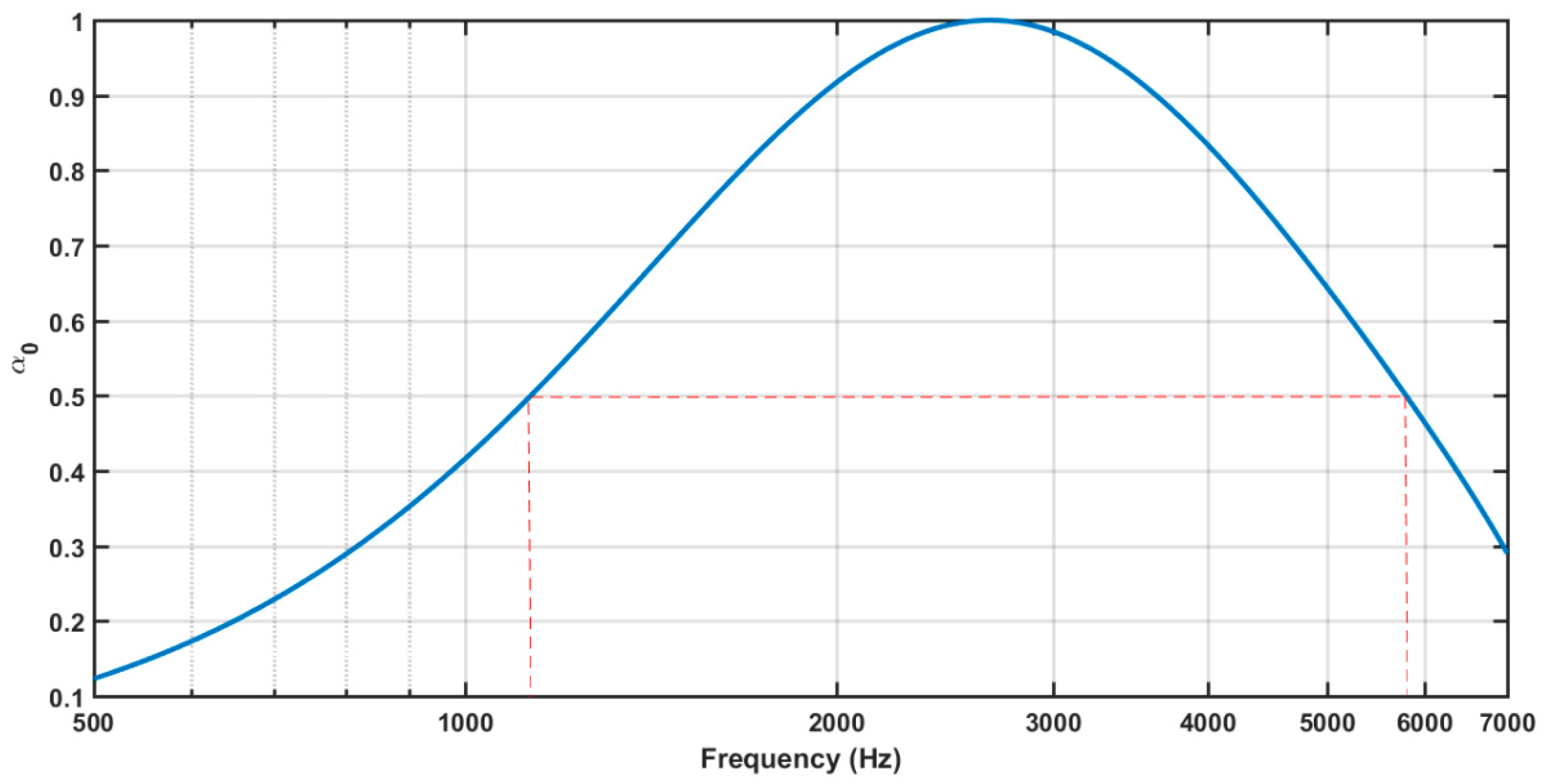
2.1. Maa Model
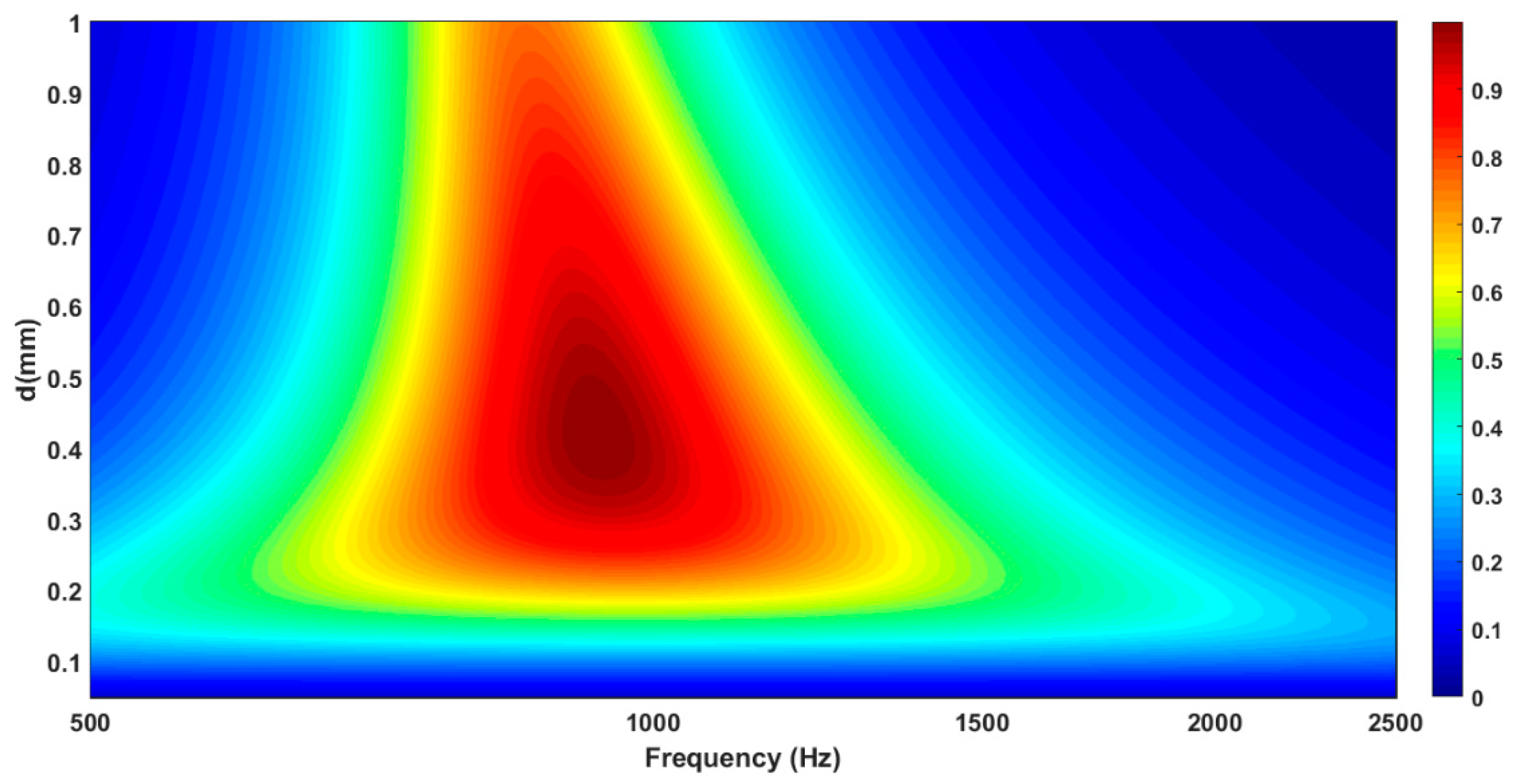
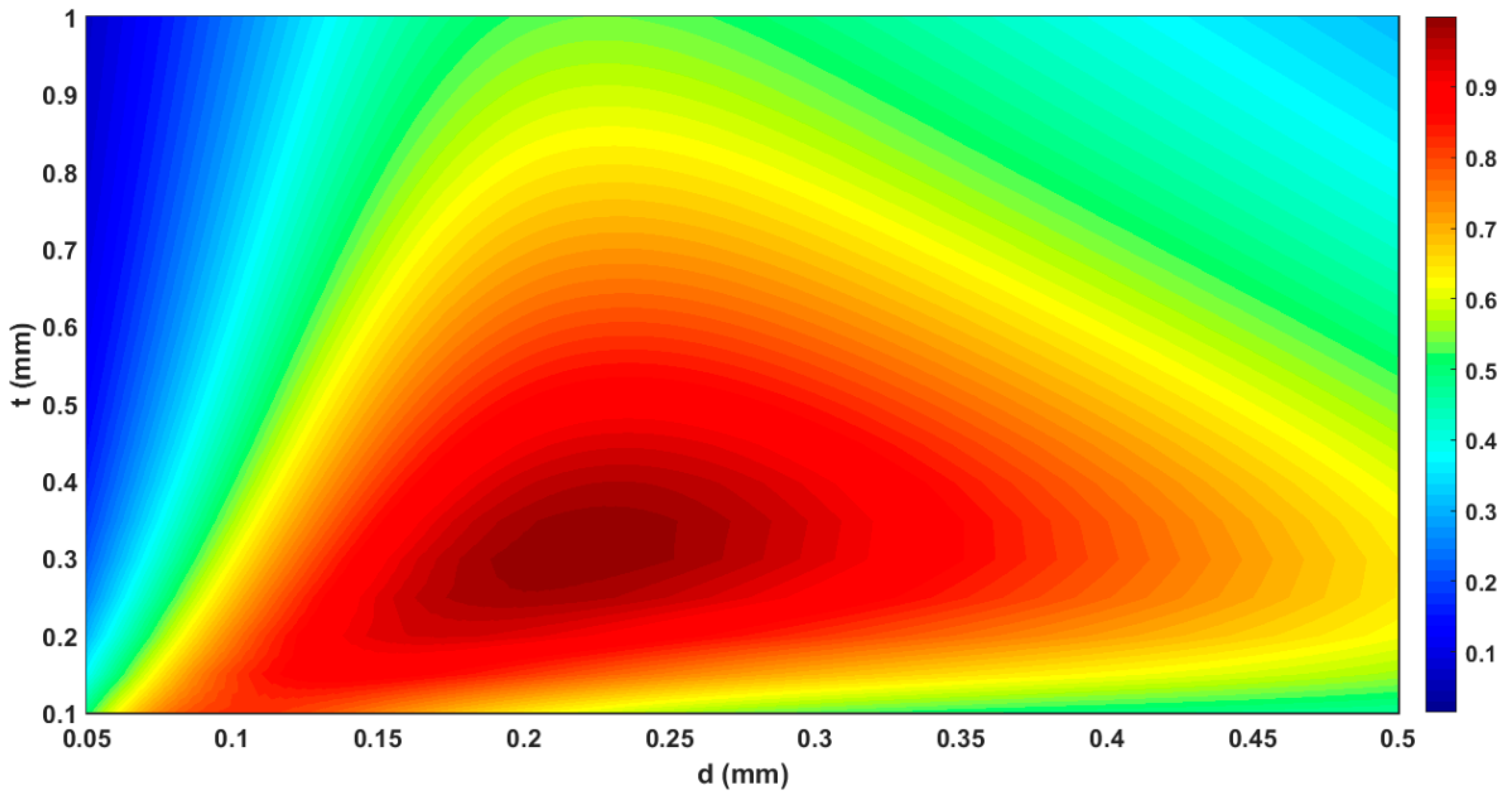
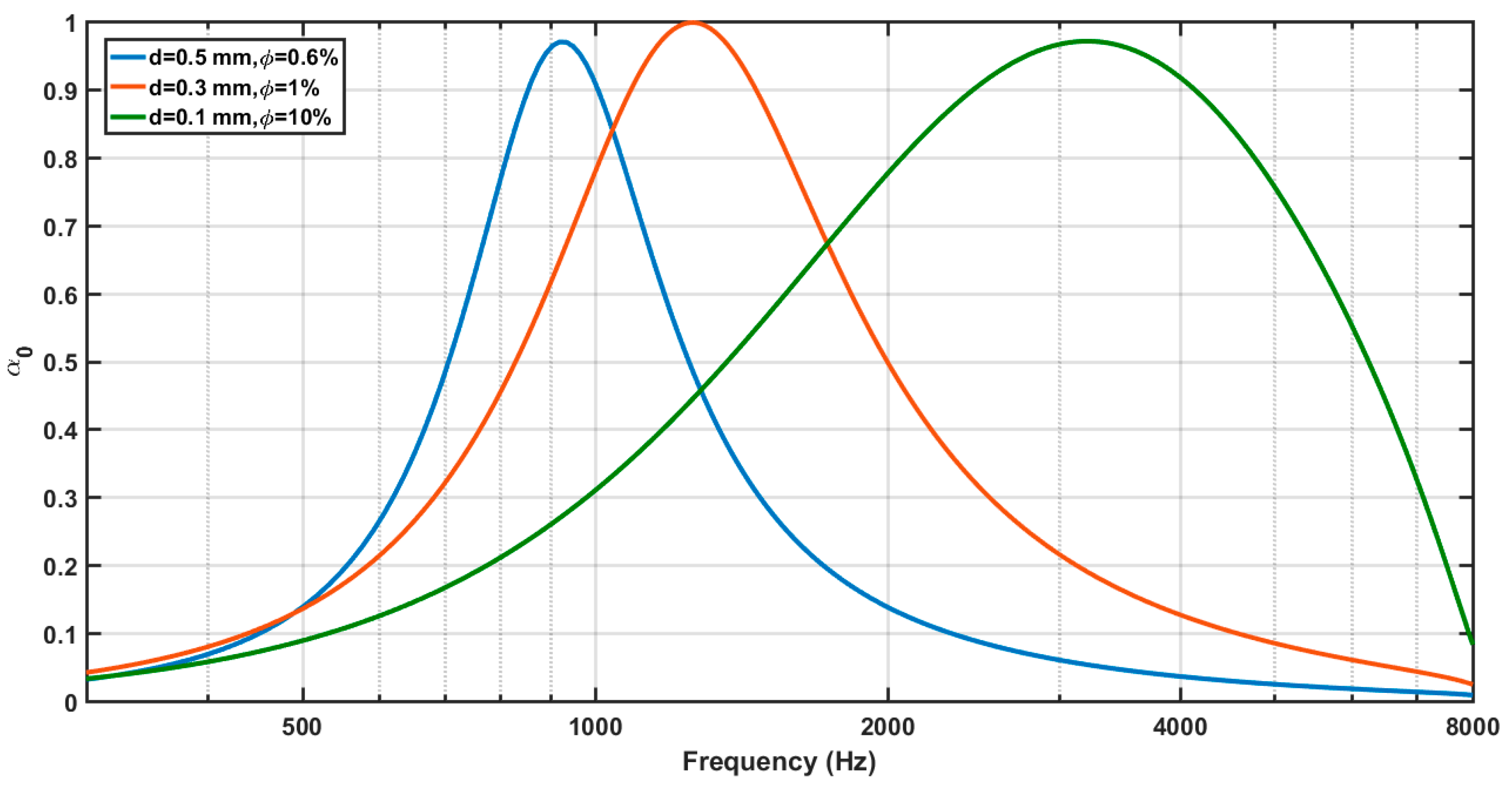
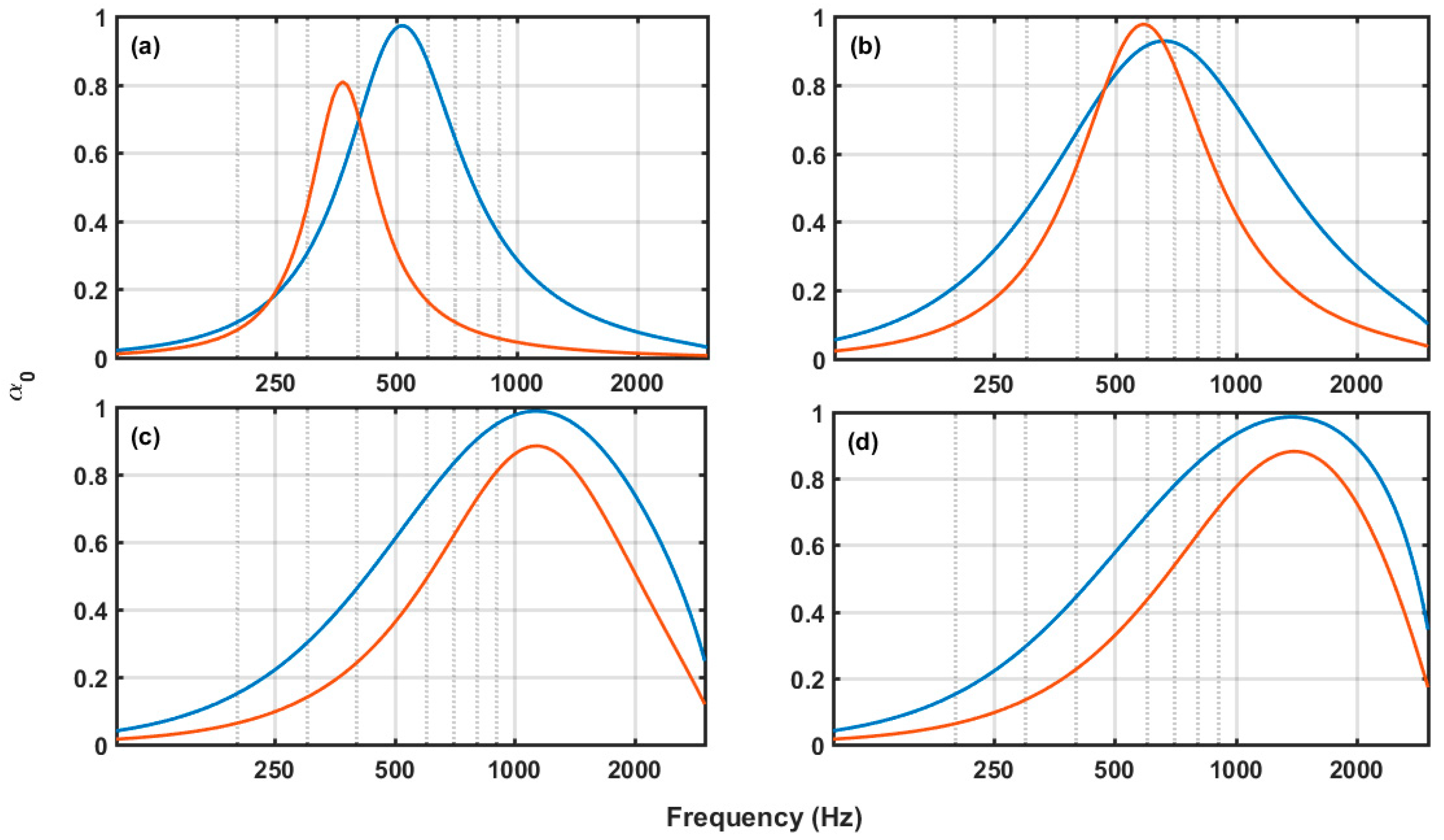
- For each combination of (t,ϕ,D), there exists a value of d providing maximum absorption (Figure 6). Furthermore, the absorption bandwidth increases as d decreases.
- For each combination of (d,ϕ,D), there is a value of t yielding maximum absorption (Figure 7). The absorption curve moves towards higher (lower) frequencies as t decreases (increases).
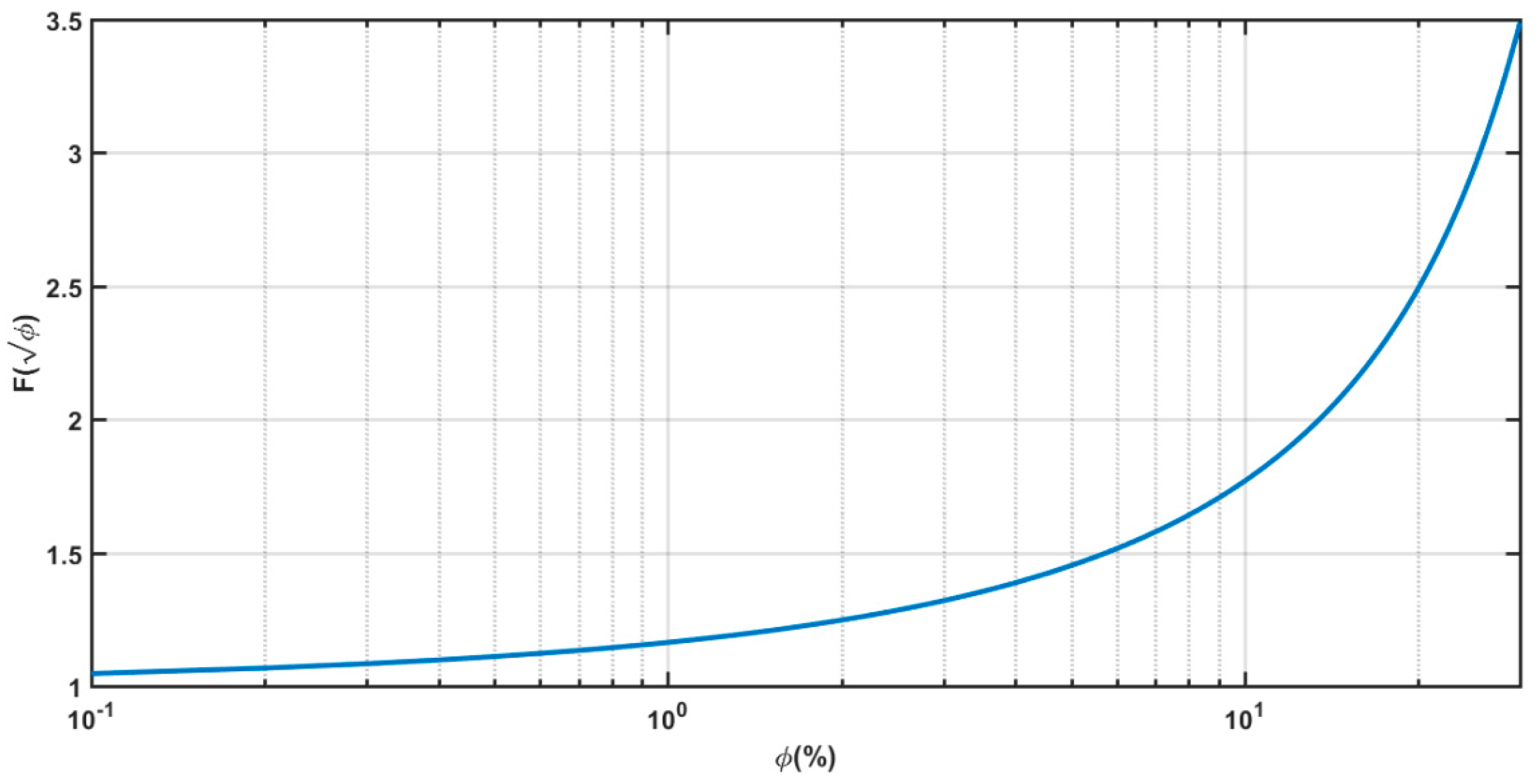
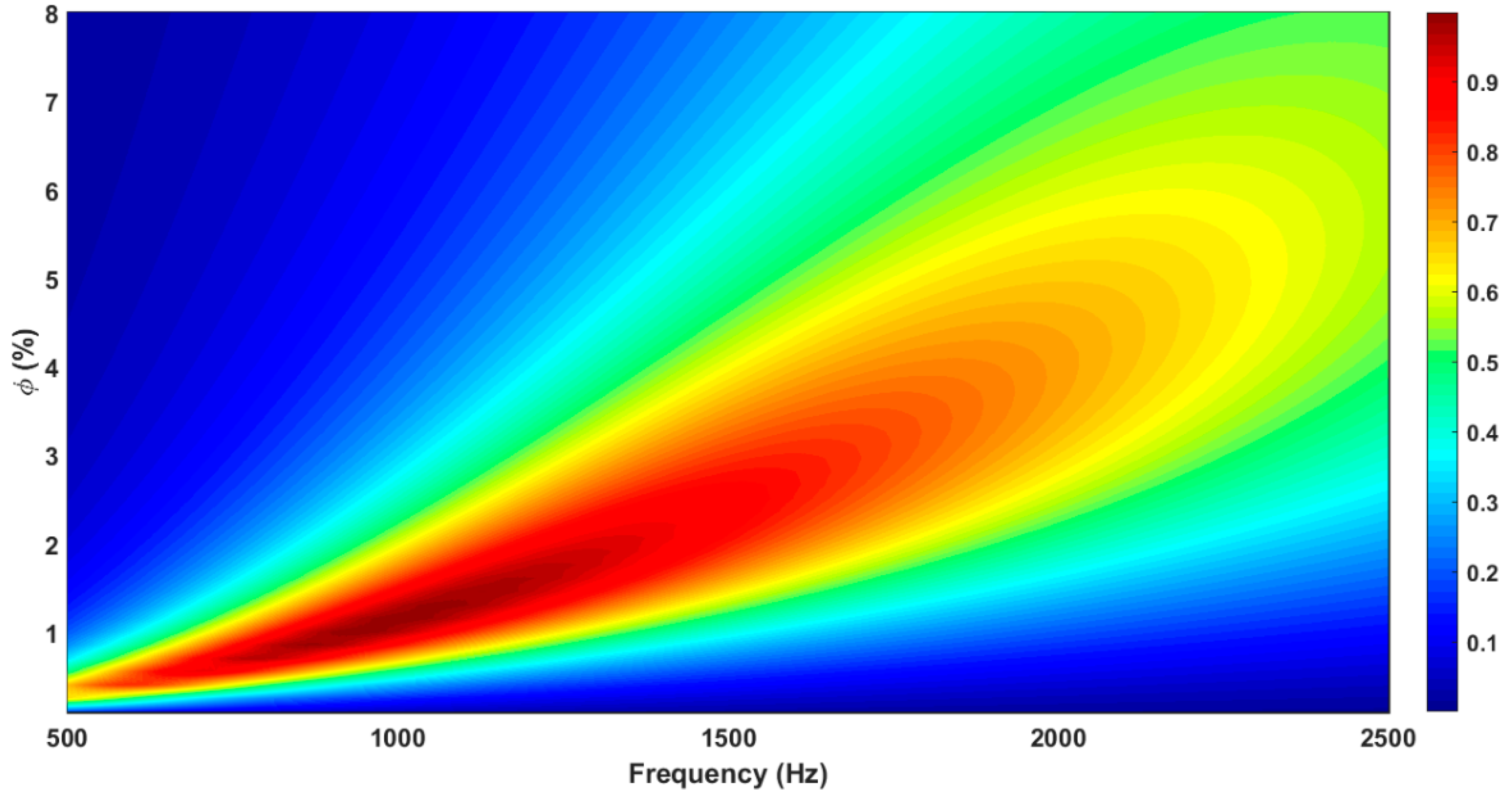
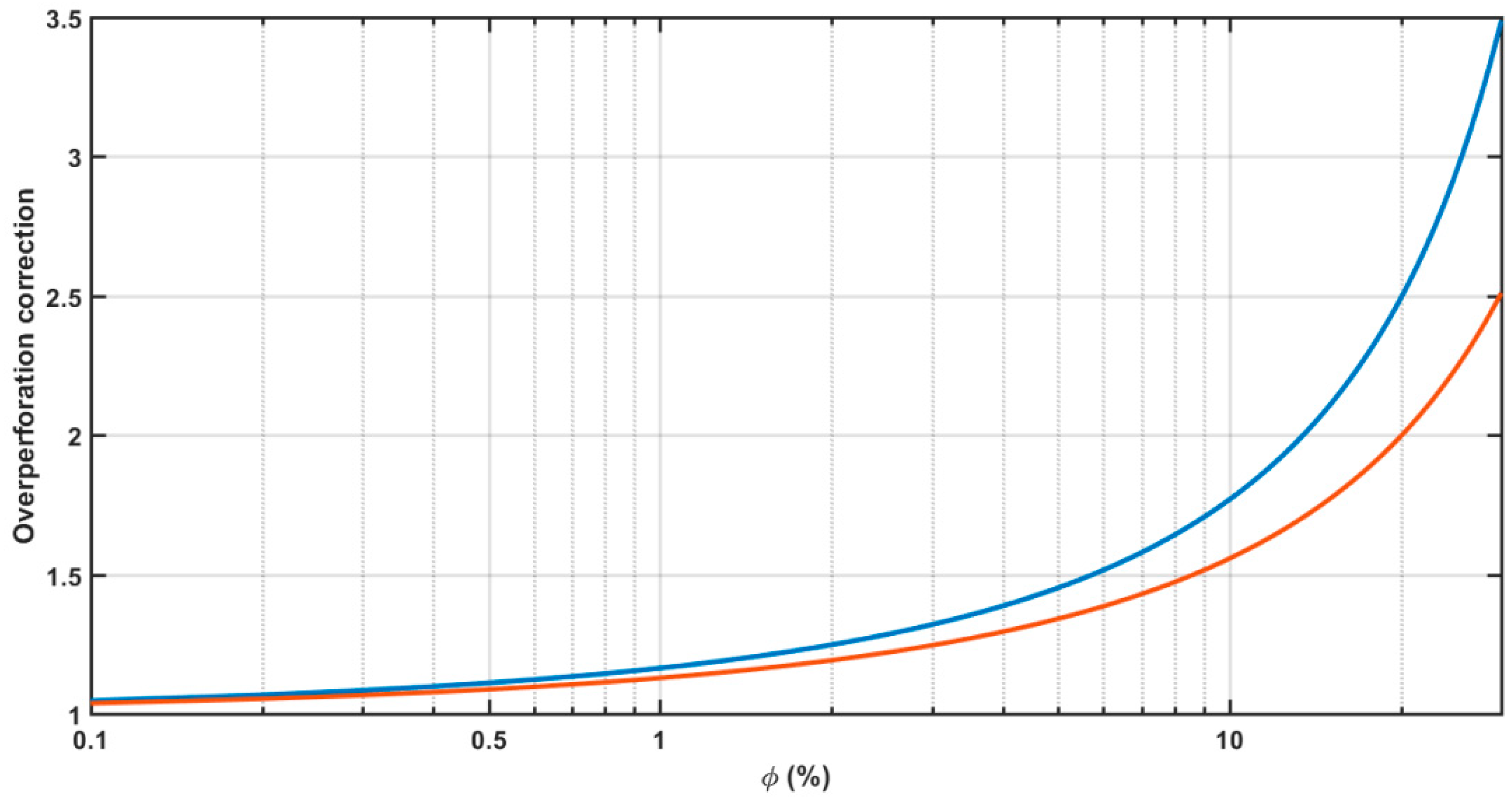
- Keeping constant the combination of parameters (d,t,D), there is a value of ϕ affording maximum absorption (Figure 8). The absorption curve moves towards higher frequencies, and the absorption bandwidth increases as ϕ increases.
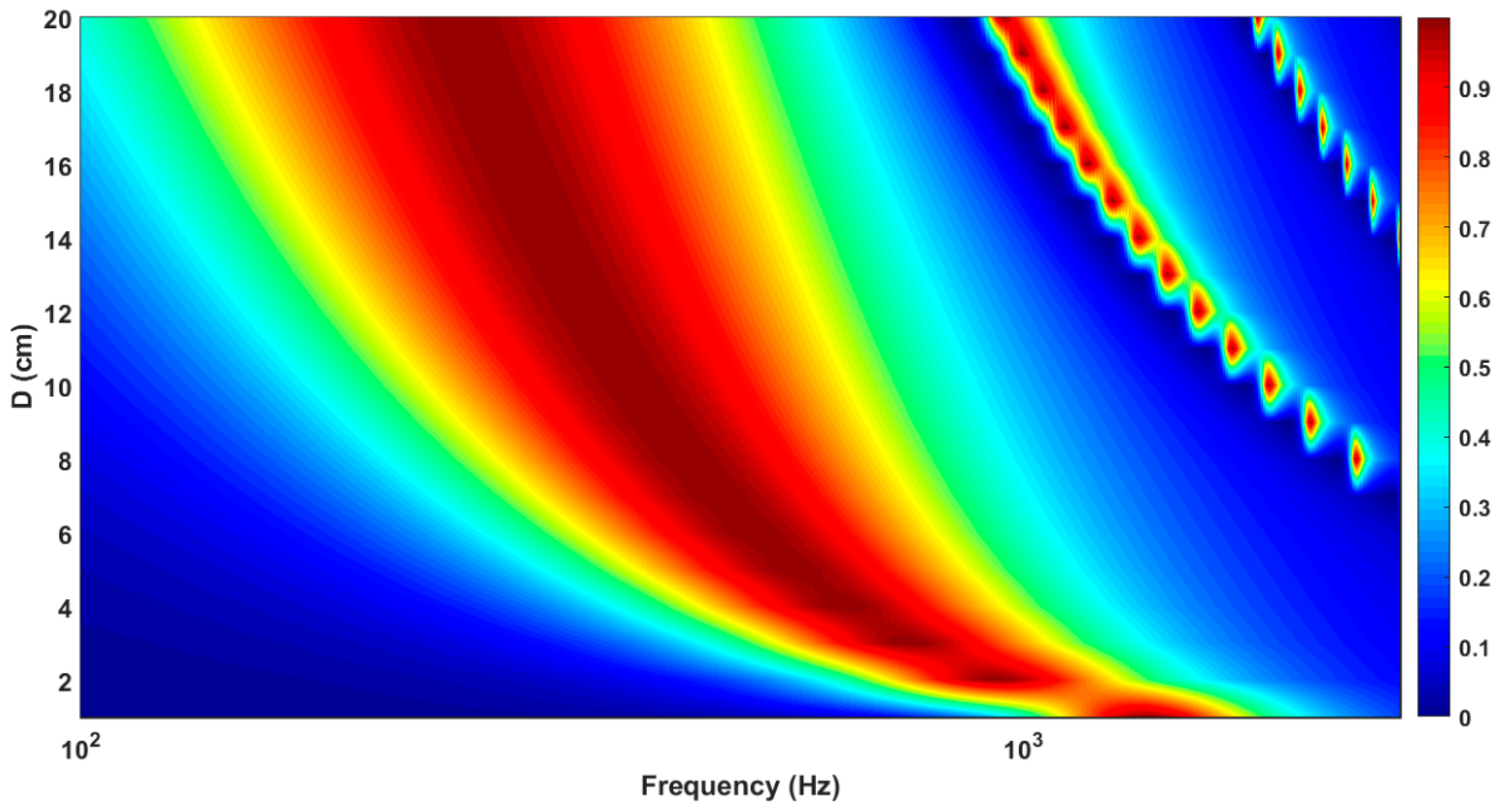
- Keeping constant the combination of parameters (d,t,ϕ), the effect of D is to move the absorption curve towards lower frequencies as D increases (Figure 9).
2.2. EF Model
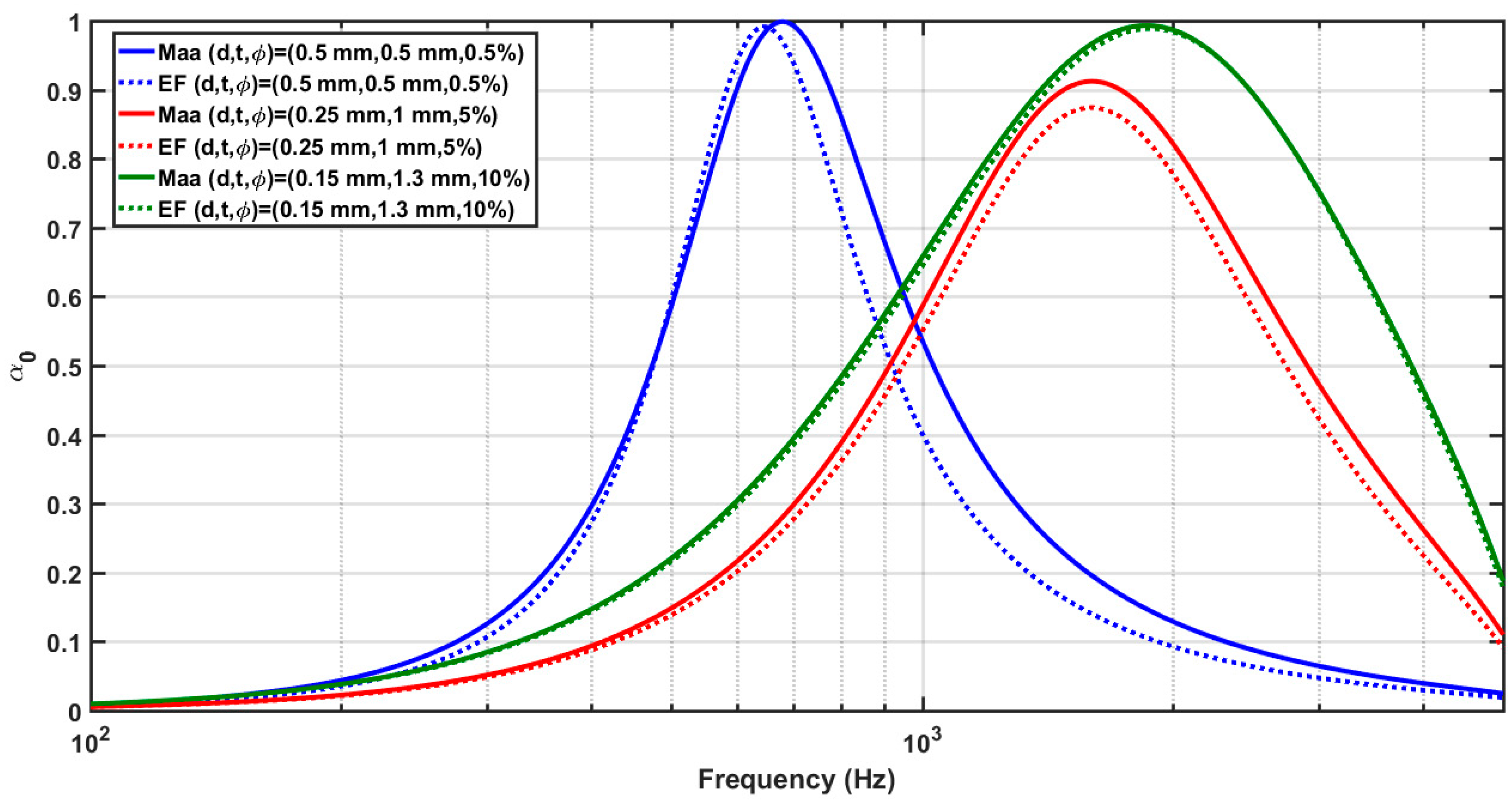
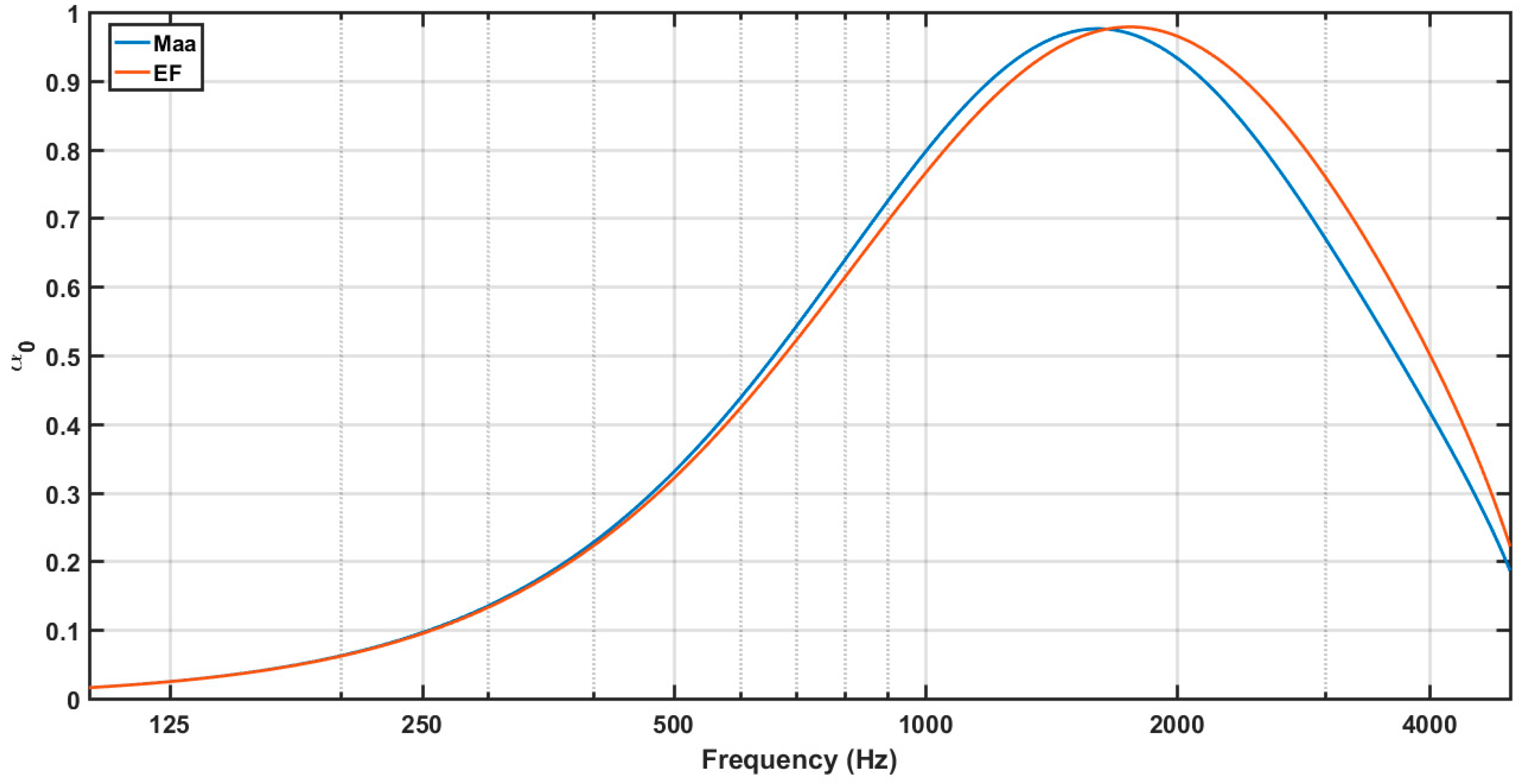
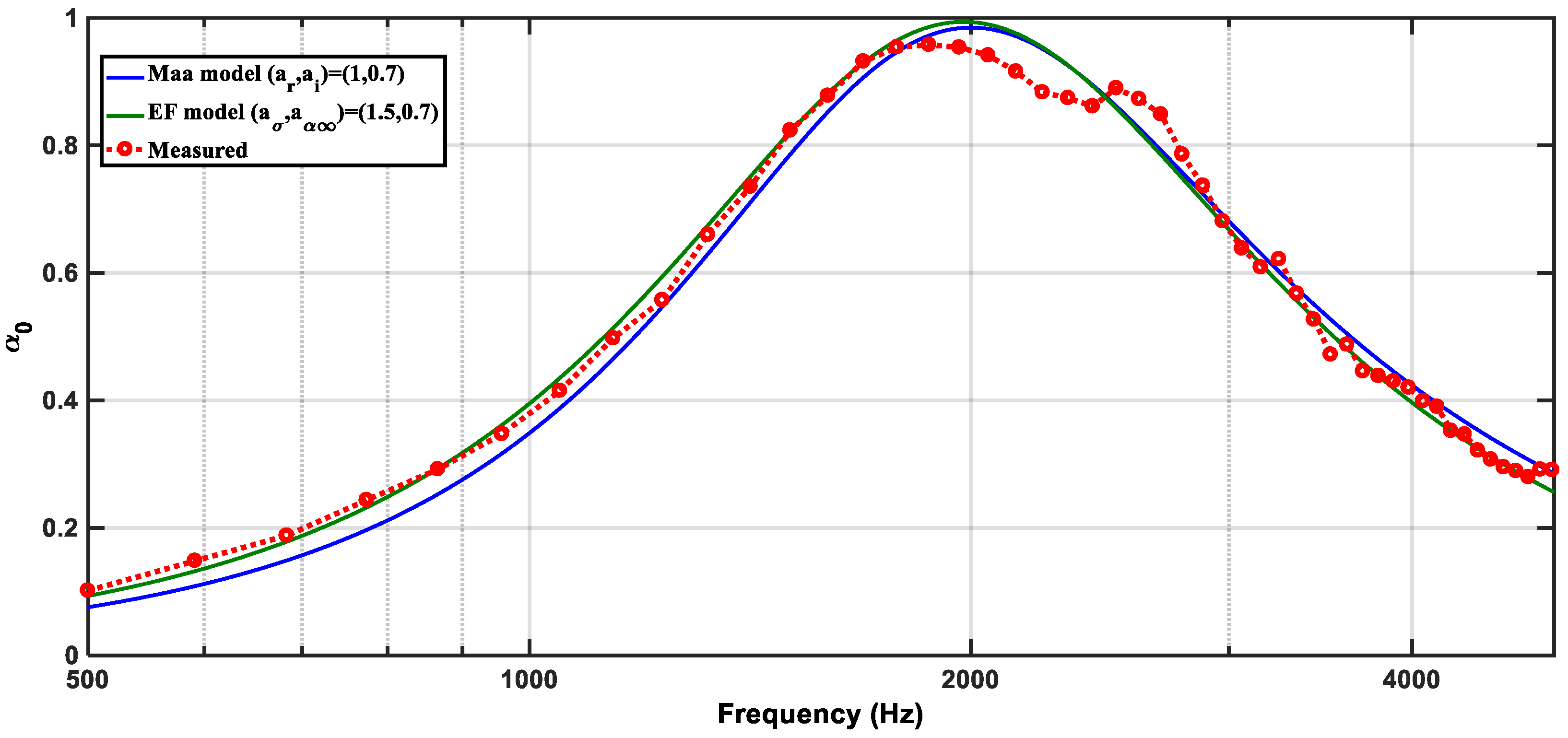
2.3. Comparison Between Maa and EF Models
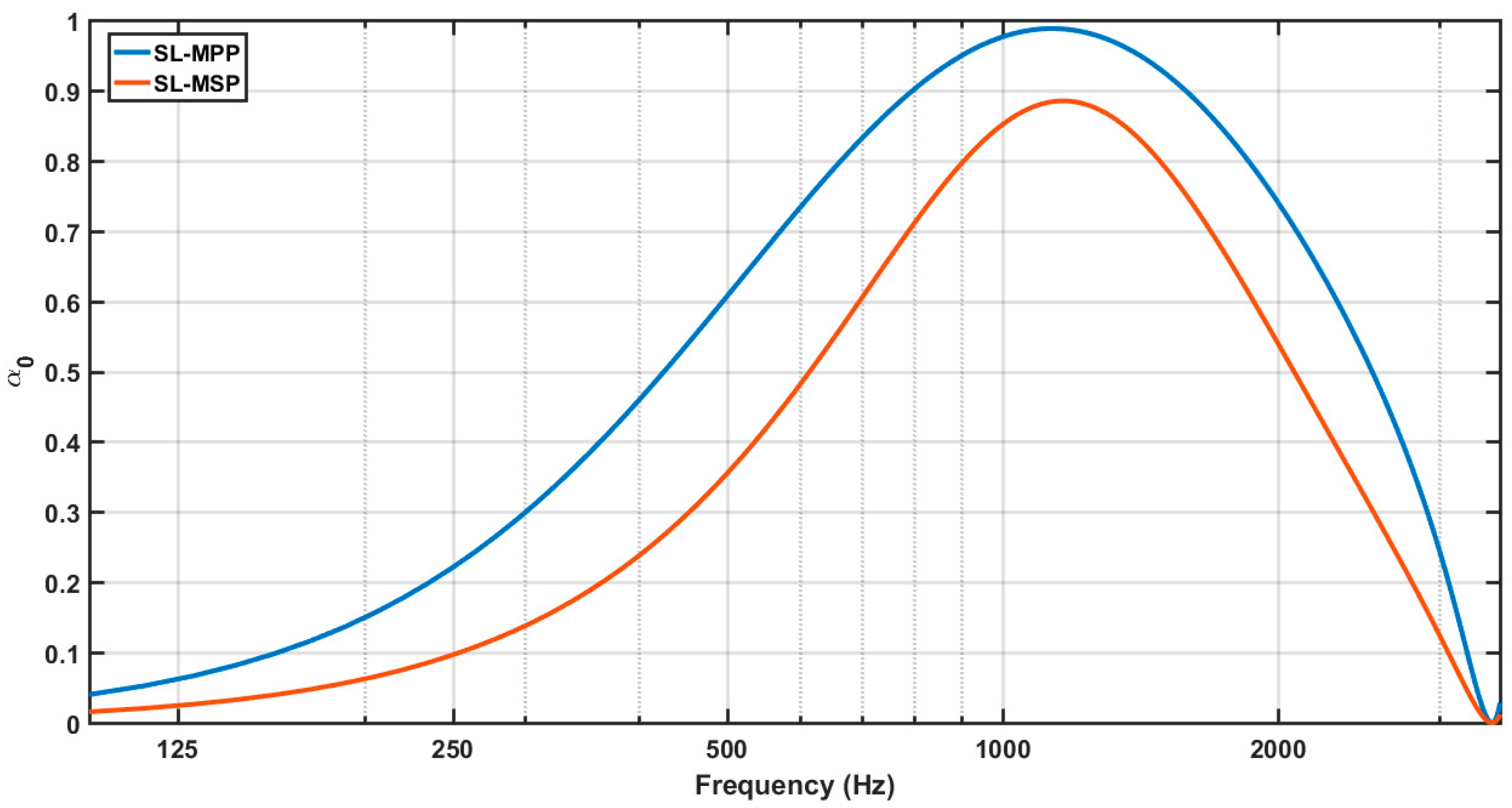
2.4. Microslotted Panels (MSP)
2.5. Microperforated Insertion Units (MIUs)
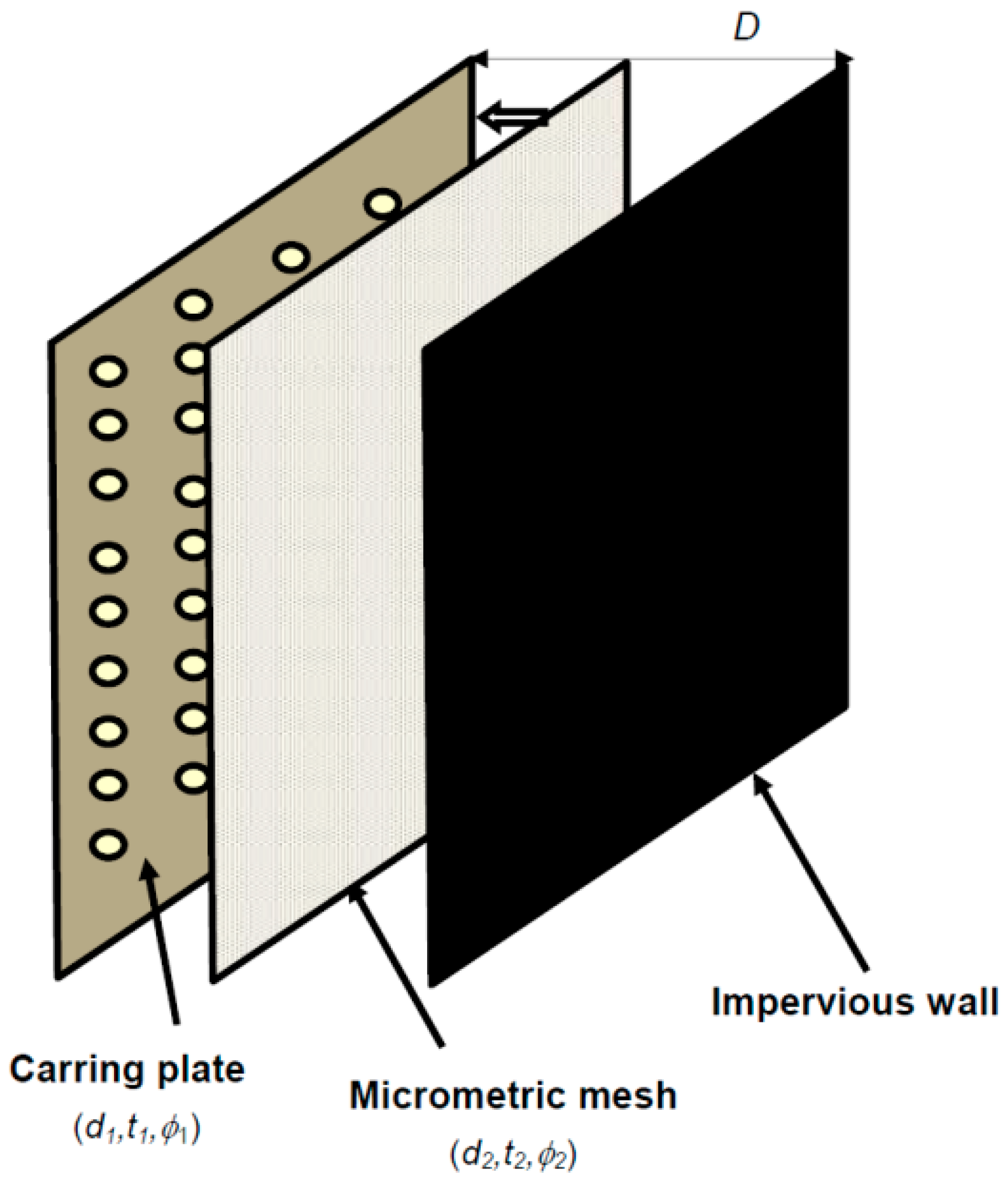
2.6. MPP Manufactured by Infiltration Technique
2.7. Absorption of an SL-MPP at Random Incidence
- The random incidence absorption coefficient of a locally reacting SL-MPP has an absorption bandwidth rather similar to the normal incidence absorption coefficient, with a slight reduction of the peak absorption.
- The random incidence absorption coefficient of a bulk reacting SL-MPP has an absorption curve quite displaced towards higher frequencies as compared to the normal incidence absorption coefficient, with a more reduced absorption peak.
3. Multiple-Layer MPP (ML-MPP)
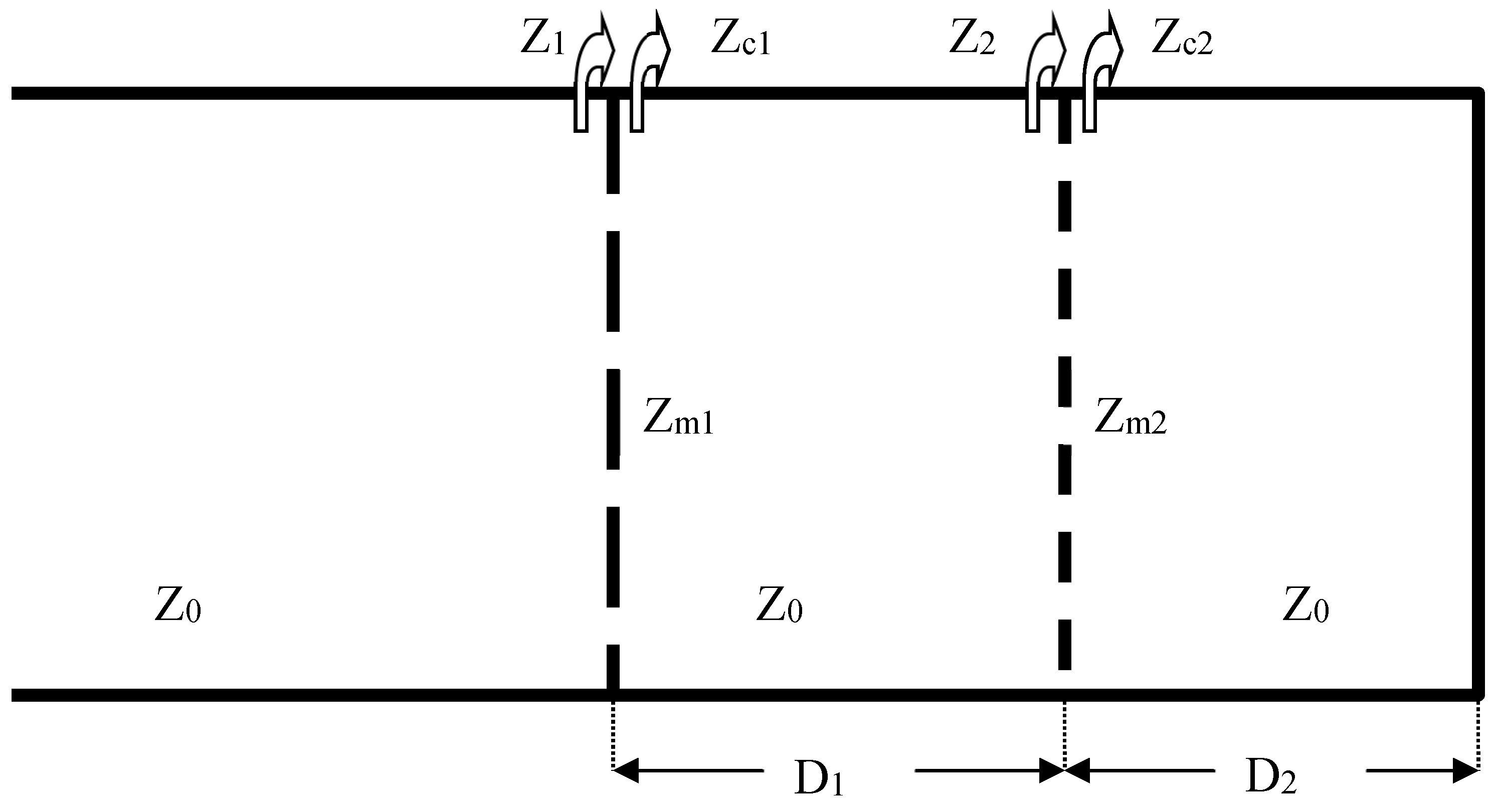
3.1. Double-Layer MPP (DL-MPP)
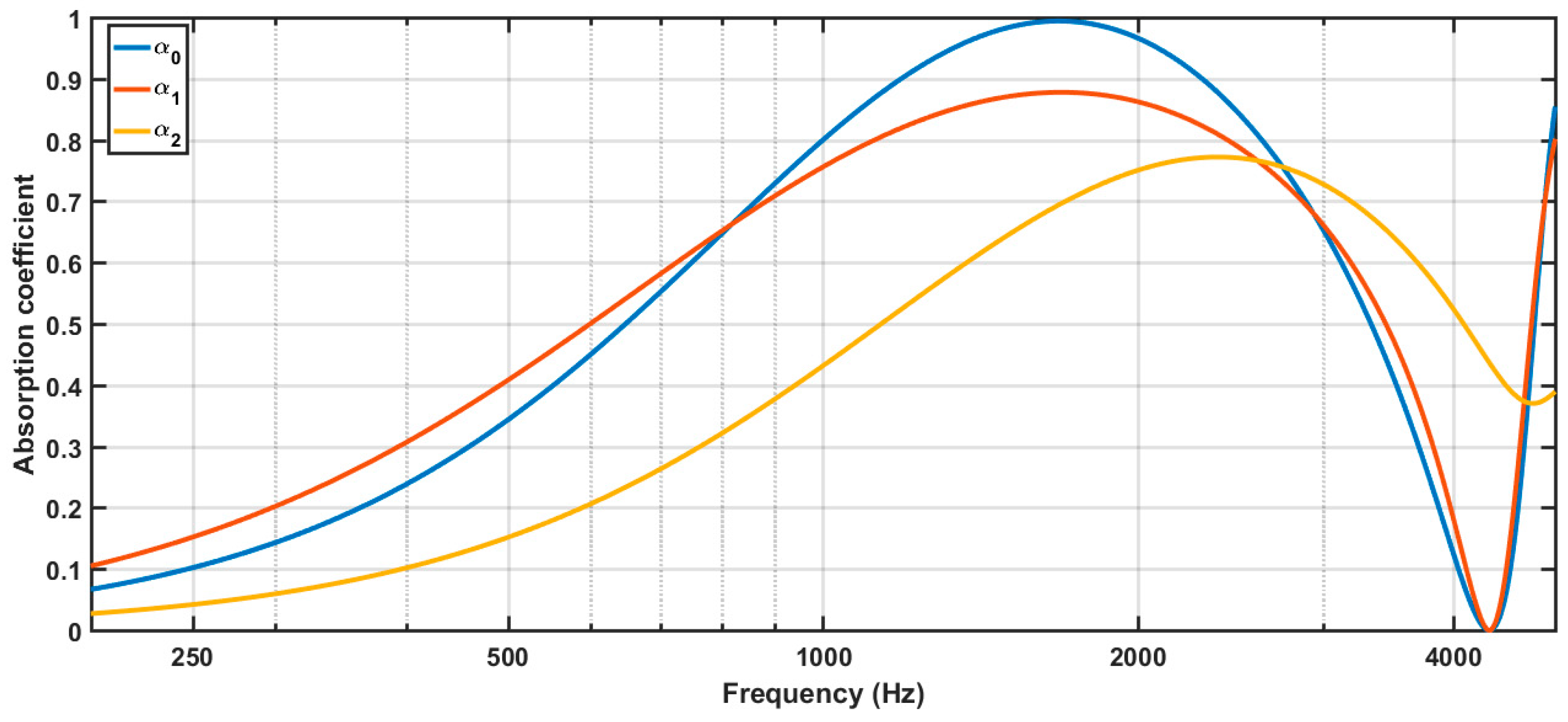
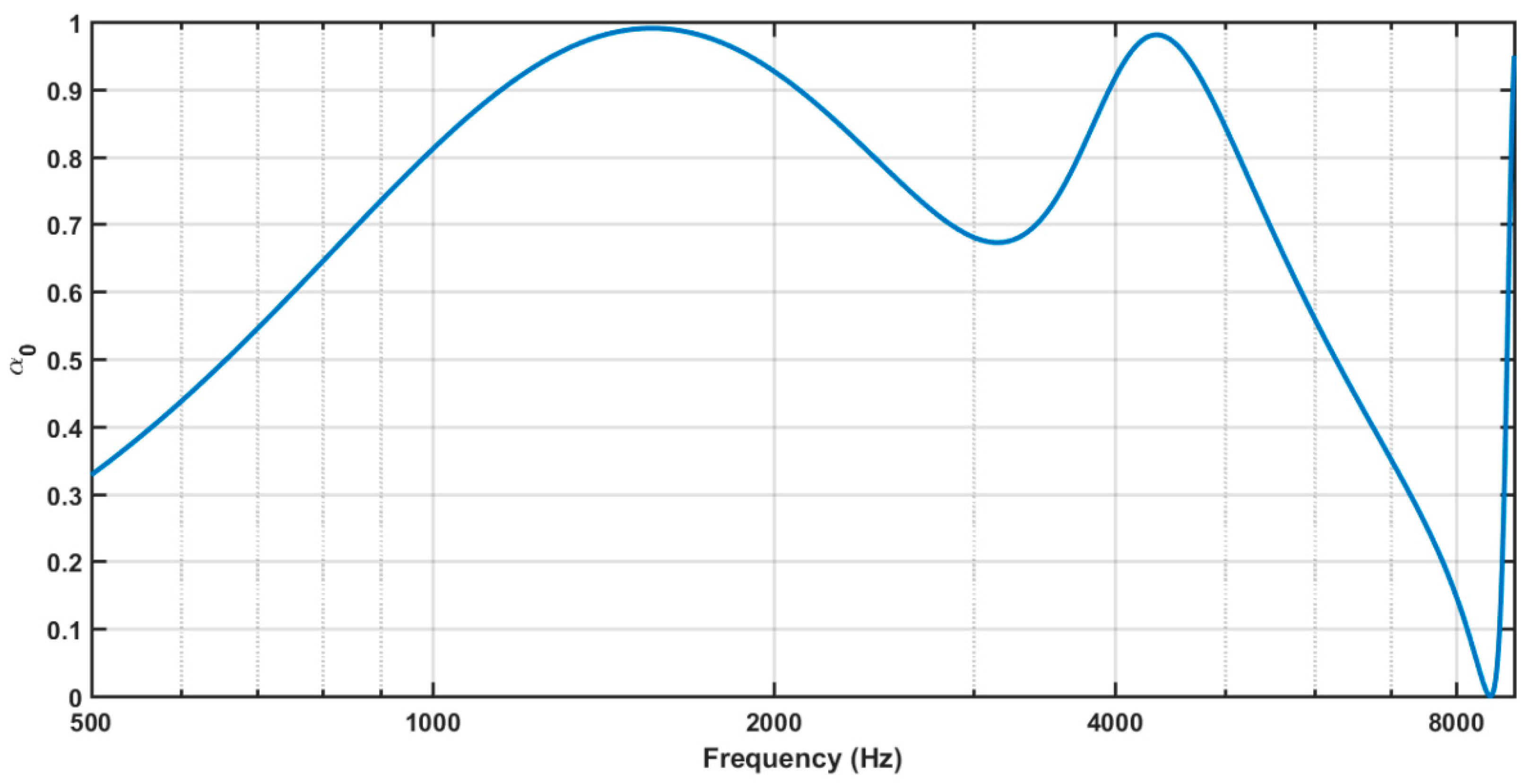
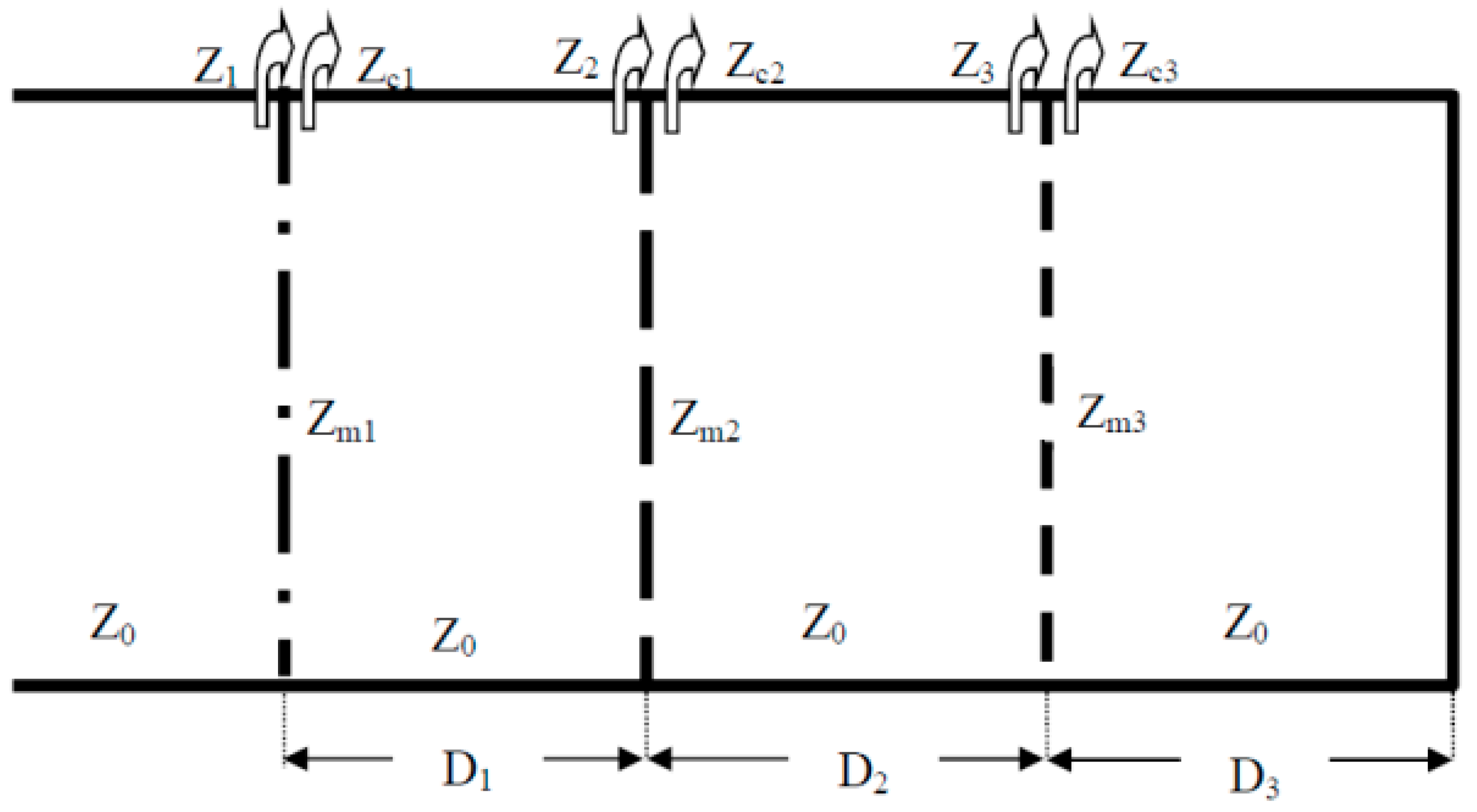
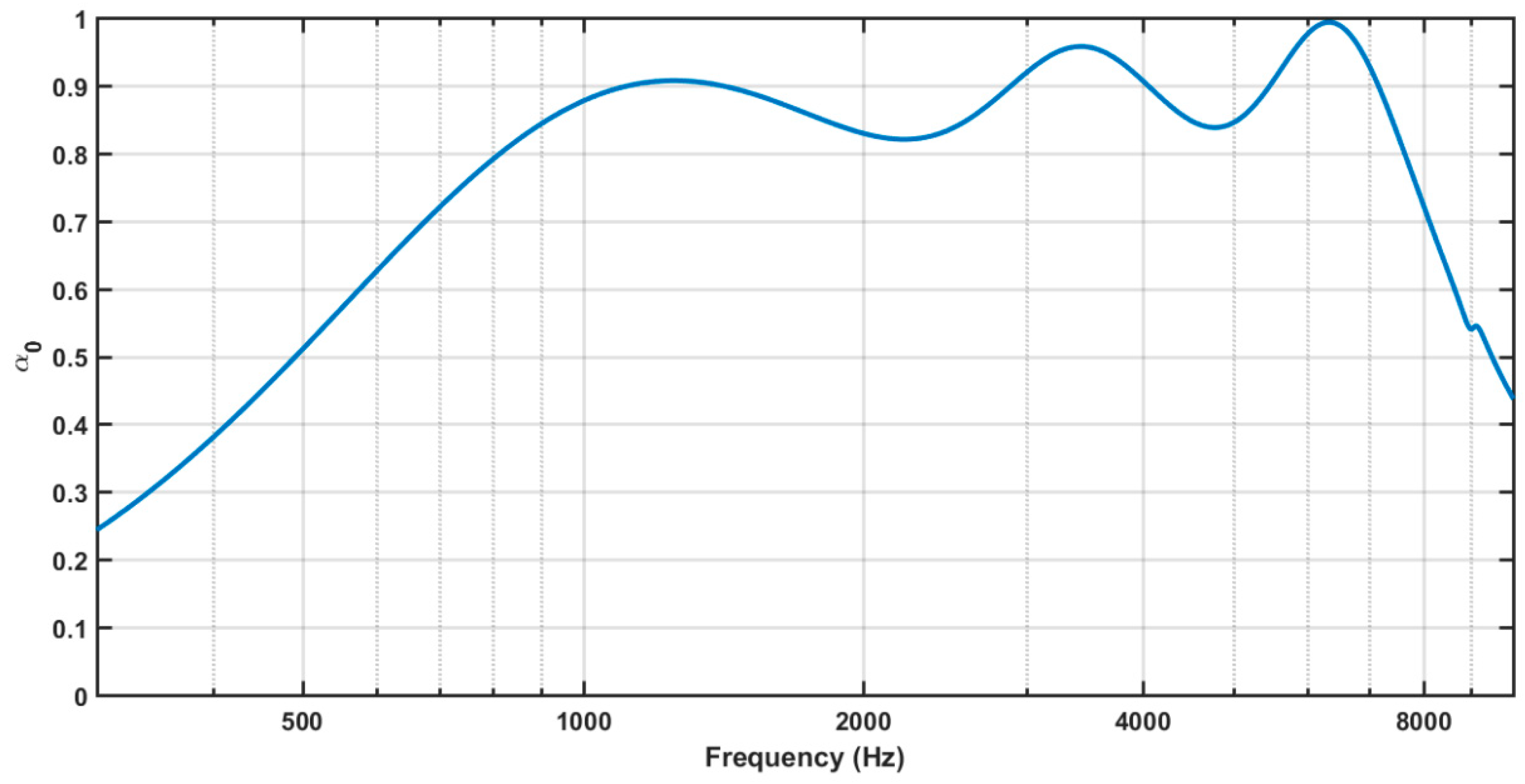
3.2. Triple-Layer MPP (TL-MPP)
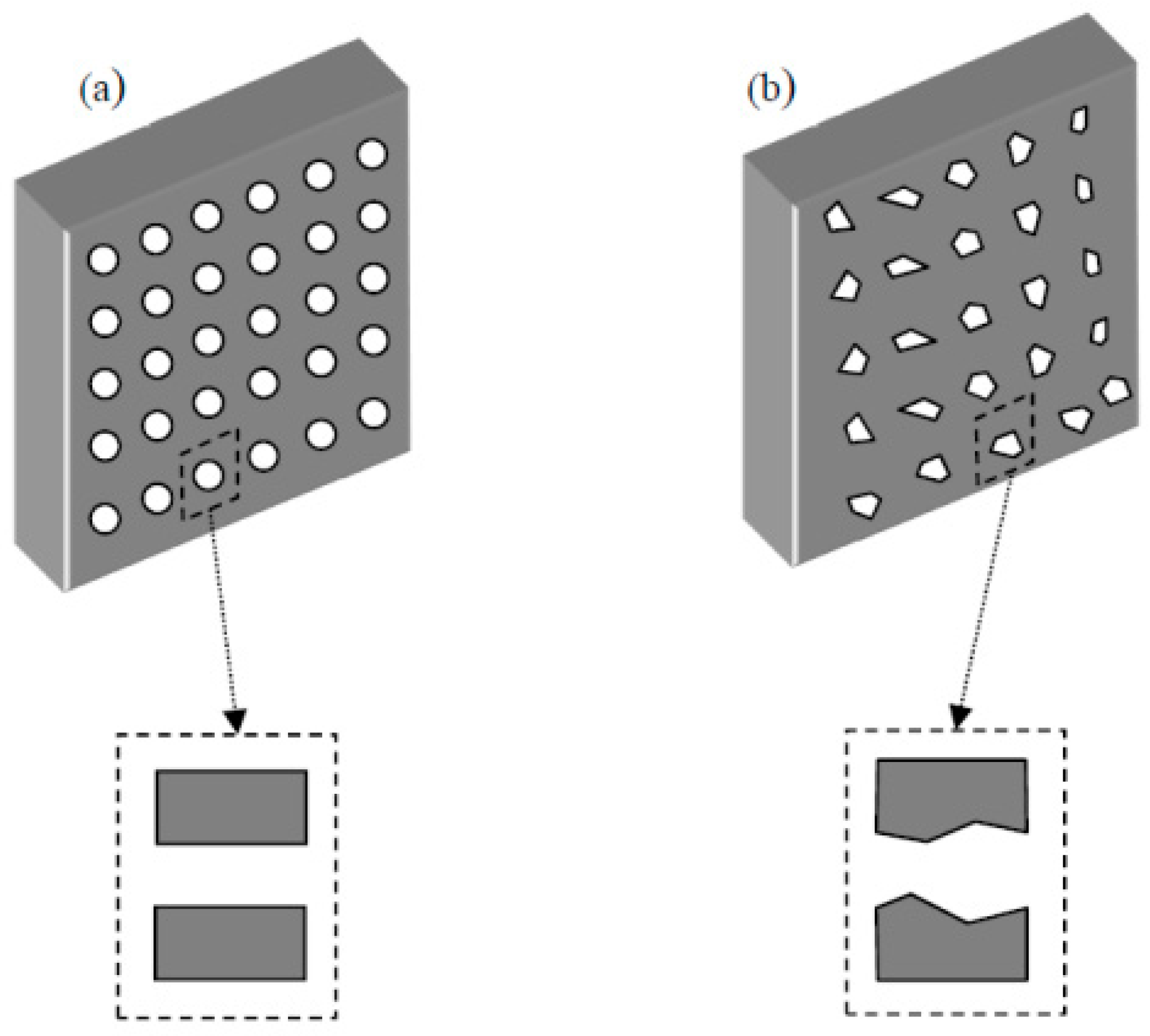
4. Machining MPPs
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cobo, P.; Ruiz, H.; Alvarez, J. Double-Layer Microperforated Panel/Porous absorber as liner for anechoic closing of the test section in wind tunnels. Acta Acust. United Acust. 2010, 96, 914–922. [Google Scholar] [CrossRef]
- Maa, D.Y. Microperforated-panel wideband absorbers. Noise Control Eng. J. 1987, 29, 77–84. [Google Scholar] [CrossRef]
- Maa, D.Y. Potential of microperforated panel absorber. J. Acoust. Soc. Am. 1998, 104, 2861–2866. [Google Scholar] [CrossRef]
- Allard, J.F. Propagation of Sound in Porous Media. Modelling Sound Absorbing Materials; Elsevier Applied Science: London, UK, 1993. [Google Scholar]
- Allard, J.F.; Atalla, N. Propagation of Sound in Porous Media. Modelling Sound Absorbing Materials; John Wiley & Sons: Chichester, West Sussex, UK, 2009. [Google Scholar]
- Atalla, N.; Sgard, J.F. Modeling of perforated plates and screens using rigid frame porous models. J. Sound Vib. 2007, 303, 195–208. [Google Scholar] [CrossRef]
- Ingard, U. On the theory and design of acoustic resonators. J. Acoust. Soc. Am. 1953, 25, 1037–1061. [Google Scholar] [CrossRef]
- Maa, D.Y. Theory of microslit absorbers. Chin. J. Acoust. 2001, 20, 1–10. [Google Scholar]
- Randeberg, R.T. Perforated Panel Absorbers with Viscous Energy Dissipation Enhanced by Orifice Design. Doctoral Thesis, Norweian University of Science and Technology, Trondheim, Norway, 2000. [Google Scholar]
- Vigran, T.O.; Pettersen, O.K.Ø. The absorption of slotted panels revisited. In Proceedings of the Forum Acusticum, Budapest, Hungary, 29 August–2 September 2005; pp. 2037–2040. [Google Scholar]
- Pfretzschner, J.; Cobo, P.; Simon, F.; Cuesta, M.; Fernández, A. Microperforated Insertion Units: an alternative strategy the design of microperforated panels. Appl. Acoust. 2006, 67, 62–73. [Google Scholar] [CrossRef]
- Ruiz, H.; Cobo, P.; Dupont, T.; Martin, B.; Leclaire, P.H. Acoustic properties of plates with unevenly distributed macroperforations backed by woven meshes. J. Acoust. Soc. Am. 2012, 132, 3138–3147. [Google Scholar] [CrossRef]
- Cobo, P.; Montero de Espinosa, F. A proposal of cheap microperforated panels manufactured by infiltration. Appl. Acoust. 2013, 74, 1069–1075. [Google Scholar] [CrossRef]
- Quian, Y.J.; Kong, D.Y.; Liu, S.M.; Sun, S.M.; Xhao, Z. Investigation on micro-perforated panel absorber with ultra-micro perforations. Appl. Acoust. 2013, 74, 931–935. [Google Scholar] [CrossRef]
- Lee, J.; Swenson, G.W., Jr. Compact sound absorbers for low frequencies. Noise Control Eng. J. 1992, 38, 109–117. [Google Scholar] [CrossRef]
- Lee, D.H.; Kwon, Y.P. Estimation of the absorption performance of multiple layer perforated panel systems by transfer matrix method. J. Sound Vib. 2004, 278, 847–860. [Google Scholar] [CrossRef]
- Cobo, P.; Cuesta, M.; Siguero, M. Comparison of models describing double layer microperforated absorbers. Noise Control Eng. J. 2009, 57, 10–15. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic properties of multilayer sound absorbers with a 3D printed micro-perforated panel. Appl. Acoust. 2017, 121, 25–32. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic measurement of a 3D printed micro-perforated panel combined with a porous material. Measurements 2017, 1041, 233–236. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Ren, L.; Ichchou, M.; Galland, M.A.; Bareille, O. Sound absorption of a new bionic multi-layer absorber. Compos. Struct. 2014, 108, 400–408. [Google Scholar] [CrossRef]
- Park, S.H. Acoustic properties of micro-perforated panel absorbers backed by Helmholtz resonators for the improvement of low-frequency sound absorption. J. Sound Vib. 2013, 332, 4895–4911. [Google Scholar] [CrossRef]
- Gai, X.-L.; Li, X.-H.; Tuo, B.Z.; Zhao, J.-J.; Ma, Z.-H. Experimental study on sound absorption performance of microperforated panel with membrane cell. Appl. Acoust. 2016, 110, 241–247. [Google Scholar] [CrossRef]
- Duan, X.H.; Wang, H.Q.; Li, Z.B.; Zhu, L.K.; Chen, R.; Kong, D.Y.; Zhao, Z. Sound absorption of a flexible micro-perforated panel absorber based on PVDF piezoelectric film. Appl. Acoust. 2015, 88, 84–89. [Google Scholar] [CrossRef]
- Guo, W.; Min, H. A compound micro-perforated panel sound absorber with partitioned cavities of different depths. Energy Procedia 2015, 78, 1617–1622. [Google Scholar] [CrossRef]
- Huang, S.; Li, S.; Wang, X.; Mao, D. Micro-perforated absorbers with incompletely partitioned cavities. Appl. Acoust. 2017, 126, 114–119. [Google Scholar] [CrossRef]
- Quian, Y.J.; Kong, D.Y.; Liu, Y.; Liu, S.M.; Li, Z.B.; Shao, D.S.; Sun, S.M. Improvement of sound absorption characteristics under low frequency for micro-perforated panel absorbers using super-aligned carbon nanotube arrays. Appl. Acoust. 2014, 82, 23–27. [Google Scholar] [CrossRef]
- Xiaodan, Z.; Xiangqian, F. Enhancing low frequency sound absorption of micro-perforated panel absorbers by using mechanical impedance plates. Appl. Acoust. 2015, 88, 123–128. [Google Scholar]
- Xiaodan, Z.; Wang, X.; Yongjie, Y. Enhancing low-frequency sound absorption of micro-perforated panel absorbers by combining parallel mechanical impedance. Appl. Acoust. 2018, 130, 300–304. [Google Scholar]
- Kim, B.S.; Cho, S.J.; Min, D.K.; Park, J. Sound absorption structure in helical shapes made using fibrous paper. Compos. Struct. 2015, 134, 90–94. [Google Scholar] [CrossRef]
- Kim, B.S.; Cho, S.J.; Min, D.K.; Park, J. Experimental study for improving sound absorption of a composite helical-shaped porous structure using carbon fiber. Compos. Struct. 2016, 145, 242–247. [Google Scholar] [CrossRef]
- Onen, O.; Caliskan, M. Design of a single layer micro-perforated sound absorber by finite element analysis. Appl. Acoust. 2010, 71, 79–85. [Google Scholar] [CrossRef]
- Carbajo, J.; Ramis, J.; Godinho, L.; Amado-Mendes, P.; Alba, J. A finite element model of perforated panel absorbers including viscothermal effects. Appl. Acoust. 2015, 90, 1–8. [Google Scholar] [CrossRef]
- Ruiz, H.; Cobo, P.; Jacobsen, F. Optimization of multiple-layer microperforated panels by simulated aneealing. Appl. Acoust. 2011, 72, 772–776. [Google Scholar] [CrossRef]
- Cobo, P.; Moraes, E.; Simon, F. Inverse estimation of the non-acoustical parameters of loose granular absorbers by Simulated Annealing. Build. Environ. 2015, 94, 859–866. [Google Scholar] [CrossRef]
- Cobo, P.; Simon, F. A comparison of impedance models for the inverse estimation of the non-acoustical parameters of granular absorbers. Appl. Acoust. 2016, 104, 119–126. [Google Scholar] [CrossRef]
- Cobo, P.; Simon, F. Using simulating annealing for the inverse estimation of the non-acoustical parameters of sound absorbers. Build. Acoust. 2017, 24, 295–306. [Google Scholar] [CrossRef]
- Jaouen, L.; Becot, F.X. Acoustical characterization of perforated facings. J. Acoust. Soc. Am. 2011, 129, 1400–1406. [Google Scholar] [CrossRef] [PubMed]
- Tayong, R.; Leclaire, P. Hole interaction effects under high and medium sound intensities for micro-perforated panels design. In Proceedings of the 10éme Congress Francais d’Acoustique, Lyon, France, 12–16 April 2010. [Google Scholar]
- Cobo, P. Absorción del Sonido; Biblioteca de Ciencias, 42, CSIC: Madrid, Spain, 2015. [Google Scholar]
- Fahy, F. Foundations of Engineering Acoustics; Academicc Press: San Diego, CA, USA, 2001. [Google Scholar]
- Hou, K. Measurement and Modeling of Micro-Perforated Panels. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2009. [Google Scholar]
- Melling, T.H. The acoustic impedance of perforates at medium and high sound pressure levels. J. Sound Vib. 1973, 29, 1–65. [Google Scholar] [CrossRef]
- Rschevkin, S.N. A Course of Lectures on the Theory of Sound; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Stinson, M.R.; Champoux, Y. Propagation of sound and the assignment of shape factors in models of porous materials having simple geometries. J. Acoust. Soc. Am. 1992, 91, 685–695. [Google Scholar] [CrossRef]
- Cobo, P.; Pfretszchner, J.; Cuesta, M.; Anthony, D.K. Hybrid passive-active absorption using microperforated panels. J. Acoust. Soc. Am. 2004, 116, 2118–2125. [Google Scholar] [CrossRef]
- Cobo, P.; Fernández, A. Hybrid passive-active absorption of broadband noise using MPPs. Noise Vib. Worldw. 2006, 37, 19–23. [Google Scholar] [CrossRef]
- Cobo, P.; Cuesta, M. Hybrid passive-active absorption of a microperforated panel in free field conditions. J. Acoust. Soc. Am. 2007, 121, EL251–EL255. [Google Scholar] [CrossRef]
- Cobo, P.; Cuesta, M. Measuring hybrid passive-active sound absorption of a microperforated liner at oblique incidence. J. Acoust. Soc. Am. 2009, 125, 185–190. [Google Scholar] [CrossRef]
- Mechel, F.P.; Ver, I.L. Sound absorbing materials and sound absorbers. In Noise and Vibration Control Engineering; Beranek, L.L., Ver, I.L., Eds.; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Ortiz, S.; González, C.; Cobo, P.; Montero de Espinosa, F. Attenuating open cavity tones by lining its walls with microperforated panels. Noise Control Eng. J. 2014, 62, 145–151. [Google Scholar] [CrossRef]
- Mechel, F.P. Formulas of Acoustics; Spriger: Berlin, Germany, 2002. [Google Scholar]
- Morfey, C.L. Dictionary of Acoustics; Academic Press: London, UK, 2001. [Google Scholar]
- Cox, T.J.; D’Antonio, P. Acoustic Absorbers and Diffusers. Theory, Design, and Application; Spon Press: New York, NY, USA, 2004. [Google Scholar]
- Ingard, U. Notes on Sound Absorption; Kittery Point: Kittery, ME, USA, 1999. [Google Scholar]
- Kang, J.; Fuchs, H.V. Predicting the sound absorption of open weave textiles and microperforated membranes backed by an air space. J. Sound Vib. 1999, 220, 905–920. [Google Scholar] [CrossRef]
- Cobo, P.; de la Colina, C.; Roibás, E.; Chimeno, M.; Simón, F. A wideband triple-layer microperforated panel sound absorber. Compos. Struct. 2019. submitted. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cobo, P.; Simón, F. Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings 2019, 9, 53. https://doi.org/10.3390/buildings9020053
Cobo P, Simón F. Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings. 2019; 9(2):53. https://doi.org/10.3390/buildings9020053
Chicago/Turabian StyleCobo, Pedro, and Francisco Simón. 2019. "Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review" Buildings 9, no. 2: 53. https://doi.org/10.3390/buildings9020053
APA StyleCobo, P., & Simón, F. (2019). Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings, 9(2), 53. https://doi.org/10.3390/buildings9020053





