Formula for Determining the Construction Workers Productivity Including Environmental Factors
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Factors Affecting Labour Productivity
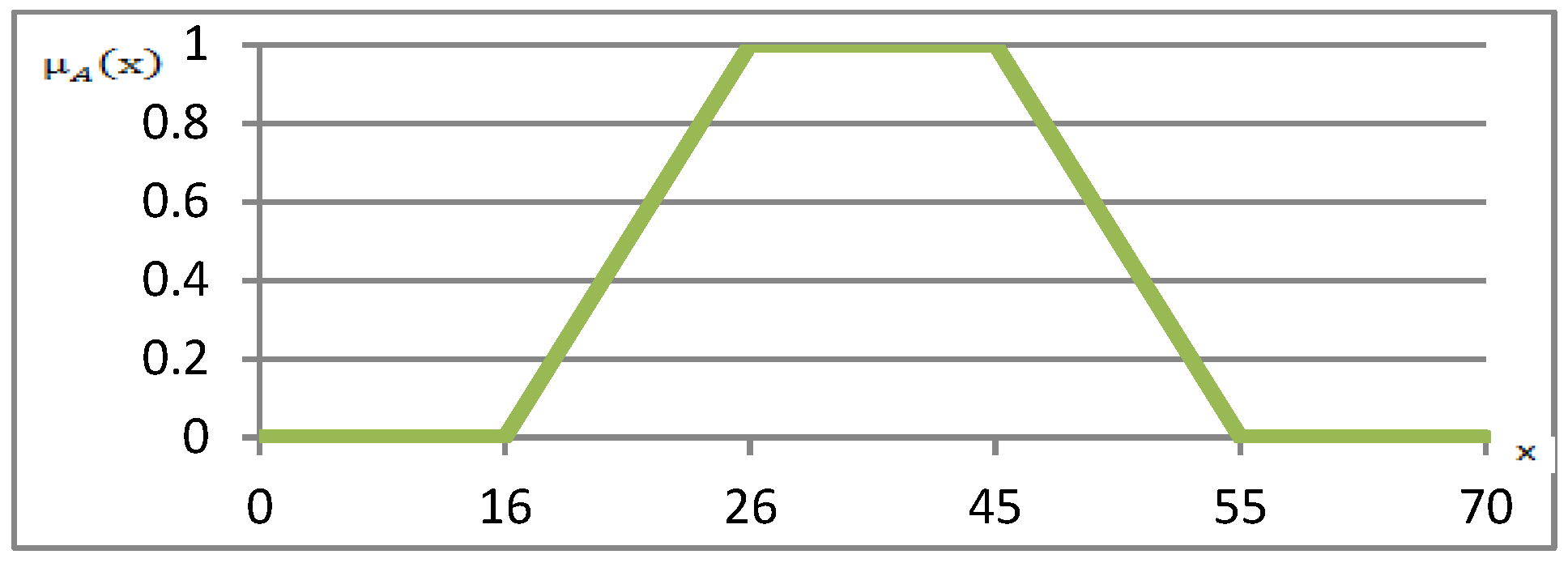
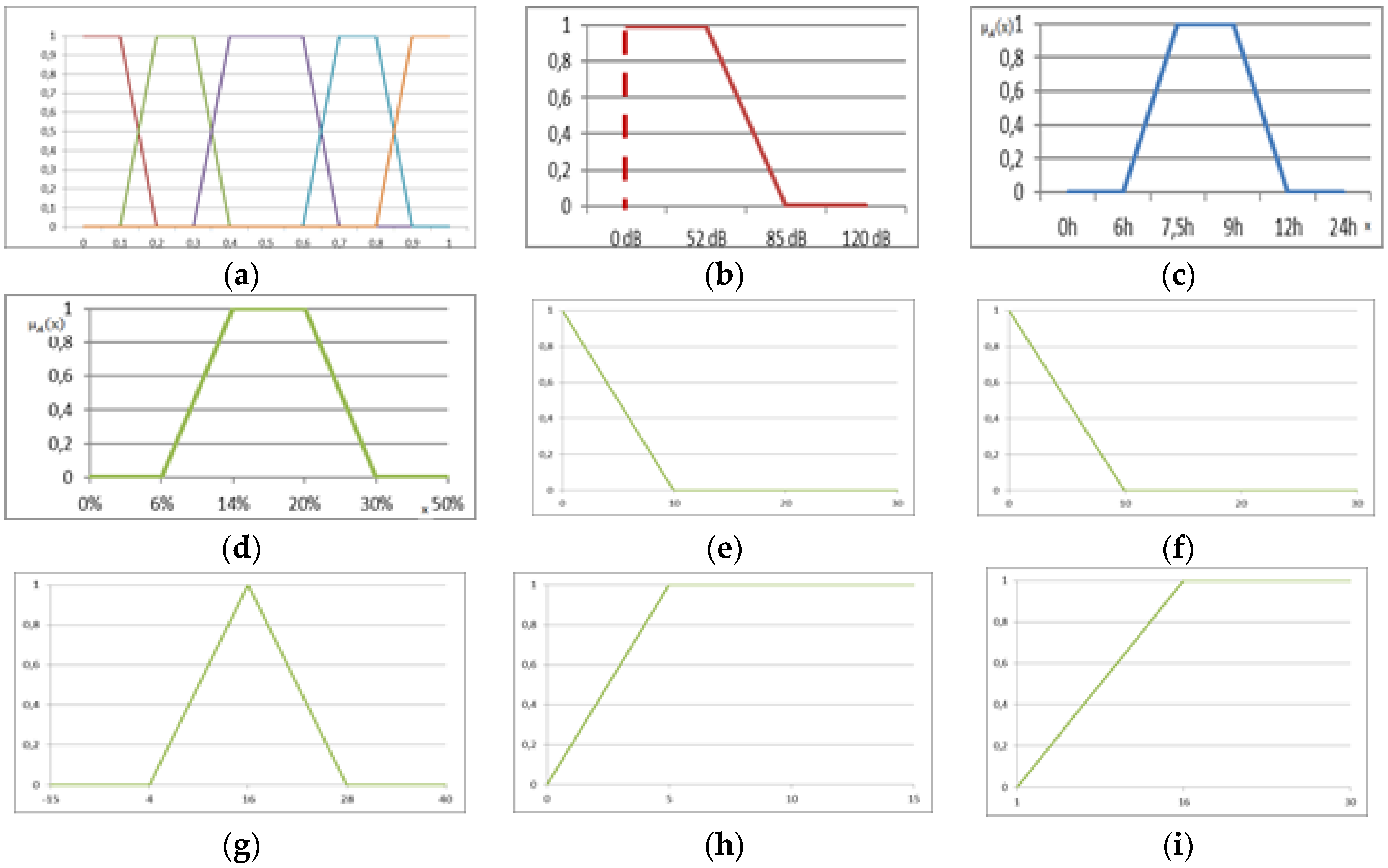
3.2. Parameterization of the Factors
- The membership functions of the following factors are captured as linguistic values: ergonomics of equipment and tools; wage; organization of work and work stations; stress; fatigue of the employee; and health. The membership function is:
- Very good (0.8; 0.9; 1.0; 1.0);
- Good (0.6; 0.7; 0.8; 0.9)
- Average (0.3; 0.4; 0.6; 0.7);
- Weak (0.1; 0.2; 0.3; 0.4)
- Bad (0.0; 0.0; 0.1; 0.2)
- For the factor: noise, the membership function is described in Equation (2).where dB stands for decibels.
- For the factor: duration of work shift, the membership function is described in Equation (3).where h is hours worked.
- For the factor: regeneration of strength, the membership function is described in Equation (4).where: T is time available; Tfo is time to rest; and
- For the factor: precipitation, the membership function is described in Equation (5).
- For the factor: wind, the membership function is described in Equation (6).
- For the factor: air temperature, the membership function is described in Equation (7).
- For the factor ‘worker’s absence,’ the membership function is described in Equation (8).where: r − d represents workdays.
- For the factor: adaptation to new working conditions, the membership function is described in Equation (9).
- For the factor ‘time spent with family,’ the membership function is described in Equation (10).
- For the factor ‘day of the week,’ the membership function is described in Equation (11).
3.3. Impact of Identified Factors on Work Productivity of Construction Workers
3.4. Formula for Determining the Productivity of Construction Workers by Considering the Influencing Factors
3.5. Example of Formula Usage
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Juszczyk, M.; Leśniak, A.; Zima, K. ANN based approach for estimation of construction costs of sports fields. Complexity 2018, 2018, 11. [Google Scholar] [CrossRef]
- Leśniak, A.; Juszczyk, M.; Piskorz, G. Modelling delays in bridge construction projects based on the logit and probit regression. Arch. Civ. Eng. 2019, 65, 107–120. [Google Scholar] [CrossRef]
- Hoła, B.; Nowobilski, T. Analysis of the influence of socio-economic factors on occupational safety in the construction industry. Sustainability 2019, 11, 4469. [Google Scholar] [CrossRef]
- Halligan, D.W.; Demsetz, L.A.; Brown, J.D.; Pace, C.B. Action-response model and loss of productivity in construction. J. Constr. Eng. Manag. 1994, 120, 47–64. [Google Scholar] [CrossRef]
- Moselhi, O.; Khan, Z. Significance ranking of parameters impacting construction labor productivity. Constr. Innov. 2012, 12, 272–296. [Google Scholar] [CrossRef]
- Hwang, B.; Soh, C.K. Trade-level productivity measurement: Critical challenges and solutions. J. Constr. Eng. Manag. 2013, 139, 04013013. [Google Scholar] [CrossRef]
- Yi, W.; Chan, A.P.C. Critical review of labor productivity research in construction journals. J. Manag. Eng. 2014, 30, 214–225. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Nguyen, L.D. Relationship between building floor and construction labor productivity. Eng. Constr. Arch. Manag. 2013, 20, 563–575. [Google Scholar] [CrossRef]
- Panas, A.; Pantouvakis, J.P. Evaluating Research Methodology in Construction. Built Hum. Environ. Rev. 2010, 3, 63–85. [Google Scholar]
- Smith, S.D. Earthmoving productivity estimation using linear regression techniques. J. Constr. Eng. Manag. 1999, 125, 133–141. [Google Scholar] [CrossRef]
- Sander, S.R.; Thomas, H.R. Masonry productivity forecasting model. J. Constr. Eng. Manag. 1993, 119, 163–179. [Google Scholar] [CrossRef]
- Thomas, H.R.; Sakarcan, A.S. Forecasting labor productivity using the factor model. J. Constr. Eng. Manag. 1994, 120, 228–239. [Google Scholar] [CrossRef]
- Zayed, T.M.; Halpin, D.W. Pile Construction Productivity Assessment. J. Constr. Eng. Manag. 2005, 131, 705–714. [Google Scholar] [CrossRef]
- Fayek, A.R.; Oduba, A. Predicting Industrial Construction Labor Productivity Using Fuzzy Expert Systems. J. Constr. Eng. Manag. 2005, 131, 938–941. [Google Scholar] [CrossRef]
- El-Rayes, K.; Moselhi, O. Impact of Rainfall on the Productivity of Highway Construction. J. Constr. Eng. Manag. 2001, 127, 125–131. [Google Scholar] [CrossRef]
- Song, L.; AbouRizk, S.M. Measuring and Modeling Labor Productivity Using Historical Data. J. Constr. Eng. Manag. 2008, 134, 786–794. [Google Scholar] [CrossRef]
- Portas, J.; AbouRizk, S.M. Neural network model for estimating construction productivity. J. Constr. Eng. Manag. 1997, 123, 399–410. [Google Scholar] [CrossRef]
- Choy, E.; Ruwanpura, J.Y. Situation Based Modeling for Construction Productivity. Can. J. Civil. Eng. 2006, 33, 1585–1600. [Google Scholar] [CrossRef]
- Hanna, A.S.; Peterson, P.; Lee, M.J. Benchmarking productivity indicators for electrical/mechanical projects. J. Constr. Eng. Manag. 2002, 128, 331–337. [Google Scholar] [CrossRef]
- Graham, D.; Smith, S.D. Estimating the productivity of cyclic construction operations using case-based reasoning. Adv. Eng. Inform. 2004, 18, 17–28. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Sun, K. Planning gang formwork operations for building construction using simulations. Automat. Constr. 2004, 13, 765–779. [Google Scholar] [CrossRef]
- Hsie, M. A model used in creating a work-rest schedule for labores. Automat. Constr. 2009, 18, 762–769. [Google Scholar] [CrossRef]
- Townsend, K.; Lingard, H.; Bradley, L.; Brown, K. Complicated working time arrangements: Construction industry case study. J. Constr. Eng. Manag. 2012, 138, 443–448. [Google Scholar] [CrossRef]
- Ahn, S.; Lee, S.; Steel, R.P. Effects of workers social learning: Focusing on absence behaviour. J. Constr. Eng. Manag. 2013, 139, 1015–1025. [Google Scholar] [CrossRef]
- Lee, H.S.; Shin, J.W.; Park, M.; Ryu, H.G. Probabilistic duration estimation model for high-rise structural work. J. Constr. Eng. Manag. 2009, 135, 1289–1298. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, N.; Lu, S.L. Productivity model in hot and humid environment based on heat tolerance time analysis. Build. Environ. 2009, 44, 2202–2207. [Google Scholar] [CrossRef]
- Helmer, O. Social Technology; Basic Books: New York, NY, USA, 1966. [Google Scholar]
- Chan, A.P.C.; Wong, F.K.W.; Wong, D.R.; Lam, E.W.M.; Yi, W. Determining an optimal recovery time after exercising to exhaustion in controlled climatic environment: Application to construction works. Build. Environ. 2012, 56, 28–37. [Google Scholar] [CrossRef]
- Bowen, P.; Edwards, P.; Lingard, H. Workplace stress experienced by construction professionals in South Africa. J. Constr. Eng. Manag. 2013, 139, 393–403. [Google Scholar] [CrossRef]
- Malara, J. Research on working time in the construction sector. Tech. Trans. 2014, 19, 169–175. [Google Scholar]
- Plebankiewicz, E.; Juszczyk, M.; Malara, J. Estimation of task completion times with the use of the PERT method on the example of a real construction project. Arch. Civ. Eng. 2015, 61, 51–62. [Google Scholar] [CrossRef]
- Chen, J.; Yang, L.; Su, M. Comparison of som-based optimization and particle swarm optimization for minimizing the construction time of a secant pile wall. Automat. Constr. 2009, 18, 844–848. [Google Scholar] [CrossRef]
- Gonzalez, V.; Alarcon, L.; Maturana, S.; Bustamante, J. Site management of work-in-process buffers to enhance project performance using the reliable commitment model: Case study. J. Constr. Eng. Manag. 2011, 137, 707–715. [Google Scholar] [CrossRef]
- Gouett, M.; Haas, C.; Goodrum, P.; Caldas, C. Activity analysis for direct-work rate improvement in construction. J. Constr. Eng. Manag. 2011, 137, 1117–1124. [Google Scholar] [CrossRef]
- Renna, P. Influence of maintenance policies on multi-stage manufacturing systems in dynamic conditions. Int. J. Prod. Res. 2012, 2, 345–357. [Google Scholar] [CrossRef]
- Russell, M.M.; Howell, G.; Hsiang, S.M.; Liu, M. Causes of time buffers in construction project task duration. J. Constr. Eng. Manag. 2014, 140, 325–336. [Google Scholar] [CrossRef]
- Wambeke, B.W.; Hsiang, S.M.; Liu, M. Causes of variation in construction project task starting times and duration. J. Constr. Eng. Manag. 2011, 9, 663–677. [Google Scholar] [CrossRef]
- Chao, L.C. Fuzzy logic model for determining minimum bid markup. Comput.-Aided Civ. Infrastruct. Eng. 2007, 22, 449–460. [Google Scholar] [CrossRef]
- Tah, J.H.M.; Carr, V. A proposal for construction project risk assessment using fuzzy logic. Constr. Manag. Econom. 2000, 18, 491–500. [Google Scholar] [CrossRef]
- Taylor, P. Employment Initiatives for an Ageing Workforce in the eu15; European Foundation for the Improvement of Living and Working Conditions: Dublin, Ireland, 2006.
- Naegele, G.; Walker, A. A Guide to Good Practice in Age Management; European Foundation for the Improvement of Living and Working Conditions: Dublin, Ireland, 2006.
| Factor Group | Factors | Study |
|---|---|---|
| Time spent outside work | worker’s absence | Hsie (2009) [22]; Ahn et al. (2013) [24] |
| time spent with the family (WLB) | Townsend (2012) [23] | |
| Weather conditions | air temperature | Moselhi and Khan (2012) [5]; Lee et al. (2009) [25]; Zhao et al. (2009) [26] |
| wind | ||
| precipitation | ||
| Psychophysical conditions | stress | Bowen et al. (2013) [29] |
| fatigue | Bowen et al. (2013) [29] | |
| health | Helmer (1996) [27] | |
| age | Helmer (1996) [27] | |
| recovery | Chan et al. (2012) [28] | |
| Organization and management of the worker | ergonomics noise duration of work shift salary organization of work and workstations | Malara (2014) [30]; Plebankiewicz et al. (2015) [31] |
| Remaining factors | day of the week adaptation to new operating conditions or a new technology | Malara (2014) [30] |
| Factor Number | Factor Name | Average Value |
|---|---|---|
| c1 | Ergonomics | 4.01 |
| c2 | Noise | 3.65 |
| c3 | Duration of work shift | 3.20 |
| c4 | Salary | 4.51 |
| c5 | Organization of the workstations | 4.17 |
| c6 | Stress | 3.38 |
| c7 | Fatigue | 4.18 |
| c8 | Health | 4.27 |
| c9 | Age of the worker | 3.83 |
| c10 | Recovery of strength | 3.09 |
| c11 | Precipitation | 3.49 |
| c12 | Air temperature | 3.49 |
| c13 | Wind | 3.49 |
| c14 | Time spent with the family | 3.16 |
| c15 | Worker’s absence | 3.16 |
| c16 | Day of the week | 3.65 |
| c17 | Adaptation to new operating conditions | 3.73 |
| Group Name—Influence on Work Performance of Construction Workers | Low | Average | High (Important) | Very High (Very Important) |
|---|---|---|---|---|
| Factors assigned | c3, c10, c14, c15 | c2, c6, c9, c11, c12, c13, c16, c17 | c1, c5, c7, c8 | c4 |
| Weight coefficient | 0.25 | 0.5 | 0.75 | 1 |
| y | 0 | 0.25 | 0.5 | 0.75 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| z1 | 1 | 0.84 | 0.71 | 0.59 | 0.5 | 0.25 | 0.13 | 0.06 | 0.03 |
| z2 | 1 | 1.11 | 1.22 | 1.36 | 1.5 | 2.25 | 3.38 | 5.06 | 7.59 |
| Factor Symbol | Factor Name | Measurement Result | Function µA(ci) Value |
|---|---|---|---|
| c1 | Ergonomics | good | 0.75 |
| c2 | Noise | approx. 78 dB | 0.2 |
| c3 | Duration of work shift | 9 h | 1 |
| c4 | Salary | good | 0.8 |
| c5 | Organization of the workstations | good | 0.8 |
| c6 | Stress | low | 0.8 |
| c7 | Fatigue | high | 0.25 |
| c8 | Health | average | 0.5 |
| c9 | Age of the worker | approx. 42 years | 1 |
| c10 | Recovery of strength | 8% | 0.28 |
| c11 | Precipitation | N/A | 1 |
| c12 | Air temperature | 8 °C | 0.33 |
| c13 | Wind | 5 m/s | 0.5 |
| c14 | Time spent with the family | 2 days | 1 |
| c15 | Worker’s absence | 1 workday | 0.2 |
| c16 | Day of the week | Thursday | 0.88 |
| c17 | Adaptation to new operating conditions | 2nd day | 0.07 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malara, J.; Plebankiewicz, E.; Juszczyk, M. Formula for Determining the Construction Workers Productivity Including Environmental Factors. Buildings 2019, 9, 240. https://doi.org/10.3390/buildings9120240
Malara J, Plebankiewicz E, Juszczyk M. Formula for Determining the Construction Workers Productivity Including Environmental Factors. Buildings. 2019; 9(12):240. https://doi.org/10.3390/buildings9120240
Chicago/Turabian StyleMalara, Jarosław, Edyta Plebankiewicz, and Michał Juszczyk. 2019. "Formula for Determining the Construction Workers Productivity Including Environmental Factors" Buildings 9, no. 12: 240. https://doi.org/10.3390/buildings9120240
APA StyleMalara, J., Plebankiewicz, E., & Juszczyk, M. (2019). Formula for Determining the Construction Workers Productivity Including Environmental Factors. Buildings, 9(12), 240. https://doi.org/10.3390/buildings9120240







