Probabilistic Seismic Assessment of Existing Masonry Buildings
Abstract
:1. Introduction
2. Assessment of the Seismic Performance of Existing Masonry Buildings
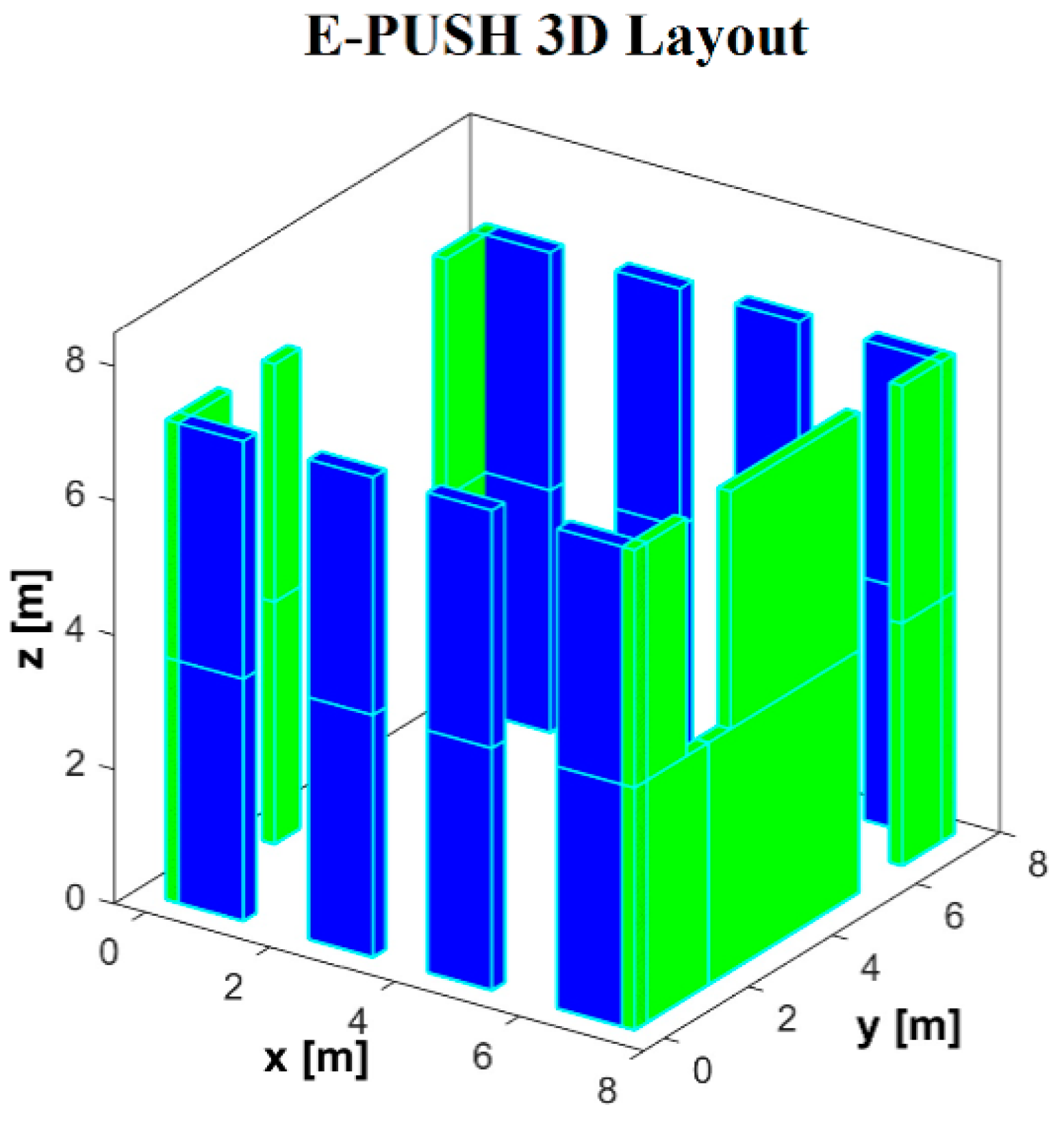
2.1. The E-PUSH Program
- only lateral stiffness of masonry walls is taken into account, disregarding transverse stiffness;
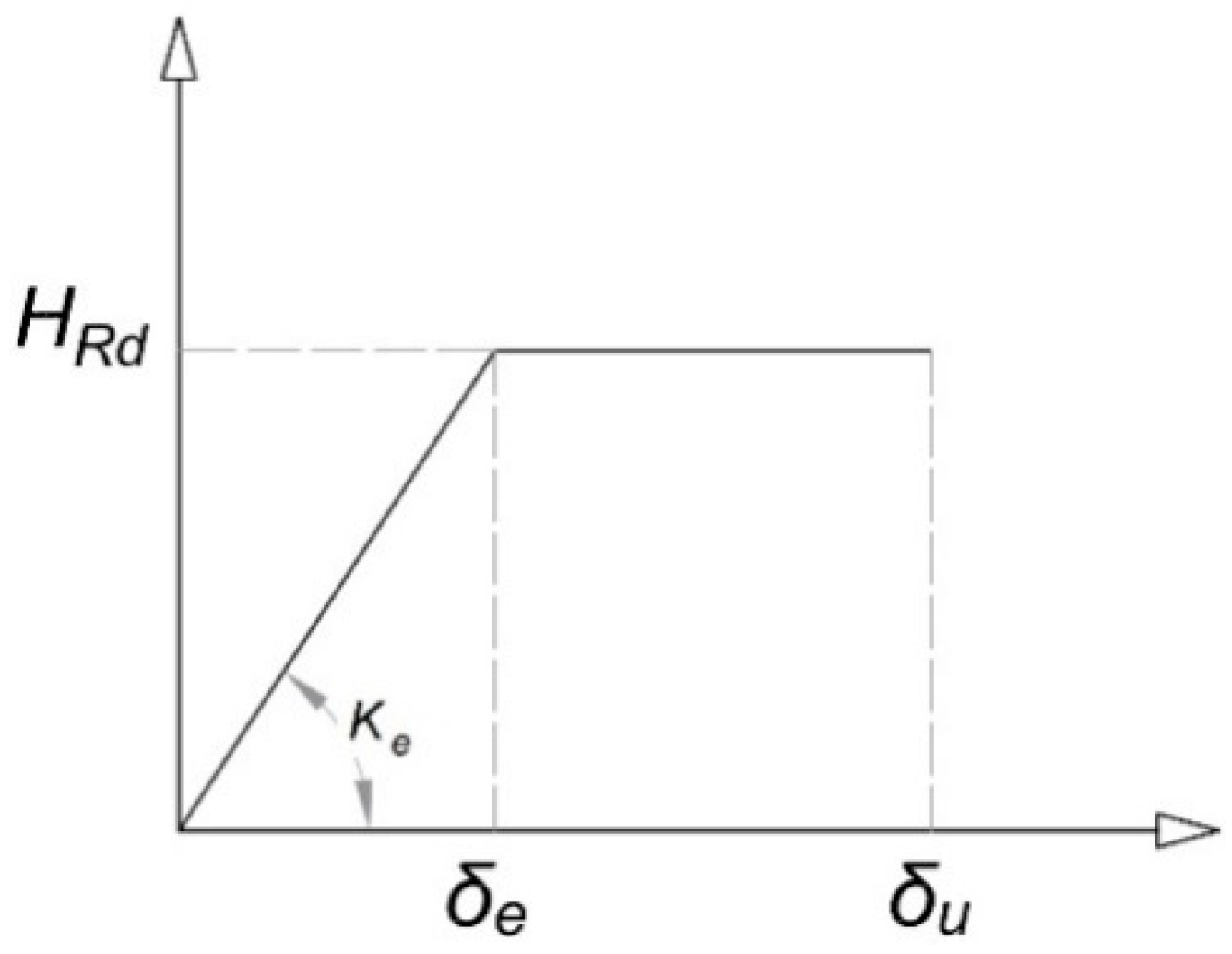
- horizontal force-lateral displacement diagram of the wall is elastic-plastic, with the plastic plateau limited by the elastic drift and the ultimate drift .
- verification is performed in terms of seismic capacity and demand using the acceleration-displacement response spectra (ADRS) taking into account the story displacements.
- , the wall is still in the elastic range;
- , the wall is in the plastic range, it achieved its shear force resistance and its equivalent stiffness is reduced;
- , the wall sustains only vertical loads and its shear resistance and its lateral stiffness are set to zero.
- the non-linear capacity curve of the structure is transformed in an equivalent bi-linear elastic-plastic curve as described in [14]; the curve is characterized by the maximum force , calculated averaging the maximum base shear in the non-linear capacity curve and the base shear corresponding to the attainment of the elastic limit; by the yield displacement , evaluated as the ratio between and the effective stiffness of the structure ; and by the ultimate displacement which is the maximum displacement in the capacity curve;
- the bi-linear, force-displacement capacity curve, , of the multi-degree of freedom (MDOF) system is converted in an acceleration-displacement, , capacity diagram, for an equivalent single degree of freedom (SDOF) system, according to the following formulaewhere Γ is the mass participation factor given byand is the mass of the equivalent SDOF system.
- 3.
- in order to obtain the demand diagram, the elastic design spectrum defined in the Italian Building code [15] from the standard pseudo acceleration-natural period, is converted into the pseudo acceleration-displacement format through:
- 4.
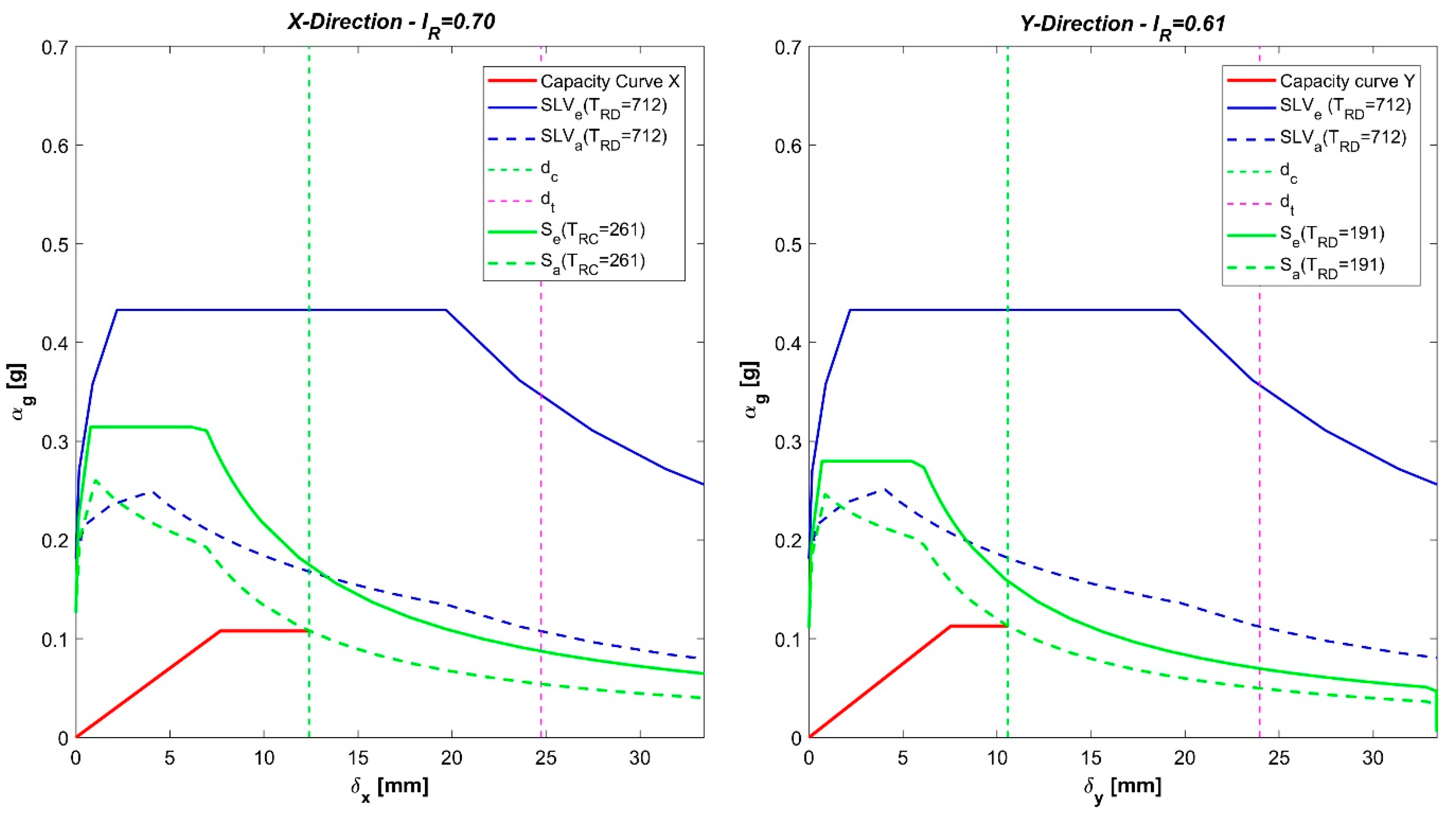
- the capacity spectrum and demand spectrum curves are plotted in the same graph, to define displacement demand. If the capacity curve intersects the demand curve, the displacement demand is assumed equal to the intersection point . Otherwise, the displacement demand is determined starting from the intersection of the radial line corresponding to the elastic period of the structure with the elastic design spectrum defining the acceleration demand . A reduction factor is defined as the ratio between the acceleration demand and the yield acceleration Sa,y.
- 5.
- the seismic performance of the structure is evaluated comparing the displacement demand with the ultimate displacement defined by the capacity curve .
- the bi-linear capacity curve of the structure (red solid line);
- the design spectrum (blue solid curve) for a return period of 712 years (), referring to the ultimate limit state for life safety () of occupants in a given location (Florence Municipality in this case);
- the design inelastic spectrum (blue dashed curve);
- the displacement demand (scarlet dashed line) to be compared with the ultimate displacement (green dashed line);
- the elastic spectrum (green solid curve) for the return period TRC consistent with the capacity of the structure () and the corresponding inelastic spectrum (green dashed curve).
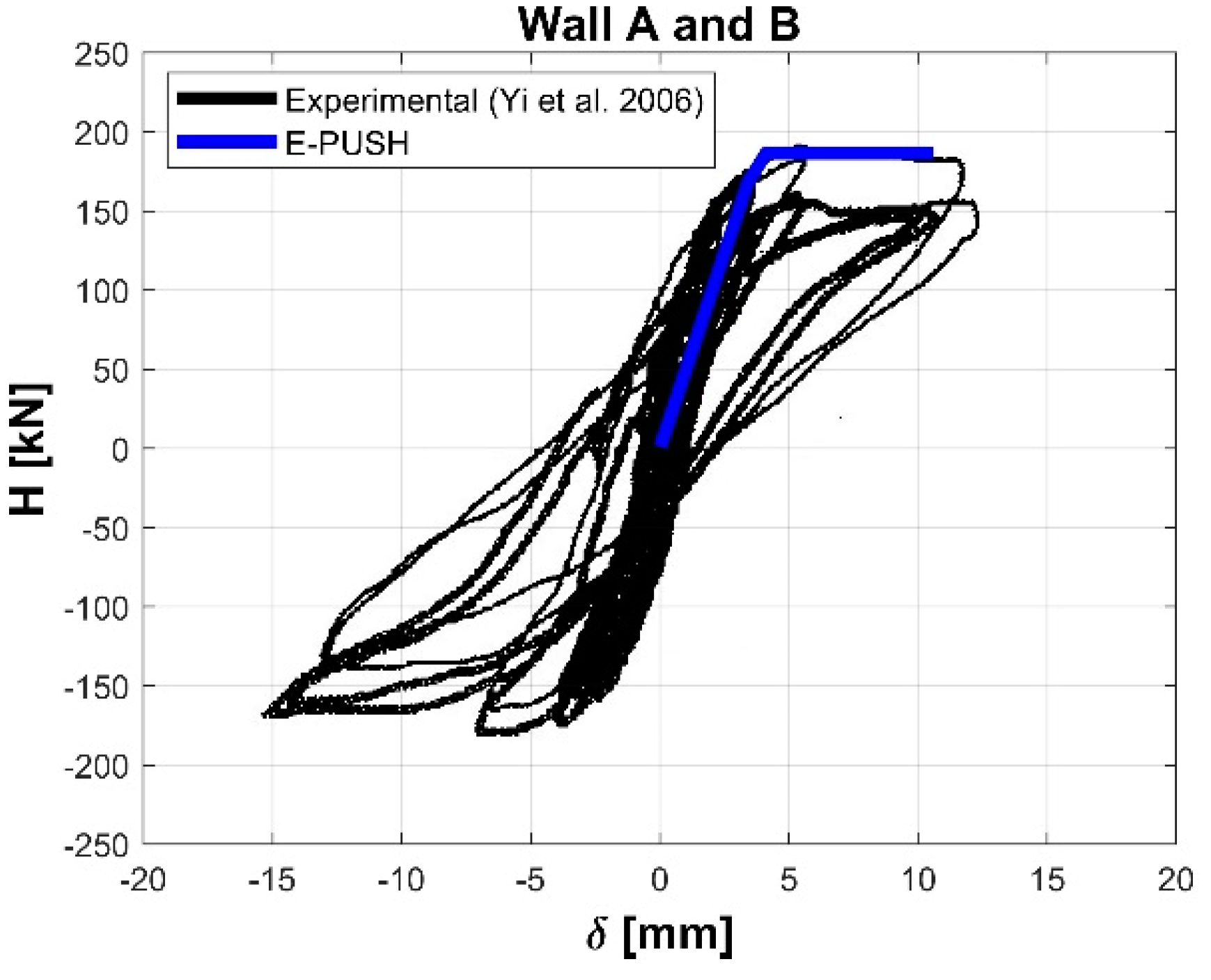
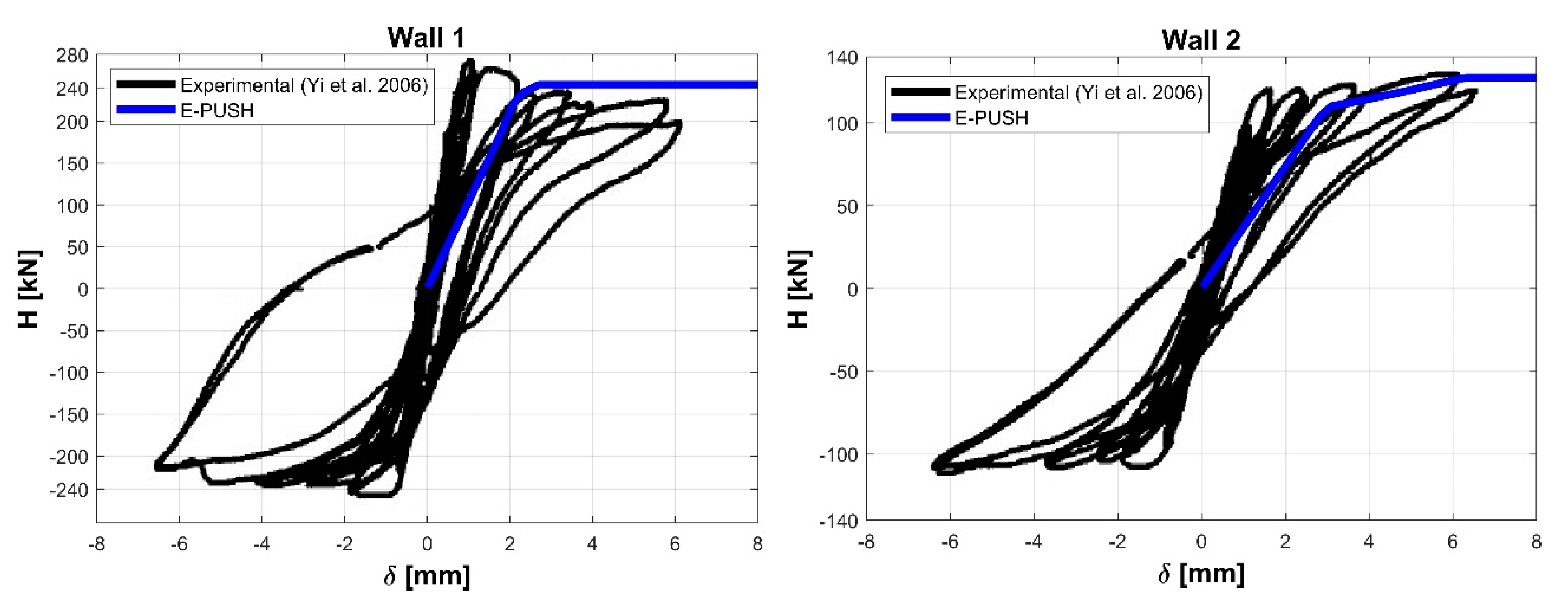
2.2. Validation of the E-PUSH Program
2.3. Challenges in the Assessment of the Seismic Performance
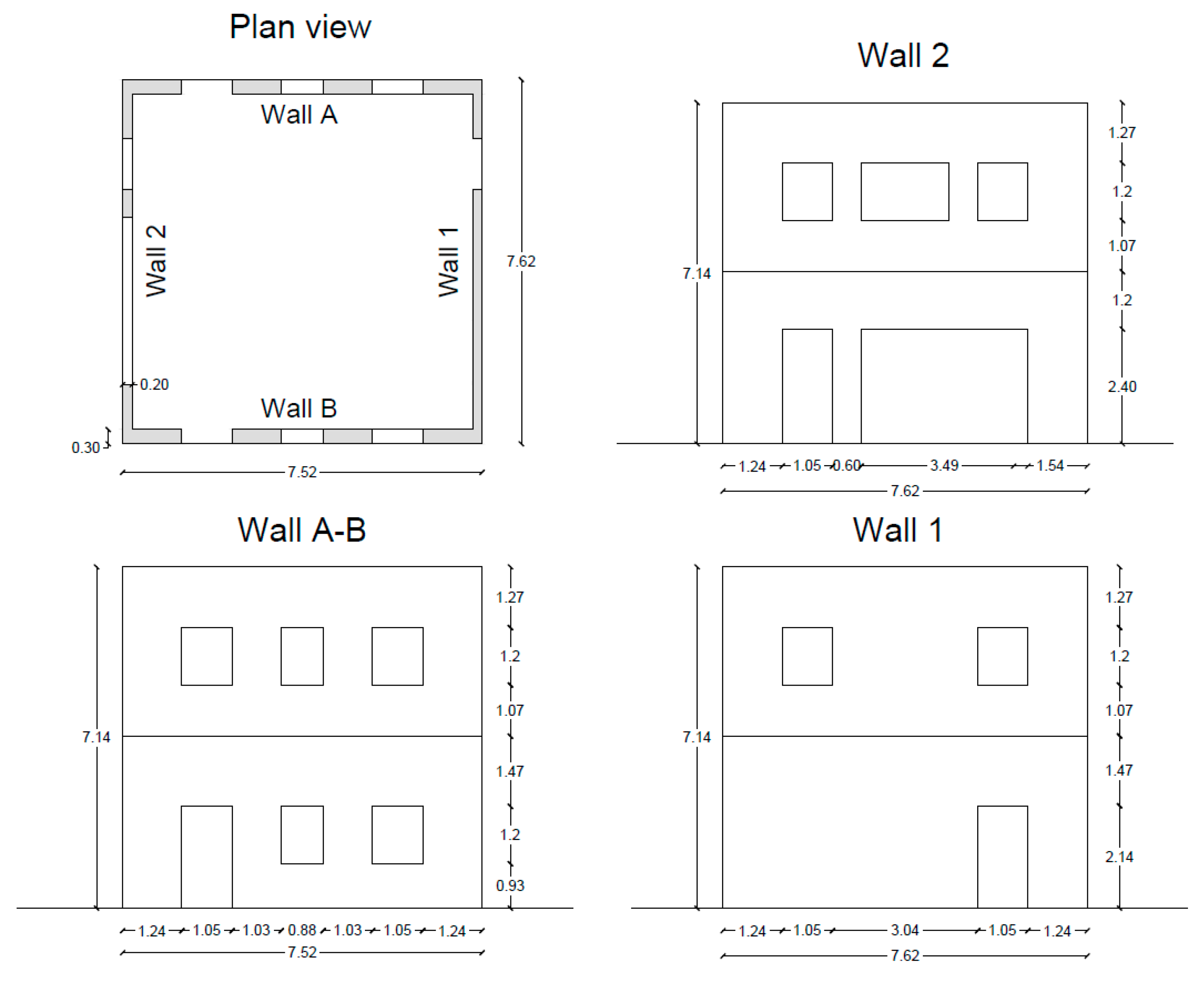
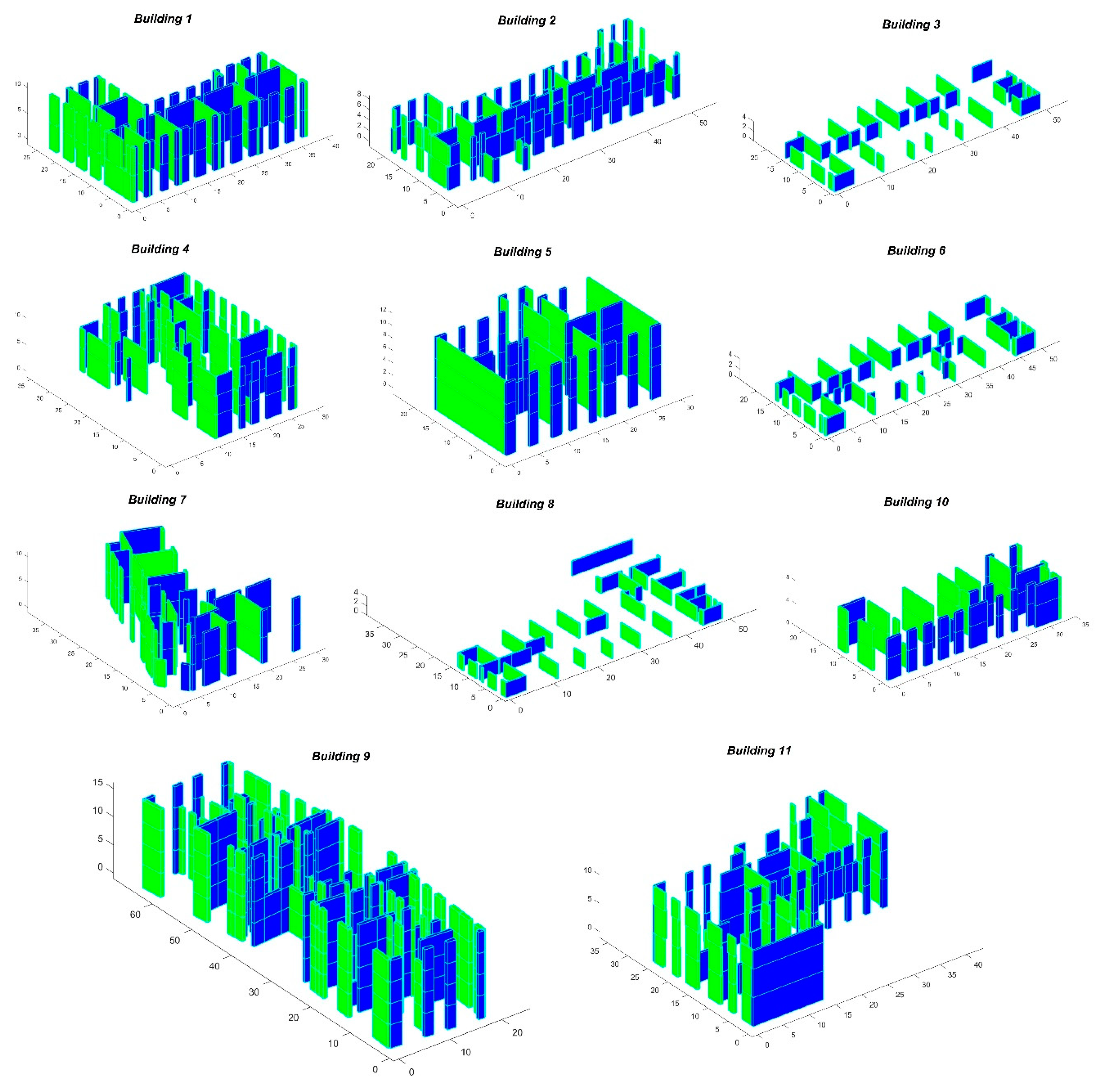
3. Case Studies
4. Methodology
4.1. Identification of Uncertain Parameters
- the shear modulus G and the elastic modulus E of masonry;
- the shear strength ;
- the ultimate displacement .
4.2. Sensitivity Analysis
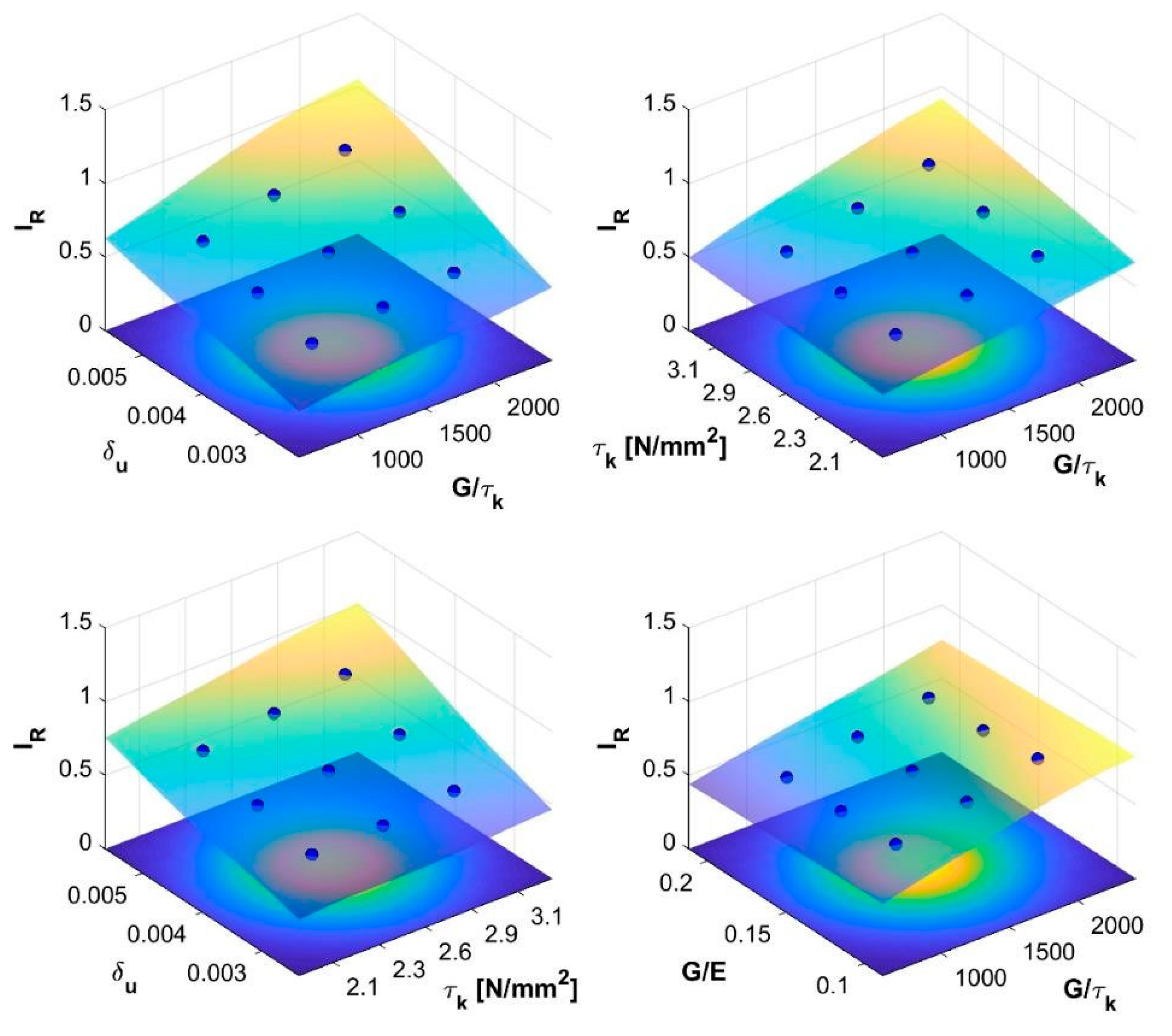
4.2.1. Response Surface via generalized Polynomial Chaos Expansion
- in terms of and , assuming mean values for and ;
- in terms of and , assuming mean values for and ;
- in terms of and , assuming mean values for and ;
- in terms of and assuming mean values for and .
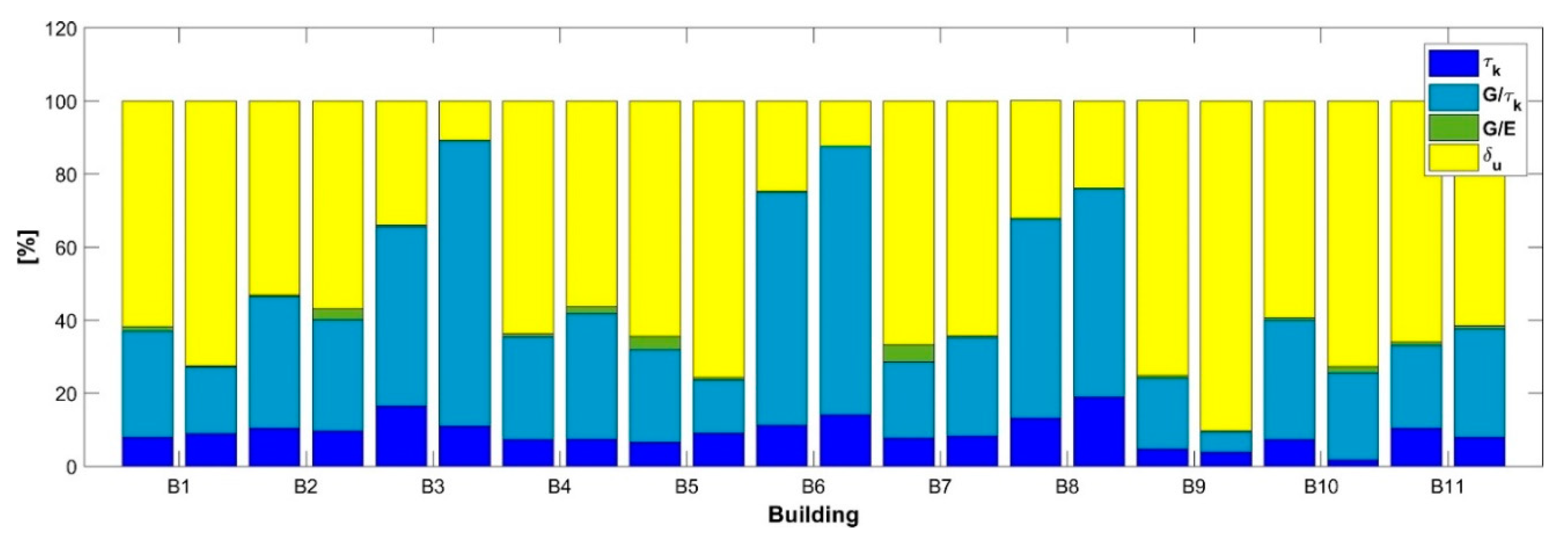
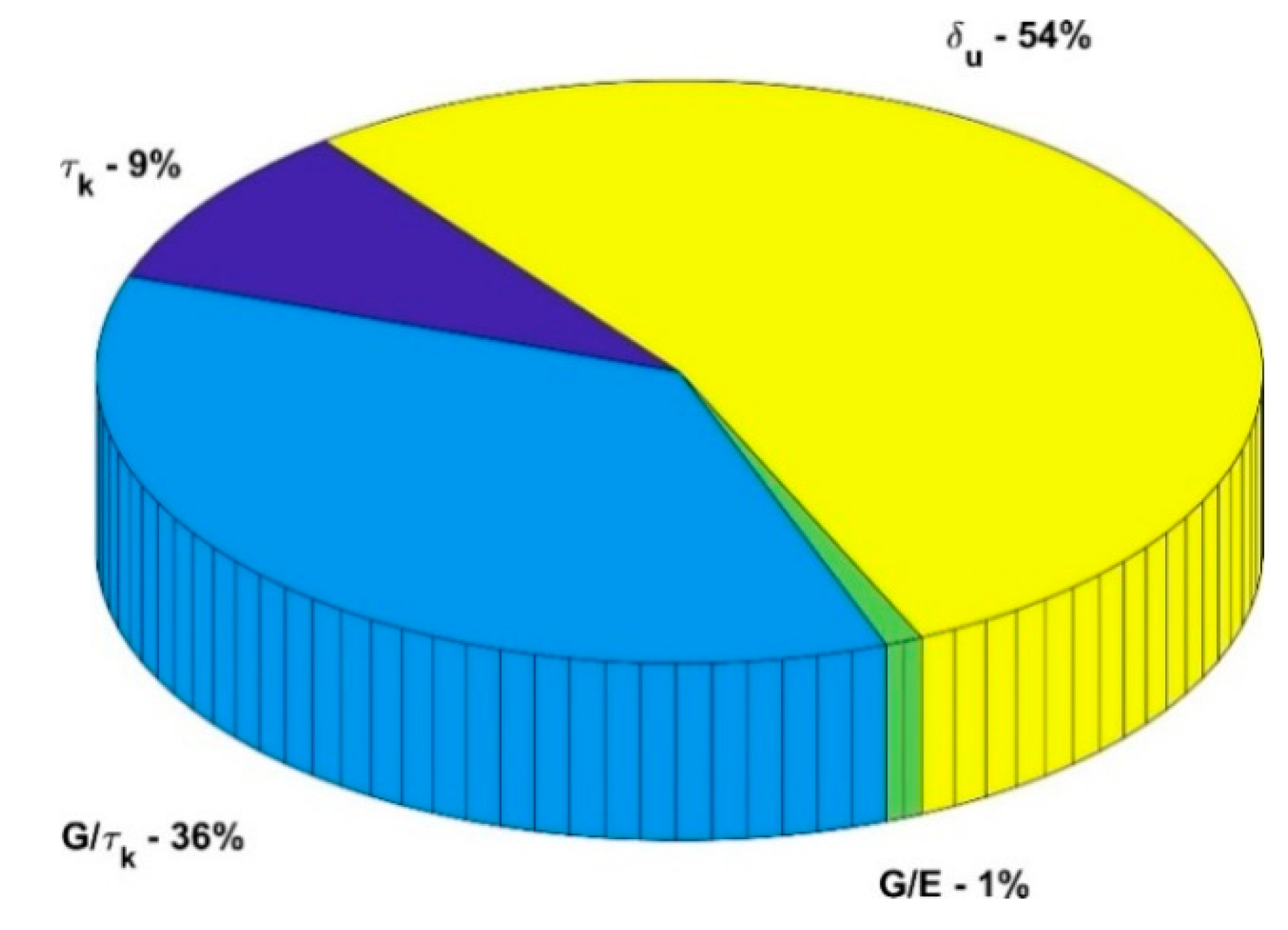
4.2.2. Evaluation of Sobol Indices
4.3. Uncertainty Quantification
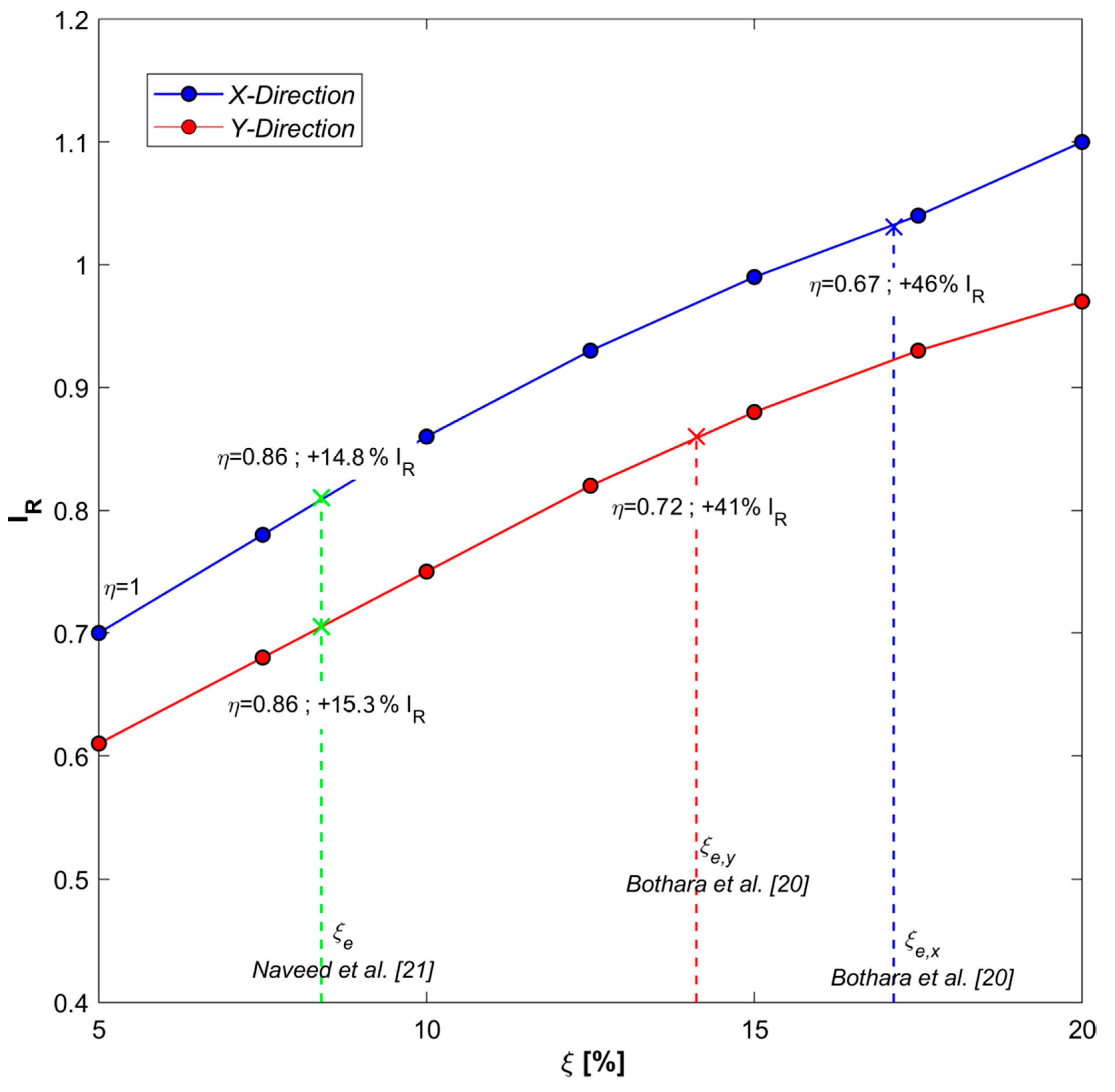
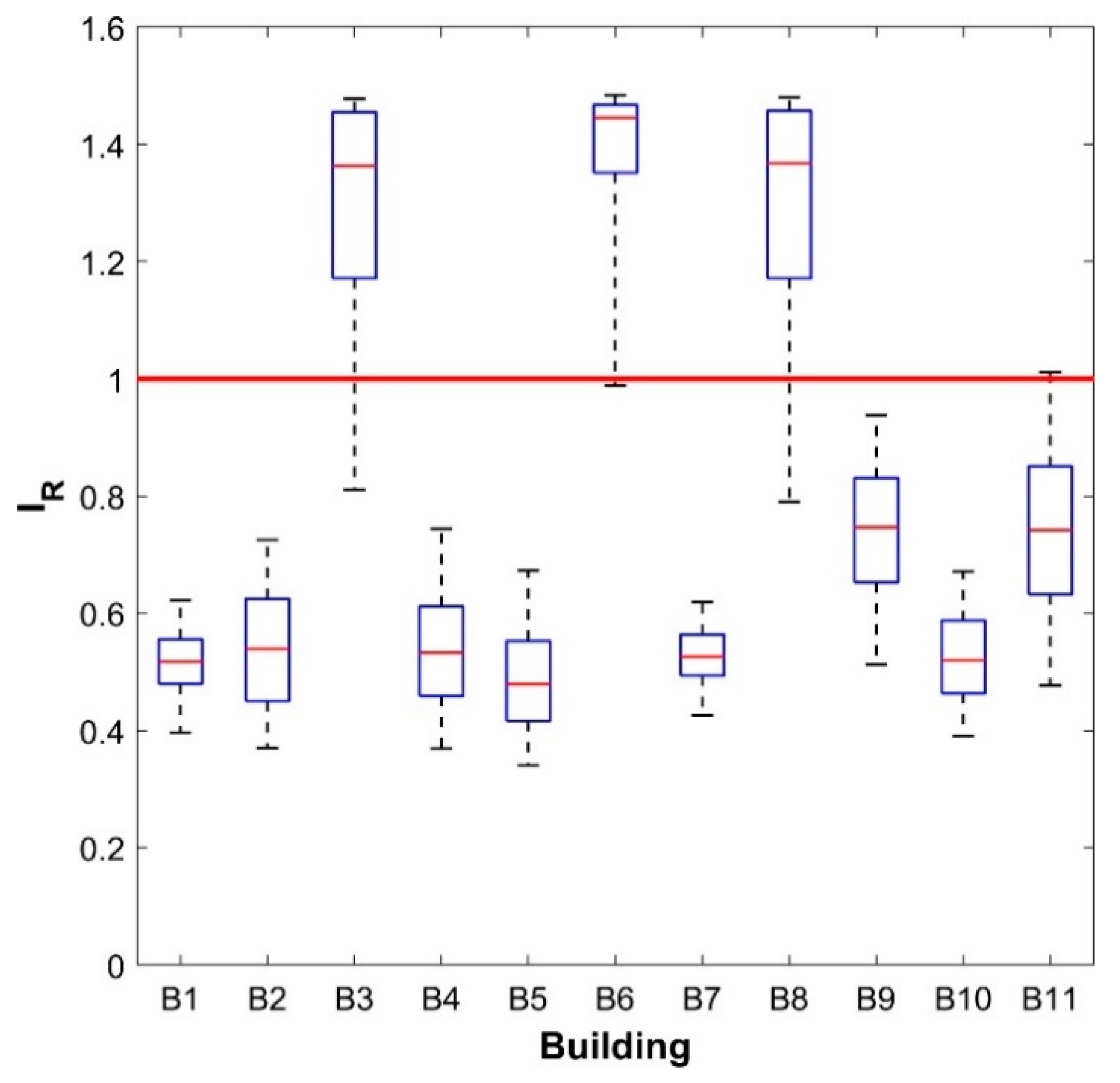
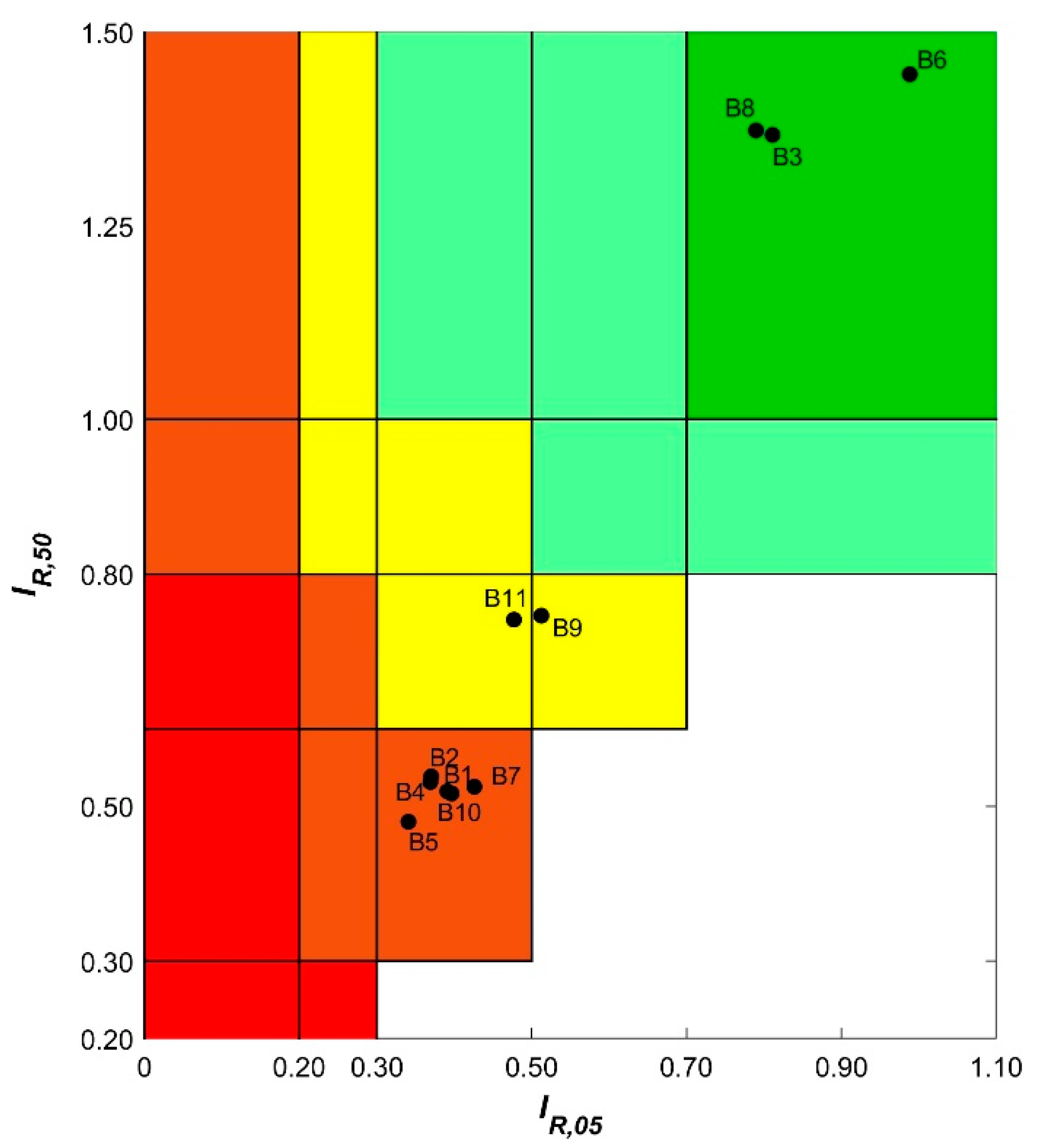
5. Seismic Performance Classification
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Croce, P.; Beconcini, M.L.; Formichi, P.; Cioni, P.; Landi, F.; Mochi, C.; Castelluccio, R. Expeditious assessment of seismic vulnerability of existing buildings from a statistic sample of school buildings, property of the Comune di Firenze (in Italian). Proceedings of XVII convegno ANIDIS “L’ingegneria sismica in Italia”, Pistoia, Italy, 17–21 September 2017; Pisa University Press: Pisa, Italy. [Google Scholar]
- Roca, P.; Cervera, M.; Gariup, G.; Luca, P. Structural analysis of masonry historical constructions. Classical and advanced approaches. Arch. Comput. Methods Eng. 2010, 17, 299–325. [Google Scholar] [CrossRef]
- Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- Croce, P.; Beconcini, M.L.; Formichi, P.; Cioni, P.; Landi, F.; Mochi, C.; Giuri, R. Influence of mechanical parameters on non linear static analysis of masonry walls: A relevant case study. Procedia Struct. Integr. 2018, 11, 331–338. [Google Scholar] [CrossRef]
- Borri, A.; Corradi, M.; Castori, G.; De Maria, A. A method for the analysis and classification of historic masonry. Bull. Earthq. Eng. 2015, 13, 2647–2665. [Google Scholar] [CrossRef]
- Bracchi, S.; Rota, M.; Magenes, G.; Penna, A. Seismic assessment of masonry buildings accounting for limited knowledge on materials by Bayesian updating. Bull. Earthq. Eng. 2016, 14, 2273–2297. [Google Scholar] [CrossRef]
- Beconcini, M.L.; Cioni, P.; Croce, P.; Formichi, P.; Landi, F.; Mochi, C. Non-linear static analysis of masonry buildings under seismic actions. In Proceedings of the 12th International Multi-Conference on Society, Cybernetics and Informatics: IMSCI 2018, Orlando, FL, USA, 8–11 July 2018. [Google Scholar]
- Croce, P.; Holicky, M. Operational Methods for the Assessment and Management of Aging Infrastructure; TEP: Pisa, Italy, 2015. [Google Scholar]
- Tomazevic, M.; Turnsek, V.; Tertelj, S. Computation of the Shear Resistance of Masonry Buildings; Report ZRMK-ZK; Institute for Testing and Research in Materials and Structures: Ljubljana, Slovenia, 1978. (In Slovene) [Google Scholar]
- Tomazevic, M. Improvement of Computer Program POR; Report ZRMK-IK; Institute for Testing and Research in Materials and Structures: Ljubljana, Slovenia, 1978. (In Slovene) [Google Scholar]
- Regione Autonoma Friuli Venezia Giulia. TD n.2—Guidelines for Strengthening and Repair of Masonry Buildings; Gruppo Interdisciplinare Centrale: Udine, Italy, 1980. (In Italian) [Google Scholar]
- Ministry of Public Works. Guidelines for Application of Structural Code for Strengthening and Repair of Masonry Buildings; Istituto Poligrafico e Zecca dello Stato: Roma, Italy, 1981. (In Italian) [Google Scholar]
- Magenes, G. A method for pushover analysis in seismic assessment of masonry buildings. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Fajfar, P.; Eeri, M. A Nonlinear Analysis Method for Performance Based Seismic Design. Earthq. Spectra 2000, 16, 573–592. [Google Scholar] [CrossRef]
- Italian Ministry of Infrastructure and Transport. NTC 2018—Italian Building Code; D.M. 17 January 2018; Istituto Poligrafico e Zecca dello Stato: Roma, Italy, 2018. (In Italian) [Google Scholar]
- Vidic, T.; Fajfar, P.; Fischinger, M. Consistent inelastic design spectra: Strength and displacement. Earthq. Eng. Struct. Dyn. 1994, 23, 502–521. [Google Scholar] [CrossRef]
- Miranda, E.; Bertero, V.V. Evaluation of Strength Reduction Factors for Earthquake-Resistant Design. Earthq. Spectra 1994, 10, 357–379. [Google Scholar] [CrossRef]
- Miranda, E. Inelastic displacement ratios for displacement based earthquake resistant design. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- EN1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Brussels, Belgium, 2004. [Google Scholar]
- Bothara, J.K.; Dhakal, R.P.; Mander, J.B. Seismic performance of an unreinforced masonry building: An experimental investigation. Earthq. Eng. Struct. Dyn. 2010, 39, 45–68. [Google Scholar] [CrossRef]
- Ahmad, N.; Crowley, H.; Pinho, R.; Ali, Q. Simplified formulae for the displacement capacity, energy dissipation, and characteristic vibration period of brick masonry buildings. In Proceedings of the 8IMC-International Masonry Conference, Dresden, Germany, 4–7 July 2010; pp. 1385–1394. [Google Scholar]
- Yi, T.; Moon, F.L.; Leon, R.T.; Kahn, L.F. Lateral Load Tests on a Two-Story Unreinforced Masonry Building. J. Struct. Eng. 2006, 132, 643–652. [Google Scholar] [CrossRef]
- Aedes Software. Aedes PCM User’s Manual; Aedese Software per Ingegneria Civile: San Miniato, Italy, 2016. (In Italian) [Google Scholar]
- Bosiljkov, V.Z.; Totoev, Y.Z.; Nichols, J.M. Shear modulus and stiffness of brickwork masonry: An experimental perspective. Struct. Eng. Mech. 2005, 20, 21–43. [Google Scholar] [CrossRef]
- Croce, P.; Beconcini, M.L.; Formichi, P.; Cioni, P.; Landi, F.; Mochi, C.; De Lellis, F.; Mariotti, E.; Serra, I. Shear modulus of masonry walls: A critical review. Procedia Struct. Integr. 2018, 11, 339–346. [Google Scholar] [CrossRef]
- Petry, S.; Beyer, K. Influence of boundary conditions and size effect on the drift capacity of URM walls. Eng. Struct. 2014, 65, 76–88. [Google Scholar] [CrossRef]
- Wilding, B.V.; Beyer, K. Analytical and empirical models for predicting the drift capacity of modern unreinforced masonry walls. Earthq. Eng. Struct. Dyn. 2018, 47, 2012–2031. [Google Scholar] [CrossRef]
- Beconcini, M.L.; Cioni, P.; Croce, P.; Formichi, P.; Landi, F.; Mochi, C. Influence of shear modulus and drift capacity on non-linear static analysis of masonry buildings. In IABSE Symposium, Guimaraes 2019: Towards a Resilient Built Environment Risk and Asset Management, Report; International Association for Bridge and Structural Engineering (IABSE): Zurich, Switzerland, 2019; pp. 876–883. ISBN 978-385748163-5. [Google Scholar]
- Italian Public Works Council. Guidelines for Application of Italian Building Code; Istituto Poligrafico e Zecca dello Stato: Roma, Italy, 2019. (In Italian) [Google Scholar]
- Tomazevic, M. Shear resistance of masonry walls and Eurocode 6: Shear versus tensile strength of masonry. Mater. Struct. 2009, 42, 889–907. [Google Scholar] [CrossRef]
- Lang, K. Seismic Vulnerability of Existing Buildings. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2002. [Google Scholar]
- Ganz, H.R.; Thürlimann, B. Versuche an Mauerwerksscheiben unter Normalkraft und Querkraft; Inst. für Baustatik und Konstruktion, ETH Zürich, Report Nr. 7502-4; Birkhäuser Verlag: Basel, Switzerland, 1984. [Google Scholar]
- EN1998-3. Eurocode 8: Design of Structures for Earthquake Resistance—Part 3: Assessment and Retrofitting of Buildings; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Croce, P.; Beconcini, M.L.; Formichi, P.; Landi, F.; Puccini, B.; Zotti, V. Seismic risk evaluation of existing masonry buildings: Methods and uncertainties. In IABSE Congress New York: The Evolving Metropolis; IABSE: Zurich, Switzerland, 2019; pp. 2510–2515. ISBN 978-385748165-9. [Google Scholar]
- EN1996-1-1. Eurocode 6: Design of Masonry Structures—Part 1-1: Common Rules for Reinforced and Unreinforced Masonry Structures; CEN: Brussels, Belgium, 2005. [Google Scholar]
- Zimmermann, T.; Strauss, A.; Wendner, R. Old Masonry under Seismic Loads: Stiffness Identification and Degradation. In Proceedings of the Structures Congress 2011 ASCE, Las Vegas, NV, USA, 14–16 April 2011; pp. 1736–1747. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements—A Spectral Approach; Springer: Berlin, Germany, 1991. [Google Scholar]
- Landi, F.; Marsili, F.; Friedman, N.; Croce, P. A comparison of stochastic inverse methods with sampling and functional-based linear and non-linear update procedures Beton. und Stahlbetonbau Spezial 2018. In Proceedings of the 16th International Probabilistic Workshop, Extended Abstract, Vienna, Austria, 12–14 September 2018. [Google Scholar] [CrossRef]
- Xiu, D. Numerical Methods for Stochastic Computations; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Matthies, H.G.; Zander, E.K.; Rosic, B.V.; Litvinenko, A.; Pajonk, O. Inverse Problems in a Bayesian Setting. In Computational Methods for Solids and Fluids; Ibrahimbegovic, A., Ed.; Springer: Cham, Switzerland, 2016; Volume 41, pp. 245–286. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Sobol, I. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Saltelli, A.; Sobol, I. About the use of rank transformation in sensitivity of model output. Reliab. Eng. Syst. Saf. 1995, 50, 225–239. [Google Scholar] [CrossRef]

| Random Variable | COV | |
|---|---|---|
| Mean Value for each masonry class in [29], e.g., 0.026 N/mm2 for stone | 0.14 | |
| 1500 | 0.3 | |
| 0.15 | 0.2 | |
| 0.004 | 0.2 |
| School Building | |||
|---|---|---|---|
| B1 | 0.40 | 0.52 | 0.62 |
| B2 | 0.37 | 0.54 | 0.73 |
| B3 | 0.81 | 1.37 | 1.48 |
| B4 | 0.37 | 0.53 | 0.74 |
| B5 | 0.34 | 0.48 | 0.67 |
| B6 | 0.99 | 1.45 | 1.48 |
| B7 | 0.43 | 0.53 | 0.62 |
| B8 | 0.79 | 1.37 | 1.48 |
| B9 | 0.51 | 0.75 | 0.94 |
| B10 | 0.39 | 0.52 | 0.67 |
| B11 | 0.48 | 0.74 | 1.01 |
| <0.2 | 0.2–0.3 | 0.3–0.5 | 0.5–0.7 | >0.7 | ||
|---|---|---|---|---|---|---|
| <0.3 | E | E | - | - | - | |
| 0.3–0.6 | E | D | D | - | - | |
| 0.6–0.8 | E | D | C | C | - | |
| 0.8–1 | D | C | C | B | B | |
| >1 | D | C | B | B | A | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croce, P.; Landi, F.; Formichi, P. Probabilistic Seismic Assessment of Existing Masonry Buildings. Buildings 2019, 9, 237. https://doi.org/10.3390/buildings9120237
Croce P, Landi F, Formichi P. Probabilistic Seismic Assessment of Existing Masonry Buildings. Buildings. 2019; 9(12):237. https://doi.org/10.3390/buildings9120237
Chicago/Turabian StyleCroce, Pietro, Filippo Landi, and Paolo Formichi. 2019. "Probabilistic Seismic Assessment of Existing Masonry Buildings" Buildings 9, no. 12: 237. https://doi.org/10.3390/buildings9120237
APA StyleCroce, P., Landi, F., & Formichi, P. (2019). Probabilistic Seismic Assessment of Existing Masonry Buildings. Buildings, 9(12), 237. https://doi.org/10.3390/buildings9120237







