Durability of Stone Cladding in Buildings: A Case Study of Marble Slabs Affected by Bowing
Abstract
:1. Introduction
- Density: 2680 to 2710 (kg/m3);
- Compressive strength: 79 to 100 (×106 Pa);
- Flexural strength/Modulus of rupture: 9 to 26 (×106 Pa);
- Elasticity modulus (dynamic/static): 40 to 50/16 to 25 (×109 Pa);
- Poisson coefficient: 0.25 to 0.41.
2. Marble Slabs Affected by Bowing and Wind Pressure—A Case Study
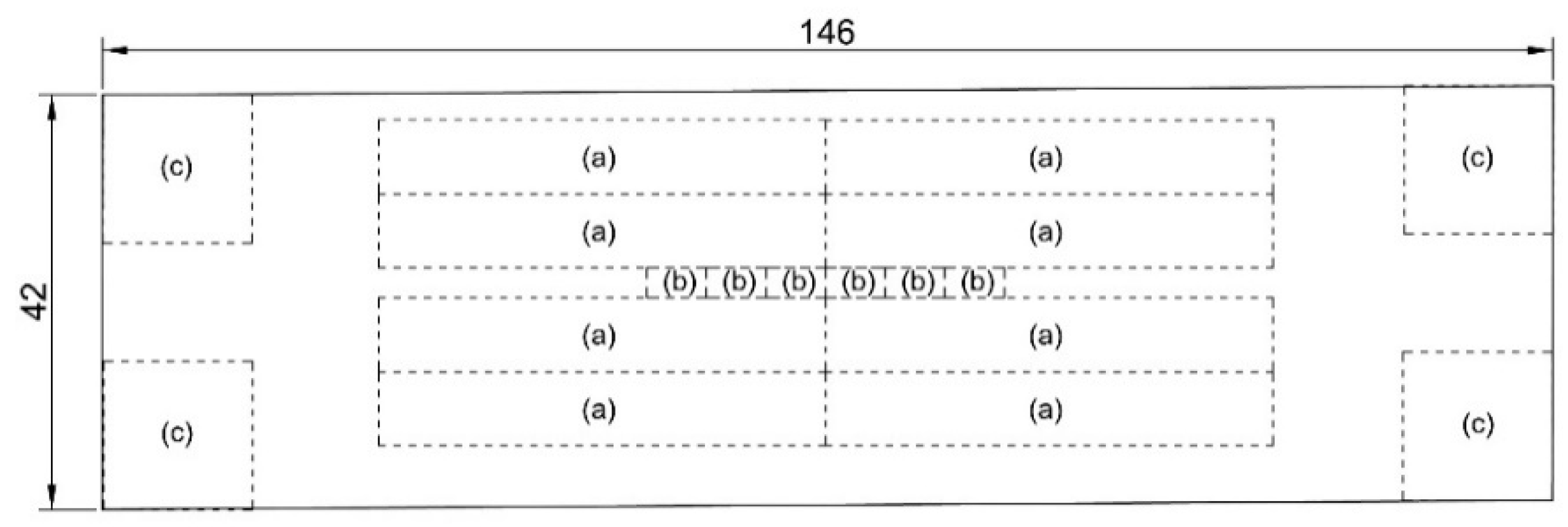
2.1. Construction Aspects of the Stone Cladding
2.2. Bowing of the Marble Cladding
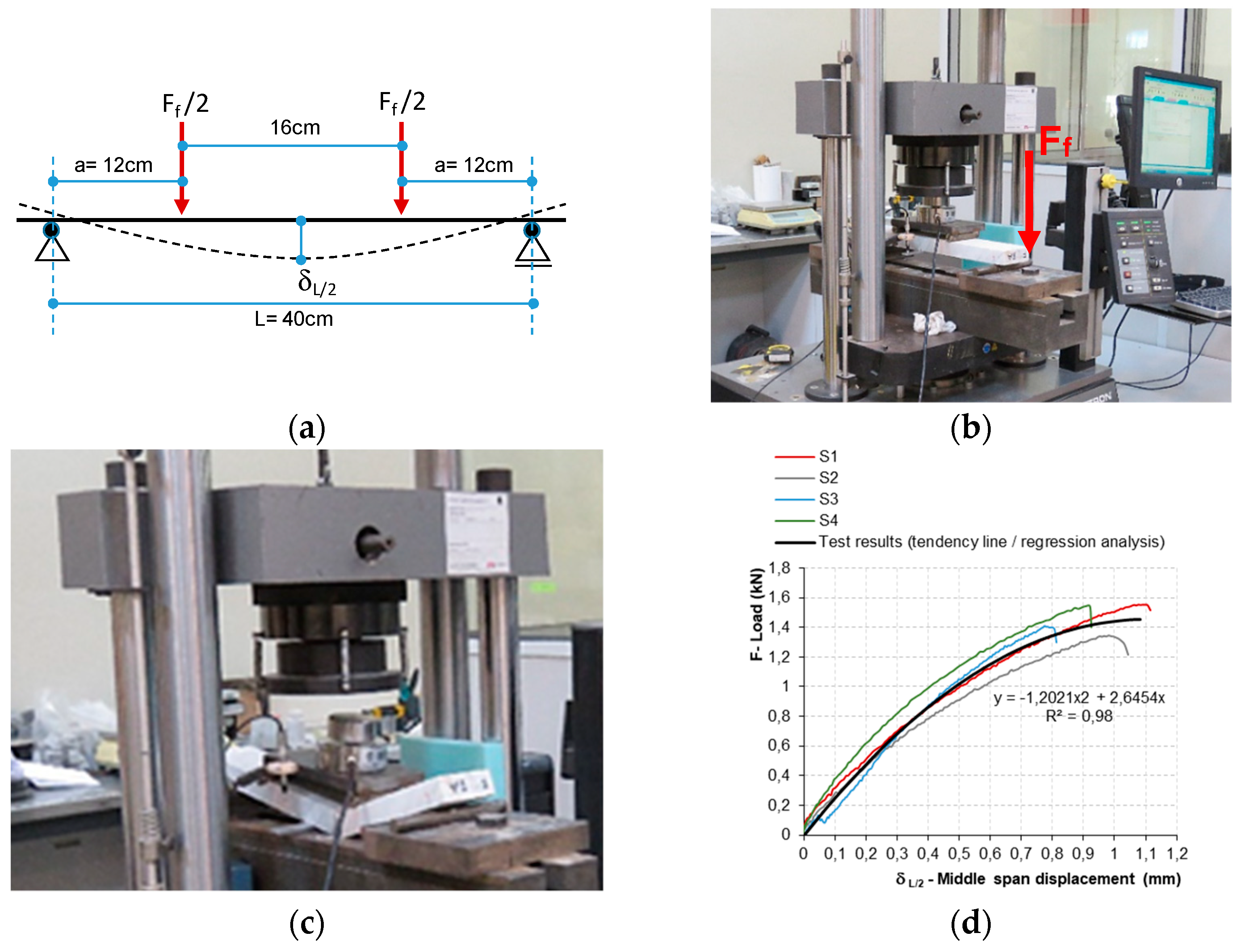
2.3. Experimental Tests
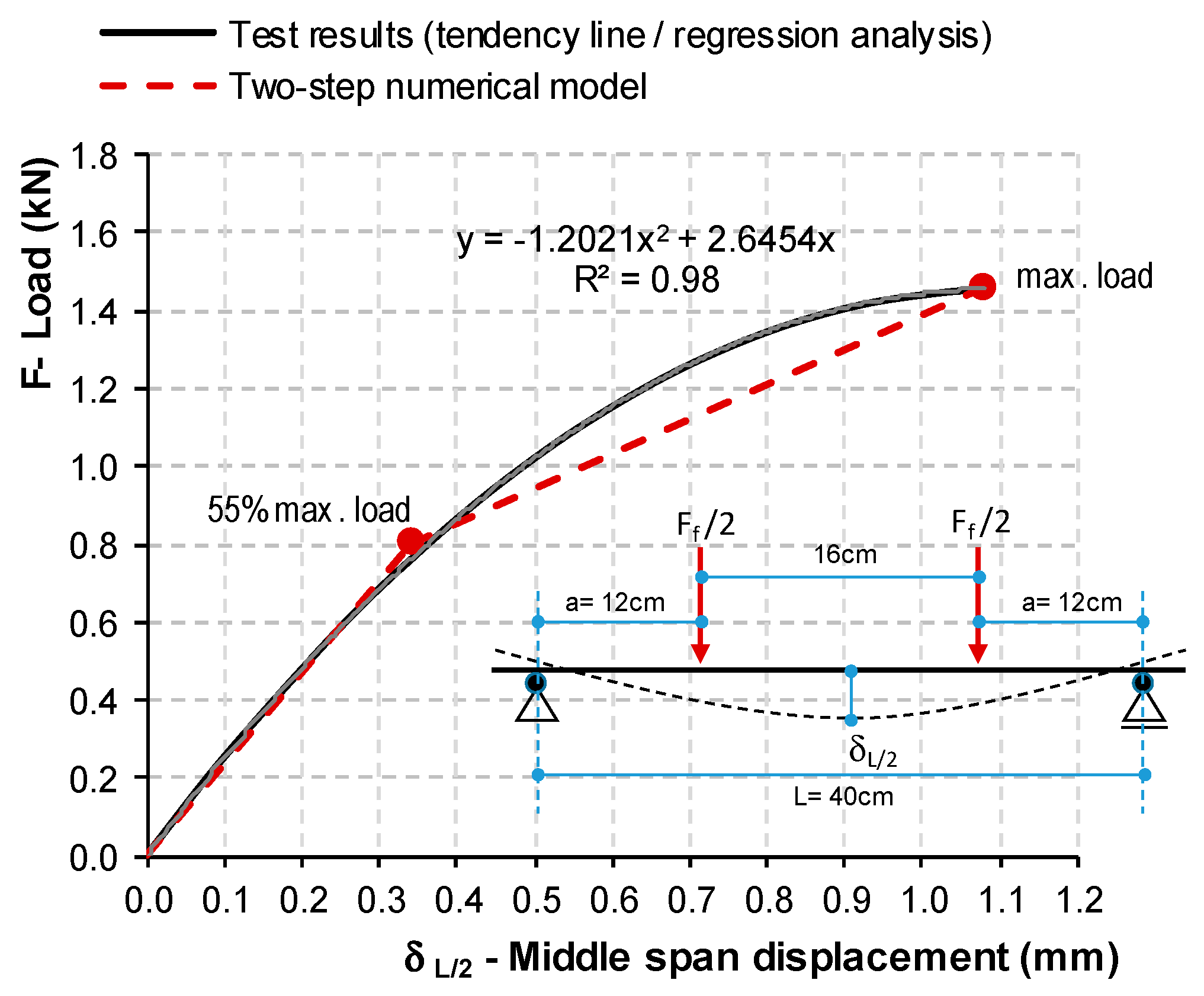
2.4. Numerical Simulations
- For h ≤ 9 m − Wk = 1.3 kN/m2;
- For 9 m < h ≤ 18 m − Wk = 2.1 kN/m2.
- Combination SLS: Ssd = Gk + Wk;
- Combination ULS: Ssd = 1.35 Gk + 1.5 Wk.
- Rrk—Characteristic value obtained from statistical analysis of the lab tests results obtained in this study (minimum values obtained from a log-normal distribution with 75% confidence level and 5% fractile distribution—see Table 1);
- γm—Partial safety factor determined through a semi-probabilistic approach adapted for stone cladding [18], using the experimental results obtained from lab tests performed in this study (for ULS γm equal to 2.4 and for SLS γm equal to 1);
- η—Conversion factor to take into account several effects, namely temperature and humidity (since the stone in this case study was not in its initial conditions, i.e., it was submitted to 15 years of climate exposure, this factor was assumed equal to 1).
2.5. Lab Tests Results
- The mineralogical/petrographic study revealed that the marble was made mainly of calcite, thus classified as a calcite marble, although containing other minerals in smaller quantities (dolomite, quartz, biotite and chlorite), and possessing a homogenous structure (granoblastic texture of fine equigranular grains);
- The variation coefficient (C.V.) presents higher values for marble stone affected by bowing, being lower than 20% for most of the properties, except for the case of breaking load at the dowel hole (without bowing, 38%), which may be related to insufficient fixing of the test samples (provided by clamps);
- Considering the experimental force-vertical displacements (Ff-δL/2) obtained from flexural tests, the marble exhibits a linear behavior until 40 to 55% of the maximum/breaking load;
- Relatively small differences between stone slabs with and without bowing were found for the flexural strength (5% for the mean value and 20% for the characteristic value) and for the compressive strength (11% for the mean value and 9% for the characteristic value);
- Therefore, in average terms, there is no significant difference between the mechanical properties of stone slabs with and without bowing, which can be related with the scarce number of samples available for testing in this study;
- The mechanical properties of marble in initial conditions of use (unaffected by aging/deterioration agents) were not available in this case study; however, comparing the experimental results obtained in this study with the range of average values found in literature for similar calcite marbles in initial conditions of use, a reduction between 23% to 70% was found for the flexural strength, 3% to 23% for the compressive strength and 3% to 34% for the static modulus of elasticity;
2.6. Numerical Simulations Results
- The flexural/bending resistance of all marble slabs is verified for serviceability conditions (SLS security ratios are lower than 1, i.e., between 0.3 to 0.7), therefore presenting a low risk of damage/fracture due to bending caused by moderate wind pressures (as observed in the inspections made);
- The load resistance at the dowel hole for serviceability conditions is not verified for slabs located higher than 9 m (SLS security ratios are, in general, higher than 1, i.e., between 1.2 to 1.7), thus presenting a high risk of occurring permanent damage/fracture near the slabs fixing points (as observed in the inspections made—see Figure 3);
- The bending/flexural resistance and load resistance at the dowel hole are not verified for almost every case analyzed in ultimate limit states (ULS security ratios between 1 to 2.6 for bending and 1.2 to 6 for the load dowel hole), meaning that the stone slabs have a high risk of collapsing when exposed to extreme wind pressures, especially due to failure of the marble near the slab fixing points (ULS security ratios for the load dowel hole are higher than bending stress).
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Loughran, P. Failed Stone: Problems and Solutions with Concrete and Masonry; Birkhäuser—Publishers for Architecture: Basel, Switzerland, 2007; pp. 1–159. [Google Scholar]
- Neto, N.; de Brito, J. Validation of an inspection and diagnosis system for anomalies in natural stone cladding (NSC). Constr. Build Mater. 2012, 30, 224–236. [Google Scholar] [CrossRef]
- Akesson, U.; Lindqvist, J.E.; Schouenborg, B.; Grelk, B. Relationship between microstructure and bowing properties of calcite marble claddings. Bull. Eng. Geol. Environ. 2006, 65, 73–79. [Google Scholar] [CrossRef]
- Siegesmund, S.; Ruedrich, J.; Koch, A. Marble bowing: Comparative studies of three different public building façade. Environ. Geol. 2008, 56, 473–494. [Google Scholar] [CrossRef]
- Koch, A.; Siegesmund, S. The combined effect of moisture and temperature on the anomalous expansion behaviour of marble. Environ. Geol. 2004, 46, 350–363. [Google Scholar] [CrossRef]
- Erlin, B. Contribution to a better understanding of the mechanism causing dishing failures of the Carrara marble used for outside on building facades. In Dimension Stone Cladding: Design, Construction, Evaluation, and Repair; Hoigard, K.R., Ed.; ASTM International: West Conshohocken, PA, USA, 2000; pp. 71–78. [Google Scholar]
- Beouch, R.; Fichet, O.; Bigas, J.P.; Teyssie, D.; Berthier, B.; Prichystal, J.B. Cracks and stains on facade-cladding made of carbonate rock thin panels. Struct. Surv. 2012, 30, 130–144. [Google Scholar]
- Logan, J.M. On-site and laboratory studies of strength loss in marble on building exteriors. In Fracture and Failure of Natural Building Stones; Kourkoulis, S.K., Ed.; Springer: Houten, The Netherlands, 2006; pp. 345–362. [Google Scholar]
- de Gennaro, R.; Calcaterra, D.; di Girolamo, P.; Langella, A.; de Gennaro, M. Discovering the stone heritage of southern Italy: Technical properties of the Mondragone marble from Campania region. Environ. Geol. 2003, 44, 266–276. [Google Scholar] [CrossRef]
- Papamichos, E.; Papanicolopulos, S.A.; Larsen, I. Mechanical properties and damage diagnosis of natural building stones. In Fracture and Failure of Natural Building Stones; Kourkoulis, S.K., Ed.; Springer: Houten, The Netherlands, 2006; pp. 71–92. [Google Scholar]
- Siegesmund, S.; Dürrast, H. Physical and Mechanical Properties of Rocks. In Stone in Architecture, 4th ed.; Siegesmund, S., Snethlage, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 97–225. [Google Scholar]
- Amaral, P.M.; Fernandes, J.C.; Pires, V.; Rosa, L.G. Ornamental Stones. In Materials for Construction and Civil Engineering; Gonçalves, M.C., Margarido, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 397–445. [Google Scholar]
- Rochas Ornamentais Portuguesas. Available online: http://rop.lneg.pt/rop/ (accessed on 23 January 2018).
- Grelk, B.; Christiansen, C.; Schouenborg, B.; Malaga, K. Durability of Marble Cladding—A Comprehensive Literature Review. J. ASTM Int. 2007, 4, 1–19. [Google Scholar] [CrossRef]
- Bellopede, R.; Castelletto, E.; Schouenborg, B.; Marini, P. Assessment of the European Standard for the determination of resistance of marble to thermal and moisture cycles: Recommendations for improvements. Environ. Earth Sci. 2016, 75, 1–9. [Google Scholar] [CrossRef]
- CEN. EN 16306—Natural Stone Test Methods: Determination of Resistance of Marble to Thermal and Moisture Cycles; European Committee for Standardization: Brussels, Belgium, 2013. [Google Scholar]
- CEN. EN 1991-1-4—Eurocode 1: Actions on Structures, Part 1–4: General Actions—Wind Actions; European Committee for Standardization: Brussels, Belgium, 2010. [Google Scholar]
- Camposinhos, R.S. Stone Cladding Engineering; Springer: Dordrecht, The Netherlands, 2014; pp. 1–171. [Google Scholar]
- ASTM. Dimension Stone Cladding: Design, Construction, Evaluation, and Repair; ASTM International: West Conshohocken, PA, USA, 2000; pp. 1–194. [Google Scholar]
- AFNOR. DTU 55.2 (NF P 65-202-1): Travaux de Bâtiment—Revêtements Muraux Attachés en Pierre Mince—Partie 1: Cahier des Clauses Techniques; Association Française de Normalisation: La Plaine Saint-Denis, France, 2000. [Google Scholar]
- Lewis, M.D. Modern Stone Cladding: Design and Installation of Exterior Dimension Stone Systems; ASTM International: West Conshohocken, PA, USA, 1995; pp. 1–146. [Google Scholar]
- Marble Institute of America. Dimension Stone Design Manual, 8th ed.; Marble Institute of America: East Lorain St. Oberlin, OH, USA, 2016. [Google Scholar]
- Camposinhos, R.S.; Camposinhos, R.A. Dimension-stone cladding design with dowel anchorage. Proc. Inst. Civ. Eng. Constr. Mater. 2009, 162, 95–104. [Google Scholar] [CrossRef]
- Moreiras, S.; Paraguassu, A.; Ribeiro, R. Dimension stone for building facades: Methodology for structural design. Bull. Eng. Geol. Environ. 2008, 67, 53–57. [Google Scholar] [CrossRef]
- Camposinhos, R. Dimension stone design—Partial safety factors: A reliability based approach. Proc. Inst. Civ. Eng. Constr. Mater. 2012, 165, 145–159. [Google Scholar] [CrossRef]
- Piresa, V.; Pacheco, A.; Infante, V.; Amaral, P.M.; Rosa, L.G. Finite element model development applied to portuguese granites for contact analysis of two dowel fixing conditions used in cladding. Key Eng. Mater. 2013, 548, 255–266. [Google Scholar] [CrossRef]
- Camposinhos, R.S.; Camposinhos, R.A. Dimension stone design – kerf anchorage in limestone and marble. Proc. Inst. Civ. Eng. Constr. Mater. 2012, 165, 161–175. [Google Scholar]
- Mahabadi, O.K.; Cottrell, B.E.; Grasselli, G. An example of realistic modelling of rock dynamics problems: FEM/DEM simulation of dynamic Brazilian test on barre granite. Rock Mech. Rock Eng. 2010, 43, 707–716. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic damage model for concrete. Int. J. Solid Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Jankowiak, T.; Lodygowski, T. Identification of parameters of concrete damage plasticity constitutive model. Found. Civ. Environ. Eng. 2005, 6, 53–69. [Google Scholar]
- Sousa, R.; Sousa, H.; Guedes, J. Diagonal compressive strength of masonry samples-experimental and numerical approach. Mater. Struct. 2013, 46, 765–786. [Google Scholar] [CrossRef]
- Sousa, R.; Guedes, J.; Sousa, H. Characterization of the uniaxial compression behaviour of unreinforced masonry—Sensitivity analysis based on a numerical and experimental approach. Arch. Civ. Mech. Eng. 2015, 15, 532–547. [Google Scholar] [CrossRef]
- CEN. EN 1990—Eurocode 0: Basis of Structural Design; European Committee for Standardization: Brussels, Belgium, 2010. [Google Scholar]
- CEN. EN 1469—Natural Stone Products, Slabs for Cladding, Requirements; European Committee for Standardization: Brussels, Belgium, 2015. [Google Scholar]
- EOTA. Kits for External Wall Claddings Mechanically Fixed (EAD 090062-00-0404); European Organization for Technical Assessment: Brussels, Belgium, 2018. [Google Scholar]
- CEN. EN 13161—Natural Stone Test Methods: Determination of Flexural Strength under Constant Moment; European Committee for Standardization: Brussels, Belgium, 2008. [Google Scholar]
- CEN. EN 1926—Natural Stone Test Methods: Determination of Uniaxial Compressive Strength; European Committee for Standardization: Brussels, Belgium, 2006. [Google Scholar]
- CEN. EN 14146—Natural Stone Test Methods: Determination of the Dynamic Modulus of Elasticity (by Measuring the Fundamental Resonance Frequency); European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- CEN. EN 13364—Natural Stones Test Methods: Determination of Breaking Load at Dowel Hole; European Committee for Standardization: Brussels, Belgium, 2001. [Google Scholar]









| Property | Bowing Effect | N° Specimens | Units | Mean Value | Characteristic Value | C.V. (%) |
|---|---|---|---|---|---|---|
| Flexural strength (σr) | Without | 8 | Pa × 106 | 8.2 | 6.5 | 9.8 |
| With | 14 | 7.8 | 5.3 | 17.8 | ||
| With + Without | 22 | 7.9 | 5.8 | 15.1 | ||
| Compressive strength (Rr) | Without | 5 | Pa × 106 | 81.5 | 63.8 | 5.0 |
| With | 5 | 72.5 | 57.9 | 8.6 | ||
| With + Without | 10 | 77.0 | 62.2 | 9.2 | ||
| Breaking load at dowel hole (Fr) | Without | 5 | N × 103 | 1.19 | 0.671 | 18.7 |
| With | 4 | 1.15 | 0.433 | 38.4 | ||
| With + Without | 9 | 1.17 | 0.596 | 29.2 | ||
| Dynamic modulus of elasticity (EdL/EdT for ν = 0.25) | With | 4 | Pa × 109 | 38.8/40.9 | 33.8/28.0 | 4.8/11.8 |
| Dynamic modulus of elasticity (EdL/EdT for ν = 0.40) | With | 4 | Pa × 109 | 21.7/22.9 | 18.9/15.7 | |
| Static modulus of elasticity (EsL) | With | 4 | Pa × 109 | 16.5 | 8.5 | 18.0% |
| Stone Slabs and Surface Dimensions (m) | Security Criteria | Bending Stress (106 × Pa) | Load at Dowel Hole (103 × N) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SLS | ULS | SLS | ULS | ||||||
| h ≤ 9 m | 9 < h ≤ 18 m | h ≤ 9 m | 9 < h ≤ 18 m | h ≤ 9 m | 9 < h ≤ 18 m | h ≤ 9 m | 9 < h ≤ 18 m | ||
 | Max.Value | 1.7 | 2.7 | 2.5 | 4.0 | 0.54 | 0.87 | 0.80 | 1.3 |
| Sd/Rd | 0.3 | 0.5 | 1.0 | 1.7 | 0.9 | 1.5 | 3.2 | 5.2 | |
| Result | S | S | NS | NS | S | NS | NS | NS | |
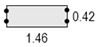 | Max.Value | 2.0 | 3.2 | 3.0 | 4.8 | 0.20 | 0.32 | 0.30 | 0.49 |
| Sd/Rd | 0.3 | 0.6 | 1.2 | 2.0 | 0.3 | 0.5 | 1.2 | 2.0 | |
| Result | S | S | NS | NS | S | S | NS | S | |
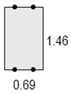 | Max.Value | 3.1 | 4.3 | 4.46 | 6.25 | 0.53 | 0.73 | 0.76 | 1.0 |
| Sd/Rd | 0.5 | 0.7 | 1.8 | 2.6 | 0.9 | 1.2 | 3.1 | 4.1 | |
| Result | S | S | NS | NS | S | NS | NS | NS | |
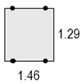 | Max.Value | 1.6 | 2.6 | 2.4 | 4.0 | 0.60 | 0.99 | 0.92 | 1.5 |
| Sd/Rd | 0.3 | 0.5 | 1.0 | 1.6 | 1.0 | 1.7 | 3.7 | 6.0 | |
| Result | S | S | NS | NS | S | NS | NS | NS | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sousa, H.; Sousa, R. Durability of Stone Cladding in Buildings: A Case Study of Marble Slabs Affected by Bowing. Buildings 2019, 9, 229. https://doi.org/10.3390/buildings9110229
Sousa H, Sousa R. Durability of Stone Cladding in Buildings: A Case Study of Marble Slabs Affected by Bowing. Buildings. 2019; 9(11):229. https://doi.org/10.3390/buildings9110229
Chicago/Turabian StyleSousa, Hipólito, and Rui Sousa. 2019. "Durability of Stone Cladding in Buildings: A Case Study of Marble Slabs Affected by Bowing" Buildings 9, no. 11: 229. https://doi.org/10.3390/buildings9110229
APA StyleSousa, H., & Sousa, R. (2019). Durability of Stone Cladding in Buildings: A Case Study of Marble Slabs Affected by Bowing. Buildings, 9(11), 229. https://doi.org/10.3390/buildings9110229






