Automation of Measuring Actual Productivity of Earthwork in Urban Area, a Case Study from Montreal
Abstract
:1. Introduction and Literature
1.1. Accuracy of GPS as a Data Collection Tool
1.2. Problem Statment
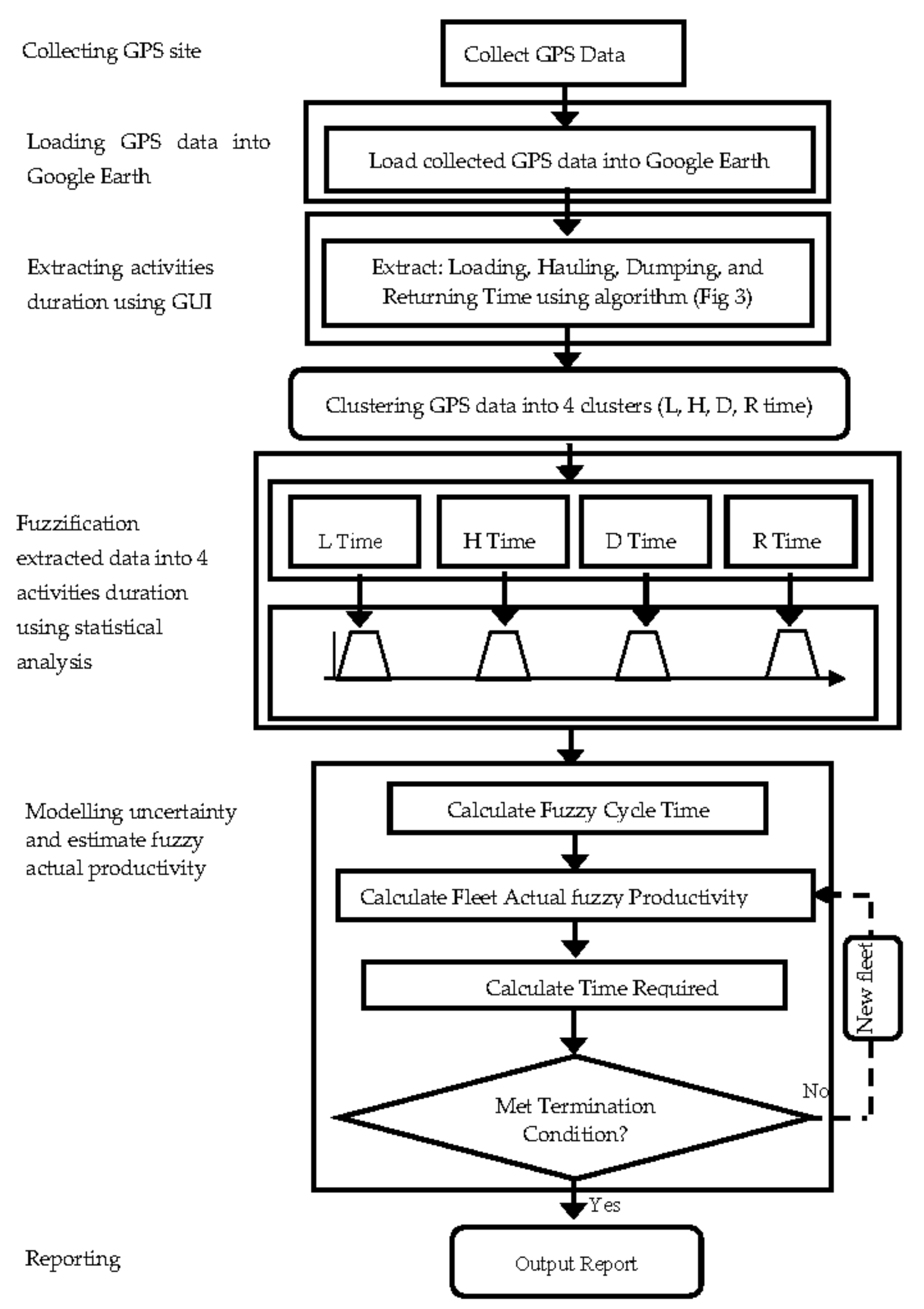
2. Developed Methodology
2.1. Data Collection
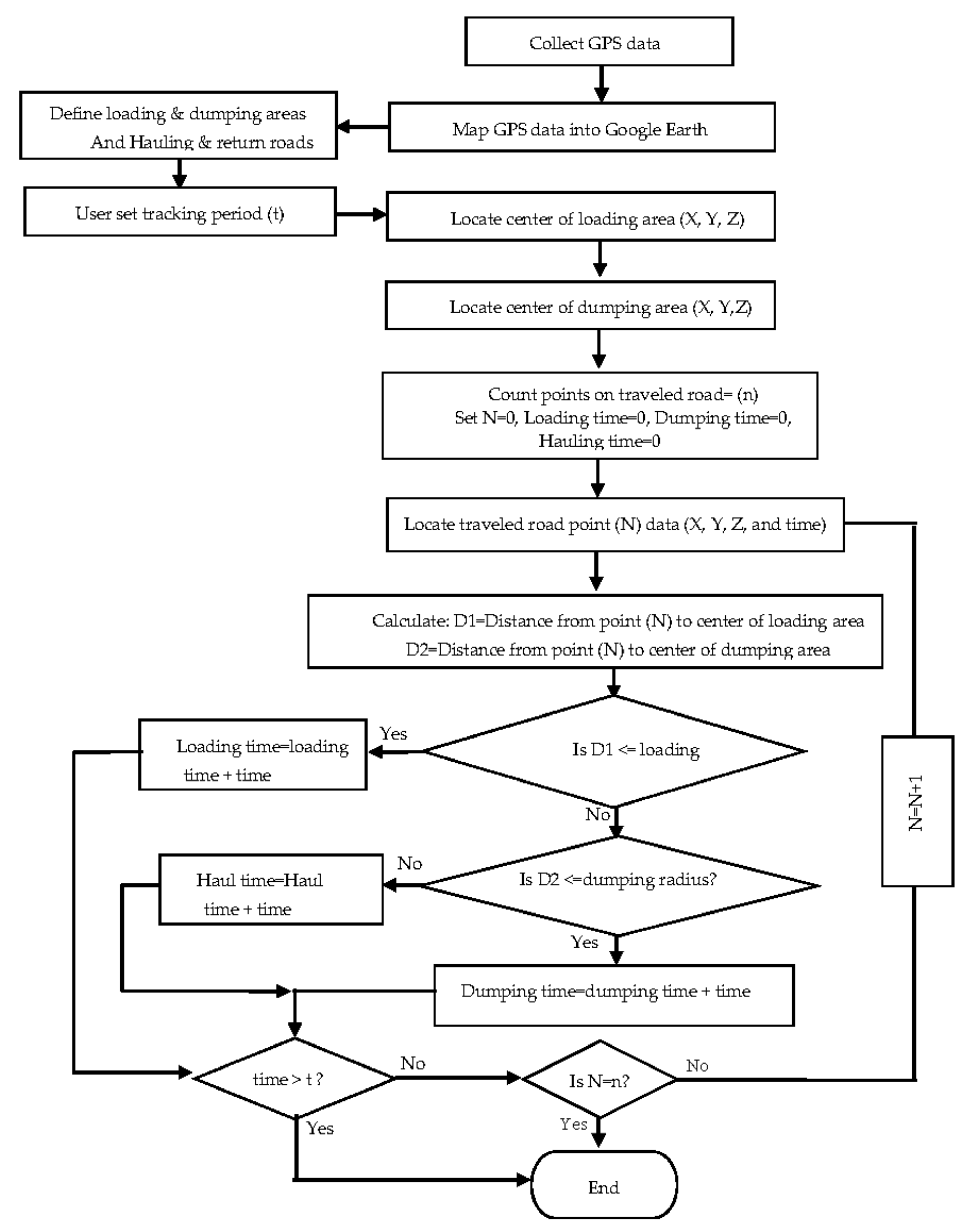
2.2. Extraction of Activities duration from GPS Data
- Uploading the collected GPS data into Google Earth.
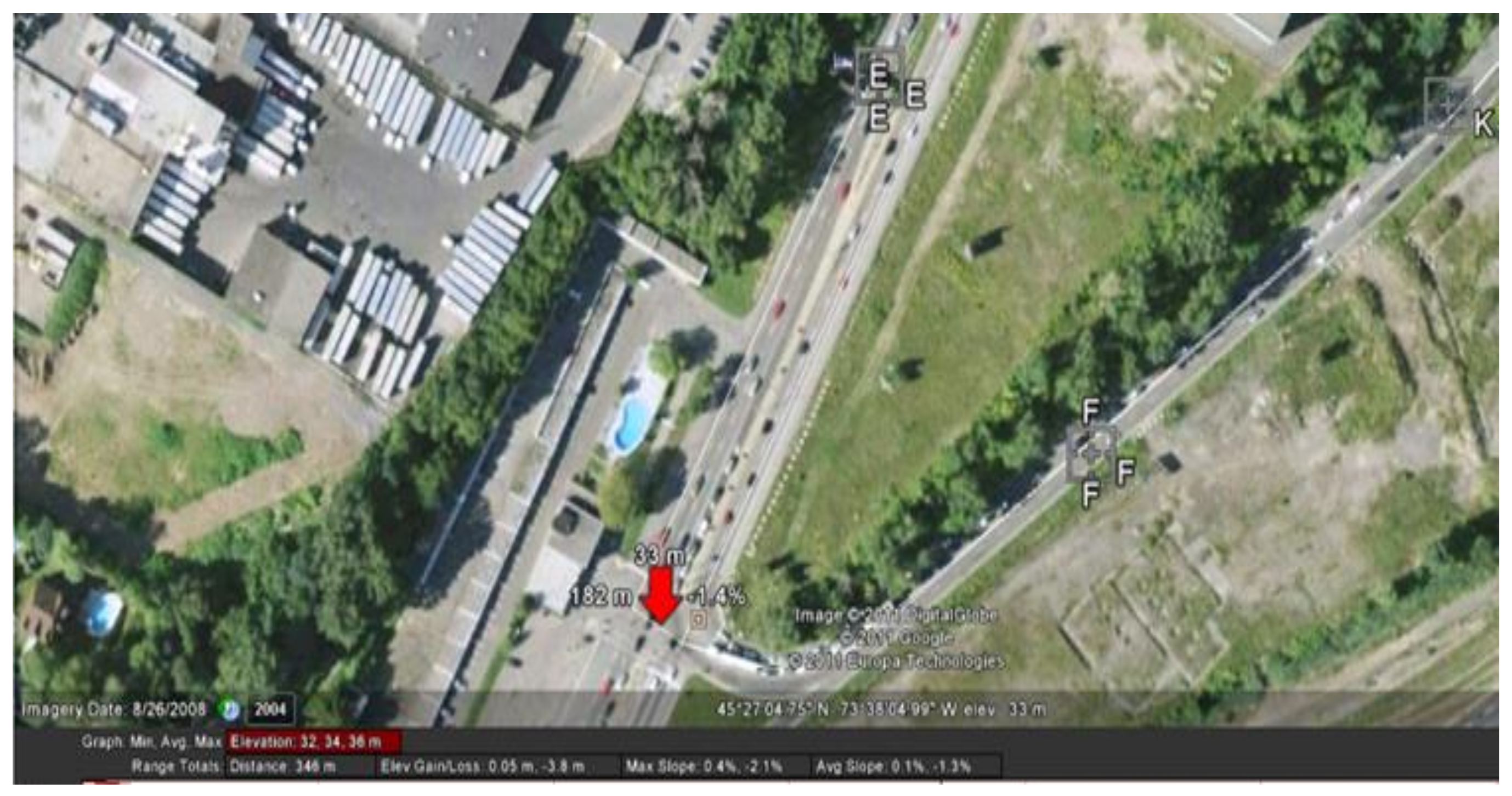
- Locating and defining the loading and dumping sites on Google map using a developed drawing tool to facilitate the identification of departure and arrival times required to compute the truck cycle time. Here, the user on Google Earth needs to define locations of loading and dumping sites so that these locations can be recognized when the truck is in the loading or dumping sites. The coordinates of the identified loading and dumping area are saved in a central database in form of dbf format. The user can define several loadings and dumping sites dynamically as the work progress. Different shapes can be used to display loading and dumping sites to fit certain job site.
- Having defined the loading and dumping sites, the developed algorithm of extracting duration then extracts the coordination (XYZ) of positions on the traveled road from GPS data.
- Computing the distance between mid-points (center) of identified dumping and loading areas and the position of the point under consideration using Haversine formula [20]. Recognizing the location of the tracked truck based on the calculated distance in step 2. One of two conclusions can be reached; (1) If calculated distance is longer than the radius of dumping and loading sites, the truck is identified as in traveling or returning; (2) If the calculated distance is smaller than the specific radius of loading and dumping sites, the truck in this case would be within loading or dumping area. Dumping time can be determined as time illustrated when the truck is within the dumping site, and likewise loading time is computed as a time taken for the truck to stay in the loading area. Hauling and returning times were differentiated by the direction of the moving unit. If the direction was from the loading to the dumping area, time computed would be for hauling. Otherwise it would be for the returning time.
- Repeating step 4 till all locations on the travelled roads are identified. Table 2 depicts a sample of the extracted duration of cycle times of the case study project.
- Clustering the extracted cycle times into four groups. Group four is selected to present the loading, dumping, hauling, and returning time of the tracked truck, which are the main components of the truck cycle time.
- Performing statistical analysis on the extracted durations includes calculating minimum, maximum, mean, and median of loading, dumping, hauling, and returning time of the tracked truck to form fuzzy numbers of the cycle time.
2.3. Modelling Uncertainty and Estimate Productivity
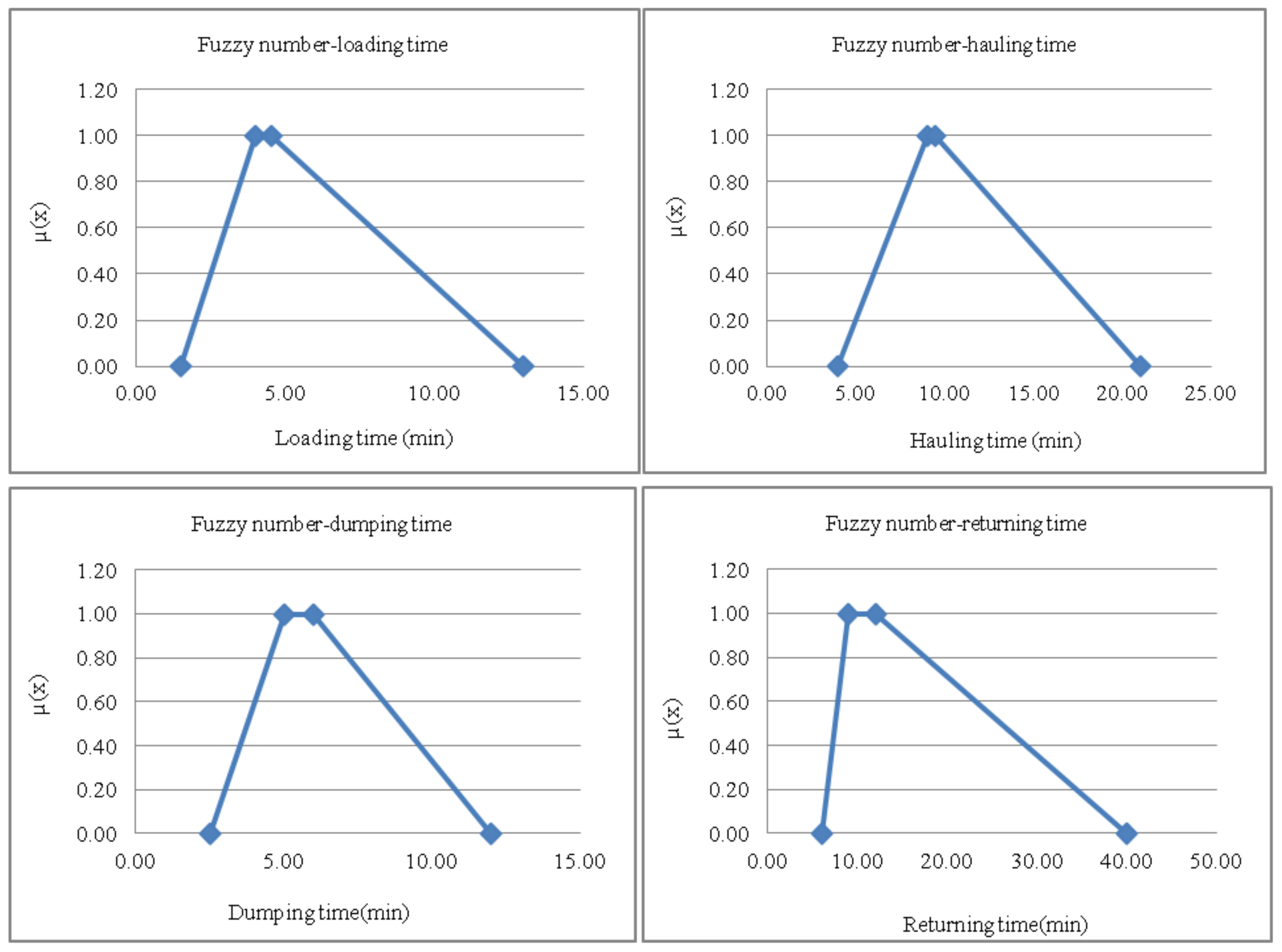
- Defining the functions of membership to the four fuzzy numbers (a, b, c, and d) based on computed mean, median, standard deviation, minimum, and maximum values. Mean and median were used to define the lower and upper modes (i.e., b and c) with full membership (i.e., f(x) = 1.0) and minimum and maximum were used to define lower and upper bounds (i.e., a and d) with no membership (i.e., f(x) = 0.0). The contractor can set different membership functions of the four activity durations, based on his/her judgment. In the example project provided in this paper trapezoidal and triangular shapes were used, with full membership at the median.
- Calculating the fuzzy cycle time of the monitored truck by adding the bases of the cycle time’s fuzzy numbers. Figure 4 illustrates the calculated fuzzy activity durations of the case project presented in this paper.
- Defuzzifing the calculated fuzzy cycle time by calculating a crisp expected value of the cycle time through center of area (COA) technique [12].
- Calculating the fleet fuzzy onsite productivity based on the hauling unit’s fuzzy cycle time using Equation (1).where m = number of trucks model in the fleet being considered; nt is number of trucks of the same model in the fleet under consideration; Pa = estimated fleet productivity; FCT = the calculated fuzzy cycle time; Tc = the capacity of the truck of the same model taking into consideration the soil type; FF = adjustment factor that accounts for the fill factor which is relied upon soil type.
- Analyzing the calculated fuzzy cycle time and the estimated fleet fuzzy productivity, using a set of indices as described in the case project.
3. Case Project
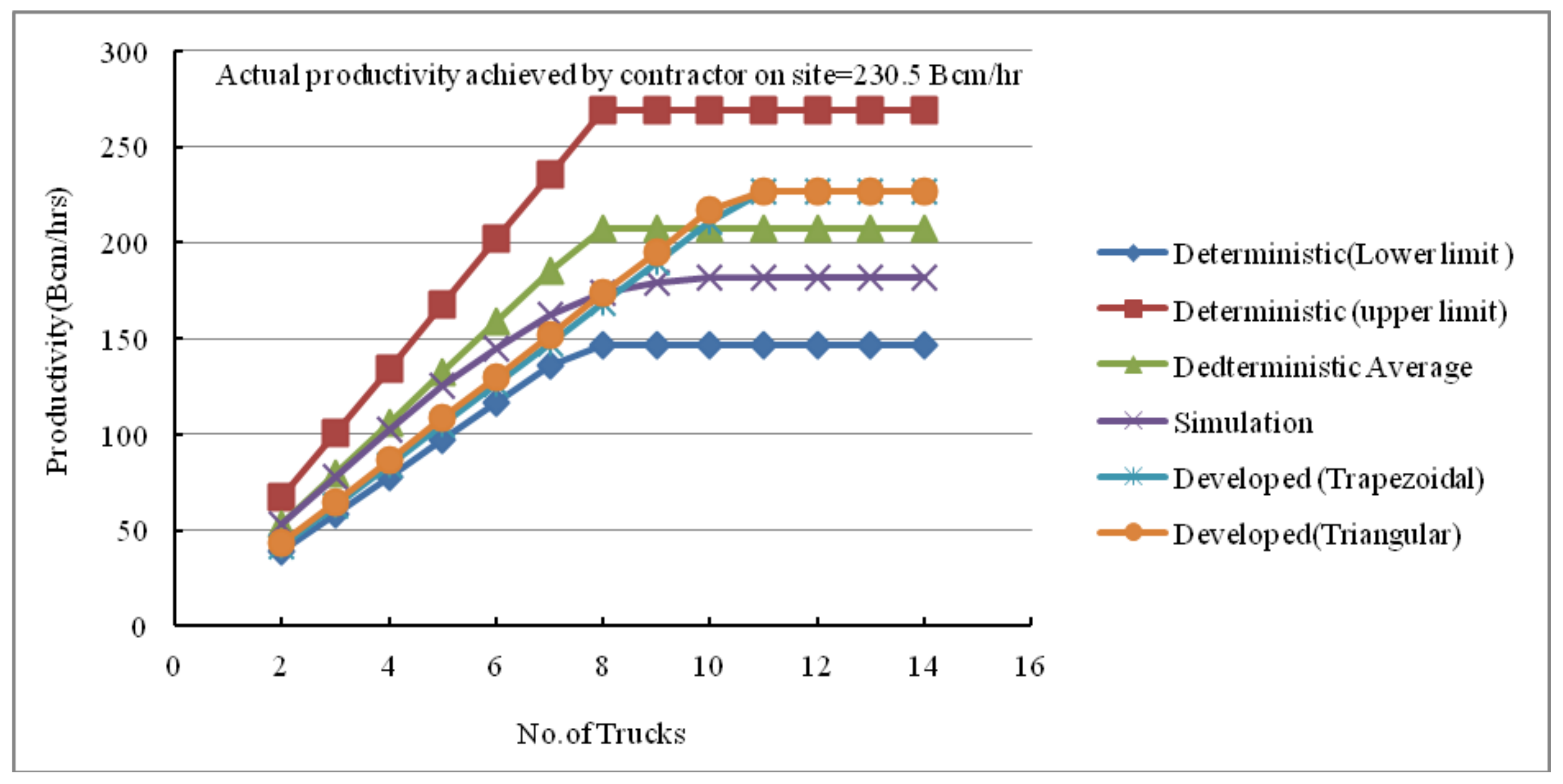
3.1. Results and Discussions
- The output of the developed methodology is very close to the actual productivity the contractor achieved and measured.
- The output of the developed methodology is in an agreement with the output of the simulation-based model for identifying the most productive fleet formation (11 trucks) required to serve an excavator.
- The developed methodology requires only a one step calculation to estimate productivity compared to that of simulation-based models, which need multi runs (e.g., 1000 iteration) to generate significant productivity estimates.
- The fleet productivity would be between 400 Bcm/hr and 500 Bcm/hr.
- Fleet productivity is exactly 300 Bcm/hr.
3.2. Features of the Proposed Methodology
3.3. Limitations of the Study and Recommendation of Future Work
4. Conclusions
Funding
Conflicts of Interest
References
- Zhang, C.; Hammad, A.; Bahnassi, H. Collaborative multi-agent systems for construction equipment based on real-time field data capturing. J. Inf. Technol. Constr. 2009, 14, 204–228. [Google Scholar]
- Christian, J.; Xie, T. Improving earthmoving estimation by more realistic knowledge. Can. J. Civ. Eng. 1996, 23, 250–259. [Google Scholar] [CrossRef]
- Paek, J.; Lee, Y.; Ock, J. Pricing construction risk: Fuzzy set theory application. J. Constr. Eng. Manag. 1993, 119, 743–756. [Google Scholar] [CrossRef]
- Tam, C.M.; Tong, T.K.L.; Tse, S.L. Artificial neural networks model for predicting excavator productivity. Eng. Constr. Archit. Manag. 2002, 2002, 446–452. [Google Scholar] [CrossRef]
- Montaser, A.; Moselhi, O. RFID+ for tracking earthmoving operations. In Proceedings of the Construction Research Congress 2012, West Lafayette, IN, USA, 21–23 May 2012; pp. 1011–1020. [Google Scholar] [CrossRef]
- Montaser, A.; Azram, R.; Moselhi, O. Experimental study for efficient use of Rfid in construction. In Proceedings of the 30th ISARC, Montréal, QC, Canada, 11–15 August 2013; pp. 618–625. [Google Scholar]
- Montaser, A.; Bakry, I.; Alshibani, A.; Moselhi, O. Estimating productivity of earthmoving operations using spatial technologies. Can. J. Civ. Eng. 2012, 39, 1072–1082. [Google Scholar] [CrossRef]
- Montaser, A.; Moselh, O. Truck+ for earthmoving operations. J. Inf. Technol. Constr. 2014, 19, 412–433. [Google Scholar]
- Rashidi, A.; Nejad, H.R.; Maghiar, M. Productivity estimation of bulldozers using generalized linear mixed models. KSCE J. Civ. Eng. 2014, 18, 1580–1589. [Google Scholar] [CrossRef]
- Montaser, A.; Moselhi, O. Automated site data acquisition technologies for construction progress reporting. In Proceedings of the CSCE 2014 General Conference—Congrès général 2014 de la SCGC, Halifax, UK, 28–31 May 2014. [Google Scholar]
- Hajjar, D.; AbouRizk, S. Unified modeling methodology for construction simulation. J. Constr. Eng. Manag. 2002, 128, 174–185. [Google Scholar] [CrossRef]
- Shaheen, A.; Fayek, A.; AbouRizk, S. Fuzzy numbers in cost range estimating. J. Constr. Eng. Manag. 2007, 133, 325–334. [Google Scholar] [CrossRef]
- Chung, T. Simulation—Based Productivity Modeling for Tunnel Construction Operations. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of Alberta, Edmonton, AB, Canada, 2007. [Google Scholar]
- Kannan, G. A Methodology for the Development of a Production Experience Database for Earthmoving Operations Using Automated Data Collection. Ph.D. Thesis, Department of Civil Engineering, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1999. [Google Scholar]
- Montaser, A.; Moselhi, O. Tracking scraper-pusher fleet operations using wireless technologies. In Proceedings of the 4th Construction Specialty Conference, Montréal, QC, Canada, 29 May–1 June 2013. [Google Scholar]
- Yang, Y.; Farrell, J.; Barth, M. High-accuracy, high-frequency differential carrier phase GPS aided low-cost INS. In Proceedings of the IEEE Position, Location and Navigation Symposium, San Diego, CA, USA, 13–16 March 2000. [Google Scholar]
- Navon, R.; Goldschmidt, E. Monitoring labor inputs: Automated-data collection model and enabling technologies. J. Autom. Constr. 2002, 12, 185–199. [Google Scholar] [CrossRef]
- Shi, H.; Qiao, D. Experimental study on accuracy of GPS positioning. Appl. Mech. Mater. 2013, 263–266, 346–349. [Google Scholar] [CrossRef]
- Montaser, A.; Bakry, I.; Alshibani, A.; Moselhi, O. Estimating productivity of earthmoving operations using spatial technologies. In Proceedings of the 3rd International/9th Construction Specialty Conference, Ottawa, ON, Canada, 14–17 June 2011. [Google Scholar]
- Sinnott, W.W. Virtues of the Haversine. Sky Telesc. 1984, 68, 159. [Google Scholar]
- Zadeh, L. Fuzzy Sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]

| Time | Information | Location | Speed (KM/h) | Heading | Latitude | Longitude |
|---|---|---|---|---|---|---|
| 15:27:11 | Stopped for 23 h 16 m | 7545 Henri-Bourassa BOUL E, Montréal, QC, CA | - | - | 45.62079 | −73.58962 |
| 14:43:38 | Stopped for 4 m | 3496 West Broadway AV, Montréal, QC, CA | - | - | 45.45708 | −73.64221 |
| 14:48:09 | Stopped for 9 m | 3905 West Broadway AV, Montréal, QC, CA | - | - | 45.45717 | −73.64181 |
| 14:57:17 | Moving | 12 | SW | 45.4553 | −73.6413 | |
| 14:59:17 | Moving | 31 | SE | 45.45396 | −73.63862 | |
| 15:01:17 | Moving | 20 | NE | 45.45433 | −73.63397 | |
| 15:05:17 | Moving | 2 | NE | 45.45573 | −73.62775 |
| Cycle No | Total Cycle Time (min) | Loading Time (T1) min | Travel Time (T2) min | Dumping Time (T3) min | Return Time (T4) min |
|---|---|---|---|---|---|
| 1 | 33.75 | 7.75 | 10.00 | 8.00 | 8.00 |
| 2 | 31.00 | 3.00 | 10.00 | 8.00 | 10.00 |
| 3 | 29.08 | 3.08 | 9.00 | 5.00 | 12.00 |
| 4 | 33.54 | 4.13 | 10.78 | 5.00 | 13.63 |
| 5 | 43.00 | 2.00 | 7.00 | 5.00 | 29.00 |
| 6 | 28.00 | 2.13 | 9.87 | 7.00 | 9.00 |
| 7 | 25.00 | 2.75 | 8.25 | 6.00 | 8.00 |
| 8 | 27.00 | 4.00 | 9.00 | 5.00 | 9.00 |
| 9 | 67.00 | 2.15 | 46.85 | 9.00 | 9.00 |
| 10 | 28.00 | 3.10 | 8.90 | 5.00 | 11.00 |
| 11 | 27.05 | 3.05 | 8.00 | 6.00 | 10.00 |
| 12 | 28.15 | 3.00 | 8.00 | 6.00 | 11.15 |
| 13 | 28.00 | 4.00 | 10.00 | 5.00 | 9.00 |
| n | - | - | - | - | - |
| Activity | Trapezoidal Representation (Minutes) | |||
|---|---|---|---|---|
| a | b | c | d | |
| Loading | 1.50 | 2.75 | 4.00 | 13.00 |
| Hauling | 4.00 | 9.00 | 10.00 | 21.00 |
| Dumping | 2.50 | 5.00 | 6.00 | 12.00 |
| Returning | 6.00 | 9.00 | 12.00 | 40.00 |
| No. of Trucks | Deterministic Model | Simulation Based Model | Developed Method | ||||
|---|---|---|---|---|---|---|---|
| Lower Limit Production Bcm/hr | Upper Limit Production Bcm/hr | Average Bcm/hr | µ | Trapezoidal Fuzzy Numbers Bcm/hr | Triangular Fuzzy Number Bcm/hr | Developed vs. Probabilistic (%) | |
| 2 | 38.89 | 67.23 | 53.06 | 53.27 | 42.18 | 43.4 | −26.29 |
| 3 | 58.34 | 100.85 | 79.59 | 78.37 | 63.26 | 65.10 | −23.89 |
| 4 | 77.79 | 134.47 | 106.13 | 102.97 | 84.35 | 86.80 | −22.07 |
| 5 | 97.24 | 168.09 | 132.66 | 125.74 | 105.44 | 108.50 | −19.25 |
| 6 | 116.69 | 201.71 | 159.2 | 145.14 | 126.53 | 130.20 | −14.71 |
| 7 | 136.14 | 235.33 | 185.73 | 162.14 | 147.62 | 151.90 | −9.84 |
| 8 | 146.77 | 268.95 | 207.86 | 173.60 | 168.70 | 173.60 | −2.90 |
| 9 | 146.77 | 269.08 | 207.86 | 179.43 | 189.79 | 195.30 | 5.46 |
| 10 | 146.77 | 269.08 | 207.86 | 181.81 | 210.88 | 217.00 | 13.79 |
| 11 | 146.77 | 269.08 | 207.86 | 182.19 | 226.63 | 226.63 | 19.61 |
| 12 | 146.77 | 269.08 | 207.86 | 182.29 | 226.63 | 226.63 | 19.56 |
| 13 | 146.77 | 269.08 | 207.86 | 182.29 | 226.63 | 226.63 | 19.56 |
| 14 | 146.77 | 269.08 | 207.86 | 182.29 | 226.63 | 226.63 | 19.56 |
| Method | Input Distribution | Output Distribution | Most Productive Fleet (Bcm/hr) | |
|---|---|---|---|---|
| µ | σ | |||
| Simulation | Lognormal | - | 182.19 | - |
| Deterministic | Crisp | Crisp | 207.927 | NA |
| Developed Method | Trapezoidal | Trapezoidal | (86.00, 231.24, 287.36, 528.55) ** 174.56 *** | - |
| Method | Fleet Productivity (Bcm/hr) | Probability (p > 300 Bcm/hr) | Possibility (p = 300 Bcm/hr) | Is It More Possible That (p = 182.19) > (p = 226.63)? | Expected Value | Fuzziness Measure | Ambiguity Measure | FNQI |
|---|---|---|---|---|---|---|---|---|
| Simulation | 182.19 | - | NA | NA | - | NA | NA | NA |
| Deterministic | 146.77–269.00 | NA | NA | NA | 207.88 | NA | NA | NA |
| Developed Method | (86.00, 231.24, 287.36, 528.55) | 0.54 e | 0.95 f | No f | 287.48 | 193.22 | 92.46 | 142.84 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshibani, A. Automation of Measuring Actual Productivity of Earthwork in Urban Area, a Case Study from Montreal. Buildings 2018, 8, 178. https://doi.org/10.3390/buildings8120178
Alshibani A. Automation of Measuring Actual Productivity of Earthwork in Urban Area, a Case Study from Montreal. Buildings. 2018; 8(12):178. https://doi.org/10.3390/buildings8120178
Chicago/Turabian StyleAlshibani, Adel. 2018. "Automation of Measuring Actual Productivity of Earthwork in Urban Area, a Case Study from Montreal" Buildings 8, no. 12: 178. https://doi.org/10.3390/buildings8120178
APA StyleAlshibani, A. (2018). Automation of Measuring Actual Productivity of Earthwork in Urban Area, a Case Study from Montreal. Buildings, 8(12), 178. https://doi.org/10.3390/buildings8120178




