Investigation of the Optical Performance of a Novel Planar Static PV Concentrator with Lambertian Rear Reflectors

Abstract

Due to the demands for energy saving and environmental conservation, the development of sustainable zero-carbon buildings has become an inevitable trend. Building Integrated Photovoltaics (BIPV) is a promising technology capable of producing clean electricity onsite and replacing conventional building materials. This paper designs and investigates the performance of a planar Lambertian reflector-based concentrating BIPV system. A comprehensive 3D ray-tracing simulation was applied to study the optical characteristics of the proposed module. It was found that when the geometric concentration ratio is 2.0, the optical efficiency of the investigated Concentrating Photovoltaics (CPV) module is 62.5% and the radiant flux received by the solar cells is about 1.4 times that of the counterpart module without solar concentrators. Through parametric analyses, it was concluded that the optical performance can be enhanced by selecting a suitable glass thickness and type, integrating the glazing cover with edge mirrors, adjusting the distance between the solar cells and improving the reflectivity of the Lambertian reflectors. Comparative analysis was also conducted for the CPV systems integrated with Lambertian and v-groove rear reflectors under different incident light angles, respectively. It was confirmed that the system integrated with Lambertian rear reflectors shows less angular dependence.

1. Introduction

Nowadays, the world is facing the problems of energy shortage, environmental pollution, and global warming. The building sector is responsible for 40% of total energy use and 36% of CO₂ emission in the EU [1]. In light of this, a series of energy legislations have been established, for instance, all new buildings in EU countries should be constructed to be nearly zero-energy after 2020, and the reduction in carbon emissions should be no less than 40% by 2030 [1]. Under the background, the expansion of renewable energy utilization becomes increasingly significant. Photovoltaics (PV) are a promising technology that can convert solar energy into electric power without concern about pollution and noise. In recent years, the rapid advance in the PV industry has shifted the developers’ sights to the integration of PV into the building envelope, named Building Integrated Photovoltaics (BIPV). BIPV is a versatile technology that can produce renewable power at the point of use, replace the building materials for cost saving, serve as shading devices, and improve the aesthetic outlook [2]. Nonetheless, the low efficiency of PV associated with the high cost remains the major obstacle to the popularization of BIPV. One prospective approach is to use relatively cheap refractive or reflective optics to guide the sunlight onto the solar cells, therefore increasing the unit flux intensity on the PV surface (named Concentrating PV (CPV)), thus increasing the unit power output. Hence, the solar cell areas can be scaled down and the overall system cost can be reduced.

Based on geometric concentration ratio (C_g) (see Equation (1)), the CPV systems can be divided into three categories: high (C_g > 100), medium (10 < C_g < 100), and low (C_g < 10) concentration PV systems [3]. A High Concentration PV (HCPV) system is generally composed of point/line-focus optics, high-efficiency solar cells (such as multi-junction cells) and other auxiliary equipment [4]. The HCPV system can be designed to achieve a high optical efficiency (see Equation (2)), however, which is comprised of the acceptance angle and irradiance uniformity [5]. To prevent the drop of optical efficiency due to the acceptance angle, a precise two-axis solar tracker is required to continually rotate the concentrator to orient towards the sun and collect the normal irradiation. The pointing accuracy of a typical tracker for a HCPV system is generally +/−0.1° [6]. In addition, due to intensified illumination, the PV receiver can overheat and the surface temperature distribution can be heterogeneous. Therefore, active or passive cooling mechanisms become a necessity to remove the accumulated heat that can cause the reduction of PV efficiency and quality degradation [4]. All these requirements increase the system cost and complexity. Similarly, Medium Concentration PV (MCPV) systems also demand expensive tracking and cooling devices for effective system operation and require large-sized infrastructure to support the systems [7]. Due to the mobility, protrusive shapes, and large sizes, high and medium concentration PV systems are difficult to be directly integrated into buildings as part of the elements, such as façades and windows. Low Concentration PV (LCPV) systems have wider acceptance angle ranges and can harvest a fraction of diffuse solar radiation [5]. This means the requirement of tracking is low and the system can be operated even on cloudy days. When the geometric concentration ratios (C_g) are below 2.5, the need of tracking system can be eliminated and the LCPV systems can be stationary [3]. In addition, cell cooling is less required for the static LCPV systems, because of relatively low PV operating temperatures and more uniform illumination distribution on the PV surfaces [4]. With the above features, LCPV systems show enormous potentiality in the integration of PV concentrators into buildings.

$${\mathrm{C}}_{\mathrm{g}}=\frac{{\mathrm{A}}_{\mathrm{c}}}{{\mathrm{A}}_{\mathrm{pv}}}$$

(1)

where ${\mathrm{C}}_{\mathrm{g}}$ is the geometric concentration ratio, ${\mathrm{A}}_{\mathrm{c}}$ is the aperture area of the solar concentrator (m²), and ${\mathrm{A}}_{\mathrm{pv}}$ is the aperture area of the solar cells (m²).

$${\mathsf{\eta }}_{\mathrm{op}}=\frac{{\mathsf{\varphi }}_{\mathrm{pv}}}{{\mathsf{\varphi }}_{\mathrm{c}}}$$

(2)

where ${\mathsf{\eta }}_{\mathrm{op}}$ is the optical efficiency, ${\mathsf{\varphi }}_{\mathrm{c}}$ is the solar flux received by the concentrator aperture (W), and ${\mathsf{\varphi }}_{\mathrm{pv}}$ is the solar flux received by the PV aperture (W).

There are many types of LCPV systems, such as the Compound Parabolic Concentrator (CPC) [8,9,10], the V-trough solar concentrator, the wedge-shaped solar concentrator [11], and the Luminescent Solar Concentrator (LSC) [12,13,14]. A planar PV concentrator with Lambertian rear reflectors is another category and has the advantages, such as good optical efficiency, high angular acceptance, low cost, simple fabrication, and suitability for architectural integration [15,16,17]. The system generally consists of a transparent front cover, one or multiple reflective sheet(s), and mono-facial or bi-facial solar cells. The solar cells can be mounted to the rear or lateral sides of the front cover. The reflective sheet(s) can be placed behind or between the back-mounted cells. There are different types of reflectors, among which the reflectors formed by v-grooves and Lambertian diffuse materials are the most commonly used. Figure 1a,b display the light-travelling mechanisms of the planar CPV systems with a v-groove reflector and a Lambertian reflector, respectively. In principle, when the incident light passes through the transparent medium (e.g., glazing cover) and strikes the reflector surface, it bounces back to the air-medium interface. The reflected light cannot escape from the medium unless it hits the interface at an angle smaller than the critical angle (${\mathsf{\theta }}_{\mathrm{c}}$) (see Equation (3)). After multiple internal reflection, the trapped light can be collected by the solar cells for power generation or absorbed by the components, such as the medium and reflective sheet.

$${\mathsf{\theta }}_{\mathrm{c}}={\sin }^{-1}\frac{{\mathrm{n}}_{\mathrm{a}}}{{\mathrm{n}}_{\mathrm{m}}}$$

(3)

where ${\mathsf{\theta }}_{\mathrm{c}}$ is the critical angle, ${\mathrm{n}}_{\mathrm{m}}$ is the refractive index of the transparent medium, and ${\mathrm{n}}_{\mathrm{a}}$ is the refractive index of the neighboring air.

Figure 1. Light propagation within (a) a v-groove reflector based Photovoltaics (PV) concentrator and (b) a Lambertian reflector-based PV concentrator.

Uematsu et al. [16] designed and fabricated two planar solar concentrators with v-groove rear reflectors and different types of solar cells. The geometric concentration ratios of the modules with monofacial and bifacial cells are 1.5 and 2.0, respectively. The corresponding optical efficiencies under the normal incident light were measured to be 87.6% and 85.6%, respectively. Yoshioka et al. [18] studied the relationship between the optical efficiency and the geometric concentration ratio of the planar solar concentrators with v-groove rear reflectors. It was reported that the optical efficiency decreases with the increase of the geometric concentration ratio at both experimental measurement and simulation. Weber et al. [19] compared the performance of the planar bifacial-cell-type solar concentrators with a v-groove rear reflector and a Lambertian rear reflector. It was concluded that the average yearly performance of the two modules are similar when C_g = 2, however, the performance of the Lambertian reflector-based module is less sensitive to the variation of incident light angle. Mcintosh [20] used a ray-tracing simulation to characterize the optical behaviour of a flat-plate solar concentrator with a Lambertian backsheet. The results show that around 25% of the photons hitting on the backsheet are internally reflected onto the neighbouring cells, and the proportion can be improved if the backsheet’s reflectivity is lifted increased from 75% to 85%. Moehlecke et al. [21] fabricated two planar CPV modules with 36 bifacial solar cells and white-diffuse rear reflectors, and compared the electrical performance of the solar cells with, and without, a solar concentrator. It was suggested that, by utilizing the proposed reflector, the electricity output of the modules can be improved by approximately 29%. Van Dijk et al. [22] proposed several light-trapping schemes for solar modules for efficient power conversion. In the design, a conventional solar module was integrated with a glass cover that has a lens array on the front side and a reflector (metal or white-diffuse paint) on the backside. The incident light can be funneled through the aperture in the reflector, and then collected by the solar cells or recycled. The researchers revealed that the light absorption by the proposed module depends on the factors including solar cell absorption, diffuse light fraction, and concentration factor.

In this project, a flat-plate static CPV system with Lambertian rear reflectors is developed, which can potentially be integrated into the building envelope components such as roof, wall façade, and windows. The optical efficiency and effective concentration ratio of the proposed system are calculated via a 3D ray-tracing simulation. Parametric analysis is undertaken by varying the width and optical properties of the Lambertian reflectors, changing the type and thickness of the front glazing cover, and coupling the glass edges with mirrors. The optical performance of the planar CPV systems with Lambertian and v-groove rear reflectors are, respectively, investigated at different solar zenith angles and solar azimuths.

2. Methodology

2.1. Ray-Tracing Approach

Non-sequential ray-tracing is a method widely used to analyze the optical characteristics of static non-imaging CPV systems. Different from sequential ray-tracing, non-sequential ray-tracing allows rays to intersect the objects/surfaces in any sequence and for repeated times, which can predict the spatial flux distribution [23]. With this approach, the light diffusion induced by Total Internal Reflection (TIR) and diffuse surfaces can be simulated and the global light collection by absorbers (such as solar cells) can be evaluated. In the simulation, multiple rays with same flux intensity are launched from a light source and maintain straight propagation until encountering the physical surfaces/objects. At the intersection points, the ray directions are changed as a result of reflection, refraction, diffraction, or scattering depending on the properties of the surface. The rays are continually tracked until they cannot reach the next intersected surface. The tracing of the rays also stops when the rays are collected by the detectors (such as solar cells) or meet the cut-off condition (e.g., when the flux of a ray drops below the defined flux threshold after multiple internal reflection) [13,20]. The detector surface is divided into numbers of small pixels to collect the incident rays. After counting the flux of the rays entering into the pixels, the irradiance on the detector surface can be obtained.

A Monte Carlo algorithm is generally used to characterize the scattering of light when striking a diffused surface. In the simulation, the number of rays remains unchanged before and after intersecting the surface, and the directions of scattered rays are assigned stochastically [23]. The incident flux are weighted and distributed to the random rays according to the probabilities (i.e., absorptivity, reflectance, and transmittance) [24]. In order to obtain realistic outcomes, the number of incident rays should be large enough. Nevertheless, a compromise is made between the simulation accuracy and time cost. According to that, it is necessary to perform ray independence tests where the ray number for simulation is progressively raised until the result errors between successive tests are not significant. On the other hand, the pixel size needs to be defined properly in order to obtain accurate results with minimal ray numbers [23].

2.2. Method Validation

The reliability of the ray-tracing model is checked by validating the work from reported experimental results. According to the work of Yoshioka et al. [18], the optical efficiencies of the planar static CPV systems with aluminum (Al) and silver (Ag)-coated v-grooves when C_g = 2 were measured to be 81% and 84%, respectively. A ray-tracing simulation was applied for the CPV system designed by Yoshioka et al. [18]. It was found that the optical efficiencies of the Al and Ag-coated type modules are 80.9% and 84.8%, respectively. The errors between the results from the literature and the simulation are less than 1%, which indicates the developed ray-tracing model is reliable and can be used to predict the optical performance of other solar systems.

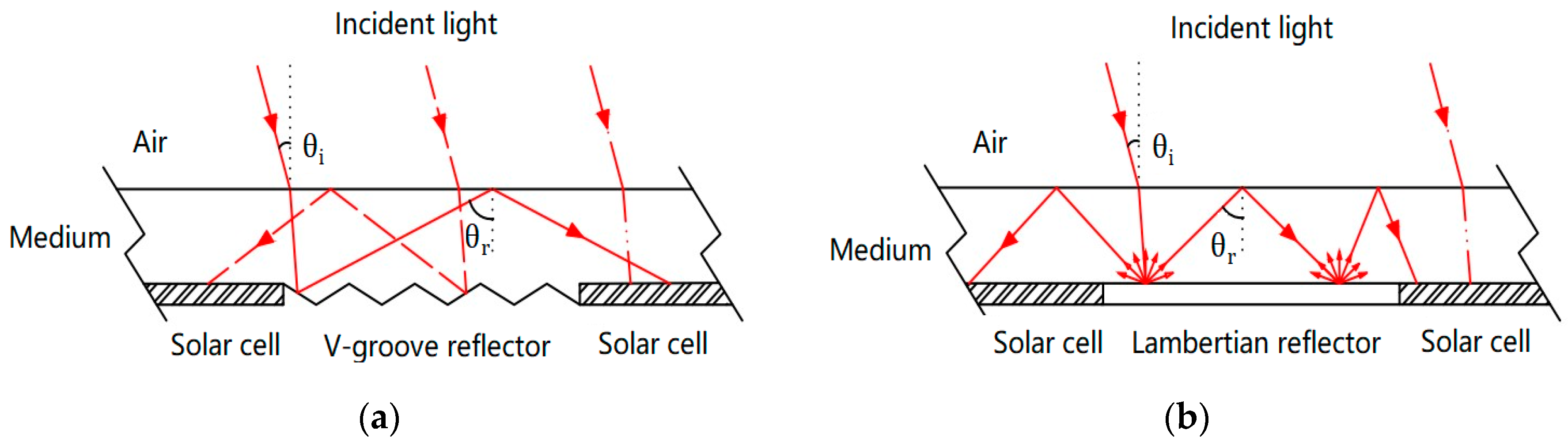
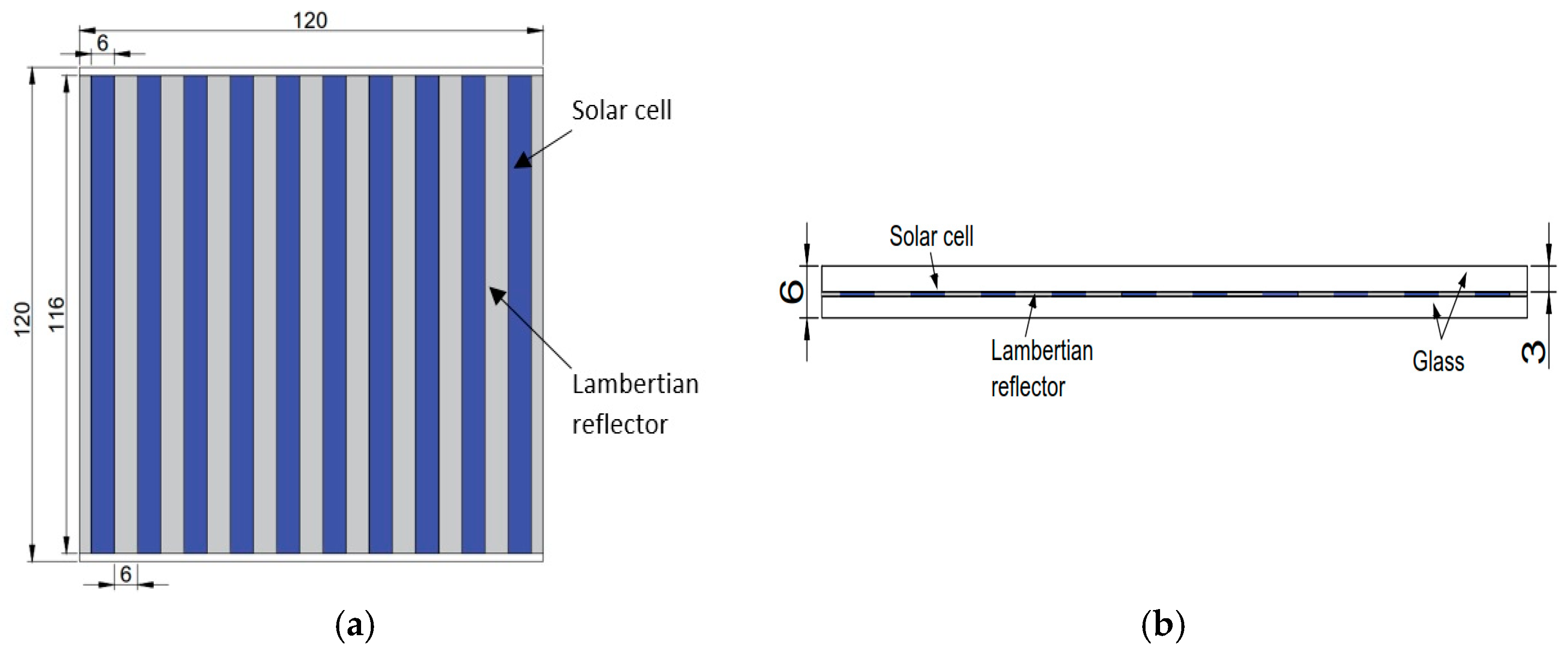
2.3. Model Description

A 3D ray-tracing model is developed for a novel planar CPV system comprising of two glass panes, 10 mono-facial solar cells and Lambertian reflectors installed between the solar cells. The solar cells and Lambertian reflectors are optically adhered between the glass panes by encapsulate coating (i.e., there is no air gap between the solar cells and two glass panes, and also between the reflectors and two glass panes). The dimension of the CPV module is 120 mm × 120 mm × 6 mm and the area of each solar cell is 116 mm × 6 mm (see Figure 2a). Pilkington Optiwhite^TM (Pilkington, Lathom, UK) low-iron glass [25] with the thickness of 3 mm is selected as the front and rear covers (see Figure 2b). In this study, the thicknesses of the solar cells and Lambertian reflectors are neglected. The geometric concentration ratio of the module is approximately 2.0.

Figure 2. Diagrams of (a) the layout; and (b) the cross-section of the novel Lambertian reflector-based Concentrating Photovoltaics (CPV) module.

In the model setup, the surface and bulk optical properties of the module components are defined, respectively. The light reflectance (r) and transmittance (τ) at the air-glass interface are calculated according to Fresnel equations (see Equations (4) and (5)) where the average refractive index of the Pilkington Optiwhite^TM low-iron glass is 1.51. The light absorption (a) of the glass medium is calculated according to Beer’s law and expressed as Equation (6) [26]. For simplification, the solar cells are defined as perfect light absorbers with an absorptivity of 100% and the rear reflectors are assumed to be isotropic scattering sheets (i.e., the reflected light are randomly oriented) with a diffuse reflectivity of 99%:

$$\mathrm{r}=\frac{{({\mathrm{n}}_{\mathrm{a}}\cos {\mathsf{\theta }}_1-{\mathrm{n}}_{\mathrm{g}}\cos {\mathsf{\theta }}_2)}^2}{{({\mathrm{n}}_{\mathrm{a}}\cos {\mathsf{\theta }}_1+{\mathrm{n}}_{\mathrm{g}}\cos {\mathsf{\theta }}_2)}^2}$$

(4)

$$\mathsf{\tau }=1-\mathrm{r}$$

(5)

$$\mathrm{a}=1-\exp (-\frac{\mathsf{\alpha }\mathrm{L}}{\cos {\mathsf{\theta }}_2})$$

(6)

where ${\mathrm{n}}_{\mathrm{g}}$ is the refractive index of the glass, ${\mathsf{\theta }}_1$ and ${\mathsf{\theta }}_2$ are the angles of the incident and refracted light with respect to the normal of the air-glass interface, α is the glass absorption coefficient (m⁻¹) and L is the glass cover thickness (m).

In terms of the light source, multiple light rays are emitted perpendicular to the module with an intensity of 1000 W/m² and at a single wavelength of 0.54 μm. Through ray independence tests, 1,000,000 rays are used for the further studies. Sensitivity analysis is performed by varying the parameters, including reflector width, reflector reflectivity, glazing cover thickness, glass type, and solar incidence angle. To access the optical performance of each design, the values of optical efficiency and effective concentration ratio (see Equation (7)) are investigated and compared:

$${\mathrm{C}}_{\mathrm{e}}=\frac{{\mathrm{I}}_{\mathrm{pv}}}{{\mathrm{I}}_{\mathrm{c}}}={\mathrm{C}}_{\mathrm{g}}\times {\mathsf{\eta }}_{\mathrm{op}}$$

(7)

where ${\mathrm{C}}_{\mathrm{e}}$ is the effective concentration ratio, ${\mathrm{I}}_{\mathrm{pv}}$ is the irradiance on the concentrator aperture (W/m²), and ${\mathrm{I}}_{\mathrm{c}}$ is the irradiance on the aperture of solar cells (W/m²).

3. Results and Discussion

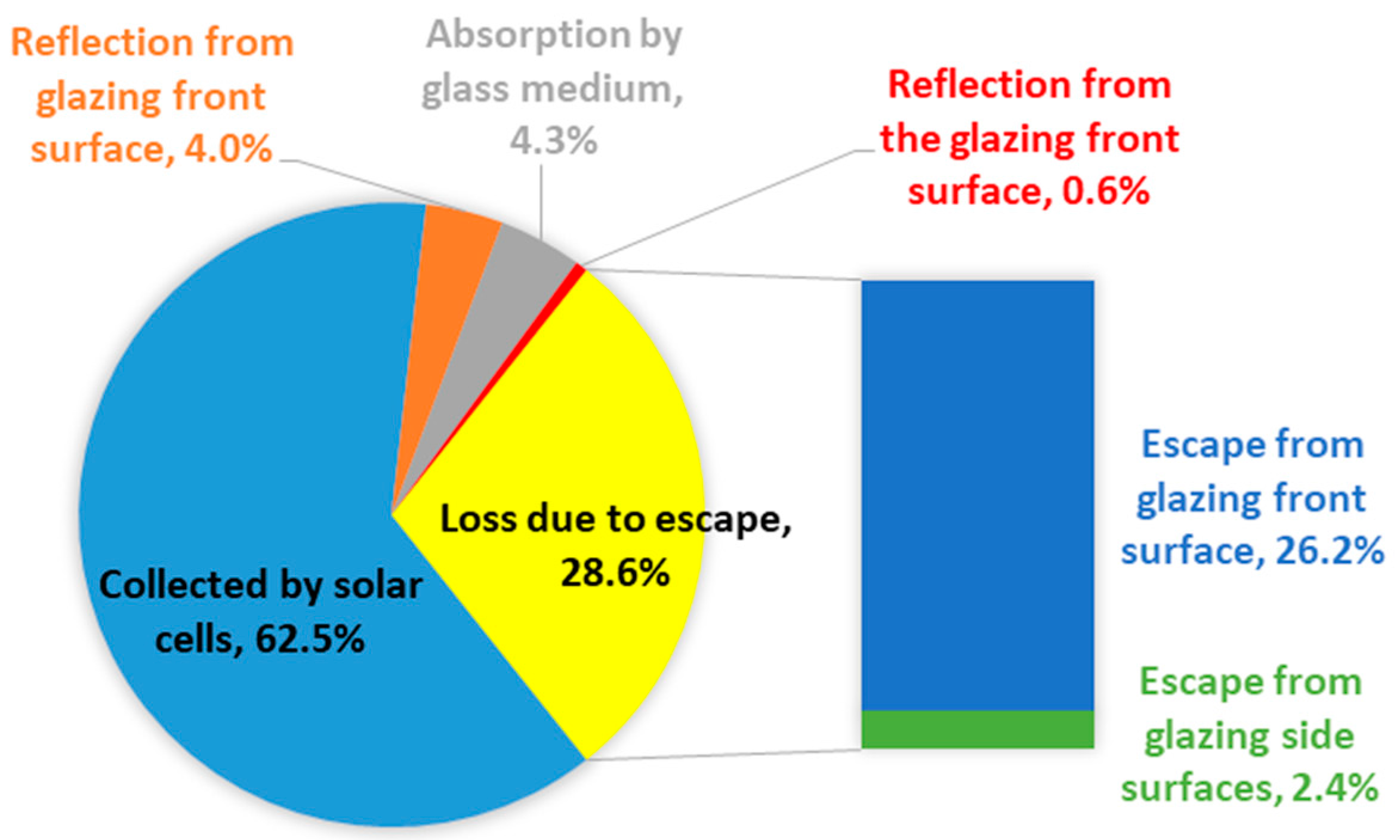
3.1. Optical Characteristics of the Base Model

From the ray-tracing simulation, the optical efficiency and effective concentration ratio of the novel CPV system with Lambertian rear reflectors are 62.5% and 1.29, respectively. When the incidental solar radiation is 1000 W/m², the radiant flux received by the solar cells in the proposed CPV system is 9 W, which is 1.4 times over its counterpart PV module without a solar concentrator (η_op = 45% and received radiant flux = 6.5 W). This indicates that the power output of the solar cells can be enhanced with the use of Lambertian rear reflectors. Figure 3 shows the light distribution within the proposed CPV system. It is found that 28.6% of the total incident irradiation is lost due to the light escape from the glazing cover, followed by the glass medium absorption (4.3%) and reflection at the air-glass interface (4.0%). As observed, the largest portion of the escaped light is through the front surface of the glazing cover. This might be because the interaction of the internal reflection at the front surface is more significant, resulting a greater amount of rays being scattered outwards.

Figure 3. Light distribution within the CPV module with Lambertian rear reflectors.

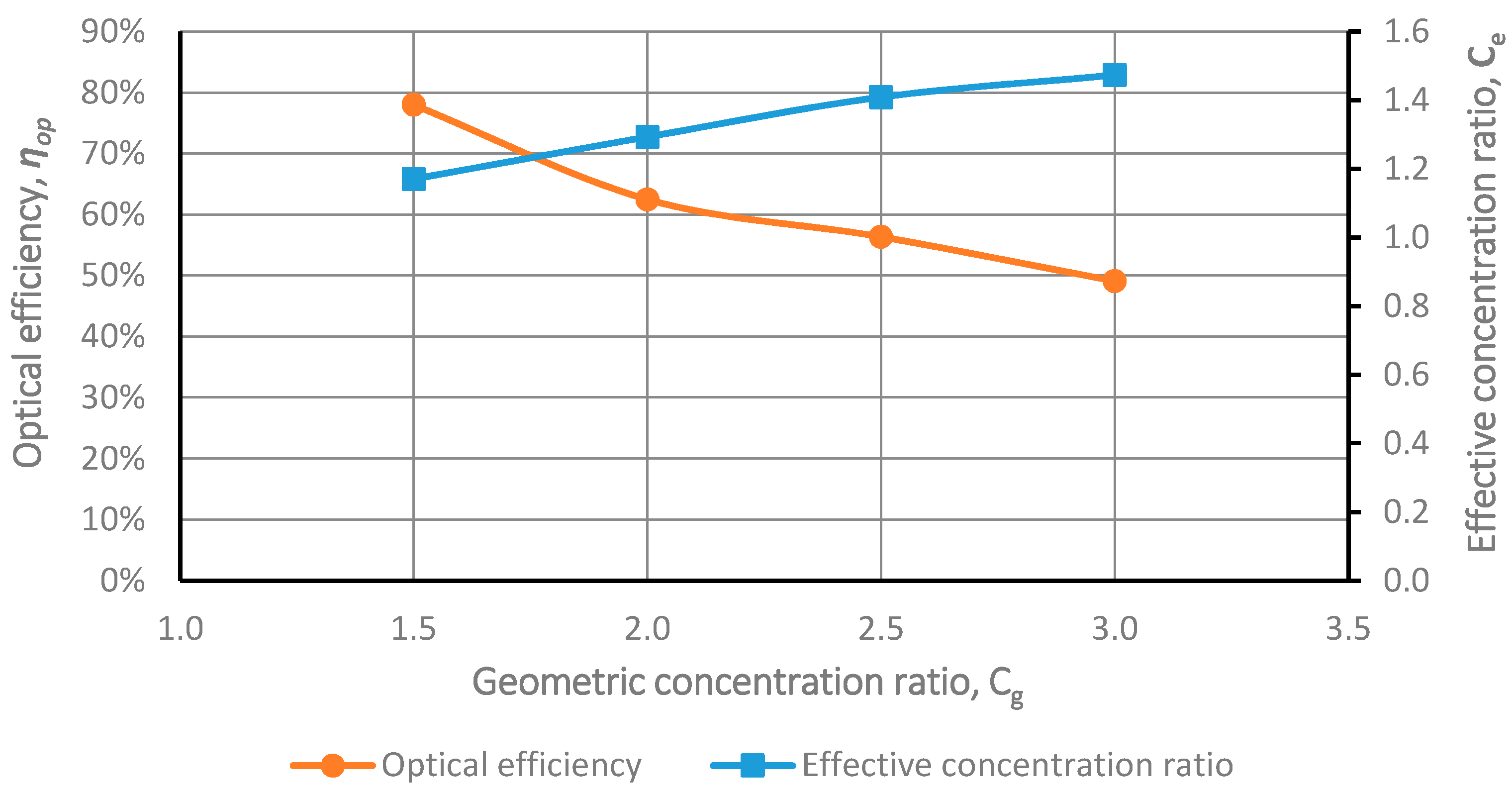
3.2. Influence of the Geometric Concentration Ratio

When changing the interval distance between the solar cells to 3, 6, 9, and 12 mm, the glazing cover dimensions turn out to be 120 × 90, 120 × 120, 120 × 150, and 120 × 180 mm², respectively. The corresponding geometric concentration ratios of the modified modules are calculated to be approximately 1.5, 2.0, 2.5, and 3.0. The relationships between the geometric concentration ratio and the effective concentration ratio, and the optical efficiency are displayed in Figure 4. It is found that raising C_g can lead to the increase of C_e, but the decrease of η_op. The reason for the increase of C_e is because of the larger-size rear reflectors that scatter more incident flux and increase the irradiance levels on the PV surfaces. The reason for the decrease of η_op is because of the larger-area glazing cover that aggravates the light escape through the front surface and contributes to higher optical loss.

Figure 4. The optical efficiency and effective concentration ratio as a function of the geometric concentration ratio.

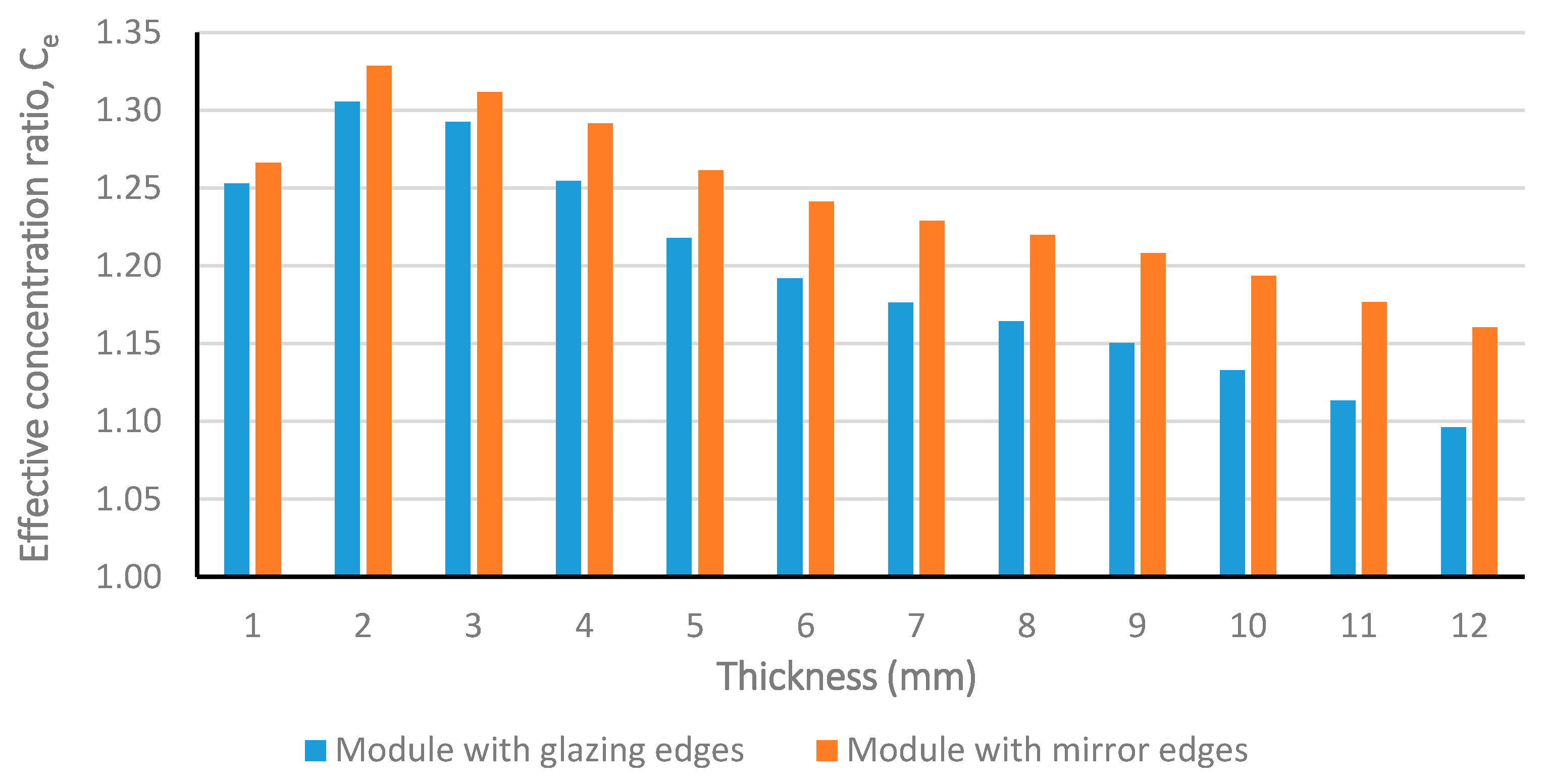
3.3. Influence of the Glass Thickness and Edge Mirror

Glass cover thickness is another significant parameter for the optimum system design. The influence of the front glazing cover thickness and edge mirrors on the effective concentration ratio are shown in Figure 5. It can be found that the effective concentration ratio increases, when the thickness of the front glazing cover increases from 1 to 2 mm. A possible reason is because the amount of the light pass between the glazing front surface and the Lambertian reflector reduces as the glass cover thickness increases and, thus, the probability of light escaping at the front surface decreases and the optical loss reduces. Consequently, fewer scattered rays are collected by the solar cells and the irradiances on the PV surfaces become lower. On the other hand, when the glazing thickness increases from 2 to 12 mm, the value of C_e reduces. This is because the optical path of the light travel within the glass is prolonged and the surface areas of the glass edges are enlarged, which causes more energy absorption by the glass medium and escaping through the glass edges. To relieve the negative impact, an alternative is to integrate the front glazing cover with edge mirrors. As observed from Figure 5, when the four edges of the glazing cover are coupled with mirrors (specular reflectivity = 100%), the values of C_e are significantly improved. The effect of edge mirrors is more apparent when the CPV module has a thicker front glazing cover.

Figure 5. The effective concentration ratio as a function of glass thickness with and without edge mirrors.

3.4. Influence of the Glazing Optical Properties

A range of Pilkington optical glasses are selected for the front glazing cover for the comparative analysis. The optical properties of the glasses are listed in Table 1. From Figure 6, it is observed that C_e and η_op increase with the increase of glazing refractive index. The reason is because the critical angle becomes smaller and the light-trapping ability is improved. Nevertheless, it should be noted that more incident light would be reflected off the air-glass interface if the glass has a higher refractive index, as seen from Table 1. One feasible solution is to apply an antireflection coating on the glazing cover to enhance the light transmission. In another aspect, the optical glass BSC517642 exhibits better optical performance, compared with the Optiwhite^TM low-iron glass that has a similar refractive index (1.51). This might be because the optical glass has a lower absorption coefficient, thus, less energy is absorbed by the glazing cover.

Table 1. Optical properties of the Pilkington optical glasses at the wavelength of 0.54 μm.

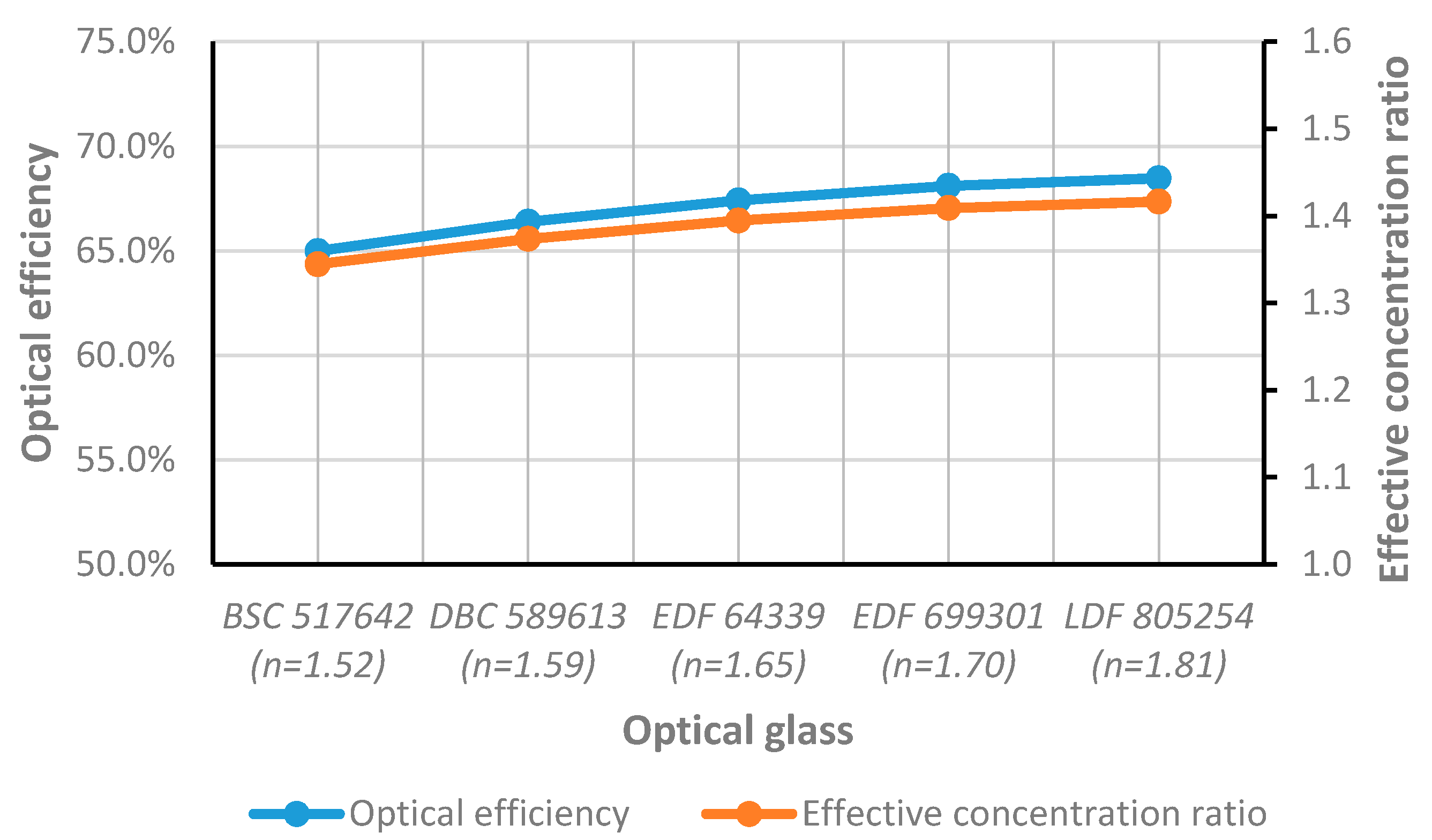
	BSC 517642	DBC 589613	EDF 648339	EDF 699301	LDF 805254
Refractive index	1.52	1.59	1.65	1.70	1.81
Critical angle (°)	41.5	41.1	39.0	37.3	36.0
Reflectivity at the air-glass interface	4.3%	5.2%	6.0%	6.7%	8.3%
Absorption coefficient (cm−1)	0.003	0.003	0.002	0.002	0.001

Figure 6. Optical efficiencies and effective concentration ratios of the systems with different optical glasses.

3.5. Influence of the Reflectivity of the Lambertian Reflector

In the study, the optical performance of the modules with the opaque reflectors (r + a = 100%) and the semitransparent reflectors (τ + r = 100%) are respectively analyzed. For opaque reflectors, when the diffuse reflectivity varies from 99% to 30%, it is observed that η_op descends from 62.5% to 49.9%, and the value of C_e drops from 1.29 to 1.03, as shown from in Figure 7. When the reflectivity is further reduced, C_e becomes less than 1.0, which means the CPV system starts to become ineffective in solar concentration. Therefore, the use of opaque reflectors with a reflectivity higher than 30% in order to maintain effective solar concentration is suggested. For semi-transparent reflectors, the decreasing rates of the optical efficiency and effective concentration ratio are relatively lower compared with the module with opaque reflectors. It can be seen that the effective concentration ratio remains above 1.0 when the transmittance is increased to 100%. This might be because some of the light transmitted through the transparent reflectors may be trapped in the back glass sheet via TIR, and transported back to the front cover to be collected by the solar cells.

Figure 7. The optical efficiency and effective concentration ratio as a function of the diffuse reflectivity of the opaque and semi-transparent reflectors.

3.6. Influence of the Solar Incident Angle

A ray-tracing simulation is performed for the CPV modules with Lambertian and v-groove rear reflectors under different solar incident angles, respectively. As indicated in Figure 8a,b, the module is placed horizontally and the sun trajectory changes in both solar azimuth angles (0°, 45° and 90°) and solar zenith angles (from 0° to 90°). The edges of the glazing covers are masked by mirrors and only the oblique rays entering the front surface are traced. The v-grooves are designed with the parameters referred from the literatures [18,27]: v-groove width = 0.2 mm, length = 116 mm, depth = 0.058 mm, slope angle = 30°, and specular reflectivity = 80%. The rear reflector between the solar cells is 6 mm wide, consisting of 30 v-grooves (see Figure 8c).

Figure 8. Raytracing simulation at (a) three different solar azimuths and (b) at the solar zenith angles from 0 to 90°; (c) diagram of the module with v-grooves; (d) optical efficiencies of the Lambertian reflector based module at different solar zenith angles and solar azimuths; and (e) optical efficiencies of the v-groove reflector based module at different solar zenith angles and solar azimuths.

According to Figure 8d, it is found that the optical efficiencies of the module with Lambertian reflectors are less dependent on the solar azimuth angles and change insignificantly when the zenith angle is below 70°. Beyond 70°, the optical efficiencies drop dramatically, because the reflectivity of the air-glass interface starts to increase sharply. Based on the findings, it is concluded that the proposed CPV module has a wide angular acceptance range, therefore, it can be integrated into the building envelope for power generation without tracking demand. As seen in Figure 8e, when the solar azimuth is constant, the optical efficiency of the CPV module with v-groove reflectors varies with the solar zenith angle. However, the extent of the variation is relatively smaller when the solar azimuth is 90° (east), which might be because the long-axis of the v-grooves is in the west-east direction and, thus, the change of the solar zenith angle in the east direction does not largely influence the number of the internally-reflected rays that are collected by each solar cell. On the other hand, when the solar zenith angle is constant, it is found that the optical efficiency of the module changes with the solar azimuth. By comparison, the optical performance of the CPV module with Lambertian rear reflectors is relatively less sensitive to the variation of incident light angle.

4. Conclusions

A numerical study based on a 3D ray-tracing simulation is conducted to evaluate the optical performance of a novel planar static concentrating PV module with Lambertian rear reflectors, which can be integrated into building envelope for on-site power generation. By investigation, the optical efficiency and effective concentration ratio of the proposed CPV module with a geometric concentration ratio of 2.0 are 62.5% and 1.29, respectively. The radiant flux received by the solar cells in the proposed module is about 1.4 times than that of the counterpart module without a solar concentrator. To improve the effective concentration ratio, it is suggested to reduce the interval distance between the adjacent solar cells, use a front glazing cover with appropriate small thickness and high refractive index, and increase the reflectivity of the rear reflectors. In addtion, coupling the front glazing cover with edge mirrors can effectively reduce the optical loss of the system, especially when a thick glazing cover is used. From the angular dependence study, it is known that the proposed CPV module with Lambertian rear reflectors has a good angular acceptance and its optical efficiency is relatively less sensitive to the solar incident angle, compared with the counterpart module with v-groove rear reflectors. In future work, the numerical work will be improved by taking diffuse solar radiation and the solar spectrum into consideration. More realistic optical parameters of the solar cells and Lambertian reflector will be applied in the simulation. Prototypes with different parametric designs will be fabricated for building applications, and the energy and daylighting control performance will be measured and evaluated. Bifacial solar cells, glazing surface treatment technologies, and/or the combination of different reflectors will also be considered in future work to improve the system overall perofrmance.