Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice
Abstract
:1. Introduction
2. The Use of Hedonic Approach for the Assessment or Urban Quality
3. The Methodology
3.1. The Valuation Model
3.1.1. The Hedonic Price Method
- Market offers properties with a continuous combination of public and private characteristics (A and z);
- Purchasers behave according to the principle of decreasing marginal utility of environmental and urban qualities;
- Purchasers have the same access opportunity to the real estate market; in other words, they have the same information, transaction and transfer costs, and the same income and mobility;
- The real estate market is transparent regarding prices and properties characteristics;
- Market prices adapt immediately to changes in environmental and urban quality; and
- Market offers many transactions.
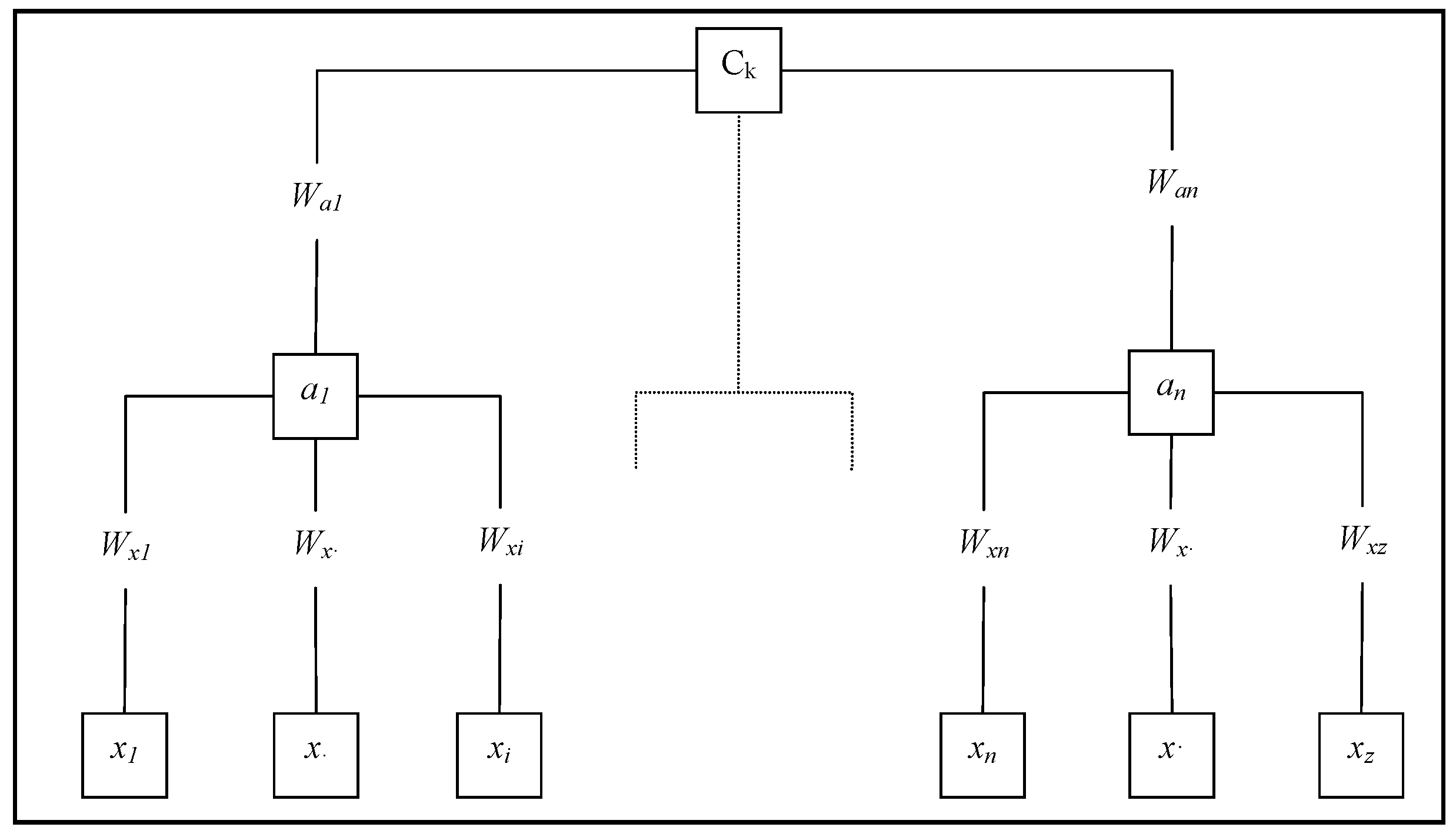
3.1.2. The Multi Attribute Procedure
- Structures indicators in hierarchical trees that summarize the real estate characteristics at various aggregation levels;
- Estimates aggregate indicators from a comparison between detailed characteristics rather than from a comparison between the real estates in the sample; and
- Uses a direct weights assignment procedure for characterization instead of the pairwise comparison.
- More detailed identification and characterization of the variables and indicators affecting market value;
- The possibility to build more general models than those built with reference to specific real estate sample;
- Eliminates the risk of “rank reversal” in the estimate of the cardinal aggregate indicator, inherent in the pairwise comparison approach;
- The possibility to apply econometric analysis to indicators at various aggregation levels.
- Individuation of the characteristics (xi) potentially influencing the value of real estate goods in the specific urban context and aggregation of characteristics (xi) in indicators (aj, ck);
- The elicitation of weights (wi) which represent the relative importance of the various characteristics (xi) at each level of hierarchical decomposition for the definition of the aggregated indicators (ck).
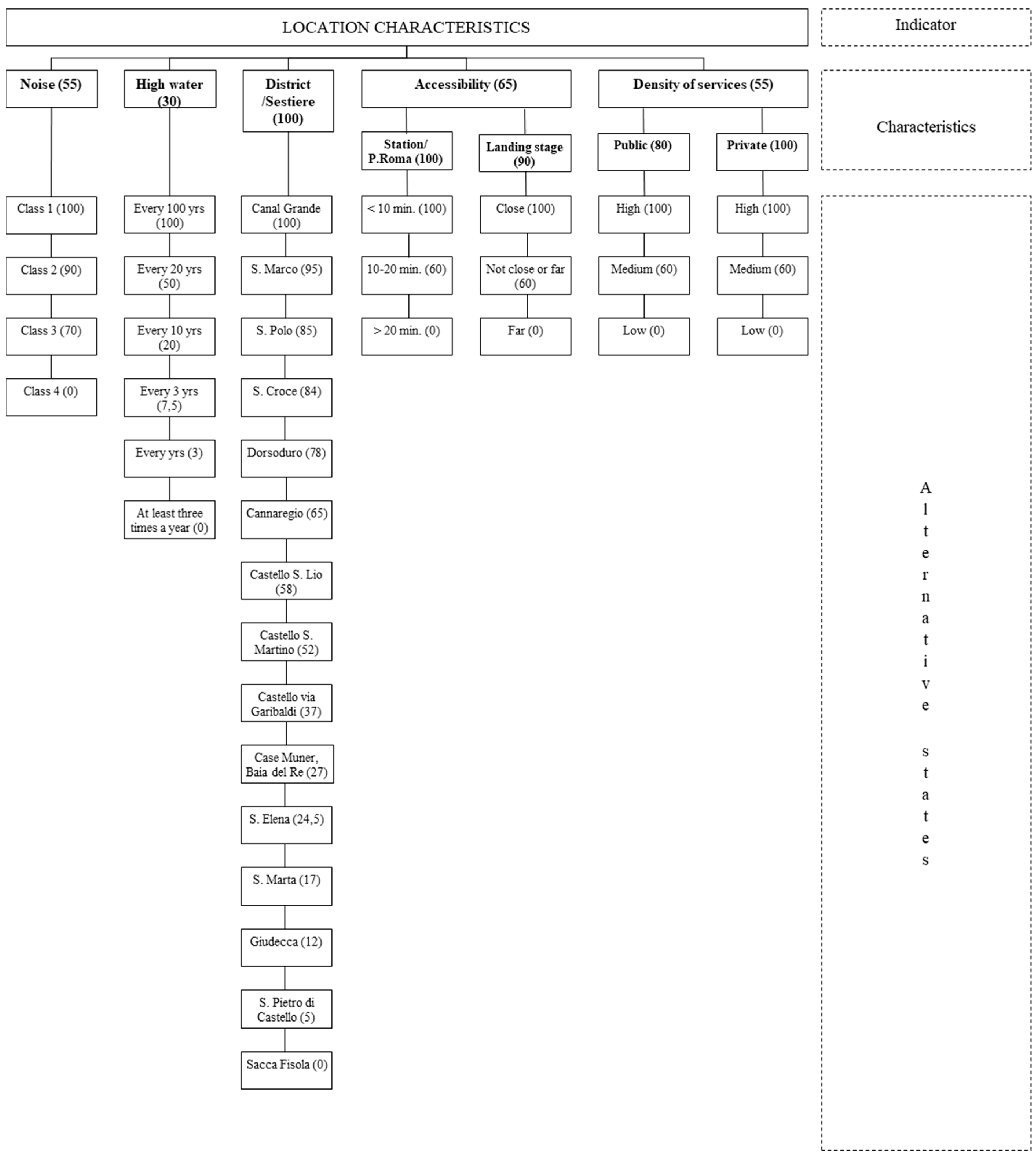
- Location characteristics, which include environmental and urban quality;
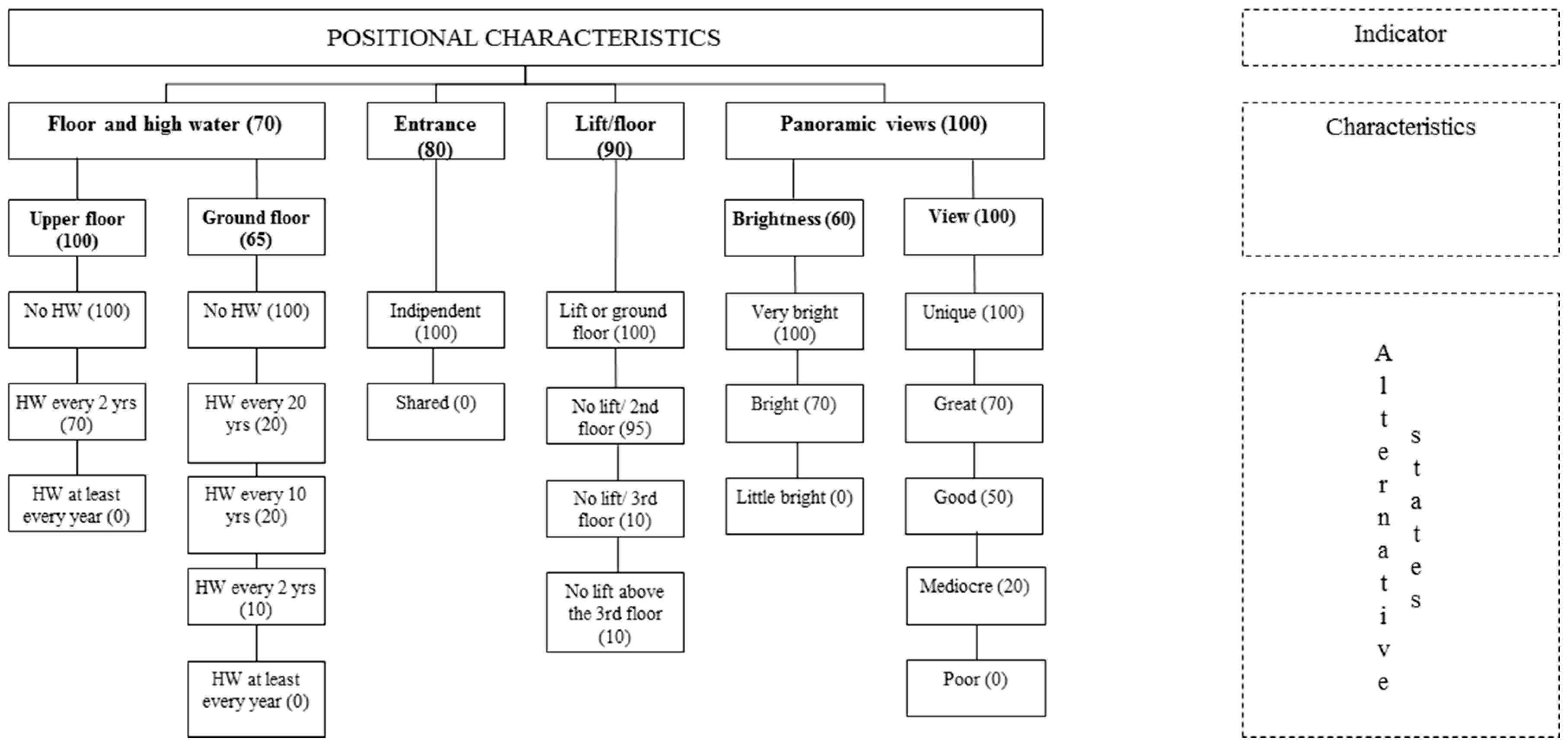
- Position characteristics, which describe the way the building is related to the surrounding context;
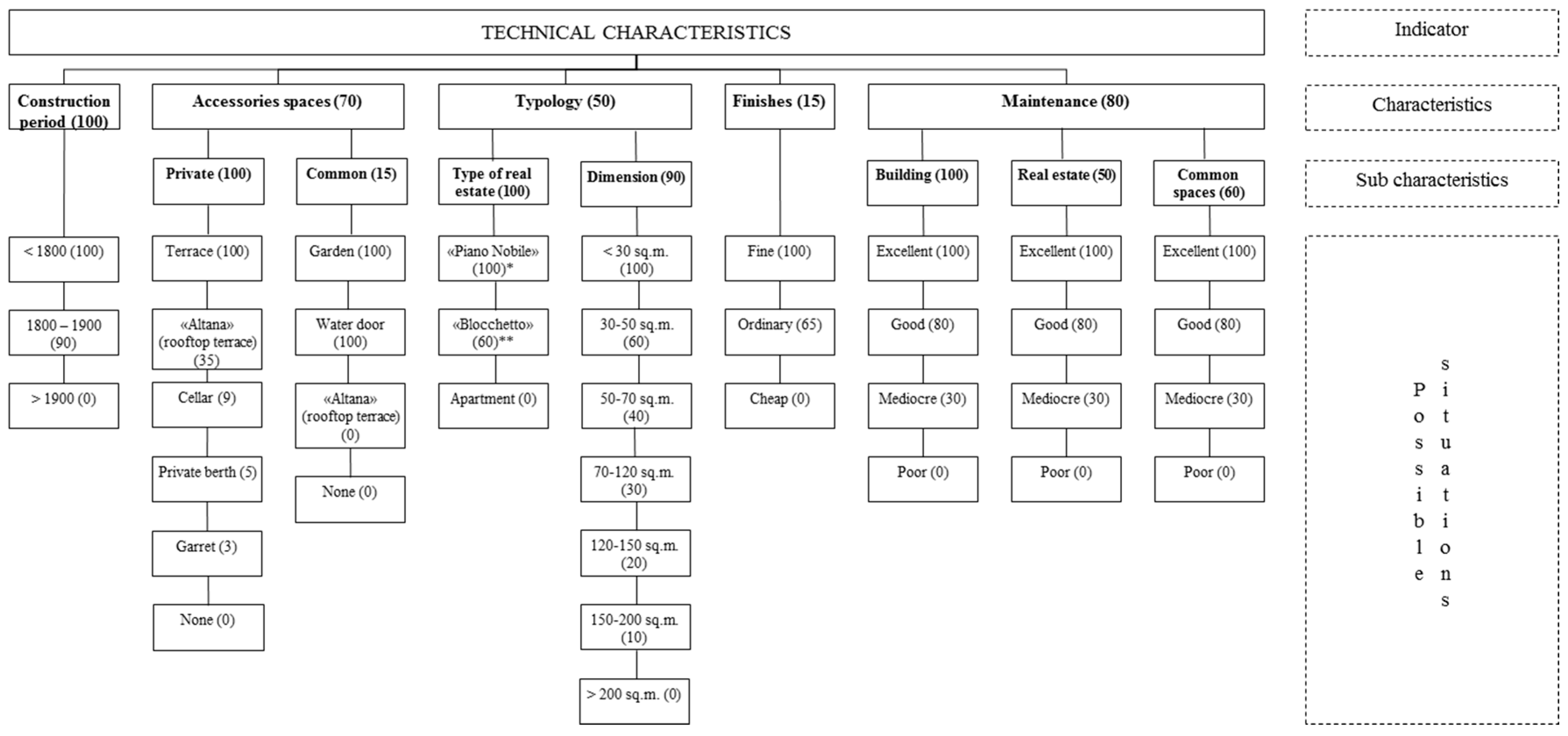
- Technical characteristics, which comprehend dimension, architecture typology, finishing and maintenance;
- Economic characteristics, which regard particular aspects, such as third party rights and usufruct.
- For each node (an) of the hierarchy, the relative characteristics (xi) are identified
- For each characteristic, the best and the worst possible state is defined to obtain a set of maximum possible improvements on each characteristic.
- The characteristics (xi) are ordered according to the contribution in defining the complex variable represented by a node (an).
- Score are fixed out of 100, the score of the most important characteristics, with the remainders receiving a score according to their relative importance.
- Scores are normalized.
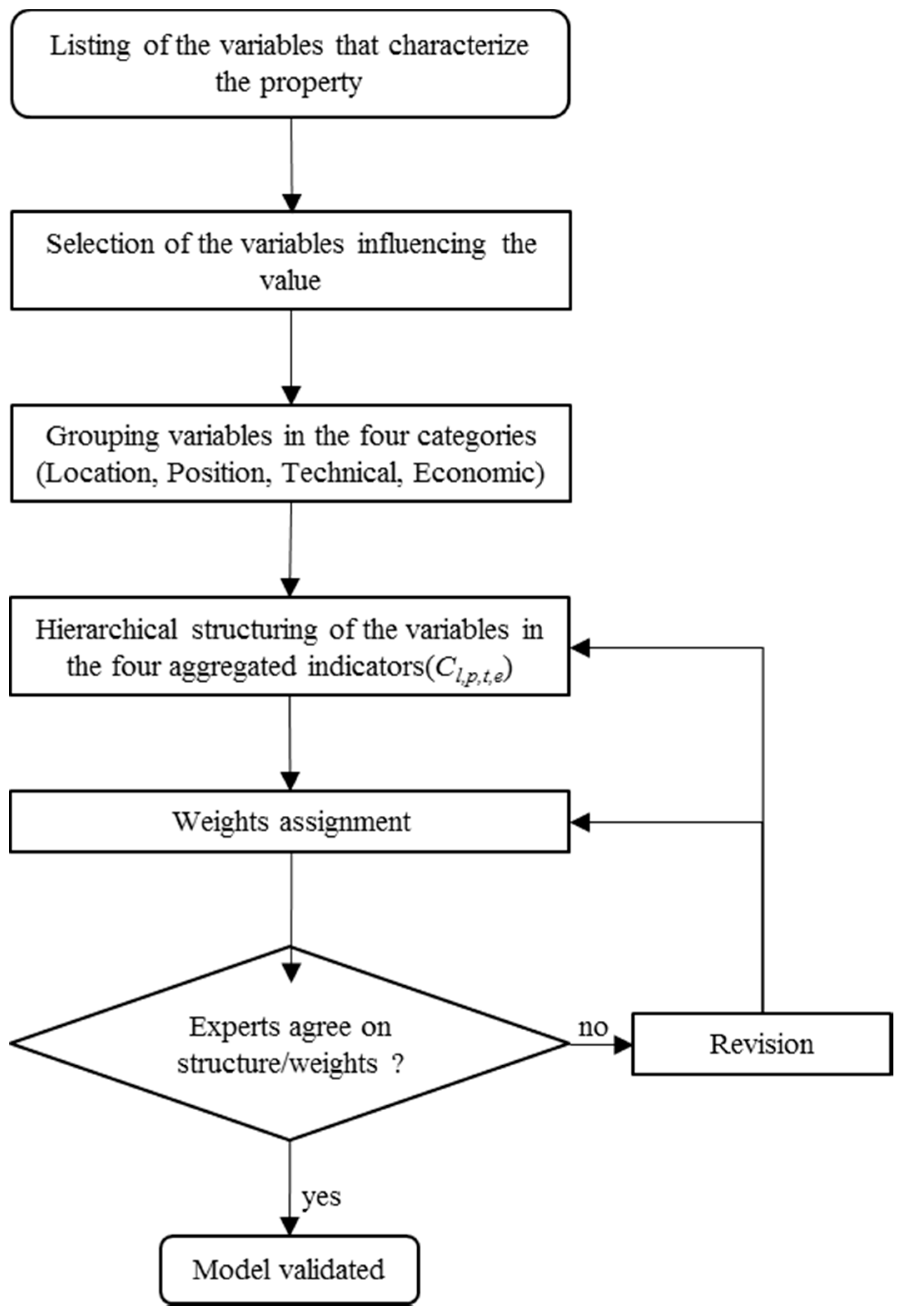
3.1.3. The Model Estimation
- Identification of modified characteristics by eliminating high flooding (tides greater than 110 cm);
- Identification of the variation induced on the state of these variables;
- Calculus of the modified aggregated indicators (cl,p,t,e) using MAA models of Figures 3–6; and
- Calculus of the modified value using Equation (2).
3.2. A Hedonic-Multi Attribute Model for the Historic Center of Venice
- Location characteristics (cl), which includes environmental and urban quality like services, accessibility, infrastructure, amenities, pollution, noise, etc.;
- Position characteristics (cp), which describe the way the building is related to the surrounding context like views, brightness, etc.;
- Technical characteristics (ct), which comprehend architecture typology, finishing, maintenance, etc.; and
- Economic characteristics (ce), which regard those aspects that influence income, profitability, costs, etc.
- Calculation for each market data (comparable) of the aggregate indicators described above (cl,p,t,e);
- Stepwise OLS (ordinary least square) regression with the aggregate indicators as independent variables and the property prices (€ m−2) as dependent variables.
3.3. The Geographic Model
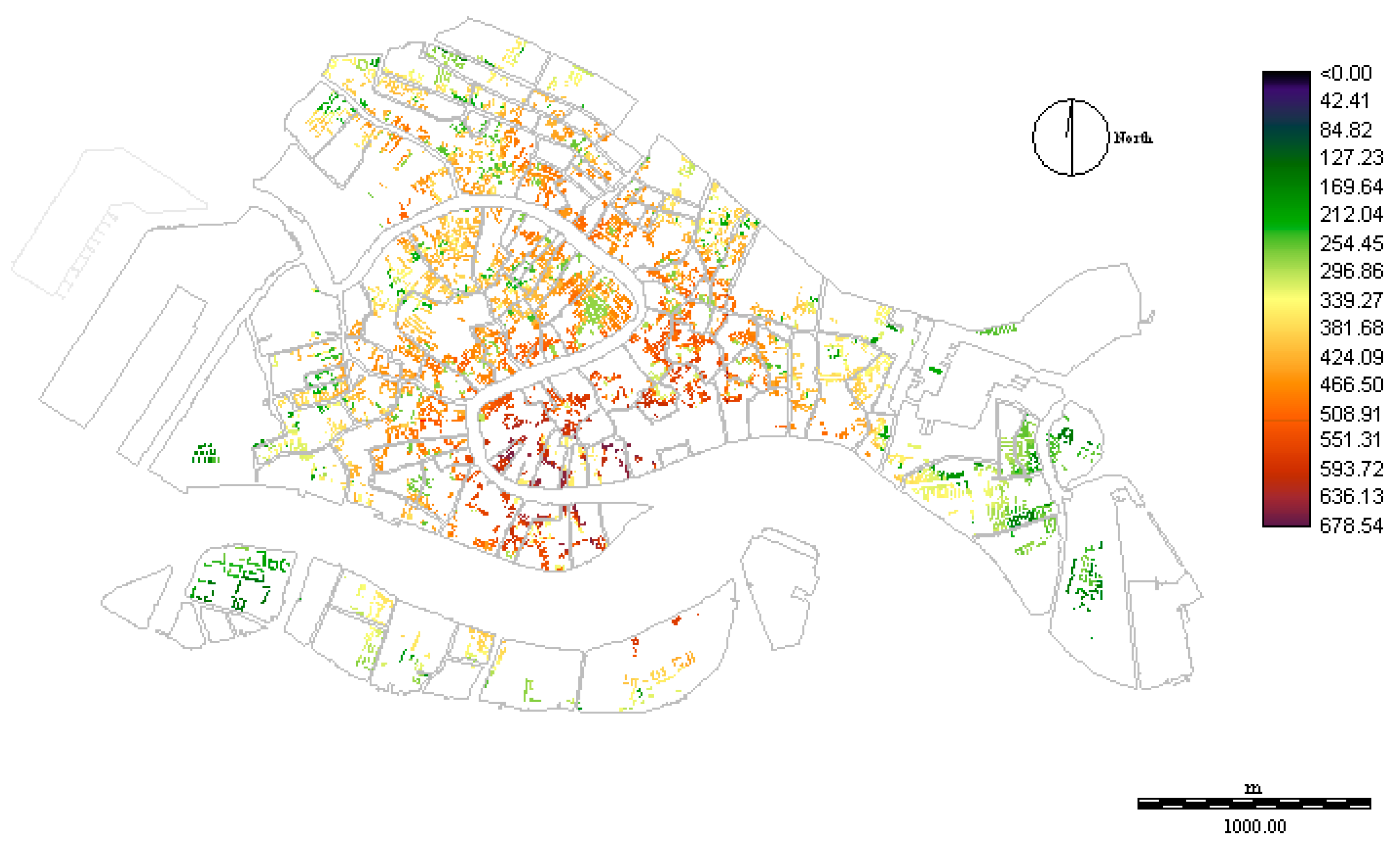
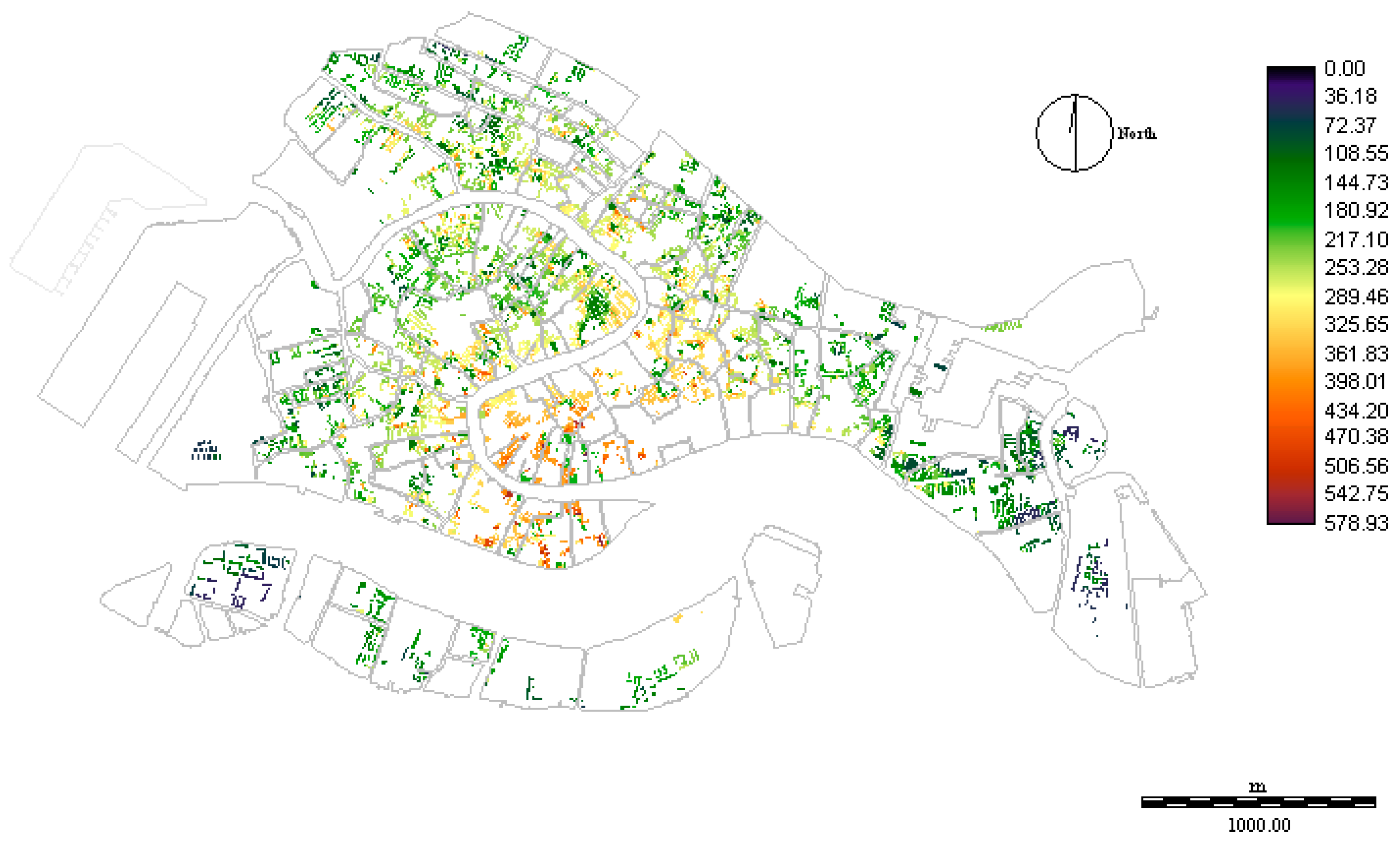
3.3.1. The Distribution of Location Characteristics
3.3.2. The Distribution of Position Characteristics
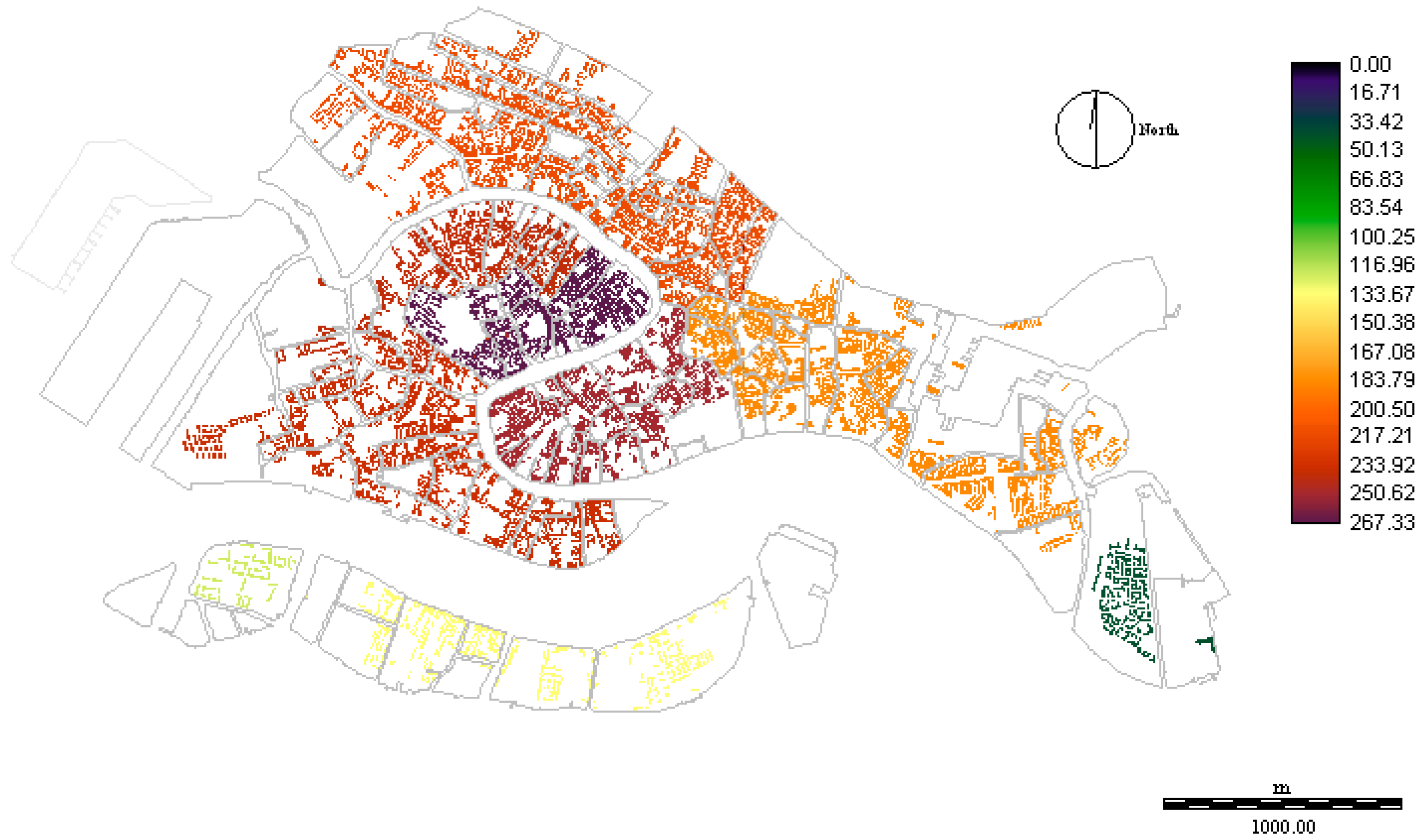
3.3.3. The Present Distribution of Residential Property Value
4. The Simulation of Urban Improvements
- Identification of modified characteristics by eliminating high flooding (tides greater than 110 cm);
- Identification of the variation induced on the state of these variables;
- Calculating the modified value using Equation (2).
- Location characteristics: The frequency of flooding was set to zero for areas situated above 110 cm above sea level, thus diminishing the flood frequency. For buildings situated in areas under 110 cm, the frequencies were reduced consequently.
- Position: Analogously, the frequency of building flooding was modified by eliminating those caused by tides higher than 110 cm above sea level.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A.
| Property _________ | |||
| Date of purchase (month/year) | |||
| Price (€) | |||
| Floor area (m2) | |||
| Location (house number or position on the map) | |||
| Positional Characteristics | |||
| 1. | Flooding with high water | Tide level at which the ground floor of building is flooded (cm) | |
| Flooding frequency per year (average) | |||
| 2. | Entrance/Lift | Independent entrance | |
| Is there a lift serving the property? | |||
| 3. | Construction period | Before 1800 | |
| 1800–1900 | |||
| 1900–1945 | |||
| After 1945 | |||
| 4. | Brightness of the property | Very bright | |
| Bright | |||
| Little bright | |||
| Quality of the view from the property | Unique | ||
| Great | |||
| Good | |||
| Mediocre | |||
| Poor | |||
| 5. | Accessory | Terrace | |
| “Altana” | |||
| Cellar | |||
| Private berth | |||
| Garret | |||
| Technical Characteristics | |||
| 1. | Dimension | <30 m2 | |
| 30–50 m2 | |||
| 50–70 m2 | |||
| 70–120 m2 | |||
| 120–150 m2 | |||
| 150–200 m2 | |||
| 2. | Typology | “Piano Nobile” | |
| “Blocchetto” | |||
| Apartment | |||
| 3. | Finishes | Fine | |
| Ordinary | |||
| Cheap | |||
| 4. | Building maintenance | Excellent | |
| Good | |||
| Mediocre | |||
| Poor | |||
| Real estate maintenance | Excellent | ||
| Good | |||
| Mediocre | |||
| Poor | |||
| Common spaces maintenance | Excellent | ||
| Good | |||
| Mediocre | |||
| Poor | |||
| 5. | Floor | GF, 1st, 2nd, 3rd, 4th or 5th floor | |
| Economic Characteristics | |||
| 1. | Availability | Free | |
| Rented | |||
| Free with usufruct | |||
| Rented with usufruct | |||
References
- Hanley, N.; Knight, J. Valuing the environment: Recent UK experience and an application to Green Belt Land. J. Environ. Plan. Manag. 1992, 35, 145–160. [Google Scholar] [CrossRef]
- Bullock, C.H. Valuing Urban Green Space: Hypothetical Alternatives and the Status Quo. J. Environ. Plan. Manag. 2008, 51, 15–35. [Google Scholar] [CrossRef]
- Whitehead, J.C.; Haab, T.C.; Huang, J.-C. Measuring recreation benefits of quality improvements with revealed and stated behavior data. Resour. Energy Econ. 2000, 22, 339–354. [Google Scholar] [CrossRef]
- Pearce, D.; Atkinson, G.; Mourato, S. Cost-Benefit Analysis and the Environment: Recent Developments; Organisation for Economic Co-Operation and Development: Paris, France, 2006; ISBN 978-92-64-01004-8. [Google Scholar]
- Crompton, J.L. The impact of parks on property values. empirical evidence from the past two decades in the United States. Manag. Leisure 2005, 10, 203–218. [Google Scholar] [CrossRef]
- Cloudburst Management Pays Off 2014—Climate-ADAPT. Available online: http://climate-adapt.eea.europa.eu/repository/11286781.pdf/view (accessed on 16 October 2017).
- Bender, A.; Din, A.; Favarger, P.; Hoesli, M.; Laakso, J. An analysis of perceptions concerning the environmental quality of housing in Geneva. Urban Stud. 1997, 34, 503–513. [Google Scholar] [CrossRef]
- Din, A.; Hoesli, M.; Bender, A. Environmental variables and real estate prices. Urban Stud. 2001, 38, 1989–2000. [Google Scholar] [CrossRef]
- Baranzini, A.; Ramirez, J.V. Paying for quietness: The impact of noise on Geneva rents. Urban Stud. 2005, 42, 633–646. [Google Scholar] [CrossRef]
- Lake, I.R.; Lovett, A.A.; Bateman, I.J.; Langford, I.H. Modelling environmental influences on property prices in an urban environment. Comput. Environ. Urban Syst. 1998, 22, 121–136. [Google Scholar] [CrossRef]
- Del Giudice, V.; De Paola, P. The Effects of Noise Pollution Produced by Road Traffic of Naples Beltway on Residential Real Estate Values; Trans Tech Publications: Zürich, Switzerland, 2014; Volume 587, pp. 2176–2182. [Google Scholar]
- Del Giudice, V.; De Paola, P.; Manganelli, B.; Forte, F. The monetary valuation of environmental externalities through the analysis of real estate prices. Sustainability 2017, 9, 229. [Google Scholar] [CrossRef]
- Gao, X.; Asami, Y. The external effects of local attributes on living environment in detached residential blocks in Tokyo. Urban Stud. 2001, 38, 487–505. [Google Scholar] [CrossRef]
- Zabel, J.E.; Kiel, K.A. Estimating the demand for air quality in four US cities. Land Econ. 2000, 76, 174–194. [Google Scholar] [CrossRef]
- Irwin, E.G. The effects of open space on residential property values. Land Econ. 2002, 78, 465–480. [Google Scholar] [CrossRef]
- Kim, C.W.; Phipps, T.T.; Anselin, L. Measuring the benefits of air quality improvement: A spatial hedonic approach. J. Environ. Econ. Manag. 2003, 45, 24–39. [Google Scholar] [CrossRef]
- Crane, R.; Daniere, A.; Harwood, S. The contribution of environmental amenities to low-income housing: A comparative study of Bangkok and Jakarta. Urban Stud. 1997, 34, 1495–1512. [Google Scholar] [CrossRef]
- Coulson, N.E.; Leichenko, R.M. The internal and external impact of historical designation on property values. J. Real Estate Financ. Econ. 2001, 23, 113–124. [Google Scholar] [CrossRef]
- Votsis, A. Planning for green infrastructure: The spatial effects of parks, forests, and fields on Helsinki’s apartment prices. Ecol. Econ. 2017, 132, 279–289. [Google Scholar] [CrossRef]
- Bond, M.T.; Seiler, V.L.; Seiler, M.J. Residential real estate prices: A room with a view. J. Real Estate Res. 2002, 23, 129–138. [Google Scholar]
- Tajani, F.; Morano, P.; Locurcio, M.; Torre, C.M. Data-driven techniques for mass appraisals. Applications to the residential market of the city of Bari (Italy). Int. J. Bus. Intell. Data Min. 2016, 11, 109–129. [Google Scholar] [CrossRef]
- Walsh, P.; Griffiths, C.; Guignet, D.; Klemick, H. Modeling the Property Price Impact of Water Quality in 14 Chesapeake Bay Counties. Ecol. Econ. 2017, 135, 103–113. [Google Scholar] [CrossRef]
- Tomkins, J.; Topham, N.; Twomey, J.; Ward, R. Noise versus access: The impact of an airport in an urban property market. Urban Stud. 1998, 35, 243–258. [Google Scholar] [CrossRef]
- Mei, Y.; Hite, D.; Sohngen, B. Demand for urban tree cover: A two-stage hedonic price analysis in California. For. Policy Econ. 2017, 83, 29–35. [Google Scholar] [CrossRef]
- Saginor, J.; Ge, Y. Do hurricanes matter?: A case study of the residential real estate market in Brunswick County, North Carolina. Int. J. Hous. Mark. Anal. 2017, 10, 352–370. [Google Scholar] [CrossRef]
- Chay, K.Y.; Greenstone, M. Does air quality matter? Evidence from the housing market. J. Polit. Econ. 2005, 113, 376–424. [Google Scholar] [CrossRef]
- Paterson, R.W.; Boyle, K.J. Out of sight, out of mind? Using GIS to incorporate visibility in hedonic property value models. Land Econ. 2002, 78, 417–425. [Google Scholar] [CrossRef]
- Wu, J.; Adams, R.M.; Plantinga, A.J. Amenities in an urban equilibrium model: Residential development in Portland, Oregon. Land Econ. 2004, 80, 19–32. [Google Scholar] [CrossRef]
- Anselin, L.; Lozano-Gracia, N.; Deichmann, U.; Lall, S. Valuing Access to Water-A Spatial Hedonic Approach, with an Application to Bangalore, India. Spat. Econ. Anal. 2010, 5, 161–179. [Google Scholar] [CrossRef]
- Curto, R.; Fregonara, E.; Semeraro, P. A spatial analysis for the real estate market applications. In Advances in Automated Valuation Modeling; Springer: Cham, Switzerland, 2017; pp. 163–179. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Chichester, UK, 2003; ISBN 0-470-85525-8. [Google Scholar]
- Herath, S.; Choumert, J.; Maier, G. The value of the greenbelt in Vienna: A spatial hedonic analysis. Ann. Reg. Sci. 2015, 54, 349–374. [Google Scholar] [CrossRef]
- Bin, O.; Poulter, B.; Dumas, C.F.; Whitehead, J.C. Measuring the Impact of Sea-Level Rise on Coastal Real Estate: A Hedonic Property Model Approach. J. Reg. Sci. 2011, 51, 751–767. [Google Scholar] [CrossRef]
- Orford, S.; Dorling, D.; Harris, R. Review of Visualisation in the Social Sciences: A State of the Art Survey and Report; Advisory Group on Computer Graphics: Bristol, UK, 1998. [Google Scholar]
- Roebeling, P.; Saraiva, M.; Palla, A.; Gnecco, I.; Teotónio, C.; Fidelis, T.; Martins, F.; Alves, H.; Rocha, J. Assessing the socio-economic impacts of green/blue space, urban residential and road infrastructure projects in the Confluence (Lyon): A hedonic pricing simulation approach. J. Environ. Plan. Manag. 2017, 60, 482–499. [Google Scholar] [CrossRef]
- Wen, H.-Z.; Jia, S.-H.; Guo, X.-Y. Hedonic price analysis of urban housing: An empirical research on Hangzhou, China. J. Zhejiang Univ. 2005, 6, 907–914. [Google Scholar] [CrossRef]
- Donnelly, W.A. Hedonic Price Analysis of the Effect of a Floodplain on Property Values. J. Am. Water Resour. Assoc. 1989, 25, 581–586. [Google Scholar] [CrossRef]
- Harrison, D.T.; Smersh, G.; Schwartz, A. Environmental determinants of housing prices: The impact of flood zone status. J. Real Estate Res. 2001, 21, 3–20. [Google Scholar]
- Bin, O.; Polasky, S. Effects of flood hazards on property values: Evidence before and after Hurricane Floyd. Land Econ. 2004, 80, 490–500. [Google Scholar] [CrossRef]
- Bin, O.; Kruse, J.B. Real estate market response to coastal flood hazards. Nat. Hazards Rev. 2006, 7, 137–144. [Google Scholar] [CrossRef]
- Bin, O.; Kruse, J.B.; Landry, C.E. Flood hazards, insurance rates, and amenities: Evidence from the coastal housing market. J. Risk Insur. 2008, 75, 63–82. [Google Scholar] [CrossRef]
- Daniel, V.E.; Florax, R.J.; Rietveld, P. Flooding risk and housing values: An economic assessment of environmental hazard. Ecol. Econ. 2009, 69, 355–365. [Google Scholar] [CrossRef]
- Samarasinghe, O.; Sharp, B. Flood prone risk and amenity values: A spatial hedonic analysis. Aust. J. Agric. Resour. Econ. 2010, 54, 457–475. [Google Scholar] [CrossRef]
- McKenzie, R.; Levendis, J. Flood Hazards and Urban Housing Markets: The Effects of Katrina on New Orleans. J. Real Estate Financ. Econ. 2010, 40, 62–76. [Google Scholar] [CrossRef]
- Bin, O.; Landry, C.E.; Meyer, G.F. Riparian buffers and hedonic prices: A quasi-experimental analysis of residential property values in the Neuse River basin. Am. J. Agric. Econ. 2009, 91, 1067–1079. [Google Scholar] [CrossRef]
- Rambaldi, A.N.; Fletcher, C.S.; Collins, K.; McAllister, R.R. Housing shadow prices in an inundation-prone suburb. Urban Stud. 2013, 50, 1889–1905. [Google Scholar] [CrossRef]
- Bin, O.; Landry, C.E. Changes in implicit flood risk premiums: Empirical evidence from the housing market. J. Environ. Econ. Manag. 2013, 65, 361–376. [Google Scholar] [CrossRef]
- Fu, X.; Song, J.; Sun, B.; Peng, Z.-R. “Living on the edge”: Estimating the economic cost of sea level rise on coastal real estate in the Tampa Bay region, Florida. Ocean Coast. Manag. 2016, 133, 11–17. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Freeman, A.M., III. Hedonic prices, property values and measuring environmental benefits: A survey of the issues. In Measurement in Public Choice; Springer: London, UK, 1981; pp. 13–32. [Google Scholar]
- Witte, A.D.; Sumka, H.J.; Erekson, H. An estimate of a structural hedonic price model of the housing market: An application of Rosen’s theory of implicit markets. Econom. J. Econom. Soc. 1979, 1151–1173. [Google Scholar] [CrossRef]
- Diamond, D.B.; Smith, B.A. Simultaneity in the market for housing characteristics. J. Urban Econ. 1985, 17, 280–292. [Google Scholar] [CrossRef]
- Curto, R. Mercato delle abitazioni e valori: Il caso di Torino. Genio Rurale 1990, 5, 11–27. [Google Scholar]
- Ozanne, L.; Malpezzi, S. The efficacy of hedonic estimation with the annual housing survey. Evidence from the demand experiment. J. Econ. Soc. Meas. 1985, 13, 153–172. [Google Scholar]
- Curto, R. L’uso Delle Tecniche Multicriteri Come Procedimenti Pluriparametrici; CELID: Torino, Italy, 2005. [Google Scholar]
- Rosato, P.; Lisini, L. I metodi di analisi quantitativa nell’estimo immobiliare: Una valutazione comparata. In Estimo E Valutazione Metodol. E Casi Studio; DEI Tipogr. Genio Civ.: Roma, Italy, 2007; pp. 45–60. [Google Scholar]
- Forte, C.; De’Rossi, B.; Ruffolo, G. Principi di Economia ed Estimo; Etas Libri: Milano, Italy, 1974. [Google Scholar]
- Belton, V.; Stewart, T. Multiple Criteria Decision Analysis: An Integrated Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002; ISBN 0-7923-7505-X. [Google Scholar]
- Von Winterfeldt, D.; Edwards, W. Decision Analysis and Behavioral Research; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Comune di Venezia Distribuzione Annuale Alte e Basse Maree. Available online: http://www.comune.venezia.it/it/content/distribuzione-annuale-delle-alte-maree-110-cm (accessed on 26 November 2017).
- Umgiesser, G.; Matticchio, B. Simulating the mobile barrier (MOSE) operation in the Venice Lagoon, Italy: Global sea level rise and its implication for navigation. Ocean Dyn. 2006, 56, 320–332. [Google Scholar] [CrossRef]
- Vergano, L.; Umgiesser, G.; Nunes, P.A. An economic assessment of the impacts of the MOSE barriers on Venice port activities. Transp. Res. Part D Transp. Environ. 2010, 15, 343–349. [Google Scholar] [CrossRef]


| Variable | Min | Max | Average | Std. Dev. |
|---|---|---|---|---|
| Price (€) | 70,000 | 2,500,000 | 402,956 | 271.518 |
| Price (€ m−2) | 1679 | 9000 | 4528 | 1.298 |
| Residential area (m2) | 27 | 400 | 92 | 56 |
| Height above sea level (cm) | 85 | 210 | 145 | 28 |
| Variable | Freq. | % | Cum. (%) | |
|---|---|---|---|---|
| Urban Areas | Cannaregio | 57 | 28.9 | 28.9 |
| Castello, San Pietro, via Garibaldi | 6 | 3.0 | 32.0 | |
| Sant’Elena | 2 | 1.0 | 33.0 | |
| Dorsoduro | 26 | 13.2 | 46.2 | |
| Giudecca/Sacca Fisola | 25 | 12.7 | 58.9 | |
| San Marco/Canal Grande | 13 | 6.6 | 65.5 | |
| S. Polo | 24 | 12.2 | 77.7 | |
| S. Croce | 17 | 8.6 | 86.3 | |
| Castello San Lio | 5 | 2.5 | 88.8 | |
| Castello S. Martino | 19 | 9.6 | 98.5 | |
| Case Muner, Baia del Re | 1 | 0.5 | 99.0 | |
| Santa Marta | 2 | 1.0 | 100.0 | |
| Distance from Venice access | >20 min | 107 | 54.3 | 54.3 |
| 10–20 min | 48 | 24.4 | 78.7 | |
| <10 min | 42 | 21.3 | 100.0 | |
| Entrance | Shared | 145 | 73.6 | 73.6 |
| Independent | 52 | 26.4 | 100.0 | |
| Lift/Floor | Lift or ground floor | 63 | 32.0 | 32.0 |
| No lift/2nd floor | 102 | 51.8 | 83.8 | |
| No lift/3rd floor | 24 | 12.2 | 95.9 | |
| No lift above 3rd floor | 8 | 4.1 | 100.0 | |
| Brightness | Very bright | 59 | 29.9 | 29.9 |
| Bright | 96 | 48.7 | 78.7 | |
| Little bright | 42 | 21.3 | 100.0 | |
| View | Unique | 10 | 5.1 | 5.1 |
| Great | 24 | 12.2 | 17.3 | |
| Good | 83 | 42.1 | 59.4 | |
| Mediocre | 70 | 35.5 | 94.9 | |
| Poor | 10 | 5.1 | 100.0 | |
| Maintenance | Excellent | 62 | 31.5 | 31.5 |
| Good | 69 | 35.0 | 66.5 | |
| Mediocre | 51 | 25.9 | 92.4 | |
| Poor | 15 | 7.6 | 100.0 | |
| Finishes | Fine | 63 | 32.0 | 32.5 |
| Ordinary | 90 | 45.7 | 77.7 | |
| Cheap | 44 | 22.3 | 100.0 | |
| Variables | Characteristics | ||
|---|---|---|---|
| Position | Technical | ||
| Characteristics | Location | −0.052 | −0.007 |
| (0.637) | (0.952) | ||
| Position | – | 0.283 | |
| – | (0.09) | ||
| Variables | Coefficient | Std Error | Ratio | p-Value |
|---|---|---|---|---|
| Constant (β0) | 753.305 | 1169.05 | 0.6444 | 0.5212 |
| Location characteristics (Cl) | 4963.65 | 1300.15 | 3.818 | 0.0003 |
| Position characteristics (Cp) | 2057.32 | 1044.43 | 1.970 | 0.0523 |
| Technical characteristics (Ct) | 3430.75 | 1195.61 | 2.869 | 0.0052 |
| Variables | Characteristics | ||
|---|---|---|---|
| Position | Technical | ||
| Characteristics | Location | −0.224 | 0.164 |
| (0.18) | (0.085) | ||
| Position | – | 0.244 | |
| – | (0.10) | ||
| Variables | Coefficient | Std Error | Ratio | p-Value |
|---|---|---|---|---|
| Constant (β0) | 1211.81 | 323.094 | 3.751 | 0.0003 |
| Location characteristics (Cl) | 794.464 | 360.194 | 2.206 | 0.0295 |
| Position characteristics (Cp) | 1254.08 | 381.914 | 3.284 | 0.0014 |
| Technical characteristics (Ct) | 1950.08 | 350.888 | 5.558 | <0.0001 |
| Sestiere | Average Value Increments |
|---|---|
| S. Polo | 267.33 |
| S. Marco | 249.73 |
| S. Croce | 239.52 |
| Dorsoduro | 235.42 |
| Canareggio | 215.34 |
| Castello | 184.17 |
| Giudecca | 134.09 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosato, P.; Breil, M.; Giupponi, C.; Berto, R. Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice. Buildings 2017, 7, 112. https://doi.org/10.3390/buildings7040112
Rosato P, Breil M, Giupponi C, Berto R. Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice. Buildings. 2017; 7(4):112. https://doi.org/10.3390/buildings7040112
Chicago/Turabian StyleRosato, Paolo, Margaretha Breil, Carlo Giupponi, and Raul Berto. 2017. "Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice" Buildings 7, no. 4: 112. https://doi.org/10.3390/buildings7040112
APA StyleRosato, P., Breil, M., Giupponi, C., & Berto, R. (2017). Assessing the Impact of Urban Improvement on Housing Values: A Hedonic Pricing and Multi-Attribute Analysis Model for the Historic Centre of Venice. Buildings, 7(4), 112. https://doi.org/10.3390/buildings7040112






