1. Introduction
There are a number of situations where an increase in structural capacity or rehabilitation of reinforced concrete (RC) columns are required. Those may include deterioration due to environment effects, overloads, aging, design and/or construction errors, damages due to blasts, and collision or earthquake effects. The engineering application of FRP is increasing for strengthening and retrofitting of the elements of reinforced concrete (RC) structures. Reasons behind this may include light weight, high strength, corrosion resistance, good durability and simply construction in comparison with other retrofitting techniques [
1]. FRP materials, depending on the fiber layout and orientation (transverse or longitudinal with respect to the column axis), can lead to the improvement of behavior of reinforced columns from both strength and ductility points of view via either enhancement of core concrete confinement or increasing the moment capacity of the section.
There are numerous studies available in the literature, for example [
2,
3], concerning the behavior of FRP-retrofitted RC columns. Those studies have primarily dealt with how different design parameters such as the number of FRP sheet layers, the mechanical properties of the fibers used, orientation of the fibers with respect to the column axis, etc. affect the strength and ductility properties of the member. Previous studies on strengthening of FRP-retrofitted RC columns have been generally carried out on short columns under different loading conditions [
4]. Despite the extensive body of knowledge of theoretical and experimental studies on FRP-retrofitted short columns, studies on slender columns subjected to eccentric loads—and particularly biaxial eccentric loads—are quite limited. Bournas et al. [
5] present an analytical model for the analysis of reinforced concrete (RC) members with rectangular cross sections, strengthened in flexure with various types of externally applied reinforcement. The Effects of strengthening of square columns using carbon fiber reinforced polymer (CFRP) composites under uniaxial and biaxial conditions was the subject of an experimental study conducted by Tao and Yu [
6]. The study indicated that the ultimate strength of the columns retrofitted by transverse CFRP sheets did not differ significantly from the non-retrofitted columns. Nonetheless, they demonstrated that remarkable enhancement is achieved in load bearing capacity of the column in cases where simultaneous transverse and longitudinal FRP sheets were utilized. Furthermore, they showed that longitudinal fibers have a larger impact on improving the loading capacity of tension-controlled columns. In an analytical and experimental study, Rocca et al. [
7] developed a simplified design interaction curve of reinforced concrete columns in the compression-controlled region of behavior using transverse FRP composites under uniaxial bending. The methodology developed in that study is in good accordance with the experimental results. As will be discussed later, in this paper, the compatibility equations of the aforementioned study are incorporated.
Fitzwilliam et al. [
8] analyzed the effect of retrofit of short and slender concrete columns using CFRP sheets and with two and four-sheet layouts in both transverse and longitudinal direction of small-scale samples. Their study shows that transverse CFRP layout with respect to longitudinal axis of column leads to enhancement of loading capacity in short columns whereas longitudinal fiber layout might lead to improvement of behavior of slender columns and increase their ultimate strength similar to short columns. Gajdosova et al. [
9] conducted an experimental study on eight real scale concrete columns under eccentric loading. The samples included slender columns. Among all, there were two non-retrofitted samples (control samples), two samples retrofitted using transverse CFRP sheets, two samples retrofitted by Near Surface Mounted (NSM) strips, and two samples retrofitted using combined transverse CFRP and NSM sheets. The most obvious finding to emerge from their study is that retrofitting using the NSM method has the largest effect on enhancement of loading capacity of columns in cases where the bending moment is remarkable and/or the loading is eccentric. Teng and Jiang [
10] also proposed a theoretical model for predicting the behavior of FRP-retrofitted RC columns.
Punurai et al. [
11] Performed an experimental study on five small-scale square RC columns confined with transverse CFRP sheets under axial load and biaxial bending moments. Very good consistency was observed between the experimental results with those obtained from the finite element analytical models. Rahai and Akbarpour [
2] also conducted an experimental study on rectangular FRP-jacketed RC columns under uniaxial eccentric loading conditions. In their study, several parameters including thickness of the FRP sheet, the fiber orientation, and loading eccentricity were taken into account. It was demonstrated that the strength and ductility of specimens increased with increasing FRP thickness and that the fiber orientation has a great impact on both the strength and ductility characteristics of the retrofitted member. It was also observed that adding one longitudinal-oriented FRP sheet to the control model with only one transverse-oriented FRP sheet led to significant improvement of ductility characteristics of the member.
The available knowledge on the subject have matured to a state that the impact of confinement provided by FRP composites on load-bearing capacity of both short and slender columns can be estimated with good accuracy. However, from a ductility capacity point of view, notable biases are typically observed between theoretical models and experimental results [
12,
13]. This may be due to the fact that eccentric loading conditions significantly affects the ultimate axial strain of the confined column, an issue that is of great significance for predicting deformation capacity of retrofitted RC columns under seismic loading conditions. Various theoretical and experimental studies can also be found in literature regarding the behavior of FRP-confined RC columns subjected to axial force and bending moment [
14,
15,
16,
17,
18,
19]. Most of those studies have ignored the effect of the presence of biaxial bending in real cases despite the fact that the presence of combined axial force and biaxial bending moments are very common in practical engineering design due to gravitational and/or lateral load effects or their combination. This includes current FRP retrofitting design guidelines such as ACI440 [
20]. This guideline deals with the subject of retrofitting of RC columns under axial loads without direct attention to biaxial moments. It seems that current design procedures consider primarily the increase in axial load capacity of RC columns merely due to the increase in compressive strength of concrete resulting from confinement effects of FPR sheets.
However, previous studies (see above) suggest notable advantages in using FRP composites (in longitudinal and transverse layouts) to enhance the strength and ductility of reinforced concrete columns.
The present research is an extension of the interaction curve method developed in Rocca’s study [
7] in which the procedure of creating interaction curves for FRP-jacketed RC columns is taken into account based on principles of equilibrium and strain compatibility in tension-controlled region as well. Moreover, the requirements for proper anchorage (bond length) of fiber reinforcement or anchors through the joints (or footings) are satisfied. Additionally, besides extending the current methods for the conditions of strengthening with transverse fiber (Regarding the longitudinal axis of the column), new equations will be proposed for the longitudinal fiber alone as well as the combined layout. Also, an engineering method will be suggested for evaluating the effect of strengthening the FRP-retrofitted RC columns under the impacts of axial force and biaxial bending as a very important case in practical retrofitting works. The proposed procedures will be illustrated through a case study along with it will be validated against experimental results.
2. Design Philosophy for the Columns Strengthened with Transverse FRP Materials
The present section reviews the procedure of generating simplified interaction curves of non-retrofitted and retrofitted columns under uniaxial bending conditions and using transverse RFP materials. In subsequent sections, additional cases employing longitudinal fibers and combination of longitudinal and transverse fibers by considering biaxial bending will also be developed and discussed.
Table 1 presents the notations used in this paper. Other parameters are mentioned in the text. Analysis of RC columns confined with transverse FRP sheets is similar to typical reinforced concrete columns (without FRP sheets); the only difference is the stress-strain model of concrete in the compressive region [
21,
22].
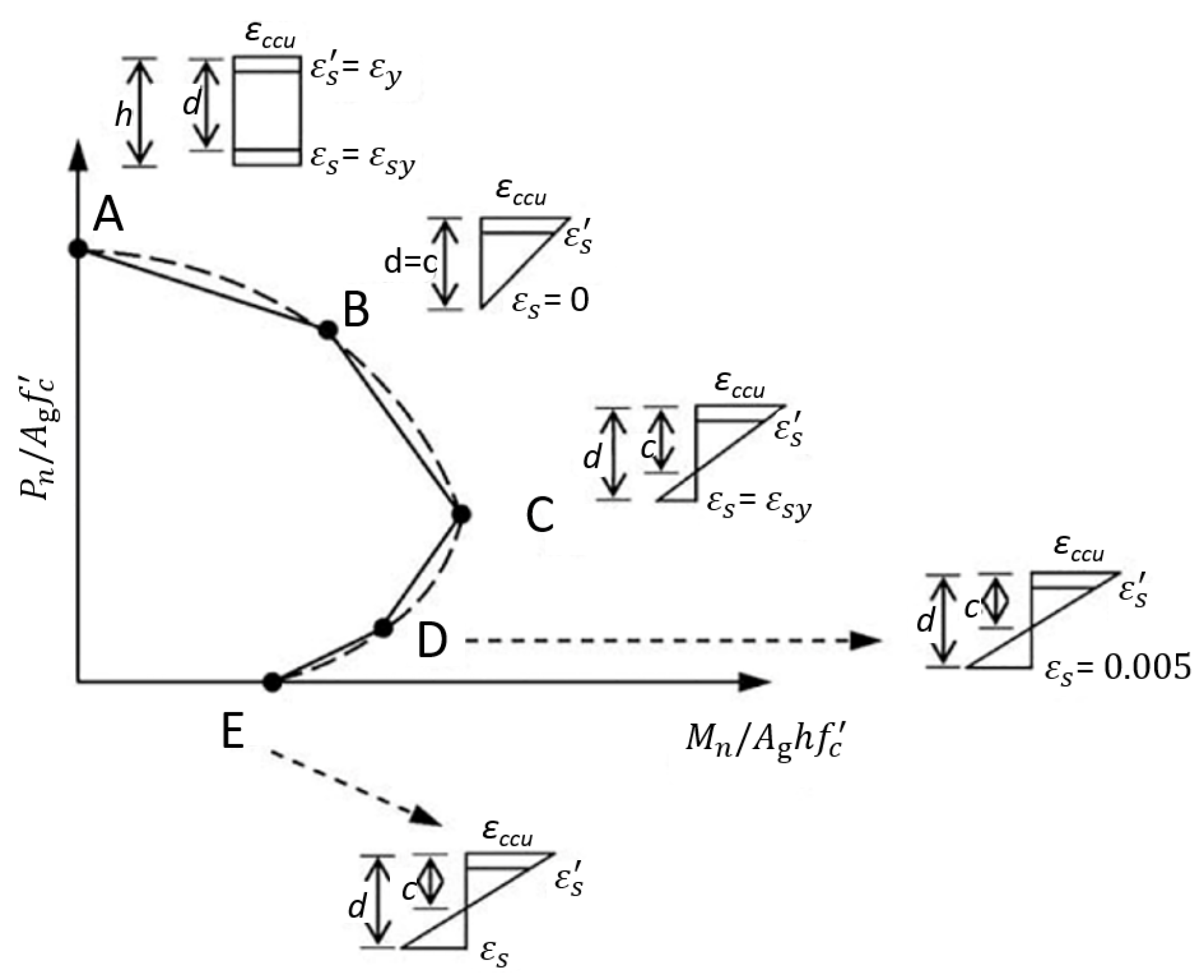
It is basically assumed in analysis of strengthened columns that the section does not undergo distortion, tensile strength of concrete is negligible and no slippage occurs between the concrete and reinforcements or between the concrete and fibers. Often for simplification, interaction curves of retrofitted and non-retrofitted columns can be generated with appropriate accuracy by linear connecting the five key points of column behavior corresponding to different response modes at failure (
Figure 1) [
7]. Generation and application of the simplified curve for evaluation of FRP-retrofitted columns is simple and relatively straightforward [
7].
Due to the significance of this section, the equations available in the technical literature for strengthening with transverse fibers are presented in the present paper with a slight modification. The key points in the aforementioned simplified interaction curve using ordinary assumptions in analysis of reinforced concrete elements [
7] according to
Figure 1 include:
Point A: uniform axial compressive strain in the confined concrete.
Point B: This point corresponds to the state of strain distribution in which maximum compressive strength is εccu and strain in the last rebar sheet in the tensile region is equal to zero. εccu is the ultimate compressive strength of the confined concrete. In non-confined conditions, εcu i.e., ultimate compressive strength of unconfined concrete is used.
Point C: This point represents the state of strain distribution in which simultaneously the maximum ultimate compressive strain of concrete is εccu and maximum tensile strain in the last rebar sheet is equal to yield stress. This point is the same as equilibrium (balance) point of the column behavior.
Point D: This point corresponds to the state of strain distribution in which maximum compressive strain equals εccu (or εcu in unconfined conditions) and strain in the last longitudinal rebar sheet of section is equal to 0.005.
Point E: This point is associated with the conditions for pure bending without axial force.
In the interaction curve shown in
Figure 1, point “A” represents the pure axial compression capacity without any bending moment. For the points “B”, “C” and “D”, location of the neutral axis is obtained based on similarity of triangles in the strain diagram. Point “E” is representative of pure bending without axial force which can be calculated based on classical theories of analysis of RC flexural members (beams). Nominal axial force
corresponding to point “A” can be determined using Equation (1):
For longitudinal fiber,
Pn is the same as Equation (1) because confinement effect of longitudinal fiber is neglected. Nominal axial force (
Pn) and nominal bending moment (
Mn) are calculated at points B, C, and D via integration of stress. This integration for non-circular sections is shown in Equations (2) and (3);
In the above equations,
c is the distance of neutral axis from the farthest compressive axis of section.
Asi,
fsi, and
dsi are respectively area, stress, and distance to the centroid of area in
i-th sheet of longitudinal (bending) rebars. “
y” is integration variable in compressive region of section. Compressive strength function
fc is used based on the Lam and Teng model [
23,
24]. This model has been chosen based on the assessment of a series of FRP-confined column models with minimal dimension of 300 mm under pure axial compression [
25].
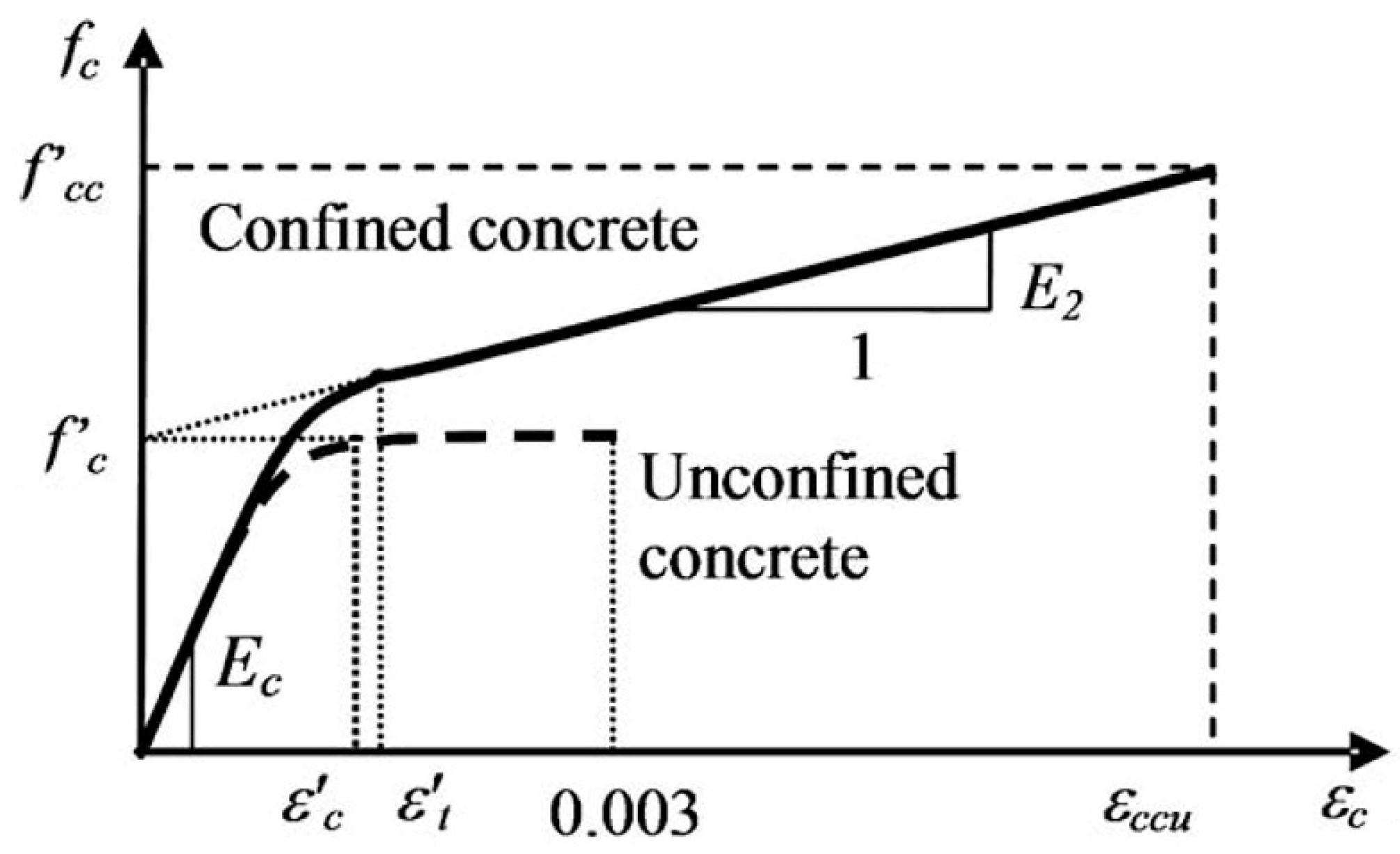
Several models that simulate the stress-strain behavior of FRP-confined compression sections are available in the literature. The stress-strain model by Lam and Teng’s, illustrated in
Figure 2, for FRP-confined concrete has been used in many experimentally-verified papers [
7]. Stress-strain curve of this model consists of two parabolic and linear parts (
Figure 2) which intersect at transient strain
. The second part of the curve (which is linear) reaches to the point at the end corresponding to maximum compressive strength
fcc and maximum axial strain of confined concrete
εccu. This model follows the equations below in different strain intervals:
where,
fc and
εc are axial stress and strain of the concrete,
Ec is elasticity module of the confined concrete,
E2 is the slope of linear part of the curve, and
is the maximum axial strain of the FRP-confined concrete. Compressive strength of FRP-confined concrete is expressed according to Equation (7):
In the equation above,
ka parameter is the “geometrical effect” coefficient which will be explained later. FRP confinement stress (
f1) is computed based on principles of equilibrium and compatibility of strains through the following equations:
In Equation (8), effective strain (
εfe) is calculated based on
kε effect factor and maximum tensile strain (
εfu) (
). Other parameters are included in
Table 1. Based on experimental studies by Lam and Teng, value of
is recommended [
23]. Similarly, Cary and Harries [
26] suggested a value of 0.58 for this parameter. In the present paper, the authors have assumed a value of 0.55 for
kε parameter for designing purposes and further assurance. Based on recommendations of ACI-440 Committee [
27], the effective FRP strain in deformation state (
εfe) in elements under combination of axial force and bending moment is limited to two values of 0.004 and
.
In Lam and Teng’s model, maximum compressive strain of FRP-confined concrete is expressed via the following equation:
Compressive strain of unconfined concrete (ε
c) in the equation above is assumed equal to 0.002. Value of ultimate compressive strain of unconfined concrete (
εcu) is considered equal to 0.003 based on ACI318-08 Directive [
28]. Geometric effect coefficients
ka and
kb can be evaluated based on Equations (10) and (11). These values equal 1 for circular sections and depend on two parameters of effective confined area ratio (
) and aspect ratio (
h/
b):
If the FRP effect is disregarded in the previous equations, the relationships will hold for the case of no reinforcement too.
4. Design Philosophy for Columns Strengthened with Combined Longitudinal and Transverse FRP Materials
This section deals with the procedure of generating simplified interaction curves for unconfined and FRP-confined columns under uniaxial bending conditions and equipped with both longitudinal and transverse fibers. It will be shown in the subsequent sections that simultaneous longitudinal and transverse confining technique is very efficient for columns with bending moment (load eccentricity) in one or two directions. As depicted in
Section 2, in order to plot the simplified interaction curves of confined columns (retrofitted using FRP materials) and also unconfined columns (non-retrofitted), it is necessary to calculate five points (A, B, C, D, and E as previously introduced in
Figure 1).
As implied earlier, in case of applying the longitudinal fiber, it is reasonable to ignore enhancement in axial strength due to insufficient confinement provided by this fiber type. As a result, Equations (12)–(14) of the previous section are rewritten as Equations (15)–(17) below for the case of combined transverse and longitudinal fibers:
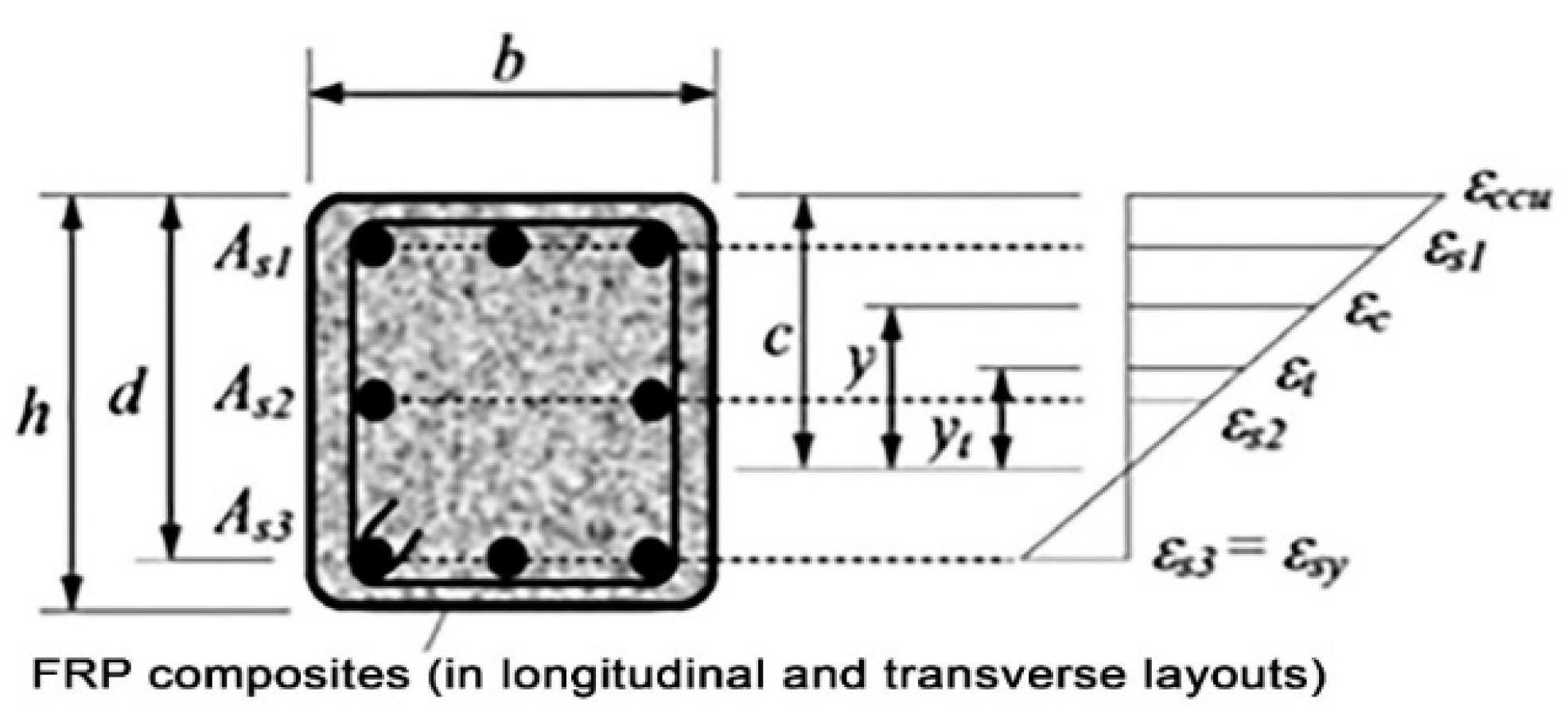
The coordinate parameter
yt lies on the cross section has the neutral axis as its origin and is within the compression region of the concrete and is associated with transient strain center. This parameter can be determined using Equation (18) and according to
Figure 3 as:
Following integration and rearrangement of Equations (15)–(17) using coefficients A, B, C, D, E, F, G, H, and I, Equations (19)–(21) are derived as below. The aforementioned coefficients are separately included in Equations (22)–(30). Equations (20) and (21) have been, respectively, written for the cases of transverse fiber and combined transverse and longitudinal fibers:
Values of
fsi and
ffi, respectively, represent the stress in rebar sheets and FRP materials which are calculated based on similarity of triangles in the strain distribution diagram. The respective values are dependent on the position of the neutral axis. Stress in rebar sheets is assumed to be positive for compression and negative for tension. It must be noted that FRP materials merely have tensile capacity, and in practice, the strength of supporting compression is not defined for them. On the other hand, for simplifications in the design formulation, FRP fibers have been modeled separately in the same row as rebar sheets. It should be reminded that nominal axial compressive capacity under net axial compression (Point A in interaction curve) for columns with transverse rebar is limited equal to 80% of value of nominal net axial capacity according to the design procedure of ACI318-08 code of practice [
28]. For columns with transverse rebar, based on ACI 318-08 recommendations [
28], strength reduction factors should be considered in loading capacity computations.
The equations provided above have been written for the state of uniaxial bending moment and axial force. To extend this method to the more general state of biaxial bending moment, the ultimate biaxial bending moments can be converted into uniaxial moments using credible references [
29]. The equivalent uniaxial moments depend on ratio of biaxial bending moments and can be evaluated via Equation (31):
In this equation, Mux and Muy are, respectively, the ultimate bending moments of column under the effect of gravity loads about x and y axes of the section. “b” and “h” also represent the dimensions of section along x and y axes, respectively.
5. Validation of the Procedure
To evaluate the proposed formulation proposed in the present study, the interaction curve for the experimental samples studied by Rahai and Akbarpour [
2] is computed and plotted using the proposed equations. The test specimens of that study were tested at actual scale. In
Table 2, geometrical and strength specifications of columns are shown from reference [
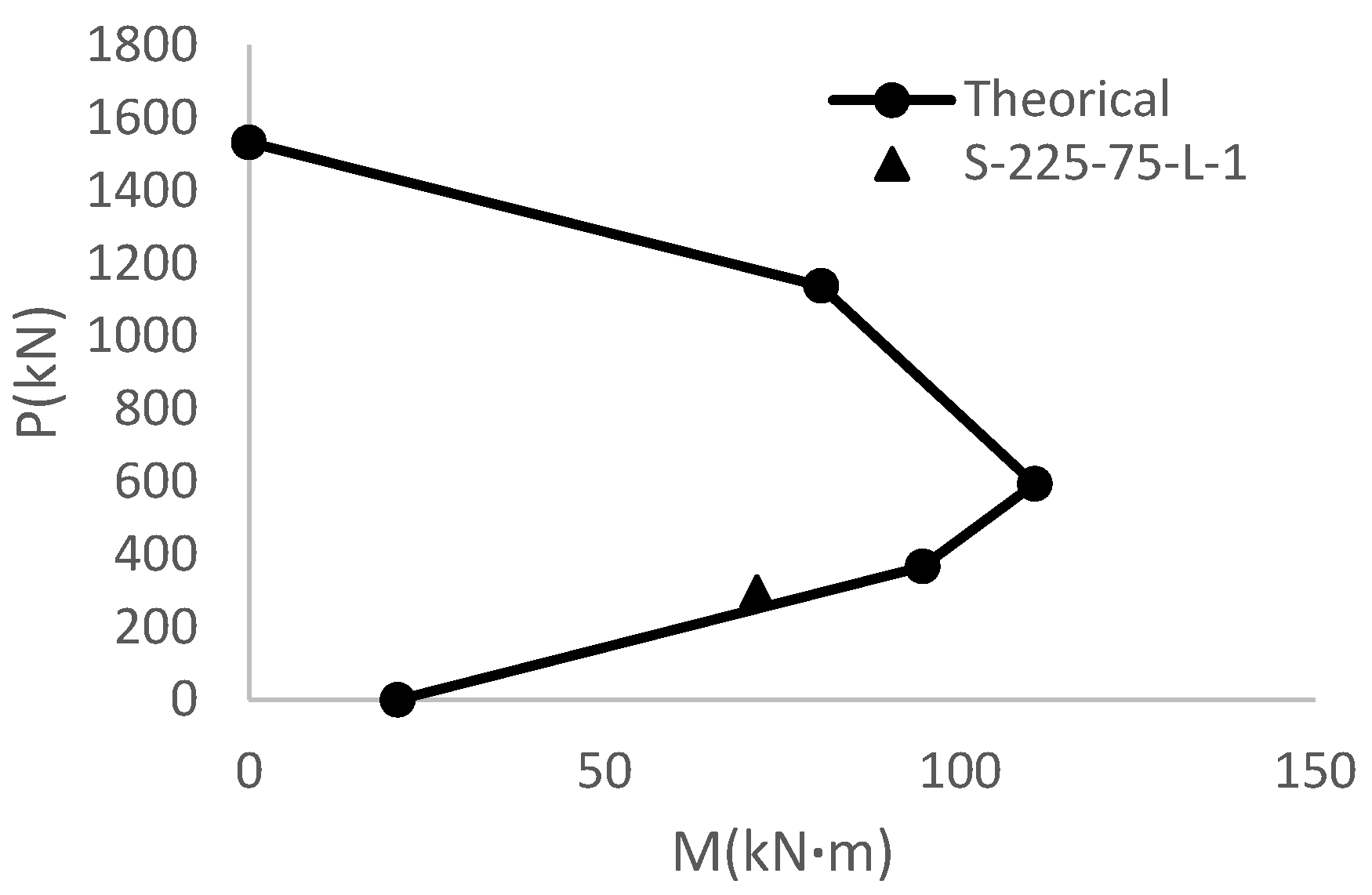
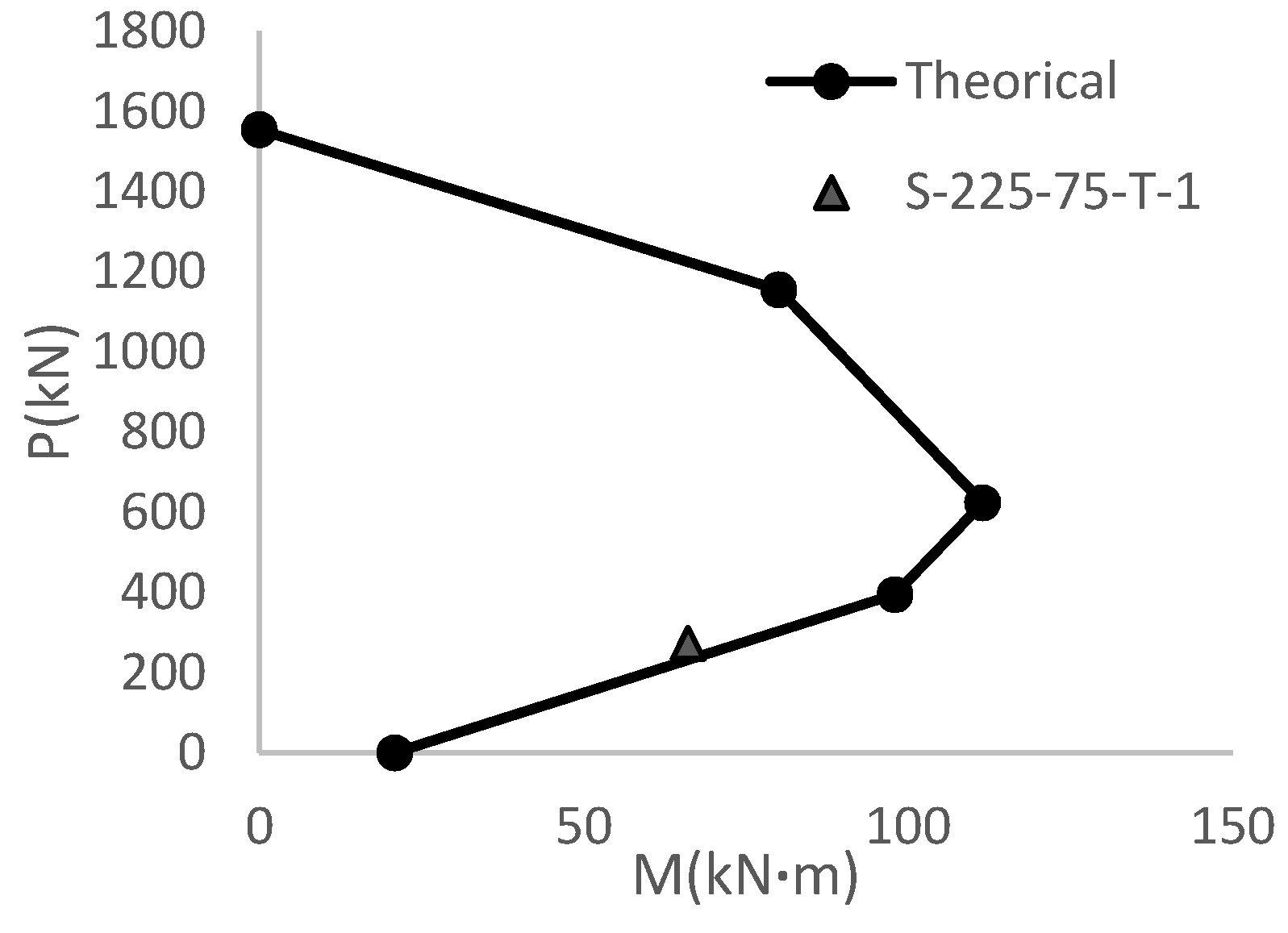
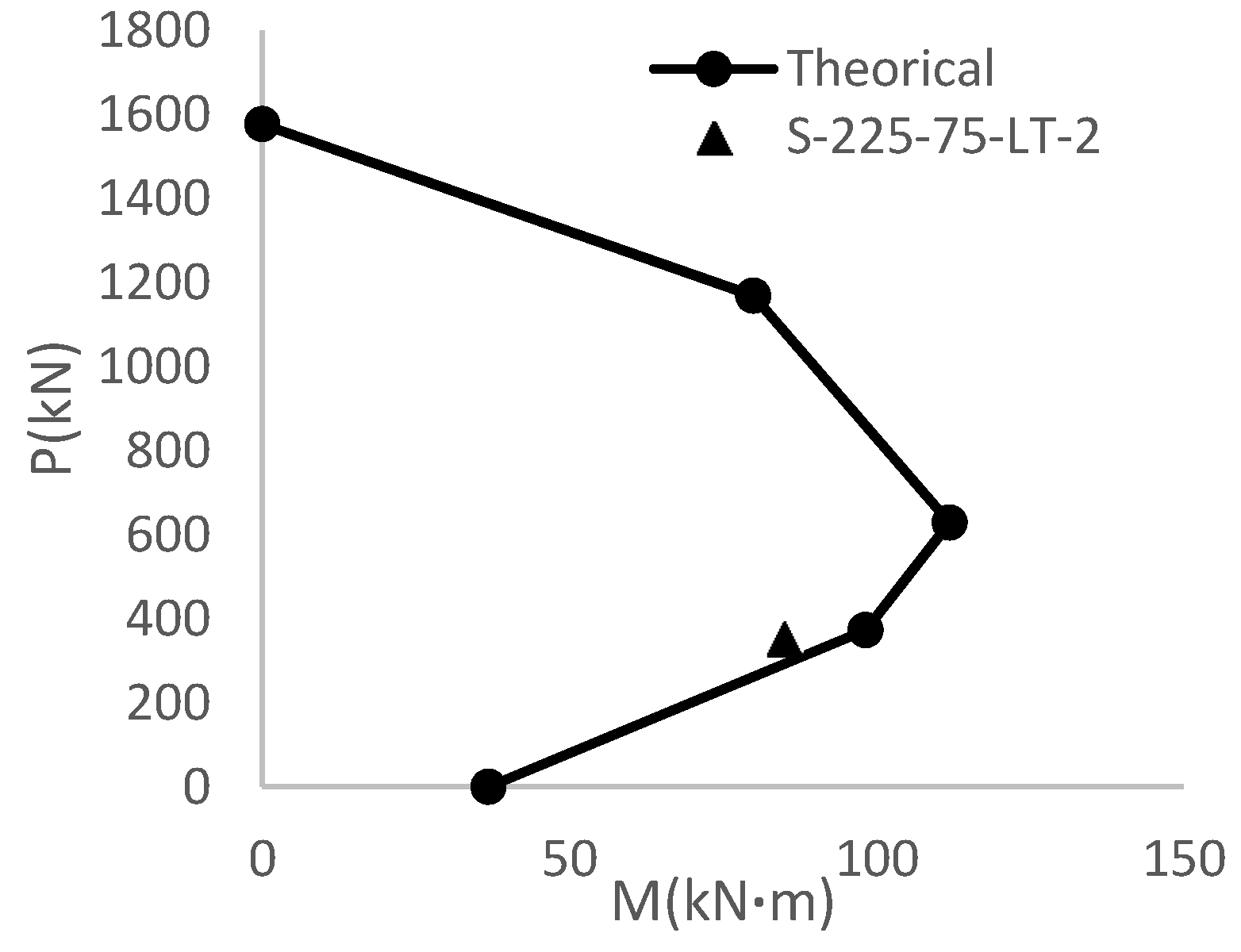
2]. Among the experimental results in the aforementioned study, three column specimens were selected as follows: strengthened with only longitudinal fiber (designated as S-225-75-L-1), strengthened with only transverse fiber (designated as S-225-75-T-1) and strengthened with a longitudinal sheet and a transverse sheet (designated as S-225-75-LT-2).
Numbers 225 and 75 in the designations respectively represent the eccentricity of axial force along y and x direction under which the columns are subjected to axial force and biaxial bending moments. The maximum load and moment exerted as such to each specimen are shown in
Table 3.
In the first stage, interaction curves of the columns under analysis are plotted using the equations proposed in the present paper and substitution of biaxial bending moments included in
Table 3 by equivalent uniaxial bending moment (calculated using Equation (31)) as separately illustrated for each column in
Figure 4,
Figure 5 and
Figure 6. Also, axial force and equivalent uniaxial bending moment pairs are shown by solid circles on the curves in
Figure 4,
Figure 5 and
Figure 6 according to the values of
Table 3. These values actually represent the maximum strength demands exerted on the column. Proximity of the circles to the interaction curve is suggestive of good match between theoretical and experimental results. Thus, the theoretical results acquired in the present research are considered to be acceptable in normal design usages with adequate accuracy. It is worth mentioning that design strength reduction factor was set to be 1 in computation of the interaction curves in
Figure 4,
Figure 5 and
Figure 6.
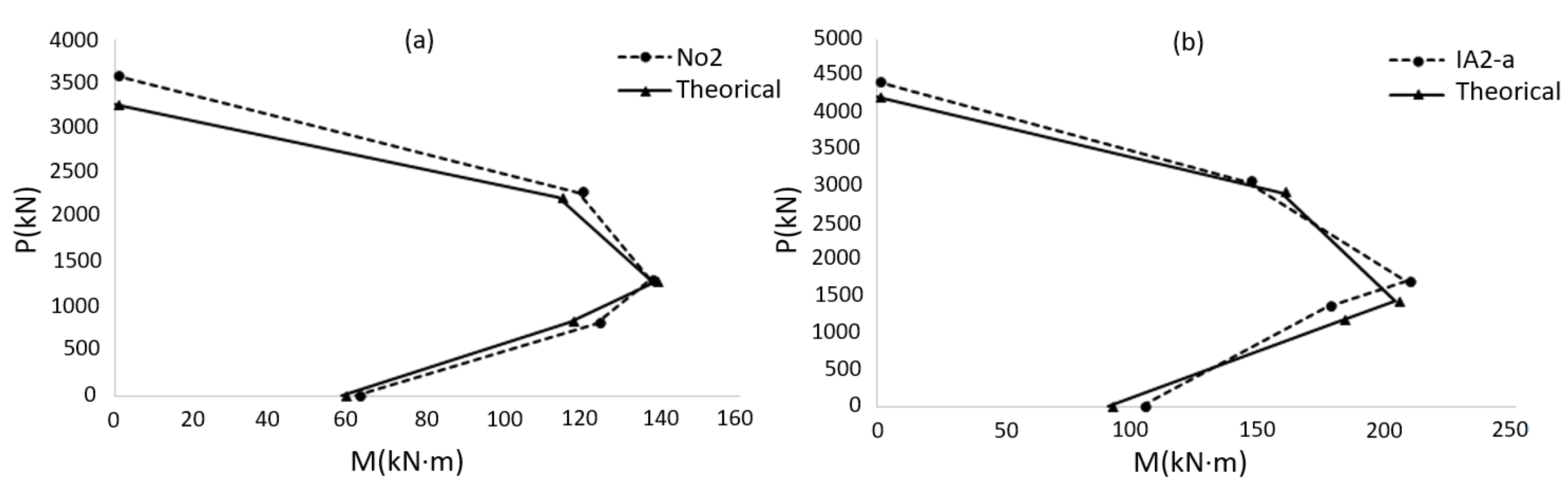
In order to compare the proposed theoretical interaction curves with the experimental results, the interaction curves of specimens No2 and IA2-a from the Rocca [
7] study have been considered.
Figure 7 shows the theoretical as well as the experimental interaction curves. No environmental and strength reduction factors were considered in developing these interaction diagrams. As seen, the theoretical interaction curves developed with the proposed procedure of this paper are in good agreement with those derived from experimental results in Reference [
7].
6. Case Study
In the present section, strengthening of a column of a 4-story residential building with FRP sheets by using the procedure suggested in the previous sections is investigated. The structure has been designed based on ACI 318-08 code of practice [
28] for a site with high seismicity and special ductility level. The lateral load-resisting system is moment-resisting frames in both plan directions.
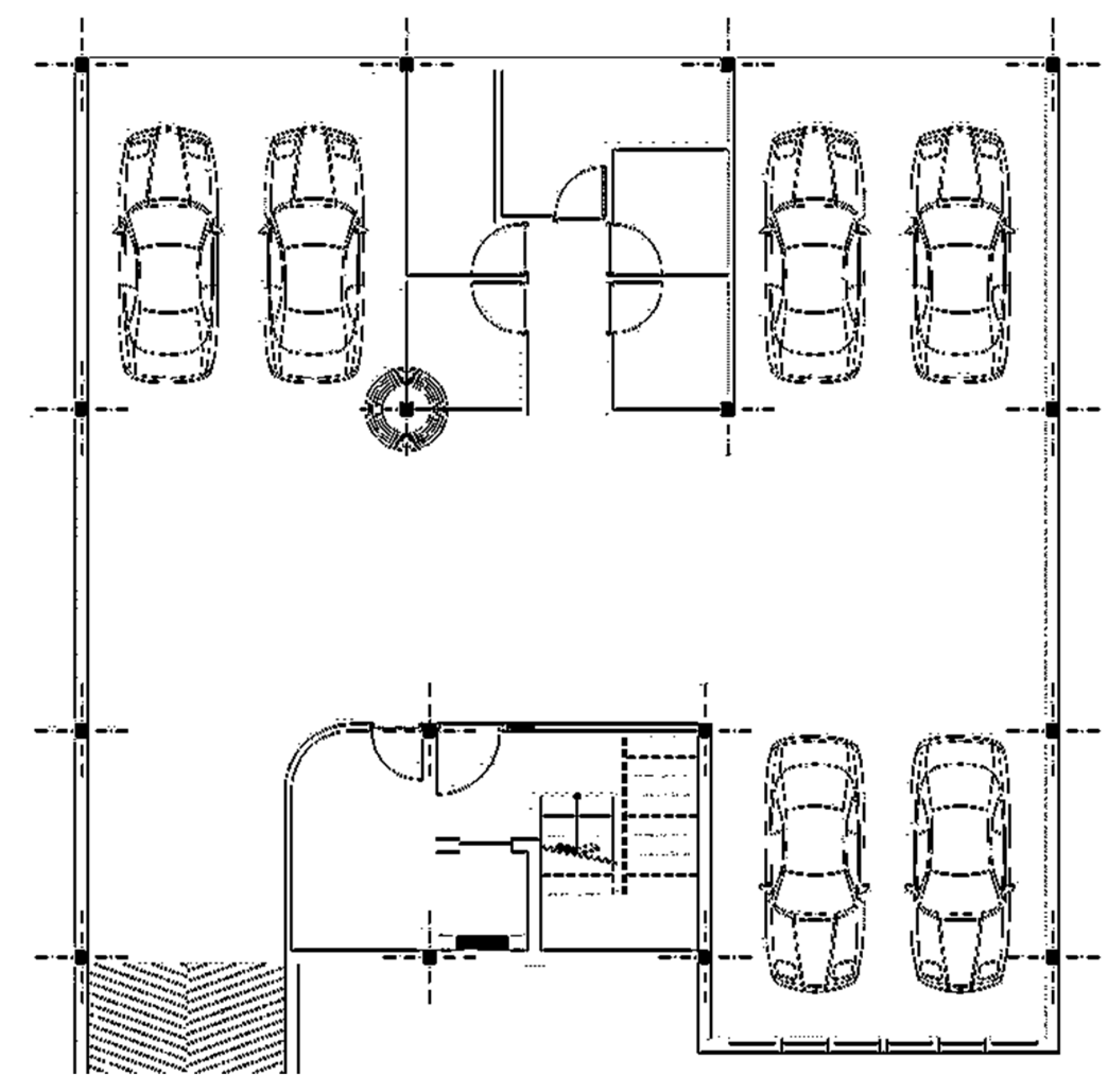
Figure 8 represents the building plan and the respective column. The column is located in the ground floor of the structure. Specifications of materials, sections, and internal efforts of the respective non-retrofitted column are included in
Table 4. The concrete strength mentioned in
Table 4 is the characteristic strength (28-day) of standard cylindrical sample. Structural analysis was performed assuming cracked section properties. Secondary (P-∆) effects were also considered in the structural analysis. The selected column is to support maximum axial force of 562 kN (12% increase compared to its pre-strengthened condition), bending moments of 198.2 kN·m (23.7% increase) and 33.4 kN·m (15.5% increase) about its cross-section local axes.
Specifications of the FRP jacket sheets are included in
Table 5. These specifications belong to sheets made of carbon and have been extracted from available commercial catalogues. The column has been strengthened based on the simplified procedure of the present research. Therefore, aimed at enhancing loading capacity of the column, retrofitting by using one-layer FRP sheets was taken into account. Interaction curves can be plotted using the design equations presented in previous sections (
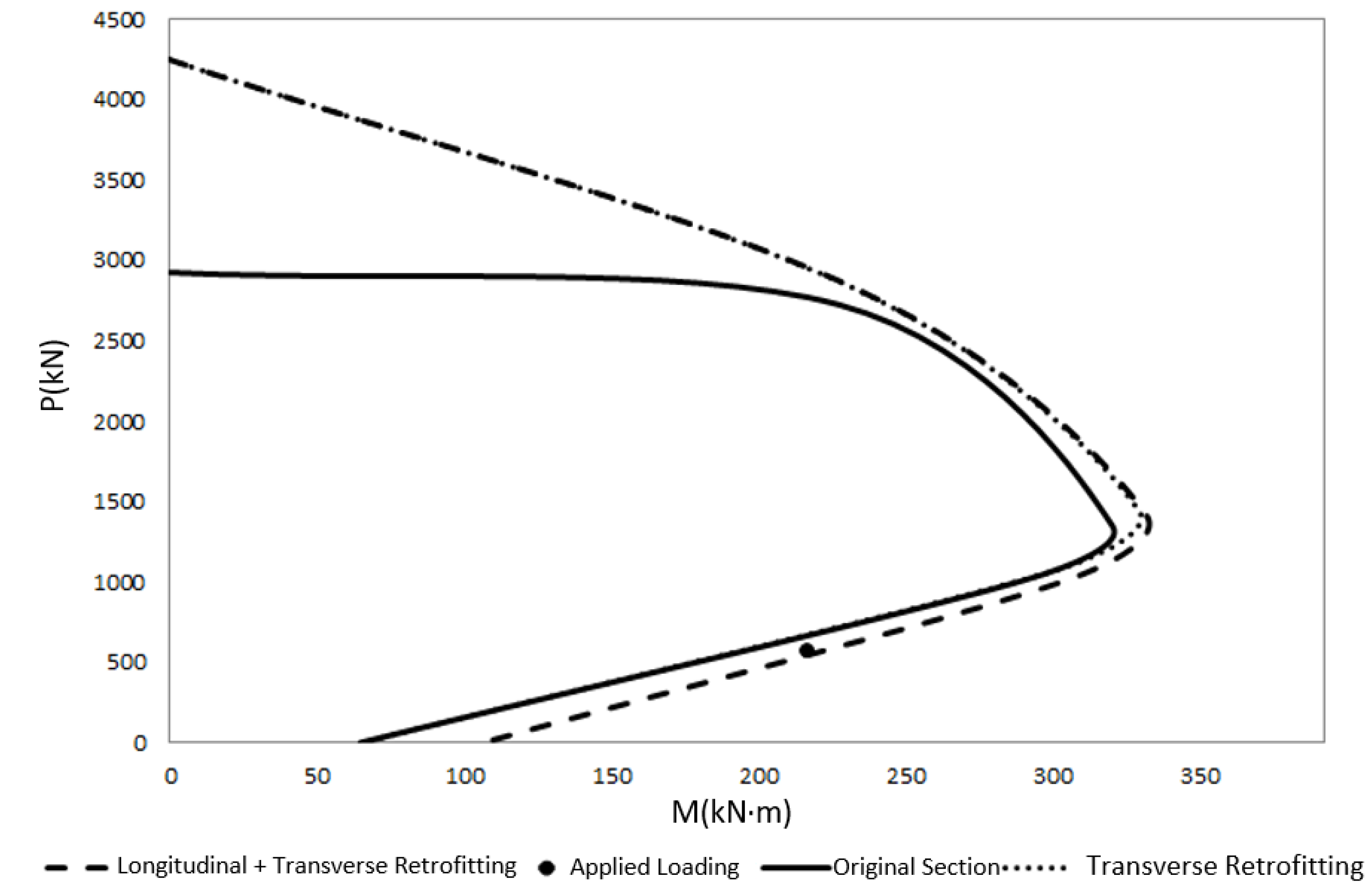
Figure 9). Solid, dashed and dotted-line diagrams, respectively, correspond to interaction curves of the column without retrofitting, retrofitting with transverse fibers and retrofitting with combined longitudinal and transverse fibers.
Confinement effects of FRP with combined longitudinal and transverse fiber sheets are more pronounced in enhancing the load bearing capacity of both the compression- and tension-controlled columns.
Figure 9 also illustrates this significant finding. The mentioned constraint in current design rules for using FRP materials in strengthening of columns can be alleviated using the equations developed in the present study for longitudinal or combined transverse and longitudinal fiber orientations. It must be noted that previous experimental studies [
2,
30] have demonstrated that longitudinal fibers also have some effects on confinement level of the column, which have been neglected in the equations developed in the current research. For the same reason, as a practical recommendation, in the case of applying the combined method of strengthening with both longitudinal and transverse fibers, the longitudinal fibers can only be used in critical areas of the column which require reinforcement and strength enhancement (in general, upper and lower parts of the column in normal moment frames); meanwhile, transverse fibers can be used for the entire height of the column. The authors believe that such a method will considerably help the economics of the operations. The final detail of the retrofitted column is illustrated in
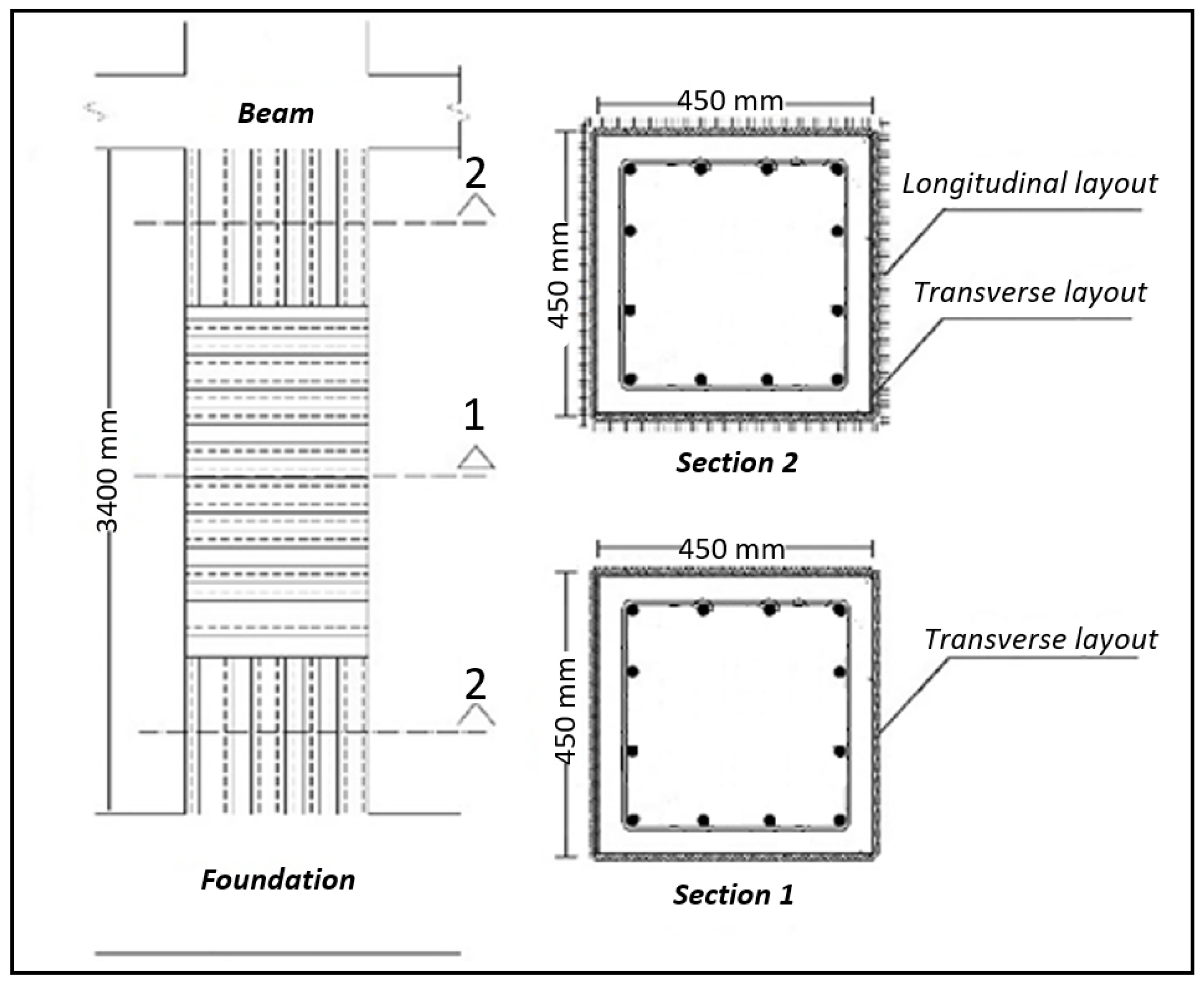
Figure 10.
The dashed lines represent areas with combined longitudinal and transverse fibers overlaps the dashed line curve (merely longitudinal fiber) in the tension-controlled region, and, overlaps the interaction curve of transverse fiber in the compression-controlled region. Accordingly, as observed, column strengthening is possible using each of the three methods. It is thus preferable to use a combination of transverse and longitudinal fibers in critical regions.