Computational Combination of the Optical Properties of Fenestration Layers at High Directional Resolution
Abstract
:1. Introduction
1.1. Modeling Complex Fenestration Systems with Bidirectional Scattering Distribution Functions
1.2. Computational Combination of Bidirectional Scattering Distribution Functions
1.3. Data-Driven Models of the Bidirectional Scattering Distribution Function in Daylight Simulation
2. Objectives
- BSDFs of different directional resolution shall be combined. This reflects the fact that descriptions of layers with very different optical characteristics, often leading to different approaches in their characterization by measurement or simulation, have to be combined.
- The directional resolution of the resulting BSDF shall be configurable. The target resolution of the system’s BSDF depends on factors such as the characteristics of the CFS, as well as the later application of the model in assessments requiring different degrees of accuracy.
- Support for the data-driven reflection and transmission model in Radiance shall ensure the applicability of the method in visual comfort assessments and leverage the data-reduction algorithm implemented in Radiance. The compact representation allows one to make use of libraries of BSDF data in analogy to the CGDB and is crucial to employ data-driven models in simulations with often complex and detailed architectural models.
3. Method
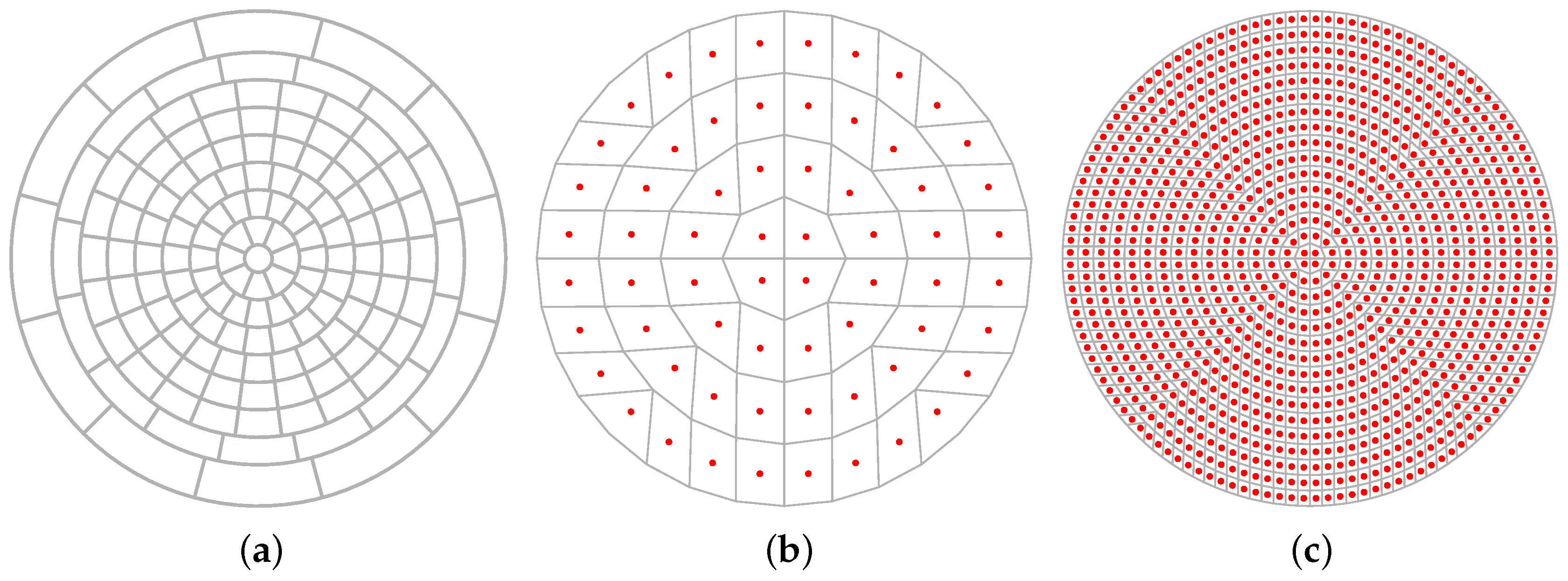
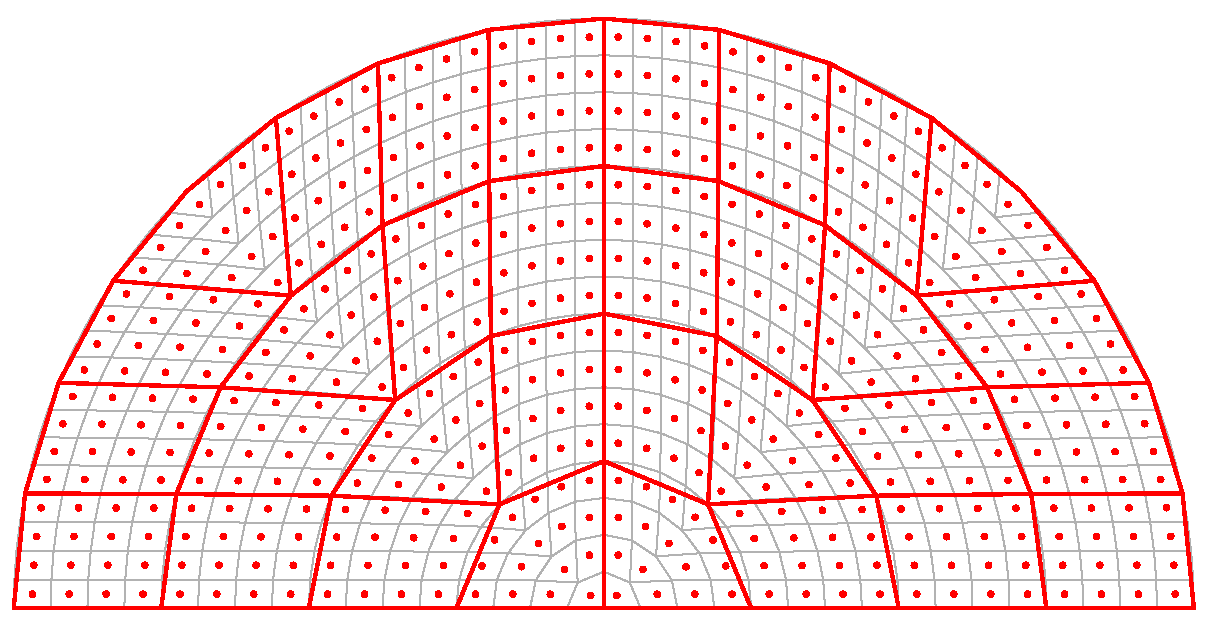
3.1. Matrix Formalism Employing a Subdivision Algorithm of Variable Resolution
3.2. Pair-Wise Combination of Bidirectional Scattering Distribution Functions at Variable Resolution
3.3. Combination of Bidirectional Scattering Distribution Functions of Different Resolutions
3.4. Testing the Method and Its Impact on the Predicted Performance of Multilayer Fenestration Systems
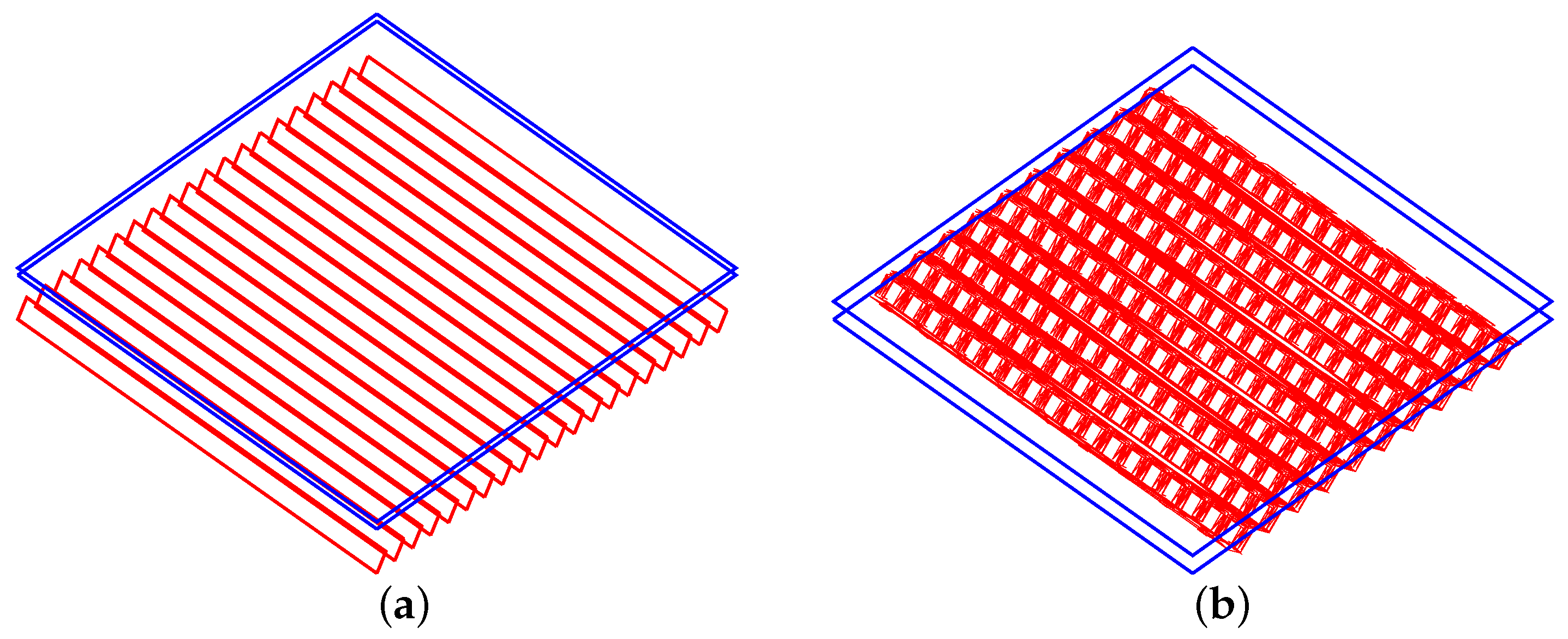
3.4.1. Cases and Computational Generation of Bidirectional Scattering Distribution Functions
- CFS1
- Flat specular blinds embedded in a double glazing unit comprise a simple case of a CFS with predictable scattering properties.
- CFS2
- Tilted light-shafts embedded in a triple glazing unit redirect light admitted from a range of given incident directions. The array of light shafts is highly directionally selective, aiming at a complete exclusion of direct sunlight in overhead applications.
3.4.2. Comparison of the Results of the Extended Matrix Formalism and Ray-Tracing
3.4.3. Comparing the Performance of the Matrix Formalism to Ray-Tracing
3.4.4. Testing the Down-Sampling of Bidirectional Scattering Distribution Functions
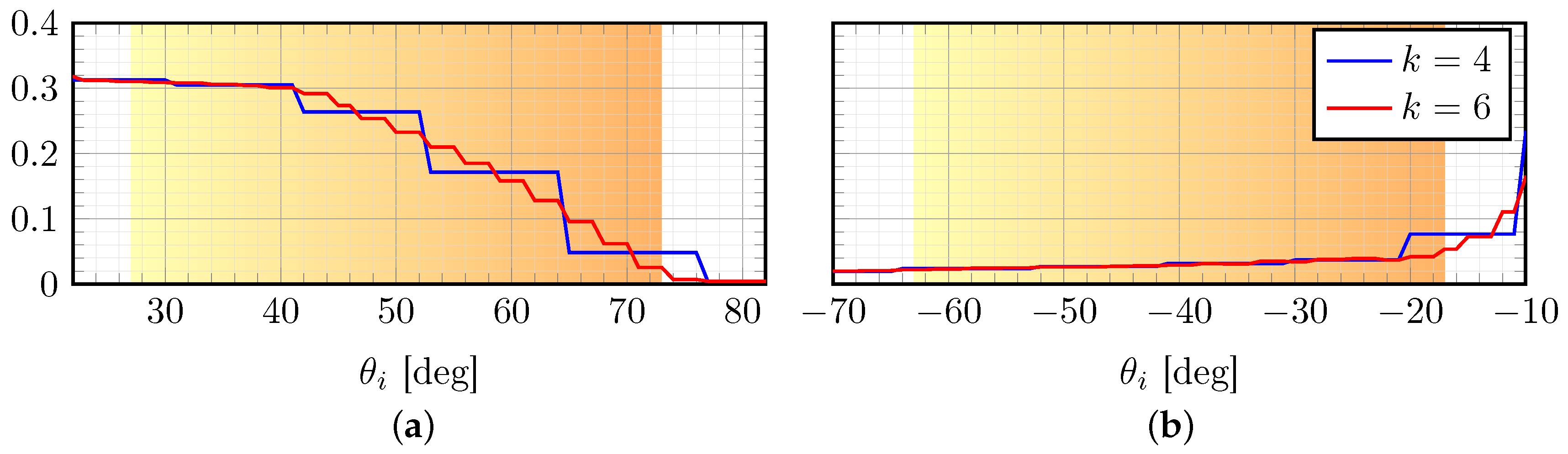
3.4.5. Impact of Directional Resolution on the Predicted Performance of Fenestration Systems
4. Results
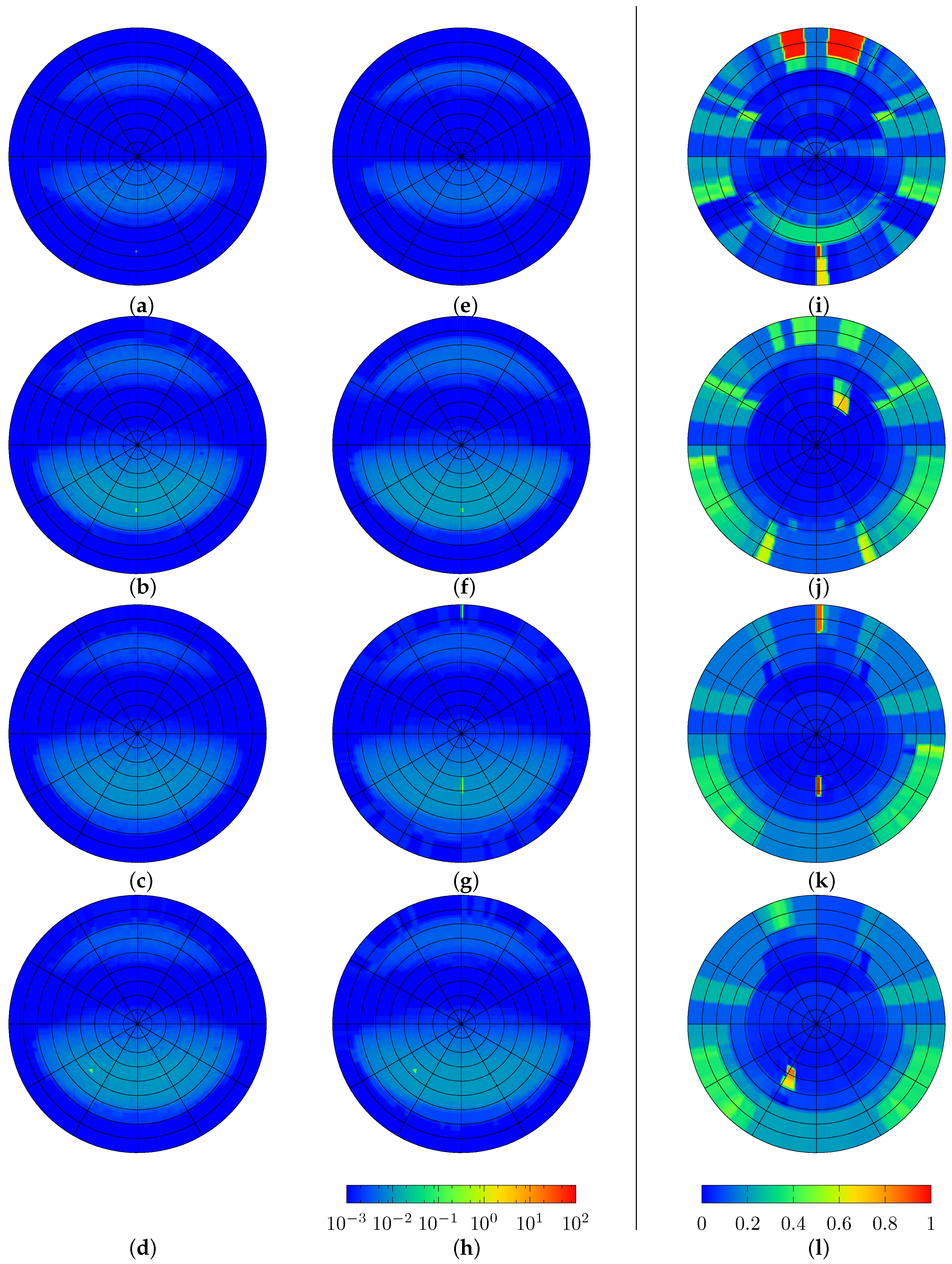
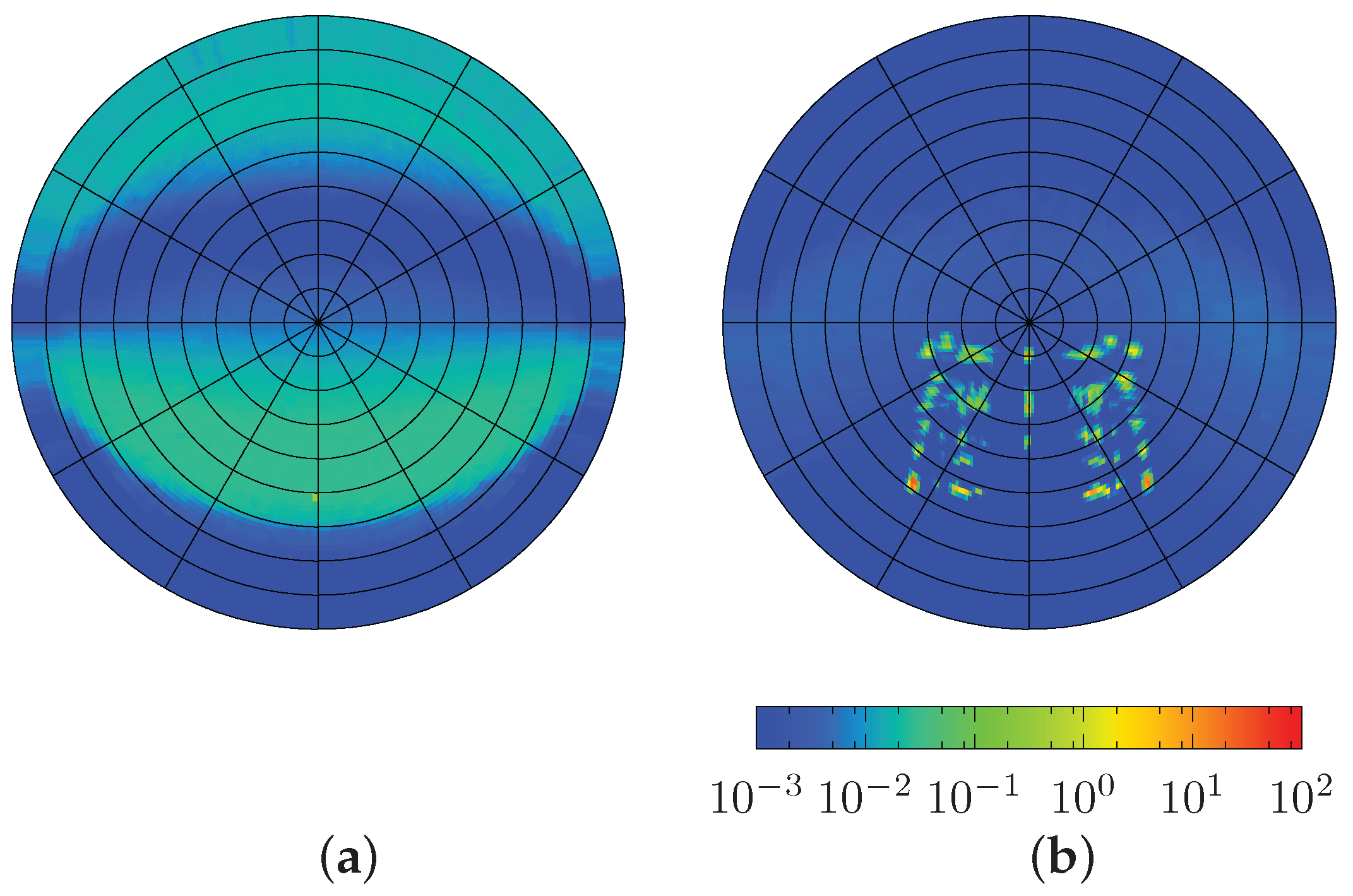
4.1. Computed BSDFs of the Fenestration Layers
4.2. Re-Sampling of the Bidirectional Scattering Distribution Function
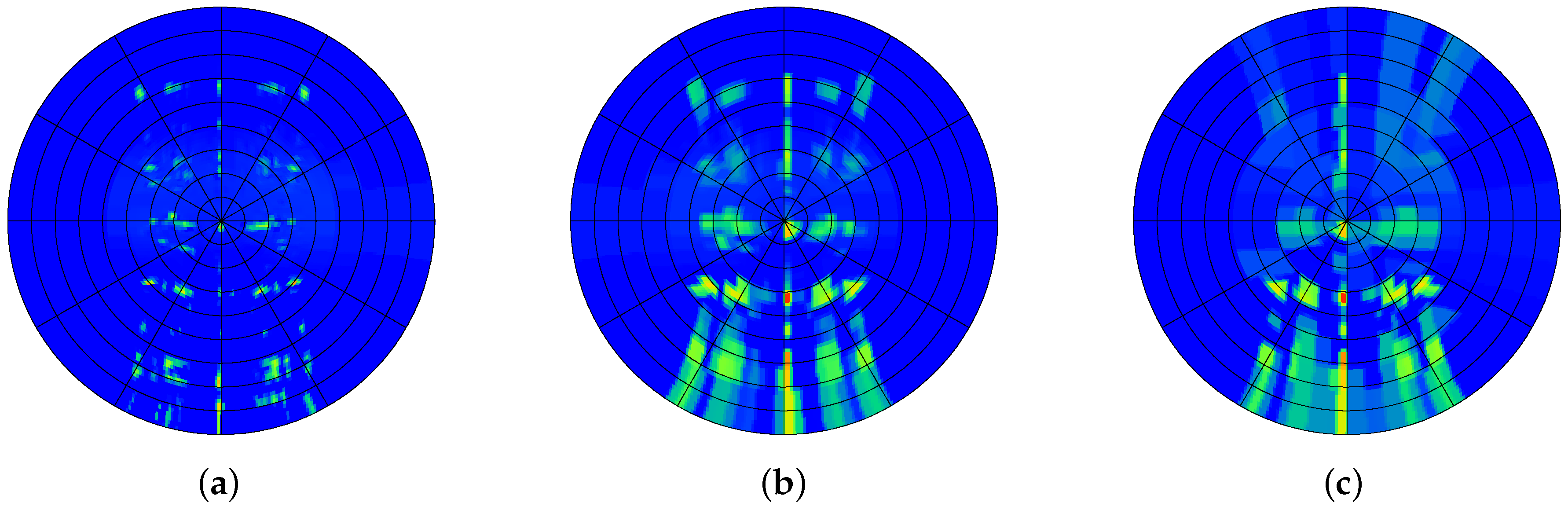
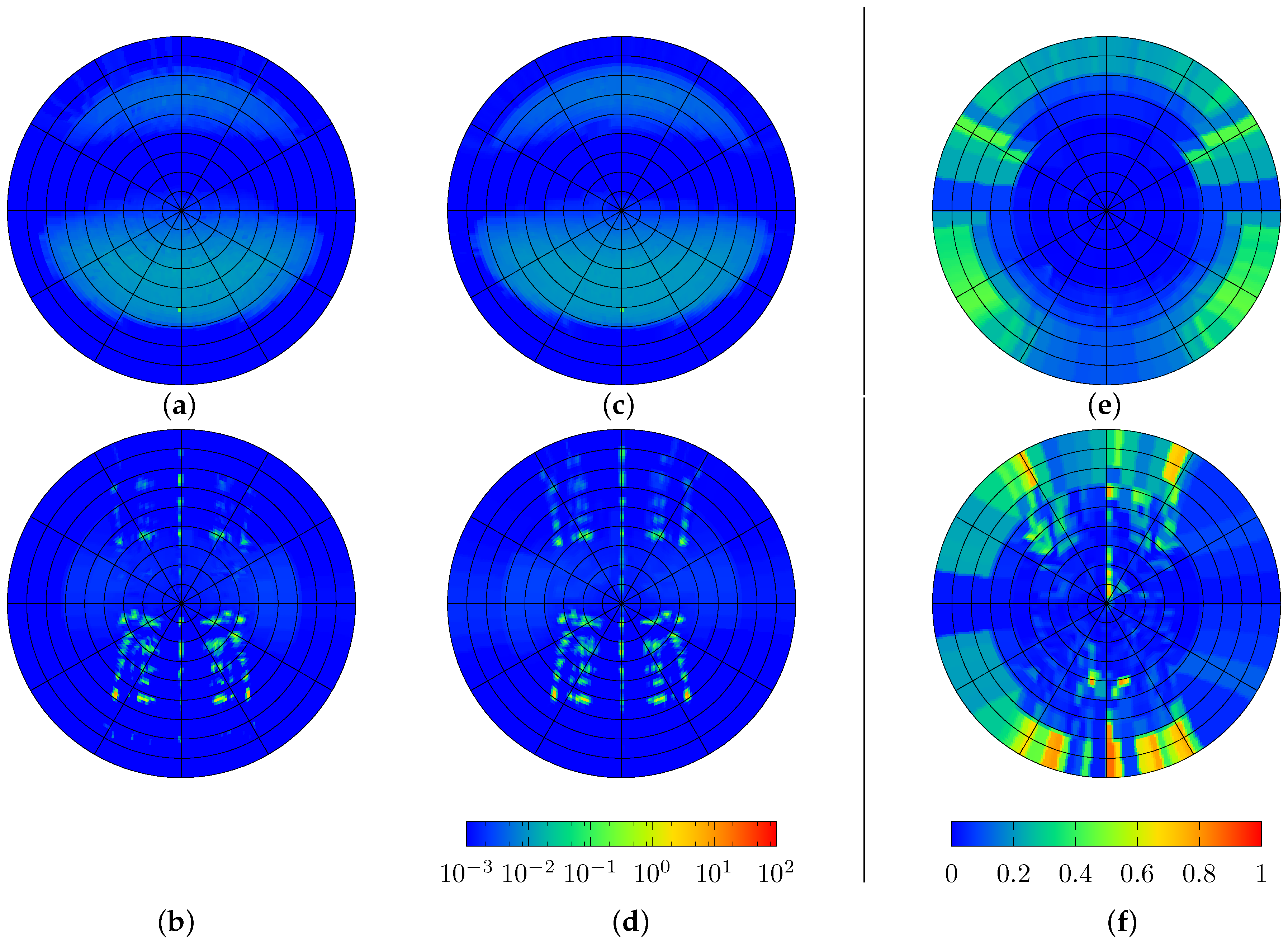
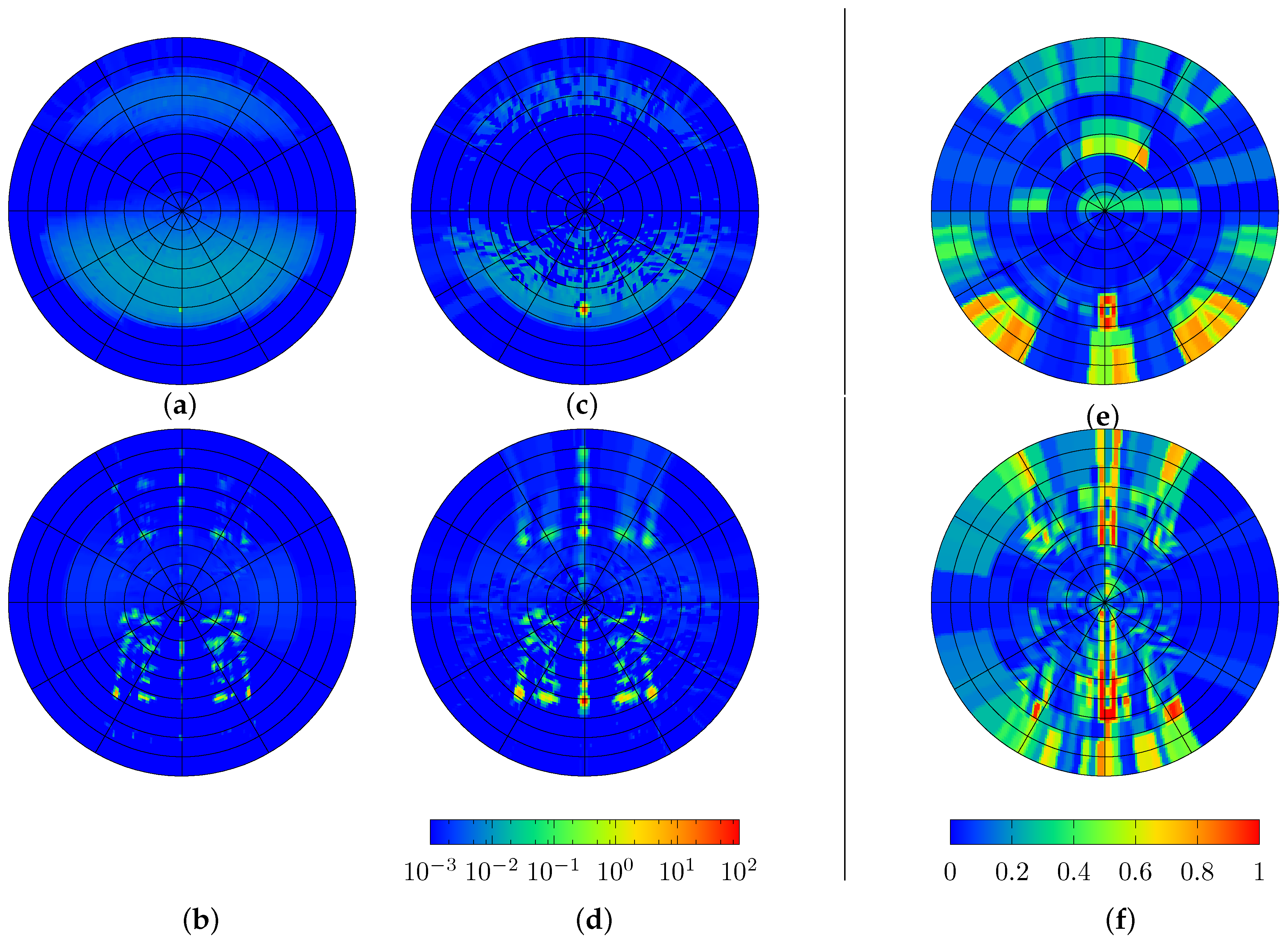
4.3. Combined Bidirectional Scattering Distribution Functions and Comparison to Results of Ray-Tracing
4.4. Evaluating the Performance of the Matrix Formalism
4.5. Evaluating the Impact of Directional Resolution
5. Discussion and Conclusion
Acknowledgments
Conflicts of Interest
Appendix

References
- Ruck, N.; Aschehoug, Ø.; Aydinli, S.; Christoffersen, J.; Courret, G.; Edmonds, I.; Jakobiak, R.; Kischkoweit-Lopin, M.; Klinger, M.; Lee, E.; et al. Daylight in Buildings—A Source-book on Daylighting Systems and Components; Lawrence Berkeley National Laboratory: Washington, DC, USA, 2000.
- Gago, E.; Muneer, T.; Knez, M.; Köster, H. Natural light controls and guides in buildings. Energy saving for electrical lighting, reduction of cooling load. Renew. Sustain. Energy Rev. 2015, 41, 1–13. [Google Scholar] [CrossRef]
- Nair, M.; Ramamurthy, K.; Ganesan, A. Classification of indoor daylight enhancement systems. Light. Res. Technol. 2014, 46, 245–267. [Google Scholar] [CrossRef]
- Papamichael, K.; Winkelmann, F. Solar-optical properties of multilayer fenestration systems. In Proceedings of the International Daylighting Conference, Long Beach, CA, USA, 4–7 November 1986; Volume 1.
- Janak, M. Coupling building energy and lighting simulation. In Proceedings of the Fifth International IPBSA Conference, Prague, Czech Republic, 8–10 September 1997; pp. 8–10.
- Bueno, B.; Wienold, J.; Katsifaraki, A.; Kuhn, T.E. Fener: A Radiance-based modeling approach to assess the thermal and daylighting performance of complex fenestration systems in office spaces. Energy Build. 2015, 94, 10–20. [Google Scholar] [CrossRef]
- Kuhn, T.E.; Herkel, S.; Frontini, F.; Strachan, P.; Kokogiannakis, G. Solar control: A general method for modeling of solar gains through complex facades in building simulation programs. Energy Build. 2011, 43, 19–27. [Google Scholar] [CrossRef]
- Appelfeld, D.; McNeil, A.; Svendsen, S. An hourly based performance comparison of an integrated micro-structural perforated shading screen with standard shading systems. Energy Build. 2012, 50, 166–176. [Google Scholar] [CrossRef]
- Nicodemus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance; Technical Report; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1977.
- American Society for Testing and Materials (ASTM). ASTM E2387-05. Standard Practice for Goniometric Optical Scatter Measurements; The ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Kajiya, J.T. The Rendering Equation. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 1986; pp. 143–150. [Google Scholar]
- Lawrence, J.; Ben-Artzi, A.; DeCoro, C.; Matusik, W.; Pfister, H.; Ramamoorthi, R.; Rusinkiewicz, S. Inverse shade trees for non-parametric material representation and editing. In ACM Transactions on Graphics; ACM: New York, NY, USA, 2006; Volume 25, pp. 735–745. [Google Scholar]
- Kaempf, J.H.; Scartezzini, J. Integration of BT(R)DF Data into Radiance Lighting Simulation Programme; Technical Report; Ecole Polytechnique Federale de Lausanne: Lausanne, Switzerland, 2004. [Google Scholar]
- Greenup, P.; Edmonds, I.; Compagnon, R. Radiance algorithm to simulate laser-cut panel light-redirecting elements. Light. Res. Technol. 2000, 32, 49–54. [Google Scholar] [CrossRef]
- Ward, G.; McNeil, A. A variable-resolution BSDF implementation. In Proceedings of the 10th International Radiance Workshop, Berkeley, CA, USA, 24–26 August 2011.
- Stover, J.C. Optical Scattering: Measurement and Analysis; SPIE Optical Engineering Press: Bellingham, WA, USA, 1995; Volume 2. [Google Scholar]
- Apian-Bennewitz, P. New scanning gonio-photometer for extended BRTF measurements. In Proceedings of the International Society for Optics and Photonics SPIE Optical Engineering+ Applications, Santiago, CA, USA, 1–5 August 2010; p. 779200.
- McNeil, A.; Lee, E.S.; Jonsson, J.C. Daylight performance of a microstructured prismatic window film in deep open plan offices. Build. Environ. 2016, 113, 280–297. [Google Scholar] [CrossRef]
- Kostro, A.; Scartezzini, J.L.; Schueler, A. Mixed-Dimensionality Approach for Advanced Ray Tracing of Lamellar Structures for Daylighting and Thermal Control. In Proceedings of the CISBAT 2013 Cleantech for Smart Cities and Buildings. EPFL Solar Energy and Building Physics Laboratory (LESO-PB), Lausanne, Switzerland, 4–6 September 2013; Volume 2, pp. 1115–1120.
- Krehel, M.; Grobe, L.O.; Wittkopf, S. A hybrid BSDF model comprising measured and simulated data. J. Facade Des. Eng. 2017. preprint. [Google Scholar]
- Lawrence Berkeley National Laboratory. Complex Glazing Database. Available online: https://windows.lbl.gov/software/CGDB (accessed on 8 March 2017).
- Stokes, G.G. On the intensity of light reflected from or transmitted through a pile of plates. Proc. R. Soc. Lond. 1860, 11, 545–556. [Google Scholar] [CrossRef]
- Jakob, W.; d’Eon, E.; Jakob, O.; Marschner, S. A Comprehensive Framework for Rendering Layered Materials. ACM Trans. Graph. 2014, 33, 118:1–118:14. [Google Scholar] [CrossRef]
- Eisenlohr, J.; Tucher, N.; Höhn, O.; Hauser, H.; Peters, M.; Kiefel, P.; Goldschmidt, J.C.; Bläsi, B. Matrix formalism for light propagation and absorption in thick textured optical sheets. Opt. Express 2015, 23, A502–A518. [Google Scholar] [CrossRef] [PubMed]
- Klems, J.H. New method for predicting the solar heat gain of complex fenestration systems - 1. Overview and derivation of the matrix layer calculation. ASHRAE Trans. 1994, 100, 1065–1072. [Google Scholar]
- Klems, J.H. New method for predicting the solar heat gain of complex fenestration systems - 2. Detailed description of the matrix layer calculation. ASHRAE Trans. 1994, 100, 1073–1086. [Google Scholar]
- Mitchell, R.; Kohler, C.; Klems, J.; Rubin, M.; Arasteh, D.; Huizenga, C.; Yu, T.; Curcija, D. Window 6.2/Therm 6.2 Research Version User Manual; Technical Report LBNL-941; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2008.
- Aydinli, H.; Kaase, H. Measurement of Luminous Characteristics of Daylighting Materials; Technical Report, International Energy Agency Task 21; IEA: Paris, France, 1999. [Google Scholar]
- de Boer, J. Modeling Indoor Illumination by CFS Based on Bidirectional Photometric Data; Technical Report, International Energy Agency Task 31; IEA: Stuttgart, Germany, 2005. [Google Scholar]
- Kämpf, J.H.; Scartezzini, J.L. Ray-tracing simulation of complex fenestration systems based on digitally processed BTDF data. In Proceedings of the CISBAT, Lausanne, Switzerland, 14–16 September 2011; pp. 349–354.
- Klems, J.H. Complex Fenestration Calculation Module. In EnergyPlus Engineering Reference; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2013; chapter Window Calculation Module. [Google Scholar]
- Basurto Dávila, C. On advanced daylighting simulations and integrated performance assessment of complex fenestration systems for sunny climates. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2014. [Google Scholar]
- McNeil, A. On the Sensitivity of Daylight Simulations to the Resolution of The Hemispherical Basis Used to Define Bidirectional Scattering Distribution Functions; Technical Report; DOE Technical Memo: Berkeley, CA, USA, 2011. [Google Scholar]
- Ward, G.; Kurt, M.; Bonneel, N. A Practical Framework for Sharing and Rendering Real-World Bidirectional Scattering Distribution Functions; Technical Report; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2012.
- Shirley, P.; Chiu, K. A low distortion map between disk and square. J. Gr. Tools 1997, 2, 45–52. [Google Scholar] [CrossRef]
- Eigen is a C++ Template Library for Linear Algebra: Matrices, Vectors, Numerical Solvers, and Related Algorithms. Eigen v3. Available online: http://eigen.tuxfamily.org (accessed on 8 March 2017).
- Noback, A.; Grobe, L.O.; Wittkopf, S. Accordance of light scattering from design and de-facto variants of a daylight redirecting component. Buildings 2016, 6, 30. [Google Scholar] [CrossRef]
- Bergen, A. A practical method of comparing luminous intensity distributions. Light. Res. Technol. 2012, 44, 27–36. [Google Scholar] [CrossRef]
- The Linux man-pages project. time(1). Available online: http://man7.org/linux/man-pages/man1/time.1.html (accessed on 8 March 2017).



| Forward | Backward | ||||
|---|---|---|---|---|---|
| Reflection | front to front | = 0 to 90 | = 0 to 90 | ||
| back to back | = 90 to 180 | = 90 to 180 | |||
| Transmission | front to back | = 0 to 90 | = 90 to 180 | ||
| back to front | = 90 to 180 | = 0 to 90 |
| Parameter | Description | Value |
|---|---|---|
| −t4 k | Tensor resolution exponent, results in coefficients | 7 |
| −c n | Number of sample rays per hemisphere | 163,840 |
| Percentage of data reduction applied to tensor (constant set in genBSDF) | 90 |
| Parameter | Description | Value |
|---|---|---|
| −t4 g | Tensor resolution exponent, results in coefficients | 7 |
| −c n | Number of sample rays per hemisphere | 32,768 |
| −ad n | Number of daughter rays at each ambient ray intersection | 128 |
| Percentage of data reduction applied to tensor (constant set in genBSDF) | 90 |
| Parameter | Description | Value |
|---|---|---|
| −aa k | Ambient accuracy, disables ambient caching | 0 |
| −ad n | Ambient divisions, number of child rays in indirect-diffuse calculation | 16,384 |
| −lw w | Limit weight, maximum contribution of one ray | 5 × 10 |
| −ss s | Specular sampling, number of rays to send in indirect-specular calculation | 1024 |
| −ps t | Pixel sample spacing, disables adaptive sampling | 1 |
| CFS | |||||
|---|---|---|---|---|---|
| CFS1 | 0.010 | 88.943 | 97.864 | 98.938 | 97.760 |
| CFS2 | 67.677 | 95.410 | 97.992 | 96.361 | 98.738 |
| CFS | genBSDF | ||||
|---|---|---|---|---|---|
| CFS1 | 0.26 | 0.26 | 0.39 | 7.09 | 289 |
| CFS2 | 0.26 | 0.26 | 0.40 | 7.07 | 1981 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grobe, L.O. Computational Combination of the Optical Properties of Fenestration Layers at High Directional Resolution. Buildings 2017, 7, 22. https://doi.org/10.3390/buildings7010022
Grobe LO. Computational Combination of the Optical Properties of Fenestration Layers at High Directional Resolution. Buildings. 2017; 7(1):22. https://doi.org/10.3390/buildings7010022
Chicago/Turabian StyleGrobe, Lars Oliver. 2017. "Computational Combination of the Optical Properties of Fenestration Layers at High Directional Resolution" Buildings 7, no. 1: 22. https://doi.org/10.3390/buildings7010022
APA StyleGrobe, L. O. (2017). Computational Combination of the Optical Properties of Fenestration Layers at High Directional Resolution. Buildings, 7(1), 22. https://doi.org/10.3390/buildings7010022






