Experimental Study on Seismic Performance of Rammed Earth and Rubble Masonry Walls

Abstract

Rammed earth and rubble masonry walls are constructed using raw stones as aggregate and native soil as binding material. To investigate the impact of different configurations on the seismic performance of rammed earth and rubble masonry wall, four wall specimens were subjected to quasi-static testing. Through comparative analysis of hysteresis curves, skeleton curves, stiffness degradation curves, and energy dissipation capacity, the failure modes and seismic performance of the walls were elucidated. Research indicates that under horizontal low-cycle cyclic loading, rammed earth and rubble masonry walls undergo three stages of failure: microcrack initiation and propagation, macrocrack formation and local failure, and ultimate collapse. The arched counter-arch joint wall exhibits the highest energy dissipation capacity and maximum shear bearing capacity, demonstrating an 18.7% improvement over the standard wall. Timber reinforcement walls exhibited lower energy dissipation capacity than curved joint walls but higher than standard walls, with shear bearing capacity being 1.3% greater than standard walls. The opening wall demonstrated the poorest energy dissipation capacity, with shear bearing capacity being 35% lower than standard walls and having the weakest seismic performance. These findings provide theoretical support for optimizing the seismic design of traditional rammed earth and rubble masonry dwellings.

1. Introduction

Rubble stone walls, an ancient construction technique that is widely used, have left an indelible mark across the globe due to their convenience in sourcing local materials and the inherent durability of stone itself. From humble field walls to monumental civilizational relics, they collectively showcase humanity’s ingenuity in adapting and harnessing nature for construction. Among these, Peru’s Machu Picchu stands as the pinnacle of dry-stone masonry, with its masterfully crafted walls featuring stones interlocked without mortar, enduring earthquakes while remaining steadfast. Additionally, the Trulli houses of Italy’s Puglia region and the watchtowers of China’s Tibetan areas, respectively, demonstrate the exceptional performance of rough-hewn stone in residential and military defense applications, collectively forming the most brilliant examples in the world’s heritage of rough-stone architecture.

The main structure of the earth-filled rubble stone house is a masonry wall system, using rammed earth as the binding material and stone as the building blocks [1,2,3]. Walls serve as primary load-bearing and enclosing components, with common forms including ashlar masonry, rubble masonry, slate masonry, and pebble masonry. Among these, rubble masonry—constructed from roughly hewn natural stones—offers advantages such as cost-effectiveness, environmental sustainability, and readily available materials, making it the most prevalent wall type in ordinary residential buildings [4,5]. Taking Tibetan-style houses in China as an example, these structures are situated in seismic zones with high intensity requirements, where frequent and intense earthquakes occur. This region has experienced multiple destructive major earthquakes (such as the Dingri County earthquake in Shigatse, the Wenchuan earthquake, and the Lushan earthquake), making seismic resistance the primary consideration in local architectural design. Current systematic research on the seismic performance of rammed earth and rubble masonry walls primarily focuses on the compressive strength of stone masonry, failure patterns of mortar joints, the impact of masonry techniques on the mechanical properties of stone masonry, and the overall seismic performance of structures. For instance, Tian Xun established an evaluation system for the compressive performance of stone masonry walls based on axial compression tests [6]; Yang Na revealed through an improved double-shear test that mortar joint shear failure is actually a coupled process of mortar plastic deformation and interfacial debonding, providing key parameters for shear constitutive models [7]; Wu Aojun quantified the influence of masonry techniques on compressive strength by integrating digital image correlation technology with finite element modeling [8]; Zhang Qiang used a micromechanical model to elucidate how yellow clay content affects wall failure modes and energy dissipation mechanisms [9]. Regarding overall structural seismic performance, Cui Lifu replicated typical Ganbao Tibetan village houses in shake table tests, discovering that wall-to-wall connections are prone to failure during strong earthquakes due to low-strength mortar and structural defects [10]. Romanazzi et al. investigated the failure mechanisms of a substructure composed of rammed earth walls and timber framing under out-of-plane seismic loads, as well as the restraining effect of the timber framing, through shake table testing [11]. Senaldi et al. conducted shake table tests on a half-scale model of a terraced masonry building complex, revealing the complex’s cooperative dynamic response, damage evolution process, and collapse mechanism during earthquakes [12]. Kallioras et al. investigated the failure mechanisms, seismic performance, and ultimate collapse process of unreinforced clay brick masonry buildings with chimneys under seismic loading through shake table collapse tests [13]. Guerrini et al. investigated the seismic performance and reinforcement effectiveness of a row of stone masonry buildings with reinforcement measures and flexible floor slabs under seismic loading through shake table tests [14]. Kouris et al. analyzed the evolution of dynamic characteristics and the accumulation and propagation mechanisms of seismic damage in a two-story full-scale masonry building through dynamic testing [15]. Zhao et al. evaluated the overall seismic performance and failure modes of a hybrid structural system combining masonry and traditional cave dwellings through scaled model shake table tests [16]. Xue et al. specifically investigated the seismic response, failure mechanisms, and seismic capacity of brick-masonry cave dwellings-a unique earthen architecture- through shake table testing [17]. Tomic et al. further validated and explored the interaction, damage evolution, and seismic vulnerability of semi-scale terraced stone masonry complexes during strong earthquakes through shake table testing [18]. The aforementioned studies on masonry walls have primarily focused on stone masonry structures, with seismic performance research predominantly centered on shake table testing of buildings. Such testing can only reveal the overall failure patterns of buildings during seismic events. However, there remains a lack of systematic and in-depth research on the seismic performance implications of key structural elements in rammed earth and rubble masonry walls, including the stabilizing effect of timber wall ties, the seismic contribution of counter-arch masonry, and the weakening effects of openings.

This study investigates Tibetan-style rammed earth and rubble masonry walls in China. Through quasi-static testing, it quantitatively evaluates the contribution and influence mechanisms of typical structural measures, identifies the failure patterns and mechanisms of the walls, and analyzes the degradation patterns of wall stiffness and the energy dissipation capacity of the walls. Through this analysis, the study identifies effective ductile seismic design measures within rammed earth and rubble masonry walls. These findings guide the engineering design and construction of traditional rammed earth and rubble masonry houses, thereby enhancing their seismic resistance.

2. Test Overview

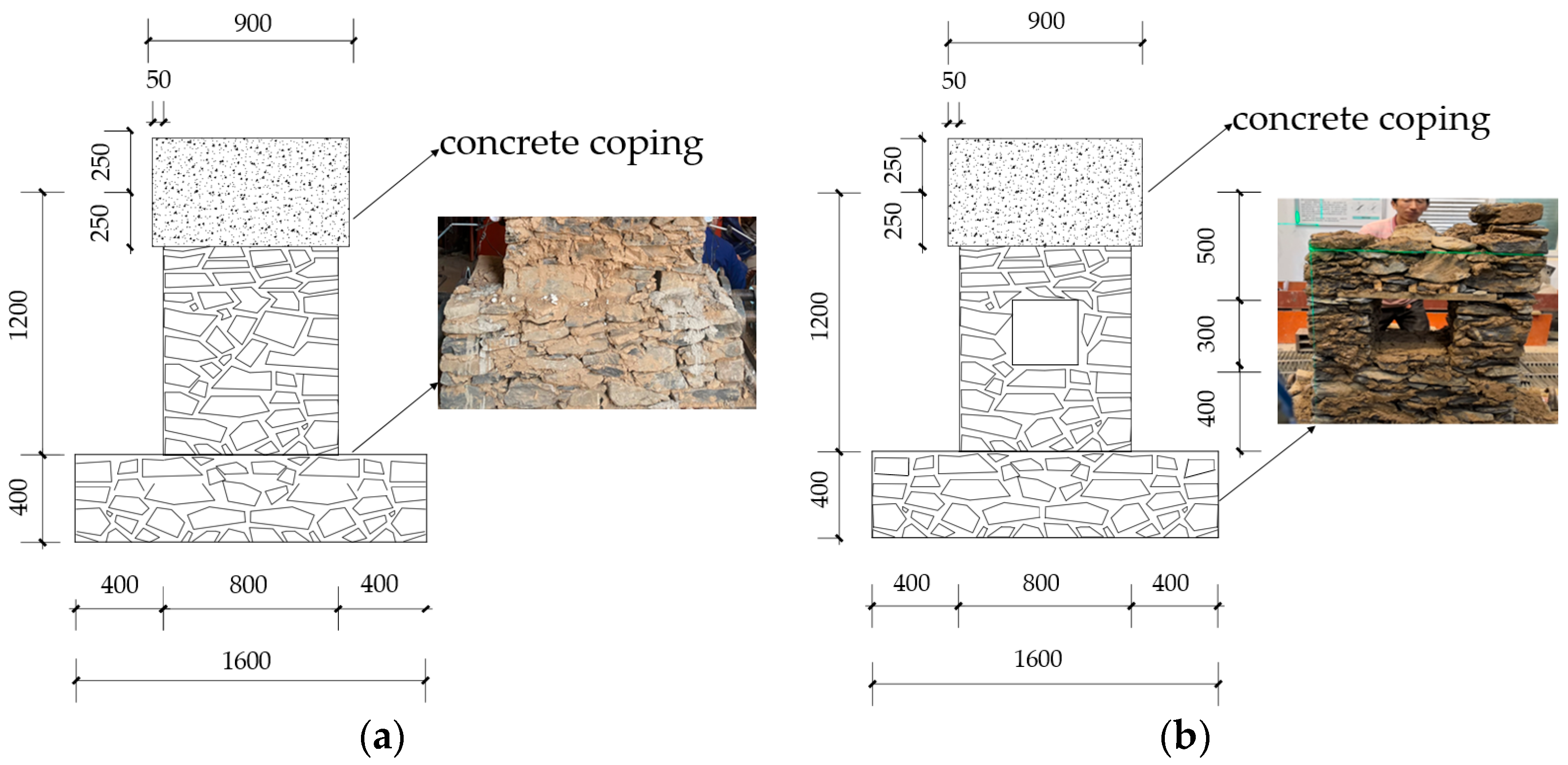
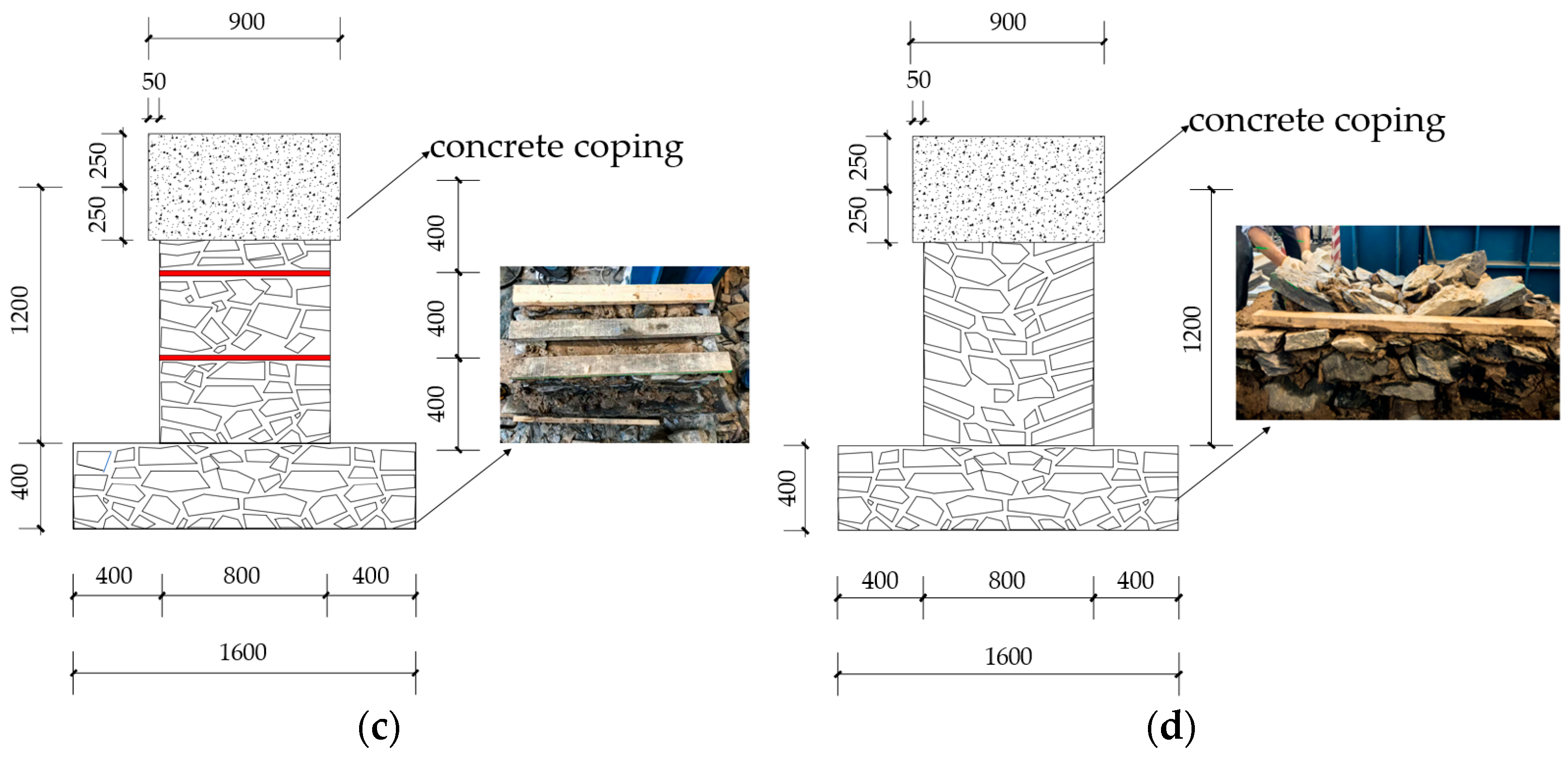
2.1. Test Specimen Design

The wall prototype is based on an actual Tibetan-style house in Heishui County, Aba Prefecture of China. Its dimensions were scaled down to 1/4 size according to the “standard for test method of basic mechanics properties of masonry” (GBT50129-2011) [19], laboratory equipment, and site conditions, measuring 800 mm × 400 mm × 1200 mm. A base measuring 1600 mm × 400 mm × 800 mm was installed beneath the wall to simulate the foundation. To investigate the impact of different construction methods on seismic performance in Tibetan dwellings, four test specimens were prepared: a standard specimen (Figure 1a), an opening specimen (Figure 1b), a timber reinforcement specimen (Figure 1c), and a curved joint specimen (Figure 1d). To prevent localized failure under horizontal thrust, a concrete coping was cast atop the wall, measuring 410 mm × 500 mm × 900 mm. This coping encased the stone wall by 250 mm and extended upward 250 mm along the wall top (Figure 1).

The yellow clay and rubble used in the walls were sourced from Heishui County, Aba Prefecture of China. The ultimate compressive strength of the yellow clay was determined using a universal testing machine (Figure 2a). The ultimate compressive strength of the stone was also determined using a universal testing machine (Figure 2b). The ultimate bond strength between yellow clay and stone was determined through triaxial compression tests (Figure 2c). The standard vertical ultimate failure load of the wall was obtained from axial compression tests (Figure 2d). The material test specifications for various components within the wall are listed in

Table 1. Material test specifications for various components in the wall.

Material Type	Material Performance Specifications	Experimental Measured Values
Stone	Compressive strength	42.7 MPa
	Density	2811 kg·m−3
	Elastic modulus	2682 MPa
Yellow clay	compressive strength	0.676 MPa
	Density	1388.59 kg·m−3
	Elastic modulus	120 MPa
Bond strength between yellow clay and stone	Ultimate bond strength	3.6134 × 10−5 MPa
Wall	Ultimate failure load	577 kN

.

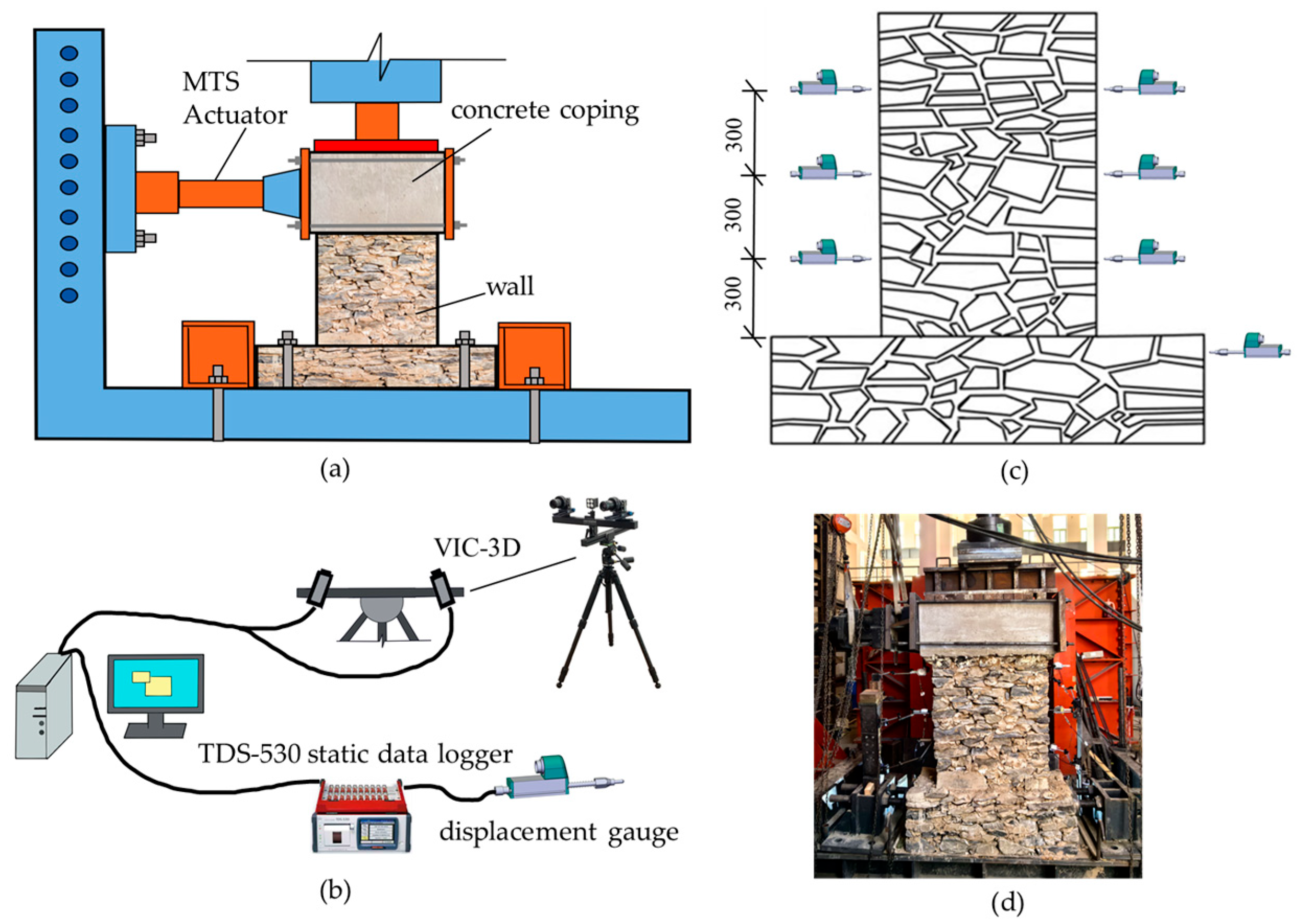
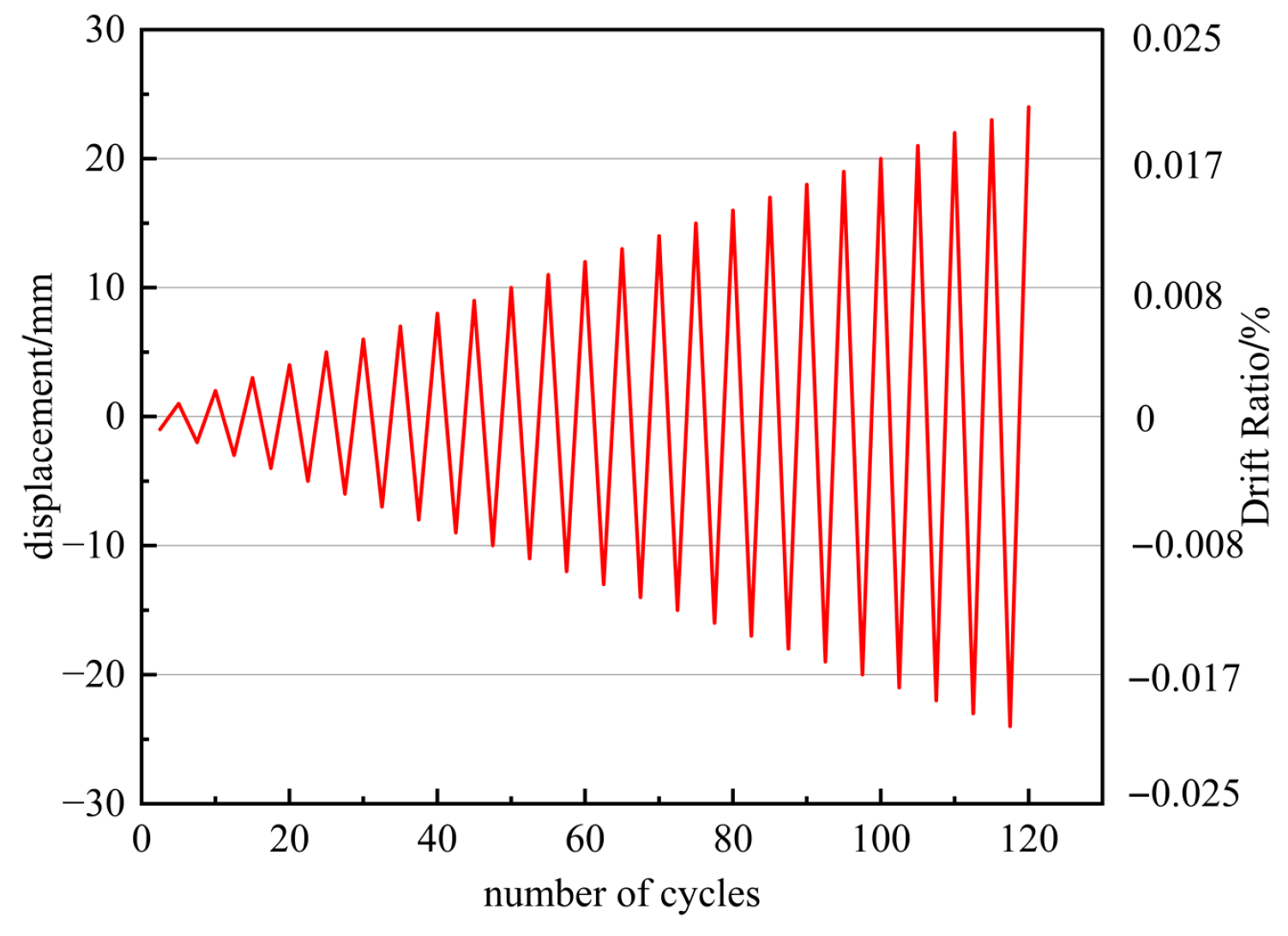
2.2. Test Setup and Loading Regime

The loading and data acquisition system is shown in Figure 3. Horizontal low-cycle cyclic tests were conducted on the components in accordance with the “specification for seismic test of buildings” (JGJ/T101-2015) [20]. An MTS electro-hydraulic servo loading system was employed for loading, with a schematic of the loading system presented in Figure 3a. The vertical load was set at 40–60% of the ultimate compressive failure load of the standard specimen (577 kN). Considering the weakening effect of the opening in the specimen, the vertical load for this test was set at 190 kN.

The schematic diagram of the data acquisition system is shown in Figure 3b. Wall lateral deformation is measured using displacement transducers, with a total of seven transducers selected: WY1, WY2, WY4, and WY5 measure upper wall displacement; WY3 and WY6 measure lower wall displacement; and WY7 verifies whether the wall base has shifted (Figure 3c). Displacement data is acquired using the TDS-530 static data logger. The VIC-3D captures the evolution of surface cracks during loading (Volumetric Image Correlation in 3 Dimensions), a non-contact full-field strain measurement system, documenting the progression of surface damage characteristics. A camera records the testing process and associated phenomena.

Due to the extremely low cohesive strength of yellow clay in Tibetan-style rammed earth and rubble masonry walls, force control accelerated wall failure and failed to reflect the actual failure process accurately. Therefore, displacement control was adopted for the test. Vertical loading was performed first, with the vertical load applied in three stages (50%, 70%, 100%). After each stage was applied, the load was stabilized for 2 min before proceeding to the next stage, continuing until the target load was reached and maintained at a constant level. Horizontal loading was then initiated under displacement control, with increments of 0.5 mm per stage and one cycle per stage. Testing ceased upon wall failure or instability. The loading protocol is illustrated in Figure 4.

The flowchart for the entire experimental process is shown in Figure 5.

3. Primary Test Phenomena and Failure Patterns

The damage progression of Tibetan-style rammed earth walls with rough stones is categorized into three stages based on the magnitude of horizontal control displacement values: the formation and expansion of microcracks, the development of macrocracks and localized failure, and overall collapse. Details are as follows.

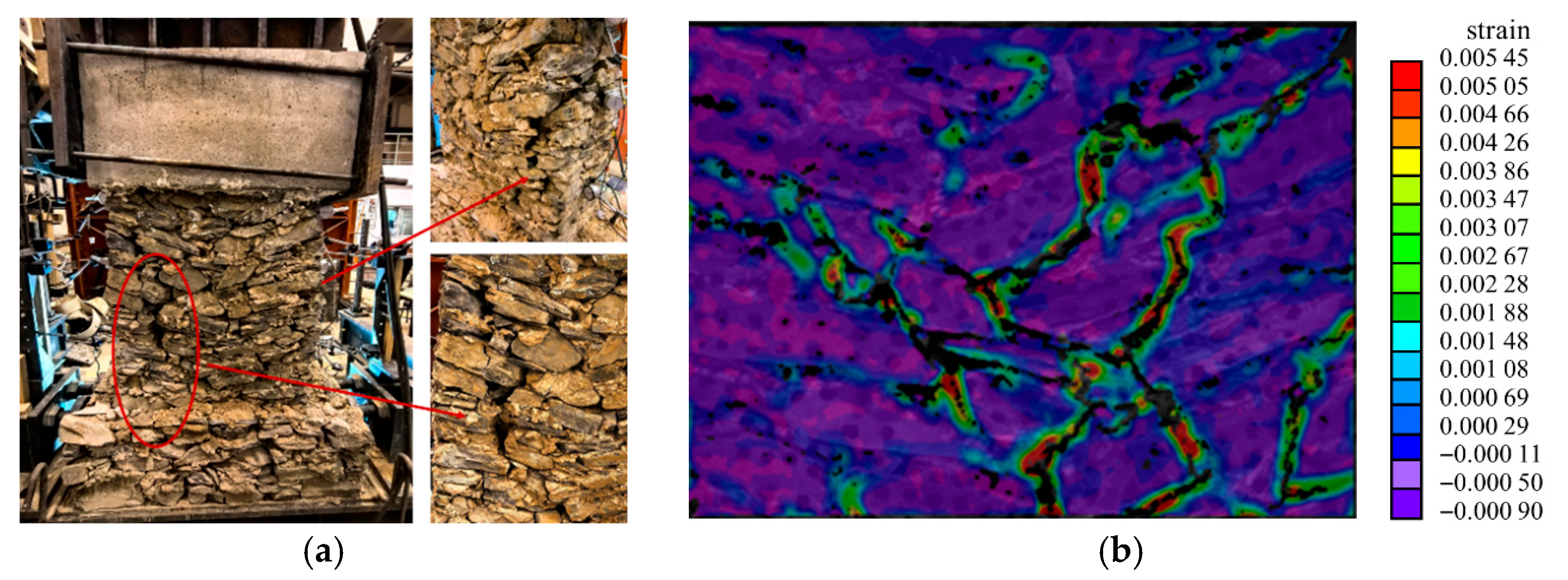
3.1. Formation and Propagation of Microcracks

When the horizontal displacement controlled by the actuator is small, stresses and strains at all points within the wall are minimal, exhibiting a nearly linear relationship between force and displacement. Small, scattered cracks appear in the yellow clay mortar joints with the weakest bonding strength. These cracks are initially invisible, and the wall exhibits almost no residual deformation. During this stage, the maximum displacement applied by the horizontal actuator was 2.5 mm for standard specimens and opening specimens, 3 mm for timber reinforcement specimens, and 1.5 mm for curved-joint specimens. This indicates that in the elastic stage, the load-bearing capacity of standard and opening specimens was comparable, with the weakening effect of openings not yet evident. The displacement of the timber reinforcement specimen was slightly higher, indicating that wood reinforcement has a specific inhibitory effect on cracking. Due to the influence of masonry techniques, the curved masonry specimen exhibited the lowest displacement value.

At this stage, shear slippage or crushing occurs in the yellow clay bonding at stress concentration points (such as sharp corners of rubble stones, opening edges, and ends of wooden ties), forming initial micro-voids and slippage. Key influencing factors include irregular protrusions and sharp edges on stones acting as “nucleation sites” for microcracks, as well as vertical self-weight loads compacting joints to provide friction, but load redistribution above openings creates an “arch effect” that generates higher compressive and shear stresses at the arch feet on both sides of the opening, potentially accelerating microcrack development there.

3.2. Macro Crack Formation and Local Failure

As the horizontal control displacement increases, the load gradually rises. When the tensile stress at the horizontal mortar joints exceeds the ultimate tensile strength of the yellow clay, cracks form in the masonry joints. Due to the uneven distribution of stone blocks within the wall, cracking occurs asymmetrically on the left and right sides. The side with relatively more minor stone blocks cracks first at the mortar joints. As the horizontal control displacement is applied, the gaps in this area gradually widen, resembling shear failure. When the load exceeds 50% of the ultimate load, visible cracks in the wall increase progressively, gaps widen, macro-cracks form, and the structure enters the initial stage of elastic–plastic behavior. During this stage, the maximum horizontal displacement recorded for the standard specimen was 4 mm; the maximum displacement for the opening specimen was 3.5 mm, indicating the weakening effect of the opening; the maximum displacement for the timber reinforcement specimen was 4 mm; and the maximum displacement for the curved joint specimen was 2 mm.

As horizontal displacement control increases further, macro-cracks partially penetrate to form stepped cracks. Stones at the intersection of cracks become loose and dislodge, causing localized bulging or indentation in the wall. When the maximum principal tensile stress generated by the horizontal displacement control exceeds the tensile strength of the stone, shear diagonal cracks penetrating the blocks appear in the wall. These cracks exhibit slightly varying angles, and during reverse loading, the diagonal cracks show a noticeable closing phenomenon. As the horizontal cyclic loading continues, cracks increase on both sides of the wall, the wall undergoes greater elastic–plastic deformation, and it progresses toward a stage of local failure. The phenomena observed in the four component groups are as follows: ① After the standard specimen displacement reached 5.48 mm, with a horizontal thrust of 8.68 kN, yellow clay continuously cracked and peeled off the outer wall surface. Cracks appeared in the mortar joints, and stepped cracks gradually increased. At this stage, the maximum horizontal displacement borne by the standard specimen was 6 mm, with cracks primarily concentrated in the upper left wall section (Figure 6a). The evolution of the maximum principal strain on the surface is shown in Figure 6b, with the principal strain range being: −0.0018 to 0.0242. ② After the opening specimen reached 3 mm displacement, the stones above the opening exhibited noticeable lateral displacement. Simultaneously, cracks appeared in the mortar joints of the side walls, the yellow clay lost its bonding strength, and the side rubble stones also shifted laterally. At this stage, the maximum horizontal displacement borne by the opening specimen reached 5.5 mm, with cracks primarily concentrated on both sides of the opening (Figure 7a). The evolution of the maximum principal strain on the surface is shown in Figure 7b, with a principal strain range of −0.0019 to 0.01647. ③ After the wall displacement of the timber-reinforced specimen reached 4 mm, compressive cracks appeared in the central section of the double-layer timber-reinforced wall. Under horizontal cyclic loading, tensile cracks alternated with compressive cracks, but tensile cracks were more prevalent. Additionally, significant tensile cracks developed in the mortar joints between stones in the central wall section. When the displacement of the timber-reinforced specimen wall reached 6 mm, the horizontal thrust was 13.94 kN, and stepped cracks appeared in the mortar joints at the wall’s midpoint. Due to the presence of wooden ribs, these cracks did not widen during subsequent loading. At this stage, the maximum horizontal displacement experienced by the timber-reinforced specimen was 7 mm, with cracks primarily concentrated in the lower-middle section of the wall (Figure 8a). The evolution of the maximum principal strain on the surface is shown in Figure 8b, with the principal strain range being: −0.00023 to 0.00193. ④ In the curved joint specimen, the inclined masonry made the stones more prone to fracture. During initial loading, the stones cracked before the yellow clay was applied. When displacement reached 3 mm and horizontal thrust reached 5.66 kN, continued displacement control caused stone displacement. The yellow clay reached its shear strength limit and lost bonding strength. However, under cyclic loading, the displaced stones did not recover to their original state as observed in other specimens. Instead, a primary tensile crack developed in the wall’s central region, accompanied by numerous small tensile cracks around it. During this stage, the curved joint specimen experienced a maximum horizontal displacement of 3.5 mm. Cracks were primarily concentrated on the wall’s sides and central region (Figure 9a). The evolution of maximum principal strain on the surface is shown in Figure 9b, with the principal strain range ranging from −0.0021 to 0.0206.

At this stage, microcracks propagate along weak mortar joints, forming distinct diagonal or stepped macrocracks that segment the wall into several relatively independent load-bearing units. Key influencing factors include the complete failure of yellow clay bonding, with shear resistance relying entirely on friction and geometric interlock between blocks. The geometric interlock effect of irregular stones is crucial for the wall’s continued load-bearing capacity at this stage. Curved masonry promotes the formation of an “arch effect,” causing macro-cracks to develop more readily along potential arch lines. This facilitates more effective force chain reconfiguration, thereby enhancing load-bearing capacity and ductility during this phase. The tensile reinforcement of wooden ties became prominent, preventing the complete separation of blocks on either side of cracks and forcing continued collaborative action. Simultaneously, compression between ties and stones provided additional lateral restraint, increasing effective normal stress on slip planes and thereby strengthening frictional resistance. The opening forces the flow of forces to detour, fixing the macro-crack pattern as distinct diagonal cracks extending from the opening corners toward the load point. This shortens the path for force chain reconstruction, making this stage shorter and more fragile. Furthermore, vertical loads are transmitted through the reconfigured local block assemblies. The presence of wooden ties enables more uniform load distribution, delaying overload in any single local assembly.

3.3. Failure Stage

As residual deformation accumulates, crack width and length gradually increase, progressively reducing the wall’s load-bearing capacity until the specimen ultimately fails. The phenomena observed in the four groups of components are as follows:

Standard Specimen: When the actuator-controlled displacement reached 7 mm, stones within the wall cracked, emitting a relatively muffled “thudding” sound, with a horizontal thrust of 14.24 kN. Continued loading caused smaller rubble stones to fracture, further widening the cracks. At 8 mm actuator displacement (horizontal thrust: 21.66 kN), cracks in the rubble stones connected with mortar joints to form through cracks. Under subsequent horizontal cyclic loading and vertical loading, the wall bulged outward along the through-crack toward both ends, ultimately collapsing under compression. The bearing capacity decreased to 13.28 kN. The failure crack is shown in Figure 10a, while the evolution of the maximum principal strain on the surface is depicted in Figure 10b. The principal strain range was −0.0012 to 0.04537.

The opening specimen: As the shear force in the wall gradually increased, the yellow clay cracked and fell away. Under the action of horizontal cyclic loading, the contact surface between the stones at the upper corner of the opening and the wooden lintel was separated. With continued loading, the rocks at the edges of the opening fractured due to stress concentration. At a displacement of 7 mm, the wall emitted a dull “thudding” sound as rubble stones shifted noticeably. With a horizontal force of 13.45 kN, the stones at the bottom of the opening cracked and connected with the yellow clay mortar joints, forming cracks beneath the opening. At 11 mm displacement, the maximum horizontal thrust reached 18.18 kN. The walls on both sides of the opening bulged outward, cracks proliferated around the opening, and the wall ultimately failed due to instability. The failure cracks are shown in Figure 11a, while the evolution of the maximum principal strain on the surface is depicted in Figure 11b. The principal strain range was −0.00083 to 0.0286.

Timber-reinforced specimen: When displacement reached 8 mm, the horizontal thrust was 15.61 kN, causing stones at the wall-to-base connection to crack successively. At 9.5 mm displacement, the horizontal thrust reached 19.55 kN, causing the first layer of wooden reinforcement to crack. When wall displacement reached 11 mm, the horizontal load peaked at 22.14 kN. At this stage, the wall maintained overall integrity without any outward bulging tendency. Mortar joints in the wall’s mid-section gradually developed into stepped cracks, while stones in the lower-middle section of the wall’s sides fractured. When the wall displacement reached 14 mm, the wall failed, and the load dropped to 60% of the peak value. The cracks are shown in Figure 12a, and the evolution of the maximum principal strain on the surface is shown in Figure 12b. The range of principal strain was −0.00101 to 0.00268.

Curved joint specimen: When displacement reached 5 mm, the wall exhibited noticeable misalignment, and the joints between stones gradually widened under horizontal forces, with a faster widening rate than the other three specimens. When wall displacement reached 5.5 mm, the horizontal load peaked at 12.09 kN. At 7 mm displacement, the load decreased to 3.02 kN, with a large through-crack forming in the wall’s center, ultimately leading to wall failure. Reasons for accelerated wall failure are as follows: Uneven stone selection during masonry work led to more pronounced stone displacement, accelerating mortar joint separation. Each masonry layer could only achieve approximate curvature similarity, resulting in weak overall integrity and increased susceptibility to crushing. The failure crack pattern is shown in Figure 13a, while the evolution of the maximum principal strain on the surface is depicted in Figure 13b. The principal strain range was −0.0009 to 0.00545.

During this stage, cracks gradually widen as residual deformation continues to accumulate, resulting in a decline in load-bearing capacity and ultimately leading to failure. The dominant failure mechanism involves the instability of critical load-bearing elements, such as the sliding or rotation of internal stones, which disrupts primary load transfer pathways. This causes the wall to lose its vertical load-bearing capacity, resulting in overall overturning or fragmentation. Among key influencing factors, ultimate failure is often triggered by the slippage or rotation of rubble stones that provide critical restraint. The failure of the restraint system primarily manifests as the pulling out, breaking, or shearing of wooden ties, signifying the loss of overall restraint and accelerating the collapse. However, the ductility inherent in wooden tie materials can provide buffering for load redistribution, delaying complete instability. Openings, as inherent weak planes, often cause failure to manifest as the overall overturning of walls on one side or above the opening. The curved masonry technique facilitates the formation of an overall multi-hinged arch mechanism during the failure stage, enabling progressive collapse and increasing the visibility of failure precursors. Additionally, potential energy within vertical loads partially converts to kinetic energy. Timber reinforcement constraints dissipate some energy, moderating the collapse speed and slightly controlling the extent of failure. Overall, timber reinforcement primarily functions not to prevent microcracking but to significantly prolong and intensify macrocracking. By providing tensile connection and increased friction, it enables “cracking without disintegration” and delays ultimate instability, serving as the primary source of toughness. The curved masonry technique enhances load-bearing capacity and stability by optimizing force flow and promoting the formation of internal arch effects, thereby improving the efficiency of post-damage force chain reconfiguration. In contrast, opening weakening exerts detrimental effects throughout all stages, accelerating damage concentration, shortening the macro-cracking phase, and leading to more abrupt and patterned failure. It represents a clear weak link.

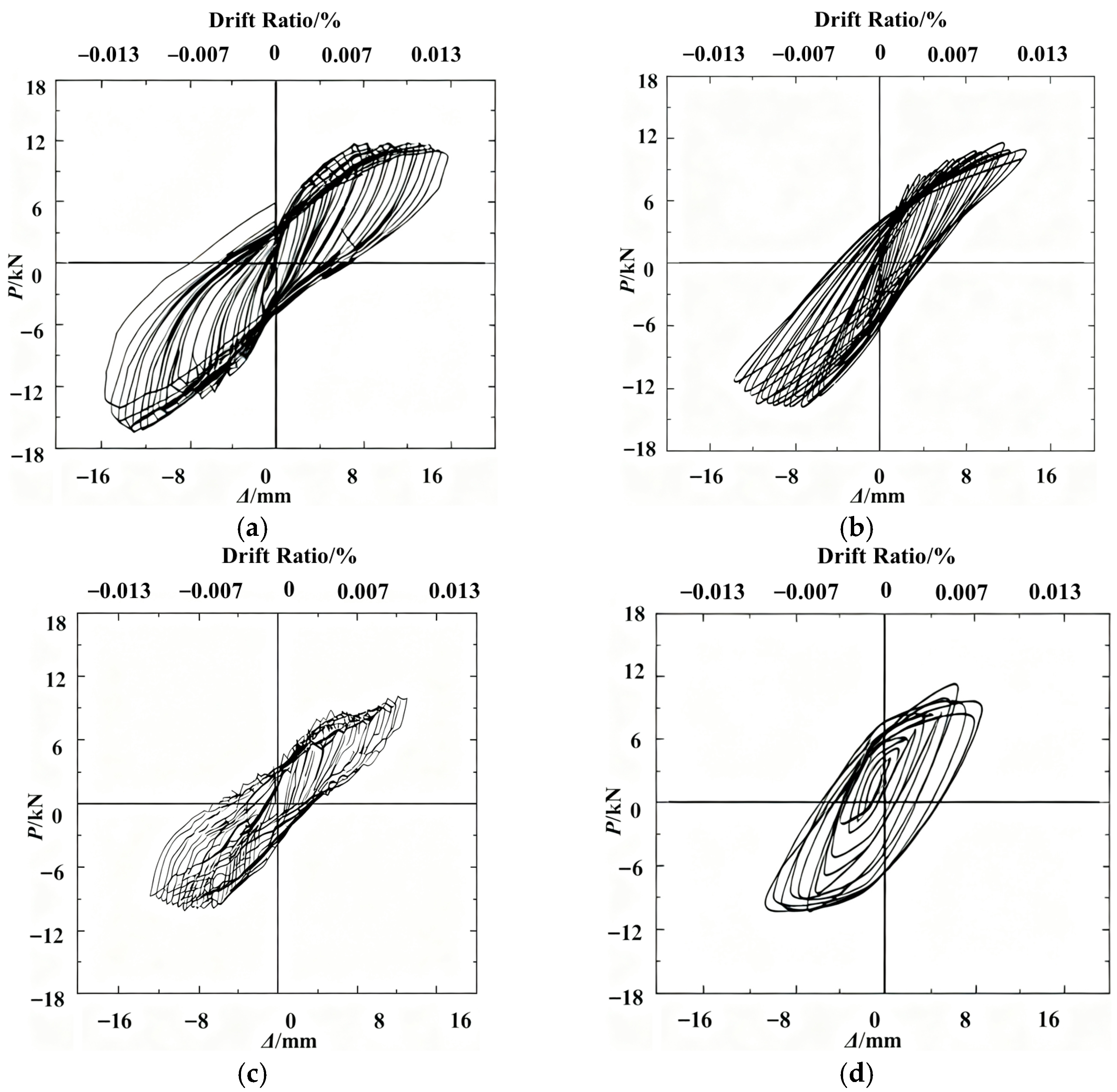
3.4. Hysteresis Curves

The hysteresis curves for each wall type are shown in Figure 14. As shown in Figure 14a, during the initial loading phase, the hysteresis curves of the standard specimens largely overlap, exhibiting small hysteresis loop areas with a typical spindle shape. After displacement increases to 2 mm, the hysteresis loops tend toward parallel spindle shapes. When displacement reaches 4 mm, the hysteresis curves remain spindle-shaped without significant pinching, indicating stable energy dissipation in the walls. However, the curves exhibit asymmetry in the first and third quadrants, primarily due to uneven material distribution and variations in stiffness within the walls. Concurrently, material asymmetry and inconsistent crack development lead to differing forward and reverse responses. Additionally, the curves fail to return to zero after unloading, primarily due to plastic deformation in the compression zone and stone block slippage resulting from cohesive failure in the tension zone.

Comparing the hysteresis loops of each wall reveals that the opening specimen (Figure 14b) and the standard specimen (Figure 14a) exhibit broadly similar hysteresis loops. However, the opening specimen’s hysteresis loop shifts to the right. This shift primarily results from the formation of a distinct slip plane on the left wall of the opening specimen, where the wall experiences tension on the left side and compression on the right. The entire fence tends to tilt to the right, resulting in irreversible plastic deformation. After unloading, the specimen cannot return to its initial position, causing the starting point of subsequent cycles to shift gradually to the right. Simultaneously, cracks in the opening specimen failed to close fully during unloading. Residual cracks increased the specimen’s effective length, requiring greater displacement to achieve the same load in subsequent loading cycles. The timber-reinforced specimen (Figure 14c) exhibited a relatively fuller, spindle-shaped profile compared to the standard specimen, indicating that timber reinforcement enhances the wall’s energy dissipation capacity. The hysteresis curve of the timber-reinforced specimen also exhibits asymmetry, primarily due to vertical cracks forming between the two layers of timber reinforcement. This causes bond failure between the stone and yellow clay in the tension zone, leading to relative slip between stones during reverse loading. The bonding at wood-to-stone interfaces relies on standard friction, physical adsorption, and mechanical interlocking. Its mechanical behavior exhibits significant nonlinearity and displacement-related characteristics due to the absence of chemical cementation, fundamentally differing from stone-to-concrete interfaces that form integral chemical bonds through cement hydration products. The corresponding failure modes are also distinctly different: the latter often manifests as brittle delamination of the cementitious layer or brittle fracture of the stone itself, whereas the timber-to-stone interface exhibits typical progressive interlayer shear failure. This progression begins with initial elastic slip, progresses to friction decay due to the shear softening of the natural yellow clay fill, and ultimately culminates in directional slip and the extraction of the timber reinforcement. This forms a friction-dissipative process accompanied by continuous energy dissipation. The hysteresis curve of the curved joint specimen (Figure 14d) is more pronounced than that of the standard group specimens, indicating that curved joints significantly enhance the wall’s energy dissipation capacity. Curved joints enhance the plastic deformation capacity of the entire wall structure, resulting in excellent seismic performance. The non-smooth hysteresis curve of curved masonry joint specimens fundamentally stems from the inherent instability of their geometric and physical properties. Compared to walls with regular joints, the non-uniform contact caused by curved joints leads to highly concentrated stress transfer and variable paths. Under cyclic loading, this readily induces intermittent sliding and rotation between masonry units, resulting in abrupt changes in stress response. Simultaneously, the weak cohesion and susceptibility to damage of rammed earth jointing material cause continuous degradation of interface performance under cyclic shear, further amplifying response dispersion. Compared to conventional walls with better integrity, reinforced walls featuring ductile energy dissipation mechanisms with wood reinforcement, or walls with openings possessing relatively defined force flow paths, curved masonry walls lack effective internal force redistribution capabilities. Damage concentrates in a few vulnerable joint zones, manifesting as sudden localized crushing or sliding instability. This results in hysteresis curves exhibiting pronounced pinching effects, abrupt stiffness changes, and irregular degradation, leading to insufficient overall energy dissipation capacity and deformation stability.

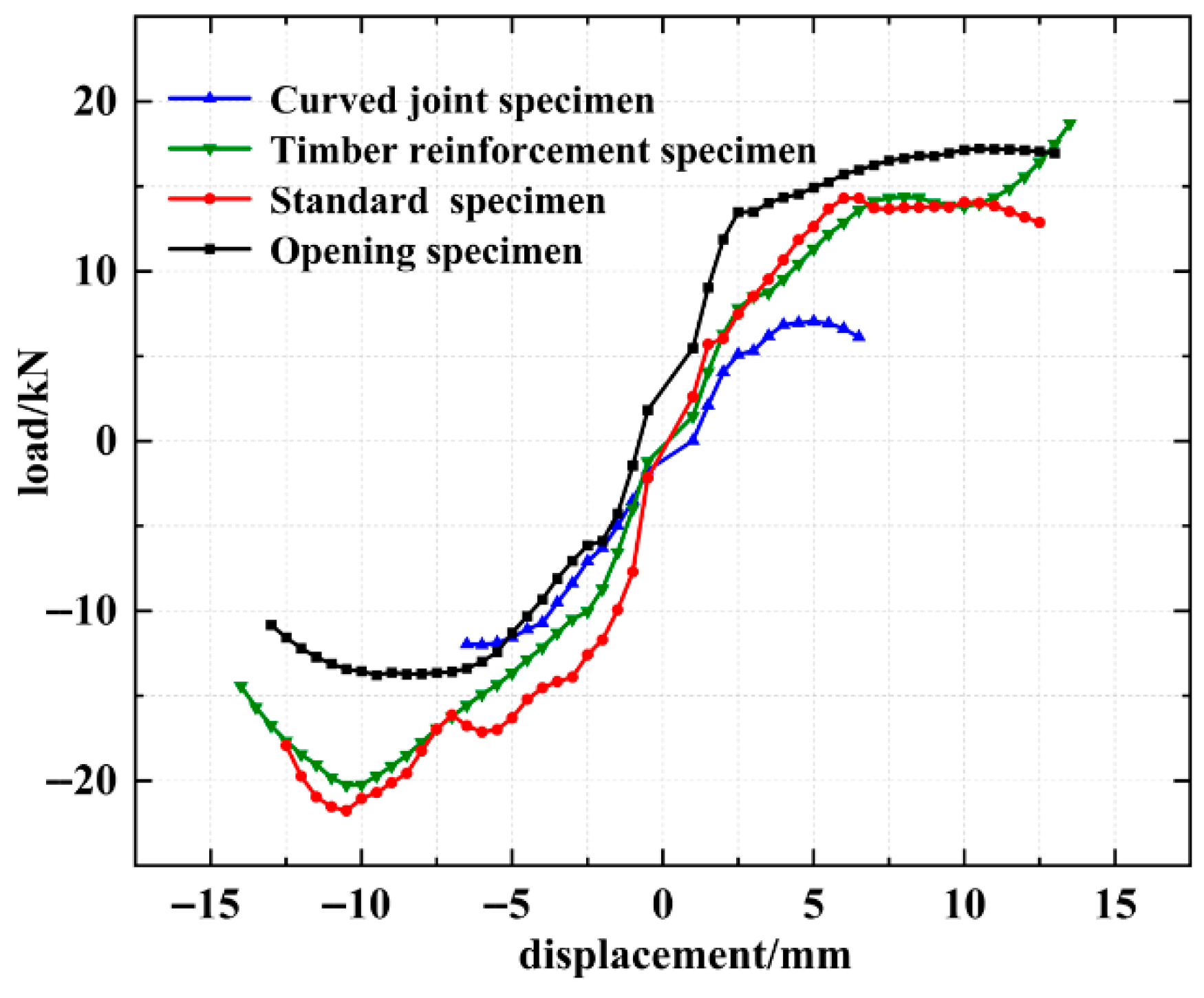
3.5. Skeleton Curves

The skeleton curves for each wall are shown in Figure 15. Before cracking, the walls are in the elastic stage, with skeleton curves that are essentially straight but asymmetrical, representing a result of inconsistent lateral friction forces on either side of the wall. The opening specimen exhibits lower initial stiffness, while the timber-reinforced specimen and the curved joint specimen demonstrate roughly equivalent initial stiffness. After cracking, the walls enter the elastic–plastic stage, where the skeleton curves exhibit significant bending, yet the load-bearing capacity of the walls still increases. As displacement increases, cracks continue to develop, and the walls enter the horizontal yielding stage, indicating that the walls possess a specific deformation resistance. At this stage, the differences between the walls become apparent, primarily due to the distribution of yellow clay in the wall stone and differences in construction methods. Upon reaching the cracking load, the curve exhibits fluctuations due to stress redistribution caused by mortar joints and stone cracks, resulting in a temporary increase in shear resistance. After reaching the ultimate load, the wall’s load-bearing capacity gradually decreases with increasing displacement, ultimately leading to failure.

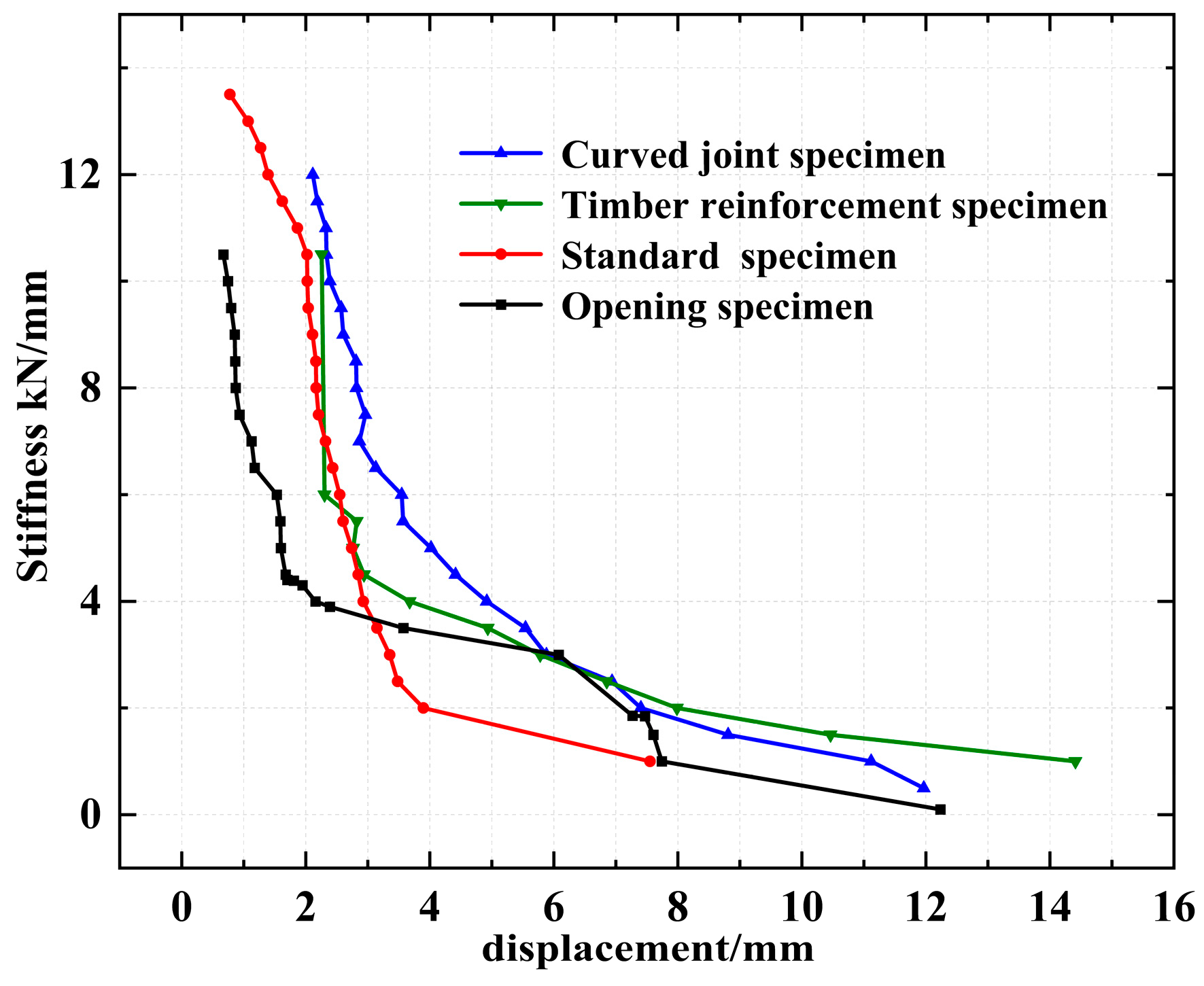
3.6. Stiffness Deterioration Curves

The stiffness deterioration curves for each wall are shown in Figure 16. Before cracking, stiffness degradation primarily resulted from the development of microcracks within the wall and localized plastic deformation, leading to a decrease in the wall’s shear modulus. After cracking, stiffness declined significantly, primarily due to the continuous development of diagonal cracks, reduced cohesion of the yellow clay, and diminished overall wall integrity. As shown in Figure 16, the opening specimen exhibits lower initial stiffness and experiences a greater reduction in wall stiffness compared to the standard specimen after reaching the cracking load. Wall stiffness decreases again after reaching the cracking load. The initial stiffness of the standard specimen, timber-reinforced specimen, and curved-joint specimen is nearly identical. After reaching the cracking load, the rate of stiffness change for the timber-reinforced and curved-joint specimens is relatively gradual. However, the timber-reinforced specimen exhibits a gradual decrease in stiffness after reaching the ultimate load, eventually stabilizing. The curved joint specimen exhibited a rapid rate of stiffness change before reaching the cracking load. This was attributed to the inherent gaps within the wall structure, which accelerated gap development under horizontal loading, leading to a faster change in wall stiffness.

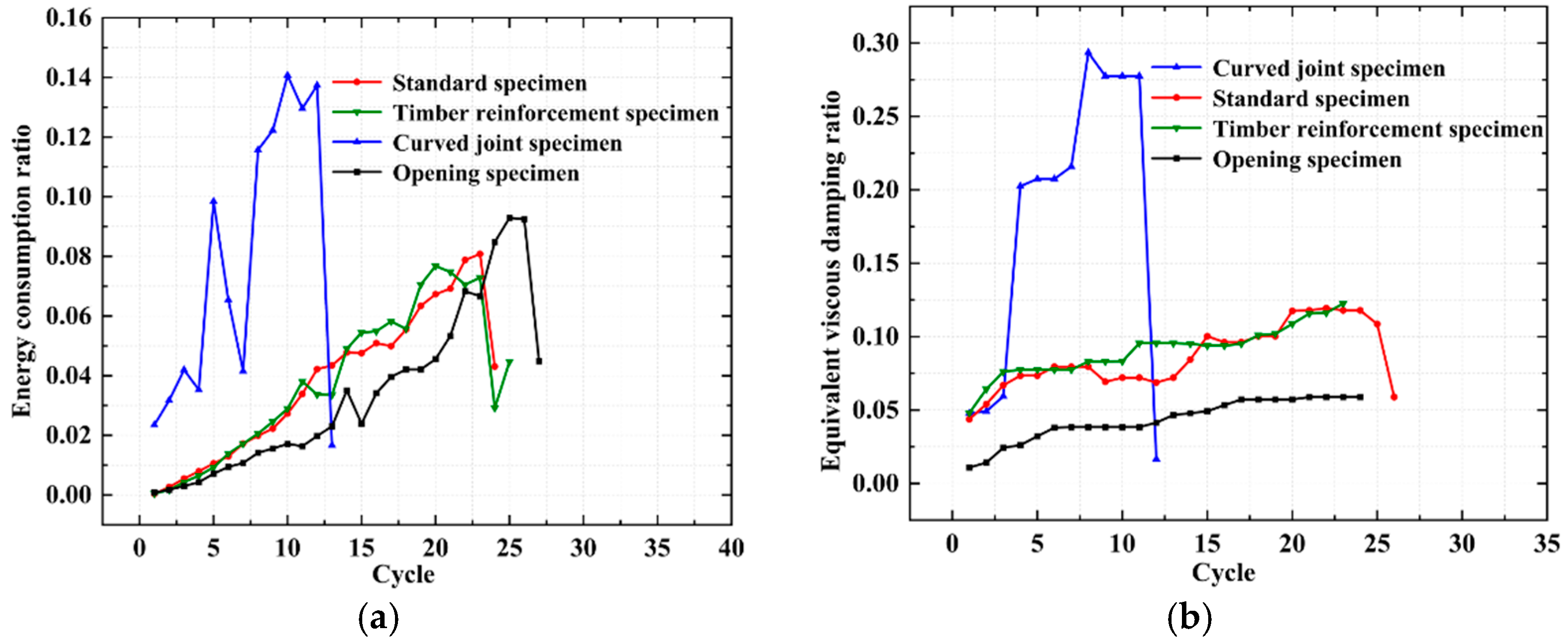
3.7. Energy Dissipation Capacity

The energy dissipation ratio versus equivalent viscous coefficient damping ratio curve for masonry is shown in Figure 17. The figure indicates that during the initial loading phase, the energy dissipation ratios of standard specimens, timber reinforcement specimens, and curved joint specimens are roughly consistent, exhibiting a linear increase with an increasing number of cycles. Upon reaching the cracking load, the three specimen groups diverged: the opening specimen first attained its peak, indicating it reached maximum energy dissipation earliest under identical cycles, thus exhibiting the weakest energy dissipation capacity. The standard specimen peaked next, while the timber-reinforced specimen peaked last, confirming its strongest energy dissipation capacity among the three. Notably, before reaching its peak, the timber reinforcement specimen exhibited weaker energy dissipation capacity than the other two specimens. However, its delayed peak attainment indirectly indicates superior ductility and greater overall deformation capacity. The curved mortar joint specimen clearly exhibits superior energy dissipation capacity compared to the timber reinforcement specimen. Its maximum energy dissipation per cycle reaches 1.5 times that of the standard specimen. However, fluctuations in its energy dissipation curve indicate significant crack development within the specimen, resulting in the redistribution of internal forces within the wall. Subsequently, energy dissipation capacity recovers before abruptly declining due to further crack propagation, resulting in sudden wall failure.

4. Shear Capacity of Raw Rammed Earth and Rubble Masonry Wall

Shear capacity serves as the foundation and a crucial component of seismic performance, representing the maximum shear force a wall can withstand before it fails due to shear. Key factors influencing the shear capacity of the rammed earth and rubble masonry walls include masonry shear strength, construction methods, vertical normal pressure, and construction quality. Calculating the shear bearing capacity of the rammed earth and rubble masonry walls necessitates a comprehensive consideration of various structural factors. This includes accounting for area reduction at openings, friction between timber reinforcement and stone in timber-reinforced walls, and the impact of curved joint shapes on shear stress distribution within the shear plane. Based on the above analysis, the shear bearing capacity formula for Tibetan-style rammed earth and rubble masonry walls is derived from the “Code for design of masonry structures” (GB50003-2011) [21] and the “General code for masonry structures” (GB55007-2021) [22], incorporating the bond strength and friction effects under vertical loads. It references Shi Yanghang’s modified shear strength formula for stone masonry and Huang Liang’s theory [23,24], which introduces geometric shape coefficients to correct the curved joint shear capacity [14,25,26]. Calculations employ the superposition method, as shown in Equation 1:

V = k·(f_v + αµ₁δ₀)·A·γ_αη + μ₂f_t,wA_wn

(1)

In the formula, V represents the shear bearing capacity of the rammed earth and rubble masonry wall; k denotes the curved joint correction factor, which is taken as 1.2 for a gentle curve (curvature radius R ≥ 3t, where t is the wall thickness), and k = 1 when no curved masonry exists; f_v represents the design shear strength of masonry, directly related to the strength grade of yellow clay, in this experiment, the strength grade of yellow clay is comparable to that of M2.5 mortar, set at f_v = 0.08; α denotes the friction correction factor, typically taken as 0.64; μ₁ is the friction coefficient between rubble and yellow clay, typically 0.6~0.7 for rubble masonry; δ₀ is the vertical compressive stress (MPa), which must satisfy δ₀ ≤ 0.8f, where f is the design compressive strength of the masonry; and A represents the horizontal cross-sectional area of the wall (m²), A = b × l, where b is the wall thickness and l is the effective length. For specimens with openings, the net cross-sectional area of the wall must be calculated. For specimens with curved joints, the projected cross-sectional area must be calculated: A_net = A∙cosθ, where θ is the angle between the joint and the horizontal plane; γ_α is the correction factor for construction quality, typically 0.8 to 1; η is the opening reduction factor, set to 1.0 if the opening area is less than 15%. For areas exceeding 15%, the value is reduced by 0.1 for every additional 10%; μ₂ is the friction coefficient between the wooden reinforcement and the wall, generally 0.4 to 0.6; f_t,w is the design value of wood tensile strength along grain, determined according to the “Code for Design of Timber Structures” (GB50005-2017) [27]; A_w is the cross-sectional area of a single timber reinforcement; n is the number of timber reinforcements contributing to shear resistance.

The shear bearing capacities of each specimen calculated using Equation (1) are shown in

Table 2. Shear bearing capacity of rammed earth and rubble masonry wall.

Specimen Type	A (mm2)	δ0 (MPa)	Fcr (kN)	Fu (kN)	V (kN)
Standard specimen	32,000	0.59375	13.3324	21.27353	7.88480
Opening specimen	23,000	0.59375	10.14874	18.18453	5.10048
Curved joint specimen	32,000	0.59375	10.8398	12.99544	9.31801
Timber reinforcement specimen	32,000	0.59375	15.6134	22.14756	7.98492

Note: The adjustment factor γ_α for construction quality is set to 0.8; the friction coefficient μ₁ is set to 0.6; the opening reduction factor η is set to 0.9; and the friction coefficient μ₂ between wooden reinforcement and masonry is set to 0.5. F_cr represents the measured cracking load value; F_u represents the measured ultimate load value.

. The key mechanical indicators for all four specimens are shown in

Table 3. Key mechanical indicators for all four specimens.

Specimen Type	Peak Displacements (mm)	Peak Loads (kN)	Stiffness Values (kN/mm)	Energy-Dissipation Metrics
Standard specimen	8	21.66	13.5	0.119
Opening specimen	11	18.18	10.5	0.059
Curved joint specimen	7	12.09	12	0.293
Timber reinforcement specimen	14	22.14	10.5	0.123

.

Table 2 and Table 3 indicate that the shear bearing capacity calculated using the formula in this paper is lower than the experimental cracking load value, showing relatively good agreement with the measured values. This validates the correctness and conservative nature of the formula. Table 1 results indicate that the shear bearing capacity of the opening specimens is 35% lower than that of the standard specimens, demonstrating a significant weakening effect. The shear bearing capacity of the timber-reinforced specimens increased by only 1.2% compared to the standard specimens, showing limited improvement. In contrast, the curved mortar joint specimens exhibited a 19% increase in shear bearing capacity relative to the standard specimens, indicating a marked enhancement.

5. Discussions

5.1. Analysis of Factors Affecting Testing

This study reveals the general mechanical patterns of rammed earth rubble walls during their three-stage failure evolution, while also highlighting their pronounced discrete characteristics, which are influenced by material and process variability. Yellow clay binders exhibit fluctuations in cohesion and internal friction angle spanning tens of percentage points due to variations in soil composition and moisture content. These variations directly influence the threshold for microcrack initiation, potentially blurring the boundaries between failure stages. The random distribution of rubble stones in terms of strength and geometric shape also exerts a significant impact. Premature crushing of weak stones or slippage of specific-shaped blocks may alter force chain reconfiguration paths and overall stability. During construction, the subjective nature of joint filling and block placement introduces uncontrollable weak interfaces, leading to crack development that deviates from theoretical trajectories.

Furthermore, both point-sensor monitoring and surface visual observation suffer from locality and lag, making it challenging to fully capture the continuous evolution of internal damage and introducing uncertainty in phase transition judgments. These factors collectively cause dispersed responses in specimens, where load–displacement curves should be interpreted as statistical trends, with stages representing continuous transition processes. The strengthening effects of measures like wooden reinforcement and curved masonry techniques also vary with actual craftsmanship quality, with their contributions becoming more pronounced in poorly constructed masonry. Therefore, future research requires repeatability tests and statistical analyses to quantify the variation range of key mechanical parameters, providing a basis for structural reliability assessment.

5.2. Research Outlook

In the mechanical study of rammed earth rubble walls, two core challenges stand out: first, the inherent uncertainty in material and interface behavior, such as the dispersion of yellow clay binder strength, the random distribution of irregular stone geometry, and the complex mechanical response at their contact interfaces; second, the strong nonlinearity of structural response and the discrete nature of failure pathways, manifested as friction-induced slip between stones, the initiation and propagation of discontinuous cracks, and ultimately, global collapse triggered by the instability of key blocks. Traditional homogenized finite element models and macroscopic experimental methods often struggle to accurately analyze the evolution of this “force chain network,” which is dominated by micro-scale heterogeneity, the accumulation of local damage, and the catastrophic failure process. This not only leads to significant discrepancies between numerical predictions and experimental results but also hinders the effective revelation of intrinsic mechanisms governing the progression from micro-crack development to macro-scale instability. Consequently, developing novel analytical methods that can simultaneously accommodate material randomness, geometric irregularities, and the strong nonlinearity of failure processes has become an imperative requirement for deepening the understanding of such structures and achieving precise performance evaluation and reliable control. Specifically, traditional methods struggle to accurately characterize the evolution of the “arch effect”—dominated by the interlocking of irregular block geometries—during wall damage progression, as well as the nonlinear influence of discrete constraint elements, such as wooden ribs, on overall mechanical behavior before and after failure. To overcome this limitation, this study proposes that integrating advanced data-driven modeling with physics-informed fusion represents a viable pathway to deepen understanding of such structural mechanics. In recent years, the hierarchical deep learning neural network framework proposed by Zhang et al. [28] has provided new insights for computational mechanics. By deeply integrating deep neural networks with the finite element method, this framework enables adaptive analysis—simultaneously optimizing network parameters and computational node spatial locations during training—significantly enhancing solution accuracy. This capability is particularly suited for problems involving local stress concentrations and complex damage pathways, such as those in rammed earth and rubble masonry walls, offering the potential for more refined simulation of heterogeneous, nonlinear processes from microcrack initiation to macrocrack propagation. Concurrently, the physics-assisted deep learning framework developed by Xu et al. offers a powerful tool for reconstructing probability density functions in structural random dynamic response analysis [29]. This method demonstrates that probabilistic models incorporating material and geometric randomness can be established using deep learning and experimental data. Such models enable the quantitative analysis of the statistical distribution characteristics of the bearing capacity, deformation capability, and failure modes of earth-retaining walls, providing a more scientific basis for reliability assessment.

6. Conclusions

Through four sets of quasi-static tests on rammed earth and rubble masonry walls, this study analyzed the effects of different construction details, such as opening weakening, timber reinforcement, and curved mortar joints, on the walls’ seismic performance. It elucidated the failure modes and mechanisms of rammed earth rubble walls. Key conclusions are as follows:

(1)

The ultimate failure of rammed earth and rubble masonry walls occurs when cumulative damage reaches a critical threshold, leading to final instability failure. Wall failure progresses through three stages: microcrack initiation and propagation, macrocrack formation and local failure, and ultimate failure. However, as damage accumulates, a large through-crack forms in the wall’s midsection, ultimately causing the wall to collapse.

(2)

The placement of openings weakens the integrity and load-bearing capacity of rammed earth and rubble masonry walls, reducing their lateral stiffness. Stress concentration is easily induced around openings, particularly at corners, leading to the initiation and propagation of cracks, which results in low deformation resistance. The timber tie-in technique effectively enhances wall integrity and seismic performance, limiting out-of-plane deformation and preventing disintegration during earthquakes. Curved walls exhibit arching effects that improve structural stability. They convert horizontal seismic forces into pressure along the wall’s curved surface, improving overall stability and collapse resistance.

(3)

The calculated shear capacity of the opening specimen is 14% lower than that of the standard specimen, and its energy dissipation capacity is slightly lower than that of the standard specimen. As long as the opening area of the wall remains below the corresponding threshold, it will not significantly impact the seismic performance of the wall. The shear capacity of timber-reinforced specimens increased by no more than 5% compared to standard specimens. However, timber reinforcement enhances the wall’s integrity, significantly improving its ductility relative to standard specimens. Walls with curved mortar joints exhibit the most robust hysteresis curves, demonstrating the highest energy dissipation capacity and superior seismic performance. The shear capacity of curved mortar joint specimens increased by 19.8% compared to standard specimens. Correctly setting the curvature radius of curved mortar joints and ensuring high-quality construction can significantly enhance the seismic performance of Tibetan-style rammed earth and rubble masonry walls.

In summary, the traditional construction techniques of rammed earth and rubble masonry walls embody profound seismic wisdom, featuring distinct seismic mechanisms and demonstrable effectiveness. In post-disaster reconstruction and traditional building preservation, these conventional techniques should be understood scientifically and utilized appropriately. By integrating modern seismic technologies to enhance the ductility and energy dissipation mechanisms of rammed earth and rubble masonry structures, their overall seismic performance can be comprehensively improved. This transforms them from brittle structures into ones possessing deformation capacity and energy dissipation capabilities. “Seismic tolerance” is far more crucial than mere “seismic resistance.”