An Evolutionary Game-Based Governance Mechanism for Sustainable Medical and Elderly Care Building Retrofits in Urban Renewal

Abstract

The retrofit of vacant buildings into sustainable integrated medical and elderly care facilities represents an important pathway for promoting urban regeneration and addressing population aging challenges. However, conflicts of interest among key stakeholders frequently compromise the quality of retrofit and long-term operational sustainability. To address this issue, this study develops a tripartite evolutionary game model comprising investors, builders, and operators to examine the behavioral evolution and cooperative mechanisms of these stakeholders across the investment, construction, and operation phases. Simulations were conducted based on a real-world retrofit project in Lanzhou, China, and the results suggest that: (1) Policy preference or reputational incentives alone appear insufficient to maintain cooperation, whereas their integration with economic incentives can effectively enhance the stability of cooperation among the three parties. (2) Builders exhibit higher sensitivity to penalties than operators, underscoring the pivotal role of the construction phase in ensuring retrofit quality. (3) When investors shift their role from short-term compliance regulation to long-term governance, it is more conducive to promoting operators to provide high-quality services in the long run. This paper proposes several suggestions and countermeasures, to provide practical guidance for the multi-party collaborative governance and sustainable operation of integrated medical and elderly care retrofit projects in China under the background of urban renewal.

1. Introduction

Population aging and rising life expectancy are reshaping China’s demographic structure [1,2]. By the end of 2024, more than 300 million people in China were aged 60 or above, accounting for 22% of the total population. The elderly care sector comprised 5.077 million beds, 65.7% of which were medical and elderly care beds. Yet this still fell short of the 14th Five-Year Plan target by over 1.3 million beds [3]. The growing complexity of older adults’ health and care needs has exceeded the capacity of traditional elderly care facilities and spatial layouts, posing substantial challenges to the national elderly care service system [4,5]. Meanwhile, within the broader agenda of high-quality urban development, urban renewal places greater emphasis on the retrofitting and adaptive reuse of vacant buildings, and the Chinese government encourages enterprises to revitalize idle assets and expand the supply of elderly care services [6,7]. This has created favorable conditions for converting vacant buildings into integrated medical and elderly care facilities. Driven by both demographic pressures and policy support, repurposing vacant buildings into integrated medical and elderly care institutions not only helps alleviate the supply-demand mismatches in traditional elderly care but also enhances the sustainability and vitality of urban renewal initiatives [8].

However, age-friendly retrofit projects involve complex interactions among multiple stakeholders, including investors, builders, and operators [9]. These actors pursue distinct interests and exhibit heterogeneous behavioral motivations, often resulting in misaligned strategies, low cooperation efficiency, and even project stagnation [10]. In particular, retrofit-oriented integrated medical and elderly care projects have strong public welfare attributes, long investment payback periods, and substantial construction and operational risks. Coordinating the dynamic evolution of cooperation among investors, builders, and operators, and designing incentive and constraint mechanisms that guide stakeholders toward mutually beneficial strategies, are therefore core issues for project governance and sustainable development in this field.

Existing stakeholder and social network analyses help describe multi-stakeholder coordination in building retrofit and adaptive reuse [11,12,13,14,15], but their static nature makes it difficult to capture bounded rationality and dynamic strategic adjustments, limiting their ability to reflect complex challenges in quality, cost, and long-term performance [16]. Given the limitations of static analytical methods, evolutionary game models have been widely used to study urban renewal and elderly care service systems. By capturing bounded rationality, imitation, and dynamic strategy adjustment, they are well-suited to examine how stakeholder behavior evolves under different incentive and regulatory mechanisms [17,18,19,20,21,22].

Existing research reveals collaborative mechanisms among elderly care service providers, focusing primarily on post-operation service delivery, government regulation, and platform governance [23,24,25,26], with less attention paid to the construction and retrofit phases and market-driven regulatory mechanisms. Existing evolutionary game theory studies typically view regulators as external public institutions, rarely considering the regulatory powers that investors exercise over builders and operators while bearing life-cycle financial risks in retrofit projects. Furthermore, most existing studies are limited to new public–private partnership (PPP) projects or general construction quality management, thus neglecting the unique characteristics of integrated healthcare and elderly care retrofits, such as complex quality assessment standards and long-term service performance requirements.

This study employs evolutionary game theory to analyze the behavioral strategies and interactions of key stakeholders in integrated medical and elderly care retrofit projects across the investment, construction, and operation phases. It constructs a tripartite evolutionary game model for investors, builders, and operators that links decisions at each phase and examines how economic incentives, penalties, and quality evaluation parameters are transmitted across phases to shape the evolutionary trajectories of stakeholder behavior and the stability of different equilibrium states. Investors are conceptualized as market-oriented regulators and “value guardians” who combine fund provision, regulatory authority, and brand value concerns. On this basis, the study derives governance implications for designing effective reward–penalty portfolios, quality evaluation mechanisms, and benefit-sharing schemes to support high-quality cooperation in integrated medical and elderly care retrofit projects.

The remainder of this paper is organized as follows. Section 2 reviews the relevant literature and clarifies the research gaps. Section 3 develops the evolutionary game model for investors, builders, and operators. Section 4 analyzes the replicator dynamics, evolutionary stability, and strategic evolution. Section 5 presents sensitivity analyses of key parameters. Section 6 discusses practical implications, and Section 7 concludes the study.

2. Literature Review

2.1. Evolutionary Game Applications in Integrated Medical and Elderly Care Collaboration

Evolutionary game theory has been widely applied to analyze stakeholder interactions in integrated medical and elderly care systems. Existing studies mainly model strategic behaviors among governments, medical and elderly care service providers, platforms, residents, and data-sharing institutions, and examine how reputation mechanisms, differentiated subsidies, credit constraints, and dynamic reward–penalty schemes affect cooperation and service quality [23,24,25,26,27,28]. These studies show that evolutionary game models can effectively capture bounded rationality, incentive conflicts, and dynamic strategy adjustments in multi-actor elderly care governance, including community services, “Internet + elderly care” platforms, and medical data sharing [24,25,26]. However, this literature largely concentrates on the operation phase and on regulatory relationships between governments and service providers or platforms. It rarely addresses lifecycle interactions among investors, builders, and operators in age-friendly retrofit projects, nor does it incorporate building retrofit decisions and integrated quality evaluation mechanisms into the payoff structure.

2.2. Governance, Incentive Mechanisms, and Opportunistic Behavior in the Transformation of Integrated Medical and Elderly Care

Additionally, many studies have examined governance and incentive mechanisms that shape stakeholder behavior in elderly care services. Zhang et al. [29] developed a tripartite evolutionary game among government, the private sector, and residents, showing that resource coordination and effective supervision promote cooperative stability. Wang et al. [30] analyzed interactions among government agencies, private elderly care institutions, and the public, and compared static and dynamic reward–penalty mechanisms, finding that dynamic regulatory schemes are more conducive to desirable stable states. But both of them mainly focus on the operation phase and on relationships between governments and service providers.

More recent research has turned to the retrofit and build stages of medical and elderly care facilities. Fu et al. [31] modeled the evolution of speculative behavior under different penalty intensities and underscored the importance of robust collaboration mechanisms to curb opportunism. Under conditions of information asymmetry, Yue et al. [32] explored the root causes of low quality in PPP-based integrated care projects, revealing how hidden actions and weak oversight can distort contractual performance. Extending this line of inquiry to integrated urban renewal, Zhang et al. [33] linked home-based medical services, age-friendly retrofits, and urban renewal demands, and proposed evolutionarily stable strategies and incentive measures through case simulations. However, they typically focus on multi-stakeholder interactions at a single stage of a project, and these projects are mostly government-led and regulated, either newly built or redeveloped existing residential areas. They rarely involve the retrofit of vacant buildings.

2.3. Limitations of Existing Research and Contributions of This Study

Overall, existing research provides valuable insights into governance, incentives, and opportunism in integrated medical and elderly care services, but remains fragmented. Most studies examine government-led regulation at specific stages, especially the operation phase, focusing on service provision, quality supervision, and PPP governance, while paying less attention to how stakeholder behavior evolves during building retrofit phases, even though these phases shape project quality and long-term service performance. In addition, evolutionary game models primarily analyze government–social capital interactions and rarely consider investors as market coordinators, nor do they capture the continuous lifecycle interactions among investors, builders, and operators in integrated medical and elderly care retrofit projects [34]. These limitations provide the context and rationale for the present study.

Against this backdrop, and unlike previous evolutionary game studies that center on government–enterprise regulation at single project stages, the main contents of this study are as follows. First, this study extends evolutionary game analysis to the lifecycle context of converting vacant buildings into integrated medical and elderly care facilities, thereby capturing how early investment and construction decisions influence subsequent cooperation dynamics. Second, it constructs a tripartite evolutionary game model among investors, builders, and operators along the investment–construction–operation chain, rather than centering on government–market or operator-focused interactions. Third, it introduces a market-based regulatory perspective in which investors act as “value guardians” and examines how economic incentives, penalty mechanisms, and quality assessments jointly affect collaborative governance, thereby complementing predominantly government-led regulation frameworks and aligning with the emerging trend of market-driven retrofit governance.

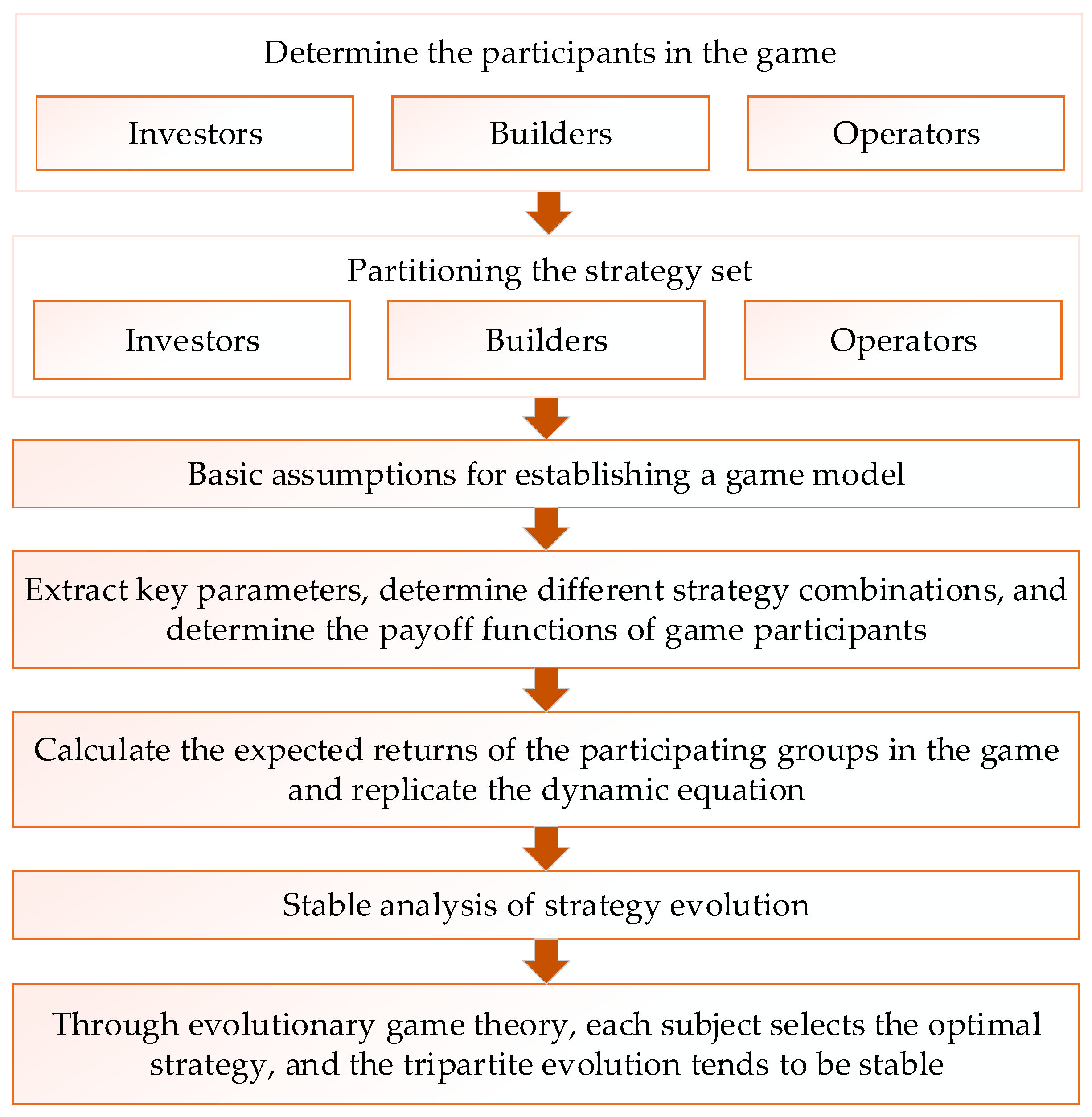
3. Methodology: Evolutionary Game Model for Building Retrofit Governance

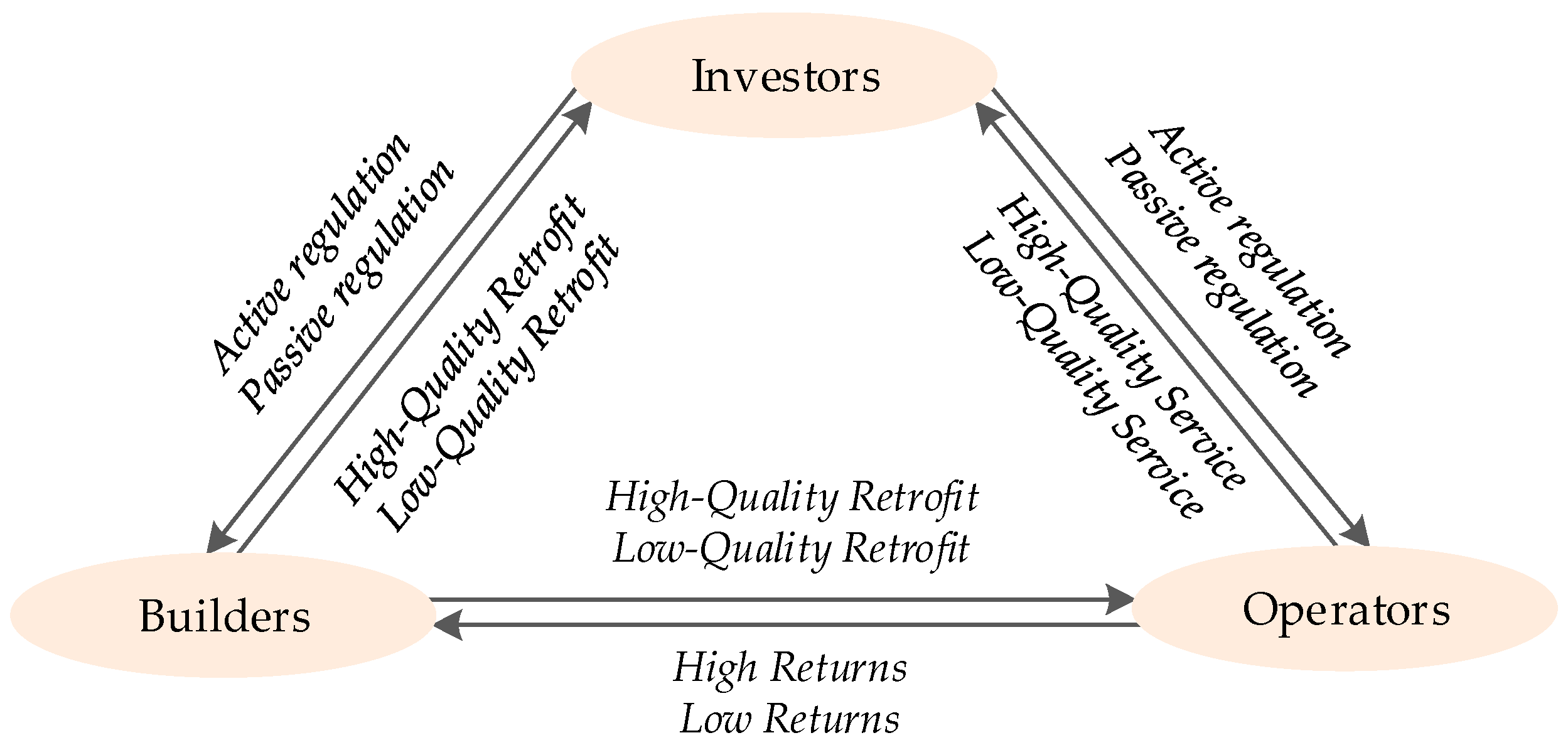
3.1. Determining the Game Players and Methodology

Integrated medical and elderly care retrofit projects involve multiple stakeholders, including government regulators, investors, builders, operators, and end-users. Drawing on the stakeholder salience framework of Mitchell et al. [35], this study evaluates stakeholder importance in terms of power, legitimacy, and urgency. Existing research shows that investors, builders, and operators typically dominate key project decisions and bear primary risks, while government agencies shape the institutional environment and end-users influence service reputation and demand [13,23,36,37,38].

Table 1. Stakeholder saliency analysis.

Stakeholders	Power	Legitimacy	Urgency
Investors	High	High	High
Builders	High	High	High
Operators	High	High	High
Governments	High	High	Low
End users	Low	High	High

summarizes the saliency analysis of the stakeholders in integrated medical and elderly care age-friendly retrofit project. Investors control capital investment and profit distribution, builders determine retrofit quality and engineering risk, and the operators are responsible for long-term service quality. Therefore, these three stakeholders have strong power, legitimacy, and urgency concerning project success and are identified as the core actors in the evolutionary game model.

In contrast, although government regulators and end-users are important, they play different roles in this model. Governments’ influence is indirectly incorporated into the model via policy preferences, while end-users’ influence is reflected through reputational rewards and the quality evaluation coefficient Δ. To ensure model tractability and focus on key behavioral interactions in the investment-construction-operation chain, investors, builders, and operators are selected as the three primary actors. The tripartite evolutionary game analysis process is shown in Figure 1.

3.2. Model Assumptions

Assumption 1.

The evolutionary game model includes three stakeholders: investors, builders, and operators. All parties possess bounded rationality and are capable of independent decision-making. Moreover, they continuously learn and adapt to environmental changes during the project retrofit process, adjusting strategies to maximize their own interests [18].

Assumption 2.

Investors act both as capital providers and regulatory agents and choose between Active regulation and Passive regulation. “Active regulation” involves monitoring and providing incentives throughout the lifecycle, incurring a basic management cost C₁₁ and an additional regulatory cost C₁₂ [20]. “Passive regulation” entails bearing only the basic management cost C₁₁, without conducting any additional oversight. When the investors adopt active regulation, and both the builders and the operators choose high-quality strategies, the investors’ payoff includes economic benefits R₁, brand benefits S, and policy-derived benefits P associated with policy preference θ. Although P, Q, and S are all linked to Q in this study, they affect stakeholder payoffs through distinct parameters, such as the policy preference θ and the number of successfully completed projects n. If investors choose Passive regulation and quality problems arise, they will lose these benefits and incur a responsibility cost K. The intensity of the economic incentives, reputational incentives, and penalties imposed by the investors on the builders and operators are denoted by β, γ and α, and the corresponding fines imposed on the builders and operators are denoted as F₁ and F₂, respectively. This reflects the standard incentive and deterrence mechanisms used in agency-based models.

Assumption 3.

Builders are assumed to choose between two strategies: High-Quality Retrofit and Low-Quality Retrofit. High-Quality Retrofit incurs a basic cost C₂₁ and an additional cost C₂₂, and yields higher revenue R₂₂. Low-Quality Retrofit incurs only C₂₁, generating revenue R₂₁, but risks investor penalties. In practice, builders’ investments (e.g., customized accessibility features and embedded medical pipeline systems) involve significant asset specificity [30]. Once committed, these investments are difficult to redeploy or recover, creating substantial sunk-cost risk. Accordingly, builders may adopt high-quality retrofit when incentives or expected brand value enhancement are sufficient, but prefer low-quality retrofit when incremental costs and risks are high and short-term returns are limited. Under these assumptions, the builders’ expected payoffs are specified as follows. When the builders adopt High-Quality Retrofit: (1) he investors adopt Active regulation and the operators provide High-Quality Service, the builders’ expected payoff is given by −C₂₁ − C₂₂ + (1 + γ) (βR₂₂ + θQ), where β and γ jointly amplify the economic and reputational returns of the high-quality strategy. (2) If the investors adopt Active regulation but the operators provide Low-Quality Service, the builders’ expected payoff is affected by the quality evaluation coefficient δ, expressed as −C₂₁ − C₂₂ + δ(1 + β) R₂₂. When the builders choose Low-Quality Retrofit and are penalized by the investors, the expected payoff is −C₂₁ + R₂₁ − αF₁.

Assumption 4.

Operators, responsible for post-retrofit operation and service delivery, choose between High-Quality Service and Low-Quality Service. High-Quality Service incurs a basic cost C31 and an additional service cost C32, and generates revenue R₃₂. Low-Quality Service means incurring only C₃₁, yielding revenue R₃₁, but risks investor penalties. Operators may choose High-Quality Service due to their commitment to retrofit sustainability or in response to investors’ regulation and incentives; otherwise, they may prefer the lower-cost Low-Quality Service strategy. The builders’ dominant strategy directly affects the final retrofit quality and thus the operators’ subsequent operational costs. Consequently, operators’ strategic choices are also influenced by builders’ strategies. The demand matching coefficient μ captures service capacity and utilization under different retrofit outcomes, reflecting demand–supply matching considerations in service-oriented governance and sustainability research [39,40]. Under these assumptions, the operators’ expected payoffs are specified as follows. When the operators provide High-Quality Service: (1) If the investors adopt Active regulation and the builders perform High-Quality Retrofit, the operators’ expected payoff is given by −C₃₁ − C₃₂ + (1 + γ) (βR₃₂ + θQ). (2) If the investors adopt Active regulation but the builders perform Low-Quality Retrofit, the operators’ expected payoff is affected by the demand matching coefficient μ, expressed as −C₃₁ − C₃₂ + μ(1 + β) R₃₂. When the operators choose Low-Quality Service, they are penalized by the investors in the payoff structure, and their expected payoff is −C₃₁ + R₃₁ − αF₂.

Assumption 5.

The proportion of investors choosing Active regulation is denoted by x, the proportion of builders choosing the High-Quality Retrofit strategy is denoted by y, and the proportion of operators choosing High-Quality Service is denoted by z, where x, y, z ϵ [0, 1]. The relationship between the stakeholders is shown in Figure 2.

Based on the assumptions above, the model parameters are described in

Table 2. Model parameters and value ranges.

Parameters	Descriptions	Range of Values
C11	Base cost under passive regulation	≥0
C12	Additional cost incurred under active regulation	≥0
C21	Base cost of implementing a low-quality retrofit	≥0
C22	Additional cost required for a high-quality retrofit	≥0
C31	Base cost of providing low-quality service	≥0
C32	Additional cost required for high-quality service	≥0
R1	Investors’ benefits when builders and operators adopt high-quality strategies	≥0
R21	Revenue obtained from a low-quality retrofit	≥0
R22	Revenue obtained from a high-quality retrofit	≥0
R31	Revenue obtained from low-quality service	≥0
R32	Revenue obtained from high-quality service	≥0
F1	Penalty imposed by the investors for low-quality retrofit	[35% × R22, 50% × R22]
F2	Penalty imposed by the investors for low-quality service	[40% × R32, 50% × R32]
K	Investors’ responsibility costs under passive regulation when project losses occur [39]	≥0
Q	Social and environmental benefits generated by the project	Fixed value
P	Policy benefits generated by policy preference, P = θQ	≥0
S	Accumulated brand benefits from the project [41]	≥0
α	Investors’ penalty intensity for low-quality behavior by builders and operators [40]	[0, 1]
β	The strength of economic incentives from investors for promoting high-quality practices by builders and operators [18]	[0, 1]
γ	The strength of reputational incentives from investors when builders and operators adopt high-quality behavior [42]	[0, 1]
θ	The investors’ policy preference [18]	[0, 1]
δ	Quality evaluation coefficient reflecting the effectiveness of the builders’ retrofit	[0.6, 1]
μ	Matching the coefficient between market demand and service supply	[0.6, 1]
I0	Total project investment	>0
R	Total economic benefits, R = 0.2 I0	>0
n	Number of successfully completed projects	[0, 20]

, and the detailed basis for these parameters can be found in Section 4.1.

3.3. Construction of the Payoff Matrix

Based on the above assumptions and parameter descriptions, the payoff matrix for the tripartite evolutionary game is constructed as shown in

Table 3. Payoff matrix of the tripartite evolutionary game.

Builders	Operators	Investors
		Active Regulation (x)	Passive Regulation (1 − x)
High-quality retrofit (y)	High-quality service (z)	−C11 − C12 + R1 + S + θQ	−C11 + R1 + S
		−C21 − C22 + (1 + γ)(βR22 + θQ)	−C21 − C22 + R22
		−C31 − C32 + (1 + γ)(βR32 + θQ)	−C31 − C32 + R32
	Low-quality service (1 − z)	−C11 − C12 + S	−C11 − K
		−C21 − C22 + δ(1 + β)R22	−C21 − C22 + ΔR22
		−C31 + R31 − αF2	−C31 + R31 − αF2
Low-quality retrofit (1 − y)	High-quality service (z)	−C11 − C12 + S	−C11 − K
		−C21 + R21 − αF1	−C21 + R21 − αF1
		−C31 − C32 + μ(1 + β)R32	−C31 − C32 + μR32
	Low-quality service (1 − z)	−C11 − C12	−C11 − K
		−C21 + R21 − αF1	−C21 + R21 − αF1
		−C31 + R31 − αF2	−C31 + R31 − αF2

.

4. Model Analysis and Theoretical Results

4.1. Equilibrium Points Solution

The expected payoffs for the investors adopting “active regulation” and “passive regulation” are denoted as I₁₁ and I₁₂, respectively, and the average expected payoff is denoted as I₁.

$$\begin{array}{c}{I}_{11}=yz(-C_{11}-C_{12}+R_1+S+\theta Q)+y(1-z)\left(-C_{11}-C_{12}+S\right)+(1-y)\mathrm{z}\left(-C_{11}-C_{12}+S\right)\\ +(1-y)(1-z)(-C_{11}-C_{12})\end{array}$$

(1)

$$I_{12}=yz(-C_{11}+R_1+S)+y(1-z)\left(-C_{11}-K\right)+(1-y)z\left(-C_{11}-K\right)+(1-y)(1-z)(-C_{11}-K)$$

(2)

$$I_1=x{I}_{11}+(1-x)I_{12}$$

(3)

The replicator dynamics equation for the investors is obtained from Equations (1)–(3):

$$f_1={\displaystyle \frac{dx}{dt}}=x(I_{11}-I_1)=x(1-x)[-C_{12}+K+S(y+z)+yz(\theta Q-2S-K)]$$

(4)

The expected payoffs for builders adopting “high-quality retrofit” and “low-quality retrofit” are denoted as B₂₁ and B₂₂, respectively, and the average expected payoff is denoted as B₂.

$$\begin{array}{c}{B}_{21}=xz[-C_{21}-C_{22}+(1+\gamma )\left(\beta R_{22}+\theta Q\right)]+x(1-z)[-C_{21}-C_{22}+\delta \left(1+\beta \right)R_{22}+0\cdot \theta Q]\\ +(1-x)z[-C_{21}-C_{22}+R_{22}]+(1-x)(1-z)[-C_{21}-C_{22}+\delta R_{22}]\end{array}$$

(5)

$$\begin{array}{c}{B}_{22}=xz[-C_{21}-C_{22}+R_{21}-\alpha F_1]+x(1-z)[-C_{21}+R_{21}-\alpha K]+(1-x)z[-C_{21}+R_{21}-\alpha K]\\ +(1-x)(1-z)[-C_{21}+R_{21}-\alpha K]\end{array}$$

(6)

$$B_2=y{B}_{21}+(1-y)B_{22}$$

(7)

Let:

$${\Delta }_B=-C_{22}+\left(1+\gamma \right)\left(\beta R_{22}+\theta Q\right)-R_{21}+\alpha F_1$$

$${\Delta }_B^{\prime }=-C_{22}+\delta \left(1+\beta \right)R_{22}-R_{21}+\alpha F_1$$

$${\Delta }_B^{\prime \prime }=-C_{22}+R_{22}-R_{21}+\alpha F_1$$

$${\Delta }_B^{\prime \prime \prime }=-C_{22}+\delta R_{22}-R_{21}+\alpha F_1$$

The replicator dynamics equation for the builders is obtained as follows:

$$f_2={\displaystyle \frac{dy}{dt}}=y(B_{21}-B_2)=y(1-y)[xz{\Delta }_B+x(1-z){\Delta }_B^{\prime }+(1-x)z{\Delta }_B^{\prime \prime }+(1-x)(1-z){\Delta }_B^{\prime \prime \prime }]$$

(8)

The expected payoffs for operators adopting “high-quality service” and “low-quality service” are denoted as O₂₁ and O₂₂, respectively, and the average expected payoff is denoted as O₃.

$$\begin{array}{c}{O}_{31}=xy[-C_{31}-C_{32}+(1+\gamma )\left(\beta R_{32}+\theta Q\right)]+x(1-y)[-C_{31}-C_{32}+\mu \left(1+\beta \right)R_{32}]\\ +(1-x)y[-C_{31}-C_{32}+R_{32}]+(1-x)(1-y)[-C_{31}-C_{32}+\mu R_{32}]\end{array}$$

(9)

$$\begin{array}{c}{O}_{32}=xy[-C_{31}+R_{31}-\alpha F_2+0\cdot \theta Q]+x(1-y)[-C_{31}+R_{31}-\alpha F_2]+(1-x)y[-C_{31}+R_{31}-\alpha F_2]\\ +(1-x)(1-y)[-C_{31}+R_{31}-\alpha F_2]\end{array}$$

(10)

$$O_3=z{O}_{31}+(1-z)O_{32}$$

(11)

Let:

$${\Delta }_O=-C_{32}+(1+\gamma )\left(\beta R_{32}+\theta Q\right)-R_{31}+\alpha F_2$$

$${\Delta }_O^{\prime }=-C_{32}+\mu \left(1+\beta \right)R_{32}-R_{31}+\alpha F_2$$

$${\Delta }_O^{\prime \prime }=-C_{32}+R_{32}-R_{31}+\alpha F_2$$

$${\Delta }_O^{\prime \prime \prime }=-C_{32}+\mu R_{32}-R_{31}+\alpha F_2$$

The replicator dynamics equation for the operators is as follows:

$$f_3={\displaystyle \frac{dz}{dt}}=z(O_{31}-O_3)=z(1-z)[xy{\Delta }_O+x(1-y){\Delta }_O^{\prime }+(1-x)y{\Delta }_O^{\prime \prime }+(1-x)(1-y){\Delta }_O^{\prime \prime \prime }]$$

(12)

Based on the analysis in Section 3.1, the system of replicator dynamic equations is formulated as Equation (13). Solving this system produces eight pure-strategy equilibrium points: E₁(1,1,1), E₂(1,1,0), E₃(1,0,1), E₄(1,0,0), E₅(0,1,1), E₆(0,1,0), E₇(0,0,1), and E₈(0,0,0). In addition, there may exist a mixed-strategy equilibrium point within the interval (0, 1), denoted as E₉(x^*, y^*, z^*).

$$\left\{\begin{array}{l}{f}_1=x(1-x)[-C_{12}+K+S(y+z)+yz(\theta Q-2S-K)]\\ f_2=y(1-y)[xz{\Delta }_B+x(1-z){\Delta }_B^{\prime }+(1-x)z{\Delta }_B^{\prime \prime }+(1-x)(1-z){\Delta }_B^{\prime \prime \prime }]\\ f_3=z(1-z)[xy{\Delta }_O+x(1-y){\Delta }_O^{\prime }+(1-x)y{\Delta }_O^{\prime \prime }+(1-x)(1-y){\Delta }_O^{\prime \prime \prime }]\end{array}\right.$$

(13)

4.2. Evolutionary Stability Strategy Analysis

According to the perspectives of Lyapunov [43], only pure-strategy Nash equilibria can be asymptotically stable. Therefore, the mixed-strategy equilibrium E₉ is not considered further. The asymptotic stability of the eight pure-strategy equilibrium points is verified by analyzing the eigenvalues of the system’s Jacobian matrix [44].

The Jacobian matrix J, derived from Equation (13), is given in Equation (14). Substituting each of the eight equilibrium points into J yields the corresponding eigenvalues, which are summarized in

Table 4. Characteristic values and stability conditions.

Equilibrium Points	Eigenvalues			Eigenvalue Sign	Stability
	λ1	λ2	λ3
E1(1,1,1)	C12 − θQ	−ΔB	−ΔO	−, −, −	ESS
E2(1,1,0)	C12 – S − K	${-\Delta }_{\mathrm{B}}^{\prime }$	ΔO	×, +, +	Saddle point/Unstable point
E3(1,0,1)	C12 − S − K	ΔB	${-\Delta }_{\mathrm{O}}^{\prime }$	×, +, +	Saddle point/Unstable point
E4(1,0,0)	C12 − K	${\Delta }_{\mathrm{B}}^{\prime }$	${\Delta }_{\mathrm{O}}^{\prime }$	×, −, −	ESS/Saddle point
E5(0,1,1)	−C12 + θQ	${-\Delta }_{\mathrm{B}}^{″}$	${-\Delta }_{\mathrm{O}}^{″}$	+, ×, ×	Saddle point/Unstable point
E6(0,1,0)	−C12 + S + K	$-{\Delta }_{\mathrm{B}}^{‴}$	${\Delta }_{\mathrm{O}}^{″}$	×, +, ×	Saddle point/Unstable point
E7(0,0,1)	−C12 + S + K	${\Delta }_{\mathrm{B}}^{″}$	$-{\Delta }_{\mathrm{O}}^{‴}$	×, ×, +	Saddle point/Unstable point
E8(0,0,0)	K − C12	${\Delta }_{\mathrm{B}}^{‴}$	${\Delta }_{\mathrm{O}}^{‴}$	×, −, −	ESS/Saddle point

Note: “×” means the eigenvalue’s sign is indeterminate and can be either positive or negative.

. A negative eigenvalue implies that such deviations reduce the relative payoff of the deviating strategy, causing the trajectory to converge back to the equilibrium, whereas a positive eigenvalue implies that deviations increase relative payoffs and drive the system away from the equilibrium. An equilibrium point is an evolutionarily stable strategy (ESS) if and only if all of its eigenvalues are negative. If all eigenvalues λ are positive, the equilibrium is unstable; if at least one eigenvalue is negative and at least one is positive, the equilibrium is a saddle point.

$$J={\displaystyle \frac{\partial (f_1,f_2,f_3)}{\partial (x,y,z)}}=\left[\begin{array}{ccc}{\displaystyle \frac{\partial f_1}{\partial x}}& {\displaystyle \frac{\partial f_1}{\partial y}}& {\displaystyle \frac{\partial f_1}{\partial z}}\\ {\displaystyle \frac{\partial f_2}{\partial x}}& {\displaystyle \frac{\partial f_2}{\partial y}}& {\displaystyle \frac{\partial f_2}{\partial z}}\\ {\displaystyle \frac{\partial f_3}{\partial x}}& {\displaystyle \frac{\partial f_3}{\partial y}}& {\displaystyle \frac{\partial f_3}{\partial z}}\end{array}\right]=\left[\begin{array}{ccc}{j}_{11}& j_{12}& j_{13}\\ j_{21}& j_{22}& j_{23}\\ j_{31}& j_{32}& j_{33}\end{array}\right]$$

(14)

$$\begin{array}{l}{j}_{11}=(1-2x)[-C_{12}+K+Sy+Sz+yz(\theta Q-2S-K)]\\ j_{12}=x(1-x)[S+z(\theta Q-2S-K)]\\ j_{13}=x(1-x)[S+y(\theta Q-2S-K)]\end{array}$$

$$\begin{array}{l}{j}_{21}=y(1-y)[z({\Delta }_B-{\Delta }_B^{\prime \prime })+(1-z)({\Delta }_B^{\prime }-{\Delta }_B^{\prime \prime \prime })]\\ j_{22}=(1-2y)[{\Delta }_{B}xz+{\Delta }_B^{\prime }x(1-z)+{\Delta }_B^{\prime \prime }(1-x)z+{\Delta }_B^{\prime \prime \prime }(1-x)(1-z)]\\ j_{23}=y(1-y)[x({\Delta }_B-{\Delta }_B^{\prime })+(1-x)({\Delta }_B^{\prime \prime }-{\Delta }_B^{\prime \prime \prime })]\end{array}$$

$$\begin{array}{l}{j}_{31}=z(1-z)[y({\Delta }_O-{\Delta }_O^{\prime \prime })+(1-y)({\Delta }_O^{\prime }-{\Delta }_O^{\prime \prime \prime })]\\ j_{32}=z(1-z)[x({\Delta }_O-{\Delta }_O^{\prime })+(1-x)({\Delta }_O^{\prime \prime }-{\Delta }_O^{\prime \prime \prime })]\\ j_{33}=(1-2z)[{\Delta }_{O}xy+{\Delta }_O^{\prime }x(1-y)+{\Delta }_O^{\prime \prime }(1-x)y+{\Delta }_O^{\prime \prime \prime }(1-x)(1-y)]\end{array}$$

Further analysis reveals that certain equilibrium points exhibit mutually exclusive stability conditions. These pairs include E₁(1,1,1) and E₅(0,1,1), E₂(1,1,0) and E₆(0,1,0), and E₃(1,0,1) and E₇(0,0,1), and the system can ultimately only converge to a stable strategy combination that is not mutually exclusive. Furthermore, equilibrium points E₂(1,1,0) and E₃(1,0,1) scenarios, which emphasize construction over operation and operation over construction, respectively, lack practical sustainability in the lifecycle management of integrated medical and elderly care projects. Points E₅(0,1,1), E₆(0,1,0), and E₇(0,0,1) depict cooperation scenarios in the absence of investors regulation, which contradicts the current policy direction that actively promotes integrated medical and elderly care in China, thus limiting their practical relevance. Therefore, this study does not delve deeply into the equilibrium points E₂, E₃, E₅, E₆, and E₇, focusing instead on E₁, E₄, and E₈.

E₁(1,1,1) represents the ideal cooperative state where investors actively regulate, builders implement high-quality retrofits, and operators provide high-quality services. This configuration corresponds to a Pareto-optimal outcome that maximizes the project’s combined social and economic value. At E₁(1,1,1), the eigenvalues of the Jacobian matrix are determined by the net regulatory payoff of investors and the incremental benefits of cooperation in the construction and operation stages. Specifically, the sign of the first eigenvalue depends on C₁₂ − θQ < 0, which captures the difference between the investors’ regulatory cost and the policy benefits generated by their policy preference. When θQ > C₁₂, this eigenvalue is negative, indicating that if investors slightly reduce their regulatory effort, their relative payoff deteriorates and the system pushes them back toward active regulation. The second and third eigenvalues are governed by Δ_B and Δ_O, the incremental returns from high-quality construction and operation, respectively. If Δ_B > 0 and Δ_O > 0, both eigenvalues are negative, implying that marginal deviations by builders or operators from high-quality strategies will reduce their payoffs. Under the joint conditions θQ > C₁₂, Δ_B > 0 and Δ_O > 0, all eigenvalues of the Jacobian at E₁ are negative, so E₁(1,1,1) is locally asymptotically stable in the evolutionary sense. Economically, this means that policy benefits are sufficient to offset investors’ regulatory costs, and cooperation in both the construction and operation stages remains strictly more profitable than opportunistic behavior. In this case, the investors’ economic and reputational incentives sustain the long-term cooperation of builders and operators, and the tripartite cooperative regime becomes reinforcing.

E₄(1,0,0) represents a non-cooperative equilibrium characterized by the absence of a responsibility-linkage mechanism. Here, investors choose active regulation, while builders and operators adopt low-quality strategies. In this regime, the high ex post responsibility cost K makes active regulation more attractive than inaction: when K > C₁₂, the eigenvalue of the Jacobian along the investors’ strategic dimension is negative, meaning that any marginal deviation toward weaker regulation would increase the investors’ expected liability. By contrast, the eigenvalues associated with the builders’ and operators’ strategy dimensions are governed by the net benefits of switching from low-quality to high-quality behavior. For builders, the payoff difference between high- and low-quality retrofit is Δ′_B, with Δ′_B < 0 when δ(1 + β) R₂₂ − C₂₂ < R₂₁ − αF₁. Similarly, for operators, the payoff difference Δ′_O satisfies Δ′_O < 0 when μ(1 + β) R₃₂ − C₃₂ < R₃₁ − αF₂). Under these conditions, the corresponding eigenvalues are negative, indicating that a small increase in the share of high-quality builders or operators would reduce their relative payoffs and be driven back toward the low-quality strategy. Therefore, when (K > C₁₂), (Δ′_B < 0), and (Δ′_O < 0), all eigenvalues of the Jacobian at E₄ are negative, and the equilibrium (E₄(1,0,0)) is locally asymptotically stable. Economically, this implies a locked-in pattern: investors are forced to maintain costly regulation to hedge responsibility risks, while builders and operators rationally adopt low-quality strategies and simply internalize expected penalties instead of engaging in cooperative behavior.

E₈(0,0,0) depicts a non-cooperative equilibrium in which investors regulate passively, builders perform low-quality retrofit, and operators deliver low-quality service. In the early stage of the project, the social, policy, and brand benefits have not yet materialized, and the incremental cost of active regulation exceeds the expected responsibility cost under passive regulation. When K < C₁₂, the eigenvalues of the Jacobi matrix along the investor strategy dimension are negative: investors will face lower net returns from active regulation than from passive regulation, thus their tendency to cooperate decreases, and the system eventually reverts to passive regulation. For builders and operators, in the absence of effective incentives, their strategy choices depend on the payoff difference between high-quality and low-quality behaviors. For builders, the incremental return of high-quality retrofit over low-quality retrofit is ${\Delta }_B^{‴}$, ${\Delta }_B^{‴}$ < 0 when δR₂₂ − C₂₂ < R₂₁ − αF₁. For operators, the corresponding payoff difference ${\Delta }_O^{‴}$ satisfies ${\Delta }_O^{‴}$ < 0 when μR₃₂ − C₃₂ < R₃₁ − αF₂. Under these conditions, both eigenvalues are negative, implying that slight increases in the proportion of high-quality builders or operators reduce their relative payoffs, so these deviations are gradually eliminated and the population converges back to low-quality strategies. Therefore, when K < C₁₂, ${\Delta }_B^{‴}$ < 0 and ${\Delta }_O^{‴}$ < 0, all eigenvalues of the Jacobian at E₈ are negative, and the equilibrium E₈(0,0,0) is locally asymptotically stable. Economically, this reflects a low-level lock-in state in the early phase of medical and elderly care retrofit projects: investors rationally choose passive regulation to minimize short-term losses, and builders and operators remain in low-quality strategies because high-quality strategies do not generate sufficient economic or reputational returns to offset their additional costs.

5. Case Simulation: Medical and Elderly Care Retrofit in Lanzhou

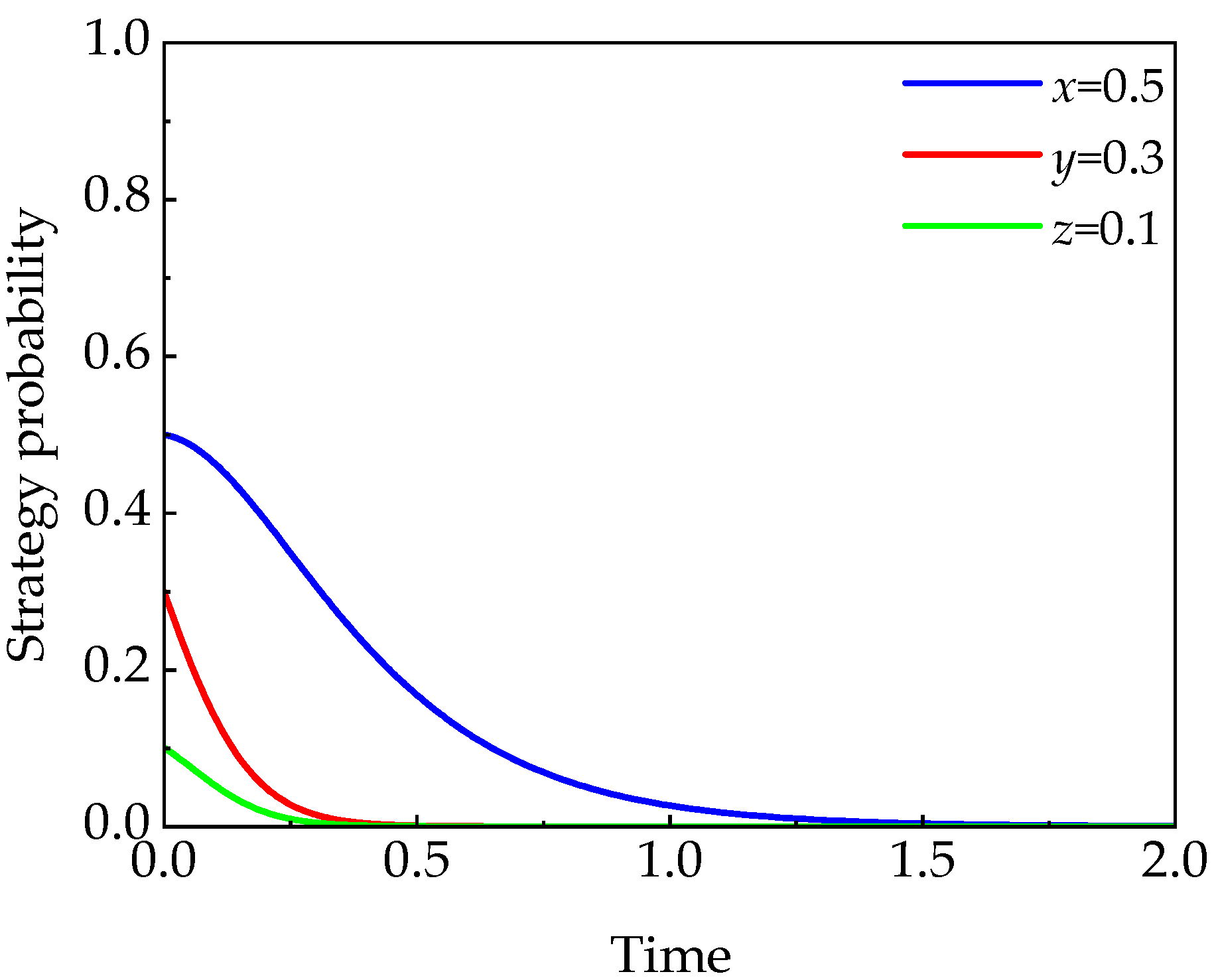
5.1. Parameter Calibration and Initial Simulation Results

Building on the above evolutionary game model and theoretical analysis, this section uses data from an actual project case [39], utilizes MATLAB R2024a [45] to simulate the evolutionary dynamics of the three stakeholders, and examines how key factors influence their equilibrium strategies.

The case concerns the retrofit of a vacant sanatorium in Lanzhou, Gansu Province, undertaken by China SDIC Health Industry Investment Co., Ltd. The project converts the vacant building into an integrated medical and elderly care facility to help alleviate the shortage of combined medical and elderly care institutions. The planned investment is I₀ = 800 (unit: one hundred thousand CNY), and the annual operational revenue is approximately 20% of the investment (R = 0.2 I₀). Revenue sharing is aligned with each party’s risk exposure, investment proportion, and lifecycle management responsibilities, such that participants bearing higher risks and greater investments receive a larger share of the returns [46]. Based on expert consultation and a review of typical contractual arrangements in integrated medical and elderly care retrofit projects, a 2:3:5 distribution ratio was adopted, which allocates a greater proportion of revenue to builders and operators, who bear substantial construction risks and long-term service obligations, and is consistent with commonly applied principles of benefit sharing [47]. Accordingly, revenue is distributed among investors, builders, and operators in a 2:3:5 ratio.

To ensure standardized and valid parameter assignments, including the revenue-sharing scheme and qualitative parameters such as policy preference, incentive strength, and penalty sensitivity, we conducted semi-structured interviews with eleven experts, comprising five staff from relevant government departments and six project managers involved in integrated medical and elderly care retrofit projects. The interview transcripts were manually coded into several key dimensions, and experts rated each dimension on a five-point Likert scale. These ratings were then normalized to the [0, 1] interval to obtain approximate parameter values. Final parameter values were derived by averaging expert responses and cross-checking with values reported in the relevant literature. The specific parameter settings are reported in

Table 5. Parameter calibration for the Lanzhou medical and elderly care building retrofit case.

Agents	Parameters	Range	Initial Value	Source
Investors	C11	-	16	Case data
	C12	2% × I0	16	Case data
	R1	20% × R	32	Case data
	θ	[0, 1]	0.5	[18]
	P	θQ	40	Case data
	K	50% × θQ	12	[39]
	n	[0, 20]	10	Case data
	S	nQ × 1%	8	[41]
Builders	C21	-	16	Case data
	C22	3.5% × I0	28	Case data
	R21	-	20	Case data
	R22	30% × R	48	Case data
	F1	[35% × R22, 50% × R22]	16.8	Case data
	δ0	[0.6, 1]	0.6	Policy document
Operators	C31	-	16	Case data
	C32	3% × I0	24	Case data
	R31	-	50	Case data
	R32	50% × R	80	Case data
	F2	[40% × R32, 50% × R32]	32	Case data
	μ	[0.6, 1]	0.6	Policy document
Global	α	[0, 1]	0.2	[40]
	β	[0, 1]	0.3	[18]
	γ	[0, 1]	0.3	[42]
	Q	Fixed value	80	Case data
	R	Fixed value	160	Case data

. In addition, Section 5 presents sensitivity analyses of key parameters to examine the robustness of the evolutionary trajectories and equilibrium outcomes.

Given that the parameter settings in Table 5 satisfy the stability conditions for implementing integrated medical and elderly care retrofit projects under current practice, based on these settings, 500 sets of different initial strategy points (x, y, z) were randomly generated using MATLAB R2024a to simulate the dynamic evolution of the system. Figure 2 illustrates the evolutionary trajectories of the tripartite game under varying initial conditions. The results show that, under the baseline profit distribution scheme of 2:3:5, approximately 71% of the simulation paths converge to the cooperative equilibrium among the tripartite, whereas about 29% evolve toward non-cooperative states, exhibiting a clear bistable structure. This pattern suggests that, due to variations in initial strategies and interaction paths, real-world projects may remain susceptible to cooperation failure.

To further verify the impact of the revenue distribution ratio on the system’s steady state, while keeping the total revenue constant, three alternative revenue distribution schemes (1.5:3.5:5.0, 2.0:3.5:4.5 and 2.5:3.5:4.0) are designed based on the baseline scenario of 2:3:5, and the proportions of trajectories converging to cooperative or non-cooperative equilibria under different initial conditions are statistically analyzed. As shown in Figure 3, adjusting the distribution structure significantly increases the proportion converging to the non-cooperative equilibrium. The proportions of convergence to non-cooperative equilibrium in the three scenarios are 91.4%, 91.6% and 99.6%, respectively, indicating a significant reduction in the “attraction domain” for cooperation. This suggests that the 2:3:5 revenue distribution structure is more conducive to cooperation, providing reasonably fair revenue compensation to entities bearing higher construction and operational risks; while distribution schemes deviating from this structure tend to weaken the appeal of cooperative strategies, causing the system to slide toward non-cooperative equilibria.

According to the “2024 National Bulletin on the Development of Aging” jointly issued by the Ministry of Civil Affairs and the China National Committee on Ageing, by the end of 2024, China had more than 8400 integrated medical and elderly care institutions and about 41,000 registered elderly care institutions, with integrated facilities accounting for 20.49% of the total, including newly ones [3]. Combining relevant research [19,42], the initial strategy probabilities for investors, builders, and operators were set to 0.5, 0.3, and 0.1, respectively, which allows evolutionary simulations to reflect current reality.

In this evolutionary game model, investors, builders, and operators are treated as three co-evolving populations in a unified strategic environment, capturing the long-term, interdependent relationships typical of modern project governance models, where their strategy choices mutually influence and adjust. To ensure comparability and readability of the simulation graphs, the time axis is normalized to a dimensionless “replication cycle” over [0.0, 2.0]. This scale does not respond to calendar time (e.g., years or months), but an abstract evolutionary step size describing the iterative convergence of strategies [48]. In the simulations, the system typically reaches a steady state at t ≈ 1.6–1.9. Thus, the interval [0.0, 2.0] fully captures the strategy evolution while facilitating comparison across different parameter scenarios. As shown in Figure 4, under this initial strategy combination, the strategies of the investors, builders, and operators converge to E₈(0,0,0). This outcome indicates that retrofitting vacant buildings into integrated medical and elderly care institutions is shaped not only by retrofit costs but also by policy preferences, investment planning, and revenue sharing. Accordingly, the subsequent analysis conducts sensitivity tests on key parameters to identify which factors, and under what conditions, promote tripartite cooperation and shift the system from an inefficient equilibrium toward a more desirable stable state.

5.2. Sensitivity Analysis of Key Policy-Level Parameters

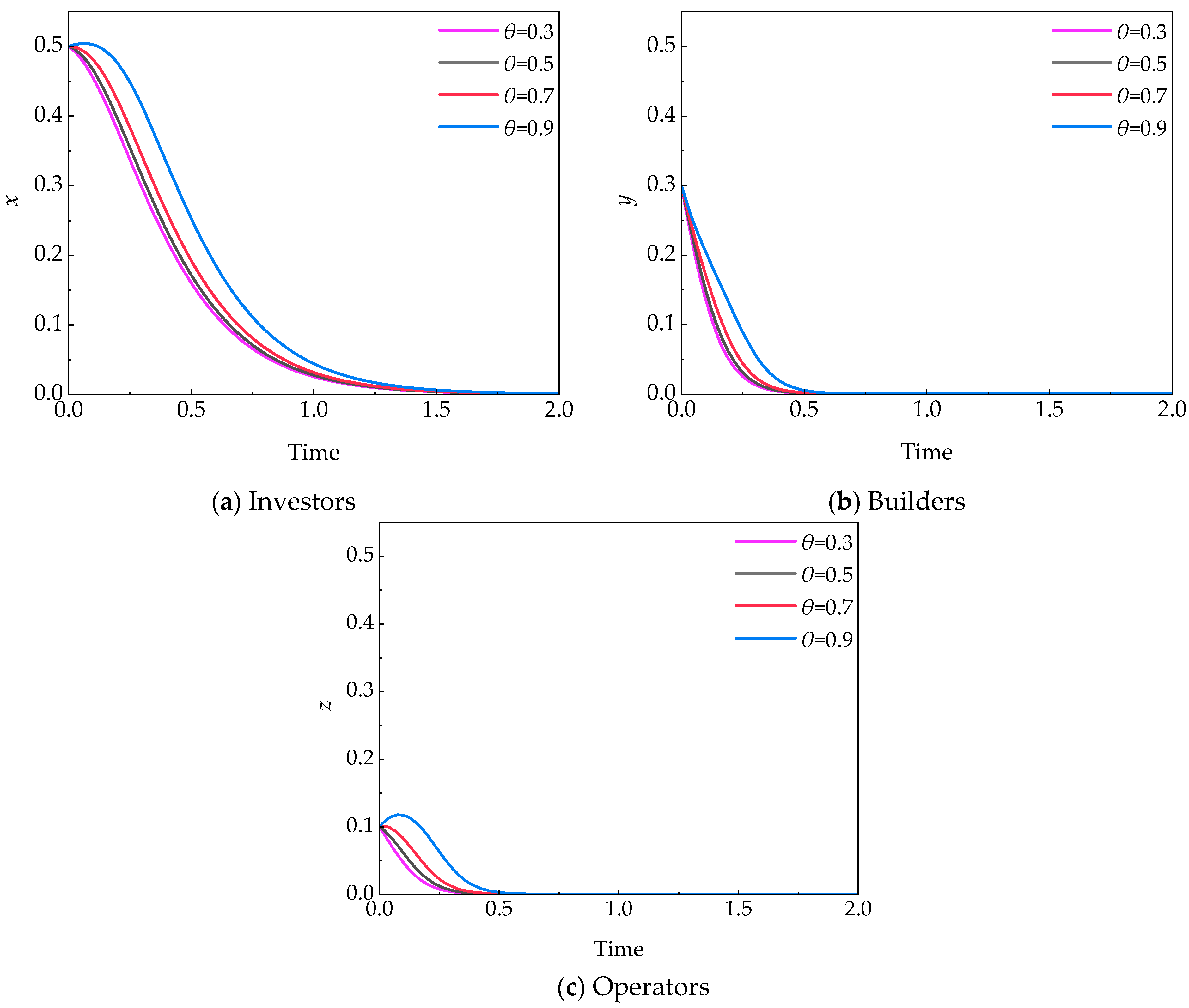
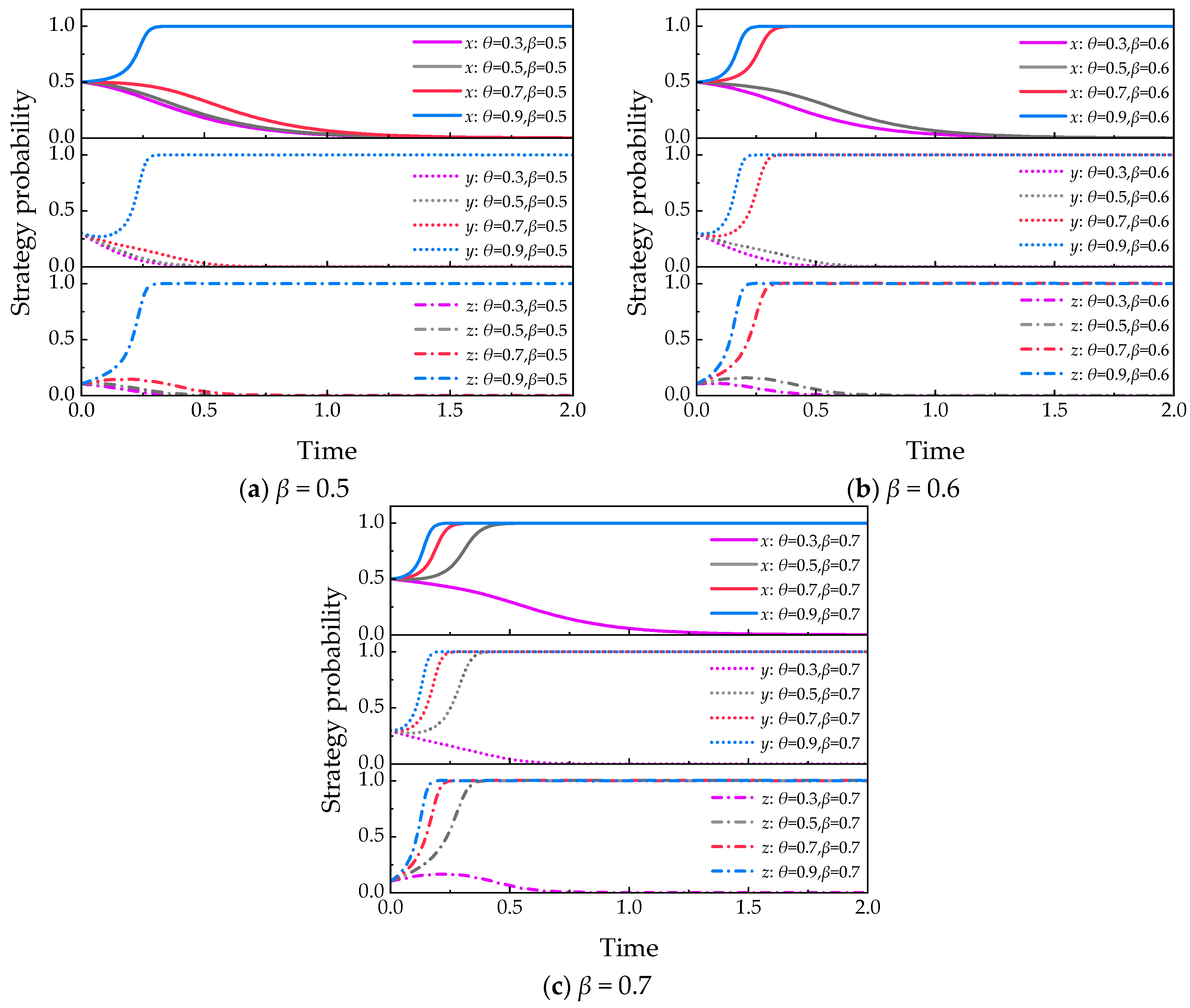
5.2.1. Policy Preference (θ)

To examine the impact of policy preference on the strategic choices of investors, builders, and operators, values of θ were set to 0.3, 0.5, 0.7, and 0.9. The resulting evolutionary trajectories are shown in Figure 5. Although increasing θ from 0.3 to 0.9 slows convergence, the evolutionary direction of the system remains unchanged, and E₈(0,0,0) remains the dominant equilibrium. This suggests that, under the current payoff and constraint structure, increasing θ does not alter the net payoff difference between cooperative and non-cooperative strategies. This result is consistent with real-world integrated medical and elderly care retrofit projects, which typically involve long payback periods, delayed capital recovery, and uncertainties in policy continuity and enforcement, all of which exacerbate stakeholders’ risk aversion [40]. In the absence of substantial economic incentives or constraints, non-cooperative strategies tend to retain a relative advantage in the evolutionary process [42].

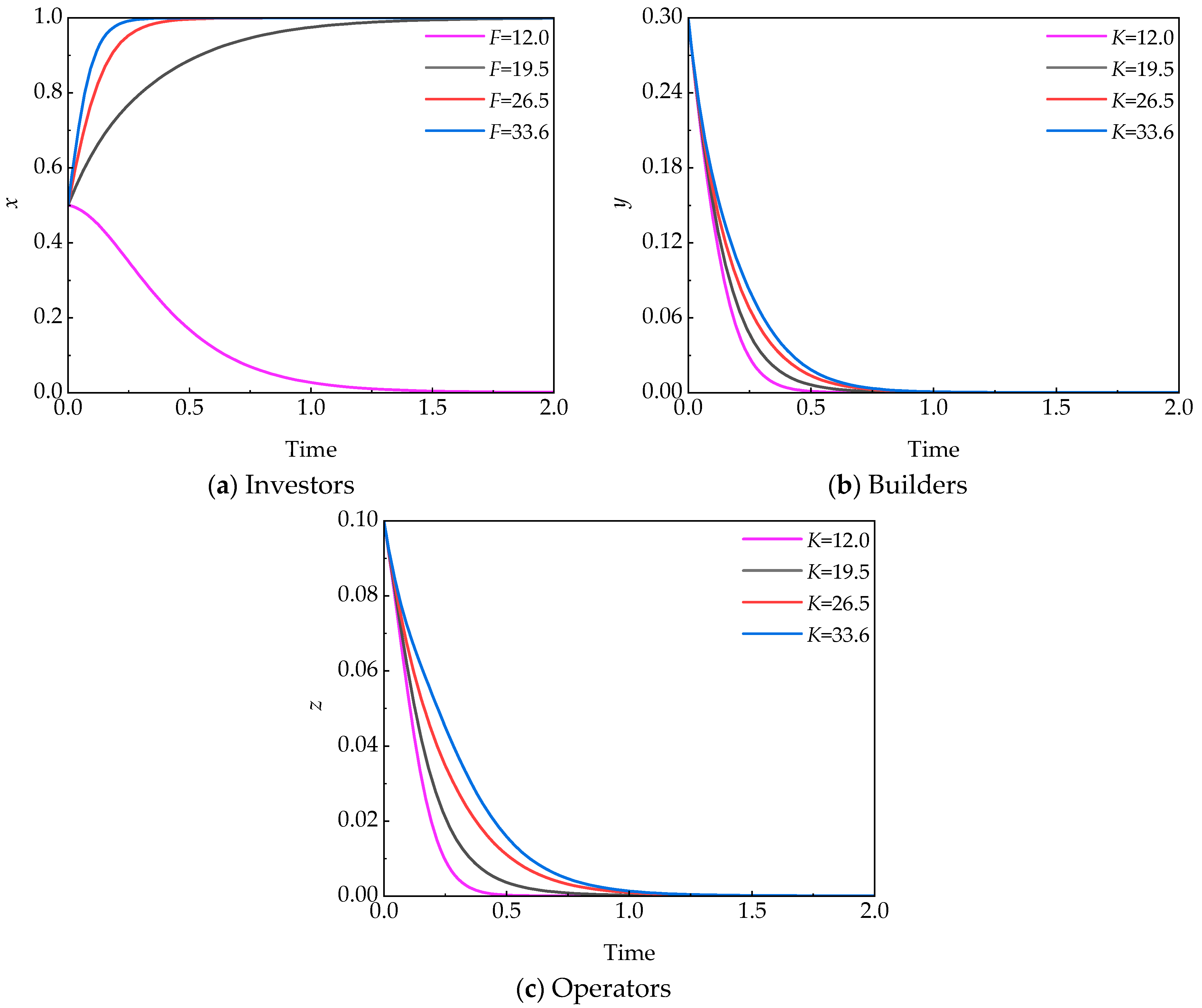
5.2.2. Responsibility Cost (K)

Effective management by investors can reduce the likelihood of project failure and secondary losses [49]. To reflect this impact, a responsibility cost K is introduced to represent the losses investors expect to incur under passive regulation. K was set at 7.5% (12.0), 12% (19.5), 16.5% (26.5), and 21% (33.6) of the total economic benefits (R = 160), and the resulting evolutionary trajectories are shown in Figure 6. When K = 12.0, the probability x that investors adopt active regulation converges to 0, indicating that the expected payoff of passive regulation is still higher than that of active regulation. As K increases from 12.0 to 19.2, x rises from 0.5 to 1, and the convergence toward active regulation accelerates, because a higher K reduces the expected payoff of passive regulation relative to active regulation and reverses the payoff difference between the two strategies.

By comparison, increasing K slows the convergence of builders’ and operators’ strategies toward non-cooperation, but their cooperation probabilities y and z still converge to 0. This aligns with the payoff structure; the K value directly affects investors, and its impact on other stakeholders is primarily achieved through changes in investor behavior. In fact, the liability costs resulting from insufficient investor oversight may also be partially borne through insurance or contractual arrangements, so their impact is not fully passed on to builders and operators [50]. This indicates a missing link in the accountability mechanism and highlights the necessity of designing enforceable liability-sharing clauses and performance-linked mechanisms that connect investor oversight with the contractual obligations of builders and operators [51].

5.3. Sensitivity Analysis of Key Economic Parameters

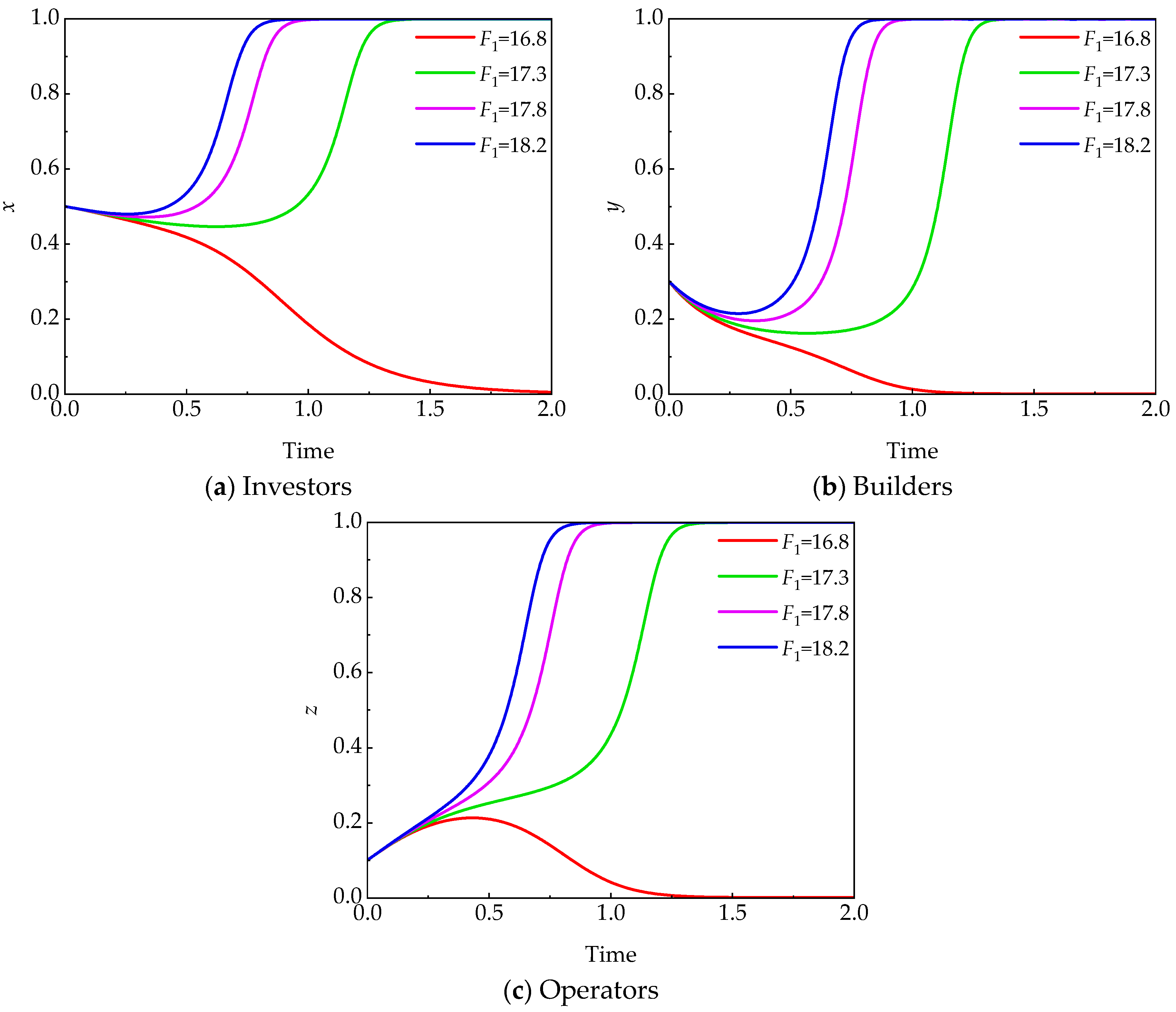
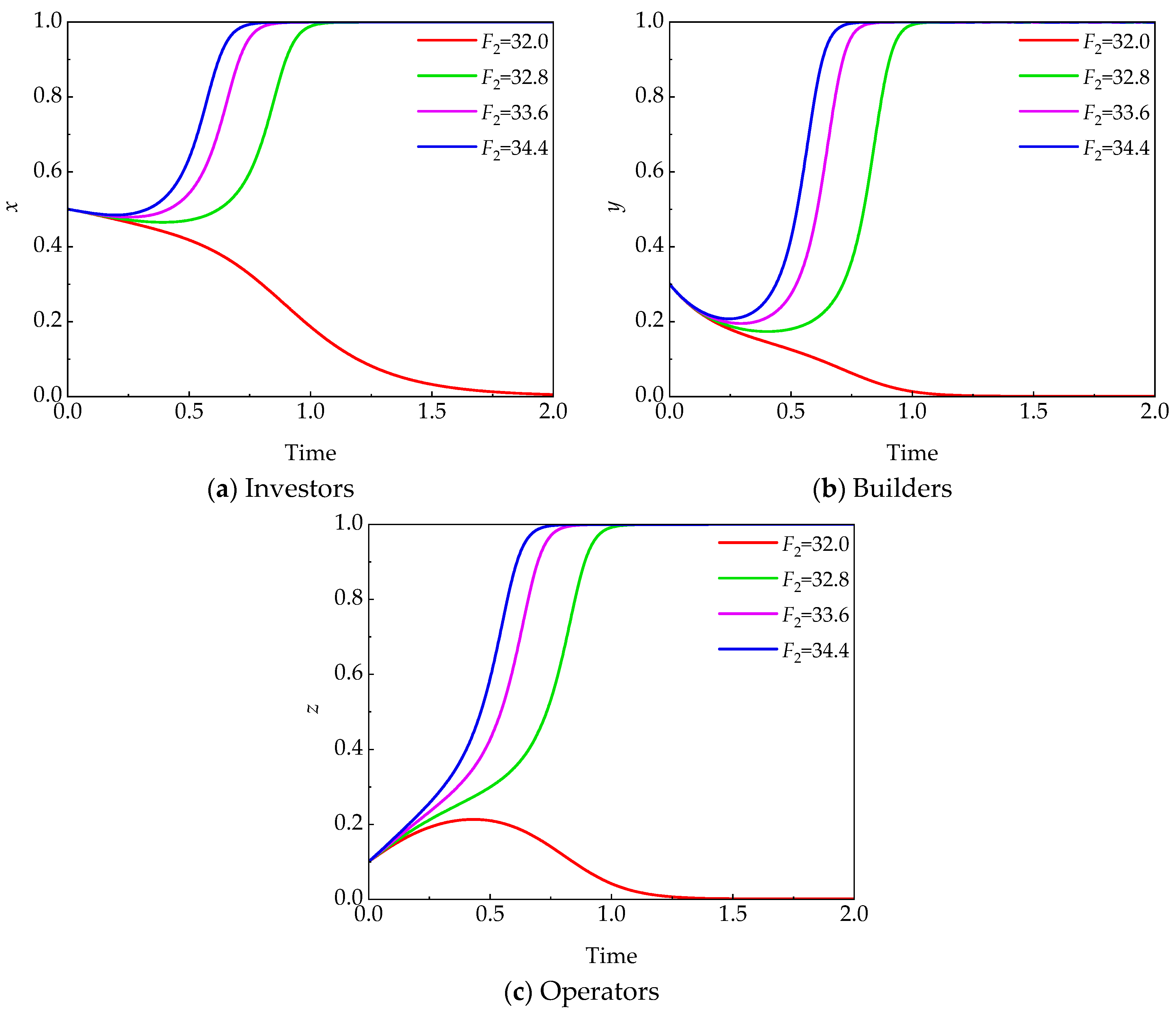
5.3.1. Penalty Cost (F_i)

Existing studies usually assume a uniform penalty cost and neglect differences in responsibility and cost structures among stakeholders. To capture these differences, this paper introduces independent penalty costs F₁ and F₂ for builders and operators, respectively, both linked to the penalty intensity α [40].

Setting α = 0.5, the values of F₁ were set to 35% (16.8), 36% (17.3), 37% (17.8), and 38% (18.2) of R₂₂, respectively. The evolution of tripartite behavioral strategies is shown in Figure 7. When F₁ = 16.8, the system converged to E₈(0,0,0). Once F₁ exceeds 17.3, the system evolves to the equilibrium point E₁(1,1,1), and higher values of F₁ further accelerate convergence. Furthermore, increasing F₁ strengthens the selection gradient in the builders’ replicator dynamics: the penalty term αF₁ lowers the payoff of low-quality retrofit relative to high-quality retrofit, so that marginal deviations toward low quality become unprofitable and leads builders to prefer high-quality retrofit. Because builders’ retrofit quality directly affects investors’ returns, this shift also increases the expected payoff of active regulation for investors, leading both x and y to converge quickly to 1. In contrast, the incremental cost for the operators to provide high-quality service are mostly controllable, allowing them to flexibly manage the pace and scale of input. Thus, the operators’ strategy probability z remains on an upward trend and eventually stabilizes at 1.

For operators, α = 0.5, and the values of F₂ were set to 40% (32.0), 41% (32.8), 42% (33.6), and 43% (34.4) of R₃₂. Figure 8 shows the impact of the penalty F₂ on tripartite behavior evolution. As with F₁, increasing F₂ accelerates convergence toward E₁(1,1,1). However, the cooperative threshold for F₂ (32.8) is 89.6% higher than that for F₁ (17.3), indicating that a substantially stronger penalty is required to induce a comparable cooperative response from operators. This difference is consistent with the model structure: In the payoff functions, F₁ acts on an upstream decision and directly reduces the net return of low-quality retrofit for builders, thereby enlarging the payoff gap between high-quality and low-quality strategies at the construction stage, whereas F₂ acts on a downstream decision and initially affects only operators’ payoffs at the operation stage, and its impact on builders and investors is transmitted indirectly through service quality, reputation, and revenue sharing, resulting a higher threshold.

In summary, different entities react differently to the penalty mechanism [39]. Considering the combined effects of F₁ and F₂, intervention measures targeting builders are a more cost-effective strategy. It can reduce regulatory costs, ensure quality, reduce long-term operational risks, and ultimately improve the overall benefits of the project [43]. In addition, early risk-sharing mechanisms or economic subsidies can be introduced to help builders overcome risk concerns and cost rigidity [44,45]. For operators, a market-oriented return mechanism can be established to link service quality with economic returns.

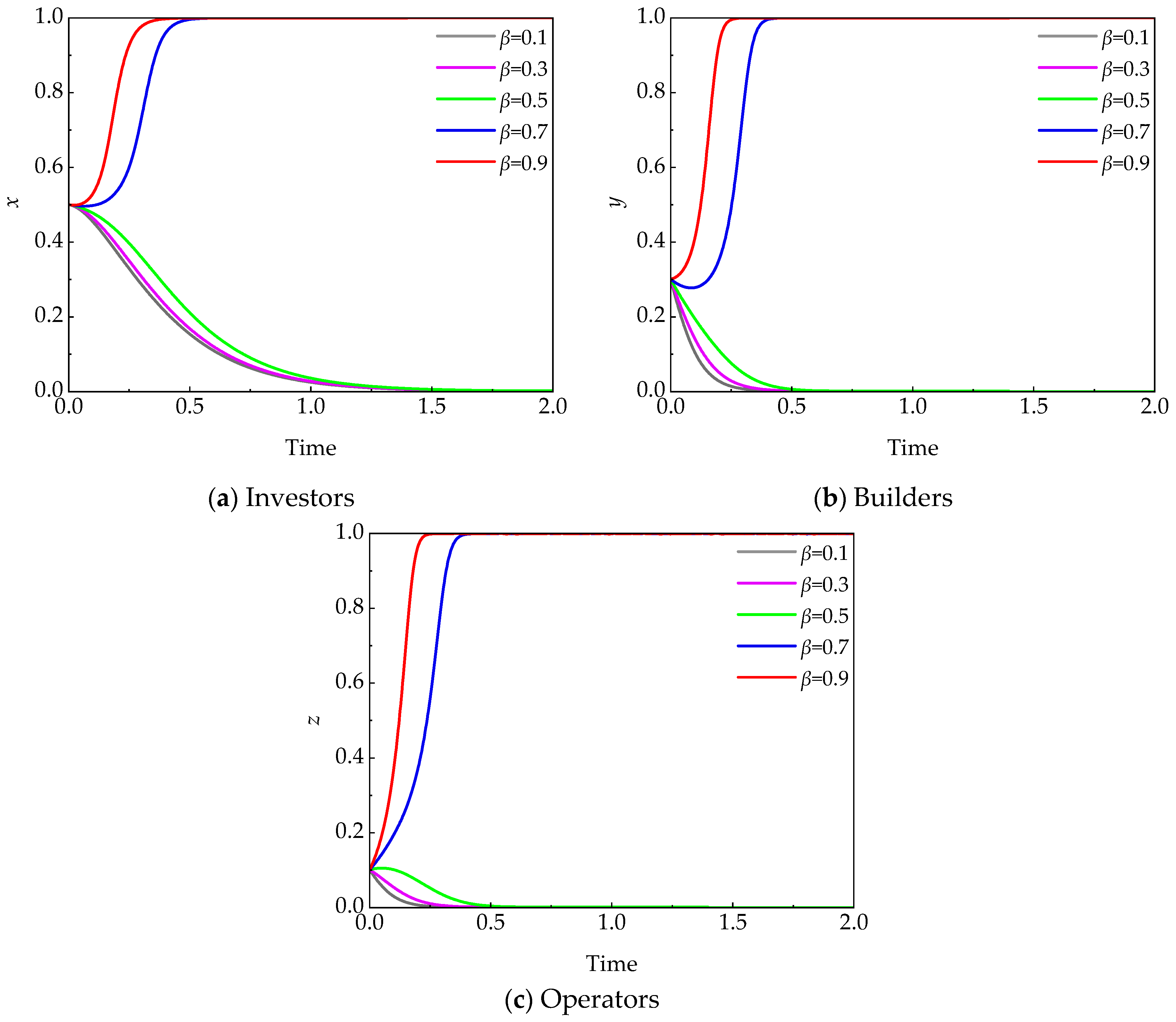
5.3.2. Economic Incentives Coefficient (β)

Figure 9 illustrates the impact of varying the economic incentives coefficient β on the evolution of tripartite behavioral strategies. When β ≤ 0.5, the probabilities x, y, and z that investors, builders, and operators adopt cooperative strategies all decrease over time, and the system eventually converges to the non-cooperative equilibrium E₈(0,0,0). The additional benefits generated by economic incentives were insufficient to offset the incremental costs and perceived risks of proactive behavior. Therefore, cooperative behavior yields lower returns than non-cooperation, and the non-cooperative equilibrium is evolutionarily stable. When β = 0.7, the probabilities x and z gradually increased and converged to 1, while y first decreased and then rose to 1. The incentive level was sufficiently high to compensate for the incremental input costs, thereby reversing the payoff inequality.

However, because of high sunk-cost risks and technical uncertainties, the probability that builders adopt a high-quality retrofit strategy initially declines. As economic incentives accumulate and cooperation between investors and operators becomes more likely, expected cost pressures on builders are alleviated, and their perceived risk decreases, which induces a strategic shift toward high-quality retrofit. Eventually, the system converges to the cooperative equilibrium E₁(1,1,1). When β = 0.9, x, y, and z all converge to 1. The expected returns from economic incentives substantially exceed those of non-cooperative strategies, leading to rapid convergence to full cooperation. Overall, the economic incentive coefficient β exhibits a clear threshold effect on tripartite cooperation. When β ≥ 0.7, E₁ becomes the dominant equilibrium. Meanwhile, builders’ strategic adjustments depend strongly on evolving signals from investors and operators, underscoring the importance of a coordinated incentive mechanism among three stakeholders.

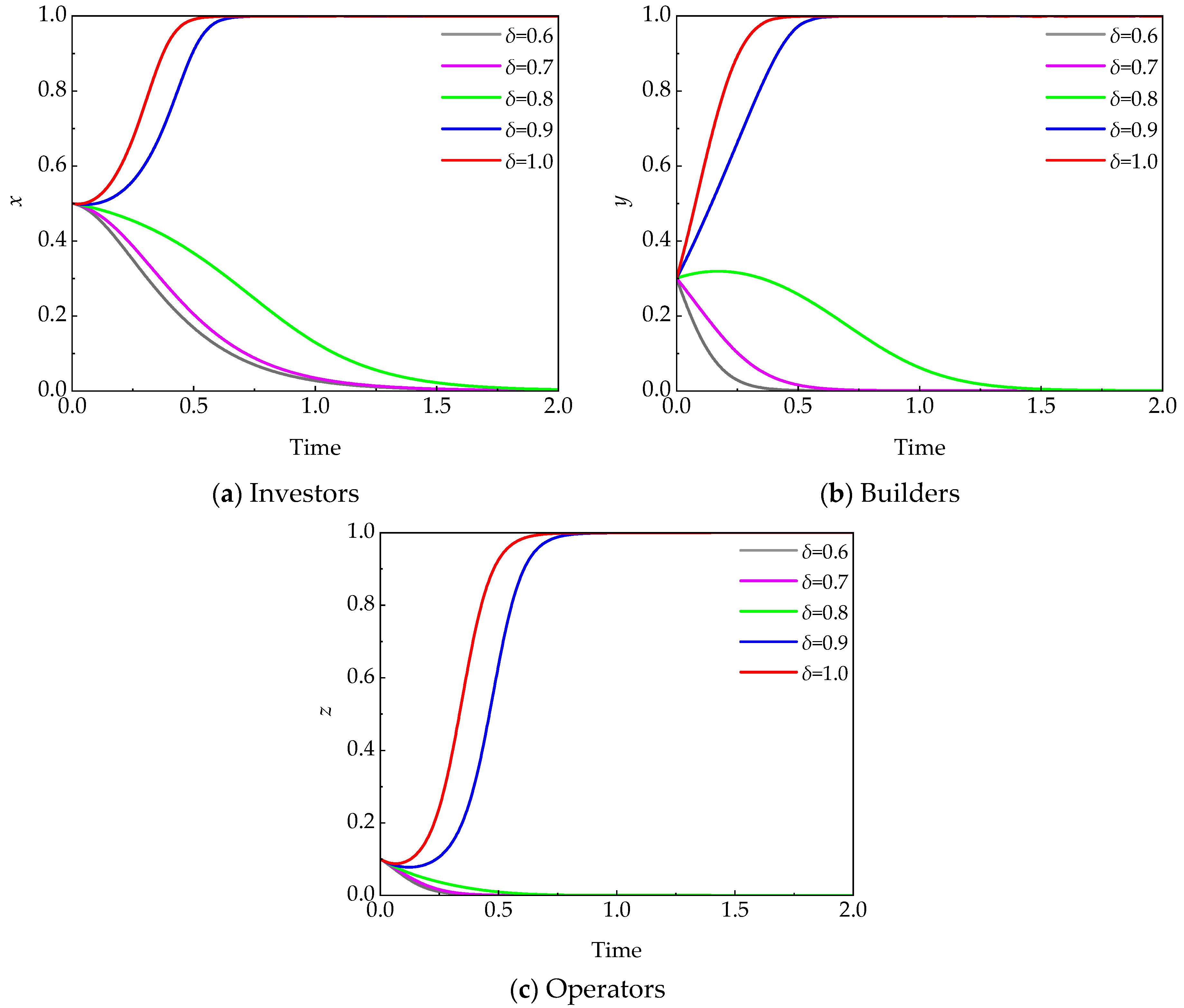
5.3.3. Quality Evaluation Coefficient (δ)

Integrated medical and elderly care retrofit projects emphasize long-term benefits, with quality linking initial investment to these outcomes. Therefore, the quality evaluation coefficient δ was introduced. The value of δ was obtained by normalizing two dimensions: the building physical environment [52] and operational service quality [53], with a baseline of 0.6.

Figure 10 illustrates the evolution of tripartite behavioral strategies. When δ ≤ 0.8, the probabilities x, y, and z that investors, builders, and operators adopt active strategies all decrease over time, and the system ultimately converges to E₈(0,0,0). Within this range, the quality evaluation level is insufficient to support the long-term return expectations for high-quality retrofit and service, leading stakeholders to avoid short-term risks through opportunistic behavior. As δ increased, the rates of decline of x, y, and z slowed, indicating that quality improvements partially alleviated stakeholder concerns about the input-output mismatch, but the non-cooperative equilibrium remained stable.

When δ was 0.9, x, y, and z showed an increasing trend, eventually converging to 1. When δ was further increased to 1, the convergence of x, y, and z to 1 became faster. This result appears to contradict the view that higher quality standards permit more relaxed regulation [52]. In this study, investors play a dual role as funders and regulators, with regulatory incentives directly tied to overall project quality and long-term value. In other words, a higher δ means that a high-quality retrofit translates into sustained returns for investors, which in turn strengthens their motivation for high-quality regulation. For builders and operators, when δ exceeds the critical threshold, the weight of high-quality retrofit and service in the revenue function increases significantly, and the linkage effect between the two parties in reputation accumulation and market share is enhanced, forming a stable cooperative evolutionary path.

Therefore, to ensure long-term interests and high-quality development, investors should not switch to passive regulation merely because short-term quality standards are met. On the contrary, high-quality retrofit requires sustained investment in regulatory and governance resources over a longer timescale. It relies on a sound and efficient regulatory system to embed quality evaluation results into stakeholder incentives.

5.4. Sensitivity Analysis of Key Reputation-Related Parameters

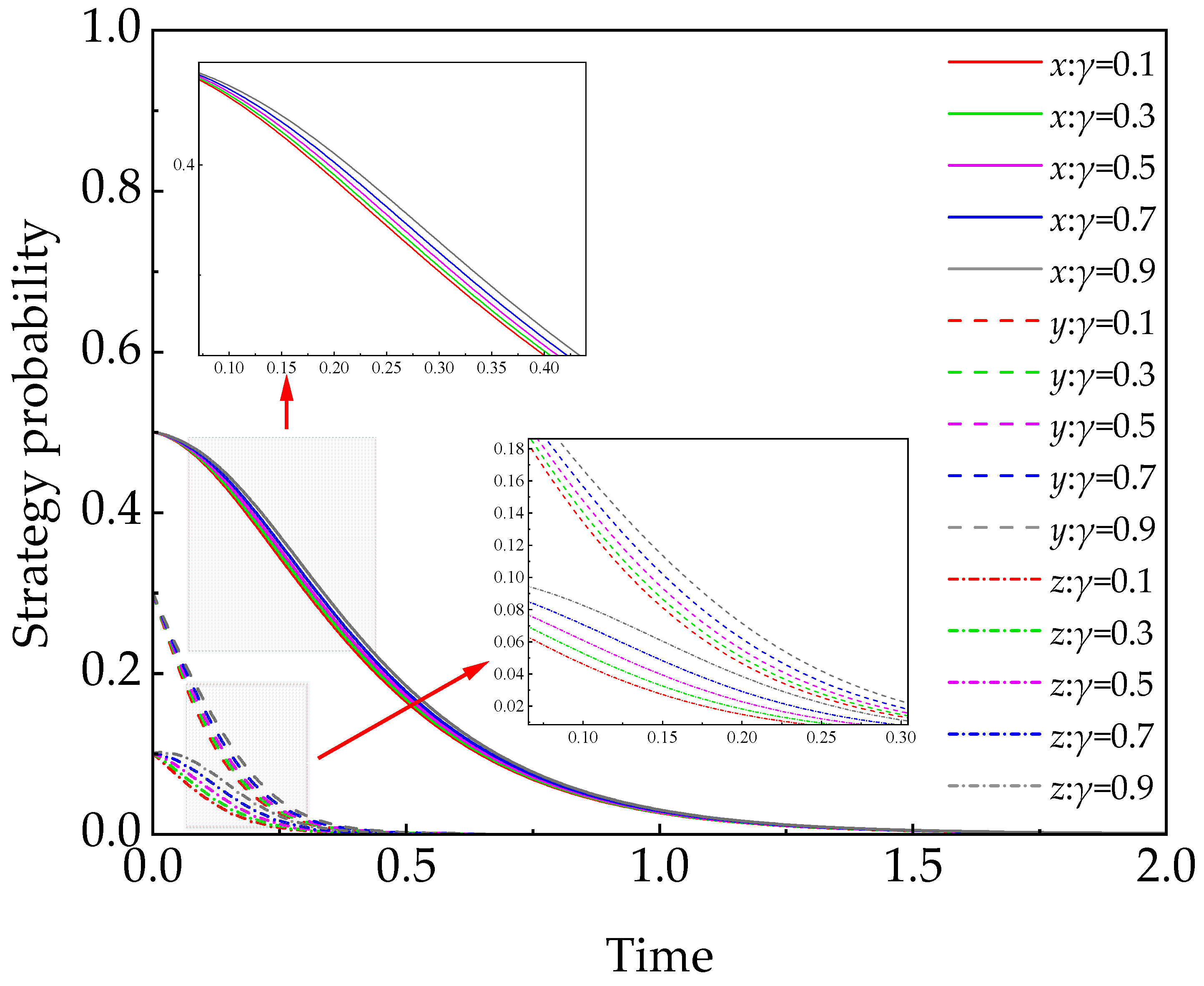
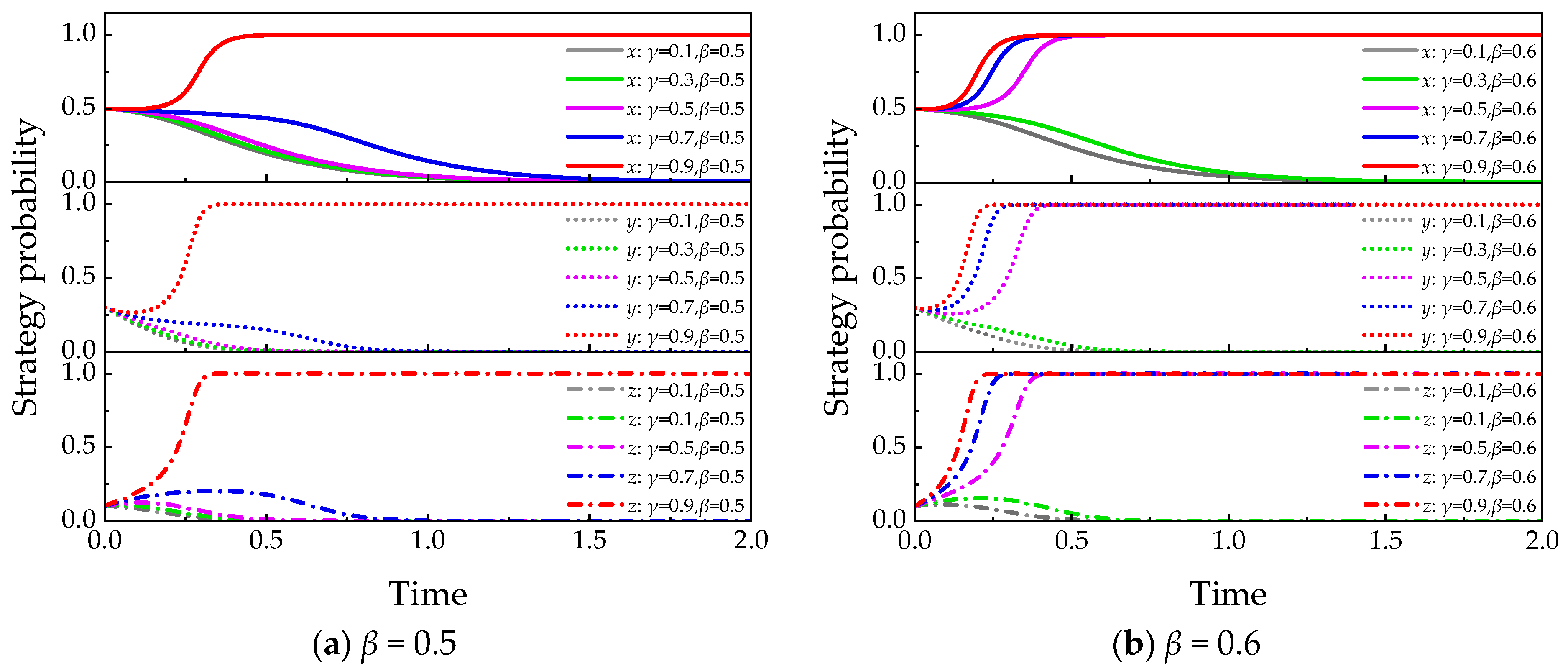
5.4.1. Reputational Incentives Coefficient (γ)

Figure 11 illustrates the impact of the reputational incentives coefficient γ on the stakeholders’ behavior evolution. As the value of γ increased, x, y, and z consistently decreased, ultimately converging to 0. Reputational incentives essentially serve as a complement to, rather than a substitute for, economic incentives [54,55].

Reputational incentives alone are insufficient to induce the three parties to bear the project’s upfront costs and risks. Accordingly, a hybrid incentive scheme that combines economic compensation with reputational rewards is required to foster cooperation. Figure 12 illustrates the impact of jointly implemented reputational and economic incentives on stakeholders’ behavioral evolution. When β = 0.5 and γ ≤ 0.7, the cooperation probabilities x, y, and z all decrease and converge to 0, indicating persistent non-cooperation. When γ increases from 0.7 to 0.9, x, y, and z instead increase and eventually converge to 1, as the higher reputational incentives generate positive net gains from proactive strategies and drive the system toward cooperation. When β = 0.6 and γ ≤ 0.3, x, y, and z all declined and converged to 0, indicating non-cooperation. When γ increased from 0.3 to 0.5, the tripartite evolved to the equilibrium point E₁(1,1,1), meaning the tripartite began to cooperate. As γ continued to increase, the speed at which x, y, and z converged to 1 accelerated. In summary, reputational incentives can effectively promote faster evolution towards cooperation among the tripartite only when β lies within the threshold range [0.5, 0.7] [56].

Comparing Figure 12a,b reveals that increasing β from 0.5 to 0.6 lowers the threshold of γ required for the stakeholders’ evolution towards cooperation. This demonstrates a complementary effect between economic and reputational incentives. Economic incentives secure the attainment of benefits, while reputational incentives reinforce project value over time. Together, they constitute a complete incentive system [54]. Consequently, in the retrofit projects of integrated medical and elderly care, economic incentives should serve as the primary means, supplemented by reputational incentives, to accelerate the evolution of cooperation among all agents and facilitate long-term development.

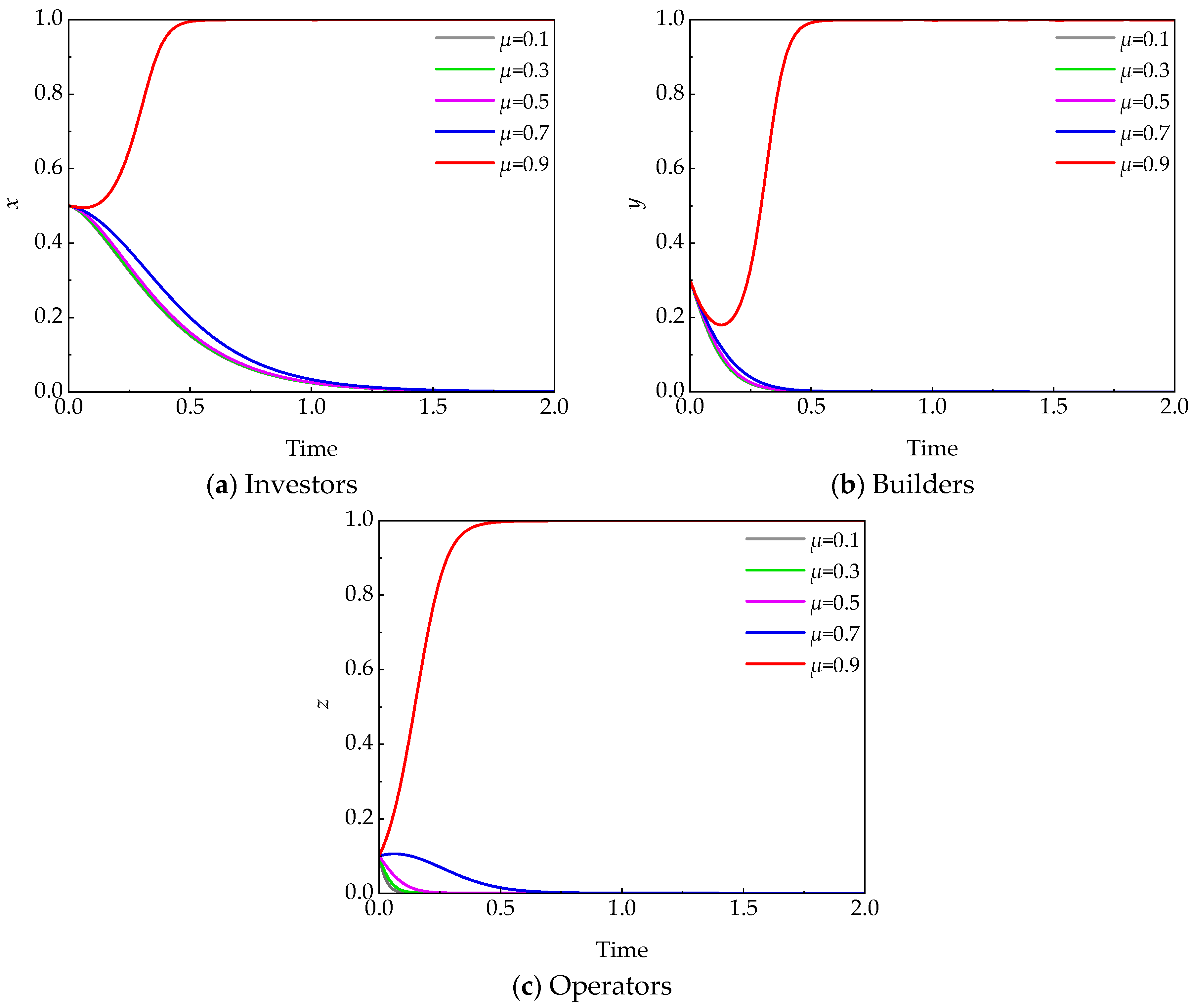
5.4.2. Demand Matching Coefficient (μ)

To assess the alignment between the completed project and market demand, the demand matching coefficient μ was introduced. Figure 13 shows the impact of μ on the stakeholders’ behavior evolution. When μ ≤ 0.7, the cooperation probabilities x, y, and z for investors, builders, and operators decrease and eventually converge to 0, indicating non-cooperation. When μ increased from 0.7 to 0.9, x, y, and z continuously rose and eventually converged to 1, whereas y first decreased and then increased to 1. This suggests that at this level of demand matching, the cooperative state in which investors adopt active regulation and the operators adopt high-quality service yields higher expected returns for both parties. Unlike investors and operators, builders exhibit significant asset specificity in their inputs (human resources, equipment, materials, etc.), which are difficult to recover or redeploy once committed. This results in a more cautious decision-making logic by builders. Even if the projected demand match is sufficiently high, builders typically do not immediately adopt a proactive, cooperative stance; their optimal strategy in the early project stages is to remain on the sidelines. As the project progresses, the probabilities that investors and operators adopt an active strategy gradually increase, alleviating builders’ concerns and causing y to reverse its trend and rise, ultimately facilitating tripartite cooperation.

6. Discussion and Implications

6.1. Building Credible Commitment: A Synergistic Mechanism of Policy Preference and Economic Incentives

As shown in Section 5.2.1, policy preferences alone are insufficient to drive system-wide collaboration, suggesting that, in the absence of tangible incentives, stakeholders tend to treat policy signals as a “soft” and uncertain commitment rather than a credible guarantee of future returns [55]. To address this dilemma, the combined effects of policy preferences and economic incentives are examined. The simulations in Figure 14 reveal a clear trade-off frontier between β and θ: higher economic incentives allow the same cooperative equilibrium to be sustained under markedly lower policy preference, indicating a synergistic and partially substitutable relationship between these two instruments, consistent with prior findings on the synergy between regulatory constraints and economic incentives in other evolutionary game settings [57]. In essence, combining policy preferences with economic incentives mitigates both the incremental costs and the perceived policy risk borne by the three parties, transforming policy support from a soft signal into a credible, budget-backed commitment and shifting their expected returns from passive to active strategies [58]. Practically, this implies that policy support for integrated medical and elderly care retrofits should be designed as a portfolio: performance-based subsidies, dedicated guarantee funds, and multi-year contractual commitments can operationalize β, while stable, transparently implemented policy schemes anchor θ [59]. Only when this combined package surpasses the minimum economic policy thresholds identified in the simulations can investors, builders, and operators reasonably commit to long-term cooperative strategies.

6.2. Reconstructing the Investors’ Role: From Passive Responder to Active Value Guardian

The analysis of the quality evaluation coefficient Δ in Section 5.3.3 reveals a pattern that runs counter to conventional regulatory intuition: as Δ increases, the probability of investors adopting active regulation (x) also rises, rather than being relaxed [55]. This suggests that improving the accuracy and salience of quality evaluation does not lead to regulatory fade-out; instead, it activates regulation as an endogenous driver of lifecycle value governance. In other words, the investor’s role evolves from a compliance inspector to a long-term value guardian.

In compliance-oriented regulation, regulators are typically treated as exogenous forces whose primary task is to ensure that retrofits meet minimum quality standards, after which regulatory intensity is expected to decline. In our project, investors assume the regulatory role, as core residual claimants and risk-sharers; their objectives extend beyond short-term compliance to safeguarding the long-term value of retrofitted assets, including stable operational cash flows and accumulated brand reputation [49]. Quality improvement thus becomes a precondition for creating and securing this value, and regulation is endogenized as an internal value-enhancing mechanism embedded in the project lifecycle [60]. Stronger investor regulation, therefore, reflects not simple distrust of builders or operators, but the need to protect and enhance investment value [61].

This reconfiguration of the investors’ role implies that governance tools should support continuous, value-oriented oversight rather than one-off compliance checks. Digital twin platforms and similar data infrastructures can convert the behaviors, strategy evolution, and user feedback of investors, builders, and operators into transparent, traceable, and analyzable information [62]. This enables regulators to monitor quality and performance trajectories in real time and adjust incentives accordingly, thereby supporting integrated medical and elderly care retrofit projects led by investor oversight.

6.3. The Builders’ Pivotal Role: Targeted Governance and Trust Building Based on Asset Specificity

The construction phase is the critical link that determines the quality of the retrofit. As shown in Section 5.3.1, the penalty threshold required to induce cooperative behavior is substantially lower for builders than for operators, suggesting that governance interventions targeted at the construction phase are easier to implement effectively. Controlling quality at source not only avoids higher governance costs in the operation phase, but also makes it more cost-effective, from an asset-specific governance perspective, to shift the regulatory focus upstream to construction [61].

Comparing Section 5.3.1 and Section 5.3.2 further indicates that when β ≥ 0.7, the level of economic incentives required to sustain cooperation is markedly higher than the penalty threshold needed to deter non-cooperation. This asymmetry reflects the behavioral economics concept of loss aversion [63], whereby agents are more sensitive to potential losses than to gains of equivalent magnitude. Builders are particularly sensitive to penalties due to the irreversibility and asset specificity of their investments [64], underscoring the need to differentiate governance priorities across lifecycle stages. And this was often overlooked in standard multi-agent EGT (Empirical Game Theoretic) models.

The pattern whereby the builders’ probability of choosing high-quality retrofit first decreases and then increases (Figure 9 and Figure 13) also reveals key prerequisites for their willingness to commit to high-quality work. Builders are more likely to adopt high-quality retrofit only when they observe effective investor regulation and credible commitments to high-quality service from operators. Under information asymmetry, builders are particularly loss-sensitive due to the irreversibility and asset specificity of their investments (e.g., embedded pipelines, access structures) [61]. They require credible commitments from both investors and operators before locking in irreversible construction assets. Therefore, it is necessary to introduce governance measures targeting builders at the early stages of a project to ensure project quality from the source [64]. For example, once initial regulatory funds are secured, advance payments to builders in the early stages can incentivize them and reduce the risk of failed collaborations due to cross-stage dependencies More broadly, future retrofit projects should integrate early incentives and trust mechanisms to reduce builders’ asset specificity and loss aversion, thereby mitigating opportunistic risks during the construction phase.

6.4. Sustained Motivation for the Operators: Building Dual Market-Based and Reputational Incentives

To enhance operators’ willingness to provide high-quality services sustainably, an effective incentive mechanism must be established. Simulation results in Section 5.4.1 show that reputational incentives alone are insufficient to drive the system to E₁(1,1,1) equilibrium (Figure 11), while purely economic incentives require a relatively high cost (β ≥ 0.7). When reputational and economic incentives are combined (Figure 12), their synergistic effect enables the three parties to maintain a cooperative equilibrium at a lower β value.

This result is consistent with the incentive theory of the complementarity between extrinsic rewards and intrinsic motivation, economic incentives can amplify weak reputation effects into more substantial incentives for cooperation [56,65,66]. In practice, this means establishing a quantifiable quality assessment system that directly links an operator’s reputation level to core economic benefits such as service fees, subsidies, and contract renewal eligibility. At the same time, clearly defining the penalties for failing to meet quality standards (e.g., forfeiting deposits or temporarily restricting market access) helps curb short-term opportunistic behavior and may direct operators’ attention to long-term service quality and reputation maintenance [27,30]. In conclusion, the dual incentive system combining economic benefits and reputation provides a more solid foundation for the sustainable development and user satisfaction of integrated medical and elderly care renovation projects.

7. Conclusions

Against the backdrop of urban renewal and accelerating population aging, retrofitting vacant buildings into integrated medical and elderly care institutions has become a key strategy for promoting synergistic, high-quality urban development and elderly service provision, with significant importance for enhancing public welfare and social benefits. The main contribution of this study lies in applying an evolutionary game theory model to the collaborative governance of age-friendly retrofit projects integrating medical and elderly care. Unlike typical multi-agent EGT models, this study integrates interactions among investors, builders, and operators with their respective lifecycle stages, thereby revealing additional governance mechanisms. Based on specific case data, model parameters are assigned values, and sensitivity analyses of key parameters such as policy preferences, economic incentives, penalty costs, and quality evaluation coefficients are conducted through numerical simulations, providing insights into incentive design and collaborative governance in age-friendly retrofit projects. The main conclusions are as follows:

(1)

Policy preferences (θ) alone are insufficient to maintain tripartite cooperation in the model. However, their impact is more significant when combined with economic incentives. As the economic incentive coefficient (β) increases from 0.5 to 0.7, the θ value required to maintain the ideal cooperative state decreases from 0.9 to 0.5, indicating that stronger economic incentives may partially compensate for the inadequacy of policy preferences.

(2)

Responsibility costs (K) reaching 12% of total economic benefits can incentivize investors to adopt active regulation. In contrast, its impact on the strategy choices of builders and operators is limited, mainly mitigating rather than reversing their tendency to non-cooperate.

(3)

Different agents exhibit varying sensitivities to penalties. In this study, a penalty cost of 17.3 (F₁) is sufficient to motivate builders to adopt a cooperative strategy, while operators require a higher penalty cost (F₂) of 32.8 to induce cooperative behavior. Meanwhile, the dominant strategy of builders still depends on the strategic choices of investors and operators, illustrating the interdependence among the stakeholders.

(4)

Economic incentives play a central role in promoting systemic cooperation. The economic incentive coefficient (β) exhibits a threshold effect (β ≥ 0.7); exceeding this value appears to be a necessary condition for accelerating the evolution of tripartite cooperation.

(5)

The higher the quality assessment coefficient (Δ), the greater the likelihood that investors choose active regulation. This suggests that when the quality of retrofit is closely related to investors’ long-term returns, investors may be motivated to maintain or even strengthen regulatory efforts, which in turn can accelerate the formation of tripartite cooperation strategies.

(6)

Reputation incentives (γ) alone are insufficient to promote stable tripartite cooperation. However, when combined with economic incentives, they help accelerate the evolution of cooperation and appear to lower the threshold of the economic incentive coefficient (β) required to trigger cooperative behavior.

In summary, the findings point to several governance principles that may be useful for integrated medical and elderly care retrofit projects. First, economic incentives can serve as a central component of mechanism design, with the β value set above the identified threshold and coordinated with policy preference θ and reputational incentives γ, so that cooperative strategies retain a relative profit advantage. Second, penalty costs and responsibility costs need to be differentiated: the responsibility cost K mainly functions to activate investor oversight, whereas the penalty costs F₁ and F₂ should be set within an effective minimum range that reflects builders’ greater sensitivity and the higher trigger threshold faced by operators. Third, linking governance tools to long-term quality performance makes them more likely to be effective, for example, by incorporating quality evaluation coefficients to capture the sustained effects of retrofit decisions. Taken together, these elements outline a collaborative governance framework characterized by incentive consistency, asymmetric penalties, and quality orientation, which may offer actionable strategic guidance for the design and implementation of such projects.

8. Limitations and Future Research

The simulation analysis in this study is based on a single integrated medical and elderly care retrofit project in Lanzhou. Its parameter settings (such as policy preferences, economic incentive intensity, and investment amount) are highly context-dependent. Therefore, although the tripartite evolutionary game model and the collaborative mechanism constructed in this study are structurally universal, when applied across different cities or contexts, the parameters still need to be recalibrated to local policies, market environments, and stakeholder characteristics. Future research can further test the robustness of the model and the generalizability of the research conclusions through multi-case comparisons, cross-regional simulations, and extended sensitivity analysis.