Impact of Public Space in Primary and Secondary Schools Based on Natural Visibility Ratio
Abstract
1. Introduction
1.1. The Paradox of Security and Pedagogy in Campus Design
- Oversimplified safety zoning: Traditional binary classifications of “safe/unsafe” zones fail to account for the gradient nature of the spatial permeability that is required for adolescent socialization. This rigid framework ignores transitional zones that facilitate both security and social interaction;
- Excessive visibility and its paradoxes: While visibility is a cornerstone of CPTED, overreliance on surveillance technologies (e.g., cameras) and transparent designs can disrupt peer socialization and raise privacy concerns [2,24]. Transparency, intended to enable casual supervision, may inadvertently expose students to unwanted attention or interruptions, undermining their perceived safety [6]. Visual connectivity between spaces can also yield counterproductive effects, such as bystander fixation during conflicts [25];
- Isolated security interventions: Conventional approaches prioritize fragmented measures over holistic spatial performance. These interventions often distort spatial layouts, creating compensatory blind spots and compromising their educational functionality.
1.2. Computational Morphology: Bridging Design and Security
- Space syntax: Introduced by Hillier and Hanson, space syntax is a theoretical and computational approach that applies graph theory to analyze spatial configurations [39,40]. Unlike traditional architectural analyses which are focused on the physical form of buildings, space syntax emphasizes topological relationships—how spaces connect, integrate, and sequence within a system [41]—and builds bridge a between spatial features and behavioral patterns [42]. Key elements in space syntax include axial lines, convex spaces, integration, connectivity, and depth. These metrics reveal how spatial arrangements influence the flow of activities, social behaviours, and interaction patterns [43];
- Parametric modelling: parametric modelling translates spatial relationships into mathematical formulations, shifting design from being qualitatively subjective to being quantitatively rigorous. Parametric design facilitates exploring design alternatives and optimizing spatial configurations based on a set of predefined constraints [44]. It is particularly useful for understanding the relationship between geometry and spatial performance, and includes visibility, circulation, and environmental factors;
- Computational methods and algorithms: These methods involve the use of computer algorithms to solve complex design problems. One popular tool is evolutionary algorithms (EAs), which can automate the exploration of complex design spaces, optimizing solutions for multi-objective problems [35]. Rule-based generative systems encode design logic into computational workflows, enabling data-driven spatial analyses and iterative refinements.
2. Material and Methods
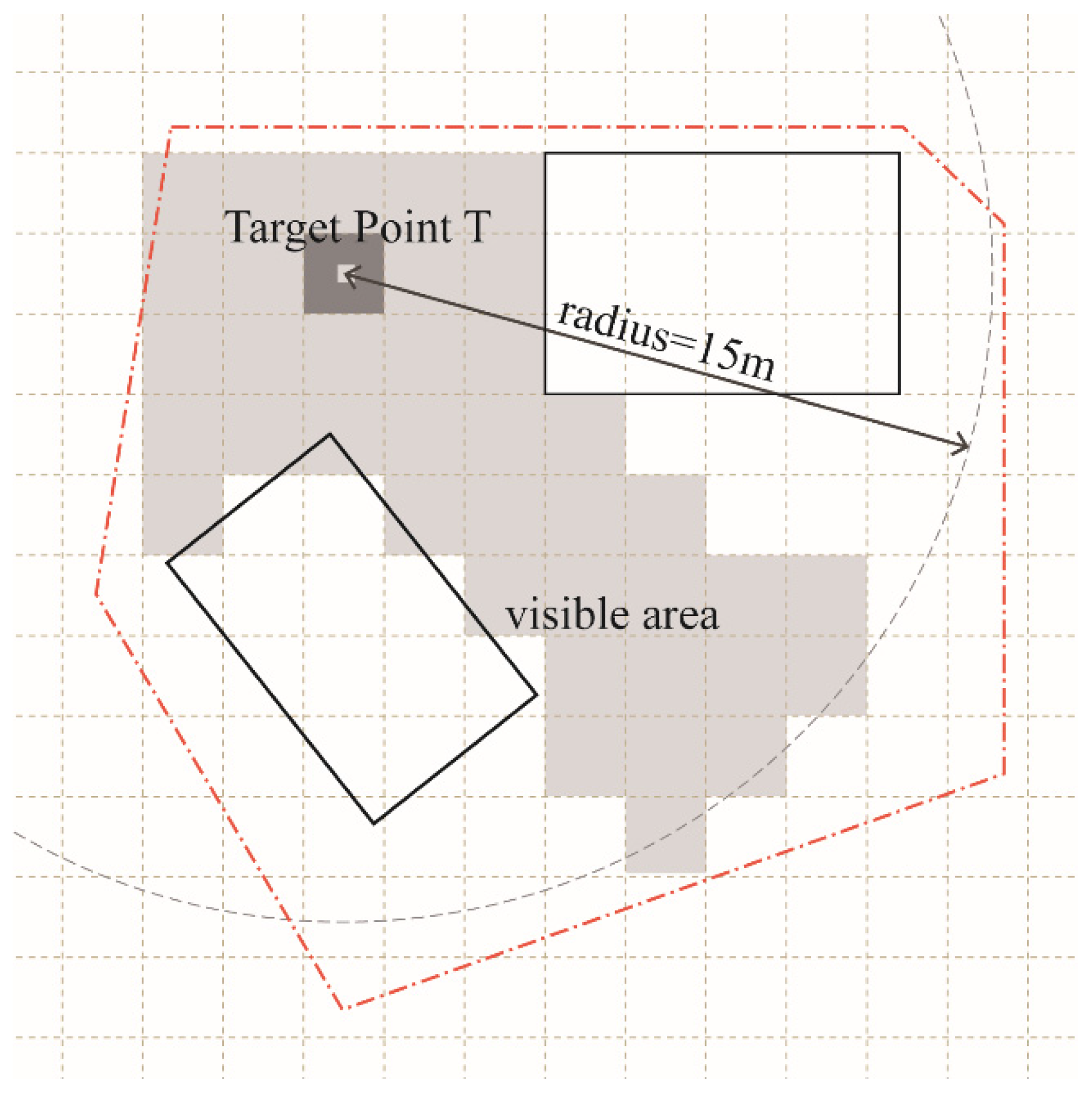
2.1. Natural Visibility Metrics in Campus Safety Evaluation
2.2. Algorithmic Iteration and Spatial Analysis for Campus Layout Optimization
2.2.1. Campus Layout Configuration Generates Simulation
- 1)
- Although the functional configuration may change, the building form generally remains unchanged, and, consequently, the morphology of public spaces typically remains consistent as well;
- 2)
- When changes in the functional configuration lead to alterations in the morphology of public spaces, the building form is often modified concurrently. In such instances, the influence cannot be attributed to a single factor, making it challenging to evaluate;
- 3)
- If vertical changes in the building layout entail modifications to the spatial relationships between different buildings, both the building form and density will undergo corresponding adjustments. In these scenarios, the variables are no longer singular.
2.2.2. Morphological Features Extraction of Public Space
- (1)
- Determine the quantity of edges n, and then generate n degrees ai (i ∈ [1, n]), sorting them in ascending order;
- (2)
- Generate n distances di. The vertices can be uniquely determined in a polar coordinate system by ai and di. These vertices are then connected sequentially to form a polygon;
- (3)
- Scale this polygon until its area equals S.
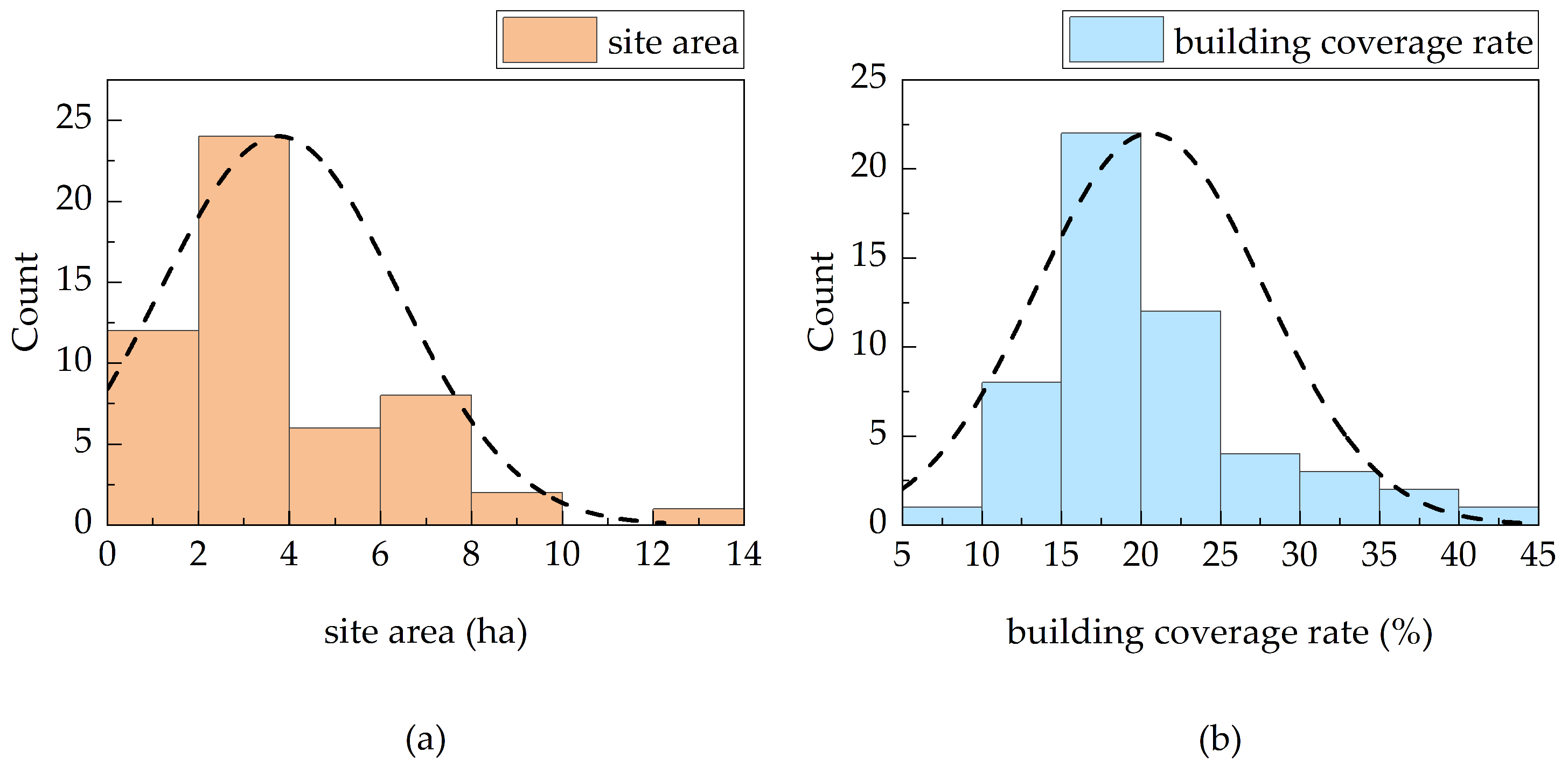
2.3. Case Selection
3. Results
3.1. Building Layout with Natural Surveillance
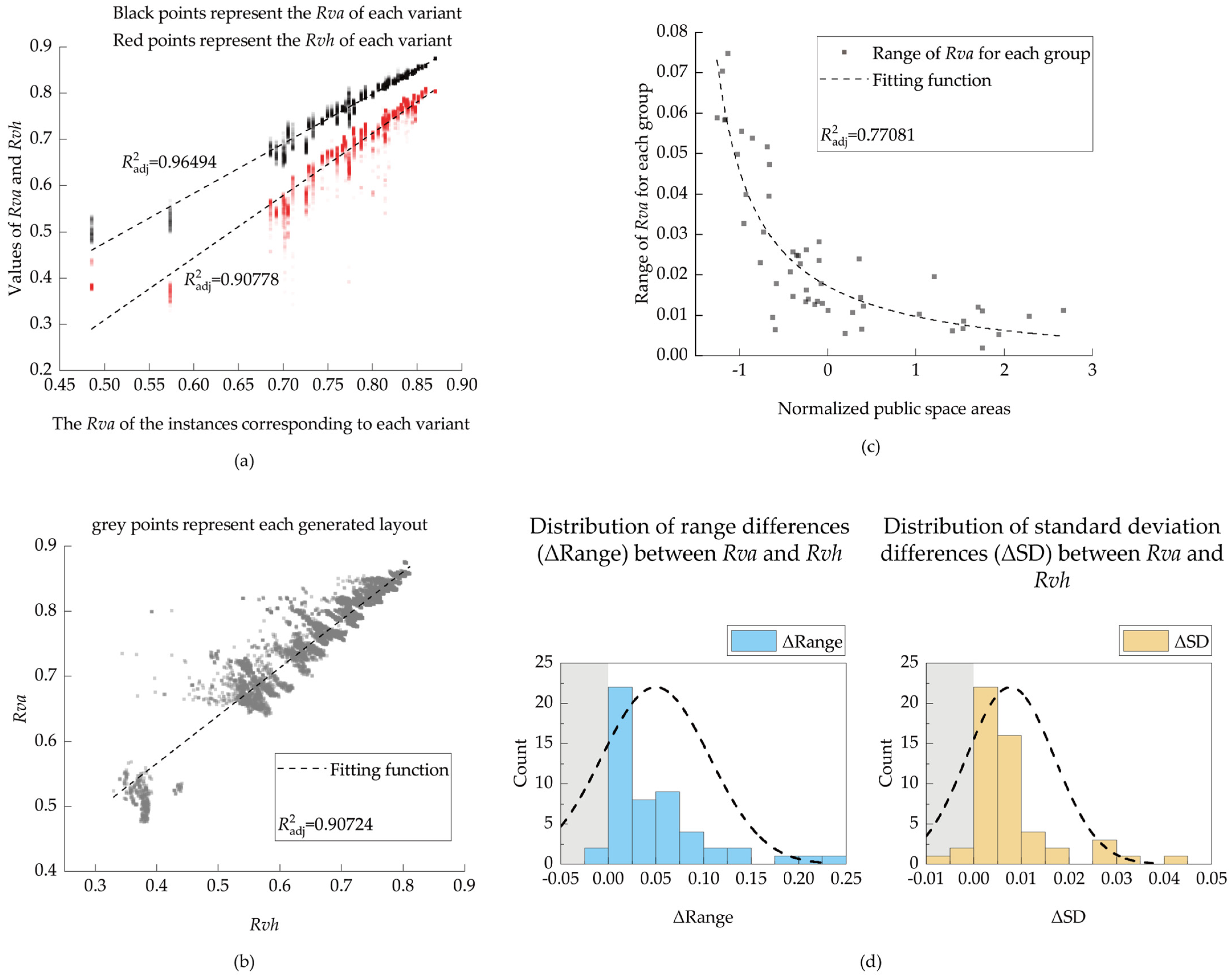
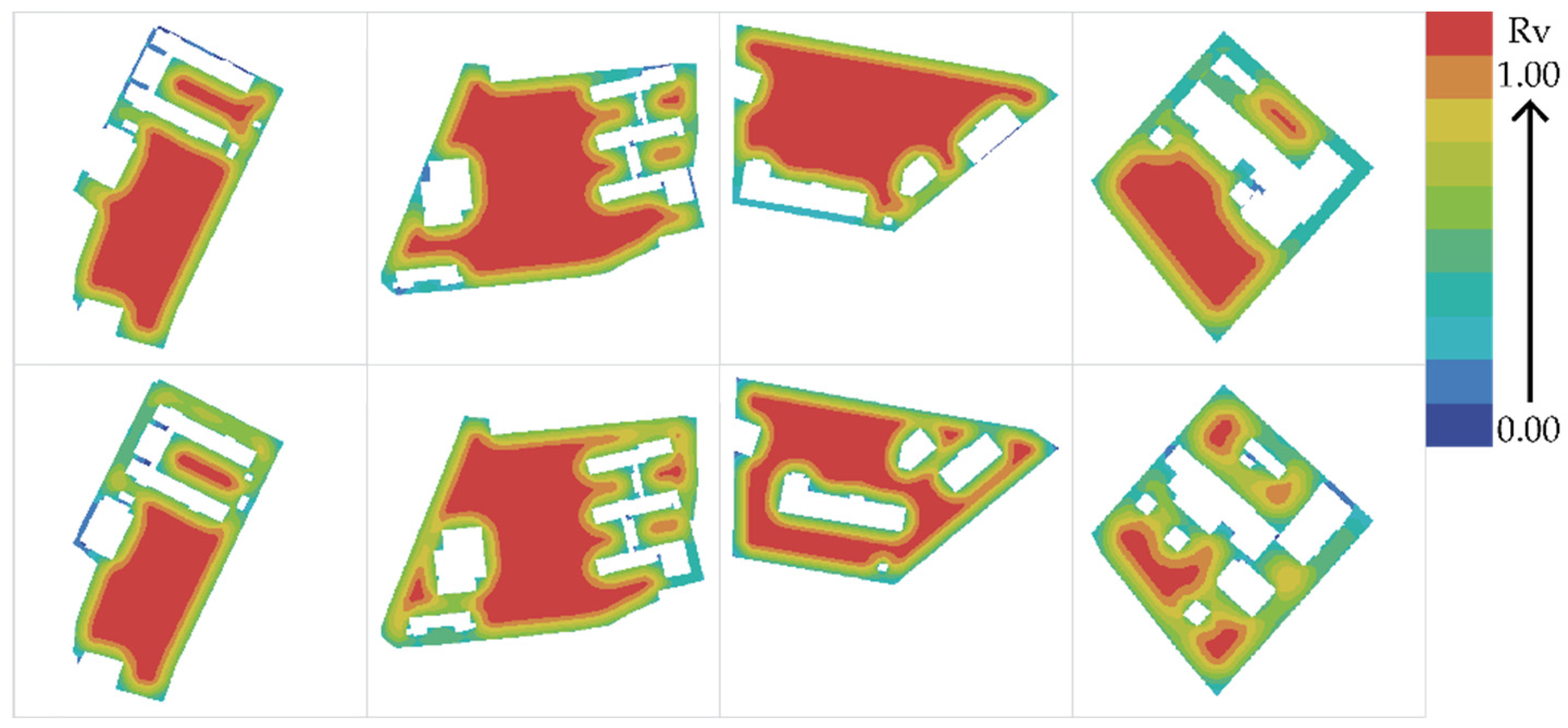
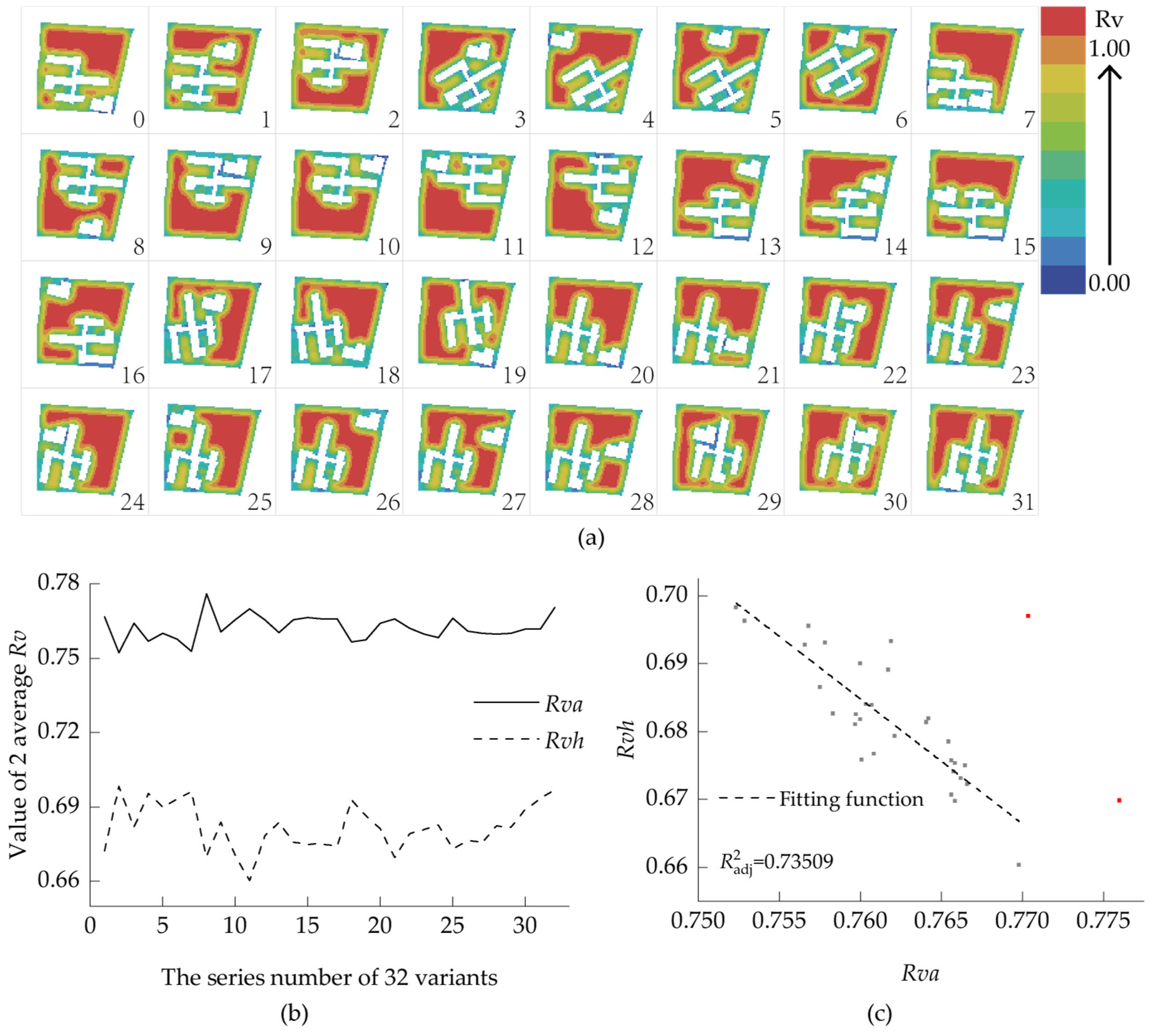
3.1.1. General Relationships Between Building Layouts and Rva
3.1.2. The Analysis of High-Occlusion Spaces
- (1)
- The Rva weights all spaces equally, favoring concentrated high-visibility clusters;
- (2)
- The Rvh penalizes low-visibility extremes, requiring homogeneous visibility distribution.
3.2. Public Space Form
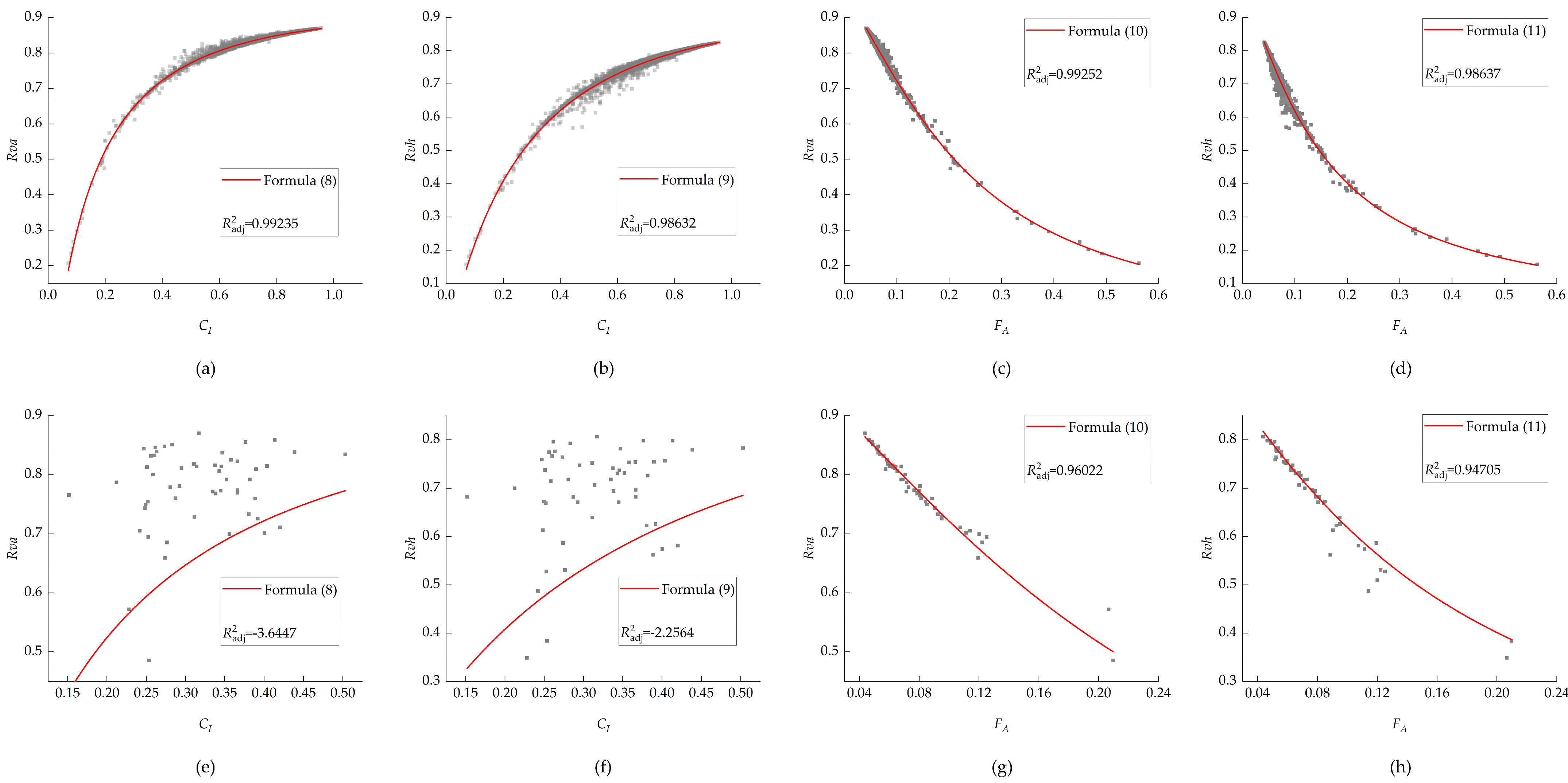
3.2.1. The Correlation Between Public Space Density and Natural Visibility
3.2.2. The Correlation Between Public Space Shape and Natural Visibility
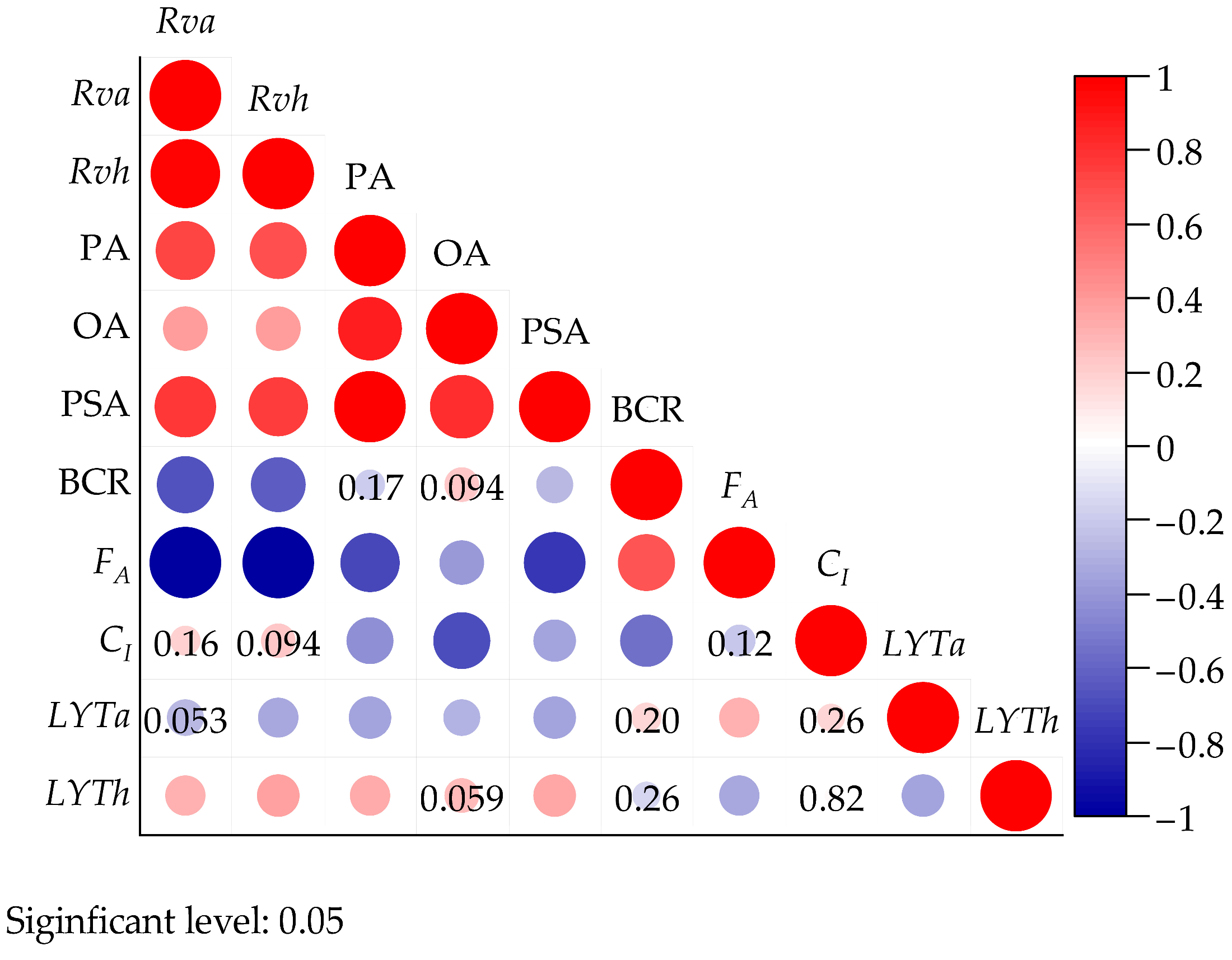
3.3. Integrated Impacts of Spatial Configurations on Natural Visibility
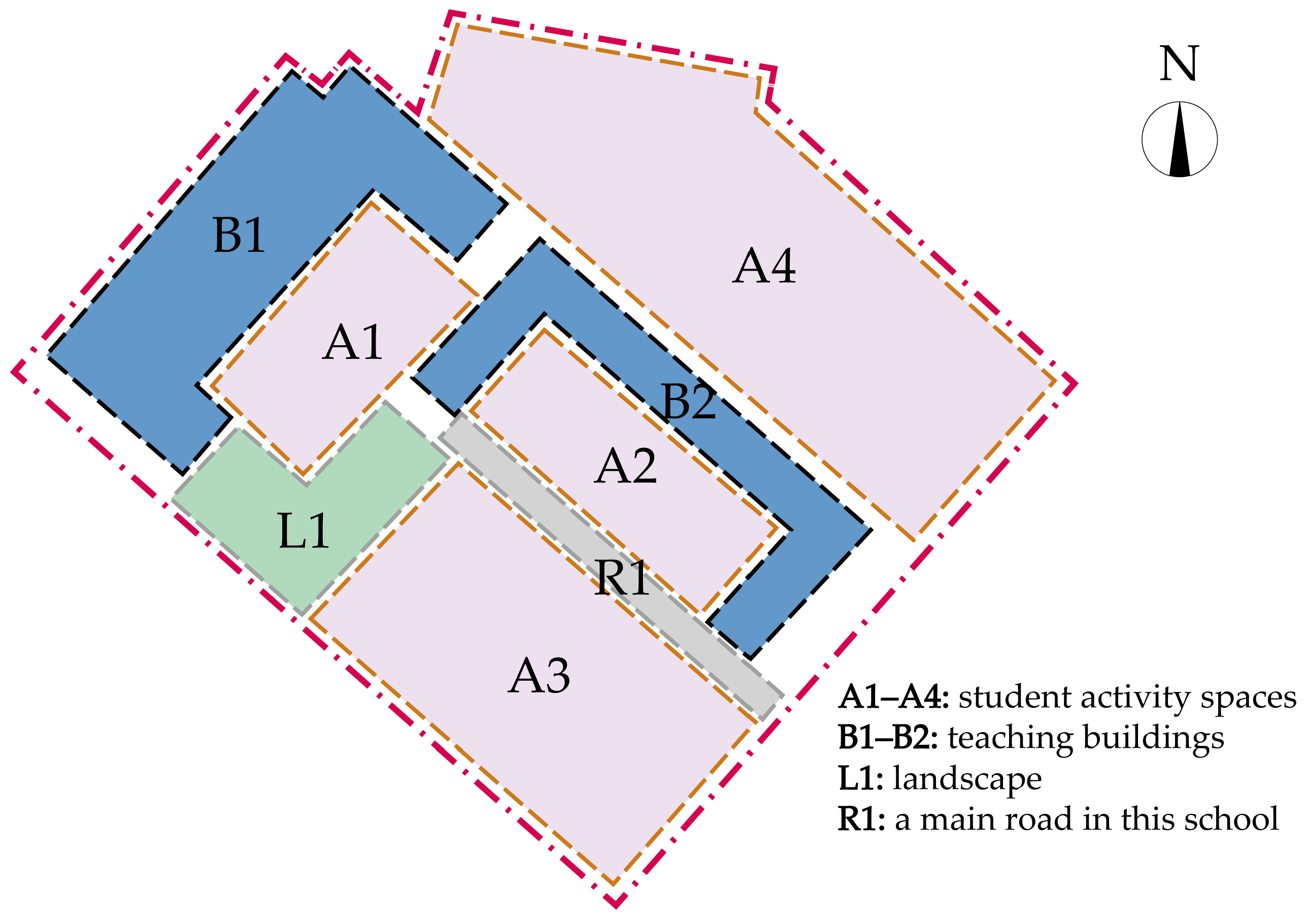
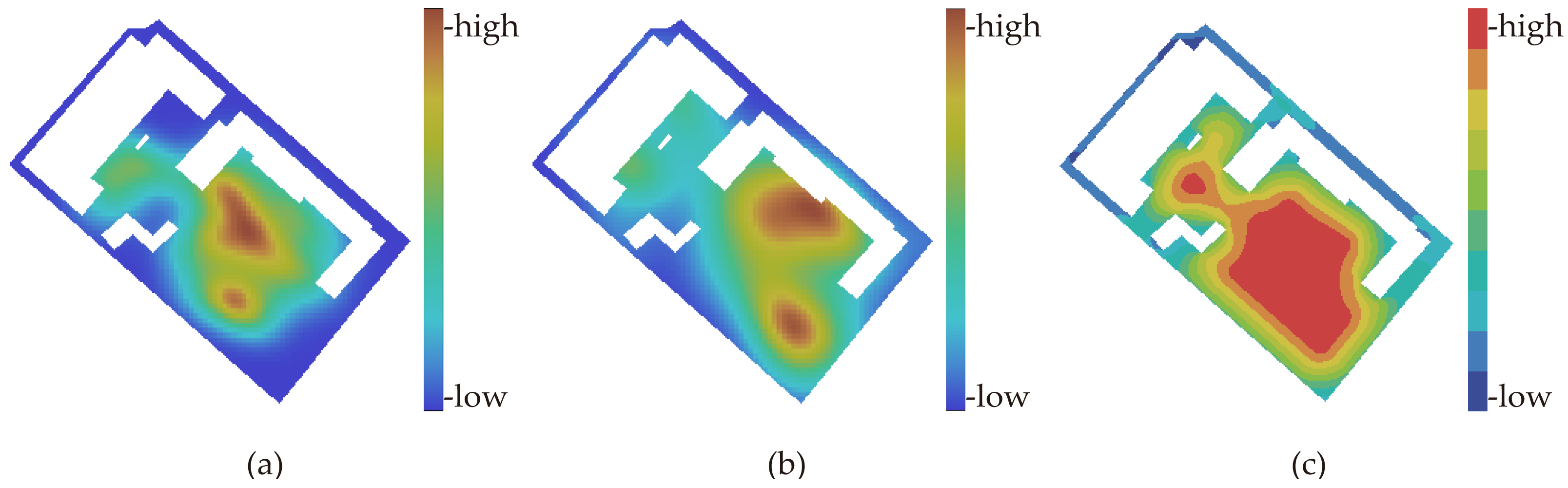
4. The Spatial Distribution of Student Activities for the Validation of the Natural Visibility Rate Results
- A1–A4: designated student congregation zones during non-instructional intervals, with specialized programmatic allocations: A3: hardscape recreational facility with basketball courts; A4: synthetic turf playground integrating football field infrastructure;
- R1: primary vehicular thoroughfare governed by temporal access restrictions (vehicle prohibition during education operations: 08:00–18:00);
- L1: ecological buffer zone exhibiting minimal pedestrian interaction frequencies, serving primarily as visual relief space.
5. Discussion
5.1. Building Layout and Campus Safety
5.2. Public Space Morphology and Campus Safety
5.3. Reconciling Natural Visibility and Safety in Campus Design
5.4. Digital Technology for Solving Architectural Problems
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
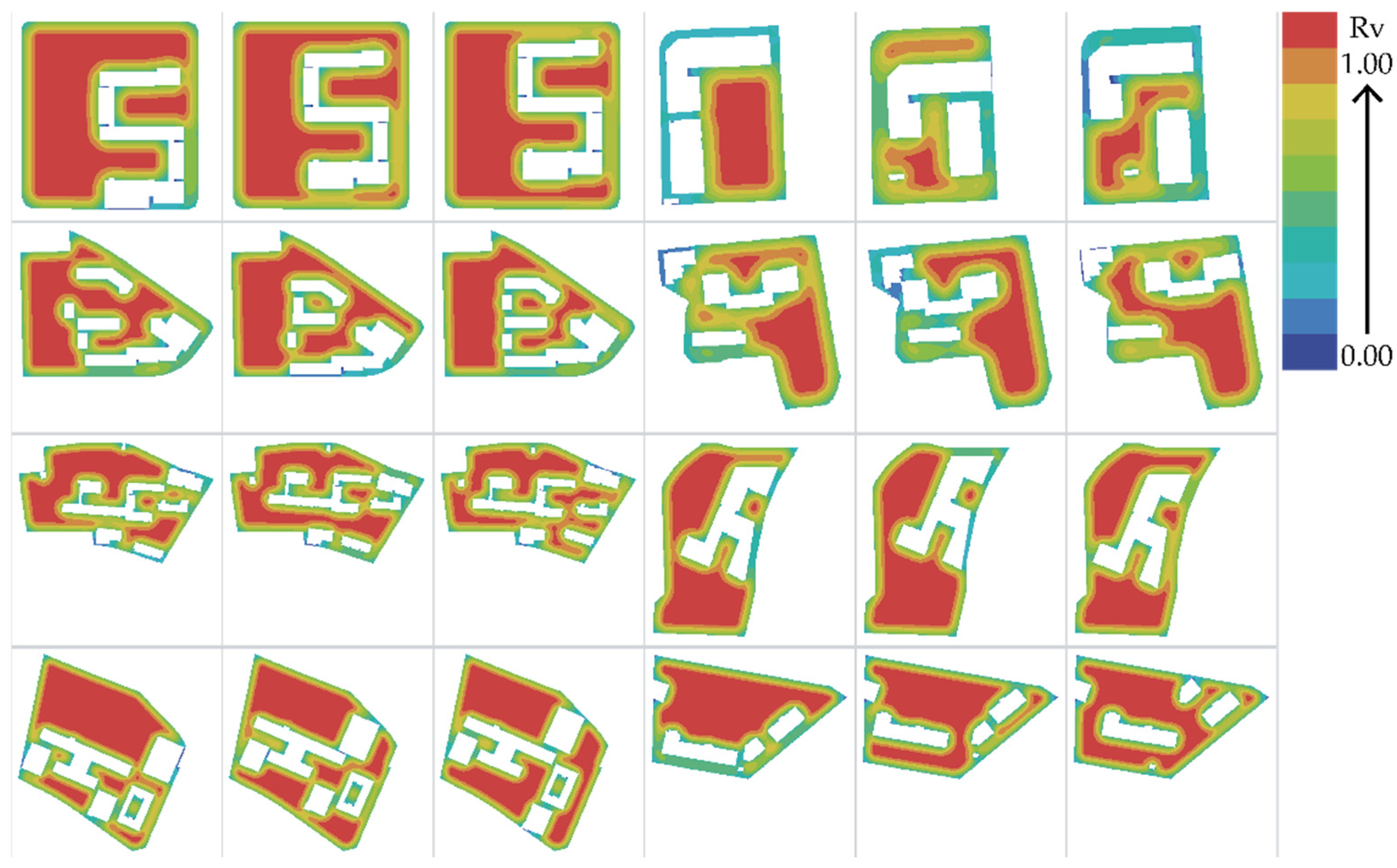
Appendix C
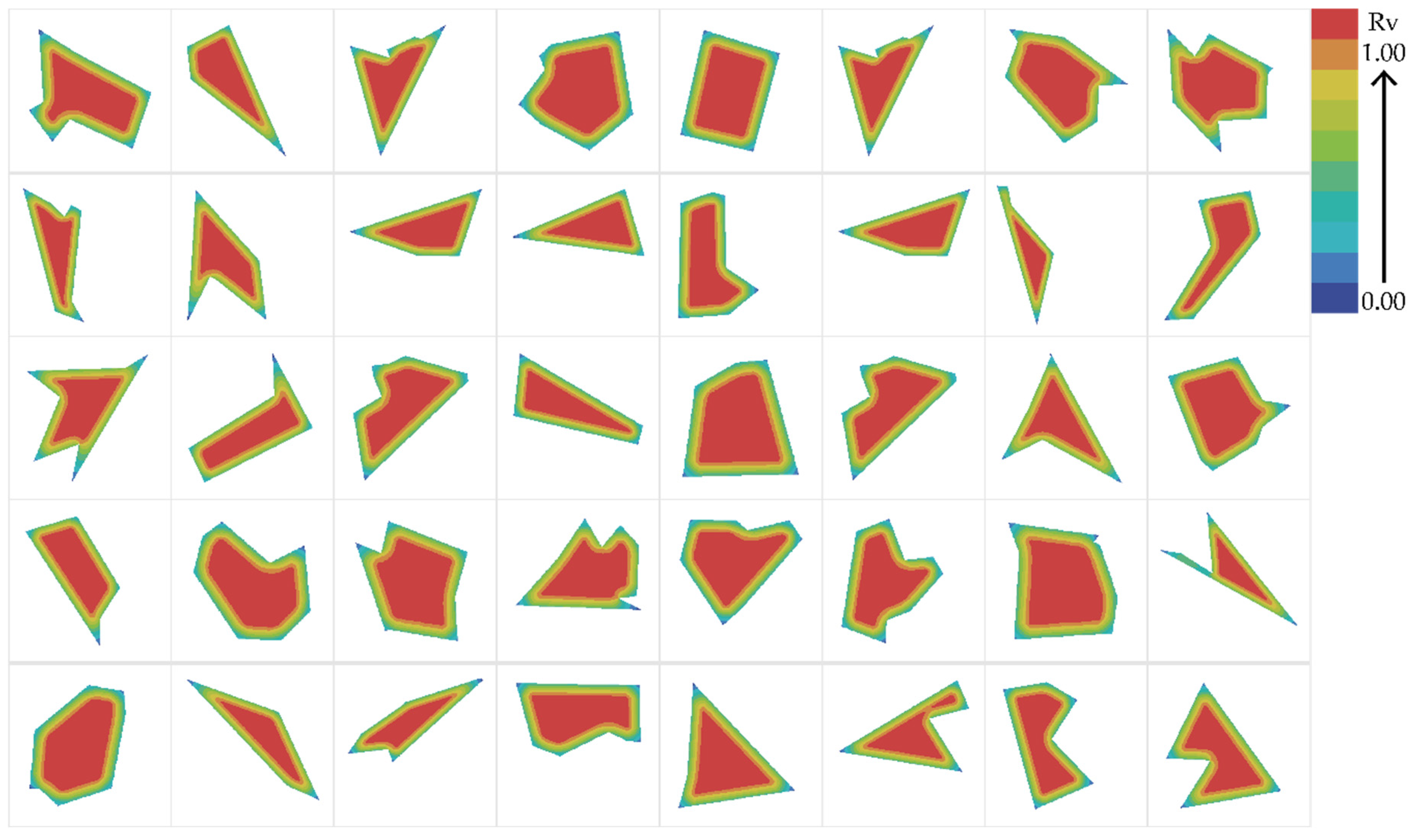
Appendix D
References
- Cornell, D.G.; Mayer, M.J.; Sulkowski, M.L. History and Future of School Safety Research. Sch. Psychol. Rev. 2020, 50, 143–157. [Google Scholar] [CrossRef]
- Addington, L.A. Cops and Cameras: Public School Security as a Policy Response to Columbine. Am. Behav. Sci. 2009, 52, 1426–1446. [Google Scholar] [CrossRef]
- Wood, S.N. Mapping School Geographies: Teaching and Learning in Unsafe Places. J. Sch. Violence 2005, 4, 71–89. [Google Scholar] [CrossRef]
- Ministry of Education of the People’s Republic of China. Fortifying Campus Safety with a Sense of Responsibility That Is “Always on Our Minds”. China Education News, 30 January 2024. [Google Scholar]
- Gooren, J. The Logic of CPTED for Public Space or the Social Potential of Physical Security. Crime Law Soc. Change 2023, 79, 417–436. [Google Scholar] [CrossRef]
- Perumean-Chaney, S.E.; Sutton, L.M. Students and Perceived School Safety: The Impact of School Security Measures. Am. J. Crim. Justice 2013, 38, 570–588. [Google Scholar] [CrossRef]
- Lamoreaux, D.; Sulkowski, M.L. An Alternative to Fortified Schools: Using Crime Prevention Through Environmental Design (CPTED) to Balance Student Safety and Psychological Well-Being. Psychol. Sch. 2020, 57, 152–165. [Google Scholar] [CrossRef]
- Sohn, D.-W. Residential Crimes and Neighbourhood Built Environment: Assessing the Effectiveness of Crime Prevention through Environmental Design (CPTED). Cities 2016, 52, 86–93. [Google Scholar] [CrossRef]
- Hunter, J.; Garius, L.; Hamilton, P.; Wahidin, A. Who Steals from Shops, and Why? A Case Study of Prolific Shop Theft Offenders. In Retail Crime; Crime Prevention and Security Management; Palgrave Macmillan: Cham, Switzerland, 2018; pp. 71–97. [Google Scholar] [CrossRef]
- Seo, S.Y.; Lee, K.H. Effects of Changes in Neighbourhood Environment Due to the CPTED Project on Residents’ Social Activities and Sense of Community: A Case Study on the Cheonan Safe Village Project in Korea. Int. J. Urban Sci. 2017, 21, 326–343. [Google Scholar] [CrossRef]
- Son, D.; Im, B.; Her, J.; Kim, S.-N. Effects of CPTED Principles on Intention to Burgle in High-Density Low-Rise Residential Areas of South Korea: A Virtual Reality Experiment. Sage Open 2024, 14, 21582440241296723. [Google Scholar] [CrossRef]
- Bradshaw, C.P.; Milam, A.J.; Furr-Holden, C.D.M.; Lindstrom Johnson, S. The School Assessment for Environmental Typology (SAfETy): An Observational Measure of the School Environment. Am. J. Community Psychol. 2015, 56, 280–292. [Google Scholar] [CrossRef]
- Vagi, K.J.; Stevens, M.R.; Simon, T.R.; Basile, K.C.; Carter, S.P.; Carter, S.L. Crime Prevention Through Environmental Design (CPTED) Characteristics Associated With Violence and Safety in Middle Schools. J. Sch. Health 2018, 88, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Schneider, R.H.; Kitchen, T.; Schneider, R.H. Planning for Crime Prevention; Routledge: London, UK, 2002. [Google Scholar]
- Liu, C.; Zhang, Y.; Zhang, J. Optimal Design for the Elementary School Campus Space Based on CPTED Theory. Urban. Archit. 2018, 2, 55–58. [Google Scholar]
- Ju, C. Research on the Status of Rural Idle Schools and Building Reform in Weihai. Master’s Thesis, China Central Academy of Fine Arts, Beijing, China, 2020. [Google Scholar]
- Hu, R. Based on CPTED Theory, the Space Design of Dormitory Area in Primary and Middle Schools Against Bullying. Master’s Thesis, University of Jinan, Jinan, China, 2021. [Google Scholar]
- Fujii, T.; Fujiwara, Y.; Oikawa, K. A Quantitative Analysis of Natural Surveillance at Elementary Schools-Evaluation Method Based on Perspectives from Both Outside Visibility and Visibility from Inside Buildings. J. Asian Archit. Build. Eng. 2013, 12, 17–23. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Hu, Z.; Tang, Y.; Xie, J. Natural Visibility Measurement of Public Space in Primary and Secondary Schools. Sci. Technol. Eng. 2019, 19, 342–349. [Google Scholar]
- Li, C. Optimization Design of Xiamen Bindong Primary School Based on Natural Visibility Rate Simulation of Public Space. Fujian Constr. Sci. Technol. 2024, 13–15. [Google Scholar]
- Cozens, T.P. Love A Review and Current Status of Crime Prevention through Environmental Design (CPTED) (Article). J. Plan. Lit. 2015, 30, 393–412. [Google Scholar] [CrossRef]
- Ekblom, P. Redesigning the Language and Concepts of Crime Prevention through Environmental Design. In Proceedings of the Criminology and Criminal Justice, Ajman, United Arab Emirates, 11–14 March 2013. [Google Scholar]
- Ekblom, P. Deconstructing CPTED… and Reconstructing It for Practice, Knowledge Management and Research. Eur. J. Crim. Policy Res. 2011, 17, 7–28. [Google Scholar] [CrossRef]
- Braggs, D. Webcams in Classrooms: How Far Is Too Far. JL Educ. 2004, 33, 275. [Google Scholar]
- Altenburger, E.; Russell, L. Safety and Exposure in Transparent School Interiors: Patterned User Perceptions of Glass. J. Inter. Des. 2023, 48, 223–241. [Google Scholar] [CrossRef]
- Yin, X. The Research on the Investigation and Countermeasures of Violent Crimes on Campus in Recent Years. J. Xingtai Polytech. Coll. 2023, 40, 69–72. [Google Scholar]
- Voight, A.; Nation, M. Practices for Improving Secondary School Climate: A Systematic Review of the Research Literature. Am. J. Community Psychol. 2016, 58, 174–191. [Google Scholar] [CrossRef] [PubMed]
- Altenburger, E.; Wellenreiter, B.R. Where to Hang Out: Interplay Between School Building Characteristics, Authority Structures, and School Micro-Climates. Child. Youth Environ. 2021, 31, 1–33. [Google Scholar] [CrossRef]
- Kwon, C. Architectural Typologies of School Outdoor Spaces by Cases Study of the School Design Guidelines. Int. J. Sustain. Build. Technol. Urban Dev. 2022, 13, 231–240. [Google Scholar] [CrossRef]
- Shach-Pinsly, D. Measuring Security in the Built Environment: Evaluating Urban Vulnerability in a Human-Scale Urban Form. Landsc. Urban Plan. 2019, 191, 103412. [Google Scholar] [CrossRef]
- Oliveira, V. Urban Morphology: An Introduction to the Study of the Physical Form of Cities; Springer International Publishing: Cham, Switzerland, 2016; ISBN 3-319-32083-1. [Google Scholar]
- Kropf, K. The Handbook of Urban Morphology; John Wiley & Sons: Hoboken, NJ, USA, 2017; ISBN 1-118-74782-8. [Google Scholar]
- Ye, Y.; Li, D.; Liu, X. How Block Density and Typology Affect Urban Vitality: An Exploratory Analysis in Shenzhen, China. Urban Geogr. 2018, 39, 631–652. [Google Scholar] [CrossRef]
- Oliveira, V. Morpho: A Methodology for Assessing Urban Form. Urban Morphol. 2013, 17, 21–33. [Google Scholar] [CrossRef]
- Makki, M.; Showkatbakhsh, M.; Tabony, A.; Weinstock, M. Evolutionary Algorithms for Generating Urban Morphology: Variations and Multiple Objectives. Int. J. Archit. Comput. 2019, 17, 5–35. [Google Scholar] [CrossRef]
- Kachroo, P.; Bhatia, S.Y.; Patil, G.R. Computational Geometry-Based Kinematic Morphology for Urban Growth. Transp. Dev. Econ. 2024, 10, 11. [Google Scholar] [CrossRef]
- Desyllas, J.; Connoly, P.; Hebbert, F. Modelling Natural Surveillance. Environ. Plan. B Urban Anal. City Sci. 2003, 30, 643–655. [Google Scholar] [CrossRef]
- Rahimbakhsh, H.; Kohansal, M.E.; Tarkashvand, A.; Faizi, M.; Rahbar, M. Multi-Objective Optimization of Natural Surveillance and Privacy in Early Design Stages Utilizing NSGA-II. Autom. Constr. 2022, 143, 104547. [Google Scholar] [CrossRef]
- Hillier, B.; Leaman, A.; Stansall, P.; Bedford, M. Space Syntax. Environ. Plan. B Plan. Des. 1976, 3, 147–185. [Google Scholar] [CrossRef]
- Hillier, B. Space Is the Machine: A Configurational Theory of Architecture; Space Syntax: London, UK, 2007. [Google Scholar]
- Fu, J.-M.; Tang, Y.-F.; Zeng, Y.-K.; Feng, L.-Y.; Wu, Z.-G. Sustainable Historic Districts: Vitality Analysis and Optimization Based on Space Syntax. Buildings 2025, 15, 657. [Google Scholar] [CrossRef]
- Karimi, K. A Configurational Approach to Analytical Urban Design: ‘Space Syntax’ Methodology. Urban Des. Int. 2012, 17, 297–318. [Google Scholar] [CrossRef]
- Cutumisu, N.; Spence, J.C. Exploring Associations Between Urban Environments and Children’s Physical Activity: Making the Case for Space Syntax. J. Sci. Med. Sport 2009, 12, 537–538. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Li, B. From Knowledge Encoding to Procedural Generation for Early-Stage Layout Design: A Case of Linear Shopping Centres. Front. Archit. Res. 2025, 14, 282–294. [Google Scholar] [CrossRef]
- Safizadeh, M.; Hedayati Marzbali, M.; Abdullah, A.; Maghsoodi Tilaki, M.J. Integrating Space Syntax and CPTED in Assessing Outdoor Physical Activity. Geogr. Res. 2024, 62, 309–330. [Google Scholar] [CrossRef]
- Nubani, L.; Wineman, J. The Role of Space Syntax in Identifying the Relationship between Space and Crime. In Proceedings of the Proceedings of the 5th Space Syntax Symposium on Space Syntax, Delft, The Netherlands, 13–17 June 2005; pp. 13–17. [Google Scholar]
- Arghyani, M. Evaluating the Effect of Physical Components on the Promotion of the Sense of Security in Educational Spaces from the Perspective of Students; Case Study: High Schools of Bojnourd. Arman. Archit. Urban Dev. 2020, 13, 1–16. [Google Scholar] [CrossRef]
- GB 50099—2011; Code for Design of School. Ministry of Housing and Urban-Rural Development of the People’s Republic of China China Architecture Publishing & Media Press: Beijing, China, 2010.
- Crowe, T.D. Crime Prevention Through Environmental Design; Butterworth-Heinemann: Oxford, UK, 1991. [Google Scholar]
- Armitage, R.; Monchuk, L.; Rogerson, M. It Looks Good, but What Is It Like to Live There? Exploring the Impact of Innovative Housing Design on Crime. Eur. J. Crim. Policy Res. 2011, 17, 29–54. [Google Scholar] [CrossRef]
- Byun, G.; Ha, M. Factors of a Surveillance Environment That Affect Burglaries in Commercial Districts. J. Asian Archit. Build. Eng. 2016, 15, 73–80. [Google Scholar] [CrossRef]
- Jong, M.D.; Wagenaar, W.A.; Wolters, G.; Verstijnen, I.M. Familiar Face Recognition as a Function of Distance and Illumination: A Practical Tool for Use in the Courtroom. Psychol. Crime Law 2005, 11, 87–97. [Google Scholar] [CrossRef]
- Loukaitou-Sideris, A.; Liggett, R.; Iseki, H.; Thurlow, W. Measuring the Effects of Built Environment on Bus Stop Crime. Environ. Plan. B Urban Anal. City Sci. 2001, 28, 255–280. [Google Scholar] [CrossRef]
- GB 50352—2019; Uniform Standard for Design of Civil Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China China Architecture Publishing & Media Press: Beijing, China, 2019.
- Alexander, C. A Pattern Language: Towns, Buildings, Construction; Oxford University Press: Oxford, UK, 1977; ISBN 0-19-972653-1. [Google Scholar]
- Wang, L.; Liu, J.; Zeng, Y.; Cheng, G.; Hu, H.; Hu, J.; Huang, X. Automated Building Layout Generation Using Deep Learning and Graph Algorithms. Autom. Constr. 2023, 154, 105036. [Google Scholar] [CrossRef]
- Bao, F.; Yan, D.-M.; Mitra, N.J.; Wonka, P. Generating and Exploring Good Building Layouts. ACM Trans. Graph. 2013, 32, 122. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, C.; Teng, M. Impact of Residential Building Layouts on Microclimate in a High Temperature and High Humidity Region. Sustainability 2020, 12, 1046. [Google Scholar] [CrossRef]
- Chang, Y.; Ai, Z.; Wargocki, P.; Liu, Y.; Hu, Y. Design of Convertible Patient Care Unit for Both Non-Pandemic and Pandemic Times: Prototype, Building Spatial Layout, and Ventilation Design. Build. Environ. 2024, 258, 111597. [Google Scholar] [CrossRef]
- Sepúlveda, G.K.; Romero, N.; Vidal-Silva, C.; Besoain, F.; Barriga, N.A. Barriga Semi-Automatic Building Layout Generation for Virtual Environments. IEEE Access 2024, 12, 87014–87022. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Ayyıldız, S.; Durak, Ş. Space Syntax Analysis of the Spatial Configuration of Yalova Traditional Rural Houses. Nexus Netw. J. 2024, 26, 27–48. [Google Scholar] [CrossRef]
- Li, W.; Goodchild, M.F.; Church, R. An Efficient Measure of Compactness for Two-Dimensional Shapes and Its Application in Regionalization Problems. Int. J. Geogr. Inf. Sci. 2013, 27, 1227–1250. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, X.; Zhang, F.; Gu, Y.; Zhou, X. Does Compact City Shape Matter to Residents’ Happiness? Cities 2023, 141, 104524. [Google Scholar] [CrossRef]
- Xing, X.; Shi, W.; Wu, X.; Liu, Y.; Wang, X.; Zhang, Y. Towards a More Compact Urban Form: A Spatial-Temporal Study on the Multi-Dimensional Compactness Index of Urban Form in China. Appl. Geogr. 2024, 171, 103368. [Google Scholar] [CrossRef]
- Properties, M.S. Polygon Shape Properties 2014. Available online: https://www.microimages.com/documentation/TechGuides/81PolyShape.pdf (accessed on 14 March 2025).
- Richardson, L.F. The Problem of Contiguity: An Appendix to Statistics of Deadly Quarrels. In General System Yearbook; The Society: Washington, DC, USA, 1961; Volume 6, pp. 139–187. [Google Scholar]
- Polsby, D.D.; Popper, R.D. The Third Criterion: Compactness as a Procedural Safeguard against Partisan Gerrymandering. Yale Law Policy Rev. 1991, 9, 301–353. [Google Scholar] [CrossRef]
- Peng, Z.; Jiang, M.; Liu, M.; He, T.; Jiang, N.; Huan, X. An Investigation into the Effects of Primary School Building Forms on Campus Wind Environment and Classroom Ventilation Performance. Appl. Sci. 2024, 14, 7174. [Google Scholar] [CrossRef]
- Gehl, J. Life Between Buildings: Using Public Space; Island Press: Washington, DC, USA, 2011. [Google Scholar]





| LYTa | LYTh | |
|---|---|---|
| LYTa | 1 | −0.357 * |
| LYTh | −0.357 * | 1 |
| LYTa | LYTh | |
|---|---|---|
| LYTa | 1 | −0.717 ** |
| LYTh | −0.717 ** | 1 |
| PA | OA | PSA | BCR | Rva | Rvh | |
|---|---|---|---|---|---|---|
| PA | / | 0.86792 *** | 0.9929 *** | −0.21593 | 0.73246 *** | 0.70424 *** |
| OA | 0.86792 *** | / | 0.82164 *** | 0.20311 | 0.41268 ** | 0.40082 ** |
| PSA | 0.9929 *** | 0.82164 *** | / | −0.2989 * | 0.78374 *** | 0.75835 *** |
| BCR | −0.21593 | 0.20311 | −0.2989 * | / | −0.68295 *** | −0.64353 *** |
| Rva | 0.73246 *** | 0.41268 ** | 0.78374 *** | −0.68295 | / | 0.96944 *** |
| Rvh | 0.70424 *** | 0.40082 ** | 0.75835 *** | −0.64353 *** | 0.96944 *** | / |
| Collinearity | Variables | VIF |
|---|---|---|
| High multicollinearity (VIF > 10) | BCR | 28.530 |
| FA | 25.174 | |
| Moderate multicollinearity (5 ≤ VIF ≤ 10) | CI | 6.390 |
| Low multicollinearity (VIF < 5) | PSA | 4.308 |
| LYTa | 1.261 | |
| LYTh | 1.160 |
| Collinearity | Variables | VIF |
|---|---|---|
| Moderate multicollinearity (5 ≤ VIF ≤ 10) | BCR | 5.670 |
| CI | 5.310 | |
| Low multicollinearity (VIF < 5) | PSA | 3.038 |
| LYTa | 1.257 | |
| LYTh | 1.142 |
| Coefficient | Standard Error | t-Value | p-Value | ||
|---|---|---|---|---|---|
| Rva (adjusted R2 = 0.970) | Intercept | 0.008 | 0.024 | 0.319 | 0.751 |
| PSA | 0.165 * | 0.050 | 3.339 | 0.002 | |
| BCR | −0.038 | 0.046 | −0.839 | 0.406 | |
| FA | −0.848 * | 0.053 | −16.046 | 0.000 | |
| CI | 0.070 | 0.045 | 1.551 | 0.128 | |
| LYTa | 0.021 | 0.027 | 0.794 | 0.431 | |
| LYTh | −0.042 | 0.026 | −1.628 | 0.110 | |
| Rvh (adjusted R2 = 0.950) | Intercept | −0.004 | 0.031 | −0.135 | 0.893 |
| PSA | 0.178 * | 0.065 | 2.760 | 0.008 | |
| BCR | −0.068 | 0.060 | −1.134 | 0.263 | |
| FA | −0.746 * | 0.069 | −10.818 | 0.000 | |
| CI | 0.090 | 0.059 | 1.527 | 0.134 | |
| LYTa | −0.029 | 0.035 | −0.830 | 0.411 | |
| LYTh | 0.125 * | 0.034 | 3.699 | 0.001 |
| Coefficient | Standard Error | t-Value | p-Value | ||
|---|---|---|---|---|---|
| Rva (adjusted R2 = 0.799) | Intercept | 0.007 | 0.061 | 0.122 | 0.903 |
| PSA | 0.677 | 0.097 | 6.976 | 0.000 | |
| BCR | −0.446 * | 0.098 | −4.568 | 0.000 | |
| CI | 0.310 * | 0.109 | 2.841 | 0.007 | |
| LYTa | 0.024 | 0.069 | 0.353 | 0.725 | |
| LYTh | −0.013 | 0.066 | −0.193 | 0.848 | |
| Rvh (adjusted R2 = 0.824) | Intercept | −0.004 | 0.058 | −0.074 | 0.941 |
| PSA | 0.628 * | 0.093 | 6.781 | 0.000 | |
| BCR | −0.426 * | 0.093 | −4.572 | 0.000 | |
| CI | 0.300 * | 0.104 | 2.889 | 0.006 | |
| LYTa | −0.027 | 0.066 | −0.402 | 0.690 | |
| LYTh | 0.150 | 0.063 | 2.385 | 0.021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhou, H.; Xie, J.; Tang, Y.; Liu, S. Impact of Public Space in Primary and Secondary Schools Based on Natural Visibility Ratio. Buildings 2025, 15, 1472. https://doi.org/10.3390/buildings15091472
Liu F, Zhou H, Xie J, Tang Y, Liu S. Impact of Public Space in Primary and Secondary Schools Based on Natural Visibility Ratio. Buildings. 2025; 15(9):1472. https://doi.org/10.3390/buildings15091472
Chicago/Turabian StyleLiu, Feng, Hao Zhou, Jiangtao Xie, Yue Tang, and Shuyu Liu. 2025. "Impact of Public Space in Primary and Secondary Schools Based on Natural Visibility Ratio" Buildings 15, no. 9: 1472. https://doi.org/10.3390/buildings15091472
APA StyleLiu, F., Zhou, H., Xie, J., Tang, Y., & Liu, S. (2025). Impact of Public Space in Primary and Secondary Schools Based on Natural Visibility Ratio. Buildings, 15(9), 1472. https://doi.org/10.3390/buildings15091472





