Application of Advanced Multi-Parameter Monitoring in Concrete Structure Defect Detection: Integrating Thermal Integrity Profiling and Strain Analysis
Abstract
1. Introduction
2. Field Monitoring of Temperature and Strain in Underground Continuous Walls During Hydration
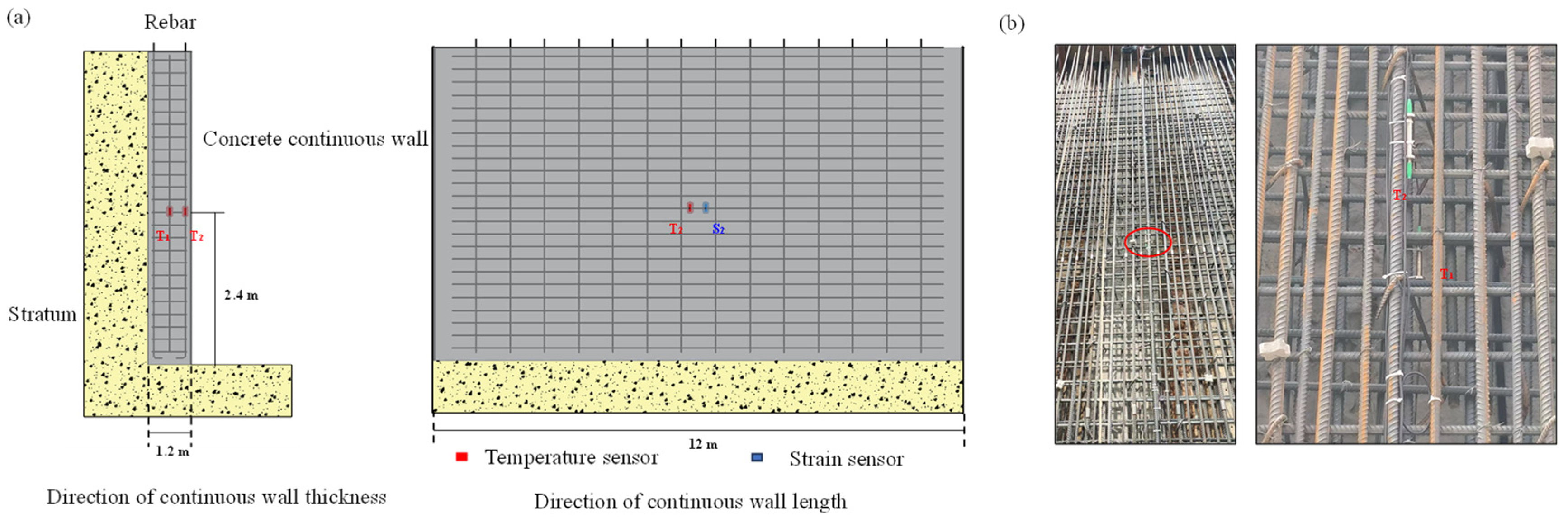
2.1. Project Overview
2.2. Sensors and Monitoring Plan
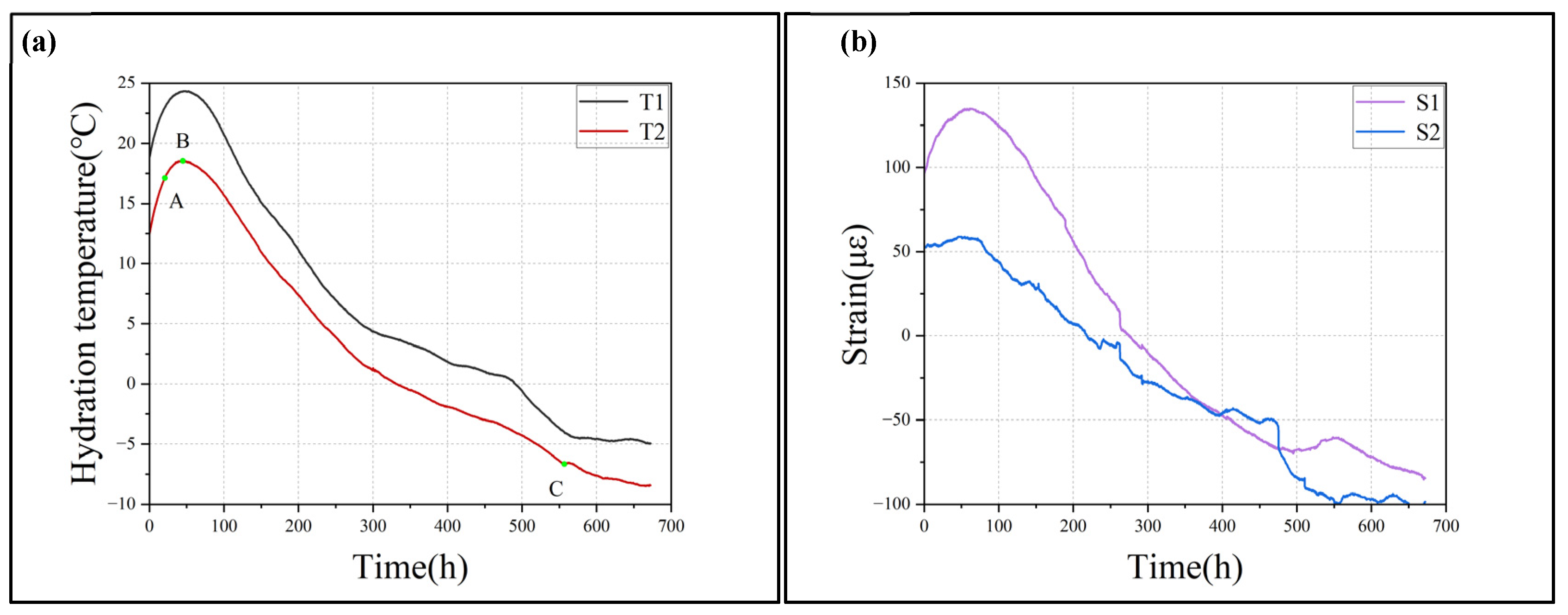
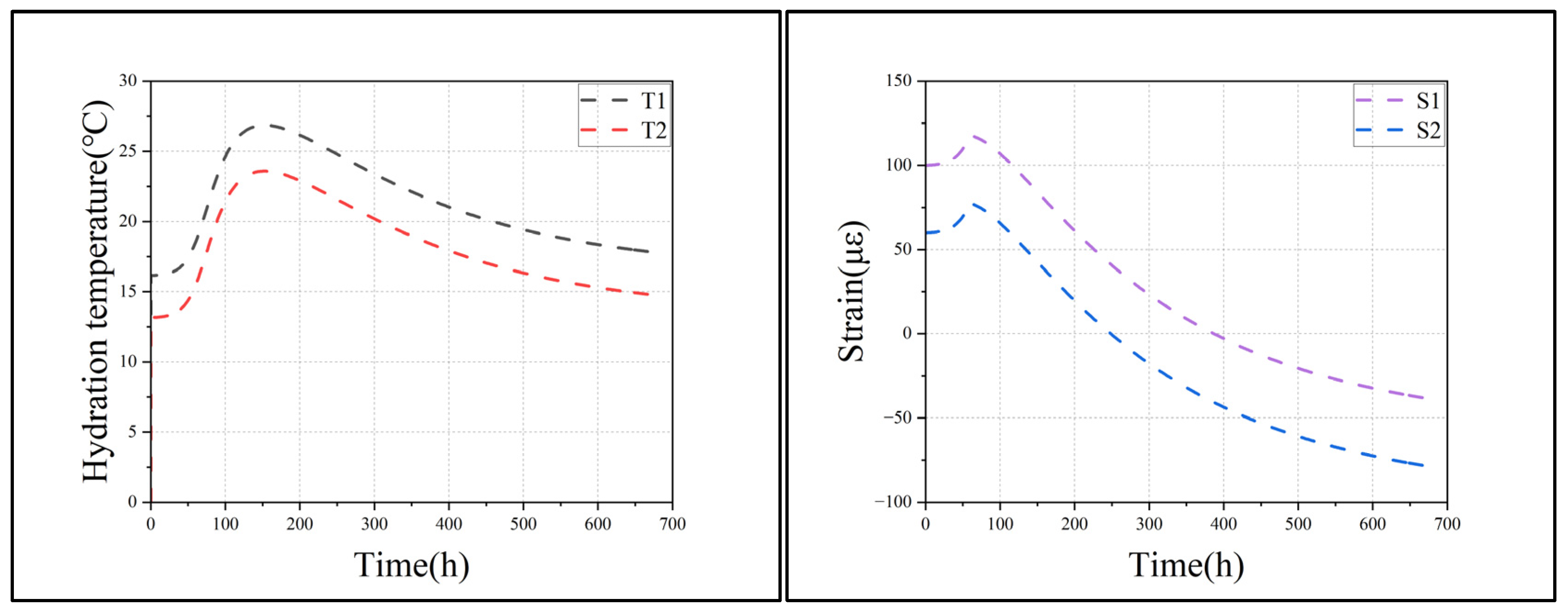
2.3. Analysis of Monitoring Results
- Rapid Hydration and Accelerated Temperature Rise: After concrete pouring is completed, the hydration effect becomes significant. During this stage, the hydration degree of the concrete increases rapidly, and the heat released from the hydration reaction exceeds heat loss from the surrounding environment due to convection and heat conduction, causing a rapid increase in concrete temperature. At 21 h after pouring (Point A), the rate of heat release reaches its maximum.
- Slower Hydration and Continuous Temperature Rise: After 21 h, the hydration heat effect slows down, and the internal temperature of the concrete continues to rise steadily until 44 h after pouring (Point B), at which point the internal and external temperatures of the wall reach their peak. This characteristic time point (44 h) was identified by analyzing the measured temperature evolution curves obtained from the fiber-optic sensing system during the transition from temperature rise to decline.
- Hydration Cooling Stage: In this phase, the hydration rate decreases, and the heat released is less than heat loss caused by convection and heat conduction. As a result, the concrete temperature decreases. The temperature continues to decrease until 153 h after pouring (Point D), when the hydration effect is essentially complete. This point (153 h) was selected based on the observation that the concrete temperature stabilized, indicating the hydration process was essentially complete. The hydration heat effect shows a phased pattern, initially slowing, and then accelerating, followed by stabilization and gradual dissipation. The temperature changes throughout the hydration stage are influenced by both the heat generated from hydration and heat dissipation from the concrete surface.
3. Finite Element Modeling
3.1. Basic Principles
3.1.1. Heat Generation and Thermal Diffusion
3.1.2. Stress–Strain Constitutive Relationship
3.1.3. Hydration Equation
3.1.4. Concrete Ageing Effects
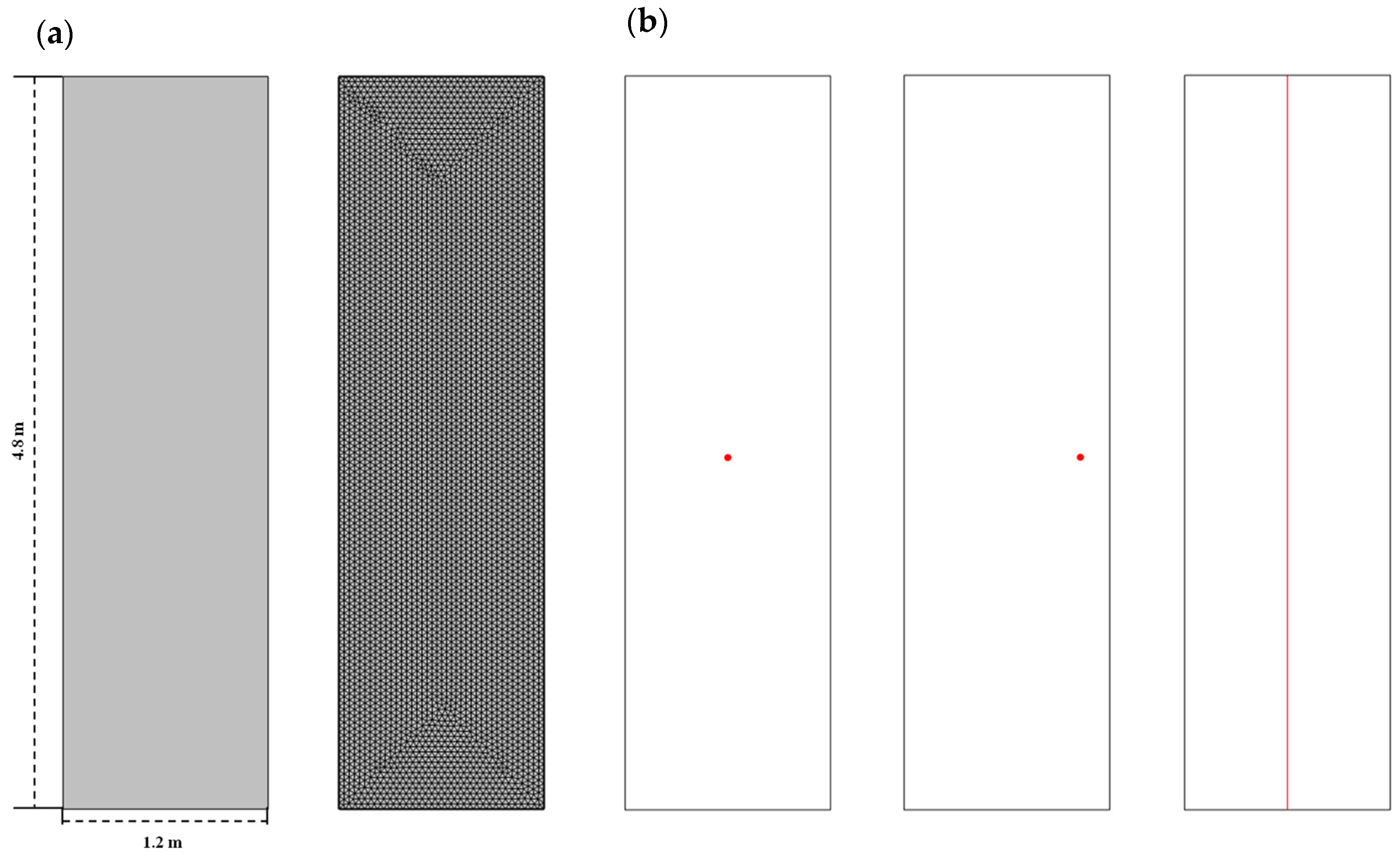
3.2. Model Parameters
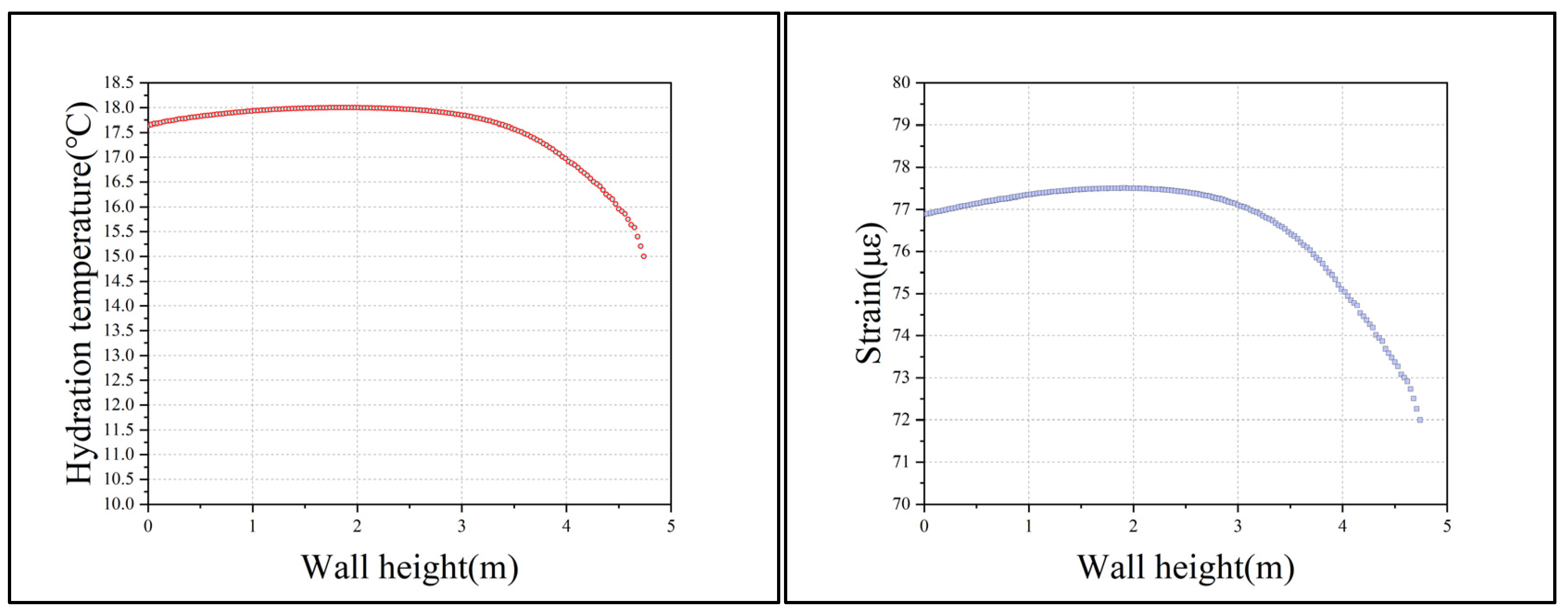
3.3. Validation with Experimental Data
4. Analysis of the Influence of Different Defect Types on the Temperature and Strain Evolution of the Wall During Hydration
4.1. Temperature and Strain Distribution of the Wall During Hydration When the Monitoring Line Does Not Pass Through the Defect Zone
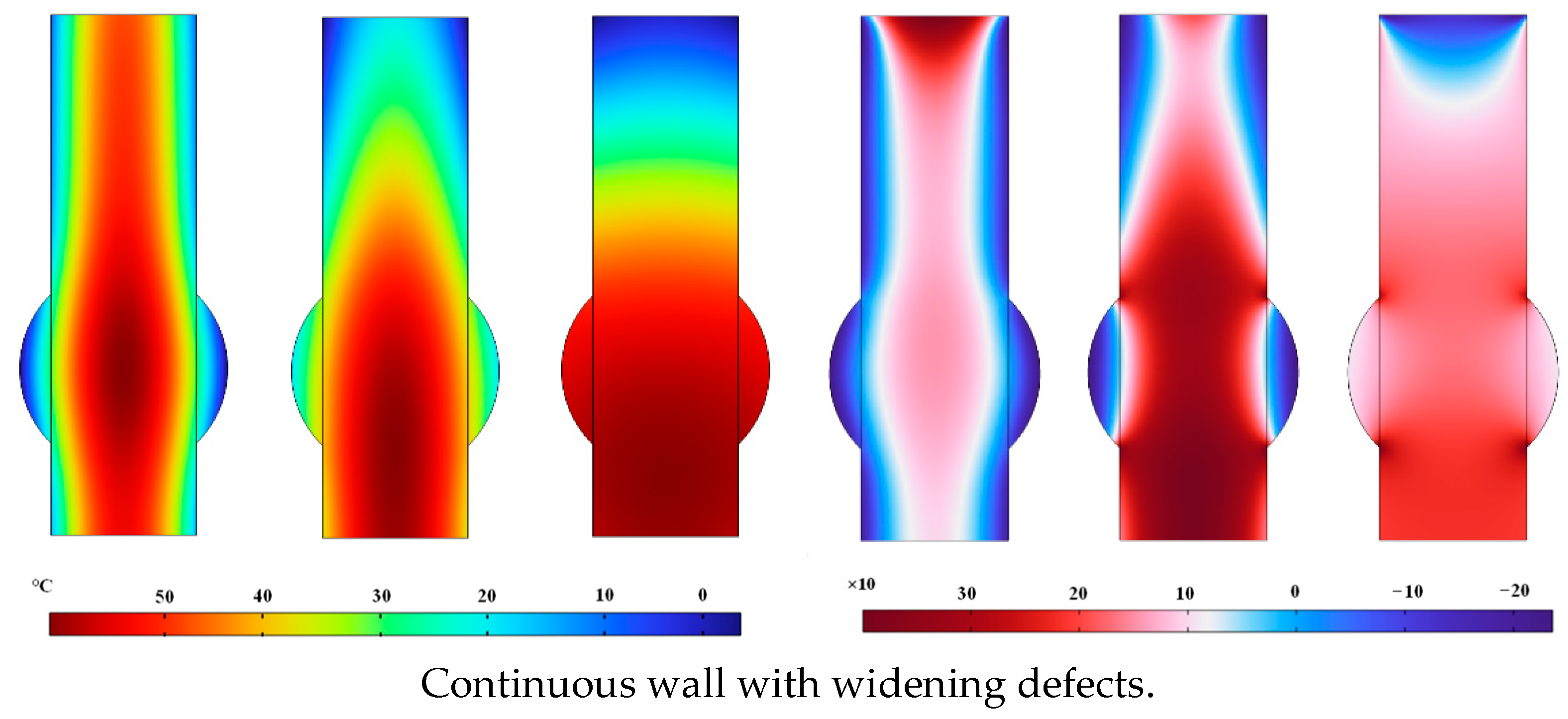
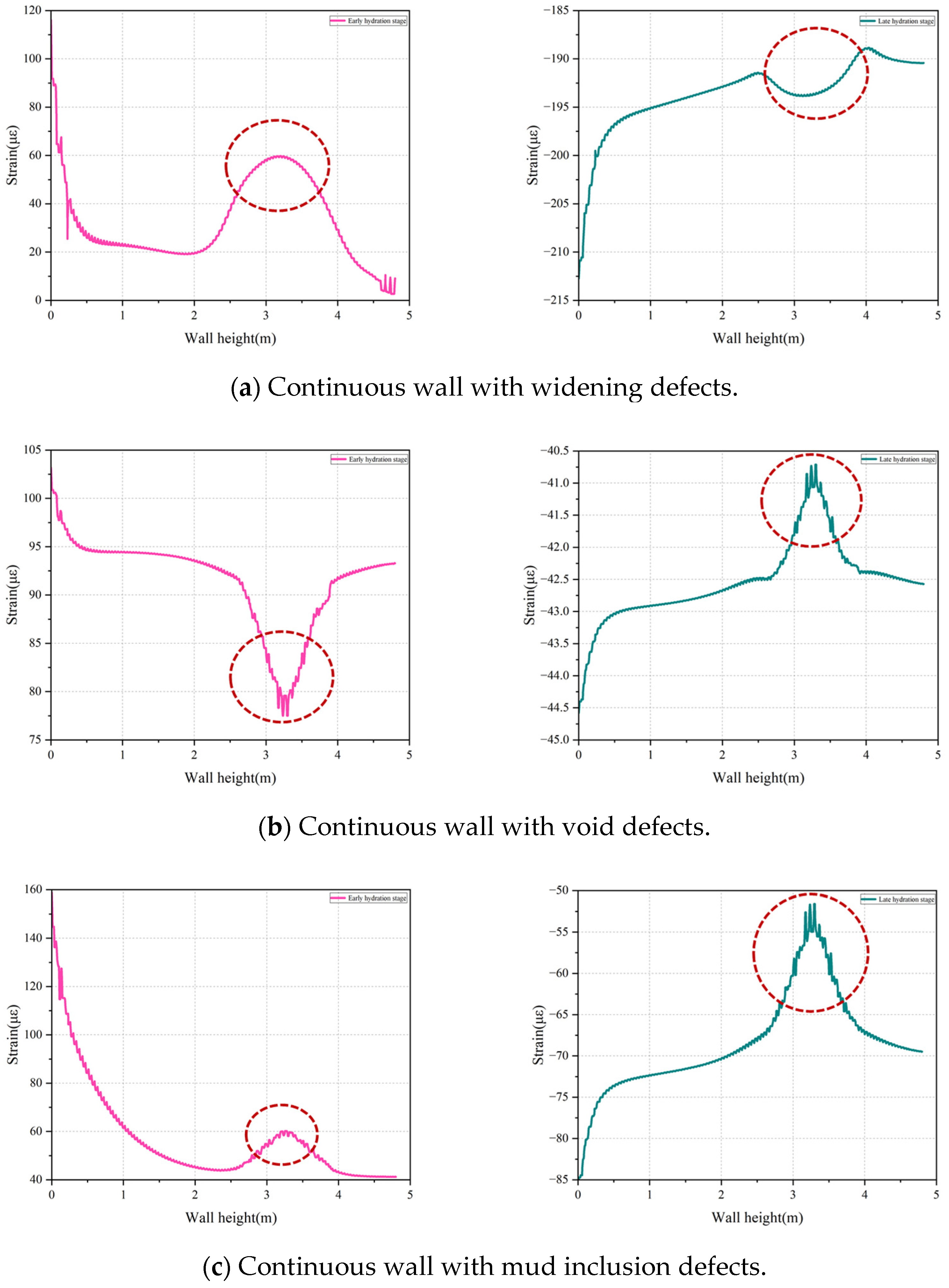
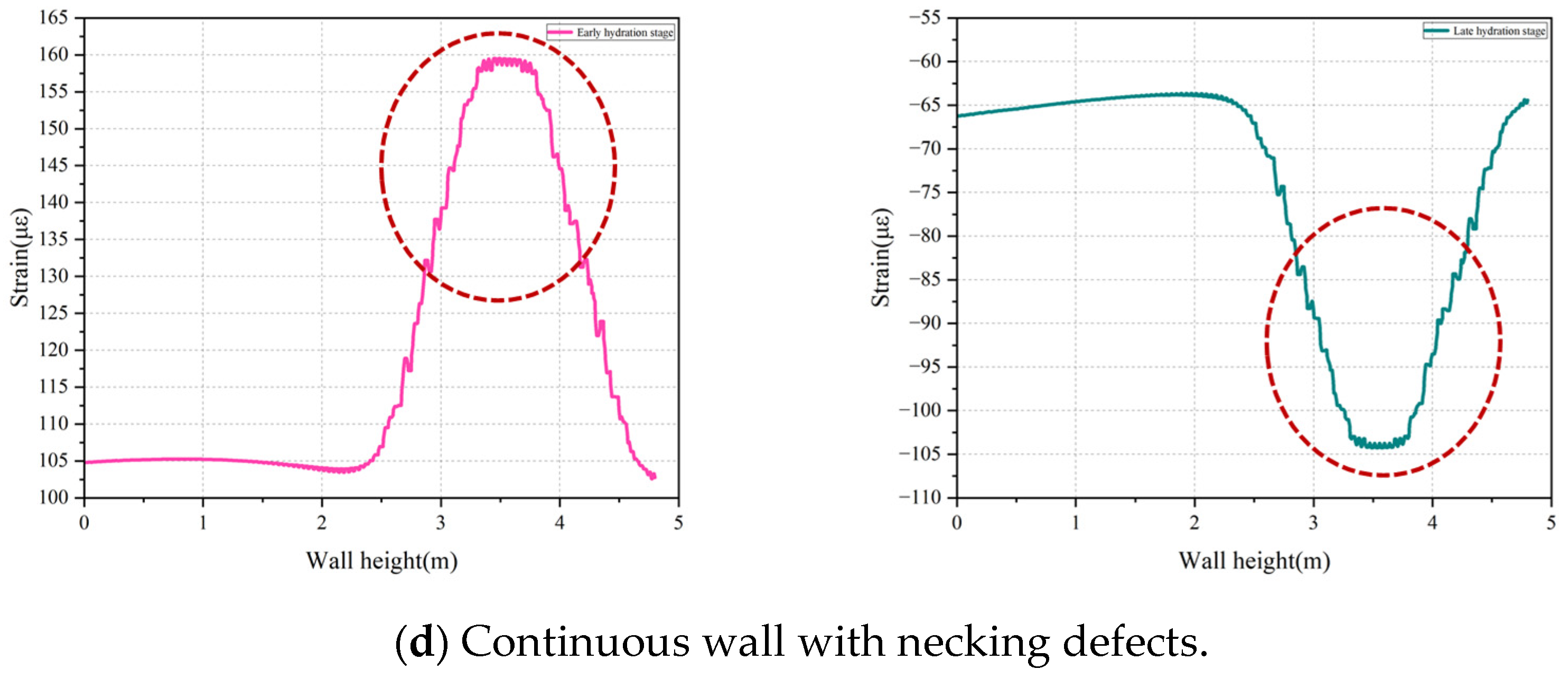
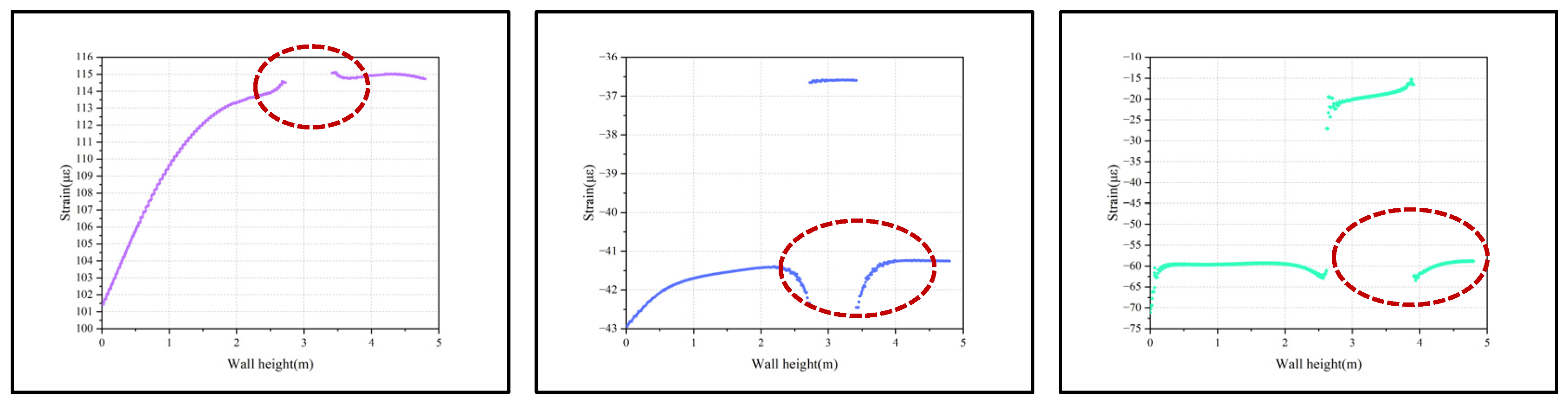
4.2. Distribution Patterns of Hydration–Temperature and Strain in the Wall When the Monitoring Line Passes Through the Defect Zone
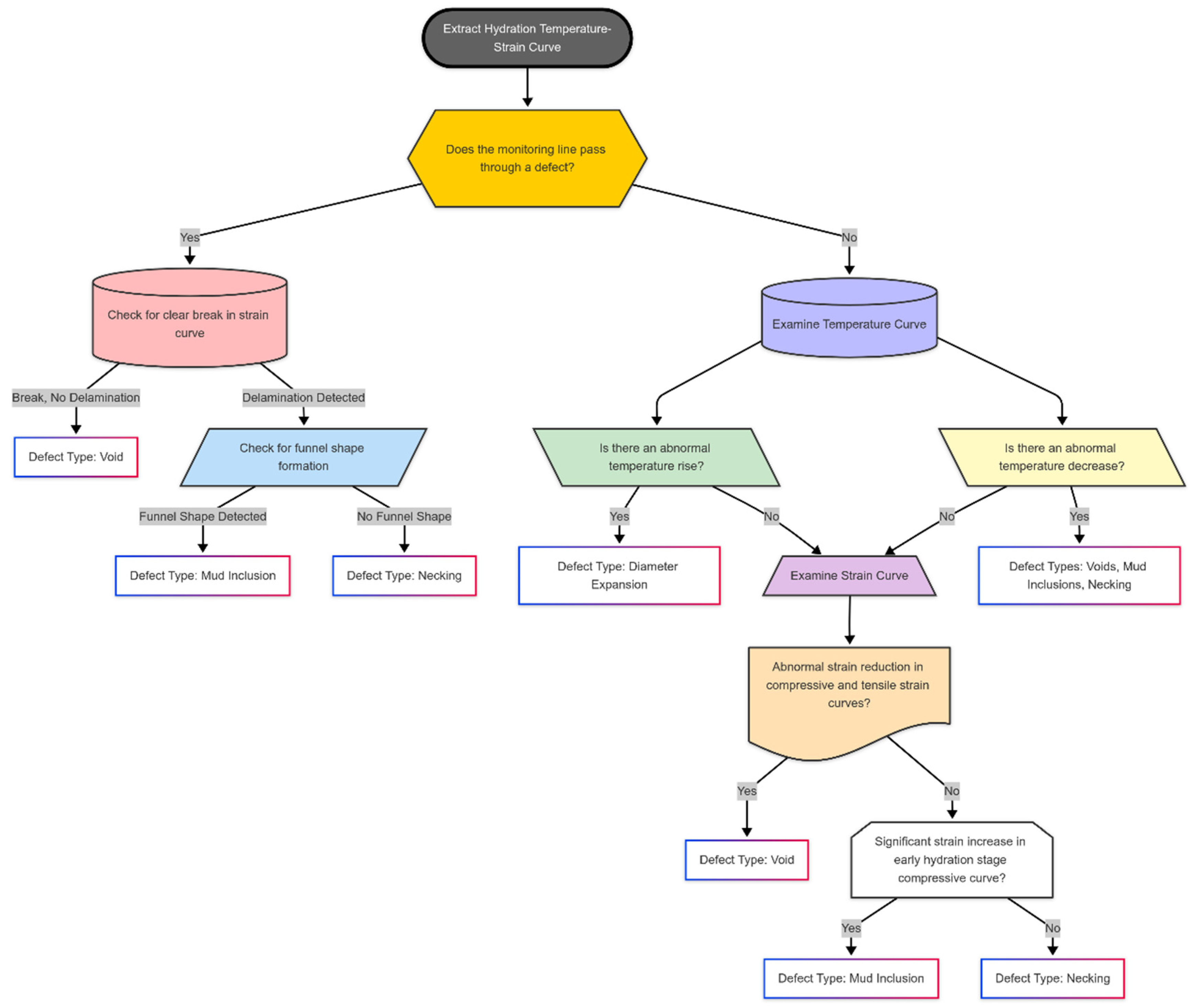
5. Concrete Defect Type Identification Process Based on Temperature–Strain Combined Monitoring and Application Study
6. Conclusions
- The combination of Thermal Integrity Profiling and fiber Bragg grating strain monitoring effectively provided the detailed, real-time tracking of the concrete hydration process within underground walls. The data verified the typical three-stage hydration process (rapid temperature rise, peak temperature, and gradual cooling) and highlighted a clear linear relationship between peak temperature and protective layer thickness. Notably, the multi-parameter approach successfully detected anomalous temperature and strain patterns, proving valuable for the early detection of hidden structural defects.
- An advanced thermal–mechanical–chemical multi-field coupled finite element model was created to simulate temperature and strain behaviors throughout the concrete hydration period, accounting for the presence of defects. This innovative model integrates chemical hydration heat generation, thermal conduction, and mechanical deformation comprehensively. The model was validated rigorously against field measurements, achieving excellent consistency between the simulation and experimental data, underscoring its potential as an effective analytical tool for studying early-stage defects in concrete structures.
- Defect Identification Mechanisms and Accuracy: By analyzing the combined temperature and strain data, the distinct impact mechanisms of different defect types were elucidated, enabling the accurate identification of defect nature and location. Four major defect types in the continuous wall—voids, mud inclusions, necking, and widening—were successfully distinguished by their unique temperature–strain signature patterns (e.g., variations in peak temperature drop, the heat dissipation rate, and strain anomalies during hydration). This dual-parameter approach overcomes the limitation of TIP alone by linking each observed anomaly to a specific defect mechanism.
- This study proposes a rapid and systematic defect identification procedure based on the integrated monitoring and modeling results, which offers a new technological approach for concrete structural health assessment. This procedure was successfully demonstrated on the Weizishan Station underground wall and is readily transferable to similar underground concrete structures (e.g., diaphragm walls, deep foundation elements, and tunnel linings). The proposed multi-parameter monitoring and analysis framework significantly enhances the efficiency and precision of defect detection in recently made concrete, enabling timely intervention and long-term health monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.X.; Zhao, J.; Zhang, Q.B. A modular automated modelling framework for cut-and-cover excavations in mixed ground conditions. Tunn. Undergr. Space Technol. 2025, 158, 106384. [Google Scholar] [CrossRef]
- Bai, B.W.; Liang, J.R.; Xu, H.Q.; Jiang, P.M.; Zhou, A.Z.; Lv, Y.Y. Study on hydraulic conductivity of dredged sediment-attapulgite vertical cutoff walls under confining pressure. Environ. Res. 2024, 255, 119110. [Google Scholar] [CrossRef]
- Choi, J.Y.; Ahn, D.H. Displacement Monitoring of Subway Tracks and Tunnels According to Adjacent Construction. Appl. Sci. 2024, 14, 1887. [Google Scholar] [CrossRef]
- Wu, J.R.; Chen, J. Experimental Research on the Floating Amount of Shield Tunnel Based on the Innovative Cumulative Floating Amount Calculation Method. Buildings 2024, 14, 1228. [Google Scholar] [CrossRef]
- Miao, R.C.; Gu, Z.H.; Wang, C.; Cui, W. Study on rock-breaking mechanism of impact trenching in underground diaphragm wall with consideration of slurry effects. Comput. Geotech. 2025, 179, 106998. [Google Scholar] [CrossRef]
- Peng, H.; Li, Y.J.; Niu, X.K.; Tang, H.D.; Meng, X.; Li, Z.C.; Wan, K.D.; Li, W.; Song, W. Characteristics analysis of leakage diseases of Beijing underground subway stations based on the field investigation and data statistics. Transp. Geotech. 2024, 48, 101317. [Google Scholar] [CrossRef]
- Liang, R.Z.; Zhang, Z.W.; Li, Z.C.; Cao, S.; El Naggar, M.H.; Xiao, M.Z.; Wu, W.B. Simplified Method for Predicting the Shield Tunnel Longitudinal Responses to Over-Crossing Tunneling Considering Circumferential Joint Effect. Int. J. Geomech. 2024, 24, 04024140. [Google Scholar] [CrossRef]
- Sun, Q.; Elshafie, M.Z.; Xu, X.; Schooling, J. Pile defect assessment using distributed temperature sensing: Fundamental questions examined. Struct. Health Monit.-Int. J. 2024, 23, 1701–1724. [Google Scholar] [CrossRef]
- Torigoe, I.; Mori, K.; Spagnoli, A. Signal processing procedure for non-destructive test of concrete structure integrity. NDT E Int. 2005, 38, 575–581. [Google Scholar] [CrossRef]
- Ni, S.-H.; Lo, K.-F.; Lehmann, L.; Huang, Y.-H. Time-frequency analyses of pile-integrity testing using wavelet transform. Comput. Geotech. 2008, 35, 600–607. [Google Scholar] [CrossRef]
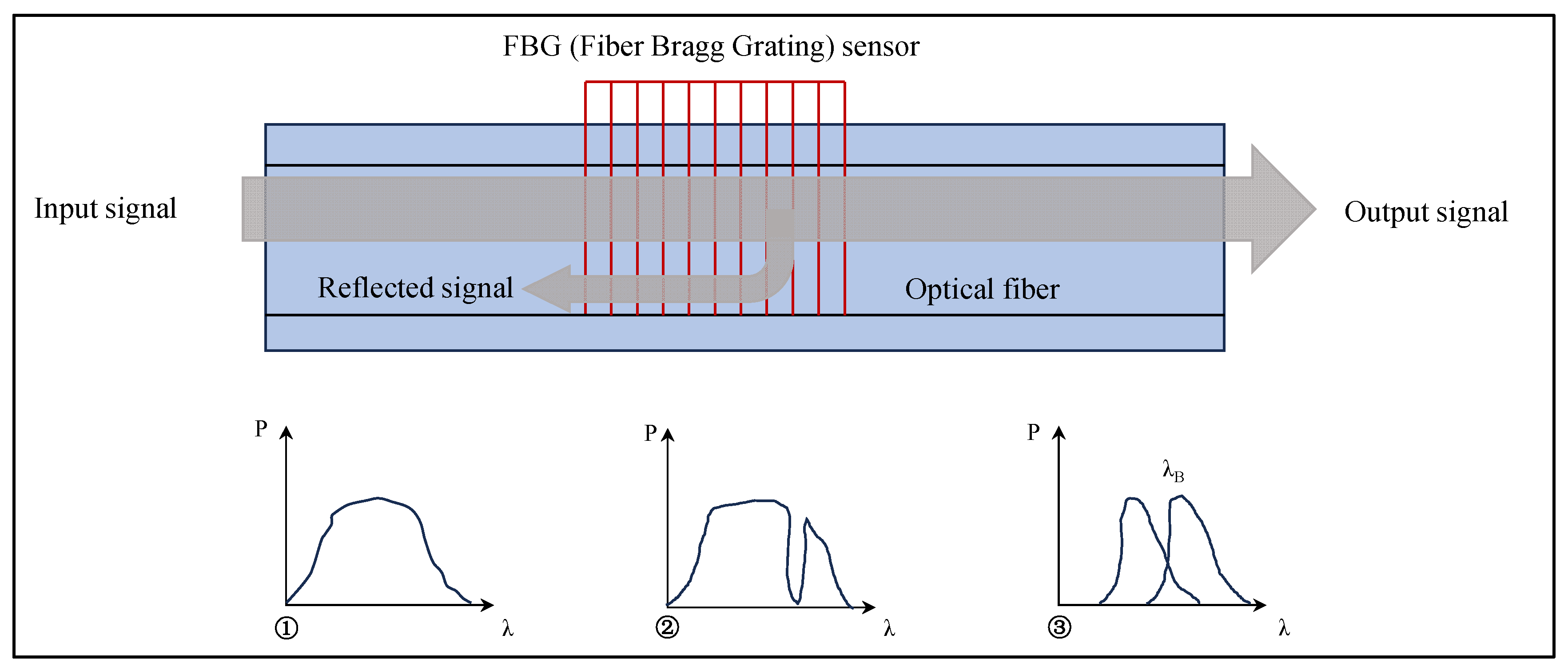
- Tennyson, R.C.; Coroy, T.; Duck, G.; Manuelpillai, G.; Mulvihill, P.; Cooper, D.J.F.; Smith, P.W.E.; Mufti, A.A.; Jalali, S.J. Fibre optic sensors in civil engineering structures. Can. J. Civ. Eng. 2000, 27, 880–889. [Google Scholar] [CrossRef]
- Pelecanos, L.; Soga, K.; Elshafie, M.Z.E.B.; de Battista, N.; Kechavarzi, C.; Gue, C.Y.; Ouyang, Y.; Seo, H.-J. Distributed Fiber Optic Sensing of Axially Loaded Bored Piles. J. Geotech. Geoenviron. Eng. 2018, 144, 04017122. [Google Scholar] [CrossRef]
- Sun, Q.; Elshafie, M.; Barker, C.; Fisher, A.; Schooling, J.; Rui, Y. Thermal integrity testing of cast in situ piles: An alternative interpretation approach. Struct. Health Monit.-Int. J. 2021, 20, 2493–2512. [Google Scholar] [CrossRef]
- Chen, J.W.; Liao, Y.S.; Ma, F.; Tang, S.W. Effect of ground granulated blast furnace slag on hydration characteristics of ferrite-rich calcium sulfoaluminate cement in seawater. J. Cent. South Univ. 2025, 32, 189–204. [Google Scholar] [CrossRef]
- He, F.F.; Chen, J.; Li, C.Z.; Xiong, F. Temperature tracer method in structural health monitoring: A review. Measurement 2022, 200, 111608. [Google Scholar] [CrossRef]
- Zhu, J.S.; Wang, Z.Y. Experimental modeling and quantitative evaluation of mitigating cracks in early-age mass concrete by regulating heat transfer. J. Build. Eng. 2024, 96, 110641. [Google Scholar] [CrossRef]
- Calo, M.; Ruggieri, S.; Nettis, A.; Uva, G. A MTInSAR-Based Early Warning System to Appraise Deformations in Simply Supported Concrete Girder Bridges. Struct. Control Health Monit. 2024, 2024, 8978782. [Google Scholar] [CrossRef]
- Chu, I.; Kwon, S.H.; Amin, M.N.; Kim, J.-K. Estimation of temperature effects on autogenous shrinkage of concrete by a new prediction model. Constr. Build. Mater. 2012, 35, 171–182. [Google Scholar] [CrossRef]
- Xiao, Z.P.; Di Murro, V.; Osborne, J.A.; Zhu, H.H.; Li, Z.L. Distributed fibre optic sensing and novel data processing method for tunnel circumferential deformation—A case study of an ageing tunnel at CERN. Tunn. Undergr. Space Technol. 2024, 153, 106014. [Google Scholar] [CrossRef]
- Sun, Q.; Elshafie, M.Z.E.B.; Barker, C.; Fisher, A.; Schooling, J.; Rui, Y. Integrity monitoring of cast in-situ piles using thermal approach: A field case study. Eng. Struct. 2022, 272, 114586. [Google Scholar] [CrossRef]
- Phan, L.T.; Lawson, J.R.; Davis, F.L. Effects of elevated temperature exposure on heating characteristics, spalling, and residual properties of high performance concrete. Mater. Struct. 2001, 34, 83–91. [Google Scholar] [CrossRef]
- Khan, I.; Yong, G.T. Role of supplementary cementiteous materials in mitigating heat of hydration in mass concrete elements. Constr. Build. Mater. 2024, 431, 136482. [Google Scholar] [CrossRef]
- Hernandez-Bautista, E.; Bentz, D.P.; Sandoval-Torres, S.; Cano-Barrita, P.F.d.J. Numerical simulation of heat and mass transport during hydration of Portland cement mortar in semi-adiabatic and steam curing conditions. Cem. Concr. Compos. 2016, 69, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Ge, Z.; Wang, K. Influence of cement fineness and water-to-cement ratio on mortar early-age heat of hydration and set times. Constr. Build. Mater. 2014, 50, 657–663. [Google Scholar] [CrossRef]
- Zhao, D.P.; Zhu, L.; Shen, Z.D.; Miu, Z.C.; Liu, X.H. Effect of hydration heat of super-large-section tunnel-lining concrete on structural stress and its mitigation measures. Tunn. Undergr. Space Technol. 2025, 157, 106324. [Google Scholar] [CrossRef]
- Wang, L.G.; Wang, Y.C.; Miao, Y.C.; Ju, S.Y.; Sui, S.Y.; Wang, F.J.; Liu, Z.Y.; Jiang, J.Y. Temperature damage assessment of mass concrete based on the coupling mechanism of hydration-temperature-humidity-constraint factors. J. Build. Eng. 2024, 90, 109211. [Google Scholar] [CrossRef]
- Gottsäter, E.; Johansson, M.; Plos, M.; Ivanov, O.L. Crack widths in base restrained walls subjected to restraint loading. Eng. Struct. 2019, 189, 272–285. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Wang, Y.; Yao, T.; Tian, Q.; Li, S. Deformation and cracking modeling for early-age sidewall concrete based on the multi-field coupling mechanism. Constr. Build. Mater. 2015, 88, 84–93. [Google Scholar] [CrossRef]
- Saeed, M.K.; Rahman, M.K.; Alfawzan, M.; Basha, S.; Dahish, H.A. Recycling of date kernel powder (DKP) in mass concrete for mitigating heat generation and risk of cracking at an early age. Constr. Build. Mater. 2023, 376, 131033. [Google Scholar] [CrossRef]
- Chu, I.; Lee, Y.; Amin, M.N.; Jang, B.-S.; Kim, J.-K. Application of a thermal stress device for the prediction of stresses due to hydration heat in mass concrete structure. Constr. Build. Mater. 2013, 45, 192–198. [Google Scholar] [CrossRef]
- Schackow, A.; Effting, C.; Gomes, I.R.; Patruni, I.Z.; Vicenzi, F.; Kramel, C. Temperature variation in concrete samples due to cement hydration. Appl. Therm. Eng. 2016, 103, 1362–1369. [Google Scholar] [CrossRef]
- Chen, B.F.; Tang, G.Q.; Lu, X.C.; Xiong, B.B.; Guan, B.; Tian, B. Thermal property evolution and prediction model of early-age low-heat cement concrete under different curing temperatures. J. Build. Eng. 2024, 82, 108020. [Google Scholar] [CrossRef]
- Mardmomen, S.; Chen, H.L. Prediction of the early age thermal behavior of mass concrete containing SCMs using ANSYS. J. Therm. Anal. Calorim. 2023, 148, 7899–7917. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Baweja, S. Justification and refinements of model b3 for concrete creep and shrinkage 1. statistics and sensitivity. Mater. Struct. 1995, 28, 415–430. [Google Scholar] [CrossRef]
- Madsen, H.O.; Bazant, Z.P. Uncertainty analysis of creep and shrinkage effects in concrete structures. J. Am. Concr. Inst. 1983, 80, 116–127. [Google Scholar]
- Dwairi, H.M.; Wagner, M.C.; Kowalsky, M.J.; Zia, P. Behavior of instrumented prestressed high performance concrete bridge girders. Constr. Build. Mater. 2010, 24, 2294–2311. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Y.; Zhou, M.; Chen, F. Control of Early-Age Cracking in Super-Long Mass Concrete Structures. Sustainability 2022, 14, 3809. [Google Scholar] [CrossRef]
- Dias, I.F.; Oliver, J.; Lemos, J.V.; Lloberas-Valls, O. Modeling tensile crack propagation in concrete gravity dams via crack-path-field and strain injection techniques. Eng. Fract. Mech. 2016, 154, 288–310. [Google Scholar] [CrossRef]
- Klemczak, B.; Knoppik-Wrobel, A. Reinforced concrete tank walls and bridge abutments: Early-age behaviour, analytic approaches and numerical models. Eng. Struct. 2015, 84, 233–251. [Google Scholar] [CrossRef]
- Boeckmann, A.Z.; Loehr, J.E. Evaluation of Thermal Integrity Profiling and Crosshole Sonic Logging for Drilled Shafts with Concrete Defects. Transp. Res. Rec. 2019, 2673, 86–98. [Google Scholar] [CrossRef]
- Farahani, M.A.; Gogolla, T. Spontaneous raman scattering in optical fibers with modulated probe light for distributed temperature Raman remote sensing. J. Light. Technol. 1999, 17, 1379–1391. [Google Scholar] [CrossRef]
- Zhu, H.H.; Ho, A.N.L.; Yin, J.H.; Sun, H.W.; Pei, H.F.; Hong, C.Y. An optical fibre monitoring system for evaluating the performance of a soil nailed slope. Smart Struct. Syst. 2012, 9, 393–410. [Google Scholar] [CrossRef]
- Schindler, A.K.; Folliard, K.J. Heat of hydration models for cementitious materials. ACI Mater. J. 2005, 102, 24–33. [Google Scholar]
- Ulm, F.J.; Coussy, O. Couplings in early-age concrete: From material modeling to structural design. Int. J. Solids Struct. 1998, 35, 4295–4311. [Google Scholar] [CrossRef]
- Briffaut, M.; Benboudjema, F.; Torrenti, J.M.; Nahas, G. Numerical analysis of the thermal active restrained shrinkage ring test to study the early age behavior of massive concrete structures. Eng. Struct. 2011, 33, 1390–1401. [Google Scholar] [CrossRef]
- De Schutter, G. Finite element simulation of thermal cracking in massive hardening concrete elements using degree of hydration based material laws. Comput. Struct. 2002, 80, 2035–2042. [Google Scholar] [CrossRef]
- Thanh-Tung, N.; Weiler, M.; Waldmann, D. Experimental and numerical analysis of early age behavior in non-reinforced concrete. Constr. Build. Mater. 2019, 210, 499–513. [Google Scholar] [CrossRef]
- De Schutter, G.; Taerwe, L. Degree of hydration-based description of mechanical properties of early age concrete. Mater. Struct. 1996, 29, 335–344. [Google Scholar] [CrossRef]
- De Schutter, G.; Taerwe, L. Fracture energy of concrete at early ages. Mater. Struct. 1997, 30, 67–71. [Google Scholar] [CrossRef]
- Rui, Y.; Kechavarzi, C.; O’Leary, F.; Barker, C.; Nicholson, D.; Soga, K. Integrity Testing of Pile Cover Using Distributed Fibre Optic Sensing. Sensors 2017, 17, 2949. [Google Scholar] [CrossRef]
- Li, Z.; Li, M.; Guo, H.; Wu, Y.; Sheng, L.; Jiao, J.; Li, Z.; Sui, W. Experimental Investigation of the Evaluation of the Cement Hydration Process in the Annular Space Using Distributed Fiber Optic Temperature Sensing. Sensors 2025, 25, 958. [Google Scholar] [CrossRef] [PubMed]
- Rui, Y.; Sun, Q.C. Measurement of Pile Cover Thickness Using Distributed Fibre Optic Sensors. In Proceedings of the 3rd International Conference on Information Technology in Geo-Engineering (ICITG), Guimaraes, Portugal, 29 September–2 October 2019. [Google Scholar]



| Material Property Name, Symbol (Unit) | Value |
|---|---|
| Concrete density, ρ (kg/m3) | 2450 |
| Convective heat-transfer coefficient of sidewall template (W/(m2 K)) | 2.75 |
| Concrete heat capacity, ct (J/(kg K)) | 940 |
| Heat conductivity, λ (W/(m K)) | 2.4 |
| Convective heat-transfer coefficient of side-wall concrete surface (W/(m2 K)) | 6.0 |
| Specific heat capacity of the foundation, (J/(kg K)) | 1005 |
| Initial temperature of concrete and environment, T0 (K) | 293 |
| Solid bulk modulus, Kr (GPa) | 44 |
| Monitoring Point | RMSE (Temperature) | R (Temperature) | RMSE (Strain) | R (Strain) |
|---|---|---|---|---|
| Point 1 | 1.1 °C | 0.98 | 5 με | 0.96 |
| Point 2 | 1.3 °C | 0.97 | 6 με | 0.95 |
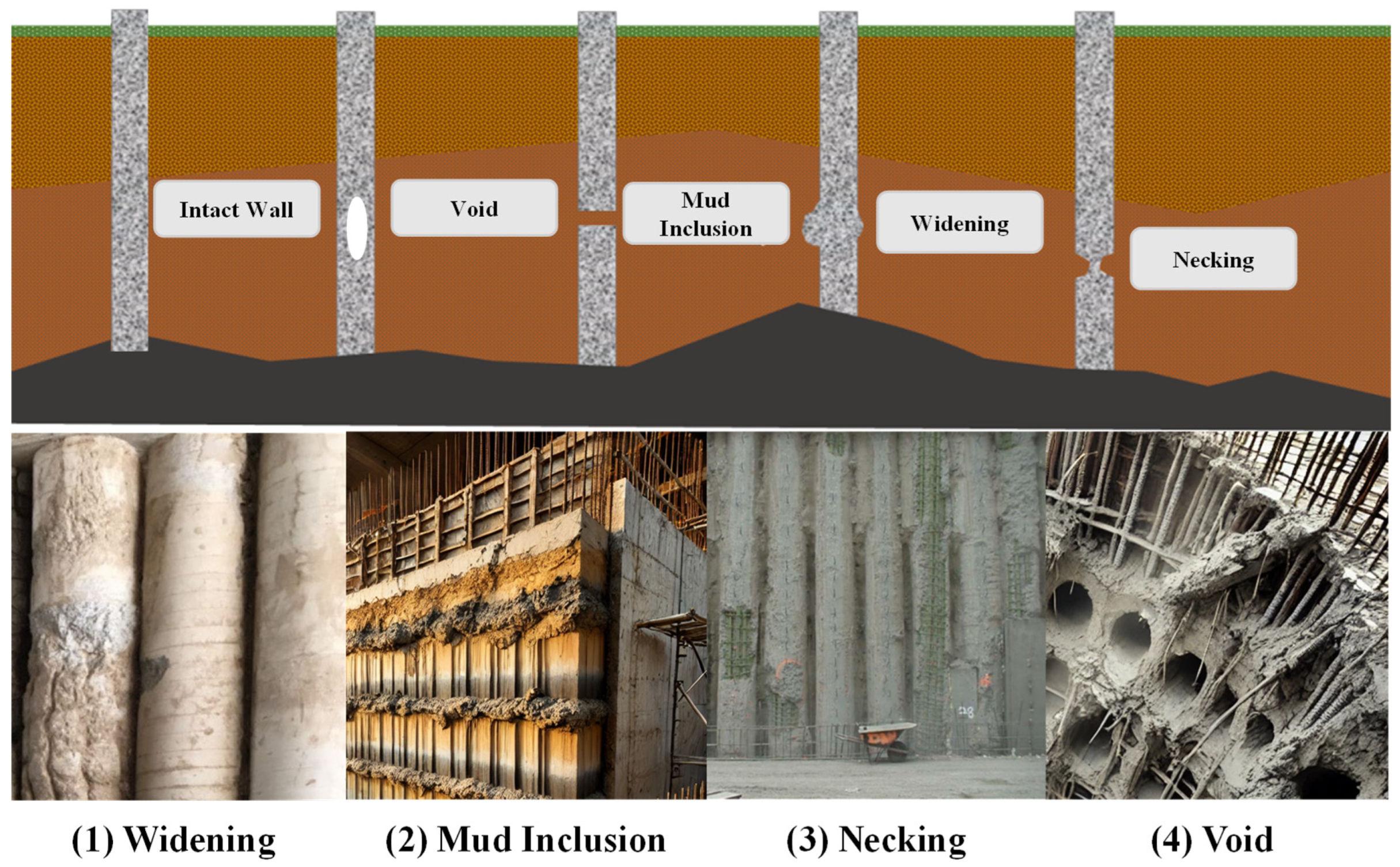
| Type | Concept |
|---|---|
| Intact Wall | A continuous wall with a uniform structure and no internal defects. |
| Void | An internal cavity in the continuous wall where concrete is absent. |
| Mud Inclusion | A layer of mud or weak material embedded within the continuous wall. |
| Necking | A local reduction in the thickness of the continuous wall. |
| Widening | A local increase in the thickness of the continuous wall. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Zhang, X.; Li, X.; Lu, Y. Application of Advanced Multi-Parameter Monitoring in Concrete Structure Defect Detection: Integrating Thermal Integrity Profiling and Strain Analysis. Buildings 2025, 15, 1350. https://doi.org/10.3390/buildings15081350
Lu L, Zhang X, Li X, Lu Y. Application of Advanced Multi-Parameter Monitoring in Concrete Structure Defect Detection: Integrating Thermal Integrity Profiling and Strain Analysis. Buildings. 2025; 15(8):1350. https://doi.org/10.3390/buildings15081350
Chicago/Turabian StyleLu, Linhai, Xin Zhang, Xiaojun Li, and Yanyun Lu. 2025. "Application of Advanced Multi-Parameter Monitoring in Concrete Structure Defect Detection: Integrating Thermal Integrity Profiling and Strain Analysis" Buildings 15, no. 8: 1350. https://doi.org/10.3390/buildings15081350
APA StyleLu, L., Zhang, X., Li, X., & Lu, Y. (2025). Application of Advanced Multi-Parameter Monitoring in Concrete Structure Defect Detection: Integrating Thermal Integrity Profiling and Strain Analysis. Buildings, 15(8), 1350. https://doi.org/10.3390/buildings15081350




