Predicting Soft Soil Settlement with a FAGSO-BP Neural Network Model ^†

Abstract

Aiming at the problem that it is difficult to consider the prediction of foundation settlement in the case of multi-parameter coupling effect by theoretical formulas and numerical analysis, the fireworks algorithm with gravitational search operator (FAGSO) is introduced into the BP neural network model, and the FAGSO algorithm aims to enhance the neural network’s weight and threshold adjustment process; so, a new soft ground settlement prediction model was developed which uses a fireworks algorithm integrated with a gravitational search operator to optimize a BP neural network (referred to as FAGSO-BP). The FAGSO-BP neural network forecasting model is used to predict the soft foundation settlement of Hunan Wuyi Expressway Project. In the soft foundation settlement prediction analysis of Hunan Wuyi Expressway Project, the average relative error of the FAGSO-BP neural network test set was 6.06%, with an RMSE of 1.6, an MAE of 1.2, a MAPE of 0.12% and an MSE of 2.56, which compared to the traditional BP, GA-BP and FWA-BP neural models, had smaller error and higher model stability.

1. Introduction

Soft soils are widely distributed in the coastal and inland areas of China, and the number of projects for infrastructure construction in soft soil areas is increasing, and it is inevitable that soft soil foundations will be encountered during construction. Due to its high water content, low strength and high compressibility, soft soil foundation is prone to settlement, thus posing a threat to the safety and stability of engineering structures [1,2,3]. With the construction of highways in China, the problem of post-construction settlement of soft ground is becoming more and more prominent, which has become a key factor affecting the quality of the project and normal operation. In order to ensure the quality and safety of engineering construction, service life, normal use and operation after construction, it is necessary to monitor and predict the settlement of soft ground. There are many existing methods for foundation settlement prediction, but there is always a gap between the calculated value and measured value of various methods. In order to improve the accuracy of calculation and prediction, and to make the calculated value closer to the measured value, so as to guide the construction more accurately and avoid foundation settlement, it is necessary to predict the settlement of soft ground in time and accurately.

There are three categories of methods for predicting soft ground settlement and deformation: theoretical formula method, numerical modeling computational analysis method and empirical formula projection method for predicting foundation settlement based on monitoring information [4]. With the rapid development of artificial intelligence and computer technology, data-driven machine learning methods have been widely used in the field of engineering [5,6,7]. BP neural network, as a classical machine learning algorithm, has a strong nonlinear fitting ability, which is suitable for the prediction problem of complex systems [8,9,10]. Liu et al. [11] established an error back propagation network prediction model for soft soil deformation characteristics based on the results of soft soil triaxial tests. It was verified that the improved BP neural network model applied to soft soil foundation settlement prediction has the characteristics of fast calculation speed, high accuracy, strong generalization ability and strong fitting ability with measured data. Minguang Li et al. [12,13,14] used a genetic algorithm to optimize the weights and thresholds of BP neural network to construct GA-BP neural network, which solved some of the problem points of BP neural network. The results show that GA-BP neural network has higher prediction accuracy and lower distortion rate. Bo Wang [15] combined genetic algorithm with BP neural network to optimize the weights and thresholds of BP neural network, and the results showed that the optimized prediction model had better generalization ability and good stability. Ming Li [16] proposed a GOM-BP neural network prediction model, and the results showed that the prediction accuracy of the model had improved compared to the GM-BP neural network model. Guo Ziqi [17] combined the particle swarm algorithm and BP neural network to establish PSO-BP prediction model with an underground project as the background, and the results showed that the PSO-BP neural network had high computational accuracy and accurate prediction results. Zhang Guopeng [18] established a BP-PSO-RBF model to simulate and predict the deep horizontal displacement and other deformations of the pit enclosure structure using the measured data of underground deep foundation pit. The results show that combinatorial neural networks can make up for the shortcomings of BP neural networks that are prone to falling into local minimum as well as the existence of problems with the implicit layer function of the error graded iterative method. Wang Biaolong [19] proposed a novel landslide reliability evaluation method that integrates a particle swarm optimization algorithm with a natural selection strategy and a BP neural network. This method enhances the global optimization capability of the model by improving the weights and threshold adjustment of the BP neural network. Chunhui Zhang [20] improved the particle swarm algorithm in the intelligent optimization algorithm and applied it to the weight threshold optimization of BP neural network to construct an effective roadbed settlement prediction model, and through Matlab simulation, the example analysis verified the effectiveness of the model in the prediction of roadbed settlement. Wu Yimin [21] proposed a BP neural network model HO-BP optimized based on the Hippo algorithm HO, and the results of the study showed that the prediction accuracy of the model had improved, and its robustness and resistance to noise interference were also strengthened. Yao Yong [22] proposed an inverse analysis method based on uniform design theory and DE-BP neural network, and the results showed that the DE algorithm can effectively improve the prediction accuracy of BP neural network and avoid the BP neural network falling into the local extreme value. Ma Chuangtao [23] proposed a prediction model based on the fireworks algorithm to improve the BP neural network to compensate for the shortcomings of the BP neural network. The model optimizes the neural network’s optimization search process for weights and thresholds by using the principle of explosive diffusion of the firework explosion operator.

With the rapid development of artificial intelligence technology, neural network as its branch is widely used in various fields. Numerous researchers have employed BP neural networks for forecasting the subsidence of soft soil, but it has the problems of easily falling into the local minimum and slow convergence [24,25,26]. To address the shortcomings of the BP neural network in predicting soft soil settlement, this paper relies on the Hunan Wuyi Expressway Project, using the global search capability of the fireworks algorithm, optimizing the weights and thresholds of BP neural network, combining the fireworks algorithm, FAGSO algorithm and BP neural network. The FWA-BP model and FAGSO-BP model were developed using PyCharm equipped with Python 3.9 programming software for predicting soft soil settlement using neural networks. This paper will introduce the construction method of FAGSO-BP model and its application effect in soft foundation settlement prediction in detail.

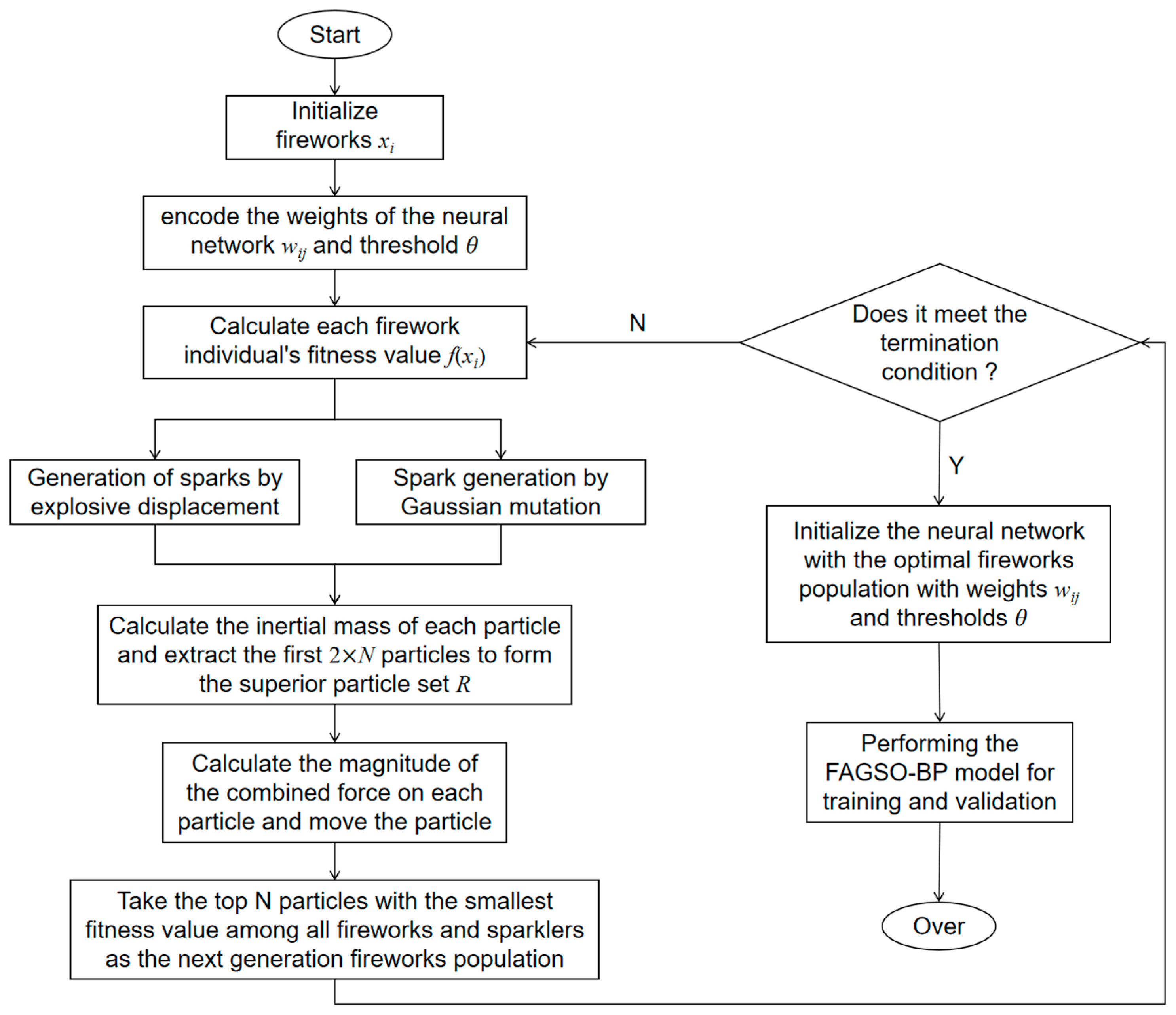
2. Principles of Optimization Neural Networks

Fireworks Algorithm is an algorithm based on group intelligence optimization proposed by Ying Tan [27], which can effectively solve the global optimal solution of complex problems. The gravitational search algorithm [28] carries out displacement operations and operations on particles through the force between the particles and then changes the position and dimension information of each particle. In the process of displacement operation, the particles can use the spatial environment information to optimize their own worse latitude values, so that the particle population enters a more optimal region for searching. The conventional backpropagation neural network exhibits limitations including sluggish convergence rates, susceptibility to local optima trapping and inadequate exploration of solution spaces. To resolve these limitations, the BP neural network is optimized through the FAGSO algorithm method, originally introduced in Zhu Qibing et al.’s foundational work [29]. The improvement strategy is as follows [30]:

(1)

Key parameter coding: In neural networks, weights and thresholds exist as multidimensional vector arrays spanning the parameter space. Let $\mathrm{X}=[{\mathrm{x}}_1,{\mathrm{x}}_2,...,{\mathrm{x}}_{\mathrm{D}}]$, X denotes a set of parameters consisting of network weights and thresholds. In network, denote ${\mathrm{n}}_{\mathrm{I}\mathrm{W}\left(\mathrm{1,1}\right)}$, ${\mathrm{n}}_{\mathrm{I}\mathrm{W}\left(\mathrm{2,1}\right)}$ as the number of weights between the implicit layer and the input layer and the output layer and the implicit layer, ${\mathrm{n}}_{\mathrm{b}\left(\mathrm{1,1}\right)}$, ${\mathrm{n}}_{\mathrm{b}\left(\mathrm{2,1}\right)}$ are the number of implicit layer and output layer thresholds, denote $\mathrm{D}={\mathrm{n}}_{\mathrm{I}\mathrm{W}\left(\mathrm{1,1}\right)}+{\mathrm{n}}_{\mathrm{b}\left(\mathrm{1,1}\right)}$ + ${\mathrm{n}}_{\mathrm{I}\mathrm{W}\left(\mathrm{2,1}\right)}$ + ${\mathrm{n}}_{\mathrm{b}\left(\mathrm{2,1}\right)}$, D is the total set of weights and thresholds.

(2)

Calculation of adaptation values: the neuronal weights and neuronal thresholds within each layer of the feedforward architecture are parameterized through a stochastic initialization process, where all values are uniformly sampled from the interval [−1,1] following the relationship, i.e., ${\mathrm{x}}_{\mathrm{i}}~\mathrm{U}[-\mathrm{1,1}]$, and use the position of the firework individual ${\mathrm{x}}_{\mathrm{i}}$ in the firework algorithm to represent the weights between the network nodes and the thresholds at each layer.

(3)

Define the fitness function: Selection of squared errors to assess the fitness value of the FAGSO-BP model, Equation (1) was used to calculate the fitness value of individual fireworks. Calculation of the actual output value of the network was done using Equation (2) and calculation of the fitness function value was done through Equation (3) as follows:

$$SSE={\displaystyle \sum _{P=1}^P{\displaystyle \sum _{t=1}^S{(t-y)}^2}}$$

(1)

where t is the target output value to be achieved by the network; P is total number of layers of the neural network; S is the number of nodes in the output layer; y is the output result actually calculated by the network.

$$y_i=f_i({\displaystyle \sum _{j=1}^n{w}_{ij}{x}_j}+{\theta }_i)$$

(2)

where $x_j$ is the input to the network; ${\mathrm{w}}_{\mathrm{i}\mathrm{j}}$ is the weights of the network nodes; ${\theta }_i$ is the threshold for the first neuron in the network.

$$f_i(x)={\displaystyle \sum _{p=1}^p{\displaystyle \sum _{t=1}^s{(t-y)}^2}}={\displaystyle \sum _{p=1}^p{\displaystyle \sum _{t=1}^s(t-f_i}}({\displaystyle \sum _{j=1}^n{w}_{ij}{x}_j}+{\theta }_i){)}^2$$

(3)

(4)

Optimization of firework populations: For each individual firework $x_i$, calculate its fitness value ${f(x}_i)$ through Equation (3). To determine the quantity of fireworks that burst, utilize Equations (4) and (5) for computation and using Equations (6)–(8) for blast, displacement and mutation operations, and make Equation (9) select the optimal fireworks individuals to form the next generation of fireworks population as follows:

$$S_i=m{\displaystyle \frac{Y_{\max }-f(x_i)+\mathsf{\epsilon }}{{\displaystyle \sum _{i=}^N(Y_{\max }-f(x_i))+\epsilon }}}$$

(4)

where $S_i$ denotes the number of sparks released by the ith firework; m is a constant that regulates the total number of sparks generated by the entire population during the initialization phase; $Y_{max}$ represents the fitness value of the least fit (i.e., the worst-performing) individual in the current population; ${f(x}_i)$ is the individual ith firework’s fitness function value; $\epsilon$ is a tiny positive number introduced to prevent the divisor from being zero.

$$A_i=d{\displaystyle \frac{f(x_i)-Y_{\min }+\epsilon }{{\displaystyle \sum _{i=1}^N(f(x_i)-Y_{\min })+\epsilon }}}$$

(5)

where $A_i$ is the range of explosion amplitude of fireworks; $d$ is a constant limiting the explosion amplitude of fireworks; $Y_{min}$ denotes the fitness value corresponding to the individual with the best fitness in the current population.

$$h=A_i\times rand(-\mathrm{1,1})$$

(6)

$${ex}_i^k=x_i^k+h$$

(7)

$${cx}_i^k=x_i^k+r$$

(8)

where h is the positional bias term in each dimension; $x_i^k$ is the kth dimension of the ith firework; ${ex}_i^k$ is the exploding spark; ${cx}_i^k$ is a Gaussian variant spark; r is a random number obeying a Gaussian distribution r~N (1,1).

$$p(x_i)=R(x_i)/{\displaystyle \sum _{j\in k}R(x_j)}$$

(9)

where $R\left(x_i\right)$ denotes the cumulative value of the distance between an individual $x_i$ and the rest of the individuals in the population.

(5)

Determine the inertial weight for each particle utilizing Equations (10) and (11) within the search domain, and the 2 × N particles with the best mass among them are selected to form an elite set of particles R as follows:

$$m_i={\displaystyle \frac{f(w_i)-\underset{w_j\in W(t)}{\max }f(w_j)}{\underset{w_j\in W(t)}{\min }f(w_j)-\underset{w_j\in W(t)}{\max }f(w_j)}}$$

(10)

$$M_i={\displaystyle \frac{m_i}{{\displaystyle \sum _{w_j\in W(t)}{m}_j}}}$$

(11)

(6)

Calculate the Euclidean distances of the elite particles from the other particles in the set R, and the magnitude of the stress in the d-dimension for each particle is calculated from Equations (12) and (13); in this network model d = 4. Generate new spark particles according to Equation (14) and the particles that are out of range are mapped according to Equation (15). All the spark particles and fireworks are sorted according to the size of the fitness value, from which the top N elite particles are selected for constituting the initial population of fireworks in the next iteration, set t = t × 1, as follows:

$$F_i^d={\displaystyle \sum _{j\in R,j\ne i}rand(0,1)}{F}_{i,j}^d$$

(12)

$$F_{i,j}^d=G{\displaystyle \frac{M_i\times M_j}{r_{ij}+\epsilon }}(w_j^d-w_i^d)$$

(13)

$$v_i^d=x_i^d+F_i^d/M_i$$

(14)

$$x_i^k=x_i^k+\left|x_i^k\right|\%(x_{\max }^k-x_{\min }^k)$$

(15)

where $w_i^d$ and $w_j^d$ are coordinate values corresponding to the ith and jth particles in the set $w\left(t\right)$ in dimension d ($\mathrm{d}\le \mathrm{D}$); $F_i^d$ is the combined force of particle i in the dth dimension; G indicates the constant used to adjust the accuracy of the particle position update; $M_i$ denotes the inertial mass parameter of the particle itself; $r_{ij}$ represents the distance in Euclidean terms between particles i and j; $x_{min}^k and x_{max}^k$ are the upper and lower bounds in the kth dimension.

(7)

If t < T, then return to step (4), otherwise the algorithm stops. Calculate the fitness value ${f(x}_i)$ for each individual firework x according to Equation (3), the firework individual with the minimum fitness value ${min\left(f\right(x}_i\left)\right)$ in the current firework population is taken as the optimal firework individual $X_{best}$.

(8)

To update the weights and thresholds, the weights $\mathrm{w}$ and thresholds $\theta$ in the BP neural network are initialized using firework individuals $X_{best}$. The weights and threshold vectors X in the network model are updated by the BP neural network.

Based on the above steps the flowchart of the whole FAGSO-BP algorithm can be obtained as shown in Figure 1.

3. Neural Network Model Building and Validation

3.1. Data Sources

The feasibility of FWA-BP and FAGSO-BP based model for soft ground settlement forecasting is verified by using the monitoring data of the deep foundation pit project in the West Third Ring Road of Zhengzhou City [31]. The surface deposition values of the monitoring data in periods 1–4 is selected as input values, and the surface deposition value of the latter period is taken as output value, so the number of neurons in the input layer is 4, and the number of neuron nodes in the output layer is 1. By analogy, the data of periods 2–5 are taken as the input of the network, and the data of period 6 are taken as the output of the network, which constitutes 31 sets of sample data.

3.2. Data Normalization

In order to overcome the adverse effects of different magnitudes on the accuracy of the prediction model, the data of different indicators need to be normalized so that they are in the same magnitude and the comparability between the data is improved. Equation (16) is used to normalize the data in this model as follows:

$$X^{\ast }={\displaystyle \frac{X_K-min\left(X\right)}{max\left(X\right)-min\left(X\right)}}$$

(16)

where max (X) is the maximum value in the data set; min (X) is the smallest value in the data set.

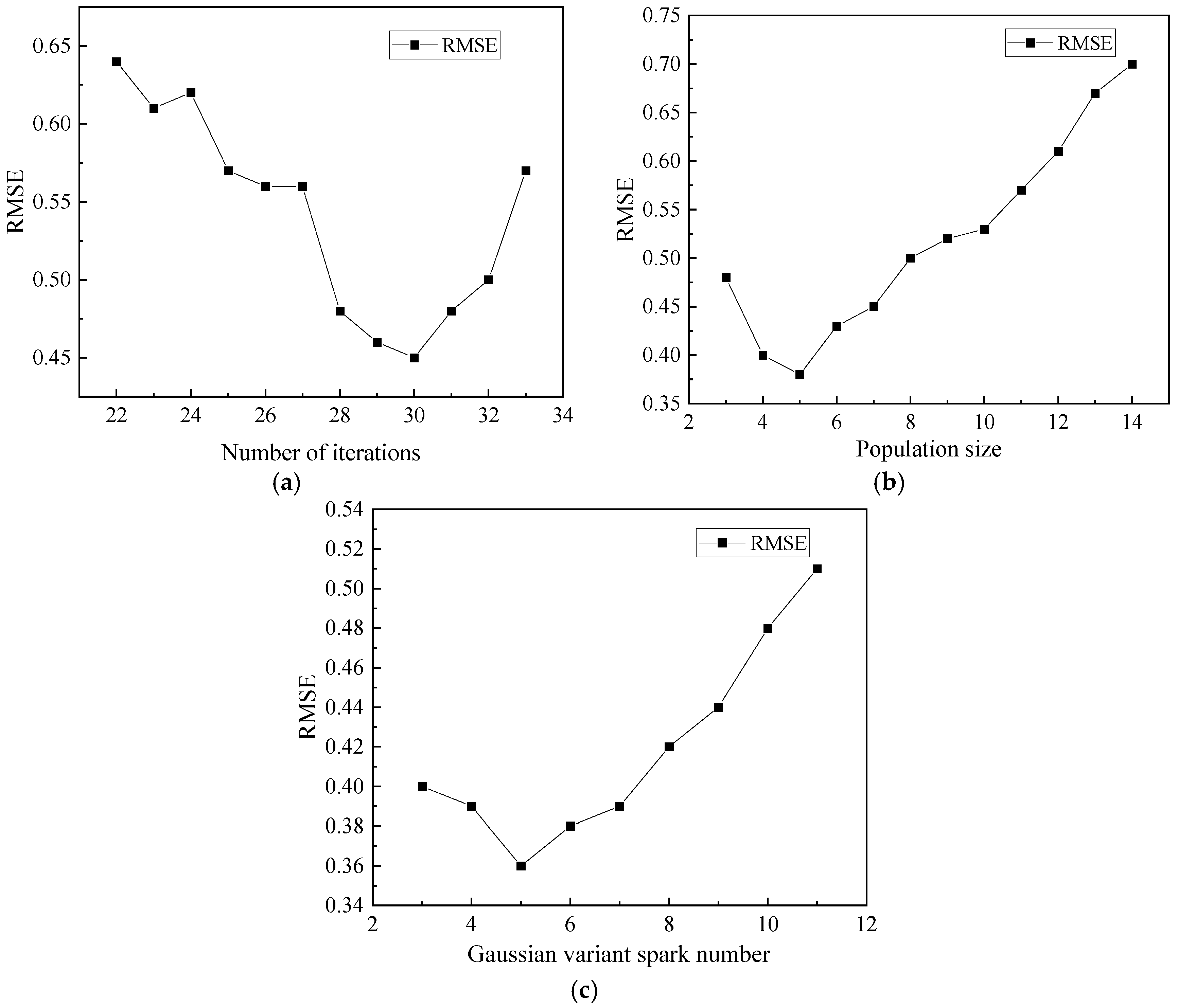
3.3. Determination of Neural Network Parameters

According to the principle of optimization neural network in Section 2, the first 23 sets of data in the sample data were used as the training set of FWA-BP neural network model and FAGSO-BP neural network model, and the last 8 sets of data were used as the testing set through Python programming operations, and the values of each parameter were determined through several trial calculations.

(1)

Determination of structural parameters of BP neural network

The predictive model for the subsidence of soft soil uses a three-layer BP neural network, the number of neurons in the input layer is 4; the number of neurons in the output layer is 1. For the determination of the number of neurons in the implied layer, the number of neurons in the implied layer is calculated by Equation (17), and the number of neurons in the implied layer is taken as s = 10, as follows:

$$s=\sqrt{m+n}+a$$

(17)

where m is the number of nodes in the input layer of the network; n is the number of nodes in the output layer of the network; a is a constant between 0 and 10.

Taking m = 4 and n = 1, the network learning rate is 0.001, the maximum number of iterations for training is 1000 and the minimum error for the training objective is 0.00065. Tanh activation function can effectively improve the model’s ability to fit complex data and training efficiency due to its nonlinear characteristics, zero-centered output and good gradient propagation ability, so in the BP neural network for forecasting, the Tanh function serves as the activation for both the input and output layers. The parameters of the BP neural network are shown in

Table 1. Key parameters of BP neural network algorithm.

Parameter Name	Parameter Overview	Corresponding Value
m	Quantity of neurons in the input layer	4
n	Neuron count in the hidden layer	10
s	Total nodes in the output layer	1
lr	The learning rate of the network	0.001
epochs	Training maximum number of iterations	1000
goal	Training target minimum error	0.00065

.

(2)

Determination of the number of iterations of the fireworks algorithm

According to the range of setting parameters of the fireworks algorithm, the preliminary setting of the population size is 10, the number of Gaussian variance sparks is 5 and the number of iterations is 25 based on the determination of the number of iterations with the smallest root mean square error. The preliminary results of the calculations for the optimal number of iterations of the FAGSO-BP neural network model are shown in Figure 2a. The optimal number of iterations can be obtained from Figure 2a to be 30.

(3)

Determination of the population size of the fireworks algorithm

Based on the preliminary setting of population size of 10, Gaussian variance spark number of 5, and iteration number of 30, the population size with the smallest root mean square error is determined. The results of the preliminary calculations of the optimal population size of the FAGSO-BP neural network model are shown in Figure 2b. From Figure 2b, the optimal population size of 5 can be obtained.

(4)

Determination of the number of Gaussian variant sparks for fireworks algorithms

Based on the preliminary setting of population size of 5, Gaussian variance spark number of 5 and the number of iterations of 30, the number of iterations with the smallest root mean square error is determined. The results of the preliminary calculations of the optimal Gaussian variance spark number for the FAGSO-BP neural network model are shown in Figure 2c. From Figure 2c, we can obtain that the optimal Gaussian variance spark number is 5.

The parameters of the fireworks algorithm were determined by the above calculations, the number of iterations was 30, the population size was 5, the number of Gaussian variant sparks was 5, the radius of fireworks was adjusted by a constant of 10, the number of fireworks exploding sparks was adjusted by a constant of 5 and the upper and lower bounds for the number of fireworks exploding sparks were 6 and 2. The key parameters of the fireworks algorithm are shown in

Table 2. Parameters of the fireworks algorithm.

Parameter Name	Parameter Description	Parameter Value
N	Size in populations of fireworks	5
d	The radius of fireworks was adjusted by a constant	10
m	The number of fireworks exploding sparks was adjusted by a constant	5
am	The upper bounds for the number of fireworks exploding sparks	6
bm	The lower bounds for the number of fireworks exploding sparks	2
g	The number of Gaussian variant sparks	5
T	Maximum iterations	30

.

3.4. Optimizing Neural Network Feasibility Analysis

After calculation, the parameters of FWA-BP neural network model and FAGSO-BP neural network model were determined. The network learning rate in BP neural network is 0.001, the maximum number of iterations for training is 1000 and the minimum error of training target is 0.00065. The number of neuron nodes in the hidden layer is 10, and Tanh activation function is used in the function of the input layer and output layer. The number of iterations of the fireworks algorithm is 30, the population size is 5, the number of Gaussian variant sparks is 5, the radius of the fireworks is adjusted by a constant of 10, the number of fireworks exploding sparks is adjusted by a constant of 5, and the upper and lower bounds of the number of fireworks exploding sparks are 6 and 2. The training process of FWA-BP neural network and FAGSO-BP neural network is shown in Figure 3. After the convergence of FWA-BP and FAGAO-BP neural network, the comparison of the prediction results with the monitoring data is shown in Figure 4, and the relative error of the neural network prediction model is shown in Figure 5.

The comparative analysis of the two neural networks after training and testing is shown in

Table 3. Comparative analysis of neural networks.

Sample Group	Monitoring Value (mm)	FWA-BP Prediction (mm)	Average Relative Error (%)	FAGAO-BP Prediction (mm)	Average Relative Error (%)
18	6.89	6.75	−1.7221	6.89	−1.6106
19	7.03	6.92		7.05
20	7.35	7.51		7.17
21	7.53	7.38		7.27
22	7.68	7.72		7.36
23	7.89	7.67		7.42
24	7.96	7.74		7.47
25	8.23	7.79		7.51

. The average relative error of the single BP neural network prediction data in the data source article is 2.6297%, and the average relative error of the GA-BP neural network is 1.7111%. The maximum relative error of the FWA-BP neural network is −5.3785%, the minimum relative error is 0.5790% and the average relative error is −1.7221%. The maximum relative error of FAGSO-BP neural network is −3.8961%, the minimum relative error is 0.0447% and the average relative error is −1.6106%. Compared with the single BP neural network, the prediction accuracy of FWA-BP and FAGSO-BP neural networks is improved, the prediction accuracy of FWA-BP is approximately equal to that of GA-BP neural network and the prediction accuracy of FAGSO-BP neural network is slightly better than that of GA-BP neural network, which verifies the feasibility of the optimization approach.

4. Example Analysis

The data come from the monitoring value of settlement and deformation of soft soil roadbed of Wuyi expressway in Hunan Province, the monitoring value includes foundation settlement and groundwater level, and the mileage number of the main line monitored ranges from K161 + 050 to K162 + 872, K167 + 110 to K175 + 600, there are 62 monitoring sections, and there is a settlement plate in the left, middle pile and right section of each section, which is used for observing the cumulative the total settlement amount of the soft soil. The total number of monitoring data is 184. The engineering characteristics of the geotechnical layer are evaluated as follows:

• Cultivated soil ①: plastic high compressibility soil, plant roots and corrosive material content of about 5%, physical and mechanical properties of large differences, poor structure, cannot be used as the road foundation bearing layer, should be dug out.
• Powdery clay ②: according to the results of geotechnical tests and field standard penetration test results for the hard plastic compressive soil, physical and mechanical properties are better, shallower buried, strength is more uniform, can be selected as the road natural foundation holding layer.
• Powdery clay ③: according to the results of geotechnical test and on-site standard penetration test results for soft-plastic high compression soil, its soil quality is poor, low strength, can be selected as a composite foundation pile foundation bearing layer.
• Fine sand ④: saturated with water, slightly dense according to standard penetration test, with general physical and mechanical properties, but with deeper burial and smaller thickness, it cannot be selected as bearing layer of foundation pile.
• Pebbles ⑤: saturated with water, in dense state, with better physical and mechanical properties, smaller deformation, more stable distribution, but deeper buried, can be selected as bearing layer of pile foundation of proposed road foundation.

4.1. Optimization Neural Network Model Building

According to the monitoring data, four factors, namely, observation time, groundwater level, soft soil roadbed disposal method, and monitoring location, are utilized as inputs to the BP neural network, which consequently shapes the input into a vector with four dimensions. The output of the model is the predicted settlement of soft soil, represented by a single-dimensional vector. And the data is normalized using Equation (19). The input variables are listed below:

(1)

Time of observation: measured data.

(2)

Groundwater level: measured data.

(3)

Soft soil roadbed disposal methods: (1) cement mixing pile; (2) dredgings and replenishment; (3) biochemical enzyme curing; (4) high pressure rotary spraying piles.

(4)

Monitoring locations: (1) general roadbed; (2) access road; (3) access road transition section; (4) round pipe culvert; (5) bridgehead transition section; (6) bridgehead encryption section; (7) bridgehead treatment section.

After the calculations in Section 3.3, the parameters of the FWA-BP neural network model and the FAGSO-BP neural network model were determined. The number of iterations of the fireworks algorithm is 30, the population size is 5, the number of Gaussian variant sparks is 5, the radius of the fireworks is adjusted by a constant of 10, the number of fireworks exploding sparks is adjusted by a constant of 5, and the upper and lower bounds for the number of fireworks exploding sparks are 6 and 2. The key parameters of the GA algorithm are shown in

Table 4. GA algorithm key parameters.

Parameter Name	Parameter Description	Parameter Value
popu	Population size	5
gen	Hereditary number	200
pcross	Crossover probability	0.08
permutation	Mutation probability	0.002

.

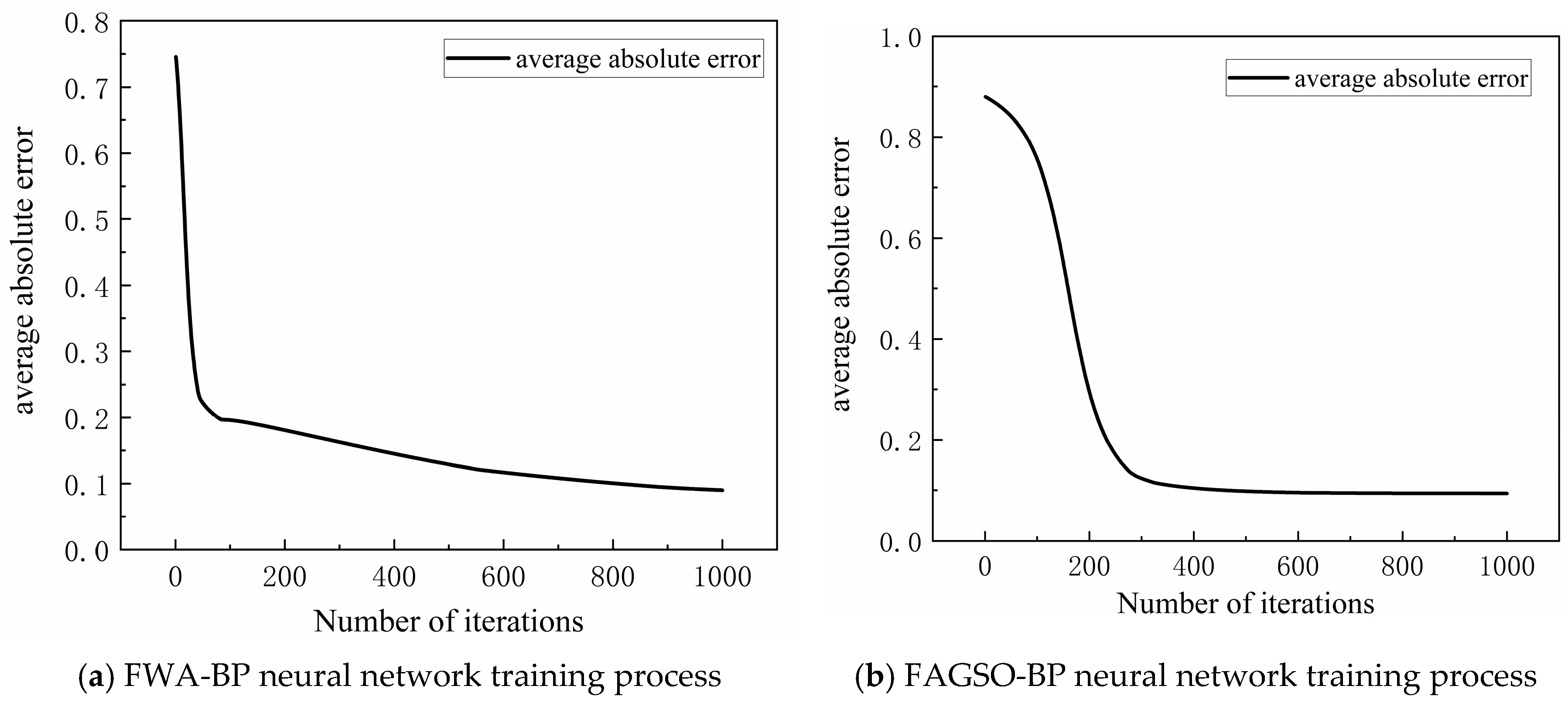
4.2. Model Training and Testing

After the calculation in Section 3.3, the network learning rate in the BP neural network is 0.001, the maximum number of iterations for training is 1000, and the minimum error of the training objective is 0.00065. The number of neuron nodes in the input layer is 4, the number of neuron nodes in the hidden layer is 10, the number of neuron nodes in the output layer is 10, and the functions of the input and output layers use tanh activation function. The first 140 sets of data from the monitoring data are used as training samples, and the last 44 sets of data are used as test samples.

In the case of the trained models for predicting soft soil settlement, specific test data are employed to evaluate the models’ predictive capabilities. Subsequently, a statistical analysis is conducted on their predictive outcomes. The performance of these models is assessed by the following five indicators:

(1)

RMSE (Root Mean Square Error): Measures the average error between the predicted value and the actual value. The smaller the RMSE, the more accurate the prediction of the model.

(2)

MAE (Mean Absolute Error): Measures the average of the absolute errors between the predicted and actual values. The smaller the MAE, the more accurate the model’s predictions.

(3)

MAPE (Mean Absolute Percentage Error): Measures the average of the absolute percentage error between the predicted value and the actual value. The smaller the MAPE, the more accurate the model’s prediction.

(4)

MSE (Mean Square Error): Measures the average of the squares of the errors between the predicted values and the actual values. The smaller the MSE, the more accurate the prediction of the model.

(5)

Mean Relative Error (%): Measures the average value of the relative error between the predicted and actual values. The smaller the average relative error, the more accurate the model’s prediction.

Finally, the predictive efficacy of the model for forecasting soft soil subsidence is further verified by comparing it with that of the soft ground settlement prediction model based on the traditional BP neural network, the fireworks algorithm-optimized BP neural network (FWA-BP), genetic algorithm-optimized BP neural network (GA-BP) and fireworks algorithm-optimized BP neural network with gravitational operator (FAGSO-BP).

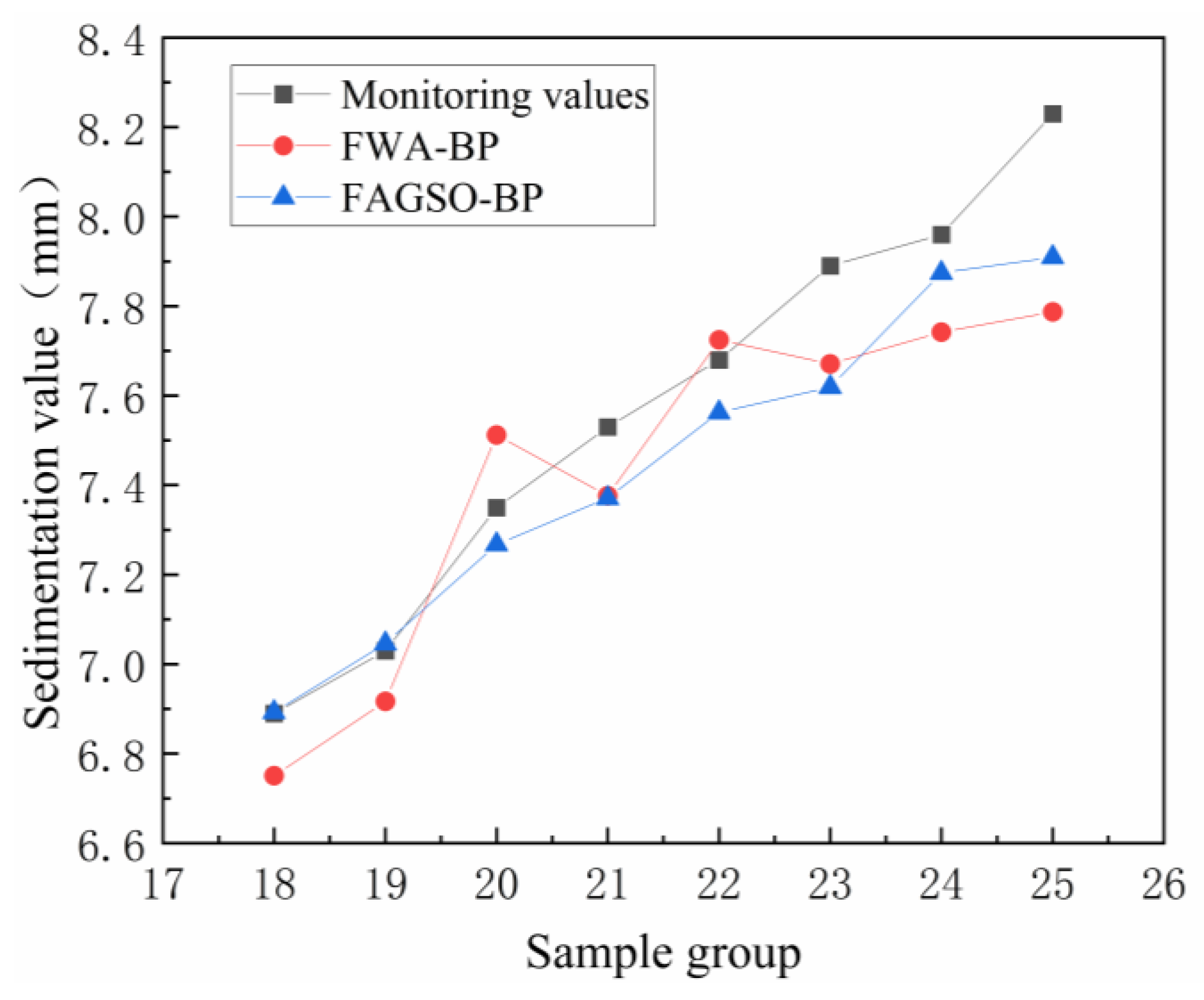
4.3. Projected Results

The comparison of the neural network training results with the true values of the training set is shown in Figure 6. The training set evaluation metrics are shown in

Table 5. Performance metrics for the training dataset.

Metrics	Network Type
	BP	GA-BP	FWA-BP	FAGSO-BP
RMSE	2.23	1.60	1.97	1.82
MAE	1.70	3.77	1.62	1.39
MAPE (%)	0.17	0.16	0.17	0.14
MSE	4.98	2.55	3.89	3.29
Average relative error (%)	7.41	7.09	6.91	5.54

.

The average relative error of the BP neural network training set is 7.41%, RMSE is 2.23, MAE is 1.70, MAPE is 0.17% and MSE is 4.98. The GA-BP neural network training set had an average relative error of 7.09%, RMSE of 1.60, MAE of 3.77, MAPE of 0.15% and MSE of 7.09. The average relative error of the FWA-BP neural network training set was 6.91%, RMSE was 1.97, MAE was 1.62, MAPE was 0.17% and MSE was 3.89. The average relative error of FAGSO-BP neural network training set is 5.54%, RMSE is 1.82, MAE is 1.39, MAPE is 0.14% and MSE is 3.29. This shows that the FWA-BP and FAGSO-BP models perform better on the training set.

From Table 5, we can see that: in the training set, the FAGSO-BP neural network model significantly improves the prediction accuracy compared to other models. Specifically, the FAGSO-BP model achieves reductions of 18.39% in RMSE and 17.65% in MAPE on the training dataset, respectively, contrasted with the standalone BP neural network model, which indicates that the FAGSO-BP model has the best fitting effect on the training set and is able to capture the data features more efficiently, which results in a higher prediction accuracy. In contrast, the BP neural network model performs the worst on these metrics, indicating that its fitting ability on the test set is limited, and its prediction accuracy needs to be improved.

The comparison of the neural network testing results with the true values of the training set is shown in Figure 7, and the evaluation indexes of the test set are shown in

Table 6. Performance metrics for the testing dataset.

Metrics	Network Type
	BP	GA-BP	FWA-BP	FAGSO-BP
RMSE	2.20	1.85	1.63	1.60
MAE	1.69	1.46	1.33	1.20
MAPE (%)	0.16	0.15	0.14	0.12
MSE	4.86	3.44	2.67	2.56
Average relative error (%)	9.27	9.74	7.03	6.06

.

When comparing the prediction performance of the four neural network models for soft soil settlement, the FAGSO-BP model demonstrated the lowest root mean square error (RMSE), mean square error (MSE), and mean absolute error (MAE), which showed that its prediction accuracy outperformed that of the traditional BP model, the GA-BP model, and the FWA-BP model.

In comparison, the higher RMSE and MAE values of the BP model in soft ground settlement prediction imply that it may be prone to fall into local optimal solutions during the training process, and thus a global optimization strategy is required to enhance its performance. Optimization of the BP neural network by the fireworks algorithm with the introduction of the gravitational search operator can enhance its global search capability, thus improving the accuracy and stability of the prediction.

5. Conclusions

In this paper, two neural network models were developed to predict the settlement of soft ground using soft ground settlement monitoring data from an engineering project. The first model is constructed based on the FWA-BP algorithm, while the second model uses the FAGSO-BP algorithm. The following conclusions are mainly obtained:

(1)

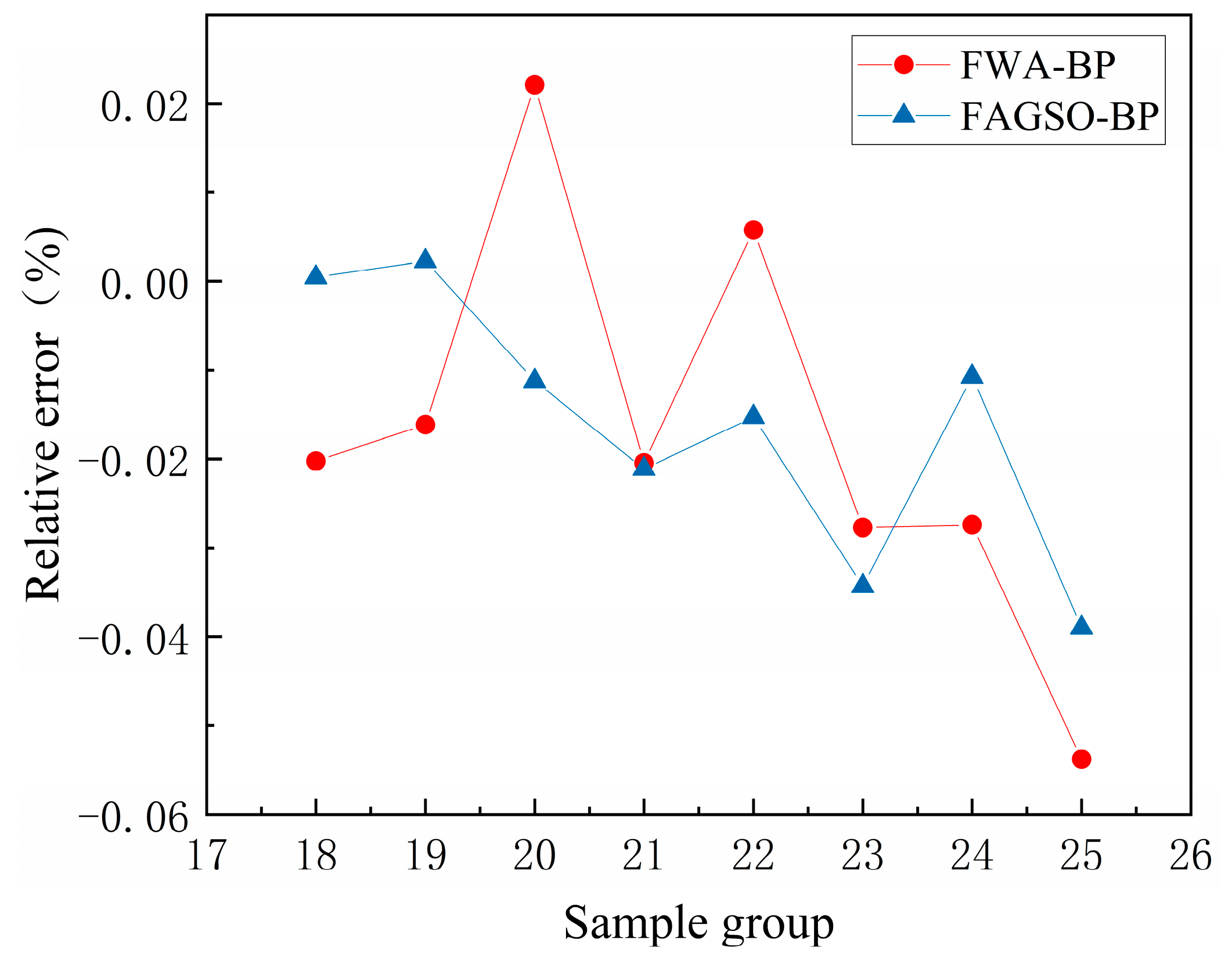
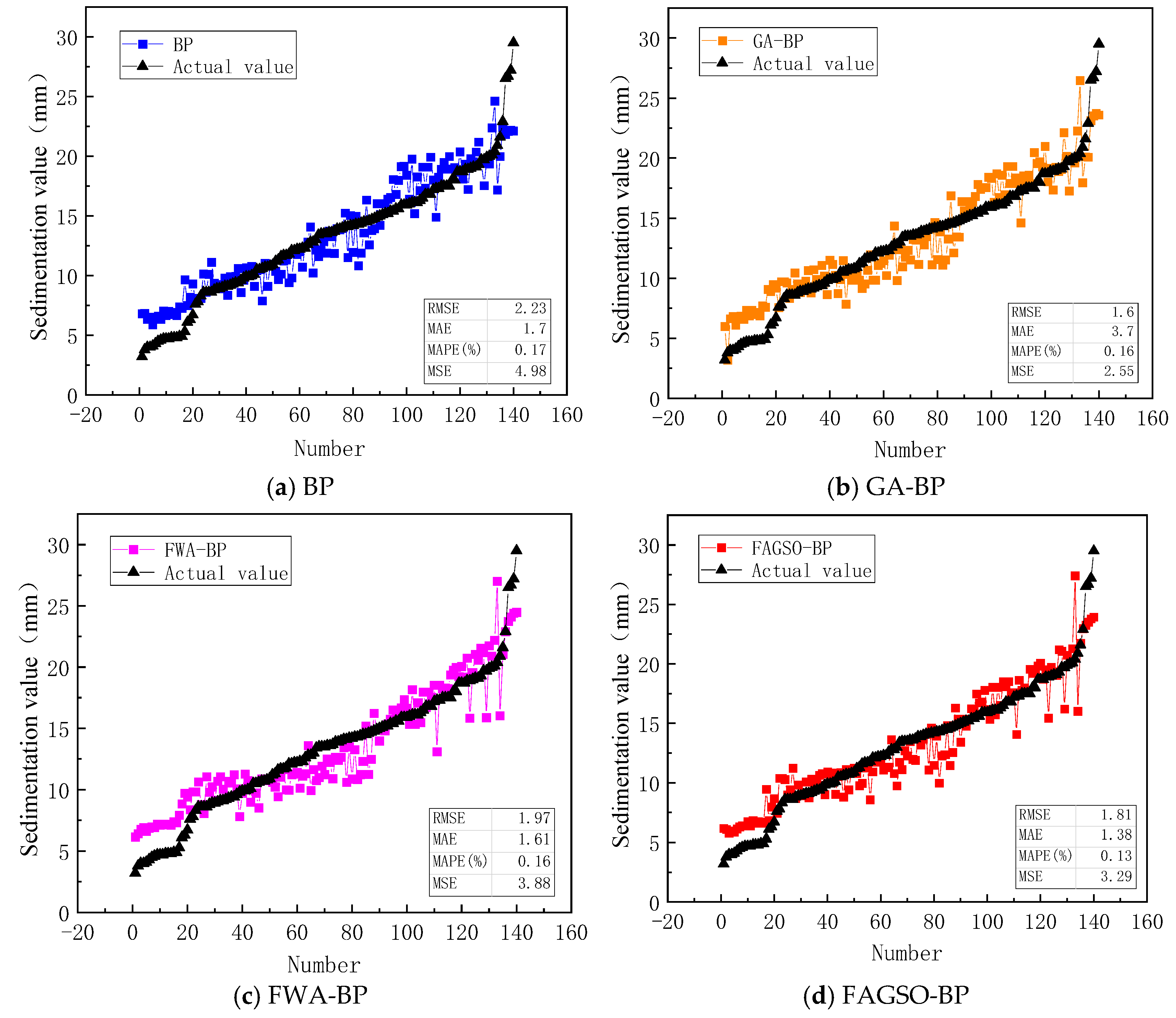
The feasibility of the FWA-BP neural network prediction model and the FAGSO-BP neural network prediction model were verified using the monitoring data of the deep foundation pit project of the West Third Ring Road in Zhengzhou City. The results show that the maximum relative error of FWA-BP neural network is −5.3785%, the minimum relative error is 0.5790% and the average relative error is −1.7221%. The maximum relative error of FAGSO-BP neural network is −3.8961%, the minimum relative error is 0.0447% and the average relative error is −1.6106%. Compared with the single BP neural network, the prediction accuracy of FWA-BP and FAGSO-BP neural network is improved, the prediction accuracy of FWA-BP is approximately equal to that of GA-BP neural network, and the prediction accuracy of FAGSO-BP neural network is slightly better than that of GA-BP neural network, which proves that the optimization approach is feasible.

(2)

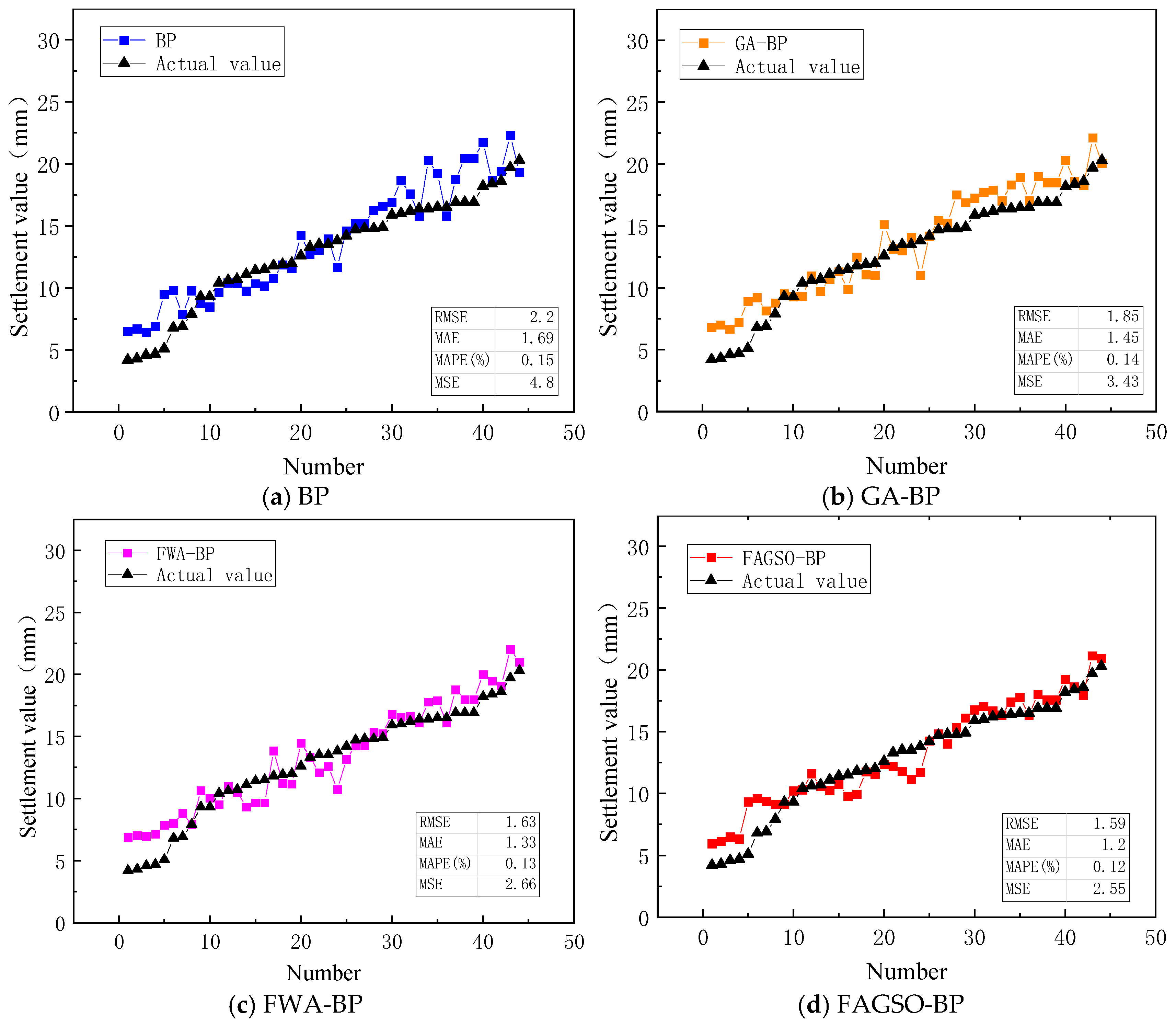
Through the soft foundation settlement prediction analysis of Hunan Wuyi Expressway Project, it can be seen that among the four neural network prediction models, the FAGSO-BP neural network model shows a lower average relative error (6.06%), mean square error MSE (2.56) and root mean square error RMSE (1.60), their reductions of 34.63%, 47.33% and 27.27%, respectively, compared to BP neural network, which verifies the efficiency and reliability of the model in real engineering projects.

(3)

By applying a combination of the fireworks algorithm and the gravitational search operator to the BP neural network, the proposed FAGSO-BP model performs well in terms of weight and threshold optimization, which indicates that the algorithm optimization can effectively improve the accuracy of soft ground settlement prediction. Compared with the traditional BP neural network, GA-BP neural network and FWA-BP neural network, the FAGSO-BP model has smaller errors and higher stability, which indicates that the introduced optimization algorithm is able to enhance the robustness of the model for soft ground settlement prediction.

(4)

Future work can focus on the following three aspects:① fusion of spatio-temporal modelling techniques (e.g., LSTM-Transformer) to enhance long-term prediction capability under dynamic loading; ② development of adaptive parameter optimization framework to expand the generalization of the model to complex geologies, such as oceanic clays, organic soils, etc.; ③ construction of real-time subsidence early warning system by combining edge computing with multi-source sensing data (InSAR, fibre optics), to promote intelligent geotechnical engineering management.