Study on the Failure Mechanism of Deep Foundation Pit of High-Rise Building: Comprehensive Test and Microstructure Coupling
Abstract
1. Introduction
- Through the multiple coupling of comprehensive testing and finite element models, the problem of quality defects in pile foundations in deep foundation pits in soft soil is solved.
- Reveals the fully coupled pile foundation defect diagnosis and field test comparative analysis process in soft soil areas.
- Provides a theoretical research framework and comprehensive analysis method for accurately evaluating and ensuring the construction quality of soft foundation pile foundations.
- Provides a rich and comprehensive research and analysis process and framework for how to study and analyze similar cases and establishes standards for better judgment of such pile foundation quality accidents.
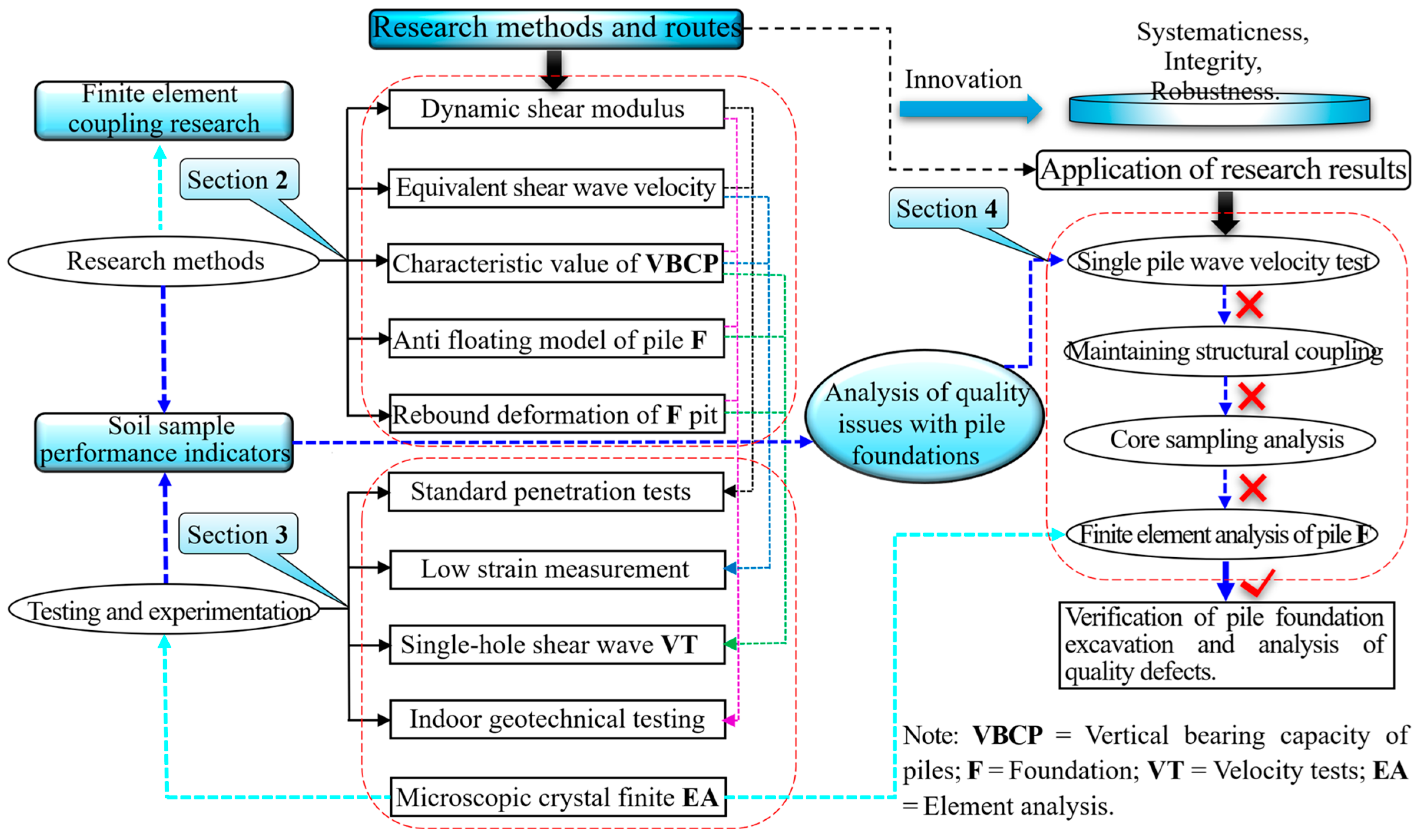
2. Methods
2.1. Main Experimental Testing
2.2. Coupling Model for the Spatiotemporal Effects
2.3. Stability Evaluation Indicators for Support System
3. Results
- The one # office building is 31 stories high, with a maximum load of 31,000 kN for a single pile. The 3rd layer of medium-weathered tuff is used as the bearing layer of the pile foundation. The pile type is a boring (punched) cast-in-place pile with a diameter of 1000 mm or more, and the design principle is to enter the 10th-3rd layer of medium-weathered tuff for more than 15 m.
- The two # scientific research office buildings are 20 stories high, with a maximum load of 18,000 kN for a single pile. The 10th-3rd layer of medium-weathered tuff is used as the bearing layer of the pile foundation. The pile type is a bored (punched) cast-in-place pile with a diameter of 800 mm or more, and the design principle is to enter the 10th-3rd layer of medium-weathered tuff for more than 10 m.
- The maximum load of a single pile for the podium and basement is 4500 kN; the 10-3 layer of medium-weathered tuff is used as the bearing layer of the pile foundation. The pile type is a bored (punched) cast-in-place pile of 600 mm and above. The entire cross-section of the pile end entering the bearing layer is not less than 1 d.
3.1. Load Analysis
- The enclosure’s lateral deformation depends on the enclosure’s stiffness, the support spacing, the effective insertion length of the enclosure, the passive soil resistance in the pit, the soil pressure outside the pit, and the axial stiffness of the elastic support.
- The lateral deformation control caused by soft soil rheology is analyzed using the Kelvin model, which is a mechanical model that represents a viscoelastic material as a spring and a damper in parallel [21].
- The soil’s dead weight is considered in the load analysis (the width is 25.95 m, and the excavation depths are 5.05 m and 9.05 m, respectively). During construction, the equivalent load is 20.0 kN/, which is evenly applied to the road surface around the foundation pit. The soil pressure generated by the deadweight of the soil around the foundation pit is 14,298.28 kN/ (the total soil pressure is 67.35 × kN; see Figure 3 for direction), and the soil pressure inside the foundation pit is 33,182.90 kN/ (the total soil pressure is 241.80 × kN, see Figure 3 for direction). A uniform surface load is applied to the road model near the foundation pit as a vehicle load, and the load value is 28 kN/. The concrete support of the retaining structure is designed to be 25.0 kN/, and the column piles and retaining piles are 25.0 kN/ [22].
3.2. Outdoor Testing and Experimentation
3.2.1. Consolidation Coupling
3.2.2. Single Hole Wave Velocity Testing
3.3. Indoor Testing and Experimentation
- The conventional physical and mechanical performance tests of undisturbed soil include indicators such as liquid limit, internal friction angle, cohesive force, etc.
- For the natural (saturated) uniaxial compressive strength test samples of rocks, the development of joints and cracks is uneven. It is necessary to analyze the maximum value, minimum value, average value, statistical sample size, and statistical coefficient of variation [31].
- One hundred forty-one sets of soil samples and 29 sets of points were collected in the geotechnical test. The average sample bottom depth is 19.89 m, and the moisture content range is 19.90%~68.50%, with an average of 34.41%. The highest water content range is concentrated in positions Z52-T3, T1, and Z60-T1, as well as the silt layer’s main distribution areas of the silt layer. The soil sample’s average dry density/average wet density is 0.75, consistent with the moisture content test result. The average value of natural porosity e is 0.96, and the porosity of the foundation soil is relatively large. The average liquid limit index is = 36.93%, and the plastic limit index is 21.30%, indicating a plastic state. The soil is relatively soft and has a high natural moisture content. Four pressure conditions were used to test the porosity of the soil layer: p = 50~400 MPa, average porosity = 0.878, = 0.832, = 0.765, = 0.690 (Figure 6).
Soil Microstructure Analysis
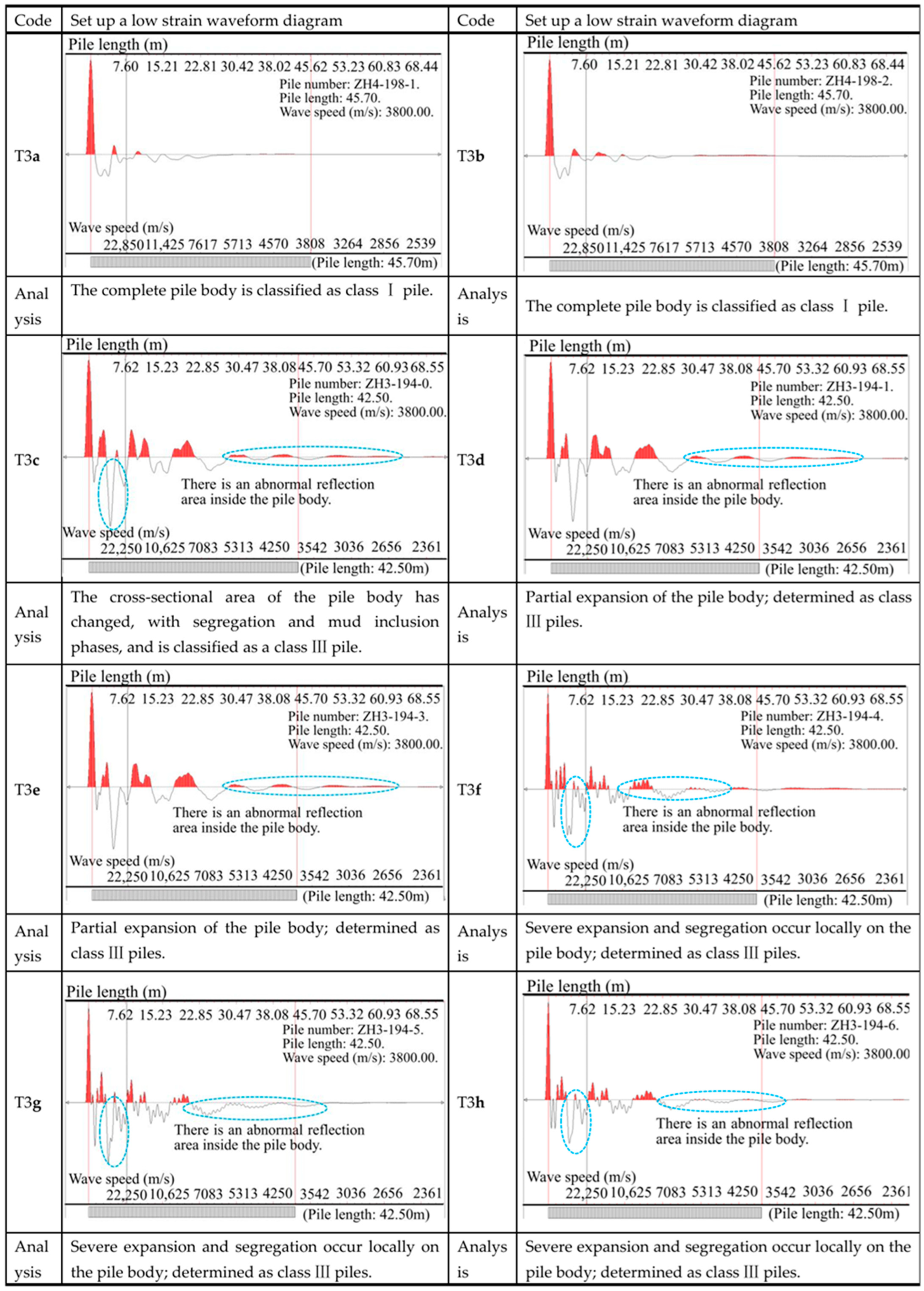
3.4. Low Strain Wave Velocity Testing
Static Load and Core Sampling
4. Discussion
4.1. Numerical Simulation Analysis
4.1.1. Overall Support System
4.1.2. Damaged Component Structures
4.2. Component Defect Inspection
- Digging down to a depth of −2.7 m (on-site pile top elevation, Figure 14a) to −5.2 m, with a pile foundation diameter R > 700 mm, there was expansion, and the pile foundation expansion range was 760~860 mm. The primary reinforcement of the pile top steel cage was offset by 60~10 mm, and a small amount of hoop reinforcement had leakage (Figure 14a,b).
- Digging down to a depth of −5.2 m, the steel cage was exposed to one side of the pile foundation, and the primary reinforcement of the steel cage was slightly deformed. There were honeycombs, pitted surfaces, and a small amount of looseness in the concrete (Figure 14a).
- Digging down to a depth of −10.4 m, the primary reinforcement of the steel cage on the excavation surface was bent and deformed, with an exposed section of 2.4 m. The deformation within a range of about 1.4 m in the upper part was relatively small; in comparison, within a range of 1 m in the lower part, the pile body necking and primary reinforcement deformation were obvious [37]. The range of about 0.25 m extension of the pile body towards the core of the pile was all loose compressed concrete aggregates (Figure 14b).
- Researchers also inspected the large volume of concrete blocks of the expanded pile body peeled off on-site and found evident traces of drilling at the bottom of the second core sampling hole (Figure 10b). The concrete at the bottom of the core sampling hole was mixed with silt and sand, losing structural strength and damaging bearing capacity and stability (Figure 14b).
- As the distance of ZH2-194 from the main tower crane pile foundation is only 3.9 m, the outer expansion of the Larssen steel sheet pile support around the pile body is small. The Larssen steel sheet pile is 12 m long, with a support excavation section of 2.8 m × 3.7 m = 10.36 .
4.3. Entity Structure Verification
- The test data for the steel cage invade the protective layer by 5 cm. From the perspective of material elasticity and strength theory, the bending and pure torsion of the pile foundation under a stress state have changed, resulting in displacement-deformation deviations (Figure 14b).
- The circular pie-shaped cushion of the steel cage does not control the protective layer in the deformation caused by the vertical S-shaped deformation of the pile hole or the creep shrinkage of the soft soil in the pile foundation in soft soil geology (Figure 14a).
- Under the superposition of the additional stress generated by the construction of soft soil and the load generated by the concrete mixer truck during concrete pouring, the soft soil layer undergoes creep deformation within a specific depth range or local and large-scale hole collapse [38,39]. The mud on the hole wall invades the pile foundation, causing quality defects such as voids and honeycomb pits (Figure 14).
- After the second hole cleaning, the concrete cannot be poured in time. The equilibrium state of the lateral pressure of the slurry inside the hole and the horizontal force of the soft soil outside the hole changes or is damaged for a short time. Plastic deformation occurs in the hole wall range with weak anti-skid (shear) strength of the soil layer, and the soft soil invades the boundary of the pile foundation concrete [40].
- The concrete used for bored piles is underwater. Due to long-distance transportation and vibration equipment not being used during pouring, the concrete should have lost its good construction workability, water retention, cohesion, and retardancy.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, X.; Li, J.; Liu, J.; Hu, Z.; Tang, C. Influence of Complex Hydraulic Environments on the Mechanical Properties of Pile-Soil Composite Foundation in the Coastal Soft Soil Area of Zhuhai. Buildings 2023, 13, 563. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, Y.; Wu, K.; Huang, X. Centrifuge Shaking Table Study on the Hydrodynamic Effects on a Pile Foundation Bridge Pier in Soft Soil under Earthquakes. Mar. Struct. 2022, 85, 103261. [Google Scholar] [CrossRef]
- Shamsi, M.; Ghanbari, A. Nonlinear Dynamic Analysis of Qom Monorail Bridge Considering Soil-Pile-Bridge-Train Interaction. Transp. Geotech. 2020, 22, 100309. [Google Scholar] [CrossRef]
- Ahmed, D.; Bt Taib, S.N.L.; Ayadat, T.; Hasan, A. Numerical Analysis of the Carrying Capacity of a Piled Raft Foundation in Soft Clayey Soils. Civ. Eng. J. 2022, 8, 622–636. [Google Scholar] [CrossRef]
- Bhattacharjee, T.; Chanda, D.; Saha, R. Influence of Soil Flexibility and Plan Asymmetry on Seismic Behaviour of Soil-Piled Raft-Structure System. Structures 2021, 33, 1775–1788. [Google Scholar] [CrossRef]
- Castro, P.; Martins, P.; Castro, M.; Amaral, L.; Urashima, B. Use of Geosynthetic in Soft Soil Foundation in Mining Area: A Case Study with Analytical and Numerical Studies. Int. J. Geosynth. Ground Eng. 2023, 9, 12. [Google Scholar] [CrossRef]
- Deb, P.; Debnath, B.; Reang, R.B.; Pal, S.K. Structural Analysis of Piled Raft Foundation in Soft Soil: An Experimental Simulation and Parametric Study with Numerical Method. Ocean Eng. 2022, 261, 112139. [Google Scholar] [CrossRef]
- Lin, C.; Huang, L.; Chen, S.; Huang, M.; Wang, R.; Tan, Q. Study on Shielding Effect of the Pile Group in a Soft-Soil Foundation. Appl. Sci. 2023, 13, 9478. [Google Scholar] [CrossRef]
- Li, C.; Sheng, Y. Large-strain Analysis for Cylindrical Cavity Contraction in Strain-softening Geomaterials. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 3012–3027. [Google Scholar] [CrossRef]
- Tan, J.J.; Ramli, H. Effect of standard penetration test corrections on the estimation of undrained shear strength. J. Civ. Eng. Manag. 2023, 29, 501–515. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, D.; Fan, T.; Sun, T. Dynamic and Residual Pore Water Pressure Response of Hybrid Foundation System Under Combined Action of Wind, Wave and Seismic Loading. Period. Polytech. Civ. Eng. 2022, 67, 1. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F. Effects of Pit-Bottom-Soil Reinforcement on the Deformation of Subway Deep Foundation Pits Based on an Improved Model. Adv. Mater. Sci. Eng. 2022, 2022, 2661311. [Google Scholar] [CrossRef]
- Farrugia, D.; Galea, P.; D’Amico, S.; Paolucci, E. Sensitivity of Ground Motion Parameters to Local Shear-Wave Velocity Models: The Case of Buried Low-Velocity Layers. Soil Dyn. Earthq. Eng. 2017, 100, 196–205. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Yang, Z.; Chen, P.; Ji, F.; Wen, B. Mechanical Behavior Analysis and Bearing Capacity Calculation of CFG Pile Composite Foundation on Coral Sand Site. Front. Earth Sci. 2023, 11, 1204989. [Google Scholar] [CrossRef]
- Kong, D.; Guan, Y.; Yuan, H. Study on the Anti-Floating Water Level of the Underground Structure’s Comprehensive Anti-Floating. Structures 2023, 56, 104921. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Alcalá, J.; Yepes, V. Research on the Optimized Environment of Large Bridges Based on Multi-Constraint Coupling. Environ. Impact Assess Rev. 2022, 97, 106914. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Ding, Z.; Wu, X. An Approach to the Selection of Target Reliability Index of Cable-Stayed Bridge’s Main Girder Based on Optimal Structural Parameter Ratio from Cost-Benefit Analysis. Structures 2020, 28, 2221–2231. [Google Scholar] [CrossRef]
- Du, D.; Liu, Z. Seismic Bearing Capacity of Strip Foundation on Rock Mass Obeying Modified Hoek-Brown Failure Criterion. Buildings 2022, 12, 2083. [Google Scholar] [CrossRef]
- Dai, E.; Lv, Z.; Yuan, P.; Liu, G.; Guo, N.; Liu, Z.; Tang, B. Ductile Fracture of Anisotropic QP980 Steel Sheet by Using the Isotropic/Anisotropic Modified Mohr-Coulomb Models. Eng. Fract. Mech. 2023, 290, 109522. [Google Scholar] [CrossRef]
- Dai, Z.; Tang, H.; Wu, S.; Habibi, M.; Moradi, Z.; Ali, H.E. Nonlinear Consecutive Dynamic Instabilities of Thermally Shocked Composite Circular Plates on the Softening Elastic Foundation. Thin-Walled Struct. 2023, 186, 110645. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Zeng, B.; Xu, Q. Cyclic Creep Model of Concrete Based on Kelvin Chain under Fatigue Loads. Constr. Build Mater. 2024, 417, 135255. [Google Scholar] [CrossRef]
- Rao, P.; Meng, J.; Cui, J.; Feng, W.; Nimbalkar, S.; Liu, Z. Stability Analysis of Unsaturated Soil Pit Under Vehicle Load. Geotech. Geol. Eng. 2024, 42, 4987–5001. [Google Scholar] [CrossRef]
- Wang, Y.; Ouyang, J.; Guo, P.; Liu, Y.; Lin, H.; Li, X.; Gong, X.; Li, J. Performance of Deep Braced Excavation Under Embankment Surcharge Load. Geotech. Geol. Eng. 2023, 41, 3575–3586. [Google Scholar] [CrossRef]
- Zhai, S.; Du, G.; He, H. Bayesian Probabilistic Characterization of the Shear-Wave Velocity Combining the Cone Penetration Test and Standard Penetration Test. Stoch. Environ. Res. Risk Assess. 2023, 38, 69–84. [Google Scholar] [CrossRef]
- Jebali, H.; Bouassida, M.; frikha, W. Numerical Study of Tunis Soft Soil Improved by Combined Vacuum Consolidation and Geodrains. Innov. Infrastruct. Solut. 2024, 9, 289. [Google Scholar] [CrossRef]
- Yuan, J.; Gan, Y.; Chen, J.; Tan, S.; Zhao, J. Experimental Research on Consolidation Creep Characteristics and Microstructure Evolution of Soft Soil. Front. Mater. 2023, 10, 1137324. [Google Scholar] [CrossRef]
- Moozhikkal, R.; Sridhar, G.; Robinson, R.G. Constant Rate of Strain Consolidation Test Using Conventional Fixed Ring Consolidation Cell. Indian Geotech. J. 2019, 49, 141–150. [Google Scholar] [CrossRef]
- Alam, M.; Chen, J.; Umar, M.; Ullah, F.; Shahkar, M. Predicting Standard Penetration Test N-Value from Cone Penetration Test Data Using Gene Expression Programming. Geotech. Geol. Eng. 2024, 42, 5587–5613. [Google Scholar] [CrossRef]
- Fan, Y.; Niu, H.; Yang, G.; Gao, Q.; Wu, J.; Tian, B. Near-Field Vibration Induced by Single-Hole Blasting under Different Initiation Modes. Eur. J. Environ. Civ. Eng. 2023, 28, 753–778. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y. Assessment of Liquefaction-Induced Differential Ground Settlement and Lateral Displacement Using Standard Penetration Tests with Consideration of Soil Spatial Variability. J. Geotech. Geoenviron. Eng. 2022, 148, 0002775. [Google Scholar] [CrossRef]
- Su, Z.; Tan, X.; Chen, W.; Ma, W.; Zhang, C.; Xu, F. A Combined Non-Destructive Prediction Method for Evaluating the Uniaxial Compressive Strength of Rocks Under Freeze–Thaw Cycles. Arab. J. Sci. Eng. 2022, 47, 13365–13379. [Google Scholar] [CrossRef]
- Pérez, J.A.; Reyes-Rodríguez, A.M.; Sánchez-González, E.; Ríos, J.D. Experimental and Numerical Flexural–Torsional Performance of Thin-Walled Open-Ended Steel Vertical Pile Foundations Subjected to Lateral Loads. Buildings 2023, 13, 1738. [Google Scholar] [CrossRef]
- Amrioui, J.; Le Kouby, A.; Duc, M.; Guedon, J.-S.; Lansac, F. Relationship between Porosity and Water Permeability for Deep Soil Mixing Material. Int. J. Geomech. 2023, 23, 8447. [Google Scholar] [CrossRef]
- Cetin, K.O.; Cevik, M.E.; Al-Suhaily, A.; Yunatci, A.A. Probabilistic Assessment of Standard Penetration Test Hammer Energy Efficiency and Rod Length Corrections. J. Geotech. Geoenviron. Eng. 2023, 149, 11136. [Google Scholar] [CrossRef]
- Bagińska, I. Comparative Analysis of Cone Resistances in Cone Penetration Test (CPTu) and Dynamic Probe Heavy Test (DPH). Geotech. Geol. Eng. 2020, 38, 5269–5278. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, X.; Zheng, F.; Sun, Y.; Liu, G. Geological Disaster Information Sharing Based on Internet of Things Standardization. Environ. Earth Sci. 2024, 83, 148. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, Y.; Alcalá, J.; Yepes, V. Research on Coupling Optimization of Carbon Emissions and Carbon Leakage in International Construction Projects. Sci. Rep. 2024, 14, 10752. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Alcalà, J.; Yepes, V. Carbon impact assessment of bridge construction based on resilience theory. J. Civ. Eng. Manag. 2023, 29, 561–576. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sheng, J.; Zhang, Z. Failure Mechanism and Treatment of Mine Landslide with Gently-Inclined Weak Interlayer: A Case Study of Laoyingzui Landslide in Emei, Sichuan, China. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 61. [Google Scholar] [CrossRef]
- Wu, C.; Yu, J.; Cao, X.; Shen, W. Study on Design Method of Pile Wall Combination Structure in a Deep Foundation Pit Considering Deformation Induced by Excavation. Front. Earth Sci. 2022, 10, 837950. [Google Scholar] [CrossRef]


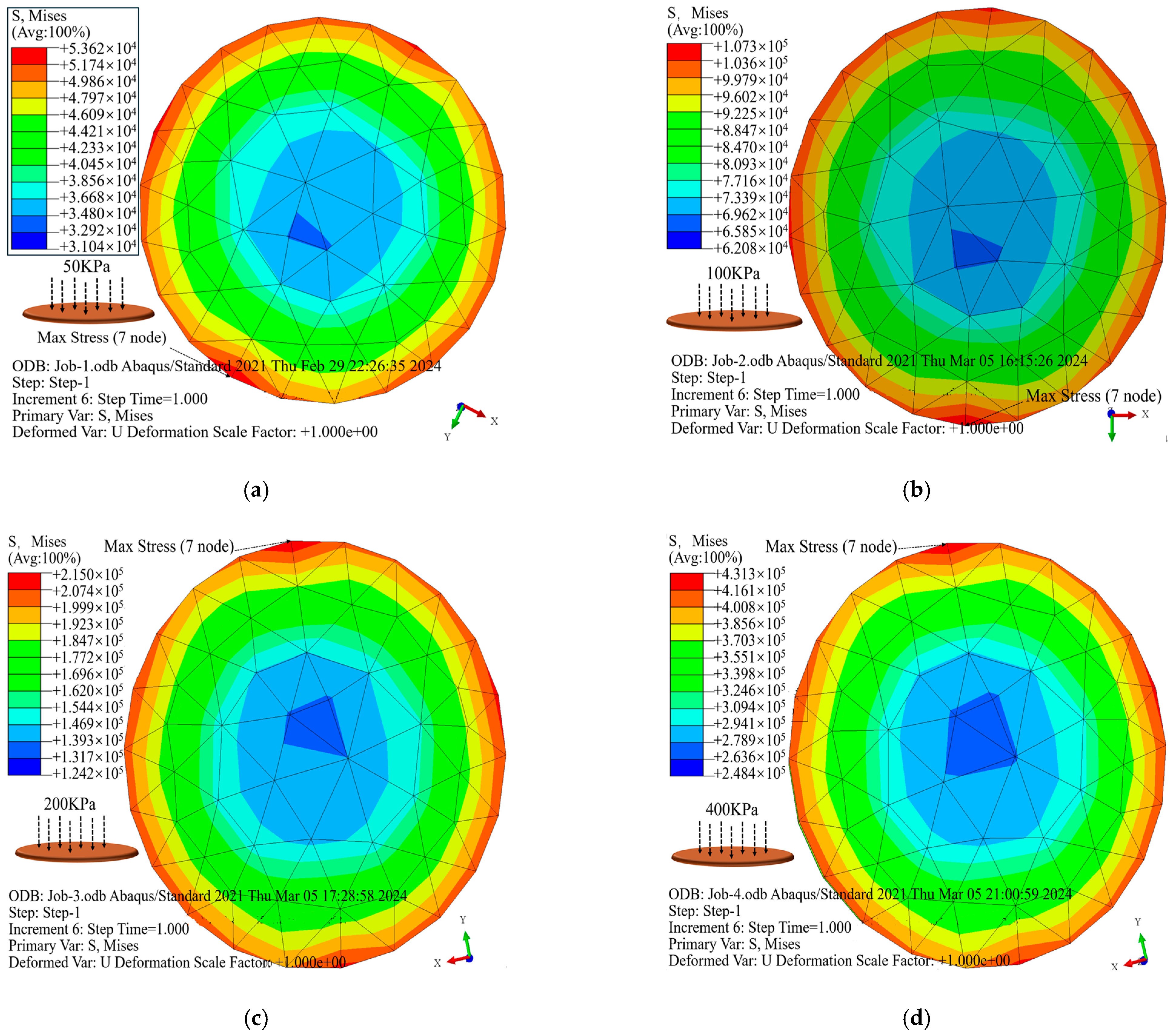
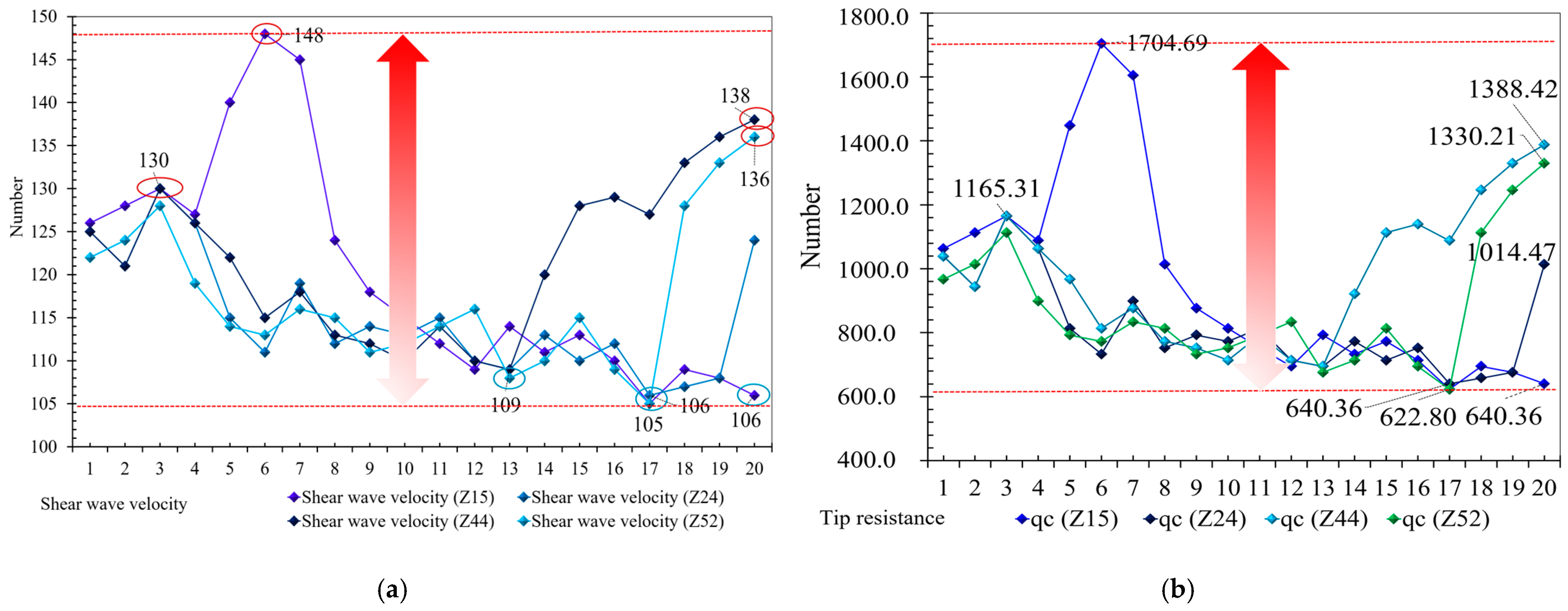

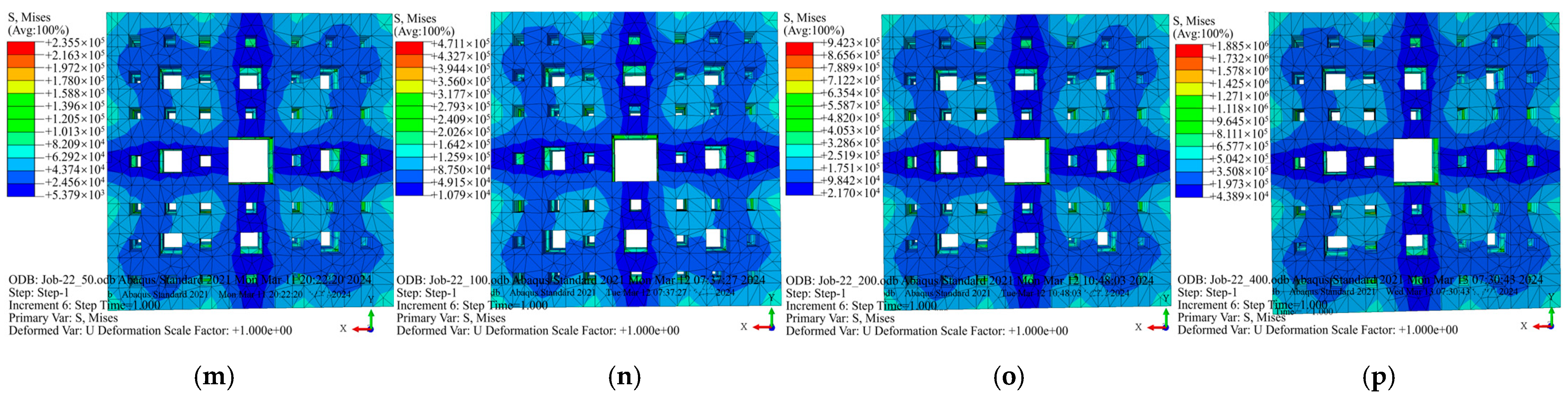

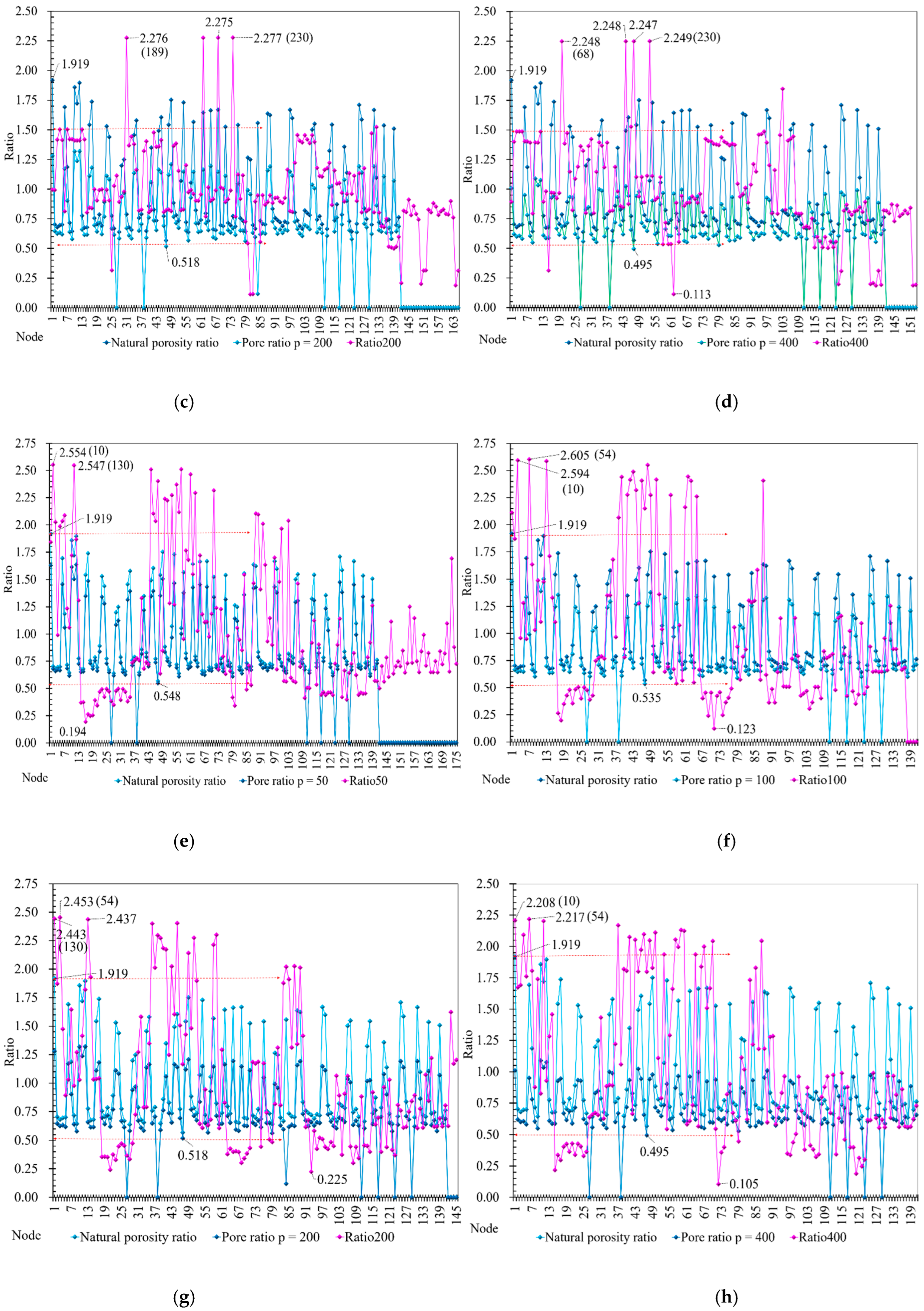



| Material Type | Density (kg/m3) | Poisson’s Ratio | Elastic Modulus (MPa) | Position |
|---|---|---|---|---|
| Cement mixing pile | 1500 | 0.32 | 31,000 | Surrounding the foundation pit |
| Supporting beam C30 | 2462 | 0.23 | 28,850 | Inside the foundation pit |
| Slope protection C20 | 2309 | 0.22 | 25,350 | Slope of foundation pit |
| Steel support | 7850 | 0.30 | 200,000 | Local reinforcement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Yepes-Bellver, L.; Alcalá, J.; Yepes, V. Study on the Failure Mechanism of Deep Foundation Pit of High-Rise Building: Comprehensive Test and Microstructure Coupling. Buildings 2025, 15, 1270. https://doi.org/10.3390/buildings15081270
Zhou Z, Yepes-Bellver L, Alcalá J, Yepes V. Study on the Failure Mechanism of Deep Foundation Pit of High-Rise Building: Comprehensive Test and Microstructure Coupling. Buildings. 2025; 15(8):1270. https://doi.org/10.3390/buildings15081270
Chicago/Turabian StyleZhou, Zhiwu, Lorena Yepes-Bellver, Julián Alcalá, and Víctor Yepes. 2025. "Study on the Failure Mechanism of Deep Foundation Pit of High-Rise Building: Comprehensive Test and Microstructure Coupling" Buildings 15, no. 8: 1270. https://doi.org/10.3390/buildings15081270
APA StyleZhou, Z., Yepes-Bellver, L., Alcalá, J., & Yepes, V. (2025). Study on the Failure Mechanism of Deep Foundation Pit of High-Rise Building: Comprehensive Test and Microstructure Coupling. Buildings, 15(8), 1270. https://doi.org/10.3390/buildings15081270








