Numerical Investigation and Factorial Analysis of Residual Displacement in Rocking Self-Centering Bridge Columns Under Cyclic Loading

Abstract

Well-designed rocking self-centering (RSC) columns are capable of achieving small residual displacement. However, quantitative assessments of residual displacement mechanisms in RSC columns remain understudied. The residual displacement is the product of the struggle between the self-centering (SC) capacity and the energy dissipation (ED) capacity. In this study, an SC factor and an ED parameter were defined to reflect the SC and ED capacity of the RSC column, respectively. The hysteretic behavior of an RSC pier under quasi-static load was studied. Based on the finite element model, the factorial analysis of two types of RSC piers was carried out, and the influence of eight common design parameters on the SC factor and ED parameters was discussed. Parametric analysis was performed to investigate the effect of the SC factor and the ED parameter with an increase in maximum displacement. According to the results of the parametric analysis, the effect of the SC factor and the ED parameter on the distribution of the residual displacement was statistically researched. A simplified formula was proposed to calculate the upper limit of the residual displacement. Furthermore, a set of predictive regression formulas was established to estimate the actual residual displacement. These regression formulas have an applicable condition that the ED parameter should be larger than 0.75. When the ED parameter is less than 0.75, the residual displacement is approximately zero. The hysteretic performance of an RSC pier is mainly determined by a single-factor effect, and the residual displacement distribution under a quasi-static load is mainly controlled by the SC factor and ED parameter.

1. Introduction

Devastating earthquakes in the past have demonstrated that reinforced concrete (RC) bridge structures are highly vulnerable to earthquakes, with extensive damage concentrated in the plastic regions of bridge piers [1,2]. This damage is likely to cause large residual displacement. It is difficult to restore a bridge structure with significant permanent displacement to its initial condition; this causes tremendous difficulties in post-earthquake recovery and huge economic losses [3]. For example, about 100 RC bridge piers were eventually demolished due to a residual displacement ratio of 1.75% after the 1995 Kobe earthquake in Japan [3]. Therefore, residual displacement is regarded as a main index to evaluate earthquake resilience, and the self-centering capacity of piers has become an important design consideration [4,5].

Based on the accelerated bridge construction philosophy, the rocking self-centering (RSC) column was proposed, and post-tensioning was considered to be an efficient way to drastically reduce residual displacement [6]. Precast segmental concrete-filled steel tubes, as suggested by Zhang et al. [7], exhibit exceptional self-centering performance and minimal plastic deformation. To date, many experimental studies have been carried out to address the seismic behavior of RSC columns [8,9,10,11,12,13,14,15,16,17,18,19]. Hewes et al. [8] performed an early cyclic test of RSC columns, and the results showed that segments of the pier basically remained elastic, and the residual displacement was very small. However, the energy dissipation (ED) capacity was extremely weak due to the lack of ED elements. To enhance the ED capacity of RSC columns, various types of dissipaters were proposed, and the ED bar is the commonest ED device among these dissipaters. The results of many cyclic tests have shown that the hysteretic curve of an RSC column equipped with ED elements is much fuller, and the ED capacity is improved, as expected [9,10,11,12,13,14,15]. Meanwhile, the added ED elements reduce the SC capacity of RSC columns, leading to the problem of residual displacement needing to be addressed if too many dissipaters are used. Some researchers have tried to use high-performance materials (e.g., shape memory alloy, fiber-reinforced polymer composite bar, and reinforcement with non-adhesive post-tensioning) to achieve a balance between SC and ED capacity [16,17,18,19,20]. Guo et al. [21] set the self-centering coefficient at approximately 1.0 to achieve a balanced trade-off between effective energy dissipation capacity and acceptable residual deformation. It can be concluded that there is a trade-off between the SC and ED capacity; the residual displacement is the product of their mutual struggle.

The harm of residual displacement has been realized gradually, and residual displacement has been regarded as an important consideration in seismic design. According to earthquake damage investigation results, the Japan Road Association code first proposed a reparability limit of 1% for RC columns [22]. Some studies focusing on the residual displacement of RC columns have been conducted; these aimed to explore the influence factors and estimate residual displacement under the influence of earthquakes. It can be concluded that residual displacement is determined by both structural properties and the characteristics of earthquake load [23,24,25,26,27,28]. However, few studies related to the residual displacement estimation of RSC columns have been reported. Li et al. [29] selected residual displacement as a performance index to conduct seismic vulnerability analysis and loss assessment of an RSC bridge system. Ou et al. [30] developed a three-dimensional model of an RSC column equipped with internal ED bars. The results of cyclic loading analyses suggested an optimum ED bar ratio of around 0.5%. Cai et al. [31] performed cyclic analyses to investigate the influence of post-tensioning force, gravity load, ED bar ratio, and aspect ratio on the residual displacement of RSC columns. Liu et al. [32] carried out parametric analyses on residual displacement under cyclic loading. Wang et al. [33] proposed a simplified formula for UHPC bridge columns with unbonded post-tensioning tendons to calculate the upper limit of residual displacement under cyclic loading. In conclusion, the residual displacement of RSC columns under cyclic loading mainly depends on structural properties. Quantitative analysis of residual displacement remains limited in previous works. Tazarv et al. [34] proposed a UHPC prefabricated column that effectively minimizes residual displacement. Jia et al. [35] introduced an intelligent high-performance material shape memory alloy (an L-shaped plate), which significantly reduces the residual displacement response of the rocking column and facilitates the prompt restoration of normal operation.

The purpose of this study is to explore the distribution of residual displacement in RSC columns under cyclic loading and achieve its prediction. Two governing parameters, including an SC factor and an ED parameter, were introduced to describe the SC capacity and ED capacity of piers. The contribution of eight common design parameters to the SC factor and ED parameter was compared. Then, the effect of the SC factor and ED parameter on the residual displacement was investigated, a set of predictive formulas for the residual displacement was obtained from regressive analyses, and an application of it was provided.

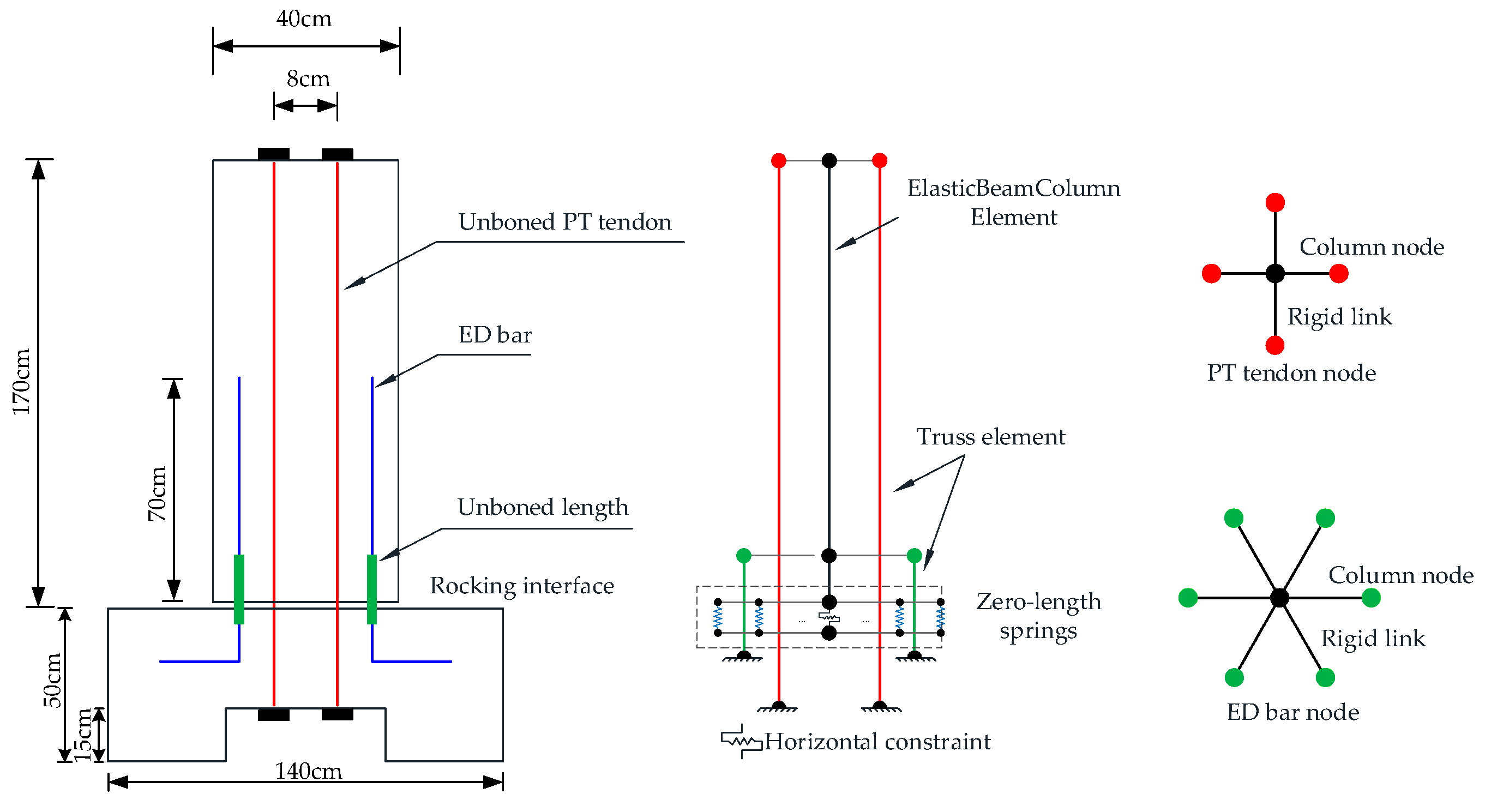
2. Simulation of RSC Columns

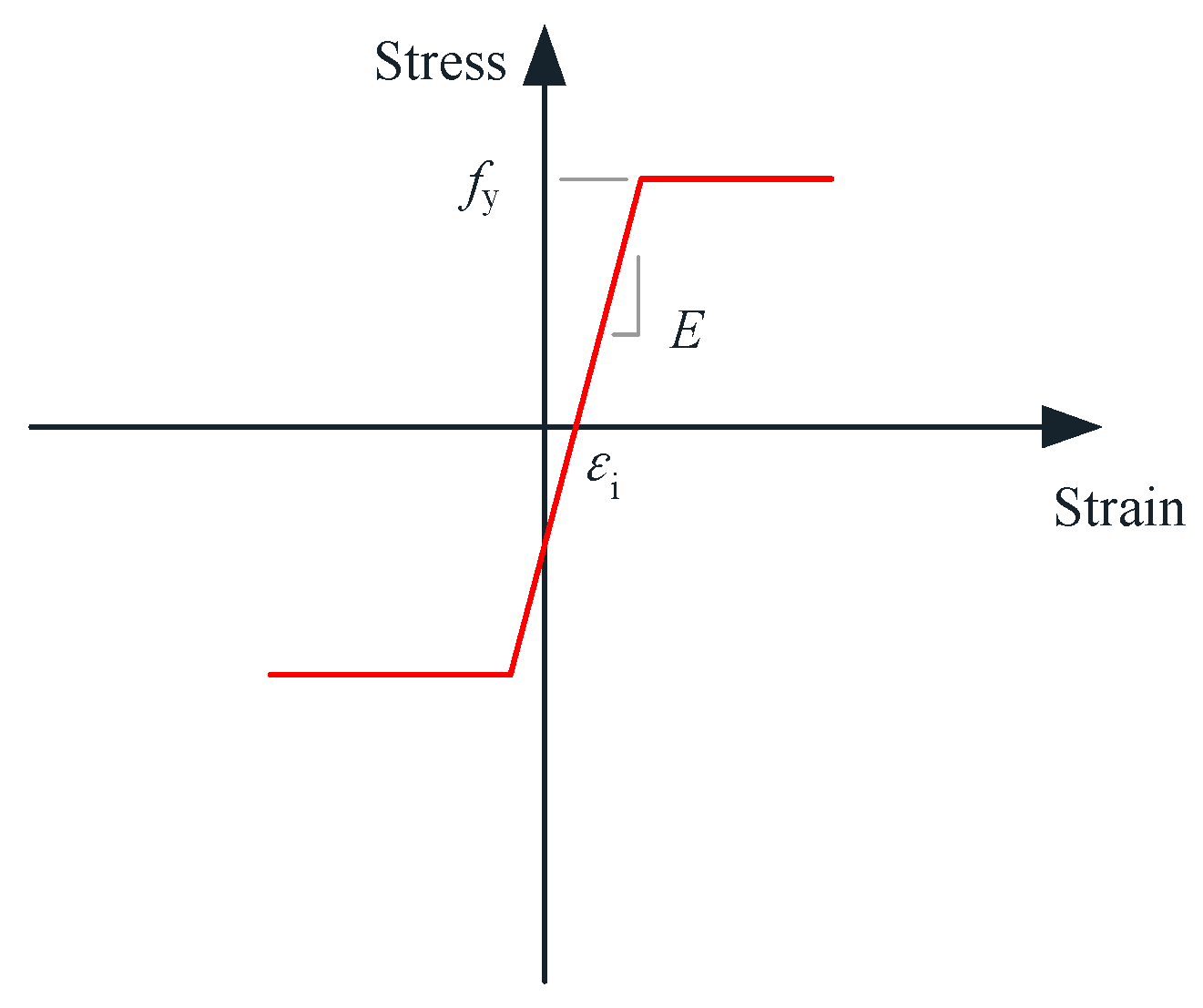
2.1. Simulation Method

To capture the hysteretic behavior of RSC columns, a numerical model was established using OpenSees. Figure 1 shows the schematic of the numerical model. The bottom segment of the structural element underwent consolidation treatment to enhance its integrity. A rigid connecting arm was employed to couple the degrees of freedom between the top node of the element and the corresponding pier node, ensuring synchronized deformation between the prestressed tendons and the pier structure. The displacement mechanism of RSC (reinforced self-consolidating) columns is predominantly governed by rigid body rotation. While minor bending deformations may occur prior to column uplift during loading phases, their contribution to the overall response remains negligible. Consequently, the adoption of elastic beam–column elements provides an appropriate and efficient modeling approach for capturing the structural behavior under consideration. This simplified approach has been used in previous studies [36,37]. A lumped mass was applied at the pier top to represent the gravity load, and a horizontal constraint was set at the bottom to prevent a relative slide between the column and the foundation. Corotational truss elements composed of elastic–perfectly plastic material were considered to model the force displacement of the unbonded post-tensioning (PT) tendons. The bottom nodes of the tendons were fixed, and the top nodes were connected to the corresponding column node with rigid links. A similar simulation method was adopted to model the unbonded segments of the energy dissipation (ED) bars. Truss elements with reinforcing steel material were used to model the ED bars, and the ultimate stress was set to 1.35 times the yield stress f_y [38]. The ratio of the tangent at initial strain hardening to the initial elastic tangent can be set to 0.01–0.05 [31]; 0.03 was selected in this study. The ratio of strain corresponding to the initial strain hardening to the yield strain can be set to 3–5 [31]; 3 was selected in this study, and the ultimate strain can be set to 0.1 [39].

The stress–strain relationship of unbonded prestressed tendons was simulated by elasticPP (elastic–perfectly plastic) uniaxial material, and its material constitutive relationship is shown in Figure 2, where f_py is the yield strength of prestressed tendons, E is the elastic modulus, and ε_i is the initial strain. Its value can be calculated from the initial pretension force.

The total unbonded length of ED bars in the numerical model, L_ub, consists of two parts. One is the designed unbonded length (L₀), which can prevent the early fracture of ED bars, the other is the equivalent unbonded length (L_eu) caused by the strain penetration. The L_ub can be expressed as:

$$L_{ub}=L_0+L_{eu}$$

(1)

If L_eu = 0, the value of L_ub is minimum; thus, the stress of ED bars is largest at the same lateral displacement. As a result, the strength of an RSC column will be overestimated. The value of L_eu is significant, but it is difficult to determine its value precisely because of the complexity of the strain penetration. For example, Mantawy et al. [40] suggested the adoption of an iterative method to determine the value of L_ub. The trial value of L_ub continues to increase until the correct bridge stiffness is calibrated.

Some formulas of L_eu can be found in studies related to the analytical pushover method for RSC columns [41,42]. According to the monolithic beam analogy, the strain of ED bars can be expressed as follows [41]:

$${\epsilon }_s={\displaystyle \frac{[(\Delta +2/3l_{sp}\alpha {\epsilon }_y)]}{(L_0+2l_{sp})}}\approx {\displaystyle \frac{\Delta }{(L_0+2l_{sp})}}$$

(2)

where Δ is the elongation of an ED bar due to the opening of the joint; ε_y is the yield strain of ED bars; α is the ratio of elastic strain and yield strain in reinforcement; l_sp is the strain penetration taken as 0.022f_yd_b, and f_y and d_b are the yield stress and diameter of ED bars, respectively. All units are in MPa and mm. From Equation (2), L_eu can be calculated as:

$$L_{eu}=2l_{sp}=2\times 0.022f_y{d}_b$$

(3)

In Bu’s study, L_eu is calculated with Equation (4) [36].

$$L_{eu}=\left\{\begin{array}{l}0, f_s\le f_y\\ {\displaystyle \frac{2.1\times (f_s-f_y)}{{(f_g)}^{1.5}}}{d}_b, f_s>f_y\end{array}\right.$$

(4)

where f_s is the stress of ED bars and f_g is the compression strength of grout.

By trial calculation, it can be found that the calculated results obtained from Equation (3) are generally much larger than the results of Equation (4). Therefore, Equation (3) is used to determine the maximum value of L_ub. Though the precise value of L_ub is hard to determine, the range of L_ub can be estimated by Equation (5). Subsequently, the influence of L_ub on residual displacement will be discussed.

$$\mathrm{Min}{L}_{ub}=L_0<L_{ub}<L_0+2\times 0.022f_y{d}_b=\mathrm{Max}{L}_{ub}$$

(5)

Several compression-only springs are used to model the opening and closing of the bottom rocking interface. Generally, the simulation result will gradually become stable as the number of springs increases. These springs are uniformly distributed with equal spacing, and all springs have the same axial stiffness. The axial stiffness, k, can be calculated as [29]:

$$k={\displaystyle \frac{2E_c{A}_g}{nH}}$$

(6)

where $E_c=4700\sqrt{f_c^{\prime }}$ is the elastic modulus of the concrete; f_c′ is the concrete compressive strength [36]; A_g is the gross area of the column section; H is the column height; and n is the number of zero-length springs.

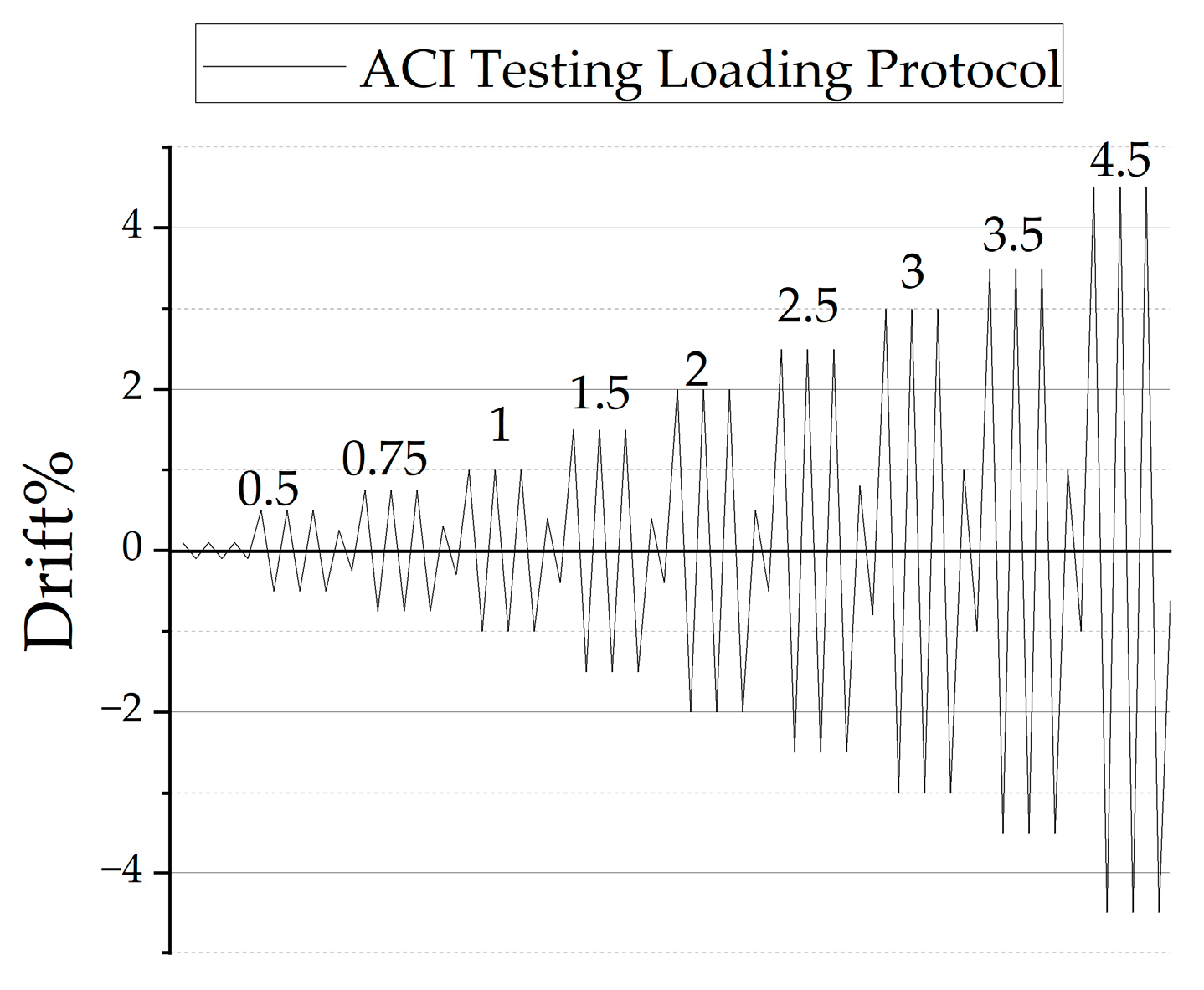
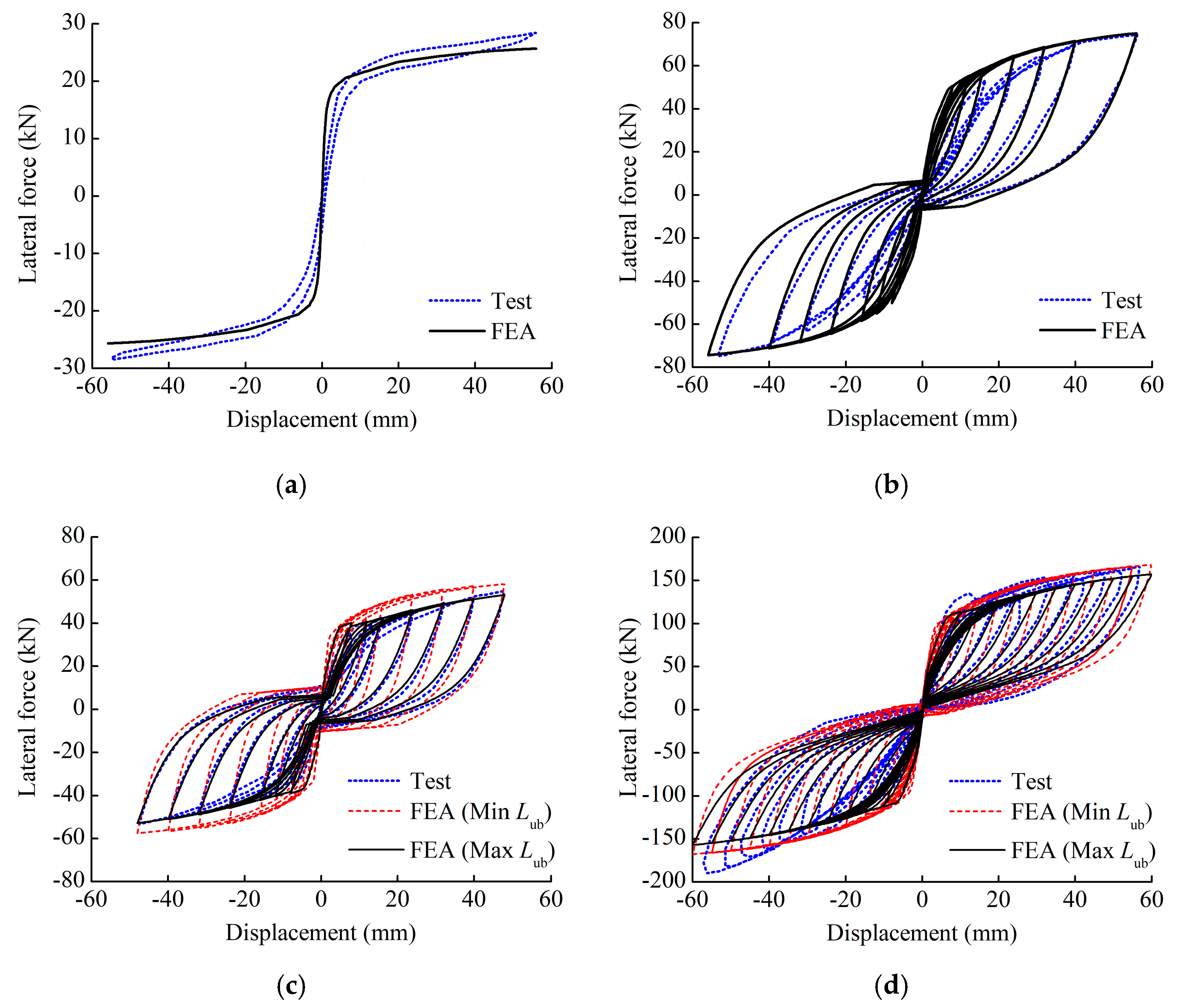
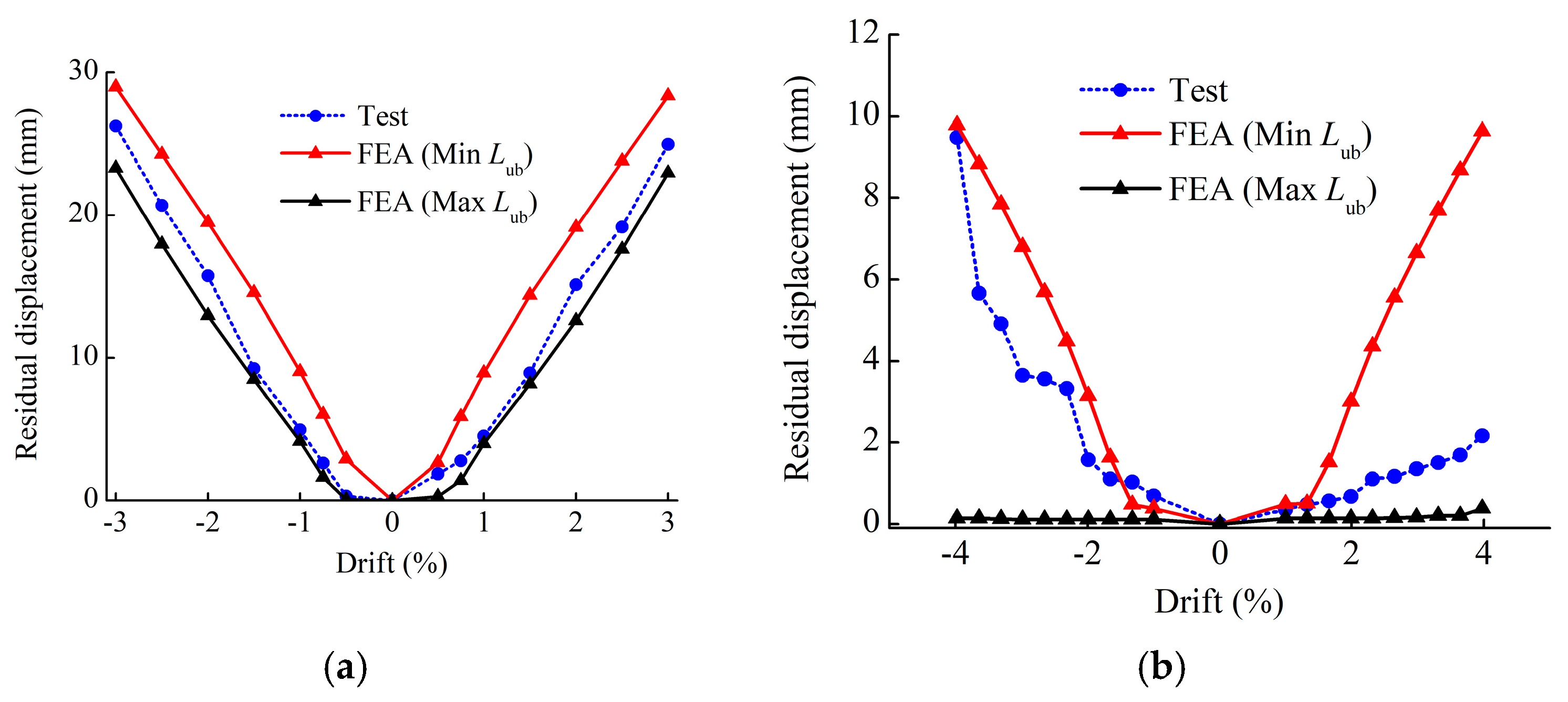
2.2. Model Validation

In order to validate the simulation method, four RSC bridge pier specimens are selected [5,43], as reported in

Table 1. Properties of selected specimens.

Specimen	PT1	HBD2	HBD1	s-SCP(I-ED)
Geometry	350 × 350 mm2	350 × 350 mm2	350 × 350 mm2	400 × 400 mm2
Aspect ratio	4.57	4.57	4.57	3.78
Total axial load	200 kN	300 kN	200 kN	533.05 kN
Tendons	2 × 99 mm2	4 × 99 mm2	2 × 99 mm2	4Φ15.2
	100 kN each	75 kN each	100 kN each	313.05 kN total
Dissipation	None	4-HD20	4-D16	4-D20
		12.5 mm diameter fuse	Reinforcing steel	Reinforcing steel
		50 mm fuse length	L0 = 50 mm	L0 = 100 mm
		fy = 586 MPa	fy = 304 MPa	fy = 349 MPa

. PT1 has no dissipation elements; it can be used to confirm the effectiveness of the modeling methods for all components in addition to ED bars. HBD2 chooses the reinforcing steel with a fuse length as the dissipation element. HBD1 and s-SCP(I-ED) dissipate energy via the internal reinforcing steel; the corresponding unbonded lengths are 50 mm and 100 mm, respectively. More detailed information about these specimens can be found in references [5,43].

Since there are few dynamic tests on RSC piers, the accuracy of the numerical model is mainly verified by comparing the hysteresis curve under a static load. Figure 3 shows the loading mode of a quasi-static load.

As shown in Figure 4, the numerical hysteretic curves are compared with the test results. For specimen PT1, as shown in Figure 4a, the simulated initial stiffness is slightly larger than the test result, and the simulated strength is slightly lower. In addition, because the elastic beam–column element is adopted to model the column, the simulated hysteretic curve is unable to reflect the low energy dissipation during the cyclic loading. On the whole, the FEA result matches well with the test result, which suggests that the simulation techniques, except for those using ED bars, are effective.

Because the reinforcing steel in specimen HBD2 has a fuse length of 50 mm, the strain will be concentrated on the fuse segment; therefore, L_ub is set to 50 mm. The hysteretic curve based on FEA is plotted in Figure 4b. As for specimens HBD1 and s-SCP(I-ED), detailed comparisons between test and simulation results are presented in Figure 4c,d. The red and black curves represent the simulation results corresponding to the minimum L_ub and the maximum L_ub, respectively. The lateral strength of the red curves is slightly larger than the black curves because a smaller L_ub will generate a larger strain under the same joint opening. A larger strain leads to a larger dissipation force. As a result, the lateral strength is improved. Meanwhile, the residual displacement per loop of the red curves is also larger than the black curves. Detailed comparisons are plotted in Figure 4. On the one hand, this phenomenon can be explained from the perspective of a larger dissipation force, which weakens the self-centering capacity of the piers. On the other hand, the increase in L_ub will significantly decrease the slope of the unloading path and thus diminish the residual displacement, as shown in Figure 4c,d. The latter reason is more important because the improvement in dissipation force is very limited.

Based on the above analysis and Figure 5, it can be concluded that the proposed simulation method is effective. However, there is uncertainty regarding L_ub in the modeling process. A conservative result for residual displacement will be obtained, in general, if the strain penetration is not considered, and it is highly possible to underestimate the residual displacement if Equation (3) is used to calculate the equivalent unbonded length.

3. Governing Design Parameters for Residual Displacement

Two design parameters, the SC factor and ED parameter, are believed to have a governing influence on the residual displacement.

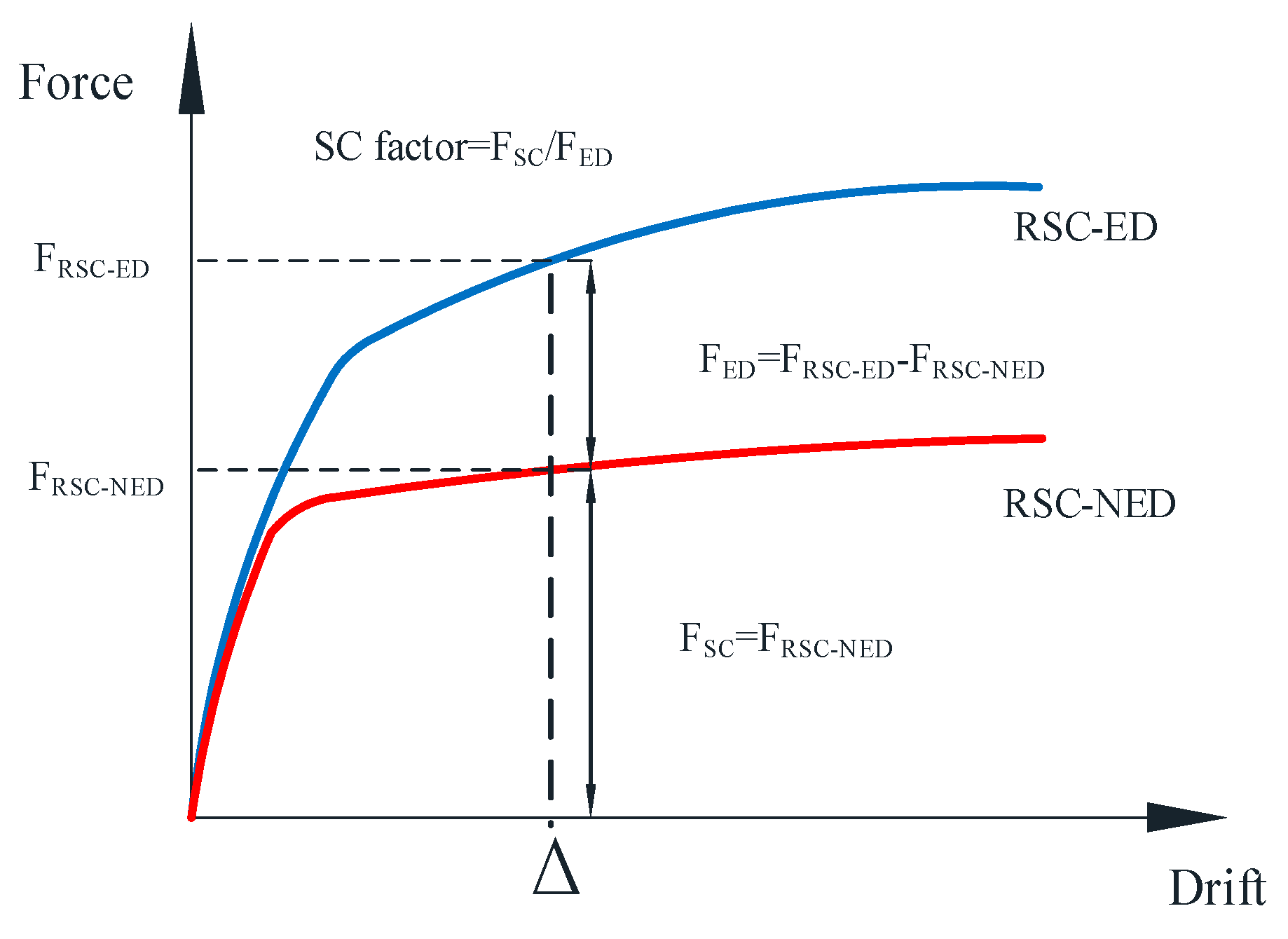
3.1. Definition and Calculation of SC Factor

Several researchers have put forward different SC factors for evaluating the self-centering capacity of RSC columns. Hieber et al. [44] proposed a recentering ratio that is equal to the ratio between the total axial force (including the gravity force and initial prestressing force) and the yielding force of ED bars. The self-centering capacity of bridge columns at different displacements is usually different, while the recentering ratio is constant for an RSC column.

The contribution ratio λ_SC is another SC factor, and it is typically adopted in the design of RSC systems [9,33]. λ_SC, in its generic form, represents the force or moment ratio between the self-centering contribution and the energy dissipation contribution, as shown in Equation (7):

$${\lambda }_{SC}={\displaystyle \frac{M_{\text{self-centering}}}{M_{\mathrm{dissipation}}}}={\displaystyle \frac{F_{\text{self-centering}}}{F_{\mathrm{dissipation}}}}$$

(7)

The self-centering and energy dissipation contribution can be derived from the monolithic beam analogy procedure [41]. However, the iterative calculation process is still relatively complicated. What is more, λ_SC is obtained from theoretical calculation, while the residual displacement is determined by simulation. In order to reduce error, it is better to use the simulation method to measure the self-centering performance index. For this reason, the SC factor λ_SC used in this study is defined as follows:

$${\lambda }_{SC}={\displaystyle \frac{F_{SC}}{F_{ED}}}$$

(8)

where F_SC is the self-centering contribution provided by gravity load and PT tendons, and F_ED is the energy dissipation contribution provided by ED bars. As shown in Figure 6, the calculation of λ_SC requires the following two steps:

• Step 1: Establish the numerical model of the RSC-ED columns and conduct a pushover analysis; then, the force-displacement curve can be obtained. The force F_RSC-ED includes the self-centering and energy dissipation contribution.
• Step 2: Delete the ED bar elements from the existing numerical model of the RSC-ED column. The corresponding numerical model of an RSC-NED pier is obtained. Then, perform a pushover analysis again. As a result, a force-displacement curve that only contains the self-centering contribution will be obtained. Therefore, the energy dissipation contribution F_ED can be derived as:

$$F_{ED}=F_{RSC\text{-}ED}-F_{RSC\text{-}NED}$$

(9)

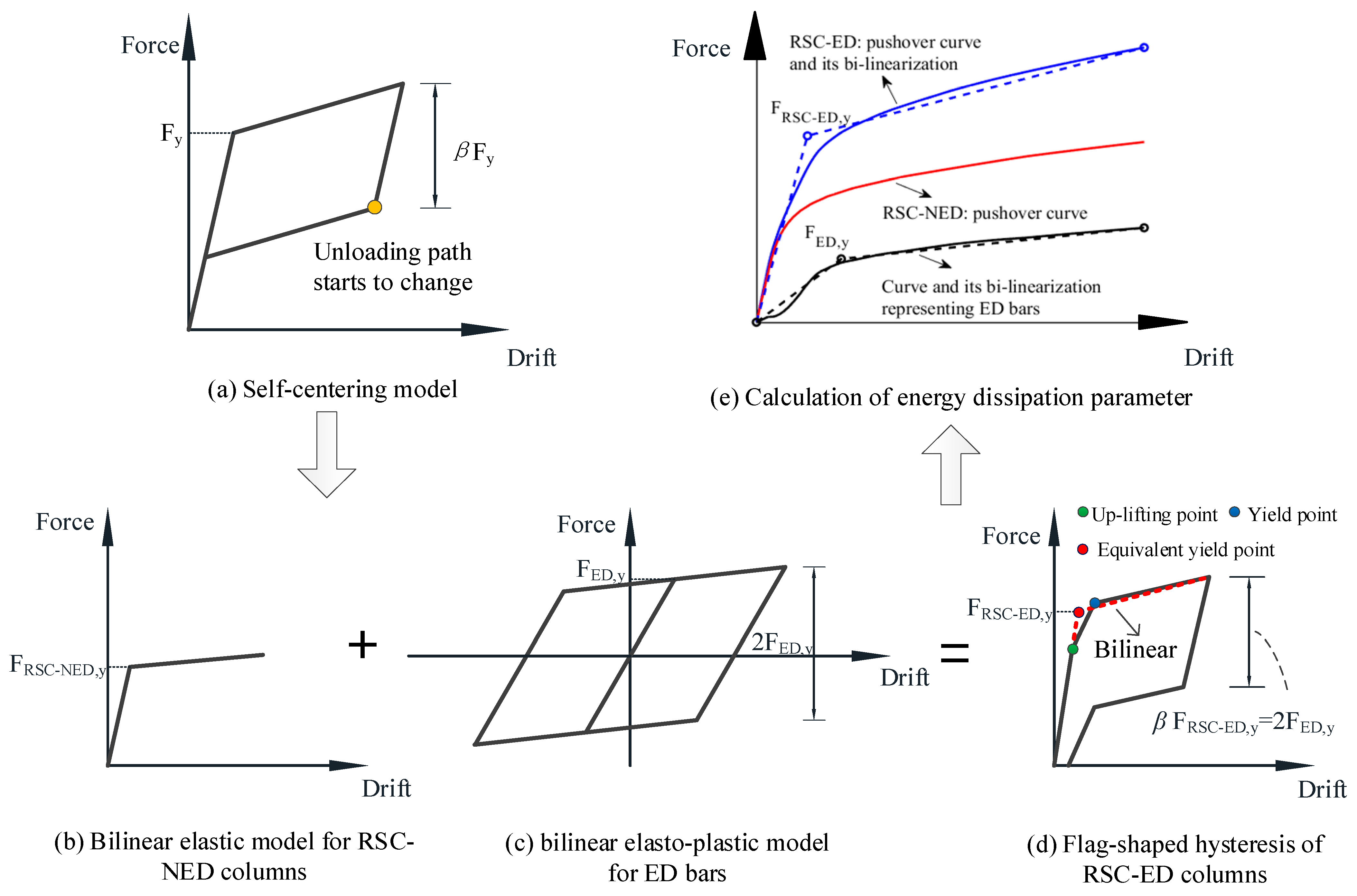
3.2. Definition and Calculation of ED Parameter

The second governing design parameter is the ED parameter. The cyclic behavior of RSC columns can be simplified into a flag-shaped hysteretic model, as shown in Figure 7a. The ED parameter β is a significant parameter in this model. This integrated methodology achieves two objectives: firstly, it rigorously quantifies the hysteretic energy dissipation capacity within self-centering structural elements, and, secondly, it strategically governs the critical transition point along the unloading trajectory through targeted control mechanisms. The smaller the ED parameter is, the earlier the unloading path changes, leading to lower residual displacement. Hence, it can be predicted that the ED parameter has a non-ignorable influence on residual displacement; recent studies related to the residual displacement of RSC systems did not consider this [2,3,4].

The self-centering model is so ideal that it is unable, in fact, to capture residual displacement. Implementing two rotational springs in parallel with appropriate hysteretic models is another simplified simulation method. The RSC column without ED bars is modeled by a bilinear elastic model, as shown in Figure 7b. The ED bar is simulated using a bilinear elastoplastic model, as shown in Figure 7c. With the coaction of the two springs, the RSC column presents a trilinear skeleton curve. To be precise, there is a reduction in stiffness after the column is lifted. Since the reduction in stiffness is very slight, the skeleton curve can be approximated to a bilinear one.

To extract the ED parameter, an equivalent linearization method is used. The ED parameter can be calculated as:

$$\beta ={\displaystyle \frac{2F_{ED,y}}{F_{RSC\text{-}ED,y}}}$$

(10)

where F_ED,y is the yielding force of the bilinear elastoplastic model and F_RSC-ED,y is the effective yielding strength of the bridge column, as shown in Figure 7d.

Equation (10) can be expressed approximately as:

$$\beta \approx {\displaystyle \frac{2F_{ED,y}}{F_{ED,y}+F_{RSC\text{-}NED,y}}}={\displaystyle \frac{2}{1+F_{RSC\text{-}NED,y}/F_{ED,y}}}={\displaystyle \frac{2}{1+{\lambda }_{SC,y}}}$$

(11)

where F_RSC-NED,y is the yielding force of the bilinear elastic model and λ_SC,y is the SC factor that corresponds to the yield displacement. It can be found that the value of β is relatively stable, and it is smaller than 1 when the value of λ_SC,y exceeds 1. As shown in Figure 7e, the calculation of β requires the following two steps:

• Step 1: Establish the FE model of an RSC-ED column and perform a pushover analysis. Then, the obtained pushover curve is bilinearized according to the equal energy principle. As a result, the parameter F_RSC-ED,y can be determined.
• Step 2: Delete the ED bar elements from the FE model and carry out a pushover analysis again. Then, the force–displacement curve representing the energy dissipation contribution can be plotted by subtraction. Conduct an equivalent linearization again, and the parameter F_ED,y is obtained.

4. Fractional Factorial Analysis

In the actual construction of RSC columns, the key design parameters are presented in the form of aspect ratio λ, concrete strength f_c, PT tendon ratio ρ_PT, axial load ratio (η_G, η_PT) caused by gravity load PG and PT force PPT, ED bar ratio PED, yield stress of ED bars f_y, and unbonded length L₀. It should be noted that the non-dimensional parameters, the SC factor and ED parameter, can be regarded as the comprehensive embodiment of these key design parameters. This part of the study uses fractional factorial analysis to discuss the effect of each parameter on the SC factor and ED parameter at different displacements.

4.1. Design Parameters of Reference Specimen

In factorial analysis, the reference specimen RS selects the prototype of the specimen HBD1, and the specimen HBD1 is 1/3 scaled, but the design parameters of specimen RS are not strictly converted by a scale of 1:3 according to those of specimen HBD1, as shown in

Table 2. Comparison of the design parameters of specimens HBD1 and RS.

Specimen	Width/mm	λ	fc/MPa	ED Bar	ρED/%	fy/MPa	L0/mm	PT Tendon	ρPT/%	PG/kN	ηG	PPT/kN	ηPT
HBD1	350	4.57	54.1	4D16	0.66	304	50	2 × 99 mm2	0.16	0	0	200	0.03
RS	1050	4.57	54.1	20D22	0.69	304	300	12D15.2	0.2	1800	0.03	600	0.01

. For example, in order to ensure that the ED bars have an adequate deformation capacity at a larger loading displacement, the value of L₀ of the specimen RS is set to 300 mm rather than 150 mm. The prototype pier of specimen HBD1 has a total mass of 180 t, but the gravity force was not applied in the test due to the limitation of the experimental prestressing. The value of P_G of the specimen RS is 1800 kN. Meanwhile, P_G will enhance the self-centering capacity of the specimen RS, which may lead to no residual displacement. Therefore, the value of P_PT is set to 600 kN rather than 1800 kN.

Figure 8a shows the cross-section of the specimen RS. Each duct holds four PT tendons, and the diameter and tensile strength of each PT tendon are 15.2 mm and 1860 MPa, respectively. The PT tendon ratio can be easily adjusted by changing the number of PT tendons in each duct, and the ED bar ratio can be changed by altering the diameter of the ED bars in the following study. The hysteretic curve of the specimen RS is plotted in Figure 8b. For specimen HBD1, the simulation result corresponding to the maximum value of L_ub matches better with the test result, as shown in Figure 4c. Thus, the maximum L_ub is adopted in this part.

4.2. Two-Level Fractional Design

The purpose of this fractional factorial analysis is to evaluate the importance of the key design parameters to the residual displacement of RSC columns.

Table 3. Two levels of the considered factors.

Level	λ	fc	Pd	ρPT	ηG	L0 (mm)	fy (MPa)	ρED
	(A)	(B)	(C)	(D)	(E)	(F = ABC)	(G = ABD)	(H = BCDE)
Range	4.42~5.29	32~65.9	0.12~0.51	0.13~0.65%	0~0.1	50~400	300~600	0.26~1.03%
− (low)	3.5	30	0.2	0.20%	0.02	150	300	0.46%
+ (high)	6	60	0.4	0.60%	0.1	450	600	1.12%

Note: P_d is the ratio between the initial stress of a PT tendon and its yield stress.

shows the key parameters and the two levels of each parameter. The ranges of the factors are determined by the investigation of 19 RSC column specimens [9,10,11,37]. The statistical results are also reported in Table 3. To prevent the PT tendon from yielding under cyclic loading, the value of P_d corresponding to its high level is set to 0.4, and the maximum loading displacement is 4%.

Factorial analysis is often used when multiple factors determine an output. However, full factorial analysis requires a great number of runs if many factors are taken into account, which may become computationally demanding. In this study, the analysis includes eight factors, and each factor has two levels. A complete factorial analysis requires 256 runs. In order to improve efficiency, one-eighth factorial analysis is performed, which decreases the number of runs required to a total of 32.

The approach that Montgomery proposed [45,46] is used to perform the fractional factorial analysis. The construction of a one-eighth factorial analysis consists of two parts. The first part is a basic design, which contains a complete fractional factorial combination (the first five columns in

Table 4. Fractional factorial design.

Case (Level)	Basic Design					Generated from Basic Design
	λ	fc	Pd	ρPT	ηG	L0	fy	ρED
	(A)	(B)	(C)	(D)	(E)	(F = ABC)	(G = ABD)	(H = BCDE)
1	−1	−1	−1	−1	−1	−1	−1	1
2	1	−1	−1	−1	−1	1	1	1
3	−1	1	−1	−1	−1	1	1	−1
4	1	1	−1	−1	−1	−1	−1	−1
5	−1	−1	1	−1	−1	1	−1	−1
6	1	−1	1	−1	−1	−1	1	−1
7	−1	1	1	−1	−1	−1	1	1
8	1	1	1	−1	−1	1	−1	1
9	−1	−1	−1	1	−1	−1	1	−1
10	1	−1	−1	1	−1	1	−1	−1
11	−1	1	−1	1	−1	1	−1	1
12	1	1	−1	1	−1	−1	1	1
13	−1	−1	1	1	−1	1	1	1
14	1	−1	1	1	−1	−1	−1	1
15	−1	1	1	1	−1	−1	−1	−1
17	−1	−1	−1	−1	1	−1	−1	−1
18	1	−1	−1	−1	1	1	1	−1
19	−1	1	−1	−1	1	1	1	1
20	1	1	−1	−1	1	−1	−1	1
21	−1	−1	1	−1	1	1	−1	1
22	1	−1	1	−1	1	−1	1	1
23	−1	1	1	−1	1	−1	1	−1
24	1	1	1	−1	1	1	−1	−1
25	−1	−1	−1	1	1	−1	1	1
26	1	−1	−1	1	1	1	−1	1
27	−1	1	−1	1	1	1	−1	−1
28	1	1	−1	1	1	−1	1	−1
29	−1	−1	1	1	1	1	1	−1
30	1	−1	1	1	1	−1	−1	−1
31	−1	1	1	1	1	−1	−1	1
32	1	1	1	1	1	1	1	1

). The other part includes three generators (the last three columns in Table 4), which determine the factors that are not included in the basic design. − and + are the symbols for low level and high level, respectively. The levels of the last three factors are determined by using generating relations.

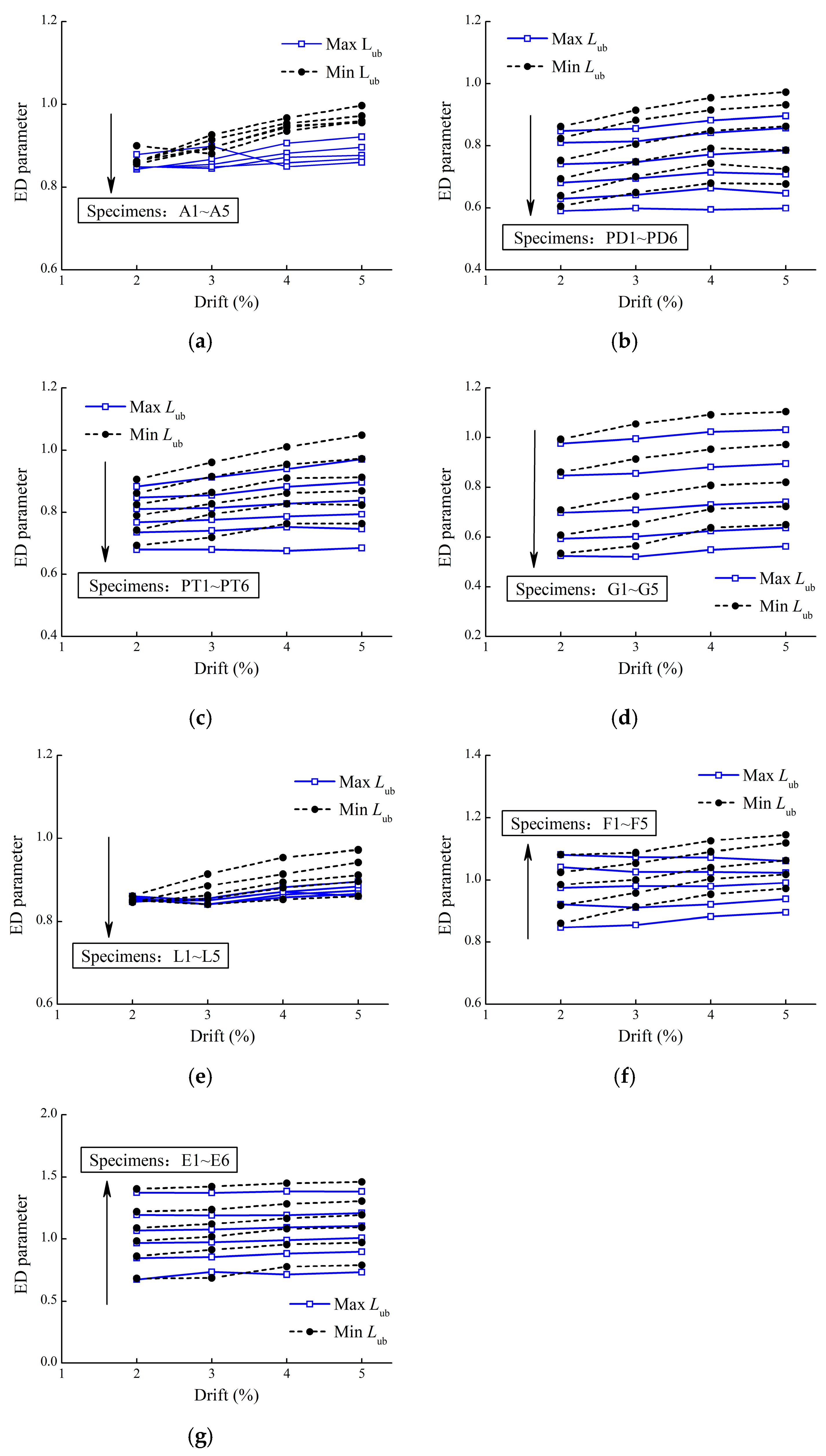
4.3. Results of Factorial Analysis

Based on the earthquake damage investigation results, the Japan Road Association (JRA) code proposed a residual displacement limitation of 1% for RC columns to measure whether the columns could be repaired or not [22]. If the residual displacement does not exceed 1%, the damaged column can generally be repaired. Because the residual displacement is always smaller than the peak displacement, the SC factor and ED parameter at 1% displacement are not considered to be significant.

The effect of each key parameter on the SC factor at 2%, 3%, and 4% displacement is compared, as shown in Figure 9. Except for λ, f_y, and ρ_ED, the other five parameters have a positive influence on the SC factor. At the considered levels of the parameters, the most important parameters are ρ_ED, f_y, ρ_TP, and η_G; the contribution of L₀ can be neglected. The change in the contribution provided by each parameter is presented in Figure 9d. It can be observed that the change in the contribution provided by λ and η_G is the most notable. With an increase in displacement, the contribution of λ increases from 1.9% to 10.5%, while the contribution of η_G declines from 17.4% to 8.9%. This is because the larger aspect ratio and displacement aggravate the P−Δeffect. Meanwhile, the contribution of ρ_TP grows by about 5%, which indicates that self-centering capacity is more dependent on ρ_TP at large displacements. The total contribution is very stable and exceeds 83%, no matter which displacement is considered, and no intense interaction between the parameters is observed.

As shown in Figure 10, the contribution of each factor to the ED parameter at 2%, 3%, and 4% displacement is compared. f_c, P_d, ρ_TP, and η_G have a negative effect, f_y and ρ_ED have a positive effect, and the effect of λ and L₀ is approximately zero. The most significant parameters are ρ_ED, f_y, η_G, and ρ_TP. As shown in Figure 10d, the contribution of these parameters, excluding f_y, basically remains the same; the contribution of f_y decreases from 21.5% to 14.9% as the displacement increases from 2% to 4%. On the other hand, the total contribution at the three loading displacements reaches 94%; thus, it can be concluded that the ED parameter is dominated by the effect of a single factor, and the interaction between the factors is very slight. Here, the ED parameter β is fitted with a linear regression model that can be expressed as follows:

$$\beta =a_0+a_1{x}_1+a_2{x}_2+a_3{x}_3+a_4{x}_4+a_5{x}_5+a_6{x}_6$$

(12)

where x₁, x₂, x₃, x₄, x₅, and x₆ are the normalized parameters representing the effect of f_c, P_d, ρ_TP, η_G, f_y, and ρ_ED. For example, x₁ = (λ − 45)/15. The normalized parameters range from −1 to 1 (corresponding to low and high levels). The obtained corresponding coefficients of the regression model are provided in

Table 5. Coefficient values of the regression model for β.

Displacement	Coefficients
	a0	a1	a2	a3	a4	a5	a6
2%	0.760	−0.062	−0.060	−0.106	−0.154	0.148	0.179
3%	0.749	−0.062	−0.062	−0.115	−0.161	0.130	0.173
4%	0.746	−0.063	−0.061	−0.118	−0.157	0.119	0.173

.

5. Formula for Predicting Residual Displacement Under Cyclic Loading

The purpose of this part is to explore the effect of the SC factor and ED parameter on the distribution of the residual displacement and predict the residual displacement under cyclic loading. Because there are two directions during a full cycle, the residual displacement D_res is defined as follows:

$$D_{res}={\displaystyle \frac{D_{-res}+D_{+res}}{2}}$$

(13)

where D_−res and D_+res are the residual displacements corresponding to the negative and positive loading directions, respectively.

5.1. Parametric Study

In order to obtain enough data to analyze the distribution of residual displacement, a parametric study is first carried out.

Table 6. Denotations of specimens in the parametric study.

Parameters	Denotation	Parameter Values for Each Specimen
λ	A1, A2, A3, A4, A5 (A1–A5)	3.6, 4.6, 5.5, 6.5, 7.4
Pd	PD1, PD2, PD3, PD4, PD5, PD6 (PD1–PD6)	0.15, 0.2, 0.3, 0.4, 0.5, 0.6
${\rho }_{\mathrm{PT}}$	PT1, PT2, PT3, PT4, PT5, PT6 (PT1–PT6)	0.13%, 0.2%, 0.26%, 0.33%, 0.4%, 0.53%
${\eta }_G$	G1, G2, G3, G4, G5 (G1–G5)	0.03, 0.045, 0.06, 0.075, 0.091
L0	L1, L2, L3, L4, L5 (L1–L5)	300 mm, 400 mm, 500 mm, 600 mm, 700 mm
fy	F1, F2, F3, F4, F5 (F1–F5)	304 MPa, 350 MPa, 400 MPa, 450 MPa, 500 MPa
${\rho }_{\mathrm{ED}}$	E1, E2, E3, E4, E5, E6 (E1–E6)	0.46%, 0.69%, 0.89%, 1.12%, 1.46%, 2.28%

is the working condition design table. There are five or six working conditions for each parameter. Each specimen has a special denotation that corresponds to a value in the parameter. For example, for the aspect ratio λ, five specimens are designed and tagged with A1, A2, A3, A4, and A5. Among these tags, A1 corresponds to a value of 3.6.

Figure 11 shows the influence of each parameter on the SC factor. The arrow represents what kind of trend the sc factor shows as the X-axis increases. The uncertainty of L_ub in the simulation process is considered. It can be concluded that the value of the SC factor corresponding to the minimum L_ub is always less than that corresponding to the maximum L_ub, which indicates that the self-centering capacity of bridge columns will be underestimated if strain penetration is not considered. The uncertainty of L_ub has little influence on the change tendency of the SC factor. The SC factor presents a downward trend as the displacement increases.

As shown in Figure 11a, the five specimens (A1–A5) have a similar SC factor at 1% displacement. With an increase in displacement, the SC factor of the specimen with a larger aspect ratio descends more rapidly because of the P−Δeffect. Specimen A1 is different from other specimens: its SC factor demonstrates slight growth when the displacement exceeds a certain value. Increasing P_d, ρ_PT, η_G, and L₀ are all benefits that improve the self-centering force. Thus, their increase will enhance the SC factor, as shown in Figure 11b–e. The improvement effect of P_d and η_G on the SC factor is very similar and dependent on the displacement. As shown in Figure 11b,d, a larger P_d and η_G can generally generate a larger SC factor, but the self-centering capacity is not stable, which decreases sharply as the displacement increases. As shown in Figure 11c, it can be concluded that increasing the PT tendon ratio is an effective method to strengthen the stability of the self-centering capacity. Compared with P_d, ρ_PT, and η_G, the effect of L₀ on the SC factor is very limited, as shown in Figure 11e. The value of L₀ increases from 300 mm to 700 mm, while the increase in the SC factor does not exceed 0.3. Increasing f_y or ρ_ED aids in improving the energy dissipation capacity. Thus, their increase will reduce the SC factor, as shown in Figure 11f,g. The greatest reduction in the SC factor occurs when ρ_ED increases from 0.46% to 0.69%, as shown in Figure 11g.

Similarly, Figure 12 shows the influence of each parameter on the ED parameter. It can be observed that the ED parameter corresponding to the minimum L_ub is frequently larger than that corresponding to the maximum L_ub. With an increase in displacement, the ED parameter shows a slight uptrend. It remains stable, on the whole, and its greatest growth does not reach 0.2. As shown in Figure 12a–e, by increasing λ, P_d, ρ_PT, η_G, and L₀, one is able to reduce the ED parameter. For η_G, P_d, and ρ_PT, in particular, their reduction effect is more remarkable, and the effect of λ and L₀ is relatively limited. By increasing f_y and ρ_ED, one can improve the ED parameter, as shown in Figure 12f,g.

5.2. Regression Analysis

As shown in Figure 13, the data obtained from the parameter analysis are collected to investigate the influence of the SC factor on the residual displacement distribution. The black points correspond to the maximum L_ub, and the red points correspond to the minimum L_ub. The red points are located at the upper boundary of the black points. The upper limit of the residual displacement is dominated by two key coordinate points: (2, 0) and (0, D_max). Point (2, 0) indicates that the residual displacement is equal to zero if the SC factor reaches 2; point (0, D_max) indicates that the residual displacement is equal to the maximum displacement if the SC factor is 0. The upper limit of residual displacement D_upres at different displacements can be expressed as Equation (14). Wang et al. (2019) [33] proposed a formula for the RSC UHPC bridge column with a hollow section to calculate the upper limit of residual displacement, as shown in Equation (15). Equation (14) is very similar to Equation (15). The only difference is that Equation (15) is based on the assumption that the residual displacement is equal to zero when the SC factor is 2.5. Therefore, Equation (15) is more conservative, as shown in Figure 13. However, this does not mean that the concrete material or the section shape have a great influence on the upper limit of residual displacement. In [33], the SC factor, defined as the moment contribution ratio, is obtained by theoretical calculation, while the residual displacement is obtained from the numerical results, which amplifies the error.

$$D_{upres}=D_{max}\times (1-0.5{\lambda }_{sc})$$

(14)

$$D_{upres}=D_{max}\times (1-0.4{\lambda }_{sc})$$

(15)

In addition, the residual displacement exhibits a feature of linear distribution. However, there are some special points at which the SC factors exceed 1, while the corresponding residual displacement is very small and approximately zero. These special points show an entirely different pattern of distribution. In order to explain the phenomenon, the source of these special points is verified. It is found that most of them are obtained from the specimens PD1–PD6, PT1–PT6, and G1–G5. P_d, ρ_PT, and η_G all have a great negative effect on the ED parameter. Thus, the influence of the ED parameter on the residual displacement distribution is studied, as shown in Figure 14. When the ED parameter exceeds 0.75, the residual displacement is very sensitive to it. Within the range of 0.75 to 1.0, in particular, the residual displacement grows rapidly as the ED parameter increases; when the ED parameter exceeds 1.0, the residual displacement increases smoothly. Meanwhile, the distribution of residual displacement is stratified because the residual displacement depends heavily on the maximum displacement. On the other hand, it can be concluded that the residual displacement is close to zero when the ED parameter is less than 0.75, which is not related to the maximum displacement.

As shown in Figure 15, the data in Figure 13 are collected, and the points in which the ED parameter is larger than 0.75 are removed. It can be found that most of the special points are filtered out, and the filtered data exhibit a more obvious linear distribution characteristic. Regression analyses are performed for the filtered data, and the relation between the residual displacement at a certain displacement and the SC factor is established as follows:

$$D_{res,2\%}=-1.4{\lambda }_{sc}+1.936$$

(16a)

$$D_{res,3\%}=-1.972{\lambda }_{sc}+2.974$$

(16b)

$$D_{res,4\%}=-2.515{\lambda }_{sc}+3.973$$

(16c)

$$D_{res,5\%}=-3{\lambda }_{sc}+4.9$$

(16d)

where D_res,2%, D_res,3%, D_res,4%, and D_res,5% are the residual displacements at 2, 3, 4, and 5% displacement. It should be noted that this set of formulas can be used to estimate the residual displacement under cyclic loading on the premise that the ED parameter exceeds 0.75. If the parameter is smaller than 0.75, the residual displacement can be ignored. The correlation coefficients of Equation (16a), Equation (16b), Equation (16c), and Equation (16d) are 86.6%, 85.6%, 85.4%, and 84.8%, respectively.

Too great a value of L₀ is a significant cause of the discreteness of the formulas. As shown in Figure 15, numerous points descend faster as the SC factor increases. This occurs because a value of L₀ that is too great will change the unloading path and aggravate the pinching effect. Meanwhile, the SC factor is not sensitive to L₀. As a result, the residual displacement is reduced at the cost of a slight reduction in strength and energy dissipation capacity. A comparison of the hysteretic curves between specimens L1 and L5 is provided as an example and shown in Figure 16. In fact, an unbonded length that is too long will not be designed, in general, because it may lead to the buckling of ED bars. As a result, it is unnecessary to pay a great deal of attention to the effect of L₀.

Palermo et al. (2007) [9] conducted a cyclic loading test on four RSC bridge pier specimens. The specimens were named PT1, HBD1, PT2, and HBD2. The only difference between specimen PT1 (PT2) and HBD1 (HBD2) was that the former lacked ED bars. The SC factors and ED parameters of specimens HBD1 and HBD2 can be obtained from the test results. A comparison of the test results with the predictive residual displacement is provided in

Table 7. Comparison of the test results with predictive results.

Specimens	Displacement	SC Factor	ED Parameter	Residual Displacement (%)
				Test	Upper Limit	Predictive Result
HBD1	2%	1	0.98	0.94	1	0.54
	3%	0.98	0.97	1.55	1.53	1.04
HBD2	2%	1.4	0.83	0.23	0.6	0

.

Analysis of Table 7 reveals that variations in the self-centering (SC) factor and energy dissipation (ED) parameters among tested specimens directly correlate with divergent residual displacement responses. Significantly, within identical structural configurations, the magnitude of displacement is identified as a critical parameter influencing both the SC factor and ED parameter.

6. Conclusions

This paper uses the numerical method to investigate and predict the residual displacement of RSC columns under cyclic loading. RC piers are categorized into two types: RSC-ED piers equipped with energy-dissipating bars and RSC-NED piers without such bars. The SC factor and ED parameter are regarded as important parameters that govern residual displacement. To explore the impact of design parameters on the hysteretic performance of RSC piers, factorial analysis is employed. The effects of eight key design parameters on equivalent stiffness, equivalent yield strength, post-yield stiffness ratio, and residual displacement are examined. Additionally, the influence of seven key parameters on the self-resetting coefficient and energy dissipation parameters is analyzed. The effect of the SC factor and ED parameter on the residual displacement distribution is statistically analyzed. During the process, the uncertainty of energy-dissipating steel bars of a set length in the numerical model is considered in order to refine residual displacement predictions, leading to a more conservative estimation approach. Finally, regression analysis is used to establish a predictive formula for the residual displacement of RSC piers, providing valuable guidance for their design. Based on the analyses, the following conclusions can be drawn:

• Simplifying the strain penetration of energy-consuming steel bars to equivalent unbonded segment lengths can lead to an underestimation of self-resetting capacity and residual displacement. Ignoring the strain penetration of ED bars will underestimate the self-centering capacity of RSC columns and conservative residual displacement will be obtained. Therefore, when establishing RSC pier models, it is essential to consider the impact of strain penetration to enhance the accuracy of prediction outcomes.
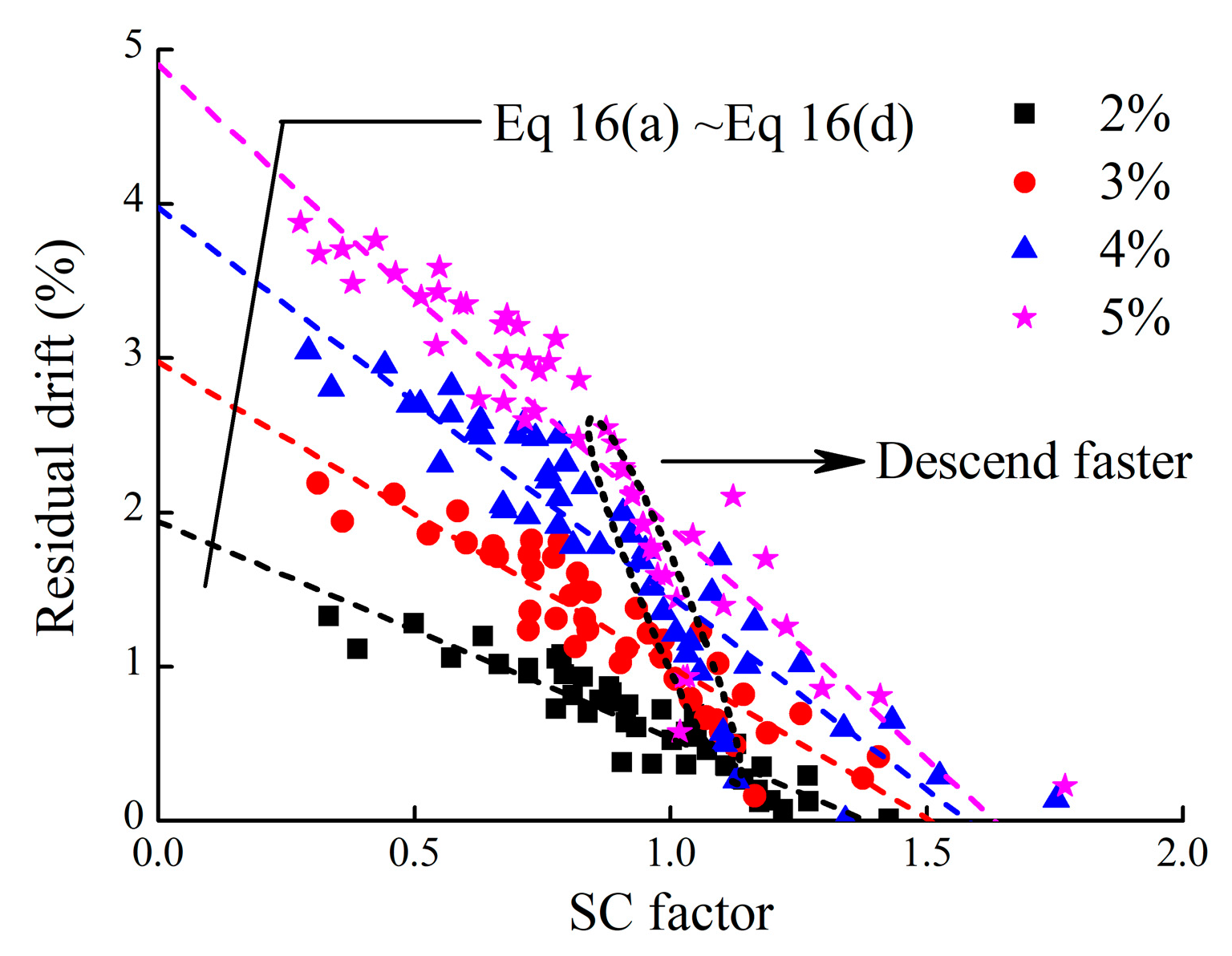
• The total contribution of the eight parameters to the SC factor and ED parameter is stable and maintained at approximately 84% and 95%, respectively. No significant interaction between these factors is observed. Due to the P−Δeffect, the contribution of the gravity loading ratio to the SC factor will decrease rapidly as the displacement increases, and the effect of the aspect ratio will grow.
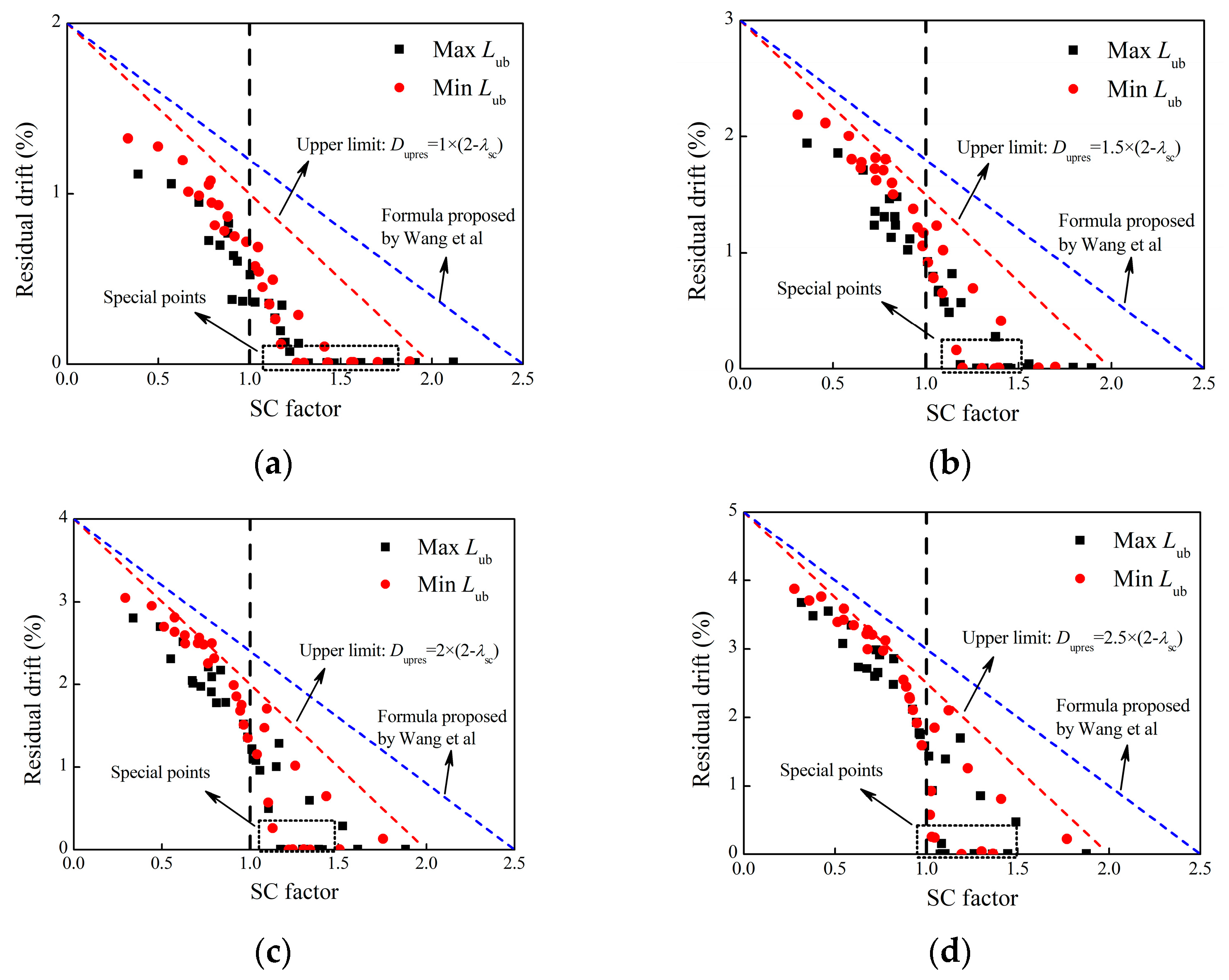
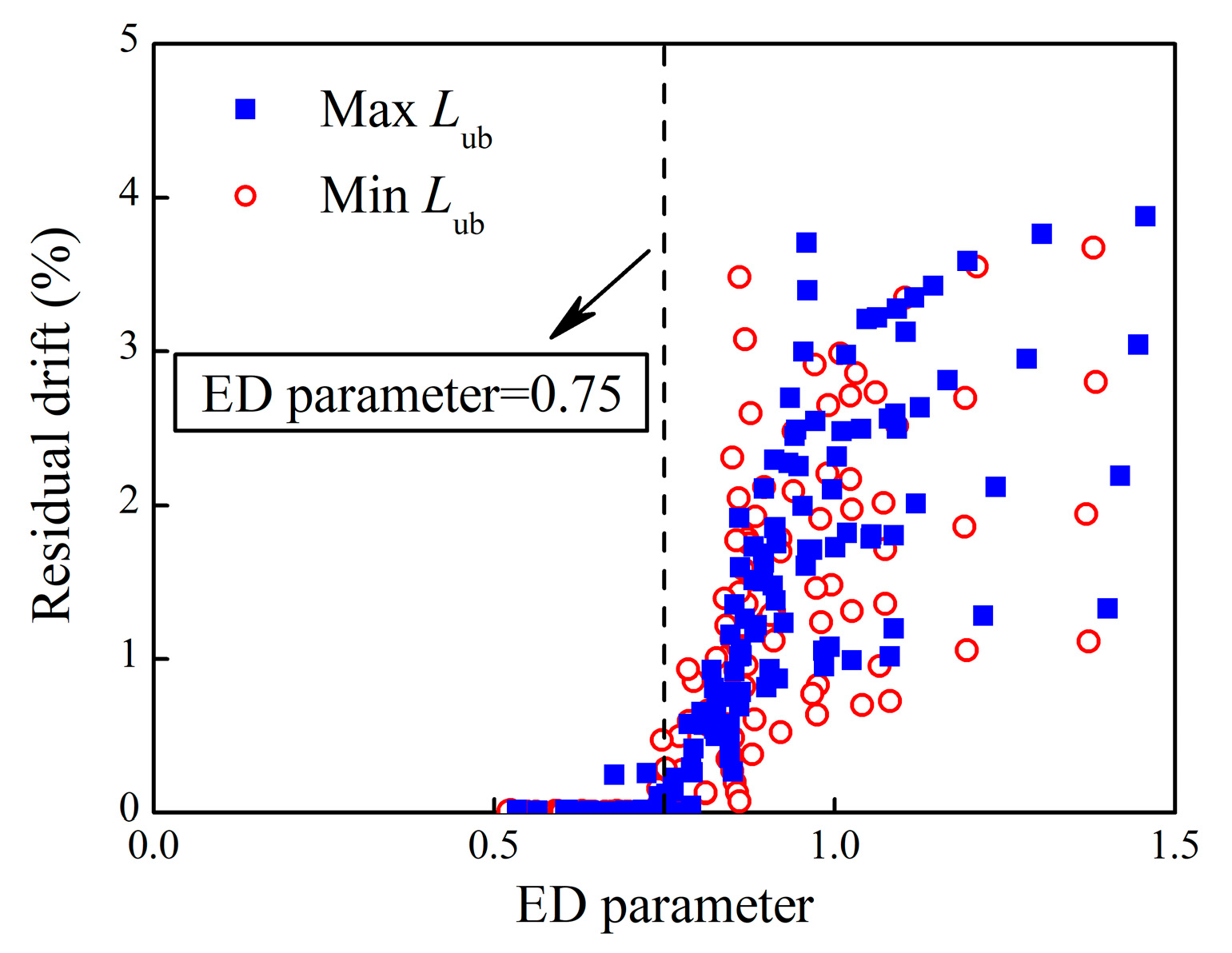
• The SC factor, ED parameter, and maximum displacement dominate the distribution of residual displacement under cyclic loading. When the SC factor exceeds 2.0 or the ED parameter is smaller than 0.75, the residual displacement can be neglected. In other situations, the residual displacement can be estimated using the upper limit formula and the regression formula. This implies that, during the design of RSC piers, controlling residual displacement can be achieved by adjusting the rocking self-resetting factor and energy dissipation capacity parameters.
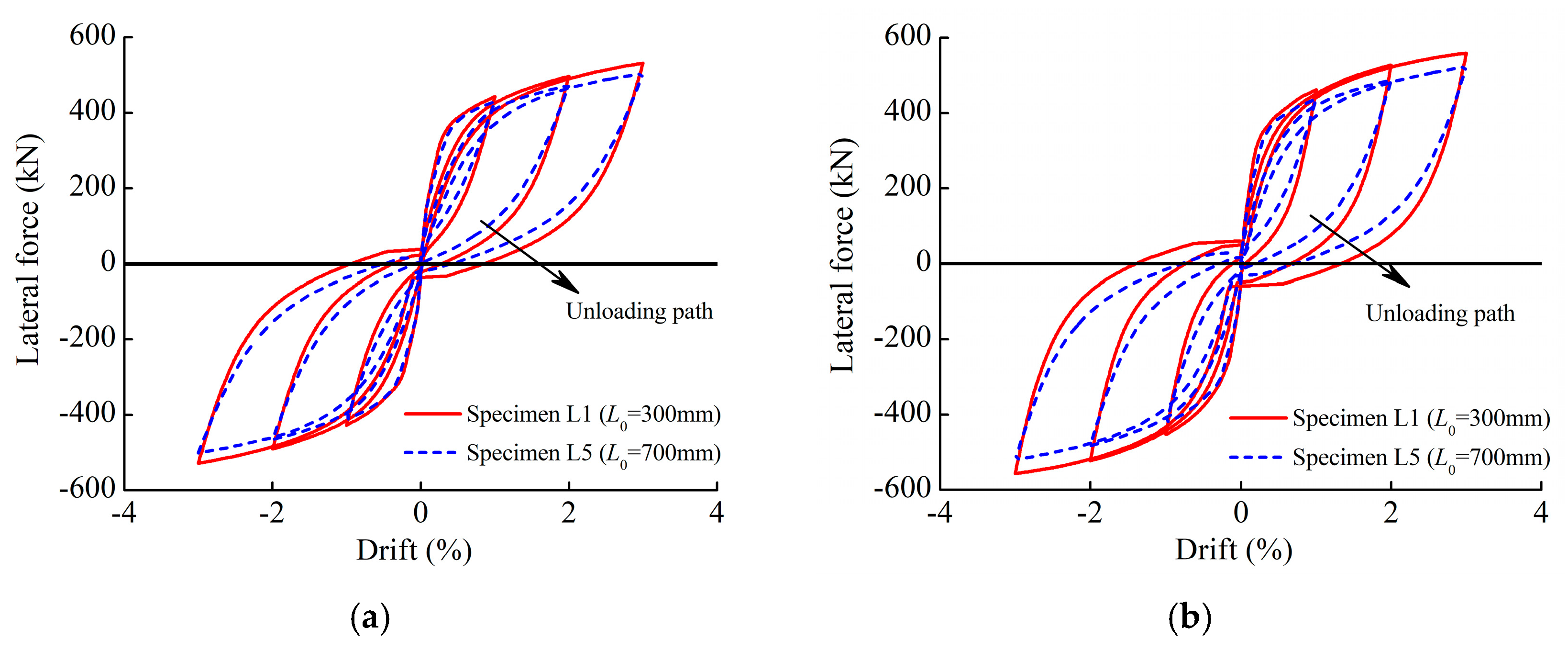
• The unbonded length of ED bars has little influence on the SC factor and the ED parameter. However, if the unbonded length is too long, the residual displacement can effectively be diminished because of the changed unloading path. This means that, when designing RSC piers, the length of unbonded energy-dissipating steel rods can be adjusted as needed to achieve the desired self-resetting capacity, energy-dissipating capacity, and residual displacement control effect.