An Edge-Computing-Driven Approach for Augmented Detection of Construction Materials: An Example of Scaffold Component Counting
Abstract
1. Introduction
2. Related Works
2.1. Vision-Based Construction Material Detection and Counting
2.2. Edge Computing in Construction
2.3. Model Compression Techniques
3. Methodology
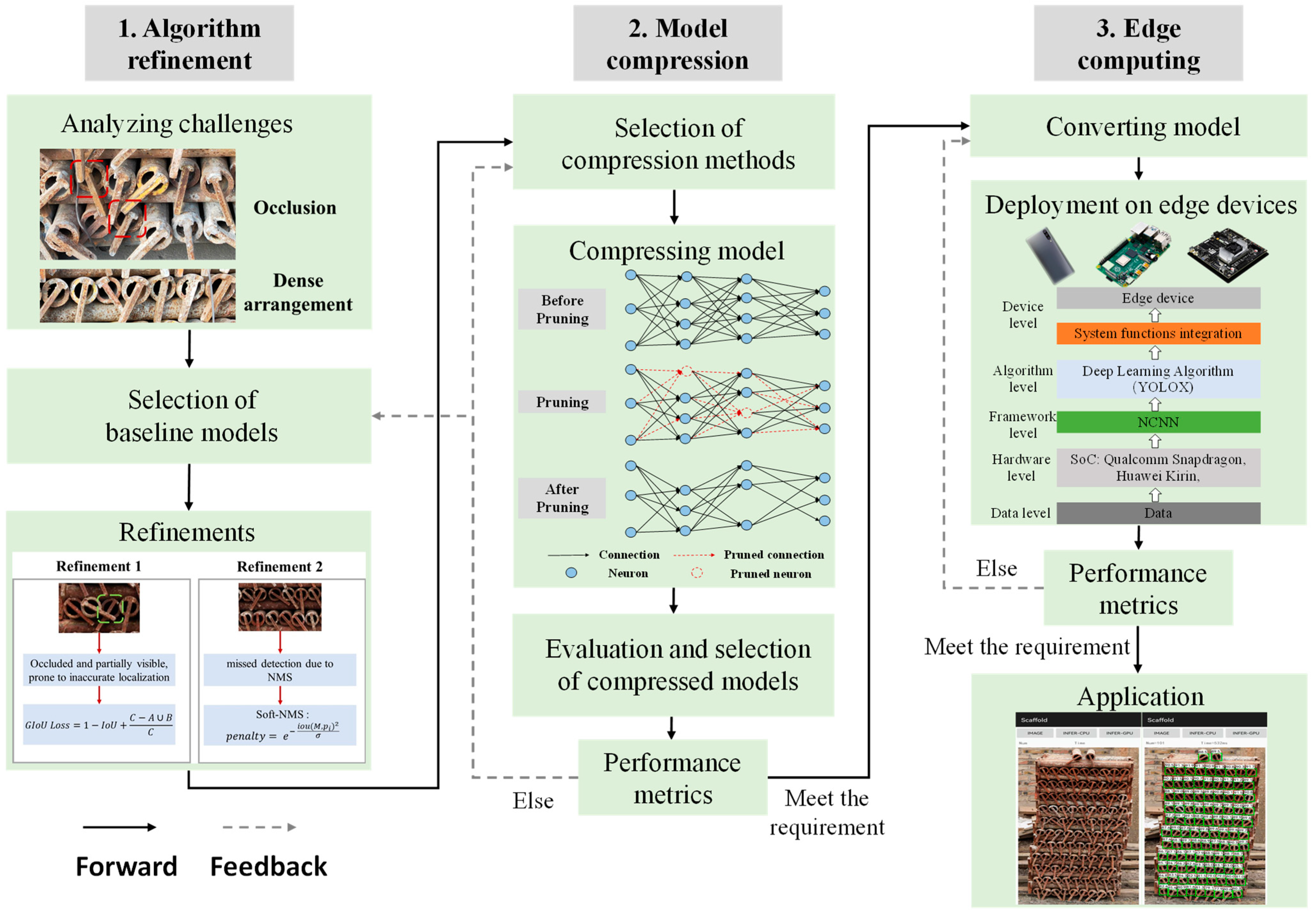
3.1. Overview of Workflow
- Challenge Analysis: Examine the characteristics of the tasks to identify the challenges and issues. For scaffold counting, the primary challenges are occlusion and dense arrangement.
- Baseline Model Selection: Choose a baseline model that essentially aligns with the real-time and accuracy requirements of the tasks.
- Algorithm Refinement: Propose a series of algorithmic refinements to address the identified challenges. Refined modules can range from pre-processing and post-processing algorithms to network architecture, loss function, and training strategies.
- Compression Method Selection: Decide on the method for model compression. Options include network pruning, knowledge distillation, quantization, etc.
- Execute Model Compression: Compress the refined model.
- Model Evaluation: Evaluate the compressed models and select the most appropriate one based on the performance metrics.
- Model Conversion: Convert the selected model into a format that is compatible with edge devices.
- Model Deployment: Deploy the model on the edge devices, integrating functionalities like data collection, pre-processing, post-processing, and model computing.
- Application: Incorporate visualization and interaction functionalities on the edge device for enhanced user experience and interaction.
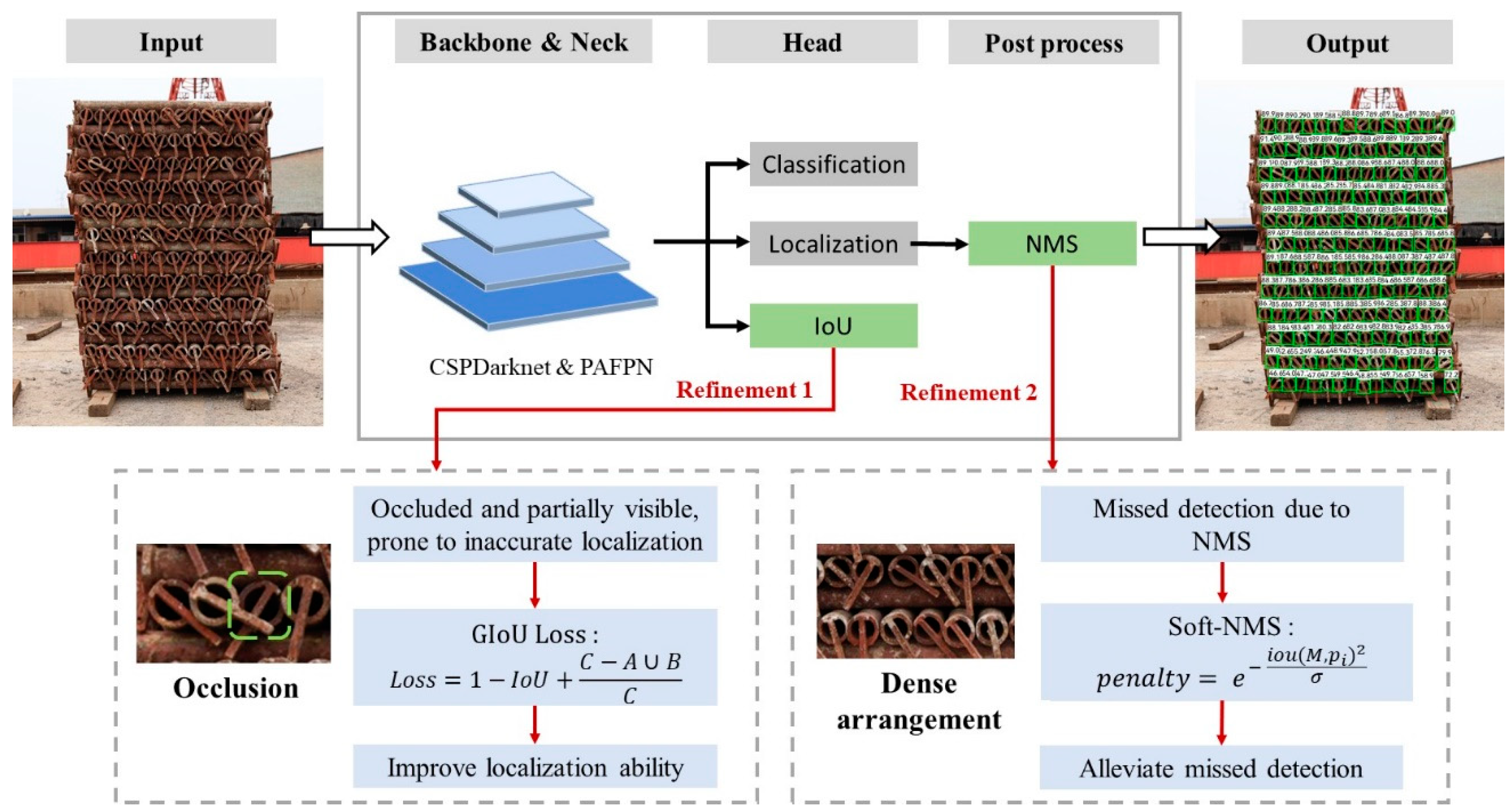
3.2. Algorithm Refinement
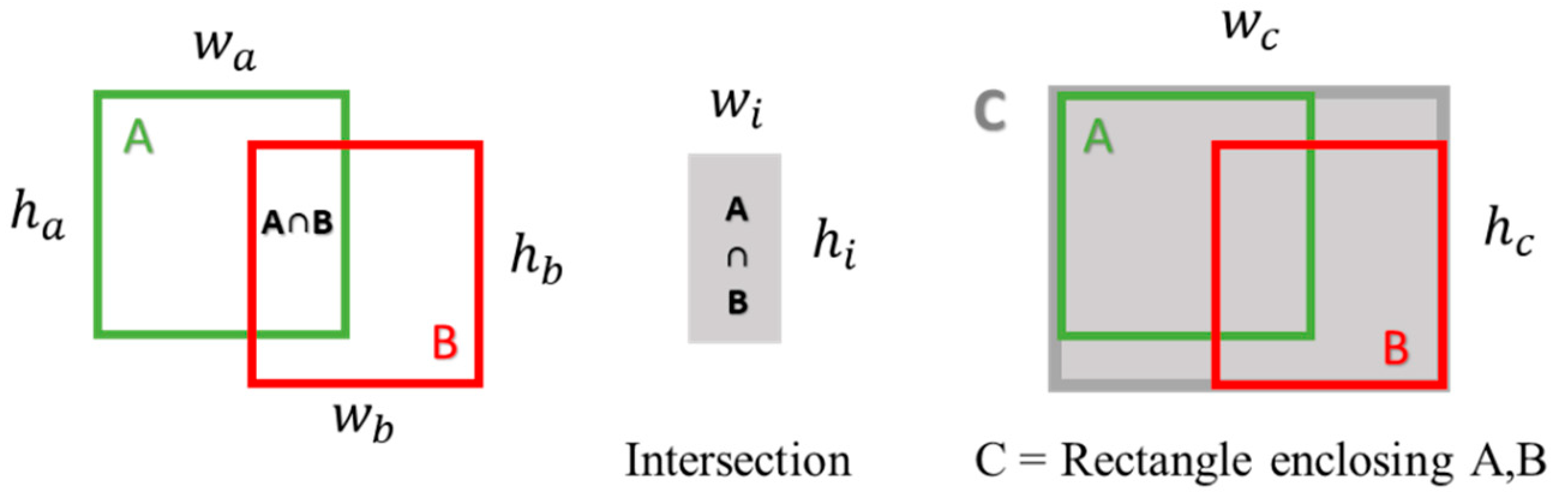
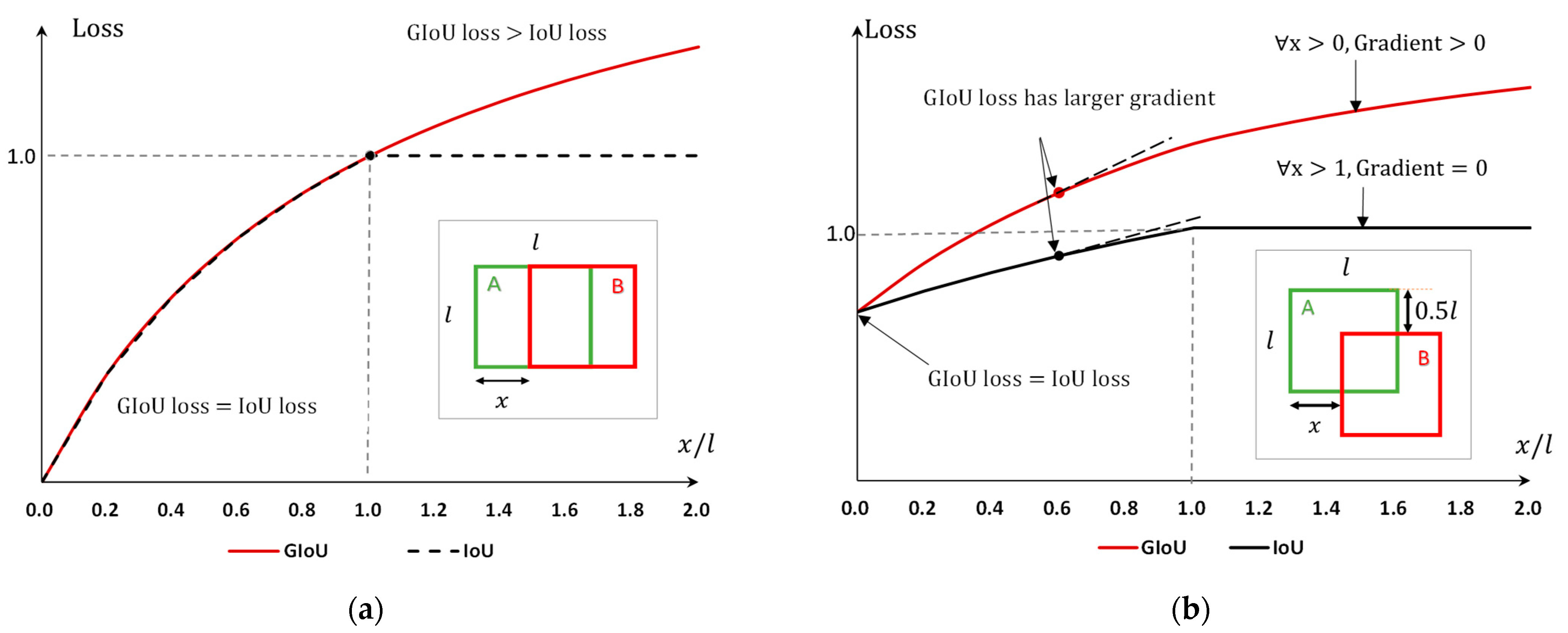
- Generalized intersection over union (GIoU)
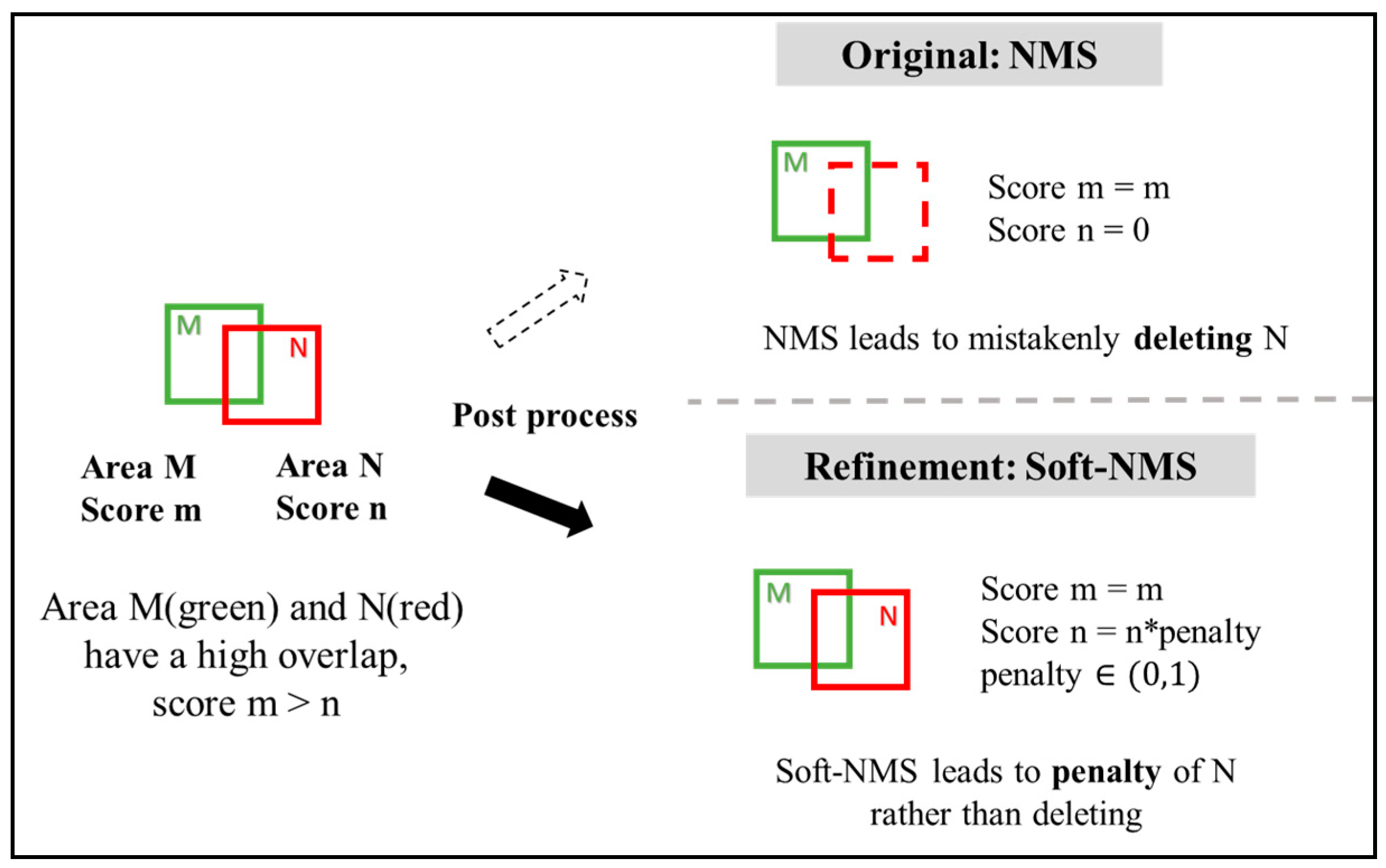
- Soft non-maximum suppression (Soft-NMS)
| Algorithm 1: Soft-NMS |
| Input |
| is the list of initial predictions |
| contains the confidence score of every prediction |
| is the penalty function for Soft-NMS |
| Output: is the result after Soft-NMS |
| contains the confidence score of every prediction after Soft-NMS |
| 1: |
| 2: while is not empty do |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: for in do |
| 8: |
| 9: |
| 10: end for |
| 11: end while |
| 12: return |
3.3. Model Compression
- Determination of Pruning Hyperparameters.
- Weight Assessment and Branch Elimination.
- Retraining.
- Performance Evaluation.
| Algorithm 2: Pruning |
| Input |
| is the list of network structures to be pruned |
| contains all the weights of network structures |
| is the pruning factor |
| Output: Performance metrics is the evaluation result of pruned network |
| 1: |
| 2: while is not empty do |
| 3: for in do |
| 4: |
| 5: if then |
| 6: |
| 7: |
| 8: end if |
| 9: end for |
| 10: end while |
| 11: retrain network with structure |
| 12: |
| 13: return Performance metrics |
3.4. Model Deployment on Edge Devices
4. Experiments
4.1. Dateset and Devices
4.2. Performance Metrics
- (1)
- Accuracy
- (2)
- Efficiency
5. Results
5.1. Results of Scaffold Detection
5.2. Results of Model Compression and Deployment
6. Discussion
6.1. The Rationale for Improved Algorithm
- GIoU loss ≥ IoU loss. GIoU loss always serves as an upper bound for IoU loss. This implies that the GIoU loss provides a more comprehensive error measurement by considering both the overlap and the relative positions.
- Greater gradient in GIoU loss. In the second case, the gradient of the GIoU loss is larger compared to that of the IoU loss. This larger gradient is beneficial for the convergence of the training process, as it provides a stronger correction signal for the model when the prediction is far from the actual target.
- Non-zero gradient for GIoU. When (i.e., when there is no overlap between the two areas), the IoU loss remains at 1, leading to a zero gradient. In such cases, optimization using IoU loss becomes infeasible since the loss function fails to provide a direction for improvement. In contrast, the gradient of GIoU loss remains greater than zero even in these scenarios, ensuring continuous optimization potential.
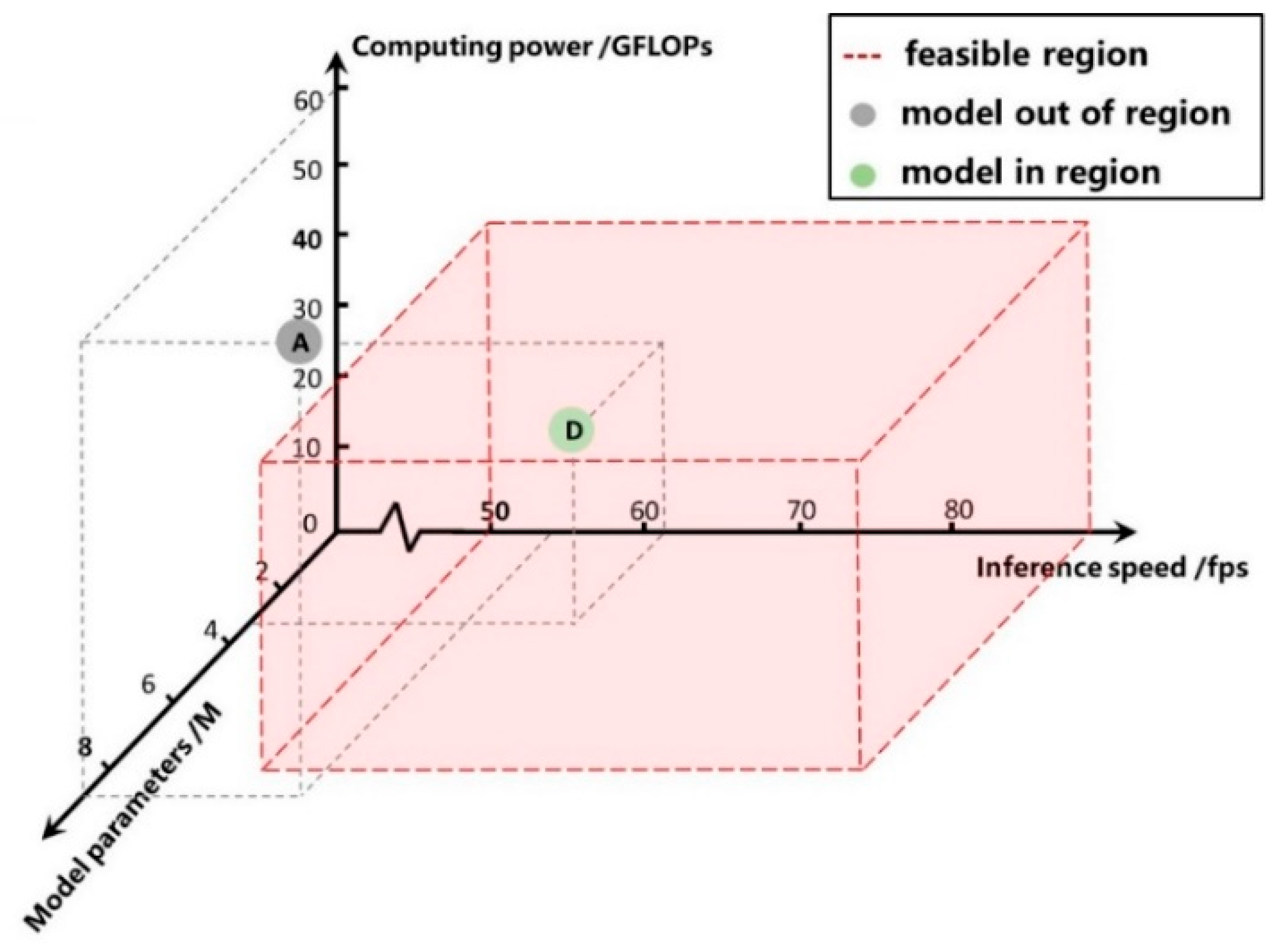
6.2. Optimal Selection of Compressed Models
6.3. Generalization Across Unseen Scenarios
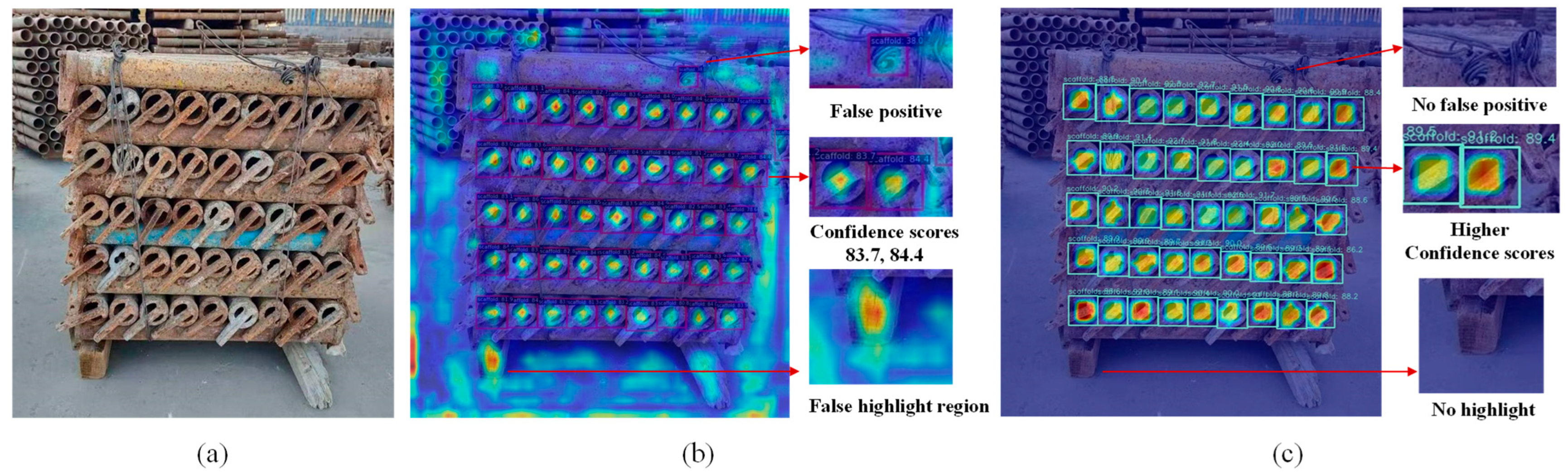
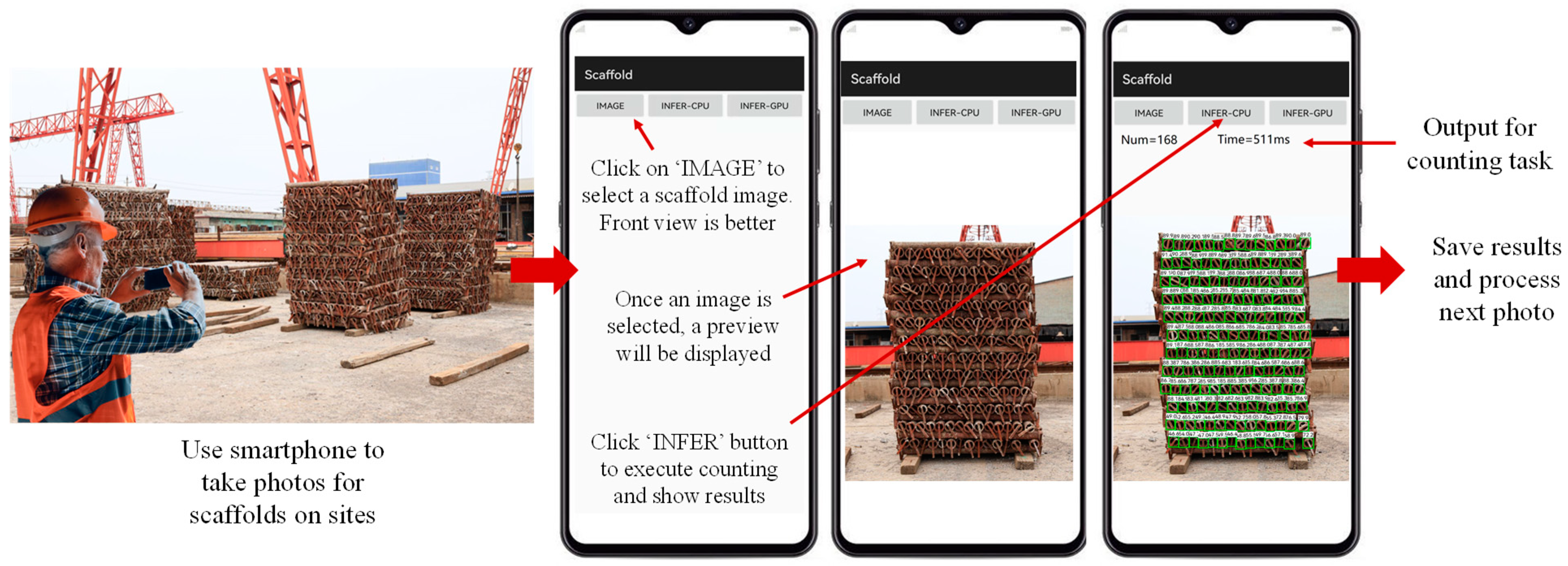
6.4. Field Application
6.5. Limitations
- Case 1
- Case 2
7. Conclusions
- The proposed approach effectively achieves accurate and rapid scaffold tube counting on edge devices, demonstrating an accuracy rate of 98.8% and a latency ranging from 0.4 to 0.8 s per image.
- The introduction of two algorithmic refinements enhanced the mean average precision by 5.3% (from 72.3% to 77.6%), without increasing the inference time. The improved YOLOX outperformed other state-of-the-art detectors in scaffold detection and counting.
- The implementation of an automated pruning method streamlined the compression process. This approach resulted in a 60.2% reduction in computational demand and a 9.1% increase in inference speed, with no significant compromise in accuracy.
- Multi-sensor fusion for enhanced robustness. The framework could integrate 2D images and RFID tag signals through a multi-sensor fusion mechanism to address occlusion and environmental interference in material management. This cross-modal alignment compensates for limitations in single sensing modalities—for instance, RFID provides spatial identity under low visibility, while visual data resolve tag collisions.
- Edge device performance benchmarking. Systematic evaluations of edge devices will be conducted to quantify their impacts on model accuracy, computational latency, energy consumption, and environmental resilience. This analysis will inform hardware selection and optimization strategies for real-world deployment.
- Model compression technique optimization. A comparative study will assess how advanced compression methods—including but not limited to quantization-aware training, teacher–student distillation, and NAS—affect the trade-off between model efficiency and accuracy performance. The findings will guide the development of lightweight yet accurate models for edge computing platforms.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GIoU | Generalized intersection over union |
| Soft-NMS | Soft non-maximum suppression |
| NMS | Non-maximum suppression |
| FLOPs | Floating point operations |
| GFLOPs | Giga Floating Point Operations per Second |
| HSV | Hue, saturation, value |
| FP | False positive |
| FN | False negative |
| GT | Ground truth |
| AP | Average precision |
| ONNX | Open Neural Network Exchange |
References
- Hou, L.; Zhao, C.; Wu, C.; Moon, S.; Wang, X. Discrete Firefly Algorithm for Scaffolding Construction Scheduling. J. Comput. Civ. Eng. 2017, 31, 04016064. [Google Scholar] [CrossRef]
- Wang, H.; Polden, J.; Jirgens, J.; Yu, Z.; Pan, Z. Automatic Rebar Counting using Image Processing and Machine Learning. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, Suzhou, China, 29 July–2 August 2019, and Intelligent Systems (CYBER); pp. 900–904.
- Li, Y.; Lu, Y.; Chen, J. A deep learning approach for real-time rebar counting on the construction site based on YOLOv3 detector. Autom. Constr. 2021, 124, 103602. [Google Scholar] [CrossRef]
- Xiang, Z.; Rashidi, A.; Ou, G. An improved convolutional neural network system for automatically detecting rebar in GPR data. In Proceedings of the ASCE International Conference on Computing in Civil Engineering, Atlanta, GA, USA, 17–19 June 2019; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 422–429. [Google Scholar]
- Han, K.K.; Golparvar-Fard, M. Appearance-based material classification for monitoring of operation-level construction progress using 4D BIM and site photologs. Autom. Constr. 2015, 53, 44–57. [Google Scholar] [CrossRef]
- Lauer, A.P.R.; Benner, E.; Stark, T.; Klassen, S.; Abolhasani, S.; Schroth, L.; Gienger, A.; Wagner, H.J.; Schwieger, V.; Menges, A.; et al. Automated on-site assembly of timber buildings on the example of a biomimetic shell. Autom. Constr. 2023, 156, 105118. [Google Scholar] [CrossRef]
- Li, Y.; Chen, J. Computer Vision–Based Counting Model for Dense Steel Pipe on Construction Sites. J. Constr. Eng. Manag. 2022, 148, 04021178. [Google Scholar]
- Katsigiannis, S.; Seyedzadeh, S.; Agapiou, A.; Ramzan, N. Deep learning for crack detection on masonry façades using limited data and transfer learning. J. Build. Eng. 2023, 76, 107105. [Google Scholar]
- Davis, P.; Aziz, F.; Newaz, M.T.; Sher, W.; Simon, L. The classification of construction waste material using a deep convolutional neural network. Autom. Constr. 2021, 122, 103481. [Google Scholar]
- Han, Q.; Liu, X.; Xu, J. Detection and Location of Steel Structure Surface Cracks Based on Unmanned Aerial Vehicle Images. J. Build. Eng. 2022, 50, 104098. [Google Scholar] [CrossRef]
- Kamari, M.; Ham, Y. Vision-based volumetric measurements via deep learning-based point cloud segmentation for material management in jobsites. Autom. Constr. 2021, 121, 103430. [Google Scholar]
- Beckman, G.H.; Polyzois, D.; Cha, Y.-J. Deep learning-based automatic volumetric damage quantification using depth camera. Autom. Constr. 2019, 99, 114–124. [Google Scholar] [CrossRef]
- Wang, P.; Yan, Z.; Han, G.; Yang, H.; Zhao, Y.; Lin, C.; Wang, N.; Zhang, Q. A2E2: Aerial-assisted energy-efficient edge sensing in intelligent public transportation systems. J. Syst. Archit. 2022, 129, 102617. [Google Scholar] [CrossRef]
- Habib, M.; Bollin, E.; Wang, Q. Edge-based solution for battery energy management system: Investigating the integration capability into the building automation system. J. Energy Storage 2023, 72, 108479. [Google Scholar] [CrossRef]
- Akhavian, R.; Behzadan, A.H. Smartphone-based construction workers’ activity recognition and classification. Autom. Constr. 2016, 71, 198–209. [Google Scholar] [CrossRef]
- Abner, M.; Wong, P.K.-Y.; Cheng, J.C.P. Battery lifespan enhancement strategies for edge computing-enabled wireless Bluetooth mesh sensor network for structural health monitoring. Autom. Constr. 2022, 140, 104355. [Google Scholar] [CrossRef]
- Maalek, R.; Lichti, D.D.; Maalek, S. Towards automatic digital documentation and progress reporting of mechanical construction pipes using smartphones. Autom. Constr. 2021, 127, 103735. [Google Scholar]
- Chen, C.; Gu, H.; Lian, S.; Zhao, Y.; Xiao, B. Investigation of Edge Computing in Computer Vision-Based Construction Resource Detection. Buildings 2022, 12, 2167. [Google Scholar] [CrossRef]
- Chen, K.; Zeng, Z.; Yang, J. A deep region-based pyramid neural network for automatic detection and multi-classification of various surface defects of aluminum alloys. J. Build. Eng. 2021, 43, 102523. [Google Scholar] [CrossRef]
- Wang, N.; Zhao, X.; Zhao, P.; Zhang, Y.; Ou, J. Automatic damage detection of historic masonry buildings based on mobile deep learning. Autom. Constr. 2019, 103, 53–66. [Google Scholar]
- Alexander, Q.G.; Hoskere, V.; Narazaki, Y.; Maxwell, A.; Spencer, B.F., Jr. Fusion of thermal and RGB images for automated deep learning based crack detection in civil infrastructure. AI Civ. Eng. 2022, 1, 3. [Google Scholar]
- Kizilay, F.; Narman, M.R.; Song, H.; Narman, H.S.; Cosgun, C.; Alzarrad, A. Evaluating fine tuned deep learning models for real-time earthquake damage assessment with drone-based images. AI Civ. Eng. 2024, 3, 15. [Google Scholar]
- Cheng, Y.; Wang, D.; Zhou, P.; Zhang, T. A Survey of Model Compression and Acceleration for Deep Neural Networks. arXiv 2017, arXiv:1710.09282. [Google Scholar]
- Cheng, J.; Wang, P.S.; Gang, L.I.; Qing-Hao, H.U.; Han-Qing, L.U. Recent advances in efficient computation of deep convolutional neural networks. Front. Inf. Technol. Electron. Eng. 2018, 19, 64–77. [Google Scholar] [CrossRef]
- Lecun, Y. Optimal Brain Damage. Neural Inf. Proceeding Syst. 1990, 2, 598–605. [Google Scholar]
- Hassibi, B.; Stork, D.G. Second order derivatives for network pruning: Optimal brain surgeon. In Proceedings of the 6th International Conference on Neural Information Processing Systems, San Francisco, CA, USA, 30 November–3 December 1992; pp. 164–171. [Google Scholar]
- Guo, Y.; Cui, H.; Li, S. Excavator joint node-based pose estimation using lightweight fully convolutional network. Autom. Constr. 2022, 141, 104435. [Google Scholar]
- Wu, P.; Liu, A.; Fu, J.; Ye, X.; Zhao, Y. Autonomous surface crack identification of concrete structures based on an improved one-stage object detection algorithm. Eng. Struct. 2022, 272, 114962. [Google Scholar]
- Gong, Y.; Liu, L.; Yang, M.; Bourdev, L. Compressing Deep Convolutional Networks using Vector Quantization. arXiv 2014, arXiv:1412.6115. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. Comput. Sci. 2015, 14, 38–39. [Google Scholar]
- Chen, Z.; Yang, J.; Chen, L.; Feng, Z.; Jia, L. Efficient railway track region segmentation algorithm based on lightweight neural network and cross-fusion decoder. Autom. Constr. 2023, 155, 105069. [Google Scholar]
- Hong, Y.; Chern, W.-C.; Nguyen, T.V.; Cai, H.; Kim, H. Semi-supervised domain adaptation for segmentation models on different monitoring settings. Autom. Constr. 2023, 149, 104773. [Google Scholar] [CrossRef]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. YOLOX: Exceeding YOLO Series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 658–666. [Google Scholar]
- Bodla, N.; Singh, B.; Chellappa, R.; Davis, L.S. Improving Object Detection with One Line of Code. arXiv 2017, arXiv:1704.04503. [Google Scholar]
- ONNX. Open Neural Network Exchange. Available online: https://github.com/onnx/onnx (accessed on 28 April 2022).
- NCNN. A High-Performance Neural Network Inference Framework Optimized for the Mobile Platform. Available online: https://github.com/Tencent/ncnn (accessed on 28 April 2022).
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Computer Vision—ECCV 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Everingham, M.; Eslami, S.M.A.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes Challenge: A Retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef]
- Berg, A.C.; Fu, C.Y.; Szegedy, C.; Anguelov, D.; Erhan, D.; Reed, S.; Liu, W. SSD: Single Shot MultiBox Detector. arXiv 2015, arXiv:1512.02325. [Google Scholar]
- U. LLC. YOLOv5. 2020. Available online: https://github.com/ultralytics/yolov5 (accessed on 28 April 2022).
- Wang, C.-Y.; Bochkovskiy, A.; Liao, H.-Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]

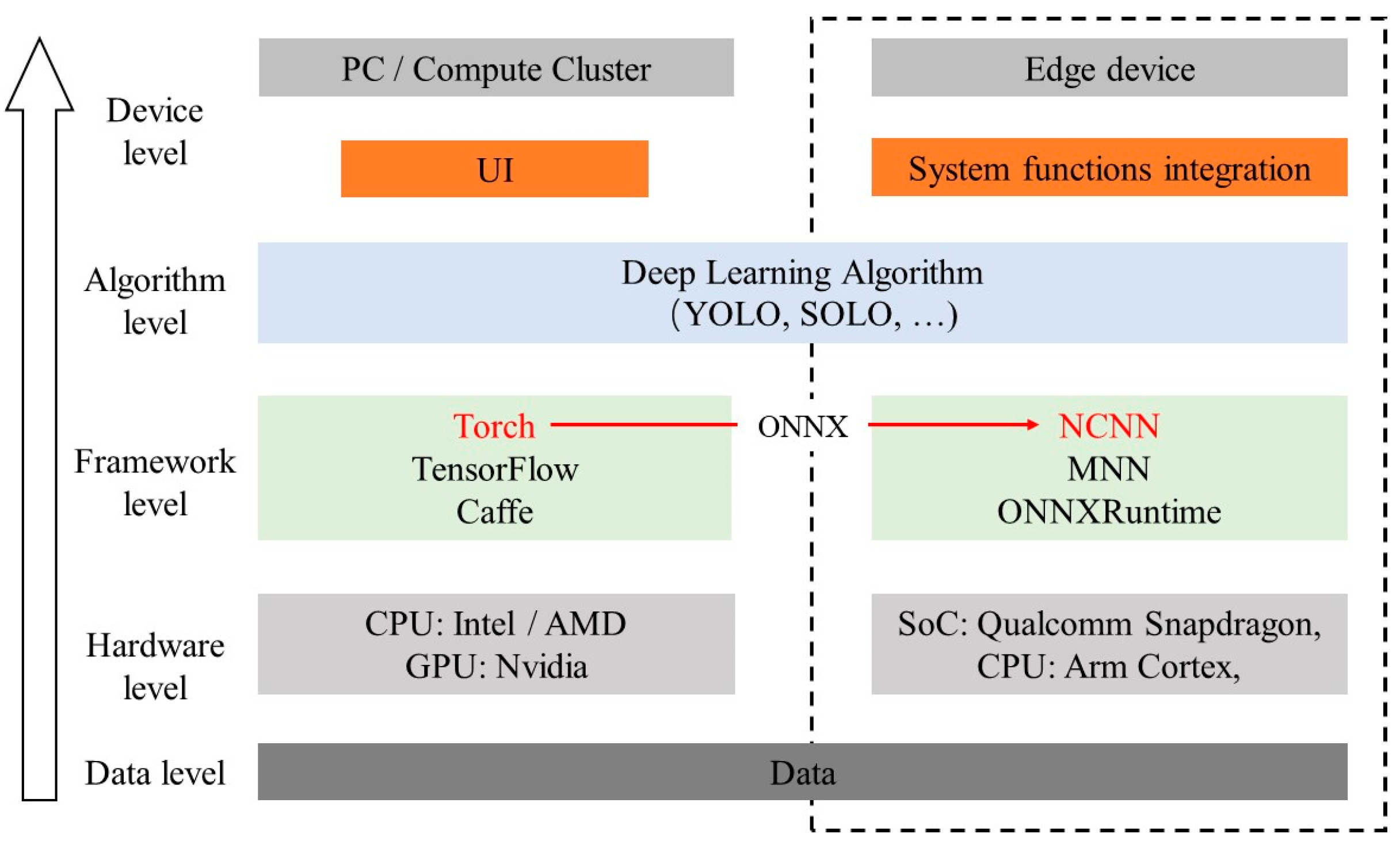



| Type of Strategy | Data Collection | Data Processing & Analyzing | Result & Feedback | Reference | Advantage | Disadvantage |
|---|---|---|---|---|---|---|
| Cloud-dominant | Edge | Cloud | Cloud | [2,4,9,11,12,19] | High computing power, extensibility | Data loss, bandwidth pressure |
| Cloud–edge collaboration | Edge | Cloud | Edge | [3,7,14,15,16,17,20,21] | High computing power, extensibility | Data loss, bandwidth pressure, high latency |
| Edge-dominant | Edge | Edge | Edge | [18,22] | Quick response, data security, convenience | Low computing power, limited accuracy |
| Device | Type | Computing Power Index |
|---|---|---|
| Windows computer (i7-RTX3090) | Professional computer | 100 |
| MacBook Pro (M2 Pro) | Personal computer | 19 |
| Huawei Mate40 pro (Kirin9000) | Smartphone/Edge device | 18 |
| iPhone14 (A16) | Smartphone/Edge device | 12 |
| Jetson-TX1 (Cortex-A57) | Minicomputer/Edge device | 4 |
| Raspberry Pi-4B (Cortex-A72) | Minicomputer/Edge device | 1 |
| YOLOX | AP/% | AP@50/% | AP@75/% | Inference Time/ms |
|---|---|---|---|---|
| Baseline | 72.3 | 91.5 | 89.5 | 17.9 |
| +Soft-NMS | 73.0 (+0.7) | 92.9 (+1.4) | 90.0 (+0.5) | 18.1 |
| +GIoU | 77.4 (+5.1) | 95.6 (+4.1) | 93.6 (+3.1) | 18.3 |
| +GIoU and Soft-NMS | 77.6 (+5.3) | 95.9 (+4.4) | 93.9 (+3.4) | 17.8 |
| Model | Backbone | AP/% | AP@50/% | Inference Time/ms |
|---|---|---|---|---|
| Faster R-CNN | ResNet50 | 73.1 | 91.1 | 61.1 |
| SSD | VGG16 | 63.2 | 78.2 | 51.8 |
| YOLOv5 | CSP-Darknet53 | 77.1 | 92.9 | 23.0 |
| YOLOv7 | ELAN | 77.2 | 93.1 | 21.9 |
| YOLOX-GIoU and Soft-NMS | CSP-Darknet53 | 77.6 | 95.9 | 17.8 |
| Model Ref | Pruning Factor | AP/% | Params/M | Computing Power/GFLOPs | Inference Time/ms |
|---|---|---|---|---|---|
| A (unpruned) | 0 | 77.6 | 8.94 | 59.93 | 17.8 |
| D | 0.375 | 74.6 (↓3.9%) | 3.50 (↓60.9%) | 23.86 (↓60.2%) | 16.3 (↓8.4%) |
| Model Ref | Three-Dimensional Space | Inside of Feasible Region | Performance | ||
|---|---|---|---|---|---|
| Params/M | Computing Power/GFLOPs | Inference Speed/fps | AP/% | ||
| A | 8.94 | 59.9 | 56.2 | No | 77.6 |
| B | 6.85 | 46.1 | 58.8 | No | 73.9 |
| C | 5.03 | 34.1 | 58.5 | Yes | 72.5 |
| D | 3.50 | 23.9 | 61.3 | Yes | 74.6 |
| E | 2.24 | 15.5 | 59.5 | Yes | 73.1 |
| F | 1.26 | 8.9 | 60.2 | Yes | 71.0 |
| G | 0.56 | 4.1 | 64.9 | Yes | 70.5 |
| H | 0.14 | 1.1 | 72.5 | Yes | 67.8 |
| Project Information | Manual | Our Method | ||||||
|---|---|---|---|---|---|---|---|---|
| ID | Type | Total Area /m2 | Number of Scaffolds | Total Count | Total Time /h | Accuracy % | Total Time /h | Accuracy % |
| 1 | Residential building | 35,225.2 | 34,650 | 69,300 | 8.09 | 98.5 | 0.98 (↓87.9%) | 98.9 (↑0.4%) |
| 2 | Bridge | 6375.7 | 25,500 | 51,000 | 5.95 | 98.1 | 0.78 (↓86.9%) | 98.8 (↑0.7%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Cheng, B.; Lu, Y.; Huang, Z. An Edge-Computing-Driven Approach for Augmented Detection of Construction Materials: An Example of Scaffold Component Counting. Buildings 2025, 15, 1190. https://doi.org/10.3390/buildings15071190
Zhao X, Cheng B, Lu Y, Huang Z. An Edge-Computing-Driven Approach for Augmented Detection of Construction Materials: An Example of Scaffold Component Counting. Buildings. 2025; 15(7):1190. https://doi.org/10.3390/buildings15071190
Chicago/Turabian StyleZhao, Xianzhong, Bo Cheng, Yujie Lu, and Zhaoqi Huang. 2025. "An Edge-Computing-Driven Approach for Augmented Detection of Construction Materials: An Example of Scaffold Component Counting" Buildings 15, no. 7: 1190. https://doi.org/10.3390/buildings15071190
APA StyleZhao, X., Cheng, B., Lu, Y., & Huang, Z. (2025). An Edge-Computing-Driven Approach for Augmented Detection of Construction Materials: An Example of Scaffold Component Counting. Buildings, 15(7), 1190. https://doi.org/10.3390/buildings15071190







