Heat Transfer Analysis of Ventilated Photovoltaic Wall Panels with Curved Ribs for Different Parametric Cavity Structures

Abstract

Photovoltaic (PV) wall panels are an integral part of Building-Integrated Photovoltaics (BIPV) and have great potential for development. However, inadequate heat dissipation can reduce power generation efficiency. To reduce the temperature of photovoltaic wall panels and improve the photovoltaic conversion efficiency, this paper constructs a computational fluid dynamics (CFD) numerical model of ventilated photovoltaic wall panels and verifies it, then simulates and analyzes the effects of three cavity structure forms on the thermal performance of photovoltaic wall panels and optimizes the dimensional parameters of the curved-ribbed cavity structure. The average surface temperatures of flat-plate, rectangular-ribbed, and arc-ribbed cavity structure PV wall panels were 59.42 °C, 57.56 °C, and 55.39 °C, respectively, under natural ventilation conditions. Among them, the arc-ribbed cavity structure PV wall panels have the best heat dissipation effect. Further studies have shown that the curvature, rib height, width, and spacing of the curved ribs significantly affect the heat dissipation performance of the photovoltaic panels. Compared to the flat-plate cavity structure, the parameter-optimized curved-rib cavity structure significantly reduces the average surface temperature of PV panels. As solar radiation intensity increases, the optimized structure’s heat dissipation effect strengthens, achieving a 6 °C temperature reduction at 1000 W/m² solar radiation.

1. Introduction

Given the increasing scarcity of nonrenewable resources and the aggravation of environmental pollution problems, the attention to the advancement of new energy sources and energy-saving technologies continues to rise globally. According to the 2024 Renewable Energy Report, the importance of solar power may be further strengthened in future energy systems. The report suggests that, from now until 2030, the incremental growth of photovoltaic systems could account for more than 80% of the global increase in renewable energy installations [1].

In the construction industry, the integration of solar photovoltaic technology has significantly increased the proportion of renewable energy in building envelopes. Building-Integrated Photovoltaics (BIPV), which integrate solar panels into buildings, have great growth potential [2,3,4]. Minelli et al. [5] introduced a photovoltaic shading device called Phlo Ver, which integrates solar power generation and tracking technology. Featuring a modular, flower-like design, this system enhances shading performance while optimizing energy production. It offers a sustainable energy solution for urban public spaces.

However, photovoltaic power generation systems are not without flaws. In China, prolonged exposure to the sun during hot summer weather can lead to a significant increase in the temperature of photovoltaic panels. When PV modules overheat, their output efficiency suffers. Photovoltaic panels typically consist of a front glass panel, a hot-melt adhesive film, a cell, and a back sheet. Studies have shown that photovoltaic cell photoelectric conversion ranges from 6% to 19%, and most of the unconverted energy accumulates inside the cell in the form of heat. In addition, high temperatures will accelerate the thermal degradation process of the cells, thus reducing the lifetime of the PV panels [6,7]. Overheating of PV cells has become an important factor limiting the performance and development of PV panels, so effective measures to prevent overheating of PV panel temperatures and maintain them within an appropriate range are essential to improve system efficiency.

To improve the photoelectric conversion efficiency of photovoltaic modules, many scholars have conducted in-depth research on the structural optimization and thermal characteristics of PV-integrated systems. According to the study by Saitoh et al. [8], a hybrid solar collector incorporating a circulating cooling fluid demonstrates enhanced performance compared to standalone photovoltaic (PV) modules and solar thermal collectors under constant temperature conditions. Specifically, the electrical conversion efficiency increases from 10% to 13%, while the thermal efficiency improves from 40% to 50%. Al-Akam et al. [9], by investigating the effect of various roof coverings on the performance of photovoltaic (PV) panels in standard environments, found that placing wet wood chips underneath the PV panels reduced the temperature. At this point, the PV panels performed optimally, and the efficiency could be increased by 5%. J.K. Tonui et al. [10] found that air channels and the addition of heatsinks in the PVT module significantly enhanced the air convection heat transfer, and the thermal efficiency of the system could be increased by more than 20%. The above studies found that it is effective to increase the photovoltaic conversion efficiency by reducing the temperature of the PV panels through system optimization.

The loss of electrical and thermal efficiency can be significantly reduced by a rational fluid circulation method. Air and water, as commonly used media, can effectively reduce the temperature of photovoltaic panels. Bayu et al. [11] used pure water and nanofluid as the cooling fluid for comparison, and the results show that the application of nanofluid can effectively reduce the temperature of the photovoltaic cells and improve their efficiency. Relative to water-cooled PV systems, air-cooled PV systems with no fluid leakage are easy to install, have a low maintenance workload, and have been the main way to dissipate heat from PV panels [12]. Shahsavar et al. [13] studied a device that uses the wind entering and exiting a building to cool photovoltaic panels. The results indicated that it could generate an additional 56 kWh of electricity per year. Ritzen et al. [14] conducted a test on BIPV roof design in the Netherlands and the results showed that ventilated BIPV roofs produce 2.6% more electricity annually than non-ventilated ones. Ibrahim et al. [15] investigated the cooling of PV panels by utilizing phase-change materials in combination with natural convection and forced convection and experimentally compared the four cooling techniques, and the results showed that forced convection PV panels with aluminum fins had the best performance with an efficiency increase of 20.36%.

Fahad et al. [16] reduced the temperature of the PV panels by applying exhaust gases from a centralized air conditioner, and the results showed that the electrical efficiency of PV panels was increased by 0.97%. Zhangyang Kang et al. [17] proposed a multiple-inlet cooling channel PV/T system that improves heat transfer, reduces peak PV temperatures, and increases efficiency.

In one study, the researchers analyzed the effect of placing curved ribs in the solar collector and the results of the study showed a 56% increase in energy consumption enhancement as compared to a flat plate solar collector [18]. Filip et al. [19] investigated the reduction in the operating temperature of the PV panels by mounting aluminum heat sinks on the back of the PV panels and consequently obtaining an increase in the efficiency of the PV panels.

D’Orazio et al. [20] examined the thermal performance of PV panels on tiled roofs and found that PV modules mounted on roofs with air gaps can help to reduce the module temperature and thus improve its performance, as shown in Figure 1, in which (a) represents a photovoltaic wall panel with an air gap, and (b) represents a photovoltaic wall panel without an air gap. The curved air gap design, with its unique airflow characteristics, can effectively increase the speed and flow path of airflow and enhance ventilation.

Currently, there are already projects to add PV panel heat dissipation air-cooling channels. Zheng et al. [21] proposed a natural-ventilation-based PV wall panel featuring rectangular ribs, and this fin-type air-cooling channel has better heat dissipation than the flat plate-type air-cooling channel.

Based on the current research, despite significant progress in PV systems, certain limitations still exist. Most existing studies primarily focus on solar thermal collectors, often overlooking the thermal performance optimization of BIPV systems. In addition, while water-cooled photovoltaic panels can improve heat dissipation, they are expensive to maintain and risk leakage. Mechanical ventilation, though more effective, poses challenges for practical implementation in engineering applications. In real projects, air-cooled channels have been integrated into PV systems. It has been shown that the inclusion of rectangular ribs in the air-cooling channels of vertical PV panels helps to improve heat dissipation. On this basis, an innovative scheme is proposed in this paper to replace the rectangular ribs in the air-cooling channel with curved ribs, and to adjust the parameters of the curved fins to further improve the heat dissipation efficiency. By lowering the operating temperature of the PV panels, this approach aims to improve overall system performance.

2. Methods

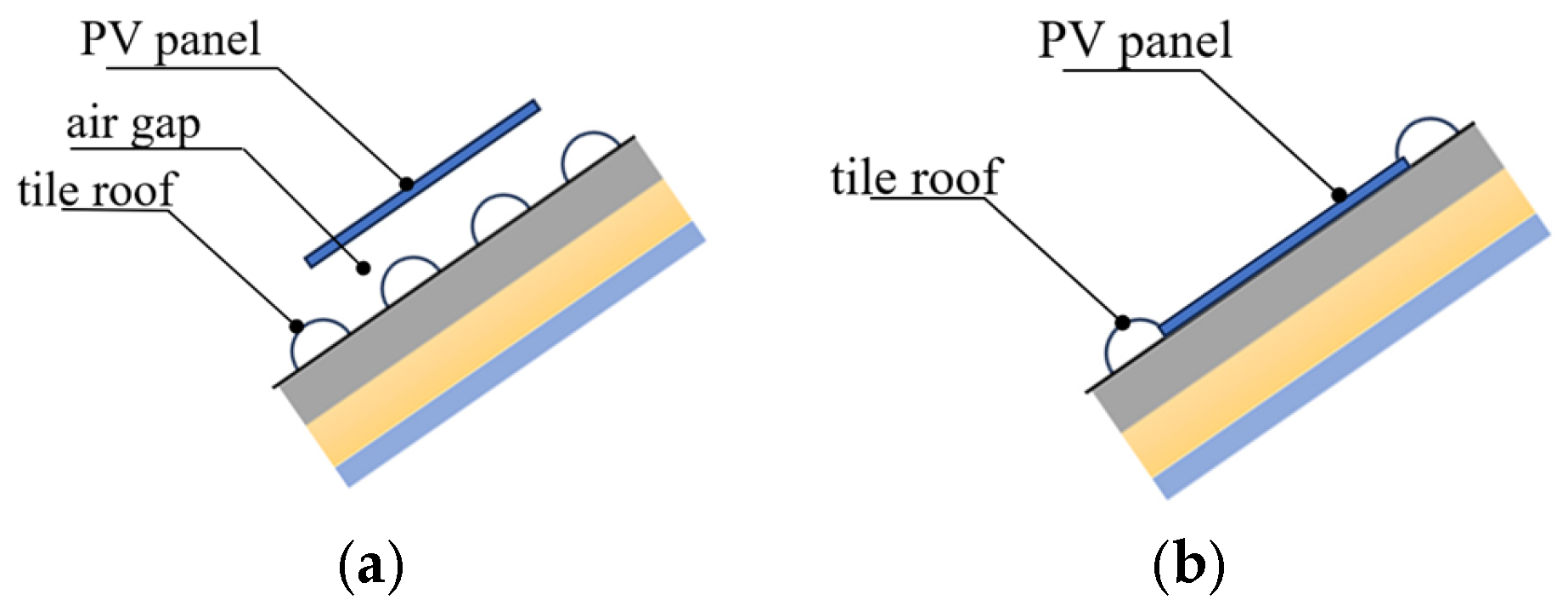
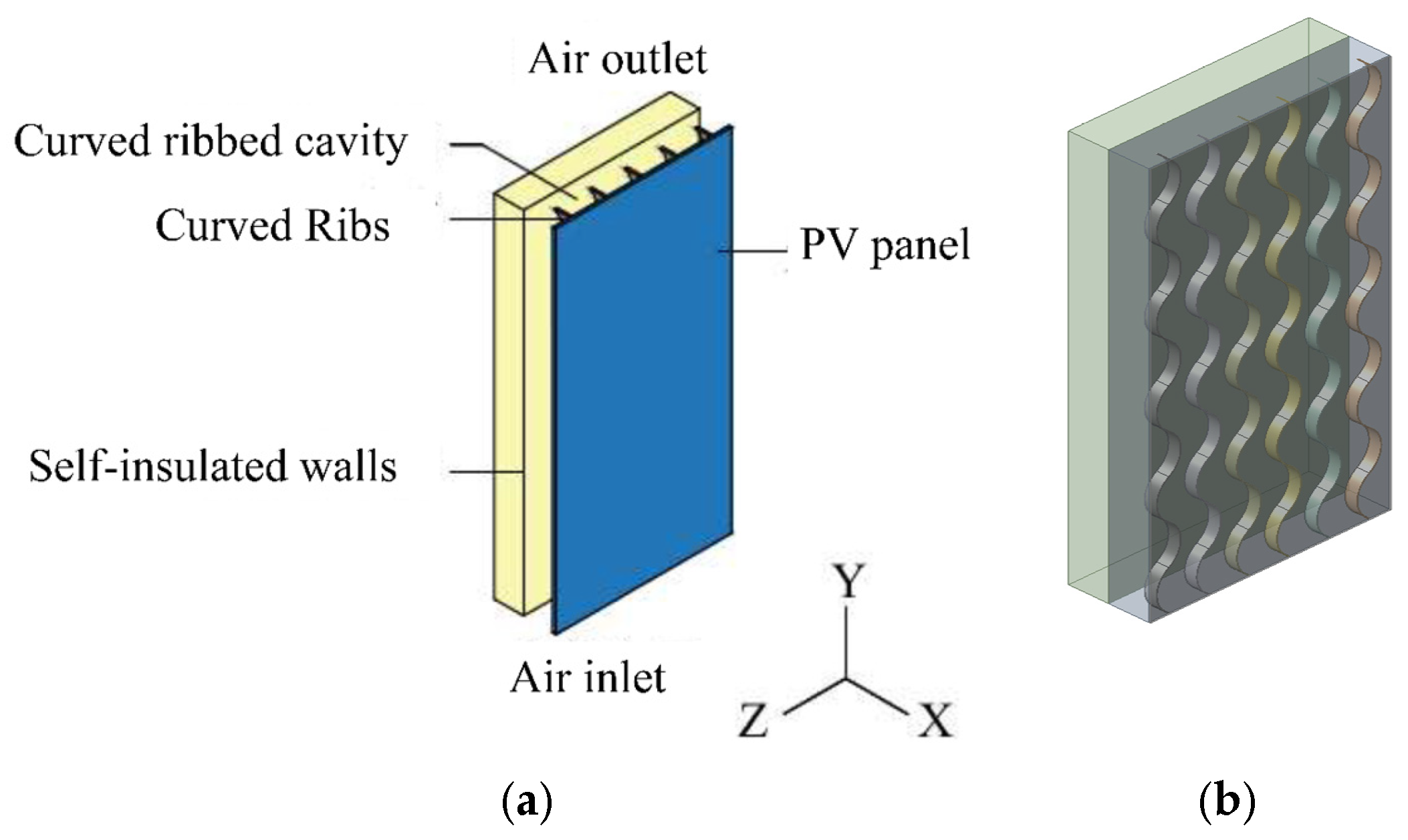
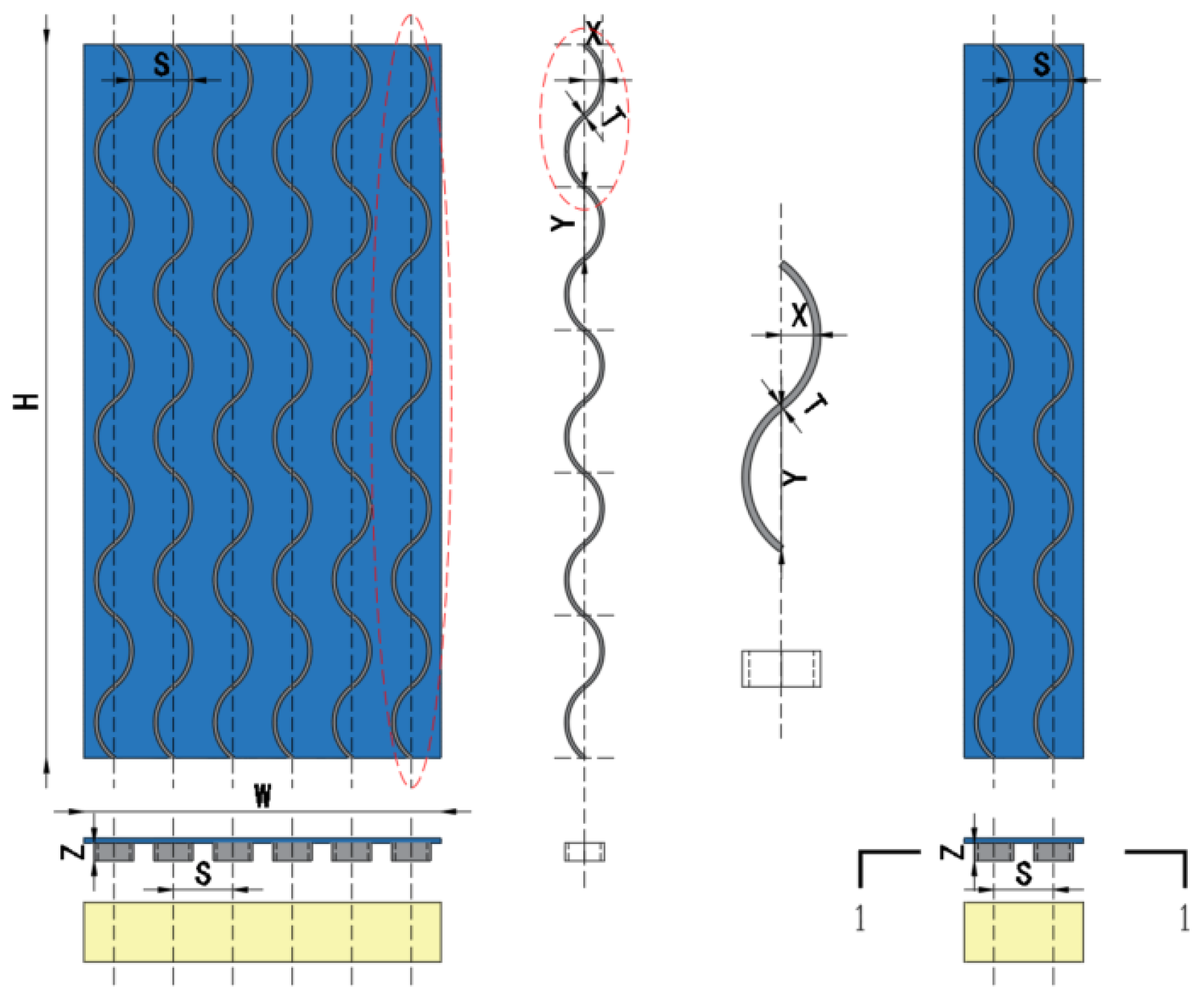
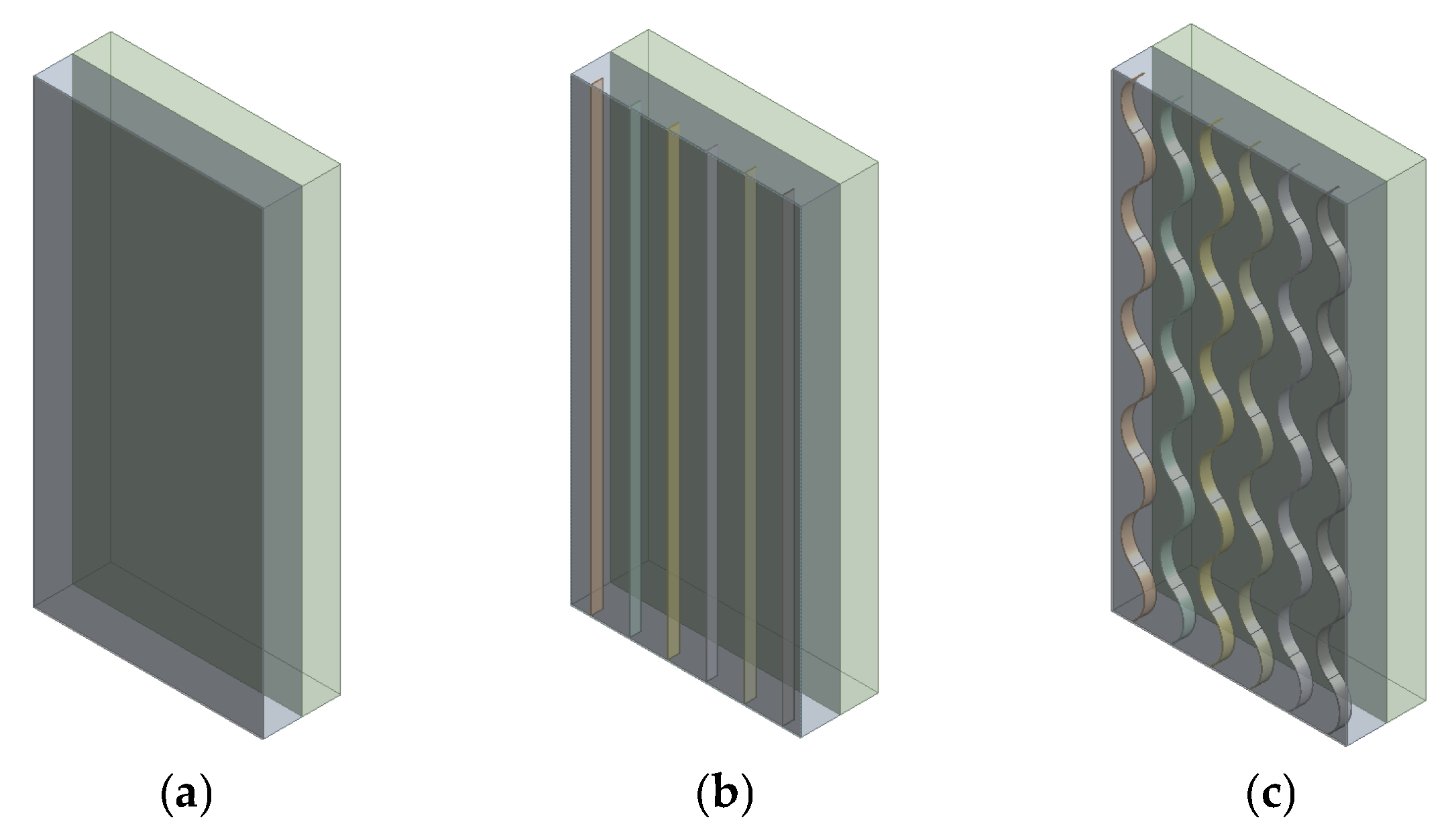
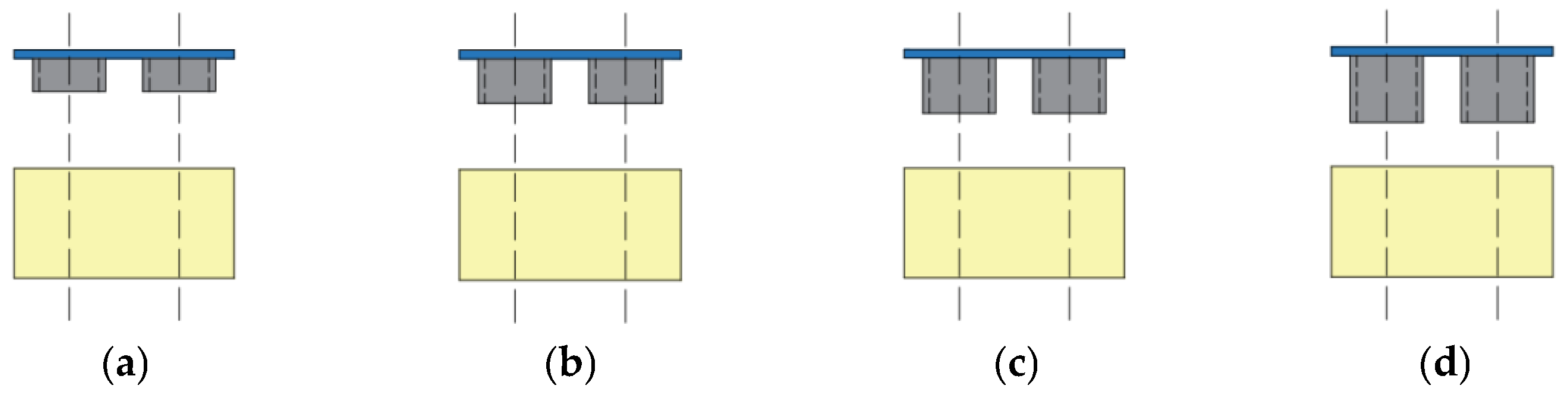
2.1. Geometric Model

The simulation is based on the actual measurements carried out by Agathokleous et al. [22], and a model of a single ventilated PV wall panel with dimensions of 600 mm (width) × 1200 mm (height) is designed to study its cavity structure. The ribs are supported by the cavity frame. For simulation simplicity, the support frame is omitted, allowing us to focus on the heat exchange driven by airflow and inlet air temperature without adding structural complexity. Taking the curved-ribbed cavity structure of the PV panel as an example, the PV wall panel is simplified into four main parts: the PV panel, the self-insulated wall, the ventilated cavity, and the curved ribs, where the thickness of the PV panel is 4 mm, the thickness of the self-insulated wall is 100 mm, and the thickness of the cavity is 100 mm. The geometric structure of the PV wall panel is presented in Figure 2, and the material parameters are shown in

Table 1. Material parameters of natural ventilation-type photovoltaic panels.

Geometry Name	Densities (kg/m3)	Specific Heat Capacity J/(kg·K)	Thermal Conductivity W/(m·K)
Photovoltaic panel	1500	1760	1.04
Self-insulating wall panel	550	1100	0.14
Atmosphere	1.177	1006.43	0.0242
Ribs (aluminum)	2719	900	202.4

.

The bottom and top of the cavity are directly connected to the external environment, where the bottom serves as the air inlet and the top as the air outlet. The cooling mechanism of the PV panel is based on the principle that when the temperature rises, the gas in the cavity accelerates due to buoyancy and is eventually discharged. This process creates a natural ventilation effect, which effectively takes away the thermal energy produced by the PV panels through the airflow in the air-cooled channel of the curved ribs, thus lowering their temperature and improving the photovoltaic conversion efficiency. In this paper, we will simulate and analyze the dimensions of the air-cooling channel through the CFD model to optimize the ventilation and heat dissipation effect of the curved-ribbed cavity structure and diminish the surface temperature of the PV panels.

The dimensional parameters of the curved ribs in the cavity structure of PV wall panels are composed of rib thickness (T), rib curvature (C), rib chord length (Y), rib chord height (X), rib width (Z), and rib spacing (S), as shown in Figure 3, in which rib curvature (C) is the ratio of the rib chord height (X) to the rib chord length (Y), which is used to characterize the bending laminarity of the ribs.

2.2. Mathematical Models

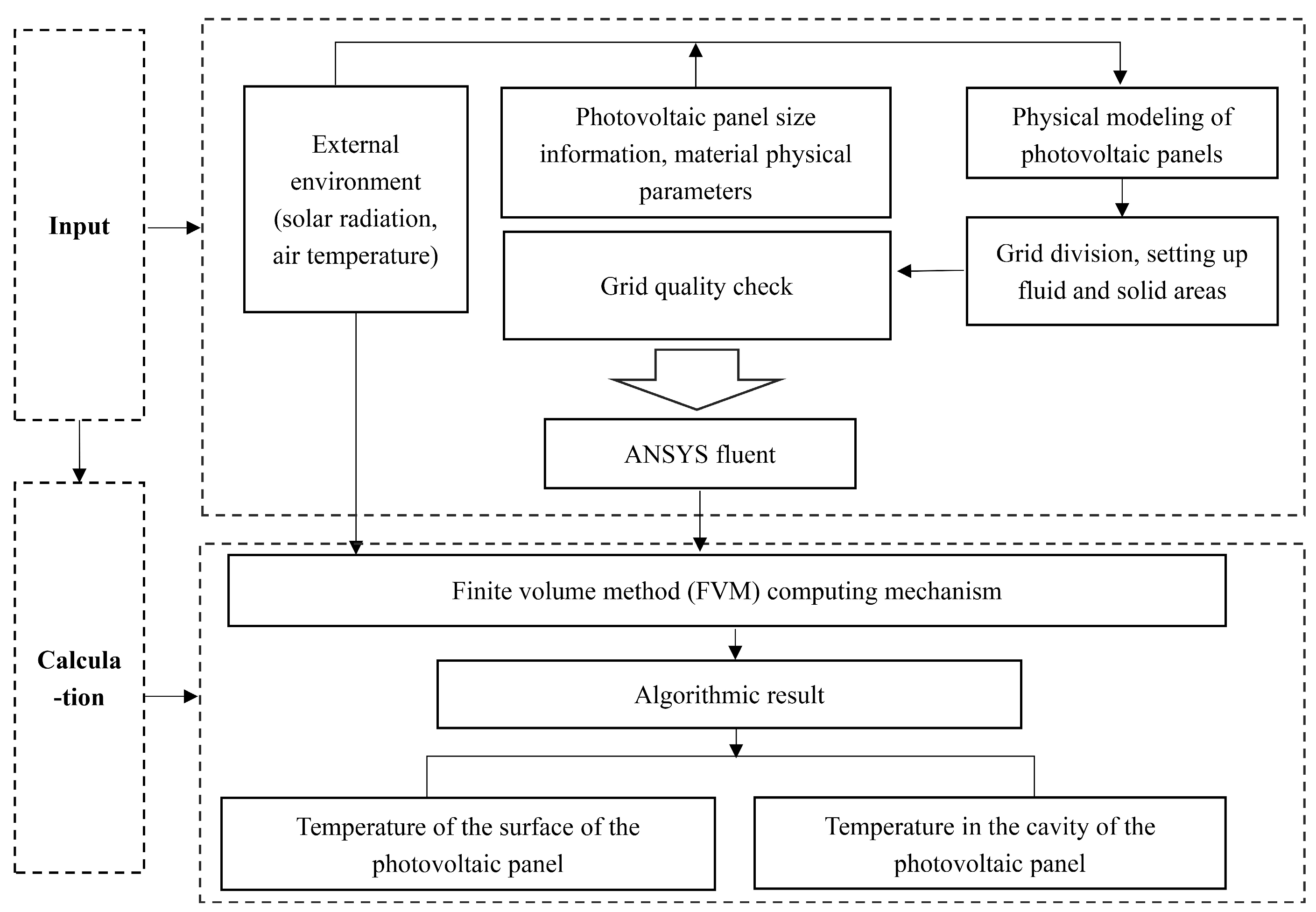
2.2.1. Computing Modules

In this study, a three-dimensional steady-state heat transfer model of ventilated photovoltaic wall panels was constructed using Fluent computational fluid dynamics software under ANSYS 2022 R1. The cavity structure of the ventilated PV wall panel is simulated and analyzed by Fluent software, and the impacts of different cavity structures on the ventilation and heat transfer performance of the ventilated PV wall panel are studied. The calculation flow is shown in Figure 4.

2.2.2. Assumptions and Boundary Condition

The numerical model is simplified appropriately to meet the prerequisites of the study, assuming that the airflow in the cavity is natural ventilation under thermal pressure and that all thermophysical parameters are fixed, except for the air density and temperature. The environmental boundary conditions adopt the parameters of the standard working conditions, set the solar radiation vertically and uniformly irradiated on the PV panels, and at the same time ignore the influence of air humidity on the temperature field inside the cavity, as well as the viscous dissipation between the air inside the cavity and the PV wall. The air density inside the cavity satisfies the Boussinesq assumption, meaning that for small density changes, the effect of density variation on the momentum equation can be neglected. Still, its effect on the buoyancy term is retained [23]. Here, ${\rho }_{amb}$ represents the air density at the ambient temperature $T_{amb}$(kg/m³), $\beta$ is the thermal expansion coefficient (1/K), and $\rho$ is the local density of the fluid, which varies with temperature and pressure. $T$ is the local fluid temperature. The difference in density with the ambient temperature produces a density difference and induces a motion of the fluid in the Boussinesq approximation. $g$ is the acceleration of gravity, which is approximately 9.81 m/s². The corresponding equation is as follows:

$$\left(\rho -{\rho }_{amb}\right)g=-{\rho }_{amb}\beta \left(T-T_{amb}\right)g$$

(1)

The effect of solar radiation absorbed by the PV cell is modeled as thermogenesis in the PV panel.

For the ventilated cooling channel, the boundary condition at both the inlet and outlet is defined by the environmental pressure, with the inlet and outlet temperatures set to the environmental temperature.

The no-slip is used for all wall surfaces. A hybrid boundary condition is set on the outer surface of the PV module including convective and radiative heat transfer. The natural convective heat transfer coefficient between the PV and the ambient is represented by Equation (2) [24], where $v_w$ is the ambient wind speed:

$$h_{out}=2.8+3.0v_w$$

(2)

The external radiant temperature is considered to be the temperature of the sky ($T_{sky}$), and the empirical formula widely used in the literature [25] is as follows:

$$T_{sky}=0.0522T_{amb}^{1.5}$$

(3)

2.2.3. Governing Equation

In the CFD simulation of PV wall panels, taking the above assumptions into account, the Navier–Stokes equation is as follows, where “f” refers to air and $\overrightarrow{V_f}$ is the velocity:

$${\displaystyle \frac{\partial {\rho }_f}{\partial t}}+\nabla ·\left({\rho }_f\overrightarrow{V_f}\right)=0$$

(4)

In the solid region, the energy transport equation is as follows:

$$\lambda \left({\displaystyle \frac{{\partial }^{2}T}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}T}{\partial y^2}}+{\displaystyle \frac{{\partial }^{2}T}{\partial z^2}}\right)+S_T=0$$

(5)

The momentum equation is as follows:

$${\displaystyle \frac{\partial }{\partial t}}\left({\rho }_f\overrightarrow{V_f}\right)+\nabla ·\left({\rho }_f\overrightarrow{V_f}\overrightarrow{V_f}\right)=-\nabla \mathrm{p}+\nabla ·\left(\begin{array}{c}=\\ \tau \end{array}\right)++{\rho }_f\overrightarrow{g}$$

(6)

In a flow field, heat transfer occurs due to the combined effects of convection and thermal conduction. However, in solid components (e.g., PV cells and walls), the heat transfer mechanisms are heat conduction and heat radiation. Therefore, the energy equation for the air in the gap as well as for the solid component can be expressed as follows:

$$\begin{array}{c}{\rho }_f{C}_{p,f}\left[{\displaystyle \frac{\partial T_f}{\partial t}}+\left(\overrightarrow{V_f}.\nabla \right)T_f\right]=k_f{\nabla }^2{T}_f\hfill \\ {\rho }_s{C}_{p,s}{\displaystyle \frac{\partial T_s}{\partial t}}=k_s{\nabla }^2{T}_s+S_h\hfill \end{array}$$

(7)

The subscripts “s” and “f” refer to the solid component and air, respectively. $k$ and $S_h$ are the thermal conductivity and heat source, respectively, and the heat source indicates the quantity of solar radiation taken in by each solid layer. The RNG k-ε model was used to describe the buoyancy-driven flow within the air gap [26]. Regarding the radiation, the discrete longitudinal coordinate radiation model DO (Discrete Ordinate) [27] was used.

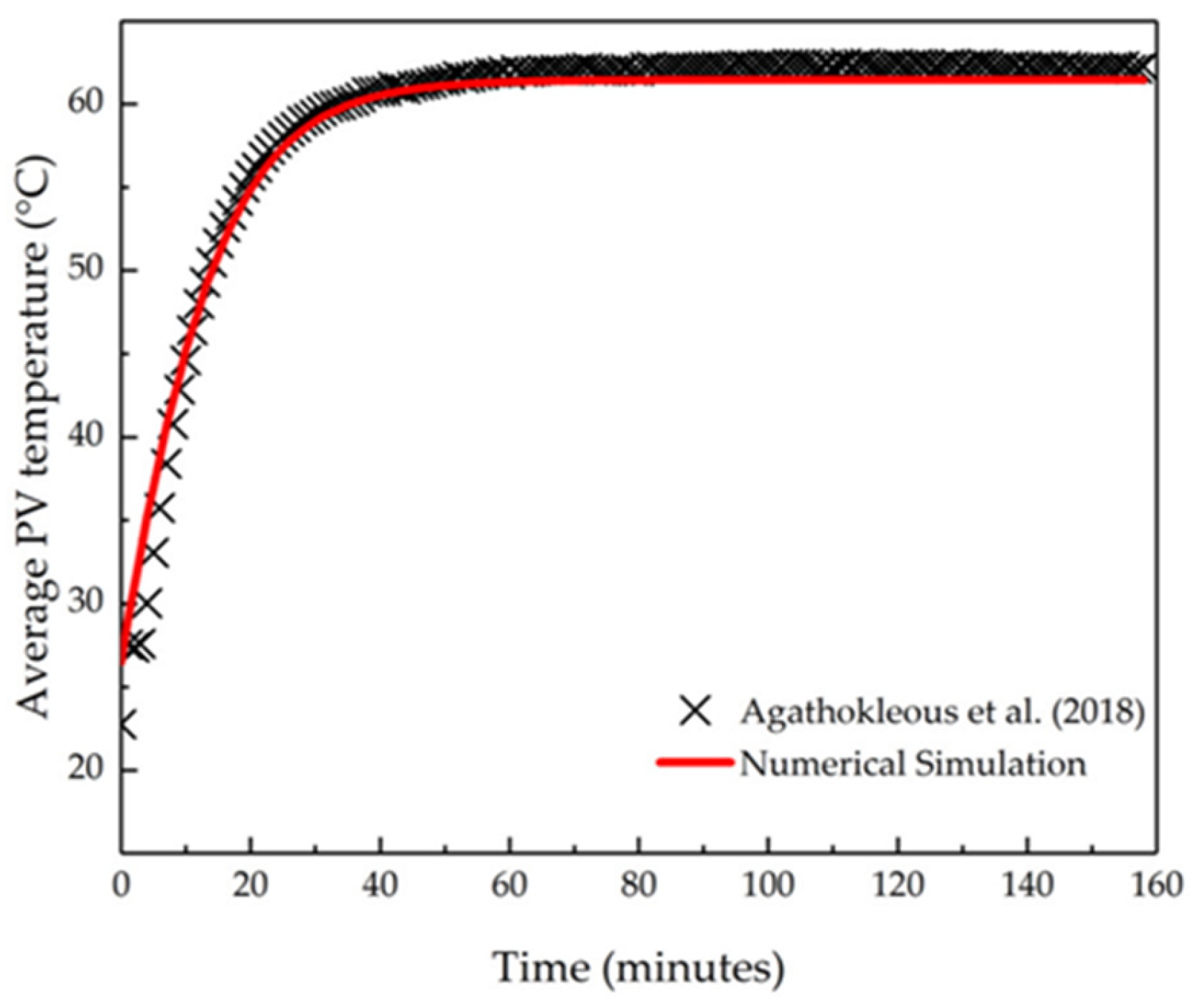
2.3. Model Validation

To evaluate the accuracy of the CFD model constructed in this study, the simulation results are analyzed and compared with the experimental data examined by Agathokleous et al. [22]. The experiments were carried out in a controlled indoor environment with a constant solar irradiance of 800 W/m² for 2 h. This paper focuses on analyzing the heat transfer characteristics of naturally ventilated photovoltaic (PV) wall panels with different cavity structures. Figure 5 illustrates the comparison of the simulation and the experimental results.

The validation study was conducted using the ASHRAE Energy Measurement Guidelines [28], which use two parameters to establish the uncertainty of the model: the Normalized Mean Bias Error (NMBE) and the coefficient of variation of Root Mean Square Error (CVRMSE), corresponding to the equations shown in (8) and (9), where $y_s$ is the numerical simulation value, $y_{ref}$ is the experimental measurement value, ${\overline{y}}_{ref}$ is the mean value of the measurements, and n is the number of measurements.

$$NMBE=\sum _{i=1}^n(y_{s\left(i\right)}-y_{ref\left(i\right)})/({\overline{y}}_{ref}\times n)\times 100$$

(8)

$$CVRMSE=\left[\sqrt{\sum _{i=1}^n{(y_{s\left(i\right)}-y_{ref\left(i\right)})}^2/n}\right]/{\overline{y}}_{ref}\times 100$$

(9)

As can be seen in Figure 5, there is a high degree of agreement between the calculated results and the experimental data. The NMBE and CVRMSE values for the average surface temperature of the PV panel are −0.79% and 1.93%, both falling within the acceptable range outlined in the ASHRAE guidelines. Consequently, the proposed CFD model is validated, confirming its reliability for analyzing the heat transfer characteristics of ventilated PV wall panels.

3. Results and Discussion

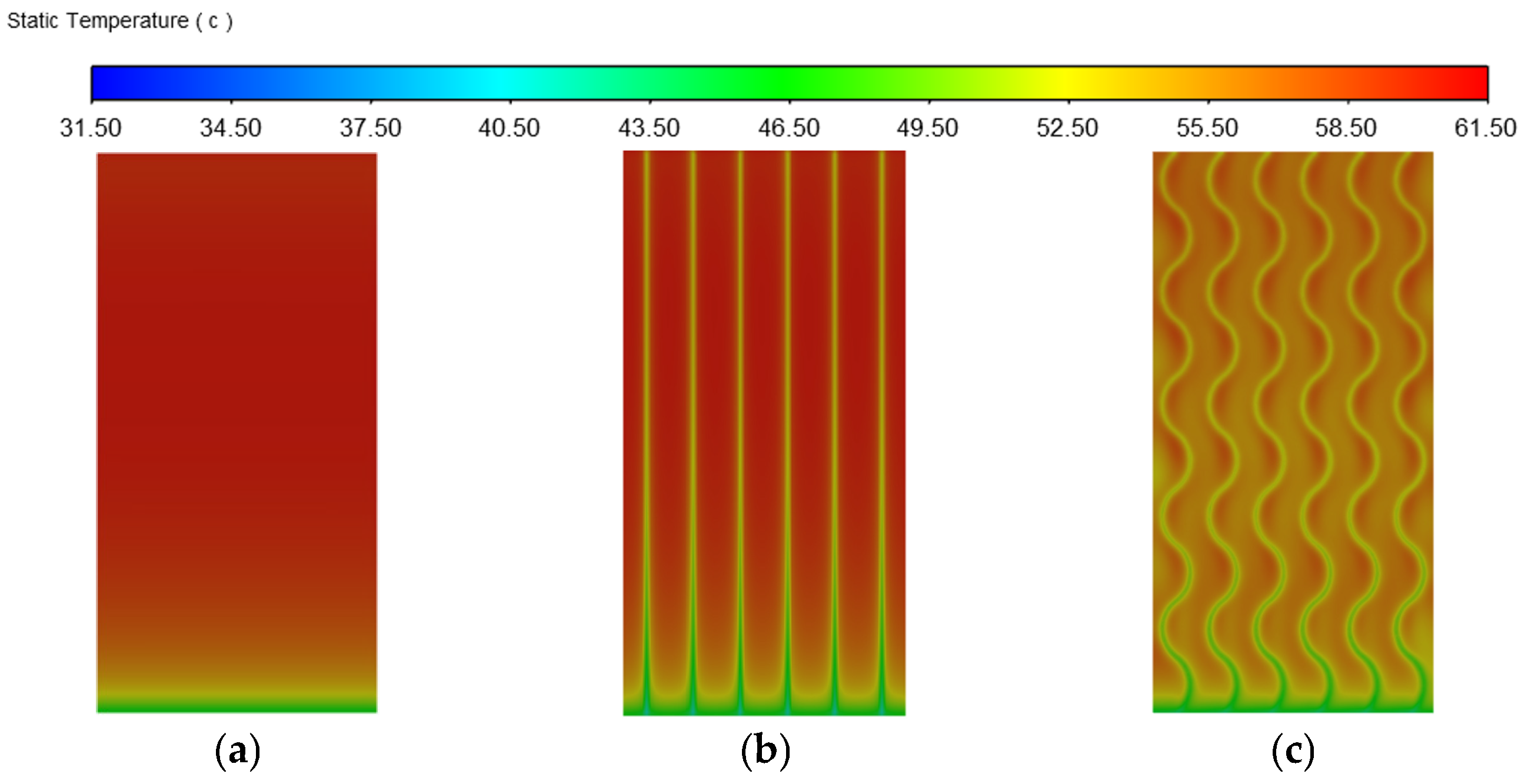
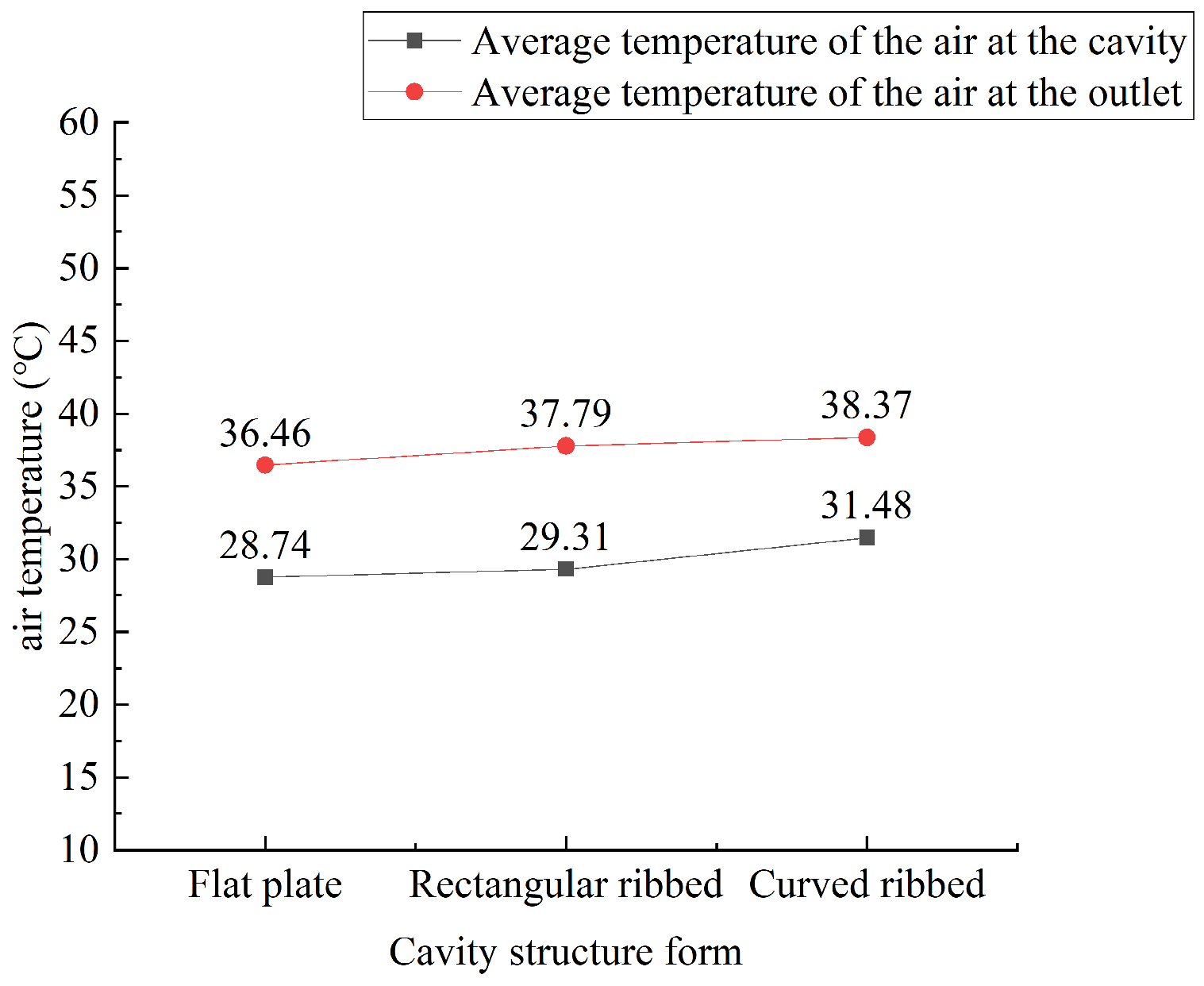
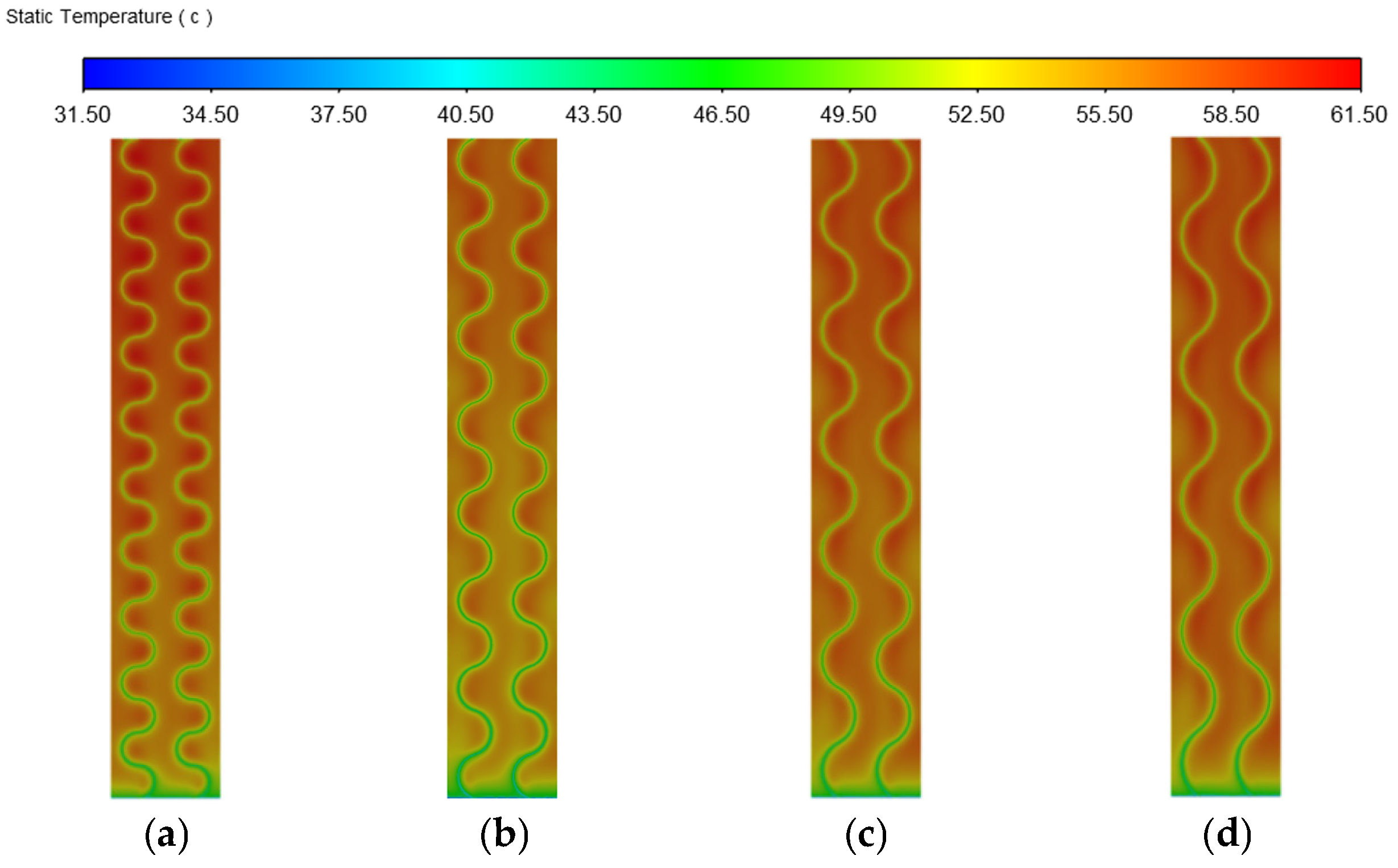
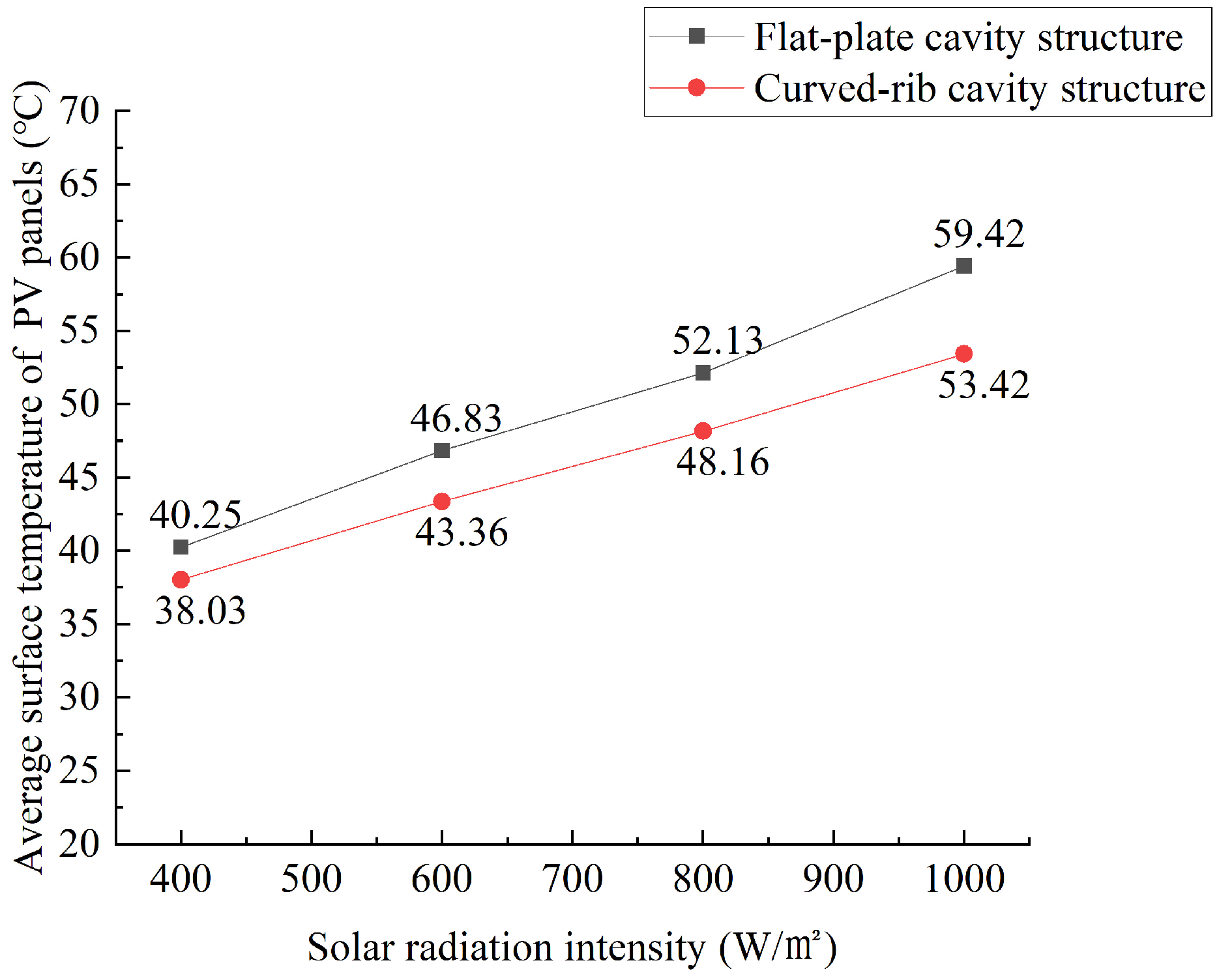
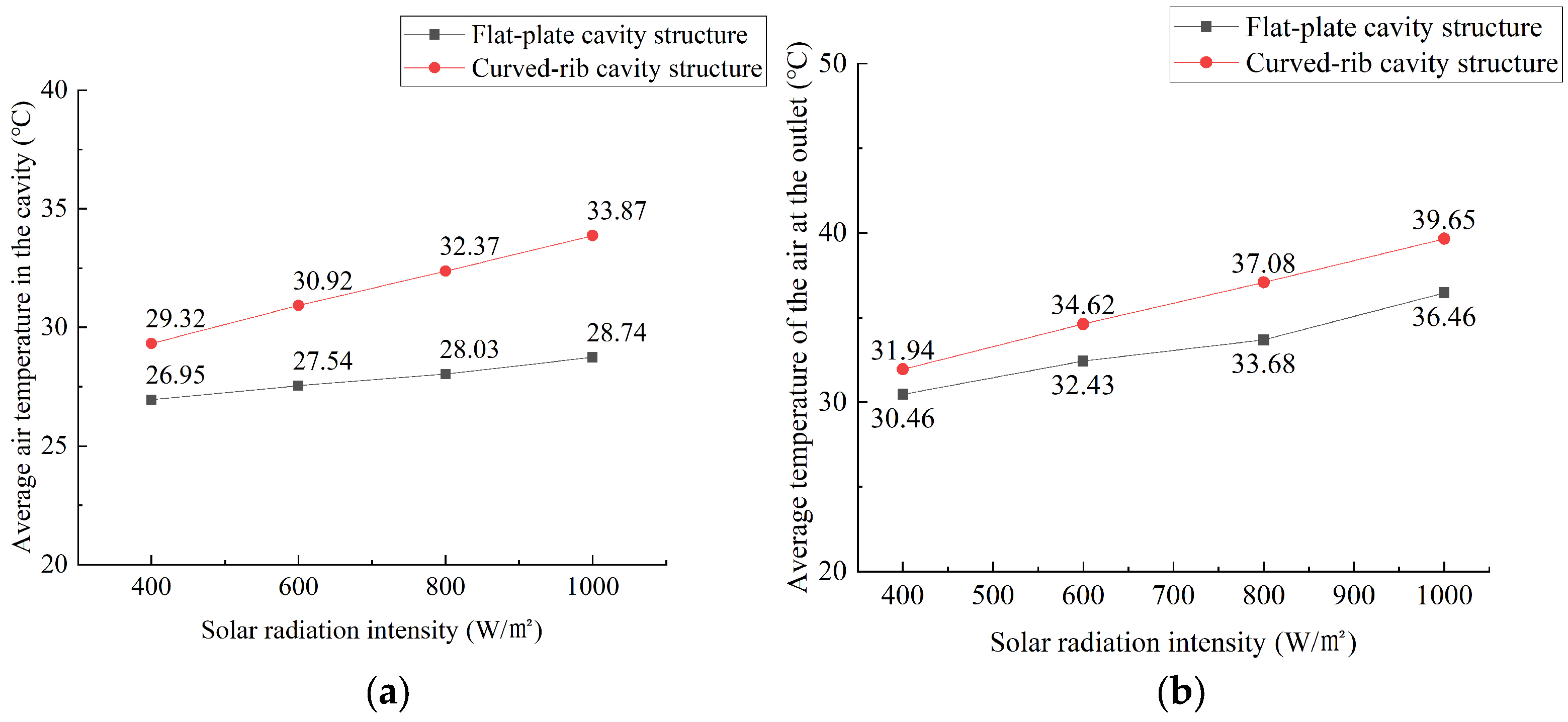
3.1. Comparative Analysis of Different Cavity Structures

The flat-plate cavity structure of PV wall panels is one of the most common practices in practical engineering, while the practice of installing ribs in the cavity is common in solar air collectors. For the curved-ribbed cavity structure proposed in this paper, a comparative study with other structural forms of photovoltaic panels is carried out, and the model established is shown in Figure 6, and the parameter settings of rectangular ribs and curved ribs are shown in

Table 2. Geometrical parameters of ribs in cavity structures.

Type of Rib	Chord Length (mm)	Chord Height (mm)	Spacing (mm)	Width (mm)	Thicknesses (mm)
Rectangular ribs	-	-	100	30	2
Curved ribs	120	30	100	30	2

.

By simulating and analyzing the ventilated PV wall panels with flat-plate, rectangular-rib, and curved-rib cavity structures, the temperature cloud diagrams are obtained, as shown in Figure 7. This figure shows the temperature distribution on the surface of the PV panels under the three cavity structures. The two main wall surfaces in the flat-plate cavity structure are flat walls, and the temperature at the entrance is lower; the installation of rectangular ribs in the flat-plate cavity structure plays a certain role in the heat dissipation of the PV panels, but it is mainly concentrated at the bottom of the PV panels, and the effect is not obvious; the installation of curved ribs in the flat-plate cavity structure is more obvious in the heat dissipation of the PV panels, and it has a better effect on the whole PV panel.

From the data in Figure 8, it can be seen that the overall temperature on the surface of the PV panels with a flat-plate cavity structure is the highest, with an average temperature of 59.42 °C; the temperature of the PV panels with a rectangular-ribbed cavity structure has been reduced to 57.56 °C; and the installation of curved ribs in the cavity structure has the best cooling effect, with an average temperature of 55.39 °C, which is a reduction in temperature of about 4 °C compared to the temperature of the PV panels with a flat-plate cavity structure. Figure 9 shows the temperature change of air in ventilated PV wall panels with different cavity structure forms. Comparison of the data shows that the air temperature in the flat-plate cavity structure is the lowest, and the installation of rectangular ribs in the flat-plate cavity structure can increase the air temperature in the cavity, and when the rectangular ribs are replaced with curved ribs, the air temperature in the cavity can be further increased. Simulation results show that the installation of curved ribs of a certain size in the flat cavity structure can increase the average temperature of the air in the cavity by 2.74 °C, and the average temperature of the air at the exit of the cavity can be increased by 1.91 °C. Therefore, the use of photovoltaic panels with curved ribs can take away the heat from the photovoltaic panels more effectively.

So, the curved-ribbed cavity structure PV wall panels can effectively reduce the temperature of the PV panels and have the best heat dissipation effect.

3.2. Parameter Setting and Optimization Study of Curved-Rib Cavity Structure

3.2.1. Parameter Setting of the Curved-Rib Cavity Structure

The simulation analysis and optimization of the curved-ribbed cavity structure is carried out using the established CFD simulation model. The simulation analysis is divided into five groups, and the curvature (chord height (X)/chord length (Y)), chord height (X), rib width (Z), and rib spacing (S) of the curved ribs are investigated in Groups 1 to 4, respectively, and the basic dimensional parameter data of their cases are presented in

Table 3. Simulation parameters of curved-rib cavity structure unit.

Case	Rib Curvature (Chord Height/Chord Length)	Chord Height (mm)	Rib Width (mm)	Rib Spacing (mm)
Case 1	1/2 3/8 3/10 1/4	30	30	100
Case 2	3/8	22.5 30 37.5 45	30	100
Case 3	3/8	30	30 40 50 60	100
Case 4	3/8	30	40	60 80 100 120

. The fifth group of models mainly investigates the impact of the curved-rib cavity structure on the ventilation and heat transfer of PV wall panels under different solar radiation intensities. The environmental parameter conditions of this PV wall panel are based on STC standard working conditions, and in the setting of environmental boundary conditions, the solar radiation intensity is 1000 W/m², and the ambient temperature is 25 °C.

3.2.2. Optimization Study of Curved-Rib Cavity Structure

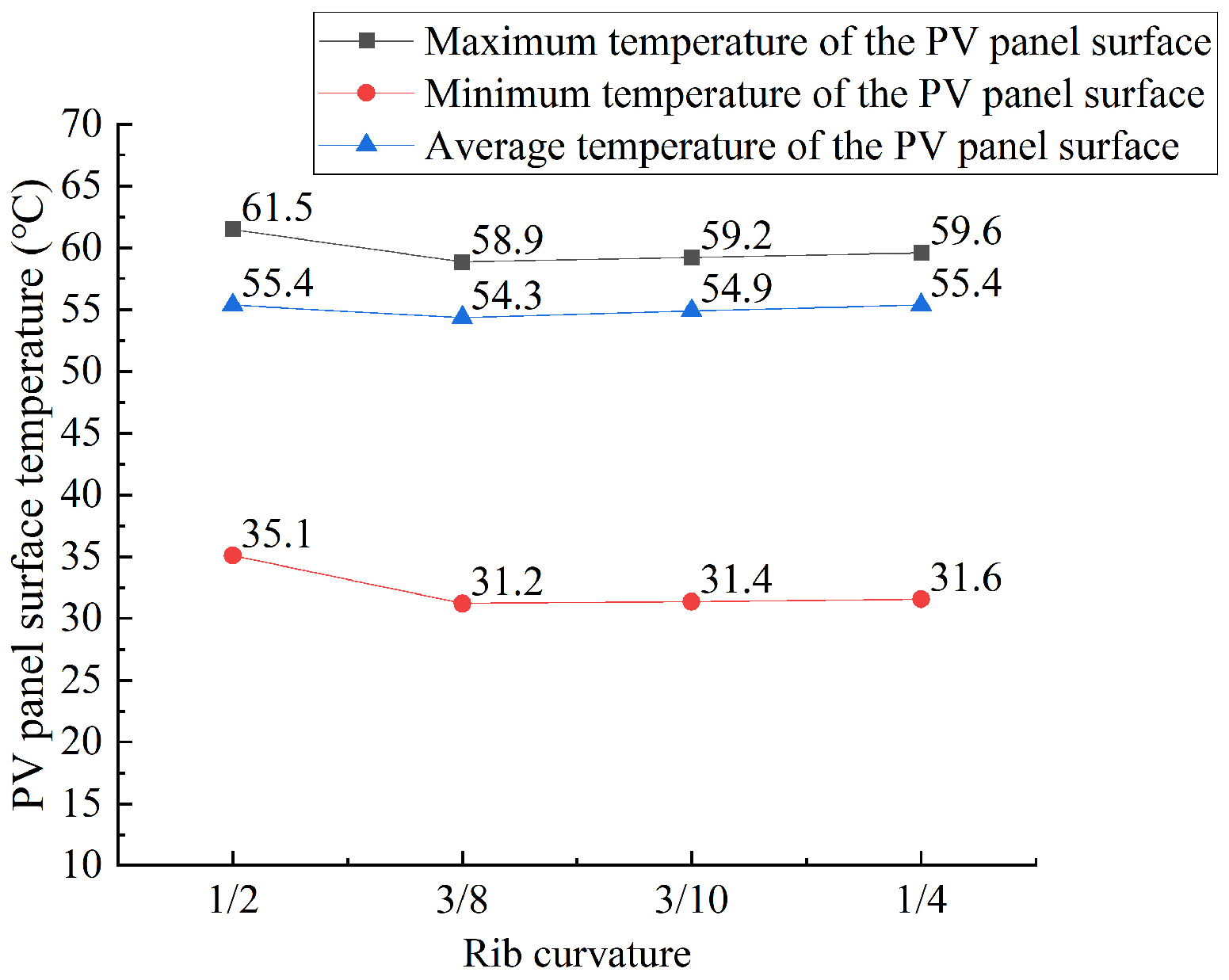
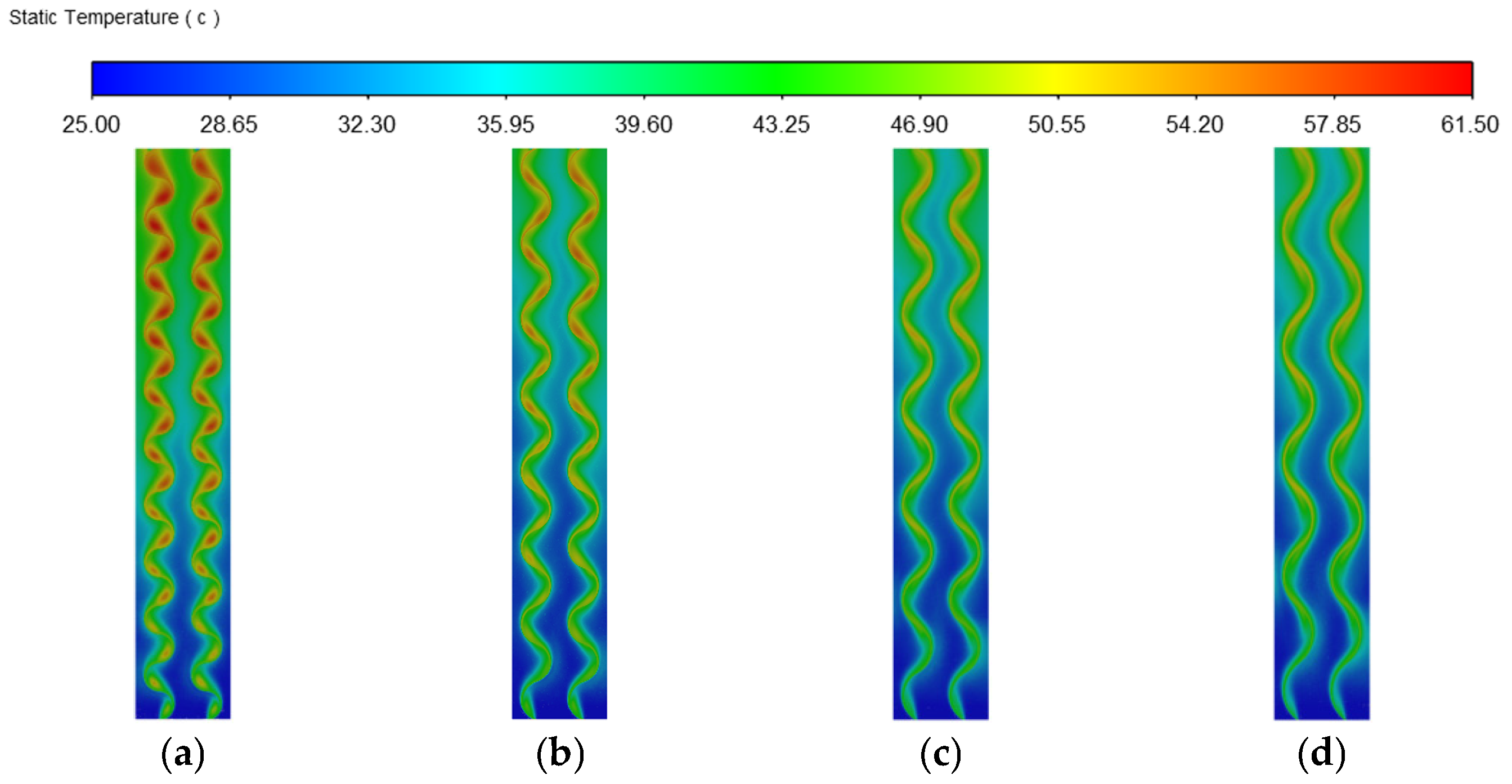
Effect of Different Rib Curvatures

To investigate the impact of rib curvature on the ventilation and heat transfer of PV wall panels, this section simulates and analyzes four sets of geometric models with rib curvature (C) of 1/2, 3/8, 3/10, and 1/4 based on the CFD three-dimensional steady-state heat transfer model established in the previous section, and the chord lengths and chord heights of the ribs are parameterized as shown in Table 3.

Through the simulation analysis, the temperature distribution cloud map of the PV panel surface is obtained as presented in Figure 10. The high-temperature region on the surface of the PV panel is mainly concentrated between the concave surfaces of the ribs, while the temperature is lower in the region of the convex surface of the ribs; with the decrease in the rib bending degree, the local high-temperature region is relatively reduced, which indicates that the appropriate rib bending degree helps to improve the heat dissipation performance.

Figure 11 demonstrates the effect of ribs with different curvatures on the surface temperature of the PV panels. The data analysis shows that among the four types of ribs simulated, the temperature is the lowest when the rib curvature is 3/8, with an average temperature of 54.34 °C, while the average temperature increases to 55.4 °C when the rib curvature is 1/2, at which time the surface temperature of the PV panel is the highest. Therefore, different rib curvatures will lead to differences in the surface temperature of the PV panel, which in turn affect its cooling effect.

The temperature contour map at position 1-1 of the cavity structure with different rib curvatures (the location is detailed and labeled in Figure 3) is shown in Figure 12. From Figure 12, it can be seen that there is a significant difference in the local air temperature under different rib bending conditions. The high temperatures are mainly concentrated on the concave side of the rib, and the temperature on the convex side is relatively low. As the rib bend decreases, the local high-temperature phenomenon is alleviated, which indicates that too large a rib bend will make the hot air on the concave surface not easy to dissipate, which in turn affects the heat dissipation performance of the PV panel; when the rib curvature is too small, the air temperature around the rib decreases, making it difficult for the airflow to effectively carry away heat from the photovoltaic panel. This phenomenon indicates that excessively small rib curvature hinders heat exchange between the air and the rib, reducing the overall cooling efficiency. Therefore, selecting an appropriate rib bending degree is crucial for optimizing the heat transfer effect.

Therefore, according to the above analysis, when the rib bending degree is 3/8, the PV panel reaches a better state, the average temperature is the lowest, and the cooling effect is significant.

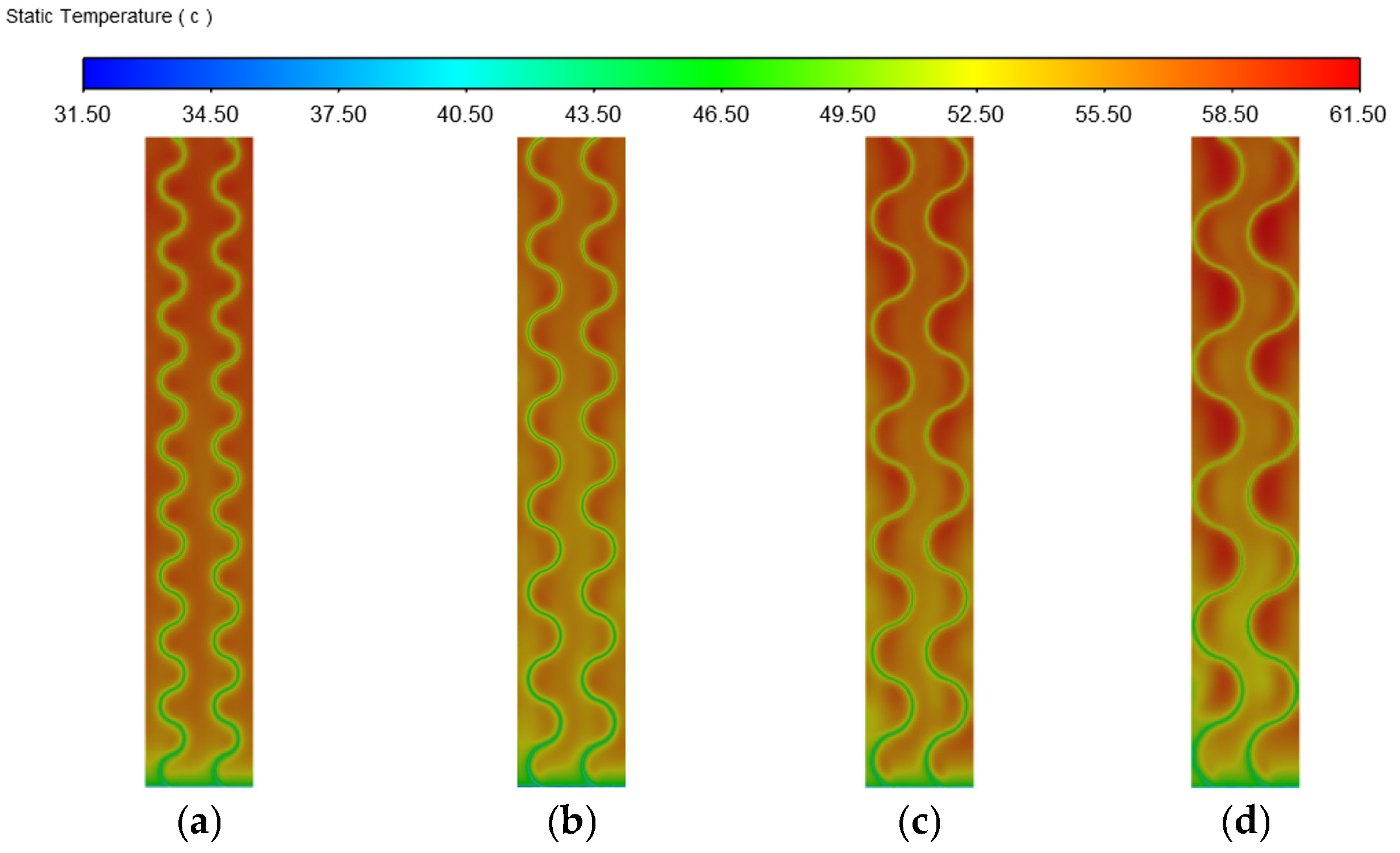
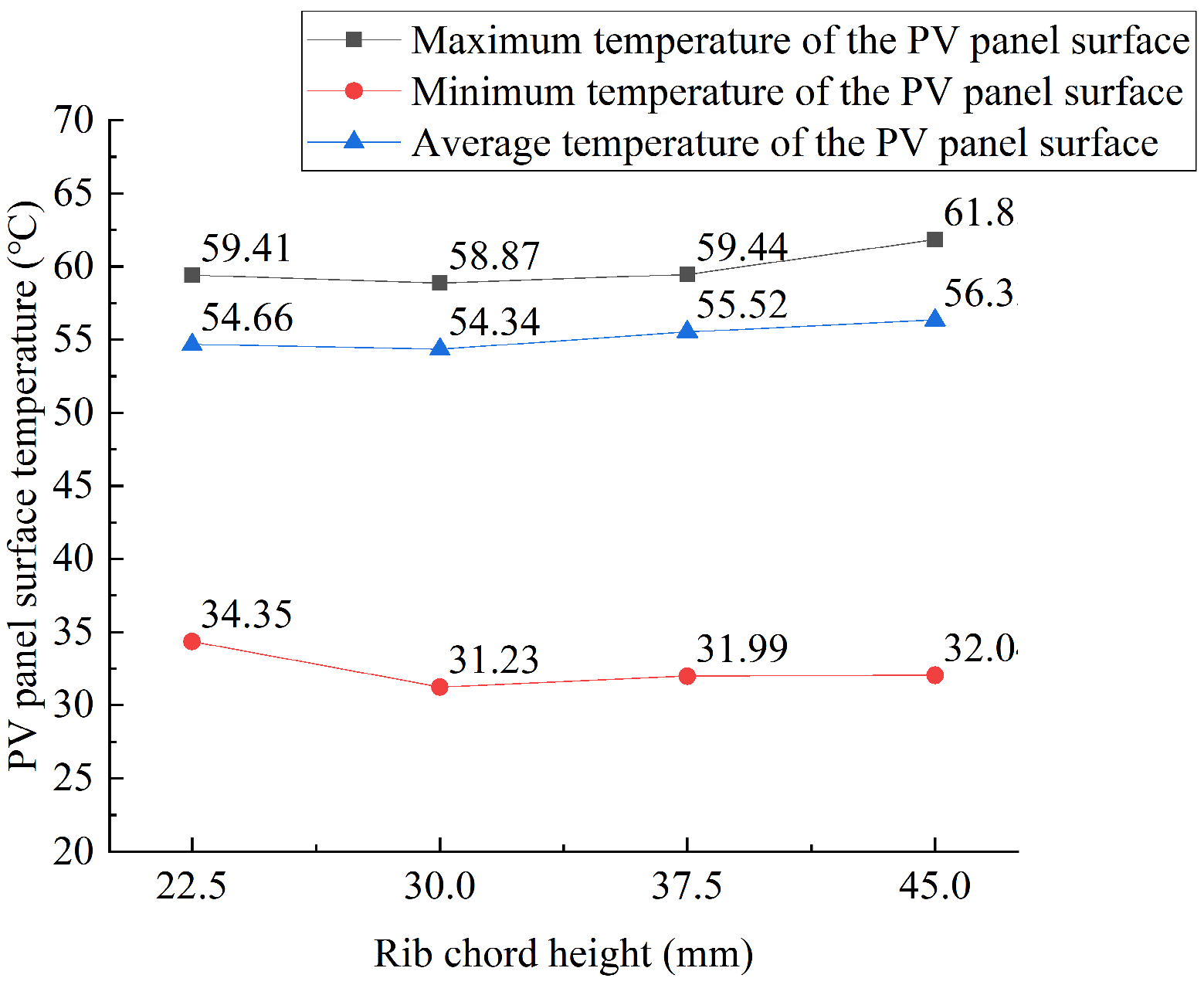
Effect of Different Rib Chord Heights

To study the influence of rib chord height on the ventilation and heat transfer of PV wall panels, the rib bending is fixed to 3/8, and the CFD three-dimensional steady-state heat transfer model is used to simulate and analyze four groups of ribs with different chord heights, with specific dimensions of chord length × chord height of 60 × 22.5 mm, 80 × 30 mm, 100 × 37.5 mm, and 120 × 45 mm, respectively.

Through the simulation analysis, the temperature cloud diagram shown in Figure 13 is obtained, which shows the temperature distribution on the surface of the PV panel under different rib chord heights. From the figure, it can be seen that when the chord height of the rib is larger, the local temperature of the PV panel surface increases significantly, and the high-temperature region is mainly concentrated between the concave surfaces of the ribs, while the convex surfaces of the ribs have relatively lower temperatures. As the rib height decreases, the rib chord length also decreases, resulting in a relative reduction in the local temperature of the photovoltaic panel. The best effect is observed when the rib height is 30 mm.

Figure 14 shows the impact of the cavity structure unit on the surface temperature of the PV panels under different rib chord heights. From the line graph, it can be observed that the temperature of the PV panel surface reaches the lowest point, i.e., 31.23 °C, when the rib chord height is 30 mm, which shows the optimal cooling effect; and the surface temperature of the PV panels is the highest when the rib chord height is 45 mm, which shows the most unsatisfactory cooling effect. Therefore, under different rib height settings, variations in the surface temperature of the photovoltaic panel occur, and the cooling effect also changes.

The temperature cloud images of the 1-1 cross-section location of the cavity structure are further analyzed, as shown in Figure 15. Observation of these images reveals that under the same bending condition, the change in the chord height of the ribs causes a change in the chord length, which affects the air temperature distribution inside the cavity. The ribs play a cooling role by enhancing the convective heat transfer efficiency between the air and the PV panel as well as the ribs. However, if the high-temperature air in the concave region fails to exchange with the low-temperature air in the convex region in time, localized overheating will be formed. Therefore, in the case of fixed rib curvature (3/8), the selection of the appropriate chord height is essential to ensure the effective exchange of hot and cold air.

Through the above analysis, it can be seen that when the rib chord height is 30 mm, the average temperature on the surface of the PV panels reaches the lowest level, which shows a good cooling effect, indicating that the reasonable configuration of the rib chord height and chord length can play a positive role in the thermal dissipation process of the PV panels.

Effect of Different Rib Widths

To investigate the impact of rib width on the ventilation and heat dissipation performance of the cavity structure, the fixed rib curvature is 3/8, the rib chord height × chord length is 30 mm × 80 mm, and four groups of ribs with different widths are simulated and analyzed, and the specific dimensions of the rib widths are 30 mm, 40 mm, 50 mm, and 60 mm, respectively. The other parameters are provided in Table 3, and the simulated top view of the cavity structure unit of the photovoltaic panels is shown in Figure 16.

Through the simulation analysis, the temperature cloud diagram shown in Figure 17 was obtained. From the figure, it can be seen that with the gradual increase in the width of the rib, the local temperature changes; when the width of the rib increases to 50 mm and 60 mm, the local temperature of the concave area of the rib rises significantly, and in the rib width of 40 mm, the local temperature of the PV panel surface is the lowest, which shows a more desirable cooling effect. Therefore, the width of the cooling ribs should be moderate, avoiding too large or too small a width.

Figure 18 shows the effect of the cavity structure unit on the surface temperature of the PV panel at different rib widths. As can be seen from the line graph, when the rib width is set to 40 mm, the average temperature is about 0.4 °C lower compared to the case with a rib width of 60 mm, showing a better cooling effect. 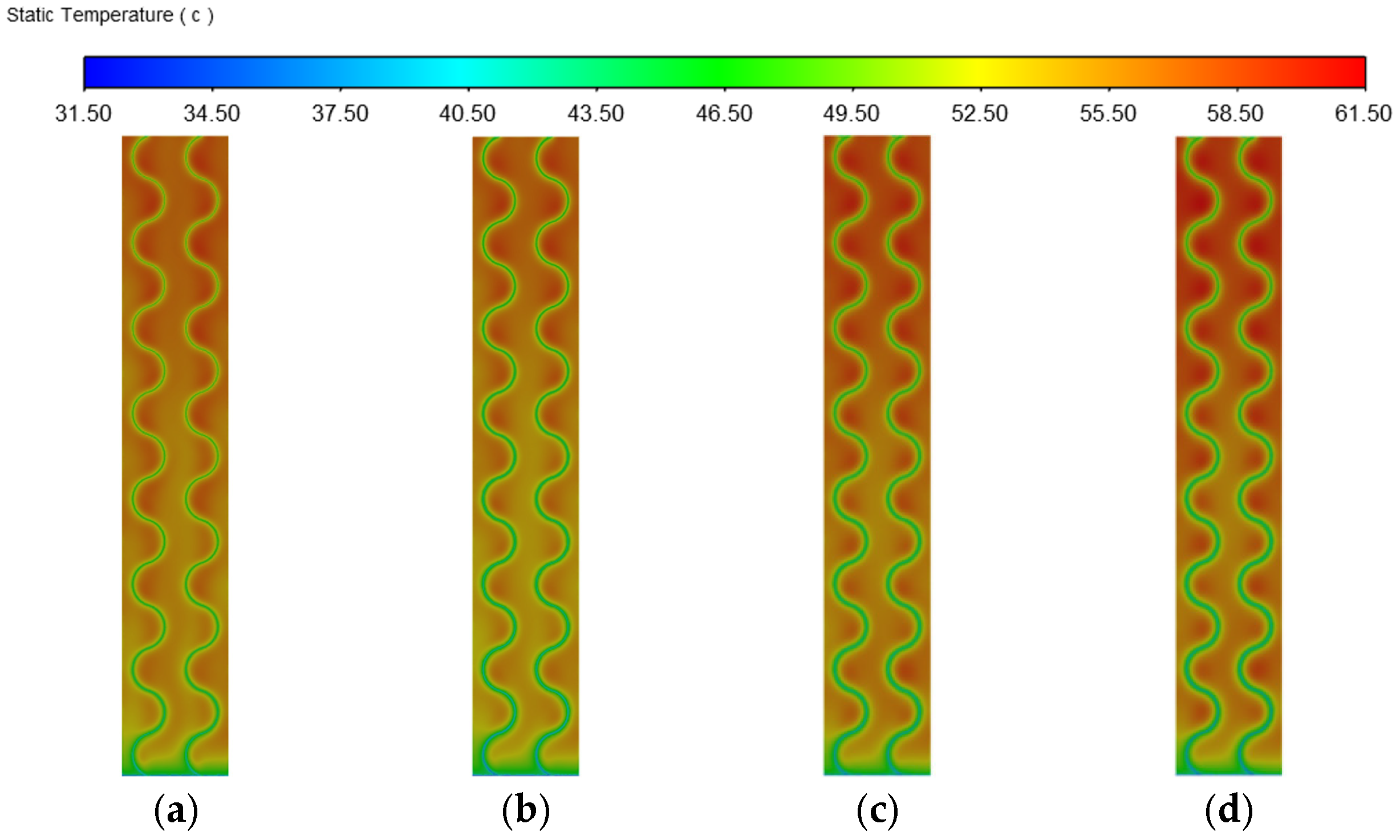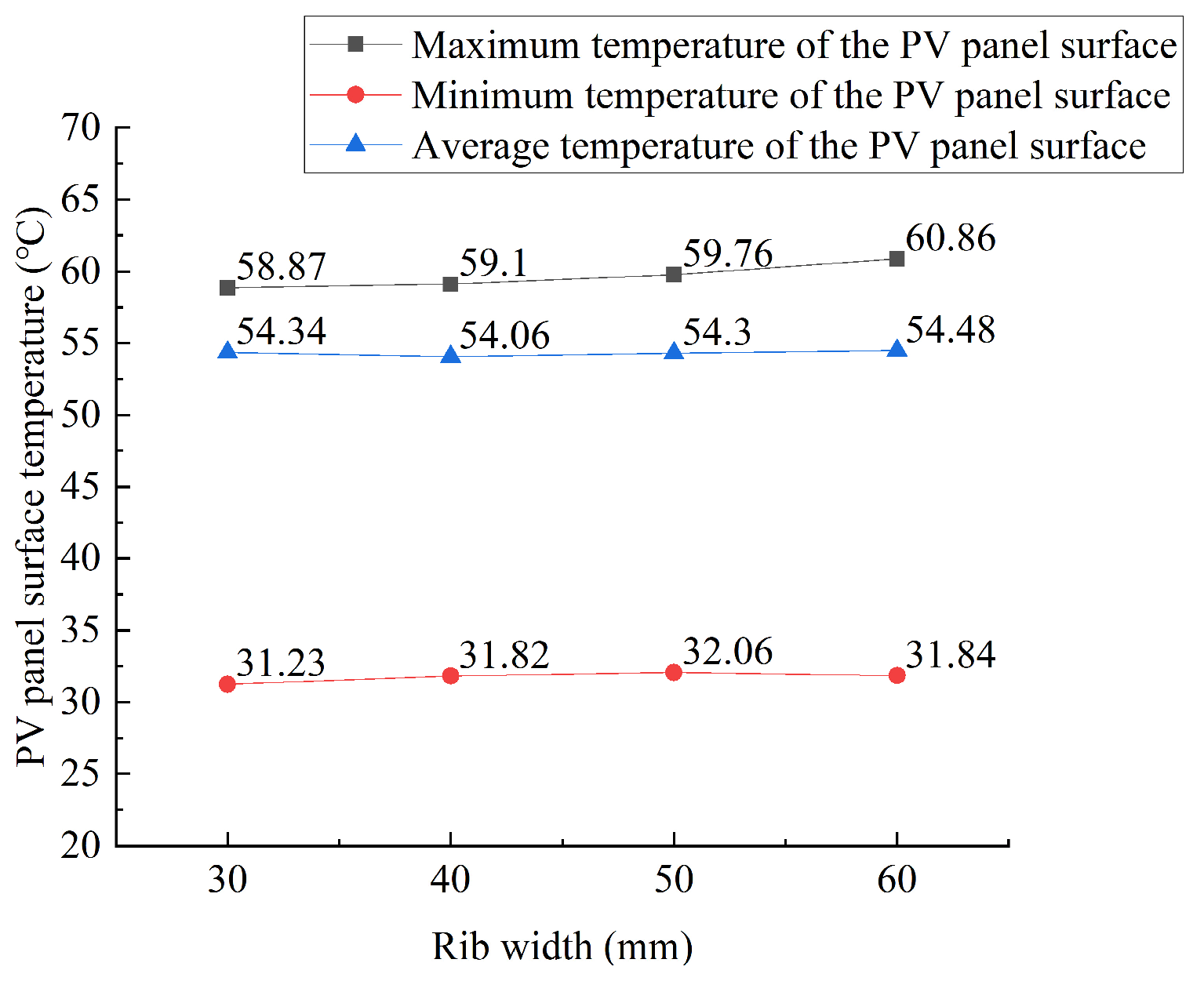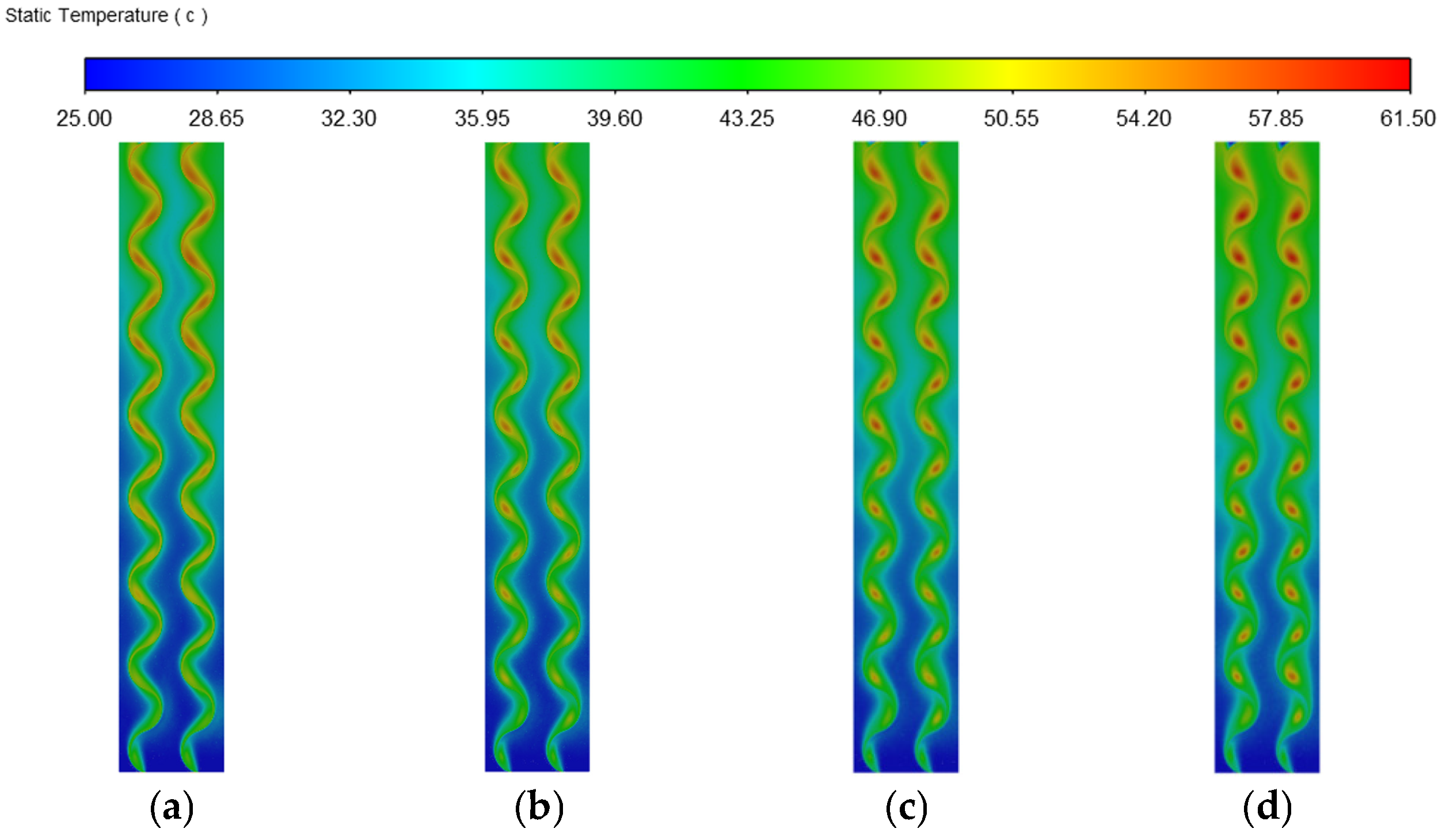Therefore, the temperature and cooling effect on the surface of the PV panels varies at different rib width settings.

As can be seen from Figure 19, there are differences in the temperature distribution of the curved-rib cavity structure at different rib widths. When the rib width is too large, the high-temperature phenomenon in the concave area is intensified, which indicates that too large a rib width will hinder the discharge of high-temperature air, whereas a rib width that is too small will result in insufficient heat exchange, thereby preventing the heat inside the voltaic panel from being discharged effectively.

From the above analysis, it can be seen that when the rib width is 40 mm, the average temperature on the surface of the PV panel reaches the lowest level, showing a better cooling effect, which indicates that the appropriate rib width has a beneficial impact in the heat dissipation process of the PV panel.

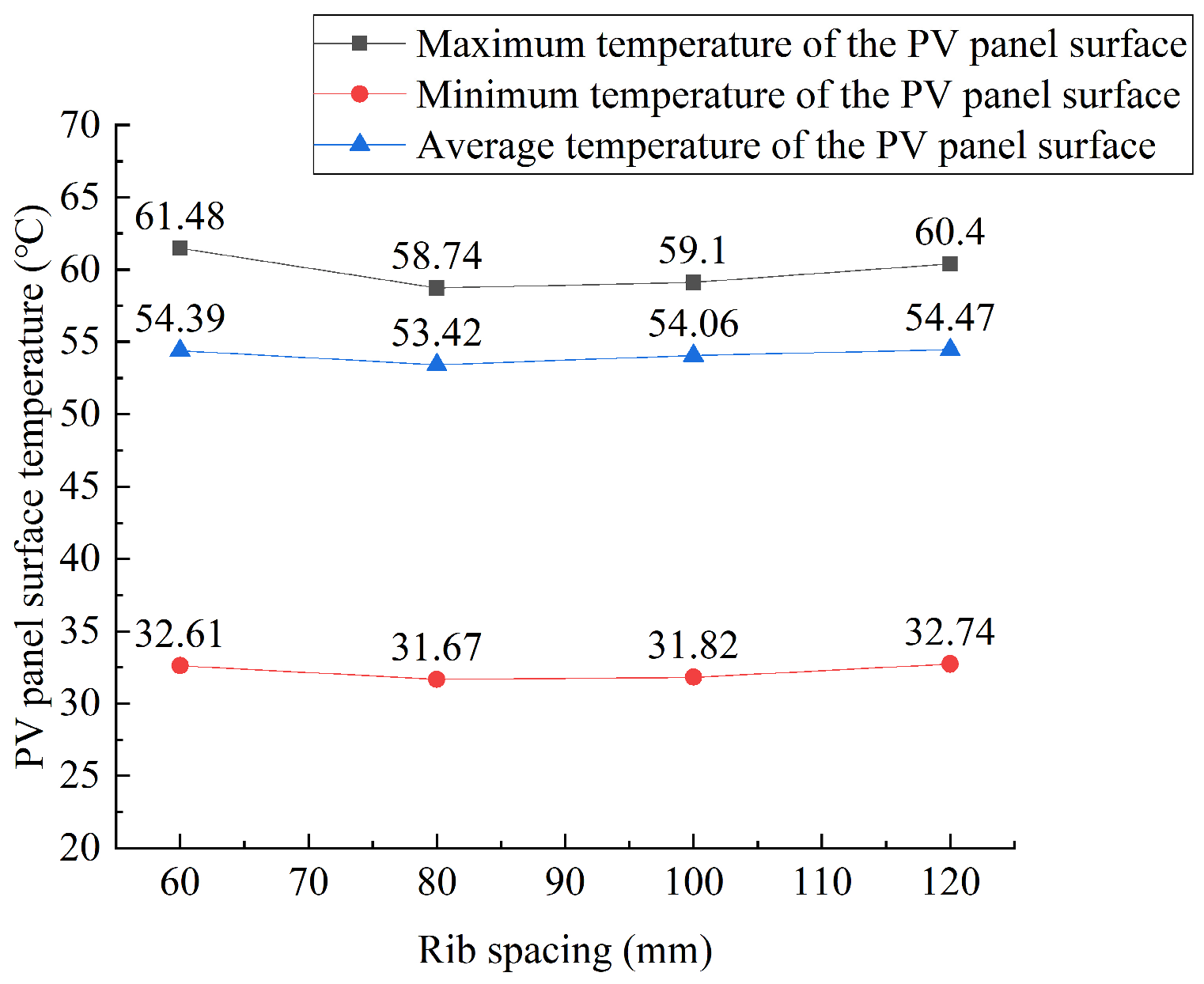
Effect of Different Rib Spacing

To investigate the impact of rib spacing on the ventilation and heat dissipation performance of the cavity structure, the fixed rib curvature is 3/8, the rib chord height is 30 mm, the rib width is 40 mm, and the CFD three-dimensional steady-state heat transfer model is used to simulate and analyze the photovoltaic wall panels with four groups of different rib spacings, with specific sizes of rib spacings of 60 mm, 80 mm, 100 mm, and 120 mm, respectively.

Through simulation and analysis, the temperature cloud diagram shown in Figure 20 is obtained. From the figure, it can be seen that the rib spacing is too large or too small, which is not conducive to the effective heat dissipation of the PV panel. When the rib installation spacing is too small, the dense arrangement of rows between ribs leads to significant localized high temperatures on the surface of the PV panel; when the rib installation spacing is too large, the overall temperature is high.

Figure 21 demonstrates the effect of cavity structure units with different rib spacings on the surface temperature of the PV panels. The data analysis shows that different rib spacings have different cooling effects. When the rib spacing is 80 mm, the temperature on the surface of the PV panel reaches the lowest point and the cooling effect is optimal, at which time the temperature is 53.42 °C, which is 1.1 °C lower than that when the rib spacing is 60 mm. Therefore, different rib spacing will lead to differences in the surface temperature of the PV panels, which in turn affects the cooling effect.

The temperature cloud at position 1-1 of the cavity structure is shown in Figure 22. The results show that when the arc-rib spacing is small, the local temperature of its concave surface increases significantly, resulting in the expansion of the high-temperature region, and as the rib spacing increases, the efficiency of air heat transfer within the cavity diminishes. Therefore, in order to give full play to the disturbance efficiency of the curved ribs, it is necessary to set the rib spacing reasonably. The air temperature in the cavity structure of the curved rib with a spacing of 60 mm is too high, and the thermal transfer between the high-temperature air and the surrounding cold air is difficult, which is not conducive to the heat dissipation of the photovoltaic wall panels. The rib spacing of 80 mm and 100 mm can realize a heat dissipation effect.

In summary, the curved-rib cavity structure with 60 mm spacing has the problem of insufficient heat exchange, which is not conducive to the heat dissipation of PV wall panels. When the rib spacing is 80 mm and 100 mm, the overall temperature on the surface of the PV panel is low, and there is no obvious local high temperature, so the cooling effect is better.

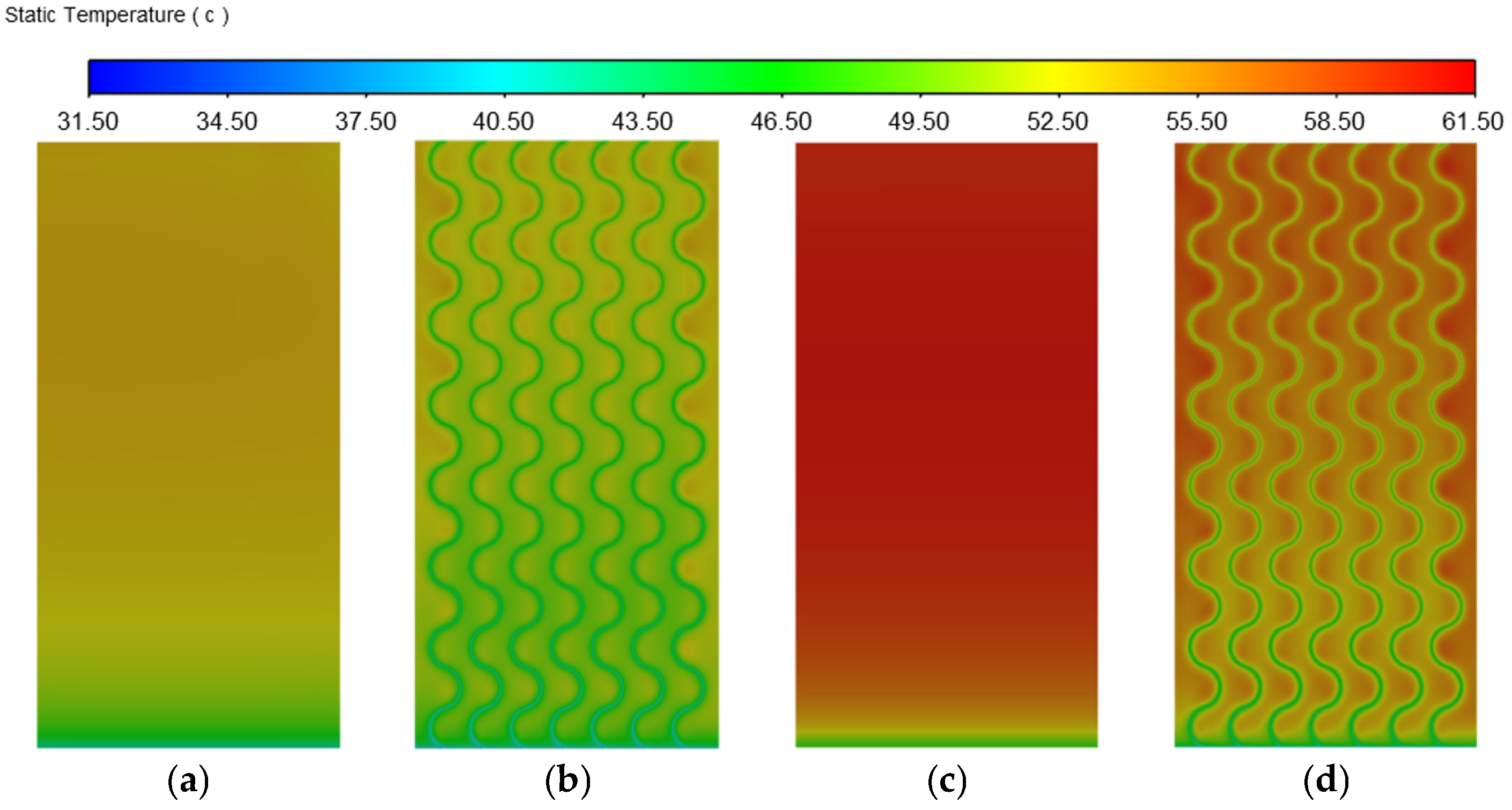
3.2.3. Effects of Solar Radiation Intensity

To investigate the impact of solar radiation intensity on the heat transfer performance of PV wall panels, CFD three-dimensional steady-state modeling was used to conduct comparative simulation experiments on two kinds of PV panels. The dimensions of the PV panels are all 600 mm × 1200 mm, and other material parameters are shown in Table 1. One of the PV wall panels is a flat plate structure without curved ribs in the cavity, and the other is an optimized structure with curved ribs in the cavity. The specific parameters of the curved-rib cavity structure are set as follows: rib curvature 3/8, chord height 30 mm, chord length 80 mm, width 40 mm, and mounting spacing 80 mm, and its geometric structure is shown in Figure 23: Schematic diagram of cavity structure of ventilated photovoltaic wall panels. The study sets the environmental temperature at 25°C and analyzes the temperature of the two types of photovoltaic panels under solar radiation strengths of 400 W/m², 600 W/m², 800 W/m², and 1000 W/m².

Through the simulation analysis, the temperature cloud diagram shown in Figure 24 is obtained, which shows the temperature distribution on the surface of PV panels with different cavity structures when the solar radiation intensity is 800 W/m² and 1000 W/m², respectively. The findings indicate that with the increase in solar radiation intensity, the surface temperature of both kinds of PV panels shows a gradual increase trend.

Figure 25 presents the variation in the average temperature of the PV panel surface of the ventilated PV wall panels under different solar radiation intensities. Simulation results show that, with the increase in solar radiation intensity, although the average temperature of the surface of the flat plate-type and the curved-rib cavity structure of the PV panel are both on the rise, the surface temperature of the PV wall panels with the curved-rib cavity structure is always lower than that of the flat plate-type PV wall panels, which suggests that installing a certain specification of the size of the curved ribs can effectively reduce the surface temperature of PV panels. When the intensity of the solar radiation is larger, the cooling effect is more significant. Specifically, when the solar radiation is 1000 W/m², the curved-rib cavity structure of the PV wall panels can be reduced by about 6 °C.

Figure 26a illustrates the average temperature change of the air within the cavity of the PV wall panels under different levels of solar irradiance. From the comparative data, it can be concluded that the installation of curved ribs in a flat cavity increases the air temperature inside the cavity by 2.37 °C, 3.38 °C, 4.34 °C, and 5.13 °C, respectively. It can be seen that the installation of curved ribs in the flat-plate cavity structure enhances the heat exchange capability of the air with the PV panels for heat exchange. Figure 26b shows the variation of the average air temperature at the outlet of the cavity of the PV wall panels under different solar radiation intensities. Comparison of the data shows that the addition of certain sizes of curved ribs in the flat-plate cavity increases the temperature of the air at the cavity outlet by 1.48 °C, 2.19 °C, 3.4 °C, and 3.19 °C, respectively, which suggests that more heat was carried away by the air with the addition of the curved ribs.

4. Conclusions

In this study, a CFD numerical model of ventilated PV wall panels is established by using ANSYS Fluent, and the simulation analysis is carried out by adding curved ribs into the air-cooling channel of the ventilated PV wall panels with a size of 600 mm (width) × 1200 mm (height), and the systematic simulation of different structural parameters of the ribs (curvature, chord height, width, and spacing) reveals the significant effect of each parameter on the ventilating and heat transfer performance of the PV wall panels. In addition, the thermal performance of the optimized curved-rib cavity structure is comparatively analyzed under different solar radiation intensity conditions to assess its influence on the cooling effect of PV wall panels. The conclusions of this study are as follows:

(1)

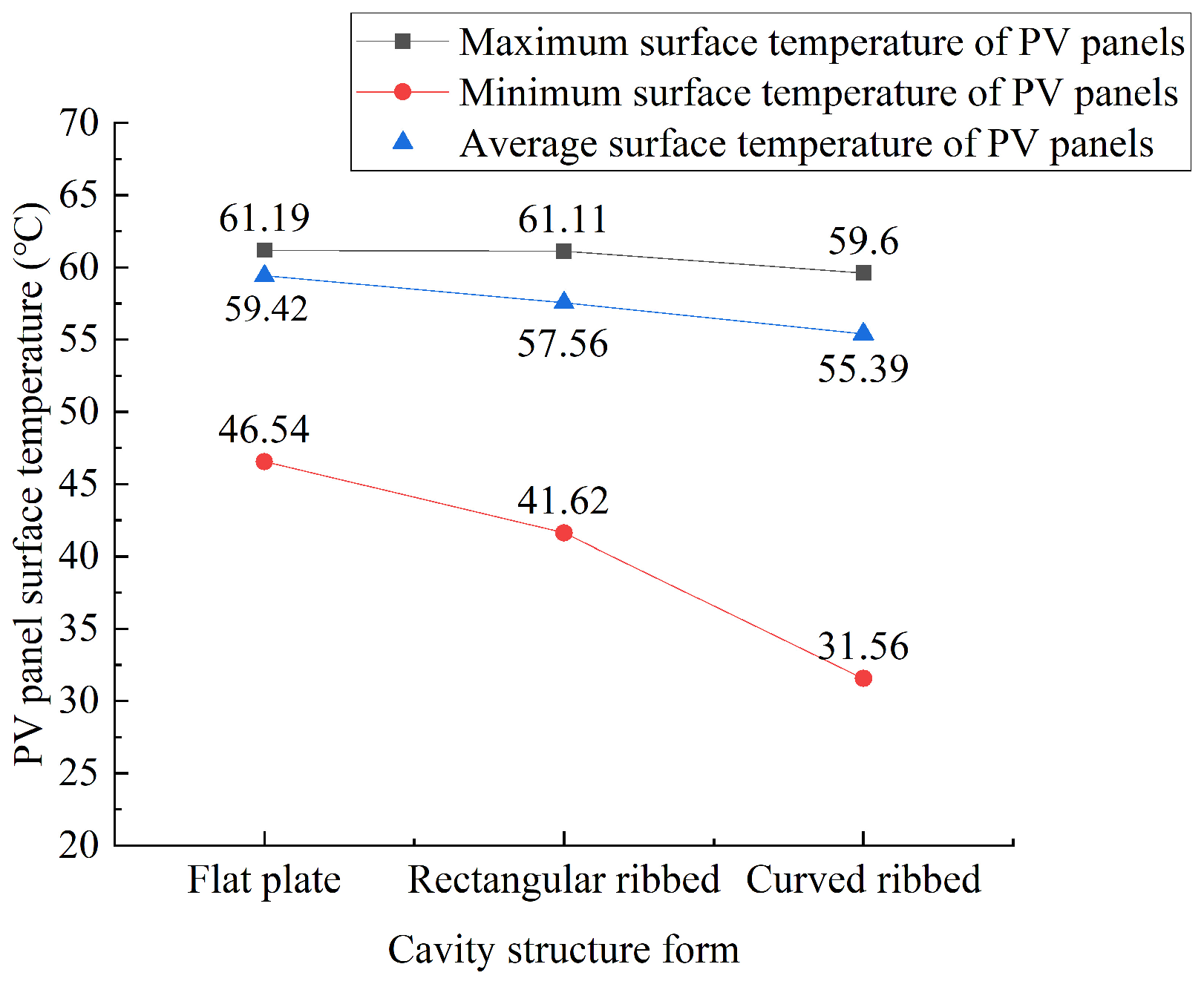
The average surface temperatures of the flat-plate, moment-ribbed, and arc-ribbed cavity structure PV wall panels under natural ventilation conditions are 59.42 °C, 57.56 °C, and 55.39°C, respectively. The arc-ribbed cavity structure PV wall panels have the best heat dissipation effect. This result aligns with previous studies on ventilated PV systems, which have demonstrated that structured modifications such as ribbing can enhance convective cooling and reduce operational temperatures.

(2)

When the rib curvature is 3/8, the heat dissipation of the photovoltaic wall panel is found to be relatively optimal. If the rib height or width is set too large or too small, it is not conducive to the heat dissipation of the photovoltaic wall panel. Based on the simulations conducted in this study, the performance is relatively better when the rib height is 30 mm and the width is 40 mm. If the rib spacing is too small, the arrangement is too compact, and the hot air cannot be expelled effectively. If the rib spacing is too large, the heat exchange within the cavity is insufficient. The optimal rib spacing is between 80 mm and 100 mm. However, it should be noted that this research only simulated a limited number of configurations and did not cover the full range of possible parameter combinations. Therefore, the results are indicative of favorable configurations in the simulation range.

(3)

Compared with the flat cavity structure of PV wall panels, the optimized curved-rib cavity structure can significantly reduce the average surface temperature of PV panels. With the increase in solar radiation intensity, the heat dissipation impact of the optimized structure is enhanced accordingly. When the intensity is 1000 W/m², the average surface temperature of PV panels can be reduced by 6 °C. These results suggest that structured modifications to PV panel cavities could play a crucial role in improving thermal regulation and operational efficiency in high-temperature environments.