Experimental Study on Flexural Behaviors and Theoretical Compression-Bending Capacity of Unreinforced Steel Fiber Reinforced Concrete
Abstract
1. Introduction
2. Experimental Programs
2.1. Materials
2.2. Fabrication of Specimens and Loading Method
2.2.1. The Cube Compressive Strength Test and Notched Beam Test
2.2.2. The Compression-Bending Test
3. Results
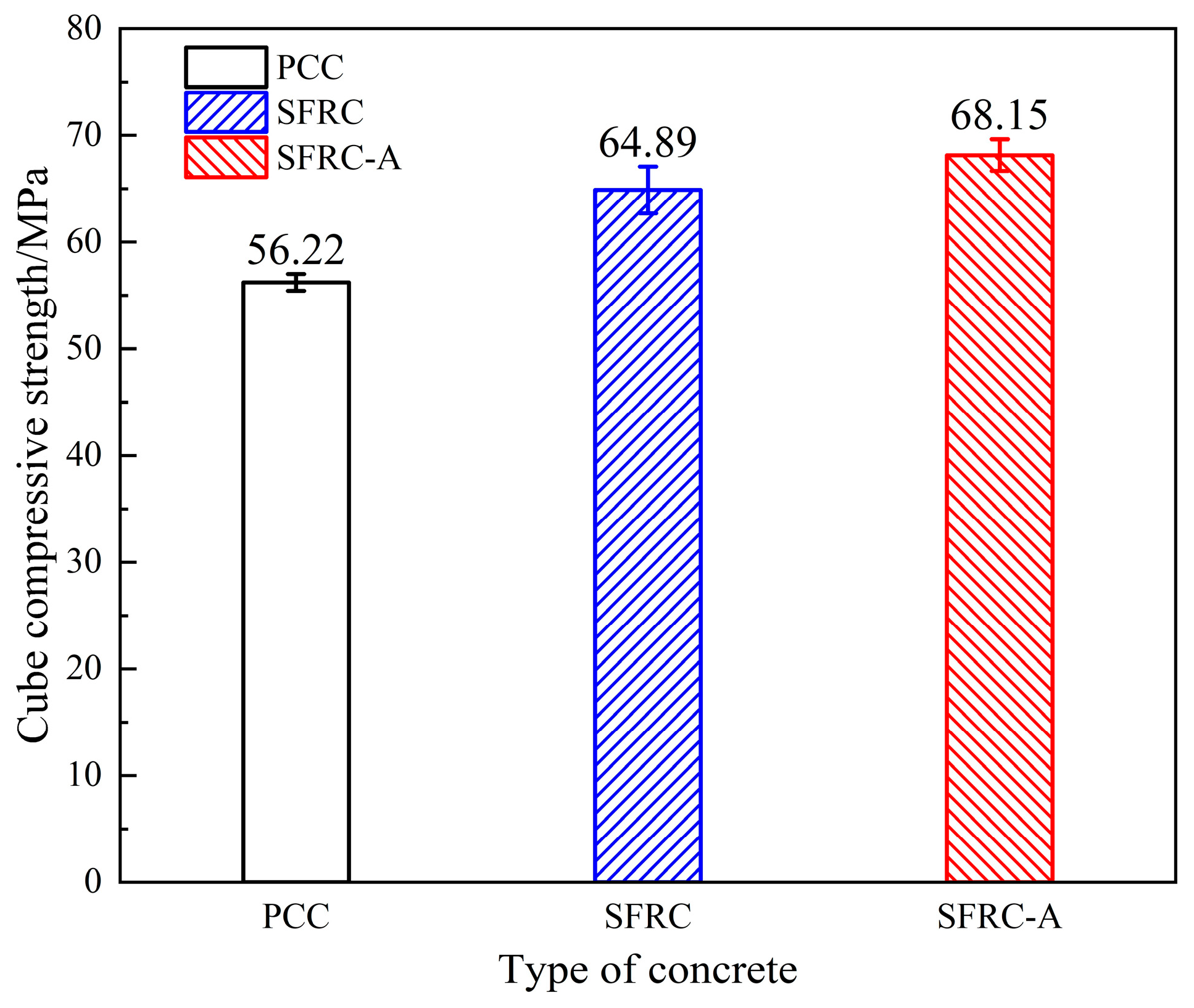
3.1. Reinforcement on Cube Compressive Strength
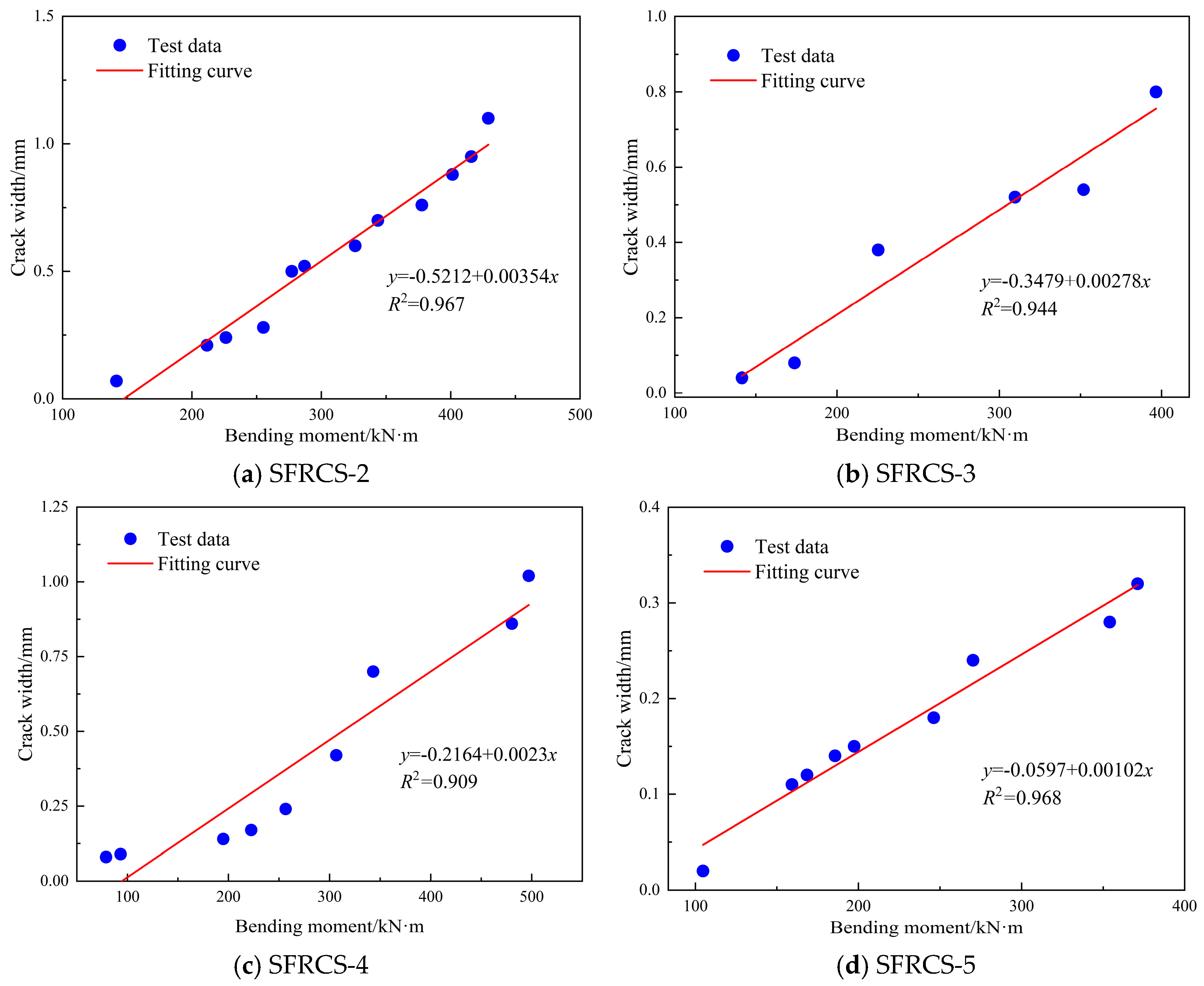
3.2. The Residual Flexural Strength
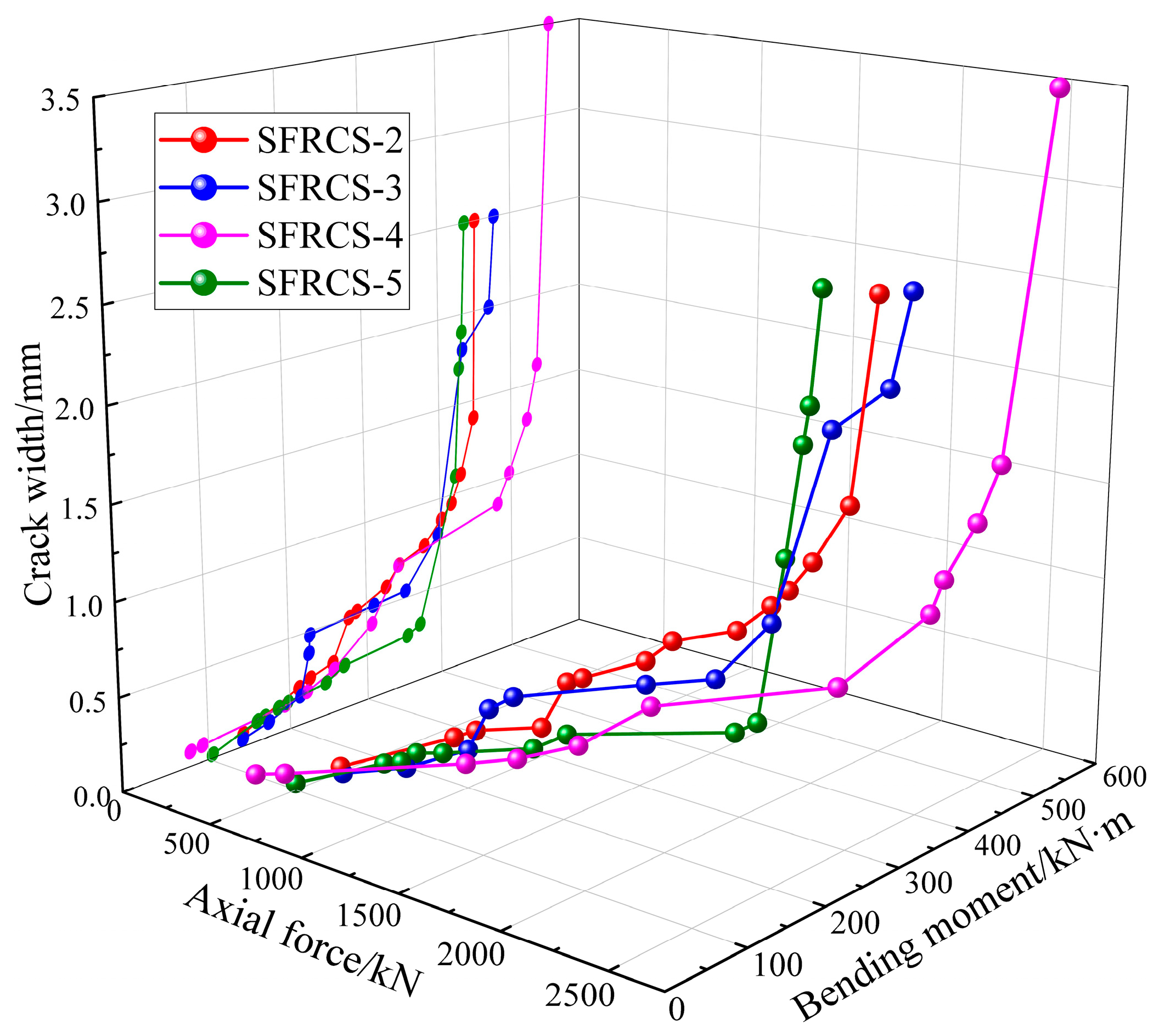
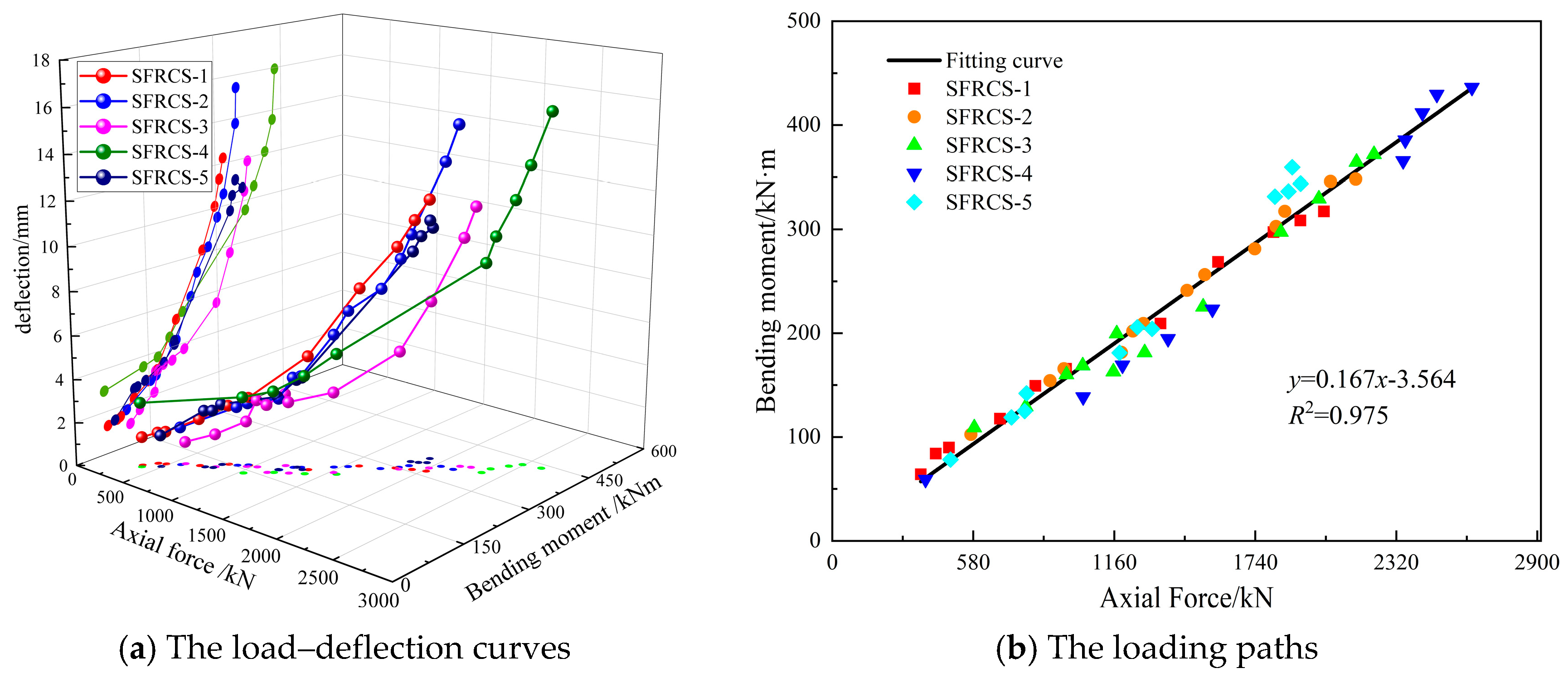
3.3. Characteristics of the Compression-Bending Capacity Curve
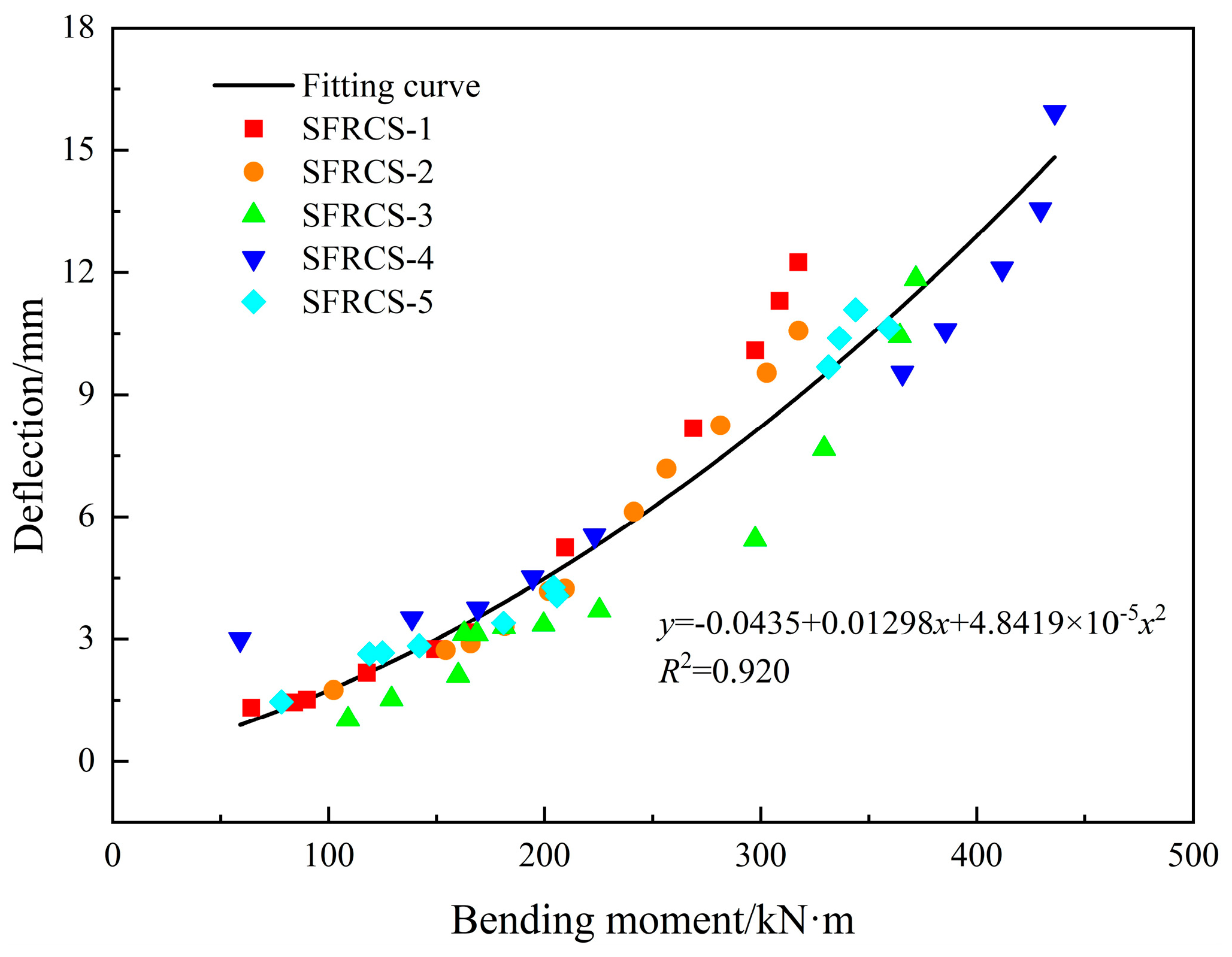
3.4. The Load–Deflection Curve
4. Discussion
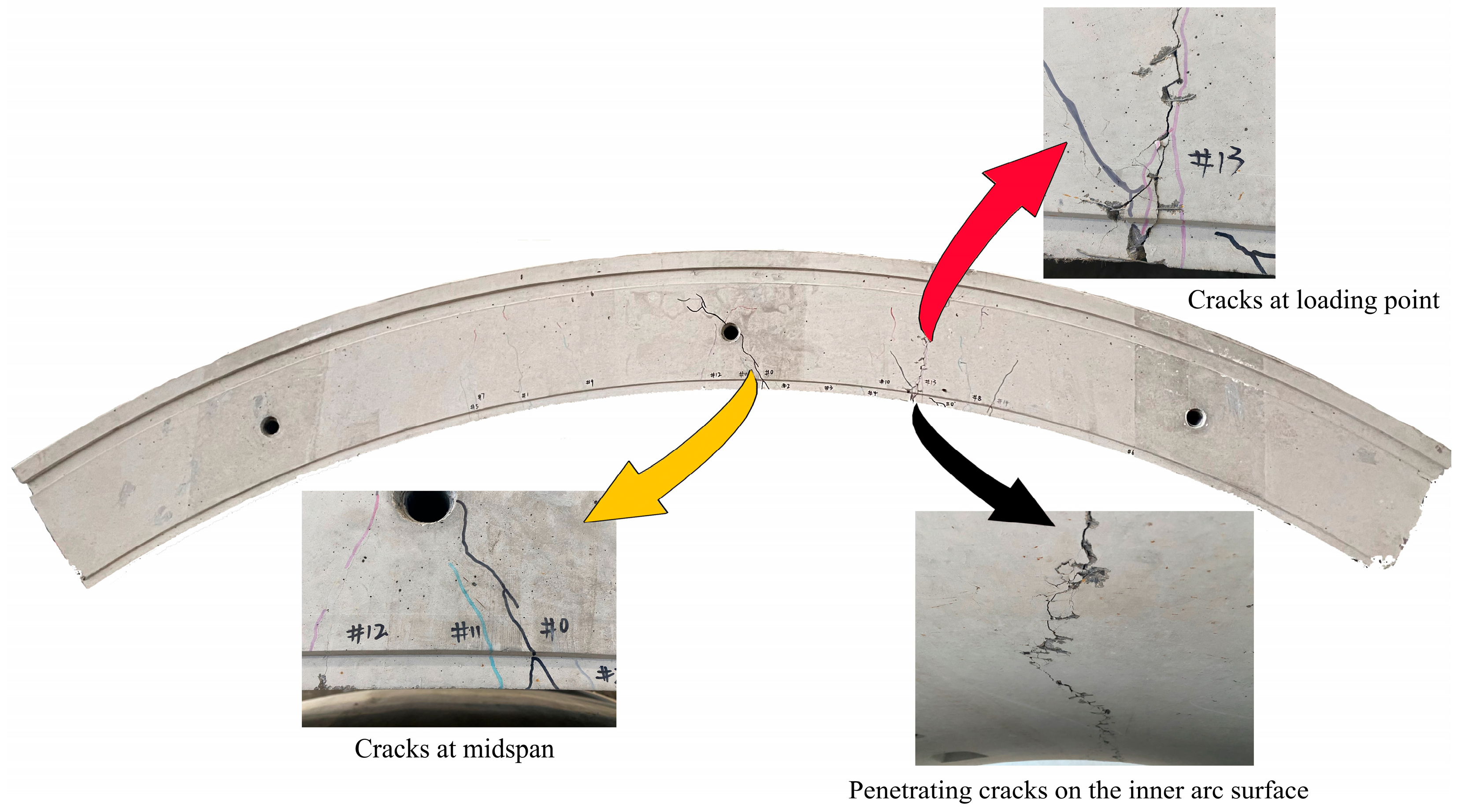
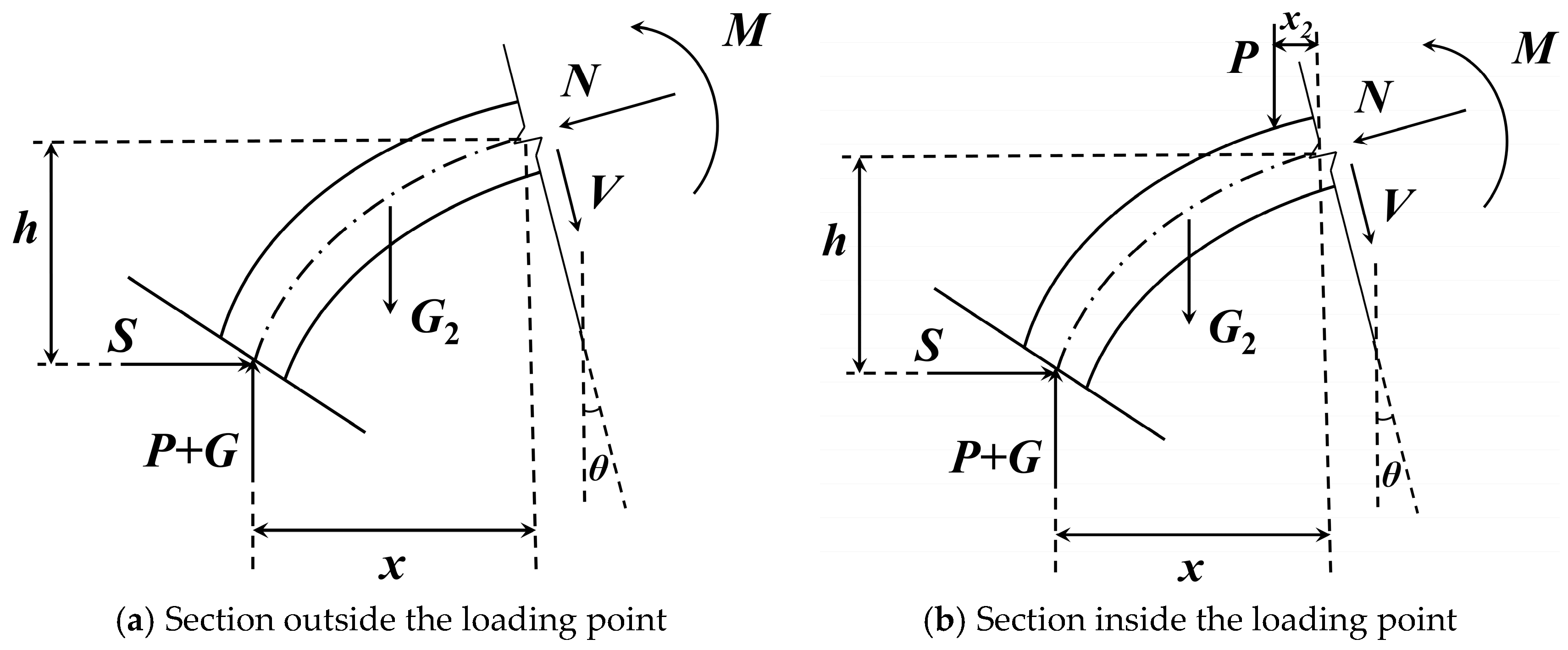
4.1. Features of Segment Surface
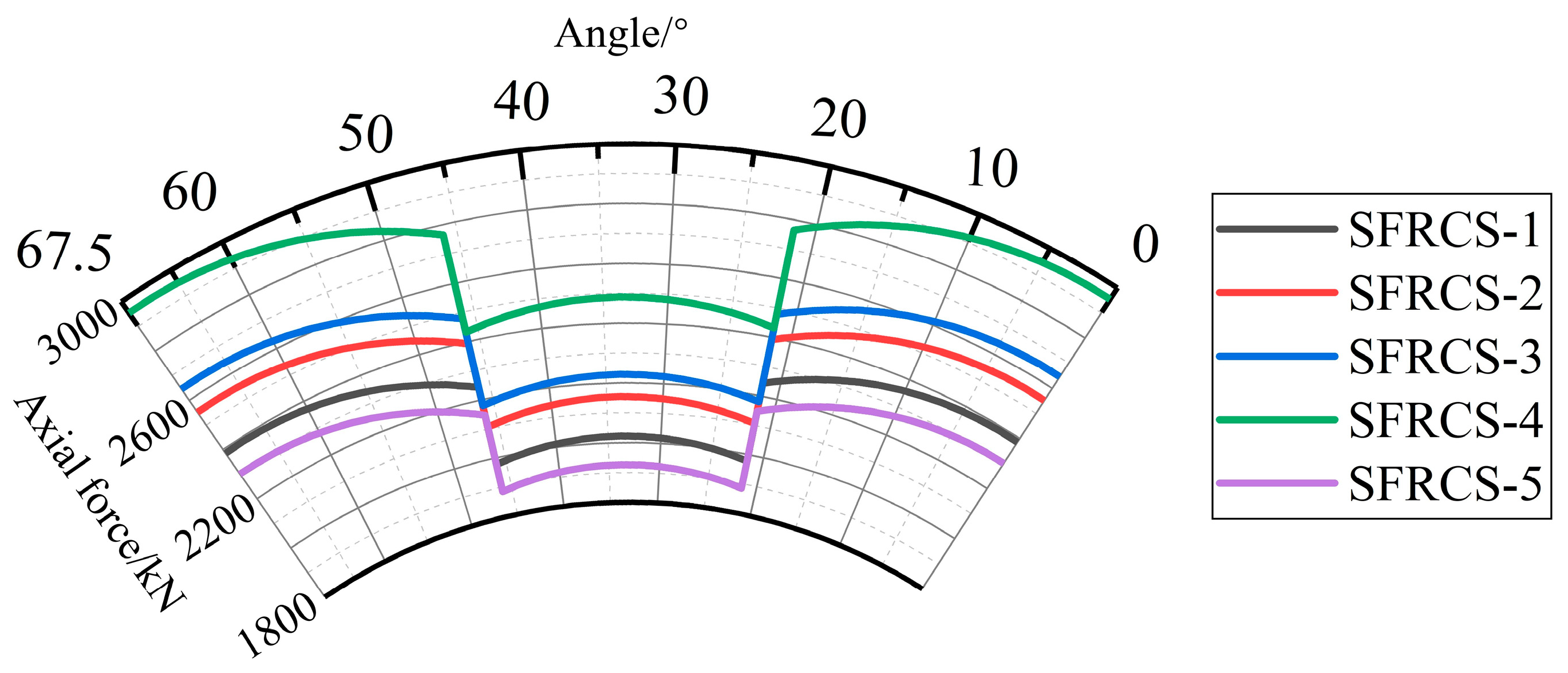
4.1.1. The Axial Force
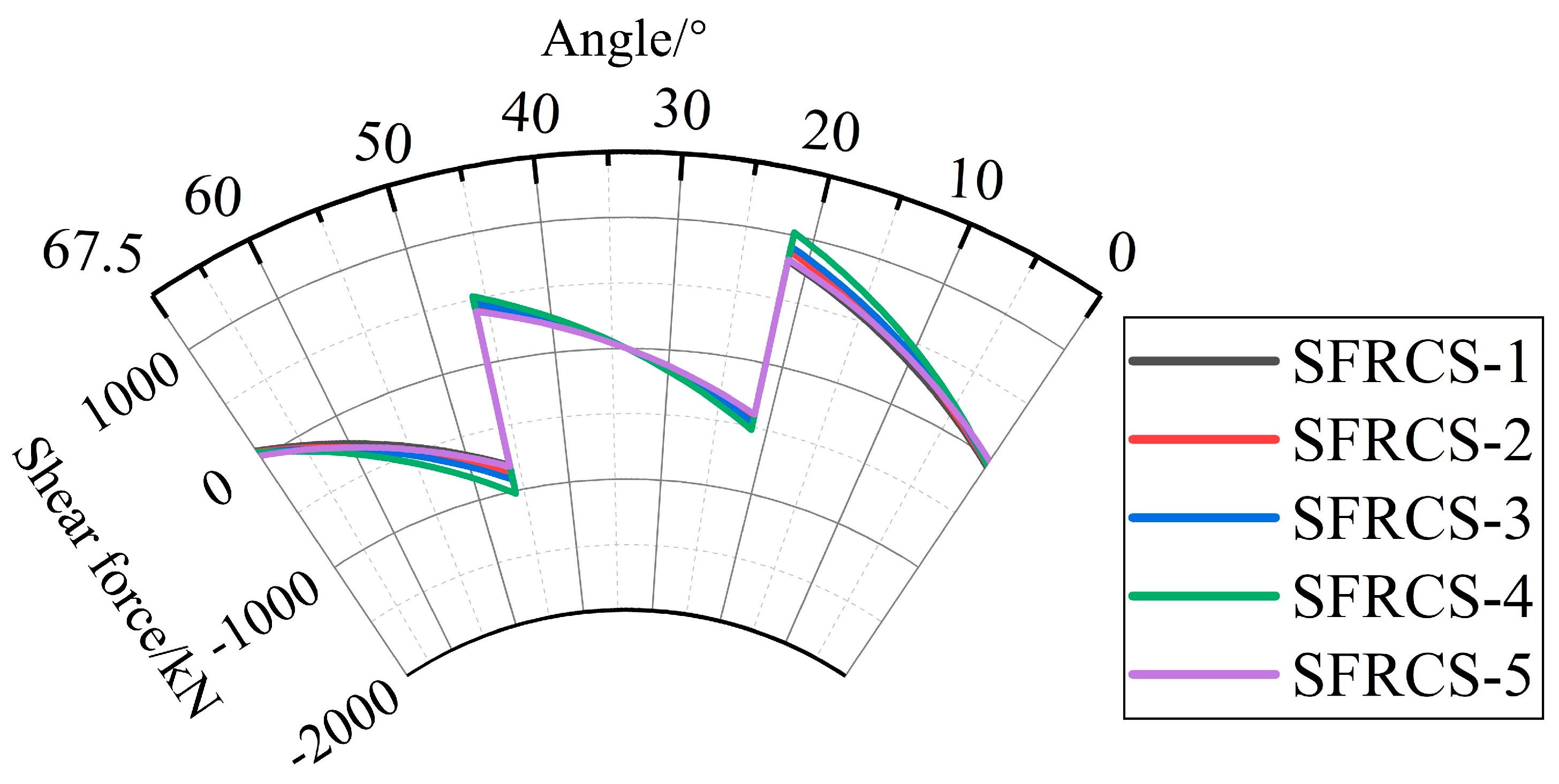
4.1.2. The Shear Force
4.1.3. The Bending Moment
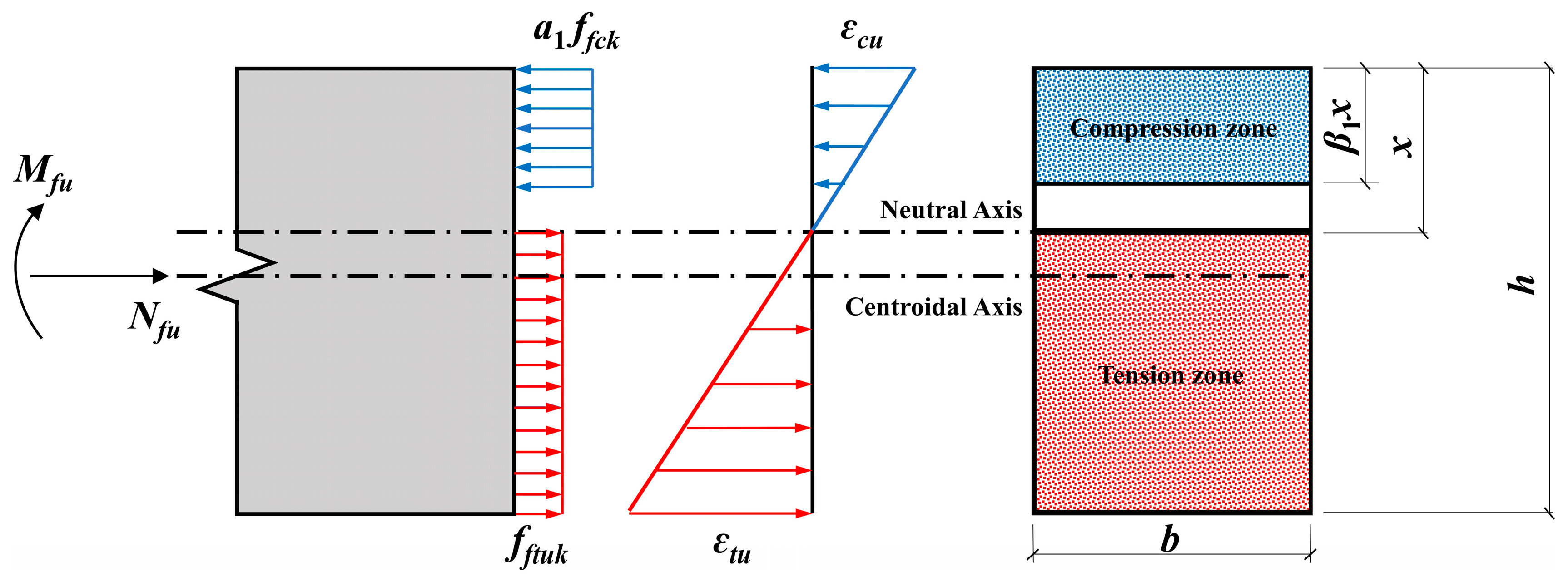
4.2. Model Review
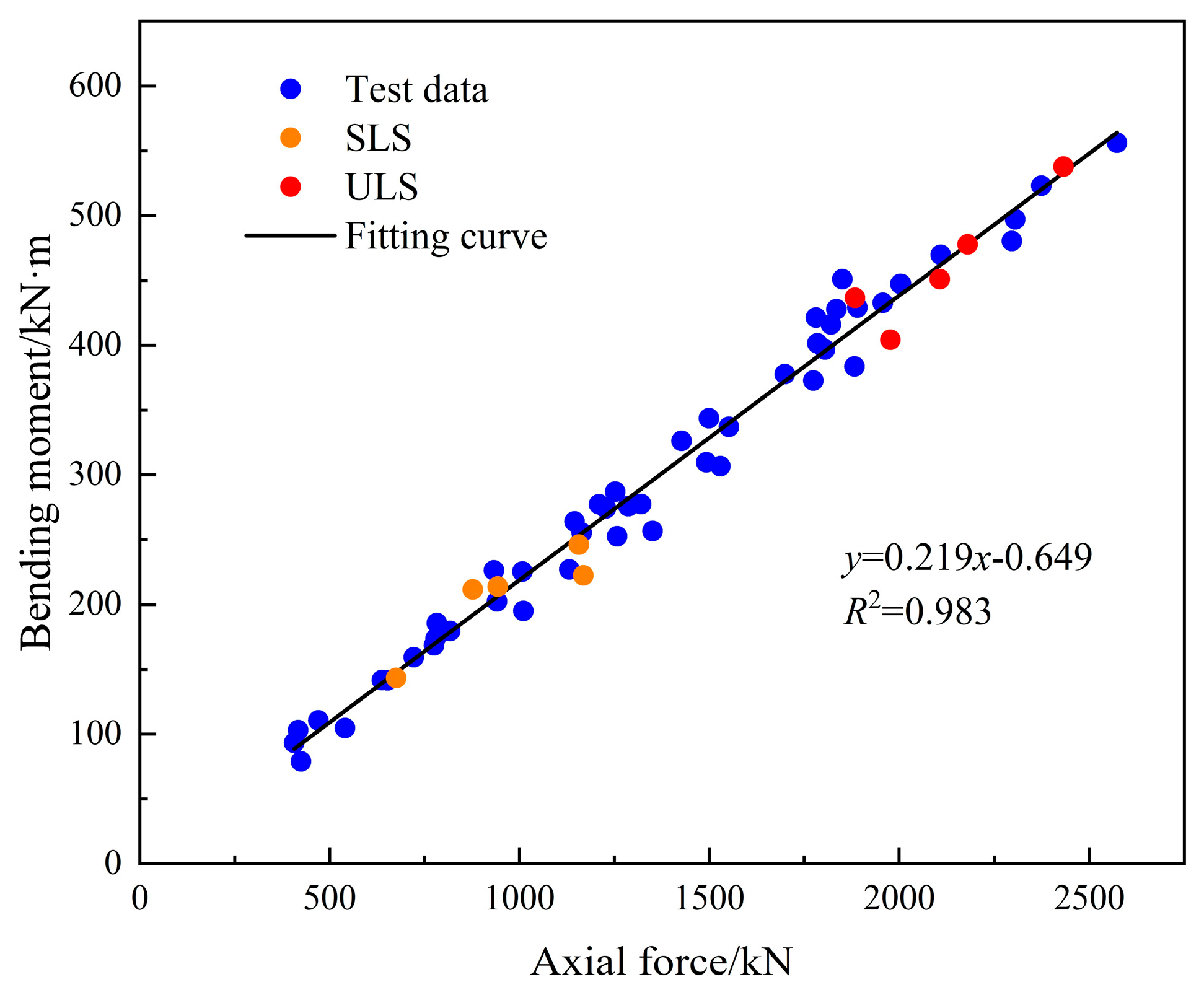
4.3. The Ultimate Strength for Compression-Bending Load
4.4. The Modification and Study of the Calculation Models
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, H.T.; Li, C.C.; Gao, D.Y.; Yang, L.; Cheng, S.Z. Study on mechanical properties and strength relation between cube and cylinder specimens of steel fiber reinforced concrete. Adv. Mech. Eng. 2019, 11, 1687814019842423. [Google Scholar] [CrossRef]
- Cao, Q.; Gao, Q.Q.; Jia, J.Q.; Gao, R.X. Early-Age Cracking Resistance of Fiber-Reinforced Expansive Self-Consolidating Concrete. ACI Mater. J. 2019, 116, 15–26. [Google Scholar] [CrossRef]
- Bolat, H.; Simsek, O. Evaluation of Energy Absorption of Macro Synthetic and Steel Fiber Reinforced Concretes. Rev. Rom. Mater. 2015, 45, 123–132. [Google Scholar]
- Nili, M.; Afroughsabet, V. Combined effect of silica fume and steel fibers on the impact resistance and mechanical properties of concrete. Int. J. Impact Eng. 2010, 37, 879–886. [Google Scholar] [CrossRef]
- Xu, S.L.; Lyu, Y.; Xu, S.J.; Li, Q.H. Enhancing the initial cracking fracture toughness of steel-polyvinyl alcohol hybrid fibers ultra high toughness cementitious composites by incorporating multi-walled carbon nanotubes. Constr. Build. Mater. 2019, 195, 269–282. [Google Scholar] [CrossRef]
- Tan, K.H.; Paramasivam, P.; Tan, K.C. Cracking characteristics of reinforced steel fiber concrete beams under short-and long-term loadings. Adv. Cem. Based Mater. 1995, 2, 127–137. [Google Scholar] [CrossRef]
- Naaman, A.E.; Argon, A.S.; Moavenzadeh, F. A fracture model for fiber reinforced cementitious materials. Cem. Concr. Res. 1973, 3, 397–411. [Google Scholar] [CrossRef]
- Olivito, R.S.; Zuccarello, F.A. An experimental study on the tensile strength of steel fiber reinforced concrete. Compos. Part B-Eng. 2010, 41, 246–255. [Google Scholar] [CrossRef]
- Thomas, J.; Ramaswamy, A. Mechanical properties of steel fiber-reinforced concrete. J. Mater. Civ. Eng. 2007, 19, 385–392. [Google Scholar] [CrossRef]
- Sloma, S.F. Influence of Hooked-end Steel Fibers on Fresh and Hardened Properties of Steel Fiber Reinforcement Self-Compacting Concrete(SFRSCC). J. Phys. Conf. Ser. 2019, 1198, 032005. [Google Scholar] [CrossRef]
- Fuente, A.D.L.; Pujadas, P.; Blanco, A.; Aguado, A. Experiences in Barcelona with the use of fibres in segmental linings. Tunn. Undergr. Space Technol. 2012, 27, 60–71. [Google Scholar] [CrossRef]
- Qi, M.S.; Liu, X. A Full-scale Experimental Study on Bearing Capacity of Fiber Reinforced Concrete Segments. Tunn. Undergr. Space Technol. 2019, 15 (Suppl. S1), 55–60. [Google Scholar]
- Liu, X.; Sun, Q.H.; Jiang, H.; Bao, H.L. Experimental Research and Theoretical Analysis of Mechanical Behaviors of Fiber Reinforced Concrete Segments. Mod. Tunn. Technol. 2018, 55 (Suppl. S2), 1080–1090. [Google Scholar] [CrossRef]
- Liu, X.; Sun, Q.; Yuan, Y.; Taerwe, L. Comparison of the structural behavior of reinforced concrete tunnel segments with steel fiber and synthetic fiber addition. Tunn. Undergr. Space Technol. 2020, 103, 103506. [Google Scholar] [CrossRef]
- Xu, H.Y.; Wang, Z.J.; Zhou, P.; Li, Z.Y.; Xu, J.X.; Tang, L.; Li, R.Y. Eccentric compression model test of steel fiber reinforced concrete lining segments. J. Build. Struct. 2018, 39 (Suppl. S2), 290–298. [Google Scholar] [CrossRef]
- Oh, B.H. Flexural Analysis of Reinforced Concrete Beams Containing Steel Fibers. J. Struct. Eng. 1991, 118, 2821–2835. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B.S. Structural behavior of ultra high performance concrete beams subjected to bending. Eng. Struct. 2010, 32, 3478–3487. [Google Scholar] [CrossRef]
- Mertol, H.C.; Baran, E.; Bello, H.J. Flexural behavior of lightly and heavily reinforced steel fiber concrete beams. Constr. Build. Mater. 2015, 98, 185–193. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Yoon, Y.S. Structural performance of ultra-high-performance concrete beams with different steel fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Biolzi, L.; Cattaneo, S. Response of steel fiber reinforced high strength concrete beams: Experiments and code predictions. Cem. Concr. Comp. 2017, 77, 1–13. [Google Scholar] [CrossRef]
- Yang, J.M.; Min, K.H.; Shin, H.O.; Yoon, Y.S. Effect of steel and synthetic fibers on flexural behavior of high-strength concrete beams reinforced with FRP bars. Compos. Part B-Eng. 2012, 43, 1077–1086. [Google Scholar] [CrossRef]
- Lin, L.; Fuente, A.D.L. Design of FRC tunnel segments considering the ductility requirements of the Model Code 2010. Tunn. Undergr. Space Technol. 2015, 47, 200–210. [Google Scholar] [CrossRef]
- Issa, M.S.; Metwally, I.M.; Elzeiny, S.M. Influence of fibers on flexural behavior and ductility of concrete beams reinforced with GFRP rebars. Eng. Struct. 2011, 33, 1754–1763. [Google Scholar] [CrossRef]
- ACI 440.1R-15; Guide for the Design and Construction of Structural Concrete Reinforced with Fiber-Reinforced Polymer (FRP) Bars. American Concrete Institute: Farmington Hills, MI, USA, 2015.
- DB21/T 3165-2019; Technical Specification for Precast Steel Fiber Reinforced Concrete Segments. Liaoning Provincial Administration for Market Regulation: Shenyang, China, 2019.
- CECS 13:2009; Standard Test Methods for Fiber Reinforced Concrete. China Association for Engineering Construction Standardization: Beijing, China, 2009.
- EN 14651:2005; Test Method for Metallic Fibre Concrete—Measuring the Flexural Tensile Strength (Limit of Proportionality (LOP), Residual). European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- fib Bulletin 83:2017; Precast Tunnel Segments in Fibre Reinforced Concrete. International Federation for Structural Concrete (FIB): Lausanne, Switzerland, 2017.
- Wang, J.W. Study on Ultimate Limit State Design Method of Steel Fiber Reinforced Concrete Segment. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar]



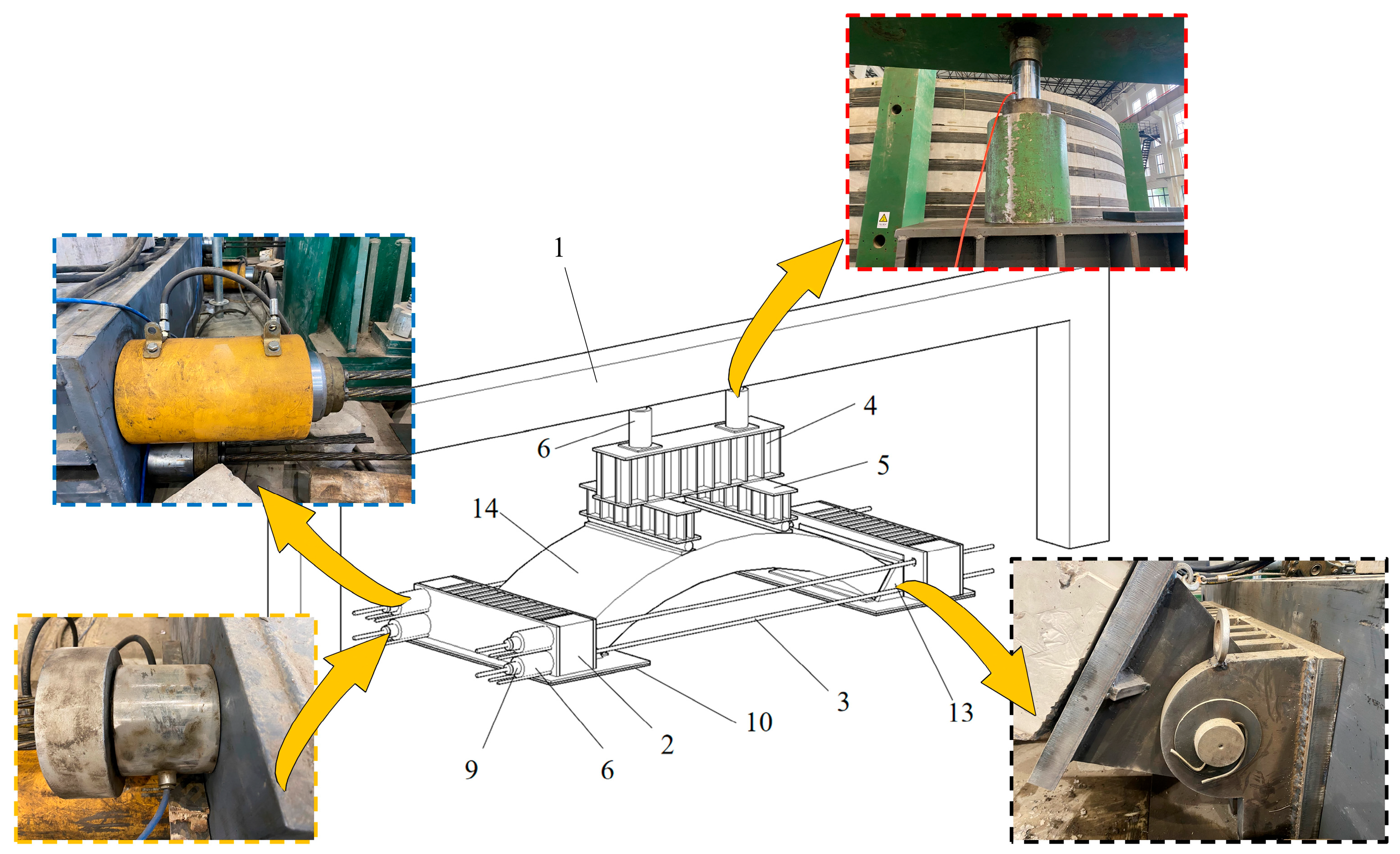




| Identifier | SF/ kg | Fly Ash/ kg | Fine Aggregate/kg | Coarse Aggregate/kg | Water Reducer/ kg | Water/kg | Cement/ kg | |
|---|---|---|---|---|---|---|---|---|
| 5.0–10.0/mm | 10.0–20.0/mm | |||||||
| PCC-1 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| PCC-2 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| PCC-3 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| PCC-4 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| PCC-5 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| PCC-6 | 0 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-1 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-2 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-3 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-4 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-5 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-6 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-7 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-8 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-9 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-10 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-11 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-12 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCC-A1 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A2 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A3 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A4 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A5 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A6 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A7 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCC-A8 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-1 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-2 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-3 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-4 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-5 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-6 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-7 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-8 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-9 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-10 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-11 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-12 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCQ-A1 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A2 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A3 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A4 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A5 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A6 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A7 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A8 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A9 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A10 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A11 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCQ-A12 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCS-1 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCS-2 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCS-3 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCS-4 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCS-5 | 40 | 70 | 690 | 452 | 678 | 11.00 | 165 | 380 |
| SFRCS-A1 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCS-A2 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| SFRCS-A3 | 30 | 70 | 639 | 330 | 586 | 7.50 | 150 | 400 |
| Identifier | t (mm) | ri (mm) | re (mm) | w (mm) | a (°) |
|---|---|---|---|---|---|
| SFRCS-1 | 350 | 2700 | 3100 | 1200 | 67.5 |
| SFRCS-2 | 350 | 2700 | 3100 | 1200 | 67.5 |
| SFRCS-3 | 350 | 2700 | 3100 | 1200 | 67.5 |
| SFRCS-4 | 350 | 2700 | 3100 | 1200 | 67.5 |
| SFRCS-5 | 350 | 2700 | 3100 | 1200 | 67.5 |
| SFRCS-A1 | 350 | 2950 | 3300 | 1500 | 72.0 |
| SFRCS-A2 | 350 | 2950 | 3300 | 1500 | 72.0 |
| SFRCS-A3 | 350 | 2950 | 3300 | 1500 | 72.0 |
| Identifier | Fiber | Content (kg/m3) | Curing Days | fcc (MPa) | fcu,m (MPa) |
|---|---|---|---|---|---|
| PCC-1 | Plain | 0 | 40 | 55.1 | 56.2 |
| PCC-2 | Plain | 0 | 40 | 56.5 | |
| PCC-3 | Plain | 0 | 40 | 55.3 | |
| PCC-4 | Plain | 0 | 40 | 56.6 | |
| PCC-5 | Plain | 0 | 40 | 57.4 | |
| PCC-6 | Plain | 0 | 40 | 56.4 | |
| SFRCC-1 | Dramix 4D 80/60BG | 40 | 40 | 65.9 | 64.9 |
| SFRCC-2 | Dramix 4D 80/60BG | 40 | 40 | 62.0 | |
| SFRCC-3 | Dramix 4D 80/60BG | 40 | 40 | 60.2 | |
| SFRCC-4 | Dramix 4D 80/60BG | 40 | 40 | 64.0 | |
| SFRCC-5 | Dramix 4D 80/60BG | 40 | 40 | 65.3 | |
| SFRCC-6 | Dramix 4D 80/60BG | 40 | 40 | 65.0 | |
| SFRCC-7 | Dramix 4D 80/60BG | 40 | 40 | 67.7 | |
| SFRCC-8 | Dramix 4D 80/60BG | 40 | 40 | 68.8 | |
| SFRCC-9 | Dramix 4D 80/60BG | 40 | 40 | 65.6 | |
| SFRCC-10 | Dramix 4D 80/60BG | 40 | 40 | 65.7 | |
| SFRCC-11 | Dramix 4D 80/60BG | 40 | 40 | 64.7 | |
| SFRCC-12 | Dramix 4D 80/60BG | 40 | 40 | 63.8 | |
| SFRCC-A1 | Dramix 4D 80/60BG | 30 | 39 | 69.3 | 68.2 |
| SFRCC-A2 | Dramix 4D 80/60BG | 30 | 39 | 69.4 | |
| SFRCC-A3 | Dramix 4D 80/60BG | 30 | 39 | 65.0 | |
| SFRCC-A4 | Dramix 4D 80/60BG | 30 | 39 | 67.3 | |
| SFRCC-A5 | Dramix 4D 80/60BG | 30 | 39 | 69.8 | |
| SFRCC-A6 | Dramix 4D 80/60BG | 30 | 39 | 69.0 | |
| SFRCC-A7 | Dramix 4D 80/60BG | 30 | 39 | 67.9 | |
| SFRCC-A8 | Dramix 4D 80/60BG | 30 | 39 | 67.5 |
| Beam | Fl (mm) | fL (N/mm2) | fR1 (N/mm2) | fR2 (N/mm2) | fR3 (N/mm2) | fR4 (N/mm2) |
|---|---|---|---|---|---|---|
| Deflection | 0.47 mm | 1.32 mm | 2.17 mm | 3.02 mm | ||
| SFRCQ-1 | 0.06 | 5.61 | 5.42 | 7.00 | 5.79 | 3.51 |
| SFRCQ-2 | 0.06 | 5.43 | 6.47 | 8.89 | 7.25 | 5.59 |
| SFRCQ-3 | 0.06 | 5.67 | 6.56 | 8.34 | 8.06 | 6.23 |
| SFRCQ-4 | 0.06 | 6.10 | 6.10 | 7.88 | 8.28 | 5.81 |
| SFRCQ-5 | 0.07 | 5.84 | 7.11 | 9.63 | 8.66 | 6.03 |
| SFRCQ-6 | 0.06 | 6.43 | 6.61 | 8.40 | 7.32 | 6.14 |
| SFRCQ-7 | 0.06 | 5.90 | 5.60 | 7.20 | 6.35 | 5.10 |
| SFRCQ-8 | 0.04 | 6.12 | 6.07 | 8.34 | 8.29 | 5.86 |
| SFRCQ-9 | 0.06 | 5.66 | 5.22 | 6.74 | 5.24 | 3.56 |
| SFRCQ-10 | 0.05 | 5.99 | 5.76 | 7.66 | 5.74 | 4.44 |
| SFRCQ-11 | 0.05 | 6.36 | 6.47 | 7.93 | 6.33 | 3.56 |
| SFRCQ-12 | 0.06 | 5.86 | 6.23 | 7.71 | 5.86 | 4.22 |
| Average | 0.06 | 5.91 | 6.14 | 7.98 | 6.93 | 5.00 |
| S.D. | 0.01 | 0.30 | 0.55 | 0.81 | 1.19 | 1.08 |
| C.V. | 13.11 | 5.12 | 9.02 | 10.20 | 17.19 | 21.65 |
| fRjk | - | - | 5.01 | 6.31 | 4.49 | 2.78 |
| fR3k/fR1k | 0.90 | |||||
| Beam | Fl (mm) | fL (N/mm2) | fR1 (N/mm2) | fR2 (N/mm2) | fR3 (N/mm2) | fR4 (N/mm2) |
|---|---|---|---|---|---|---|
| Deflection | 0.47 mm | 1.32 mm | 2.17 mm | 3.02 mm | ||
| SFRCQ-A1 | 0.06 | 5.18 | 4.49 | 6.13 | 6.89 | 6.15 |
| SFRCQ-A2 | 0.06 | 5.06 | 3.40 | 4.45 | 3.84 | 2.86 |
| SFRCQ-A3 | 0.06 | 5.31 | 3.91 | 5.11 | 4.96 | 4.59 |
| SFRCQ-A4 | 0.06 | 4.63 | 2.45 | 3.54 | 4.09 | 4.00 |
| SFRCQ-A5 | 0.05 | 5.31 | 3.75 | 5.47 | 5.53 | 5.26 |
| SFRCQ-A6 | 0.06 | 4.91 | 2.48 | 3.17 | 3.32 | 3.06 |
| SFRCQ-A7 | 0.06 | 4.56 | 3.57 | 4.83 | 4.98 | 4.11 |
| SFRCQ-A8 | 0.06 | 5.92 | 5.31 | 7.37 | 6.61 | 5.60 |
| SFRCQ-A9 | 0.06 | 4.69 | 4.11 | 5.95 | 6.04 | 4.59 |
| SFRCQ-A10 | 0.06 | 5.15 | 5.36 | 7.48 | 7.56 | 5.81 |
| SFRCQ-A11 | 0.06 | 4.99 | 4.82 | 5.80 | 5.52 | 4.45 |
| SFRCQ-A12 | 0.06 | 5.10 | 3.93 | 5.44 | 5.71 | 5.21 |
| Average | 0.06 | 5.07 | 3.97 | 5.40 | 5.42 | 4.64 |
| fRjk | - | - | 2.04 | 2.72 | 2.82 | 2.53 |
| fR3k/fR1k | 1.38 | |||||
| Number of Specimens | 6 | 9 | 12 | 15 | 20 | 25 | 100 | ∞ |
|---|---|---|---|---|---|---|---|---|
| ks | 2.336 | 2.141 | 2.048 | 1.991 | 1.932 | 1.895 | 1.760 | 1.645 |
| Identifier | Axial Force (kN) | |||
|---|---|---|---|---|
| Support | OSLP | ISLP | Mid-Span | |
| SFRCS-1 | 2954.25 | 2766.26 | 2431.63 | 2486.83 |
| SFRCS-2 | 2300.17 | 2146.78 | 1883.90 | 1926.37 |
| SFRCS-3 | 2550.42 | 2392.11 | 2105.78 | 2153.40 |
| SFRCS-4 | 2645.17 | 2477.70 | 2178.97 | 2228.30 |
| SFRCS-5 | 2384.63 | 2242.27 | 1977.58 | 2022.22 |
| Identifier | Shear Force (kN) | |||
|---|---|---|---|---|
| Support | OSLP | ISLP | Mid-Span | |
| SFRCS-1 | −71.05 | 797.76 | −422.62 | 0 |
| SFRCS-2 | −59.04 | 869.73 | −450.42 | 0 |
| SFRCS-3 | −52.05 | 910.78 | −466.30 | 0 |
| SFRCS-4 | −54.82 | 1021.74 | −521.10 | 0 |
| SFRCS-5 | −24.93 | 809.70 | −402.30 | 0 |
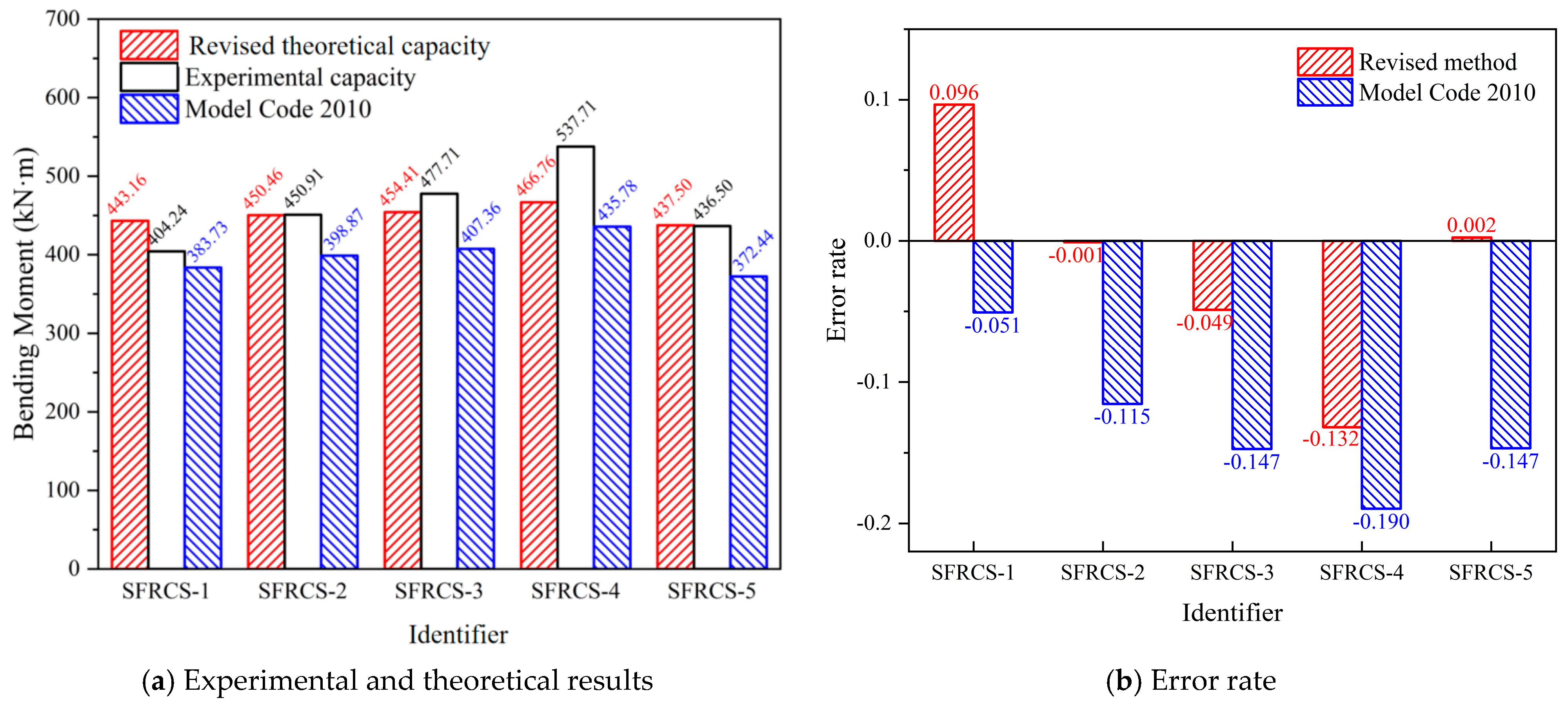
| Identifier | Test Value N (kN)/M (kN·m) | e (m) | Model Code (kN·m) |
|---|---|---|---|
| SFRCS-1 | 1977.58/404.24 | 0.204 | 383.73 |
| SFRCS-2 | 2105.78/450.91 | 0.214 | 398.87 |
| SFRCS-3 | 2178.97/477.71 | 0.219 | 407.36 |
| SFRCS-4 | 2431.63/537.71 | 0.221 | 435.78 |
| SFRCS-5 | 1883.90/436.50 | 0.232 | 372.44 |
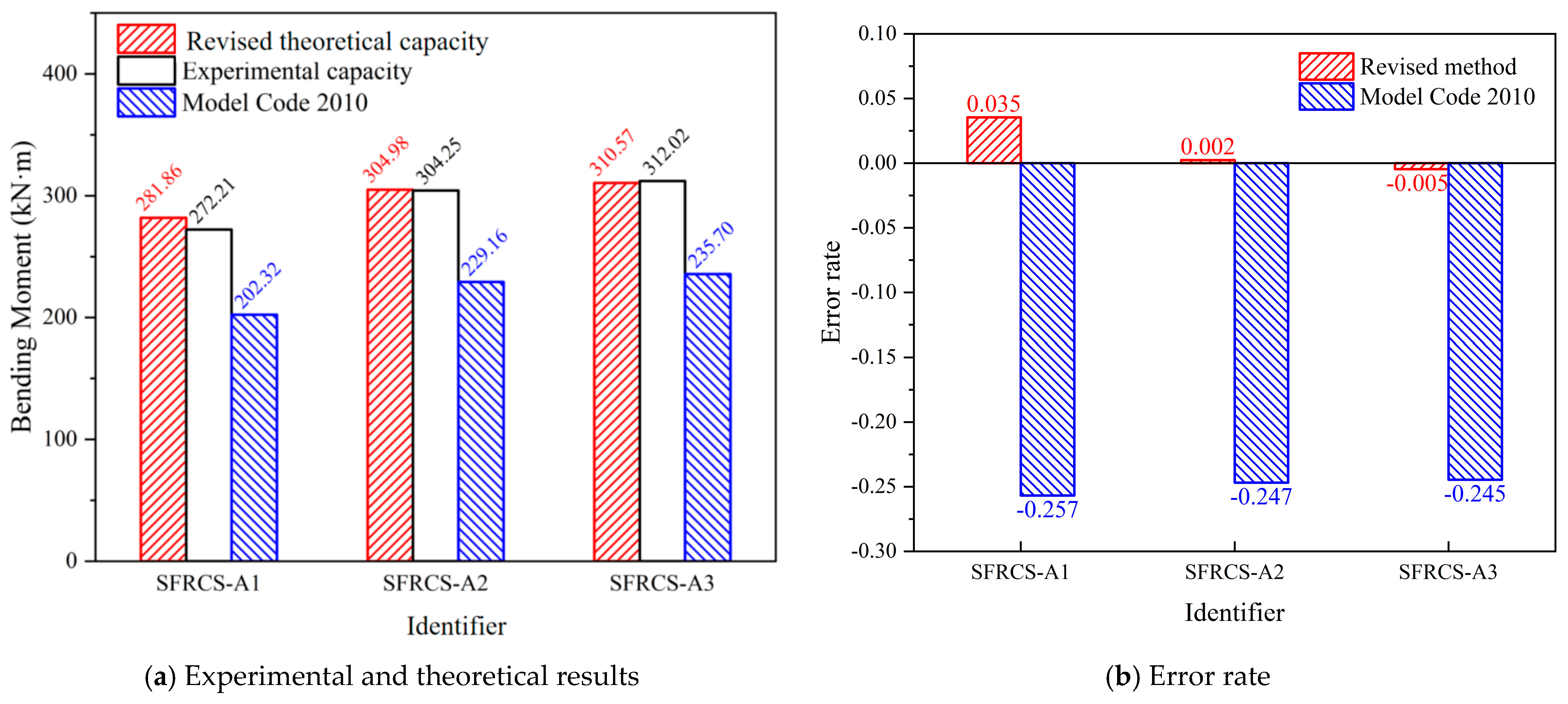
| Identifier | Horizontal Load S (kN) | Vertical Load P (kN) | Axial Force N (kN) | Bending Moment M (kN·m) | e (m) |
|---|---|---|---|---|---|
| SFRCS-A1 | 762.70 | 521.15 | 750.38 | 272.21 | 0.363 |
| SFRCS-A2 | 947.08 | 628.55 | 931.09 | 304.25 | 0.327 |
| SFRCS-A3 | 992.85 | 655.05 | 975.75 | 312.02 | 0.320 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Wang, L.; Lin, J.; Wang, Z.; Wang, Y.; Huang, Y.; Fan, Z.; Yang, Y.; Rui, X.; Xu, H. Experimental Study on Flexural Behaviors and Theoretical Compression-Bending Capacity of Unreinforced Steel Fiber Reinforced Concrete. Buildings 2025, 15, 1160. https://doi.org/10.3390/buildings15071160
Gao C, Wang L, Lin J, Wang Z, Wang Y, Huang Y, Fan Z, Yang Y, Rui X, Xu H. Experimental Study on Flexural Behaviors and Theoretical Compression-Bending Capacity of Unreinforced Steel Fiber Reinforced Concrete. Buildings. 2025; 15(7):1160. https://doi.org/10.3390/buildings15071160
Chicago/Turabian StyleGao, Cunmiao, Linjiang Wang, Junyu Lin, Zhijie Wang, Yunhui Wang, Yu Huang, Zhanfeng Fan, Youlian Yang, Xiaohao Rui, and Haiyan Xu. 2025. "Experimental Study on Flexural Behaviors and Theoretical Compression-Bending Capacity of Unreinforced Steel Fiber Reinforced Concrete" Buildings 15, no. 7: 1160. https://doi.org/10.3390/buildings15071160
APA StyleGao, C., Wang, L., Lin, J., Wang, Z., Wang, Y., Huang, Y., Fan, Z., Yang, Y., Rui, X., & Xu, H. (2025). Experimental Study on Flexural Behaviors and Theoretical Compression-Bending Capacity of Unreinforced Steel Fiber Reinforced Concrete. Buildings, 15(7), 1160. https://doi.org/10.3390/buildings15071160





