An Innovative Multi-Story Trombe Wall as a Passive Cooling and Heating Technique in Hot Climate Regions: A Simulation-Optimization Study

Abstract

This study develops an optimized multi-story Trombe Wall (MTW) as a hybrid passive system for heating, cooling, and PV electricity generation. Unlike previous research, which focused on single-story applications and heating efficiency, this study explores MTW performance in hot climates. The methodology includes four phases: identifying TW design parameters, selecting and validating a case study, applying a two-stage optimization, and developing predictive equations. Results show that the MTW achieves up to a 1.94 °C decrease in cooling mode, a 1.56 °C increase in heating mode, a 40% increase in thermal comfort hours, and a 31% rise in annual PV electricity generation. Finally, the developed regression models demonstrated strong predictive capability (R² = 70.2–95.73%) for discomfort and electricity generation. The proposed MTW provides a cost-effective and sustainable solution, supporting designers and researchers in optimizing building performance.

1. Introduction

The world is witnessing an increased demand for energy, with a 1.3% growth observed in 2022. Fossil fuels comprise about 80% of the energy supply [1]. A significant proportion of this energy is utilized by air conditioning [2], as many designs on both urban and building levels suffer from a lack of adaptation strategies to deal with thermally uncomfortable periods in interior and exterior space. As a result, about five billion people live where space conditioning is required to maintain comfortable conditions. This figure is expected to increase to seven billion by 2050 [3].

Integrating passive design techniques has gained increasing significance in pursuing ecological responsibility and energy efficiency in building practices [4]. Passive design is a sustainable approach to architectural solutions that prioritizes energy efficiency by utilizing natural components and climatic conditions to lessen reliance on mechanical heating and cooling systems. In contrast to active systems, which rely on external energy sources, passive design capitalizes on the building’s inherent characteristics, surroundings, and environment for energy conservation and emphasizes creating comfortable living spaces.

Trombe Wall (TW) is a passive design technique that can significantly improve thermal efficiency and reduce energy consumption in buildings [5]. It can potentially reduce the energy required for heating in buildings and, if used efficiently, can also impact performance during the summer [6]. This offers a cost-effective and environmentally friendly solution to utilize solar power for natural ventilation during the summer, resulting in reduced indoor temperatures [7]. Usually, TW consists of a glazing unit, an air gap, and a concrete wall. The concrete wall is positioned to face the south and features adjustable upper and lower openings to accommodate seasonal fluctuations. The internal mass of the wall is used to absorb and preserve solar heat [8].

The majority of research on TW has focused on improving their heating efficiency [9,10], demonstrating their significant potential to reduce heating energy consumption by up to 71.7% [6]. However, the performance of TW systems in regions with hot summers poses notable challenges. This limitation has driven researchers to investigate strategies to enhance their cooling performance to make TW systems more versatile and practical in diverse climatic conditions. TW can harness solar radiation to enhance natural ventilation during summertime, lowering inside temperatures [7]. Efforts to enhance the TW’s summer performance focus on improving ventilation efficiency and adopting advanced methods to control heat absorption and transfer. One of these efforts tried to solve the overheating problem in the summer using external shading [11]. Another study achieved a 73% reduction in cooling demand by adding insulation and shutters and changing the color of the massive wall [12]. Others benefited from glazing properties to regulate solar radiation by using low-emissivity (low-e) glazing [13] and double glazing [14]. Also, integrated PCM (phase change material), evaporative cooling [6], and controlling vents opening strategies [15] could lead to a significant reduction in cooling energy during the summer. Still, TW’s summer performance and potential development as a cooling technology require further investigation.

TW research has explored various types and innovations, including shape modifications such as the classic TW, zigzag-TW, and water-TW [16], as well as integrations like PCM-TW [17], photovoltaic (PV)-TW [18], and photocatalytic-thermal-catalytic TW [19]. These studies encompassed a range of methodologies, including simulation models [20], scaled-down prototypes [21], and full-scale rooms with actual dimensions [9]. However, these studies have focused primarily on their application in individual rooms. This narrow approach neglects the potential for TW systems to support multiple interconnected spaces, particularly in multi-story configurations. As a result, their applicability in more complex architectural layouts remains underexplored, limiting their broader utilization in contemporary building designs.

To maximize the efficiency of TWs and achieve optimal energy savings and occupant comfort, optimizing design parameters and control strategies is crucial [22]. Numerous studies have explored the optimization of TW systems through design parameters, including TW dimensions and configurations [23,24], the massive wall properties [25,26], glazing types [27], and ventilation mechanisms through vents [28] and the air gap [29]. Most of these studies employed parametric optimization techniques, focusing on a single design variable with limited scenarios. Few investigations have simultaneously analyzed multiple design parameters to capture their relationships, highlighting a significant gap in comprehensive TW optimization research.

Based on previous studies’ findings, TW systems’ performance efficiency is influenced by several design parameters. These parameters include TW proportions, air gap dimensions, glazing types, massive wall properties, vents, and their operational scenarios. However, most of these studies focus on examining and enhancing individual parameters independently (i.e., one factor at a time) without considering their interrelationships. Moreover, research efforts have predominantly concentrated on enhancing the heating efficiency of TWs despite the challenges associated with their application in regions characterized by hot summers.

Additionally, existing research has focused mainly on evaluating the effects of TWs on single-room configurations, leaving a significant gap in the literature regarding the assessment and optimization of a multi-story TW system. Addressing this gap represents a valuable opportunity to expand the applicability of TW technology for more complex architectural layouts.

This study contributes by developing an optimized multi-story Trombe Wall (MTW) that functions as a hybrid system for both heating and cooling. The study objectives are: (1) evaluating the thermal and energy performance of the proposed MTW; (2) optimizing the MTW design parameters to improve energy efficiency and thermal comfort in residential buildings located in hot climate regions; and (3) developing performance prediction equations to estimate the MTW’s thermal and energy performance.

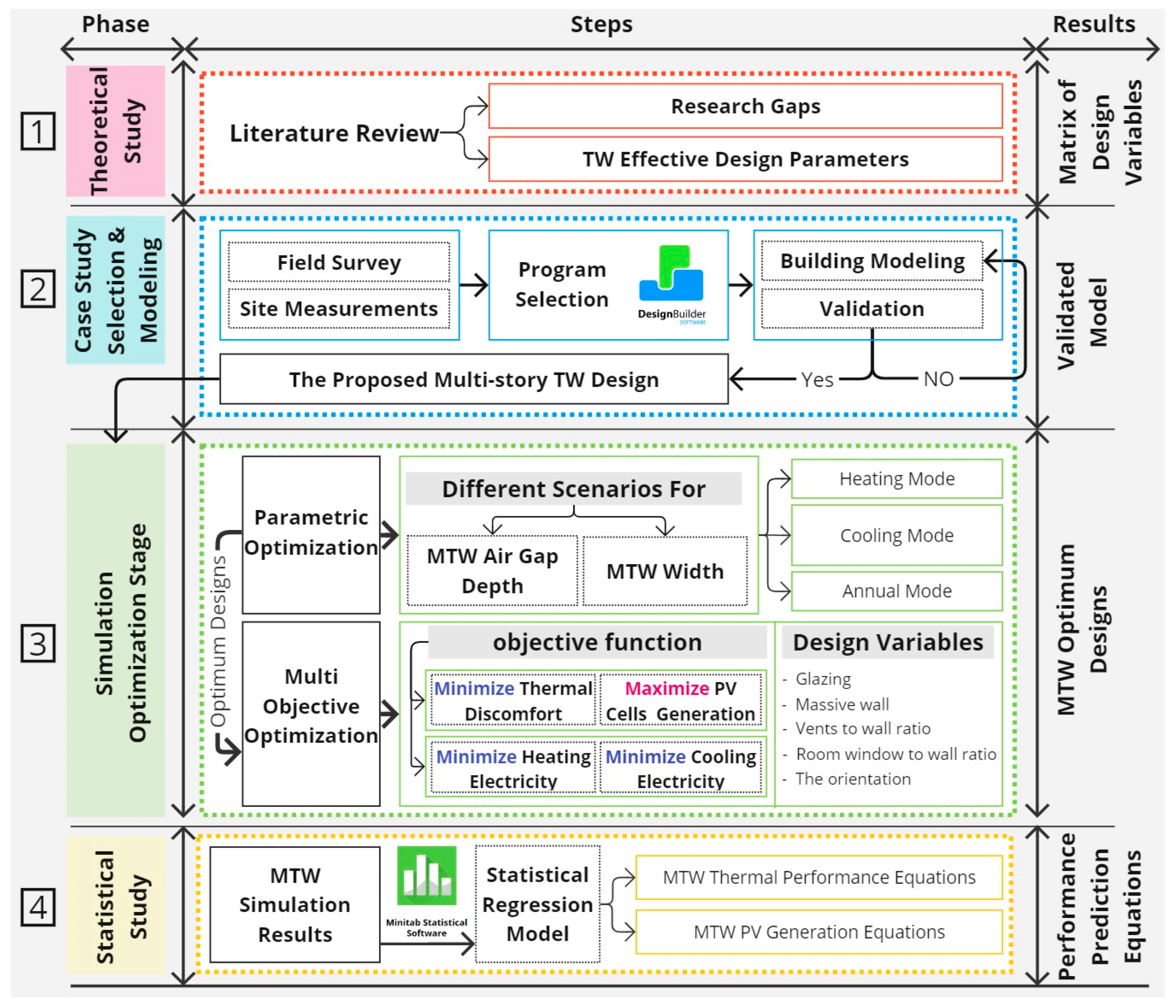
The research is structured into four distinct phases. Initially, TW design parameters’ geometric and thermal ranges and limitations were identified through a comprehensive literature review. Subsequently, a case study was selected, modeled, and validated based on field surveys and on-site measurements. Following this, a two-stage multi-objective simulation-optimization approach was conducted to identify the optimal configurations for the MTW. Finally, a multiple regression analysis was performed to develop predictive equations for the MTW’s performance.

2. Research Methodology

As shown in Figure 1, the proposed methodology consists of four main phases: In the first phase, the geometrical and thermal specifications and limitations of TW design parameters were determined based on a thorough literature review. Then, field measurements, modeling, and calibration were performed for a selected case study residential building in New Burj Al Arab City, Egypt, followed by proposing an MTW design (phase two).

The first and second phases would achieve the first objective. Subsequently, a two-stage simulation-optimization approach was applied to determine the impact of seven key design parameters on the proposed MTW system performance and to identify the optimal configurations of the MTW (objective 2). In the first stage, a parametric optimization was performed to investigate the impact of the MTW width and air gap depth and find their optimum values. In the second stage, a multi-objective simulation-optimization was conducted to find the near-optimum values of five design parameters: vents-to-wall ratio, room window-to-wall ratio, the massive wall, glazing, and building orientation, to maximize both the energy and thermal performance. Finally, a multiple regression analysis was performed to develop predictive equations for MTW performance (objective 3).

2.1. Identification of TW’s Most Effective Design Parameters

Here, TW’s most influential design parameters are identified by conducting a thorough literature review. Many studies discussed the various design parameters that affect TW performance. The design of TW and its components, including the massive wall, the air gap, the air vents, and the glazing layer, significantly influences its performance [21,30].

TW proportions have a significant impact on thermal and airflow performance. TW width-to-height ratio affects heat transfer and airflow rate. An optimal ratio of 1:5 resulted in the highest airflow rate [18]. Also, TW height directly influences airflow speed, where increasing the height of the TW results in an enhanced rate of air movement [24]. The optimal thermal performance is achieved when the air gap depth-to-height ratio is 0.05 [23], while another study determined the ratio to be 0.1 [31]. In addition, the optimum TW-to-wall area ratio is 37% in Mediterranean regions. This ratio can save approximately 32.1% of the annual heating consumption [32].

Numerous studies have investigated the performance of the massive wall, with particular emphasis on the influence of wall thickness and materials. These factors are directly linked to the U-value, which measures the heat transfer capability of the wall [33]. Most of these studies discussed the influence of varying the wall thickness between 0.1 and 1 m. For instance, utilizing 0.45 m of clay brick could achieve around 20% annual savings in heating electricity in Lyon, France [34]. In another investigation, the ideal thickness for stone was 34 cm, and for concrete, it was 32 cm; that could help to reduce heating loads by 50% [25]. Additional research has explored the integration of advanced materials, such as thermal insulators and PCM, to enhance the thermal properties of the walls and optimize their heat absorption and storage capabilities. The maximum operating time can be achieved while integrating phase change material with a 45 cm wall thickness [26]. Also, adding wool insulation to a gray color-painted massive wall reduces heating and cooling loads by 94% and 73%, respectively [12].

The performance of TW is considerably influenced by the airflow dynamics within the air gap. Many factors must be considered, especially the air gap thickness [30]. Most of the literature examined changing the air gap width between 5 and 80 cm. In a study in Kirkuk (Iraq), the massive wall has the maximum temperature at a 10 cm air gap width, while a 30 cm gap width would achieve the highest airflow rate [20]. Also, a 10 cm air gap showed the maximum air gap temperature of 30 °C in a CFD study using empirical data [35]. In addition, a 10 cm air gap thickness could achieve a maximum airflow rate of 120 m³/h [5].

The design of the vents significantly impacts TW thermal efficiency [30]. Previous investigations examined the application of various vent ratios, starting from 2% [36], and also altered the number of vents from an unvented condition [37] to a configuration with eight vents [38]. In their study, Kaya et al. examined the impact of the vent-to-wall-area ratio on TW performance for 11 different scenarios, from unvented to a 20% area ratio. Eight vents with an 8% vent-to-wall area ratio achieved the best performance [28]. In addition, controlling TW vent opening scenarios showed a reduction in heating demand by 71.7% and cooling demand by 36.1% in a warm climate and 18.2% and 42.4% in a cold climate [6]. Also, opening the air vent two to three hours after sunrise and closing it one hour before sunset could maximize heating efficiency [39].

The impact of received sunlight is directly connected to the specifications, thickness, and quality of the glass, making glazing an important factor influencing TW performance [40]. Due to its insulating properties, glass often causes substantial heat loss [41]. A glazing with a high solar heat gain coefficient (SHGC) and low heat transfer coefficient (U-value) can improve TW heating performance [22]. Studies have investigated the influence of various glazing types on TW efficacy, particularly glass with single and multi-layers. Argon-filled double glazing is more effective in reducing cooling energy than clear single and double glazing [42]. At the same time, low-e glass can improve heating performance in a ventilated TW [13]. Selecting the appropriate glazing-to-wall ratio and type could decrease the heating duration by 48.8%, leading to a 23.9% enhancement in comfort conditions [27].

As summarized in

Table 1. Summary of analysis of previous studies of TW.

Design Parameter	Location	Method	Studied Factors	H/C/V	Level	Studied Scenarios	Reference
Proportions	-	N	TW height	V	Single-story	-	[24]
	China	N	width-to-height ratio	V	Single-story	3 heights (2, 3, 4), 8 width scenarios (10 to 80 cm)	[18]
	Amman, Jordon	S	TW area ratio	H	Single-story	0:50%	[32]
	laboratory conditions	E	TW depth/height ratio	V	Single-story	0.025:0.1	[23]
	-	N	TW aspect ratio	H	Single-story	Width (0.1:0.6 m)–Height (1:3 m)	[31]
Massive wall	Tunisia	N	Wall thickness and material	H	Single-story	Four wall materials thickness (0.1:0.5 m)	[25]
	Sinai, Egypt	E & S	Wall color and insulation	H & C	Single-story	-	[12]
	Lyon, France	S	Wall thickness and material	H	Single-story	0.1 to 1 m and five wall materials	[34]
	-	N	wall thickness	H	Single-story	0.05 to 0.45 m	[26]
	Erzurum, Turkey	N	Wall colour and material	H	Single-story	-	[43]
Air gap	Kirkuk, Iraq	N	air gap thickness	H	Single-story	5 air gap scenarios (5:30 cm)	[20]
	-	N	air gap thickness	H	Single-story	9 air gap scenarios	[29]
	Tehran, Iran	S	air gap thickness	H & C	Single-story	5 air gap scenarios	[11]
	laboratory conditions	E	air gap thickness	V	Single-story	3 air gap scenarios (4:10 cm)	[5]
	-	N	air gap thickness	H	Single-story	6 air gap scenarios (10:30 cm)	[35]
Vents	Granada, Pisa, and Copenhagen	S	Vents opening scenarios	H & C	Single-story	-	[6]
	Perugia, Italy	N & S	Vent-to-wall area ratio	V	Single-story	6 vents area ratio scenarios	[44]
	Istanbul, Turkey	N	Vent-to-wall area ratio	H	Single-story	From unvented to 10 Vents with area from 0% to 20%	[28]
	Athens, Greece	S	extra window in the massive wall	H	Single-story	-	[37]
	Qinghai, China	N & E	opening and closing scenarios	H	Single-story	-	[39]
Glazing	Perak, Malaysia	N	Glazing type	H	Single-story	3 glazing types	[42]
	Tabriz, Iran	N & S	Glazing type and glazing to wall ratio	H & C	Single-story	4 glazing types for three ratios	[27]
	Izmir, Turkey	E	Single, double glass and semi-transparent PV	H	Single-story	3 glazing types	[45]
	-	N	glass blocks	H	Single-story	One glazing type	[46]
	Nanjing, China	N & S	Ventilated low-e glass TW	H	Single-story	One glazing type	[13]
Multiple design parameters	Iberian Peninsula	S	Shading, thermal mass, air gap width, and vents dimensions	H & C	Single-story	-	[40]
	Alexandria, Egypt	N & S	TW height, air gap depth, and massive wall thickness	H	Single-story	-	[47]
	Sichuan, China	N & S	TW-to-wall ratio, glazing angle, wall depth and material, and air gap depth	H	Single-story	-	[48]
	Ancona, Italy	N	Glazing and frame type wall thickness and material	H & C	Single-story	2 wall materials, 2 wall thicknesses, 2 glazing types	[14]

Note: Simulation (S); Numerical (N); Experimental (E); Heating (H); Cooling (C); Ventilation (V).

, the previous analysis highlights the significant influence of TW design parameters, including proportions, the massive wall, the air gap, vents, and glazing, on its performance. Selecting the optimal combination of these parameters, tailored to the specific climatic conditions, can enhance TW’s efficiency and reduce energy consumption.

The design variables of MTW were identified based on insights from previous studies. Particular consideration was given to the dimensions of the photovoltaic cell network, ensuring its integration was reflected in adjustments to the Trombe Wall’s width ratios and the air gap depth. The selection prioritized locally available building materials for the wall and glazing parameters while ensuring a broad range of variability in thermal properties, especially the U-value. Additionally, orientation was incorporated as a critical variable, given its significant influence on the timing and intensity of solar radiation incidents on the Trombe Wall. Figure 2 displays the matrix of design variables.

2.2. Case Study Selection and Modeling

2.2.1. Location and Climatic Conditions

In this study, New Borg El Arab is selected as a case study. New Borg El Arab is located in the northwestern region of Egypt, within the Alexandria Governorate. It lies approximately 60 km southwest of Alexandria city and about 7 km from the Mediterranean coast. The city’s geographical coordinates are approximately 30°52′54″ North latitude and 29°34′40″ East longitude. According to the Köppen Climate Classification, New Borg El Arab experiences a hot desert climate (BWh). Summers are typically long, hot, and arid, while winters are cooler and rainy. The average temperature in January, the coldest month, is approximately 15 °C, while in August, the warmest month, it averages around 27.5 °C [49].

2.2.2. Building Design and Construction

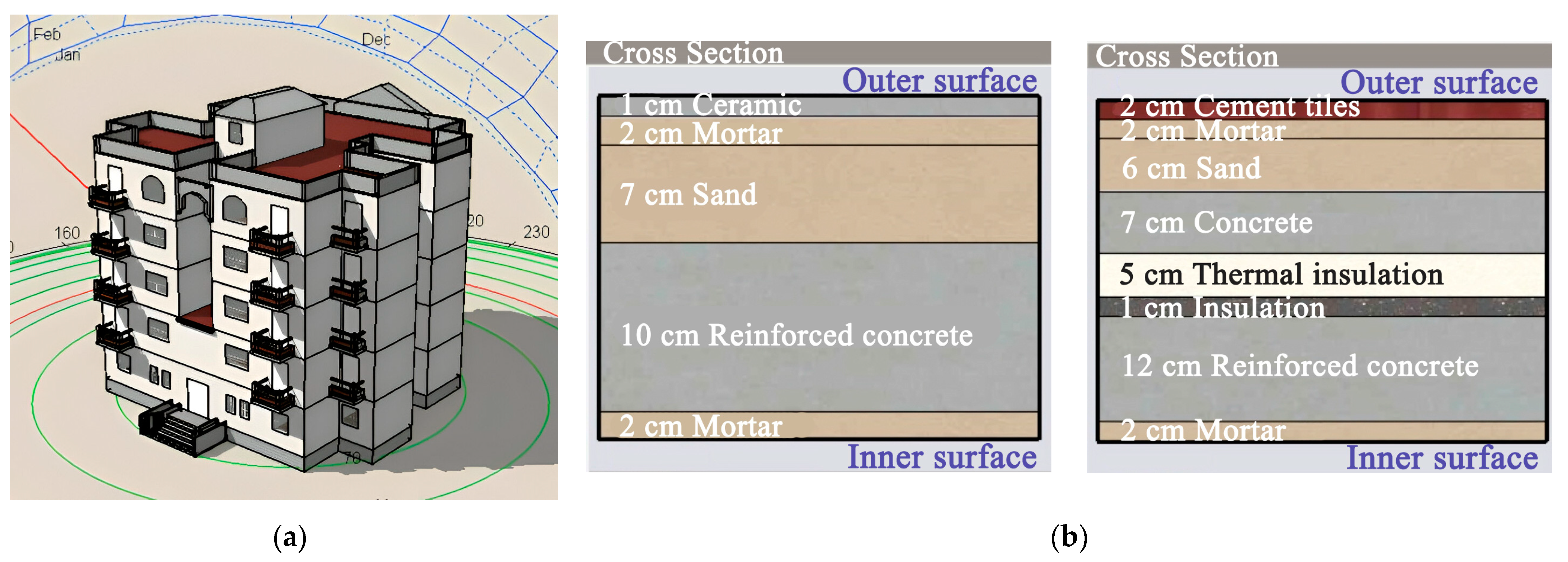
Figure 3a shows a typical residential building within the Egyptian-Japanese University’s housing complex in New Borg El Arab City. The complex comprises 28 identical detached residential buildings, organized into two groups of 14 buildings each, as shown in Figure 3b. Each building features a ground floor and four repetitive upper floors, with a floor height of 3 m and a total floor area of 325 m².

Figure 3c presents the standard floor plan, which includes four residential units per floor. Each unit comprises a reception area, a kitchen, a bathroom, and two bedrooms, each with a small terrace. The building is constructed with a reinforced concrete frame structure, incorporating red brick walls for both exterior and interior partitions. Details of the building envelope’s physical components—such as walls, roofing, flooring, and glazing—were obtained from the design drawings and are summarized in

Table 2. The building construction details.

Item	Thickness	Construction	U-Value
Roof	36 cm	Cement roof tiles 2 cm, mortar 2 cm, sand 6 cm, plain concrete 7 cm, thermal insulation (foam) 5 cm, waterproof insulation (bitumen) 2 cm, reinforced concrete slab 12 cm, mortar 2 cm.	0.458 W/m2K
Floors	24 cm	Ceramic tiles 1 cm, mortar 2 cm, sand 7 cm, reinforced concrete slab 12 cm, mortar 2 cm.	2.374 W/m2K
Outer walls	29 cm	Plaster 2 cm, brick 25 cm, plaster 2 cm.	1.303 W/m2K
Inner walls	16 cm	Plaster 2 cm, brick 12 cm, plaster 2 cm.	1.705 W/m2K
Ground floor	37 cm	Ceramic tiles 1 cm, mortar 2 cm, sand 7 cm, concrete 15 cm, waterproof insulation (bitumen) 2 cm, concrete 10 cm.	0.879 W/m2K
Windows	3 mm	Clear single glazing (3 mm) with a 5 cm aluminum frame.	5.894 W/m2K

.

2.2.3. Modeling and Validation

DesignBuilder v7 was utilized for building simulation, as it is a versatile software widely recognized for simulating building designs to improve energy efficiency and occupant comfort [47,50]. It takes into account the impact of different parameters, including air movement, pressures, and velocity and their effects on heat transfer [51].

The building model was developed by providing all relevant details as inputs; the boundary conditions were established using real hourly weather data for New Burj Al Arab City, Egypt, to account for variations in ambient temperature, solar radiation, and wind speed. The external surfaces were exposed to dynamic environmental conditions, while internal surfaces were influenced by heat transfer between adjacent zones. The simulation incorporated natural ventilation as the primary airflow mechanism. Also, the simulation considered the stack effect and pressure-driven ventilation, with airflow rates and velocities dynamically adjusted based on temperature differences between the indoor and outdoor environments. The building model was developed by providing all relevant details as inputs, including user profiles, and comprehensive specifications of the building and its components specifications based on building designs and field surveys. Figure 4a,b shows the building model and the building’s floors and roof cross-sections.

A timestep of 10 was selected. The timestep represents the discrete time interval at which calculations and system updates occur during the simulation. More timesteps per hour enhance accuracy but increase computational load. Simpler models may yield reliable results with fewer timesteps (e.g., 2 per hour), while more complex systems (e.g., containing HVAC systems) typically require 6 or more [51]. Therefore, a timestep of 10 was selected to ensure a balance between computational efficiency and result accuracy. The initial and boundary conditions were summarized in

Table 3. The initial and boundary conditions.

Parameter	Condition/Value	Parameter	Condition/Value
Location	New Burj Al Arab City, Egypt	Time Step per hour	10
Weather Data	Hourly real weather data Includes temperature, solar radiation, wind speed, and humidity	Indoor Boundary Conditions	Modeled dynamically
Infiltration Rate	0.7 ACH (Air Changes per Hour)	Initial Indoor Temperature	Dynamic adaptation based on climate.
Outdoor Boundary Conditions	(Weather file-driven) Varies based on real weather data	Surface Convection	Uses EnergyPlus heat transfer algorithms (TARP and DOE-2)

.

The actual temperatures can be compared with the simulation results to verify the accuracy of the simulation model and the extent to which its results are consistent with the actual reality in the interior spaces. The actual indoor temperatures were measured in Room a on July 25 for 24 h, and a comparison was made between the measured and simulated results during the same period. The validation was conducted only for 24 h due to data limitations and the challenges of collecting real-world measurements in an occupied building. Many studies have conducted validation within similar or even shorter time frames. For instance, Cheng et al. validated a passive solar room by comparing simulated and measured indoor temperature data over a 24 h period starting at 8:00 a.m. [52]. Similarly, Friji et al. compared measured and modeled temperatures from 10:00 a.m. to 4:00 p.m. [35]. Additionally, Zhang et al. validated a test room by comparing numerical and experimental indoor temperature data from midnight on 10 January to 6:00 p.m. on 11 January [48].

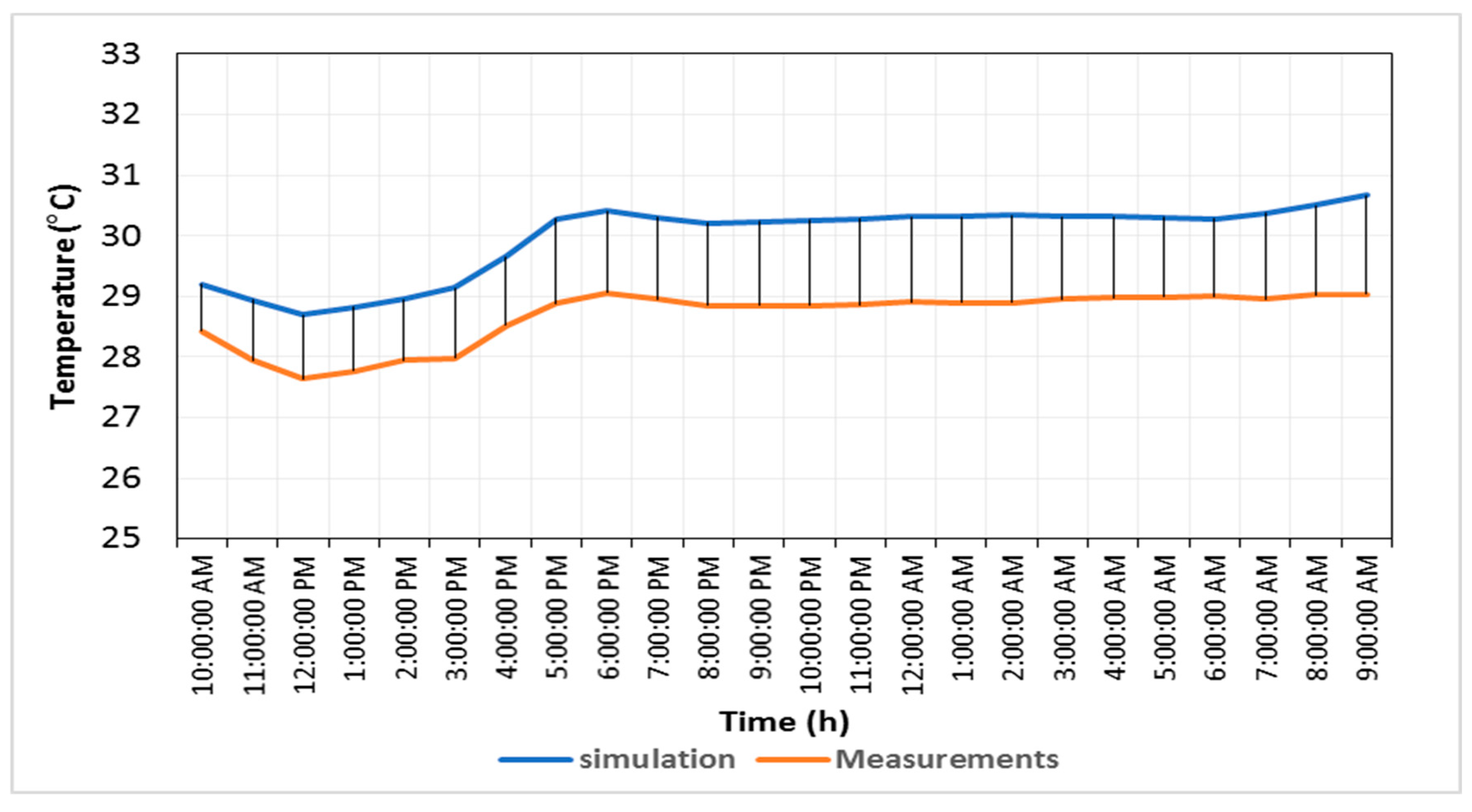
As shown in Figure 5, the results showed that the largest value of the change was 1.63 °C and the smallest was 0.77 °C. Generally, there is an agreement and consistency between the actual measurements and the simulation results.

To validate the accuracy of the simulation results, a comparative analysis was performed between the measured and simulated data. The Root Mean Square Error (RMSE) and Relative Error (RE) were utilized as evaluation metrics [53]. The calculation equations are as follows:

$$RMSE=\sqrt{{\displaystyle \frac{\sum _{i=1}^n{(T_{measured}-T_{simulated})}^2}{N}}},$$

(1)

$$RE={\displaystyle \frac{T_{measured}-T_{simulated}}{T_{measured}}}\times 100,$$

(2)

where T is the temperature and N is the number of measurements.

The analysis yielded an average relative error of 4.45%, demonstrating a strong agreement between the simulated results and the measured data [35]. Furthermore, the RMSE was 1.33, within the acceptable calibration threshold of 1.5 [54]. These findings confirm the reliability of the computational simulation and its suitability for evaluating the performance of the proposed system. Measured and simulated indoor temperatures in Room (a) on 25 July, which were used for estimating the values of the RE and RMSE, are available in

Table A1. Measured and simulated indoor temperatures in Room (a) on July 25.

Coefficient	Measured	Simulated	Difference
10:00:00 a.m.	28.43	29.2	0.77
11:00:00 a.m.	27.95	28.94	0.99
12:00:00 p.m.	27.64	28.6	0.96
1:00:00 p.m.	27.77	28.82	1.05
2:00:00 p.m.	27.94	28.96	1.02
3:00:00 p.m.	28.15	29.14	0.99
4:00:00 p.m.	28.52	29.66	1.15
5:00:00 p.m.	28.89	30.28	1.39
6:00:00 p.m.	29.07	30.41	1.34
7:00:00 p.m.	28.96	30.31	1.36
8:00:00 p.m.	28.85	30.21	1.36
9:00:00 p.m.	28.85	30.24	1.40
10:00:00 p.m.	28.85	30.26	1.42
11:00:00 p.m.	28.86	30.28	1.42
12:00:00 a.m.	28.91	30.32	1.42
1:00:00 a.m.	28.90	30.32	1.42
2:00:00 a.m.	28.90	30.34	1.44
3:00:00 a.m.	28.96	30.32	1.36
4:00:00 a.m.	28.97	30.32	1.35
5:00:00 a.m.	28.99	30.3	1.31
6:00:00 a.m.	29.00	30.28	1.28
7:00:00 a.m.	28.95	30.38	1.43
8:00:00 a.m.	29.03	30.5	1.47
9:00:00 a.m.	29.04	30.67	1.63

in Appendix A.

2.2.4. The Proposed Multi-Story Trombe Wall Design

The proposed TW design was developed as a multi-story system to accommodate the maximum number of rooms in a vertical configuration. The MTW has a 375 cm width and a 30 cm depth, featuring a 25 cm brick wall, with upper and lower vents of 0.4 m² on each floor and 6 mm clear glazing. It was integrated with the southeast-facing bedrooms.

PV blind was integrated and connected to the massive wall, adding the functionality of electricity generation. Also, the PV position can significantly minimize thermal gain into rooms since the PV cells operate as an absorber, blocking transmitted radiation. Consequently, it can control heat transfer to the interior, particularly during the summer [22].

Table 4. The PV cell specifications.

Specification	Unit	Specification	Unit
Cell Type	Monocrystalline	Maximum Power Voltage	18.6 V
Module Area–Number of Cells	0.13 m2–36 cells	Open Circuit Voltage (Voc)	22.9 V
Rated Electric Power	20 W	Maximum Power Current	1.08 A
Operating Temperature	−40 °C to 85 °C	Short Circuit Current (Isc)	1.12 A

shows the PV cell specifications.

As depicted in Figure 6, two operational modes were designed for the MTW system: one for heating and one for cooling. In the heating mode, the room window is closed, the upper and lower vents in the massive wall are opened, and the PV blind is positioned horizontally to facilitate direct heat transfer through the massive wall. Conversely, in the cooling mode, the room window is opened, the upper vents are sealed, the lower vents are left open, and the PV cells are placed vertically to minimize heat transfer through the wall.

2.3. Simulation-Optimization

Simulation tools (e.g., building energy simulation programs) can solely evaluate the impact of design variables on defined performance measures. On the other hand, optimization finds the optimum or near-optimum design variables that obtain the best performance measures. However, optimization still requires the output from simulation to evaluate the goodness of a solution. Therefore, there is a need to integrate simulation and optimization in one approach, called simulation-optimization [55]. This study applied this approach to find the near-optimum design variables of the proposed multi-story Trombe Wall (MTW).

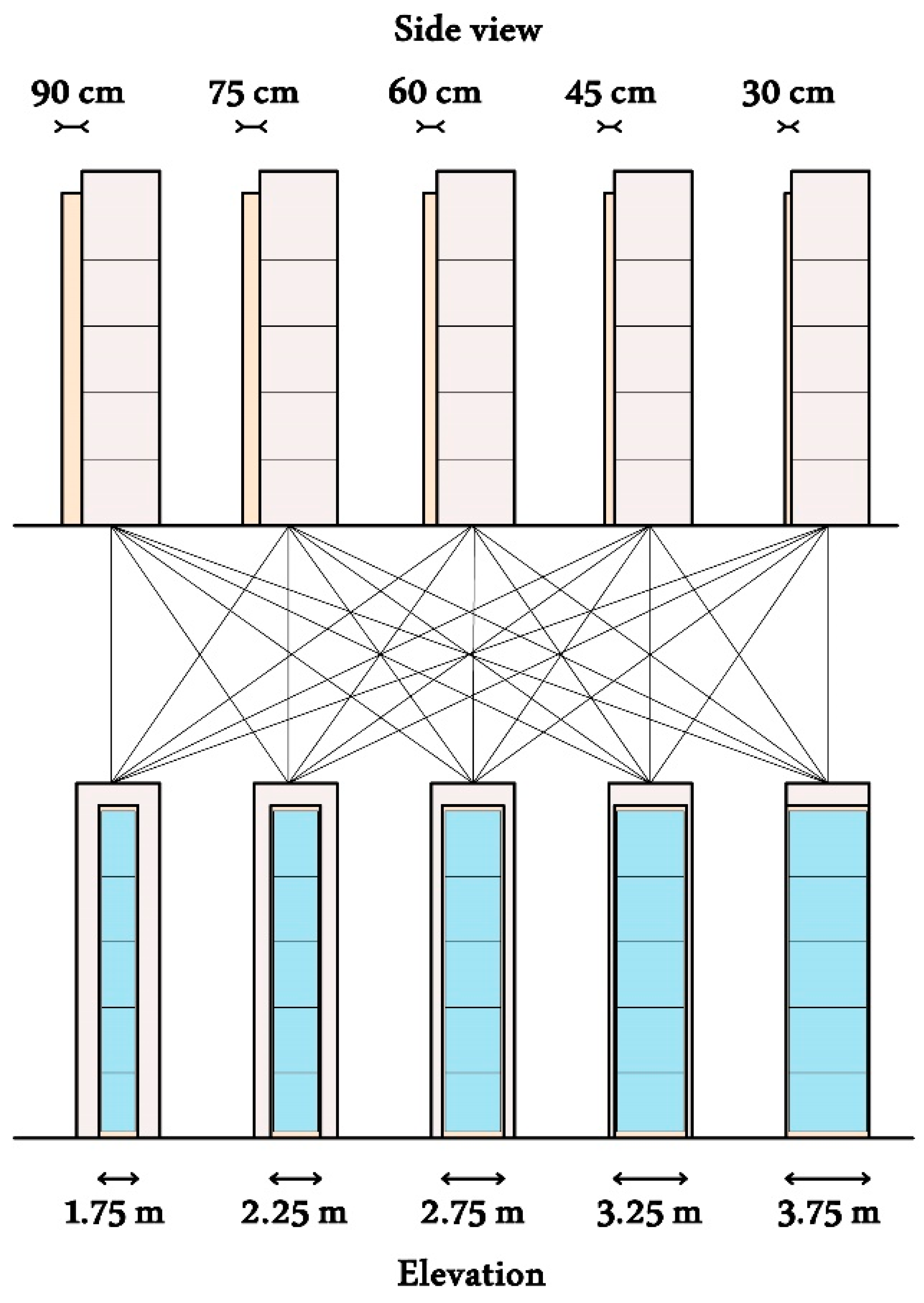
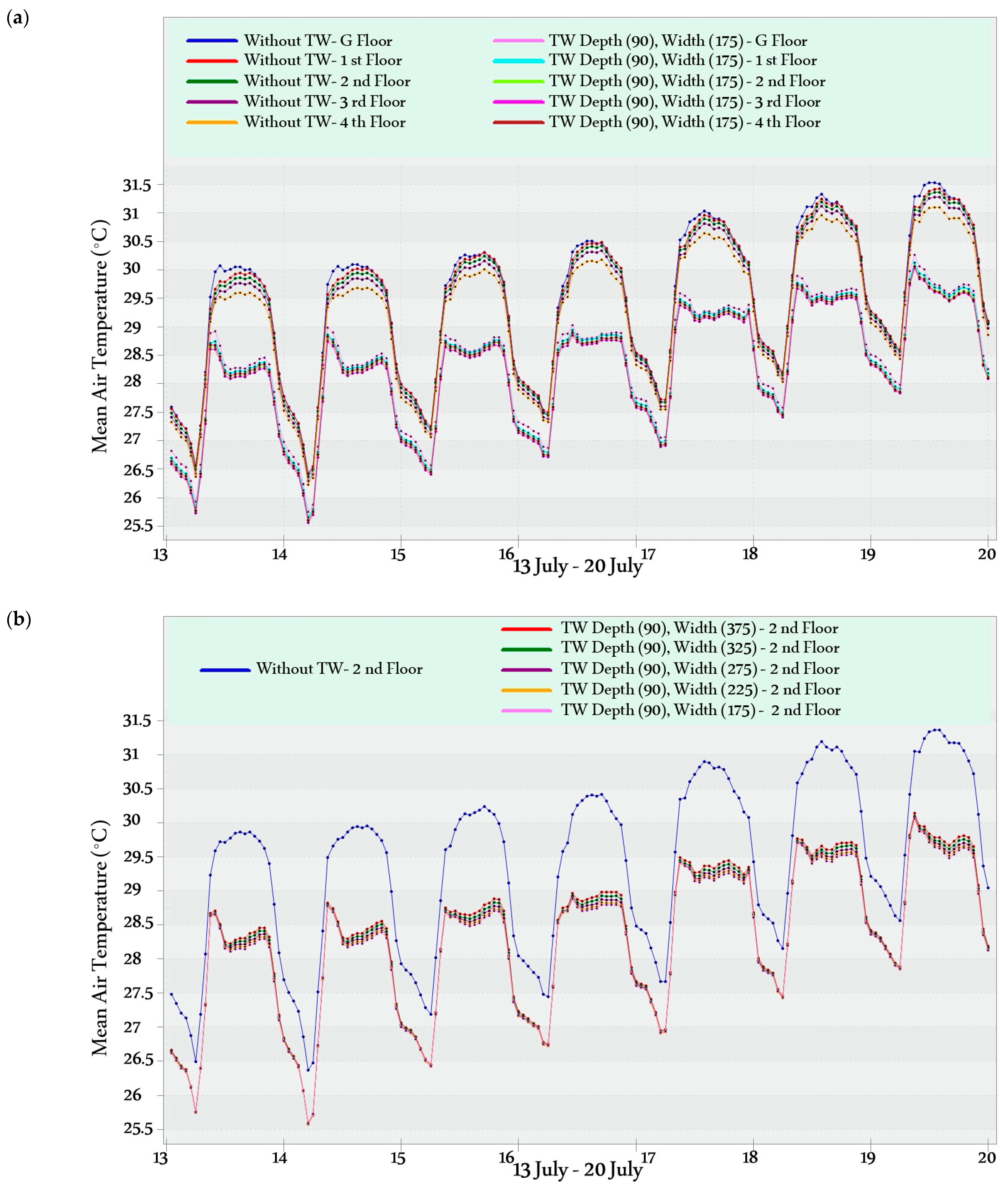
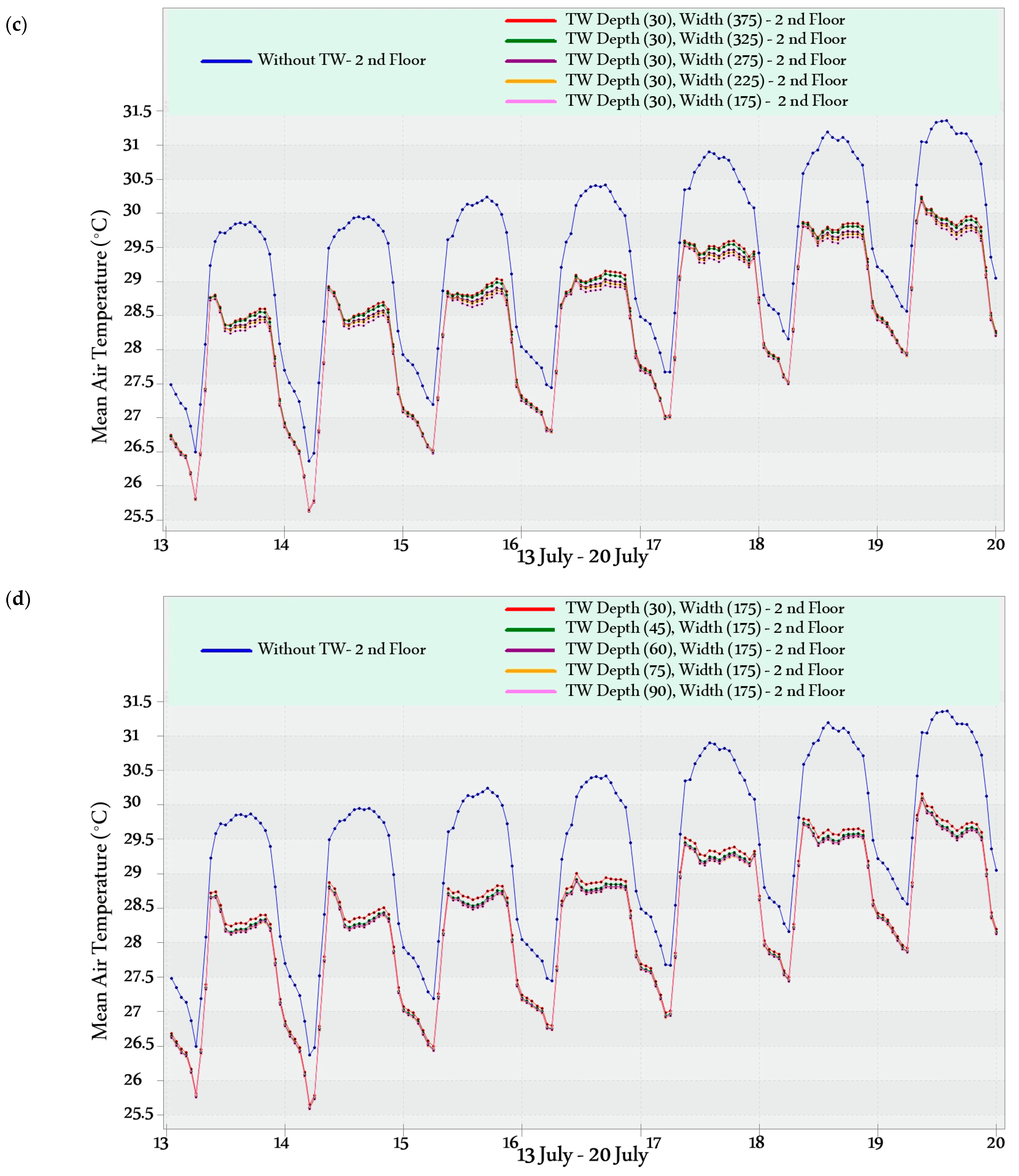
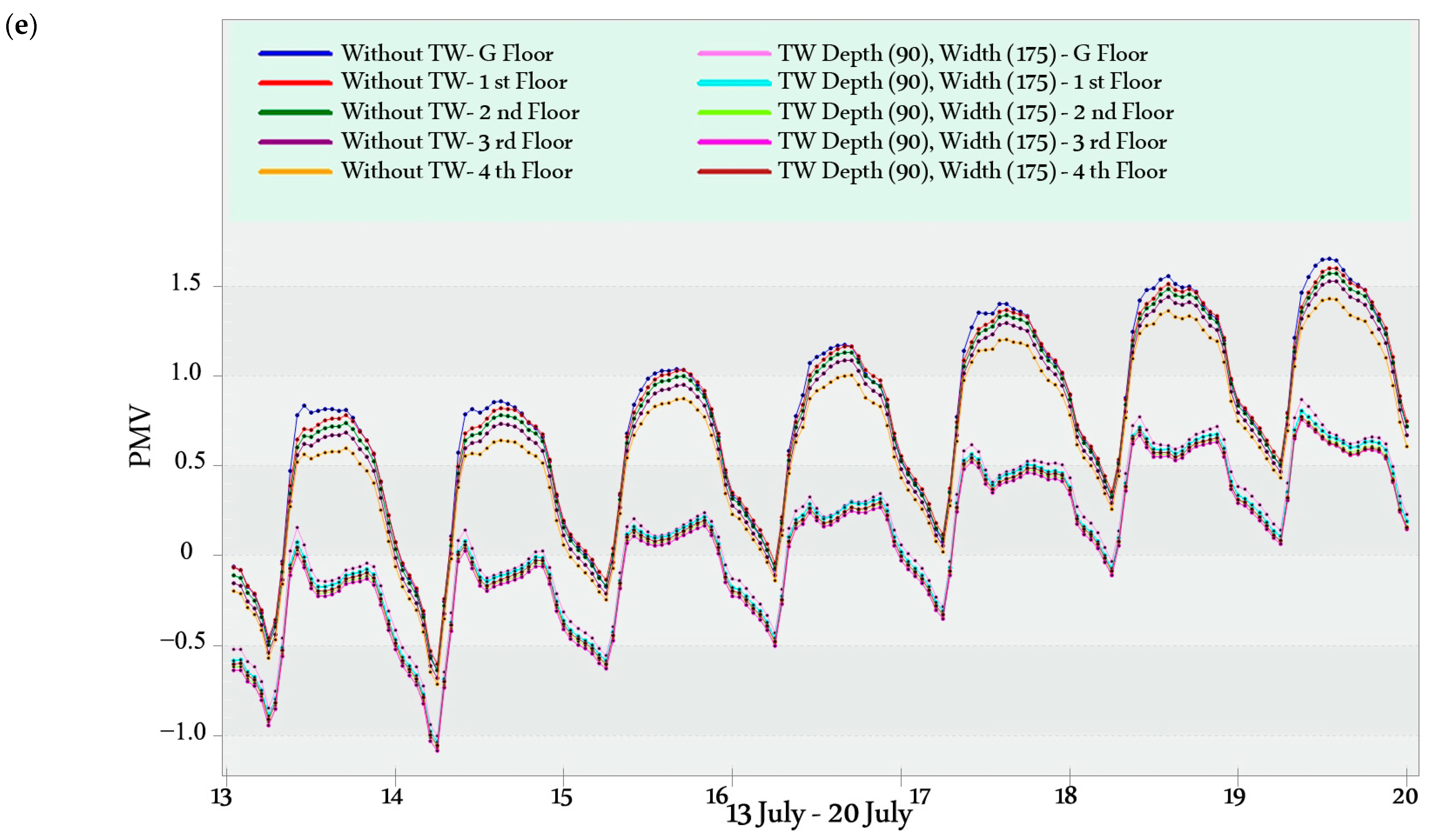
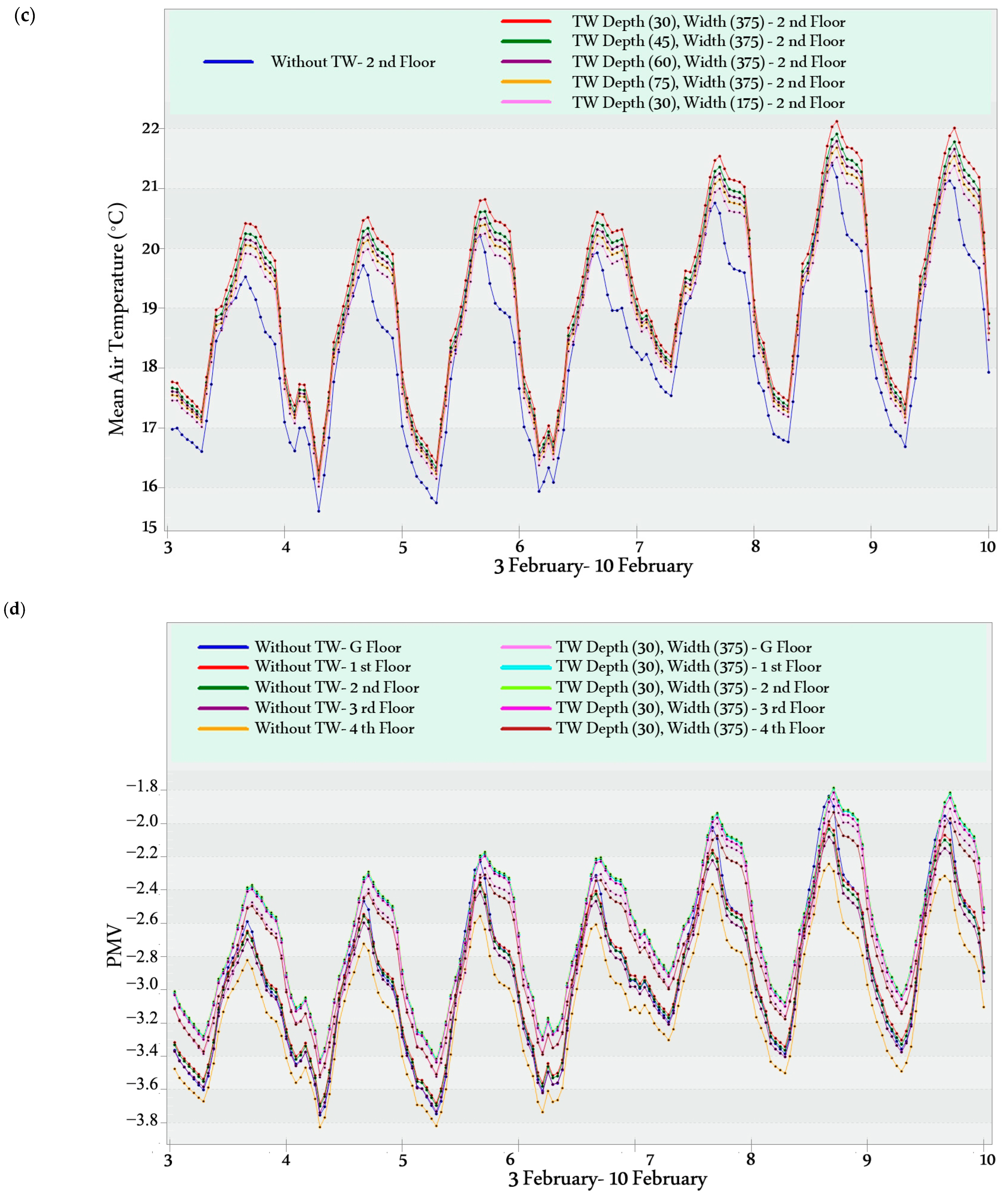
The simulation-optimization was conducted in two stages [56]. In the first stage, parametric optimization is conducted to investigate the impact of varying the MTW width and air gap depth. The width was adjusted between 175 cm and 375 cm in increments of 50 cm, while the air gap depth ranged from 30 cm to 90 cm, with 15 cm intervals resulting in 25 design alternatives, as shown in Figure 7. Then, a simulation evaluation of these 25 design alternatives is conducted to obtain the optimum MTW width and air gap depth (i.e., full enumeration).

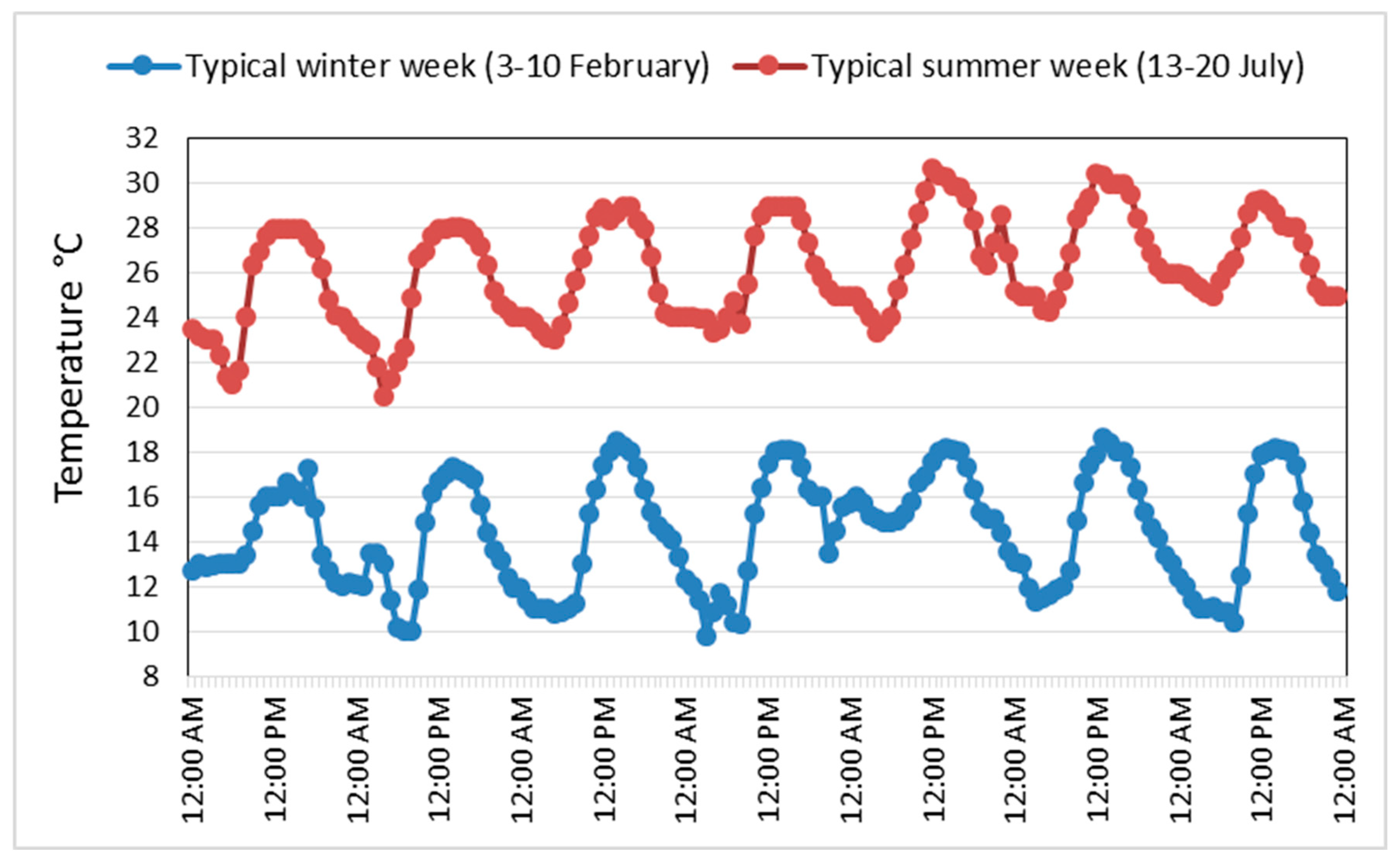
The simulation was conducted to evaluate hourly temperatures and Predicted Mean Vote (PMV) values during a typical winter week (3–10 February) and a typical summer week (13–20 July). A typical week is identified as a representative period that characterizes the climatic conditions of a specific season [51]. Figure 8 shows the design temperature in the typical winter week and the typical summer week. The PMV metric assesses thermal comfort from −3 (cold) to 3 (hot), with 0 representing optimal comfort. The advised PMV range for satisfactory thermal comfort is between −0.5 and 0.5 [57].

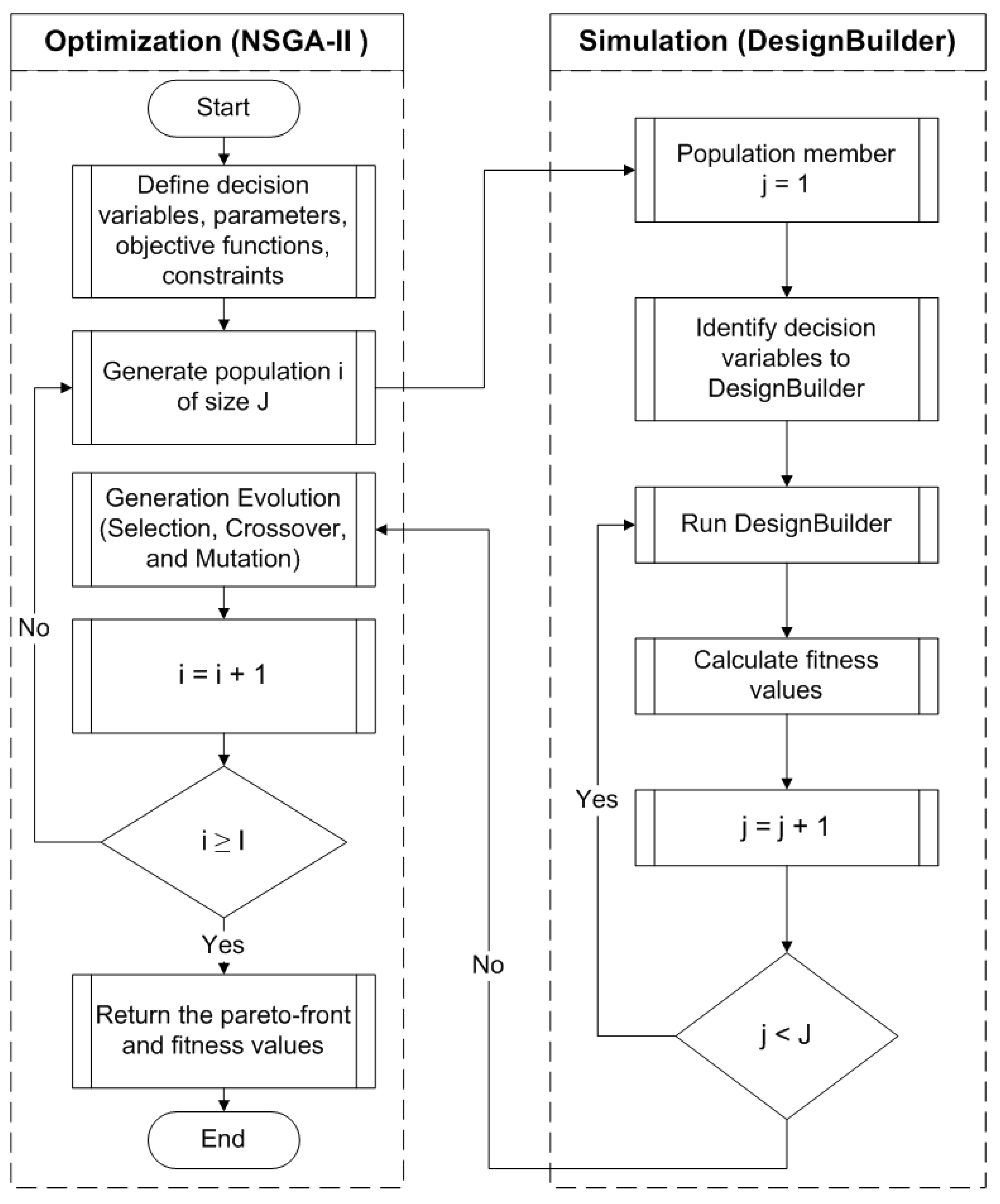
In the second stage, a multi-objective simulation-optimization is conducted, as shown in Figure 9. This figure shows the integration between simulation and optimization. This study uses the non-dominated sorting genetic algorithm (NSGA II) as the optimization algorithm. Previous studies demonstrated the efficiency of NSGA II in solving complex multi-objective simulation-optimization problems [58,59,60]. Firstly, the decision variables, parameters, objective functions, and constraints are defined. The decision variables are the design parameters of MTW (i.e., glazing, the massive wall, the vents-to-wall ratio, the room window-to-wall ratio, and the orientation). The optimum MTW width and air gap depth values obtained from the first stage are defined as optimization parameters in this stage. The objective functions are: (1) maximizing the PV cell energy generation rate and minimizing thermal discomfort according to ASHRAE 55 Adaptive 80% Acceptability; and (2) minimizing heating and cooling electricity. ASHRAE 55 is among the most widely utilized adaptive thermal comfort models globally. It indicates whether the indoor temperature aligns with the 80% acceptability limits for adaptive comfort [61].

The constraints represent the value ranges of decision variables, discussed previously in Figure 2. The second step is randomly generating an initial population of size J, where each member (j) represents a unique combination of decision variables. DesignBuilder evaluates each member performance. After estimating the values of all members of the population, they are ranked using the non-dominated sorting, and the best Pareto front is updated. Selection, crossover, and mutation processes are repeated until generating a new population. Each new population undergoes fitness evaluation in DesignBuilder, followed by repeated cycles of selection, crossover, and mutation until reaching the predefined maximum number of generations (I).

2.4. Regression Analysis

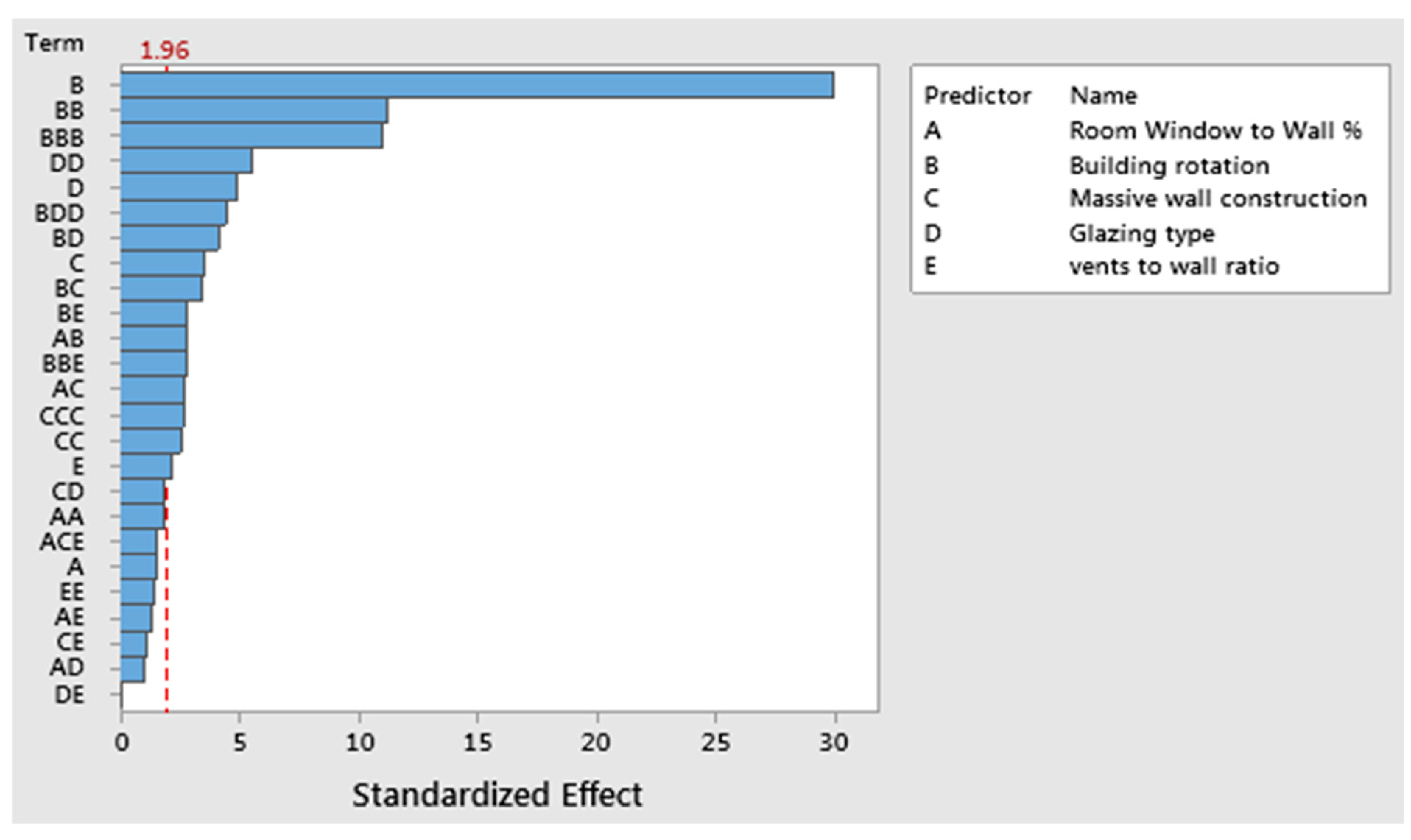
A multiple regression analysis using the least squares method was conducted via Minitab^® 19.1 statistics software [62] to examine the Model Sensitivity and to develop a regression model for the MTW system. The “multiple regression” tool is utilized to explain the relationship between a set of predictors (×1, ×2, ×3, etc.) and the response variable (Y). The general formula for multiple regression is represented as:

$$Y={\beta }_0+\sum _{i=1}^n{\beta }_i{X}_i+\sum _{i=1}^n{\beta }_{ii}{X}_i^2+\sum _{i=1}^n{\beta }_{iii}{X}_i^3+\sum _{i\ne j}{\beta }_{ij}{X}_i{X}_j+\epsilon ,$$

(3)

where $Y$ is the dependent variable: $X_1$, $X_2$,…, $X_n$ are the independent variables; ${\beta }_0$ is the intercept; ${\beta }_i,{\beta }_{ii},{\beta }_{iii}$ are the linear, quadratic, and cubic coefficients; ${\beta }_{ij}$ represents interaction terms ($X_i,X_j$, capturing interactions between predictors); and $\epsilon$ is the error term.

The predictors corresponded to five design variables: the type and thickness of the massive wall, the type and thickness of the glazing layer, the vent-to-wall ratio, the window-to-wall ratio, and the orientation. The response variable was determined as PV energy generation rates and the number of discomfort hours. Using the regression model, equations were generated to predict the number of discomfort hours and PV generation rates.

3. Results

3.1. MTW Model Sensitivity

The model sensitivity was assessed using simulation results and Minitab^® statistical and data analysis software to evaluate the impact of the design parameters on the performance of the Multi-Story Trombe Wall (MTW). Sensitivity analysis was conducted to verify the influence of these design variables, ensuring a more robust model.

As shown in Figure 10, the Pareto chart presents the absolute values of the standardized effects, ranking them from the largest to the smallest. Additionally, it includes a reference line (appears as a red dotted line in Figure 10) to identify statistically significant effects. This approach highlights not only the individual significance of each design parameter but also their interactions. The analysis confirms that all five MTW design parameters—the massive wall, glazing, vent-to-wall ratio, room window-to-wall ratio, and orientation—along with their interactions, have a substantial influence on MTW performance in terms of both energy generation and thermal comfort.

3.2. The Influence of MTW Configuration

The impact of 25 design alternatives of MTW width and air gap depth variations on thermal performance and PV generation was investigated for the heating and cooling modes.

3.2.1. The MTW Thermal Performance

At Cooling Mode: A consistent reduction in room temperatures across all floors throughout the testing period was observed. The most significant temperature reductions occurred during the peak heating hours, from 9:00 a.m. to 10:00 p.m., during which the base case exhibited the highest temperatures. Additionally, the implementation of the MTW contributed to enhanced temperature stability within the rooms. The observed temperature reductions ranged from 0.81 °C to 1.94 °C. Figure 11a presents a comparison of indoor temperatures across the five floors between the base case (without the Trombe Wall) and the scenarios incorporating the multi-story Trombe Wall (MTW) with a 90 cm depth and 175 cm width.

Throughout the measurement period, a notable temperature reduction is observed for all air gap depths. The reduction values converge across the different widths, with a slight variation of up to 0.22 °C between the widest and narrowest configurations. Consequently, a width of 175 cm is deemed optimal for the cooling period, as expected, since narrower widths mean less solar radiation reaches the MTW. Figure 11b,c compares indoor temperatures between the base case and the MTW, with the air gap depth fixed at 90 cm and 30 cm, respectively, and the width varying from 375 cm to 175 cm.

A temperature reduction is evident across all air gap depths compared to the base case. Although the temperature reduction is relatively consistent across the depths, a 90 cm depth achieves the most substantial decrease, making it the most effective configuration during the cooling period. Figure 11d highlights the effect of varying the air gap depth while maintaining a constant width of 175 cm.

Implementing the MTW resulted in a noticeable reduction in PMV values throughout the entire testing period. This improvement translated into a 40% increase in hours within the thermal comfort range. Figure 11e compares PMV values across the five floors between the base case and the optimal MTW configuration, incorporating the optimal width and air gap depth for cooling mode. Overall, the integration of the MTW significantly reduced indoor temperatures and enhanced thermal comfort during the cooling period.

At Heating Mode: An increase in room temperatures is observed across all floors throughout the test period, as shown in Figure 12a, which presents a comparison of room temperatures across the five floors for the base case (without the Trombe Wall) and the scenario with the MTW implemented.

The results reveal a positive correlation between the MTW width and the room temperatures, which can be attributed to the increased solar radiation captured by the MTW. The maximum temperature increase, ranging from 0.25 °C to 1.55 °C, is recorded at a width of 375 cm. From 10:00 a.m. to 6:00 p.m., no temperature increase is observed for MTW widths of 175 cm and 225 cm. Figure 12b compares room temperatures between the base case and the MTW, with the MTW air gap depth fixed at 30 cm and the width varying from 375 cm to 175 cm.

As the depth decreases, room temperatures increase, with the maximum temperature rise (up to 1.56 °C) observed at a depth of 30 cm. This indicates that a depth of 30 cm is the optimal configuration for the heating mode. Figure 12c demonstrates the relationship between the MTW air gap depth and temperature.

Implementing the MTW resulted in an increase in PMV values across the entire test period. However, this increase did not move PMV values into the thermal comfort range. Figure 12d compares the PMV values for the five floors between the base case and the MTW configuration with the optimal width and air gap depth for heating mode. Finally, it is evident that in heating mode, variations in width and depth have a more significant impact on MTW performance compared to the cooling mode.

3.2.2. The MTW PV Generation

The average generation rate for each mode was calculated based on the PV cell area, which varies with the MTW width. During cooling mode, the average generation rate was 815 kilowatts per square meter, compared to 572 kilowatts per square meter in heating mode. The lower power output in heating mode is primarily attributed to the horizontal alignment of the PV cells, which leads to shading. Adjusting the MTW width or depth has minimal influence on the average energy generation rate per square meter of PV cells. Consequently, the alignment and total surface area of the PV cells remain the primary factors determining electricity output.

The actual temperature of the photovoltaic (PV) module and its corresponding efficiency during the simulation were determined based on the Nominal Operating Cell Temperature model, which accounts for ambient conditions and solar radiation. The PV module temperature ranged between 20.48 °C and 59.8 °C in summer and between 11 °C and 40.9 °C in winter, depending on the time of day. Consequently, the maximum PV efficiency was 17.56% in summer and 18.29% in winter, and the minimum was 14.8% in summer and 16.15% in winter.

Table 5. PV cell electricity generation for cooling and heating modes.

MTW Width	1.75	2.25	2.75	3.25	3.75	Avg Generation	Module Temperature (°C)		PV Efficiency %
PV Cells Area (m2)	2.5	3.5	4.5	5.5	6.5		Max	Min	Max	Min
Cooling mode generation (kW)	2039	2855	3671	4487	5303	815 kW/m2	59.8	20.48	17.56	18.29
Heating mode generation (kW)	1355	2002	2640	3282.5	3682	572 kW/m2	40.9	11	14.8	16.15

summarizes the electricity generation rates of photovoltaic (PV) cells for both heating and cooling modes.

3.2.3. The Selected MTW Width and Air Gap Depth for the Annual Mode

In this section, the MTW width and air gap depth for the annual mode were obtained based on the analysis in the previous sections. As outlined in the analysis of the heating mode, increasing the width and reducing the depth of the MTW is preferred, whereas the opposite is true for the cooling mode. Consequently, identifying the most suitable annual operational mode is essential to optimize yearly performance.

The analysis of the heating and cooling modes results highlights that adjustments to the MTW width during the cooling period have a minimal effect, with only slight temperature variations observed. These variations are particularly noticeable between 1:00 p.m. and 8:00 p.m., where the temperature difference between the largest and smallest widths remains below 0.2 °C. In contrast, width adjustments during heating have a more pronounced and consistent impact throughout the day. Widths of 175 cm and 225 cm could not achieve the desired temperature improvements, especially between 10:00 a.m. and 6:00 p.m. Moreover, increasing the width enhances thermal performance, making the 375 cm width optimal for year-round operation. Regarding depth, its influence during the cooling period is limited compared to the heating period. Thus, a depth of 30 cm is deemed the most appropriate for the MTW’s annual operation. PV cells were aligned vertically, similar to their configuration in the cooling mode, as this orientation resulted in higher electricity generation.

3.3. The MTW Design Parameters Optimization

A multi-objective optimization was conducted, based on the results from the parametric optimization. The parameters of the optimization algorithm were set as follows: a population size of 50, maximum generations of 500, a mutation rate of 0.5, and a crossover rate of 0.9 [51]. The simulation-optimization experiments were conducted on a workstation (Intel(R) Xeon(R) Gold 6230R CPU @ 2.10 GHz and 128 GB Random Access Memory (RAM)) with an average computational time of 12 h for each experiment. The width and air gap depth were set to 175 cm and 90 cm for the cooling mode and 375 cm and 30 cm for the heating mode, reflecting the optimal scenarios identified in the parametric optimization.

3.3.1. Regarding the Cooling Mode

The scatter plot in Figure 13, illustrates the multi-objective optimization result for the cooling mode, aimed at minimizing thermal discomfort and maximizing electricity generation. The Pareto front (highlighted in red) represents the optimal trade-offs between these two objectives, while the gray points indicate non-optimal solutions from previous generations.

In multi-objective optimization, the Pareto front represents solutions that outperform all others within the search space. This provides the designer with a range of optimal choices to select from [63]. In DesignBuilder, generated electricity is represented with a negative sign, whereas consumed electricity is indicated with a positive sign.

A clear inverse relationship is observed between discomfort hours and electricity generation. Reducing discomfort leads to a reduction in electricity generation. This indicates a trade-off where improving thermal comfort results in a reduction in electricity generation. This suggests that achieving better thermal comfort requires design modifications that negatively impact energy production.

The higher-left section of the Pareto front represents the near-optimum solutions with minimal thermal discomfort but relatively low electricity generation. In contrast, the lower-right section corresponds to the near-optimum solutions with significantly higher electricity generation but at the cost of increased discomfort hours. The thermal discomfort hours exhibited a relatively narrow variation across all iterations, ranging from 1636 to 1779 h. In contrast, electricity generation demonstrated a significantly wider range, varying from 4604 kWh to 1334 kWh. Notably, the knee point around 1700 discomfort hours emerges as a potential balance between enhanced thermal comfort and efficient electricity generation.

The results indicate that higher building rotation angles (e.g., 195°) are associated with increased electricity generation, whereas lower angles (e.g., 5° or 10°) result in reduced electricity production but enhanced thermal comfort. Additionally, Triple Low-e glazing is consistently featured in the optimal solutions, highlighting its effectiveness in balancing energy efficiency and occupant comfort. A higher room window-to-wall ratio (30–40%) contributes to greater electricity generation but also increases discomfort hours. Furthermore, the TW massive wall 0.51 construction appears frequently in high-performing solutions, suggesting that it provides a balance between thermal insulation and energy efficiency.

Table 6. The near-optimum designs for the cooling mode.

Solution ID	Objective Values		Decision Variables
	Discomfort (h)	Generated Electricity (kWh)	Room Window to Wall %	Building Rotation	Massive Wall	Glazing	Vents to Wall %
1	1714.1	4603.95	30	195	double wall	Trp Low-e	10
2	1709.1	4594.26	20	190	Brick wall 0.51	Trp Low-e	30
3	1704.1	4561.57	10	180	Brick wall 0.38	Trp Low-e	20
4	1702.4	4543.33	10	175	Brick wall 0.51	Trp Low-e	30
5	1702.3	4522.98	25	170	Brick wall 0.51	Trp Low-e	25
6	1701.8	4495.96	30	165	Brick wall 0.51	Trp Low-e	15
7	1701.3	4289.98	35	145	Brick wall 0.51	Trp Low-e	10
8	1698.6	4214.49	20	140	Concrete block 0.16	Trp Low-e	50
9	1693.6	4132.79	20	135	Brick wall 0.51	Trp Low-e	30
10	1688.8	4042.18	50	130	Brick wall 0.51	Trp Low-e	10
11	1682.2	3945.25	30	125	double wall	Trp Low-e	35
12	1674	3840.85	25	120	Brick wall 0.51	Trp Low-e	35
13	1665.7	3728.27	40	115	Brick wall 0.51	Trp Low-e	30
14	1657.5	3608.63	35	110	Brick wall 0.51	Trp Low-e	30
15	1652.1	3483.73	35	105	Brick wall 0.51	Trp Low-e	30
16	1647.2	3352.09	30	100	Brick wall 0.51	Trp Low-e	35
17	1643.7	3216.44	35	95	Brick wall 0.25—insulated	Trp Low-e	25
18	1643.2	3077.33	30	90	Brick wall 0.51	Thermochromic	45
19	1637.2	1361.8	30	10	Brick wall 0.38	Sgl Clr 6 mm	40
20	1636.2	1337.79	40	5	Brick wall 0.51	Sgl Clr 6 mm	25

U values: Trp Low-e (1.19); Thermochromic (2.13); Sgl Clr 6 mm (5.778); Double wall (1.536); Brick wall 0.51 (0.892) Brick wall 0.38 (1.063); Brick wall 0.25-insulated (0.231); Concrete block 0.16 (3.087).

presents the near-optimum design solutions for the cooling mode (shown in red dots in Figure 13).

3.3.2. Regarding the Heating Mode

There is a clear trade-off between the two objectives. Lower discomfort hours correspond to lower electricity generation and vice versa. The scatter plot in Figure 14 illustrates the multi-objective optimization result for the heating mode.

Compared with the cooling mode, the thermal discomfort hours exhibited a relatively wider variation across all iterations, ranging from 1503 to 2022 h. In contrast, electricity generation demonstrated a significantly narrow range, varying from 3480 kWh to 4001 kWh. Also, towards the right of the graph (around 1900–2000 discomfort hours), there is greater scatter in the gray points, suggesting more variability in performance for these configurations.

Solutions with the highest electricity generation (~4000 kWh) exhibit higher discomfort (around 1910–1920 h). Conversely, solutions with the lowest discomfort (~1503 h) generate significantly less electricity (~3805 kWh). This indicates that prioritizing energy generation increases discomfort and vice versa. The choice of the optimal point depends on the relative importance of energy efficiency versus occupant comfort in the specific context of the MTW design. A balanced solution would lie somewhere in the middle of the Pareto front (around 1700 discomfort hours), where neither objective is overly sacrificed.

Table 7. The near-optimum designs for the heating mode.

Solution ID	Objective Values		Decision Variables
	Discomfort (h)	Generated Electricity (kWh)	Room Window to Wall %	Building Rotation	Massive Wall	Glazing	Vents to Wall %
1	1919.6	4001.2	25	335	Concrete block 0.20	Trp Low-e	35
2	1914.9	3992.0	40	325	Concrete block 0.16	Trp Low-e	50
3	1914.7	3987.4	15	340	Concrete block 0.20	Thermochromic	40
4	1910.1	3981.2	30	320	Brick wall 0.12	Trp Low-e	35
5	1829.4	3979.9	10	25	Brick wall 0.38	Sgl Clr 3 mm	30
6	1821.2	3975.9	45	35	Concrete block 0.16	Sgl Clr 3 mm	50
7	1812.6	3957.0	45	40	Brick wall 0.25	Sgl Clr 3 mm	5
8	1798.6	3929.8	30	45	Concrete block 0.20	Trp Low-e	35
9	1766.1	3922.5	30	50	Concrete block 0.20	Trp Low-e	35
10	1729.9	3901.3	30	55	Concrete block 0.20	Trp Low-e	35
11	1690.1	3868.8	30	60	Concrete block 0.20	Trp Low-e	30
12	1649.5	3860.2	45	65	Concrete block 0.16	Trp Low-e	40
13	1610.6	3845.7	45	70	Brick wall 0.25	Trp Low-e	35
14	1565.3	3817.8	45	75	Concrete block 0.16	Trp Low-e	40
15	1528.3	3813.5	35	80	Concrete block 0.20	Trp Low-e	30
16	1503.7	3805.2	30	85	Concrete block 0.20	Trp Low-e	40

U values: Trp Low-e (1.19); Thermochromic (2.13); Sgl Clr 3 mm (5.894); Concrete block 0.16 (3.087); Concrete block 0.20 (3.871); Brick wall 0.12 (1.726); Brick wall 0.25 (1.316); Brick wall 0.38 (1.063).

presents the near-optimal design solutions for the heating mode (shown in red dots in Figure 14). Rotation angles between 70° and 85° are associated with reduced discomfort hours and reduced energy generation; in contrast, angles range from 320° to 340°, emphasizing building orientation’s critical role in optimizing heating performance. Additionally, most optimal solutions maintain a vent-to-wall ratio of 35–40%, suggesting that this range effectively balances heat retention and air circulation.

Near-optimal solutions predominantly favor medium to high massive wall U-values (3.087–3.781) over extreme insulation levels (close to 0.23), indicating a preference for higher U values to enhance indoor comfort. Similarly, lower glazing U-values (1.19) are prevalent, highlighting the importance of well-insulated glazing in minimizing heat loss. However, some solutions use much higher glazing U-values (5.984), likely to maximize solar heat gain, suggesting a trade-off between passive solar heating and heat loss prevention.

3.3.3. Regarding the Annual Mode

The annual mode Pareto Front shows a clear trade-off between comfort and energy generation solutions with lower discomfort hours (~1500 to 1600 h), tending to have lower electricity generation (~3250 to 3750 kWh). In contrast, solutions with higher energy generation (~4600 kWh) exhibit significantly higher discomfort (~1900 h or more). A balanced solution (~1700 h, ~4000 kWh) could provide a practical compromise for sustainable and comfortable building operation. Compared with the MTW base case, optimizing the proposed MTW could increase the annually generated electricity by 31% on average. The scatter plot, shown in Figure 15, visualizes the multi-objective optimization result for the annual mode.

Table 8. The near-optimum designs for the annual mode.

Solution ID	Objective Values		Decision Variables
	Discomfort (h)	Generated Electricity (kWh)	Room Window to Wall %	Building Rotation	Massive Wall	Glazing	Vents to Wall %
1	1933.6	4618.8	30	195	Brick wall 0.12	Trp Low-e	20
2	1929.2	4609.2	50	190	Brick wall 0.51	Trp Low-e	35
3	1911.6	4593.9	30	185	Concrete block 0.20	Trp Low-e	25
4	1906.7	4576.6	50	180	Concrete block 0.20	Trp Low-e	15
5	1903.5	4538.0	25	170	Brick wall 0.12	Trp Low-e	25
6	1893.9	4510.8	15	165	Concrete block 0.16	Trp Low-e	35
7	1885.2	4474.3	25	160	Concrete block 0.16	Trp Low-e	35
8	1875.3	4428.6	35	155	Concrete block 0.16	Trp Low-e	20
9	1859.1	4372.2	25	150	Concrete block 0.16	Trp Low-e	30
10	1838.2	4305.0	15	145	Concrete block 0.20	Trp Low-e	15
11	1814.0	4229.8	10	140	Concrete block 0.16	Trp Low-e	20
12	1782.4	4148.2	35	135	Concrete block 0.20	Trp Low-e	35
13	1743.9	4057.8	35	130	Concrete block 0.20	Trp Low-e	20
14	1705.5	3961.2	15	125	Concrete block 0.20	Trp Low-e	15
15	1663.9	3856.8	35	120	Concrete block 0.20	Trp Low-e	35
16	1619.5	3744.3	50	115	Concrete block 0.20	Trp Low-e	15
17	1576.4	3625.0	15	110	Concrete block 0.20	Trp Low-e	25
18	1538.9	3500.1	40	105	Concrete block 0.20	Trp Low-e	25
19	1508.9	3368.6	20	100	Concrete block 0.20	Trp Low-e	40
20	1493.0	3233.1	30	95	Concrete block 0.20	Trp Low-e	40

U values: Trp Low-e (1.19); Brick wall 0.12 (1.726); Brick wall 0.51 (0.892); Concrete block 0.16 (3.087); Concrete block 0.20 (3.871).

presents the near-optimal design solutions for the heating mode (shown in red dots in Figure 15). Higher rotation angles (~185°) appear in higher energy-generating solutions. In comparison, lower angles (~110°) are linked to better comfort levels but slightly reduced electricity output. Also, triple Low-e glazing appears in all optimal solutions. This suggests that low U-value glazing balances comfort and energy efficiency, helping reduce heat loss while maximizing passive solar gains. In addition, concrete block walls with high U-values (~3.087–3.871) perform well in both objectives.

For the annual mode, a multi-objective optimization was performed to minimize heating and cooling electricity consumption, considering using an HVAC system to mitigate discomfort periods, as shown in Figure 16.

The resulting Pareto front follows an L-shaped pattern, highlighting two distinct trade-off regions: the left vertical section (~700 kWh heating, 2800–4000 kWh cooling) and the bottom horizontal section (~700–1200 kWh heating, ~2800 kWh cooling).

In the bottom-left corner of the Pareto front, three near-optimal design solutions stand out, representing balanced trade-offs between low heating and cooling electricity consumption. These solutions significantly reduce total energy demand, making them highly efficient choices. Compared to other points on the Pareto front, they maintain heating electricity around 700–800 kWh while keeping cooling electricity near the lowest observed values (~2800 kWh). As detailed in

Table 9. The near-optimal designs for the annual mode.

Solution ID	Objective Values		Decision Variables
	Heating Electricity (kWh)	Cooling Electricity (kWh)	Room Window to Wall %	Building Rotation	Massive Wall	Glazing	Vents to Wall %
1	676.3	2836.8	40	100	Brick wall 0.51	Trp Low-e	45
2	688.4	2824.3	15	100	Concrete block 0.16	Trp Low-e	10
3	688.8	2823	10	100	Concrete block 0.16	Trp Low-e	25

U values: Trp Low-e (1.19); Brick wall 0.51 (0.892); Concrete block 0.16 (3.087).

, all three solutions maintain a 100° building rotation and incorporate Triple Low-E glazing, emphasizing their superiority in optimizing energy efficiency.

3.4. Performance Prediction Equations

The simulation-optimization process discussed in previous sections requires significant computational resources that are rarely accessible to designers and take long processing times, making it unsuitable for rapid design and redesign decision-making. Therefore, there is a need to approximate the simulation model’s output to allow for quicker evaluation and objective prediction. To achieve this goal (Objective 3), the solutions derived from the evaluated simulation-optimization process were used as a dataset to develop multiple regression models, effectively approximating the MTW simulation model. These predictive equations provide a practical tool for assessing the performance of various MTW design configurations with minimal computational effort. Additionally, these equations can be integrated with optimization algorithms to determine the optimal MTW design parameters, further enhancing efficiency in the decision-making process.

For heating and cooling modes, two regression equations were developed—one for electricity generation and another for discomfort hours—resulting in four equations, as shown in

Table 10. MTW Performance prediction equations.

Response	Mode	Regression Equation	R2
Discomfort (h)	Heating mode	β0 + β1A + β2B + β3C + β4D + β5E + β6A2 + β7B2 + β8C2 + β9D2 + β10E2 + β11(A × B) + β12(A × C) + β13(A × D) + β14(A × E) + β15(B × C) + β16(B × D) + β17(B × E) + β18(C × D) + β19(C × E) + β20(D × E) + β21A3 + β22B3 + β23C3 + β24D3 + β25E3 + β26(A2 × B) + β27(A2 × C) + β28(A2 × D) + β29(A2 × E) + β30(A × B2) + β31(A × B × C) + β32(A × B × D) + β33(A × B × E) + β34(A × C2) + β35(A × C × D) + β36(A × C × E) + β37(A × D2) + β38(A × D × E) + β39(A × E2) + β40(B2 × C) + β41(B2 × D) + β42(B2 × E) + β43(B × C2) + β44(B × C × D) + β45(B × C × E) + β46(B × D2) + β47(B × D × E) + β48(B × E2) + β49(C2 × D) + β50(C2 × E) + β51(C × D2) + β52(C × D × E) + β53(C × E2) + β54(D2 × E) + β55(D × E2)	70.20%
	Cooling mode	β0 + β1A + β2B + β3C + β4D + β5E + β6A2 + β7B2 + β8D2 + β9E2 + β10(A × B) + β11(A × C) + β12(A × E) + β13(B × C) + β14(B × D) + β15(C × D) + β16(C × E) + β17B3 + β18C2 + β19E3 + β20(A2 × B) + β21(A2 × C) + β22(A2 × D) + β23(A2 × E) + β24(A × B2) + β25(A × B × C) + β26(A × B × D) + β27(A × B × E) + β28(A × C × E) + β29(A × D2) + β30(A × D × E) + β31(A × E2) + β32(B2 × C) + β33(B2 × D) + β34(B2 × E) + β35(B × C × D) + β36(B × C × E) + β37(B × D2) + β38(B × D × E) + β39(C × D2) + β40(C × D × E) + β41(C × E2) + β42(D × E2)	83.29%
Generated electricity (kWh)	Heating mode	β0 + β1A + β2B + β3C + β4D + β5E + β6A2 + β7B2 + β8C2 + β9D2 + β10E2 + β11(A × B) + β12(A × C) + β13(A × D) + β14(A × E) + β15(B × C) + β16(B × D) + β17(B × E) + β18(C × D) + β19(C × E) + β20(D × E) + β21A3 + β22B3 + β23C3 + β24D3 + β25E3 + β26(A2 × B) + β27(A2 × C) + β28(A2 × D) + β29(A2 × E) + β30(A × B2) + β31(A × B × C) + β32(A × B × D) + β33(A × B × E) + β34(A × C2) + β35(A × C × D) + β36(A × C × E) + β37(A × D2) + β38(A × D × E) + β39(A × E2) + β40(B2 × C) + β41(B2 × D) + β42(B2 × E) + β43(B × C2) + β44(B × C × D) + β45(B × C × E) + β46(B × D2) + β47(B × D × E) + β48(B × E2) + β49(C2 × D) + β50(C2 × E) + β51(C × D2) + β52(C × D × E) + β53(C × E2) + β54(D2 × E) + β55(D × E2)	86.49%
	Cooling mode	β0 + β1A + β2B + β3C + β4D + β5E + β6A2 + β7B2 + β8C2 + β9D2 + β10E2 + β11(A × B) + β12(A × C) + β13(A × D) + β14(A × E) + β15(B × C) + β16(B × D) + β17(B × E) + β18(C × D) + β19(C × E) + β20(D × E) + β21B3 + β22C3 + β23(A × C × E) + β24(B2 × E) + β25(B × D2)	95.73%

Note: Room window to the wall ratio (A); Building rotation (B); Massive wall U-value (C); Glazing U-value (D); Vents to the wall ratio (E).

. These equations offer a simplified and efficient representation of how various design parameters influence both thermal discomfort and energy production. R², commonly referred to as the goodness of fit, measures how well a regression model explains the variability of the dependent variable. An R² value closer to 1 indicates a stronger correlation between the predicted and actual values, signifying a well-fitted model [64]. A regression model is generally considered reliable when R² is 0.7 or higher [65].

In this study, the regression models for discomfort in heating and cooling modes exhibit high R² values of 70.20% and 83.29%, respectively, demonstrating that the selected variables and their interactions effectively explain variations in thermal discomfort across different scenarios. Similarly, the regression models for electricity generation in heating and cooling modes also show strong predictive capability, with R² of 86.49% and 95.73%, respectively. The derived equations provide a reliable framework for predicting the MTW’s efficiency, facilitating design optimization, and enhancing its applicability in improving generation performance and occupant comfort in residential buildings. The coefficient values (β) of the regression equations are available in

Table A2. Coefficient values of the regression equation to estimate discomfort (h) in the heating mode.

Coefficient	Value	Coefficient	Value	Coefficient	Value
β0	2036	β19	0.07	β38	−0.00339
β1	−8.41	β20	0.626	β39	0.00085
β2	−6.982	β21	0.00005	β40	0.000064
β3	11.2	β22	−0.000077	β41	−0.000987
β4	38.6	β23	5.27	β42	0.000013
β5	−3.12	β24	2.21	β43	−0.0192
β6	0.108	β25	0.00056	β44	−0.0258
β7	0.04315	β26	−0.000311	β45	−0.00006
β8	−23.7	β27	−0.0027	β46	−0.0152
β9	−22.3	β28	−0.0077	β47	−0.00080
β10	−0.007	β29	−0.00084	β48	−0.000355
β11	0.0223	β30	0.000019	β49	−2.52
β12	0.04	β31	−0.00231	β50	0.105
β13	1.27	β32	−0.00104	β51	−0.76
β14	0.033	β33	−0.000069	β52	0.082
β15	0.192	β34	−0.092	β53	−0.0092
β16	0.526	β35	0.238	β54	−0.0322
β17	0.0221	β36	−0.0010	β55	−0.00694
β18	8.7	β37	−0.1137

,

Table A3. Coefficient values of the regression equation to estimate discomfort (h) in the cooling mode.

Coefficient	Value	Coefficient	Value	Coefficient	Value
β0	1674.2	β15	−0.47	β30	−0.00074
β1	0.457	β16	0.109	β31	0.000519
β2	−0.8809	β17	−0.000015	β32	0.000094
β3	−0.51	β18	0.0984	β33	−0.000573
β4	−0.72	β19	−0.000035	β34	0.000005
β5	1.085	β20	−0.000079	β35	0.00120
β6	−0.0131	β21	0.00217	β36	−0.000024
β7	0.007632	β22	0.00170	β37	0.00583
β8	−0.980	β23	0.000555	β38	−0.000023
β9	−0.0148	β24	0.000004	β39	−0.058
β10	0.00642	β25	−0.000658	β40	−0.0038
β11	0.041	β26	−0.000298	β41	−0.00154
β12	−0.0583	β27	−0.000030	β42	0.000414
β13	−0.0281	β28	0.00070
β14	0.1678	β29	−0.0047

,

Table A4. Coefficient values of the regression equation to estimate generated electricity (KWh) in the heating mode.

Coefficient	Value	Coefficient	Value	Coefficient	Value
β0	3964.4	β19	−1.01	β38	0.00356
β1	−3.21	β20	−1.840	β39	−0.001721
β2	−2.554	β21	0.00098	β40	0.001038
β3	13.4	β22	0.000017	β41	0.000064
β4	37.8	β23	−3.07	β42	−0.000033
β5	5.43	β24	−0.739	β43	0.0554
β6	−0.052	β25	0.00106	β44	0.0158
β7	0.00362	β26	0.000308	β45	0.00207
β8	7.4	β27	−0.0254	β46	0.03372
β9	−1.6	β28	−0.00135	β47	−0.000223
β10	−0.1023	β29	−0.00114	β48	0.000438
β11	−0.0039	β30	−0.000013	β49	−0.38
β12	2.29	β31	−0.00096	β50	0.176
β13	0.417	β32	−0.001765	β51	0.261
β14	0.1474	β33	−0.000026	β52	0.0130
β15	−0.610	β34	−0.114	β53	−0.0070
β16	−0.2232	β35	−0.063	β54	0.2289
β17	−0.01828	β36	0.0124	β55	0.00156
β18	−0.6	β37	0.0032

and

Table A5. Coefficient values of the regression equation to estimate generated electricity (KWh) in the cooling mode.

Coefficient	Value	Coefficient	Value	Coefficient	Value
β0	774	β9	40.85	β18	−8.87
β1	6.38	β10	−0.0644	β19	−1.38
β2	33.79	β11	0.01756	β20	0.020
β3	337.6	β12	−3.10	β21	−0.000106
β4	−267.7	β13	0.407	β22	22.65
β5	9.23	β14	−0.0962	β23	0.0557
β6	−0.1033	β15	−0.2747	β24	0.000164
β7	−0.06229	β16	1.136	β25	−0.1736
β8	−126.3	β17	−0.0640

in Appendix B.

4. Discussion and Future Directions

This study explored the potential of multi-story Trombe Wall (MTW) as a hybrid passive design strategy for heating, cooling, and electricity generation. Recent studies have investigated the thermal performance of Trombe Walls and their advanced configurations, highlighting their potential for both passive cooling and heating, with a predominant focus on enhancing heating performance.

In cooling mode, the MTW in this study achieves a temperature reduction of up to 1.94 °C. This performance is comparable to the 0.78 °C cooling effect reported by Irshad et al. for PVTW but slightly lower than the reductions achieved by PVTW-venetian blind systems (2.1 °C) [66], optimized TW incorporating solar chimney (2 °C) (Rabani et al.) [67], and PCM-integrated TW (3.25 °C) (Li et al.) [68]. However, it surpasses the cooling effect of double-layer PCM TWs, which ranged from 0.4 to 0.93 °C (Kong et al.) [69]. For heating performance, the MTW increases indoor temperatures by 1.56 °C, outperforming the 0.5 °C improvement recorded by Bellos et al. for an extra window TW [37] However, it falls below the 5.5 °C increase achieved by He et al. using a Venetian blind TW [70] and the 1–4 °C improvement observed by Abbassi and Dehmani with finned TWs [71].

Regarding thermal comfort, the MTW enhances comfort hours by 40%, a value comparable to the 43.81% improvement achieved by Lin et al. using a PV-PCM TW [72] but higher than the 23.9% improvement achieved by Pourghorban and Asoodeh through adding advanced glazing [27]. Overall, while the MTW provides balanced cooling and heating effects, its key advantage lies in its multi-story application, allowing it to enhance thermal performance across multiple rooms—unlike previous studies, which primarily focused on single-room configurations, making it a viable alternative for energy-efficient multi-story building applications. Potential improvements could be achieved by integrating phase change materials (PCM), fins, blinds, and other advanced configurations, which have been shown in previous studies to enhance both passive cooling and heating performance.

While this study advances the understanding of multi-story Trombe Wall as a hybrid system, several limitations must be acknowledged. These limitations also present opportunities for further research, as outlined below:

• This study primarily focused on analyzing the impact of the proposed MTW on indoor temperatures and PMV levels. However, incorporating a CFD analysis could provide more profound insights into airflow patterns and temperature variations across different floors. Additionally, modifying the air duct cross-section may offer better control over the performance of the multi-story Trombe Wall, highlighting the need for further investigation in this area.
• Exploration of alternative building types and configurations: This research focused on a specific residential building. Investigating MTW applications in high-rise, commercial, and mixed-use buildings would help determine its broader architectural potential. Additionally, assessing the impact of different urban forms, including building density, height variations, and surrounding shading elements, would provide more insights into MTW efficiency in real-world scenarios.
• Application of machine learning: The developed regression models demonstrated high predictive accuracy; however, integrating machine learning could enhance model precision and adaptability. Future work could focus on using artificial intelligence to optimize MTW performance.
• Integration with smart control systems: Developing an intelligent control system to adjust vent openings, shading devices, and airflow rates could optimize the MTW’s performance.
• Economic and lifecycle analysis: Investigating the cost-effectiveness and environmental impact of MTW compared to traditional heating and cooling systems would provide practical insights for designers.
• The validation process was conducted over a 24 h period due to constraints in obtaining long-term real-world data in an occupied building. While this approach aligns with previous studies, we recognize that a longer validation period could further enhance the reliability of the results. Future research should consider extended validation periods to improve the robustness of the findings.
• The application of the MTW in temperate and cold climate regions may require further modifications to account for different environmental conditions, such as lower solar radiation levels and increased heating demand. This is an important aspect that warrants further exploration.

5. Conclusions

Trombe Walls, as a passive design technique, provide a cost-effective and eco-friendly solution by reducing heating and cooling energy consumption through solar-powered natural ventilation. Numerous studies have explored various TW designs and their impact on building performance. However, several research gaps remain: (1) Most studies examine TW parameters individually without considering their interrelationships; (2) Research primarily focuses on heating efficiency, with limited attention to cooling performance in hot climates; (3) Studies mainly assess TWs in single-room setups, neglecting multi-story applications; and (4) A comprehensive optimization of TW design parameters is still needed. This study contributes by developing an optimized multi-story Trombe Wall (MTW) as a hybrid system for both heating and cooling. The key objectives are: (1) assessing the thermal and energy performance of the proposed MTW, (2) optimizing its design parameters to enhance energy efficiency and thermal comfort in residential buildings within hot climate regions, and (3) developing predictive equations to estimate its thermal and energy performance.

To achieve these objectives, a four-phase methodology was adopted. Firstly, the geometric and thermal parameters of the Trombe Wall (TW) design were identified through a literature review, followed by field measurements, modeling, and calibration for a residential case study in New Burj Al Arab City, Egypt. Then, a multi-story Trombe Wall (MTW) design was proposed based on the findings of the first phase. Consequently, a two-stage simulation-optimization was employed to evaluate the impact of seven key design parameters and find their optimum values. Finally, multiple regression analysis was applied to develop predictive equations for MTW performance. The key results of the study are:

• From the literature review, the identified TW design parameters are the TW width, the air gap depth, the type and thickness of the massive wall, the type and thickness of the glazing layer, the vent-to-wall ratio, the room window-to-wall ratio, and the orientation.
• A building energy simulation model (using DesignBuilder software) for a residential building in New Burj Al Arab City, Egypt, was validated with an RMSE of 1.33 and a relative error of 4.45%, confirming the reliability of the computational simulation.
• A proposed multi-story TW system integrated with a PV blind was developed. The MTW has two operational modes: one for heating and one for cooling.
• Regarding the impact of MTW width and air gap depth on the thermal performance:
  • In the heating mode, increasing the width or reducing the air gap depth of the MTW enhances thermal performance. The optimum MTW width and air gap depth are 375 cm and 30 cm, respectively. The maximum temperature increase reached up to 1.56 °C;
  • In the cooling mode, decreasing the width or increasing the air gap depth of the MTW enhances thermal performance. The optimum MTW width and air gap depth are 175 cm and 90 cm, respectively. The maximum temperature reduction reached 1.94 °C;
  • Implementing the MTW in the cooling mode resulted in a noticeable reduction in PMV values. This improvement translated into a 40% increase in comfort hours.
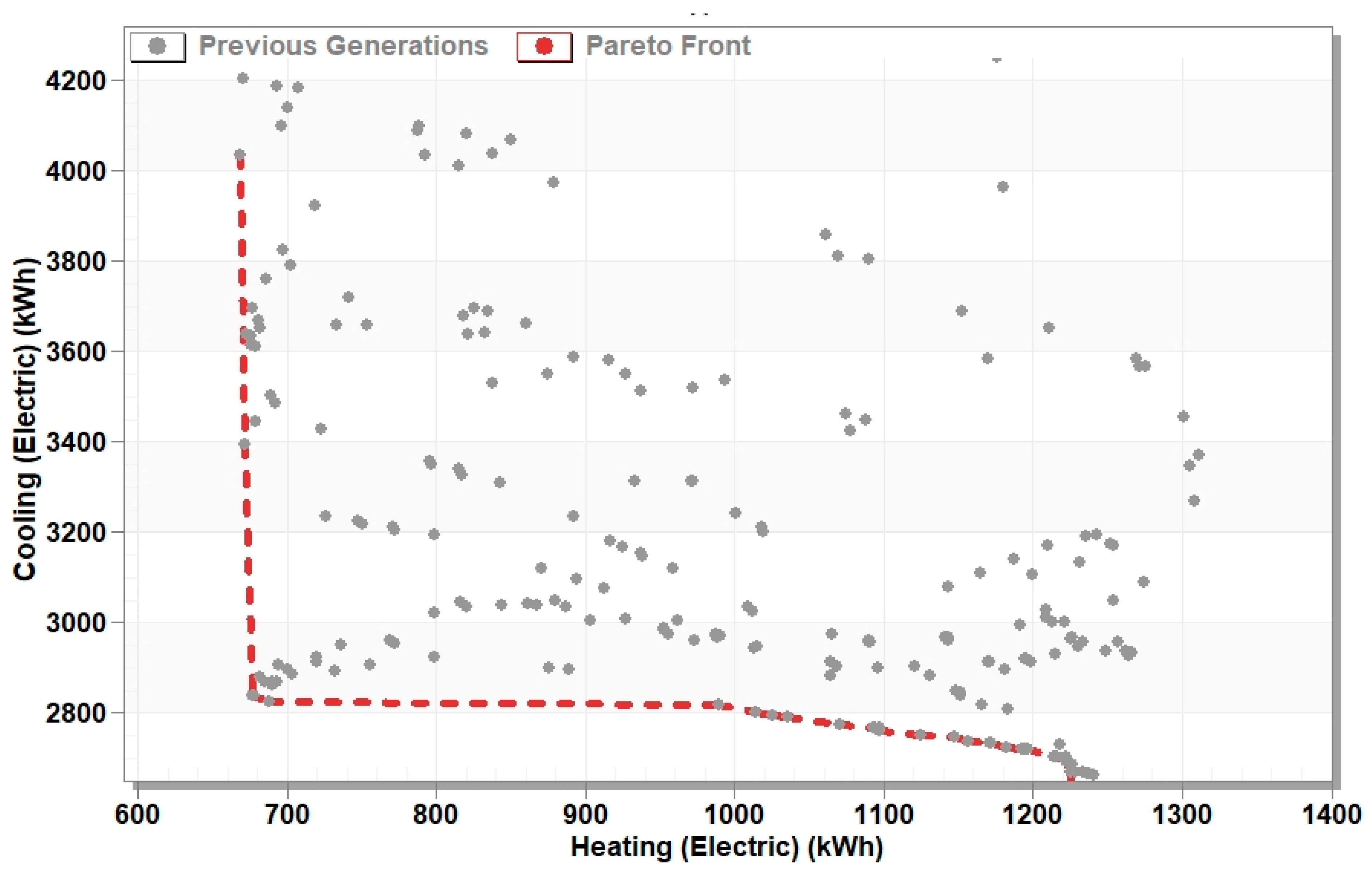
• Regarding the impact of MTW width and air gap depth on PV electricity generation, adjusting the MTW width or depth has minimal influence on the average energy generation rate per square meter of PV cells. Consequently, the PV cells’ alignment and total surface area remain the primary factors determining electricity output. During cooling mode, the average generation rate was 815 kilowatts per square meter, compared to 572 kilowatts per square meter in heating mode.
• The developed regression models for discomfort in heating and cooling modes exhibit high R² values of 70.20% and 83.29%, respectively. Also, the regression models for electricity generation in heating and cooling modes show strong predictive capability, with R² values of 86.49% and 95.73%, respectively. These R² values demonstrate that the models effectively represent variations in thermal discomfort and electricity generation.
• The multi-objective simulation-optimization key results are:

  1.

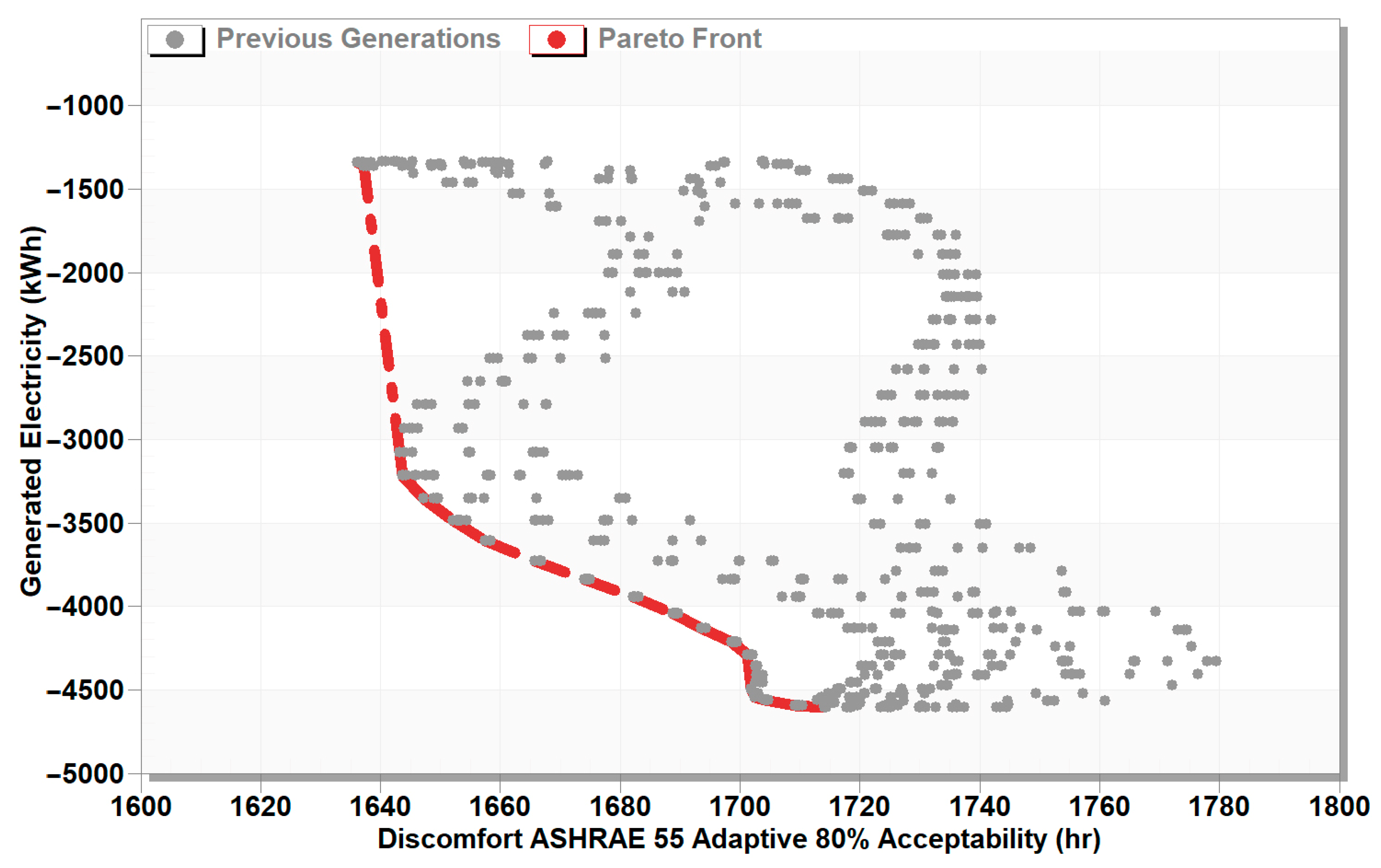
  In the cooling mode, an inverse relationship was observed between discomfort hours and electricity generation. Twenty near-optimal solutions were obtained with a maximum electricity of 4603.95 kWh and a minimum discomfort of 1636.2 h.

  2.

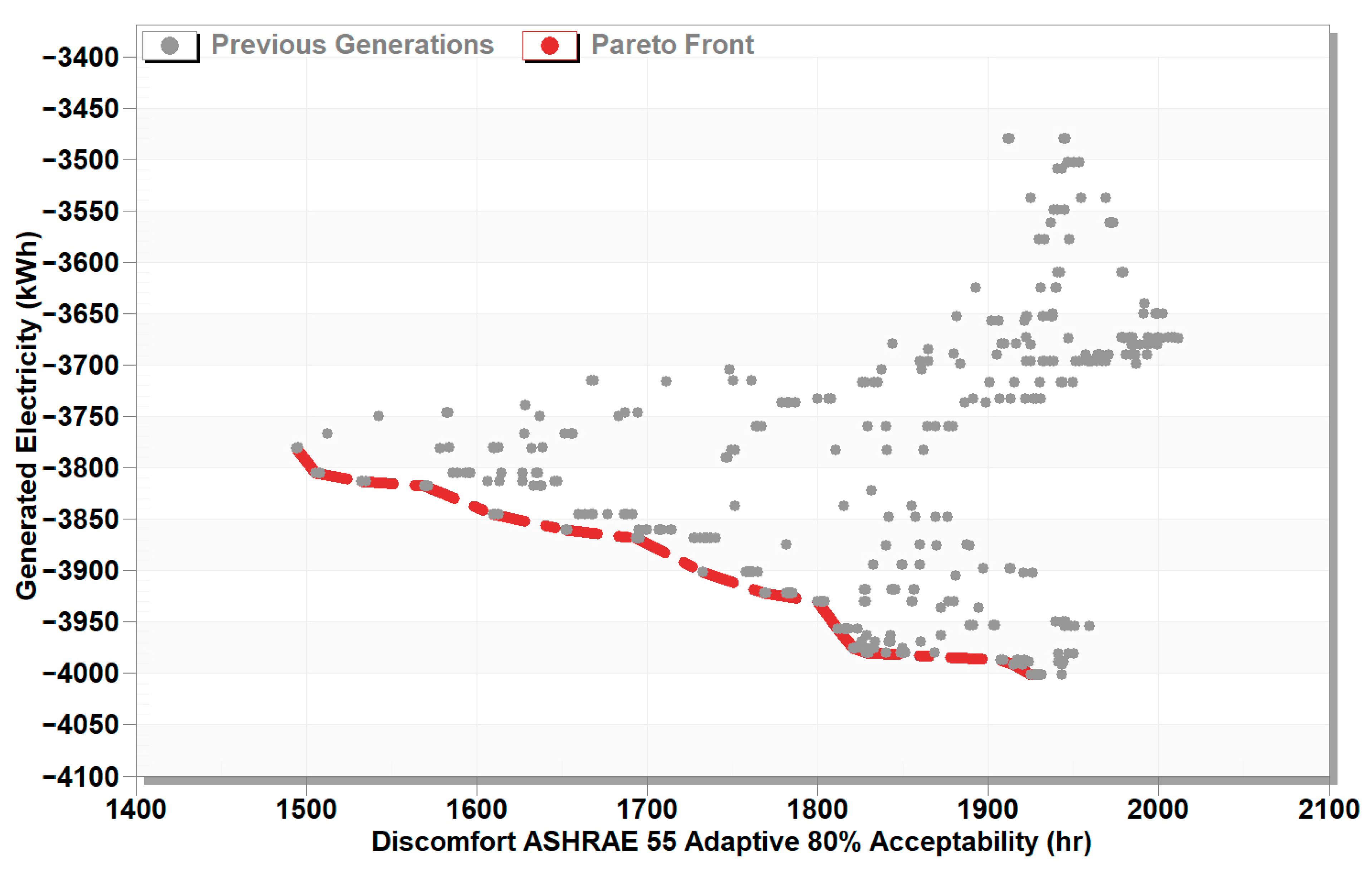
  In the heating mode: A trade-off exists between discomfort hours and electricity generation. Sixteen solutions on the Pareto front were obtained with a maximum electricity of 4001.2 kWh and a minimum discomfort of 1503.7 h.

  3.

  The following design parameters could balance heating and cooling modes: a 375 cm width, 30 cm air gap depth, Triple low-e glazing, a massive wall of 20 cm-thick concrete block (u value of 3.871), around 130° building rotation, about 20% room window to wall ratio, and nearby 20% vents to wall ratio.

  4.

  The Pareto front analysis revealed that the optimized MTW system can significantly reduce total energy demand, with near-optimal solutions maintaining low heating electricity (~700 kWh) and minimal cooling electricity (~2800 kWh) while ensuring comfortable indoor conditions.

  5.

  Optimizing the proposed MTW could increase the annually generated electricity by 31% on average.