Theoretical Analysis of Surface Settlement During Parallel Construction of a Double-Track Tunnel with Small Spacing
Abstract
1. Introduction
2. Theoretical Analysis of Ground Deformation
2.1. Theoretical Analysis of Ground Deformation Caused by Subsurface Tunnels Construction
- The stress release in the surrounding soil after excavation causes the soil to displace towards the tunnel.
- Gaps form between the support structure and the surrounding soil following excavation.
- As excavation progresses, the support structure undergoes slight shrinkage deformation.
- The tunnel structure undergoes overall downward displacement due to its self-weight.
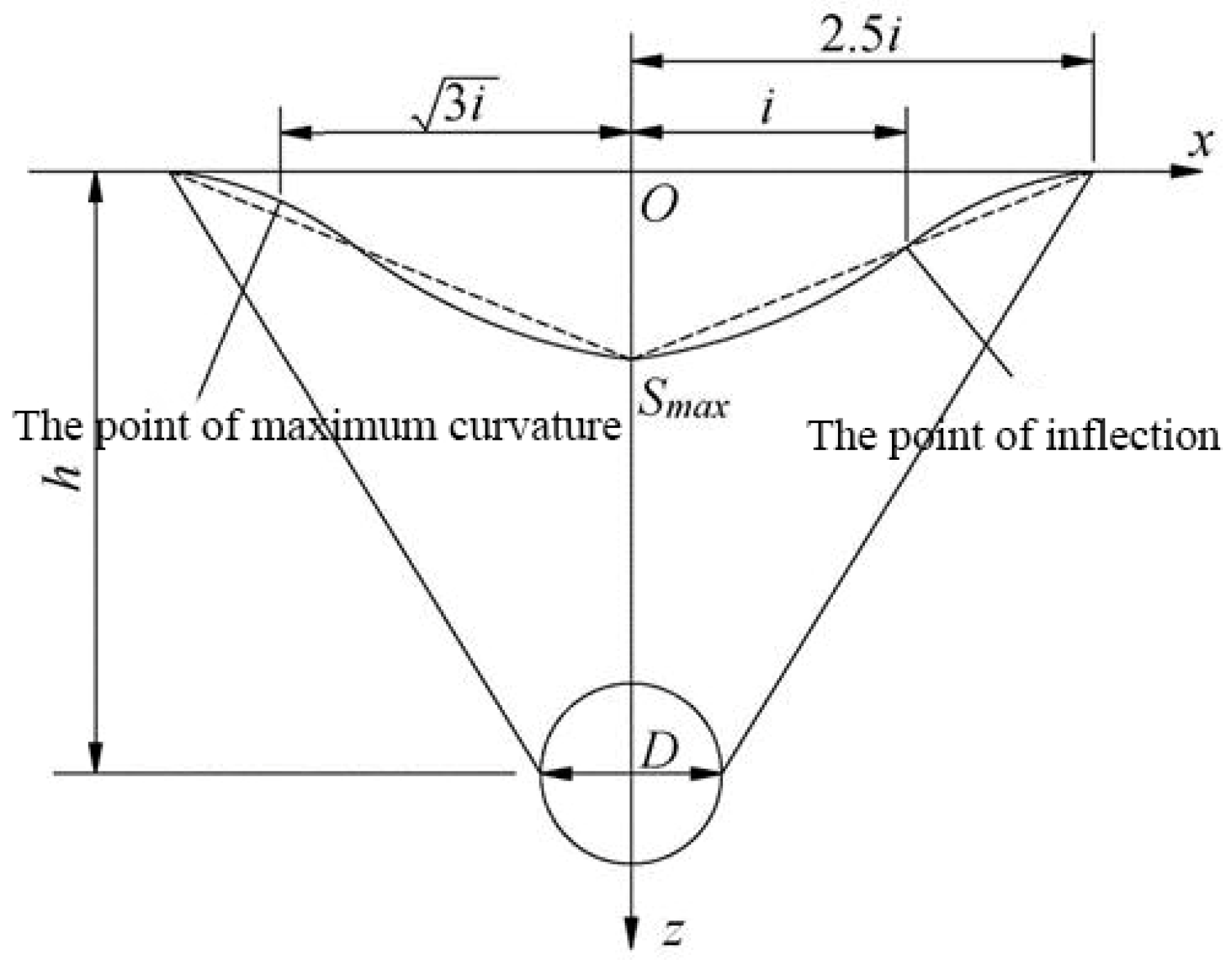
2.2. Theoretical Analysis of Ground Surface Settlement Induced by Single-Track Tunnel Construction
3. Three-Dimensional Theoretical Solution for Ground Settlement Induced by Parallel Double-Track Tunnel Construction
3.1. Current Ground Settlement Prediction Methods and Their Limitations in Double-Track Tunnel Construction
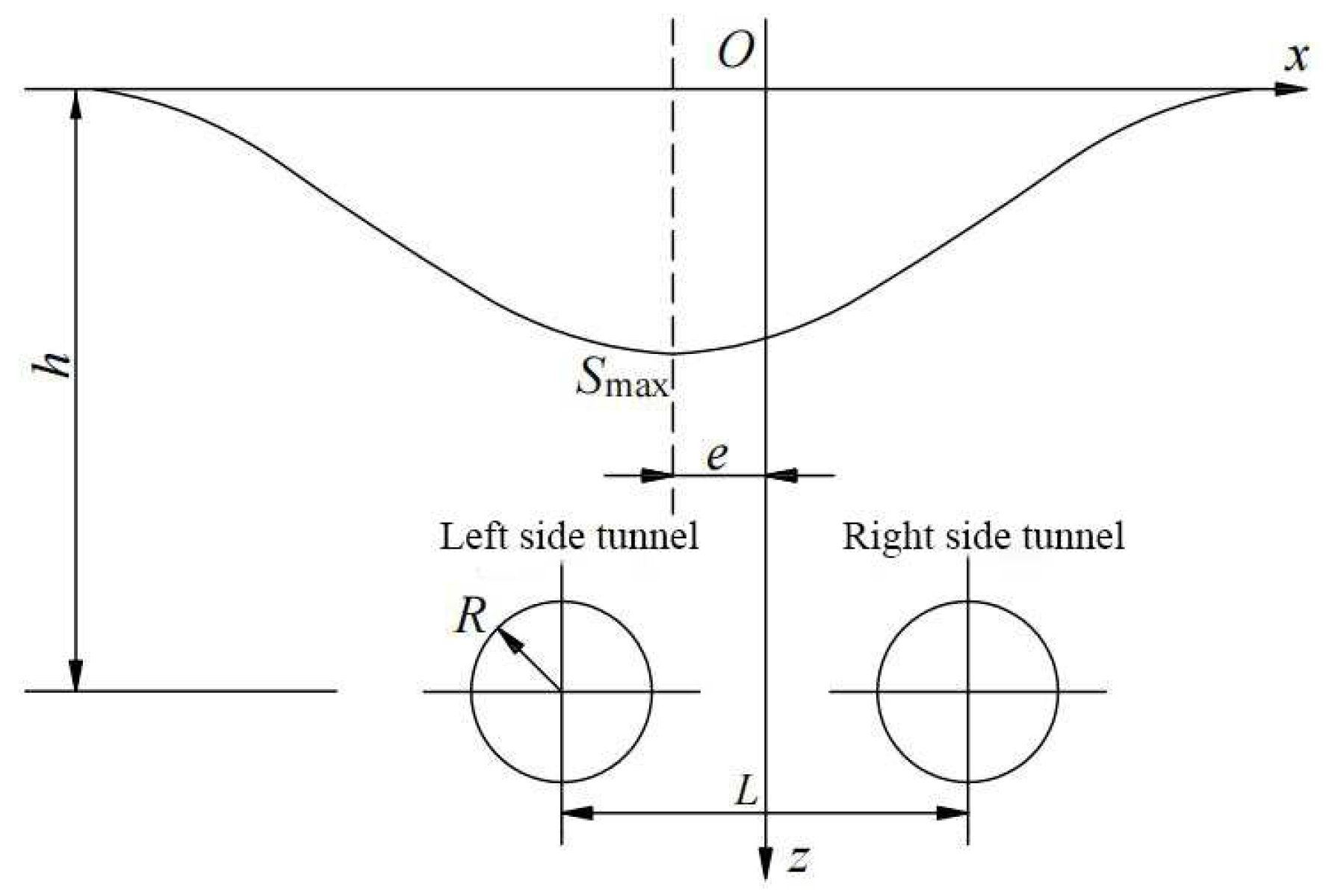
3.2. Definition of Closely Spaced Double-Track Tunnels
3.3. Derivation of the Three-Dimensional Solution for Ground Displacement Induced by Excavation of Closely Spaced Parallel Double-Track Tunnels
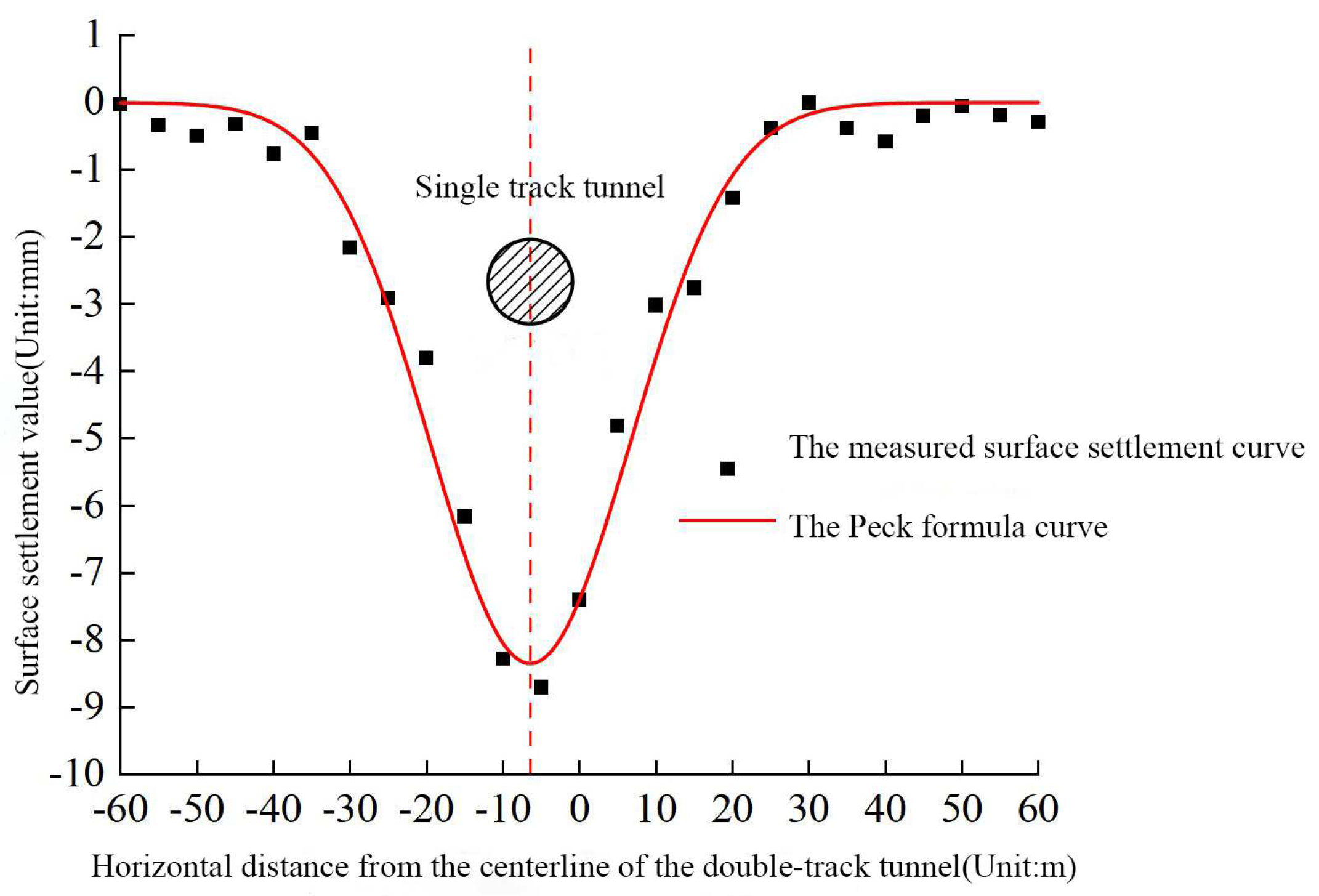
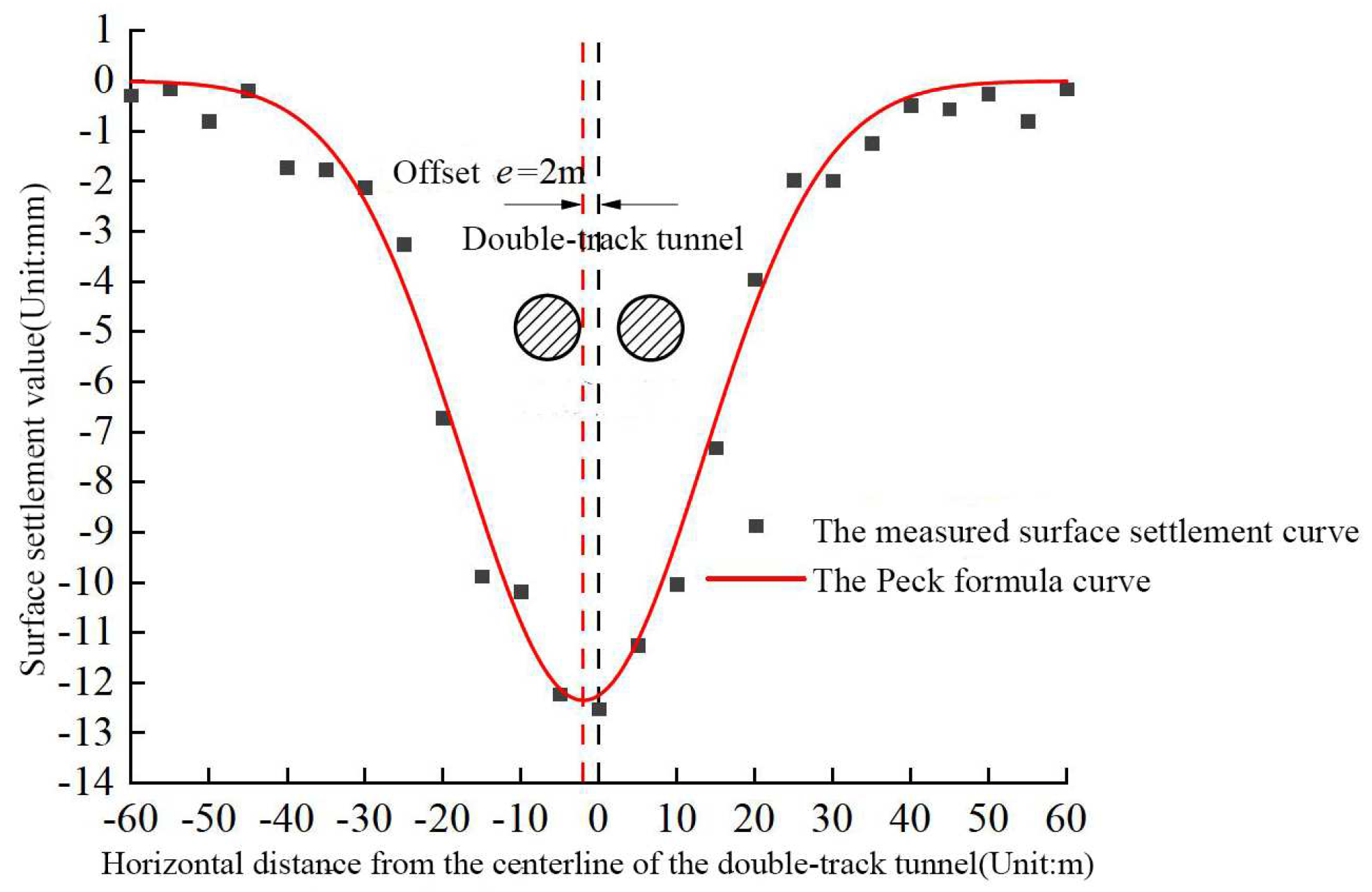
3.4. Case Verification
4. Influence of Different Parameters on Ground Settlement Caused by Excavation of Double-Track Tunnel
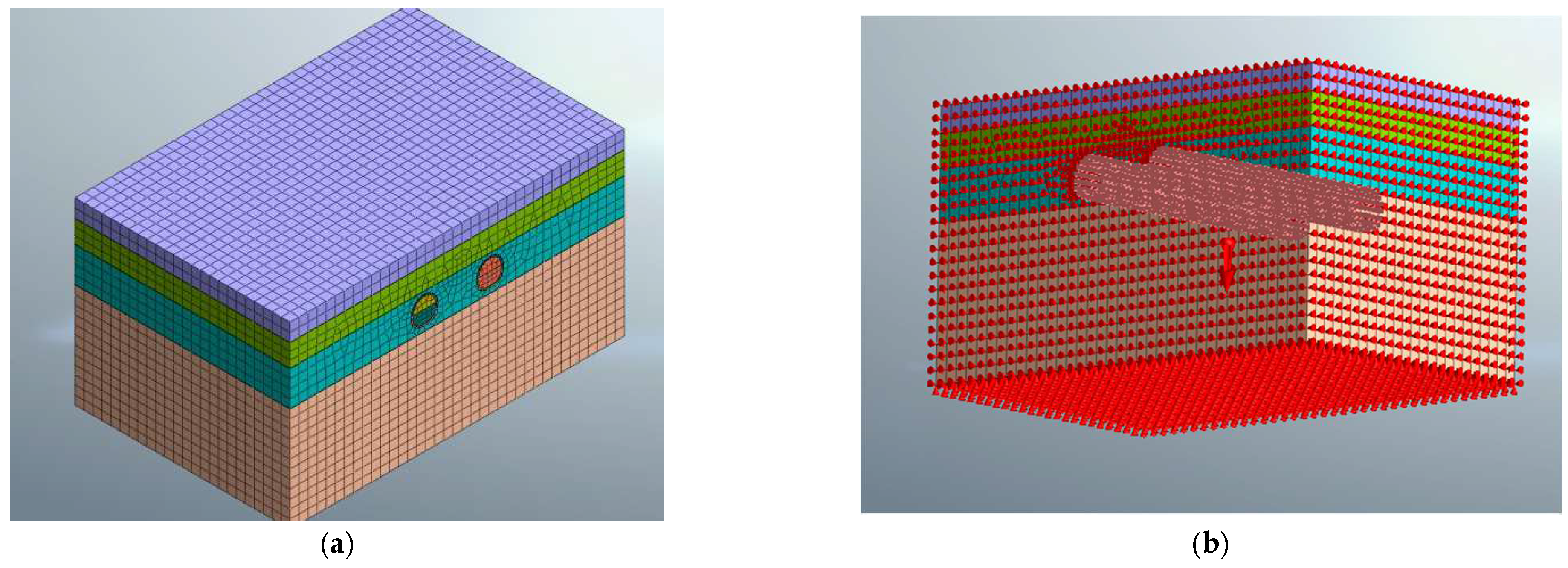
4.1. Numerical Calculation Model Establishment
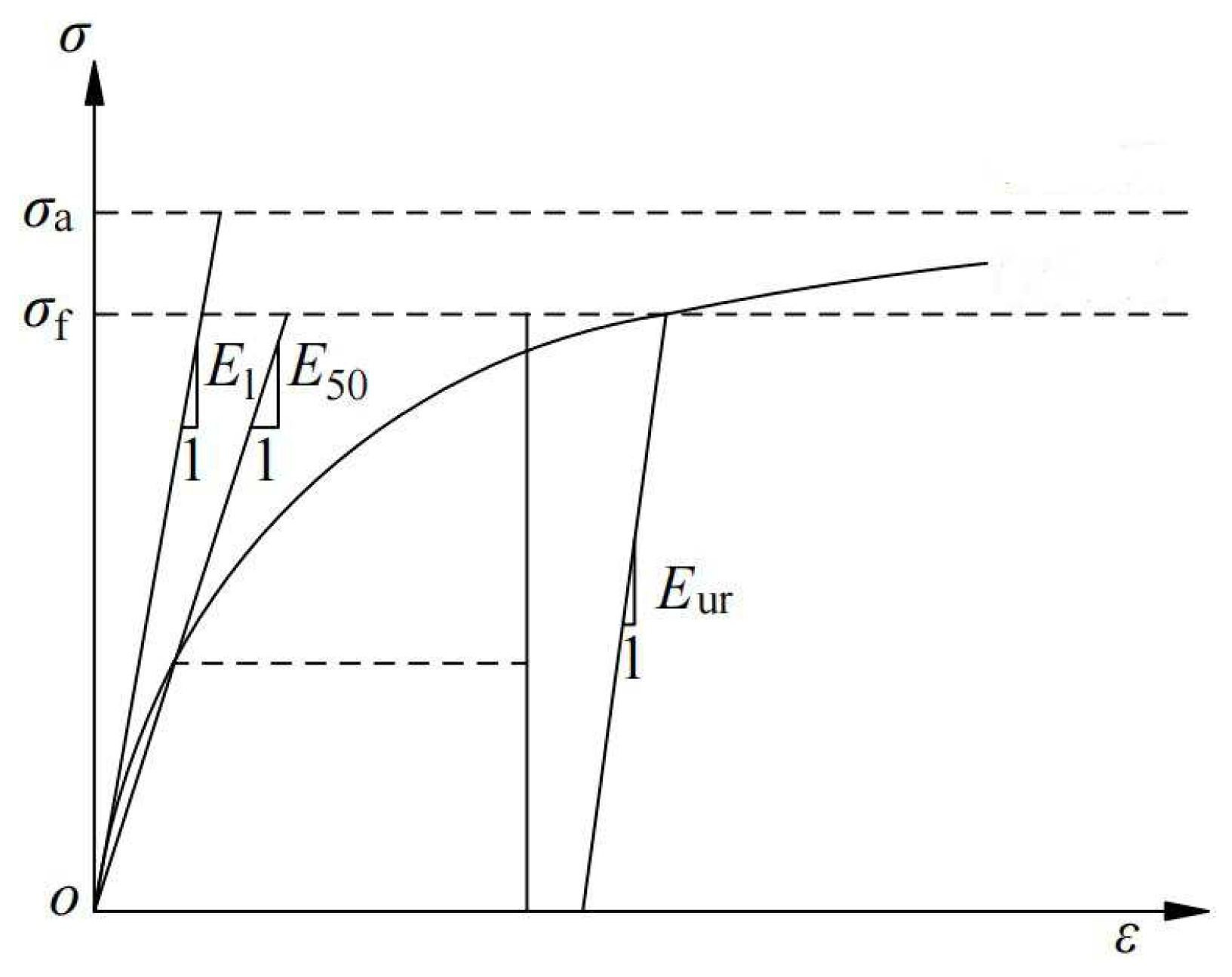
4.1.1. Soil Model Constitutive Relationships
4.1.2. Computational Parameters for Simulating the Soil Layers
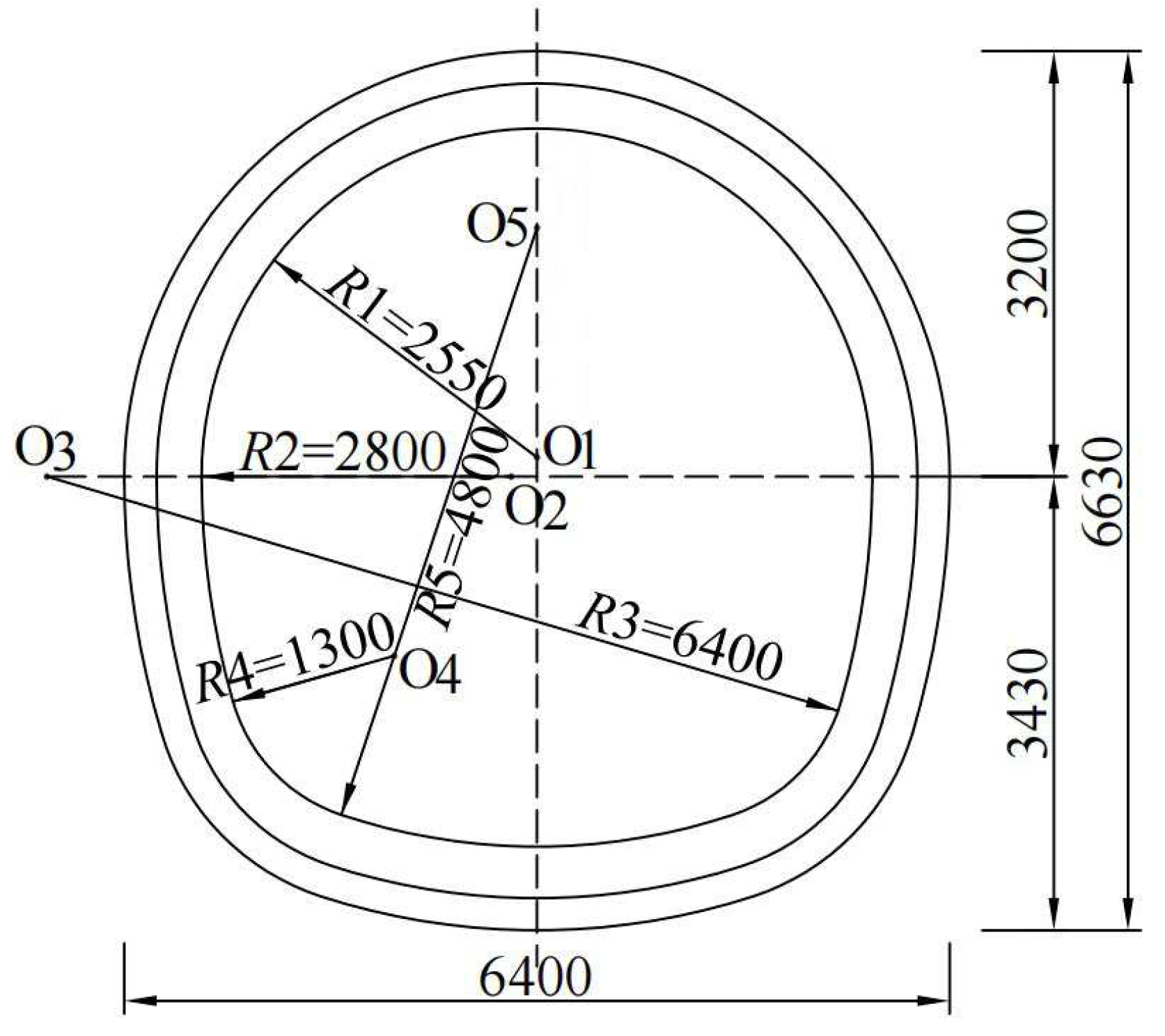
4.1.3. Computational Parameters for the Tunnel Structure
4.1.4. Model Mesh Generation
4.1.5. Load Boundary Conditions
- Model Load Conditions:
- 2.
- Model Boundary Constraint Conditions:
4.1.6. Construction Phase Simulation
- Excavate the upper bench, applying initial support to the upper section.
- Excavate the lower bench and apply the initial support to the lower section, while simultaneously proceeding with the next step for the upper bench.
- Once the initial support structure stabilizes, apply the secondary lining structure.
- Repeat steps 1–3, alternating between the upper and lower bench excavations until completion of the entire section.

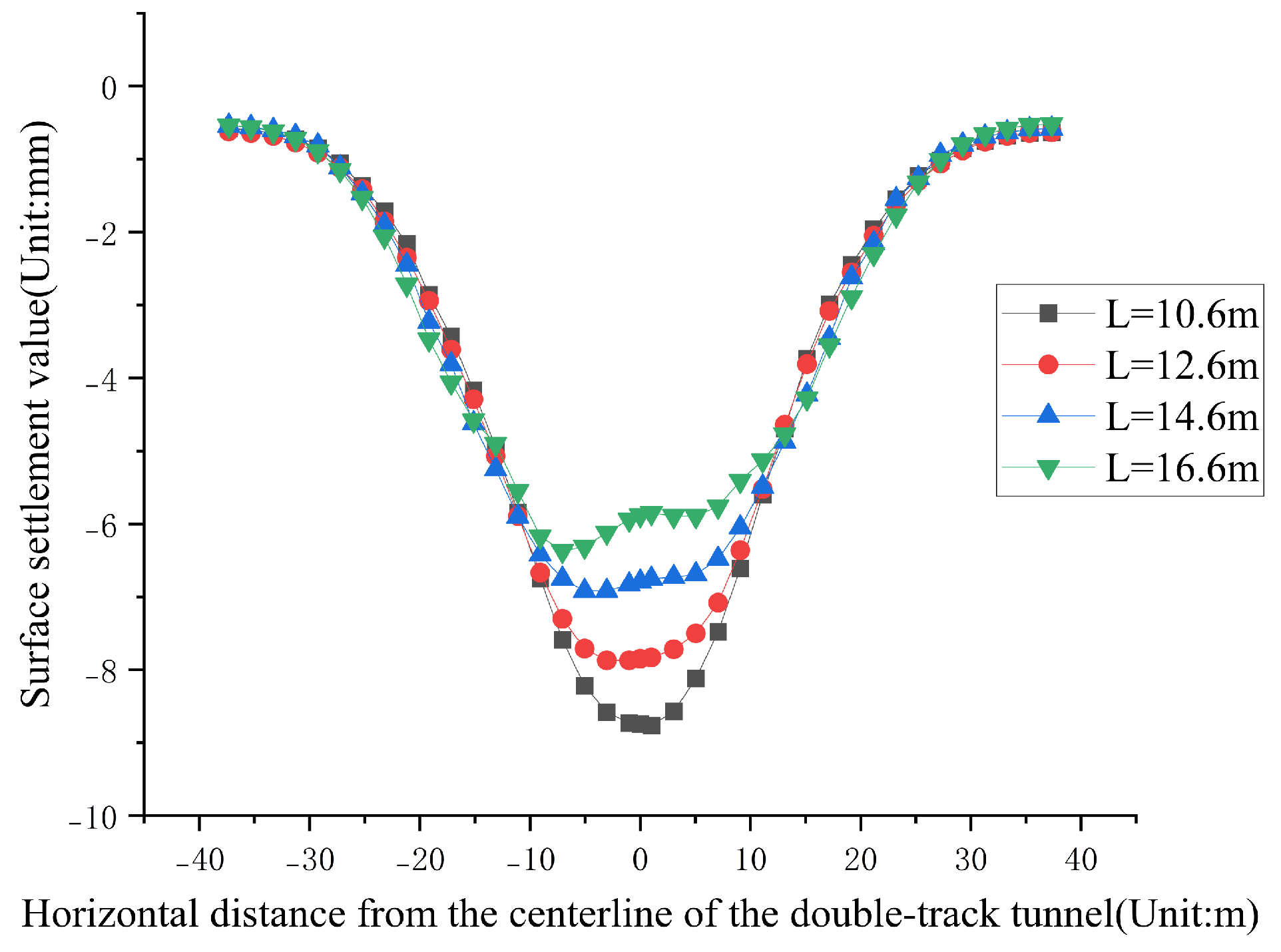
4.2. Influence of Tunnel Spacing on Ground Settlement
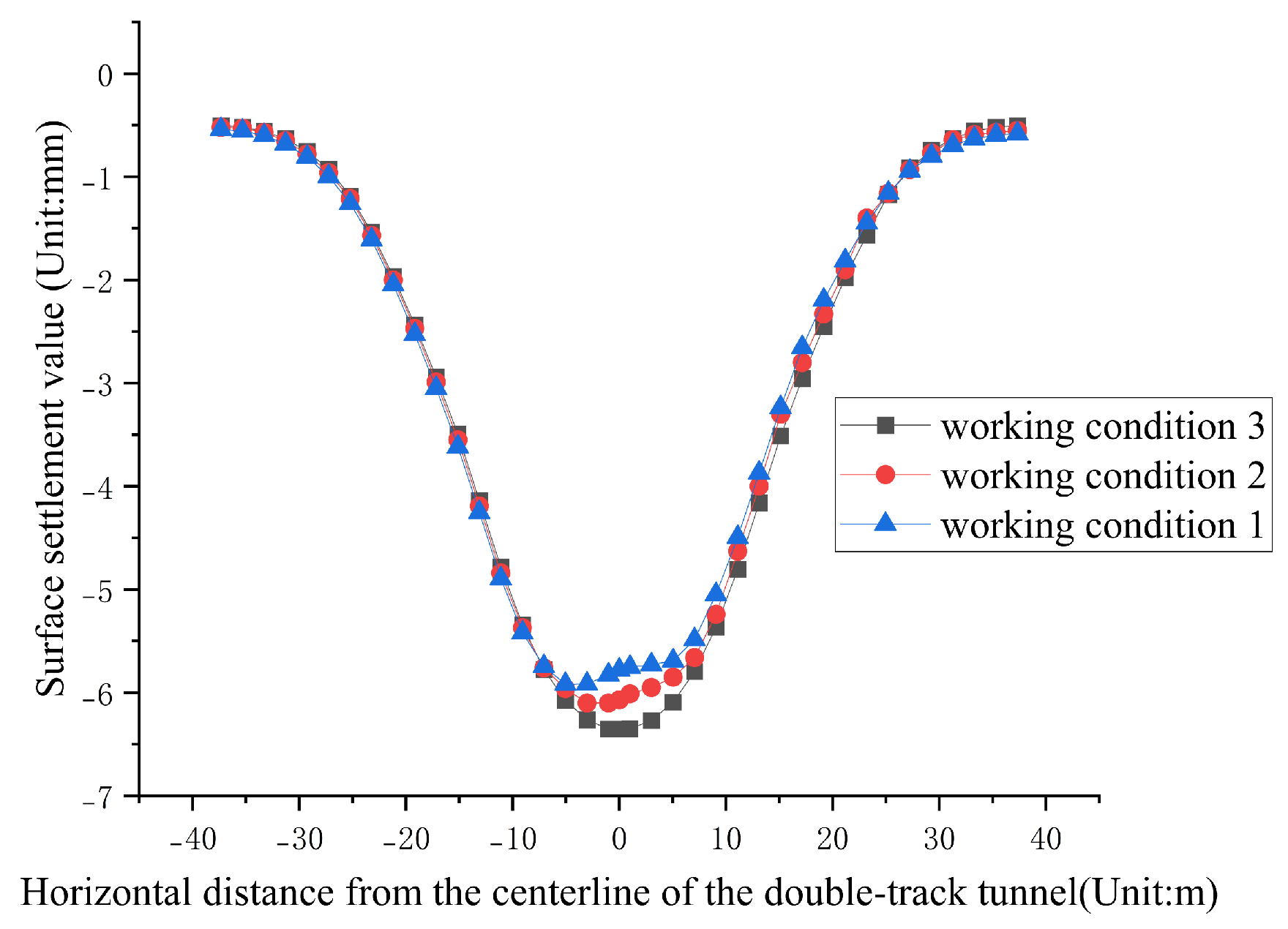
4.3. Influence of Excavation Sequence on Ground Settlement
- Sequential excavation: left tunnel excavated first, followed by the right tunnel after completion.
- The left tunnel excavated halfway before starting the right tunnel.
- Simultaneous Excavation of both Tunnels.
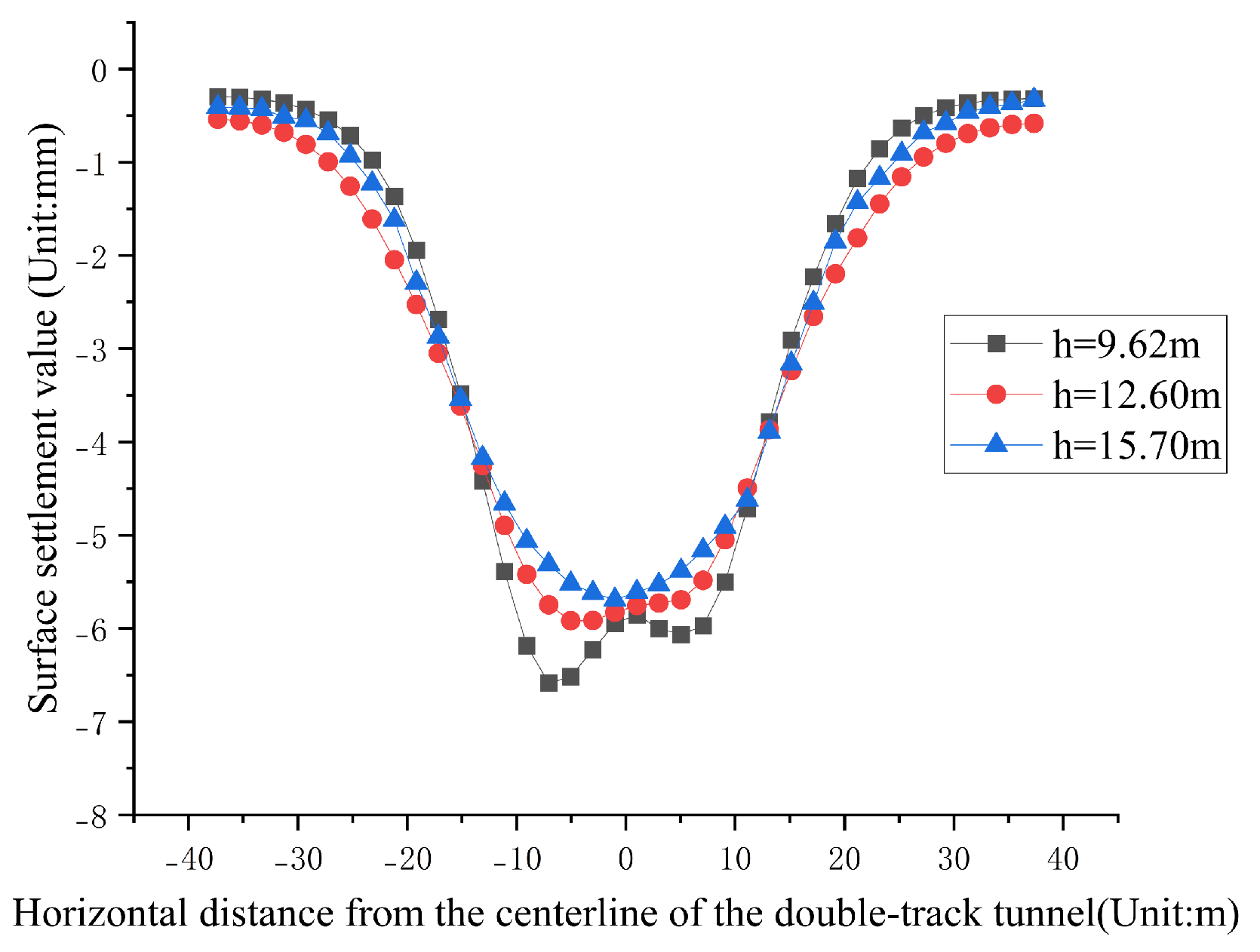
4.4. Influence of Burial Depth on Ground Settlement
5. Conclusions
- Based on the Peck formula for predicting the surface settlement induced by single-track tunnel excavation, this study proposed a definition for small-spacing double-track tunnels. The horizontal offset e and soil loss rate η (y) were introduced to derive a displacement calculation formula for soil deformation during small-spacing double-track tunnel excavation. The accuracy of the proposed formula was validated.
- The deformation patterns of ground settlement induced by small-spacing double-track tunnel excavation influenced by various parameters were characterized. As the tunnel spacing increased, the ground settlement curve transitioned from a V-shape to a U-shape, and eventually to a W-shape, and the maximum settlement gradually decreased. The location of the maximum settlement shifted towards the tunnel first excavated. Additionally, as the burial depth increased, the ground settlement curve evolved from a W-shape to a U-shape, and the maximum settlement decreased as the location of the maximum settlement shifted towards the tunnel centerline. Sequential excavation induced the smallest ground settlement; however, it was significantly influenced by the tunnel first excavated. In contrast, simultaneous excavation resulted in the largest settlement, and the maximum settlement occurred at the centerline. As the burial depth increased, the influence of the tunnel excavation on the ground settlement decreased, and the settlement distribution became increasingly uniform.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, C. Current development status and trends in urban rail transit industry. Traffic World 2019, 12, 8–9. [Google Scholar] [CrossRef]
- Mitroshin, V.A.; Mondrus, V.L. Analysis of the impact of shallow subway train traffic on urban development. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1015, 012019. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavations and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; pp. 225–290. [Google Scholar]
- Han, X.; Li, N.; Standing, J.R. Applicability analysis of Peck formula for predicting ground deformation in tunnel construction in China. Rock Soil Mech. 2007, 28, 23–28. [Google Scholar] [CrossRef]
- Yin, G.M.; Fu, H.L.; Hou, W.Z.; Yan, S. Study on the methods of selecting key parameters for Peck formula. J. Railw. Sci. Eng. 2022, 19, 2015–2022. [Google Scholar] [CrossRef]
- Chen, C.L.; Zhao, C.L.; Wei, G.; Ding, Z. Prediction of ground settlement induced by double-shield tunneling based on Peck formula. Rock Soil Mech. 2014, 35, 2212–2218. [Google Scholar] [CrossRef]
- Wu, H.J.; Wei, G. Calculation of soil settlement caused by the construction of closely spaced parallel shield tunnels. Mod. Tunn. Technol. 2014, 51, 63–69. [Google Scholar] [CrossRef]
- Zhang, Q.J.; Wu, K.; Cui, S.S.; Yu, Y.L.; Zhang, Z.; Zhao, J.H. Surface Settlement Induced by Subway Tunnel Construction Based on Modified Peck Formula. Geotech. Geol. Eng. 2019, 37, 2823–2835. [Google Scholar] [CrossRef]
- Shi, G.; Yuan, H.; Zhang, C.; Song, J. Study on the ground settlement model and parameters for double-track tunnel based on Peck formula. Urban Rail Transit Res. 2022, 25, 161–165. [Google Scholar] [CrossRef]
- Rui, Y.Q.; Yuan, J.W.; Fan, W.J.; Liu, B.Y. Numerical analysis of ground deformation control during the construction of double-track tunnel. Highway 2023, 68, 455–462. [Google Scholar]
- Rodríguez, C.A.; Rodríguez-Pérez, Á.M.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. A Finite Element Method Integrated with Terzaghi’s Principle to Estimate Settlement of a Building Due to Tunnel Construction. Buildings 2023, 13, 1343. [Google Scholar] [CrossRef]
- Wang, C.; Shan, S.B. Study on prediction model for ground settlement of double-track shield tunnel oblique undercrossing existing airport expressway. J. Saf. Sci. Technol. 2023, 19, 85–94. [Google Scholar] [CrossRef]
- Wei, G.; Wang, X. Calculation of Ground Settlement for Close-Proximity Parallel Double-Tube Shield Tunneling Based on Unified Solution. Mod. Tunn. Technol. 2017, 54, 87–95. [Google Scholar] [CrossRef]
- Yang, W.Y.; Zheng, J.J.; Zhang, R.J.; Liu, H. An analytical method for predicting equivalent gap parameter induced by 3D deformation at the face of shield tunnel in soft clay. Tunn. Undergr. Space Technol. 2022, 130, 104736. [Google Scholar] [CrossRef]
- Gao, Y.X.; Liu, Y.W.; Tang, P.J. Modification of Peck Formula to Predict Surface Settlement of Tunnel Construction in Water-Rich Sandy Cobble Strata and Its Program Implementation. Sustainability 2022, 14, 14545. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Describing Settlement Troughs over Twin Tunnels Using a Superposition Technique. J. Geotech. Geoenviron. Eng. 2007, 133, 445–468. [Google Scholar] [CrossRef]
- Chapman, D.N.; Rogers, C.D.F.; Hunt, D.V.L. Predicting the Settlements Above Twin Tunnel Constructed in Soft Ground. Tunn. Undergr. Space Technol. 2004, 19, 378. [Google Scholar] [CrossRef]
- Li, Y.X.; Lin, J.C.; Yan, S.H. Modification of the Peck Formula for a Double-Track Shield Tunnel under Expressway Subgrade. Symmetry 2022, 14, 1904. [Google Scholar] [CrossRef]
- Wei, G.; Pang, S. Definition of closely spaced parallel shield tunnels based on finite element simulation. Munic. Eng. Technol. 2014, 32, 76–80. [Google Scholar] [CrossRef]
- Cording, E.J.; Hansmire, W.H. Displacement around soft ground tunnels, General Report: Session IV, Tunnels in soil. In Proceedings of the 5th Panamerican Congress on Soil Mechanics and Foundation Engineering, Buenos Aires, Argentina, 17–22 November 1975; pp. 571–632. [Google Scholar]
- Wei, G.; Zhou, Y. Prediction of surface settlement caused by closely spaced parallel shield tunneling based on random medium theory. Rock Soil Mech. 2016, 37, 113–119. [Google Scholar] [CrossRef]
- New, B.M.; Bowers, K.H. Ground Movement Model Validation at the Heathrow Express Trial Tunnel. In Tunnelling’ 94; IMM: London, UK, 1993; pp. 301–329. [Google Scholar] [CrossRef]
- Mair, R.J.; Taylor, R.N.; Bracegirdle, A. Subsurface Settlement Profiles Above Tunnels in Clays. Geotechnique 1993, 43, 315–320. [Google Scholar] [CrossRef]
- Han, X.; Li, N.; Standing, J.R. Discussion on the Law of Ground Displacement Induced by Metro Tunnel Construction. Rock Soil Mech. 2007, 28, 609–613. [Google Scholar] [CrossRef]
- Jiang, X.L.; Zhao, Z.M.; Li, Y. Analysis and Calculation of Ground Settlement Trough Shape Induced by Tunnel Excavation. Rock Soil Mech. 2004, 25, 1542–1544. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Zhou, S.H.; Gong, Q.M. Distribution patterns of deep displacement field induced by shield tunneling in soft soil areas. Chin. J. Rock Mech. Eng. 2009, 28, 500–506. [Google Scholar] [CrossRef]
- Wei, G. Study on the calculation method for the width coefficient of deep soil settlement troughs induced by shield tunneling. J. Highw. Transp. Res. Dev. 2010, 27, 110–115. [Google Scholar] [CrossRef]
- Wei, G. Three-dimensional solution for soil deformation induced by shield tunneling. China Society for Rock Mechanics and Engineering. In Proceedings of the 2nd National Symposium on Engineering Safety and Protection, Beijing, China, 16–17 August 2010; Department of Civil Engineering, Zhejiang University City College: Hangzhou, China, 2010; Volume 16, pp. 19–24. [Google Scholar]
- Yi, C.S.; Sheng, Y.S.; Min, Y.W. Application of the Modified Mohr-Coulomb Yield Criterion in Seismic Numerical Simulation of Tunnels. Shock Vib. 2021, 2021, 117155. [Google Scholar] [CrossRef]
- Hou, G.Y.; Liu, H.W.; Li, J.J.; Gao, R.Z.; Wang, Q.; Zhang, M.D. Numerical Analysis of Subway Tunnel Construction Process Based on Excavation Unloading Effect. Chin. J. Rock Mech. Eng. 2013, 32, 2915–2924. [Google Scholar]

| Serial Number | Section Name | h/m | L/m | ifirst/m | iall/m | e/m | ηfirst/m | ηall/m |
|---|---|---|---|---|---|---|---|---|
| 1 | 23-AR-001 | 22 | 10.3 | 15 | 17 | 2 | 4.86 | 7.22 |
| 2 | 26-AR-001 | 18.5 | 20 | 13 | 18 | 4 | 4.42 | 7.71 |
| 3 | CS-8B | 19 | 17.5 | 12 | 14 | 3 | 0.74 | 1.03 |
| 4 | CS-8D | 20.1 | 14.5 | 10 | 13 | 1 | 0.69 | 1.10 |
| 5 | SS-5T-52e-s | 22.2 | 20 | 13 | 17 | 0 | 1.71 | 3.94 |
| 6 | SS-5T-52e-o | 26 | 15 | 14 | 17 | 0 | 0.92 | 1.44 |
| 7 | 23-G3-007-019 | 19 | 20 | 9 | 11 | 8 | 2.78 | 3.78 |
| 8 | HS1 | 12.6 | 20 | 9 | 11 | 8 | 2.78 | 3.78 |
| 9 | HS2 | 17.4 | 20 | 6 | 9 | 0 | 1.14 | 1.83 |
| 10 | HS3 | 18.4 | 20 | 8 | 11 | 0 | 1.07 | 1.94 |
| 11 | HS4 | 22.9 | 20 | 11 | 15 | 10 | 1.43 | 2.81 |
| 12 | HS5 | 35.6 | 20 | 15 | 18 | 0 | 0.72 | 1.71 |
| 13 | HS6 | 37.6 | 20 | 15 | 18 | 0 | 0.72 | 1.71 |
| 14 | HS7 | 44 | 20 | 22 | 25 | 0 | 0.39 | 1.08 |
| 15 | HS8 | 46.5 | 20 | 23 | 26 | 0 | 0.29 | 0.91 |
| Name | Unit Weight (KN/m3) | Secant Modulus (MPa) | Unloading Stiffness (MPa) | Poisson’s Ratio | Cohesion (kPa) | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|
| Miscellaneous fill | 17.0 | 10 | 30 | 0.28 | 10 | 6.0 |
| 3-4 Grit | 19.0 | 42 | 126 | 0.28 | 3 | 34.0 |
| 3-5-0 Boulder | 20.1 | 80 | 240 | 0.29 | 0 | 37.0 |
| 4-4-0 Grit | 20.1 | 59 | 177 | 0.29 | 0 | 37.0 |
| Name | Unit Weight (KN/m3) | Elastic Modulus (MPa) | Poisson’s Ratio |
|---|---|---|---|
| Initial support | 22 | 23,000 | 0.2 |
| Secondary lining | 25 | 32,500 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, Y.; Chen, G.; Li, Y.; Li, J.; Jin, J. Theoretical Analysis of Surface Settlement During Parallel Construction of a Double-Track Tunnel with Small Spacing. Buildings 2025, 15, 1143. https://doi.org/10.3390/buildings15071143
Liu Y, Li Y, Chen G, Li Y, Li J, Jin J. Theoretical Analysis of Surface Settlement During Parallel Construction of a Double-Track Tunnel with Small Spacing. Buildings. 2025; 15(7):1143. https://doi.org/10.3390/buildings15071143
Chicago/Turabian StyleLiu, Yanao, Yanfeng Li, Guojie Chen, Yuanhui Li, Jialong Li, and Jiaxu Jin. 2025. "Theoretical Analysis of Surface Settlement During Parallel Construction of a Double-Track Tunnel with Small Spacing" Buildings 15, no. 7: 1143. https://doi.org/10.3390/buildings15071143
APA StyleLiu, Y., Li, Y., Chen, G., Li, Y., Li, J., & Jin, J. (2025). Theoretical Analysis of Surface Settlement During Parallel Construction of a Double-Track Tunnel with Small Spacing. Buildings, 15(7), 1143. https://doi.org/10.3390/buildings15071143






