Calculating the Bearing Capacity of Foundations near Slopes Based on the Limit Equilibrium and Limit Analysis Methods
Abstract
1. Introduction
2. Analysis of the Basic Influencing Factors of Foundations near Slopes
2.1. Finite Element Modeling
2.2. Finite Element Model Test
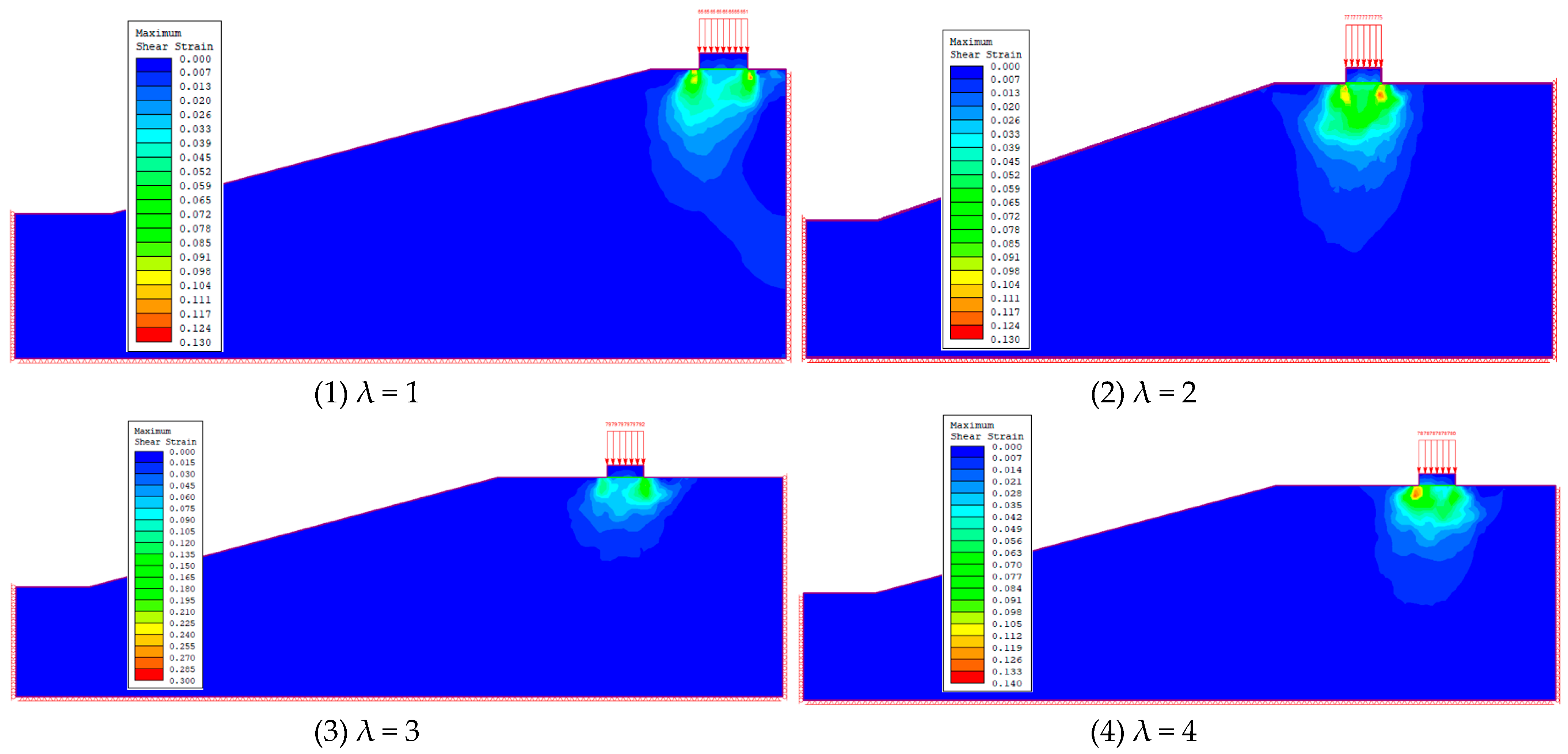
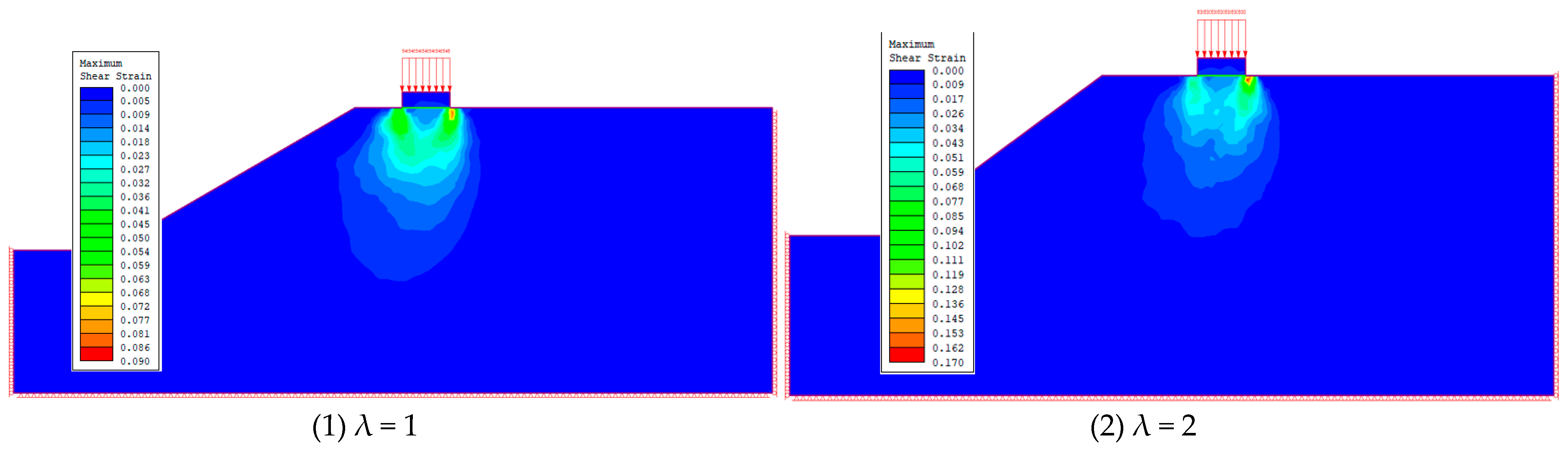
2.3. Analysis of Test Results
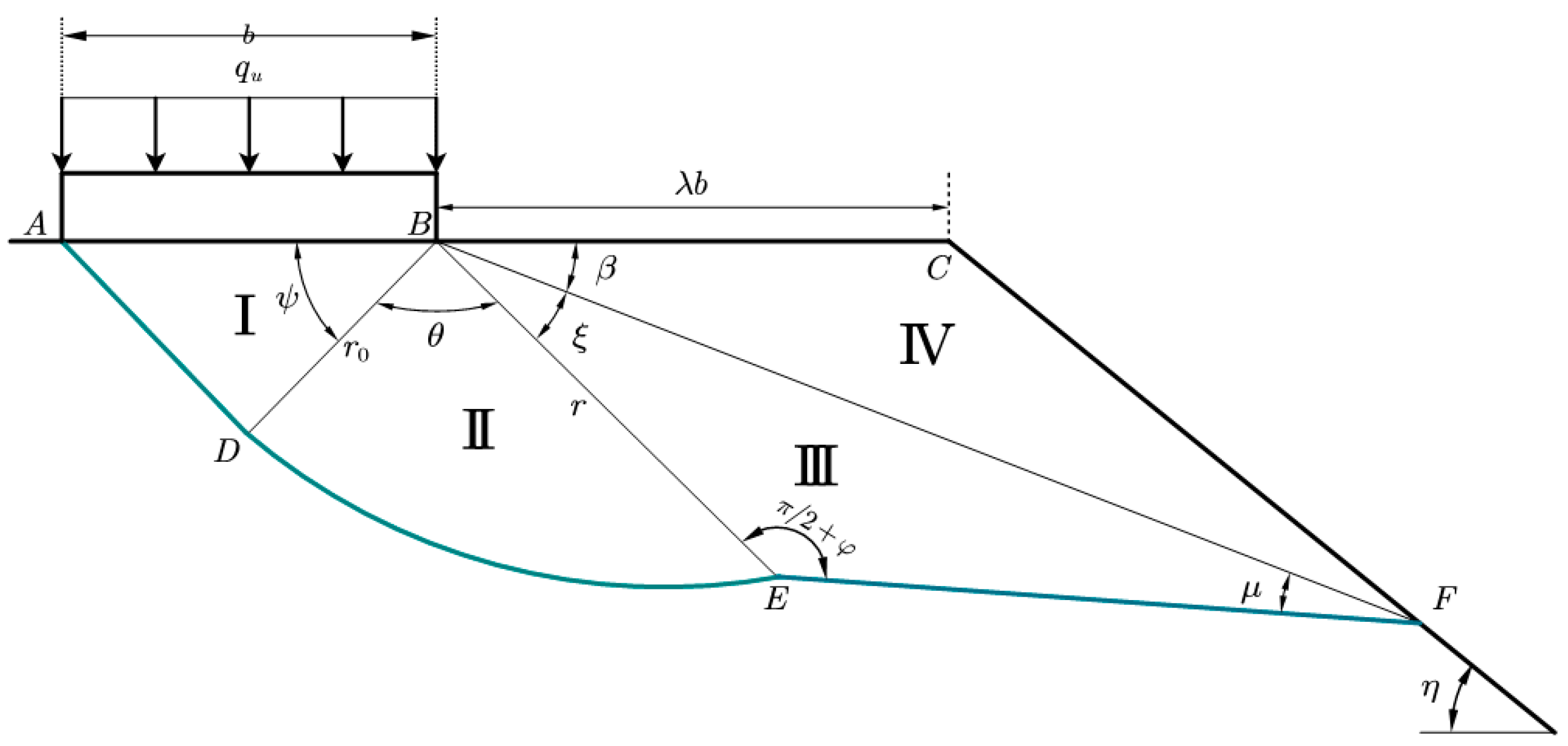
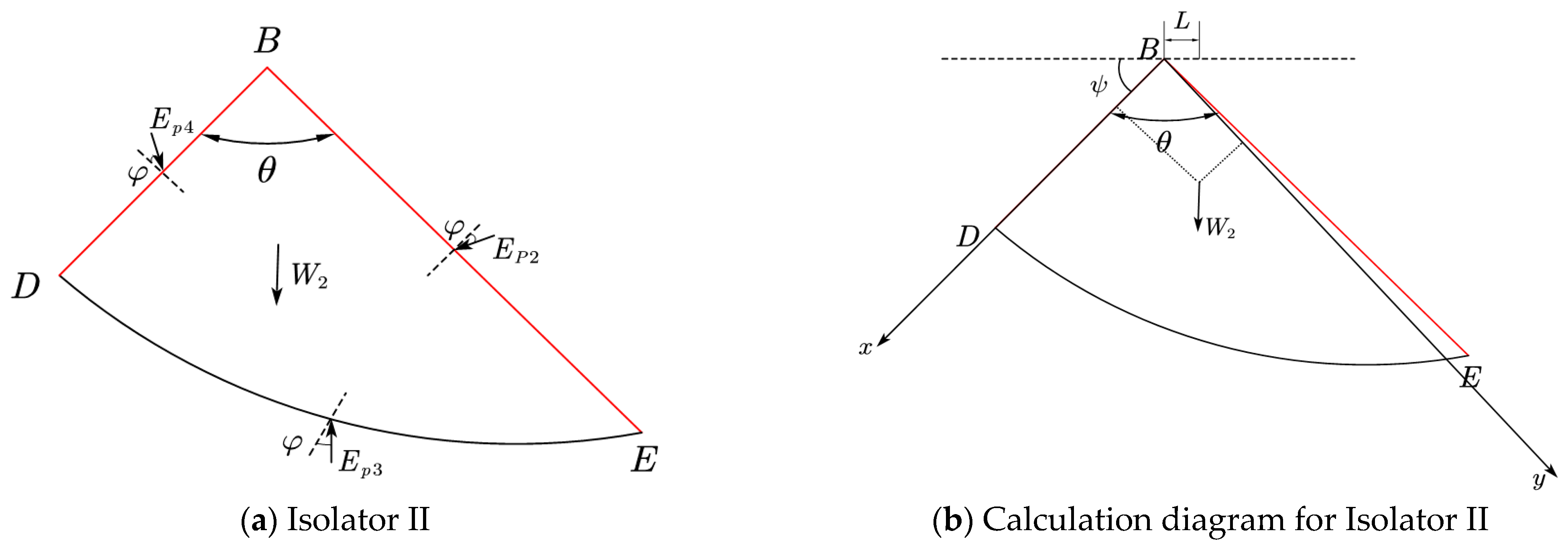
3. Formula Derivation
3.1. Basic Assumptions
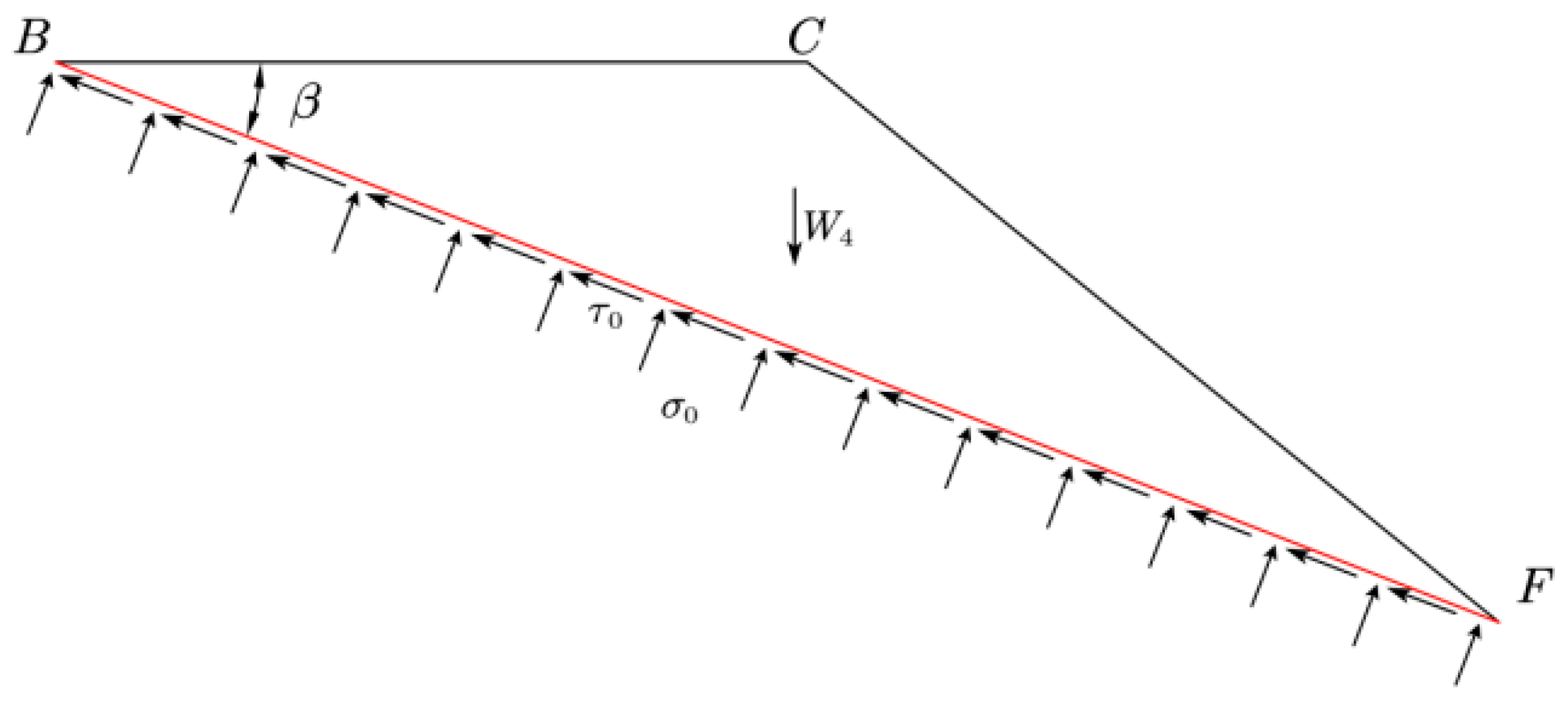
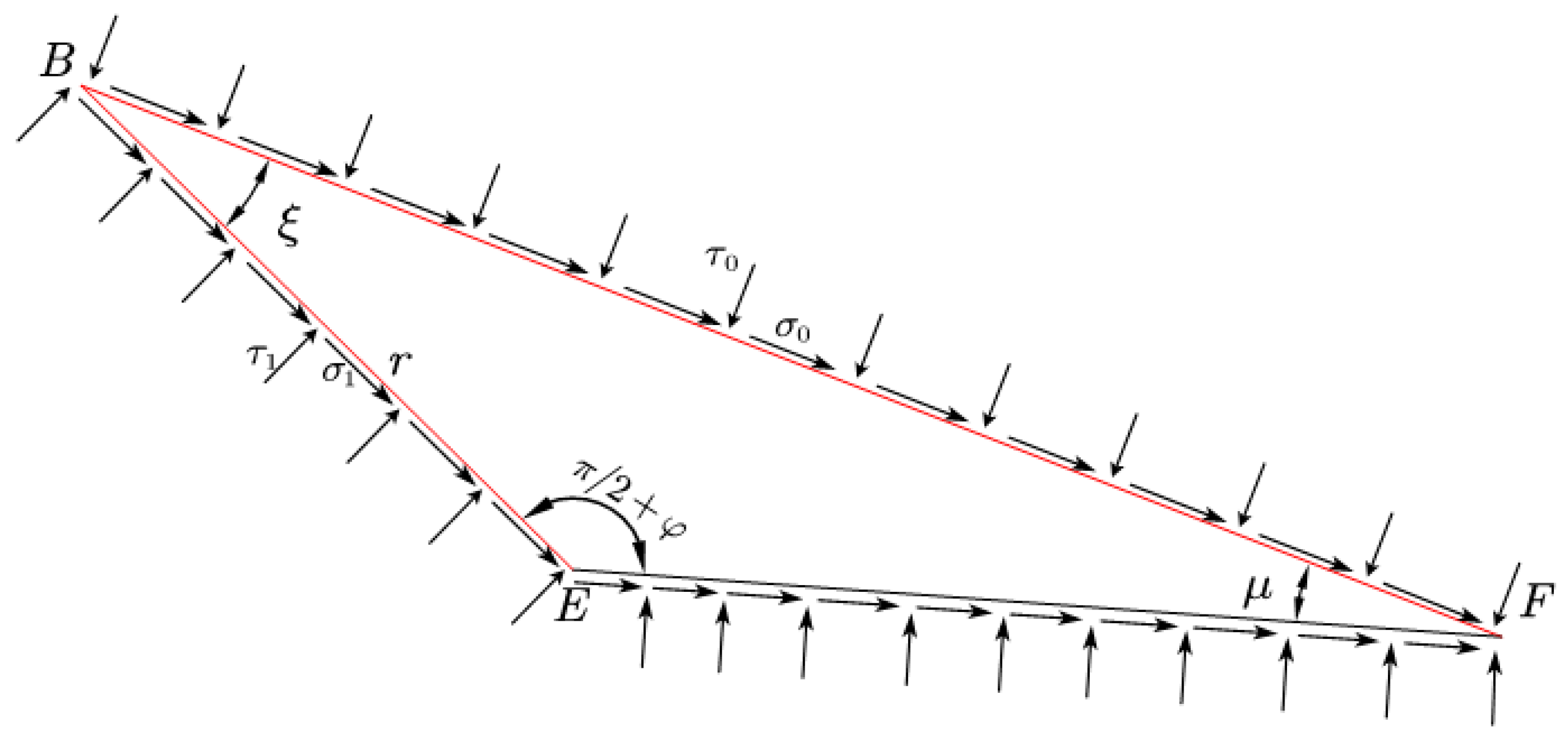
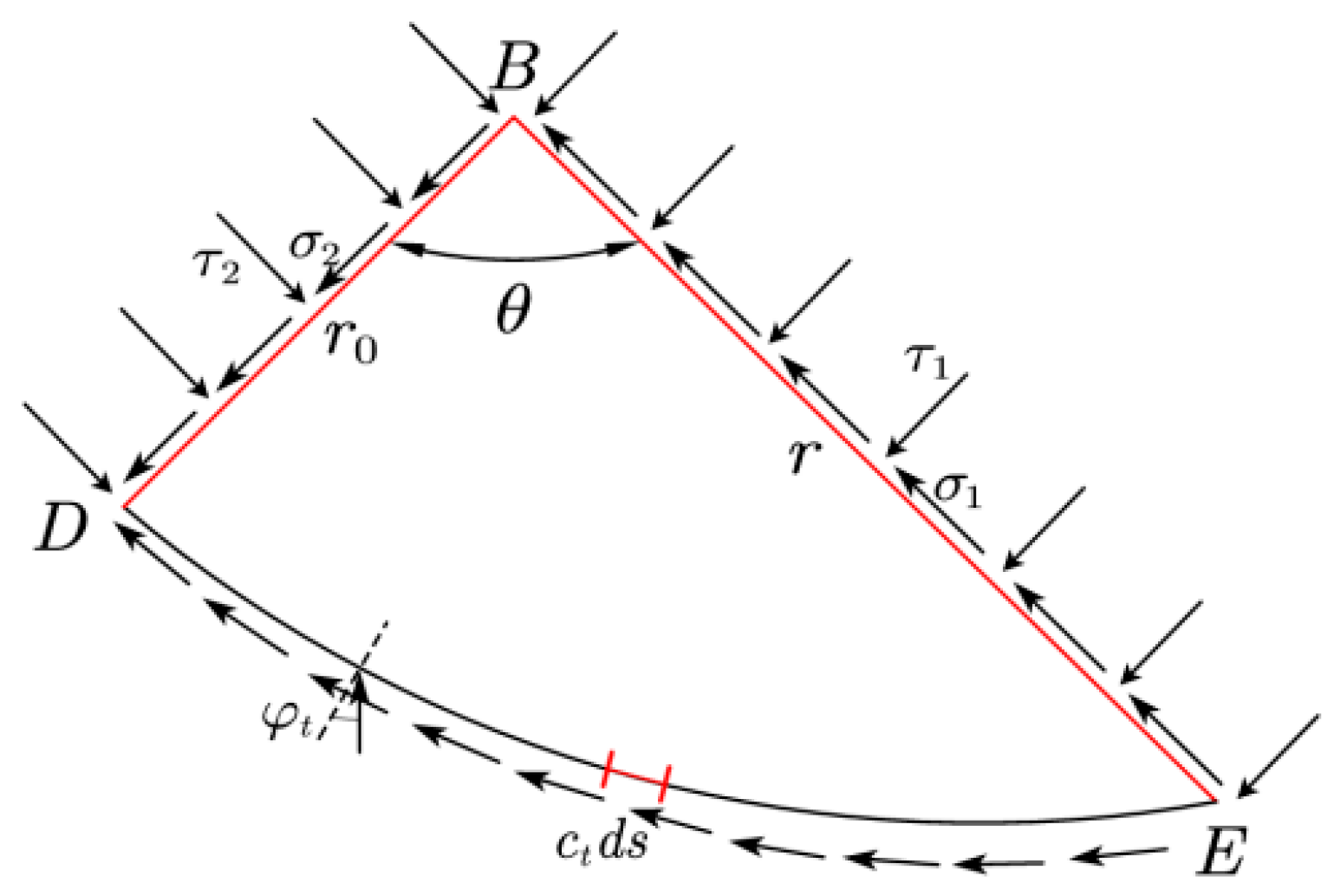
3.2. Deriving a Solution to the Isolation Body Bearing Capacity Equation
4. Application Examples and Comparative Validation
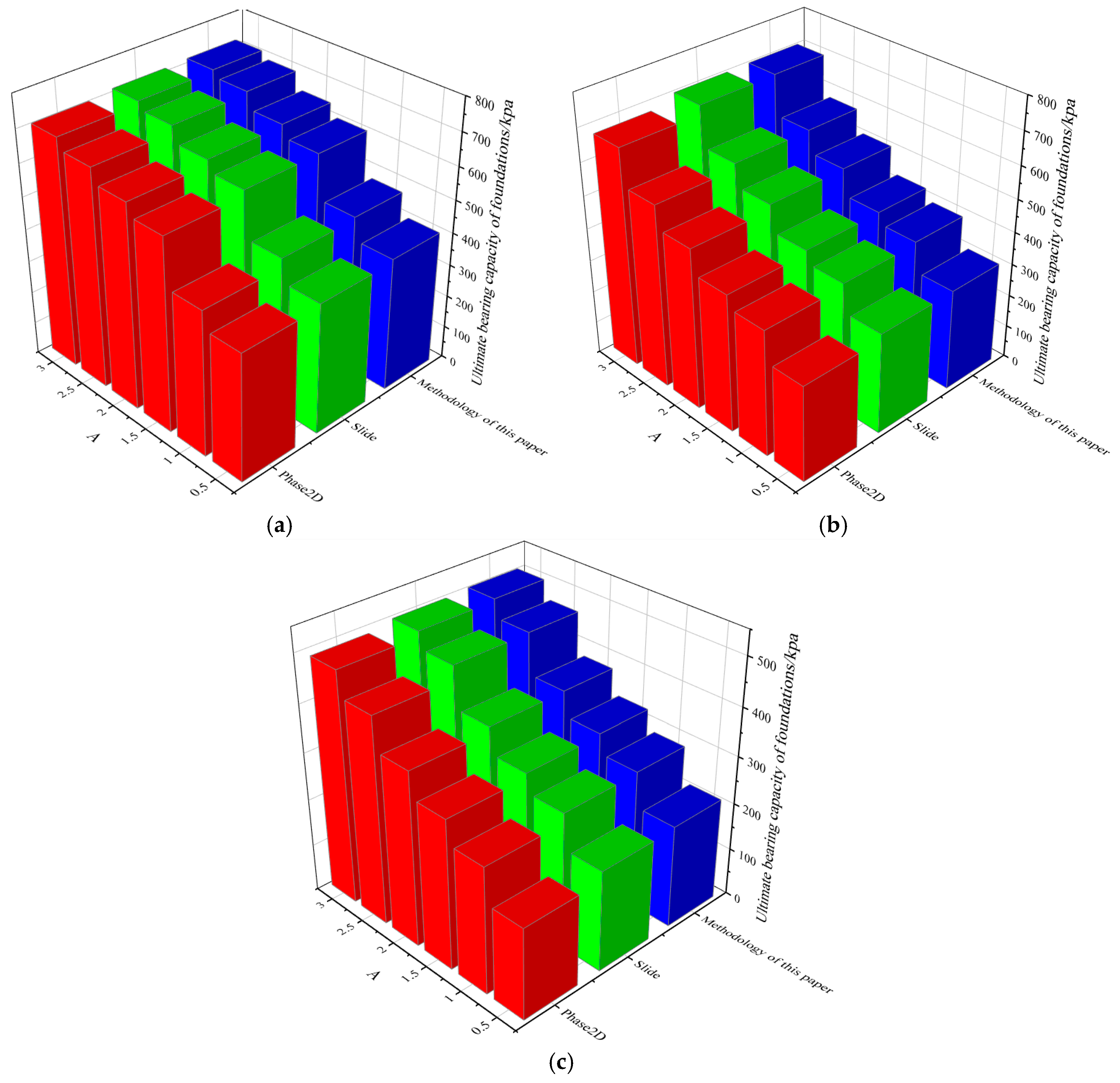
4.1. Case Studies
4.2. Comparative Numerical Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shabani, M.J.; Shamsi, M.; Ghanbari, A. Dynamic response of three-dimensional midrise buildings adjacent to slope under seismic excitation in the direction perpendicular to the slope. Int. J. Geomech. ASCE 2021, 21, 04021204. [Google Scholar] [CrossRef]
- Fatahi, B.; Huang, B.H.; Yeganeh, N.; Terzaghi, S.; Banerjee, S. Three-dimensional simulation of seismic slope-foundation-structure interaction for buildings near shallow slopes. Int. J. Geomech. ASCE 2020, 20, 04019140. [Google Scholar] [CrossRef]
- Bai, T.; Qiu, T.; Huang, X.; Li, C. Locating global critical slip surface using the Morgenstern-Price method and optimization technique. Int. J. Geomech. 2014, 14, 319–325. [Google Scholar] [CrossRef]
- Biniyaz, A.; Azmoon, B.; Liu, Z. Coupled transient saturated–unsaturated seepage and limit equilibrium analysis for slopes: Influence of rapid water level changes. Acta Geotech. 2022, 17, 2139–2156. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Numerical analysis of rainfall effects on slope stability. Int. J. Geomech. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- Cheng, Y.M. Location of critical failure surface and some further studies on slope stability analysis. Comput. Geotech. 2003, 30, 255–267. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Lau, C.K. Slope Stability Analysis and Stabilization: New Methods and Insight, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Fathipour, H.; Tajani, S.B.; Payan, M.; Chenari, R.J.; Senetakis, K. Impact of transient infiltration on the ultimate bearing capacity of obliquely and eccentrically loaded strip footings on partially saturated soils. Int. J. Geomech. 2023, 23, 1–19. [Google Scholar] [CrossRef]
- Caramana, E.J. The implementation of slide lines as a combined force and velocity boundary condition. J. Comput. Phys. 2009, 228, 3911–3916. [Google Scholar] [CrossRef]
- Clair, G.; Després, B.; Labourasse, E. A one-mesh method for the cell-centered discretization of sliding. Comput. Methods Appl. Mech. Eng. 2014, 269, 315–333. [Google Scholar] [CrossRef]
- Zhu, Y.; Du, J. Sliding Line Point Regression for Shape Robust Scene Text Detection. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 3735–3740. [Google Scholar] [CrossRef]
- Roy, A.; Noel, M.M. Design of a high-speed line following robot that smoothly follows tight curves. Comput. Electr. Eng. 2016, 56, 732–747. [Google Scholar] [CrossRef]
- Zhai, J.; Song, Z. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. Int. J. Control 2018, 92, 2255–2262. [Google Scholar] [CrossRef]
- Fraldi, M.; Guarracino, F. Evaluation of Impending Collapse in Circular Tunnels by Analytical and Numerical Approaches. Tunn. Undergr. Space Technol. 2011, 26, 507–516. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational Failure Mechanisms for the Face Stability Analysis of Tunnels Driven by a Pressurized Shield. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Wilson, D.; Abbo, A.; Sloan, S. Undrained Stability of a Square Tunnel Where the Shear Strength Increases Linearly with Depth. Comput. Geotech. 2013, 49, 314–325. [Google Scholar] [CrossRef]
- Yang, X.-L.; Qin, C.-B. Limit Analysis of Rectangular Cavity Subjected to Seepage Forces Based on Hoek-Brown Failure Criterion. Geomech. Eng. 2014, 6, 503–515. Available online: https://api.semanticscholar.org/CorpusID:129222228 (accessed on 24 March 2025).
- Yang, X.-L.; Yan, R.-M. Collapse Mechanism for Deep Tunnel Subjected to Seepage Force in Layered Soils. Geomech. Eng. 2015, 8, 741–756. [Google Scholar] [CrossRef]
- Yu, S.B.; Zhang, X.; Sloan, S.W. A 3D upper bound limit analysis using radial point interpolation meshless method and second-order cone programming. Int. J. Numer. Methods Eng. 2016, 108, 1686–1704. [Google Scholar] [CrossRef]
- Yuan, S.; Du, J.N. Effective stress-based upper bound limit analysis of unsaturated soils using the weak form quadrature element method. Method. Comput. Geotech. 2018, 98, 172–180. [Google Scholar] [CrossRef]
- Huang, M.S.; Fan, X.P.; Wang, H.R. Three-dimensional upper bound stability analysis of slopes with weak interlayer based on rotational-translational mechanisms. Eng. Geol. 2017, 223, 82–91. [Google Scholar] [CrossRef]
- Monforte, L.; Arroyo, M.; Carbonell, J.M.; Gens, A. Numerical simulation of undrained insertion problems in geotechnical engineering with the particle finite element method (PFEM). Comput. Geotech. 2017, 82, 144–156. [Google Scholar] [CrossRef]
- Singh, P.K.; Kumar, M. Hypervelocity impact behavior of projectile penetration on spacecraft structure: A review. Mater. Today Proc. 2022, 62, 67–71. [Google Scholar] [CrossRef]
- Baazouzi, M.; Benmeddour, D.; Mabrouki, A.; Nouiri, M. 2D numerical analysis of shallow foundation rested near slope under inclined loading. Procedia Eng. 2016, 143, 1234–1241. [Google Scholar] [CrossRef]
- Kusakabe, O.; Kimura, T.; Yamaguchi, H. Bearing capacity of slopes under strip load on the top surfaces. Soils Found. 1981, 21, 29–35. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.L.; Wang, Z.B.; Zou, J.F.; Li, L. Bearing capacity of foundation on slope determined by energy dissipation method and model experiments. J. Cent. South Univ. Technol. 2007, 14, 125–128. [Google Scholar] [CrossRef]
- Yang, X.L.; Guo, N.Z.; Zhao, L.H.; Li, L. Influences of nonassociated flow rules on seismic bearing capacity factors of strip footing on soil slope by energy dissipation method. J. Cent. South Univ. Technol. 2007, 14, 842–847. [Google Scholar] [CrossRef]
- Yang, S.C.; Leshchinsky, B.; Cui, K.; Zhang, F.; Gao, Y.F. Unified approach toward evaluating bearing capacity of shallow foundations near slopes. J. Geotech. Geoenviron. Eng. 2019, 145, 04019110. [Google Scholar] [CrossRef]
- Zhao, L.; Luo, Q.; Yang, F. Calculation of upper limit of bearing capacity of slope-facing strip foundation. J. Wuhan Univ. Technol. (Transp. Sci. Eng. Ed.) 2010, 34, 84–87. [Google Scholar]
- Feng, Y.; Yang, J.; Zhang, X.; Zhao, L. One-side slip failure mechanism and upper bound solution for bearing capacity of foundation on slope. Eng. Mech. 2010, 27, 162–168. [Google Scholar]
- Casablanca, O.; Biondi, G.; Cascone, E. Static and seismic bearing capacity of shallow strip foundations on slopes. Géotechnique 2022, 72, 769–783. [Google Scholar] [CrossRef]
- El Sawwaf, M.A. Behavior of strip footing on geogrid-reinforced sand over a soft clay slope. Geotext. Geomembr. 2007, 25, 50–60. [Google Scholar] [CrossRef]
- El Sawwaf, M.A.; Nazir, A.K. Cyclic settlement behavior of strip footings resting on reinforced layered sand slope. J. Adv. Res. 2012, 3, 315–324. [Google Scholar] [CrossRef]
- Faghihmaleki, H.; Nazari, H. Laboratory study of metakaolin and microsilica effect on the performance of high-strength concrete containing Forta fibers. Adv. Bridg. Eng. 2023, 4, 11. [Google Scholar] [CrossRef]
- Bagheri Kalaye, A. The Effect of Non-implementation of the Beam Roof of the Last Floor Block on the Irregularity of the Analysis and Design of the Structure. J. Civ. Asp. Struct. Eng. 2024, 1, 197–204. [Google Scholar]
- Bararpour, M.; Delfani, M. Tensile and Compressive Strength Investigations of Ordinary Concrete and Pozzolanic Concrete and the Effect of Polypropylene on Them. J. Civ. Asp. Struct. Eng. 2024, 1, 113–120. [Google Scholar]
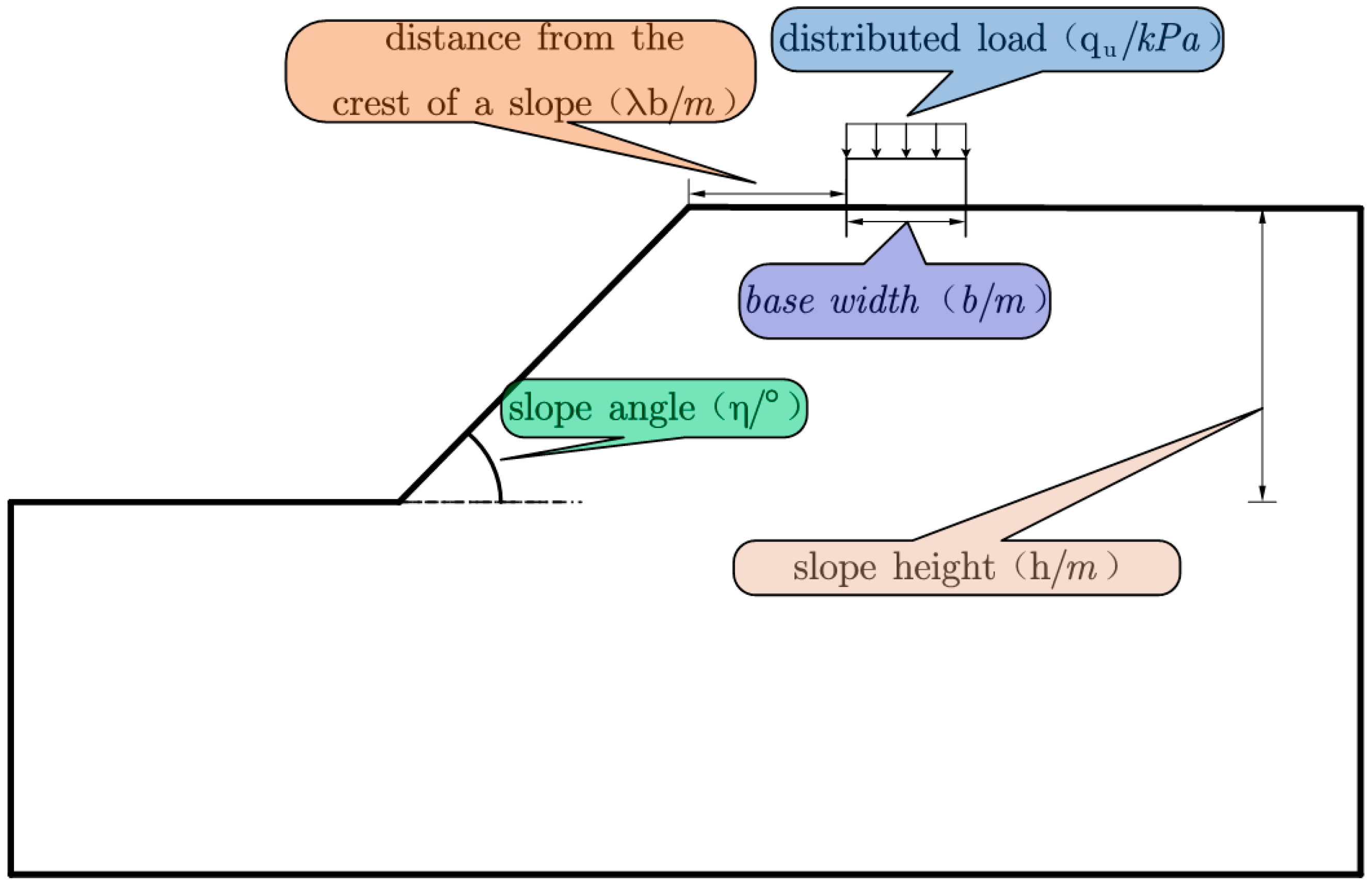
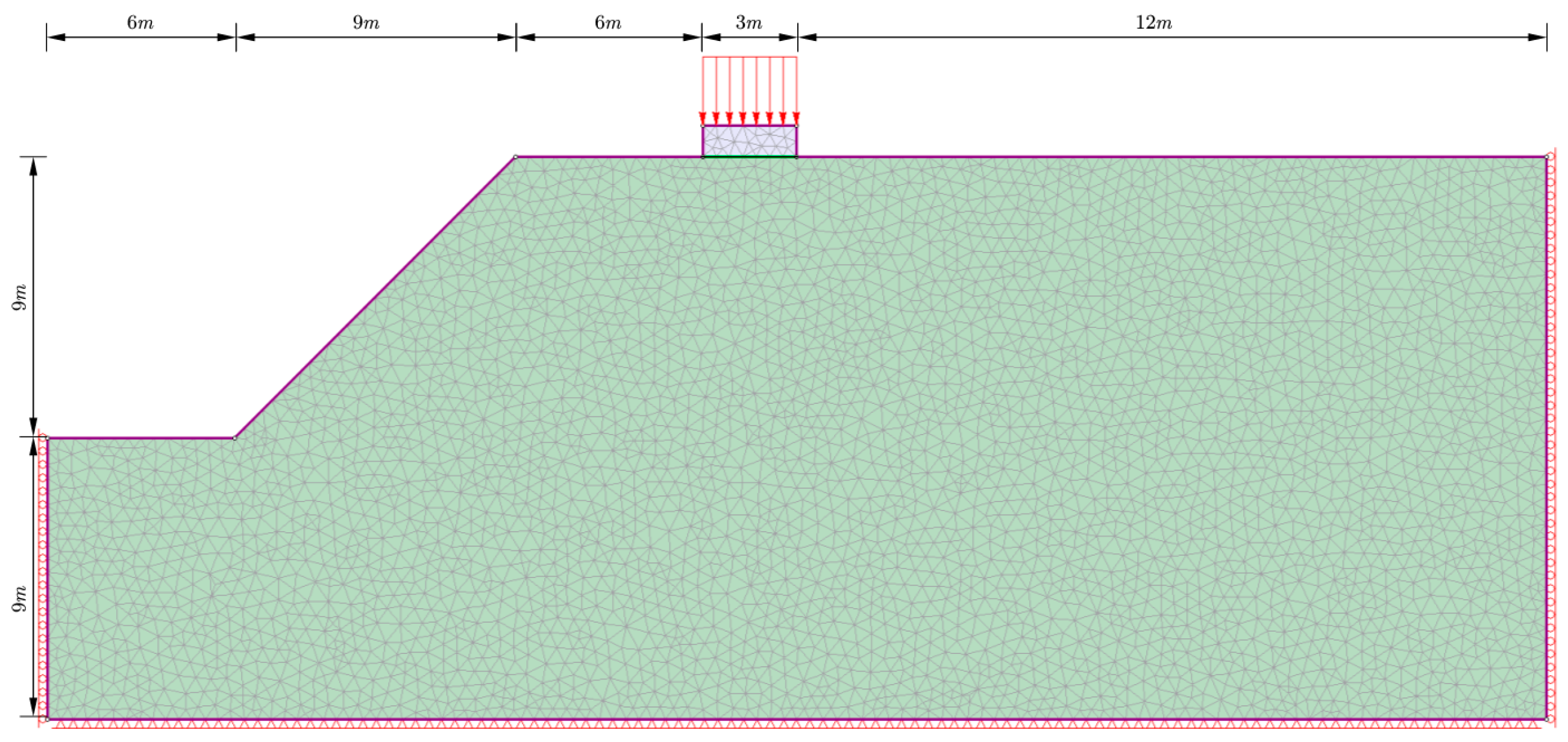
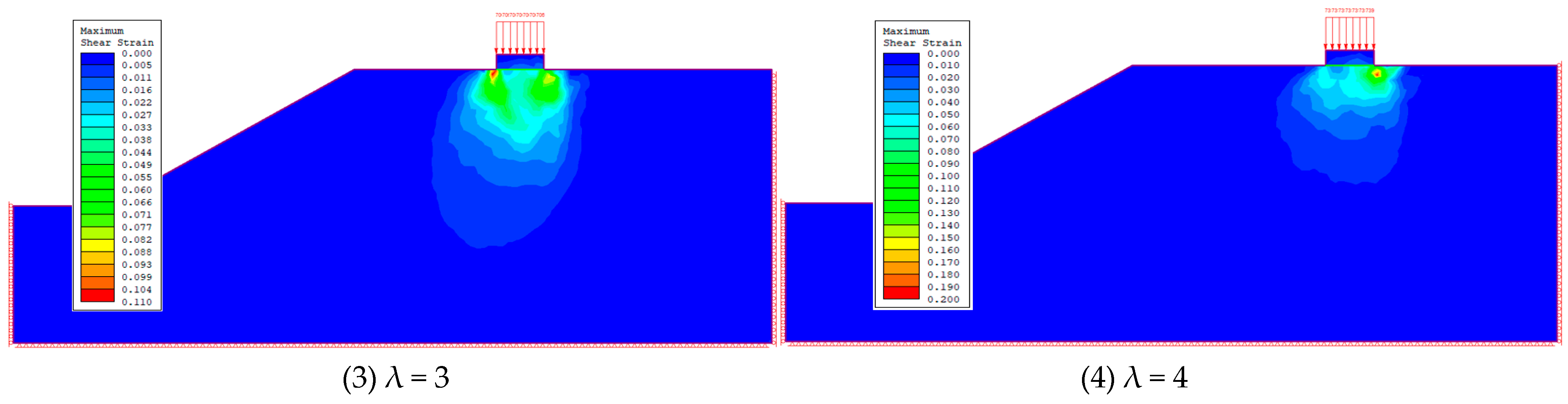
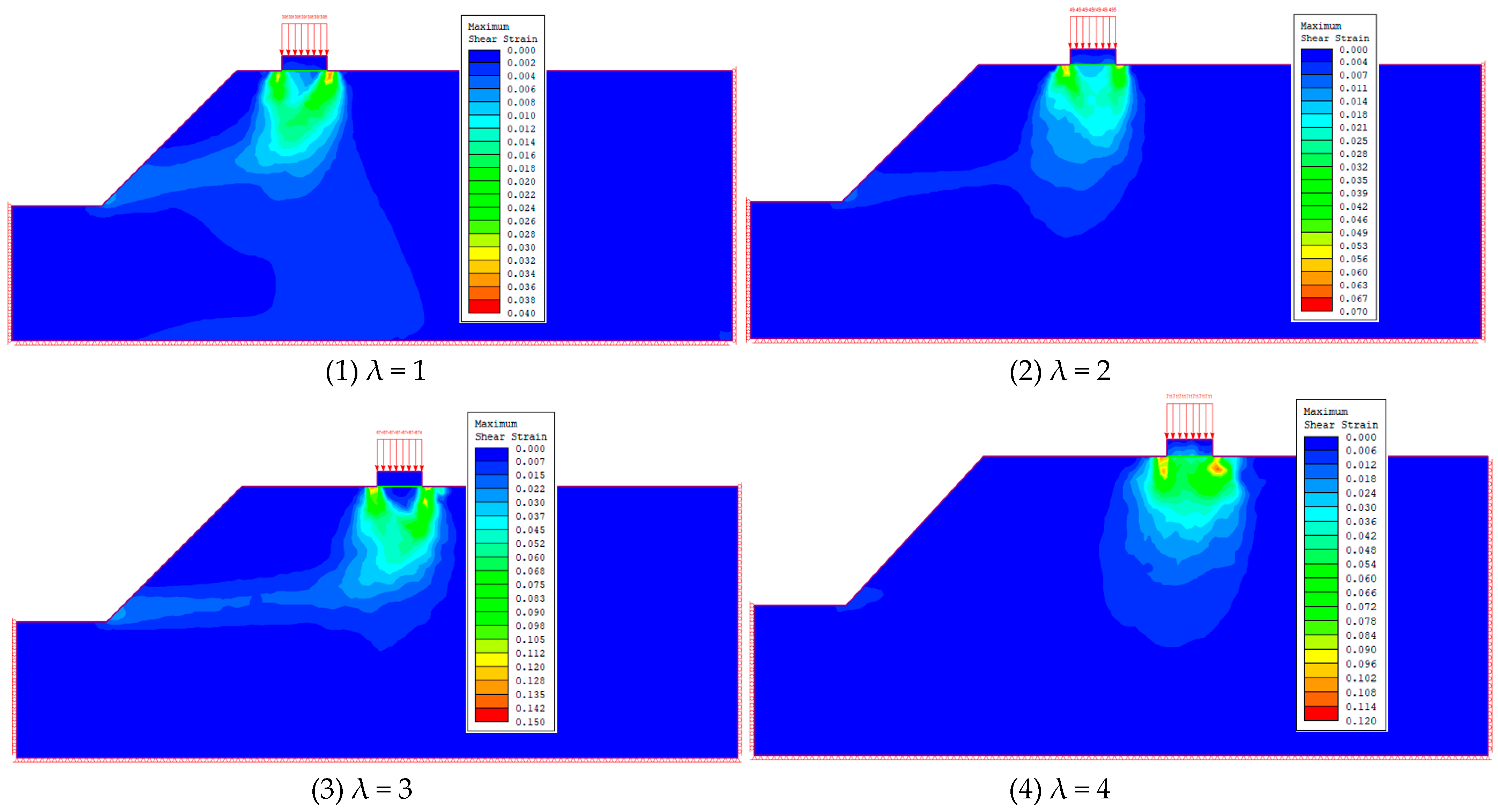

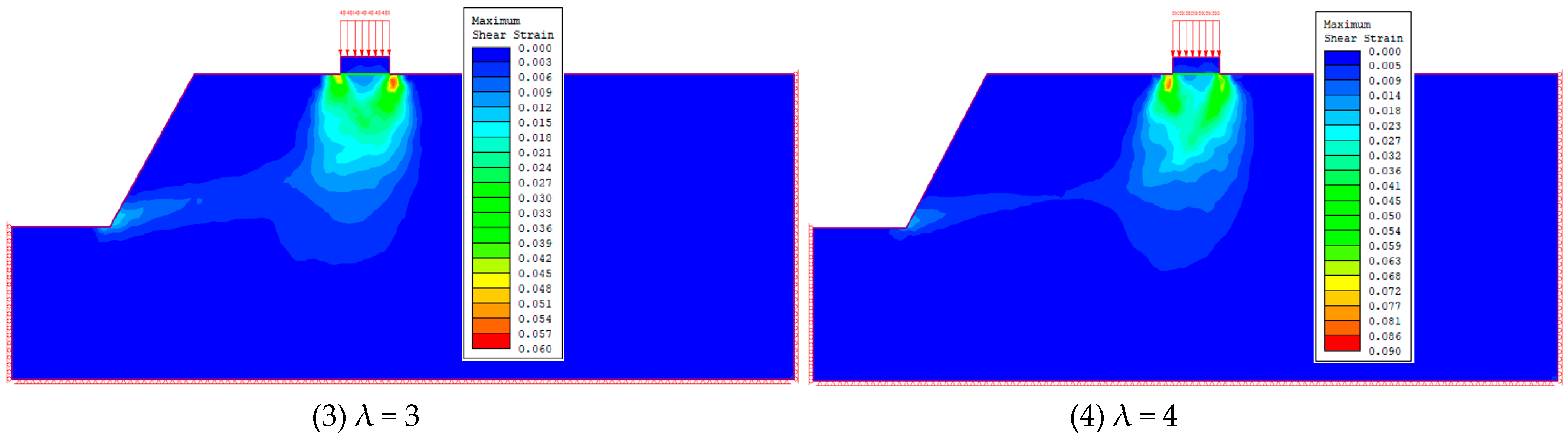

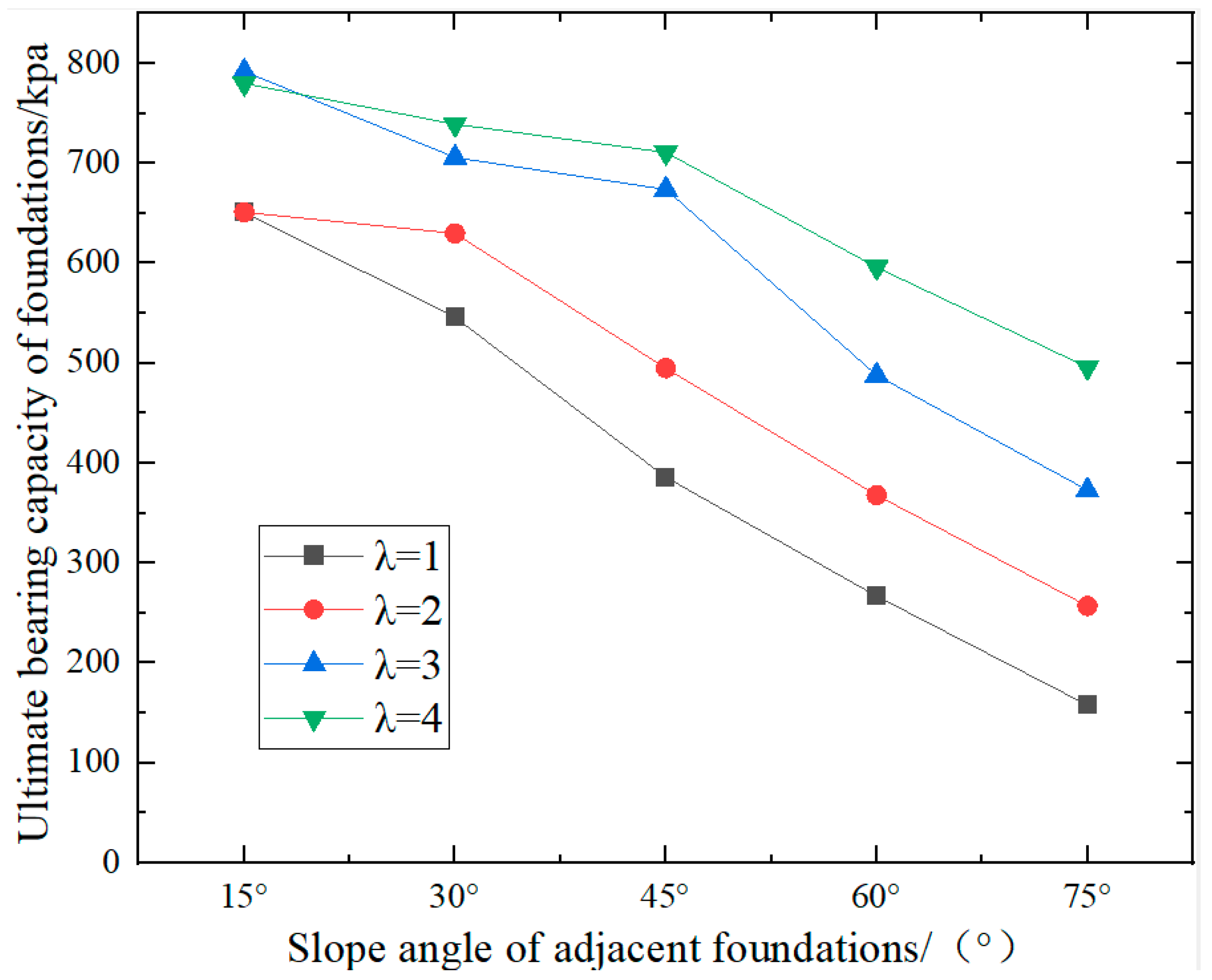




| Parameter Name | Capacity γ/(kN∙m−3) | Modulus of Elasticity E/(kpa) | Poisson’s Ratio | Tensile Strength σt/(kpa) | Angle of Internal Friction φ/(°) | Cohesive Force c/(kpa) |
|---|---|---|---|---|---|---|
| Numerical value | 19 | 50,000 | 0.38 | 5 | 15 | 50 |
| Considerations | Numerical Value | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 3 | 3 | 3 | 3 |
| η/(°) | 30 | 45 | 60 | 75 | 30 | 45 | 60 | 75 | 30 | 45 | 60 | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, M.; Tang, H. Calculating the Bearing Capacity of Foundations near Slopes Based on the Limit Equilibrium and Limit Analysis Methods. Buildings 2025, 15, 1106. https://doi.org/10.3390/buildings15071106
Ye M, Tang H. Calculating the Bearing Capacity of Foundations near Slopes Based on the Limit Equilibrium and Limit Analysis Methods. Buildings. 2025; 15(7):1106. https://doi.org/10.3390/buildings15071106
Chicago/Turabian StyleYe, Mulang, and Hua Tang. 2025. "Calculating the Bearing Capacity of Foundations near Slopes Based on the Limit Equilibrium and Limit Analysis Methods" Buildings 15, no. 7: 1106. https://doi.org/10.3390/buildings15071106
APA StyleYe, M., & Tang, H. (2025). Calculating the Bearing Capacity of Foundations near Slopes Based on the Limit Equilibrium and Limit Analysis Methods. Buildings, 15(7), 1106. https://doi.org/10.3390/buildings15071106






