Shaking Table Test and Finite Element Analysis of Isolation Performance for Diesel Engine Building in a Nuclear Power Plant
Abstract
1. Introduction
2. Test Overview
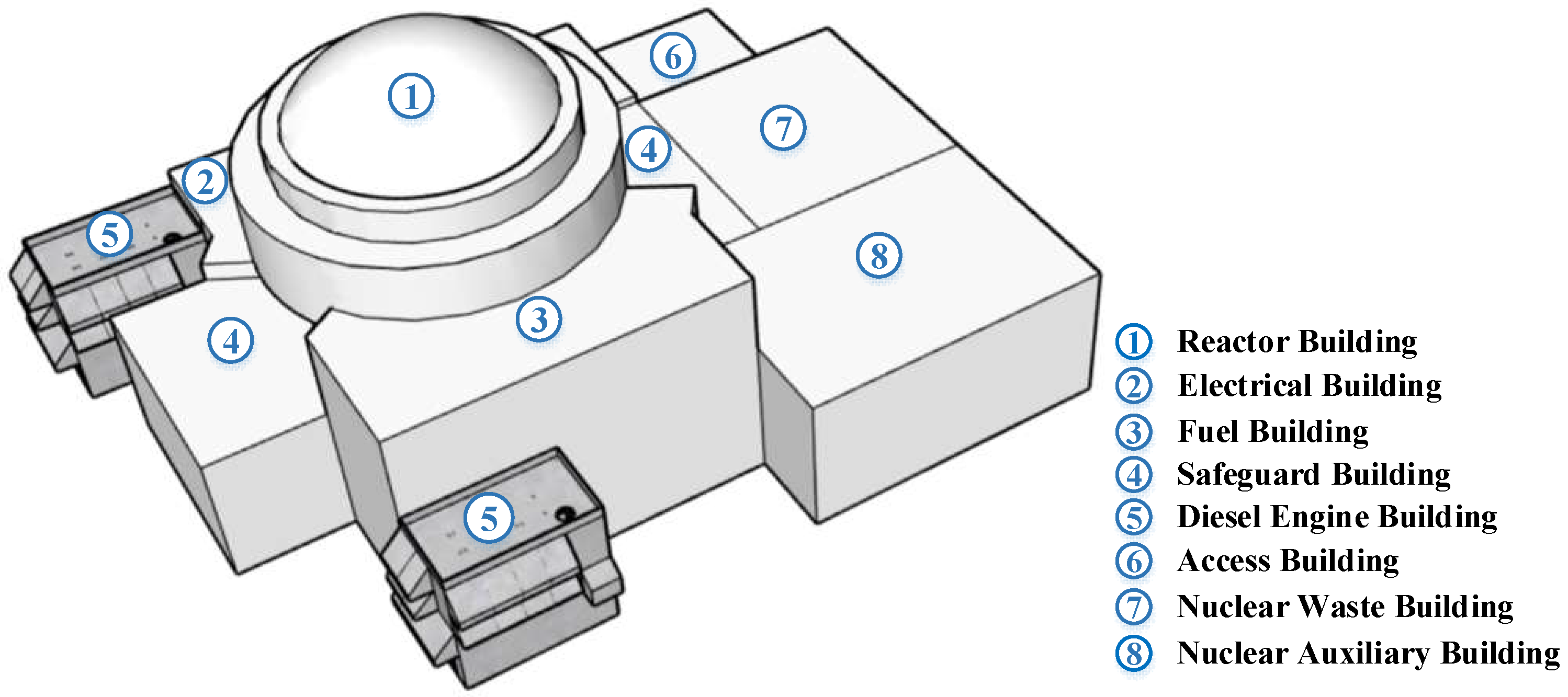
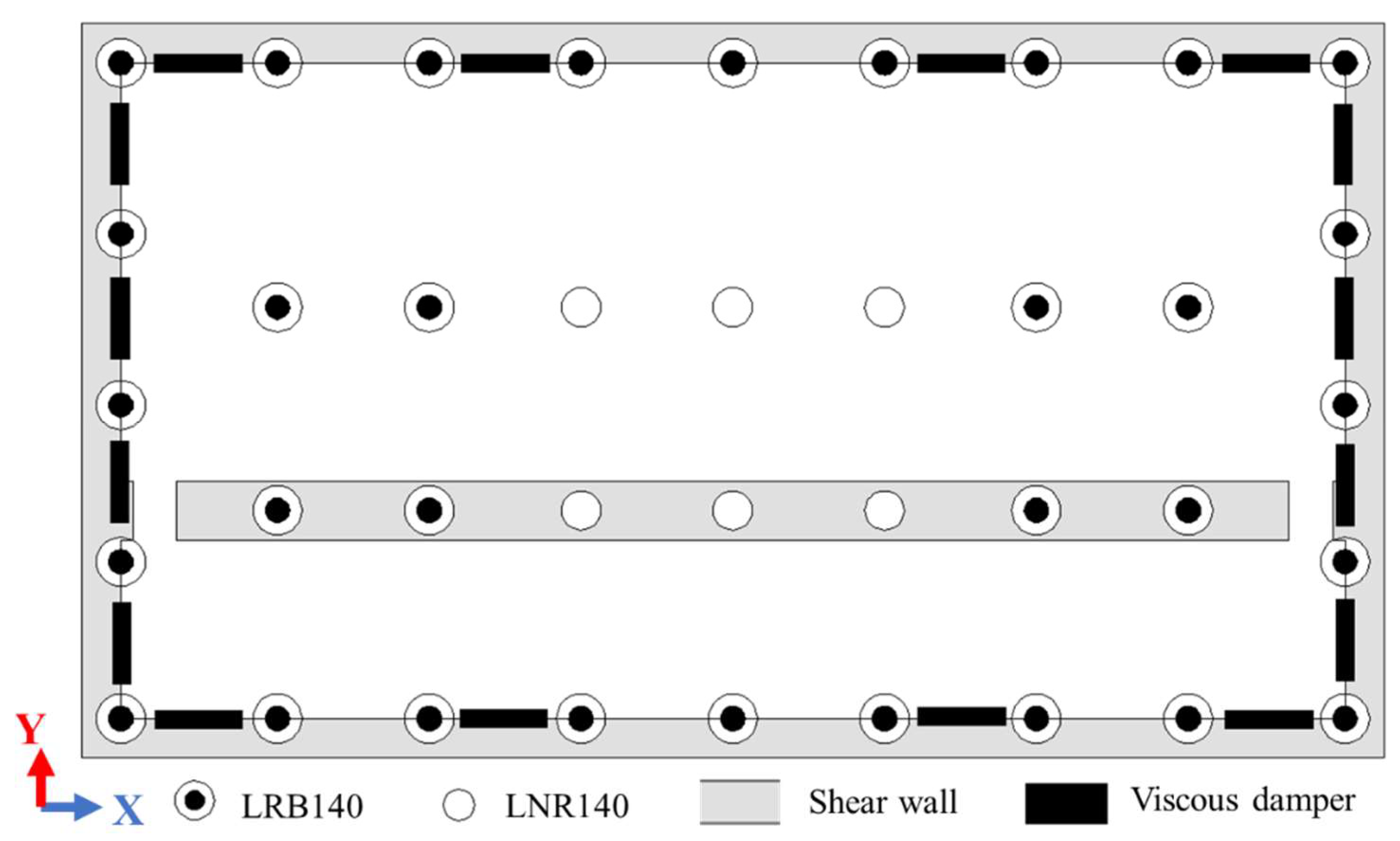
2.1. Prototype Introduction
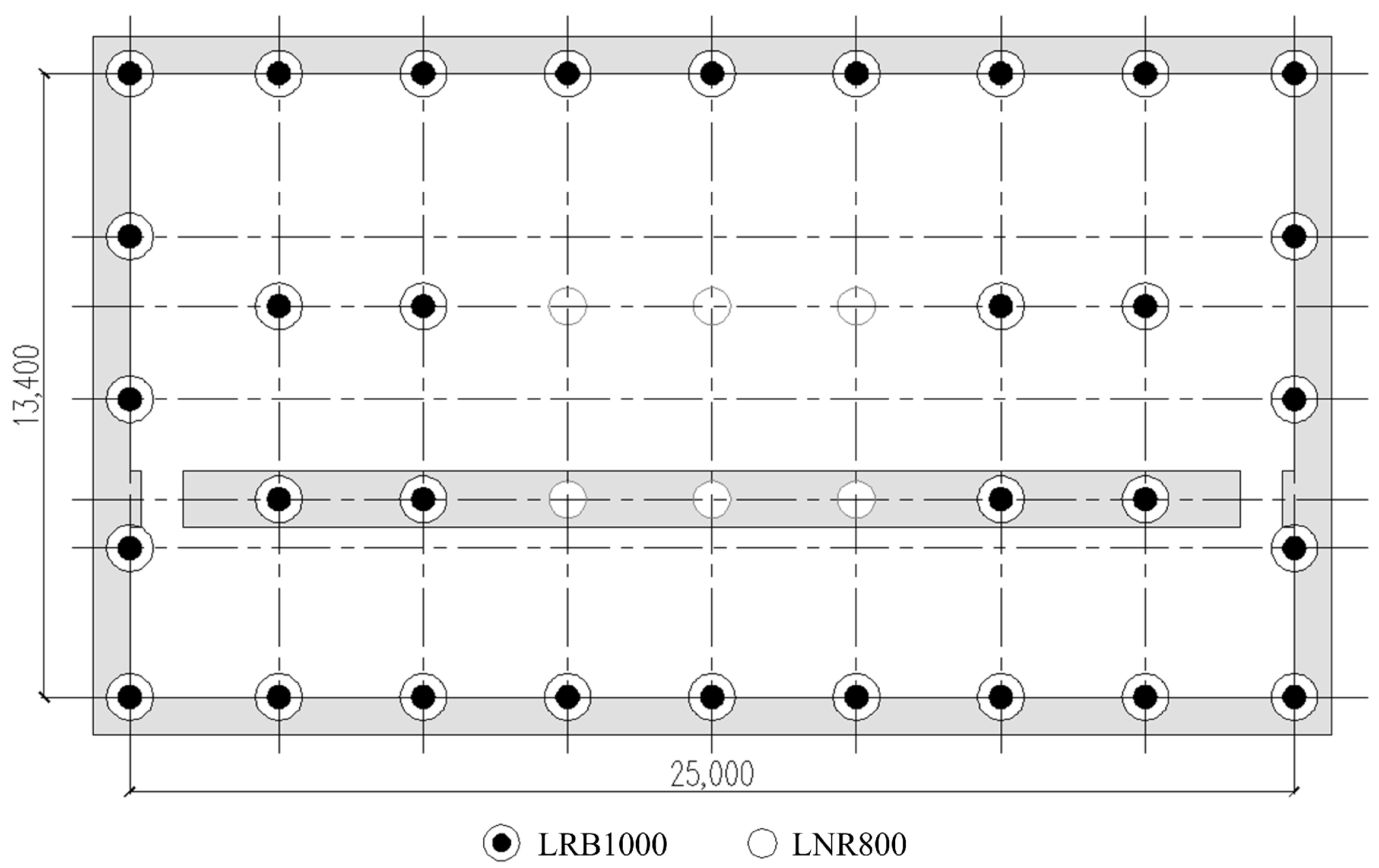
2.2. Model Design and Production
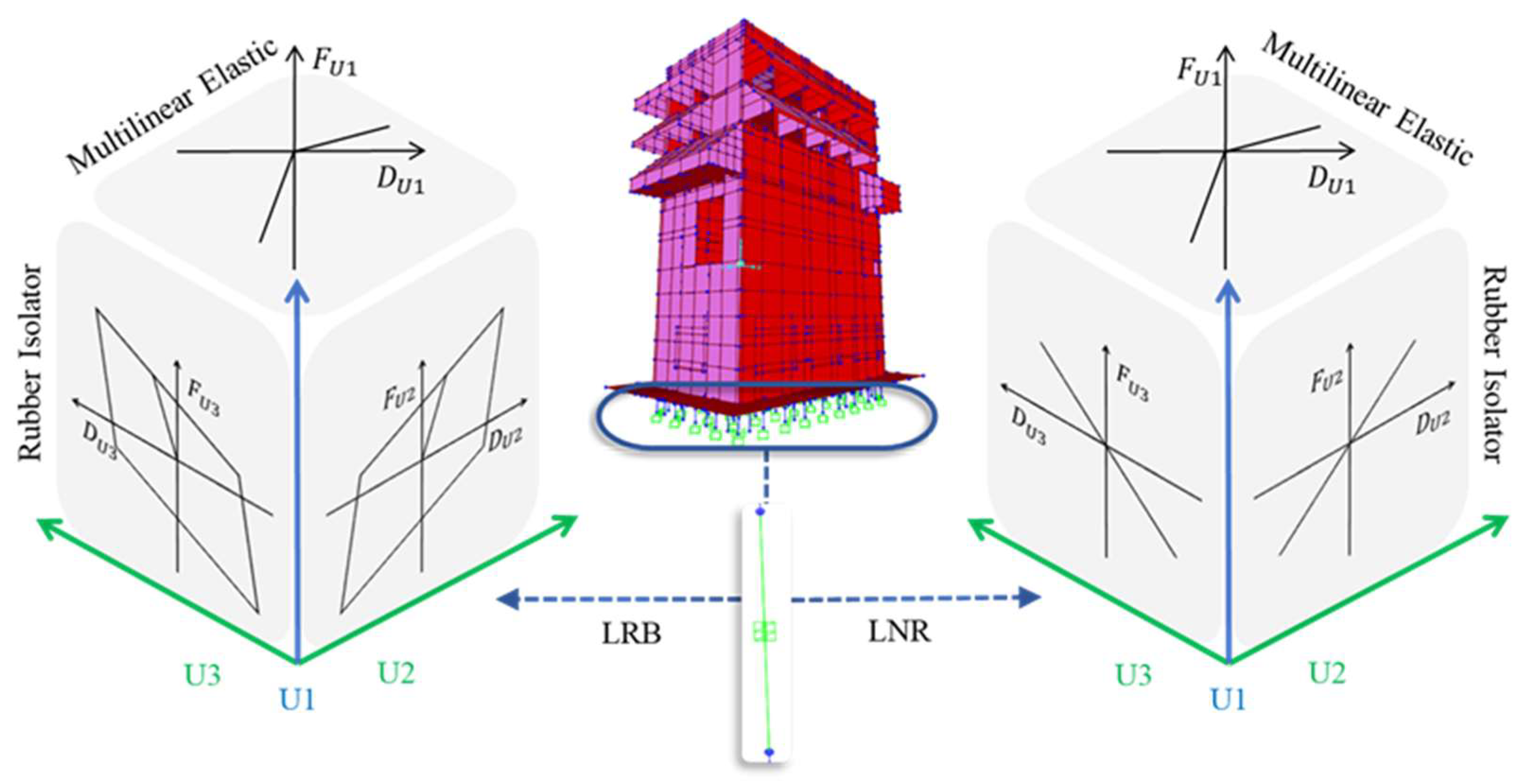
2.3. Connection Structure of Isolation Layer and Superstructure
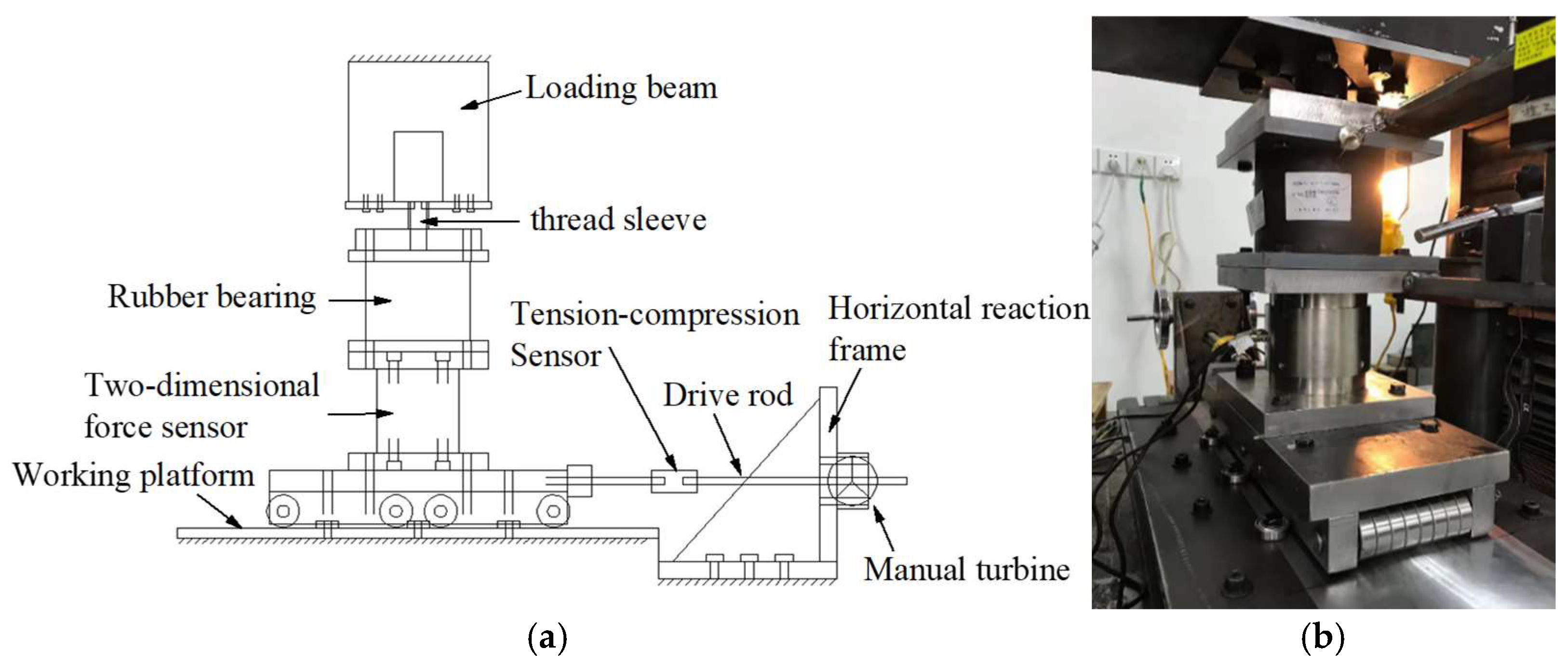
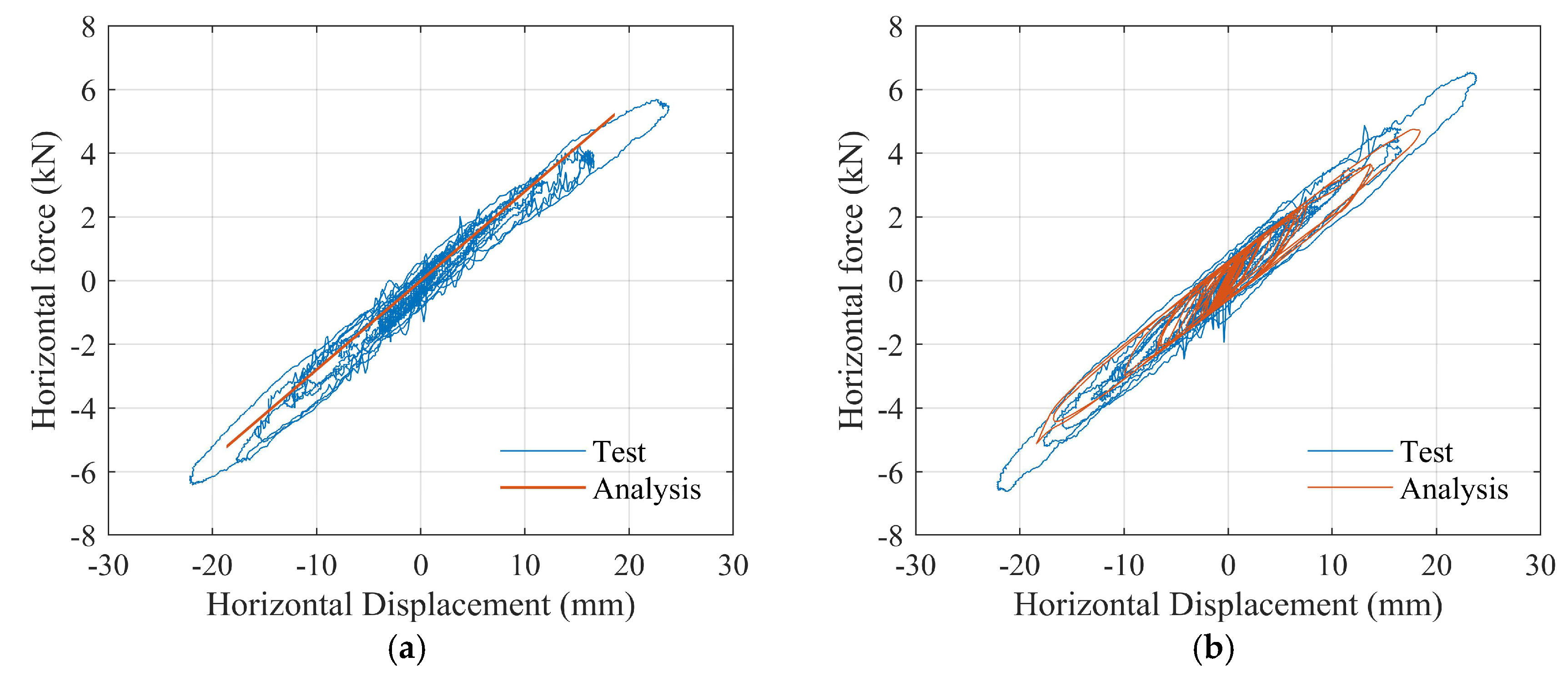
2.4. Mechanical Properties Test of Model Bearing
3. Shaking Table Test
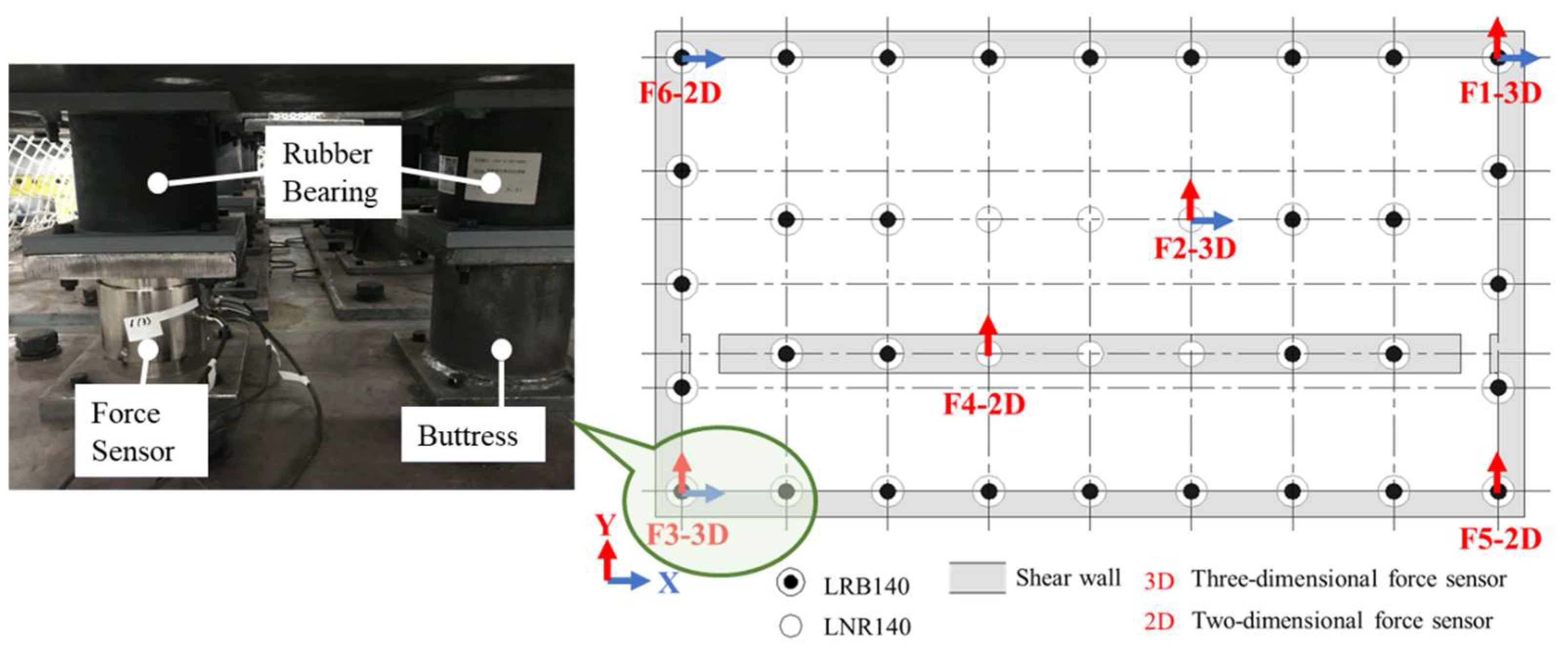
3.1. Sensor Layout and Measurement Method
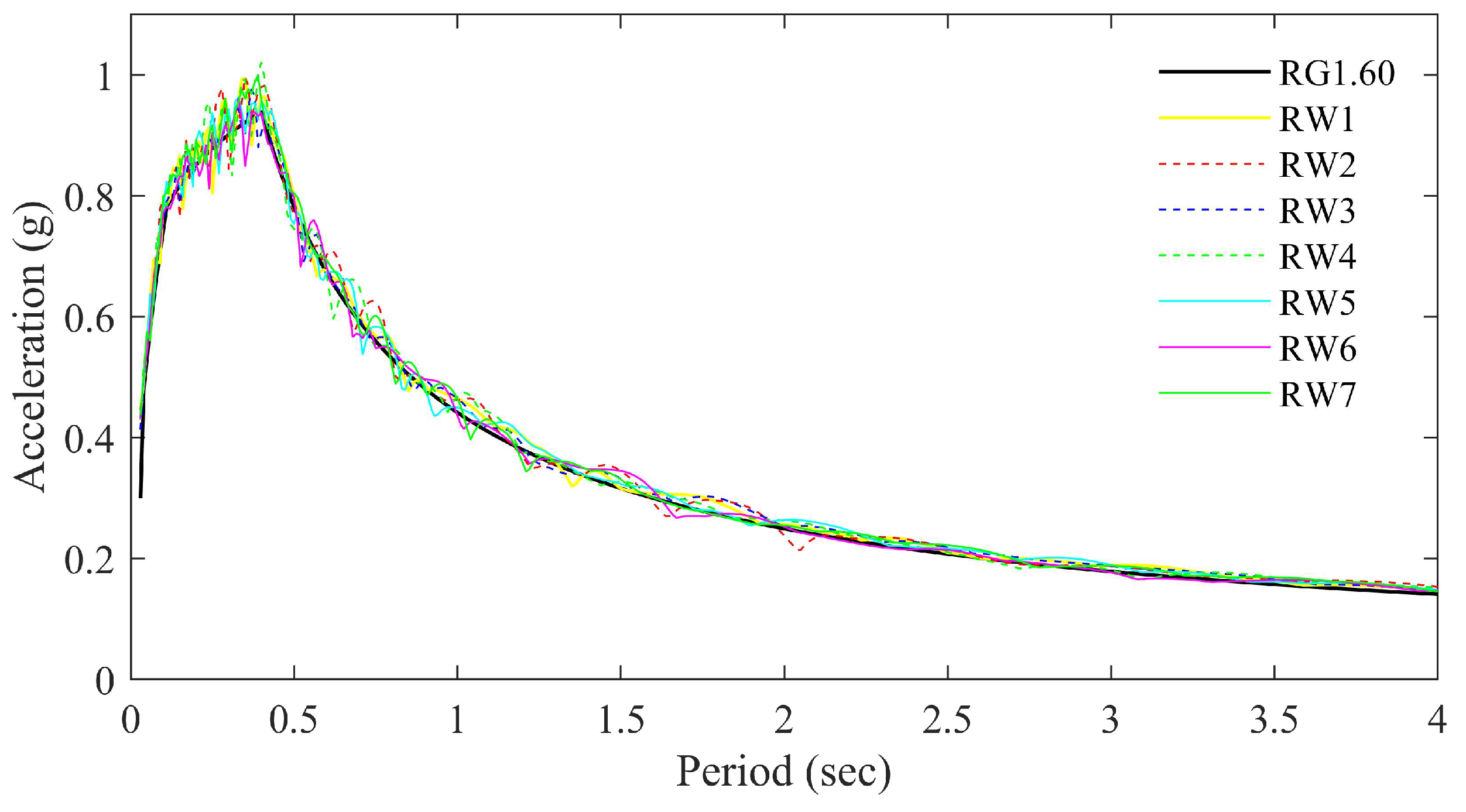
3.2. Ground Motion Selection
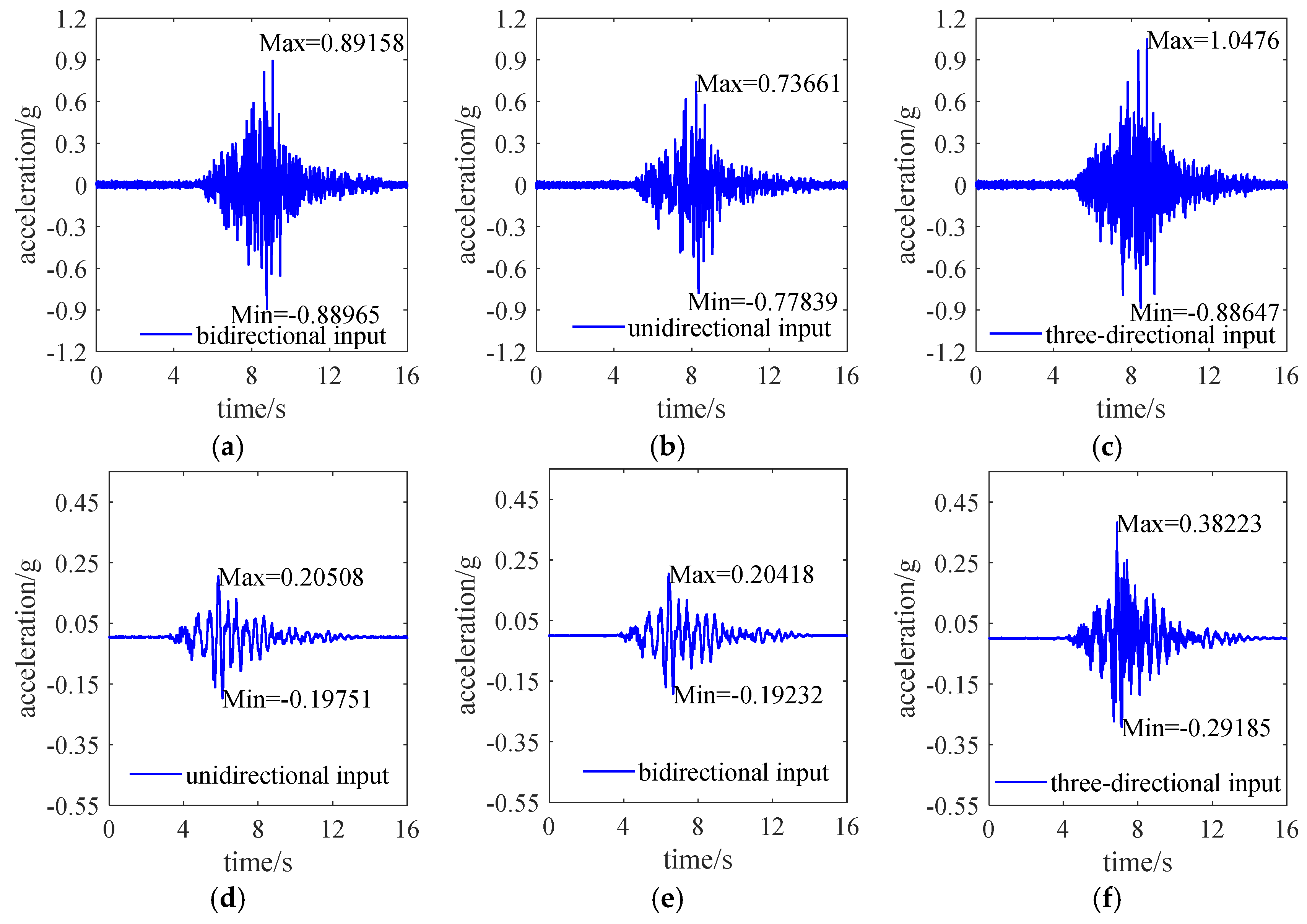
3.3. Test Conditions
3.4. Data Processing and Calibration
4. Test Results
4.1. Model Dynamic Characteristic Analysis
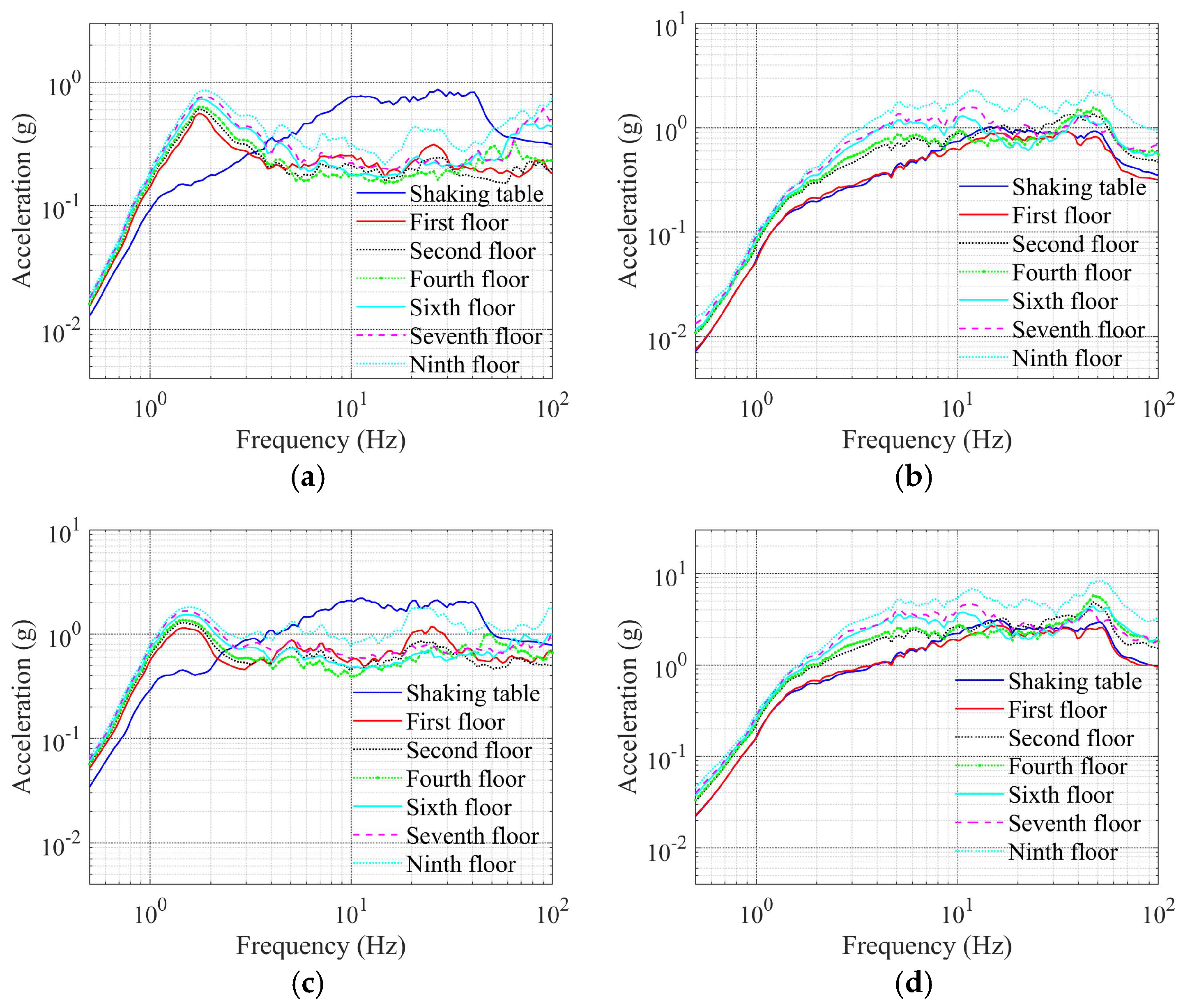
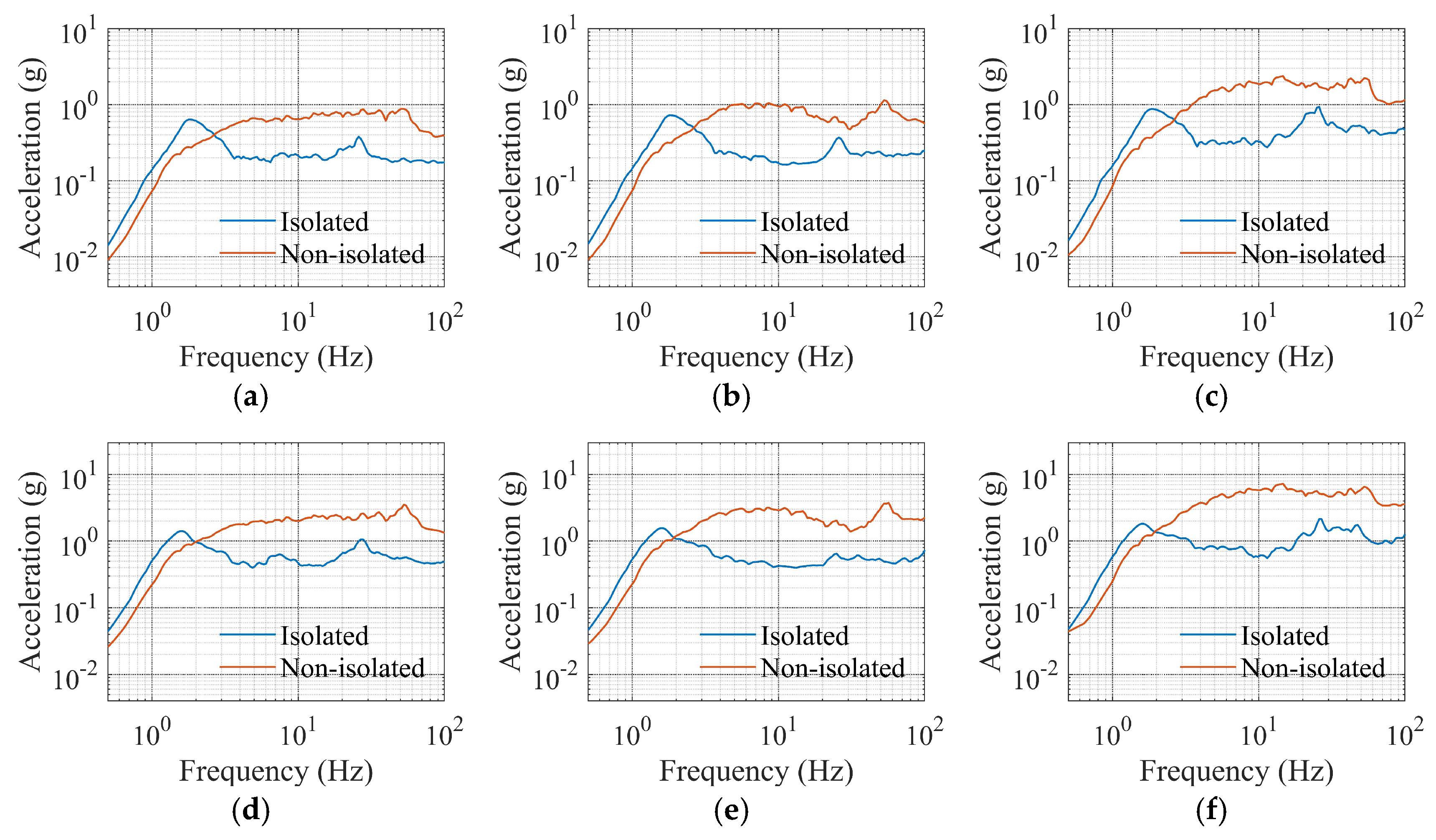
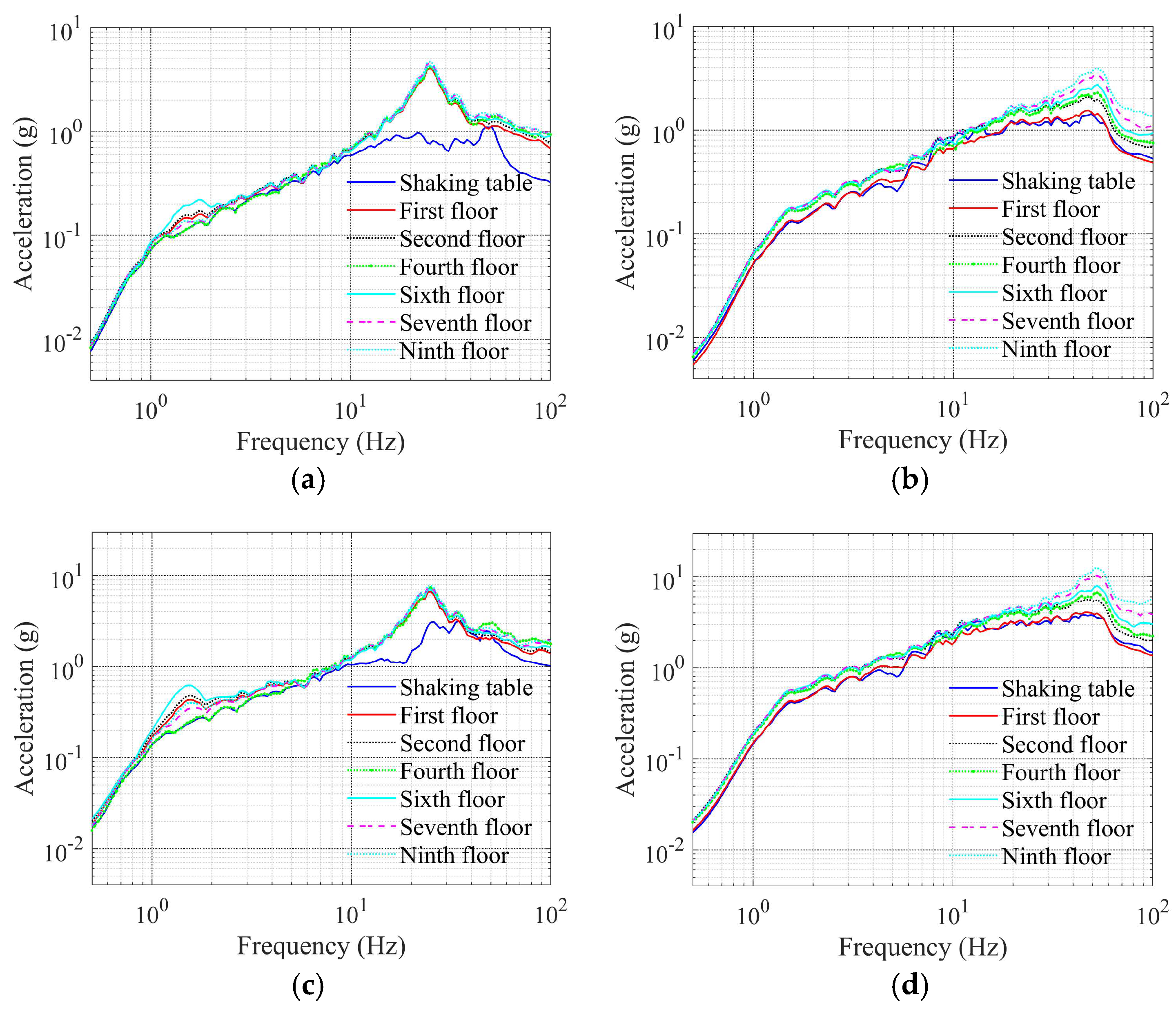
4.2. Acceleration Response
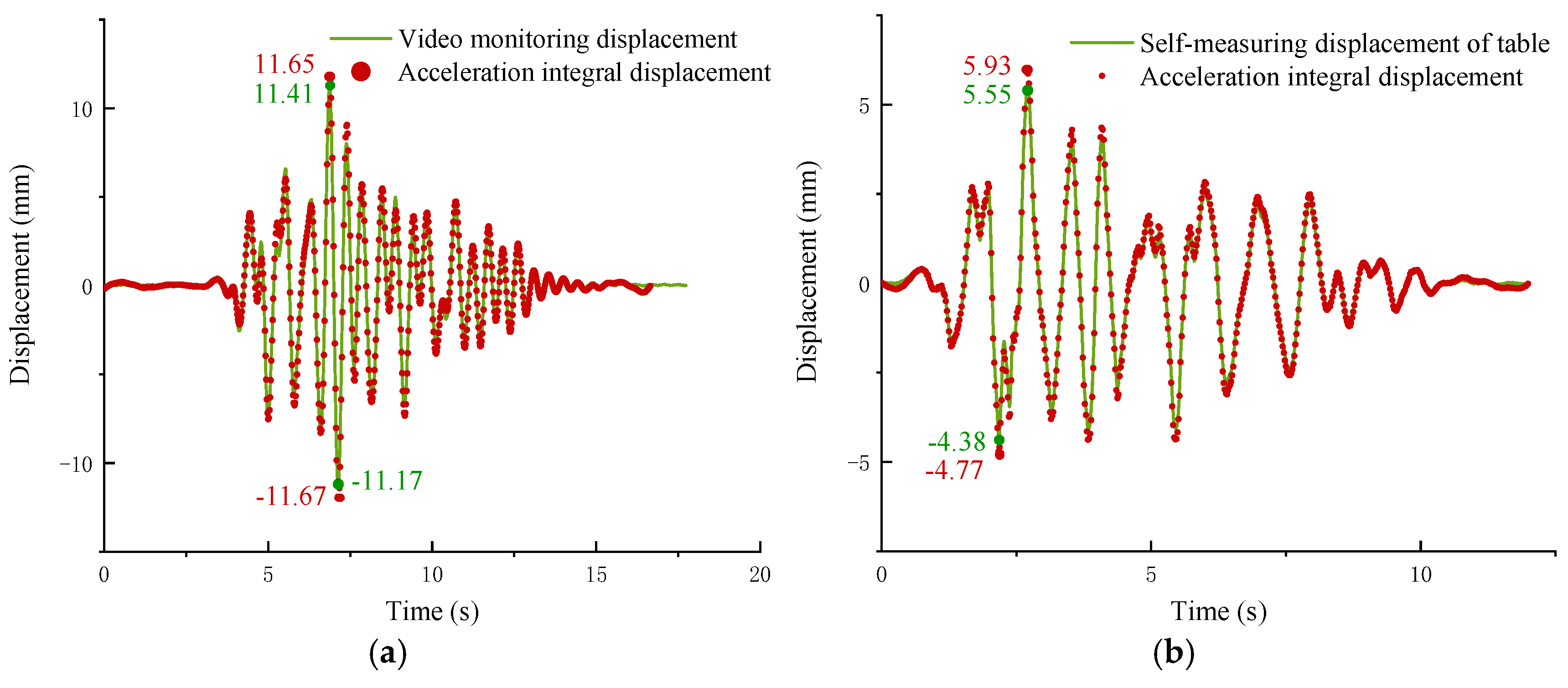
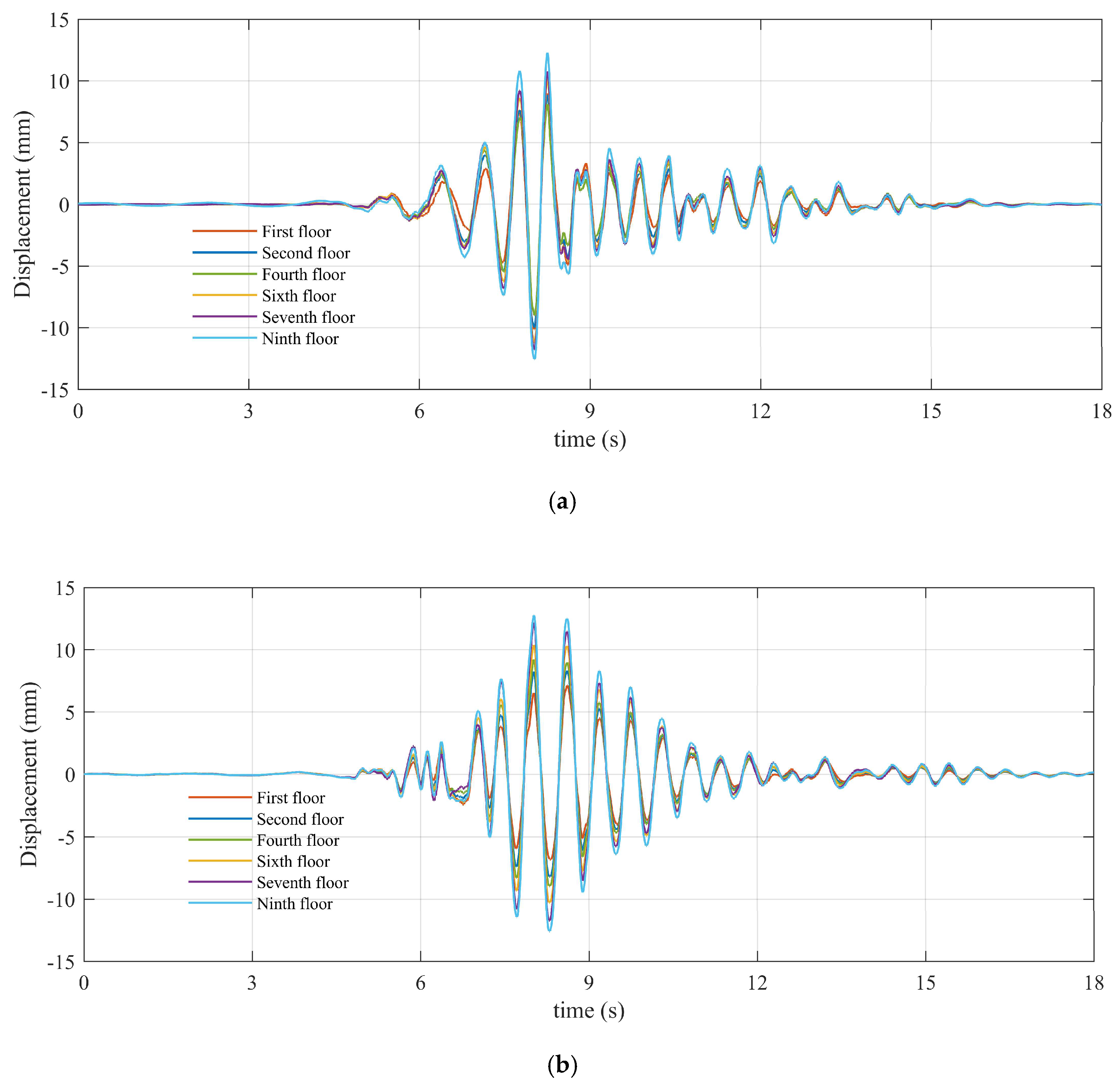
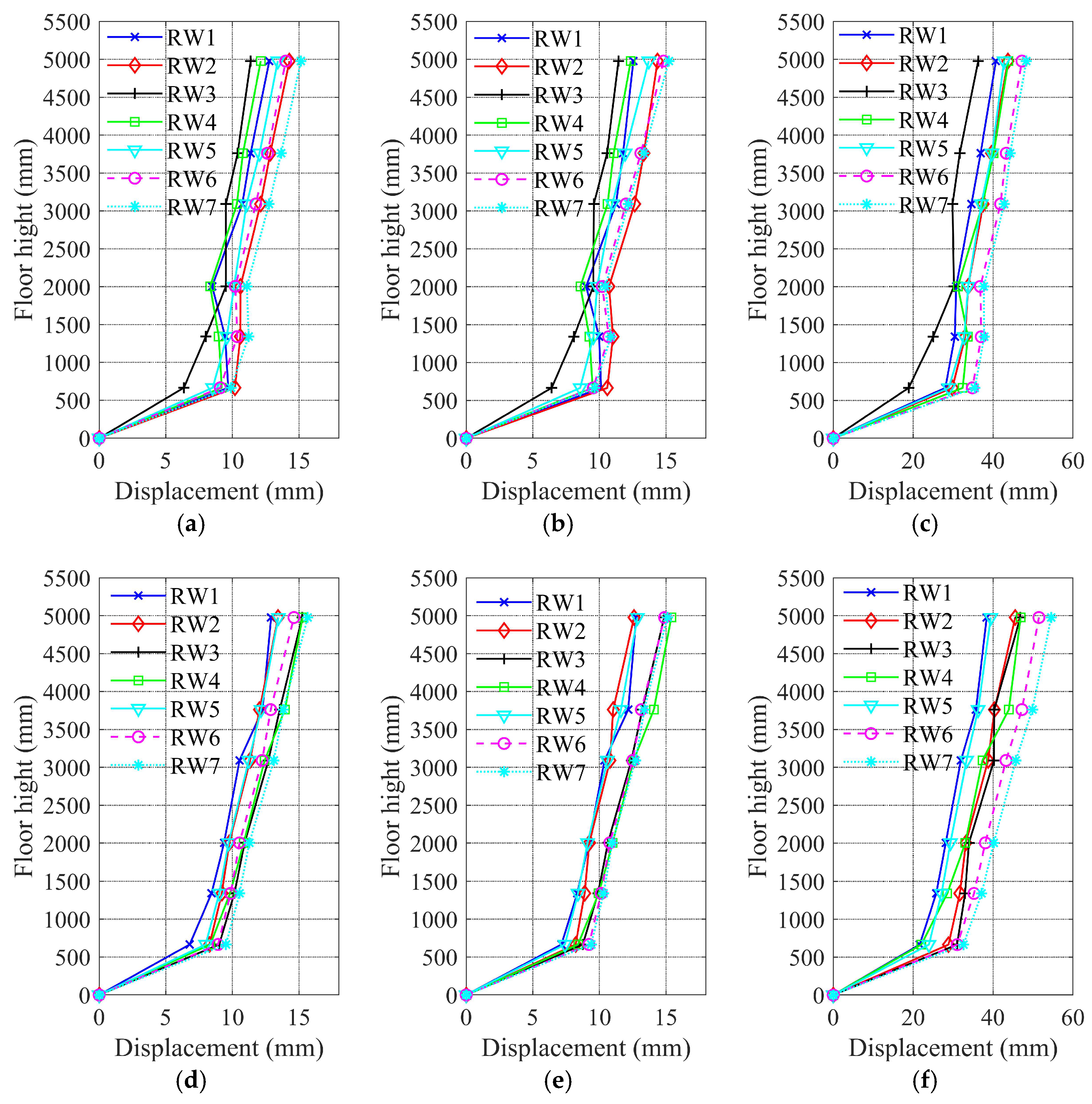
4.3. Displacement Response
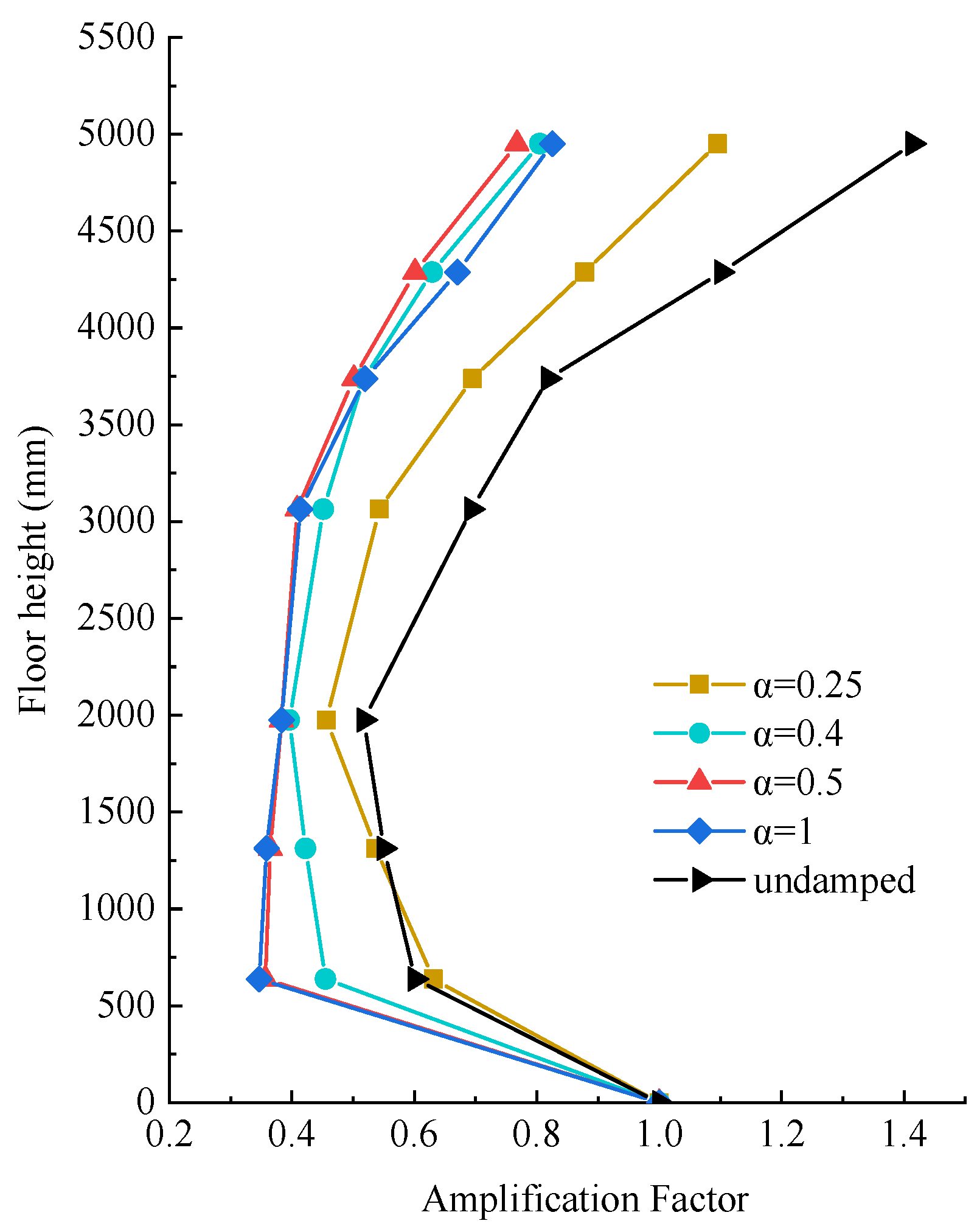
5. Finite Element Numerical Simulation
6. Deficiencies of Base Isolation and Suggestions for Improvement
7. Conclusions
- The seismic isolation model achieves a 91.5% reduction in first-order, natural frequency relative to the non-isolated structure, with the isolation layer serving as the primary energy absorber to mitigate superstructure responses.
- Horizontal isolation efficiency remains stable (<50%) under both unidirectional and bidirectional inputs. Vertical input increases horizontal efficiency, and the vertical acceleration is amplified compared to the non-isolated structure. The isolation rate of the SL-2, three-directional ground motion is lower than that of the SL-1, and the isolation effect is more significant. Under unidirectional horizontal seismic input, the isolation efficiency for the BDBE level ground motion condition is comparable to that of the SL-1 level ground motion, with enhanced performance at higher intensities.
- Under tri-directional SL-1/SL-2 inputs, the isolated structure’s horizontal floor spectra exceed non-isolated counterparts below 3 Hz, while being suppressed above this threshold. Spectral reductions intensify with floor height and seismic intensity, and the predominant frequencies of the response spectrum effectively avoid the main operating frequencies of the equipment. Moreover, the predominant frequency of the vertical floor response spectrum is close to the vertical frequency of the isolation model, which is unfavorable for vertical isolation.
- Finite element simulations demonstrate alignment with experimental modal and dynamic responses, providing a reliable analysis method for further studies in the future.
- The equivalent horizontal stiffness of the LNR bearings and the nonlinear mechanical properties of the LRB bearings change with variations in compressive stress and shear strain, as confirmed by the comparative analysis of the finite element model results and experimental results and should be considered in the modeling process.
- The horizontal displacement of the isolation model primarily occurs in the isolation layer, with a certain overturning effect observed in the superstructure. Viscous dampers should be installed in the isolation layer to mitigate the overturning effect.
- Future studies will systematically investigate the coupling effects between diesel generators’ operational frequencies and artificial wave excitation through targeted numerical simulations and experimental campaigns, aiming to quantify their potential impacts on seismic isolation performance. Furthermore, the exploration of three-dimensional isolation techniques will be prioritized to mitigate overturning risks in base-isolated structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Atomic Energy Agency (IAEA). Global Status of Nuclear Power Plants; IAEA: Vienna, Austria, 2021. [Google Scholar]
- Nuclear Energy Agency (NEA). The Role of Nuclear Power in Mitigating Climate Change; OECD/NEA: Paris, France, 2020. [Google Scholar]
- World Nuclear Association (WNA). Benefits of Nuclear Power; WNA: London, UK, 2023. [Google Scholar]
- World Nuclear Association (WNA). Fukushima Daiichi Accident; WNA: London, UK, 2011. [Google Scholar]
- Chan, R.W.K.; Lin, Y.S.; Tagawa, H. A smart mechatronic base isolation system using earthquake early warning. Soil Dyn. Earthq. Eng. 2019, 119, 299–307. [Google Scholar]
- Xu, W.Z.; Du, D.S.; Wang, S.G.; Liu, W.Q.; Li, W.W. Shaking table tests on the multi-dimensional seismic response of long-span grid structure with base-isolation. Eng. Struct. 2019, 201, 109802. [Google Scholar]
- Dicleli, M.; Karalar, M. Optimum characteristic properties of isolators with bilinear force-displacement hysteresis for seismic protection of bridges built on various site soils. Soil Dyn. Earthq. Eng. 2011, 31, 982–995. [Google Scholar]
- Karalar, M.; Padgett, J.E.; Dicleli, M. Parametric analysis of optimum isolator properties for bridges susceptible to near-fault ground motions. Eng. Struct. 2012, 40, 276–287. [Google Scholar] [CrossRef]
- Coladant, C. Seismic isolation of nuclear power plants—EDF’s philosophy. Nucl. Eng. Des. 1991, 127, 243–251. [Google Scholar] [CrossRef]
- Chen, J.Y.; Zhao, C.F.; Xu, Q.; Yuan, C.Y. Seismic analysis and evaluation of the base isolation system in AP1000 NI under SSE loading. Nucl. Eng. Des. 2014, 278, 117–133. [Google Scholar]
- Whittaker, A.S.; Kumar, M. Seismic Isolation of Nuclear Power Plants. Nucl. Eng. Technol. 2014, 46, 569–580. [Google Scholar]
- Sarebanha, A.; Mosqueda, G.; Kim, M.K.; Kim, J.H. Seismic response of base isolated nuclear power plants considering impact to moat walls. Nucl. Eng. Des. 2018, 328, 58–72. [Google Scholar]
- Zhao, C.F.; Yu, N.; Peng, T.; Lippolis, V.; Corona, A.; Mo, Y.L. Study on the dynamic behavior of isolated AP1000 NIB under mainshock-aftershock sequences. Prog. Nucl. Energy 2020, 119, 103144. [Google Scholar]
- Kennedy, R.P.; Cornell, C.A.; Campbell, R.D.; Kaplan, S.; Perla, H.F. Probabilistic seismic safety study of an existing nuclear power plant. Nucl. Eng. Des. 1980, 59, 315–338. [Google Scholar] [CrossRef]
- Lal, K.M.; Parsi, S.S.; Kosbab, B.D.; Ingersoll, E.D.; Charkas, H.; Whittaker, A.S. Towards standardized advanced nuclear reactors: Seismic isolation and the impact of the earthquake load case. Nucl. Eng. Des. 2021, 386, 111487. [Google Scholar] [CrossRef]
- Firoozabad, E.S.; Jeon, B.G.; Choi, H.S.; Kim, N.S. Seismic fragility analysis of seismically isolated nuclear power plants piping system. Nucl. Eng. Des. 2015, 284, 264–279. [Google Scholar] [CrossRef]
- Eidinger, J.M.; Kelly, J.M. Seismic isolation for nuclear power plants: Technical and non-technical aspects in decision making. Nucl. Eng. Des. 1985, 84, 383–409. [Google Scholar] [CrossRef]
- Zheng, G.Y.; Peng, X.K.; Li, X.Z.; Kang, Y.X.; Zhao, X.G. Research on the standardization strategy of China’s nuclear industry. Energy Policy 2021, 155, 112314. [Google Scholar]
- Parsi, S.S.; Lal, K.M.; Kosbab, B.D.; Ingersoll, E.D.; Shirvan, K.; Whittaker, A.S. Seismic isolation: A pathway to standardized advanced nuclear reactors. Nucl. Eng. Des. 2022, 387, 11445.1–111445.15. [Google Scholar] [CrossRef]
- Warn, G.P.; Ryan, K.L. A Review of Seismic Isolation for Buildings: Historical Development and Research Needs. Buildings 2012, 2, 300–325. [Google Scholar] [CrossRef]
- Sato, N.; Kato, A.; Fukushima, Y.; Iizuka, M. Shaking table tests on failure characteristics of base isolation system for a DFBR plant. Nucl. Eng. Des. 2002, 212, 293–305. [Google Scholar] [CrossRef]
- Kim, M.K.; Choi, I.K.; Seo, J.M. A shaking table test for an evaluation of seismic behavior of 480 V MCC. Nucl. Eng. Des. 2012, 243, 341–355. [Google Scholar] [CrossRef]
- Huang, B.F.; Lu, W.S.; Mosalam, K.M. Shaking Table Tests of the Cable Tray System in Nuclear Power Plants. J. Perform. Constr. Facil. 2017, 31, 04017018. [Google Scholar] [CrossRef]
- Huang, Y.J.; Lu, D.G.; Liu, Y.; Zheng, S. Shaking table experiments on 3/10 reduced-scale CAP1400 spent fuel storage rack considering the effect of fluid-structure interaction. Nucl. Eng. Des. 2020, 369, 110861. [Google Scholar]
- Jung, J.W.; Kim, M.K.; Kim, J.H. Experimental study on the floor responses of a base-isolated frame structure via shaking table tests. Eng. Struct. 2022, 253, 113763. [Google Scholar]
- Micheli, I.; Cardini, S.; Colaiuda, A.; Turroni, P. A sensitivity investigation upon the dynamic structural response of a nuclear plant on aseismic isolating devices. Nucl. Eng. Des. 2004, 228, 319–343. [Google Scholar]
- Zhao, C.F.; Chen, J.Y. Numerical simulation and investigation of the base isolated NPPC building under three-directional seismic loading. Nucl. Eng. Des. 2013, 265, 484–496. [Google Scholar]
- Zhou, Z.G.; Wong, J.; Mahin, S. Potentiality of Using Vertical and Three-Dimensional Isolation Systems in Nuclear Structures. Nucl. Eng. Technol. 2016, 48, 1237–1251. [Google Scholar] [CrossRef]
- Lim, H.G.; Yang, J.E.; Hwang, M.J. A quantitative analysis of a risk impact due to a starting time extension of the emergency diesel generator in optimized power reactor-1000. Reliab. Eng. Syst. Saf. 2007, 92, 961–970. [Google Scholar]
- EJ625-2004; Criteria for Diesel-Generator Units Applied as Standby Power Supplies for Nuclear Power Generating Stations. Commission of Science, Technology and Industry for National Defense: Beijing, China, 2004.
- GB/T 13625-2018; Seismic Qualification of Safety Class Electrical Equipment for Nuclear Power Plants. State Administration for Market Regulation: Beijing, China, 2018.
- GB/T 20688.1-2007; Rubber Bearings-Part 1: Seismic-Protection Isolators Test Methods. China Standards Publishing House: Beijing, China, 2007.
- NUREG-800; Standard Review Plan for the Review of Safety Analysis Reports for Nuclear Power Plants. USNRC: Rockville, MD, USA, 2007.
- RG 1.60; Regulatory Guide 1.60—Design Response Spectra for Seismic Design of Nuclear Power Plants. USNRC: Rockville, MD, USA, 2014.
- HAD 102/02–2019; Seismic Design and Identification of Nuclear Power Plants. State Bureau of Nuclear Safety: Beijing, China, 2019.
- CECS 126-2001; Technical Specification for Seismic-Isolation with Laminated Rubber Bearing Isolators. Guangzhou University: Beijing, China, 2001.







| Table Size | 5 m × 5 m | |
|---|---|---|
| Vibration direction | 3 directions and 6 degrees of freedom | |
| Table weight | 30 T | |
| Maximum specimen mass | 60 T | |
| Working frequency range | 0.1~50 Hz | |
| Maximum overturning moment | 1200 kN·m | |
| Vertical performance | Displacement | ±200 mm |
| Speed | ±1000 mm/s | |
| Acceleration | ±1.2 g | |
| Horizontal performance | Displacement | ±400 mm |
| Speed | ±1200 mm/s | |
| Acceleration | ±1.5 g | |
| Variable | Scale Factor Model/Prototype | Value | Variable | Scale Factor Model/Prototype | Value |
|---|---|---|---|---|---|
| Length | 1/8 | Frequency | 4.984 | ||
| Equivalent density | 1/0.505 | Time | 0.201 | ||
| Modulus of elasticity | 1/1.3 | Acceleration | 3.106 | ||
| Stress | 1/1.3 | Damping | 0.019 | ||
| Mass | 0.004 | Force | 0.012 | ||
| Stiffness | 0.096 | Moment | 0.002 |
| Compressive Stress (MPa) | Vertical Compressive Stiffness (N/mm) | |||||
|---|---|---|---|---|---|---|
| LNR01 | LNR02 | Mean | LRB01 | LRB02 | Mean | |
| 2 | 131,612 | 145,724 | 138,671 | 181,710 | 133,064 | 157,390 |
| 4 | 105,531 | 131,250 | 118,393 | 130,933 | 131,522 | 131,233 |
| 6 | 108,690 | 126,672 | 117,682 | 144,203 | 137,420 | 140,813 |
| Compressive Stress | Shear Strain | Horizontal Stiffness (N/mm) | Yield Strength (kN) | Equivalent Damping Ratio (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (%) | LNR01 | LNR02 | Mean | LRB01 | LRB02 | Mean | LRB01 | LRB02 | Mean | LRB01 | LRB02 | Mean |
| 1 | 100 | 150.41 | 163.75 | 157.08 | 185.4 | 189.12 | 187.26 | 1.131 | 1.125 | 1.128 | 7.70 | 7.41 | 7.56 |
| 2 | 100 | 140.13 | 154.19 | 147.16 | 173.71 | 181.59 | 177.65 | 1.136 | 1.028 | 1.082 | 8.17 | 7.65 | 7.91 |
| 3 | 100 | 126.66 | 146.25 | 136.455 | 165.55 | 180.14 | 172.845 | 1.178 | 1.062 | 1.12 | 9.47 | 8.61 | 9.04 |
| 4 | 100 | 127.22 | 138.53 | 132.875 | 160.46 | 171.26 | 165.86 | 1.264 | 1.19 | 1.227 | 10.73 | 10.69 | 10.71 |
| 5 | 100 | 124.57 | 130.68 | 127.625 | 155.23 | 164.46 | 159.845 | 1.468 | 1.329 | 1.3985 | 13.61 | 12.81 | 13.21 |
| 1 | 50 | 150.41 | 163.75 | 157.08 | 186.09 | 193.13 | 189.61 | 0.695 | 0.707 | 0.701 | 9.07 | 9.14 | 9.11 |
| 1 | 100 | 155.92 | 150.41 | 153.165 | 185.4 | 189.12 | 187.26 | 1.131 | 1.125 | 1.128 | 7.70 | 7.41 | 7.56 |
| 1 | 150 | 142.24 | 132.71 | 137.475 | 157.43 | 163.06 | 160.245 | 1.164 | 1.16 | 1.162 | 9.35 | 9.45 | 9.40 |
| 1 | 180 | — | 130.66 | 130.66 | 143.02 | 154.23 | 148.625 | 1.227 | 1.27 | 1.2485 | 10.41 | 10.10 | 10.26 |
| Parameters | LNR140 | LRB140 |
|---|---|---|
| Compression stiffness σ = 2 Mpa (N/mm) | 138,671 | 157,390 |
| Horizontal stiffness γ = 100% (N/mm) | 157.08 | 187.26 * |
| Yield strength (kN) | - | 1.128 |
| Equivalent damping ratio | - | 7.56% |
| Seismic Level | Working Condition | Input Seismic Wave | PGA/g | ||
|---|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | |||
| - | 1 | White Noise | 0.1 | 0.1 | 0.1 |
| SL-1 | 2~8 * | RW1~RW7 * | - | 0.311 | - |
| 9~15 | RW1~RW7 | 0.311 | - | - | |
| 16~22 | RW1~RW7 | 0.311 | 0.311 | - | |
| 23~29 | RW1~RW7 | 0.311 | 0.311 | 0.311 | |
| - | 30 | White Noise | 0.1 | 0.1 | 0.1 |
| SL-2 | 31~37 | RW1~RW7 | 0.932 | 0.932 | 0.932 |
| - | 38 | White Noise | 0.1 | 0.1 | 0.1 |
| BDBE | 39~41 | RW1\RW5\RW7 | - | 1.55 | - |
| - | 42 | White Noise | 0.1 | 0.1 | 0.1 |
| Test Model | First Order Frequency Y-Direction | Second Order Frequency X-Direction | Third Order Frequency Twist | Fourth Order Frequency Y-Direction |
|---|---|---|---|---|
| Isolation model | 2.30 Hz | 2.33 Hz | 2.42 Hz | 12 Hz |
| Non-isolated model | 27 Hz | 32 Hz | 45 Hz | 50 Hz |
| Seismic Level | Ground Motion Input | Direction | RW1 | RW2 | RW3 | RW4 | RW5 | RW6 | RW7 | Mean Value |
|---|---|---|---|---|---|---|---|---|---|---|
| SL-1 | Unidirectional | X | 0.25 | 0.20 | 0.21 | 0.25 | 0.21 | 0.23 | 0.23 | 0.22 |
| Y | 0.29 | 0.21 | 0.31 | 0.30 | 0.26 | 0.26 | 0.25 | 0.27 | ||
| Bidirectional | X | 0.25 | 0.22 | 0.22 | 0.22 | 0.20 | 0.23 | 0.25 | 0.23 | |
| Y | 0.26 | 0.19 | 0.25 | 0.28 | 0.23 | 0.24 | 0.23 | 0.24 | ||
| Three- dimensional | X | 0.57 | 0.37 | 0.46 | 0.33 | 0.42 | 0.50 | 0.52 | 0.45 | |
| Y | 0.59 | 0.37 | 0.69 | 0.34 | 0.37 | 0.41 | 0.59 | 0.48 | ||
| Z | 1.55 | 1.54 | 1.51 | 1.36 | 1.41 | 1.67 | 1.69 | 1.53 | ||
| SL-2 | Three- dimensional | X | 0.29 | - | 0.41 | 0.33 | 0.29 | - | 0.38 | 0.34 |
| Y | 0.43 | 0.29 | 0.41 | 0.31 | 0.30 | 0.34 | 0.32 | 0.35 | ||
| Z | 0.98 | 1.27 | 1.54 | 1.52 | 0.86 | 1.09 | 1.22 | 1.21 | ||
| BDBE | Unidirectional | Y | 0.24 | - | - | - | 0.18 | - | 0.21 | 0.21 |
| Mode | Test Result | Finite Element Model of Test Structure | Error | ||
|---|---|---|---|---|---|
| Frequency (Hz) | Direction | Frequency (Hz) | Direction | ||
| 1 | 2.30 | Y | 2.32 | Y | 0.8% |
| 2 | 2.33 | X | 2.34 | X | 0.4% |
| 3 | 2.42 | Twist | 2.39 | Twist | −1.3% |
| 4 | 12.00 | Y | 16.7 | Y | 28.1% |
| 5 | 26.00 | X | 25.68 | X | −1.3% |
| 6 | 30.50 | Z | 44.29 | Z | 31.1% |
| Scheme | Damping Index | Maximum Tensile Stress (Mpa) | Maximum X-Direction Base Shear (kN) |
|---|---|---|---|
| 1 | Undamped | 1.58 | 365.86 |
| 2 | α = 0.25 | 1.32 | 312.41 |
| 3 | α = 0.4 | 1.04 | 270.88 |
| 4 | α = 0.5 | 0.89 | 255.19 |
| 5 | α = 1 | 0.90 | 242.48 |
| Isolation Scheme | Damping Coefficient | β |
|---|---|---|
| 1 | Undamped | 1.159 |
| 2 | 0.25 | 1.986 |
| 3 | 0.4 | 2.344 |
| 4 | 0.5 | 2.511 |
| 5 | 1 | 2.544 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Gao, X.; Xu, K.; Zhou, J. Shaking Table Test and Finite Element Analysis of Isolation Performance for Diesel Engine Building in a Nuclear Power Plant. Buildings 2025, 15, 1100. https://doi.org/10.3390/buildings15071100
Xiao Y, Gao X, Xu K, Zhou J. Shaking Table Test and Finite Element Analysis of Isolation Performance for Diesel Engine Building in a Nuclear Power Plant. Buildings. 2025; 15(7):1100. https://doi.org/10.3390/buildings15071100
Chicago/Turabian StyleXiao, Yunhui, Xiangyu Gao, Kuang Xu, and Jinlai Zhou. 2025. "Shaking Table Test and Finite Element Analysis of Isolation Performance for Diesel Engine Building in a Nuclear Power Plant" Buildings 15, no. 7: 1100. https://doi.org/10.3390/buildings15071100
APA StyleXiao, Y., Gao, X., Xu, K., & Zhou, J. (2025). Shaking Table Test and Finite Element Analysis of Isolation Performance for Diesel Engine Building in a Nuclear Power Plant. Buildings, 15(7), 1100. https://doi.org/10.3390/buildings15071100






